第一章流体流动.doc
- 格式:doc
- 大小:331.00 KB
- 文档页数:23










化工原理第一章流体流动第一章 流体流动一、流体流动的数学描述在化工生产中,经常遇到流体通过管道流动这一最基本的流体流动现象。
当流体在管内作稳定流动时,遵循两个基本衡算关系式,即质量衡算方程式和机械能衡算方程式。
质量衡算方程式在稳定的流动系统中,对某一划定体积而言,进入该体积的流体的质量流量等于流出该体积的质量流量。
如图1—1所示,若取截面1—1′、2—2′及两截面间管壁所围成的体积为划定体积,则ρρρuA A u A u ==222111 (1-1a)对不可压缩、均质流体(密度ρ=常数)的圆管内流动,上式简化为2221211ud d u d u == (1-1b)机械能衡算方程式在没有外加功的情况下,流动系统中的流体总是从机械能较高处流向机械能较低处,两处机械能之差为流体克服流动阻力做功而消耗的机械能,以下简称为阻力损失。
如图1—1所示,截面1—1′与2—2′间单位质量流体的机械能衡算式为f 21w Et Et += (1-2)式中 221111u p gz Et ++=ρ,截面1—1′处单位质量流体的机械能,J /kg ;222222u p gz Et ++=ρ,截面2—2′处单位质量流体的机械能,J /kg ;∑⎥⎦⎤⎢⎣⎡∑+∑=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛∑+=2)(222f u d l l u d l w e λζλ,单位质量流体在划定体积内流动时的总阻力损失,J /kg 。
其中,λ为雷诺数Re 和相对粗糙度ε / d 的函数,即⎪⎪⎭⎫ ⎝⎛=d du εμρφλ,。
上述方程式中,若将Et 1、Et 2、w f 、λ视为中间变量,则有z 1、z 2、p 1、p 2、u 1、u 2、d 1、d 2、d 、u 、l 、∑ζ(或∑l e )、ε、ρ、μ等15个变量,而独立方程仅有式(1-1)(含两个独立方程)、式(1-2)三个。
因此,当被输送流体的物性(ρ,μ)已知时,为使方程组有唯一解,还需确定另外的10个变量,其余3个变量才能确定。
第一章 流体流动主要内容:流体静力学及其应用;流体流动中的守衡原理;流体流动的内部结构;阻力损失;流体输送管路的计算;流速、流量测量;非牛顿流体的流动。
重点内容:流体静力学基本方程及其应用;连续性方程,柏努利方程及其应用;管内流体流动助力;管路计算。
难点内容:机械能衡算式——柏努利方程;复杂管路的计算。
基本要求:熟练掌握机械能衡算式——柏努利方程, 课时安排:24第一节 流体的重要性质--流体静力学基本概念: 1.流体:具有流动性的液体和气体统称为流体。
2.连续性介质假定:流体是由连续的流体质点组成的。
3.流体静力学—研究流体处于静止平衡状态下的规律及其应用; 4.流体动力学—研究流体在流动状态下的规律及其应用。
5.不可压缩流体和可压缩流体 一、流体的密度:单位体积流体的质量 ρ=m/V [kg/m 3]重度—工程单位制中,表示密度的单位,其数值与密度相同。
3-⋅m kgf比重—物料密度与纯水(227K )密度之比,其数值的一千倍等于密度的数值。
比容——密度的倒数ρ1=v 。
1.纯流体的密度液体的密度随压强变化小,但随温度稍有变化;气体的密度随压强、温度变化大。
理想气体ρ(t 不太低,p 不太高的气体,可用理想气体状态方程)PV=nRT RTPMV m ==ρ 或004.22TP P T M ⨯=ρ对t 低,p 高的气体,可用真实气体状态方程计算 2.混合流体的密度(1)液体混合物的m ρ(1kg 基准)∑=iimw ρρ1(假设为理想溶液)ρi 液体混合物中各纯组分的密度。
W i :液体混合物中各组分的质量分率。
(2)气体混合物m ρ(1m 3基准) ii m y ∑=ρρy i :气体混合物中各组分的体积分率。
二、流体的静压强1. 静压强定义:流体垂直作用于单位面积上的压力。
AP p =2. 压强的单位(1)直接按压强定义:N/m 2,Pa (帕斯卡)(2)间接按流体柱表示:m H 2O 柱,mm Hg 柱(3)与大气压作为计量单位:标准大气压(atm),工程大气压(at ) 单位换算:1atm=1.0133×105Pa =760mmHg=10.33m H 2O=1.033kgf/cm 21 at =9.807×104Pa =735.6mmHg= 10m H 2O=1 kgf/cm 23表示压强的基准(1) 绝对压强—以绝对真空为基准测得的压强;(2) 相对压强—以当地大气压为基准测得的压强:表压和真空度p >当地大气压, 表压强=绝对压强-大气压强 p <当地大气压, 真空度=大气压强-绝对压强三、流体静力学基本方程式——研究流体柱内压强沿高度变化的规律 a) 推导:在垂直方向上,力的平衡:p 1绝对真空p 2A=p 1A+G=p 1A+ρgA (Z 1-Z 2) p 2=p 1+ρg (Z 1-Z 2)若Z 1面在水平面上 p 2=p 0+ρgh 2.讨论(1) 静止液体内任一点压强,与深度有关,越深,压强越大;(2) 在静止的、连续的同一液体内,处于同一水平面上的各点,因深度相同,压强也相同;(3) 巴斯葛原理—液面上方p 0发生变化,内部各点压强发生同样的变化。
3。
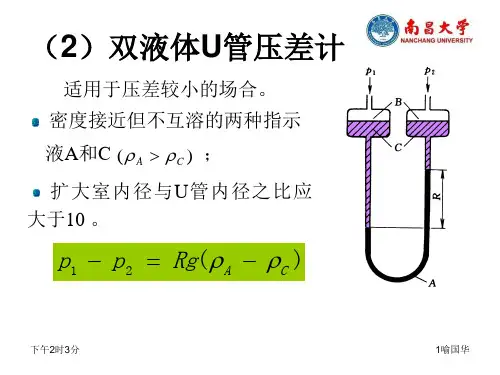
静力学方程的几种形式:2211Z g pZ g p +=+ρρ 表示:静压头+位压头=常数 g Z p g Z p 2211+=+ρρ 表示:静压能+位压能=常数四、静力学基本方程式的应用1.压强的测量(1)U 形管液柱压差计指示剂要求:不与被测液互溶、反应;密度大于被测液体。
常用的有:水,水银,四氯化碳 p a =p bp 1-ρg (m+R )= p 2-ρgm -ρ0g Rp 1- p 2=(ρ0- ρ)gR 在测量气体压强时,ρ0>> ρ所以 p 1- p 2=ρ0gR倒U 形管压差计、斜管液柱压强计、微差液柱压强计2.液面的测定结论:ρρR h o =o3.确定液封高度作用:当设备内压强超过规定值时,气体就从液封管排出,以确保设备操作的安全。
若设备要求压强不超过p 1,按静力学基本方程式,则 水封管口的液面高度h :gp h ρ(表压)1=h第二节 流体流动概述前节讨论了静止流体内部压强的变化规律,对于流体输送过程中遇到的问题,必须要找出流体在管内的流动规律——连续性方程式与柏努利方程式。
出发点——质量、动量、能量守恒 一、流量与流速1.流量:在单位时间内流过管道任一截面的流体量。
质量流量:用质量来计量,以G 表示[kg/s] 体积流量:用体积来计量,以V 表示[m 3/s]G=V ρ2.流速:单位时间内,流体质点在导管中流动方向上所流过的距离(点速度) 实验证明,在导管截面上各点的流速是不同的,具有速度分布。
在工程上为方便起见,通常使用平均速度概念:A Vu =[m/s] 质量流速:AG w = [kg/m 2.s]w = u ρ3.管径d24d uuA V π== uVd 785.0=计算后管径要圆整讨论:V —由工艺生产任务定;u —关键选择,若u 大,管道阻力大,动力消耗大,操作费用大;d 可小 若u 小,管道阻力小,但d 大,建设成本大。
所以,设计管道时,需要综合考虑这两个互相矛盾的经济因素。
一般情况下,液体流速u = 0.5-3m/s; 气体流速u = 10-30m/s 介绍: 公称压力公称直径无缝钢管与水煤气管二、定常态流动与非定常态流动1.定常态流动——流体在管道中流动时,流体在任一点上的流速、压强等有关物理参数都不随时间而改变,这种流动称为定常态流动。
2.非定常态流动——若流体在截面上的只要有一个物理量随时间而变,则称为非定常态流动。
三、流体流动类型与雷诺准数在讨论流体流动阻力产生的原因及其影响因素时,必然会想到阻力与速度有关,下面是1883年著名法国科学家雷诺作的一个实验。
1. 雷诺实验表面上看,流体流动类型由流速决定,低于某一流速,质点作直线运动,属滞流型,称滞流临界速度。
实验发现,不同流体的滞流临界速度不同。
2.雷诺数Re 及流动类型判断μρdu =Re流型判断溢流Re 2000≤——层流2000〈Re 〈4000——不稳定的过度区 Re ≥4000——湍流雷诺数Re 的含义:反映了与阻力有关的惯性力与粘性力的对比关系。
粘性力惯性力=Re3.流体流动相似原理在两根不同的管中,当流体流动的Re 数相同时,只要流体的边界几何条件相似,则流体的流动状态也相似。
第三节 流体流动的基本方程一、流体定态流动时的连续性方程式推导:以管内壁,截面1-1与2-2为衡算范围 G 1 = G 2 ρ1A 1u 1 = ρ2A 2u 2若不可压缩流体:A 1u 1 = A 2u 2212221d d u u = 说明:u 只与截面积有关,而与管路上任何设备无关。
二、柏努利方程式(Bernowlli Equation )——流动系统的机械能衡算 1. 理想流体的柏努利方程式0=++udu gdz dpρ对不可压缩流体:ρ=const ,则: const u gz p=++22ρ 对气体,若压力变化不大,%20112≤-p p p ,可看成不可压缩性流体,误差约5%,用平均密度,221ρρρ+=m2. 实际流体柏努利方程式的几种形式流体具有粘度,流动时有摩擦阻力;管路中有能量输入机械。
f h pu gz We p u gz ∑+++=+++ρρ2222121122 [J/kg]——单位质量流体的机械能守恒方程。
f e H gpg u z H g p g u z ∑+++=+++ρρ2222121122 [J/N]或[m 流体柱]——单位重量流体的机械能守恒方程。
各项为:位压头,动压头,静压头,有效压头(外加压头),压头损失1静力学方程是柏努利方程式的一个特例。
3.柏努利方程式的应用柏努利方程是流体流动的基本方程,应用范围很广,具体有:1)分析和解决流体输送问题2)体流动过程中流量的测定3)器间的相对位置,流体压强4)确定输送设备的有效功率举例:解题要点:1,绘出流程,注明流向,列出已知条件;2,确定计算系统——取截面,截面与流动方向垂直,两截面间要连续,稳定;且已知条件最多,要包括未知条件,一般规律:取起点与终点取容器的液面,u = 0,p = p03,基准高度的选取—— z为相对值,一般取地平面,水平面等较低截面;4,单位的一致性——SI制;5.注意压强,计算时应使用绝对压强。
第四节 动量传递现象一、层流—分子动量传递层流特征:流体质点无返混,整个流动区都存在速度梯度,速度分布呈二次抛物线型:()22214r R lp p u r --=μ图1-6 层流表征图平均速度是最大流速的一半,max 21u u =,如图1-6所示。
二、湍流时的速度分布湍流特征:流体质点杂乱无章,仅在管壁处存在速度梯度,速度分布服从尼古拉则的七分之一次方定律:71max ⎪⎭⎫⎝⎛=R y u u r 应用范围是5101.1Re ⨯=,平均流速是最大流速的0.8倍,max 8.0u u =,如图1-7所示。
图1-7 湍流表征图湍流时流体质点的运动状况较层流要复杂得多,截面上某一固定点的流体质点在沿管轴向前运动的同时,还有径向上的运动,使速度的大小与方向都随时变化。
湍流的基本特征是出现了径向脉动速度,使得动量传递较之层流大得多。
层流湍流的区别(1)有无径向速度脉动(2)速度分布不同(3)阻力形式不同(4)阻力系数与雷诺数的关系不同三、流体流动边界层1. 边界层的形成当一个流速均匀的流体与一个固体壁面相接触时,由于壁面对流体的阻碍,与壁面相接触的流体速度降为零。
由于流体的粘性作用,紧连着这层流体的另一流体层速度也有所下降。
随着流体的向前流动,流速受影响的区域逐渐扩大,即在垂直于流体流动方向上产生了速度梯度。
流速降为主体流速的99%以内的区域称为边界层,边界层外缘于垂直壁面间的距离称为边界层厚度。
流体在平板上流动时的边界层:由于边界层的形成,把沿壁面的流动分为两个区域:边界层区和主流区。
边界层区(边界层内):沿板面法向的速度梯度很大,需考虑粘度的影响,剪应力不可忽略。
主流区(边界层外):速度梯度很小,剪应力可以忽略,可视为理想流体。
边界层流型也分为层流边界层与湍流边界层。
在平板的前段,边界层内的流型为层流,称为层流边界层。
离平板前沿一段距离后,边界层内的流型转为湍流,称为湍流边界层。
流体在圆管内流动时的边界层如图1-24所示。
流体进入圆管后在入口处形成边界层,随着流体向前流动,边界层厚度逐渐增加,直至一段距离(进口段)后,边界层在管中心汇合,占据整个管截面,其厚度不变,等于圆管的半径,管内各截面速度分布曲线形状也保持不变,此为完全发展了的流动。