char2冲激函数和其性质

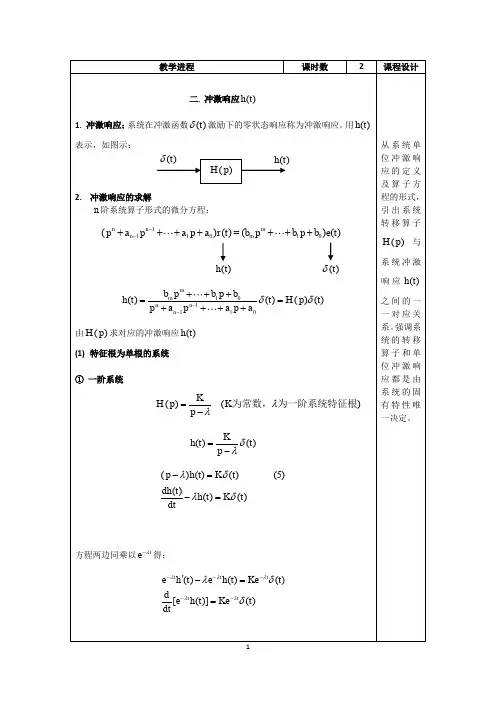
冲激信号δ(t)的三种定义与相关性质的简单讨论信息科学与工程学院1132班 樊列龙 学号：0909113224有一些物理现象，如理学中的爆炸、冲击、碰撞······，电学中的放电、闪电雷击等，它们都有共同特点： ① 持续时间短. ② 取值极大.冲击函数（或冲击信号）就是对这些物理现象的科学抽象与描述。

通常用δ(t)表示冲激信号，它是一个具有有限面积的窄而高的尖峰信号，它也可以被称作δ函数或狄拉克（Dirac ）函数，在信号领域中占有非常重要的地位. 由于冲激函数的特殊性，现给出其两种不严格的定义如下：定义一：用脉冲函数极限定义冲激信号. 如图1-1(a)的矩形脉冲，宽为τ，高为τ1，其面积为A.当A=1称之为单位冲激信号. 现保持脉冲面积不变，逐渐减小τ，则脉冲的幅度逐渐增大，当0→τ时，矩形脉冲的极限成为单位冲激函数，即：⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛+=→221lim )(0τετετδτt t t （1-1）冲击信号的波形就如1-1(b)所示.δ(t)只表示在t=0点有“冲激”，在t=0点以外的各处函数值均为0，其冲激强度（冲激面积）为1，若为A 则表示一个冲击强度为E 倍单位值得函数δ，描述为A=E δ(t)，图形表示时，在图1-2箭头旁边注上E 。

也可以用抽样函数的极限来定义δ(t)。

有⎥⎦⎤⎢⎣⎡=∞→)(lim )(kt Sa kt k πδ （1-2）对式（1-2）作如下说明：Θ Sa(t)是抽样信号，表达式为ttt a sin )(S = （1-3） 其波形如图1-2所示，Sa(t)∝1/t, 1/t 随t 的增大而减小，sint 是周 期振荡的，因而Sa(t)呈衰减振荡；并且是一个偶函数，当t=±π,±2π, ···，sint=0，从而Sa(t)=0，是其零点． 把原点两侧两个第一个零点之间的曲线部分称为“主瓣”， 其余的衰减部分称为“旁瓣”。

冲激函数卷积任意函数一、引言在信号处理领域，卷积是一种重要的运算。

卷积可以用于信号的滤波、特征提取等方面。

其中，冲激函数卷积任意函数是一种常见的卷积方式。

本文将介绍如何编写一个函数来实现冲激函数卷积任意函数。

二、什么是冲激函数在信号处理中，冲激函数是一种特殊的信号。

它在时间为0时取值为无穷大，其它时间点取值都为0。

冲激函数可以用数学公式表示为：delta(t) = {+∞, t=00, t!=0}三、什么是卷积在数学中，两个函数f和g的卷积定义为：(f * g)(t) = ∫f(τ)g(t-τ)dτ其中，*表示卷积运算符，t表示时间变量，τ表示一个虚拟变量。

四、如何计算冲激函数卷积任意函数计算冲激函数与任意函数f(t)的卷积可以分成以下步骤：1. 将f(t)反转得到f(-t)2. 将f(-t)与delta(t)进行卷积得到g(t)3. 将g(t)再次反转得到g(-t)其中，g(t)就是冲激函数与f(t)的卷积结果。

五、函数实现下面是一个Python函数，用于计算冲激函数与任意函数f(t)的卷积：```pythonimport numpy as npdef impulse_convolve(f, t):"""计算冲激函数与任意函数f(t)的卷积Args:f: 任意函数，可以是一个数组或者一个函数t: 时间变量，可以是一个数组或者一个数值范围Returns:g: 冲激函数与f(t)的卷积结果"""# 将f(t)转换为一个可调用的函数if isinstance(f, (list, tuple, np.ndarray)):f = lambda x: np.interp(x, t, f)# 反转f(-t)f_reversed = lambda x: f(-x)# 计算g(t)=delta(t)*f_reversed(-t)g = np.convolve(np.array([1]), f_reversed(t), mode='same')# 反转g(-t)g_reversed = lambda x: g[-x]return g_reversed(t)```六、使用示例下面是一个使用示例：```pythonimport matplotlib.pyplot as plt# 定义任意函数f(t)def f(x):return np.sin(x)**2 + np.cos(2*x)# 定义时间变量范围t = np.linspace(0, 10*np.pi, 1000)# 计算冲激函数与f(t)的卷积g = impulse_convolve(f, t)# 绘制f(t)和g(t)的图像plt.plot(t, f(t), label='f(t)')plt.plot(t, g, label='g(t)')plt.legend()plt.show()```运行以上代码，将会得到一个图像，其中包含了任意函数f(t)和冲激函数与f(t)的卷积结果g(t)的图像。

sql char(2)的用法
在SQL中，CHAR(n)是一种用来存储固定长度字符串的数据类型，其中n代表字符的最大长度。

对于CHAR(2)，它表示存储长度为2
的固定长度字符串。

CHAR数据类型在存储时会使用固定的存储空间，无论实际存储
的字符串长度是多少，空余的位置都会被填充。

例如，如果存储的
字符串长度小于指定的长度，那么剩余的空间会被填充为空格。

在使用CHAR(2)时，需要注意以下几点：
1. 存储空间，CHAR(2)会占用2个字节的存储空间，无论实际
存储的字符串长度是多少。

2. 字符串长度限制，存储在CHAR(2)类型中的字符串长度不能
超过2个字符，否则会被截断。

3. 比较和排序，由于CHAR类型是固定长度的，所以在比较和
排序时会占用固定的存储空间，这可能会影响查询性能。

总之，CHAR(2)用于存储固定长度为2的字符串，适合于长度固定且不太长的数据存储需求。

在实际使用中，需要根据具体的业务需求和数据特点来选择合适的数据类型。

`char(2)` 通常指的是在数据库中一个字符型字段的长度限制为2个字符。

具体取值范围取决于多个因素，包括使用的数据库系统、字符集等。

例如，在SQL中，`char(2)`表示该字段可以存储最多2个字符的字符串。

但是，取值范围不仅取决于字段的长度，还取决于数据库系统如何处理超出长度的数据。

例如，如果尝试插入超过2个字符的数据，大多数数据库系统会截断超出部分的数据。

此外，字符集也会影响取值范围。

例如，使用ASCII字符集时，`char(2)`可以存储的字符范围是可打印的ASCII字符，而使用UTF-8等字符集时，`char(2)`可以存储的字符范围更广泛，包括一些特殊符号、非打印字符等。

总的来说，`char(2)`的取值范围取决于数据库系统、字符集以及具体的插入数据。

在处理数据时，应该注意不要超出字段的长度限制，以避免数据截断或其他问题。

冲激偶函数的性质.
冲激函数的性质有：1、筛选性质。

2、取样性质。

3、导数性质。

4、尺度变换性质。

冲激函数是个奇异函数，它是对强度极大、作用时间极短暂且积分有限的一类理想化数学
模型。

冲激函数可用于对连续信号进行线性表达，也可用于求解线性非时变系统的零状态
响应。

冲激函数求导可得到冲激偶函数，单位冲激偶是这样的一种函数：当 t从负值趋于0时，它是一个强度为无限大的正的冲激函数，当t从正值趋于0时，它是一个强度为无限
大的负的冲激函数。

应用领域：
冲激函数可用于信号处理，通过冲激函数来表示复杂的信号，可以简化对复杂信号的
一些特性的研究。

冲激函数及其延时冲激函数的线性组合去则表示或迫近，再利用系统的vary原理，
可以通过直观的信号例如单位冲激函数的频谱，以及频域特性去探讨比较复杂信号的频谱。

从而增加排序繁杂信号频谱的难度。

冲激函数取样性质证明冲激函数是一种特殊的函数，也称为单位脉冲函数或Dirac函数。

它在数学分析和信号处理中有着重要的应用。

冲激函数取样性质是指冲激函数作为取样信号时，保持原信号的性质。

在这篇文章中，我将详细阐述冲激函数取样性质的证明。

首先，我们需要明确冲激函数的定义。

冲激函数通常用符号δ(t)表示，它满足以下条件：1.δ(t)在t=0时的取值为无穷大，其他时间点的取值为零：δ(0)=∞，δ(t)=0,t≠0。

2. δ(t)的面积等于1：∫δ(t)dt=1我们可以将冲激函数定义为一个函数序列的极限形式，即：δ(t) = lim(n→∞) gn(t)其中gn(t)是一系列脉冲函数。

例如，gn(t)可以是一个高度为n，宽度为1/n的矩形函数，使得gn(t)在0附近的面积为1，其他位置的面积为零。

假设我们有一个信号x(t)，我们用冲激函数对其进行取样。

取样信号可以表示为s(t)=x(t)δ(t-T)，其中T是取样时刻。

我们的目标是证明冲激函数取样信号的性质与原信号相同。

首先，我们可以推导冲激函数取样信号的时域表达式。

由于δ(t)在t=T时的取值为无穷大，假设在t=T时，x(T)的取值为X。

那么，我们可以得到：s(t)=x(t)δ(t-T)=x(t)δ(t-T)，t=T=x(T)δ(t-T)=Xδ(t-T)。

因此，冲激函数取样信号的时域表达式为s(t)=Xδ(t-T)。

这意味着取样信号在t=T时的取值为X，其他时间点的取值为零。

这与原信号在t=T时的取值相同，因此冲激函数取样信号在时域上保持了原信号的性质。

接下来，我们证明冲激函数取样信号的频域性质与原信号相同。

我们可以使用傅里叶变换来分析信号的频域特性。

假设原信号x(t)的傅里叶变换为X(ω)，即X(ω)=F{x(t)}，其中F表示傅里叶变换操作。

根据冲激函数的定义，我们可以得到取样信号的傅里叶变换为：S(ω)=F{s(t)}=F{Xδ(t-T)}。

我们可以利用傅里叶变换的性质，将傅里叶变换和冲激函数的性质结合起来。

冲激信号δ(t)的三种定义与相关性质的简单讨论信息科学与工程学院1132班 樊列龙 学号：0909113224有一些物理现象，如理学中的爆炸、冲击、碰撞······，电学中的放电、闪电雷击等，它们都有共同特点： ① 持续时间短. ② 取值极大.冲击函数（或冲击信号）就是对这些物理现象的科学抽象与描述。

通常用δ(t)表示冲激信号，它是一个具有有限面积的窄而高的尖峰信号，它也可以被称作δ函数或狄拉克（Dirac ）函数，在信号领域中占有非常重要的地位. 由于冲激函数的特殊性，现给出其两种不严格的定义如下：定义一：用脉冲函数极限定义冲激信号. 如图1-1(a)的矩形脉冲，宽为τ，高为τ1，其面积为A.当A=1称之为单位冲激信号. 现保持脉冲面积不变，逐渐减小τ，则脉冲的幅度逐渐增大，当0→τ时，矩形脉冲的极限成为单位冲激函数，即：⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛+=→221lim )(0τετετδτt t t （1-1）冲击信号的波形就如1-1(b)所示.δ(t)只表示在t=0点有“冲激”，在t=0点以外的各处函数值均为0，其冲激强度（冲激面积）为1，若为A 则表示一个冲击强度为E 倍单位值得函数δ，描述为A=E δ(t)，图形表示时，在图1-2箭头旁边注上E 。

也可以用抽样函数的极限来定义δ(t)。

有⎥⎦⎤⎢⎣⎡=∞→)(lim )(kt Sa kt k πδ （1-2）对式（1-2）作如下说明：Θ Sa(t)是抽样信号，表达式为ttt a sin )(S = （1-3） 其波形如图1-2所示，Sa(t)∝1/t, 1/t 随t 的增大而减小，sint 是周 期振荡的，因而Sa(t)呈衰减振荡；并且是一个偶函数，当t=±π,±2π···，sint=0，从而Sa(t)=0，是其零点． 把原点两侧两个第一个零点之间的曲线部分称为“主瓣”， 其余的衰减部分称为“旁瓣”。

二阶冲击函数的积分1. 定义二阶冲击函数，也称为狄拉克δ函数的导数，表示为δ′(t)，定义为：δ′(t) = dδ(t)/dt其中，δ(t) 是狄拉克δ函数，表示为：δ(t) = 0, t ≠ 0δ(t) = ∞, t = 0∫δ(t)dt = 1狄拉克δ函数的导数δ′(t)是一个奇函数，其图像是一个尖锐的脉冲，在t=0处取无穷大，而在其他地方取0。

2. 性质二阶冲击函数的积分具有以下性质：线性性：∫aδ′(t)dt = a∫δ′(t)dt导数：d/dt∫δ′(t)dt = δ(t)∫δ′(t)dt = H(t)其中，H(t)是Heaviside阶跃函数，表示为：H(t) = 0, t < 0H(t) = 1, t ≥ 03. 应用二阶冲击函数的积分在许多领域都有应用，包括：电路分析：二阶冲击函数的积分可以用来计算电容和电感电路中的电流和电压。

力学：二阶冲击函数的积分可以用来计算质点的速度和加速度。

量子力学：二阶冲击函数的积分可以用来计算波函数的导数。

信号处理：二阶冲击函数的积分可以用来滤除信号中的噪声。

4. 计算方法二阶冲击函数的积分可以通过以下方法计算：直接积分法：直接积分法是将二阶冲击函数的积分公式带入积分号中，然后进行积分。

部分积分法：部分积分法是将二阶冲击函数的积分公式与一个合适的函数相乘，然后进行积分。

微分方程法：微分方程法是将二阶冲击函数的积分公式代入一个微分方程中，然后求解微分方程。

二阶冲击函数的积分是一个重要的数学工具，在许多领域都有应用。

通过了解二阶冲击函数的积分的定义、性质、应用和计算方法，我们可以更好地理解和解决各种问题。

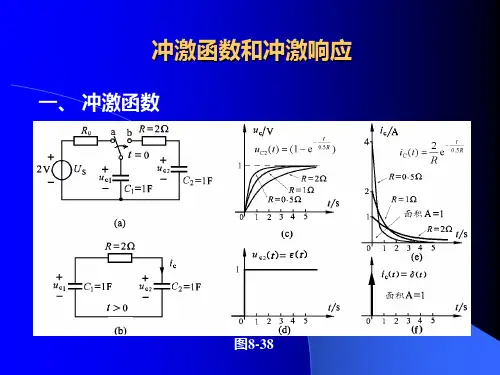
一、由理想电路引入冲激函数电流持续的时间为0，电流幅度为无穷大，但电流的时间积分有限的物理现象可以用冲激函数来描述。

二、单位冲激函数的定义和波形 1、单位冲激函数的数学符号：)(t δ2、定义单位冲激函数有若干不同的方法，下面是一种常用的单位冲激函数的定义方法单位冲激函数可由矩形脉冲面积保持为1，宽度0→τ的极限表示单位冲激函数)]2()2([1lim )(0τττδτ--+=→t u t u t ,左图中，当宽度τ不断变小的时候，幅度τ1则趋于无穷大。

面积为1，宽度趋于0，高度【幅度】趋于无穷大，那么这个极限就是单位冲激函数。

冲激函数又叫“狄拉克函数” 左图是用矩形脉冲来定义冲激函数对于一些宽度趋于0，幅度趋于无穷大，面积恒为1的三角函数也可以用来定义成单位脉冲函数。

三、单位冲激函数的幅度与强度的概念单位冲激函数的幅度指----无穷大的幅值【当0=t 时幅值无穷大；当0≠t 时，幅值为0】单位冲激函数的强度指----矩形脉冲的极限值【这个极限值叫做单位冲激函数的强度---冲激的大小】 单位冲激函数的波形中，用箭头来表示冲激函数的幅度，用小括号中加1来表示冲激函数的强度单位冲激函数的强度为1.任意0t 时刻的冲激函数的波形五、任意冲激函数的定义及波形 如上图示六、冲激函数的抽样性质1、函数)(t f 在0=t 处的冲激强度：)(t f 函数的冲激，等于t 在0=t 外的冲激：)0()()0()()(f dt t f dt t t f ==⎰⎰∞∞-∞∞-δδ )1()1(式表明，函数与冲激相乘，在无限区间上的积分结果为一个常数，这个常数代表的是该冲激的强度为)0(f2、函数)(t f 在0t t =处的冲激强度：)(t f 在0t t =的冲激：)()()()()(0000t f dt t t t f dt t t t f =-=-⎰⎰∞∞-∞∞-δδ )2(3、函数)(t f 在10t t t -=处的冲激强度：)()()()()(10101001t t f dt t t t t f dt t t t t f -=--=--⎰⎰∞∞-∞∞-δδ )3(冲激函数的性质的应用：当要抽取函数在某一时刻的函数值，只需要使该函数乘以冲激函数就行了。

冲激信号δ(t)的三种定义与相关性质的简单讨论信息科学与工程学院1132班 樊列龙 学号：0909113224有一些物理现象，如理学中的爆炸、冲击、碰撞······，电学中的放电、闪电雷击等，它们都有共同特点： ① 持续时间短. ② 取值极大.冲击函数（或冲击信号）就是对这些物理现象的科学抽象与描述。

通常用δ(t)表示冲激信号，它是一个具有有限面积的窄而高的尖峰信号，它也可以被称作δ函数或狄拉克（Dirac ）函数，在信号领域中占有非常重要的地位. 由于冲激函数的特殊性，现给出其两种不严格的定义如下：定义一：用脉冲函数极限定义冲激信号. 如图1-1(a)的矩形脉冲，宽为τ，高为τ1，其面积为A.当A=1称之为单位冲激信号. 现保持脉冲面积不变，逐渐减小τ，则脉冲的幅度逐渐增大，当0→τ时，矩形脉冲的极限成为单位冲激函数，即：⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛+=→221lim )(0τετετδτt t t （1-1）冲击信号的波形就如1-1(b)所示.δ(t)只表示在t=0点有“冲激”，在t=0点以外的各处函数值均为0，其冲激强度（冲激面积）为1，若为A 则表示一个冲击图1-2强度为E 倍单位值得函数δ，描述为A=E δ(t)，图形表示时，在箭头旁边注上E 。

也可以用抽样函数的极限来定义δ(t)。

有⎥⎦⎤⎢⎣⎡=∞→)(lim )(kt Sa kt k πδ （1-2）对式（1-2）作如下说明：Sa(t)是抽样信号，表达式为ttt a sin )(S = （1-3） 其波形如图1-2所示，Sa(t)∝1/t, 1/t 随t 的增大而减小，sint 是周 期振荡的，因而Sa(t)呈衰减振荡；并且是一个偶函数，当t=±π,±2π···，sint=0，从而Sa(t)=0，是其零点． 把原点两侧两个第一个零点之间的曲线部分称为“主瓣”， 其余的衰减部分称为“旁瓣”。

冲激函数和函数相乘的积分冲激函数和函数相乘的积分是数学中的一个重要概念，也是应用于物理学和工程学等领域的基础。

本文将介绍冲激函数的概念、性质和一些常见的函数相乘的积分，以及它们在物理学和工程学中的应用。

一、冲激函数的概念与性质1. 冲激函数的定义冲激函数是一种特殊的函数，通常用符号δ(x)表示。

它在x=0点处的取值无限大，其他点处的取值为零。

即：δ(x)={+∞}(x=0),{0}(x≠0)冲激函数在数学中是一种分布，它是用于描述非定常信号的一种数学模型。

冲激函数的概念是由英国物理学家保罗·戴拉克于20世纪20年代提出的。

2. 冲激函数的性质(1) 归一性：∫δ(x)dx=1(2) 奇偶性：δ(x)=δ(-x)(3) 积分形：∫f(x)δ(x)dx=f(0)(4) 平移性：∫f(x)δ(x-a)dx=f(a)(5) 缩放性：∫f(x)δ(ax)dx=1/|a| f(0)这些性质使得冲激函数具有在分析求解微积分方程、描写非定常信号和优化控制问题等方面的重要应用。

二、函数相乘的积分函数相乘的积分通常表示为∫f(x)g(x)dx，其中f(x)和g(x)是两个函数。

函数相乘的积分在微积分、物理学和工程学中都有广泛的应用。

下面列举的是一些常见的函数相乘的积分形式。

1. sin(x)cos(x)积分∫sin(x)cos(x)dx=1/2∫sin(2x)dx=-1/4cos(2x)+C其中C是常数。

2. xex积分∫xexdx=xex-∫exdx=xex-ex+C其中C是常数。

3. xcos(x)积分∫xcos(x)dx=xcos(x)+sin(x)+C其中C是常数。

4. x2sin(2x)积分∫x2sin(2x)dx=-x2cos(2x)/2+sin(2x)/2+2∫xcos(2x)dx=-x2cos(2x)/2+sin(2x)/2+xsin(2x)-cos(2x)/2+C其中C是常数。

这几种函数相乘的积分形式在工程数学中应用比较广泛。

冲激函数理解 -回复
冲激函数是一个在数学和物理领域常用的函数，它在时间或空间上是非常短暂的脉冲信号。

冲激函数通常用符号δ(t)或δ(x)表示，其中t表示时间，x表示空间。

冲激函数具有以下特点：
1. 首先，冲激函数在除了零点以外的所有位置上都等于零，即在δ(t)中，只有当t=0时，函数的值为无穷大，其他情况下函数值为零。

2. 其次，冲激函数在整个时间或空间范围内的积分为1，即∫δ(t)dt = 1（或∫δ(x)dx = 1）。

3. 最后，冲激函数在与其他函数进行卷积运算时，可以起到筛选、权重或调制等作用。

由于冲激函数具有非常突出和明显的特征，它经常被用于信号处理、系统分析、控制系统和电路设计等领域。

在信号处理中，冲激函
数可以用来分解信号，得到信号的频谱特性；在系统分析中，冲激函
数可以用来描述和预测系统的响应；在控制系统中，冲激函数可以用
来设计控制器的动态特性；在电路设计中，冲激函数可以用来模拟电
路的输入和输出。

总之，冲激函数在数学和物理领域中有着广泛的应用，它是一种特殊的函数，具有短暂、明显以及权重等特征，在各种实际问题中发
挥着重要的作用。