北师大版-数学-九年级上册-如何运用视点、视角和盲区的关系解决问题
- 格式：doc
- 大小：24.00 KB
- 文档页数：1
下载文档原格式
合集下载
九年级数学上册 第五章 投影与视图 1.投影 如何运用视点、视角和盲区求值？素材 (新版)北师大版
如何运用视点、视角和盲区求值？
难易度：★★★★
关键词：投影-视点、视角和盲区的运用
答案：
运用视点、视角和盲区求值，根据题意作出图形构造出相似三角形是解题的关键．
【举一反三】
典题：如示意图，小华家（点A处）和公路（l）之间竖立着一块35m长且平行于公路的巨型广告牌（DE）．广告牌挡住了小华的视线，请在图中画出视点A的盲区，并将盲区内的那段公路计为BC．一辆以60km/h匀速行驶的汽车经过公路段的时间是3s，已知广告牌和公路的距离是40m，求小华家到公路的距离．（精确到1m）
思路导引：本题考查相似三角形的判定与性质的实际应用及分析问题、解决问题的能力．利用数学知识解决实际问题是中学数学的重要内容．解决此问题的关键在于正确理解题意的基础上建立数学模型，把实际问题转化为数学问题．
根据盲区的定义，作出盲区，然后即可以通过相似三角形的性质求出距离．
标准答案：
解：如图，连接AD、AE，并延长分别交l于B、C，则BC为视点A的盲区，
BC=60 000×=50（m）．
过A点作AM⊥BC于M，交DE于N，则AN⊥DE，MN=40 m．由△ADE∽△ABC，得==，
即=，所以AM≈133（米）．
即小华家到公路的距离约为133米．。
北师大版九年级数学上册第五章投影与视图回顾与思考教学设计
3.给予学生足够的时间和空间，让他们在实践中探索、发现投影与视图的规律，培养他们的空间想象力和逻辑思维能力。
4.关注学生的情感需求，鼓励他们积极参与课堂讨论，增强他们的自信心和成就感。
三、教学重难点和教学设想
（一）教学重难点
1.理解并掌握投影与视图的基本概念及其相互关系，特别是平行投影与中心投影的区分。
3.教学过程：
（1）导入新课：
通过展示一组图片（如建筑图纸、机械零件等），引出投影与视图的概念，激发学生的学习兴趣。
（2）新课学习：
①讲解投影与视图的基本概念，引导学生认识平行投影与中心投影的区别。
②通过实物演示，让学生了解三视图的形成过程，教授绘制三视图的方法。
③介绍投影变换的基本方法，并通过实例讲解其在实际问题中的应用。
4.掌握投影变换的基本方法，如旋转、平移、缩放等，并能运用这些方法解决实际问题。
（二）过程与方法
1.通过观察、实践、探究等环节，培养学生运用投影与视图知识分析问题、解决问题的能力。
2.引导学生运用数学语言、图形、符号等表达方式，描述投影与视图的相关概念和性质。
3.培养学生运用分类、比较、归纳等方法，总结投影与视图的规律和特点。
4.通过小组合作、讨论交流等形式，提高学生合作学习、共同探究的能力。
（三）情感态度与价值观
1.培养学生对投影与视图知识的学习兴趣，激发学生学习数学的热情。
2.培养学生严谨、认真的学习态度，养成细致观察、深入思考的良好习惯。
3.使学生认识到投影与视图在现实生活中的广泛应用，体会数学与现实生活的紧密联系。
-运用任务驱动法，设置具有挑战性的任务，鼓励学生合作学习，共同解决问题。
2.教学策略：
-注重分层教学，针对学生的个体差异，设计不同难度的练习题，使每个学生都能在原有基础上得到提高。
4.关注学生的情感需求，鼓励他们积极参与课堂讨论，增强他们的自信心和成就感。
三、教学重难点和教学设想
（一）教学重难点
1.理解并掌握投影与视图的基本概念及其相互关系，特别是平行投影与中心投影的区分。
3.教学过程：
（1）导入新课：
通过展示一组图片（如建筑图纸、机械零件等），引出投影与视图的概念，激发学生的学习兴趣。
（2）新课学习：
①讲解投影与视图的基本概念，引导学生认识平行投影与中心投影的区别。
②通过实物演示，让学生了解三视图的形成过程，教授绘制三视图的方法。
③介绍投影变换的基本方法，并通过实例讲解其在实际问题中的应用。
4.掌握投影变换的基本方法，如旋转、平移、缩放等，并能运用这些方法解决实际问题。
（二）过程与方法
1.通过观察、实践、探究等环节，培养学生运用投影与视图知识分析问题、解决问题的能力。
2.引导学生运用数学语言、图形、符号等表达方式，描述投影与视图的相关概念和性质。
3.培养学生运用分类、比较、归纳等方法，总结投影与视图的规律和特点。
4.通过小组合作、讨论交流等形式，提高学生合作学习、共同探究的能力。
（三）情感态度与价值观
1.培养学生对投影与视图知识的学习兴趣，激发学生学习数学的热情。
2.培养学生严谨、认真的学习态度，养成细致观察、深入思考的良好习惯。
3.使学生认识到投影与视图在现实生活中的广泛应用，体会数学与现实生活的紧密联系。
-运用任务驱动法，设置具有挑战性的任务，鼓励学生合作学习，共同解决问题。
2.教学策略：
-注重分层教学，针对学生的个体差异，设计不同难度的练习题，使每个学生都能在原有基础上得到提高。
北师大版九年级数学上第四章视图与投影全章教案
第四章视图与投影1．视图（一）一、教学目标1. 知识与技能：经历探索基本几何体（圆柱、圆锥、球）与其三视图之间的关系。
能根据三视图描述基本几何体或实物图形，培养和发展学生推理能力和空间观念。
2. 过程与方法：结合具体实例，初步体会视图在现实生活中的应用，感受数学与现实生活的密切联系，增强学生的数学应用意识。
3. 情感态度与价值观：让学生在课堂活动中通过相互间的合作与交流，进一步发展学生合作交流的能力和数学表达能力。
二、教学重点和难点1、重点：会画圆柱、圆锥、球的三种视图，体会这几种几何体与其视图之间的相互转. 画几何体的三视图。
会画直棱柱的三种视图。
2、难点：画直棱柱的三种视图要明确图中实线和虚线的区别。
三、教学过程第一环节：情境问题引入活动内容：1还记得一个物体的主视图、左视图和俯视图吗？2你能自己或者与同伴画出下图的主视图、左视图和俯视图吗？附答案1、主视图：2、左视图：3、俯视图:第二环节：活动探究（获取信息，体会特点）活动内容：110页的图中物体的形状分别可以看成什么样的几何体？从正面、侧面、上面看这些几何体，他们的形状各是什么样的？活动目的：首先让学生经历将实物抽象成几何体的过程，培养学生的抽象能力和想象能力，并通过亲身体验归纳总结三种视图的不同特点，及在现实生活中的实际意义。
第三环节：合作学习活动内容：（1）在下图中找出上图中各物体的主视图。
（1） （2） （3）（4） （5） （6）（2） 上图中各物体的左视图是什么？俯视图呢？与同伴进行交流。
活动目的：以问题串的形式引导学生逐步深入地思考三种视图的区别与联系。
前一个问题的设置帮助培养学生的空间想象能力，问题（2）的设置帮助学生体会：三种视图在长、宽、高等方面的联系。
在以上两个问题的铺设下，图表的设置起到归纳总结的作用 。
第四环节：练习提高活动内容：如图是一个蒙古包的照片。
小明认为这个蒙古包可以看成下图所示的几何体，并画出这个几何体的三种视图，你同意小明的做法吗？主视图 左视图俯视图活动目的：对本节知识进行巩固练习。
九年级数学视点 视线与盲区
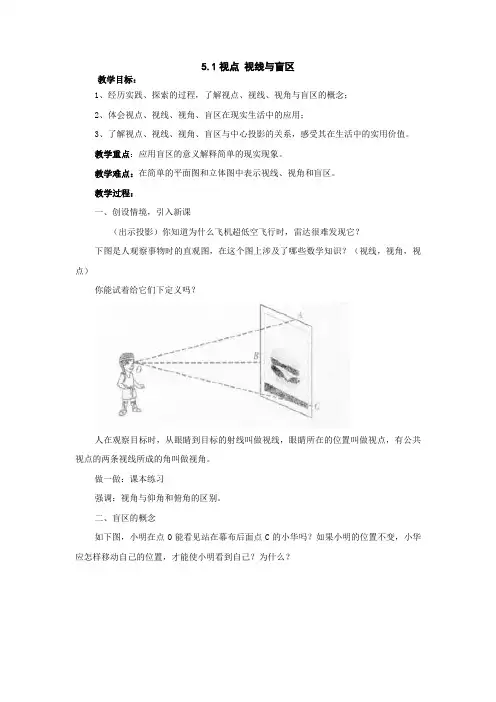
5.1视点视线与盲区教学目标：1、经历实践、探索的过程，了解视点、视线、视角与盲区的概念；2、体会视点、视线、视角、盲区在现实生活中的应用；3、了解视点、视线、视角、盲区与中心投影的关系，感受其在生活中的实用价值。
教学重点：应用盲区的意义解释简单的现实现象。
教学难点：在简单的平面图和立体图中表示视线、视角和盲区。
教学过程：一、创设情境，引入新课（出示投影）你知道为什么飞机超低空飞行时，雷达很难发现它？下图是人观察事物时的直观图，在这个图上涉及了哪些数学知识？（视线，视角，视点）你能试着给它们下定义吗？人在观察目标时，从眼睛到目标的射线叫做视线，眼睛所在的位置叫做视点，有公共视点的两条视线所成的角叫做视角。
做一做：课本练习强调：视角与仰角和俯角的区别。
二、盲区的概念如下图，小明在点O能看见站在幕布后面点C的小华吗？如果小明的位置不变，小华应怎样移动自己的位置，才能使小明看到自己？为什么？学生讨论后得出：不能；移到幕布前∠AOB的范围内；因为小华在幕布后面的区域是小明视线不能到达的区域，要使小明看到自己，必须要移到小明视线能到达的区域。
教师追问：那么图中阴影部分的区域叫做什么？为什么？小结：我们把视线不能到达的区域叫做盲区，如上图中的阴影部分的区域就是盲区。
如下图，∠AO1D，∠BO2C，分别表示人的双目水平位置上的最大视角(约120°)，在这个图上什么地方是盲区，什么地方是人眼看得最清晰的区域？盲区的意义还不局限于人观察景物，那么盲区的意义还有哪些应用呢？学生举例三、应用新知例如下图，A，B表示教室的门框位置。
小聪站在教室内的点P位置，小慧、小红、张杰三位同学分别站在教室外点C，D，E的位置。
这三位同学中，小聪能看见谁？看不见谁？请用盲区的意义给出解释。
解：如下图，作射线PA，PB.图中阴影部分表示小聪观察教室外时的盲区.小慧、小红、张杰三位同学中，只有张杰在盲区内，所以小聪能看见的是小慧、小红，看不见的是张杰.练习：课本课内练习和作业题（由学生独立完成，后指名学生口答或板书）四、小结：通过这节课的学习你学会了什么？你有什收获与困惑？五、布置作业同步练习。
北师大版数学九年级上册4.1.1《视图》教案
北师大版数学九年级上册4.1.1《视图》教案一. 教材分析北师大版数学九年级上册4.1.1《视图》是立体几何部分的一个知识点，主要让学生了解并掌握三视图的概念，学会从不同角度观察几何体，培养空间想象能力。
本节课的内容对于学生来说比较抽象，需要通过大量的实例和实践活动，让学生感受并理解三视图的含义。
二. 学情分析九年级的学生已经具备了一定的空间想象能力，但对于立体几何的概念和性质还比较陌生。
因此，在教学过程中，教师需要关注学生的认知水平，通过生动的实例和直观的演示，帮助学生理解和掌握三视图的概念。
三. 教学目标1.让学生了解并掌握三视图的概念，能正确画出一般几何体的三视图。
2.培养学生从不同角度观察几何体的能力，提高空间想象力。
3.通过对三视图的学习，培养学生直观、抽象的思维能力。
四. 教学重难点1.教学重点：三视图的概念及一般几何体的三视图。
2.教学难点：理解并掌握三视图的概念，能从不同角度观察几何体。
五. 教学方法1.采用直观演示法，通过实物和模型，让学生直观地感受三视图。
2.采用实践操作法，让学生动手画出一般几何体的三视图，提高操作能力。
3.采用讨论法，让学生分组讨论，培养合作意识。
六. 教学准备1.准备一些几何体模型，如正方体、长方体等。
2.准备幻灯片或多媒体课件，展示各种几何体的三视图。
3.准备练习题，让学生巩固所学知识。
七. 教学过程1.导入（5分钟）教师通过展示一些生活中的实物，如建筑物、家具等，引导学生从不同角度观察这些实物，从而引出本节课的主题——视图。
2.呈现（10分钟）教师通过幻灯片或多媒体课件，展示各种几何体的三视图，如正方体、长方体等。
让学生直观地感受三视图的概念，并引导学生总结三视图的特点。
3.操练（10分钟）教师让学生分组，每组选择一个几何体，动手画出其三视图。
在画图过程中，教师巡回指导，纠正学生的错误。
4.巩固（5分钟）教师选取一些练习题，让学生独立完成，检验学生对三视图概念的掌握情况。
北师大版数学九年级上册5.2视图(第三课时)教学设计
1.学生对视图概念的理解程度：通过课前测试，了解学生对主视图、左视图、俯视图的理解程度，以便在教学中有的放矢地进行针对性讲解。
2.学生的空间想象力：观察学生在课堂上的表现，了解他们在观察和想象物体形状时的困难，以便及时给予指导和帮助。
3.学生的合作与交流能力：在小组合作环节，关注学生的参与程度，鼓励他们积极发表观点，提高团队协作能力和表达能力。
二、新课讲解
1.讲解主视图、左视图、俯视图的概念，强调它们之间的相互关系。
2.通过实例演示，让学生观察和思考如何从不同角度观察物体，并绘制出相应的视图。
3.分析视图在工程设计、建筑、制造等领域的应用，让学生认识到视图知识的重要性。
三、课堂练习
1.让学生独立完成教材中的练习题，巩固所学知识。
2.引导学生运用视图知识解决实际问题，如根据视图设计物体、计算物体的表面积和体积等。
（二）过程与方法
1.通过观察、操作、实践等教学活动，让学生体验从不同角度观察物体，培养空间想象力和观察力。
2.引导学生运用类比、归纳、推理等方法，发现视图之间的内在联系，提高逻辑思维能力和解决问题的能力。
3.通过小组合作、交流讨论等形式，培养学生的团队协作能力和表达能力。
（三）情感态度与价值观
1.培养学生对视图学习的兴趣，激发学生的学习热情，使学生在轻松愉快的氛围中学习数学。
3.教师布置课后作业，要求学生运用所学知识解决实际问题，如根据视图设计物体、计算物体的表面积和体积等。
4.教师提醒学生关注生活中的视图现象，培养学生的观察力和空间想象力，为下一节课的学习打下基础。
五、作业布置
为了巩固本节课所学知识，培养学生的空间想象力和解决问题的能力，特布置以下作业：
1.完成教材课后练习题：要求学生独立完成，注意在绘制视图时保持准确性和规范性。通过完成练习题，使学生进一步熟悉三视图的绘制方法和技巧。
2.学生的空间想象力：观察学生在课堂上的表现，了解他们在观察和想象物体形状时的困难，以便及时给予指导和帮助。
3.学生的合作与交流能力：在小组合作环节，关注学生的参与程度，鼓励他们积极发表观点，提高团队协作能力和表达能力。
二、新课讲解
1.讲解主视图、左视图、俯视图的概念，强调它们之间的相互关系。
2.通过实例演示，让学生观察和思考如何从不同角度观察物体，并绘制出相应的视图。
3.分析视图在工程设计、建筑、制造等领域的应用，让学生认识到视图知识的重要性。
三、课堂练习
1.让学生独立完成教材中的练习题，巩固所学知识。
2.引导学生运用视图知识解决实际问题，如根据视图设计物体、计算物体的表面积和体积等。
（二）过程与方法
1.通过观察、操作、实践等教学活动，让学生体验从不同角度观察物体，培养空间想象力和观察力。
2.引导学生运用类比、归纳、推理等方法，发现视图之间的内在联系，提高逻辑思维能力和解决问题的能力。
3.通过小组合作、交流讨论等形式，培养学生的团队协作能力和表达能力。
（三）情感态度与价值观
1.培养学生对视图学习的兴趣，激发学生的学习热情，使学生在轻松愉快的氛围中学习数学。
3.教师布置课后作业，要求学生运用所学知识解决实际问题，如根据视图设计物体、计算物体的表面积和体积等。
4.教师提醒学生关注生活中的视图现象，培养学生的观察力和空间想象力，为下一节课的学习打下基础。
五、作业布置
为了巩固本节课所学知识，培养学生的空间想象力和解决问题的能力，特布置以下作业：
1.完成教材课后练习题：要求学生独立完成，注意在绘制视图时保持准确性和规范性。通过完成练习题，使学生进一步熟悉三视图的绘制方法和技巧。
北师大版九年级数学上册5.2.3视图教学设计
6.鼓励学生利用课余时间，查找有关视图在实际工程、设计等领域应用的案例，拓宽知识视野，提高学生的学习兴趣。
作业布置要求：
1.学生在完成作业时，要注意书写规范，保持解答过程的简洁和清晰。
2.作业完成后，要进行自我检查，确保答案的正确性。
3.教师将对作业进行详细批改，给予评价和指导，学生应认真对待反馈意见，及时改正错误。
4.掌握使用计算器、计算机等工具绘制视图的基本方法，提高动手操作能力和实际应用能力。
（二）过程与方法
1.通过观察、思考、讨论等环节，培养学生提出问题、分析问题、解决问题的能力。
2.通过小组合作、互动交流等方式，培养学生团队协作、共同探究的学习习惯。
3.运用比较、分类、归纳等方法，引导学生总结视图的特点、规律，提高学生的逻辑思维能力。
五、作业布置
为了巩固本章节所学知识，确保学生对视图的理解和应用能力得到有效提升，特布置以下作业：
1.完成课本第123页的练习题1、2、3，要求学生在完成过程中注意三视图的画法和转换方法，强化对视图概念的理解。
2.选择一个生活中的物体，如文具盒、水杯等，自行绘制其三视图，并尝试运用所学知识求解该物体的表面积和体积。此作业旨在培养学生的空间想象能力和几何计算能力。
4.结合实际生活中的例子，让学生体会数学与现实生活的联系，培养学生的应用意识和实践能力。
（三）情感态度与价值观
1.培养学生对数学学习的兴趣和热情，增强学生的自信心和自主学习能力。
2.引导学生认识到数学在科技发展、社会进步中的重要作用，树立正确的价值观。
3.培养学生严谨、细致的学习态度，提高学生的责任心和自律意识。
（五）总结归纳
1.教师引导学生回顾本节课所学内容，总结视图的概念、画法、转换方法及其在实际中的应用。
作业布置要求：
1.学生在完成作业时，要注意书写规范，保持解答过程的简洁和清晰。
2.作业完成后，要进行自我检查，确保答案的正确性。
3.教师将对作业进行详细批改，给予评价和指导，学生应认真对待反馈意见，及时改正错误。
4.掌握使用计算器、计算机等工具绘制视图的基本方法，提高动手操作能力和实际应用能力。
（二）过程与方法
1.通过观察、思考、讨论等环节，培养学生提出问题、分析问题、解决问题的能力。
2.通过小组合作、互动交流等方式，培养学生团队协作、共同探究的学习习惯。
3.运用比较、分类、归纳等方法，引导学生总结视图的特点、规律，提高学生的逻辑思维能力。
五、作业布置
为了巩固本章节所学知识，确保学生对视图的理解和应用能力得到有效提升，特布置以下作业：
1.完成课本第123页的练习题1、2、3，要求学生在完成过程中注意三视图的画法和转换方法，强化对视图概念的理解。
2.选择一个生活中的物体，如文具盒、水杯等，自行绘制其三视图，并尝试运用所学知识求解该物体的表面积和体积。此作业旨在培养学生的空间想象能力和几何计算能力。
4.结合实际生活中的例子，让学生体会数学与现实生活的联系，培养学生的应用意识和实践能力。
（三）情感态度与价值观
1.培养学生对数学学习的兴趣和热情，增强学生的自信心和自主学习能力。
2.引导学生认识到数学在科技发展、社会进步中的重要作用，树立正确的价值观。
3.培养学生严谨、细致的学习态度，提高学生的责任心和自律意识。
（五）总结归纳
1.教师引导学生回顾本节课所学内容，总结视图的概念、画法、转换方法及其在实际中的应用。
北师大版九年级上册数学教案：5.2视图
3.数学应用：将三视图应用于实际生活中，解决实际问题，培养学生学以致用的能力，增强数学与现实生活的联系。
4.团队协作：在小组合作完成视图绘制和物体形状推测的过程中，培养学生沟通协调和团队协作能力。
三、教学难点与重点
1.教学重点
-掌握三视图（主视图、左视图、俯视图）的基本概念及其画法。
-能够运用三视图识别和描述物体的空间形状。
-设计一些具有挑战性的练习题，如组合体的三视图识别，让学生在解决实际问题的过程中克服难点，提高空间思维能力和解决问题的能力。
四、教学流程
（一）导入新课（用时5分钟）
同学们，今天我们将要学习的是“5.2视图”这一章节。在开始之前，我想先问大家一个问题：“你们在日常生活中是否注意过建筑图纸或机械图纸上的不同角度的图形？”这个问题与我们将要学习的内容密切相关。通过这个问题，我希望能够引起大家的兴趣和好奇心，让我们一同探索三视图的奥秘。
（二）新课讲授（用时10分钟）
1.理论介绍：首先，我们要了解三视图的基本概念。三视图包括主视图、左视图和俯视图，它们分别从不同角度展示物体的形状。三视图在工程设计、建筑绘图等领域具有重要作用。
2.案例分析：接下来，我们来看一个具体的案例。这个案例展示了三视图在建筑图纸中的应用，以及如何通过三视图来理解建筑物的结构。
3.重点难点解析：在讲授过程中，我会特别强调三视图的画法和识别这两个重点。对于难点部分，如处理物体遮挡关系，我会通过实物模型和图解来帮助大家理解。
（三）实践活动（用时10分钟）
1.分组讨论：学生们将分成若干小组，每组讨论一个与三视图相关的实际问题，如如何从三视图中还原物体的三维形状。
2.实验操作：为了加深理解，我们将进行一个简单的实验操作，绘制一个物体的三视图。
4.团队协作：在小组合作完成视图绘制和物体形状推测的过程中，培养学生沟通协调和团队协作能力。
三、教学难点与重点
1.教学重点
-掌握三视图（主视图、左视图、俯视图）的基本概念及其画法。
-能够运用三视图识别和描述物体的空间形状。
-设计一些具有挑战性的练习题，如组合体的三视图识别，让学生在解决实际问题的过程中克服难点，提高空间思维能力和解决问题的能力。
四、教学流程
（一）导入新课（用时5分钟）
同学们，今天我们将要学习的是“5.2视图”这一章节。在开始之前，我想先问大家一个问题：“你们在日常生活中是否注意过建筑图纸或机械图纸上的不同角度的图形？”这个问题与我们将要学习的内容密切相关。通过这个问题，我希望能够引起大家的兴趣和好奇心，让我们一同探索三视图的奥秘。
（二）新课讲授（用时10分钟）
1.理论介绍：首先，我们要了解三视图的基本概念。三视图包括主视图、左视图和俯视图，它们分别从不同角度展示物体的形状。三视图在工程设计、建筑绘图等领域具有重要作用。
2.案例分析：接下来，我们来看一个具体的案例。这个案例展示了三视图在建筑图纸中的应用，以及如何通过三视图来理解建筑物的结构。
3.重点难点解析：在讲授过程中，我会特别强调三视图的画法和识别这两个重点。对于难点部分，如处理物体遮挡关系，我会通过实物模型和图解来帮助大家理解。
（三）实践活动（用时10分钟）
1.分组讨论：学生们将分成若干小组，每组讨论一个与三视图相关的实际问题，如如何从三视图中还原物体的三维形状。
2.实验操作：为了加深理解，我们将进行一个简单的实验操作，绘制一个物体的三视图。
北师大版-数学-九年级上册-4.3 灯光与影子 课时2
4.3.2 视点、视线与盲区
目标 点击 视点、视线与盲区
学习目标:
1.通过实例了解视点、视线、盲区的概念．并能体会它们在现实 生活中的应用 ．
学习重难点:
1.通过具体情境，体会视点、视线和盲区的概念，并在 生活中应用．
2.体会视点、视线和盲区的含义及在生活中的应用．
驶向胜利 的彼岸
回顾 思考
物体在光线的照射下，会在地面和墙壁上留 下它的影子，这就是投影现象. 探照灯、手电筒、路灯和台灯的光线可以看 成是从一点出发的，像这样的光线所形成的投影 称为中心投影
做一做
有一辆客车在平坦的大道上行驶,前方两座建筑物. （1）客车行驶到某一位置时，司机能看到建筑物B的一部分，如果 客车继续向前行驶，那么他所看到的部分是怎样变化的？
B
A
做一做
有一辆客车在平坦的大道上行驶,前方两座建筑物.
（2）客车行驶到位置②时，司机还能看到建筑物B吗?为 什么？
盲区
B
A
②
①
议一议
当你乘车沿一条平坦的大道向前行驶时,你会发现:前方那些高一 些的建筑物好像“沉”到了位于它们前面的那些矮一些的建筑物 后面去了.这是为什么?先想一想,再与同伴进行交流.
哇，真是“一叶障目 不见泰山”呀！
盲区
随堂练习
• 小明和小迪分别从两条小胡同走向马路,当他们分别走到图中的 位置时,哪个人看到的范围更大一些?为什么?你还能举出生活中 类似的例子吗?
小明
小迪
随堂练习
如图所示：一只猫蹲在墙前,老鼠躲在墙后.请你画出老鼠活命 的活动区域。
盲区 墙
盲区 墙
猫
大王
盲区
墙
小结与回顾
通过本节课的学习你有什么收获？ 还有什么疑问？
目标 点击 视点、视线与盲区
学习目标:
1.通过实例了解视点、视线、盲区的概念．并能体会它们在现实 生活中的应用 ．
学习重难点:
1.通过具体情境，体会视点、视线和盲区的概念，并在 生活中应用．
2.体会视点、视线和盲区的含义及在生活中的应用．
驶向胜利 的彼岸
回顾 思考
物体在光线的照射下，会在地面和墙壁上留 下它的影子，这就是投影现象. 探照灯、手电筒、路灯和台灯的光线可以看 成是从一点出发的，像这样的光线所形成的投影 称为中心投影
做一做
有一辆客车在平坦的大道上行驶,前方两座建筑物. （1）客车行驶到某一位置时，司机能看到建筑物B的一部分，如果 客车继续向前行驶，那么他所看到的部分是怎样变化的？
B
A
做一做
有一辆客车在平坦的大道上行驶,前方两座建筑物.
（2）客车行驶到位置②时，司机还能看到建筑物B吗?为 什么？
盲区
B
A
②
①
议一议
当你乘车沿一条平坦的大道向前行驶时,你会发现:前方那些高一 些的建筑物好像“沉”到了位于它们前面的那些矮一些的建筑物 后面去了.这是为什么?先想一想,再与同伴进行交流.
哇，真是“一叶障目 不见泰山”呀！
盲区
随堂练习
• 小明和小迪分别从两条小胡同走向马路,当他们分别走到图中的 位置时,哪个人看到的范围更大一些?为什么?你还能举出生活中 类似的例子吗?
小明
小迪
随堂练习
如图所示：一只猫蹲在墙前,老鼠躲在墙后.请你画出老鼠活命 的活动区域。
盲区 墙
盲区 墙
猫
大王
盲区
墙
小结与回顾
通过本节课的学习你有什么收获？ 还有什么疑问？
北师大版九年级数学上册《 第五章 投影与视图 5.2 视图》
北师大版九年级数学上册《第五章投影与视图 5.2 视图》一. 教材分析北师大版九年级数学上册《第五章投影与视图 5.2 视图》这一节主要让学生了解三视图的概念，掌握主视图、左视图、俯视图的画法，以及能够根据物体的形状确定其三视图。
教材通过生活中的实例引入视图的概念，让学生感受数学与生活的紧密联系，培养学生的数学应用能力。
二. 学情分析九年级的学生已经掌握了平面几何的基本知识，对图形有了一定的认识。
但是，对于三维空间中的物体，学生可能还比较陌生。
因此，在教学过程中，教师需要通过生动形象的实例，让学生建立起对三维空间物体的直观认识，以便于理解三视图的概念。
三. 教学目标1.让学生了解三视图的概念，掌握主视图、左视图、俯视图的画法。
2.培养学生根据物体的形状确定其三视图的能力。
3.培养学生的空间想象能力和数学应用能力。
四. 教学重难点1.重难点：三视图的概念及其画法。
2.难点：如何让学生理解并掌握三视图的画法，以及如何根据物体的形状确定其三视图。
五. 教学方法采用情境教学法、实例教学法和小组合作学习法。
通过生活中的实例引入视图的概念，让学生感受数学与生活的紧密联系；通过小组合作学习，让学生在实践中掌握三视图的画法。
六. 教学准备1.准备一些生活中的实例，如建筑物、家具等，用于导入课堂。
2.准备一些三维物体模型，如球体、长方体等，用于让学生观察和操作。
3.准备一些练习题，用于巩固所学知识。
七. 教学过程1.导入（5分钟）利用生活中的一些实例，如建筑物、家具等，引导学生观察这些物体在不同角度的投影，从而引入视图的概念。
2.呈现（10分钟）向学生介绍主视图、左视图、俯视图的定义，并通过三维物体模型让学生直观地感受三视图。
同时，讲解三视图的画法，让学生能够自己动手画出简单物体的三视图。
3.操练（10分钟）让学生分组进行合作学习，每组选择一个三维物体模型，尝试画出其三视图。
教师在旁边指导，解答学生的疑问。
4.巩固（10分钟）出示一些练习题，让学生独立完成，检验学生对三视图概念和画法的掌握程度。
北师大版数学九年级上册4.1.2《视图》教案
北师大版数学九年级上册4.1.2《视图》教案一. 教材分析北师大版数学九年级上册4.1.2《视图》一课，主要让学生掌握三视图的概念及画法，培养学生空间想象能力，体会数学与实际生活的联系。
此课内容是学生在学习了平面几何和立体几何的基础上进行学习的，对学生空间想象能力的培养起着承上启下的作用。
二. 学情分析九年级的学生已经具备了一定的空间想象能力，对平面几何和立体几何有一定的了解。
但学生在学习过程中，可能会对一些复杂几何图形的三视图难以理解和掌握。
因此，在教学过程中，教师需要关注学生的个体差异，引导学生通过观察、思考、操作、交流等途径，逐步提高空间想象能力。
三. 教学目标1.知识与技能：使学生掌握主视图、左视图、俯视图的概念，学会从不同角度观察几何体，并能画出简单几何体和组合几何体的三视图。
2.过程与方法：通过观察、操作、思考等活动，培养学生的空间想象能力。
3.情感态度与价值观：让学生感受数学与实际生活的联系，激发学习兴趣，体验成功。
四. 教学重难点1.重点：三视图的概念及画法。
2.难点：对复杂几何图形三视图的画法和空间想象能力的培养。
五. 教学方法1.情境教学法：通过生活中的实例，引导学生认识三视图，激发学习兴趣。
2.启发式教学法：引导学生主动探究、发现问题，培养空间想象能力。
3.合作学习法：分组讨论，共同完成实践操作，提高学生合作能力。
六. 教学准备1.教具：多媒体课件、几何模型、画图工具。
2.学具：学生用书、练习册、画图工具。
七. 教学过程1.导入（5分钟）教师通过生活中的实例，如建筑物的设计、机械制造等，引导学生认识三视图，激发学生学习兴趣。
2.呈现（5分钟）教师利用多媒体课件展示简单几何体和组合几何体的三视图，引导学生观察、思考，总结三视图的特点。
3.操练（10分钟）教师学生分组讨论，每组选择一个几何体，互相描述三视图，并尝试画出三视图。
教师巡回指导，解答学生疑问。
4.巩固（5分钟）教师挑选几组学生的作品，展示给大家，让大家判断其三视图是否正确。
[初中数学]九年级上册数学教案全集 北师大版166
![[初中数学]九年级上册数学教案全集 北师大版166](https://img.taocdn.com/s1/m/63642026bed5b9f3f90f1ca1.png)
宝石学校活页课时教案(首页)
班级:九年级科目:数学
一、某人在室内从窗口向外观看（如下图）.
（1）在右图中将视点用点标出.
（2）在右图中将视线画出.
（3）在下图中，画出视角，并测量视角度数.
（4）此人若想在此窗口观察室外更多的影物，应该靠近窗口，还是远离窗口？
二、如图，一个小孩在室内由窗口观察室外的一棵树.
（1）在下图中，小孩在什么位置就可以看到树干的全部，请在图中用线段表示出来.
（2）小孩站在什么位置时，只能看到树冠及树冠以上的部分，请在下图中用线段表示出来.
三、以下各图是某人站在室内，由远及近逐渐靠近窗口观察室外的一组照片。
（1）按此人逐渐靠近窗口的顺序，这5张照片的顺序应为__________.
（2）说出此人观察室外的视角由大到小的顺序.。
北师大版数学九年级上册第五章投影与视图回顾与思考教学设计
三、教学重难点和教学设想
（一）教学重难点
1.重点：理解中心投影与平行投影的概念，掌握正投影的绘制方法，学会根据三视图判断物体的空间结构。
2.难点：空间想象能力的培养，视图中的线与面、面与面关系的理解，以及在实际问题中运用投影与视图知识。
（二）教学设想
1.采用情境教学法，引入生活中的实际例子，让学生感知投影与视图在现实中的应用，激发学习兴趣。
五、作业布置
1.完成课本第五章的课后练习题，重点在于中心投影与平行投影的特点及应用，以及三视图的绘制方法。
-设计意图：通过课后习题，巩固学生对投影与视图知识的掌握，提高解题能力。
2.结合生活实际，观察并记录身边的投影现象，分析其属于中心投影还是平行投影，并尝试解释其原理。
-设计意图：培养学生的观察力，增强数学与现实生活的联系，提高实践意识。
北师大版数学九年级上册第五章投影与视图回顾与思考教学设计
一、教学目标
（一）知识与技能
1.理解并掌握中心投影与平行投影的概念，能够区分实际生活中的中心投影与平行投影现象。
2.学会使用正投影方法绘制物体的三视图，并能根据三视图判断物体的空间结构。
3.理解并掌握视图中的线与面、面与面的关系，能够运用视图知识解决实际问题。
本章内容将从投影与视图的基本概念入手，引导学生通过观察、实践、探究等学习活动，掌握投影与视图的相关知识，培养空间想象能力和创新能力。在教学过程中，注重激发学生的学习兴趣，提高学生的实践意识和团队协作能力，使学生在轻松愉快的氛围中学习数学，感受数学的魅力。
二、学情分析
九年级学生在前两年的数学学习中，已经积累了一定的空间图形知识和逻辑思维能力。在此基础上，对本章节投影与视图的学习，他们具备了一定的认知基础。但受限于生活经验，学生在理解投影与视图的应用方面可能存在一定难度。此外，空间想象能力的培养对学生来说是一个挑战，需要教师在教学过程中给予充分关注和引导。
（一）教学重难点
1.重点：理解中心投影与平行投影的概念，掌握正投影的绘制方法，学会根据三视图判断物体的空间结构。
2.难点：空间想象能力的培养，视图中的线与面、面与面关系的理解，以及在实际问题中运用投影与视图知识。
（二）教学设想
1.采用情境教学法，引入生活中的实际例子，让学生感知投影与视图在现实中的应用，激发学习兴趣。
五、作业布置
1.完成课本第五章的课后练习题，重点在于中心投影与平行投影的特点及应用，以及三视图的绘制方法。
-设计意图：通过课后习题，巩固学生对投影与视图知识的掌握，提高解题能力。
2.结合生活实际，观察并记录身边的投影现象，分析其属于中心投影还是平行投影，并尝试解释其原理。
-设计意图：培养学生的观察力，增强数学与现实生活的联系，提高实践意识。
北师大版数学九年级上册第五章投影与视图回顾与思考教学设计
一、教学目标
（一）知识与技能
1.理解并掌握中心投影与平行投影的概念，能够区分实际生活中的中心投影与平行投影现象。
2.学会使用正投影方法绘制物体的三视图，并能根据三视图判断物体的空间结构。
3.理解并掌握视图中的线与面、面与面的关系，能够运用视图知识解决实际问题。
本章内容将从投影与视图的基本概念入手，引导学生通过观察、实践、探究等学习活动，掌握投影与视图的相关知识，培养空间想象能力和创新能力。在教学过程中，注重激发学生的学习兴趣，提高学生的实践意识和团队协作能力，使学生在轻松愉快的氛围中学习数学，感受数学的魅力。
二、学情分析
九年级学生在前两年的数学学习中，已经积累了一定的空间图形知识和逻辑思维能力。在此基础上，对本章节投影与视图的学习，他们具备了一定的认知基础。但受限于生活经验，学生在理解投影与视图的应用方面可能存在一定难度。此外，空间想象能力的培养对学生来说是一个挑战，需要教师在教学过程中给予充分关注和引导。
北师大版九年级数学上册第五章投影与视图回顾与思考优秀教学案例
（三）小组合作
为了培养学生的团队合作精神和沟通能力，我会组织学生进行小组讨论活动。我会将学生分成小组，让他们共同解决一个实际问题，如设计一个建筑物的三视图。在讨论过程中，学生可以分享自己的学习心得和解决问题的方法，互相交流和启发，从而提高他们的团队合作能力和解决问题的能力。
（四）反思与评价
在教学过程中，我会引导学生进行反思和评价。例如，在解决一个实际问题时，我会让学生回顾自己的解题过程，思考哪些地方做得好，哪些地方可以改进。同时，我还会组织学生进行相互评价，让他们学会欣赏他人的优点，并给出建设性的意见。通过反思和评价，学生可以更好地了解自己的学习情况，提高自我改进的能力。
4.总结归纳与作业小结：在学生小组讨论结束后，组织学生进行总结归纳，强调投影与视图知识在实际生活中的重要性，并通过作业小结帮助学生巩固知识，提高自我改进的能力。
5.启发式教学与创新思维：在教学过程中，注重启发式教学，引导学生思考和探索，培养学生的创新思维和解决问题的能力。
这个教学案例通过以上五个亮点，充分调动了学生的学习积极性，提高了他们的数学素养。在教学过程中，注重知识的巩固与实际应用，通过实际问题情境的导入、多媒体课件的运用、小组讨论与合作、总结归纳与作业小结等方法，帮助学生更好地理解和应用投影与视图知识。同时，通过启发式教学与创新思维的培养，激发了学生的思考和创造力，使他们能够在回顾与思考中不断提升自己的数学水平。
最后，开展小组讨论活动，让学生分享自己的学习心得和解决问题的方法。通过互相交流，培养学生团队合作精神，提高他们的沟通能力。
整个教学案例注重知识的巩固与实际应用，充分调动学生的学习积极性，提高他们的数学素养。在教学过程中，注重启发式教学，培养学生的创新思维和解决问题的能力。通过这个案例，使学生在回顾与思考中断提升自己的数学水平。
为了培养学生的团队合作精神和沟通能力，我会组织学生进行小组讨论活动。我会将学生分成小组，让他们共同解决一个实际问题，如设计一个建筑物的三视图。在讨论过程中，学生可以分享自己的学习心得和解决问题的方法，互相交流和启发，从而提高他们的团队合作能力和解决问题的能力。
（四）反思与评价
在教学过程中，我会引导学生进行反思和评价。例如，在解决一个实际问题时，我会让学生回顾自己的解题过程，思考哪些地方做得好，哪些地方可以改进。同时，我还会组织学生进行相互评价，让他们学会欣赏他人的优点，并给出建设性的意见。通过反思和评价，学生可以更好地了解自己的学习情况，提高自我改进的能力。
4.总结归纳与作业小结：在学生小组讨论结束后，组织学生进行总结归纳，强调投影与视图知识在实际生活中的重要性，并通过作业小结帮助学生巩固知识，提高自我改进的能力。
5.启发式教学与创新思维：在教学过程中，注重启发式教学，引导学生思考和探索，培养学生的创新思维和解决问题的能力。
这个教学案例通过以上五个亮点，充分调动了学生的学习积极性，提高了他们的数学素养。在教学过程中，注重知识的巩固与实际应用，通过实际问题情境的导入、多媒体课件的运用、小组讨论与合作、总结归纳与作业小结等方法，帮助学生更好地理解和应用投影与视图知识。同时，通过启发式教学与创新思维的培养，激发了学生的思考和创造力，使他们能够在回顾与思考中不断提升自己的数学水平。
最后，开展小组讨论活动，让学生分享自己的学习心得和解决问题的方法。通过互相交流，培养学生团队合作精神，提高他们的沟通能力。
整个教学案例注重知识的巩固与实际应用，充分调动学生的学习积极性，提高他们的数学素养。在教学过程中，注重启发式教学，培养学生的创新思维和解决问题的能力。通过这个案例，使学生在回顾与思考中断提升自己的数学水平。
九年级数学视图与投影北师大版知识精讲
初三数学视图与投影北师大版【本讲教育信息】一. 教学内容：视图与投影二. 教学目标：1. 通过实例能够判断简单物体的视图，能根据三视图描述基本几何体或实物原型，会进行简单物体与三视图间的相互转化。
2. 通过实例了解中心投影与平行投影的含义及其简单的应用。
3. 通过实例了解视点、盲区的含义及其在生活中的应用。
三. 教学重点、难点：重点：1. 会进行简单物体与三视图间的相互转化。
2. 理解平行投影与中心投影的特征，并会应用。
3. 通过对视点、视线、盲区的理解，解决生活实际问题。
难点：1. 由三种视图想象并作出原几何体。
2. 平行投影及中心投影的应用。
四. 课堂教学：［知识要点］1. 主要概念：（1）圆柱的主视图是矩形，左视图是矩形，俯视图是圆。
（2）圆锥的主视图是三角形；左视图是三角形；俯视图是圆，还要画上圆心。
（3）球的主视图是圆；左视图是圆；俯视图是圆。
（4）投影：物体在光线的照射下，会在地面或墙上留下它的影子，这就是投影现象。
（5）平行投影：太阳光线可以看成是平行光线，像这样的光线所形成的投影称为平行投影。
（6）中心投影：由一点发出的光线形成的投影是中心投影。
（7）视点：眼睛的位置称为视点。
（8）视线：由视点出发的线称为视线。
（9）盲区：视线看不到的地方称为盲区。
2. 主要原理：（1）画视图时，看得见的部分的轮廓通常画成实线，看不见部分的轮廓线通常画成虚线。
（2）我们在画三视图时，主、左视图的高要相等；俯、左视图的宽要相等。
（3）在同一时刻，不同物体的影子与它们的高度是成比例的。
（4）在同一天中，由早晨到傍晚，物体的影子由正西、北偏西、正北、北偏东、正东的方向移动。
（5）当投影光线与投影面垂直时，形成的投影就是物体的正投影。
【典型例题】例1. 如图，画出正三棱柱在这两种位置时的视图。
位置（一）位置（二）解：图中正三棱柱在位置（一）时的三视图如下图所示。
主视图左视图俯视图图中正三棱柱在位置（二）时的三视图如下图所示：主视图左视图俯视图例2. 如图所示，画出下列物体的三视图。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
初中-数学-打印版
如何运用视点、视角和盲区的关系解决问题？
难易度：★★★★
关键词：投影-视点、视角和盲区
答案：
眼睛的位置称为视点；由视点发出的线称为视角；看不到的地方称为盲区。
【举一反三】
典题：人离窗子越远，向外眺望时此人的盲区是（）
A、变小
B、变大
C、不变
D、以上都有可能
思路导引：本题是结合实际问题来考查学生对视点，视角和盲区的理解能力．根据视角与盲区的关系来判断
标准答案：
解：通过想象我们可以知道，离窗子越远，视角就会越小，盲区就会变大．故选B．
初中-数学-打印版。