高一指数与指数函数练习题

高一数学指数与指数函数试题答案及解析1.设函数（x）＝，则满足的的取值范围是（）．A．[－1,2]B．[0,2]C．[1，＋∞）D．[0，＋∞）【答案】D．【解析】当时，，，解得，因此，当时，，解得，因此，综上【考点】分段函数的应用．2.设函数则使得成立的的取值范围是（）A．B．C．D．【答案】C【解析】当时，由，可得，即；当时，由，可得，即，综上.故选C【考点】函数的求值.3.已知定义在R上的函数满足，当时，，且.（1）求的值；（2）当时，关于的方程有解，求的取值范围.【答案】（1），（2）【解析】（1）由可知，代入表达式可求得的值.又，可求出的值；（2）由（1）可知方程为，对x进行讨论去绝对值符号，可得，据结合指数函数，二次函数的性质可求得的取值范围.试题解析：解：（1）由已知，可得又由可知 . 5分（2）方程即为在有解.当时，，令,则在单增，当时，，令,则，,综上： . 14分【考点】本题主要考查指数函数，二次函数求值域和分类讨论的数学思想方法.4.函数的图象必经过定点___________．【答案】【解析】∵指数函数过定点，∴函数过定点．【考点】函数图象．5.已知，，且，则与的大小关系_______.【答案】【解析】由，又由，所以，所以由可得，所以，，所以即.【考点】1.分数指数幂的运算；2.对数的运算；3.指数函数的单调性.6.函数在上的最大值比最小值大，则 .【答案】【解析】因为，根据指数函数的性质可知在单调递增，所以最大值为，最小值为，依题意有即，而，所以.【考点】指数函数的图像与性质.7.设，则的大小关系是（）A．B．C．D．【答案】B【解析】把看成函数当时的函数值,因为,所以；把看成函数当时的函数值,因为,所以；把看成函数当时的函数值,因为 ,所以 .综上, ,故选B【考点】1、指数函数的性质；2、对数函数的性质.8.若，则__________．【答案】【解析】【考点】指数函数的运算法则9.已知，则的大小关系是．【答案】【解析】因为指数函数在R上单调递减，所以。

第二章函数2.4.2 指数函数（针对练习）针对练习针对练习一指数与指数幂的运算1．用分数指数幂的形式表示下列各式(a>0，b>0)．(1)a222．计算或化简下列各式：（1）(a－2)·(－4a－1)÷(12a－4)(a>0)；（2）213-233+0.0028-⎛⎫- ⎪⎝⎭－2)－1＋0. 3．计算：(1)1111242 114310.7562)164300---⎫⎛⎫⎛⎫⨯⨯+-++⎪ ⎪⎝⎭⎝⎭⎝⎭111133420,0)a ba b a b->>⎛⎫⎪⎝⎭4．计算：(1)10132114(2)924---⎛⎫⎛⎫-⨯-+-⎪ ⎪⎝⎭⎝⎭；(2)2932)-⨯5．(1)()2163278()[2]8---；(2)()())1213321()0040.1a b a b ---＞，＞.针对练习二 指数函数的概念6．在①4x y =；①4y x =；①4x y =-；①()4xy =-；①()121,12xy a a a ⎛⎫=->≠ ⎪⎝⎭中，y 是关于x 的指数函数的个数是（ ） A ．1 B ．2 C ．3 D ．47．下列函数是指数函数的是（ ）A ．y ＝()2x πB ．y ＝(－9)xC ．y ＝2x －1D ．y ＝2×5x8．下列函数中为指数函数的是（ ） A ．23x y =⋅ B ．3x y =-C ．3x y -=D ．1x y =9．函数()244xy a a a =-+是指数函数，则有（ ）A ．a ＝1或a ＝3B ．a ＝1C ．a ＝3D ．a ＞0且a ≠110．若函数()x f x a =（a >0，且a ≠1）的图象经过(12,)3，则(1)f -=（ ） A．1 B ．2C D ．3针对练习三 指数函数的图像11．函数2x y -=的图象大致是（ ）A ．B ．C ．D ．12．函数①x y a =；①x y b =；①x y c =；①x y d =的图象如图所示，a ，b ，c ，d 分别是下列四个数：5413，12中的一个，则a ，b ，c ，d 的值分别是（ ）A ．5413，12 B 54，12，13C ．12，1354D ．13，12，5413．若0a >且1a ≠，则函数()11x f x a -=+的图象一定过点（ ）A ．()0,2B ．()0,1-C ．()1,2D ．()1,1-14．已知函数f （x ）= ax +1的图象恒过定点P ，则P 点的坐标为（ ） A ．(0，1) B ．(0，2) C ．(1，2)D ．()1,1a +15．对任意实数01a <<，函数()11x f x a -=+的图象必过定点（ ）A ．()0,2B ．()1,2C ．()0,1D ．()1,1针对练习四 指数函数的定义域16．函数y ） A ．(,3]-∞ B ．[3,)+∞ C ．(,2]-∞ D ．[2,)+∞17．函数()22f x x -的定义域为（ ） A ．[0,2) B ．(2,)+∞C ．()(),22,-∞+∞D ．[0,2)(2,)⋃+∞18．设函数f （x ），则函数f （x 4）的定义域为（ ） A ．(],4∞- B ．1,4∞⎛⎤- ⎥⎝⎦C ．(]0,4D ．10,4⎛⎤⎥⎝⎦19．已知函数()y f x =的定义域为()0,1，则函数()()21xF x f =-的定义域为（ ）A ．(),1-∞B ．()(),00,1-∞⋃C ．()0,∞+D ．[)0,120．函数y (－∞，0]，则a 的取值范围为( ) A ．a ＞0 B ．a ＜1 C ．0＜a ＜1 D ．a ≠1针对练习五 指数函数的值域21．函数2212x xy -⎛⎫= ⎪⎝⎭的值域为（ ） A ．1,2⎡⎫+∞⎪⎢⎣⎭B ．1,2⎛⎤-∞ ⎥⎝⎦C ．10,2⎛⎤⎥⎝⎦D ．(]0,222．若23x ，则函数1()421x x f x +=-+的最小值为（ ） A ．4 B ．0 C ．5 D ．923．函数2121x x y -=+的值域是（ ）A ．()(),11,-∞--+∞B ．(),1-∞-C ．()1,1-D ．()(),11,-∞+∞24．已知函数()()1123,12,1x a x a x f x x -⎧-+<=⎨≥⎩的值域为R ，则实数a 的取值范围是（ ）A ．10,2⎡⎫⎪⎢⎣⎭B ．1,2⎛⎫-∞ ⎪⎝⎭C ．(),0-∞D ．[)0,225．函数2x y a =-（0a >且1a ≠，11x -≤≤）的值域是5,13⎡⎤-⎢⎥⎣⎦，则实数=a （ ）A ．3B ．13C ．3或13D ．23或32针对练习六 指数函数的单调性26．函数2435x x y -+-=的单调递减区间是（ ） A ．[2,)+∞ B ．(,2]-∞ C ．(,1]-∞ D ．[1,)+∞27．函数223112x x y -+⎛⎫= ⎪⎝⎭的单调递减区间为（ ） A ．(1,)+∞ B ．3,4⎛⎤-∞ ⎥⎝C ．(),1-∞D ．3,4⎡⎫+∞⎪⎢⎣⎭28．若函数()215x axf x +⎛⎫= ⎪⎝⎭在[]1,2单调递减，则a 的取值范围（ ）A ．4a ≤-B ．2a ≤-C ．2a ≥-D ．4a ≥-29．若函数()(),1,513,13x a x f x a x x ⎧≥⎪=⎨-+<⎪⎩在R 上单调递减，则实数a 的取值范围是（ ） A ．12,33⎛⎤⎥⎝⎦B ．1,2C ．11,32⎡⎫⎪⎢⎣⎭D ．20,3⎛⎫⎪⎝⎭30．已知函数()()4211xa x x f x a x ⎧-≤=⎨>⎩，，是R 上的单调函数，那么实数a 的取值范围为（ ）A ．()01，B ．()13，C ．423⎡⎫⎪⎢⎣⎭，D ．312⎛⎤ ⎥⎝⎦，针对练习七 比较大小与解不等式31．已知412a ⎛⎫= ⎪⎝⎭，124b =，122c =，则a ，b ，c 的大小关系是（ ） A ．a b c << B ．c b a << C ．a c b << D ．b a c <<32．已知1313422,3,4a b c ===，则a ，b ，c 的大小关系为（ ） A ．a <b <c B ．c <a <b C ．a <c <b D ．c <b <a33．若2141122a a+-⎛⎫⎛⎫> ⎪⎪⎝⎭⎝⎭，则实数a 的取值范围是（ ） A ．(,1)-∞ B ．(1,)+∞C ．(3,)+∞D ．(3),-∞34．若x 满足不等式221139x x -+⎛⎫ ⎪⎝⎭，则函数2x y =的值域是（ ）A ．1,28⎡⎫⎪⎢⎣⎭B ．1,28⎡⎤⎢⎥⎣⎦C ．1,8⎛⎤-∞ ⎥⎝⎦D ．[2,)+∞35．若1133ab⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭，则下列正确的是（ ）A ．33a b <B ．ac bc >C ．11a b<D ．b c a c -<-针对练习八 指数函数的应用36．专家对某地区新型流感爆发趋势进行研究发现，从确诊第一名患者开始累计时间t （单位：天）与病情爆发系数()f t 之间，满足函数模型：0.22(340)1()1t f t e --=+，当()0.1f t =时，标志着疫情将要局部爆发，则此时t 约为（参考数据： 1.13e ≈）（ ）A ．10B ．20C ．30D ．4037．基本再生数0R 与世代间隔T 是流行病学基本参数，基本再生数是指一个感染者传染的平均人数，世代间隔指两代间传染所需的平均时间，在α型病毒疫情初始阶段，可以用指数函数模型(e )rt I t =描述累计感染病例数()I t 随时间t （单位：天）的变化规律，指数增长率r 与0R 、T 近似满足01R rT =+，有学者基于已有数据估计出0 3.22R =，10T =.据此，在α型病毒疫情初始阶段，累计感染病例数增加至(0)I 的4倍，至少需要（ ）（参考数据：ln 20.69≈） A ．6天 B ．7天 C ．8天 D ．9天38．某灭活疫苗的有效保存时间T （单位：小时h ）与储藏的温度t （单位：①）满足的函数关系为e ht b T +=（k ，b 为常数，其中e 2.71828=⋅⋅⋅，是一个和π类似的无理数，叫自然对数的底数），超过有效保存时间，疫苗将不能使用.若在0①时的有效保存时间是1080h ，在10①时的有效保存时间是120h ，则该疫苗在15①时的有效保存时间为（ ） A ．15h B ．30h C ．40h D ．60h39．某食品的保鲜时间y （单位：小时）与储藏温度x （单位：C ︒）满足函数关系e kx b y +=（e 2.718=为自然对数的底数，,k b 为常数）．若该食品在0C ︒的保鲜时间是192小时，在33C ︒的保鲜时间是24小时，则该食品在22C ︒的保鲜时间是（ ） A ．20 小时 B ．24小时 C ．36小时 D ．48小时40．牛顿曾经提出了常温环境下的温度冷却模型：()100e ktθθθθ-=-+，其中为时间（单位：min ），0θ为环境温度，1θ为物体初始温度，θ为冷却后温度），假设在室内温度为20C 的情况下，一桶咖啡由100C 降低到60C 需要20min .则k 的值为（ ） A ．ln 220B ．ln 320C ．ln 210-D ．ln 310-第二章 函数2.4.2 指数函数（针对练习）针对练习针对练习一 指数与指数幂的运算1．用分数指数幂的形式表示下列各式(a >0，b >0)．(1)a2 2．【答案】(1)52a ； (2)136a ； (3)7362a b ； (4)76a . 【解析】 【分析】由根式与有理数指数幂的关系，结合指数幂的运算性质化简求值即可. (1)原式＝11522222a a a a +⋅==. (2)原式＝22313333262a a a a +⋅==． (3)原式＝1221711333233332622222()()a ab a a b a b a b +⋅===.(4)原式＝55722666a a a a --⋅==． 2．计算或化简下列各式： （1）(a －2)·(－4a －1)÷(12a －4)(a >0)；（2）213-233+0.0028-⎛⎫- ⎪⎝⎭－2)－1＋0.【答案】（1）－13a ；（2）－1679.【解析】 【分析】直接根据指数幂的运算性质计算即可. 【详解】(1)原式21434114(12)33a a a a ----+=-÷=-=-(2)原式213227118500--⎛⎫⎛⎫=-+ ⎪ ⎪⎝⎭⎝⎭213323()5002)12-⎡⎤=-+-+⎢⎥⎣⎦＝49＋20＋1＝－ 1679. 3．计算：(1)1111242114310.7562)164300---⎫⎛⎫⎛⎫⨯⨯+++ ⎪ ⎪⎝⎭⎝⎭⎝⎭111133420,0)a b a b a b ->>⎛⎫ ⎪⎝⎭【答案】(1)-16 (2)(0,0)a a b b>> 【解析】 【分析】（1）根据分数指数幂的运算规则化简计算即可； （2）根据分数指数幂的运算规则化简得出结果. (1)原式=111222411010233-⎫⎫⎛⎫⨯⨯++⨯+ ⎪⎝⎭⎝⎭⎝⎭(12410223⎫=⨯-⨯+⎝⎭220216=-+=-(2)原式543311233(0,0)a baa b bab a b-==>> 4．计算：(1)1132114(2)924---⎛⎫⎛⎫-⨯-+- ⎪ ⎪⎝⎭⎝⎭；(2)2932)-⨯【答案】(1)196(2)【解析】 【分析】（1）利用指数幂的运算性质即可求解.（2）利用根式与分数指数幂的互化以及指数幂的运算性质即可求解. (1)原式1111924()1218236=-⨯-+=++-=. (2)原式24119555636333222221[(8)](10)10(2)1010102---=⨯÷=⨯÷=⨯721102=⨯=== 5．(1)()21603278()[2]8---；(2)()())1213321()0040.1a b a b ---＞，＞.【答案】(1)8π+；(2)85. 【解析】 【分析】(1)(2)均根据指数幂的运算性质即可计算； 【详解】(1)原式233(2)=-1＋|3﹣π|162(2)+=4﹣1＋π﹣3＋23＝π＋8.(2)原式3332223322248510a b a b--⋅==.针对练习二 指数函数的概念6．在①4x y =；①4y x =；①4x y =-；①()4xy =-；①()121,12xy a a a ⎛⎫=->≠ ⎪⎝⎭中，y 是关于x 的指数函数的个数是（ ） A ．1 B ．2 C ．3 D ．4【答案】B 【解析】 【分析】直接根据指数函数的定义依次判断即可. 【详解】根据指数函数的定义，知①①中的函数是指数函数， ①中底数不是常数，指数不是自变量，所以不是指数函数； ①中4x 的系数是1-，所以不是指数函数； ①中底数40-<，所以不是指数函数． 故选：B ．7．下列函数是指数函数的是（ ）A ．y ＝()2x πB ．y ＝(－9)xC ．y ＝2x －1D ．y ＝2×5x【答案】A 【解析】 【分析】根据指数函数定义判断． 【详解】B 中底数90-<，C 中指数是1x -，不是x ，D 中5x 前面系数不是1，根据指数函数定义，只有A 中函数是指数函数， 故选：A.8．下列函数中为指数函数的是（ ）A ．23x y =⋅B ．3x y =-C ．3x y -=D ．1x y =【答案】C 【解析】 【分析】根据指数函数的定义，逐项判定，即可求解. 【详解】根据指数函数的定义知，()0,1xy a a a =>≠，可得函数23x y =⋅不是指数函数；函数3x y =-不是指数函数；函数3x y -=是指数函数；函数1x y =不是指数函数. 故选：C.9．函数()244xy a a a =-+是指数函数，则有（ ）A ．a ＝1或a ＝3B ．a ＝1C ．a ＝3D ．a ＞0且a ≠1【答案】C 【解析】 【分析】根据已知条件列不等式，由此求得正确选项. 【详解】由已知得244101a a a a ⎧-+=⎪>⎨⎪≠⎩，即2301a a a a ⎧+=⎪⎨⎪≠⎩，解得3a =．故选：C10．若函数()x f x a =（a >0，且a ≠1）的图象经过(12,)3，则(1)f -=（ ） A ．1 B ．2 CD ．3【答案】C 【解析】 【分析】由指数函数所过的点求解析式，进而求(1)f -的值. 【详解】由题意，21(2)3f a ==，又a >0，则a =①()x f x =，故1(1)f --== 故选：C针对练习三 指数函数的图像11．函数2x y -=的图象大致是（ ）A ．B ．C ．D ．【答案】D 【解析】 【分析】根据函数的解析式可得函数2x y -=是以12为底数的指数函数，再根据指数函数的图像即可得出答案. 【详解】解：由122xxy -⎛⎫== ⎪⎝⎭，得函数2x y -=是以12为底数的指数函数，且函数为减函数，故D 选项符合题意. 故选：D.12．函数①x y a =；①x y b =；①x y c =；①x y d =的图象如图所示，a ，b ，c ，d 分别是下列四个数：5413，12中的一个，则a ，b ，c ，d 的值分别是（ ）A ．5413，12 B 54，12，13C ．12，1354D ．13，12，54【答案】C 【解析】 【分析】由直线1x =与函数图象的交点的纵坐标从上到下依次为c ，d ，a ，b 即可求解. 【详解】解：直线1x =与函数图象的交点的纵坐标从上到下依次为c ，d ，a ，b ，511423>>， 所以a ，b ，c ，d 的值分别是12，1354， 故选：C.13．若0a >且1a ≠，则函数()11x f x a -=+的图象一定过点（ ）A ．()0,2B ．()0,1-C ．()1,2D ．()1,1-【答案】C 【解析】 【分析】令10x -=求出定点的横坐标，即得解. 【详解】解：令10,1-=∴=x x .当1x =时，()1111=2f a -=+，所以函数()f x 的图象过点()1,2. 故选：C.14．已知函数f （x ）= ax +1的图象恒过定点P ，则P 点的坐标为（ ） A ．(0，1) B ．(0，2) C ．(1，2)D ．()1,1a +【答案】B 【解析】 【分析】由指数函数过定点的性质进行求解. 【详解】()x f x a =的图象恒过定点()0,1，所以()1x f x a =+的图象恒过定点()0,2故选：B15．对任意实数01a <<，函数()11x f x a -=+的图象必过定点（ ）A ．()0,2B ．()1,2C ．()0,1D ．()1,1【答案】B 【解析】 【分析】根据指数函数的知识确定正确选项. 【详解】当10x -=，即1x =时，()12f =， 所以()f x 过定点()1,2. 故选：B针对练习四 指数函数的定义域16．函数y ） A ．(,3]-∞ B ．[3,)+∞C ．(,2]-∞D ．[2,)+∞【答案】D 【解析】 【分析】根据函数的定义域定义求解即可. 【详解】要使得函数y 则390x -≥，39x ≥，233x ≥，解得2x ≥.故函数y [2,)+∞. 故选：D.17．函数()22f x x -的定义域为（ ） A ．[0,2) B ．(2,)+∞C ．()(),22,-∞+∞D ．[0,2)(2,)⋃+∞【答案】D 【解析】求出使函数式有意义的自变量的范围即得、 【详解】由21020x x ⎧-≥⎨-≠⎩得02x x ≥⎧⎨≠⎩，即[0,2)(2,)x ∈⋃+∞.故选：D.18．设函数f （x ），则函数f （x 4）的定义域为（ ） A ．(],4∞- B ．1,4∞⎛⎤- ⎥⎝⎦C ．(]0,4D ．10,4⎛⎤⎥⎝⎦【答案】A 【解析】 【分析】求得4x f ⎛⎫= ⎪⎝⎭0，结合指数函数的性质求解即可． 【详解】因为()f x =所以4x f ⎛⎫= ⎪⎝⎭因为44440,44,1,44x x x x -≥≤≤≤，所以4xf ⎛⎫⎪⎝⎭的定义域为(],4-∞，故选A ．【点睛】本题主要考查函数的定义域以及指数函数的单调性的应用，是基础题．定义域的三种类型及求法：(1)已知函数的解析式，则构造使解析式有意义的不等式(组)求解；(2) 对实际问题：由实际意义及使解析式有意义构成的不等式(组)求解；(3) 若已知函数()f x 的定义域为[],a b ，则函数()()f g x 的定义域由不等式()a g x b ≤≤求出.19．已知函数()y f x =的定义域为()0,1，则函数()()21xF x f =-的定义域为（ ）A ．(),1-∞B ．()(),00,1-∞⋃C ．()0,∞+D ．[)0,1【答案】B 【解析】 【分析】抽象函数的定义域求解，要注意两点，一是定义域是x 的取值范围；二是同一对应法则下，取值范围一致. 【详解】()y f x =的定义域为()0,1，1021x-∴<<，即121121x x ⎧-<-<⎨≠⎩，10x x <⎧∴⎨≠⎩，解得：1x <且0x ≠， ()()21x F x f ∴=-的定义域为()(),00,1-∞⋃.故选：B .20．函数y (－∞，0]，则a 的取值范围为( ) A ．a ＞0 B ．a ＜1 C ．0＜a ＜1 D ．a ≠1【答案】C 【解析】 【分析】由题意可得10x a -≥，对a 讨论，分1,01a a ><<,运用指数函数的单调性，列不等式即可得到a 的范围. 【详解】要使函数0y a >且1)a ≠有意义, 则10x a -≥, 即01x a a ≥=, 当1a >时，0x ≥；当01a <<时，0x ≤，因为y =的定义域为(],0-∞ 所以可得01a <<符合题意，a ∴的取值范围为01a <<，故选C.【点睛】本题考查函数的定义域以及指数函数的单调性，注意运用偶次根式被开方式非负，意在考查分类讨论思想与运算能力，属于中档题.针对练习五 指数函数的值域21．函数2212x xy -⎛⎫= ⎪⎝⎭的值域为（ ） A ．1,2⎡⎫+∞⎪⎢⎣⎭B ．1,2⎛⎤-∞ ⎥⎝⎦C ．10,2⎛⎤⎥⎝⎦D ．(]0,2【答案】D 【解析】 【分析】令22t x x =-，则12ty ⎛⎫= ⎪⎝⎭，转求二次函数与指数函数的值域即可.【详解】令22t x x =-，则12ty ⎛⎫= ⎪⎝⎭，①()222111t x x x =-=--≥-，①(],2120ty ⎛⎫⎪⎭∈= ⎝，①函数2212x xy -⎛⎫= ⎪⎝⎭的值域为(]0,2，故选：D22．若23x ，则函数1()421x x f x +=-+的最小值为（ ） A ．4 B ．0C ．5D ．9【答案】A 【解析】 【分析】设23x t =，则2()21=-+f t t t 利用函数()f t 单调性可得答案. 【详解】设23x t =，则()22()211=-+=-f t t t t （3t ）， 对称轴为1t =，所以()f t 在[)3,+∞上单调递增，所以2min ()(3)32314f t f ==-⨯+=.故选：A.23．函数2121x x y -=+的值域是（ ）A ．()(),11,-∞--+∞B ．(),1-∞-C ．()1,1-D ．()(),11,-∞+∞【答案】C 【解析】 【分析】将函数化为121xyy+=-，利用20x >列出关于y 的不等式，解出不等式即可. 【详解】设2121x x y -=+，由原式得121xy y +=-，20x >, 101yy+∴>-， ①11y -<<，即函数()f x 的值域为(1,1)-. 故选：C24．已知函数()()1123,12,1x a x a x f x x -⎧-+<=⎨≥⎩的值域为R ，则实数a 的取值范围是（ ） A ．10,2⎡⎫⎪⎢⎣⎭B ．1,2⎛⎫-∞ ⎪⎝⎭C ．(),0-∞D ．[)0,2【答案】A 【解析】 【分析】先求出12x y -=在[)1,+∞上的取值范围，再利用分段函数的值域进行求解．【详解】因为12x y -=在[)1,+∞上单调递增， 所以当1≥x 时，1022=1x y -=≥， 若函数()f x 的值域为R ，则1201231a a a ->⎧⎨-+≥⎩， 解得102a ≤<． 故选：A.25．函数2x y a =-（0a >且1a ≠，11x -≤≤）的值域是5,13⎡⎤-⎢⎥⎣⎦，则实数=a （ ）A ．3B ．13C ．3或13D ．23或32【答案】C 【解析】当0a >且1a ≠时，函数为指数型函数，需要分情况进行讨论解决．当1a >时，函数2x y a =-是增函数；当01a <<时，函数2x y a =-是减函数，由此结合条件建立关于a的方程组，解之即可求得答案． 【详解】当1a >时，2xy a =-在[]1,1-上为增函数， 211523a a-=⎧⎪∴⎨-=-⎪⎩，解得3a =；当01a <<时，2xy a =-在[]1,1-上为减函数，523121a a⎧-=-⎪⎪∴⎨⎪-=⎪⎩，解得13a =．综上可知：3a =或13． 故选：C 【点睛】关键点点睛：本题主要考查了指数函数的单调性和值域，解题的关键是利用函数的单调性求解函数值域，但含有参数时往往需要讨论.针对练习六 指数函数的单调性26．函数2435x x y -+-=的单调递减区间是（ ） A ．[2,)+∞ B ．(,2]-∞ C ．(,1]-∞ D ．[1,)+∞【答案】A 【解析】 【分析】利用复合函数的单调性“同增异减”来解题. 【详解】设243x x μ=-+-，在(,2]-∞单调递增，在[2,)+∞单调递减，5y μ=在(,)-∞+∞单调递增，根据“同增异减”可得，函数2435x x y -+-=的单调递减区间是[2,)+∞. 故选：A.27．函数223112x x y -+⎛⎫= ⎪⎝⎭的单调递减区间为（ ） A ．(1,)+∞ B ．3,4⎛⎤-∞ ⎥⎝⎦C ．(),1-∞D ．3,4⎡⎫+∞⎪⎢⎣⎭【答案】D 【解析】 【分析】根据复合函数单调性法则“同增异减”求解即可. 【详解】解：因为函数2231y x x =-+在区间3,4⎛⎫-∞ ⎪⎝⎭上单调递减，在3,4⎡⎫+∞⎪⎢⎣⎭上单调递增，函数12xy ⎛⎫= ⎪⎝⎭在定义域内是单调递减函数，所以，根据复合函数单调性法则“同增异减”得223112x x y -+⎛⎫= ⎪⎝⎭的单调递减区间为3,4⎡⎫+∞⎪⎢⎣⎭. 故选：D28．若函数()215x axf x +⎛⎫= ⎪⎝⎭在[]1,2单调递减，则a 的取值范围（ ）A ．4a ≤-B ．2a ≤-C ．2a ≥-D ．4a ≥-【答案】C 【解析】 【分析】根据复合函数单调性来求得a 的取值范围. 【详解】依题意函数()215x axf x +⎛⎫= ⎪⎝⎭在[]1,2单调递减，15xy =在R 上递减， 2y x ax =+的开口向上，对称轴为2ax =-，根据复合函数单调性同增异减可知，122a a -≤⇒≥-. 故选：C29．若函数()(),1,513,13x a x f x a x x ⎧≥⎪=⎨-+<⎪⎩在R 上单调递减，则实数a 的取值范围是（ ） A ．12,33⎛⎤⎥⎝⎦B ．1,2C ．11,32⎡⎫⎪⎢⎣⎭D ．20,3⎛⎫⎪⎝⎭【答案】A 【解析】 【分析】根据分段函数的性质，以及函数()f x 在R 上单调递减，结合指数函数的性质，可知011305133a a a a⎧⎪<<⎪-<⎨⎪⎪-+≥⎩，求解不等式，即可得到结果. 【详解】①函数()f x 在R 上单调递减，①011305133a a a a⎧⎪<<⎪-<⎨⎪⎪-+≥⎩，解得1233a <≤，实数a 的取值范围是12,33⎛⎤⎥⎝⎦. 故选：A.30．已知函数()()4211xa x x f x a x ⎧-≤=⎨>⎩，，是R 上的单调函数，那么实数a 的取值范围为（ ）A ．()01，B ．()13，C ．423⎡⎫⎪⎢⎣⎭，D ．312⎛⎤ ⎥⎝⎦，【答案】C 【解析】 【分析】根据()f x 的单调性列不等式组，由此求得a 的取值范围. 【详解】 函数()()4211xa x x f x a x ⎧-≤=⎨>⎩，，，若()f x 在R 上为单调递增函数，则()14201421a a a a ⎧->⎪>⎨⎪-⨯≤⎩，解得423a ≤<；若()f x 在R 上为单调递减函数，则()142001421a a a a ⎧-<⎪<<⎨⎪-⨯≥⎩，无解． 综上所述，实数a 的取值范围为423⎡⎫⎪⎢⎣⎭，． 故选：C针对练习七 比较大小与解不等式31．已知412a ⎛⎫= ⎪⎝⎭，124b =，122c =，则a ，b ，c 的大小关系是（ ） A ．a b c << B ．c b a << C ．a c b << D ．b a c <<【答案】C 【解析】 【分析】根据指数函数的单调性判断指数式的大小关系. 【详解】由题设，42a -=，2b =，122c =，又2x y =在定义域上递增， ①a c b <<. 故选：C.32．已知1313422,3,4a b c ===，则a ，b ，c 的大小关系为（ ） A ．a <b <c B ．c <a <b C ．a <c <b D ．c <b <a【答案】B 【解析】 【分析】结合指数函数、幂函数的单调性确定正确选项. 【详解】4x y =在R 上递增，14y x =在()0,∞+上递增.123111334442422893c a b ==<==<==.故选：B33．若2141122a a+-⎛⎫⎛⎫> ⎪⎪⎝⎭⎝⎭，则实数a 的取值范围是（ ） A ．(,1)-∞ B ．(1,)+∞C ．(3,)+∞D ．(3),-∞【答案】A 【解析】 【分析】根据指数函数的单调性，将函数不等式转化为自变量的不等式，解得即可； 【详解】解：因为12xy ⎛⎫= ⎪⎝⎭在定义域上单调递减，所以2141122a a+-⎛⎫⎛⎫> ⎪⎪⎝⎭⎝⎭等价于214a a +<-，解得1a <，即原不等式的解集为(,1)-∞ 故选：A34．若x 满足不等式221139x x -+⎛⎫ ⎪⎝⎭，则函数2x y =的值域是（ ）A ．1,28⎡⎫⎪⎢⎣⎭B ．1,28⎡⎤⎢⎥⎣⎦C ．1,8⎛⎤-∞ ⎥⎝⎦D ．[2,)+∞【答案】B 【解析】【分析】利用指数函数的单调性得到自变量的范围，进而得到指数函数的值域. 【详解】 由221139x x -+⎛⎫ ⎪⎝⎭可得2212(2)1339x x x -+--⎛⎫= ⎪⎝⎭，因为3x y =在R 上单调递增， 所以2124x x +-+即x 2+2x -3≤0， 解得：31x -≤≤ ， 所以31222x y -=，即函数2x y =的值域是1,28⎡⎤⎢⎥⎣⎦，故选:B .35．若1133ab⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭，则下列正确的是（ ）A ．33a b <B ．ac bc >C ．11a b<D ．b c a c -<-【答案】D 【解析】 【分析】先根据题干条件和函数13xy ⎛⎫= ⎪⎝⎭的单调性得到a b >，A 选项可以利用函数的单调性进行判断，BC 选项可以举出反例，D 选项用不等式的基本性质进行判断. 【详解】因为13xy ⎛⎫= ⎪⎝⎭在R 上单调递减，若1133a b⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭，则a b >，对于选项A ：若a b >，因为()3f x x =单调递增，所以33a b >，故A 错误；对于选项B ：当a b >时，若0c ，则ac bc =，故B 错误；对于选项C ：由a b >，不妨令1a =，2b =-，则此时11ab>，故C 错误； 对于选项D ：由不等式性质，可知D 正确. 故选：D.针对练习八 指数函数的应用36．专家对某地区新型流感爆发趋势进行研究发现，从确诊第一名患者开始累计时间t （单位：天）与病情爆发系数()f t 之间，满足函数模型：0.22(340)1()1t f t e--=+，当()0.1f t =时，标志着疫情将要局部爆发，则此时t 约为（参考数据： 1.13e ≈）（ ）A ．10B ．20C ．30D ．40【答案】A 【解析】 【分析】根据()0.1f t =列式，并根据给出参考数据，结合指数函数的性质解相应的指数方程，即可得答案. 【详解】解：因为()0.1f t =，0.22(340)1()1t f t e--=+，所以0.22(340)10.11t e--=+，即0.22(340)011t e --=+，所以0.22(340)9t e --=，由于 1.13e ≈，故()21.12.29e e =≈， 所以0.22(23).240t e e --≈，所以()0.22340 2.2t --≈，解得10t ≈. 故选：A.37．基本再生数0R 与世代间隔T 是流行病学基本参数，基本再生数是指一个感染者传染的平均人数，世代间隔指两代间传染所需的平均时间，在α型病毒疫情初始阶段，可以用指数函数模型(e )rt I t =描述累计感染病例数()I t 随时间t （单位：天）的变化规律，指数增长率r 与0R 、T 近似满足01R rT =+，有学者基于已有数据估计出0 3.22R =，10T =.据此，在α型病毒疫情初始阶段，累计感染病例数增加至(0)I 的4倍，至少需要（ ）（参考数据：ln 20.69≈） A ．6天 B ．7天 C ．8天 D ．9天【答案】B 【解析】 【分析】根据题意将给出的数据代入公式即可计算出结果 【详解】因为0 3.22R =，10T =，01R rT =+，所以可以得到01 3.2210.22210R r T --===0.2220(0)1I e ⨯==，由题意可知0.2224t e >，ln 42ln 220.696.20.2220.2220.222t ⨯>=≈≈ 所以至少需要7天，累计感染病例数增加至(0)I 的4倍 故选：B38．某灭活疫苗的有效保存时间T （单位：小时h ）与储藏的温度t （单位：①）满足的函数关系为e ht b T +=（k ，b 为常数，其中e 2.71828=⋅⋅⋅，是一个和π类似的无理数，叫自然对数的底数），超过有效保存时间，疫苗将不能使用.若在0①时的有效保存时间是1080h ，在10①时的有效保存时间是120h ，则该疫苗在15①时的有效保存时间为（ ） A ．15h B ．30h C ．40h D ．60h【答案】C 【解析】 【分析】根据已知的函数模型以及已知数据，待定系数即可求得结果. 【详解】由题意知1080e b =，1010120e e e k b k b +==⋅，所以()21051201ee 10809kk===， 所以51e 3k =，所以151e 27k =，所以15151ee e 10804027k bk b +=⋅=⨯=. 故选：C ．39．某食品的保鲜时间y （单位：小时）与储藏温度x （单位：C ︒）满足函数关系e kx b y +=（e 2.718=为自然对数的底数，,k b 为常数）．若该食品在0C ︒的保鲜时间是192小时，在33C ︒的保鲜时间是24小时，则该食品在22C ︒的保鲜时间是（ ） A ．20 小时 B ．24小时 C ．36小时 D ．48小时【答案】D 【解析】 【分析】根据题意建立方程组，进而解出11e ,e b k ，然后将22代入即可求得答案. 【详解】由题意，331133e 1922411e e 19282e24b k k k b+⎧=⇒==⇒=⎨=⎩，所以该食品在22C ︒的保鲜时间是2222e e e 1192484k b k b +=⋅=⨯=.故选：D.40．牛顿曾经提出了常温环境下的温度冷却模型：()100e ktθθθθ-=-+，其中为时间（单位：min ），0θ为环境温度，1θ为物体初始温度，θ为冷却后温度），假设在室内温度为20C 的情况下，一桶咖啡由100C 降低到60C 需要20min .则k 的值为（ ） A ．ln 220B ．ln 320C ．ln 210-D ．ln 310-【答案】A 【解析】 【分析】把020θ=，1100θ=，60θ=，20t =代入()100e ktθθθθ-=-+可求得实数k 的值.【详解】由题意，把020θ=，1100θ=，60θ=，20t =代入()100e ktθθθθ-=-+中得2080e 2060k -+=，可得201e2k-=， 所以，20ln 2k -=-，因此，ln 220k =. 故选：A.。

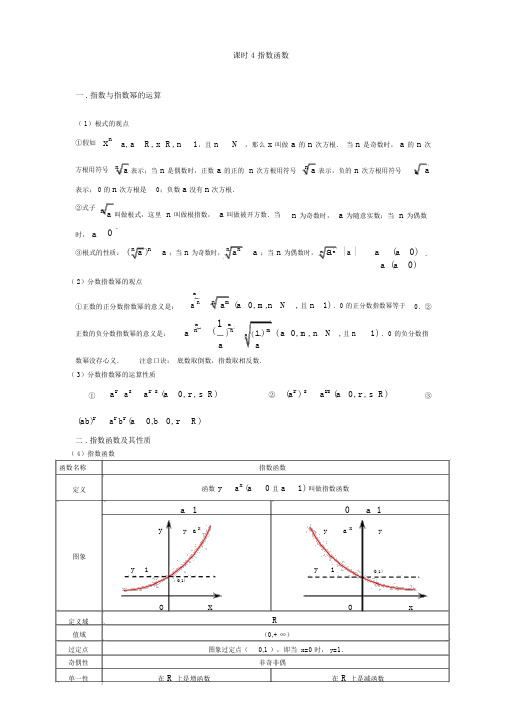
课时 4 指数函数一 . 指数与指数幂的运算（ 1）根式的观点①假如xna, a R, x R, n 1，且 nN ，那么 x 叫做 a 的 n 次方根． 当 n 是奇数时， a 的 n 次方根用符号 na 表示；当 n 是偶数时，正数 a 的正的 n 次方根用符号na 表示，负的 n 次方根用符号na表示； 0 的 n 次方根是 0；负数 a 没有 n 次方根．②式子 n a 叫做根式，这里 n 叫做根指数， a 叫做被开方数．当n 为奇数时， a 为随意实数；当 n 为偶数时， a．③根式的性质： (na )n a ；当 n 为奇数时， n a n a ；当 n 为偶数时， n a n | a |a (a 0) ．a (a 0)（ 2）分数指数幂的观点mna m (a①正数的正分数指数幂的意义是：a n 0, m,n N , 且 n 1) ．0 的正分数指数幂等于0．②m(1m1 ) m( a正数的负分数指数幂的意义是：a n)n n (0, m, n N , 且 n1) ．0 的负分数指aa数幂没存心义． 注意口诀： 底数取倒数，指数取相反数．（ 3）分数指数幂的运算性质①a r a s a r s (a 0, r , s R)② (ar) sa rs (a 0, r , s R)③(ab)ra rb r (a0,b 0, rR)二 . 指数函数及其性质（ 4）指数函数函数名称指数函数定义函数 ya x (a 0 且 a1) 叫做指数函数a 1a 1yy a xya xy图象y1y1(0,1)(0,1)OxOx定义域 R值域（0,+ ∞）过定点 图象过定点（0,1 ），即当 x=0 时， y=1．奇偶性非奇非偶单一性在 R 上是增函数在 R 上是减函数函数值的 y ＞ 1(x ＞ 0), y=1(x=0), 0＜ y ＜ 1(x ＜ 0)y ＞ 1(x ＜ 0), y=1(x=0), 0＜ y ＜ 1(x ＞ 0)变化状况a 变化对在第一象限内， a 越大图象越高，越凑近 y 轴； 在第一象限内， a 越小图象越高，越凑近 y 轴； 图象影响在第二象限内，a 越大图象越低，越凑近x 轴．在第二象限内，a 越小图象越低，越凑近x 轴．三 .例题剖析1.设 a 、 b 知足 0<a<b<1,以下不等式中正确的选项是 ( C)A.a a <a bB.b a <b bC.a a <b aD.b b <a b 分析： A 、B 不切合底数在 (0,1) 之间的单一性 ; C 、 D 指数同样 , 底小值小 . 应选 C. 2.若 0<a<1,则函数 y=a x 与 y=(a-1)x 2 的图象可能是 (D )分析： 当 0<a<1 时 ,y=a x 为减函数 ,a-1<0, 因此 y=(a-1)x2张口向下 , 应选 D.3.设指数函数 f(x)=a x (a>0 且 a ≠ 1),则以下等式中不正确的选项是 ( D )A.f(x+y)=f(x)f(y)f (x)B.f(x-y)=f ( y)C.f(nx)= ［ f(x) ］ nD.f ［ (xy) n ］ =［ f(x) ］ n ［ f(y) ］ n (n ∈ N * )分析： 易知 A 、 B 、 C 都正确 .对于 D,f ［(xy)n］ =a (xy)n , 而［ f(x) ］ n ·［f(y) ］ n =(a x ) n ·(a y ) n =a nx+ny , 一般状况下 D 不建立 .11 34.设 a= ( 3) 3,b= ( 4)4,c= ( 3) 4,则 a 、b 、 c 的大小关系是 ( B )43 2A.c<a<b3分析： a= ( )B.c<b<aC.b<a<cD.b<c<a1 111(8133( 4)3 ( 4) 4=b, b=(4) 4)4(3) 4 =c.∴ a>b>c.3 332725.设 f(x)=4 x -2x+1,则 f -1 (0)=______1____________. 分析： 令 f -1 (0)=a, 则 f(a)=0 即有 4a -2 · 2a =0.2a · (2 a -2)=0, 而 2a >0,∴ 2a =2 得 a=1.6.函数 y=a x-3 +4(a>0 且 a ≠ 1)的反函数的图象恒过定点 ______(5,3)____________.分析： 因 y=a x 的图象恒过定点 (0,1), 向右平移 3 个单位 , 向上平移 4 个单位获得 y=a x-3 +4 的图象 , 易知恒过定点 (3,5).故其反函数过定点 (5,3).10 x 10 x.证明 f(x) 在 R 上是增函数 .7.已知函数 f(x)=x10 x10x1010x102x1,设 x 1<x 2∈ R,则f(x 1)-f(x2)=10x 1 1010x 1 10x 110x 210 x 2102 x 11 102 x 21 2(102 x 1102 x2).x 110x2 10x2 102 x1 1102 x21(102 x11)(102 x 2 1)∵ y=10 x是增函数 ,∴ 10 2x 1 10 2x 2 <0.而 10 2x 1 +1>0, 102 x 2 +1>0,故当 x <x 时 ,f(x)-f(x )<0,1212即 f(x 1)<f(x 2). 因此 f(x) 是增函数 .8.若定义运算 a b=b, ab,则函数 f(x)=3 x3-x 的值域为 ( A )a, a b,A.(0,1]B. ［ 1,+∞ )C.(0,+ ∞ )D.(- ∞ ,+∞ )分析： 当 3x ≥3-x , 即 x ≥ 0 时 ,f(x)=3-x∈(0,1 ］ ;x-x, 即 x<0 时 ,f(x)=3x∈ (0,1).3 x , x 0, 当 3<3∴ f(x)=x值域为 (0,1).3x ,0,9.函数 y=a x 与 y=-a -x (a>0,a ≠1) 的图象 ( C )A. 对于 x 轴对称B.对于 y 轴对称C.对于原点对称D.对于直线 y=-x 对称分析： 可利用函数图象的对称性来判断两图象的关系.10.当 x ∈［ -1,1］时 ,函数 f(x)=3 x-2 的值域为 _______［ -5,1 ］ ___________.3分析： f(x) 在［ -1,1 ］上单一递加 .11.设有两个命题 :(1)对于 x 的不等式 x 2+2ax+4>0对全部 x ∈ R 恒建立 ;(2) 函数 f(x)=-(5-2a) x是减函数 .若命题 (1)和 (2)中有且仅有一个是真命题 ,则实数 a 的取值范围是 _______(- ∞ ,-2)__________.分析： (1) 为真命题=(2a) 2-16<0-2<a<2. (2)为真命题 5-2a>1 a<2.若 (1) 假 (2) 真 , 则 a ∈ (- ∞ ,-2]. 若 (1) 真 (2) 假, 则 a ∈ (-2,2)∩［ 2,+ ∞］=.故 a 的取值范围为 (- ∞ ,-2).12.求函数 y=4 -x -2-x +1,x ∈［ -3,2］的最大值和最小值 .解： 设 2-x=t, 由 x ∈［ -3,2 ］得 t ∈［ 1,8 ］ , 于是 y=t 2-t+1=(t-1)2+3. 当 t= 1时 ,y3 .424有最小值 这时 x=1.当 t=8 时 ,y 有最大值57.这时 x=-3.2413.已知对于 x 的方程 2a2x-2-7a x-1 +3=0 有一个根是 2,求 a 的值和方程其他的根 . 解： ∵ 2 是方程 2a2x-2-9a x-1+4=0 的根 , 将 x=2 代入方程解得 a= 1或 a=4.2(1) 当 a= 1时 , 原方程化为 2· ( 1)2x-2-9(1) x-1 +4=0.①222x-1 2令 y=( 1) , 方程①变成 2y -9y+4=0,2解得 y 1=4,y 2= 1.∴ ( 1) x-1 =42x=-1,2( 1 ) x-1 = 1x=2.22(2) 当 a=4 时 , 原方程化为 2· 42x-2 -9 · 4x-1 +4=0. ②令 t=4 x-1 , 则方程②变成 2t 2-9t+4=0. 解得 t 1=4,t 2= 1.x-12=4x=2,∴44x-1 = 1x=- 1 .22故方程此外两根是当 a= 1时 ,x=-1;1 .2当 a=4 时 ,x=-214.函数 y= (1) 3 4xx 2的单一递加区间是 ( D )3A. ［ 1,2］B.［ 2,3］C.(-∞ ,2]D.［ 2,+∞ )分析： 由于 y=3x2-4x+3 , 又 y=3t 单一递加 ,t=x 2-4x+3 在 x ∈［ 2,+ ∞ ) 上递加 , 故所求的递加区间为［ 2,+ ∞ ).15.已知 f(x)=3 x-b (2≤ x ≤ 4,b 为常数 ) 的图象经过点 (2,1), 则 F(x)=f 2(x)-2f(x) 的值域为 ( B )A. ［ -1,+∞ )B. ［ -1,63)C.［ 0,+∞ )D.(0,63 ］分析： 由 f(2)=1, 得 32-b =1,b=2,f(x)=3 x-2.∴ F (x)= ［ f(x)-1 ］2-1=(3 x-2 -1) 2-1. 令 t=3 x-2 ,2 ≤x ≤4.2∴g(t)=(t-1) - 1,t ∈［ 1,9 ］.2.1 指数函数练习1．以下各式中建立的一项A ． ( n)71n 7 m 7B ．12 ( 3)433m3C ． 4 x 3y 3( x y) 4D ．393321111 1 52．化简 (a 3 b 2 )( 3a 2 b 3 ) ( a 6 b 6 ) 的结果3D ． 9a 2 A ． 6aB ． aC ． 9a3．设指数函数 f ( x)a x ( a 0, a1) ，则以下等式中不正确的选项是f (x) A ． f(x+y)=f(x) ·f(y)B ． f （ x y ）f ( y)C ． f (nx)[ f ( x)]n (nQ )D ． f ( xy) n [ f ( x)] n ·[f ( y)] n1 4．函数 y (x5) 0 ( x 2)2A ． { x | x 5, x 2}B ． { x | x 2}C ． { x | x 5}D ． { x | 2 x 5或 x 5}（）（）（）(n N )（ ）5．若指数函数 y a x 在 [－ 1,1]上的最大值与最小值的差是1，则底数 a 等于 （）A ．15 B ．1 5 C ．15D ．5 122 226．当 a0 时，函数 y axb 和 yb ax 的图象只可能是（）7．函数 f ( x)2 |x| 的值域是（）A ． (0,1]B ． (0,1)C ． (0, )D ． R8．函数 f ( x)2 x 1, x 0，知足 f ( x)1的 x 的取值范围1x 2 , x（）A ． ( 1,1)B ． ( 1, )C ． { x | x 0或 x2}D ． { x | x 1或 x1}9．函数 y(1) x 2x2得单一递加区间是2（）A ．[ 1,1]B ． ( , 1]C ．[2,)D ．[ 1,2]2exe x210．已知 f ( x)（）2 ，则以下正确的选项是A ．奇函数，在 R 上为增函数B ．偶函数，在 R 上为增函数C ．奇函数，在 R 上为减函数D ．偶函数，在 R 上为减函数11．已知函数 f (x)的定义域是（1， 2），则函数 f (2 x ) 的定义域是.12．当 a ＞0 且 a ≠1 时，函数 f (x)=a x －2－ 3 必过定点.三、解答题：13．求函数 y1的定义域 .x5 x 1114．若 a ＞0， b ＞ 0，且 a+b=c ，求证： (1) 当r ＞1时， a r +b r ＜ c r ； (2) 当r ＜ 1时， a r +b r ＞ c r .a x 1 15．已知函数 f ( x)(a ＞1) .a x1（ 1）判断函数 f (x) 的奇偶性；（ 2）证明 f (x)在 (－∞， +∞ )上是增函数 .xa16．函数 f(x) ＝ a (a>0 ，且 a ≠1) 在区间 [1,2] 上的最大值比最小值大2，求 a 的值．参照答案一、 DCDDD AADDA二、 11． (0,1)；12． (2，－ 2) ；三、 13． 解：要使函数存心义一定：x 1 0x 1x0 x 0x 1∴ 定义域为 ： x xR 且 x0, x 1a rrrb r此中a1,0b114． 解：ba，c rcccc.r ＞1 ，a rb ra b 1，r r r当因此+b＜ c ；时c c c crrrrr当 r ＜ 1 时， aba b1， 因此 a +b ＞c .ccc c15． 解 ：(1)是奇函数 .(2) 设x ＜x ，则 f (x 1 )ax11 ax21 。

高一数学指数与指数函数试题答案及解析1.设，则的大小关系是（）.A．B．C．D．【解析】，，，因此.【考点】指数函数和对数函数的性质.2.三个数，，之间的大小关系（）A．B．C．D．【答案】B【解析】对于，当时；对于，当时，；对于，当时，；故.【考点】对数函数，指数函数的性质.3.．【答案】【解析】原式=【考点】指数与对数4.如图，在平面直角坐标系中，过原点O的直线与函数的图象交于A，B两点，过B作y轴的垂线交函数的图象于点C，若AC平行于y轴，则点A的坐标是．【答案】【解析】设，则，因为AC平行于y轴，所以，因此.又三点三点共线，所以由得，因此.【考点】指数函数运算，向量共线.5.将函数的图像向左平移一个单位，得到图像，再将向上平移一个单位得到图像，作出关于直线对称的图像，则的解析式为 .【答案】【解析】根据平移口诀“上加下减”可得函数解析式为，函数解析式为，因为图像与图像关于直线对称，所以函数与函数互为反函数。

因为，所以，解得，所以，所以函数的反函数为，即的解析式为。

【考点】图像平移，指数和对数的互化。

6.已知,且，则A的值是（）A．15B．C．±D．225【答案】B【解析】由得到代入到得：，利用换底法则得到，所以故选B【考点】指数函数综合题．7.三个数，之间的大小关系是A．B．C．D．【答案】C【解析】，所以；；。

所以。

故C正确。

【考点】指数函数和对数函数的单调性及运算。

8.计算:⑴ ;⑵．【答案】（1）；（2）．【解析】对于（1），主要是利用指数幂的运算性质进行化简求值；对于（2），主要是利用对数的运算性质进行化简求值，要求熟练的掌握指数幂和对数的运算性质．试题解析:（1）原式；（2）原式.【考点】本题主要考查了指数幂的运算性质和对数的运算性质，属于基础题．.9.【答案】(1)；（2）1.【解析】（1）由指数的运算法则，原式==；（2）由对数的运算法则，原式===1.试题解析：（1）原式= 5分= 7分（2）原式= 10分= 12分=1 14分考点:1、有理数指数幂的运算性质；2、对数的运算性质.10.已知，.（1）求的解析式；（2）解关于的方程（3）设，时，对任意总有成立，求的取值范围.【答案】（1）（2）当时，方程无解当时，解得若，则若，则（3）【解析】(1)利用换元法求解函数的解析式,设,则,代入即得解析式(2)依题意将方程中化简得,然后分和分别求解,(3)对任意总有成立，等价于当时，,然后分的取值来讨论.试题解析：解：（1）令即，则即(2)由化简得：即当时，方程无解当时，解得若，则若，则（3）对任意总有成立，等价于当时，令则令①当时，单调递增，此时，即（舍）②当时,单调递增此时，即③当时，在上单调递减，在上单调递增且即，综上:【考点】本题考查指数函数的性质及闭区间上的最值问题，考查了恒成立问题转化为求函数最值及分类讨论.11.计算 .【答案】14【解析】【考点】指数幂的运算；对数的运算12. (1)(2)计算【答案】(1) (2)【解析】（1）通过指数形式转化为对数的形式，让后再运算.（2）通过把除号改写为分数线，再把负指数化为正指数.再运算.试题解析：【考点】1.指数转化为对数形式.2.分式的运算.13.已知，则____________________．【答案】1【解析】由已知得，，，所以，，故.【考点】1.指数式与对数式之间的互化；2.对数运算.14.已知，则的增区间为_______________．【答案】（或）【解析】令函数，因为，，由函数零点存在性定理知，所以函数为减函数，又由函数的单调递减区间为，故所求函数的增区间为.【考点】1.函数的零点；2.指数函数；3.二次函数.15.函数的图象可能是（）【答案】D【解析】，，排除A；当时，排除B；当时，排除C.故选D.【考点】指数函数的图像变换16.对于函数)中任意的有如下结论：①；②；③；④；⑤.当时，上述结论中正确结论的个数是( )A．2个B．3个C．4个D．5个【答案】B【解析】当时,，①错误；，②正确；，③正确；当时，，④错误；因为是上的递增函数，即：时，，或时，，因此与同号，所以，⑤正确.【考点】指数函数的性质17.化简或求值：（1）;（2）计算.【答案】(1)；(2)1.【解析】(1)将小数化成分数，利用指数幂的运算法则；（2）对于比较复杂的式子，把它拆成几部分分别化简或计算.本小题利用对数的运算法则分别对分子和分母进行求值.试题解析：（1）原式= 3分. 6分（2）分子=； 9分分母=；原式=. 12分【考点】指数幂与对数的运算法则.18.指数函数f(x)的图象上一点的坐标是(－3，)，则f(2)＝______________．【答案】4【解析】令指数函数为，其过点(－3，)，则，求得，所以，f(2)＝。

高一数学指数运算及指数函数试题一．选择题1．若xlog 23=1，则3x+9x的值为（B）A．3B．6C．2D．解：由题意x=，所以3x==2，所以9x=4，所以3x+9x=6故选B2．若非零实数a、b、c满足，则的值等于（B）A．1B．2C．3D．4解答：解：∵，∴设=m，a=log5m，b=log2m，c=2lgm，∴==2lgm（log m5+log m2）=2lgm•log m10=2．故选B．3．已知，则a等于（）A．B．C． 2 D． 4解：因为所以解得a=4故选D4．若a＞1，b＞1，p=，则a p等于（）A．1B．b C．l og b a D．a log b a解：由对数的换底公式可以得出p==log a（log b a），因此，a p等于log b a．故选C．5．已知lg2=a，10b=3，则log125可表示为（C）A．B．C．D．解：∵lg2=a，10b=3，∴lg3=b，∴log125===．故选C．6．若lgx﹣lgy=2a，则=（C）A．3a B．C．a D．解：∵lgx﹣lgy=2a，∴lg﹣lg=lg﹣lg=（lg﹣lg）=lg=（lgx﹣lgy）=•2a=a；故答案为C．7．已知函数，若实数a，b满足f（a）+f（b﹣2）=0，则a+b= A．﹣2 B．﹣1 C．0D．2解：f（x）+f（﹣x）=ln（x+）+ln（﹣x+=0∵f（a）+f（b﹣2）=0∴a+（b﹣2）=0∴a+b=2故选D．8．=（）A．1B．C．﹣2 D．解：原式=+2×lg2+lg5=+lg2+lg5=+1=，故选B．9．设，则=（）A．1B．2C．3D．4解：∵，∴==（）+（）+（）==3故选C10．，则实数a的取值区间应为（C）A．（1，2）B．（2，3）C．（3，4）D．（4，5）解：=log34+log37=log328∵3=log327＜log328＜log381=4∴实数a的取值区间应为（3，4）故选C．11．若lgx﹣lgy=a，则=（A）A．3a B．C．a D．解：=3（lgx﹣lg2）﹣3（lgy﹣lg2）=3（lgx﹣lgy）=3a故选A．12．设，则（）A．0＜P＜1 B．1＜P＜2 C．2＜P＜3 D．3＜P＜4 解：=log112+log113+log114+log115=log11（2×3×4×5）=log11120．∴log1111=1＜log11120＜log11121=2．故选B．13．已知a，b，c均为正数，且都不等于1，若实数x，y，z满足，则abc的值等于（A）A．1B．2C．3D．4解：∵a，b，c均为正数，且都不等于1，实数x，y，z满足，∴设a x=b y=c z=k（k＞0），则x=log a k，y=log b k，z=log c k，∴=log k a+log k b+log k c=log k abc=0，∴abc=1．故选A．14．化简a2•••的结果是（C）A．a B．C．a2D．a3解：∵a2•••=a2•••==a2，故选C15．若x，y∈R，且2x=18y=6xy，则x+y为（）A．0B．1C．1或2 D．0或2解：因为2x=18y=6xy，（1）当x=y=0时，等式成立，则x+y=0；（2）当x、y≠0时，由2x=18y=6xy得，xlg2=ylg18=xylg6，由xlg2=xylg6，得y=lg2/lg6，由ylg18=xylg6，得x=lg18/lg6，则x+y=lg18/lg6+lg2/lg6=（lg18+lg2）/lg6=lg36/lg6=2lg6/lg6=2．综上所述，x+y=0，或x+y=2．故选D．16．若32x+9=10•3x，那么x2+1的值为（D）A．1B．2C．5D．1或5解：令3x=t，（t＞0），原方程转化为：t2﹣10t+9=0，所以t=1或t=9，即3x=1或3x=9所以x=0或x=2，所以x2+1=1或5故选Dx x2A．﹣2＜a＜2 B．C．D．解；令t=2x，则t＞0若二次函数f（t）=t2﹣at+a2﹣3在（0，+∞）上有2个不同的零点，即0=t2﹣at+a2﹣3在（0，+∞）上有2个不同的根∴解可得，即故选D18．若关于x的方程=3﹣2a有解，则a的范围是（A）A．≤a＜B．a≥C．＜a＜D．a＞解：∵1﹣≤1，函数y=2x在R上是增函数，∴0＜≤21=2，故0＜3﹣2a≤2，解得≤a＜，故选A．二．填空题19．，则m=10．解：由已知，a=log2m，b=log5m．∴+=log m2+log m5=log m10=1∴m=10故答案为：10．20．已知x+y=12，xy=9，且x＜y，则=．解：由题设0＜x＜y∵xy=9，∴∴x+y﹣2==12﹣6=6x+y+2==12+6=18∴=，=∴=故答案为：21．化简：=（或或）．解：====．故答案为：（或或）．22．=1．解：===1．故答案为：1．23．函数在区间[﹣1，2]上的值域是[，8]．解：令g（x）=x2﹣2x=（x﹣1）2﹣1，对称轴为x=1，∴g（x）在[﹣1，1]上单调减，在[1，8]上单调递增，又f（x）=2g（x）为符合函数，∴f（x）=2g（x）在[﹣1，1]上单调减，在[1，，2]上单调递增，∴f（x）min=f（1）==；又f（﹣1）==23=8，f（2）==1，∴数在区间[﹣1，2]上的值域是[，8]．故答案为：[，8]．24．函数的值域为（0，8]．解：令t=x2+2|x|﹣3==结合二次函数的性质可得，t≥﹣3∴，且y＞0故答案为：（0，8]．25．函数（﹣3≤x≤1）的值域是[3﹣9，39]，单调递增区间是（﹣2，+∞）．．解：可以看做是由y=和t=﹣2x2﹣8x+1，两个函数符合而成，第一个函数是一个单调递减函数，要求原函数的值域，只要求出t=﹣2x2﹣8x+1，在[1，3]上的值域就可以，t∈[﹣9，9]此时y∈[3﹣9，39]函数的递增区间是（﹣∞，﹣2]，故答案为：[3﹣9，39]；（﹣2，+∞）三．解答题26．计算：（1）；（2）．解：（1）==（2）===2+2﹣lg3+lg2+lg3﹣lg2+2=627．（1）若，求的值；（2）化简（a＞0，b＞0）．解：（1）∵，∴x+x﹣1=9﹣2=7，x2+x﹣2=49﹣2=47，∴==3×6=18，∴==．（2）∵a ＞0，b ＞0，∴====．28．已知函数f （x ）=4x ﹣2x+1+3． （1）当f （x ）=11时，求x 的值；（2）当x ∈[﹣2，1]时，求f （x ）的最大值和最小值．解：（1）当f （x ）=11，即4x ﹣2x+1+3=11时，（2x ）2﹣2•2x ﹣8=0 ∴（2x ﹣4）（2x +2）=0 ∵2x ＞02x +2＞2，∴2x ﹣4=0，2x =4，故x=2﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（4分） （2）f （x ）=（2x ）2﹣2•2x +3 （﹣2≤x ≤1） 令∴f （x ）=（2x ﹣1）2+2当2x =1，即x=0时，函数的最小值f min （x ）=2﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（10分）当2x =2，即x=1时，函数的最大值f max （x ）=3﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（12分）29．已知函数||22)(x x x f -=. （1）若2)(=x f ，求x 的值；（2）若0)()2(2≥+t mf t f t 对于]2,1[∈t 恒成立，求实数m 的取值范围。

高一数学指数运算与指数函数试题一：选择题 1．下列等式=2a ；=；﹣3=中一定成立的有解：由于2．设a ＞0，将表示成分数指数幂，其结果是（ ）B解：由题意3．根式（式中a ＞0）的分数指数幂形式为（ ）BA 【答案】B5．下列结论中正确的个数是( )①当0a <时， 域是[)2,+∞；④若1005,102ab==，则21a b +=．A 、 0B 、1C 、2D 、3【答案】B 6．若0.90.481.54,8,0.5a b c -===则（ ）A .c b a >> B. a c b >> C.b a c >> D.b c a >> 【答案】D7a ，b ，c 的大小关系是( ) A.b ＞c ＞a B.a ＞b ＞c C.c ＞a ＞b D.a ＞c ＞b【答案】D8． 设函数f （x ）＝a>0），且f （2）＝4，则DA. f （－1）>f （－2）B. f （1）>f （2）C. f （2）<f （－2）D.f （－3）>f （－2） 【答案】D9．设函数221()x f x x -⎧-=⎨⎩00>≤x x ，若1)(0>x f ，则0x 的取值范围是（ D ）A ．(1,1)-B ．(1,)-+∞C ．(,2)(0,)-∞-+∞D ．(,1)(1,)-∞-+∞ 【答案】D10．设函数若f （x ）的值域为R ，则常数a 的取值范围是A 、B 、C 、D 、【答案】A11．已知　　则实数　时均有 当 且a x f x a x x f a a x ,21)()1,1(,)(,102<-∈-=≠>的取值范围是（ ）A ．[)∞+⎥⎦⎤ ⎝⎛，，221 0B ．(]4,11,41 ⎪⎭⎫⎢⎣⎡C ．(]2 11,21， ⎪⎭⎫⎢⎣⎡D ．[)∞+⎥⎦⎤ ⎝⎛， 441,0 【答案】C12m 的取值范围是（ ） A D ．[1,)+∞【答案】C13R上的单调递增函数，则实数a的取值范围为A、()∞+,1 B、()8,1 C、()8,4 D、[)8,4【答案】D14．关于x的方程kx=-|12|给出下列四个命题①存在实数k，使得方程恰有1个零根；②存在实数k，使得方程恰有1个正根③存在实数k，使得方程恰有1个正根、一个负根④存在实数k，使得方程没有实根，其中真命题的个数是（）A．1 B．2 C．3 D．4【答案】D二：填空题15．0.5＋0.1－23π0= .【答案】10016．求值：=1．故答案为：1．17．=1．18．化简：（1）= ．（a ＞0，b ＞0）（2）=100 ． ）×+×﹣故答案为：，19．设函数2(1)()[1)x f x x x ⎧∈-∞⎪=⎨∈+∞⎪⎩-x 2，，，，，若()4f x >，则x 的取值范围是______________．【答案】2x <-或2x >；20为常数)在定义域上是奇函数，则a= . 【答案】1±21．已知[]3,2x ∈-，则的值域为 .22．当(],1x ∈-∞时，不等式1230x x t ++⋅>恒成立，则实数t 的取值范围为________ 【答案】(1,)-+∞ 三：解答题 23．求值：（1）；（2）．24．已知函数1()42x x f x aa +=⋅--.⑴若0a =,解方程(2)4f x =; ⑵若函数1()42x x f x a a +=⋅--在[1，2]上有零点，求实数a 的取值范围【答案】（1（2）若存在0[1,2],4 2.20x xx a a ∈⋅--=使25．已知函数()f x的定义域为R,并满足(1)对于一切实数x，都有0)(>xf；(2)对任意的,,()[()]yx y R f xy f x∈=；利用以上信息求解下列问题：(1)求)0(f；(2)证明(1)1()[(1)]xf f x f>=且；(3)若1(3)(932)0x x xf f K+--->对任意的[0,1]x∈恒成立，求实数K的取值范围。

2021-2022年高一数学人教版A 版(2019)必修第一册同步练习题4-1 指数与指数函数【含答案】一、选择题（本大题共8小题，每小题5分，共40分）在每小题所给出的四个选项中，只有一项是符合题目要求的．1．（2017·内蒙古集宁一中高一期中（文））()()3343112222--⎛⎫⎛⎫--+-+--- ⎪ ⎪⎝⎭⎝⎭的值（ ） A ．374B ．8C ．24-D ．8-【答案】C【解析】原式111682488⎛⎫=-----=- ⎪⎝⎭.故选：C. 2．232a a⋅的结果为（ ）A ．32aB ．16aC ．56a D ．65a【答案】C【解析】7522226627132362a a aa a aa aa-====⋅⋅，故选：C3．（2020·全国高一专题练习）若103,104x y ==，则3210x y -=( )A ．1-B ．1C ．2716D ．910【答案】C【解析】依题意，()()333322221010327101041610x xx yy y -====.故选：C.4．若a >1，b >0，a b ＋a －b ＝22，则a b －a －b等于( ) A ．4 B ．2或－2 C ．－2 D ．2【答案】D【解析】设a b －a －b＝t .∵a >1，b >0，∴a b >1，a －b <1.∴t ＝a b －a －b>0. 则t 2＝(a b －a －b )2＝(a b ＋a －b )2－4＝(22)2－4＝4.∴t ＝2. 5．设x ，y 是正数，且x y＝y x，y ＝9x ，则x 的值为( ) A.91 B ．43C ．1D ．39【答案】B【解析】∵x y＝y x，y ＝9x ，∴x 9x＝(9x )x ，∴(x 9)x ＝(9x )x ，∴x 9＝9x .∴x 8＝9.∴x ＝4839=.6．已知f (x )是奇函数，当x >0时，f (x )＝x ·2x ＋a－1，若f (－1)＝43，则a 等于( ) A ．－3 B ．－2 C ．－1 D ．0【答案】A 【解析】∵f (－1)＝43，∴f (1)＝－f (－1)＝－43，即21＋a－1＝－43，即1＋a ＝－2，得a ＝－3. 7.（多选）（2019·广东禅城佛山一中高一月考）下列运算结果中，一定正确的是（ ） A ．347a a a ⋅= B ．()326a a -=C 88a a =D ()55ππ-=-【答案】AD【解析】34347a a a a +==，故A 正确；当1a =时，显然不成立，故B 不正确；88a a =，故C ()55ππ-=-，D 正确，故选AD.8.(多选下列各式中一定成立的有（ ）A ．7177n n m m ⎛⎫= ⎪⎝⎭B ．()431233-=C ()33344x y x y +=+ D 3393=【答案】BD【解析】777n n m m -⎛⎫= ⎪⎝⎭，A 错误；()143312333-=，B 正确；()1333344x y x y+=+，C 11112333329993⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭D 正确故选：BD二、填空题（本大题共4小题，每小题5分，共20分．不需写出解答过程，请把答案直接填写在横线上）9．（2020·上海高一开学考试）当2x <3838(2)(2)x x --=_______________.【答案】22【解析】,nn n na a aa ==，因为2x <，所以原式=2222x x -+故答案为：2210．（2020·全国高一课时练习）设0a >，232a a⋅表示成分数指数幂的形式，其结果是________.【答案】76a【解析】∵0a >117222361231223a aa aa a b--⋅===.故答案为：76a.11．2a a=，则1a a +=______；当0a <3231a a a -=______.【答案】2；a -.【解析】12a a +=222a a ∴= 124a a ∴++=12a a∴+=，32311a a a a a a a--⨯⨯==0a <3231a a a a -∴=-故答案为：2；a -12化简：3216842111111111111222222⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++++⋅+= ⎪⎪⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭________. 【答案】63122-【解析】原式43216821111111111111122222222⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=+++++⋅+-⨯ ⎪⎪⎪⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭321682421111111111112222222⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=+++++⋅-⨯ ⎪⎪⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭32164481111111111222222⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=++++-⨯ ⎪⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭3216881111111122222⎛⎫⎛⎫⎛⎫⎛⎫=+++-⨯ ⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭3216161111112222⎛⎫⎛⎫⎛⎫=++-⨯ ⎪⎪⎪⎝⎭⎝⎭⎝⎭32321111222⎛⎫⎛⎫=+-⨯ ⎪⎪⎝⎭⎝⎭641122⎛⎫=-⨯ ⎪⎝⎭63122=-.三、解答题（本大题共4小题，共40分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）13.（2020·全国高一课时练习）将下列根式化成分数指数幂的形式.（1）13·a a(a >0)；（2())25230x xx >；（3）23243b--⎝⎭(b >0). 【答案】（1）512a；（2）35x-；（3）19b .【解析】（1）原式＝1132·a a56a 1526a ⎛⎫⎪⎝⎭＝512a. （22325·()x x 435·x x935x＝91531()x ＝351x＝35x -.（3）原式＝[2134()b -]23-＝212()343b -⨯⨯-＝19b .14．（2020·全国高一课时练习）若本例变为：已知a ，b 分别为x 2－12x ＋9＝0的两根，且a ＜b ，求11221122a b a b-+的值.【答案】3【解析】11221122a b a b-+＝1122211112222()()()a b a b a b -+-＝12()2()a b ab a b +--.①∵a ，b 分别为x 2－12x ＋9＝0的两根， ∴a ＋b ＝12，ab ＝9，②∴(a －b )2＝(a ＋b )2－4ab ＝122－4×9＝108. ∵a ＜b ，∴a －b ＝－3③将②③代入①，得11221122a ba b -+12963-＝－33. 15．已知2a ·3b ＝2c·3d＝6，求证：(a －1)(d －1)＝(b －1)(c －1)． 证明：∵2a·3b＝6，∴2a －1·3b －1＝1. ∴(2a －1·3b －1)d －1＝1，即2(a －1)(d －1)·3(b －1)(d －1)＝1.①又∵2c ·3d＝6，∴2c －1·3d －1＝1.∴(2c －1·3d －1)b －1＝1，即2(c －1)(b －1)·3(d －1)(b －1)＝1.②由①②知2(a －1)(d －1)＝2(c －1)(b －1)，∴(a －1)(d －1)＝(b －1)(c －1)．16.（2020·黑龙江萨尔图�大庆实验中学高一期末）已知()442xx f x =+.（1）求()()1f a f a +-（0a >且1a ≠）的值；（2）求12320182019201920192019f f f f ⎛⎫⎛⎫⎛⎫⎛⎫++++⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭的值.【答案】（1）1；（2）1009.【解析】（1）()442xxf x =+，()()()1111444441424242442a a a a aa a a a a f a f a ----⨯∴+-=+=++++⨯+()444442142424424242224a a a a a a a a a =+=+=+=++⨯++++； （2）原式120182201710091010201920192019201920192019f f f f f f ⎡⎤⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=++++++⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦⎣⎦1009=.专题4.1.2 指数函数姓名：__________________ 班级：______________ 得分：_________________注意事项：本试卷满分100分，考试时间45分钟，试题共16题．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．一、选择题（本大题共8小题，每小题5分，共40分）在每小题所给出的四个选项中，只有一项是符合题目要求的．1．（2020·全国高一课时练习）若函数()21xy a =-（x 是自变量）是指数函数，则a 的取值范围是（ ） A ．0a >且1a ≠ B ．0a ≥且1a ≠ C ．12a >且1a ≠ D ．12a ≥【答案】C【解析】由于函数()21xy a =-（x 是自变量）是指数函数，则210a ->且211a -≠，解得12a >且1a ≠.故选：C. 2．（2020·全国高一课时练习）已知函数1()4x f x a +=+的图象经过定点P ，则点P 的坐标是（ ） A ．(－1，5) B ．(－1，4)C ．(0，4)D ．(4，0)【答案】A【解析】当10x +=，即1x =-时，011x a a +==，为常数，此时()415f x =+=，即点P 的坐标为(－1，5).故选：A. 3．（2020·全国高一课时练习）函数f (x )＝a x －b的图象如图，其中a ，b 为常数，则下列结论正确的是（ ）A ．a ＞1，b ＜0B ．a ＞1，b ＞0C ．0＜a ＜1，b ＞0D ．0＜a ＜1，b ＜0 【答案】D 【解析】由f (x )＝ax －b的图象可以观察出，函数f (x )＝ax －b在定义域上单调递减，所以0＜a ＜1.函数f (x )＝a x －b的图象是在f (x )＝a x的基础上向左平移得到的，所以b ＜0.故选：D.4．（2020·陆良县联办高级中学高一开学考试）函数112xy ⎛⎫=- ⎪⎝⎭）A ．()0,+∞B ．(),0-∞C ．[)0,+∞D ．(],0-∞【答案】C【解析】要是函数有意义须满足1102x ⎛⎫-≥ ⎪⎝⎭，即011122x ⎛⎫⎛⎫≤= ⎪ ⎪⎝⎭⎝⎭，解得0x ≥， 因此，函数112xy ⎛⎫=- ⎪⎝⎭[)0,+∞.故选：C. 5．（2020·内蒙古集宁一中高二月考（文））若a ＝12⎛⎫ ⎪⎝⎭23，b ＝15⎛⎫ ⎪⎝⎭23，c ＝12⎛⎫ ⎪⎝⎭13，则a ，b ，c 的大小关系是( ) A ．a ＜b ＜c B ．c ＜a ＜b C ．b ＜c ＜a D ．b ＜a ＜c【答案】D【解析】∵y ＝x 23 (x >0)是增函数，∴a ＝12⎛⎫⎪⎝⎭23>b ＝15⎛⎫ ⎪⎝⎭23. ∵y ＝12⎛⎫⎪⎝⎭x 是减函数，∴a ＝12⎛⎫ ⎪⎝⎭23＜c ＝12⎛⎫ ⎪⎝⎭13，∴b ＜a ＜c .故本题答案为D. 6．（2020·浙江高一单元测试）函数1()31x f x =+的值域是（ ）． A ．(,1)-∞ B ．(0,1)C ．(1,)+∞D ．(,1)(1,)-∞⋃+∞【答案】B【解析】∵30x >∴311x +>，∴10131x<<+，∴函数值域为(0,1)．故选：B 7．（多选）（2020·全国高一课时练习）设函数||()x f x a -=（0a >，且1a ≠），若(2)4f =，则（ ）A ．(2)(1)f f ->-B ．(1)(2)f f ->-C ．()1)(2f f > D.(4)(3)f f ->【答案】AD【解析】由2(2)4f a -==得12a =，即||||1()22x x f x -⎛⎫== ⎪⎝⎭，故(2)(1)f f ->-，(2)(1)f f >，(4)(4)(3)f f f -=>，所以AD 正确.故选：AD8．（多选）（2020·山东临沂�高一期末）如图，某池塘里浮萍的面积y （单位：2m ）与时间t （单位：月）的关系为t y a =．关于下列说法正确的是（ ）A ．浮萍每月的增长率为2B ．浮萍每月增加的面积都相等C ．第4个月时，浮萍面积不超过280mD ．若浮萍蔓延到22m 、24m 、28m 所经过的时间分别是1t 、2t 、3t ，则2132t t t =+ 【答案】AD【解析】将点()1,3的坐标代入函数t y a =的解析式，得13a =，函数的解析式为3t y =.对于A 选项，由13323n nn+-=可得浮萍每月的增长率为2，A 选项正确； 对于B 选项，浮萍第1个月增加的面积为()102332m -=，第2个月增加的面积为()212336m -=，26≠，B 选项错误；对于C 选项，第4个月时，浮萍的面积为438180=>，C 选项错误；对于D 选项，由题意可得132t =，234t =，338t =，2428=⨯，()2122333t t t ∴=⨯，即132233t t t +=，所以，2132t t t =+，D 选项正确. 故选：AD.二、填空题（本大题共4小题，每小题5分，共20分．不需写出解答过程，请把答案直接填写在横线上）9．（2019·定远县育才学校高一月考）若函数()xf x a =（0a >且1a ≠）在[]1,2上最大值是最小值的2倍，则a =______.【答案】2或12【解析】当01a <<时，函数()xf x a =为R 上的减函数，故()()122f f =，即22a a =，解得12a =. 当1a >时，函数()xf x a =为R 上的增函数，故()()221f f =，即22a a =，解得2a =.故a 的值为2或12.故填：2或12. 10．（2020·江苏秦淮�高三期中）不等式21124x x-⎛⎫>⎪⎝⎭的解集为_________.【答案】(1,2)-【解析】22111()242x x-⎛⎫>=⎪⎝⎭，化为220x x --<，解得12x -<<，所以不等式的解集是(1,2)-. 故答案为:(1,2)-.11．（2019·深州长江中学高一期中）函数28212x x y --⎛⎫=⎪⎝⎭的单调递增区间为_________．【答案】[)1,-+∞【解析】函数12xy ⎛⎫= ⎪⎝⎭在R 上递减，函数228y x x =--+的对称轴是1x =-，且在(],1-∞-上递增，在[)1,-+∞上递减.根据复合函数单调性同增异减可知：函数28212x x y --⎛⎫=⎪⎝⎭的单调递增区间为[)1,-+∞.故填：[)1,-+∞.12．（一题两空）（2020·上海高一课时练习）函数2x y =的图象与函数2x y -=的图象关于________对称，它们的交点坐标是_________. 【答案】y 轴 ()0,1【解析】函数2x y =的图象与函数2x y -=的图象如下：由指数函数的性质可知，函数2x y =的图象与函数2x y -=的图象关于y 轴对称，它们的交点坐标是()0,1.故答案为：y 轴；()0,1.三、解答题（本大题共4小题，共40分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）13．（2020·浙江高一课时练习）已知函数21,0()21,1x c cx x cf x c x -+<<⎧⎪=⎨⎪+≤<⎩，满足928c f ⎛⎫= ⎪⎝⎭. （1）求常数c 的值.（2）解关于x 的不等式2()1f x >+. 【答案】（1）12；（2）2548x ⎧⎫⎪⎪<<⎨⎬⎪⎪⎩⎭. 【解析】（1）由928c f ⎛⎫=⎪⎝⎭，得9128c c ⋅+=，解得12c =. （2）由（1）得4111,022()121,12x x x f x x -⎧+<<⎪⎪=⎨⎪+≤<⎪⎩.由2()18f x >+得，当102x <<时，121128x +>+， 212x <<； 当112x ≤<时，42211x -+>+，解得1528x ≤<.综上，不等式2()18f x >+的解集为2548x ⎧⎫⎪⎪<<⎨⎬⎪⎪⎩⎭.14．（2019·陕西临渭�高一期末）已知函数()2121x x f x -=+.（1）判断并证明函数()f x 的奇偶性； （2）判断并证明()f x 在其定义域上的单调性. 【答案】（1）详见解答；（2）详见解答. 【解析】（1）()f x 的定义域为实数集R ，2112()()2112x xx x f x f x -----===-++，所以()f x 是奇函数；（2）()21212121x x xf x -==-++，设12x x <， 12121212222(22)()()2121(21)(21)x x x x x x f x f x --=-+=+++⋅+， 12121212,022,220,()()x x x x x x f x f x <<<-<<，所以()f x 在实数集R 上增函数.15．（2019·黑龙江松北�哈九中高一期末）已知函数()1124x xf x a =--． （1）若1a =时，求满足()11f x =-的实数x 的值；（2）若存在[]0,1x ∈，使()0f x >成立，求实数a 的取值范围． 【答案】（1）12log 3x =（2）34a >【解析】（1）当1a =时，()1111124x x f x =--=-，令()102x t t =>，则2120t t +-=， 解得3t =或4t =-（舍），由132x=，得12log 3x =， 所以12log 3x =．（2）由已知，存在[]0,1x ∈，使()0f x >成立可转化为存在[]0,1x ∈，使得1124x xa >+， 只需求出函数11()24x xh x =+的最小值即可， 令12x t =，∴1,12t ⎡⎤∈⎢⎥⎣⎦．则2y t t =+，易知2y t t =+在1,12⎡⎤⎢⎥⎣⎦上单调递增，所以 2min 113()224y =+=，∴min 3()4h x =，∴34a >．16．（2019·安徽合肥�高二开学考试）设函数()(2)x x f x a k a -=-+（0a >且1a ≠）是定义域为R 的奇函数. （1）求实数k 的值； （2）若3(1)2f =，22()2()x xg x a a mf x -=+-，且()g x 在[1,)+∞上的最小值为1，求实数m 的值.【答案】（1）1-；（2）1312. 【解析】（1）因为()f x 是定义域为R 的奇函数，所以(0)0f =，所以1(2)0k -+=，即1k =-，当1k =-时，()))((()x x x x x x f f x a a f x a a a x a ---⇒=---=-=-=-符合条件.（2）因为13(1)2f a a =-=，所以22320a a --=，解得2a =或12a =-（舍）. 故()()()222()22222222222x x x x x xx x g x m m ----=+--=---+，令22x x t -=-，由1x ≥，故113222t -≥-=， 所以2322,2y t mt t =-+≥函数222y t mt =-+图象的对称轴为t m =，①32m ≥时，22min 221y m m =-+=，解得1m =±（舍去）； ②32m <时，min 93214y m =-+=，解得133122m =<. 所以，1312m =.。

高一数学指数运算及指数函数试题一．选择题x x=22．若非零实数a、b、c满足，则的值等于（B）∴设=3．已知，则a等于（）解：因为4．若a＞1，b＞1，p=，则a p等于（）p=b．6．若lgx﹣lgy=2a，则=（C）lg lg=lg﹣lg=lg﹣lglg（=7．已知函数，若实数a，b满足f（a）+f（b﹣2）=0，则a+b=x+8．=（）×+1=9．设，则=（）解：∵∴（（）10．，则实数a的取值区间应为（C）=log11．若lgx﹣lgy=a，则=（A）解：12．设，则（）13．已知a，b，c均为正数，且都不等于1，若实数x，y，z满足，满足=log14．化简a2•••的结果是（C）••x y xy2x x2x x2解可得，18．若关于x的方程=3﹣2a有解，则a的范围是（A）≤a＜≥＜a＜≤≤，二．填空题19．，则m=10．+=log20．已知x+y=12，xy=9，且x＜y，则=．=x+y+2=12+6=18，故答案为：21．化简：=（或或）．．故答案为：（或或22．=1．23．函数在区间[﹣1，2]上的值域是[，8]．=；=[，[24．函数的值域为（0，8]．25．函数（﹣3≤x≤1）的值域是[3﹣9，39]，单调递增区间是（﹣2，+∞）．．y=三．解答题26．计算：（1）；（2）．）27．（1）若，求的值；（2）化简（a＞0，b＞0）．=3=．．28．已知函数f （x ）=4x﹣2x+1+3． （1）当f （x ）=11时，求x 的值；（2）当x ∈[﹣2，1]时，求f （x ）的最大值和最小值．29．已知函数||22)(x x x f -=. （1）若2)(=x f ，求x 的值；（2）若0)()2(2≥+t mf t f t 对于]2,1[∈t 恒成立，求实数m 的取值范围。

（1）当0<x 时，0)(=x f ；当0≥x 时，x x x f 212)(-=. 由条件可知 2212=-x x ，即 012222=-⋅-x x ， 解得 212±=x . 02>x ，()21log 2+=∴x . （2）当]2,1[∈t 时，021*******≥⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-t t t t t m ， 即 ()()121242--≥-t t m . 0122>-t ， ∴ ()122+-≥t m . ()]5,17[21],2,1[2--∈+-∴∈t t ，故m 的取值范围是),5[∞+-.30．如果函数)1,0(122≠>-+=a a a ay x x 在区间[—1，1]上的最大值是14，求a 的值。

高一数学指数与指数函数试题答案及解析1.已知函数的图象恒过定点，若点与点、在同一直线上，则的值为 .【答案】1.【解析】令，求得，，可得函的图象恒过定点．再根据点与点、在同一直线上，可得，化简得，即.【考点】指数函数的单调性与特殊点．2.若函数有两个零点，则实数a的取值范围为【答案】【解析】研究函数与函数图像交点个数.当时，由于直线在轴的截距大于，所以函数与函数图像在及时各有一个交点. 当时，由于单调减，直线单调增，所以函数与函数图像只3在时有一个交点.【考点】指数函数图像3.设，则，，的大小关系是（）A．B．C．D．【答案】A【解析】∵，，，∴，故选A．【考点】对数函数与指数函数的性质．4.已知幂函数的图象过点，则．【答案】4【解析】因为为幂函数,所以设因为过点,所以本题易错点在将幂函数的定义写成指数函数的形式,即【考点】幂函数定义,指数的运算5.设函数,如果，求的取值范围.【答案】【解析】对分段函数需分情况讨论，再解指数及对数不等式时，需将实数转化为同底的指数或对数，然后根据指数、对数的单调性解不等式。

试题解析：解：当2分,. 5分当时7分， 10分综上. 12分【考点】分段函数，指数、对数不等式。

6.计算:⑴ ;⑵．【答案】（1）；（2）．【解析】对于（1），主要是利用指数幂的运算性质进行化简求值；对于（2），主要是利用对数的运算性质进行化简求值，要求熟练的掌握指数幂和对数的运算性质．试题解析:（1）原式；（2）原式.【考点】本题主要考查了指数幂的运算性质和对数的运算性质，属于基础题．.7.函数在区间[0,1]上的最大值和最小值之和为．【答案】4【解析】因为在[0,1]上单调递增，在[0,1]上单调递减，所以在 [0,1]单调递增，所以y的最大值为，最小值为，所以最大值和最小值之和为4.【考点】指数函数和对数函数的单调性及利用单调性求最值8.已知，，，则这三个数从小到大排列为 .【答案】【解析】...【考点】本题考果不等的比较大小,考查指数函数与对数函数的性质.9.三个数大小的顺序是（）A．B．C．D．【答案】A【解析】由题意得，.，，，，故选A【考点】考察指数函数，和对数函数，分别与1和0的之对比.10.计算【答案】（1）.（2）44.【解析】（1）底数相同的对数先加减运算，根号化为分数指数.（2）根号化为分数指数，再用积的乘方运算.试题解析：【考点】1.对数运算，指数运算.2.分数指数，零指数等运算.11.若函数是函数的反函数，其图象过点，且函数在区间上是增函数，则正数的取值范围是．【答案】【解析】由题意可得，所以函数，由该函数在区间上是增函数，得函数在区间上为增函数，且，考虑到函数在上单调递增，所以当时，有得，当时，有即得，从而求得所求正数的取值范围为.【考点】1.反函数；2.函数的单调性；3.对数函数；4.常用函数.12.若，则=____________.【答案】-4【解析】由且得所以【考点】指数与对数运算.13.设，且，则=【答案】【解析】对等式两边同时取对数得：，，，，.【考点】对数与指数的基本运算14.设，，，则的大小关系是（）A．B．C．D．【答案】D【解析】由对数函数的性质知：，所以答案选.【考点】1.指数大小比较；2.对数函数的性质.15.计算：（1）；（2）【答案】（1）6；（2）.【解析】（1）直接采用换底公式计算即可；（2）利用指数幂的运算性质逐个运算即可.试题解析：（1）原式=（2）原式=【考点】1.换底公式的应用；2.指数幂的化简求值.16.已知函数（1）若存在，使得成立，求实数的取值范围；（2）解关于的不等式；（3）若，求的最大值.【答案】（1）（2）；②；③，，（3）【解析】（1）令，即成立 1分的最小值为0，当时取得 4分5分（2），令 6分① 7分② 8分③ⅰ 9分ⅱ 10分（3）令则12分13分，的最大值为 14分【考点】二次函数点评：主要是考查了二次函数的最值以及不等式的性质的运用，属于基础题。

+⎩ + 指数函数2.1.1 指数与指数幂的运算〔1〕根式的概念 ①如果 xn= a , a ∈ R , x ∈ R , n > 1，且 n ∈ N ，那么 x 叫做 a 的 n 次方根．当 n 是奇数时，a 的 n 次 方根用符号 n a 表示；当 n 是偶数时，正数 a 的正的 n 次方根用符号 n a 表示，负的 n 次方根用符号 - na表示；0 的 n 次方根是 0；负数 a 没有 n 次方根．②式子 n a 叫做根式，这里 n 叫做根指数， a 叫做被开方数．当 n 为奇数时， a 为任意实数；当 n 为偶数时， a ≥ 0 ．nnn n⎧a (a ≥ 0)③根式的性质：( a ) = a ；当 n 为奇数时， a = a ；当 n 为偶数时，=| a |= ⎨-a ．(a < 0)〔2〕分数指数幂的概念m①正数的正分数指数幂的意义是： a n= n a m(a > 0, m , n ∈ N , 且 n > 1) ．0 的正分数指数幂等于 0．②- m1 m1正数的负分数指数幂的意义是： an= ( ) n = n ( )m (a > 0, m , n ∈ N + , 且 n > 1) ．0 的负分数指a a数幂没有意义． 注意口诀：底数取倒数，指数取相反数． 〔3〕分数指数幂的运算性质①a r ⋅ a s = a r +s (a > 0,r , s ∈ R )②(a r )s = a rs (a > 0, r , s ∈ R )③(ab )r = a r b r (a > 0, b > 0, r ∈ R )2.1.2 指数函数及其性质〔4〕指数函数 函数名称 指数函数定义函数 y = a(a > 0 且 a ≠ 1)叫做指数函数图象a > 10 < a < 1y = 1 yOy = ax(0, 1)xy = a xy = 1Oy( 0 , 1 )x定义域 R值域 〔0,+∞〕过定点 图象过定点〔0,1〕，即当 x=0 时，y=1．奇偶性 非奇非偶单调性在 R 上是增函数在 R 上是减函数函数值的变化情况y ＞1(x ＞0), y=1(x=0), 0＜y ＜1(x ＜0)y ＞1(x ＜0), y=1(x=0), 0＜y ＜1(x ＞0)a 变化对图象影响在第一象限内， a 越大图象越高，越靠近 y 轴； 在第二象限内， a 越大图象越低，越靠近 x 轴．在第一象限内， a 越小图象越高，越靠近 y 轴； 在第二象限内， a 越小图象越低，越靠近 x 轴．n a n39 1 + 5 1 ± 5 12.1 指数函数练习1．以下各式中成立的一项〔〕A ． ( n )7 = n 7m 7mB ． 12(-3)4 =C ． 4x 3+ y 33(x + y )4D ．=2 11 1 1 1 52．化简(a 3 b 2)(-3a 2 b 3) ÷ ( 3a 6b 6 )的结果〔〕A ． 6aB ． - aC ． - 9aD ． 9a23．设指数函数 f (x ) = a x(a > 0, a ≠ 1) ，那么以下等式中不正确的选项是〔 〕A ．f (x +y )=f(x )·f (y )B ． f 〔x - y 〕=f (x )f ( y )C ． f (nx ) = [ f (x )]n(n ∈ Q )- 1D ． f (xy )n= [ f (x )]n·[ f ( y )]n(n ∈ N + )4．函数 y = (x - 5)0+ (x - 2)2A ．{x | x ≠ 5, x ≠ 2} C ．{x | x > 5}〔〕B ．{x | x > 2}D ．{x | 2 < x < 5或x > 5}5．假设指数函数 y = a x在[－1,1]上的最大值与最小值的差是1，那么底数a 等于 〔〕A ．B ． 2 2C ．D ．2 26．当 a ≠ 0 时，函数 y = ax + b 和 y = b ax的图象只可能是〔〕7．函数 f (x ) = 2-|x |的值域是〔 〕A ． (0,1]B ． (0,1)⎧⎪2- x- 1, x ≤ 0 C ． (0,+∞)D ．R8．函数 f (x ) = ⎨ 1 ，满足 f (x ) > 1的 x 的取值范围⎪⎩x 2 , x > 0〔 〕A ． (-1,1)B ． (-1,+∞)C ．{x | x > 0或x < -2}D ．{x | x > 1或x < -1}9．函数 y = ( 1 ) 2- x 2 + x +2 得单调递增区间是〔 〕11A ． [-1, ]2B ． (-∞,-1]C ． [2,+∞)D ． [ 2,2]3 - 33 3- 1 + 5 5 ± 1⎩ x e x - e - x10． f (x ) =，那么以下正确的选项是 〔 〕2A ．奇函数，在 R 上为增函数B ．偶函数，在 R 上为增函数C ．奇函数，在 R 上为减函数D ．偶函数，在 R 上为减函数11．函数 f (x )的定义域是〔1，2〕，那么函数 f (2 x) 的定义域是 .12．当 a ＞0 且 a ≠1 时，函数 f (x )=a x －2－3 必过定点 .三、解答题：13．求函数 y = 1的定义域.5 x -1 - 114．假设a ＞0，b ＞0，且a +b =c ，求证：(1)当r ＞1时，a r +b r ＜c r ；(2)当r ＜1时，a r +b r ＞c r .15．函数 f (x ) =a x - 1 a x + 1(a ＞1).〔1〕判断函数f (x )的奇偶性；〔2〕证明f (x )在(－∞，+∞)上是增函数.16．函数 f(x)＝a x (a>0，且 a ≠1)在区间[1,2]上的最大值比最小值大 a，求 a 的值． 2参考答案一、DCDDDAAD D A二、11．(0,1)；12．(2，－2)；三、13． 解：要使函数有意义必须：⎧x - 1 ≠ 0⎧x ≠ 1⎪x ⇒⎨ ≠ 0 ⎩ x - 1⎨x ≠ 0∴定义域为： {x x ∈ R 且x ≠ 0, x ≠ 1}⎪1 a +1 a +12 14． 解： a r + br⎛ a ⎫r⎛ b ⎫r，其中 0 < a < 1,0 < b < 1.= ⎪ c rc + ⎪c ⎝ ⎭ ⎝ ⎭ 当r ＞1时，⎛ a ⎫ r ⎛ b ⎫r a b ，所以a r+b r ＜c r ；⎪ + ⎪ < + = 1⎝ c ⎭ ⎝ c ⎭ c c当 r ＜1 时，⎛ a ⎫r⎛ b ⎫ra b，所以 a r +b r ＞c r . ⎪ + ⎪ > + = 1 ⎝ c ⎭ ⎝ c ⎭ c c15．解：(1)是奇函数.(2) x ＜x ，a x 1 -1 a x2 -1 。

指数与指数函数巩固训练题1．462(a b )(a, b 为正数)的结果是（ ） A. b a B. ab C. a bD. 2a b 2．化简1111132168421212121212-----⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++++ ⎪⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭，结果是（ ）A. 11321122--⎛⎫- ⎪⎝⎭B. 113212--⎛⎫- ⎪⎝⎭ C. 13212-- D. 1321122-⎛⎫- ⎪⎝⎭ 3．已知1335a -⎛⎫= ⎪⎝⎭， 1235b -⎛⎫= ⎪⎝⎭， 1332c -⎛⎫= ⎪⎝⎭，则,,a b c 的大小关系是（ ） A. c b a << B. c a b << C. a c b << D. b a c <<4．函数()12f x ⎛= ⎪⎝⎭的单调递增区间为（ ）A ．1,2⎛⎤-∞ ⎥⎝⎦B ．10,2⎡⎤⎢⎥⎣⎦C ．1,2⎡⎫+∞⎪⎢⎣⎭D ．1,12⎡⎤⎢⎥⎣⎦5．函数1x y e --=的图象大致形状是（ ）A ．B ．C ．D ． 6．若方程111042x x a -⎛⎫⎛⎫++= ⎪ ⎪⎝⎭⎝⎭有正数解，则实数a 的取值范围是（ ） A ．（0，1） B ．（﹣3，0） C ．（﹣2，0） D ．（﹣1，0）7．设,,a b c 均为正数，且133log a a =， 131log 3b b ⎛⎫= ⎪⎝⎭， 31log 3cc ⎛⎫= ⎪⎝⎭. 则（ ） A. b a c ＜＜ B. c b a ＜＜ C. c a b ＜＜ D. a b c ＜＜8．设函数()2log 2x f x x -=-， 的零点分别为1x ， 2x ，则下列结论正确的是（ ）A. 1201x x <<B. 121x x =C. 1212x x <<D. 122x x ≥9．已知函数()20ln 0x x f x x x -⎧≤=⎨->⎩关于x 的方程()()20f x f x m ++=有三个不同实数根，则m 的取值范围是（ ）A. mB. mC.D.m10．已知定义在R 上的函数()2x m f x +=（m 为实数）为偶函数，记()1213l o g 2,3,1a f b f c f m ⎛⎫⎛⎫===+ ⎪ ⎪⎝⎭⎝⎭，则,,a b c 的大小关系为（ ）A.a b c <<B.a c b <<C.c a b <<D.c b a <<11．设函数1()421x x f x +=-+-，2()lg(41)g x ax x =-+，若对任意1x R ∈，都存在2x R ∈，使12()()f x g x =，则实数a 的取值范围为（ ）A ．(0,4]B ．(,4]-∞C ．(4,0]-D ．[4,)+∞12．已知定义在R 上的奇函数()f x 和偶函数()g x 满足()()()20,1x x f x g x a a a a -+=-+>≠,若()2g a =,则()2f =（ ）A ．2B ．2a13．已知函数()132221x x x f x +++=+的最大值为M ，最小值为m ，则M+m 等于 .14.已知1(x)42x x f m +=-，()2121x x g x -=+，若存在实数,a b 同时满足方程()()0g a g b +=和()()0f a f b +=，则实数m 的取值范围 ．15.已知定义在()1,1-上的奇函数()f x ．在()1,0x ∈-时,()22x x f x -=+．（1）试求()f x 的表达式；（2）用定义证明()f x 在()1,0-上是减函数；（3）若对于()0,1x ∈上的每一个值，不等式()241x x t f x <-恒成立，求实数t 的取值范围．16．设函数()x x f x a a -=-（a ＞0且a ≠1）．（1）判断函数()f x 的奇偶性；（2）若()10f <，试判断 函数()f x 的单调性．并求使不等式()()240f x tx f x ++-<对一切x R ∈恒成立的t 的取值范围；（3）若()312f =，()()222x xg x a a mf x -=+-且()g x 在[)1,+∞ 上的最小值为2-,求m 的值．17.设函数()3x f x =,且()218f a +=，函数()()34ax x g x x R =-∈.（1）求()g x 的解析式；（2）判断函数()g x 在[]0,1上的单调性并用定义证明；（3）若方程()0g x b -=在[]2,2-上有两个不同的解，求实数b 的取值范围.18．已知函数()()2210g x ax ax b a =-++>在区间[]2,3上有最大值4和最小值 1.设()()g x f x x=. （1）求,a b 的值；（2）若不等式()22x x f k -⋅≥在[]1,1x ∈-上有解，求实数的取值范围；（3）若()2213021x x f k k --⋅-=-有三个不同的实数解，求实数的取值范围.参考答案：1．C 2.A 3.B 4.D 5.B 6.B 7.D 8.A 9.B 10.B 11.B 12.B13. 4 14. 1,2⎡⎫+∞⎪⎢⎣⎭15.（1） ()()()()()2210002201x x x x x f x x x --⎧+-<<⎪⎪==⎨⎪-+<<⎪⎩ （2）用定义证明；（3）[)0,+∞16.（1）奇函数, (2)()3,5- (3)m=217.(1) ()24x x g x =-(2)单调递减，用定义证明。

指数和指数函数一、选择题 1．（369a ）4（639a ）4等于（ ）（A ）a16（B ）a8（C ）a4（D ）a 22.若a>1,b<0,且a b+a -b=22,则a b-a -b的值等于（ ）（A ）6 （B ）±2 （C ）-2 （D ）23．函数f （x ）=(a 2-1)x在R 上是减函数，则a 的取值范围是（ ） （A ）1>a （B ）2<a （C ）a<2 （D ）1<2<a4.下列函数式中，满足f(x+1)=21f(x)的是( ) (A)21(x+1) (B)x+41 (C)2x (D)2-x5.下列f(x)=(1+a x )2xa-⋅是（ ）（A ）奇函数 （B ）偶函数 （C ）非奇非偶函数 （D ）既奇且偶函数6．已知a>b,ab 0≠下列不等式（1）a 2>b 2,(2)2a>2b,(3)b a 11<,(4)a 31>b 31,(5)(31)a <(31)b中恒成立的有（ ）（A ）1个 （B ）2个 （C ）3个 （D ）4个7．函数y=1212+-x x 是（ ）（A ）奇函数 （B ）偶函数 （C ）既奇又偶函数 （D ）非奇非偶函数 8．函数y=121-x 的值域是（ ） （A ）（-1,∞） （B ）（-,∞0）⋃（0，+∞） （C ）（-1，+∞） （D ）（-∞，-1）⋃（0，+∞）9．下列函数中，值域为R +的是（ ） （A ）y=5x-21 （B ）y=(31)1-x （C ）y=1)21(-x （D ）y=x 21- 10.函数y=2xx e e --的反函数是（ ）（A ）奇函数且在R +上是减函数 （B ）偶函数且在R +上是减函数（C ）奇函数且在R +上是增函数 （D ）偶函数且在R +上是增函数 11．下列关系中正确的是（ ）（A ）（21）32<（51）32<（21）31 （B ）（21）31<（21）32<（51）32（C ）（51）32<（21）31<（21）32（D ）（51）32<（21）32<（21）3112．若函数y=3+2x-1的反函数的图像经过P 点，则P 点坐标是（ ） （A ）（2，5） （B ）（1，3） （C ）（5，2） （D ）（3，1）13．函数f(x)=3x +5,则f -1(x)的定义域是（ ） （A ）（０，＋∞） （B ）（５，＋∞） （C ）（６，＋∞） （D ）（－∞，＋∞）14.若方程a x-x-a=0有两个根，则a 的取值范围是（ ） （A ）（1，+∞） （B ）（0，1） （C ）（0，+∞） （D ）φ15．已知函数f(x)=a x+k,它的图像经过点（1，7），又知其反函数的图像经过点（4，0），则函数f(x)的表达式是（ ）(A)f(x)=2x +5 (B)f(x)=5x +3 (C)f(x)=3x +4 (D)f(x)=4x+3 16.已知三个实数a,b=a a ,c=aaa ,其中0.9<a<1,则这三个数之间的大小关系是（ ）（A ）a<c<b （B ）a<b<c （C ）b<a<c （D ）c<a<b17．已知0<a<1,b<-1,则函数y=a x+b 的图像必定不经过（ ） (A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限 二、填空题 1．若a 23<a2,则a 的取值范围是 。

高一数学指数与指数函数试题答案及解析1.设，则的大小关系是（）.A．B．C．D．【解析】，，，因此.【考点】指数函数和对数函数的性质.2.若点在函数的图象上，则的值为．【答案】【解析】由点在函数的图象上得，所以，故应填入．【考点】指数函数及特殊角的三角函数．3.设，则下列不等式成立的是（）A．若，则B．若，则C．若，则D．若，则【答案】A【解析】对于A,B考查函数f（x）=2x+2x，g（x）=2x+3x的单调性与图象：可知函数f（x）、g（x）在R上都单调递增，若2a+2a=2b+3b，则a＞b，因此A正确；对于C,D分别考查函数u（x）=2x-2x，v（x）=2x-3x单调性与图象：当时，u′（x）＜0，函数u（x）单调递减；当时，u′（x）＞0，函数u（x）单调递增．故在x=取得最小值．当0＜x＜时，v′（x）＜0，函数v（x）单调递减；当x＞时，v′（x）＞0，函数v （x）单调递增．故在x＝取得最小值，据以上可画出图象．据图象可知：当2a-2a=2b-3b，a＞0，b＞0时，可能a＞b或a＜b．因此C,D不正确．综上可知：只有A正确．故答案为A．【考点】用导数研究函数的单调性和图象；命题的真假判断与应用．4.若，则（）A．B．C．D．【答案】D【解析】由得，所以.【考点】指对数式的互化，指数运算法则.5.若函数的图像与轴有公共点，则的取值范围是（）A．B．C．D．【答案】B【解析】函数与轴有公共点，即设函数,,有交点，函数如图: ,即,故选B.【考点】函数图像6.三个数的大小关系为（）A．B．C．D．【答案】D【解析】；；。

所以，故D正确。

【考点】指数对数函数的单调性。

7.已知幂函数的图象过点，则．【答案】4【解析】因为为幂函数,所以设因为过点,所以本题易错点在将幂函数的定义写成指数函数的形式,即【考点】幂函数定义,指数的运算8.如图，在平面直角坐标系中，过原点O的直线与函数的图象交于A，B两点，过B作y轴的垂线交函数的图象于点C，若AC平行于y轴，则点A的坐标是．【答案】【解析】设，则，因为AC平行于y轴，所以，因此.又三点三点共线，所以由得，因此.【考点】指数函数运算，向量共线.9.已知指数函数（且）的图像过点，则实数___________.【答案】【解析】因为指数函数（且）的图像过点，则，得.【考点】指数函数的定义.10.我国大西北某地区荒漠化土地面积每年平均比上一年增长，专家预测经过年可能增长到原来的倍，则函数的图像大致为（）【答案】D【解析】设初始年份的荒漠化土地面积为，则1年后荒漠化土地面积为，2年后荒漠化土地面积为，3年后荒漠化土地面积为，所以年后荒漠化土地面积为，依题意有即，，由指数函数的图像可知，选D.【考点】1.指数函数的图像与性质；2.函数模型及其应用.11.若，则下列结论正确的是（）A．B．C．D．【答案】C【解析】指数函数、对数函数的底数大于1 时,函数为增函数,反之,为减函数，对于幂函数而言，当时，在上递增，当时，在上递减，而，所以，故选C.【考点】1.指数函数；2.对数函数；3.幂函数的性质.12.设函数,如果，求的取值范围.【答案】【解析】对分段函数需分情况讨论，再解指数及对数不等式时，需将实数转化为同底的指数或对数，然后根据指数、对数的单调性解不等式。

1．分数指数幂(1)规定：正数的正分数指数幂的意义是a m n ＝na m (a >0，m ，n ∈N *，且n >1)；正数的负分数指数幂的意义是a －m n ＝1na m (a >0，m ，n ∈N *，且n >1)；0的正分数指数幂等于0；0的负分数指数幂没有意义．(2)有理数指数幂的运算性质：a s a t ＝a s ＋t ，(a s )t ＝a st ，(ab )t ＝a t b t ，其中a >0，b >0，s ，t ∈Q . 2．指数函数的图象与性质y ＝a xa >10<a <1图象定义域 (1)R 值域(2)(0，＋∞) 性质(3)过定点(0,1)(4)当x >0时，y >1；当x <0时，0<y <1 (5)当x >0时，0<y <1； 当x <0时，y >1 (6)在(－∞，＋∞)上是增函数(7)在(－∞，＋∞)上是减函数判断下面结论是否正确(请在括号中打“√”或“×”) (1)n a n ＝(na )n ＝a .( × )(2)分数指数幂a m n可以理解为mn 个a 相乘．( × )(3)(－1)24＝(－1)12＝－1.( × ) (4)函数y ＝a －x 是R 上的增函数．( × ) (5)函数y ＝21＋x a (a >1)的值域是(0，＋∞)．( × )(6)函数y ＝2x－1是指数函数．( × )1．函数f (x )＝a x －1 (a >0，且a ≠1)的图象经过定点坐标为__________． 答案 (1,1)解析 令x －1＝0得x ＝1，此时y ＝a 0＝1，所以点(1,1)与a 无关，所以函数f (x )＝a x －1(a >0，且a ≠1)的图象过定点(1,1)．2．函数f (x )＝a x －1a(a >0，a ≠1)的图象可能是______．(填图象序号)答案 ④解析 函数f (x )的图象恒过(－1,0)点，只有图象④适合． 3．计算：3×31.5×612＋lg 14－lg 25＝________.答案 1解析3×31.5×612＋lg 14－lg 25＝312×131332×316×213－lg 4－lg 25＝3－lg 100＝3－2＝1.4．若函数y ＝(a 2－1)x 在(－∞，＋∞)上为减函数，则实数a 的取值范围是________________． 答案 (－2，－1)∪(1，2)解析 由y ＝(a 2－1)x 在(－∞，＋∞)上为减函数，得0<a 2－1<1，∴1<a 2<2，即1<a <2或－2<a <－1.5．函数y ＝8－23－x (x ≥0)的值域是________． 答案 [0,8)解析 ∵x ≥0，∴－x ≤0，∴3－x ≤3， ∴0<23－x ≤23＝8，∴0≤8－23－x <8， ∴函数y ＝8－23－x 的值域为[0,8)．题型一 指数幂的运算例1 化简：(1)a 3b 23ab 2(a 14b 12)4a13-b13(a >0，b >0)；(2)(－278)－23＋(0.002)12-－10(5－2)－1＋(2－3)0.解 (1)原式＝1122323311233a b a b ab a b -⎛⎫ ⎪⎝⎭＝3111111226333＋－＋＋－－a b ＝ab －1. (2)原式＝(－278)23-＋(1500)12-－105－2＋1＝(－827)23＋50012－10(5＋2)＋1＝49＋105－105－20＋1＝－1679. 思维升华 (1)指数幂的运算首先将根式、分数指数幂统一为分数指数幂，以便利用法则计算，还应注意：①必须同底数幂相乘，指数才能相加；②运算的先后顺序． (2)当底数是负数时，先确定符号，再把底数化为正数．(3)运算结果不能同时含有根号和分数指数，也不能既有分母又含有负指数．(1)[(0.06415)－2.5]23－3338－π0＝________________________________________________________________________. (2)(14)12-·(4ab －1)3(0.1)－1·(a 3·b －3)12＝________. 答案 (1)0 (2)85解析 (1)原式＝253125641000-⎧⎫⎡⎤⎪⎪⎪⎪⎛⎫⎢⎥⎨⎬ ⎪⎢⎥⎝⎭⎪⎪⎣⎦⎪⎪⎩⎭－⎝⎛⎭⎫27813－1＝⎣⎡⎦⎤⎝⎛⎭⎫4103152()523⨯-⨯－⎣⎡⎦⎤⎝⎛⎭⎫32313－1＝52－32－1＝0. (2)原式＝2×432×a 32b32-10a 32b32-＝85. 题型二 指数函数的图象及应用例2 (1)函数f (x )＝a x－b的图象如图所示，其中a ，b 为常数，则下列结论正确的是________． ①a >1，b <0； ②a >1，b >0； ③0<a <1，b >0； ④0<a <1，b <0.(2)(2015·衡水模拟)若曲线|y |＝2x ＋1与直线y ＝b 没有公共点，则b 的取值范围是________． 答案 (1)④ (2)[－1,1]解析 (1)由f (x )＝a x －b 的图象可以观察出，函数f (x )＝a x －b 在定义域上单调递减，所以0<a <1.函数f (x )＝a x －b 的图象是在f (x )＝a x 的基础上向左平移得到的，所以b <0. (2)曲线|y |＝2x ＋1与直线y ＝b 的图象如图所示，由图象可知：如果|y |＝2x ＋1与直线y ＝b 没有公共点，则b 应满足的条件是b ∈[－1,1]．思维升华 (1)已知函数解析式判断其图象一般是取特殊点，判断所给的图象是否过这些点，若不满足则排除．(2)对于有关指数型函数的图象问题，一般是从最基本的指数函数的图象入手，通过平移、伸缩、对称变换而得到．特别地，当底数a 与1的大小关系不确定时应注意分类讨论．(3)有关指数方程、不等式问题的求解，往往利用相应的指数型函数图象，数形结合求解．(1)在同一坐标系中，函数y ＝2x 与y ＝⎝⎛⎭⎫12x的图象之间的关系，下列判断正确的是________．①关于y 轴对称； ②关于x 轴对称； ③关于原点对称；④关于直线y ＝x 对称．(2)已知函数f (x )＝|2x －1|，a <b <c 且f (a )>f (c )>f (b )，则下列结论中，一定成立的是________． ①a <0，b <0，c <0; ②a <0，b ≥0，c >0； ③2－a <2c; ④2a ＋2c <2. 答案 (1)① (2)④ 解析 (1)∵y ＝⎝⎛⎭⎫12x＝2－x ， ∴它与函数y ＝2x 的图象关于y 轴对称． (2)作出函数f (x )＝|2x －1|的图象，如图， ∵a <b <c ，且f (a )>f (c )>f (b )，结合图象知 0<f (a )<1，a <0，c >0， ∴0<2a <1.∴f (a )＝|2a －1|＝1－2a <1， ∴f (c )<1，∴0<c <1.∴1<2c <2，∴f (c )＝|2c －1|＝2c －1， 又∵f (a )>f (c )，∴1－2a >2c －1， ∴2a ＋2c <2.题型三 指数函数的图象和性质命题点1 比较指数式的大小例3 (1)下列各式比较大小正确的是________． ①1.72.5>1.73; ②0.6－1>0.62； ③0.8－0.1>1.250.2;④1.70.3>0.93.1.(2)设a ＝⎝⎛⎭⎫3525，b ＝⎝⎛⎭⎫2535，c ＝⎝⎛⎭⎫2525，则a ，b ，c 的大小关系是________． 答案 (1)②④ (2)a >c >b解析 (1)①中， ∵函数y ＝1.7x 在R 上是增函数， 2．5<3，∴1.72.5<1.73，错误；②中，∵y ＝0.6x 在R 上是减函数，－1<2， ∴0.6－1>0.62，正确；③中，∵(0.8)－1＝1.25，∴问题转化为比较1.250.1与1.250.2的大小． ∵y ＝1.25x 在R 上是增函数，0.1<0.2， ∴1.250.1<1.250.2，即0.8－0.1<1.250.2，错误； ④中，∵1.70.3>1,0<0.93.1<1， ∴1.70.3>0.93.1，正确． (2)∵y ＝⎝⎛⎭⎫25x为减函数， ∴⎝⎛⎭⎫2535<⎝⎛⎭⎫2525 即b <c ，又a c ＝⎝⎛⎭⎫3525⎝⎛⎭⎫2525＝⎝⎛⎭⎫3225>⎝⎛⎭⎫320＝1， ∴a >c ，故a >c >b .命题点2 解简单的指数方程或不等式例4 设函数f (x )＝⎩⎪⎨⎪⎧⎝⎛⎭⎫12x －7，x <0，x ，x ≥0，若f (a )<1，则实数a 的取值范围是__________．答案 (－3,1)解析 当a <0时，不等式f (a )<1可化为⎝⎛⎭⎫12a－7<1，即⎝⎛⎭⎫12a <8，即⎝⎛⎭⎫12a <⎝⎛⎭⎫12－3，因为0<12<1，所以a >－3，此时－3<a <0；当a ≥0时，不等式f (a )<1可化为a <1，所以0≤a <1.故a 的取值范围是(－3,1)．命题点3 和指数函数有关的复合函数的性质例5 设函数f (x )＝ka x －a －x (a >0且a ≠1)是定义域为R 的奇函数． (1)若f (1)>0，试求不等式f (x 2＋2x )＋f (x －4)>0的解集；(2)若f (1)＝32，且g (x )＝a 2x ＋a －2x －4f (x )，求g (x )在[1，＋∞)上的最小值．解 因为f (x )是定义域为R 的奇函数，所以f (0)＝0，所以k －1＝0，即k ＝1，f (x )＝a x －a －x . (1)因为f (1)>0，所以a －1a>0，又a >0且a ≠1，所以a >1.因为f ′(x )＝a x ln a ＋a －x ln a ＝(a x ＋a －x )ln a >0，所以f (x )在R 上为增函数，原不等式可化为f (x 2＋2x )>f (4－x )， 所以x 2＋2x >4－x ，即x 2＋3x －4>0， 所以x >1或x <－4.所以不等式的解集为{x |x >1或x <－4}． (2)因为f (1)＝32，所以a －1a ＝32，即2a 2－3a －2＝0，所以a ＝2或a ＝－12(舍去)．所以g (x )＝22x ＋2－2x －4(2x －2－x ) ＝(2x －2－x )2－4(2x －2－x )＋2.令t (x )＝2x －2－x (x ≥1)，则t (x )在(1，＋∞)为增函数(由(1)可知)，即t (x )≥t (1)＝32，所以原函数为ω(t )＝t 2－4t ＋2＝(t －2)2－2，所以当t ＝2时，ω(t )min ＝－2，此时x ＝log 2(1＋2)． 即g (x )在x ＝log 2(1＋2)时取得最小值－2. 思维升华 指数函数的性质及应用问题解题策略(1)比较大小问题．常利用指数函数的单调性及中间值(0或1)法．(2)简单的指数方程或不等式的求解问题．解决此类问题应利用指数函数的单调性，要特别注意底数a 的取值范围，并在必要时进行分类讨论．(3)解决指数函数的综合问题时，要把指数函数的概念和性质同函数的其他性质(如奇偶性、周期性)相结合，同时要特别注意底数不确定时，对底数的分类讨论．(1)已知函数f (x )＝2|2x －m |(m 为常数)，若f (x )在区间[2，＋∞)上是增函数，则m的取值范围是________．(2)函数f (x )＝⎝⎛⎭⎫1422－x x 的值域为__________． 答案 (1)(－∞，4] (2)(0,4]解析 (1)令t ＝|2x －m |，则t ＝|2x －m |在区间[m 2，＋∞)上单调递增，在区间(－∞，m2]上单调递减．而y ＝2t 为R 上的增函数，所以要使函数f (x )＝2|2x －m |在[2，＋∞)上单调递增，则有m2≤2，即m ≤4，所以m 的取值范围是(－∞，4]．(2)令t ＝x 2－2x ，则有y ＝⎝⎛⎭⎫14t，根据二次函数的图象可求得t ≥－1，结合指数函数y ＝⎝⎛⎭⎫14x的图象可得0<y ≤⎝⎛⎭⎫14－1，即0<y ≤4.4．换元法在和指数函数有关的复合函数中的应用典例 (1)函数y ＝⎝⎛⎭⎫14x －⎝⎛⎭⎫12x ＋1在区间[－3,2]上的值域是________． (2)函数f (x )＝2211()2－＋＋x x 的单调减区间为_________________________．思维点拨 (1)求函数值域，可利用换元法，设t ＝⎝⎛⎭⎫12x，将原函数的值域转化为关于t 的二次函数的值域．(2)根据复合函数的单调性“同增异减”进行探求． 解析 (1)因为x ∈[－3,2]， 所以若令t ＝⎝⎛⎭⎫12x ，则t ∈⎣⎡⎦⎤14，8， 故y ＝t 2－t ＋1＝⎝⎛⎭⎫t －122＋34. 当t ＝12时，y min ＝34；当t ＝8时，y max ＝57.故所求函数值域为⎣⎡⎦⎤34，57. (2)设u ＝－x 2＋2x ＋1，∵y ＝⎝⎛⎭⎫12u在R 上为减函数， ∴函数f (x )＝2211()2－＋＋x x 的减区间即为函数u ＝－x 2＋2x ＋1的增区间．又u ＝－x 2＋2x ＋1的增区间为(－∞，1]， ∴f (x )的减区间为(－∞，1]． 答案 (1)⎣⎡⎦⎤34，57 (2)(－∞，1]温馨提醒 (1)解决和指数函数有关的复合函数的单调性或值域问题时，要熟练掌握指数函数的单调性，搞清复合函数的结构，利用换元法转化为基本初等函数的单调性或值域问题；(2)换元过程中要注意“元”的取值范围的变化．[方法与技巧]1．通过指数函数图象比较底数大小的问题，可以先通过令x ＝1得到底数的值，再进行比较． 2．指数函数y ＝a x (a >0，a ≠1)的性质和a 的取值有关，一定要分清a >1与0<a <1. 3．对与复合函数有关的问题，要弄清复合函数由哪些基本初等函数复合而成． [失误与防范]1．恒成立问题一般与函数最值有关，要与方程有解区别开来． 2．复合函数的问题，一定要注意函数的定义域．3．对可化为a 2x ＋b ·a x ＋c ＝0或a 2x ＋b ·a x ＋c ≥0 (≤0)形式的方程或不等式，常借助换元法解决，但应注意换元后“新元”的范围．A 组 专项基础训练 (时间：40分钟)1．已知函数f (x )＝⎩⎪⎨⎪⎧2x ，x <1，f (x －2)，x ≥1，则f (log 27)的值为________．答案 74解析 由于log 24<log 27<log 28，即2<log 27<3，log 27－2＝log 274<1，因此f (log 27)＝f (log 27－2)＝f ⎝⎛⎭⎫log 274＝227log 4＝74. 2．已知a ＝22.5，b ＝2.50，c ＝(12)2.5，则a ，b ，c 的大小关系是__________．答案 a >b >c解析 a >20＝1，b ＝1，c <(12)0＝1，∴a >b >c .3．若函数f (x )＝a |2x －4|(a >0，a ≠1)，满足f (1)＝19，则f (x )的单调递减区间是____________．答案 [2，＋∞)解析 由f (1)＝19得a 2＝19，所以a ＝13或a ＝－13(舍去)，即f (x )＝(13)|2x －4|.由于y ＝|2x －4|在(－∞，2]上递减，在[2，＋∞)上递增， 所以f (x )在(－∞，2]上递增，在[2，＋∞)上递减．4．若关于x 的方程|a x －1|＝2a (a >0且a ≠1)有两个不等实根，则a 的取值范围是__________． 答案 ⎝⎛⎭⎫0，12 解析 方程|a x －1|＝2a (a >0且a ≠1)有两个实数根转化为函数y ＝|a x －1|与y ＝2a 有两个交点． ①当0<a <1时，如图(1)，∴0<2a <1，即0<a <12.②当a >1时，如图(2)，而y ＝2a >1不符合要求．综上，0<a <12.5．计算：⎝⎛⎭⎫3213-×⎝⎛⎭⎫－760＋814×42－ ⎝⎛⎭⎫－2323＝________.答案 2 解析 原式＝113133442222 2.331＋－＝⎛⎫⎛⎫⨯⨯⎪ ⎪⎝⎭⎝⎭6．已知函数y ＝a x ＋b (b >0)的图象经过点P (1,3)，如图所示，则4a －1＋1b 的最小值为______． 答案 92解析 由函数y ＝a x＋b (b >0)的图象经过点P (1,3)，得a ＋b ＝3，所以a －12＋b 2＝1，又a >1，则4a －1＋1b ＝⎝ ⎛⎭⎪⎫4a －1＋1b ⎝ ⎛⎭⎪⎫a －12＋b 2＝2＋12＋2b a －1＋a －12b ≥52＋22b a －1·a －12b＝92，当且仅当2b a －1＝a －12b ，即a ＝73，b ＝23时取等号，所以4a －1＋1b 的最小值为92. 7．已知正数a 满足a 2－2a －3＝0，函数f (x )＝a x ，若实数m 、n 满足f (m )>f (n )，则m 、n 的大小关系为________．答案 m >n解析 ∵a 2－2a －3＝0，∴a ＝3或a ＝－1(舍)．函数f (x )＝3x 在R 上递增，由f (m )>f (n )，得m >n . 8．已知函数f (x )＝2x －12x ，函数g (x )＝⎩⎪⎨⎪⎧f (x )，x ≥0，f (－x )，x <0，则函数g (x )的最小值是________． 答案 0解析 当x ≥0时，g (x )＝f (x )＝2x －12x 为单调增函数，所以g (x )≥g (0)＝0；当x <0时，g (x )＝f (－x )＝2－x －12－x 为单调减函数，所以g (x )>g (0)＝0，所以函数g (x )的最小值是0. 9．已知函数()43132－＋＝ax x f x ⎛⎫⎪⎝⎭(1)若a ＝－1，求f (x )的单调区间；(2)若f (x )有最大值3，求a 的值．解 (1)当a ＝－1时，f (x )＝⎝⎛⎭⎫13－x 2－4x ＋3，令g (x )＝－x 2－4x ＋3，由于g (x )在(－∞，－2]上单调递增，在(－2，＋∞)上单调递减，而y ＝⎝⎛⎭⎫13t 在R 上单调递减，所以f (x )在(－∞，－2]上单调递减，在(－2，＋∞)上单调递增，即函数f (x )的单调递增区间是(－2，＋∞)，单调递减区间是(－∞，－2]．(2)令g (x )＝ax 2－4x ＋3，f (x )＝⎝⎛⎭⎫13g (x )，由于f (x )有最大值3，所以g (x )应有最小值－1，因此必有⎩⎨⎧ a >0，3a －4a ＝－1，解得a ＝1，即当f (x )有最大值3时，a 的值为1.10．已知函数f (x )＝e x －e －x (x ∈R ，且e 为自然对数的底数)．(1)判断函数f (x )的单调性与奇偶性；(2)是否存在实数t ，使不等式f (x －t )＋f (x 2－t 2)≥0对一切x ∈R 都成立？若存在，求出t ；若不存在，请说明理由．解 (1)∵f (x )＝e x －⎝⎛⎭⎫1e x ，∴f ′(x )＝e x ＋⎝⎛⎭⎫1e x ，∴f ′(x )>0对任意x ∈R 都成立，∴f (x )在R 上是增函数．∴f (x )的定义域为R ，且f (－x )＝e －x －e x ＝－f (x )，∴f (x )是奇函数．(2)存在．由(1)知f (x )在R 上是增函数和奇函数，则f (x －t )＋f (x 2－t 2)≥0对一切x ∈R 都成立，⇔f (x 2－t 2)≥f (t －x )对一切x ∈R 都成立，⇔x 2－t 2≥t －x 对一切x ∈R 都成立，⇔t 2＋t ≤x 2＋x ＝⎝⎛⎭⎫x ＋122－14对一切x ∈R 都成立， ⇔t 2＋t ≤(x 2＋x )min ＝－14⇔t 2＋t ＋14＝⎝⎛⎭⎫t ＋122≤0， 又⎝⎛⎭⎫t ＋122≥0，∴⎝⎛⎭⎫t ＋122＝0，∴t ＝－12. ∴存在t ＝－12，使不等式f (x －t )＋f (x 2－t 2)≥0对一切x ∈R 都成立． B 组 专项能力提升(时间：20分钟)11．函数f (x )＝a |x ＋1|(a >0，a ≠1)的值域为[1，＋∞)，则f (－4)与f (1)的大小关系是____________． 答案 f (－4)>f (1)解析 由题意知a >1，∴f (－4)＝a 3，f (1)＝a 2，由单调性知a 3>a 2，∴f (－4)>f (1)．12．已知函数f (x )＝x －4＋9x ＋1，x ∈(0,4)，当x ＝a 时，f (x )取得最小值b ，则在直角坐标系中函数g (x )＝⎝⎛⎭⎫1a |x ＋b |的图象为________．答案 ②解析 f (x )＝x －4＋9x ＋1＝x ＋1＋9x ＋1－5≥29－5＝1，取等号时x ＋1＝9x ＋1，此时x ＝2.所以a ＝2，b ＝1，则g (x )＝⎝⎛⎭⎫12|x ＋1|.g (x )的图象可以看作是y ＝⎝⎛⎭⎫12|x |的图象向左平移一个单位得到的，②符合要求．13．关于x 的方程⎝⎛⎭⎫32x ＝2＋3a 5－a 有负数根，则实数a 的取值范围为__________．答案 ⎝⎛⎭⎫－23，34 解析 由题意，得x <0，所以0<⎝⎛⎭⎫32x <1，从而0<2＋3a 5－a<1，解得－23<a <34. 14．当x ∈(－∞，－1]时，不等式(m 2－m )·4x －2x <0恒成立，则实数m 的取值范围是________． 答案 (－1,2) 解析 原不等式变形为m 2－m <⎝⎛⎭⎫12x ，因为函数y ＝⎝⎛⎭⎫12x 在(－∞，－1]上是减函数，所以⎝⎛⎭⎫12x ≥⎝⎛⎭⎫12－1＝2，当x ∈(－∞，－1]时，m 2－m <⎝⎛⎭⎫12x 恒成立等价于m 2－m <2，解得－1<m <2.15．已知定义在实数集R 上的奇函数f (x )有最小正周期2，且当x ∈(0,1)时，f (x )＝2x4x ＋1. (1)求函数f (x )在(－1,1)上的解析式；(2)判断f (x )在(0,1)上的单调性；(3)当λ取何值时，方程f (x )＝λ在(－1,1)上有实数解？解 (1)∵f (x )是x ∈R 上的奇函数，∴f (0)＝0.设x ∈(－1,0)，则－x ∈(0,1)，f (－x )＝2－x4－x ＋1＝2x4x ＋1＝－f (x )， ∴f (x )＝－2x 4x ＋1，∴f (x )＝⎩⎪⎨⎪⎧ －2x 4x ＋1，x ∈(－1，0)，0，x ＝0，2x4x ＋1，x ∈(0，1).(2)设0<x 1<x 2<1，f (x 1)－f (x 2)＝(1222x x -)＋(221221＋2＋2－x x x x )(41x ＋1)(42x ＋1)＝(21x －22x )(1－212＋x x )(41x ＋1)(42x ＋1)， ∵0<x 1<x 2<1，1222，x x ∴< 120221＋＝，x x >∴f (x 1)－f (x 2)>0，∴f (x )在(0,1)上为减函数．(3)∵f (x )在(0,1)上为减函数，∴2141＋1<f (x )<2040＋1，即f (x )∈⎝⎛⎭⎫25，12. 同理，f (x )在(－1,0)上时，f (x )∈⎝⎛⎭⎫－12，－25. 又f (0)＝0，当λ∈⎝⎛⎭⎫－12，－25∪⎝⎛⎭⎫25，12， 或λ＝0时，方程f (x )＝λ在x ∈(－1,1)上有实数解.。