华东理工大学《物理化学》课件7.8 Arrhenius公式

物理化学公式大全物理化学是研究物质的物理性质和化学性质之间的关系的学科。

以下是一些在物理化学中常用的公式：1.热力学方程：-理想气体状态方程：PV=nRT其中P为气体压强，V为气体体积，n为气体摩尔数，R为气体常数，T为气体温度。

-内能变化公式：ΔU=q+w其中ΔU为系统内能变化，q为系统吸取或放出的热量，w为系统对外界做的功。

-能量守恒定律：ΔE=q+w其中ΔE为系统总能量变化，q为系统吸取或放出的热量，w为系统对外界做的功。

2.动力学方程：-反应速率公式：r=k[A]^m[B]^n其中r为反应速率，k为反应速率常数，[A]和[B]分别为反应物A和B的浓度，m和n为反应物的反应级数。

- Arrhenius 公式：k = A * e^(-Ea/RT)其中 k 为反应速率常数，A 为 Arrhenius 常数，Ea 为活化能，R为气体常数，T 为反应温度。

3.量子力学方程：- 波函数公式：Ψ = Σcnφn其中Ψ 为波函数，cn 为系数，φn 为基态波函数。

- Schroedinger 方程：HΨ = EΨ其中H为哈密顿算符，Ψ为波函数，E为能量。

4.热力学方程：- 熵变公式：ΔS = q_rev / T其中ΔS 为系统熵变，q_rev 为可逆过程吸放热量，T 为温度。

- Gibbs 自由能公式：ΔG = ΔH - TΔS其中ΔG 为 Gibbs 自由能变化，ΔH 为焓变化，ΔS 为熵变化，T 为温度。

5.电化学方程：- Nerst 方程：E = E° - (RT / nF) * ln(Q)其中E为电池电势，E°为标准电势，R为气体常数，T为温度，n为电子数，F为法拉第常数，Q为电化学反应的反应物浓度比。

- Faraday 定律：nF = Q其中n为电子数，F为法拉第常数，Q为电荷数。

以上公式只是物理化学中的一小部分，这里列举的是一些常见的、基本的公式，实际上物理化学领域有非常多的公式和方程可供使用。

华东理工大学（物理化学）一：系统处于热力学平衡状态的条件1.热平衡条件：T（1）=T（2）＝．．．=T(∏) =T2.力平衡条件Ｐ（1）=Ｐ（2）＝．．．=Ｐ(∏) =Ｐ3.相平衡条件μｉ（1）=μｉ（2）＝．．．=μｉ(∏) =μｉ4.化学平衡条件ΣⅴBμB＝０二：存在弯曲界面时的力平衡条件Ｐ（α）＝Ｐ（β）+ σ*ｄＡｓ/dV(α)三：对于组成恒定的均相封闭系统，公式dH m=C p,m dT 的适用条件是：衡压。

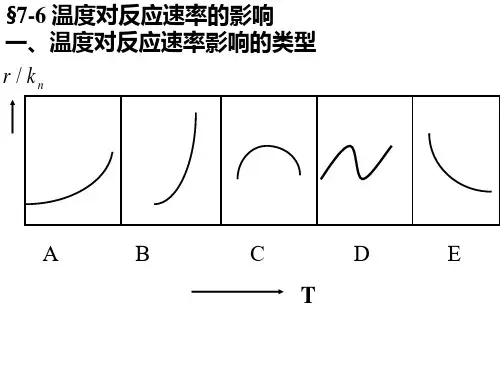
四：阿累尼乌斯方程适用范围：基元反应或有明确级数且K随温度升高增大的非基元反应。

阿累尼乌斯活化能定义：Ea=RT2d ln{k}/dT甲乙两个不同的化学反应，其活化能之间的关系是Ea（甲)大于Ea（乙)。

若将二者的温度都从Ｔ１升至Ｔ２，则甲反应的反应速率增加得快。

因为Ea越大，温度影响越显著，升高温度能更显著地加快反应速率。

五：dS≥0作为平衡判据，适用于绝热或孤立系统。

附：T环dS -δQ≥0 封闭系统，只做体积功；任意过程。

dS U,V,W’=0≥0 封闭系统，只做体积功，孤立系统或绝热过程dA T,V,W’=0≤0 恒温恒容过程dG T,P,W’=0≤0 恒温恒压过程例题：对于包含界面相σ以及两个体相，其平衡判据为：Σδ=α，β，σΣiμi（δ）dn i（δ）=0i六：热力学基本方程各种基本关系:U=Q+WH =U+PVA=U-TSG=H-TS=A+PVdS=δQ R/T对组成可变的多相多组分系统的热力学方程dG =-SdT+Vdp 的适用条件是组成恒定的均相封闭系统，只做体积功。

七：克希霍夫公式可用于计算温度对标准摩尔反应焓的影响，但是要注意其适用条件是在积分的温度范围内不能有相变化。

八：b已占体积：它相当于一摩尔气体中所有分子本身体积的4倍。

范德华方程：（p+a/V m2）(V m-b)=RT九：有关K的所有题目。

质量作用定律(反应速率与各反应物的浓度的幂乘积成正比)：只适用于基元反应.影响各种K 的因素：1.实际气体反应 Kө——仅是温度的函数K f——仅是温度的函数K p——温度、压力及组成的函数2.理想气体反应 3个都仅是温度的函数3. 液态或固态混合物中的反应Kө——仅是温度的函数K a——温度、压力的函数k x——温度、压力及组成的函数4.理想混合物中的反应 Kө——仅是温度的函数K a——温度、压力的函数K x——温度、压力的函数各种反应中K的相互关系：1.理想气体：K p= Kө(pө)ΣⅴBK p=K c(RT)ΣⅴB若ΣⅴB =0，K p=K c=Kө2.液态或固态理想混合物：Kө=K a = K x3.理想稀溶液：Kө=K a =K c (c ө)-ΣⅴB十：子配分函数(宏观性质)的析因子性质：子配分函数是相应运动形式配分函小数之积。

arrhenius 公式Arrhenius公式是研究化学反应速率与温度之间关系的重要工具。

该公式由瑞典化学家Arrhenius在1889年提出，揭示了化学反应速率与温度之间的指数关系。

这一公式在化学动力学研究中被广泛应用，对于理解和预测化学反应速率的变化具有重要意义。

Arrhenius公式可以表述为：k=Ae^(-Ea/RT)，其中k为反应速率常数，A为预指数因子，Ea为活化能，R为理想气体常数，T为反应温度。

该公式中的指数项e^(-Ea/RT)描述了温度对反应速率的影响。

根据Arrhenius公式，当温度升高时，指数项e^(-Ea/RT)的值会减小，从而导致反应速率常数k的增大。

也就是说，随着温度的升高，化学反应会更加迅速进行。

这是因为高温条件下，分子的平均动能增加，使得反应物分子能够更容易地克服反应的活化能，从而提高反应速率。

另一方面，Arrhenius公式中的预指数因子A则描述了反应速率在温度为0K时的理论值。

这个值取决于反应物分子的几何构型、反应物浓度以及反应机理等因素。

预指数因子A越大，说明反应物分子之间的碰撞频率和反应性越高，反应速率常数k也就越大。

活化能Ea是指化学反应中需要克服的能垒，也可以理解为反应物到达转变态所需的最小能量。

Arrhenius公式中的活化能Ea越大，说明反应物分子之间的碰撞需要更高的能量才能引发反应，反应速率常数k也就越小。

理想气体常数R是一个普适的常数，与化学反应的具体性质无关。

其数值为8.314 J/(mol·K)。

该常数在Arrhenius公式中起到单位换算的作用，将温度的单位从开尔文转换为摄氏度。

通过Arrhenius公式，我们可以定量地描述化学反应速率与温度之间的关系。

通过实验测定不同温度下的反应速率常数k，并利用Arrhenius公式进行拟合，可以确定预指数因子A和活化能Ea的数值。

这样，我们就能够预测在不同温度条件下反应速率的变化趋势，进一步研究和控制化学反应过程。

arrhenius 公式Arrhenius公式是描述化学反应速率与温度关系的重要公式，由瑞典化学家Arrhenius于1889年提出。

该公式为：k = A * exp(-Ea/RT)其中，k表示反应速率常数，A表示频率因子，Ea表示活化能，R表示气体常数，T表示反应温度。

Arrhenius公式揭示了温度对化学反应速率的影响。

根据公式可以看出，反应速率常数k与温度T呈指数关系，温度越高，反应速率常数越大，反应速率也就越快。

而活化能Ea则是影响反应速率的重要因素，活化能越高，反应速率常数越小，反应速率越慢。

Arrhenius公式的推导基于化学反应速率与碰撞理论。

根据碰撞理论，化学反应需要分子间的碰撞才能发生，而碰撞的能量必须大于等于活化能，才能使反应发生。

因此，活化能在反应速率中起到了关键作用。

Arrhenius公式通过引入活化能来描述反应速率与温度的关系，提供了一种定量的描述方法。

在实际应用中，Arrhenius公式被广泛用于化学反应动力学研究和工业生产中的温度控制。

通过测量不同温度下的反应速率常数，可以利用Arrhenius公式拟合出温度对反应速率的影响规律，从而预测在不同温度下的反应速率或者选择合适的反应温度。

除了温度，Arrhenius公式中的频率因子A也是一个重要参数。

频率因子A与反应物的摩尔浓度相关，代表了反应物分子在单位时间内发生反应的频率。

频率因子的确定需要实验测定或者通过理论计算得出。

Arrhenius公式的应用不仅仅局限于化学反应速率的研究，还可以推广到其他领域。

例如，在材料科学中，反应速率常数k与温度的关系可以用于研究材料的热稳定性和热分解动力学。

在生物学中，Arrhenius公式可以用于分析酶催化反应的速率与温度的关系，从而了解生物体内化学反应的特性。

Arrhenius公式是化学反应速率与温度关系的重要定量描述方法。

通过该公式，可以揭示温度对反应速率的影响规律，并在实际应用中提供了温度控制和反应速率预测的方法。

arrhenius方程简化Arrhenius方程是化学中用于描述温度对反应速率的影响的重要工具。

它由瑞典化学家Arrhenius于1889年提出，被广泛应用于化学动力学和热力学领域。

本文将介绍Arrhenius方程的基本原理和应用。

让我们来了解一下Arrhenius方程的基本形式。

Arrhenius方程可以用以下公式表示：k = A * exp(-Ea/RT)其中，k表示反应速率常数，A表示预指数因子，Ea表示活化能，R 表示气体常数，T表示反应温度。

这个方程表明，反应速率常数k 与温度T呈指数关系，且活化能Ea越大，反应速率越小。

Arrhenius方程的应用十分广泛。

首先，它可以用于预测不同温度下的反应速率。

通过测定不同温度下的反应速率常数，我们可以利用Arrhenius方程推导出反应的活化能。

这对于研究复杂的化学反应机理和优化化学工艺具有重要意义。

Arrhenius方程还可以用于推断反应的温度范围。

根据Arrhenius 方程，反应速率随温度的升高而增加，因此我们可以根据反应速率的变化情况来推断反应在哪个温度范围内进行。

Arrhenius方程还可以帮助我们理解化学反应速率与能量的关系。

活化能Ea表示反应物转变为过渡态所需的能量，而预指数因子A则表示反应物在过渡态降解为产物的速率。

通过分析A和Ea的数值大小，我们可以了解反应的难易程度和速率控制步骤。

除了以上应用，Arrhenius方程还可以用于预测和评估化学反应在不同温度下的稳定性和安全性。

通过了解反应速率和活化能的关系，我们可以避免在高温下发生剧烈的反应，从而保证实验和工业过程的安全性。

Arrhenius方程是描述温度对反应速率影响的重要工具。

通过测定反应速率常数和活化能，我们可以预测不同温度下的反应速率，推断反应的温度范围，理解反应速率与能量的关系，以及预测和评估反应的稳定性和安全性。

Arrhenius方程的应用使得我们能够更好地理解和控制化学反应过程，为化学研究和工业应用提供了重要的理论基础。

第三章 化学反应速率化学反应速率（υ）是指在一定条件下，某化学反应的反应物转变为生成物的速率。

研究化学反应速率的目的，就是要找出有关反应速率的规律并加以利用。

在实际生产中，如合成氨，人们总是希望氢气与氮气反应的速率越快越好，以便提高劳动生产率。

一些对人类不利的化学反应，如铁的生锈、金属的腐蚀、食物的变质、染料的褪色、橡胶和塑料的老化等，人们总是希望反应速率越慢越好，不发生更好，以减少损失。

因此，研究化学反应速率问题对生产实践及人类的日常生活具有重要的现实意义。

3.1化学反应速率3.1.1化学反应速率的表示方法 1.平均速率化学反应的平均速率(v ）是在定容条件下，用单位时间内某一反应物浓度的减少或生成物浓度的增加来表示。

tc t t c c v i∆∆±=--=1212 （3—1）由于反应速率只能是正值，式（3—1）中“+”表示用生成物浓度的变化表示反应速率，“-”表示用反应物浓度的变化表示反应速率；△c i 表示某物质在△t 时间内浓度的变化量，单位常用mol ·L -1；△t 表示时间的变化量，根据实际需要，单位常用秒(s)、分(min) 或时(h)等；v 是用某物质浓度变化表示的平均速率。

如反应：2N 2O 5 (g) === 4NO 2 (g) + O 2 (g)反应起始时N 2O 5 (g)浓度为1.15mol ·L —1， 100s 后测得N 2O 5 (g)浓度为1.0 mol ·L -1，则反应在100s 内的平均速率为：1131152s L mol 105.1s100L mol 15.1L mol 0.1)O N (-----⋅⋅⨯=⋅-⋅-=∆∆-=t c v如果用生成物NO 2(g)或O 2(g)浓度的变化来表示平均速率，则为：11312s L mol 100.3s1000L mol )2/415.0()NO (----⋅⋅⨯=-⋅⨯=∆∆=t c v11412s L mol 105.7s1000L mol )2/115.0()O (----⋅⋅⨯=-⋅⨯=∆∆=t c v由计算可知，分别用三种物质浓度的变化表示该反应速率的数值各不相等，这是因为它们的计量系数不相等而引起的。