2012年吉林省中考数学试题及答案解析

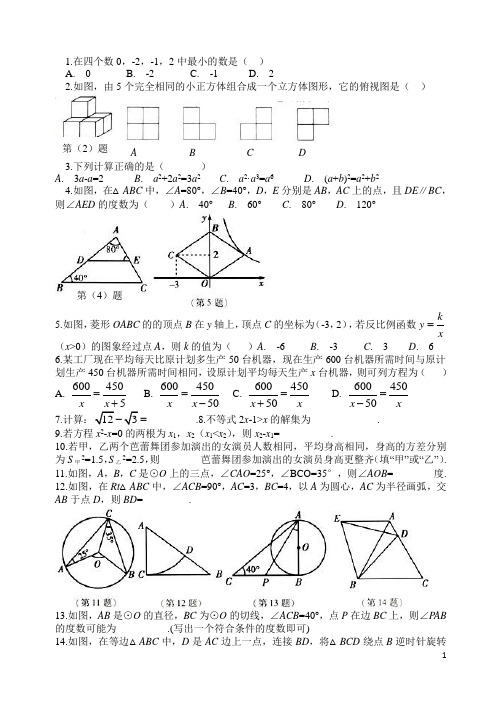
1.在四个数0，-2，-1，2中最小的数是（）A. 0B. -2C. -1D. 22.如图，由5个完全相同的小正方体组合成一个立方体图形，它的俯视图是（）3.下列计算正确的是（）A. 3a-a=2B. a2+2a2=3a2C. a2·a3=a6D. (a+b)2=a2+b24.如图，在△ABC中，∠A=80°，∠B=40°，D，E分别是AB，AC上的点，且DE∥BC，则∠AED的度数为（）A. 40°B. 60°C. 80°D. 120°5.如图，菱形OABC的的顶点B在y轴上，顶点C的坐标为（-3，2），若反比例函数kyx=（x>0）的图象经过点A，则k的值为（）A. -6 B. -3 C. 3 D. 6 6.某工厂现在平均每天比原计划多生产50台机器，现在生产600台机器所需时间与原计划生产450台机器所需时间相同，设原计划平均每天生产x台机器，则可列方程为（）A.6004505x x=+B.60045050x x=-C.60045050x x=+D.60045050x x=-7.=_________.8.不等式2x-1>x的解集为_____________.9.若方程x2-x=0的两根为x1，x2（x1<x2），则x2-x1=__________.10.若甲，乙两个芭蕾舞团参加演出的女演员人数相同，平均身高相同，身高的方差分别为S甲2=1.5，S乙2=2.5，则________芭蕾舞团参加演出的女演员身高更整齐（填“甲”或“乙”）.11.如图，A，B，C是⊙O上的三点，∠CAO=25°，∠BCO=35°，则∠AOB=________度.12.如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，以A为圆心，AC为半径画弧，交AB于点D，则BD=_________.13.如图，AB是⊙O的直径，BC为⊙O的切线，∠ACB=40°，点P在边BC上，则∠P AB 的度数可能为__________.(写出一个符合条件的度数即可)14.如图，在等边△ABC中，D是AC边上一点，连接BD，将△BCD绕点B逆时针旋转第（4）题A B C D第（2）题60°，得到△BAE ，连接ED ，若BC =10，BD =9，则△AED 的周长是___________. 15.先化简，在求值：（a +b ）(a -b )+2a 2，其中a =1，b16.如图，在东北秧歌的踩高跷表演中，已知演员身高是高跷长度的2倍，高跷与腿重合部分的长度为28cm ，演员踩在高跷上时，头顶距离地面的高度为224cm ，设演员的身高为xcm ,高跷的长度为ycm ，求x ，y 的值.17.如图，有一盘棋和一个质地均匀的正四面体骰子（各面上依次标有1，2，3，4四个数字），游戏规则是游戏者每掷依次骰子，棋子按骰子着地一面所示的数字前进相应的格数.例如：若棋子位于A 处，游戏者所掷骰子着地一面所示数字为3，则棋子由A 处前进3个方格到达B 处.请用画树形图法（或列表法）求掷骰子两次后，棋子恰好由A 处前进6个方格到达C 处的概率.18.在如图所示的三个函数图像中，有两个函数图象能近似地刻画如下a ，b 两个情景：情景a ：小芳离开家不久，发现把作业本忘在家里，于是返回家里找到了作业本再去学校； 情景b ：小芳从家出发，走了一段路程后，为了赶时间，以更快的速度前进.（1） 情景a ，b 所对应的函数图象分别为___________，______________.(填序号) （2） 请你为剩下的函数图象写出一个合适的情景.19.在平面直角坐标系中，点A 关于y 轴的对称点为点B ，点A 关于原点O 的对称点为点C . （1）若点A 的坐标为（1,2）,请你在给出的坐标系中画出△ABC .设AB 与y 轴的交点为D ，则=A D O ABCS S △△__________;（2）若点A 的坐标为（a ，b ）（ab ≠0）,则△ABC 的形状为___________.20.如图，沿AC方向开修一条公路，为了加快施工进度，要在小山的另一边寻找点E同时施工，从AC上的一点B取∠ABD=127°，沿BD的方向前进，取∠BDE=37°，测得BD=520m，并且AC，BD和DE在同一平面内.（1）施工点E离D多远正好能使A，C，E成一条直线（结果保留整数）；（2）在（1）的条件下，若BC=80m，求公路CE段得长（结果保留整数）.（参考数据：sin37°=0.60，cos37°=0.80，tan37°=0.75）.21.为了宣传节约用水，小明随机调查了某小区家庭5月份的用水情况，并将收集的数据整理成如下统计图.（1）小明一共调查了多少户家庭？（2）求所调查家庭5月份用水量的众数、平均数；（3）若该小区有400户居民，请你估计这个小区5月份的用水量.22.如图，在△ABC中，AB=AC，D为BC边上一点，以AB，BD为邻边□ABDE，连接AD，EC.（1）求证：△ADC≌△ECD;(2)若BD=CD，求证：四边形ADCE是矩形.23.如图，在扇形OAB中，∠AOB=90°，半径OA=6，将扇形OAB沿过点B的直线折叠，点O恰好落在 AB上点D处，折痕交OA于点C，求整个阴影部分的周长和面积.24.如图1，A，B，C为三个超市，在A通往C的道路（粗实线部分）上有一点D点，D与B有道路（细实线部分）相同，A与D，D与C，D与B之间的路程分别为25km，10km，5km.现计划在A通往C的道路上建一个配货中心H，每天有一辆货车只为这三个超市送货，该货车每天从H出发，单独为A送货1次，为B送货1次，为C送货2次，货车每次仅能给一家超市送货，每次送货后均返回配货中心H，设H到A的路程为xkm，这辆货车每天行驶的路程为ykm.（1）用含有x的代数式填空当0≤x≤25时.货车从H到A往返1次得路程为2xkm，货车从H到B往返1次得路程为______km.货车从H到C往返2次的路程为_________km，这辆货车每天行驶的路程y=___________km.当25<x≤35时，这辆货车每天行驶的路程y=__________;（2）请在图2中画出y与x（0≤x≤35）的函数图象；（3）配货中心H建在哪段，这辆货车每天行驶的路程最短？25.如图，在△ABC中，∠A=90°，AB=2cm,AC=4cm，动点P从点A出发，沿AB方向以1cm/s的速度向点B运动，动点Q从点B同时出发，沿BA方向以1cm/s的速度向点A运动，当点P到达B点时，P，Q两点同时停止运动，以AP为一边向上作正方形APDE，过点Q作QF∥BC，交AC于点F，设点P的运动时间为ts，正方形APDE和梯形BCFQ重合部分面积为Scm2.(1)当t=_________s时,点P与点Q重合；（2）当t=_______s时，点D在QF上；（3）当点P在Q，B两点之间（不包括Q，B两点）时，求S与t之间的函数关系式.26.问题情境如图，在x轴上有两点A(m,0)，B（n,0）（n>m>0），分别过点A，点B作x 轴的垂线，交抛物线y=x2于点C，点D，直线OC交直线BD于点E，直线OD交直线AC于点F，点E，点F的纵坐标分别为y E，y F.特例探究：填空：当m=1，n=2时，y E=________，y F =__________.当m=3，n=5时，y E=________，y F =__________.归纳证明：对任意m，n(n>m>0)，猜想y E与y F的大小关系，并证明你的猜想.拓展应用：（1）若将“抛物线y=x2”改为“抛物线y=ax2(a>0)”其他条件不变，请直接写出y E与y F的大小关系；（2）连接EF，AE.当S=3S△OFE时，直四边形OFEB接写出m与n的关系及四边形OFEA的形状.。

2012年长春市初中毕业生学业考试数 学本试卷包括七道大题，共26小题．共6页．全卷满分120分．考试时间为120分钟．考试结束后，将本试卷和答题卡一并交回． 注意事项：1．答题前，考生务必将自己的姓名、准考证号填写在答题卡上，并将条形码准确粘贴在条形码区域内． 2．答题时，考生务必按照考试要求在答题卡上的指定区域内作答，在草稿纸上、试卷上答题无效．一． 选择题（每小题3分，共24分）1. 在2、0、-2、-1这四个数中，最大的数是( ) （A ）2 (B) 0. (C) -2. (D) -1.2. 神舟九号飞船发射成功，一条相关的微博被转发了3570000次，3570000这个数用科学计数法表示为( ) (A)435710⨯． (B) 535.710⨯ (C) 61057.3⨯ (D) 73.5710⨯ 3.不等式3x-6≥0的解集为( )(A) x ＞2 (B) x ≥2. (C)x ＜2 (D)x ≤2.4. 在下列正方体的表面展开图中，剪掉1个正方形（阴影部分），剩余5个正方形组成中心对称图形的是( )5.右图是2012年伦敦奥运会吉祥物，某校在五个班级中对认识它的人数进行了调查，结果为（单位：人）：30，31，27，26，31.这组数据的中位数是( )(A) 27 (B)29 (C) 30 (D)316.有一道题目：已知一次函数y=2x+b,其中b ＜0，…，与这段描述相符的函数图像可能是( )7.如图，在Rt △ABC 中，∠C=90°．D 为边CA 延长线上的一点，DE ‖AB,∠ADE=42°，则∠B 的大小为( )(A) 42° (B) 45°(C) 48° (D)58°8. 如图，在平面直角坐标系中，在x轴、y轴的正半轴上分别截取OA、OB,使OA=OB;再分别以点A, B为圆心，以大于12AB长为半径作弧，两弧交于点C．若点C的坐标为(m-1,2n),则m与n的关系为( )(A)m+2n=1 (B)m-2n=1 (C)2n-m=1 (D)n-2m=1二、填空题（每小题3分，共18分）9.计算：23-3___10.学校购买了一批图书，共a箱，每箱有b册，将这批图书的一半捐给社区，则捐给社区的图书为册（用含a、b的代数式表示）．11.如图，⊙O与正六边形OABCDE的边OA、OE分别交于点F、G,则弧FG所对的圆周角∠FPG 的大小为度．12．如图，在△ABC中，AB=5,AC=4,点D在边AB上，∠ACD=∠B，则AD的长为.13.如图，ABCD的顶点B在矩形AEFC的边EF上，点B与点E、F不重合．若△ACD的面积为3，则图中的阴影部分两个三角形的面积和为。

2012年长春市初中毕业生学业考试(数学)参考答案本试卷包括七道大题，共26小题，共6页.全卷满分120分，考试时间为120分钟.考试结束后，将本试卷和答题卡一并交回.注意事项：1.答题前，考生务必将自己的姓名、准考证号填写在答题卡上，并将条形码准确粘贴在条形区域内.2.答题时，考试务必按照考试要求在答题卡上的指定区域作答，在草稿纸、试卷上答题无效.一. 选择题(每小题3分，共24分)1.在2、0、-2、-1这四个数中，最大的数是(A)(A) 2 (B) 0. (C) -2. (D) -1.2.神舟九号飞船发射成功，一条相关的微薄被转发了 3570000次，3570000这个数用科学计数法表示为(C)(A) 357xlO4. (B) 35.7xlO5(C) 3.57xlO6(D) 3.57xlO73.不等式3x-6>0的解集为(B)(A) x>2 (B) xN2. (C)x<2 (D)xW2.4.在下列正方体的表面展开图中，剪掉1个正方形(阴影部分)，剩余5个正方形组成中心对称图形的是(D)5.右图是2012年伦敦奥运会吉祥物，某校在五个班级中对认识它的人数进行了调查，结果为 (单位：人)：30, 31, 27, 26, 31.这组数据的中位数是(C)(A) 27 (B)29 (C) 30 (0)316.有一道题目：巳知一次函数y=2x+b,其中b<0,…，与这段描述相符的函数图像可能是(A)7.如图，在 RtAABC 中，ZC=90° . D 为边 CA 延长线上的一点，DE || AB, ZADE=42° ,则ZB 的大小为(C)8.如图，在平面直角坐标系中，在x轴、y轴的正半轴上分别截取OA、0B,使OA=OB;再分别以点A, B为圆心，以大于L AB长为半径作弧，两孤交于点C.若点C的坐标为(m-l,2n),则m2与n的关系为(B)(A)m+2n=l (B)m-2n=l (C)2n-m=l (D)n-2m=l二、填空题(每小题3分，共18分)9.计算：2吏)-也= V310.学校购买了一批图书，共a箱，每箱有b册，将这批图书的一半捐给社区，则捐给社区的图书为Lab册(用含a、b的代数式表示).2 —11.如图，。

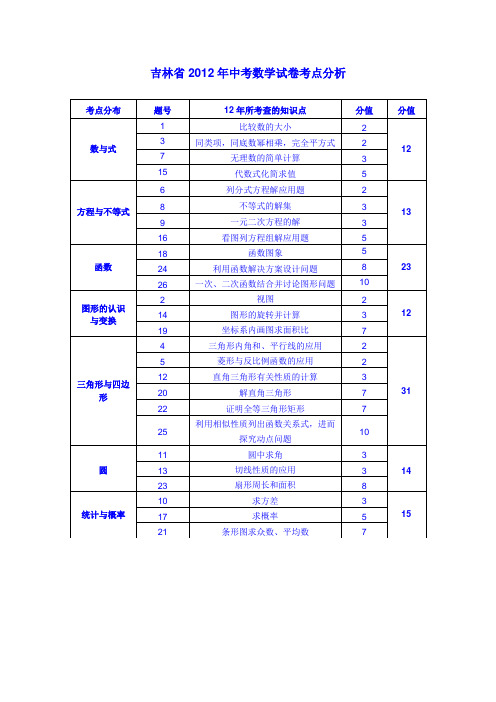
吉林省2012年中考数学试卷分析一、基本情况：本卷共有26道题，其中单项选择题6小题，填空题8小题，解答题12小题，满分120分，数与代数、图形与空间、统计与概率试题分数分别为48分、57分、15分，占总分的40%、47.5%、12.5%。

本卷十分注重体现课程标准的评价理念，题目立意新，结构合理，突出对知识发生过程以及实际应用和创新意识的考查，将传统题型与创新题型相结合，同时试题的难度表现出一定的坡度，既考察了学生是否达到课程标准所规定的毕业水平，又照顾了升学考试的分流要求。

二、试题分析（一）各考点所占分值情况：（1）数与式占12分；（2）方程与不等式占13分；（3）函数占23分；（4）图形的认识与变换占12分；（5）三角形与四边形占31分；（6）圆占14分；（7）统计与概率占15分。

（二）从试卷考查的内容来看，基本覆盖了《数学课程标准》所列的主要知识点，对初中数学的主要内容：数与式、方程、三角形、四边形、统计与概率都作了重点考查。

出现了视图、代数式化简求值、解不等式、列分式方程和二元一次方程组、二次函数图像性质、求函数解析式、等腰三角形、四边形、相似三角形、圆的相关知识、坐标系画图、统计与概率计算等考点。

（三）注重基础知识和基本技能的考查。

试题利用填空题、选择题和解答题三种题型，全面考查了初中数学的基础知识和基本技能。

有不少题目紧扣课标，源于课本，又着重于对考生能力的考查。

从试题分布情况来看，直接运用有关知识进行解答的容易题和稍难题近70%，试题编排从最基本的知识（数的比较）开始，由易到难，逐步提高难度，学生动手很容易。

选择题、填空题基本上是课本练习题的改编，解答题中的大部分题目都立足于考查初中数学核心的基础知识、基本技能和基本数学思想方法，如15题先化简再求值，16题列方程组解应用题，17题求概率，18题函数图象，20题解直角三角形，都是历年中考的热点，也是考查的核心部分。

（四）评卷过程中发现的学生答题存在的问题：1、选择题（1—6）选择题是电脑自动阅卷，看不到答题情况，从试题上看，选择题突出了对学生基础知识和基本技能的考查，试题难度不大。

2012年长春市初中毕业生学业考试数 学本试卷包括七道大题，共26小题.共6页．全卷满分120分．考试时间为120分钟．考试结束后，将本试卷和答题卡一并交回． 注意事项：1．答题前，考生务必将自己的姓名、准考证号填写在答题卡上，并将条形码准确粘贴在条形码区域内．2．答题时，考生务必按照考试要求在答题卡上的指定区域内作答，在草稿纸、试题卷上答题无效．一、选择题（每小题3分，共24分） 1．在2，0，2-，1-这四个数中，最大的数是（A ）2. （B ）0. （C ）2-. （D ）1-.2．神舟九号飞船发射成功，一条相关的微博被转发了3 570 000次．3 570 000这个数用科学记数法表示为（A ）357×104． （B ）35.7×105． （C ）3.57×106． （D ）3.57×107． 3．不等式3x -6≥0的解集为（A ）2x >． （B ）x ≥2． （C ）2x <． （D ）x ≤2．4．在下列正方体的表面展开图中，剪掉1个正方形（阴影部分），剩余5个正方形组成中心对称图形的是（A ） （B ） （C ） （D ）5．右图是2012年伦敦奥运会吉祥物,某校在五个班级中对认识它的人数进行了调查，结果为（单位：人）：30,31,27,26,31. 这组数据的中位数是 （A ）27. （B ）29. （C ）30.（D ）31. 6．有一道题目： ，与这段描述相符的函数图象可能是（A ） （B ） （C ） （D ） 7．如图，在Rt ∆ABC 中，90C ∠=︒,D 为边CA 延长线上一点，DE //AB ,∠ADE =42︒，则∠B 的大小为（A ）42︒. （B ）45︒. （C ）48︒. （D ）58︒.已知一次函数2y x b =+，其中b<0,…（第5题）（第7题）（第8题）8．如图，在平面直角坐标系中，在x轴、y轴的正半轴上，分别截取OA、OB，使OA=OB；再分别以点A、B为圆心，以大于12AB长为半径作弧，两弧交于点C.若点C的坐标为（1m-，2n），则m与m的关系为（A）21m n+= .（B）21m n-=.（C）21n m-=.（D）21n m-=.二、填空题（每小题3分，共18分）9．计算：= .10．学校购买了一批图书，共a箱，每箱有b册.将这批图书的一半捐给社区，则捐给社区的图书有册（用含a、b的代数式表示）.11．如图，⊙O与正六边形OABCDE的边OA、OE分别交于点F、G，则⌒FG所对的圆周角∠FPG 的大小为度.(第11题) (第12题)12．如图，在∆ABC中，AB=5,AC=4,点D在边AB上，若ACD∠=B∠,则AD的长为.13．如图，□ABCD的顶点B在矩形AEFC的边EF上，点B与点E、F不重合.若ACD∆的面积为3，则图中阴影部分两个三角形的面积和为.(第13题) (第14题)14．如图，在平面直角坐标系中，点A是抛物线2(3)y a x k=-+与y轴的交点，点B是这条抛物线上另一点.且AB//x轴，则以AB为边的等边三角形ABC的周长为.三、解答题（每小题5分，共20分）15．先化简，再求值：2(2)(2)2(3)a a a+-++，其中13a=．16.有甲、乙两个不透明的口袋，甲袋中有3个球，分别标有数字0,2,5；乙袋中有3个球，分别标有数字0,1,4 .这6个球除所标数字以外没有任何其他区别.从甲、乙两袋各随机摸出1个球，用画树状图（或列表）的方法，求摸出的两个球上数字之和是6的概率.2数学试题 第 页（共 6 页）317. 某班有45名同学参加紧急疏散演练.对比发现：经专家指导后，平均每秒撤离的人数是指导前的3倍，这45名同学全部撤离的时间比指导前快30秒.求指导前平均每秒撤离的人数.18. 如图，在同一平面内，有一组平行线1l 、2l 、3l ，相邻两条平行线之间的距离均为4.点O 在直线1l 上，⊙O 与直线3l 的交点为A 、B ，AB =12，求⊙O 的半径.四、解答题（每小题6分，共12分）19．长春市某校准备组织七年级学生游园．供学生选择的游园地点有：东北虎园、净月潭、长影世纪城，每名学生只能选择其中一个地点．该校学生会从七年级学生中随机抽取了a 名学生，对他们选择各游园地点的情况进行了调查，并根据调查结果绘制成如下条形统计图．（1）求a 的值.（2）求这a 名学生选择去净月潭游园的学生人数的百分比.（3）按上述调查结果，估计该校七年级650名学生中选择去净月潭游园的人数.20．如图，有一个晾衣架放置在水平地面上.在其示意图中，支架OA 、OB 的长均为108cm ，支架OA 与水平晾衣杆OC 的夹角AOC 为59º，求支架两个着地点之间的距离AB ．（结果精确到0.1cm ）【参考数据：sin59º=0.86,cos59º=0.52,tan59º=1.66】4五、解答题（每小题6分，共12分）21. 图①、图②均为44⨯的正方形网格，线段AB 、BC 的端点均在格点上. 按要求在图①、图②中以AB 和BC 为边各画一个四边形ABCD .要求：四边形ABCD 的顶点D 在格点上，且有两个角相等（一组或两组角相等均可）；所画的两个四边形不全等.22. 如图，在平面直角坐标系中，□ABCO 的顶点A 、C 的坐标分别为A (2,0) 、C (1-,2),反比例函数(0)ky k x=≠的图象经过点B . （1）求k 的值.（2）将□ABCO 沿x 轴翻折，点C 落在点C ＇处.判断点C ’是否落在反比例函数(0)ky k x=≠的图象上，请通过计算说明理由.六、解答题（每小题7分，共14分）23．某加工厂为赶制一批零件，通过提高加工费标准的方式调动工人积极性.工人每天加工零件获得的加工费y （元）与加工个数x （个）之间的部分函数图象为折线OA -AB -BC ，如图所示.（1）求工人一天加工零件不超过20个时每个零件的加工费. （2）求40≤x ≤60时y 与x 的函数关系式.（3）小王两天一共加工了60个零件，共得到加工费220元.在这两天中，小王第一天加工零件不足20个，求小王第一天加工的零件个数.数学试题 第 页（共 6 页）5 24．感知：如图①，点E 在正方形ABCD 的BC 边上，BF ⊥AE 于点F ，DG ⊥AE 于点G .可知△ADG ≌△BAF .(不要求证明)拓展：如图②，点B 、C 在∠MAN 的边AM 、AN 上，点E 、F 在∠MAN 内部的射线AD上, ∠1 、∠2分别是△ABE 、△CAF 的外角.已知AB =AC ，∠1 =∠2= ∠BAC .求证：△ABE ≌△CAF .应用：如图③，在等腰三角形ABC 中， AB =AC ，AB >BC .点D 在边BC 上，CD =2BD ，点E 、F 在线段AD 上，∠1=∠2=∠BAC .若△ABC 的面积为9，则△ABE 与△CDF 的面积之和为 .七、解答题（每小题10分，共20分）25. 如图，在平面直角坐标系中，直线242y x =-+交x 轴于点A ，交直线y x =交于点B .抛物线22y ax x c =-+分别交线段AB 、OB 于点C 、D ，点C 和点D 的横坐标分别为16和4，点P 在这条抛物线上. (1)求点C 、D 的纵坐标. (2)求a 、c 的值.(3)若Q 为线段OB 上一点，且P 、Q 两点的纵坐标都为5，求线段PQ 的长.(4)若Q 为线段OB 或线段AB 上一点，PQ ⊥x 轴.设P 、Q 两点之间的距离为d （d >0），点Q 的横坐标为m ，直接写出d 随m 的增大而减小时m 的取值范围.【参考公式：二次函数2y ax bx c =++（a ≠0）图象的顶点坐标为24()24,b ac b a a --】26.如图，在Rt △ABC 中,∠ACB =90°，AC =8cm ,BC =4cm ,D 、E 分别为边AB 、BC 的中点，连结DE .点P 从点A 出发，沿折线AD -DE -EB 运动,到点B 停止．点P 在AD的速度运动，在折线DE -EB 上以1cm/s 的速度运动.当点P 与点A 不重合时，过点P 作PQ ⊥AC 于点Q ，以PQ 为边作正方形PQMN ，使点M 落在线段AC 上.设点P 的运动时间为t （s ）.（1）当点P 在线段DE 上运动时，线段DP 的长为 cm （用含t 的代数式表示）. （2）当点N 落在AB 边上时，求t 的值.（3）当正方形PQMN 与△ABC 重叠部分图形为五边形时，设五边形的面积为S (cm 2)，求S与t的函数关系式.（4）连结CD.当点N与点D重合时，有一点H从点M出发，在线段MN上以2.5cm/s 的速度沿M-N-M连续做往返运动，直至点P与点E重合时，点H停止往返运动；当点P在线段EB上运动时，点H始终在线段MN的中点处.直接写出在点P的整个运动过程中,点H落在线段CD上时t的取值范围.6数学试题 第 页（共 6 页）7 2012年长春市初中毕业生学业考试数学参考答案及评分标准一、选择题（每小题3分，共24分）1．A 2．C 3．B 4．D 5．C 6．A 7．C 8．D 二、填空题（每小题3分，共18分） 910．2ab 11．60 12．16513．3 14．18 三、解答题（每小题5分，共20分）15．解：原式=22242632a a a -++=+． （3分）当13a =时，原式=2173()233⨯+=． （5分） 16．解：（3分）∴P （两个数字之和是6）=29． （5分） 17． 解：设指导前平均每秒撤离x 人． （1分）根据题意，得4545303x x-=． （3分） 解得1x =.经检验，1x =是原方程的解，且符合题意．答：指导前平均每秒撤离1人． （5分）18. 解：过点O 作OC ⊥AB 于C ，连结OA ． （1分）∴1112622AC AB ==⨯=． 在Rt △AOC 中，∠ACO =90°，OC =428⨯=， （3分） ∴10OA =．∴⊙O 的半径为10 ． （5分）或8四、解答题（每小题6分，共12分） 19．解：（1）18201250++=，所以a 值为50. （2分） （2）20100%40%50⨯=， 所以这50名学生选择去净月潭游园的人数的百分比为40%. （4分） （3）650×40％=260(人).所以该校七年级650名学生中会选择净月潭游园的人数约为260人.（6分）20．解：过点O 作OD ⊥AB 于D . （1分）∵OA =OB , ∴ AB=2 AD ． ∵CO ∥AB ,∴∠OAD =∠AOC =59º . （2分） 在Rt △ADO 中，∠ADO =90，cos ADOAD OA∠=， （4分） ∵OA =108，∴cos 108cos591080.5256.16AD OA OAD =⋅∠=⨯=⨯=. ∴AB =2×56.16=112.32≈112.3(cm).答：支架两个着地点之间的距离AB 约为112.3cm ． (6分)五、解答题（每小题6分，共12分） 21．解：以下答案供参考．画对一个得3分，共6分．(画出符合要求的凹四边形同样赋分)22．解：（1） ∵四边形OABC 是平行四边形，∴CB = OA , CB ∥OA . ∵A (2，0) ,C (1-，2),∴B （1，2）. （3分）数学试题 第 页（共 6 页）9 ∵反比例函数ky x=(k ≠0)的图象经过点B ， ∴21k=，2k =. （4分） （2） 点C ＇在反比例函数2y x=的图象上.理由：由翻折可知，点C ＇与点C 关于x 轴对称， ∵C (1-，2)， ∴C ＇（－1，－2）.由（1）知，反比例函数解析式为 2y x= . ∵当1x =-时，221y ==--， ∴点C ＇在反比例函数2y x=的图象上. (6分)六、解答题（每小题7分，共14分） 23．解：（1）∵60320=（元）， ∴工人一天加工零件不超过20个时每个零件的加工费为3元. （1分） （2）当40≤x ≤60 时，设y 与x 的函数关系式为y kx b =+.∵图象经过（40,140）、（60,240）,∴40140,60240.k b k b +=⎧⎨+=⎩解得5,60.k b =⎧⎨=-⎩∴当40≤x ≤60 时，y 与x 的函数关系式为560y x =- . （4分） （3）设小王第一天加工a 个零件,则第二天加工(60)a -个零件.∵小王第一天加工零件不足20个， ∴0≤a ＜20. ∴40＜60a -≤60. 根据题意，得()356060220a a +--= . 解得a =10.∴小王第一天加工10个零件. (7分)24.拓展: ∵1ABE BAE ∠=∠+∠， BAC CAF BAE ∠=∠+∠,又∵1BAC ∠=∠,∴ABE BAE CAF BAE ∠+∠=∠+∠.10∴ABE CAF ∠=∠. (2分) ∵∠1 =∠2, 1180AEB ∠+∠=︒，2180CFA ∠+∠=︒,∴AEB CFA ∠=∠. (4分) 又∵AB =AC ，∴△ABE ≌△CAF . (5分)应用: 6 (7分) 七、解答题（每小题10分，共20分）25．解：（1）在242y x =-+中，当x =16时，y =10.在y x =中，当x =4时y =4.∴点C 的纵坐标为10，点D 的纵坐标为4. （2分） （2）由（1）知，点C 的坐标为(16,10)，点D 的坐标为(4,4).∵抛物线图象经过点C 、D ，∴2563210,168 4.a c a c -+=⎧⎨-+=⎩解得1,810.a c ⎧=⎪⎨⎪=⎩ ∴a 的值为18， c 的值为10. （4分） （3） 在y x =中，当x =5时y =5.∴点Q 的横坐标为5.由（2）可知，抛物线的解析式为212108y x x =-+. 当y =5时，2121058x x -+=，解得8x =±∴点P的横坐标为8±①当点P 在点Q 左侧时，线段PQ的长为5(83--=. ②当点P 在点Q 右侧时，线段PQ的长为(853+-=+ ∴线段PQ的长为3或3+（8分） （4）当0≤m ＜4或12≤m ＜16时，d 随m 增大而减小. (10分)26．解：（1）（2t -） （不要求写t 的取值范围） （1分）（2）①当点P 在线段DE 上时，如图①.PD = PN =PQ =2.数学试题 第 页（共 6 页） 11 ∴22t -=.∴t =4.②当点P 在线段BE 上时，如图②.PN =2PB .∵PN =PC =(t －6)+2=t －4，BP=2-(t －6)=8－t ，∴42(8)t t -=-,解得 203t =. ∴当点N 落在AB 边上时，t 的值为4或203. （3分） （3）①当2＜t ＜4时，如图③，S =2212(4)4t --， 即2124S t t =-+. ②当203＜t ＜8时，如图④， S =()221(4)3204t t ---, 即2522844S t t =-+-. （7分） （4）143t =或5t =或6≤t ≤8. （10分） 提示：当点H 第一次落在线段CD 上时，12.5(4)(4)22t t -+-=，解得143t =. 当点H 第二次落在线段CD 上时，12.5(4)2(4)2t t --=-，解得5t =. 当点H 第三次落在线段CD 上时，16 2.5(4)(4)2t t --=-，解得6t =. 当6≤t ≤8时，点H 恒在线段CD 上.。

2012年长春市初中毕业生学业考试 数 学 试 卷 解 析本试卷包括七道大题，共26小题，共6页．全卷满分120分，考试时间为120分钟．考试结束后，将本试卷和答题卡一并交回． 注意事项：1. 答题前，考生务必将自己的姓名、准考证号填写在答题卡上，并将条形码准确粘贴在条形区域内． 2. 答题时，考试务必按照考试要求在答题卡上的指定区域作答，在草稿纸、试卷上答题无效． 一． 选择题（每小题3分，共24分） 1. 在2、0、-2、-1这四个数中，最大的数是（A ） 2. (B) 0. (C) -2. (D) -1.解析：A 根据正数大于0,0大于负数。

考查知识：有理数的大小比较2. 神舟九号飞船发射成功，一条相关的微薄被转发了3570000次，3570000这个数用科学计数法表示为(A)435710⨯． (B) 535.710⨯ (C) 61057.3⨯ (D) 73.5710⨯解析：C 3570000=3.57×1000000=61057.3⨯ 。

考查知识：科学计数法3.不等式3x-6≥0的解集为(A) x ＞2 (B)x ≥2. (C)x ＜2 (D)x ≤2.解析：B 3x-6≥0 x 3≥6 x ≥2。

考查知识：解不等式4. 在下列正方体的表面展开图中，剪掉1个正方形（阴影部分），剩余5个正方形组成中心对称图形的是解析：D 根据中心对称图形的概念可得。

考查知识：解不等式中心对称图形的概念5.右图是2012年伦敦奥运会吉祥物，某校在五个班级中对认识它的人数进行了调查，结果为（单位：人）：30，31，27，26，31.这组数据的中位数是(A) 27 (B)29 (C) 30 (D)31解析：C 根据中位数是把数据从小到大的顺序排列，取中间的数。

考查知识：中位数的计算6.有一道题目：已知一次函数y=2x+b,其中b＜0，…，与这段描述相符的函数图像可能是解析：A 一次函数y=2x+b,当b＜0时交y轴负半轴。

2012年吉林省中考数学试卷参考答案与试题解析一、选择题（每小题2分，共12分）1．（2012•吉林）在四个数0，﹣2，﹣1，2中，最小的数是（）A．0B．﹣2C．﹣1D．22．（2012•吉林）如图，有5个完全相同的小正方体组合成一个立方体图形，它的俯视图是（）A．B．C．D．3．（2012•吉林）下列计算正确的是（）A．3a﹣a=2B．a2+2a2=3a2C．a2•a3=a6D．（a+b）2=a2+b2 4．（2012•吉林）如图，在△ABC中，∠A=80°，∠B=40°．D、E分别是AB，AC上的点，且DE∥BC，则∠AED的度数是（）A．40°B．60°C．80°D．120°5．（2012•吉林）如图，菱形OABC的顶点B在y轴上，顶点C的坐标为（﹣3，2），若反比例函数y=（x＞0）的图象经过点A，则k的值为（）A．﹣6B．﹣3C．3D．66．（2012•吉林）某工厂现在平均每天比原计划多生产50台机器，现在生产600台机器所需的时间与原计划生产450台机器所需时间相同．设原计划每天生产x台机器，则可列方程为（）A．B．C．D．二、填空题（每小题3分，共24分）7．（2012•吉林）计算：= ．8．（2012•吉林）不等式2x﹣1＞x的解集为．9．（2012•吉林）若方程x2﹣x=0的两根为x1，x2（x1＜x2），则x2﹣x1= ．10．（2012•吉林）若甲，乙两个芭蕾舞团参加演出的女演员人数相同，平均身高相同，身高的方差分别为=1.5，=2.5，则芭蕾舞团参加演出的女演员身高更整齐（填：“甲”或“乙”）．11．（2012•吉林）如图，A，B，C是⊙O上的三点，∠CAO=25°，∠BCO=35°，则∠AOB=度．12．（2012•吉林）如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，以点A为圆心，AC长为半径画弧，交AB于点D，则BD= ．13．（2012•吉林）如图，AB是⊙O的直径，BC为⊙O的切线，∠ACB=40°，点P在边BC上，则∠PAB的度数可能为（写出一个符合条件的度数即可）14．（2012•吉林）如图，在等边△ABC中，D是边AC上一点，连接BD．将△BCD绕点B逆时针旋转60°得到△BAE，连接ED．若BC=10，BD=9，则△AED的周长是．三、解答题（每小题5分，共20分）15．（2012•吉林）先化简，再求值：（a+b）（a﹣b）+2a2，其中a=1，b=．16．（2012•吉林）如图，在东北大秧歌的踩高跷表演中，已知演员身高是高跷长度的2倍，高跷与腿重合部分的长度为28cm，演员踩在高跷上时，头顶距离地面的高度为224cm．设演员的身高为xcm，高跷的长度为ycm，求x，y 的值．17．（2012•吉林）如图，有一游戏棋盘和一个质地均匀的正四面体骰子（各面依次标有1，2，3，4四个数字）．游戏规则是游戏者每掷一次骰子，棋子按着地一面所示的数字前进相应的格数．例如：若棋子位于A处，游戏者所掷骰子着地一面所示数字为3，则棋子由A处前进3个方格到达B处．请用画树形图法（或列表法）求掷骰子两次后，棋子恰好由A处前进6个方格到达C处的概率．18．（2012•吉林）在如图所示的三个函数图象中，有两个函数图象能近似地刻画如下a，b两个情境：情境a：小芳离开家不久，发现把作业本忘在家里，于是返回了家里找到了作业本再去学校；情境b：小芳从家出发，走了一段路程后，为了赶时间，以更快的速度前进．（1）情境a，b所对应的函数图象分别是、（填写序号）；（2）请你为剩下的函数图象写出一个适合的情境．四、解答题（每小题7分，共28分）19．（2012•吉林）在平面直角坐标系中，点A关于y轴的对称点为点B，点A关于原点O的对称点为点C．（1）若A点的坐标为（1，2），请你在给出的坐标系中画出△ABC．设AB与y轴的交点为D，则= ；（2）若点A的坐标为（a，b）（ab≠0），则△ABC的形状为．20．（2012•吉林）如图，沿AC方向开山修一条公路，为了加快施工速度，要在小山的另一边寻找点E同时施工．从AC上的一点B取∠ABD=127°，沿BD的方向前进，取∠BDE=37°，测得BD=520m，并且AC，BD和DE在同一平面内．（1）施工点E离D多远正好能使成A，C，E一条直线（结果保留整数）；（2）在（1）的条件下，若BC=80m，求公路段CE的长（结果保留整数）．（参考数据：sin37°=0.60，cos37°=0.80，tan37°=0.75）21．（2012•吉林）为宣传节约用水，小明随机调查了某小区部分家庭5月份的用水情况，并将收集的数据整理成如下统计图．（1）小明一共调查了多少户家庭？（2）求所调查家庭5月份用水量的众数、平均数；（3）若该小区有400户居民，请你估计这个小区5月份的用水量．22．（2012•吉林）如图，在△ABC中，AB=AC，D为边BC上一点，以AB，BD为邻边作▱ABDE，连接AD，EC．（1）求证：△ADC≌△ECD；（2）若BD=CD，求证：四边形ADCE是矩形．五、解答题（每小题8分，共16分）23．（2012•吉林）如图，在扇形OAB中，∠AOB=90°，半径OA=6．将扇形OAB沿过点B的直线折叠，点O恰好落在上点D处，折痕交OA于点C，求整个阴影部分的周长和面积．24．（2012•吉林）如图1，A，B，C为三个超市，在A通往C的道路（粗实线部分）上有一D点，D与B有道路（细实线部分）相通．A与D，D与C，D与B之间的路程分别为25km，10km，5km．现计划在A通往C的道路上建一个配货中心H，每天有一辆货车只为这三个超市送货．该货车每天从H出发，单独为A送货1次，为B送货1次，为C送货2次．货车每次仅能给一家超市送货，每次送货后均返回配货中心H，设H到A的路程为xkm，这辆货车每天行驶的路程为ykm．（1）用含的代数式填空：当0≤x≤25时，货车从H到A往返1次的路程为2xkm，货车从H到B往返1次的路程为km，货车从H到C往返2次的路程为km，这辆货车每天行驶的路程y= ．当25＜x≤35时，这辆货车每天行驶的路程y= ；（2）请在图2中画出y与x（0≤x≤35）的函数图象；（3）配货中心H建在哪段，这辆货车每天行驶的路程最短？六、解答题（每小题10分，共20分）25．（2012•吉林）如图，在△ABC中，∠A=90°，AB=2cm，AC=4cm．动点P从点A出发，沿AB方向以1cm/s的速度向点B运动，动点Q从点B同时出发，沿BA方向以1cm/s的速度向点A运动．当点P到达点B时，P，Q两点同时停止运动，以AP为一边向上作正方形APDE，过点Q作QF∥BC，交AC于点F．设点P的运动时间为ts，正方形和梯形重合部分的面积为Scm2．（1）当t= s时，点P与点Q重合；（2）当t= s时，点D在QF上；（3）当点P在Q，B两点之间（不包括Q，B两点）时，求S与t之间的函数关系式．26．（2012•吉林）问题情境如图，在x轴上有两点A（m，0），B（n，0）（n＞m＞0）．分别过点A，点B作x轴的垂线，交抛物线y=x2于点C、点D．直线OC交直线BD于点E，直线OD交直线AC于点F，点E、点F的纵坐标分别记为y E，y F．特例探究填空：当m=1，n=2时，y E= 2 ，y F= 2 ；当m=3，n=5时，y E= 15 ，y F= 15 ．归纳证明对任意m，n（n＞m＞0），猜想y E与y F的大小关系，并证明你的猜想．拓展应用（1）若将“抛物线y=x2”改为“抛物线y=ax2（a＞0）”，其他条件不变，请直接写出y E与y F的大小关系；（2）连接EF，AE．当S四边形OFEA=3S△OFE时，直接写出m与n的关系及四边形OFEA的形状．2012年吉林省中考数学试卷参考答案与试题解析一、选择题（每小题2分，共12分）考点：有理数大小比较。