中考三角函数应用题

三角函数专项训练（中考23题）1.如图，在菱形ABCD 中，AE ⊥BC ，E 为垂足，cosB= 54，EC=2， （1）求菱形ABCD 的边长．（2）若P 是AB 边上的一个动点，则线段EP 的长度的最小值是多少？2.如图，在矩形ABCD 中，CE ⊥BD 于点E ，BE=2，DE=8，则tan ∠ACE 的值为（ ） A ．21 B ．34 C ．43 D ．23.如图，水坝的横断面是梯形，迎水坡AD 的坡角∠A=45°，背水坡BC 的坡度为31，坝顶DC 宽25米，坝高45米，求：（1）背水坡的坡角；（2）坝底AB 的长．4.小刚在一山坡上依次插了三根木杆，第一根木杆与第二根木杆插在倾斜角为30°，且坡面距离是6米的坡面上，而第二根与第三根又在倾斜角为45°，且坡面距离是8米的坡面上．则第一根与第三根木杆的水平距离是______米．（如图）（精确到0.01米）5.如图，是学校背后山坡上一棵原航空标志的古柏树AB 的示意图，在一个晴天里，数学教师带领学生进行测量树高的活动．通过分组活动，得到以下数据： 一是AC 是光线的方向，并且测得水平地面2m 的竹竿影长为0.5m ．二是测得树在斜坡上影子BC 的长为10m ；三是测得影子BC 与水平线的夹角∠BCD 为30°；请你帮助计算出树的高度AB（根号 3 =1.732，精确到0.1m）．6.如图，在航线l的两侧分别有观测点A和B，点A到航线l的距离为2km，点B位于点A北偏东60°方向且与A相距10km处．现有一艘轮船从位于点B南偏西76°方向的C处，正沿该航线自西向东航行，5min后该轮船行至点A的正北方向的D处．（1）求观测点B到航线l的距离；（2）求该轮船航行的速度（结果精确到0.1km/h）．（参考数据：3 ≈1.73，sin76°≈0.97，cos76°≈0.24，tan76°≈4.01）7.如图，某高速公路建设中需要确定隧道AB的长度．已知在离地面1500m，高度C处的飞机，测量人员测得正前方A、B两点处的俯角分别为60°和45°，求隧道AB的长．8.如图，某防洪指挥部发现长江边一处长500米，高10米，背水坡的坡角为45°的防洪大堤（横断面为梯形ABCD）急需加固．经调查论证，防洪指挥部专家组制定的加固方案是：背水坡面用土石进行加固，并使上底加宽3米，加固后背水坡EF的坡比i=1：根号3 ．（1）求加固后坝底增加的宽度AF；（2）求完成这项工程需要土石多少立方米？（结果保留根号）9.在日常生活中，我们经常看到一些窗户上安装着遮阳蓬，如图（1）．现在要为一个面向正南的窗户设计安装一个遮阳蓬，已知该地区冬天正午太阳最低时，光线与水平线的夹角为34°．夏天正午太阳最高时，光线与水平线的夹角为76°．把图（1）画成图（2），其中AB表示窗户的高，BCD表示直角形遮阳蓬．（1）遮阳蓬BCD怎样设计，才能正好在冬天正午太阳最低时光线最大限度地射入室内而夏天正午太阳最高时光线刚好不射入室内，请在图（3）中画图表示；（2）已知AB=150cm，在（1）的条件下，求出BC，CD的长度．（精确到1cm）10.两艘渔船同时从O点出发，甲船以40海里/小时的速度沿北偏东45°的方向航行，乙船沿正东方向航行，2小时后甲船到达小岛P处，发现乙船恰好位于甲船正南方向的H处，以O为坐标原点，建立如图所示的直角坐标系．（1）P点的坐标是______，乙船的速度是______海里/小时（结果保留根号）；（2）若乙船发现正东方向有另一小岛M，且M位于P点南偏东60°的方向上，若乙船速度不变，它再航行多长时间可以到达小岛M？（根号3 取1.7，结果保留两个有效数字）．11.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验：先在公路旁边选取一点C，再在笔直的车道l上确定点D，使CD与l垂直，测得CD的长等于21米，在l上点D的同侧取点A、B，使∠CAD=30°，∠CBD=60°．（1）求AB的长（精确到0.1米，参考数据：根号3 =1.732，根号2 =1.414）；（2）已知本路段限速为50千米/小时，若测得某辆汽车从A到B用时2秒，这辆车是否超速？说明理由．12.如图是某货站传送货物的平面示意图．为了提高传送过程的安全性，工人师傅欲减小传送带与地面的夹角，使其由45°改为30°．已知原传送带AB长为4米．如果需要在货物着地点C的左侧留出2米的通道，试判断距离B点4米的货物MNPQ是否需要挪走，通过计算说明理由．13.小明要测量河的宽度．如图所示是河的一段，两岸ABCD，河岸AB上有一排大树．小明先用测角仪在河岸CD的M处测得∠α=36°，然后沿河岸走50米到达N点，测得∠β=72°．请你根据这些数据帮小明算出河宽．（参考数据：sin36°≈0.59，cos36°≈0.81，tan36°≈0.73，sin72°≈0.95，cos72°≈0.31，tan72°≈3.08）14.如图．是一座人行天桥的示意图，天桥的高是10米，坡面的倾斜角为45°，为了方便行人安全过天桥，市政部门决定降低坡度，使新坡面的倾斜角为30°．若新坡脚前需留2.5米的人行道，问离原坡脚10米的建筑物是否需要拆除？请说明理由．15.如图，甲楼AB的高度为123m，自甲楼楼顶A处，测得乙楼顶端C处的仰角（参考数据：sin31°为45°，测得乙楼底部D处的俯角为31°，求乙楼CD的高度．≈0.52，cos31°≈0.86，tan31°≈0.60，结果精确到1m）．16.如图，在某中学教学楼A西南方向510米的C处，有一辆货车以60km/h的速度沿北偏东60°方向的道路CF行驶、（1）若货车以60km/h的速度行驶时其噪声污染半径为100米，试问教学楼是否受到货车噪声的影响？（2）假设货车以60km/h的以上速度行驶时，其行驶速度每增加10km/h时其噪声污染半径约增大15米，要使教学楼不受货车的噪声影响，在此路段应该限速多少？（精确到10km/h)17.如图所示，小杨在广场上的A处正面观测一座楼房墙上的广告屏幕，测得屏幕下端D处的仰角为30°，然后他正对大楼方向前进5m到达B处，又测得该屏幕上端C处的仰角为45°．若该楼高为26.65m，小杨的眼睛离地面1.65m，广告屏幕的上端与楼房的顶端平齐．求广告屏幕上端与下端之间的距离．（3≈1.732，结果精确到0.1m）18.如图，矩形ABCD是供一辆机动车停放的车位示意图．请你参考图中数据（BC=2.2m，CD=5.4m，∠DCF=40°），计算车位所占街道的宽度EF．（参考数据：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84，结果精确到0.1m．）19.小楠家附近的公路上通行车辆限速为60千米/小时．小楠家住在距离公路50米的居民楼（如图中的P点处），在他家前有一道路指示牌MN正好挡住公路上的AB段（即点P、M、A和点P、N、B分别在一直线上），已知MN∥AB，∠MNP=30°，∠NMP=45°，小楠看见一辆卡车通过A处，7秒后他在B处再次看见这辆卡车，他认定这辆卡车一定超速，你同意小楠的结论吗？请说明理由．20.如图所示，A，B两地之间有条河，原来从A地到B地需要经过桥DC，沿折线A⇒D⇒C⇒B到达．现在新建了桥EF，可直接沿直线AB从A地到达B地．已知BC=11km，∠A=45°，∠B=37°，桥DC和AB平行，则现在从A地到B地可比原来少走多少路程（结果精确到0.1km．参考数据： sin37°≈0.60，cos37°≈0.80）21.如图，河流的两岸PQ、MN互相平行，河岸PQ上有一排小树，已知相邻两树之间的距离CD=50米，某人在河岸MN的A处测得∠DAN=35°，然后沿河岸走了120米到达B处，测得∠CBN=70°．求河流的宽度CE（结果保留两个有效数字）．（参考数据：sin35°≈0.57，cos35°≈0.82，tan35°≈0.70，sin70°≈0.94，cos70°≈0.34，tan70°≈2.75）22.如图，某旅游区有一个景观奇异的望天洞，点D是洞的入口，游人从入口进洞游览后，要经山洞到达山顶的出口凉亭A处观赏旅游区风景，最后做缆车沿索道AB返回山脚下的B处．在同一平面内，若测得斜坡BD的长为100米，坡角∠DBC=10°，在A处测得的仰角∠ABC=40°，在D处测得的仰角∠ADF=45°，过点D做地面BE的垂线，垂足为点C．（1）求∠ADB的度数；（2）求索道AB的长（结果仅保留根号）．23.如图是一座人行天桥的示意图，天桥的高BC为10米，坡面AC的坡角为53°．（1）求AB的长度．（精确到0.01米）（2）为了方便行人推车过天桥，市政部门决定降低坡度，使新坡面DC的坡角为30°，且新的坡角外侧需留3米宽的人行道，问离原坡角12米的建筑物EF是否需要拆除？24.为缓解“停车难”的问题，某单位拟建筑地下停车库，建筑设计师提供了该地下停车库的设计示意图，按规定，地下停车库坡道口上方要张贴限高标志，以便告知停车人车辆能否安全驶入，为标明限高，请你根据该图计算CE．（精确到0.1m）（下列数据提供参考：sin20°=0.3420，cos20°=0.9397，tan20°=0.3640）25.如图，A、B是两座现代化城市，C是一个古城遗址，C城在A城的北偏东30°，在B城的北偏西45°，且C城与A城相距120千米，B城在A城的正东方向，以C为圆心，以60千米为半径的圆形区域内有古迹和地下文物，现要在A、B两城市修建一条笔直的高速公路．（1）请你计算公路的长度（保留根号）；（2）请你分析这条公路有没有可能对文物古迹造成损毁，并说明理由．26.人民海关缉私巡逻艇在东海海域执行巡逻任务时，发现在其所处位置O点的正北方向10海里处的A点有一涉嫌走私船只，正以24海里/小时的速度向正东方向航行．为迅速实施检查，巡逻艇调整好航向，以26海里/小时的速度追赶，在涉嫌船只不改变航向和航速的前提下，问：（1）需要几小时才能追上（点B为追上时的位置）？（2）确定巡逻艇的追赶方向．（精确到0.1°）参考数据：sin66.8°≈0.9191；cos66.8°≈0.393sin67.4°≈0.9231；cos67.4°≈0.3846sin68.4°≈0.9298；cos68.4°≈0.3681sin70.6°≈0.9432；cos70.6°≈0.3322．27.如图，为了测量河宽，在河的一边沿岸选取A、B两点，对岸岸边有一块石头C．在△ABC中，测得∠A=60°，∠B=45°，AB=60米．（1）求河宽（用精确值表示，保留根号）；（2）如果对岸岸边有一棵大树D，且CD∥AB，并测得∠DAB=37°，求C、D两点之间的距离（结果精确到0.1米）．（参考数据： sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，cot37°≈1.33）28.如图，在一个坡角为15°的斜坡上有一棵树，高为AB．当太阳光与水平线成50°时，测得该树在斜坡上的树影BC的长为7m，求树高．（精确到0.1m）29.阳光明媚的一天，数学兴趣小组的同学测量学校旗杆AB的高度（如图），发现旗杆AB的影子刚好落在水平面BC和斜坡的CD上，其中BC=48米，CD=4米，斜坡CD的坡角为27°．同一时刻，测得高为1米标杆的影长是2.5米．求出旗杆AB的高度？（结果精确到0.01米）。

中考三角函数的应用专题训练1、如图，小刚同学在綦江南州广场上观测新华书店楼房墙上的电子屏幕CD，点A是小刚的眼睛，测得屏幕下端D处的仰角为30°，然后他正对屏幕方向前进了6米到达B处，又测得该屏幕上端C处的仰角为45°，延长AB与楼房垂直相交于点E，测得BE=21米，请你帮小刚求出该屏幕上端与下端之间的距离CD．（结果保留根号）2、丁丁想在一个矩形材料中剪出如图阴影所示的梯形，作为要制作的风筝的一个翅膀．请你根据图中的数据帮丁丁计算出BE、CD的长度（精确到个位，≈1.7）．3、为倡导“低碳生活”，常选择以自行车作为代步工具，如图1所示是一辆自行车的实物图．车架档AC 与CD的长分别为45cm，60cm，且它们互相垂直，座杆C E的长为20cm，点A，C，E在同一条直线上，且∠CAB=75°，如图2．（1）求车架档AD的长；（2）求车座点E到车架档AB的距离．（结果精确到1cm．参考数据：sin75°≈0.9659，cos75°≈0.2588，tan75≈3.7321）4、生活经验表明，靠墙摆放的梯子，当50°≤α≤70°时（α为梯子与地面所成的角），能够使人安全攀爬．现在有一长为6米的梯子AB，试求能够使人安全攀爬时，梯子的顶端能达到的最大高度AC．（结果保留两个有效数字，sin70°≈0.94，s in50°≈0.77，cos70°≈0.34，cos50°≈0.64）（355、如图，在昆明市轨道交通的修建中，规划在A 、B 两地修建一段地铁，点 B 在点 A 的正东方向，由于 A 、B 之间建筑物较多，无法直接测量，现测得古树 C 在点 A 的北偏东 45°方向上，在点 B 的北偏西 60°方向上，BC=400m ，请你求出这段地铁 AB 的长度． 结果精确到 1m ，参考数据： 2 ≈ 1.414，3 ≈ 1.732 ）6、如图，甲、乙两船同时从港口出发，甲船以 60 海里/时的速度沿北偏东 60°方向航行，乙船沿北偏西 30° 方 向 航行， 半小 时后甲 船到达 C 点， 乙船正 好到 达甲船 正西 方向的 B 点，求 乙船 的速度．7．某校课外活动小组，在距离湖面7 米高的观测台 A 处，看湖面上空一热气球 P 的仰角为 37°，看 P 在 湖中的倒影 P’的俯角为 53°，（P ’为 P 关于湖面的对称点），请你计算出这个热气球 P 距湖面的高度 PC 约为多少米？3 4 3注：sin37°≈ ，cos37°≈ ，tan37°≈ ;5 5 4 P4 4 Sin53°≈ ，cos53°≈ ，tan53°≈5 3A 37°53°湖面BCP'8、某校兴趣小组坐游轮拍摄海河两岸美景．如图，游轮出发点A与望海楼B的距离为300m．在一处测得望海校B位于A的北偏东30°方向．游轮沿正北方向行驶一段时间后到达C．在C处测得望海楼B位于C的北偏东60°方向．求此时游轮与望梅楼之间的距离BC(3取l.73．结果保留整数)．9、如图，飞机沿水平方向（A、B两点所在直线）飞行，前方有一座高山，为了避免飞机飞行过低，就必须测量山顶M到飞行路线AB的距离MN.飞机能够测量的数据有俯角和飞行的距离（因安全因素，飞机不能飞到山顶的正上方N处才测飞行距离），请设计一个距离MN的方案，要求：(1)指出需要测量的数据（用字母表示，并在图中标出)；(2)用测出的数据写出求距离MN的步骤.A B NM(9题图)10、放风筝是大家喜爱的一种运动．星期天的上午小明在大洲广场上放风筝．如图他在A处时不小心让风筝挂在了一棵树的树梢上，风筝固定在了D处．此时风筝线AD与水平线的夹角为30°．为了便于观察．小明迅速向前边移动边收线到达了离A处7米的B处，此时风筝线BD与水平线的夹角为45°．已知点A、B、C在冋一条直线上，∠ACD=90°．请你求出小明此吋所收回的风筝线的长度是多少米？（本题中风筝线均视为线段，≈1.414，≈1.732．最后结果精确到1米）11、在一次数学课外活动中，一位同学在教学楼的点A处观察旗杆BC，测得旗杆顶部B的仰角为30°，测得旗杆底部C的俯角为60°，已知点A距地面的高AD为15cm．求旗杆的高度．12、如图，一艘船以每小时60海里的速度自A向正北方向航行，船在A处时，灯塔S在船的北偏东30°，航行1小时后到B处，此时灯塔S在船的北偏东75°，（运算结果保留根号）（1）求船在B处时与灯塔S的距离；（2）若船从B处继续向正北方向航行，问经过多长时间船与灯塔S的距离最近．13、某校初三课外活动小组，在测量树高的一次活动中．如图所示，测得树底部中心A到斜坡底C的水平距离为8.8m，在阳光下某一时刻测得l米的标杆影长为0.8m，树影落在斜坡上的部分CD=3.2m，已知斜坡CD的坡比i=1:3，求树高AB．（结果保留整数，参考数据：3≈1.7）．14、我市某建筑工地，欲拆除该工地的一危房AB(如图)，准备对该危房实施定向爆破．已知距危房AB水平距离60米（BD＝60米）处有一居民住宅楼，该居民住宅楼CD高15米，在该该住宅楼顶C处测得此危房屋顶A的仰角为30°，请你通过计算说明在实施定向爆破危房AB时，该居民住宅楼有无危险？(在地面上以点B为圆心，以AB长为半径的圆形区域为危险区域，参考数据:2≈1.414，3≈1.732)A30°C15、如图，在亚丁湾一海域执行护航任务的我海军某军舰由东向西行驶．在航行到B处时，发现灯塔A 在我军舰的正北方向500米处；当该军舰从B处向正西方向行驶至达C处时，发现灯塔A在我军舰的北偏东60°的方向．求该军舰行驶的路程．（计算过程和结果均不取近似值）16、如图，某校综合实践活动小组的同学欲测量公园内一棵树DE的高度．他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°，朝着这棵树的方向走到台阶下的点C处，测得树顶端D 的仰角为60°．已知A点的高度AB为2米，台阶AC的坡度为1:3(即AB：BC=1:3)，且B、C、E三点在同一条盲线上。

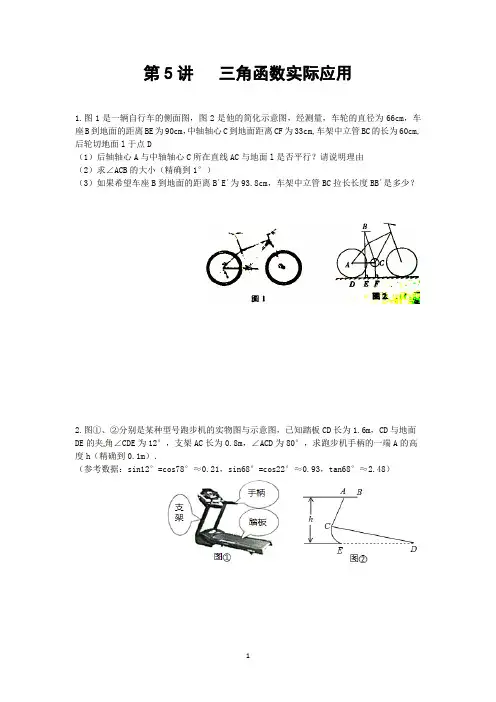
第5讲三角函数实际应用1.图1是一辆自行车的侧面图，图2是他的简化示意图，经测量，车轮的直径为66cm，车座B到地面的距离BE为90cm，中轴轴心C到地面距离CF为33cm,车架中立管BC的长为60cm,后轮切地面l于点D（1）后轴轴心A与中轴轴心C所在直线AC与地面l是否平行？请说明理由（2）求∠ACB的大小（精确到1°）（3）如果希望车座B到地面的距离B´E´为93.8cm，车架中立管BC拉长长度BB´是多少？2.图①、②分别是某种型号跑步机的实物图与示意图，已知踏板CD长为1.6m，CD与地面DE的夹角∠CDE为12°，支架AC长为0.8m，∠ACD为80°，求跑步机手柄的一端A的高度h（精确到0.1m）．（参考数据：sin12°=cos78°≈0.21，sin68°=cos22°≈0.93，tan68°≈2.48）3.如图1，某种三角形台历被放置在水平桌面上，其左视图如图2所示，其中点O是台历支架OA,OB 的交点，同时又是台历顶端连接日历的螺旋线圈所在圆的圆心，现测得OA=OB=14cm，CA=CB=4cm,∠ACB=120°（1）求点O到直线AB的距离（2）求张角∠AOB的大小（3）把某月的日历从台历支架正面翻到背面（即OB与OA重合），求点B所经历路径长（参考：sin14.33°≈0.25，cos14.33°≈0.97，tan14.33°≈0.26，π取 3.14，所有结果精确到0.01）4.如图，李华晚上在两盏相距50cm的路灯下来回踱步，已知李华的身高AB=1.7m,灯柱高OP=OP´=8.5m,两灯柱之间的距离OO´=50m，（1）若李华距灯柱OP´的水平距离OA=xm,他的影子AC=ym,求y关于x的函数关系式（2）若李华在两路灯之间行走，则他前后两个影子的长度和（DA+AC）是否发生变化？请说明理由5.图1是小华在健身器材上进行仰卧起坐锻炼时情景．图2是小华锻炼时上半身由EM 位置运动到与地面垂直的EN 位置时示意图．已知BC=0.64米，AD=0.24米，AB=1.30米． （1）求AB 的倾斜角α的度数（精确到1）；（2）若测得EN=0.85米，试算小华头顶由M 点运动到N 点的路径 MN 长度（精确到0.01米）（参考数据：sin18︒≈0.31,cos18︒≈0.95,tan18︒≈0.32）6如图，某投影仪E 正对投影幕布AB 中央，其距离EG=3.60米，为方便教学，现将投影幕布由黑板正中AB 位置调整到左面DB 位置处，测得AB=BD=2.6米，∠DBC=39.85°，此时投影仪E 调整到线段EB 上点F 处且恰好正对投影幕布DB 中央，若投影仪与投影幕布安装距离控制在3.45米到3.65米之间视觉效果最好，则调整后投影仪F 与投影幕布BD 之间的距离是否符合要求？（参考数据：tan70.15°≈2.770，tan70°≈2.747，cos39.85°≈0.7677，tan39.85°≈0.8346，可用科学计算器，结果精确到0.01）图1图2BCED AM α N7.下图是躺椅结构示意图，扶手AB与座板CD都平行于地面，靠背DM与支架OE平行，前支架OE与后支架OF分别与CD交于点G和点D，AB与DM交于点N，∠EOF=90°，∠ODC=30°，ON=40cm,EG=30cm, (1)求两支架落点E,F之间的距离(2)若MN=60cm,求躺椅高度（点M到地面的距离，结果取整数）8.身高1.65米的兵兵在建筑物前放风筝，风筝不小心挂在了树上，在如图所示的平面图形中，矩形CDEF代表建筑物，兵兵位于建筑物前点B处，风筝挂在建筑物上方的树枝点G处（点G在FE的延长线上），经测量，兵兵与建筑物的距离BC=5米，建筑物底部宽FC=7米，风筝所在点G与建筑物顶点D及风筝线在手中的点A在同一条直线上，点A据地面的高度AB=1.4米，风筝线与水平线夹角为37°。

九年级三角函数应用题1.在某高速公路建设中，需要确定隧道AB的长度。

已知在离地面1500m高度C处的飞机上，测量人员测得正前方A、B两点处的俯角分别为60°和45°。

求隧道AB的长度（3≈1.73）。

2.在一次数学活动课上，老师带领学生去测一条南北流向的河的宽度。

如图所示，某学生在河东岸点A处观测到河对岸水边有一点C，测得C在A北偏西31°的方向上。

沿河岸向北前行40米到达B处，测得C在B北偏西45°的方向上。

请根据以上数据求这条河的宽度（参考数值：tan31°≈0.6）。

3.甲、乙两船同时从港口出发。

甲船以60海里/时的速度沿XXX方向航行，乙船沿北偏西30°方向航行。

半小时后，甲船到达C点，乙船正好到达甲船正西方向的B点。

求乙船的速度。

4.港口B在港口A的西北方向。

上午8时，一艘轮船从港口A出发，以15海里/时的速度向正北方向航行。

同时，一艘快艇从港口B出发也向正北方向航行。

上午10时，轮船到达D处，同时快艇到达C处。

测得C处在D处的北偏西30°的方向上，且C、D两地相距100海里。

求快艇每小时航行多少海里（结果精确到0.1海里/时，参考数据2≈1.41，3≈1.73）。

5.平放在地面上的直角三角形铁板ABC的一部分被沙堆掩埋，其示意图如图所示。

量得角A为54°，斜边AB的长为2.1m，BC边上露出部分BD长为0.9m。

求铁板BC边被掩埋部分CD的长（结果精确到0.1m，参考数据sin54°=0.81，cos54°=0.59，tan54°=1.38）。

6.如图，放置在水平桌面上的台灯的灯臂AB长为40cm，灯罩BC长为30cm，底座厚度为2cm，灯臂与底座构成的∠BAD=60°。

使用发现，光线最佳时灯罩BC与水平线所成的角为30°，此时灯罩顶端C到桌面的高度CE是多少cm（结果精确到0.1cm，参考数据3≈1.732）。

中考数学三角函数汇编(总16页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--24题汇编1. 如图，在一笔直的海岸线上有A、B两个观测站，A在B的正东方向，23=BP（单位：km）。

有一艘小船停在点P处，从A测得小船在北偏西60°的方向，从B测得小船在北偏东45°的方向。

（1）求A、B两观测站之间的距离；（2）小船从点P处沿射线AP的方向以3千米／时的速度进行沿途考察，航行一段时间后到达点C处，此时，从B测得小船在北偏西15°的方向，求小船沿途考察的时间。

（结果有根号的保留根号）2. 如图，在哈市轨道交通的修建中，规划在A、B两地修建地铁2号线，点B在点A 的正东方向，由于A、B之间建筑物较多，无法直接测量，现测得点C在点A的北偏东45°方向上，在点B的北偏西60°方向上，BC = 400 m ，请你求出这段地铁AB的长度。

（结果精确到1m，参考数据：732.13,414.12≈≈）23. 如图，AB、CD为两个建筑物，建筑物AB的高度为60米，从建筑物AB的顶部A 点测得建筑物CD的顶部C点的俯角∠EAC为30°，测得建筑物CD的底部D点的俯角∠EAD为45°。

（1）求两建筑物底部之间水平距离BD的长度；（2）求建筑物CD的高度（结果保留根号）。

4. 如图，我市某乡镇学校教学楼后面靠近一座山坡，BC∥AD，斜坡AB=40米，坡角∠BAD=60°，为防夏季因暴雨引发山体滑坡，学校决定对山坡进行改造，经地质人员勘测，当坡角不超过45°时，可确保山体不滑坡，改造时保持坡脚A不动，从坡顶B沿BC削进到E处，问BE至少是多少米？3（结果保留根号）。

5. 如图，一艘轮船位于灯塔B的正西方向A处，且A处与灯塔B相距60海里，轮船沿东北方向匀速航行，速度为20海里／时。

（1）多长时间后轮船行驶到灯塔B的西北方向；（2）轮船不改变航向行驶到达位于灯塔B的北偏东15°方向上的C处，求灯塔B到C 处的距离。

初中三角函数应用题10道(1)求步道AC 的长度（结果保留根号）；(2)游客中心Q 在点A 的正东方向，步道AC 与步道BQ 交于点P 小明和爸爸分别从B 处和A 处同时出发去游客中心，小明跑步的速度是每分钟请计算说明爸爸的速度要达到每分钟多少米，他俩可同时到达游客中心．0.1）（参考数据：2 1.414≈，3 1.732≈，6 2.449≈）2．（2023春·重庆沙坪坝·九年级重庆八中校考阶段练习）下图是儿童游乐场里的一个娱乐项目转飞椅的简图，该设施上面有一个大圆盘（圆盘的半径是 3.5OA =米），圆盘离地面的高度1 6.5OO =米，且1OO ⊥地面l ，圆盘的圆周上等间距固定了一些长度相等的绳子，绳子的另一端系着椅子（将椅子看作一个点，比如图中的点B 和1B ），当旋转飞椅静止时绳子是竖直向下的，如图中的线段AB ，绳长为4.8米固定不变．当旋转飞椅启动时，圆盘开始旋转从而带动绳子和飞椅一起旋转，旋转速度越大，飞椅转得越高，当圆盘旋转速度达到最大时，飞椅也旋转到最高点，此时绳子与竖直方向所成的夹角为57α=︒．（参考数据：sin 570.84︒≈，cos570.55︒≈，tan 57 1.54︒≈）(1)求飞椅离地面的最大距离（结果保留一位小数）；(2)根据有关部门要求，必须在娱乐设施周围安装安全围栏，而且任何时候围栏和飞椅的水平距离必须超过2米．已知该旋转飞椅左侧安装有围栏EF ，且EF l ⊥，19.8O E =米，请问圆盘最大旋转速度的设置是否合规？并说明理由．3．（2023春·重庆渝北·九年级校联考阶段练习）如图，某大楼的顶部竖有一块宣传牌AB ，小明在斜坡的坡脚D 处测得宣传牌底部B 的仰角为45︒，沿斜坡DE 向上走到E 处测得宣传牌顶部A 的仰角为31︒，已知斜坡DE 的坡度3:4，10DE =米，22DC =米，求宣传牌AB 的高度．（测角器的高度忽略不计，参考数据：sin 310.52︒≈，cos310.86︒≈，tan 310.6)︒≈。

专题08《三角函数的实际应用》题型一、利用仰角和俯视解决问题【例1】如图为放置在水平桌面上的台灯的平面示意图，灯臂AO长为40cm，与水平面所形成的夹角∠OAM为75°．由光源O射出的边缘光线OC，OB与水平面所形成的夹角∠OCA，∠OBA分别为90°和30°，求该台灯照亮水平面的宽度BC（不考虑其他因素，结果精确到0.1cm．温馨提示：sin75°≈0.97，cos75°≈0.26，）．【变式1-1】小明在楼高AB＝15米的楼顶A处测得一电视塔底部C的俯角为31°，测得塔顶D的仰角为52°，求楼顶A到塔顶D的距离（结果保留整数）．（参考数据：sin31°＝0.52，cos31°＝0.86，tan31°＝0.80，sin52°＝0.79，cos52°＝0.62，tan52°＝1.28）【变式1-2】如图，C地在A地的正东方向，因有大山阻隔，由A地到C地需绕行B地．已知B地位于A地北偏东67°方向，距离A地520km，C地位于B地南偏东30°方向．若打通穿山隧道，建成两地直达高铁，求A地到C地之间高铁线路的长．（结果保留整数）（参考数据：sin67°≈，cos67°≈，tan67°≈，≈1.73）【变式1-3】如图，两幢建筑物AB和CD，AB⊥BD，CD⊥BD，AB＝15m，CD＝20m．AB 和CD之间有一景观池，小双在A点测得池中喷泉处E点的俯角为42°，在C点测得E点的俯角为45°，点B、E、D在同一直线上．求两幢建筑物之间的距离BD．（结果精确到0.1m）【参考数据：sin42°＝0.67，cos42°＝0.74，tan42°＝0.90】【例2】如图，小明想测山高和索道的长度．他在B处仰望山顶A，测得仰角∠B＝31°，再往山的方向（水平方向）前进80m至索道口C处，沿索道方向仰望山顶，测得仰角∠ACE ＝39°．（1）求这座山的高度（小明的身高忽略不计）；（2）求索道AC的长（结果精确到0.1m）．（参考数据：tan31°≈，sin31°≈，tan39°≈，sin39°≈）【变式2-1】为了测量竖直旗杆AB的高度，某综合实践小组在地面D处竖直放置标杆CD，并在地面上水平放置一个平面镜E，使得B，E，D在同一水平线上（如图所示）．该小组在标杆的F处通过平面镜E恰好观测到旗杆顶A（此时∠AEB＝∠FED），在F处测得旗杆顶A 的仰角为45°，平面镜E的俯角为67°，测得FD＝2.4米．求旗杆AB的高度约为多少米？（结果保留整数，参考数据：sin67°≈，cos67°≈，tan67°≈）【变式2-2】如图，为了测量山顶铁塔AE的高，小明在27m高的楼CD底部D测得塔顶A的仰角为45°，在楼顶C测得塔顶A的仰角36°52′．已知山高BE为56m，楼的底部D 与山脚在同一水平线上，求该铁塔的高AE．（参考数据：sin36°52′≈0.60，tan36°52′≈0.75）【变式2-3】某公园的人工湖边上有一座假山，假山顶上有一竖起的建筑物CD，高为10米，数学小组为了测量假山的高度DE，在公园找了一水平地面，在A处测得建筑物点D（即山顶）的仰角为35°，沿水平方向前进20米到达B点，测得建筑物顶部C点的仰角为45°，求假山的高度DE．（结果精确到1米，参考数据：sin35°≈，cos35°≈，tan35°≈）题型二、方位角的应用【例1】钓鱼岛自古以来就是我国的神圣领土，为维护国家主权和海洋权利，我国海监和渔政部门对钓鱼岛海域实现了常态化巡航管理．如图，某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A 、B ，B 船在A 船的正东方向，且两船保持20海里的距离，某一时刻两海监船同时测得在A 的东北方向，B 的北偏东15°方向有一我国渔政执法船C ，求此时船C 与船B 的距离是多少．（结果保留根号）【变式1-1】如图，某旅游景区为方便游客，修建了一条东西走向的木栈道AB ，栈道AB 与景区道路CD 平行．在C 处测得栈道一端A 位于北偏西42︒方向，在D 处测得栈道另一端B 位于北偏西32︒方向．已知120CD m =，80BD m =，求木栈道AB 的长度（结果保留整数）．（参考数据：17sin 3232︒≈，17cos3220︒≈，5tan 328︒≈，27sin 4240︒≈，3cos 424︒≈，9tan 42)10︒≈【变式1-2】如图，位于A 处的海上救援中心获悉：在其北偏东68︒方向的B 处有一艘渔船遇险，在原地等待营救．该中心立即把消息告知在其北偏东30︒且距离A 点20海里的C 处救生船，此时，遇险船在救生船的正东方向B 处，现救生船沿着航线CB 前往B 处救援，求救生船到达B 处行驶的距离？（参考数据：sin 680.90︒≈，cos680.36︒≈，tan 68 2.50︒≈，1.7)≈【例2】我国北斗导航装备的不断更新，极大方便人们的出行．某中学从A 地出发，组织学生利用导航到B 、C 两个地区进行研学考察活动，出发时，发现C 地恰好在A 地正北方向，且距离A 地15.3千米．但是导航显示路线应沿北偏东45°方同走到B 地，再沿北偏西37°方向走一段距离才能到达C地，求B，C两地的距离（精确到1千米）．（参考数据sin37°≈0.6，cos37°≈0.8，tan37°≈0.7）【变式2-1】某区域平面示意图如图，点O在河的一侧，AC和BC表示两条互相垂直的公路．甲勘测员在A处测得点O位于北偏东45°，乙勘测员在B处测得点O位于南偏西73.7°，测得AC＝840m，BC＝500m．请求出点O到BC的距离．参考数据：sin73.7°≈，cos73.7°≈，tan73.7°≈【变式2-2】码头A、B位于东西走向的河岸线l上，一游轮在P处测得码头A在其北偏东70°，游轮向东航行10分钟后到达Q处，此时测得码头B在其北偏东35°．已知游轮的速度为30千米/小时，两码头A、B相距2千米．（1）求点P到河岸线l的距离；（2）若该游轮按原速度从点Q驶向码头B，则它至少需要多长时间才能到达码头B？（参考数据：sin35°≈，cos35°≈，tan35°≈，sin70°≈，cos70°≈，tan70°≈）【变式2-3】海岛A 的周围8 n mile 内有暗礁，渔船跟踪鱼群由西向东航行，在点B 处测得海岛A 位于北偏东67︒，航行12n mlie 到达C 点，又测得小岛A 在北偏东45︒方向上．如果渔船不改变航线继续向东航行，那么它有没有触礁的危险？请说明理由．（参考数据：12sin 6713︒≈，5cos 6713︒，12tan 67)5︒≈题型三、综合类【例1】如图，马路的两边CF ，DE 互相平行，线段CD 为人行横道，马路两侧的A ，B 两点分别表示车站和超市．CD 与AB 所在直线互相平行，且都与马路的两边垂直，马路宽20米，A ，B 相距62米，∠A ＝67°，∠B ＝37°．（1）求CD 与AB 之间的距离；（2）某人从车站A 出发，沿折线A →D →C →B 去超市B ．求他沿折线A →D →C →B 到达超市比直接横穿马路多走多少米．（参考数据：sin67°≈，cos67°≈，tan67°≈，sin37°≈，cos37°≈，tan37°≈）【变式1-1】如图，某学校教学楼AB的后面有一建筑物CD，在距离CD正后方28米的观测点P处，以22︒的仰角测得建筑物的顶端C恰好挡住教学楼的顶端A，而在建筑物CD 上距离地面2米高的E处，测的教学楼的顶端A的仰角为45︒，求教学楼AB的高度（结果保留整数，2 tan22)5︒≈．【变式1-2】如图，校园内有两幢高度相同的教学楼AB，CD，大楼的底部B，D在同一平面上，两幢楼之间的距离BD长为24米，小明在点E（B，E，D在一条直线上）处测得教学楼AB顶部的仰角为45°，然后沿EB方向前进8米到达点G处，测得教学楼CD顶部的仰角为30°．已知小明的两个观测点F，H距离地面的高度均为1.6米，求教学楼AB的高度AB长．（精确到0.1米）参考值：≈1.41，≈1.73．【变式1-3】在一次综合实践课上，同学们为教室窗户设计一个遮阳篷，小明同学绘制的设计图如图所示，其中AB表示窗户，且AB＝2米，BCD表示直角遮阳蓬，已知当地一年中正午时刻太阳光与水平线CD的最小夹角∠PDN＝18.6°，最大夹角∠MDN＝64.5°请你根据以上数据，帮助小明同学计算出遮阳篷中CD的长是多少米？（结果精确到0.1）（参考数据：sin18.6°≈0.32，tan18.6°≈0.34，sin64.5°≈0.90，tan64.5°≈2.1）【变式1-4】如图是某斜拉桥引申出的部分平面图，AE，CD是两条拉索，其中拉索CD与水平桥面BE的夹角为72°，其底端与立柱AB底端的距离BD为4米，两条拉索顶端距离AC为2米，若要使拉索AE与水平桥面的夹角为35°，请计算拉索AE的长．（结果精确到0.1米）（参考数据：sin35°≈，cos35°≈，tan35°≈，sin72°≈，cos72°≈，tan72°≈）【变式1-5】2018年2月17日上午10点34分，我国自主研制的第二架C919大型客机在上海浦东国际机场进行首次飞行，这意味着C919大型客机逐步拉开全面试验试飞的新征程．这大大激发了同学们对航空科技的兴趣，如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸，图中AB∥CD，AM∥BN∥ED，AE⊥DE，请根据图中数据，求出线段BE和CD的长．（sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，结果保留小数点后一位）【变式1-6】如图，在一条河流的两岸分别有A，B，C，D四棵景观树，已知AB∥CD，某数学活动小组测得∠DAB＝45°，∠CBE＝73°，AB＝10m，CD＝30m，请计算这条河的宽度．（参考数据：sin73°≈，cos73°≈，tan73°≈）【课堂练习】1、如图所示，小河中学九年级数学活动小组选定测量学校前面小河对岸大树BC的高度，他们在斜坡上D处测得大树顶端B的仰角是30°，朝大树方向下坡走6米到达坡底A处，在A处测得大树顶端B的仰角是48°．若斜坡FA的坡比i＝1：，求大树的高度．（结果保留整数，参考数据：sin48°≈0.74，cos48°≈0.67，tan48°≈1.11，≈1.73）2、小明家所在居民楼的对面有一座大厦AB，AB＝80米，为测量这座居民楼与大厦之间的距离，小明从自己家的窗户C处测得大厦顶部A的仰角为37°，大厦底部B的俯角为48°．求小明家所在居民楼与大厦的距离CD的长度．（结果保留整数）（参考数据：）3、若商场为方便消费者购物，准备将原来的阶梯式自动扶梯改造成斜坡式动扶梯，如图所示，已知原阶梯式自动扶梯AB长为10m，扶梯AB的坡度i为1：．改造后的斜坡式动扶梯的坡角∠ACB为15°，请你计算改造后的斜坡式自动扶梯AC的长度．（结果精确到0.1m．参考数据：sin15°≈0.26，cos15°≈0.97，tanl5°≈0.27）4、共享单车为人们的生活带来了极大的便利．如图，一辆单车放在水平的地面上，车把头下方A处与坐垫下方B处在平行于地面的水平线上，A，B之间的距离为49cm，现测得AC，BC与AB的夹角分别为45°，68°．若点C到地面的距离CD为28cm，坐垫中轴E处与点B的距离BE为5cm，求点E到地面的距离．（结果保留一位小数，参考数据：sin68°≈0.93，cos68°≈0.37，tan68°≈2.50）。

中考三角函数应用题1.甲楼楼高50米，乙楼坐落在甲楼的正北面，已知当地冬至中午12时太阳光线与水平面的夹角为30°，此时，求：（1）如果两楼相距50米，那么甲楼的影子落在乙楼上有多高？（2）小明住在乙楼16m高（地板距地面的距离）的五层楼上，要是冬至中午12时阳光不被挡住，两楼至少距离多少米（结果精确到1m，参考数据：≈1.732）？2.某煤矿发生瓦斯爆炸，该地救援队立即赶赴现场进行救援，救援队利用生命探测仪在地面A、B两个探测点探测到C处有生命迹象．已知A、B两点相距6米，探测线与地面的夹角分别是30°和45°，试确定生命所在点C的深度．（精确到0.1米，参考数据：≈1.41，≈1.73）3.如图，A、B两地之间有一座山，汽车原来从A地到B地经过C地沿折线A→C→B行驶，现开通隧道后，汽车直接沿直线AB行驶．已知AC=10千米，∠A=30°，∠B=45°．则隧道开通后，汽车从A地到B地比原来少走多少千米？（结果保留根号）4.如图，某校教学楼AB的后面有一建筑物CD，当光线与地面的夹角是22°时，教学楼在建筑物的墙上留下高2m的影子CE；而当光线与地面的夹角是45°时，教学楼顶A在地面上的影子F与墙角C有13m的距离（B、F、C在一条直线上）．求教学楼AB的高度．（参考数据：sin22°≈，cos22°≈，tan22°≈）5.如图，在一个坡角为40°的斜坡上有一棵树BC，树高4米．当太阳光AC与水平线成70°角时，该树在斜坡上的树影恰好为线段AB，求树影AB的长．（结果保留一位小数）（参考数据：sin20°=0.34，tan20°=0.36，sin30°=0.50，tan30°=0.58，sin40°=0.64，tan40°=0.84，sin70°=0.94，tan70°=2.75）6.如图，从热气球C上测得两建筑物A、B底部的俯角分别为30°和60度．如果这时气球的高度CD为90米．且点A、D、B在同一直线上，求建筑物A、B间的距离．三角函数练习题1.如图，山顶建有一座铁塔，塔高CD=20m，某人在点A处，测得塔底C的仰角为45°，塔顶D的仰角为60°，求山高BC（精确到1m，参考数据：≈1.41，≈1.73）2.如图，河对岸有一高层建筑物AB，为测其高，在C处由点D用测量仪测得顶端A的仰角为30°，向高层建筑物前进50米，到达E处，由点F测得顶点A的仰角为45°，已知测量仪高CD=EF=1.2米，求高层建筑物AB的高．（结果精确到0.1米，，）3.如图所示，当一热气球在点A处时，其探测器显示，从热气球看高楼顶部点B的仰角为45°，看高楼底部点C的俯角为60°，这栋楼高120米，那么热气球与高楼的水平距离为多少米？（结果精确到0.1米，参考数据：）4.如图，大楼AB高16米，远处有一塔CD，某人在楼底B处测得塔顶的仰角为38.5°，爬到楼顶A处测得塔顶的仰角为22°，求塔高CD及大楼与塔之间的距离BD的长．（参考数据：sin22°≈0.37，cos22°≈0.93，tan22°≈0.40，sin38.5°≈0.62，cos38.5°≈0.78，tan38.5°≈0.80 ）5.如图，为测量某物体AB的高度，在D点测得A点的仰角为30°，朝物体AB方向前进20米，到达点C，再次测得点A的仰角为60°，则物体AB的高度为多少？6.如图，某建筑物BC上有一旗杆AB，小明在与BC相距12m的F处，由E点观测到旗杆顶部A的仰角为52°、底部B的仰角为45°，小明的观测点与地面的距离EF为1.6m．（1）求建筑物BC的高度；（2）求旗杆AB的高度．（结果精确到0.1m．参考数据：≈1.41，sin52°≈0.79，tan52°≈1.28）。

初中三角函数的应用例题1.一座山峰高度为1800米，从山脚测得与山顶的夹角为30°，求山脚到山顶的实际水平距离。

解：设山脚到山顶的水平距离为x，则根据三角函数的定义，有tan30°=1800/x。

将30°转化为弧度制，即tan(π/6)=1800/x，解得x=1800/(tan(π/6)) ≈ 3600米。

所以山脚到山顶的实际水平距离约为3600米。

2.一条船从港口出发，先顺时针航行90°，然后逆时针航行120°，最后顺时针航行150°，求船的最终航向与出发港口到最终位置的直线之间的夹角。

解：根据题意，船的最终航向与出发港口到最终位置的直线之间的夹角等于船的顺时针航行角度减去船的逆时针航行角度，即90°-120°+150°=120°。

所以船的最终航向与出发港口到最终位置的直线之间的夹角为120°。

3.一个轮半径为40厘米的车轮以每秒10米的速度匀速滚动，求车轮的角速度。

解：车轮每滚动一周，车轮上的任意一点都绕轮心旋转360°，所以车轮的角速度是360°/一周所需要的时间。

滚动一周的时间可以通过速度和距离的关系求得，即一周所需时间为2πr/v，其中r为半径，v为速度。

所以车轮的角速度为360°/(2πr/v)=(360°v)/(2πr)。

代入半径r=40厘米和速度v=10米/秒，计算可得车轮的角速度约为(360°×10米/秒)/(2π×40厘米)≈0.90弧度/秒。

4.一架飞机从A地飞往B地，两地相距1200公里。

飞机的地速为400千米/小时，假设直飞过程中风速与飞机速度方向相反，风速为120公里/小时，求飞机的实际航速和方向。

解：设飞机的实际航速为v，飞机速度与风速的夹角为θ。

根据三角函数的定义，有cosθ=(400-120)/v。

像是石窟中最大的佛像.某数学活动小组到龙门石窟景区测量这尊佛像的高度.如图，
他们选取的测量点A与佛像BD的底部D在同一水平线上.已知佛像头部BC为4 m，在A
处测得佛像头顶部B的仰角为45°，头底部C的仰角为37.5°，求佛像BD的高度（结
果精确到0.1 m.参考数据：sin 37.5°≈0.61，cos 37.5°≈0.79，tan 37.5°≈0.77）.
在Rt△DHE中，∠DEH＝34°，


＝
.
tan34° tan34°
∴EH＝
∵EF＝15，∴EH－FH＝15，

－x＝15.
tan34°
即
解得x≈30.5.
∴DC≈30.5＋1.5＝32.
答：拂云阁DC的高度约为32 m.
方法总结
解锐角三角函数实际应用题的一般步骤
1.正确画出平面图或截面示意图，并通过图形找出已知量和未知量.
端D的仰角为45°.已知测角仪的高度为1.5 m，测量点A，B与拂云阁DC的底部C在同
一水平线上，求拂云阁DC的高度（结果精确到1 m.参考数据：sin 34°≈0.56，cos
34°≈0.83，tan 34°≈0.67）.
解：延长EF交DC于点H，由题意知，EH⊥DC.
设DH＝x m，在Rt△DHF中，∠DFH＝45°，∴FH＝DH＝x.
∴BC＝
≈25，
sin53°
∴x＝
∴B船到达C船处约需时间：25÷25＝1（小时）.
在Rt△ADC中，AC＝ 2x≈1.41×20＝28.2，
∴A船到达C船处约需时间：28.2÷30＝0.94（小时），
而0.94＜1，所以C船至少要等待0.9ห้องสมุดไป่ตู้小时才能得到救援.

三角函数的应用题第一阶梯[例1]如图，AD∥BC，AC⊥BC，若AD=3，DC=5，且∠B=30°，求AB的长。

解：∵∠DAC=90°由勾股定理，有CD2=AD2+AC2∵AD=3，DC=5∴AC=4∵∠B=30°∴AB=2AC∴AB=8[例2]如图，△ABC中，∠B=90°，D是BC上一点，且AD=DC，若tg∠DAC=,求tg∠BAD。

探索：已知tg∠DAC是否在直角三角形中？如果不在怎么办？要求∠BAD的正切值需要满足怎样的条件？点拨：由于已知中的tg∠DAC不在直角三角形中，所以需要转化到直角三角形中，即可地D点作AC的垂线。

又要求∠BAD的正切值应已知Rt△BAD的三边长，或两条直角边AB、BD的长，根据已知可知没有提供边长的条件，所以要充分利用已知中的tg∠DAC的条件。

由于AD=DC，即∠C=∠DAC，这时也可把正切值直接移到Rt△ABC中。

解答：过D点作DE⊥AC于E，且设DE=k，则AE=4k∵AD=DC,∴∠DAC=∠C，AE=EC∴AC=8k∵设AB=m，BC=4m由勾股定理，有AB2+BC2=AC2∴由勾股定理，有CD2=DE2+EC2由正切定理，有[例3]如图，四边形ABCD中，∠D=90°，AD=3，DC=4，AB=13，BC=12，求sinB。

探索：已知条件提供的图形是什么形？其中∠D=90°，AD=3，DC=4，可提供什么知识？求sinB应放在什么图形中。

点拨：因已知是四边形所以不能求解，由于有∠D=90°，AD=3，DC=4，这样可求AC=5，又因有AB=13，BC=12，所以可证△ABC是Rt△，因此可求sinB。

解：连结AC∵∠D=90°由勾股定理，有AC2=CD2+CD2∵AD=3，CD=4，∴AC=5∵AB=13，BC=12∴132=122+52∴∠ACB=90°由正弦定义，有第二阶梯[例1]如图，在河的对岸有水塔AB，今在C处测得塔顶A的仰角为30°，前进20米后到D处，又测得A的仰角为45°，求塔高AB。

3 3精典例题：【例 1】如图，塔 AB 和楼 CD 的水平距离为 80 米，从楼顶 C 处及楼底 D 处测得塔顶 A 的仰角分别为 450 和 600，试求塔高与楼高（精确到 0.01 米）。

（参考数据： ＝1.41421…， ＝1.73205…）分析：此题可先通过解 Rt △ABD 求出塔高 AB ，再利用 CE ＝BD ＝80 米，解 Rt △AEC 求出 AE ，最后求出 CD ＝BE ＝AB －AE 。

解：在 Rt △ABD 中，BD ＝80 米，∠BAD ＝600 A∴AB ＝ BD tan 6080 138.56 （米）450C在 Rt △AEC 中，EC ＝BD ＝80 米，∠ACE ＝450 ∴AE ＝CE ＝80 米∴CD ＝BE ＝AB －AE ＝ 80 80 58.56 （米）EBD F例 1 图答：塔 AB 的高约为 138. 56 米，楼 CD 的高约为 58. 56 米。

【例 2】如图，直升飞机在跨河大桥 AB 的上方 P 点处，此时飞机离地面的高度 PO ＝450 米，且 A 、B 、 O 三点在一条直线上，测得大桥两端的俯角分别为300 ， 450 ，求大桥 AB 的长（精确到 1 米，选用数据： ＝1.41， ＝1.73）分析：要求 AB ，只须求出 OA 即可。

可通过解 Rt △POA 达到目的。

解：在 Rt △PAO 中，∠PAO ＝300∴OA ＝ PO cot PAO450 cot 300450 （米）在 Rt △PBO 中，∠PBO ＝ ∴OB ＝OP ＝450（米）∴AB ＝OA －OB ＝ 450 450450 P329 （米） 答：这座大桥的长度约为 329 米。

OBA例 2 图评注：例 1 和例 2 都是测量问题（测高、测宽等）， 解这类问题要理解仰角、俯角的概念，合理选择关系式，按要求正确地取近似值。

【例 3】一艘渔船正以 30 海里／小时的速度由西向东追赶鱼群，在 A 处看见小岛 C 在船的北偏东 600方向，40 分钟后，渔船行至 B 处，此时看见小岛 C 在船的北偏东 300 方向，已知以小岛 C 为中心周围 10 海里以内为我军导弹部队军事演习的着弹危险区，问这艘渔船继续向东追赶鱼群，是否有进入危险区域的可能？分析：此题可先求出小岛 C 与航向（直线 AB ）的距离，再与 10 海里进行比较得出结论。

姓 名学 号密封教师填写内容 考试类型 考试【 】 考查【 】 审 批绝密★启用前三角函数的应用测试时间:35分钟一、选择题1、在台风来临之前,有关部门用钢管加固树木(如图),固定点A 离地面的高度AC=m,钢管与地面所成角∠ABC=∠α,那么钢管AB 的长为( )A.mcosα B.m·sin α C.m·cos α D.msinα2、如图,两根竹竿AB 和AD 斜靠在墙CE 上,量得∠ABC=α,∠ADC=β,则竹竿AB 与AD 的长度之比为( )A.tanαtanβB.sinβsinαC.sinαsinβD.cosβcosα3、如图,要测量小河两岸相对的两点P 、A 的距离,可以在小河边取PA 的垂线PB 上一点C,测得PC=100米,∠PCA=35°,则小河宽PA 等于( )A.100sin 35°米B.100sin 55°米C.100tan 35°米D.100tan 55°米4、在东西方向的海岸线上有A,B 两个港口,甲货船从A 港口沿东北方向以5海里/小时的速度出发,同时乙货船从B 港口沿北偏西60°的方向出发,2 h 后在点P 处相遇,如图所示,则A 港口和B 港口之间的距离为( )A.10√2 海里B.(5√2+5√6)海里C.(10+5√6)海里D.20海里5、如图,旗杆及升旗台的剖面和教学楼的剖面在同一平面上,旗杆与底面垂直,在教学楼底部E 点处测得旗杆顶端的仰角∠AED=58°,升旗台底部到教学楼底部的距离DE=7米,升旗台的坡面CD 的坡度i=1∶0.75,坡长CD=2米,若旗杆底部到坡面CD 的水平距离BC=1米,则旗杆AB 的高度约为( ) (参考数据:sin 58°≈0.85,cos 58°≈0.53,tan 58°≈1.60)A.12.6米B.13.1米C.14.7米D.16.3米二、填空题6、为加强防汛工作,某市对一拦水坝进行加固,如图,加固前拦水坝的横断面是梯形ABCD.已知迎水坡面AB=12米,背水坡面CD=12√3米,∠B=60°,加固后拦水坝的横断面为梯形ABED,tan E=3√313,则CE 为 米.7、我国海域辽阔,渔业资源丰富.如图,现有渔船B 在海岛A,C 附近捕鱼作业,已知海岛C 位于海岛A 的北偏东45°方向上,在渔船B 上测得海岛A 位于渔船B 的北偏西30°的方向上,此时海岛C 恰好位于渔船B 的正北方向的18(1+√3)n mile 处,则海岛A,C 之间的距离为 n mile.三、解答题8、如图,沿AC 方向开山修路.为了加快施工进度,要在小山的另一边同时施工.从AC 上取一点B 使∠ABD=120°,BD=520 m,∠D=30°,当另一边开挖点E 离D 多远时,正好使A,C,E 三点在同一条直线上?(√3取1.732,结果取整数)横线以内不许答题9、如图,埃航MS804客机失事后,国家主席亲自发电进行慰问,埃及政府出动了多艘舰船和飞机进行搜救,其中一艘潜艇在海面下500 m 的A 点处测得俯角为45°的前下方海底有黑匣子信号发出,继续沿原方向直线航行2 000 m 后到达B 点,在B 处测得俯角为60°的前下方海底有黑匣子信号发出,求海底黑匣子C 点距离海面的深度(结果保留根号).10、由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图,航母由西向东航行,到达A 处时,测得小岛C 位于它的北偏东70°方向,且与航母相距80海里,再航行一段时间后到达B 处,测得小岛C 位于它的北偏东37°方向.如果航母继续航行至小岛C 的正南方向的D 处,求还需航行的距离BD 的长.(参考数据:sin 70°≈0.94,cos 70°≈0.34,tan 70°≈2.75,sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)11、据调查,超速行驶是引发交通事故的主要原因之一.小强用所学知识对一条笔直公路上的车辆进行测速,如图所示,观测点C 到公路的距离CD=200 m,检测路段的起点A 位于点C 的南偏东60°方向上,终点B 位于点C 的南偏东45°方向上.一辆轿车由东向西匀速行驶,测得此车由A 处行驶到B 处的时间为10 s,问此车是否超过了该路段16 m/s 的限制速度?(观测点C 离地面的距离忽略不计,参考数据:√2≈1.41,√3≈1.73)参考答案一、选择题1.答案 D 在Rt △ABC 中,AC=m,∠ABC=∠α,sin ∠ABC=AC AB ,∴AB=msinα,故选D.2.答案 B 根据直角三角形中边与角的关系即可得到答案.在Rt △ABC 中,AB=ACsinα,在Rt △ADC中,AD=AC sinβ,所以AB AD =ACsinαAC sinβ=sinβsinα.3.答案 C 在Rt △PCA 中,PC=100米,∠PCA=35°,∠APC=90°,tan ∠PCA=PAPC,所以PA=PC·tan ∠PCA=100tan 35°米.4.答案 B 如图,作PC ⊥AB 于点C,∵甲货船从A 港口沿东北方向以5海里/小时的速度出发,2 h 到P 处, ∴∠PAC=45°,AP=5×2=10海里,∴PC=AC=5√2 海里, ∵乙货船从B 港口沿北偏西60°的方向出发, ∴∠PBC=30°,∴BC=√3PC=5√6 海里, ∴AB=AC+BC=(5√2+5√6)海里,故A 港口与B 港口之间的距离为(5√2+5√6)海里,故选B.5.答案 B 如图,延长AB 交ED 的延长线于M,作CJ ⊥DM 于J,则四边形BMJC 是矩形.在Rt △CJD 中,CJ DJ =10.75=43,设CJ=4k 米,DJ=3k 米,k>0,∵CD=2米,∴9k 2+16k 2=4,解得k=25, ∴BM=CJ=85米,DJ=65米,又∵BC=MJ=1米, ∴EM=MJ+DJ+DE=465米, 在Rt △AEM中,tan ∠AEM=AMEM ,∴tan 58°=AB+85465≈1.60,∴AB≈13.1米.故旗杆AB 的高度约为13.1米.故选B.横线以内不许答题二、填空题6.答案 8解析 分别过A 、D 作AF ⊥BC,DG ⊥BC,垂足分别为F 、G,如图所示.在Rt △ABF 中,AB=12米,∠B=60°,sin B=AFAB ,∴AF=AB·sin B=12×sin 60°=12×√32=6√3米, ∴DG=6√3米.在Rt △DGC 中,CD=12√3米,DG=6√3米, ∴GC=√CD 2-DG 2=18米. 在Rt △DEG中,tan E=DG GE =3√313,∴6√3GE =3√313,∴GE=26米,∴CE=GE -CG=26-18=8(米), 即CE 为8米. 7.答案 18√2解析 如图,过A 作AD ⊥BC 于D,由题意可得,∠ABC=30°,∠DAC=45°,设AC=x n mile,在Rt △ACD 中,AD=AC·cos ∠DAC=√22x n mile,则CD=√22x n mile,在Rt △ABD 中,BD=AD tan∠ABD =√62x n mile,则√22x+√62x=18(1+√3),解得x=18√2.故海岛A,C 之间的距离为18√2 n mile.三、解答题8.解析 ∵∠ABD=120°,∠D=30°,∴∠E=90°.∵在Rt △BDE 中,cos D=DEBD ,∴DE=BD·cos D=BD·cos 30°=520×√32=260√3=260×1.732≈450(m). 答:当另一边开挖点E 离D 约450 m 时,正好使A,C,E 三点在同一条直线上. 9.解析 如图,过C 作CD ⊥AB,交AB 的延长线于D,交海面于点E,设BD=x m,∵∠CBD=60°,∠CDB=90°, ∴tan ∠CBD=CDBD , ∴CD=√3x m.∵AB=2 000 m,∴AD=(x+2 000)m.∵∠CAD=45°,∴tan ∠CAD=CDAD ,∴CD=AD·tan 45°=AD, ∴√3x=x+2 000,解得x=1 000√3+1 000, ∴CD=√3×(1 000√3+1 000)=(3 000+1 000√3)m, ∴CE=CD+DE=3 000+1 000√3+500=(3 500+1 000√3)m. 答:海底黑匣子C 点距离海面的深度为(3 500+1 000√3)m. 10.解析 由题意可知,∠ACD=70°,∠BCD=37°,AC=80海里. 在Rt △ADC 中,cos ∠ACD=CD AC ,∴CD=AC·cos ∠ACD=80×cos 70°≈80×0.34=27.2(海里). 在Rt △BDC 中,tan ∠BCD=BD CD , ∴BD=CD·tan ∠BCD=27.2×tan 37°≈27.2×0.75=20.4(海里). 答:还需航行的距离BD 的长约为20.4海里. 11.解析 ∵CD=200 m,∠DCB=45°, ∴BD=CD=200 m.在Rt △ACD 中,∠DCA=60°,AD=CD·tan ∠DCA=200√3 m. ∴AB=AD -BD=200√3-200≈146 m. ∴此车的实际车速为146÷10=14.6 m/s. ∵14.6<16,∴此车没有超过该路段16 m/s 的限制速度.。

考向5.11 用三角函数解决函数问题例1、（2020·山东济南·中考真题）如图，矩形OABC 的顶点A ，C 分别落在x 轴，y 轴的正半轴上，顶点B （2，k y x =（x >0）的图象与BC ，AB 分别交于D ，E ，BD ＝12．（1）求反比例函数关系式和点E 的坐标；（2）写出DE 与AC 的位置关系并说明理由；（3）点F 在直线AC 上，点G 是坐标系内点，当四边形BCFG 为菱形时，求出点G 的坐标并判断点G 是否在反比例函数图象上．解：（1）∵B （2，BC ＝2，而BD ＝12，∴CD ＝2﹣12＝32，故点D （32，将点D 的坐标代入反比例函数表达式得：32K，解得k ＝，故反比例函数表达式为y，当x ＝2时，yE （2（2）由（1）知，D （32，），点E （2B （2，则BD ＝12，BE故BD BC ＝122＝14，EB AB＝14＝BD BC ，∴DE ∥AC；（3）①当点F 在点C 的下方时，如下图，过点F 作FH ⊥y 轴于点H ，∵四边形BCFG 为菱形，则BC ＝CF ＝FG ＝BG ＝2，在RT △OAC 中，OA ＝BC ＝2，OB ＝AB ＝则tan ∠OCA ＝AO CO ∠OCA ＝30°，则FH ＝12FC ＝1，CH ＝CF•cos ∠OCA ＝故点F （1G （3当x ＝3时，y G 在反比例函数图象上；②当点F 在点C 的上方时，同理可得，点G （1，同理可得，点G 在反比例函数图象上；综上，点G 的坐标为（31，一、单选题1．（2021·重庆万州·模拟预测）在平面直角坐标系中，平行四边形ABCD的顶点A在y轴上，点C坐标为（﹣4，0），E为BC上靠近点C的三等分点，点B、E均在反比例函数y＝kx（k＜0，x＜0）的图象上，若tan∠OAD＝12，则k的值为（ ）A．﹣2B．﹣C．﹣6D．﹣2．（2019·山东济南·中考模拟）如图，菱形OABC的一条边OA在x轴上，将菱形OABC绕原点O顺时针旋转75°至OA′B′C′的位置，若OA＝2，∠C＝120°，则点B′的坐标为（ ）A）B）C．（3D．（33．（2019·湖北武汉·中考模拟）如图，平面直角坐标系xOy中，四边形OABC的边OA在x轴正半轴上，BC∥x轴，∠OAB＝90°，点C（3，2），连接OC．以OC为对称轴将OA翻折到OA′，反比例函数y＝kx的图象恰好经过点A′、B，则k的值是（ ）A．9B．133C．16915D．4．（2020·浙江·育海外国语学校一模）如图，在Rt △ABC 中，∠ABC=90°，tan ∠BAC=2，A （0，a ），B （b ，0），点C 在第二象限，BC 与y 轴交于点D （0，c ），若y 轴平分∠BAC ，则点C 的坐标不能表示为（ ）A ．（b+2a ，2b ）B ．（﹣b ﹣2c ，2b ）C ．（﹣b ﹣c ，﹣2a ﹣2c ）D ．（a ﹣c ，﹣2a ﹣2c ）5．（2017·河南·中考模拟）如图，在平面直角坐标系系中，直线y=k 1x+2与x 轴交于点A ，与y 轴交于点C ，与反比例函数y=2k x在第一象限内的图象交于点B ，连接BO ．若S △OBC =1，tan ∠BOC=13，则k 2的值是（ ）A ．﹣3B ．1C ．2D ．36．（2019·广东·中考模拟）如图，在平面直角坐标系系中，直线y=k 1x+2与x 轴交于点A ，与y 轴交于点C ，与反比例函数y=2k x在第一象限内的图象交于点B ，连接BO ．若S △OBC =1，tan ∠BOC=13，则k 2的值是（ ）A ．﹣3B ．1C ．2D ．37．（2015·福建莆田·一模）如图（1），点E 为矩形ABCD 边AD 上一点，点P ，Q 同时从点B 出发，点P 沿BE→ED→DC 运动到点C 停止，点Q 沿BC 运动到点C 停止，它们的运动速度都是1cm/s,设P ，Q 出发ts时，△BPQ的面积为ycm2，已知y与t的函数关系的图象如图（2）则下列正确的是（）A．AE=6cm；B．sin∠EBC=C．当0＜t≤10时，D．当t=12时，△BPQ是等腰三角形8．（2014·江苏苏州·二模）如图，直线y=12x+2交x轴于A（-4，0）点，将一块等腰直角三角形纸板的直角顶点置于原点O，另两个顶点M、N恰落在直线y=12x+2上，若N点在第二象限内，则tan∠AON的值为（ ）A．12B．13C．14D．159．（2014·江苏无锡·一模）如图，点A在反比例函数y＝4x(x>0)的图像上，点B在反比例函数y＝－9x(x<0)的图像上，且∠AOB＝90°，则tan∠OAB （）．A．B．C．D．二、填空题10．（2022·浙江温州·一模）如图，矩形OABC的边OA，OC分别在x轴、y轴上，点B在反比例函数k yx（0k >，0x >）的图象上，且AB =．将矩形OABC 沿x 轴正方向平移32个单位得矩形O A B C '''，A B ''交反比例函数图象于点D ，且30DAA '∠=︒，则k 的值为______．11．（2021·广东·东莞市石龙第二中学一模）如图，在平面直角坐标系中，已知点A （10，0），OA 绕点O 逆时针旋转60°得到OB ，连接AB ，双曲线y ＝k x（x ＞0）分别与AB ，OB 交于点C ，D （C ，D 不与点B 重合）．若CD ⊥OB ，则k 的值为______________．12．（2020·广东·深圳市龙岗区布吉贤义外国语学校模拟预测）如图，Rt △ABC 中，∠A=30°，∠C=90°，BC ⊥y轴，交y 轴于点F ，点C 在第一象限，斜边AB 与x 轴，y 轴分别相交于E 、D 两点，且AD BE ⋅=，设过C 点的双曲线为k y x=，则k =_______．13．（2019·浙江温州·一模）如图，矩形OABC 的边OA ，OC 分别在x 轴、y 轴上，点B ，5），△ACD 与△ACO 关于直线AC 对称（点D 和O 对应），反比例函数y ＝k x（k ≠0）的图象与AB ，BC 分别交于E ，F 两点，连结DE ，若DE ∥x 轴，则点F 的坐标为_____．14．（2019·吉林吉林·一模）如图，在平面直角坐标系中，抛物线y=ax 2+x 的对称轴为x=2，顶点为A ．点P 为抛物线的对称轴上一点，连接OA 、OP.当OA ⊥OP 时，点P 的坐标为________．15．（2019·广东深圳·一模）如图，在△ABC 中，∠ACB=90°，BC 在x 轴中，且点B 与点C 关于原点对称，边AC 上的点P 满足∠COP=∠CAO,且双曲线y=k x经过P 点，则k 值等于_____________.16．（2018·四川成都·中考模拟）如图，直线-8分别交x 轴，y 轴于点A 和点B ，点C 是反比例函数y=k x（x ＞0）的图象上位于直线上方的一点，CD ∥x 轴交AB 于D ，CE ⊥CD 交AB 于E ，AD ·BE=4，则k 的值为_______．17．（2016·河南·模拟预测）如图，点P （a ，a ）是反比例函数16y x=在第一象限内的图象上的一个点，以点P 为顶点作等边△PAB ，使A 、B 落在x 轴上(点A 在点B 左侧)，则△POA 的面积是___________.18．（2017·广东深圳·中考模拟）如图，矩形AOCB 的两边OC 、OA 分别位x 轴、y 轴上，点B 的坐标为B (203-，5)，D 是AB 边上的一点．将△ADO 沿直线OD 翻折，使A 点恰好落在对角线OB 上的点E 处，若点E 在一反比例函数的图象上，那么该函数的解析式是_____．19．（2015·河北石家庄·一模）如图，抛物线y=13x 2与x 轴交于A ，B 两点，与y 轴交于点C ，点M 的坐标为（ 1）．以M 为圆心，2为半径作⊙M ．则下列说法正确的是________ （填序号）．①tan ∠②直线AC 是⊙M 的切线；③⊙M 过抛物线的顶点；④点C 到⊙M 的最远距离为6；⑤连接MC ，MA ，则△AOC 与△AMC 关于直线AC 对称．三、解答题20．（2022·河南信阳·一模）如图，点P 为函数112y x =+与函数(0)m y x x =>图象的交点，点P 的纵坐标为4，PB x ⊥轴，垂足为点B ．（1）求m 的值；（2）点M 是函数(0)m y x x =>图象上一动点，过点M 作MD BP ⊥于点D ，若1tan 2PMD ∠=，求点M 的坐标．21．（2021·四川成都·二模）如图，在平面直角坐标系中，抛物线y ＝ax 2+bx ﹣3过点A (﹣3，0)，B (1，0)，与y 轴交于点C ，顶点为点D ，连接AC ，BC ．（1）求抛物线的解析式；（2）在直线CD 上是否存在点P ，使∠PBC ＝∠BCO ？若存在，求出点P 的坐标；若不存在，请说明理由；（3）若点M 为抛物线对称轴l 上一点，点N 为抛物线上一点，当直线AC 垂直平分线段MN 时，请直接写出点M 和点N 的坐标．一、单选题1．（2013·四川乐山·中考真题）如图，已知第一象限内的点A 在反比例函数y=的图象上，第二象限内的点B 在反比例函数y=的图象上，且OA ⊥OB ，cosA=，则k 的值为（ ）A ．﹣3B ．﹣4C ．﹣D ．﹣22．（2015·贵州铜仁·中考真题）如图，在平面直角坐标系系中，直线y=k 1x+2与x 轴交于点A ，与y 轴交于点C ，与反比例函数y=2k x在第一象限内的图象交于点B ，连接BO ．若S △OBC =1，tan ∠BOC=13，则k 2的值是（ ）A ．﹣3B ．1C ．2D ．33．（2021·辽宁鞍山·中考真题）如图，ABC 是等边三角形，6cm AB ＝，点M 从点C 出发沿CB 方向以1cm/s 的速度匀速运动到点B ，同时点N 从点C 出发沿射线CA 方向以2cm/s 的速度匀速运动，当点M 停止运动时，点N 也随之停止．过点M 作//MP CA 交AB 于点P ，连接MN ，NP ，作MNP △关于直线MP 对称的MN P ' ，设运动时间为ts ，MN P ' 与BMP 重叠部分的面积为2cm S ，则能表示S 与t 之间函数关系的大致图象为（ ）A ．B ．C ．D ．4．（2020·辽宁辽宁·中考真题）如图，在Rt ABC ∆中，90ACB ∠=︒，AC BC ==，CD AB ⊥于点D ．点P 从点A 出发，沿A D C →→的路径运动，运动到点C 停止，过点P 作PE AC ⊥于点E ，作PF BC ⊥于点F ．设点P 运动的路程为x ，四边形CEPF 的面积为y ，则能反映y 与x 之间函数关系的图象是（ ）A ．B ．C ．D ．5．（2020·黑龙江牡丹江·中考真题）如图，在菱形OABC 中，点B 在x 轴上，点A 的坐标为（2，，将菱形绕点O 旋转，当点A 落在x 轴上时，点C 的对应点的坐标为（ ）A ．(2--,或2)-B ．(2,C ．(2,-D ．(2--,或(2,6．（2020·贵州黔西·中考真题）如图，在菱形ABOC 中，AB ＝2，∠A ＝60°，菱形的一个顶点C 在反比例函数y ＝k x（k≠0）的图象上，则反比例函数的解析式为（ ）A ．y ＝B ．y ＝C ．y ＝3x -D ．y 7．（2019·内蒙古赤峰·中考真题）如图，点P 是反比例函数(0)k y k x=≠的图象上任意一点，过点P 作PM x ⊥轴，垂足为M ．若POM 的面积等于2，则k 的值等于（ ）．A ．-4B ．4C ．-2D ．28．（2015·山东烟台·中考真题）如图，Rt △ABC 中∠C=90°，∠BAC=30°，AB=8，以DEFG 的一边GD 在直线AB 上，且点D 与点A 重合，现将正方形DEFG 沿A ﹣B 的方向以每秒1个单位的速度匀速运动，当点D 与点B 重合时停止，则在这个运动过程中，正方形DEFG 与△ABC 的重合部分的面积S 与运动时间t 之间的函数关系图象大致是（ ）A ．B ．C ．D ．9．（2021·湖南怀化·中考真题）如图，菱形ABCD 的四个顶点均在坐标轴上，对角线AC 、BD 交于原点O ，AE BC ⊥于E 点，交BD 于M 点，反比例函数0)y x =>的图象经过线段DC 的中点N ，若4BD =，则ME 的长为（ ）A ．53ME = B ．43=ME C ．1ME = D ．23ME =二、填空题10．（2016·内蒙古包头·中考真题）如图，在平面直角坐标系中，点A 在第二象限内，点B 在x 轴上，∠AOB＝30°，AB ＝BO ，反比例函数y ＝k x(x ＜0)的图象经过点A ，若S △AOB k 的值为________．11．（2021·海南·中考真题）如图，ABC 的顶点B C 、的坐标分别是(1,0)、，且90,30ABC A ∠=︒∠=︒，则顶点A 的坐标是_____．12．（2021·湖北荆门·中考真题）如图，在平面直角坐标系中，Rt OAB 斜边上的高为1，30AOB ∠=︒，将Rt OAB 绕原点顺时针旋转90︒得到Rt OCD △，点A 的对应点C 恰好在函数(0)k y k x=≠的图象上，若在k y x=的图象上另有一点M 使得30MOC ∠=︒，则点M 的坐标为_________．13．（2021·江苏淮安·中考真题）如图（1），△ABC 和△A ′B ′C ′是两个边长不相等的等边三角形，点B ′、C ′、B 、C 都在直线l 上，△ABC 固定不动，将△A ′B ′C ′在直线l 上自左向右平移．开始时，点C ′与点B 重合，当点B ′移动到与点C 重合时停止．设△A ′B ′C ′移动的距离为x ，两个三角形重叠部分的面积为y ，y 与x 之间的函数关系如图（2）所示，则△ABC 的边长是___．14．（2021·辽宁本溪·中考真题）如图，AB 是半圆的直径，C 为半圆的中点，(2,0)A ，(0,1)B ，反比例函数(0)ky x x=>的图象经过点C ，则k 的值为________．15．（2020·湖南永州·中考真题）AOB ∠在平面直角坐标系中的位置如图所示，且60AOB ∠=︒，在AOB ∠内有一点()4,3P ，M ，N 分别是,OA OB 边上的动点，连接,,PM PN MN ，则PMN 周长的最小值是_________．16．（2020·湖南怀化·中考真题）如图，11OB A △，122A B A △，233A B A △，…，1n n n A B A -△，都是一边在x 轴上的等边三角形，点1B ，2B ，3B ，…，n B 都在反比例函数0)y x =>的图象上，点1A ，2A ，3A ，…，n A ，都在x 轴上，则n A 的坐标为________．17．（2019·辽宁铁岭·中考真题）如图，Rt Rt AOB COD ≌，直角边分别落在x 轴和y 轴上，斜边相交于点E ，且tan 2OAB ∠=．若四边形OAEC 的面积为6，反比例函数()0k y x x=>的图象经过点E ，则k 的值为_____．18．（2019·福建·中考真题）如图,菱形ABCD顶点A在例函数y=3x(x>0)的图象上，函数y=kx(k>3，x>0)的图象关于直线AC对称，且经过点B、D两点，若AB＝2，∠DAB＝30°，则k的值为______.19．（2018·湖南郴州·中考真题）如图，在平面直角坐标系中，菱形OABC的一个顶点在原点O处，且∠AOC=60°，A点的坐标是（0，4），则直线AC的表达式是_____．20．（2018·湖北随州·中考真题）如图，在平面直角坐标系xOy中，菱形OABC的边长为2，点A在第一象限，点C在x轴正半轴上，∠AOC=60°，若将菱形OABC绕点O顺时针旋转75°，得到四边形OA′B′C′，则点B的对应点B′的坐标为_____．三、解答题21．（2021·山东泰安·中考真题）如图，点P 为函数112y x =+与函数(0)m y x x =>图象的交点，点P 的纵坐标为4，PB x ⊥轴，垂足为点B ．（1）求m 的值；（2）点M 是函数(0)m y x x =>图象上一动点，过点M 作MD BP ⊥于点D ，若1tan 2PMD ∠=，求点M 的坐标．22．（2019·江苏宿迁·中考真题）如图，抛物线2y x bx c =++交x 轴于A 、B 两点，其中点A 坐标为()1,0，与y 轴交于点()0,3C -.（1）求抛物线的函数表达式；（2）如图①，连接AC ，点P 在抛物线上，且满足2PAB ACO ∠=∠．求点P 的坐标；（3）如图②，点Q 为x 轴下方抛物线上任意一点，点D 是抛物线对称轴与x 轴的交点，直线AQ 、BQ 分别交抛物线的对称轴于点M 、N ．请问DM DN +是否为定值？如果是，请求出这个定值；如果不是，请说明理由．23．（2013·黑龙江牡丹江·中考真题）如图，平面直角坐标系中，矩形OABC 的对角线AC=12，tan ∠ACO=，（1）求B 、C 两点的坐标；（2）把矩形沿直线DE 对折使点C 落在点A 处，DE 与AC 相交于点F ，求直线DE 的解析式；（3）若点M 在直线DE 上，平面内是否存在点N ，使以O 、F 、M 、N 为顶点的四边形是菱形？若存在，请直接写出点N 的坐标；若不存在，请说明理由．1．C【解析】【分析】根据已知条件运用点B，E都在反比例函数图象上，再运用tan∠OAD＝12即可求解．【详解】如图所示，过点B作BN⊥x轴，过点E作EM⊥x轴∴EM∥BN∴△ECM∽△BCN∵E为BC三等分点∴EC=13 BC∴13 EC EM CM BC BN CN===设B点的坐标为：（-m，n）∵C（-4,0）∴OC=4∴ON=m，BN=n则CN=4-m∴EM=13BN=3nCM=13CN=4-3mOM=OC-CM=4-4-3m=83m+∴E（-83m+，3n）∵tan ∠OAD =12∴tan ∠OAD =12=OF OA 则OA =2OF∴tan ∠AFO =2∵四边形ABCD 是平行四边形∴AD ∥BC∴∠ECM =∠AFO∴tan ∠ECM =2EM CM=即3n ÷4-3m =2n =8-2m∴B （-m ，8-2m ）E （-83m +，823m -），两点都在k y x =上∴-m （8-2m ）=-83m +×823m -解得m =1∴B （-1,6）∴k =-1×6=-6故选：C ．【点拨】本题考查了反比例函数上点的坐标特征平行四边形的性质及解直角三角形，本题的解题关键是确定B ，E 点的坐标，利用tan ∠OAD =12的关系即可得出答案．2．A【解析】【分析】首先根据菱形的性质，即可求得∠AOB 的度数，求出OB 的长，又由将菱形OABC 绕原点O 顺时针旋转75°至OA ′B ′C ′的位置，可求得∠B ′OA 的度数，然后在Rt △B ′OF 中，利用三角函数即可求得OF 与B ′F 的长，则可得点B ′的坐标．【详解】解：连接AC 交OB 于G ，过点B 作BE ⊥OA 于E ，过点B ′作B ′F ⊥OA 于F ，∴∠BE 0＝∠B ′FO ＝90°，∵四边形OABC 是菱形，∴OA ∥BC ，∠AOB ＝12∠AOC ，OG ＝BG ，∴∠AOC +∠C ＝180°，∵∠C ＝120°，∴∠AOC ＝60°，∴∠AOB ＝30°，∴AG ＝12OA ＝1，∴OG ＝3√AG ＝3√，∴OB ＝23√，∵菱形OABC 绕原点O 顺时针旋转75°至OA ′B ′C ′的位置，∴∠BOB ′＝75°，OB ′＝OB ＝23√，∴∠B ′OF ＝45°，在Rt △B ′OF 中，OF ＝OB ′•cos45°＝23√×22√＝6√，∴B ′F ＝6√，∴点B ′的坐标为：（6√，﹣6√）．故选A ．【点拨】此题考查了平行四边形的性质，旋转的性质以及直角三角形的性质与三角函数的性质等知识．此题综合性较强，难度适中，解题的关键是注意数形结合思想的应用．3．C【解析】【分析】设B （2k ，2），由翻折知OC 垂直平分AA′，A′G ＝2EF ，AG ＝2AF ，由勾股定理得OC，根据相似三角形或锐角三角函数可求得A′（526，613），根据反比例函数性质k ＝xy 建立方程求k ．【详解】如图，过点C 作CD ⊥x 轴于D ，过点A′作A′G ⊥x 轴于G ，连接AA′交射线OC 于E ，过E 作EF ⊥x 轴于F ，设B （2k ，2），在Rt △OCD 中，OD ＝3，CD ＝2，∠ODC ＝90°，∴OC由翻折得，AA′⊥OC ，A′E ＝AE ，∴sin ∠COD ＝AE CD OA OC=，∴AE＝CD OA OC⋅=，∵∠OAE+∠AOE ＝90°，∠OCD+∠AOE ＝90°，∴∠OAE ＝∠OCD ，∴sin ∠OAE ＝EF OD AE OC =＝sin ∠OCD ，∴EF＝313OD AE k OC ⋅==，∵cos ∠OAE ＝AF CD AE OC =＝cos ∠OCD ，∴213CD AF AE k OC =⋅=，∵EF ⊥x 轴，A′G ⊥x 轴，∴EF ∥A′G ，∴12EF AF AE A G AG AA ===''，∴6213A G EF k '==，4213AG AF k ==，∴14521326OG OA AG k k k =-=-=，∴A′（526k ，613k），∴562613k k k ⋅=，∵k≠0，∴169=15k ，故选C ．【点拨】本题是反比例函数综合题，常作为考试题中选择题压轴题，考查了反比例函数点的坐标特征、相似三角形、翻折等，解题关键是通过设点B 的坐标，表示出点A′的坐标．4．C【解析】【分析】作CH ⊥x 轴于H ，AC 交OH 于F ．由△CBH ∽△BAO ，推出2BH CH BC AO BO AB ===，推出BH=﹣2a ，CH=2b ，推出C （b+2a ，2b ），由题意可证△CHF ∽△BOD ，可得CH HF BO OD=,推出2b FH b c =，推出FH=2c ，可得C （﹣b ﹣2c ，2b ），因为2c+2b=﹣2a ，推出2b=﹣2a ﹣2c ，b=﹣a ﹣c ，可得C （a ﹣c ，﹣2a ﹣2c ），由此即可判断；【详解】解：作CH ⊥x 轴于H ，AC 交OH 于F ．∵tan ∠BAC=BC AB=2，∵∠CBH+∠ABH=90°，∠ABH+∠OAB=90°，∴∠CBH=∠BAO ，∵∠CHB=∠AOB=90°，∴△CBH ∽△BAO ，∴2BH CH BC AO BO AB===，∴BH=﹣2a ，CH=2b ，∴C （b+2a ，2b ），由题意可证△CHF ∽△BOD ，∴CH HF BO OD =，∴2b FH b c=，∴FH=2c ，∴C （﹣b ﹣2c ，2b ），∵2c+2b=﹣2a ，∴2b=﹣2a ﹣2c ，b=﹣a ﹣c ，∴C （a ﹣c ，﹣2a ﹣2c ），故选C ．【点拨】本题考查解直角三角形、坐标与图形的性质、相似三角形的判定和性质等知识，解题的关键是正确寻找相似三角形解决问题，属于中考选择题中的压轴题．5．D【解析】【详解】试题分析：先求得直线y=k 1x+2与y 轴交点C 的坐标为（0，2），然后根据△BOC 的面积求得BD 的长为1，然后利用∠BOC 的正切求得OD 的长为3,，从而求得点B 的坐标为（1，3），代入y=2k x求得k 2=3．故答案选D.考点：反比例函数与一次函数的交点问题．6．D【解析】【详解】试题分析：先求得直线y=k 1x+2与y 轴交点C 的坐标为（0，2），然后根据△BOC 的面积求得BD 的长为1，然后利用∠BOC 的正切求得OD 的长为3,，从而求得点B 的坐标为（1，3），代入y=2k x 求得k 2=3．故答案选D.考点：反比例函数与一次函数的交点问题．7．B【解析】【详解】试题分析：根据动点和函数图象可得sin ∠EBC=45．考点：函数图形的性质．8．B【解析】【详解】试题分析：过O 作OC ⊥AB 于C ，过N 作ND ⊥OA 于D ，∵N 在直线y=12x+2上，∴设N 的坐标是（x ，12x+2），则DN=12x+2，OD=-x ，∵y=12x+2，∴当x=0时，y=2，∴A （-4，0），B （0，2），即OA=4，OB=2，在△AOB 中，由勾股定理得：=∵在△AOB 中，由三角形的面积公式得：AO×OB=AB×OC ，∴，∴∵在Rt △NOM 中，OM=ON ，∠MON=90°，∴∠MNO=45°，∴sin45°=OC ON =∴在Rt △NDO 中，由勾股定理得：ND 2+DO 2=ON 2，即（12x+2）2+（-x ）2=325，解得：x 1=-1225，x 2=3725，即ND=425，OD=1225，∴tan ∠AON=13ND OD =．故选B ．考点：1.全等三角形的判定与性质；2.一次函数图象上点的坐标特征．9．C【解析】【详解】试题分析：过点A 作AC ⊥x 轴于C ，过点B 作BD ⊥x 轴于D ，∴∠ACO=∠ODB=90°，∴∠OBD+∠BOD=90°，∵∠AOB=90°，∴∠BOD+∠AOC=90°，∴∠OBD=∠AOC ，∴△OBD ∽△AOC ∴2()OBD AOC S OB S OA= ，∵点A 在反比例函数y=4x的图象上，点B 在反比例函数y=-9x 的图象上，∴S △OBD =4．5，S △AOC =2，∴32OB OA =，∴tan ∠OAB=32OB OA =．故选C ．考点：1．反比例函数图象上点的坐标特征；2．相似三角形的判定与性质．10【解析】【分析】由矩形的性质可得出点B将x=即可求出点A和B的横坐标为．再根据平移方式可得出点A'和D32+，再将32x=+代入反比例函数解析式，可求得点D的纵坐标．最后根据30DAA∠'=︒，结合锐角三角形函数和两点的距离公式即可求得k的值．【详解】∵AB=OABC为矩形，∴点B将y=kx=，解得：x=，∴点A和B．∴点A'和D32+，将32x=+代入反比例函数解析式，得：y==∴点D．∵30DAA∠'=︒，∴tanA DDAAAA'∠'==',∴D AA Ay yx x'-=-=，解得：k=．【点拨】本题考查矩形的性质，反比例函数图象上点的坐标特征，锐角三角形函数和两点的距离公式．根据各知识点用k表示出各点坐标是解题关键．11．【解析】【分析】如图，作DE⊥x轴于点E，作CF⊥x轴于点F，设OE＝a，由等边三角形性质及三角函数可表示出点D坐标（a ）、点C 坐标（15﹣2a )25a -），因为点D 、C 在反比例函数图象上，故根据k ＝xy建立方程())15225a a a =-﹣求解满足要求的a 值，然后得到D 点坐标，代入k ＝xy 中计算求解即可．【详解】解：如图，作DE ⊥x 轴于点E ，作CF ⊥x 轴于点F由题意知△OAB 为等边三角形∴∠BOA ＝∠B ＝∠BAO ＝60°设OE ＝a ，则DE ，OD ＝2a∴D （a ），BD ＝10﹣2a∴BC ＝cos 60BD ︒＝2×（10﹣2a ）＝20﹣4a ∴AC ＝10﹣（20﹣4a ）＝4a ﹣10∴FA ＝AC •cos60°＝12（4a ﹣10）＝2a ﹣5，CF ＝AC •sin60°))41025a a -=-∴OF ＝AO ﹣FA ＝10﹣2a +5＝15﹣2a∴C （15﹣2a )25a -）∵点D 、C 在反比例函数图象上∴())15225a a a =-﹣解得：a 1＝3，a 2＝5（不合题意，舍去）∴a ＝3，D （3，∴3k xy ==⨯=故答案为：．【点拨】本题考查了反比例函数与几何综合，三角函数值，等边三角形，旋转的性质．解题的关键在于表示出C D 、两点坐标．12．34．【解析】【分析】过B 点作BM x ⊥轴于点M ，过D 点作DN AC ⊥交AC 于点N ，设C 点的坐标为（x ，y ），则BM y =，DN x =，则有//AC BM ，//DN BC ，根据30MBE A ∠=∠=︒，得到BE =，22AD DN x ==，再根据AD BE ⋅=，化简即可得34xy =，即可得到结果．【详解】解：如图示，过B 点作BM x ⊥轴于点M ，过D 点作DN AC ⊥交AC 于点N ，设C 点的坐标为（x ，y ），则BM y =，DN x =，Rt △ABC 中，∠A=30°，∠C=90°，BC ⊥y 轴，则有：//AC BM ，//DN BC ，∴30MBE A ∠=∠=︒，∴BM BE ，12DN AD =，∴BE y ==，22AD DN x ==，又∵AD BE ⋅，∴2x AD BE == 即有：34xy =，∵C 点在双曲线k y x =上，∴34xy k ==，故答案为：34．【点拨】本题考查了特殊锐角的三角函数，平行线的性质和反比例函数的性质，熟悉相关性质是解题的关键．13．5）【解析】【分析】由已知条件可知OA、OC的长，利用勾股定理求出AC，在利用等积法求出OD的值．过点D作DG⊥x轴于点G，连接OD，则∠OAC＝∠ODG，利用角的余弦即可求出DG的长，从而求出E点的坐标，再利用待定系数法求出反比例函数的解析式，从而求出F点的坐标．【详解】过点D作DG⊥x轴于点G，连接OD，则∠OAC＝∠ODG．∵点B5），∴OA OC＝5，由勾股定理得AC=∴cos∠OAC=＝cos∠ODG，∵OD＝=，∴在Rt△ODG中，DG＝OD×cos∠ODG53 =，∵DE∥x轴，∴点E的坐标为53⎫⎪⎭，∵点E在反比例函数y＝kx（k≠0）的图象上，代入E点坐标得k∴，∵点F也在反比例函数y＝kx（k≠0）的图象上，点F的纵坐标为5，∴点F，点F5）．5）．【点拨】本题考查了反比例函数与图形的综合，熟练掌握对称的性质、三角函数定义及待定系数法求反比例函数解析式是解题的关键．14．（2，-4）【解析】【分析】根据抛物线的对称轴求出a的值，即可得到抛物线解析式，从而求出顶点A的坐标，根据锐角三角函数的定义求出tan∠OAE的值，然后根据同角的余角相等得到∠OAE=∠EOP，再次利用锐角三角函数的定义求出EP 的长，从而求出点P的坐标.【详解】解：如图∵抛物线y=ax2+x的对称轴为x=2 ，∴-12a=2，∴a=-1 4 ,∴抛物线y=-14x2+x，∴A（2，1）∴在Rt△AOE中，tan∠OAE=OEAE=2，∠OAE+∠AOE=90°，∵ OA⊥OP ，∴∠AOP=∠AOE+∠EOP=90°，∴∠OAE=∠EOP，∴tan∠EOP=EPOE=2，∵OE=2，∴EP=4，∴P（2，-4）故答案为（2，-4）.【点拨】本题是二次函数综合题型，主要利用了二次函数的对称轴公式，二次函数图象上点的坐标特征，锐角三角函数的定义，正确的理解题意是解题的关键．15．8 3【解析】【分析】根据勾股定理求出OC＝2，AC＝3，再由tan∠COP＝tan∠CAO，求出PC＝43，进而求出P点坐标（2，43），即可求解；【详解】解：∵点B与点C关于原点对称，∴BC＝2OC，在Rt△ABC中，AB2＝AC2＋BC2，∵AB＝5，∴25＝AC2＋4OC2，在Rt△AOC中，AO2＝AC2＋OC2，∵AO∴13＝AC2＋OC2，∴OC＝2，AC＝3，∵∠COP＝∠CAO，∴tan∠COP＝tan∠CAO，∴2 23 PC，∴PC ＝43，∴P （2，43），∴k ＝83，故答案为83.【点拨】本题考查反比例函数的图象及性质，直角三角形勾股定理，三角函数值；熟练掌握直角三角形的边角关系是解题的关键．16．【解析】【详解】分析：过点E 作EM ⊥y 轴于点M ，过点D 作DF ⊥x 轴于点F ，然后求出OA 与OB 的长度,即可求出∠OAB 的正弦值与余弦值，再设C(x ，y)，从而可表示出AD 与BE 的长度，根据AD·BE=4列出即可求出k 的值．详解：过点E 作EM ⊥y 轴于点M ，过点D 作DF ⊥x 轴于点F ，，∴点B 的坐标为(0，－8)，点A 的坐标为0)，∴OB=8，，由勾股定理可知： ∴sin ∠OAB=OB AB =，cos ∠OAB=12，设C(x ，y)， ∴DF=－y ，ME=x ， sin ∠OAB=DF AD ，∴AD=y ，∵cos ∠OAB=cos ∠MEB=ME Be ，∴BE=2x ，∵AD·BE=4，∴y ×2x=4，∴xy= 即k=点睛：本题主要考查的是三角函数的应用以及反比例函数的性质，综合性比较强，难度较大．解决这个问题的关键就是将AD 和BE 用点C 的坐标表示出来．17【解析】【详解】如图，过点P 作PH ⊥OA 于点H ，∵点P （a ，a ）是反比例函数16y x=在第一象限内的图象上的一个点，∴16=a 2，且a ＞0，解得，a=4. ∴PH=OH=4.∵△PAB 是等边三角形，∴∠PAH=60°.∴根据锐角三角函数，得∴OA=4﹣∴S △POA =12OA•PH=12.考点：1.反比例函数系数k 的几何意义；2.等边三角形的性质；3.锐角三角函数定义；1.特殊角的三角函数值.18．y ＝－12x．【解析】【详解】解：过E 点作EF ⊥OC 于F由条件可知：OE=OA=5，EF OF =tan ∠BOC=BC OC =5203=34所以EF=3，OF=4则E 点坐标为（-4，3）设反比例函数的解析式是y=k x 则有k=-4×3=-12∴反比例函数的解析式是y=12x -19．①②③④【解析】【详解】试题分析：过点M 作MN ⊥AB 于点N ，交⊙M 于点D ，则AN=BN ，∵抛物线y=13x 2与x 轴交于A ，B 两点，与y 轴交于点C ，∴A ，B 0），（0），点C 的坐标为（0，3），∴OC=3，∴tan ∠OAC=OC OA =∴①正确，∠CAO=60°，∵点M 的坐标为（1），∴MN=1，∵tan ∠MAN=MN AN ==，∴∠MAN=30°，∴MA ⊥AC ，∴直线AC 是⊙M 的切线，∴②正确，∵⊙M 的半径为2，∴DN=1，∴D点的坐标为（-1），∵抛物线y=13x 2的顶点坐标为（-1），∴⊙M 过抛物线的顶点，∴③正确，∵∠ACO=30°，∴∵MA ⊥AC ，∴4==，∴点C 到⊙M 的最远距离为4+2=6，∴④正确，∵∠AOC=90°，∠AMC≠90°，∴△AOC 与△AMC 关于直线AC 不对称，∴⑤错误，故答案为①②③④．考点：二次函数综合题．20．（1）24；（2）M 点的坐标为(8,3)【解析】【分析】(1)根据交点坐标的意义，求得点P 的横坐标，利用k =xy 计算m 即可；（2）利用分类思想，根据正切的定义，建立等式求解即可.【详解】解：（1）∵点P 纵坐标为4，∴1412x =+，解得6x =，(6,4)P ∴∴4=6m ，∴24m =．（2）∵1tan 2PMD ∠=，∴12PD PM =，设(0)PD t t =>，则2DM t =，当M 点在P 点右侧，∴M 点的坐标为(62,4)t t +-，∴（6+2t ）（4-t ）=24，解得：11t =，20t =（舍去），当11t =时，(8,3)M ，∴M 点的坐标为(8,3)，当M 点在P 点的左侧，∴M 点的坐标为(62,4)t t -+，∴（6-2t ）（4+t ）=24，解得：10t =，21t =-，均舍去．综上，M 点的坐标为(8,3)．【点拨】本题考查了一次函数与反比例函数的交点问题，反比例函数解析式的确定，三角函数，一元二次方程的解法，熟练掌握函数图像交点的意义，灵活运用三角函数的定义，构造一元二次方程并准确解答是解题的关键．21．（1）y ＝x 2+2x ﹣3；（2）存在，(1，﹣2)或(﹣5，﹣8)；（3）M (﹣1﹣2)，N (﹣1，﹣2)或M '(﹣12)，N '(﹣，﹣2)．【解析】【分析】（1）23(3)(1)y ax bx a x x =+-=+-，即可求解；（2）分点P （P ′）在点C 的右侧、点P 在点C 的左侧两种情况，分别求解即可；（3）设()()21,,,23M m N n n n -+-，根据MN AC l l ⊥，可求出:3AC l y x =--，进而可得结论．【详解】解：（1）根据二次函数交点式为()()()120=--≠y a x x x x a ，抛物线过A (﹣3，0)，B (1，0)两点，∴设()()2331y ax bx a x x =+-=+-，∵x =0时，y ＝ax 2+bx ﹣3=-3，∴将()0,3-代入()()31y a x x =+-∴﹣3a ＝﹣3，∴a ＝1，故抛物线的表达式为：y ＝x 2+2x ﹣3．（2）由抛物线的表达式知，点C 、D 的坐标分别为（0，﹣3）、（﹣1，﹣4），由点C 、D 的坐标知，直线CD 的表达式为：y ＝x ﹣3①，1tan 3BCO ∠=，则cos BCO ∠=当点P （P ′）在点C 的右侧时，如图所示：∵∠P 'BC ＝∠BCO ，故P ′B ∥y 轴，则点P ′（1，﹣2），当点P 在点C 的左侧时，设直线PB 交y 轴于点H ，过点H 作HN ⊥BC 于点N ，∵∠P 'BC ＝∠BCO ，∴△BCH 为等腰三角形，则2cos 2BC CH BCO CH =⋅∠=⨯= 解得：53CH =，则433OH CH =-=，故点4(0,3H =，由点B 、H 的坐标得，直线BH 的表达式为：4433y x =-②，联立①②并解得：58x y =-⎧⎨=-⎩， 故点P 的坐标为（﹣5，﹣8）,综上所述，满足条件的点P 坐标为（1，﹣2）或（﹣5，﹣8）．（3）如图2中，设M （﹣1，m ），2(,23)N n n n +-，∵(3,0),(0,3)A C --，则313AC k -==-，∵MN AC l l ⊥，∴1MN k =，则22311n n m n +--=+，∴240n n m +--=，且AC 垂直平分MN ，则MN 的中点在直线AC 上，则中点坐标可得为：2123(,21n n n m n -+--+，且由A 、C 坐标可得：:3AC l y x =--，则2231322n n m n +---=--，∴2320n n m +++=，联立240n n m +--=，可得：1n =或1n =，则2m =或2m =，∴N (12)--，N ′(12)--，∴M (2)--，M ′(1,2)-，综上所述，M (2)-，N (12)---或M '(1,2)-，N '(12)--．【点拨】本题是二次函数综合运用，考查了二次函数的性质，一次函数的性质，解直角三角形等知识，解题的关键是学会用分类讨论的思想思考问题．参考答案：1．B【解析】【详解】过A 作AE ⊥x 轴，过B 作BF ⊥x 轴，∵OA ⊥OB ，∴∠AOB=90°，∴∠BOF+∠EOA=90°，∵∠BOF+∠FBO=90°，∴∠EOA=∠FBO ，∵∠BFO=∠OEA=90°，∴△BFO ∽△OEA ，在Rt △AOB 中，cos ∠BAO==，设AB=，则OA=1，根据勾股定理得：BO=，∴OB ：OA=：1，∴S △BFO ：S △OEA =2：1，∵A 在反比例函数y=上，∴S △OEA =1，∴S △BFO =2，则k=﹣4．故选B2．D【解析】【详解】试题分析：先求得直线y=k 1x+2与y 轴交点C 的坐标为（0，2），然后根据△BOC 的面积求得BD 的长为1，然后利用∠BOC 的正切求得OD 的长为3,，从而求得点B 的坐标为（1，3），代入y=2k x求得k 2=3．故答案选D.考点：反比例函数与一次函数的交点问题．3．A【解析】【分析】首先求出当点N '落在AB 上时，t 的值，分02t <≤或23t <≤两种情形，分别求出S 的解析式，可得结论．【详解】解：如图1中，当点N '落在AB 上时，取CN 的中点T ，连接MT ．CM t = ，2CN t =，CT TN =，CT TN t ∴==，ABC 是等边三角形，60C A ∴∠=∠=︒，MCT ∴ 是等边三角形，TM TC TN ∴==，90CMN ∴∠=︒，//MP AC ，60BPM A MPN ∴∠=∠=∠=︒，60BMP C ∠=∠=︒，180C CMP ∠+∠=︒，120CMP ∴∠=︒，BMP 是等边三角形，BM MP ∴=，180CMP MPN ∠+∠=︒ ，//CM PN ∴，//MP CN ，∴四边形CMPN 是平行四边形，2PM CN BM t ∴===，36t ∴=，2t ∴=，如图2中，当02t <≤时，过点M 作MK AC ⊥于K ，则sin60MK CM =⋅︒=，21(6)2S t ∴=⋅-=．如图3中，当23t <≤时，21)2S t =-，观察图象可知，选项A 符合题意，故选：A ．【点拨】本题考查动点问题，等边三角形的性质，二次函数的性质等知识，解题的关键是学会用分类讨论的思想思考问题，属于中考选择题中的压轴题．4．A【解析】【分析】分两段来分析：①点P 从点A 出发运动到点D 时，写出此段的函数解析式，则可排除C 和D ；②P 点过了D 点向C 点运动，作出图形，写出此阶段的函数解析式，根据图象的开口方向可得答案．【详解】解：∵90ACB ∠=︒，AC BC ==，∴45A ∠=︒，4AB =，又∵CD AB ⊥，∴2AD BD CD ===，45ACD BCD ∠=∠=︒，∵PE AC ⊥，PF BC ⊥，∴四边形CEPF 是矩形，I ．当P 在线段AD 上时，即02x <≤时，如解图1∴sin AE PE AP A ===，∴CE =，∴四边形CEPF 的面积为2122y x x ⎛⎫==-+ ⎪ ⎪⎝⎭，此阶段函数图象是抛物线，开口方向向下，故选项CD 错误；II ．当P 在线段CD 上时，即24x <≤时，如解图2：依题意得：4CP x =-，∵45ACD BCD ∠=∠=︒，PE AC ⊥，∴sin CE PE CP ECP ==⨯∠，∴())4sin 454CE PE x x ==-︒=-，∴四边形CEPF 的面积为)2214482x x x y ⎤-=-+⎥⎦=，此阶段函数图象是抛物线，开口方向向上，故选项B 错误；故选：A ．【点拨】本题考查了动点问题的函数图象，分段写出函数的解析式并数形结合进行分析是解题的关键．5．D【解析】【分析】如图所示，过点A 作AE ⊥x 轴于点E ，根据题意易得△AOB 为等边三角形，在旋转过程中，点A 有两次落在x 轴上，当点A 落在x 轴正半轴时，点C 落在点C′位置，利用旋转的性质和菱形的性质求解，当A 落在x 轴负半轴时，点C 落在点C′′位置，易证此时C′′与点A 重合，即可求解．【详解】解：如图所示，过点A 作AE ⊥x 轴于点E ，则tan ∠，∴∠AOE=60°，∵四边形ABCD 是菱形，∴△AOB是等边三角形，当A落在x轴正半轴时，点C落在点C′位置，此时旋转角为60°，∵∠BOC=60°，∠COF=30°，∴∠C′OF=60°-30°=30°，∵OC′=OA=4，∴OF=C'O cos∠，∠，C′F=C'Osin C'OF=2∴C′（2,--当A落在x轴负半轴时，点C落在点C′′位置，∵∠AOC=∠AOC+∠BOC=120°，∴∠A′′OC=120°，∠GOC′=30°又∵OA=OC′′，∴此时C′′点A重合，C C′′(2,，综上，点C的对应点的坐标为(2--,或(2,，故答案为：D．【点拨】本题考查菱形的性质，解直角三角形和旋转的性质，解题的关键是根据题意，分析点A的运动情况，分情况讨论．6．B【解析】【分析】根据菱形的性质和平面直角坐标系的特点可以求得点C的坐标，从而可以求得k的值，进而求得反比例函数的解析式．【详解】解：因为在菱形ABOC中，∠A＝60°，菱形边长为2，所以OC＝2，∠COB＝60°．如答图，过点C作CD⊥OB于点D，则OD＝OC·cos∠COB＝2×cos60°＝2×1＝1，CD＝OC·sin∠COB＝2×sin60°＝2因为点C在第二象限，所以点C的坐标为（－1。

中考19题（三角函数的应用）2013.19.（9分）我国南水北调中线工程的起点是丹江口水库，按照工程计划，需对原水库大坝进行混凝土培厚加高，使坝高由原来的162米增加到176.6米，以抬高蓄水位. 如图是某一段坝体加高工程的截面示意图，其中原坝体的高为BE ，背水坡坡角∠BAE =68°，新坝体的高为DE ，背水坡坡角∠DCE =60°. 求工程完工后背水坡底端水平方向增加的宽度AC （结果精确到0.1米. 参考数据：sin68°≈0.93，cos68°≈0.37，tan68°≈2.50，3≈1.73）.2014.19.（9分）在中俄“海上联合—2014”反潜演习中，我军舰A 测得潜艇C 的俯角为300．位于军舰A 正上方1000米的反潜直升机B 侧得潜艇C 的俯角为680.试根据以上数据求出潜艇C 离开海平面的下潜深度.（结果保留整数。

参考数据:sin680≈0.9,cos680≈0.4,,tan680≈≈1.7)C D A图海平面2015.20.（9分）如图所示，某数学活动小组选定测量小河对岸大树BC 的高度，他们在斜坡上D 处测得大树顶端B 的仰角是30º，朝大树方向下坡走6米到达坡底A 处，在A 处测得大树顶端B 的仰角是48°. . 若坡角∠FAE =30°，求大树的高度. （结果保留整数，参考数据：sin 48°≈0.74，cos 48°≈0.67，tan 48°≈1.11，3≈1.73）2016.19如图，小东在教学楼距地面9米高的窗口C 处，测得正前方旗杆顶部A 点的仰角为37°，旗杆底部B 点的俯角为45°，升旗时，国旗上端悬挂在距地面2.25米处，若国旗随国歌声冉冉升起，并在国歌播放45秒结束时到达旗杆顶端，则国旗应以多少米/秒的速度匀速上升？（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）FD 第20题30°48° E AC B2017.19.如图所示，我国两艘海监船A ，B 在南海海域巡航，某一时刻，两船同时收到指令，立即前往救援遇险抛锚的渔船C .此时，B 船在A 船的正南方向5海里处，A 船测得渔船C 在其南偏东45︒方向，B 船测得渔船C 在其南偏东53︒方向.已知A 船的航速为30海里/小时，B 船的航速为25海里/小时，问C 船至少要等待多长时间才能得到救援？（参考数据：4sin 535︒≈，3cos535︒≈，4tan 533︒≈，2 1.41≈）2018. 20．（9分）“高低杠”是女子体操特有的一个竞技项目，其比赛器材由高、低两根平行杠及若干支架组成，运动员可根据自己的身高和习惯在规定范围内调节高、低两杠间的距离．某兴趣小组根据高低杠器材的一种截面图编制了如下数学问题，请你解答．如图所示，底座上A ，B 两点间的距离为90cm ．低杠上点C 到直线AB 的距离CE 的长为155cm ，高杠上点D 到直线AB 的距离DF 的长为234cm ，已知低杠的支架AC 与直线AB 的夹角∠CAE 为82.4°，高杠的支架BD 与直线AB 的夹角∠DBF 为80.3°．求高、低杠间的水平距离CH 的长．（结果精确到1cm ，参考数据sin82.4°≈0.991，cos82.4°≈0.132，tan82.4°≈7.500，sin80.3°≈0.983，cos80.3°≈0.168，tan80.3°≈5.850）2019.19.（9分）数学兴趣小组到黄河风景名胜区测量炎帝塑像的高度，如图所示，炎帝塑像DE 在高55m的小山EC上，在A处测得塑像底部E的仰角为34°，再沿AC方向前进21m到达B 处，测得塑像顶部D的仰角为60°，求炎帝塑像DE的高度（精确到1m. 参考数据：sin34°≈0.56，cos34°≈0.83，tan34°≈0.67，3 1.73）。

九年级三角函数的应用练习题：1、右图：在甲楼A处测得乙楼顶的仰角为30°，测得乙楼底的俯角为45°，两楼相距60米。

求两楼高度2、右图：在甲楼A处测得乙楼顶的仰角为60°，测得乙楼底的俯角为45°，甲楼高100米。

求乙楼高度和两楼距离3、右图：在甲楼顶测得乙楼顶的仰角为30°，在甲楼底测得乙楼顶的仰角为60°，甲楼的高为50米。

求乙楼高度4、右图：小明在A处测得塔顶仰角为30°，前进100米至B处,测得塔顶仰角为45°。

求塔高5、如图，一飞机从一高炮C的正上方D点2 000 m 经过，沿水平方向飞行，稍后到达B 点，此时仰角45°，一分钟后飞机到达A点，仰角为30°，求飞机从B到A的速度?6、右图：身高1．80米的同学测得旗杆顶的仰角为60°，他与旗杆的距离为5米，求旗杆高7、右图：发射塔AB在山顶上，在距离山100米的C处，测得A、B的仰角为60°和45°求发射塔AB高度8、右图：小明在A处测得塔顶仰角为45°，前进100米至B处,测得塔顶仰角为60°，已知山高50米，求CD9.一轮船以每小时20海里的速度沿正东方向航行，上午8时，该船在A处测得某灯塔位于它的北偏东30º的B处。

上午9时行至C处，测得灯塔恰好在它的正北方向，此时它与灯塔的距离是海里。

（结果保留根号）10.在一次实践活动中，小兵从A 地出发，沿东北方向行进了5 千米到达B 地，然后再沿西北方向行进了5千米到达目的地C 。

（1）A 、C 两地的距离为 千米。

（2）试确定目的地C 在A 地的什么地方？11.如图,某地为响应市政府“形象重于生命”的号召,在甲建筑物上从点A 到点E 挂一长为30米的宣传条幅,在乙建筑物的顶部D 点测得条幅顶端A 点的仰角为40°,测得条幅底端E 的俯角为26°,求甲、乙两建筑物的水平距离BC 的长(精确到0.1米).12.如图,小山上有一座铁塔AB,在D 处测得点A 的仰角为∠ADC=60°,点B 的仰角为∠BDC=45°;在E 处测得A 的仰角为∠E=30°,并测得DE=90米, 求小山高BC 和铁塔高AB(精确到0.1米).13.某民航飞机在大连海域失事,为调查失事原因,决定派海军潜水员打捞飞机上的黑匣子,如图所示,一潜水员在A 处以每小时8海里的速度向正东方向划行,在A 处测得黑匣子B 在北偏东60°的方向,划行半小时后到达C 处,测得黑匣子B 在北偏东30 °的方向,在潜水员继续向东划行多少小时,距离黑匣子B 最近,并求最近距离. BDA CE FF30︒北A 60︒C14.在拓宽工程中, 要伐掉一棵树AB,在地面上事先划定以B 为圆心,半径与AB 等长的圆形危险区,现在某工人站在离B 点3米远的D 处测得树的顶点A 的仰角为60°,树的底部B 点的俯角为30°, 如图所示,问距离B 点8米远的保护物是否在危险区内?B30︒DA60︒C E。