下载文档原格式
五年级奥数综合应用题1、两筐重量相同的梨。
甲筐取出7千克，乙筐加入19千克，这时乙筐的重量是甲筐的3倍。
两筐原来各有梨多少千克？2、一根电线长180米，将它截成三段，第一段比第二段长20米，第三段长为第一段长的2倍，则第二段的长度为多少米？3、五、一班的男生人数和女生人数同样多，抽去18名男生和26名女生参加合唱团，剩下的男生人数是女生人数的3倍。
五、一班原有男女生各多少人？4、哥哥现存的钱是弟弟的5倍，如果哥哥再存20元，弟弟再存100元。
两人的存款正好相等，哥哥原来存有多少钱？5、有两块同样长的布，第一块用去27米，第二块用去18米，结果所剩的布第二块是第一块的4倍，两块布原来各长多少米？6、甲乙两人同时从两地骑车相向而行，甲的速度每小时20千米，乙每小时行18千米，两人相遇时距中点4千米，全路程是多少千米？7、六一班同学参加学校运动会，参加田赛的有26人，参加径赛的有30人，以上的两项都参加的有12人，这两项都没参加的有4人，全班有学生多少人？8、有两块同样长的布，第一块用去32米，第二块用去20米，结果所剩的米数第二块是第一块的3倍，两块布原来有多少米？9、副食店原有的白糖比红糖多200千克，当卖出红糖50千克时，白糖比红糖的千克数正好是红糖所剩千克数的一半，原来有白糖、红糖各多少克？10、有一个长方形，如果长增加6厘米，或者宽增加4厘米，面积都比原来增加48平方厘米，求这个长方形原来面积是多少平方厘米？11、甲乙两筐水果个数一样多，从第一筐中取出31个，第二筐中取出19个后，第二筐剩下的个数是第一筐的4倍，原来两筐水果各有多少个？12、有两筐水果，甲筐水果的个数是乙筐的3倍，如果从乙筐中拿15个放进甲筐，这是甲筐的水果恰好是乙筐的5倍，原来两筐水果各有多少个水果？13、第一筐有280个桔子，第二只筐有40只桔子，每次从第一只筐取出8个放入第二只筐，去多少次后两筐桔子相等14、一个班有学生42人，参加体育队的有30人，参加文艺队的有25人，并且全班没人至少参加一个队，两个队都参加的有多少人?15、甲乙两个学校共有学生1245人，如果从甲校调20人去乙校后，甲校比乙校还多5人，两校原有学生多少人？16、把200个苹果分成四堆，第一堆比第二堆的2倍多10个，第三堆如去掉15个刚好与第二堆相等，第四堆比第二堆的2倍少5个，四堆苹果各有多少个？17、A、B、C、D、E五人进行乒乓球单循环赛，比赛进行一段时间之后，对已赛果的场次作一个小统计，A赛4场，B赛3场，C赛2场，D赛1场，这时E赛了几场？到比赛结束还需要几场比赛？应用题练习11、小红有1角、5角的硬币共35枚，一共是9元5角，问两种硬币各多少枚？（两种假设）2、有鸡兔共20只，脚44只，鸡兔各几只？3、班主任张老师带五年级（2）班50名同学栽树，张老师一人载5课，男生每人栽3棵，女生每人栽2棵，总共栽树120棵，问有几名男生，几名女生？4、某玻璃杯厂要为商店运送1000个玻璃杯，双方商定每个运费为1元，如果打碎一个，这一个不但不给运费，而且要赔偿4元，结果运到目的地后结算时，玻璃杯厂共得运费895元，求打碎几个玻璃杯？5、小张、小李两人进行射击比赛，约定每中一发记20分，脱靶一发扣20分，两人各打了10发，共得208分，其中小张比小李多64分，问小张、小李两人各中几发。
五年级上册奥数题1、分数的分子和分母同时乘以或除以一个数(0除外)，分数大小不变。
（）2、两个面积相等的三角形，底和高也相等。
（）3、假如是一个假分数，那么a一定大于b。
（）4、一个分数的分子和分母都是质数，它一定是最简分数。
（）5、如果A是奇数，那么1093+89+A+25的结果还是奇数。
（）二、我会选择。
5分1、算一个上底是acm，下底是bcm，高是3cm的梯形面积，应该使用（）公式。
A、S＝abB、S＝3a÷2C、S＝3（a＋b）÷2D、S＝ab÷22、在60＝12×5中，12和5是60的（）。
A、倍数B、偶数C、质数D、因数3、分子加上12，分数的大小不变，分母应该加上( )。
A、12B、36C、27D、不能做。
三、数学迷宫。
1、最小的自然数是（），最小的奇数是（），最小的质数是（），最小的合数是（）。
2、一个三角形的面积是24cm ，与它等底等高的平行四边形的面积是（）cm 。
3、的分数单位是（），有（）个这样的单位，再去掉（）个分数单位就是3。
4、把5米长的绳子平均分成8段，每段长（），每段占全长的（），每段是5米的（）。
5、（）÷8＝＝＝9÷（）＝6、填质数：21＝（）＋（）；（）＝（）×（）。
7、要把36个球装在盒子里，每个盒子装得同样多，有（）种装法。
8、今年在多哈举行的亚运会上，中国代表团共夺得316枚奖牌，其中金牌有165个，银牌有88个，其余的是铜牌。
金牌、银牌、铜牌各占奖牌总数的、、。
五、解决问题：1、一块平行四边形广告牌，底长14cm，高,如果每平方米用油漆千克，这块广告牌至少用多少千克油漆2、36个红球与24个黄球，大小一样，分别装在同一种盒子里,每种球正好装完，每盒最多能装几个这时共需几个盒子3、甲乙两个工程队修一条长1400米的公路，他们从两端同时开工，甲队每天修80米，乙队每天修60米，多少天后能够修完这条公路（用方程解答）4、有20张5元和10元的人民币，一共是175元，5元和10的人民币各有多少张5、某校春季植树100棵，活了93棵，活了的棵树和未成活的棵数各占总数的几分之几6、一条拦河堤的横截面是梯形，上面宽4cm,下面宽7cm,高，求这个拦河坝的横截面面积。
1.计算：①：9999×9999+19999= ②：99999×22222+33333×33334=2.1÷（2÷3）÷（3÷4）÷……÷（8÷9）÷（9÷10）=3.有一个三位数，保留两位小数后的近似值是15.20，这样的三位小数中，最小的是，最大的是。
4.3÷7的商用循环小数表示是，商的小数点后第99位上的数字是。
5.一只蜗牛从24米深的井底沿着井壁往上爬，每天白天向上爬4.5米，晚上又落下3米，这只蜗牛一共要天才能爬上井口。
6.两个数的和是19.91，如果大数的小数点向左移动一位就等于小数，则大数是，小数是。
7.一桶油连桶称有8.4千克，用去一半后连桶还重4.6千克。
这桶里原来装有油千克，空桶重千克。
8.大小两数的差是1.998，若小数的小数点向右移动一位就与大数一样大，则大数是，小数是。
9.一个梯形，它的高与上底、下底的乘积分别是17.8平方米、15.4平方米，这个梯形的面积是平方米。
10.三个数的平均数是1.2，后来又加入一个数，平均数减少了0.05，后来加入的这个数是。
11.小明在计算一道乘法题时，把乘数67错写成76，结果积就比原来增加了1116，这道题的正确结果是。
12.把1～9这9个数字分别填入下面的□内，使算式成立：□□÷□－□=□□×□＋□=□13.图中梯形的面积是平方厘米，三角形（阴影部分）的面积是平方厘米。
14.如果某年二月份有5个星期三，那么这年的一月一日是星期。
15.已知三位数的各位上数字之和为25，这样的三位数一共有个。
16.一个长方形，长和宽都增加5厘米，得到的新长方形比原长方形面积多125平方厘米，原来长方形的周长是厘米。
17.两个修路队，甲队有138人，乙队有96人，现因甲队增加任务，要求从乙队调若干人到甲队，使甲队的人数是乙队的2倍，乙队要调人到甲队。
分列组合常识构造一、分列问题在现实生涯中经常会碰到如许的问题,就是要把一些事物排在一路,构成一列,盘算有若干种排法,就是分列问题．在排的进程中,不但与介入分列的事物有关,并且与各事物地点的先后次序有关．一般地,从个不合的元素中掏出()个元素,按照必定的次序排成一列,叫做从个不合元素中掏出个元素的一个分列．依据分列的界说,两个分列雷同,指的是两个分列的元素完整雷同,并且元素的分列次序也雷同．假如两个分列中,元素不完整雷同,它们是不合的分列;假如两个分列中,固然元素完整雷同,但元素的分列次序不合,它们也是不合的分列．分列的根本问题是盘算分列的总个数．从个不合的元素中掏出()个元素的所有分列的个数,叫做从个不合的元素的分列中掏出个元素的分列数,我们把它记做．依据分列的界说,做一个元素的分列由个步调完成：步调：从个不合的元素中任取一个元素排在第一位,有种办法;步调：从剩下的()个元素中任取一个元素排在第二位,有()种办法;……步调：从剩下的个元素中任取一个元素排在第个地位,有(种)办法;由乘法道理,从个不合元素中掏出个元素的分列数是,即,这里,,且等号右边从开端,后面每个因数比前一个因数小,共有个因数相乘．二、分列数一般地,对于的情形,分列数公式变成．暗示从个不合元素中取个元素排成一列所构成分列的分列数．这种个分列全体掏出的分列,叫做个不合元素的全分列．式子右边是从开端,后面每一个因数比前一个因数小,一向乘到的乘积,记为,读做的阶乘,则还可以写为：,个中．在分列问题中,有时刻会请求某些物体或元素必须相邻;求某些物体必须相邻的办法数量,可以将这些物体当作一个整体绑缚在一路进行盘算．三、组合问题日常生涯中有许多“分组”问题．如在体育比赛中,把参赛队分为几个组,从全班同窗中选出几人介入某项运动等等．这种“分组”问题,就是我们将要评论辩论的组合问题,这里,我们将侧重研讨有若干种分组办法的问题．一般地,从个不合元素中掏出个()元素构成一组不计较组内各元素的次序,叫做从个不合元素中掏出个元素的一个组合．从分列和组合的界说可以知道,分列与元素的次序有关,而组合与次序无关．假如两个组合中的元素完整雷同,那么不管元素的次序若何,都是雷同的组合,只有当两个组合中的元素不完整雷同时,才是不合的组合．从个不合元素中掏出个元素()的所有组合的个数,叫做从个不合元素中掏出个不合元素的组合数．记作．一般地,求从个不合元素中掏出的个元素的分列数可分成以下两步：第一步：从个不合元素中掏出个元素构成一组,共有种办法;第二步：将每一个组合中的个元素进行全分列,共有种排法．依据乘法道理,得到．是以,组合数．这个公式就是组合数公式．四、组合数的主要性质一般地,组合数有下面的主要性质：()这个公式的直不雅意义是：暗示从个元素中掏出个元素构成一组的所有分组办法．暗示从个元素中掏出()个元素构成一组的所有分组办法．显然,从个元素中选出个元素的分组办法恰是从个元素中选个元素剩下的()个元素的分组办法．例如,从人中选人开会的办法和从人中选出人不去开会的办法是一样多的,即．划定,．五、插板法一般用来解决求分化必定命量的无不同物体的办法的总数,应用插板法一般有三个请求：①所要分化的物体一般是雷同的：②所要分化的物体必须全体分完：③介入分物体的组至少都分到1个物体,不克不及有没分到物体的组消失．在有些标题中,已知前提与上面的三个请求其实不必定完整相符,对此应该对已知前提进行恰当的变形,使得它与一般的请求相符,再实用插板法．六、应用插板法一般有如下三种类型：⑴小我分个器械,请求每小我至少有一个．这个时刻我们只须要把所有的器械排成一排,在个中的个闲暇中放上个插板,所以分法的数量为．⑵小我分个器械,请求每小我至少有个．这个时刻,我们先发给每小我个,还剩下个器械,这个时刻,我们把剩下的器械按照类型⑴来处理就可以了．所以分法的数量为．⑶小我分个器械,许可有人没有分到．这个时刻,我们无妨先借来个器械,每小我多发1个,如许就和类型⑴一样了,不过这时刻物品总数变成了个,是以分法的数量为．例题精讲【例 1】4个男生2个女生6人站成一排合影留念,有若干种排法？假如请求2个女生紧挨着排在正中央有若干种不合的排法？【巩固】4男2女6小我站成一排合影留念,请求2个女的紧挨着有若干种不合的排法？【例 2】将A.B.C.D.E.F.G七位同窗在操场排成一列,个中学生B与C必须相邻．请问共有若干种不合的分列办法？【巩固】6名小同伙站成一排,若两人必须相邻,一共有若干种不合的站法？若两人不克不及相邻,一共有若干种不合的站法？【例 3】书架上有4本不合的漫画书,5本不合的童话书,3本不合的故事书,全体竖起排成一排,假如同类型的书不要离开,一共有若干种排法？假如只请求童话书和漫画书不要离开有若干种排法？【巩固】四年级三班举办六一儿童节联欢运动．全部运动由2个跳舞.2个演唱和3个小品构成．请问：假如请求同类型的节目持续表演,那么共有若干种不合的出场次序？【例 4】8人围圆桌会餐,甲.乙两人必须相邻,而乙.丙两人不得相邻,有几种坐法？【巩固】a,b,c,d,e五小我排成一排,a与b不相邻,共有若干种不合的排法？【例 5】一台晚会上有个演唱节目和个跳舞节目．求：⑴当个跳舞节目要排在一路时,有若干不合的安插节目标次序？⑵当请求每个跳舞节目之间至少安插个演唱节目时,一共有若干不合的安插节目标次序？【巩固】由个不合的独唱节目和个不合的合唱节目构成一台晚会,请求随意率性两个合唱节目不相邻,开端和最后一个节目必须是合唱,则这台晚会节目标编排办法共有若干种？【例 6】有10粒糖,分三天吃完,天天至少吃一粒,共有若干种不合的吃法？【巩固】小红有10块糖,天天至少吃1块,7天吃完,她共有若干种不合的吃法？【巩固】有12块糖,小光要6天吃完,天天至少要吃一块,问共有种吃法．【例 7】10只无差此外橘子放到3个不合的盘子里,许可有的盘子空着．请问一共有若干种不合的放法？【巩固】将个雷同的苹果放到个不合的盘子里,许可有盘子空着.一共有种不合的放法.【例 8】把20个苹果分给3个小同伙,每人起码分3个,可以有若干种不合的分法？【巩固】三所黉舍组织一次联欢晚会,共表演14个节目,假如每校至少表演3个节目,那么这三所黉舍表演节目数的不合情形共有若干种？【例 9】(1)小明有10块糖,天天至少吃1块,8天吃完,共有若干种不合吃法?(2)小明有10块糖,天天至少吃1块,8天或8天之内吃完,共有若干种吃法?【巩固】有10粒糖,天天至少吃一粒,吃完为止,共有若干种不合的吃法？【例 10】马路上有编号为,,,…,的十只路灯,为勤俭用电又能看清路面,可以把个中的三只灯关失落,但又不克不及同时关失落相邻的两只,在两头的灯也不克不及关失落的情形下,求知足前提的关灯办法有若干种？【巩固】黉舍新建筑的一条道路上有盏路灯,为了节俭用电而又不影响正常的照明,可以熄灭个中盏灯,但两头的灯不克不及熄灭,也不克不及熄灭相邻的盏灯,那么熄灯的办法共有若干种？【例 11】在四位数中,列位数字之和是4的四位数有若干？【巩固】大于2000小于3000的四位数中数字和等于9的数共有若干个？【例 12】所有三位数中,与456相加产生进位的数有若干个？【巩固】从1到2004这2004个正整数中,共有几个数与四位数8866相加时,至少产生一次进位？教室检测【随练1】某小组有12个同窗,个中男少先队员有3人,女少先队员有人,全组同窗站成一排,请求女少先队员都排一路,而男少先队员不排在一路,如许的排法有若干种？【随练2】把7支完整雷同的铅笔分给甲.乙.丙3小我,每人至少1支,问有若干种办法？【随练3】在三位数中,至少消失一个6的偶数有若干个？家庭功课【作业1】将三盆同样的红花和四盆同样的黄花摆放成一排,请求三盆红花互不相邻,共有种不合的放法.【作业2】黉舍合唱团要从个班中填补名同窗,每个班至少名,共有若干种抽调办法？【作业3】能被3整除且至少有一个数字是6的四位数有个.【作业4】黉舍乒乓球队一共有4名男生和3名女生．某次比赛后他们站成一排拍照,请问：（1）假如请求男生不克不及相邻,一共有若干不合的站法？（2）假如请求女生都站在一路,一共有若干种不合的站法？【作业5】由0,1,2,3,4,5构成的没有反复数字的六位数中,百位不是2的奇数有个．【作业6】泊车站划出一排个泊车地位,今有辆不合的车须要停放,若请求残剩的个空车位连在一路,一共有若干种不合的泊车计划?教授教养反馈学生对本次课的评价○特殊知足○知足○一般家长看法及建议家长签字：。
【五年级奥数举一反三—全国通用】测评卷11《盈亏问题》试卷满分：100分考试时间：100分钟姓名：_________班级：_________得分：_________一．选择题（共9小题，满分18分，每小题2分）1．（2分）（2017•奥林匹克）某市对城区主千道进行绿化，计划把某一段公路的一侧全部栽上银杏树，要求道路两端各裁一棵，并且每两棵树的间隔相等。
如果每隔5米栽1棵树，则树苗缺21棵，如果每隔6米栽一棵树，则树苗正好用完，原有树苗_____棵。
()A．56 B．72 C．94 D．106【解答】解：651-=（米）÷=（段）515⨯=（段）215105+=（棵）1051106答：原有树苗106棵。
故选：D。
2．（2分）（2014•华罗庚金杯）某次考试有50道试题，答对一道题得3分，答错一道题扣1分，不答题不得分．小龙得分120分，那么小龙最多答对了()道试题．A．40 B．42 C．48 D．50【解答】解：依题意可知：当小龙答对40题时，得分正好为403120⨯=分．那么需要剩余的10题得分和扣分相等．当小龙再答对1题时可以错3题剩余6题不答．当小龙再答对2题时可以错6题剩余2题不答．当小龙再答对3题时最多错7题，不能平衡分数．那么小龙最多答对42题．故选：B。
3．（2分）（2017•奥林匹克）平安夜圣诞节商城打折促销，某商品如按照标价的七五折出售将赔25元；若按照标价的九折出售将赚20元，该商品标价是_____元。
()A．250 B．270 C．280 D．300【解答】解：(2025)(90%75%)+÷-=÷4515%=（元）300答：这种商品的标价为300元。
故选：D。
4．（2分）（2014•迎春杯）动物园的饲养员把一堆桃子分给若干只猴子，如果每只猴子分6个，剩57个桃子；如果每只猴子分9个，就有5只猴子一个也分不到，还有一只猴子只分到3个．那么，有()个桃子．A．216 B．324 C．273 D．301【解答】解：依题意可知：如果每只猴子分6个，剩57个桃子．如果每只猴子分9个，就有5只猴子一个也分不到，还有一只猴子只分到3个证明少了59651⨯+=；猴子共有(5751)(96)36+÷-=（只）；桃子共有36657273⨯+=．故选：C。
循环小数与分数拆分考试要求（1）掌握循环小数化分数的基本方法与规律；（2）在计算中能灵活运用循环小数化分数的方法进行简便运算。
知识框架【基本概念】纯小数——整数部分是零的小数。
循环小数——从后某一位开始不断地重复出现前一个或一节数字的。
循环小数有以下两类类：混循环小数、纯循环小数。
混循环小数——循环节不是从小数部分第一位开始的循环小数。
纯循环小数——循环节从小数部分第一位开始的循环小数。
【基本方法】（1）纯循环小数化分数：这个分数的分子等于一个循环节所组成的数，分母由9构成，9的个数等于一个循环节中的位数。
（2）混循环小数化分数：这个分数的分子是第二个循环节以前的小数部分组成的数与小数部分中不循环部分组成的数的差；分母的头几位数是9，末几位是0，9的个数与一个循环节中的位数相同，0的个数与不循环部分的位数相同。
重难点重点：循环小数化分数的基本方法与规律；难点：灵活运用循环小数化分数的规律进行运算。
例题精讲一、 分数拆分【例1】110=()()11--()1=()()()111++【巩固】在下面的括里填上不同的自然数，使等式成立．()()()()()()111111110=--=++【例2】 如果1112009A B=-，A B ，均为正整数，则B 最大是多少？【巩固】若1112004a b =+，其中a 、b 都是四位数，且a<b ，那么满足上述条件的所有数对（a,b ）是哪些？二、 纯循环小数化分数 【例3】 把纯循环小数化分数：（1）6.0 （2）201.3【巩固】把纯循环小数化成分数（1）612.0 （2）321.4三、混循环小数化分数【例4】 把混循环小数化分数。
（1）512.0 （2）335.6【巩固】把混循环小数化成分数。
（1）627.0 （2）24.7四、循环小数的四则运算与周期运算循环小数化成分数后，循环小数的四则运算就可以按分数四则运算法则进行。
从这种意义上来讲，循环小数的四则运算和有限小数四则运算一样，也是分数的四则运算。
五年级奥数综合练习1、0。
2＋0。
4＋…＋0.8＋0.10＋0.12＋…＋0。
98＋0.1002、1994十199。
4十19。
94十1.9943、(2000－1）＋（1999－2）＋（1998－3）＋……＋（1002－999)＋（1001－1000）4、在110~130这21个数中，在所有奇数（即单数)的十位与个位之间加上小数点，如119加上小数点后变为11。
9,再在所有偶数（即双数)的百位与十位之间加上小数点,如124加上小数点变为1。
24。
那么,经过变换后的21个数的和是.5、在一个整数的某两个数字间点上小数点后，把得到的小数与原来的整数相加，和是10063。
64，原来的整数是。
6、把一个小数去掉小数点后再与原数的4倍相加，和是702，原来的小数是。
7、今年陈老师42岁，张平8岁，李云9岁，王八11岁，当陈老师的年龄和张平、李云、王八年龄的和相等时,张平岁。
8、1998年父与子年龄的和是36岁，2004年父亲年龄是儿子年龄的3倍，公元年父亲年龄是儿子年龄的2倍。
9、如果两数的和是64，两数的积可以整除4，那么这两个数的差等于.10、有一些糖，每人分5块多10；如果现有的人数增加到原来的1.5倍，那么每人4块就少2块。
这些糖在块到块之间。
11、用两个质数之和来表示100有许多种方法，在所有这些方法中，两个质数中大数减小数的差最小是.12、甲乙丙三人在圆形的跑道上跑步。
甲跑完一周要用3分，乙跑完一周要用4分，丙跑完一周要用6分。
如果他们同时从同一地点同向起跑，那么他们第二次相遇要经过分钟。
13、一个国家的居民不是骑士就是无赖，骑士不说谎，无赖永远说谎。
我们遇到该国A与B两位居民，B 对我们说：“A和我不同，一个是骑士，一个是无赖。
”请问A是骑士还是无赖？14、下面的算式是按一定的规律排列的：4＋2，5＋8，6＋14，7＋20,……，那么和为83的算式是＋。
15、李林喝了一杯牛奶的，然后加满水，又喝了一杯的水，再倒满水后又喝了半杯，又加满了水,最后把一杯都喝了,那么李林喝的牛奶多，还是水多？16、用若干个只含有数字“8”组成的自然数连加，使和为1000,至少需要个“8”。
五年级奥数综合训练试卷12套五年级奥数综合训练试卷一小学五年级奥数竞赛试卷姓名：班级：（时间：80分钟）1. 15.48×35－154.8×1.9+15.48×84＝2.解方程。
5×(2x+7)－30=3×(2x+7)x=3.循环小数0.37 205小数点右面第106位上的数字是。
4.一排电线杆，原来两根之间的距离是35米，现改为45米，如果起点的一根位置不移动，至少米又有一根电线杆不需要移动。
5.一船在静水中每小时18千米，在一条顺水用4小时行了80千米，这条河的水流速度是。
6.同学们去春游，带水壶的有78人，带水果的有77人，既带水壶又带水果的有48人。
参加春游的同学共有人。
- 1 -7.同时被3、4、5整除的最小四位数是。
8.某个游戏，满分为100分，每人可以做4次，以平均分为游戏的成绩。
小王的平均分为85分，那么，他任何一次游戏的得分都不能低于分。
9.五年级数学竞赛，小明的名次乘以他的年龄和竞赛成绩的乘积是2134。
小明排名名和成绩都是分。
10.有一个六位数2002能被88整除。
这个六位数是。
11.用5、5、5、1四个数字组成一个算式，使其结果为24。
算式是。
12.五年级有六个班，每个班人数相等。
每个班选16名学生参加少先队活动，其余学生与原来4个班人数相等。
13.连续5个奇数的和是95，其中最大的是，最小的是。
14.…之和是。
(奇数或偶数)-2-15.在八个房间里，有七个房间开着灯，如果每次同时拨动四个房间的开关，（能或不能）把全部房间的灯关上，每次拨动5个房间的开关，（能或不能）把全部房间的灯关上。
16.大年三十，花灯明亮，三三个小时就能数完。
五五个小时剩一个灯笼，七七个小时正好，八八个小时还缺三个。
请你自己猜，至少有一个彩灯。
17.甲、乙、丙、丁四位同学在篮球比赛中犯规的次数各不相同，A、B、C、D四位裁判有一段对话：A说：“甲犯规4次，乙犯规3次。
平面图形1、 和差法：分割、合并、倍数比2、 运动法：3、 等积变换法：等底、等高则等积；等积、等高则等底；等积、等底则等高。
例1、求阴影部分的面积。
例2、大、小两个正方形的边长分别是8厘米和6厘米， 求阴影部分的面积。
例3、两个相同的直角三角形如图重叠在一起， 求阴影部分的面积。
例4、求阴影部分面积。
例5、图中长方形ABCD 中AB=5厘米，BC=8厘米。
三角形DEF （甲）的面积 比三角形ABF （乙）的面积大8平方厘米。
求DE 的长。
3cm4cm6cm5cm2cm12cm甲ABCDEF乙AD B C 10cm 10cm24cm45° E5cm例6、在三角形ABC 中，DC=2BD ，CE=3AE ，三角形ADE 的面积是 8平方厘米。
求三角形ABC 的面积。
例7、四边形ABCD 中，AC 和BD 互相垂直，AC=20厘米，BD=15厘米。
求四边形的面积。
例8、在四边形ABCD 中，∠C=45°，∠B=90°，∠D=90°， AD=4cm ，BC=12cm 。
求四边形ABCD 的面积。
例9、AF=2cm,AB=4cm,CD=5cm,DE=8cm,∠B=∠E=90°。
求四边形ACDF 的面积。
例10、已知大正方形比小正方形边长多2厘米，大正方形比小正方形的面积大10平方厘米。
求大、小正方形的面积各数多少平方厘米。
ABCDC45°AB CDABCDEF 4cm8cm2cm练习1、图中两个正方形的边长是10厘米和7厘米，求阴影部分的面积（如图）练习2、如下图，在三角形ABC中，AD=BD,CE=3BE。
若三角形BED的面积是1平方厘米，则三角形ABC的面积是多少平方厘米？练习3、三角形ABC是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方厘米. A B长40厘米, BC长多少厘米.练习4、在右图中(单位:厘米),两个阴影部分面积的和是平方厘米.练习5、ABC是等腰直角三角形. D是半圆周的中点,BC是半圆的直径,已知:AB=BC=10,那么阴影部分的面积是多少?练习6、已知右图中大正方形边长是6厘米,中间小正方形边长是4厘米.求阴影部分的面积. C②①A B121520A10DCB练习7、右图中三角形是等腰直角三角形, 阴影部分的面积是 (平方厘米).练习8、如右图,阴影部分的面积是 .练习9、如图所求,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是 厘米.)14.3(=π练习10、ABC 是等腰直角三角形. D 是半圆周的中点, BC 是半圆的直径,已知: AB =BC =10,那么阴影部分的面积是多少?练习11、在四边形ABCD 中，∠C=135°，∠D=90°。
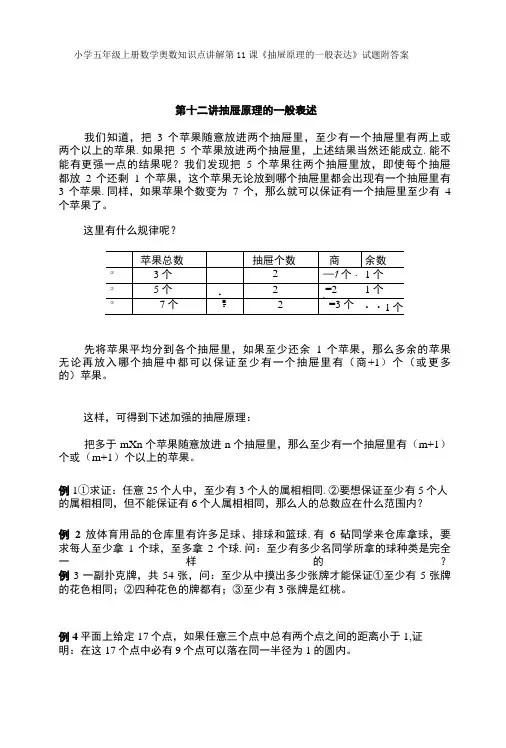
小学五年级上册数学奥数知识点讲解第11课《抽屉原理的一般表达》试题附答案第十二讲抽屉原理的一般表述我们知道，把3个苹果随意放进两个抽屉里，至少有一个抽屉里有两上或两个以上的苹果.如果把5个苹果放进两个抽屉里，上述结果当然还能成立.能不能有更强一点的结果呢？我们发现把5个苹果往两个抽屉里放，即使每个抽屉都放2个还剩1个苹果，这个苹果无论放到哪个抽屉里都会出现有一个抽屉里有3个苹果.同样，如果苹果个数变为7个，那么就可以保证有一个抽屉里至少有4 个苹果了。
这里有什么规律呢？先将苹果平均分到各个抽屉里，如果至少还余1个苹果，那么多余的苹果无论再放入哪个抽屉中都可以保证至少有一个抽屉里有（商+1）个（或更多的）苹果。
这样，可得到下述加强的抽屉原理：把多于mXn个苹果随意放进n个抽屉里，那么至少有一个抽屉里有（m+1）个或（m+1）个以上的苹果。
例1①求证：任意25个人中，至少有3个人的属相相同.②要想保证至少有5个人的属相相同，但不能保证有6个人属相相同，那么人的总数应在什么范围内？例2放体育用品的仓库里有许多足球、排球和篮球.有6砧同学来仓库拿球，要求每人至少拿1个球，至多拿2个球.问：至少有多少名同学所拿的球种类是完全一样的？例3一副扑克牌，共54张，问：至少从中摸出多少张牌才能保证①至少有5张牌的花色相同；②四种花色的牌都有；③至少有3张牌是红桃。
例4平面上给定17个点，如果任意三个点中总有两个点之间的距离小于1,证明：在这17个点中必有9个点可以落在同一半径为1的圆内。
例5把1、2、3、…、10这十个数按任意顺序排成一圈，求证在这一圈数中一定有相邻的三个数之和不小于17o例6在边长为3米的正方形内，任意放入28个点，求证：必有4个点，以它们为顶点的四边形的面积不超过1平方米。
分析与解答根据题目的结论，考虑把这个大正方形分割成面积为1平方米的9个小正方形（如右图）。
答案例1①求证：任意25个人中，至少有3个人的属相相同.②要想保证至少有5个人的属相相同，但不能保证有6个人属相相同，那么人的总数应在什么范围内?分析与解答①把12种属相看作12个抽屉。
小学五年级奥数竞赛试卷姓名：班级：（时间：80分钟）1. 15.48×35－154.8×1.9+15.48×84＝2.解方程。
5×(2x+7)－30=3×(2x+7) x=3.循环小数0.37 205 小数点右面第106位上的数字是。
4. 一排电线杆，原来两根之间的距离是35米，现改为45米，如果起点的一根位置不移动，至少米又有一根电线杆不需要移动。
5.一船在静水中每小时18千米，在一条顺水用4小时行了80千米，这条河的水流速度是。
6.同学们去春游，带水壶的有78 人，带水果的有77 人，既带水壶又带水果的有48 人。
参加春游的同学共有人。
7. 如图，E、F、G分别是平行四边形ABCD中AD、BC、DC边上的中点，求平行四边形的面积是阴影部分面积的倍。
8. 同时被3、4、5整除的最小四位数是。
9. 某个游戏，满分为100分，每人可以做4次，以平均分为游戏的成绩。
小王的平均分为85分，那么，他任何一次游戏的得分都不能低于分。
10. 五年级数学竞赛，小明获得的名次与他的年龄和竞赛的成绩相乘之积是2134，小明获得的名次名，成绩是分。
11.有一个六位数□2002□能被88整除，这个六位数是。
12.用5、5、5、1四个数字组成一个算式，使其结果为24。
算式是。
13. 五年级有六个班，每班人数相等。
从每班选16人参加少先队活动，剩下的同学相当于原来4个班的人数，原来每班人。
14.连续5个奇数的和是95，其中最大的是，最小的是。
15.1＋2＋3＋4＋5……＋2007＋2008的和是。
（奇数或偶数）16.在八个房间里，有七个房间开着灯，如果每次同时拨动四个房间的开关，（能或不能）把全部房间的灯关上，每次拨动5个房间的开关，（能或不能）把全部房间的灯关上。
17.大年三十彩灯悬,彩灯齐明光灿灿,三三数时能数尽,五五数时剩一盏,七七数时刚刚好,八八数时还缺三。
请你自己猜一猜，彩灯至少有盏18.甲、乙、丙、丁四位同学在篮球比赛中犯规的次数各不相同，A、B、C、D 四位裁判有一段对话：A说：“甲犯规4次，乙犯规3次。
”B说：“丙犯规4次，乙犯规2次。
”C说：“丁犯规2次，丙犯规3次。
”D说：“丁犯规1次，乙犯规3次。
”记录员说：“A、B、C、D四位裁判每人只说对了一半。
”甲犯规次。
19.甲、乙、丙分别在南京、苏州、西安工作，他们的职业分别是工人，农民和教师。
已知⑴甲不在南京工作，⑵乙不在苏州工作，⑶在苏州工作的是工人，⑷在南京工作的不是教师，⑸乙不是农民。
那么，甲是，在工作。
20.如图，在梯形ABCD中，DE=3ECBC=3FC，四边形AECF的面积是14平方米。
求梯形ABCD的面积是平方米。
图形弄不了，有两个图形五年级奥数试卷一、简算：20分1746＋1747＋1748 7.81×48＋78.1×4.1＋0.78×9038×29＋84×71＋46×29 34÷17＋29÷17＋27÷17＋46÷17二、有趣的数字：（10分）六一庆六一＋庆祝六一1 9 9 4四、解决问题。
（65分）1、如果数A减去数B的3倍，差是51。
数A加上数B的2倍，和是111，那么数A=（），数B=（）。
2、一次数学竞赛有10道题，做对一题得10分，做错一题倒扣2分，小明得了76分，小明做对了（）题。
3、甲站有222辆汽车，乙站有78辆汽车，每天从甲站开往乙站22辆，从乙站开往甲站26辆，（）天后，甲站的汽车是乙站5倍。
4、一排电线杆，原来两根之间的距离是35米，现改为45米，如果起点的一根位置不移动，至少（）米又有一根电线杆不需要移动。
5、一列火车通过长221米的桥需要42秒，用同样的速度通过长172米的隧道需36秒，列车长（）米，列车的速度是（）米。
6、甲、乙、丙、丁四个数的和是175，甲加上4，乙减去4，丙乘上4，丁除以4后，四个数就相等了，则甲=（），乙=（），丙=（），丁=（）。
7、甲买了4千克苹果，3千克的梨，乙买了3千克苹果，2千克的梨，丙买了3千克的苹果，4千克梨，甲比乙多花了3.45元，乙比丙少花了2.9元，则甲花了（）元，乙花了（）元。
8、一个自然数被3除余1，被5除余2，被7除余3，这个自然数最小是（）。
1、在1、2、3……499、500中，数字2在一共出现了（）次。
2、食堂有大米和面粉共351袋，如果大米增加20袋，面粉减少50袋，那么大米的袋数比面粉的袋数的3倍还多1袋，原来大米有（）袋，面粉有（）袋。
3、279是甲乙丙丁四个数的和，如果甲减少2，乙增加2，丙除以2，丁乘以2后，则四个数都相等，那么甲是（），乙是（），丙是（），丁是（）。
4、兄弟俩比年龄，哥哥说:“当我是你今年岁数的那一年，你刚5岁。
”弟弟说：“当我长到你今年的岁数时，你就17岁了。
”哥哥今年（）岁，弟弟今年（）岁。
5、甲对乙说：“我的年龄是你的3倍。
”乙对甲说：“我5年后的年龄和你11年前的年龄一样。
”甲今年（）岁，乙今年（）岁。
6、A、B两地相距21千米，上午9时甲、乙分别从A、B两地出发，相向而行，甲到达B地后立即返回，乙到达A地后立即返回，中午12时他们第二次相遇。
此时甲走的路程比乙走的路程多9千米。
甲每小时走（）千米。
7、一条轮船在两码头间航行，顺水航行需4小时，逆水航行需5小时，水速是每小时5千米，这条船在静水中每小时行（）千米。
8、一座铁路桥全长1200米，一列火车开过大桥需要75秒，火车开过路旁的电线杆只需15秒，那么火车全长是（）米。
9、蜗牛从一个枯井网上爬，白天向上爬110厘米，夜里向下滑40厘米，若要第五天的白天爬到井口，这口井至少深（）厘米。
10、周老师给学是发练习本，每人分7本还多出7本，如果每人多发2本，就有一个同学分不到，那么一共有（）个同学，（）个练习本。
11、王飞以每小时40千米的速度行了240千米，按原路返回时每小时行60千米，王飞往返的平均速度是每小时行（）千米。
12、“IMO”是国际数学奥林匹克竞赛的缩写，把这三个字母写成三种不同的颜色，现有五种不同的颜色，按上述要求可以写出（）中不同颜色搭配的“IMO”。
一、填空题1.把20个梨和25个苹果平均分给小朋友，分完后梨剩下2个，而苹果还缺2个，一共有_____个小朋友.2. 幼儿园有糖115颗、饼干148块、桔子74个，平均分给大班小朋友;结果糖多出7颗，饼干多出4块，桔子多出2个.这个大班的小朋友最多有_____人.3. 用长16厘米、宽14厘米的长方形木板来拼成一个正方形，最少需要用这样的木板_____块.4. 用长是9厘米、宽是6厘米、高是7厘米的长方体木块叠成一个正方体，至少需要这种长方体木块_____块.5. 一个公共汽车站,发出五路车,这五路车分别为每隔3、5、9、15、10分发一次，第一次同时发车以后，_____分又同时发第二次车.6. 动物园的饲养员给三群猴子分花生,如只分给第一群,则每只猴子可得12粒;如只分给第二群，则每只猴子可得15粒;如只分给第三群，则每只猴子可得20粒.那么平均给三群猴子,每只可得_____粒.7. 这样的自然数是有的:它加1是2的倍数,加2是3的倍数,加3是4的倍数,加4是5的倍数,加5是6的倍数,加6是7的倍数,在这种自然数中除了1以外最小的是_____.8. 能被3、7、8、11四个数同时整除的最大六位数是_____.9. 把26,33,34,35,63,85,91,143分成若干组,要求每一组中任意两个数的最大公约数是1, 那么至少要分成_____组.10. 210与330的最小公倍数是最大公约数的_____倍.二、解答题11.公共汽车总站有三条线路，第一条每8分发一辆车，第二条每10分发一辆车，第三条每16分发一辆车，早上6:00三条路线同时发出第一辆车.该总站发出最后一辆车是20:00,求该总站最后一次三辆车同时发出的时刻.12. 甲乙两数的最小公倍数除以它们的最大公约数,商是12.如果甲乙两数的差是18,则甲数是多少?乙数是多少?13. 用、、分别去除某一个分数，所得的商都是整数.这个分数最小是几?14. 有15位同学,每位同学都有编号,他们是1号到15号,1号同学写了一个自然数,2号说:“这个数能被2整除”，3号说:“这个数能被他的编号数整除.1号作了检验:只有编号连续的二位同学说得不对,其余同学都对,问:(1)说的不对的两位同学,他们的编号是哪两个连续自然数?(2)如果告诉你,1号写的数是五位数,请找出这个数.参考答案:1、9 若梨减少2个,则有20-2=18(个);若将苹果增加2个,则有25+2=27(个),这样都被小朋友刚巧分完.由此可知小朋友人数是18与27的最大公约数.所以最多有9个小朋友.2、36 根据题意不难看出,这个大班小朋友的人数是115-7=108,148-4=144,74-2=72的最大公约数. 所以,这个大班的小朋友最多有36人.3、56 所铺成正方形的木板它的边长必定是长方形木板长和宽的倍数,也就是长方形木板的长和宽的公倍数,又要求最少需要多少块,所以正方形木板的边长应是14与16的最小公倍数.先求14与16的最小公倍数.216 1487故14与16的最小公倍数是287=112.因为正方形的边长最小为112厘米,所以最少需要用这样的木板=78=56(块)4、5292 与上题类似，依题意，正方体的棱长应是9，6，7的最小公倍数，9，6，7的最小公倍数是126.所以,至少需要这种长方体木块=142118=5292(块)[注]上述两题都是利用最小公倍数的概念进行“拼图”的问题，前一题是平面图形，后一题是立体图形，思考方式相同，后者可看作是前者的推广.将平面问题推广为空间问题是数学家喜欢的研究问题的方式之一.希望引起小朋友们注意.5、90依题意知,从第一次同时发车到第二次同时发车的时间是3,5,9,15和10的最小公倍数.因为3,5,9,15和10的最小公倍数是90,所以从第一次同时发车后90分又同时发第二次车.6、5依题意得花生总粒数=12第一群猴子只数=15第二群猴子只数=20第三群猴子只数由此可知,花生总粒数是12,15,20的公倍数,其最小公倍数是60.花生总粒数是60,120,180,……，那么第一群猴子只数是5，10，15，……第二群猴子只数是4，8，12，……第三群猴子只数是3，6，9，……所以，三群猴子的总只数是12，24，36，…….因此,平均分给三群猴子,每只猴子所得花生粒数总是5粒.7、421依题意知,这个数比2、3、4、5、6、7的最小公倍数大1,2、3、4、5、6、7的最小公倍数是420，所以这个数是421.8、999768由题意知,最大的六位数是3,7,8,11的公倍数,而3,7,8,11的最小公倍数是1848.因为9999991848=541……231，由商数和余数可知符合条件的最大六位数是1848的541倍，或者是999999与231的差.所以,符合条件的六位数是999999-231=999768.9、3根据题目要求,有相同质因数的数不能分在一组,26=213,91=713,143=1113,所以,所分组数不会小于3.下面给出一种分组方案:(1)26，33，35;(2)34，91;(3)63，85，143.因此,至少要分成3组.[注]所求组数不一定等于出现次数最多的质因数的出现次数，如15=35，21=37，35=57，3，5，7各出现两次，而这三个数必须分成三组，而不是两组.除了上述分法之外,还有多种分组法,下面再给出三种:(1)26,35;33，85，91;34，63，143.(2)85,143,63;26，33，35;34，91.(3)26,85,63;91，34，33;143，35.10、77根据“甲乙的最小公倍数甲乙的最大公约数=甲数乙数”，将210330分解质因数，再进行组合有210330=235723511=223252711=(235)(235711)因此，它们的最小公倍数是最大公约数的711=77(倍).11、根据题意,先求出8,10,16的最小公倍数是80,即从第一次三车同时发出后,每隔80分又同时发车.从早上6:00至20:00共14小时,求出其中包含多少个80分601480=10…40分由此可知,20:00前40分,即19:20为最后一次三车同时发车的时刻. 12、甲乙两数分别除以它们的最大公约数,所得的两个商是互质数.而这两个互质数的乘积,恰好是甲乙两数的最小公倍数除以它们的最大公约数所得的商--12.这一结论的根据是:(我们以“约”代表两数的最大公约数，以“倍”代表两数的最小公倍数) 甲数乙数=倍约=，所以:=，=12将12变成互质的两个数的乘积:①12=43，②12=112先看①,说明甲乙两数:一个是它们最大公约数的4倍，一个是它们最大公约数的3倍.甲乙两数的差除以上述互质的两数(即4和3)之差,所得的商,即甲乙两数的最大公约数.18(4-3)=18甲乙两数,一个是:183=54，另一个是:184=72.再看②,18(12-1)=,不符合题意,舍去.13、依题意,设所求最小分数为,则=a =b =c即=a =b =c其中a,b,c为整数.因为是最小值,且a,b,c是整数,所以M是5,15,21的最小公倍数,N是28,56,20的最大公约数,因此,符合条件的最小分数: ==14、(1)根据2号~15号同学所述结论,将合数4,6,…，15分解质因数后，由1号同学验证结果，进行分析推理得出问题的结论.4=22,6=23,8=23,9=32,10=25,12=223,14=27,15=35由此不难断定说得不对的两个同学的编号是8与9两个连续自然数(可逐次排除,只有8与9满足要求).(2)1号同学所写的自然数能被2,3,4,5,6,7,10,11,12,13,14,15这12个数整除,也就是它们的公倍数.它们的最小公倍数是223571113=60060因为60060是一位五位数,而这12个数的其他公倍数均不是五位数,所以1号同学写的五位数是60060.一、填空题1.把20个梨和25个苹果平均分给小朋友，分完后梨剩下2个，而苹果还缺2个，一共有_____个小朋友.2. 幼儿园有糖115颗、饼干148块、桔子74个，平均分给大班小朋友;结果糖多出7颗，饼干多出4块，桔子多出2个.这个大班的小朋友最多有_____人.3. 用长16厘米、宽14厘米的长方形木板来拼成一个正方形，最少需要用这样的木板_____块.4. 用长是9厘米、宽是6厘米、高是7厘米的长方体木块叠成一个正方体，至少需要这种长方体木块_____块.5. 一个公共汽车站,发出五路车,这五路车分别为每隔3、5、9、15、10分发一次，第一次同时发车以后，_____分又同时发第二次车.6. 动物园的饲养员给三群猴子分花生,如只分给第一群,则每只猴子可得12粒;如只分给第二群，则每只猴子可得15粒;如只分给第三群，则每只猴子可得20粒.那么平均给三群猴子,每只可得_____粒.7. 这样的自然数是有的:它加1是2的倍数,加2是3的倍数,加3是4的倍数,加4是5的倍数,加5是6的倍数,加6是7的倍数,在这种自然数中除了1以外最小的是_____.8. 能被3、7、8、11四个数同时整除的最大六位数是_____.9. 把26,33,34,35,63,85,91,143分成若干组,要求每一组中任意两个数的最大公约数是1, 那么至少要分成_____组.10. 210与330的最小公倍数是最大公约数的_____倍.二、解答题11.公共汽车总站有三条线路，第一条每8分发一辆车，第二条每10分发一辆车，第三条每16分发一辆车，早上6:00三条路线同时发出第一辆车.该总站发出最后一辆车是20:00,求该总站最后一次三辆车同时发出的时刻.12. 甲乙两数的最小公倍数除以它们的最大公约数,商是12.如果甲乙两数的差是18,则甲数是多少?乙数是多少?13. 用、、分别去除某一个分数，所得的商都是整数.这个分数最小是几?14. 有15位同学,每位同学都有编号,他们是1号到15号,1号同学写了一个自然数,2号说:“这个数能被2整除”，3号说:“这个数能被他的编号数整除.1号作了检验:只有编号连续的二位同学说得不对,其余同学都对,问:(1)说的不对的两位同学,他们的编号是哪两个连续自然数?(2)如果告诉你,1号写的数是五位数,请找出这个数.参考答案:1、9 若梨减少2个,则有20-2=18(个);若将苹果增加2个,则有25+2=27(个),这样都被小朋友刚巧分完.由此可知小朋友人数是18与27的最大公约数.所以最多有9个小朋友.2、36 根据题意不难看出,这个大班小朋友的人数是115-7=108,148-4=144,74-2=72的最大公约数. 所以,这个大班的小朋友最多有36人.3、56 所铺成正方形的木板它的边长必定是长方形木板长和宽的倍数,也就是长方形木板的长和宽的公倍数,又要求最少需要多少块,所以正方形木板的边长应是14与16的最小公倍数.先求14与16的最小公倍数.216 1487故14与16的最小公倍数是287=112.因为正方形的边长最小为112厘米,所以最少需要用这样的木板=78=56(块)4、5292 与上题类似，依题意，正方体的棱长应是9，6，7的最小公倍数，9，6，7的最小公倍数是126.所以,至少需要这种长方体木块=142118=5292(块)[注]上述两题都是利用最小公倍数的概念进行“拼图”的问题，前一题是平面图形，后一题是立体图形，思考方式相同，后者可看作是前者的推广.将平面问题推广为空间问题是数学家喜欢的研究问题的方式之一.希望引起小朋友们注意.5、90依题意知,从第一次同时发车到第二次同时发车的时间是3,5,9,15和10的最小公倍数.因为3,5,9,15和10的最小公倍数是90,所以从第一次同时发车后90分又同时发第二次车.6、5依题意得花生总粒数=12第一群猴子只数=15第二群猴子只数=20第三群猴子只数由此可知,花生总粒数是12,15,20的公倍数,其最小公倍数是60.花生总粒数是60,120,180,……，那么第一群猴子只数是5，10，15，……第二群猴子只数是4，8，12，……根据题目要求,有相同质因数的数不能分在一组,26=213,91=713,143=1113,所以,所分组数不会小于3.下面给出一种分组方案:(1)26，33，35;(2)34，91;(3)63，85，143.因此,至少要分成3组.[注]所求组数不一定等于出现次数最多的质因数的出现次数，如15=35，21=37，35=57，3，5，7各出现两次，而这三个数必须分成三组，而不是两组.除了上述分法之外,还有多种分组法,下面再给出三种:(1)26,35;33，85，91;34，63，143.(2)85,143,63;26，33，35;34，91.(3)26,85,63;91，34，33;143，35.10、77根据“甲乙的最小公倍数甲乙的最大公约数=甲数乙数”，将210330分解质因数，再进行组合有210330=235723511=223252711=(235)(235711)因此，它们的最小公倍数是最大公约数的711=77(倍).11、根据题意,先求出8,10,16的最小公倍数是80,即从第一次三车同时发出后,每隔80分又同时发车.从早上6:00至20:00共14小时,求出其中包含多少个80分601480=10…40分由此可知,20:00前40分,即19:20为最后一次三车同时发车的时刻. 12、甲乙两数分别除以它们的最大公约数,所得的两个商是互质数.而这两个互质数的乘积,恰好是甲乙两数的最小公倍数除以它们的最大公约数所得的商——12.这一结论的根据是:(我们以“约”代表两数的最大公约数，以“倍”代表两数的最小公倍数) 甲数乙数=倍约=，所以:=，=12将12变成互质的两个数的乘积:①12=43，②12=112先看①,说明甲乙两数:一个是它们最大公约数的4倍，一个是它们最大公约数的3倍.甲乙两数的差除以上述互质的两数(即4和3)之差,所得的商,即甲乙两数的最大公约数.18(4-3)=18甲乙两数,一个是:183=54，另一个是:184=72.再看②,18(12-1)=,不符合题意,舍去.13、依题意,设所求最小分数为,则=a =b =c即=a =b =c其中a,b,c为整数.因为是最小值,且a,b,c是整数,所以M是5,15,21的最小公倍数,N是28,56,20的最大公约数,因此,符合条件的最小分数: ==14、(1)根据2号~15号同学所述结论,将合数4,6,…，15分解质因数后，由1号同学验证结果，进行分析推理得出问题的结论.4=22,6=23,8=23,9=32,10=25,12=223,14=27,15=35由此不难断定说得不对的两个同学的编号是8与9两个连续自然数(可逐次排除,只有8与9满足要求).(2)1号同学所写的自然数能被2,3,4,5,6,7,10,11,12,13,14,15这12个数整除,也就是它们的公倍数.它们的最小公倍数是223571113=60060因为60060是一位五位数,而这12个数的其他公倍数均不是五位数,所以1号同学写的五位数是60060.第三群猴子只数是3，6，9，……所以，三群猴子的总只数是12，24，36，…….因此,平均分给三群猴子,每只猴子所得花生粒数总是5粒.7、421依题意知,这个数比2、3、4、5、6、7的最小公倍数大1,2、3、4、5、6、7的最小公倍数是420，所以这个数是421.8、999768由题意知,最大的六位数是3,7,8,11的公倍数,而3,7,8,11的最小公倍数是1848.因为9999991848=541……231，由商数和余数可知符合条件的最大六位数是1848的541倍，或者是999999与231的差.所以,符合条件的六位数是999999-231=999768.。
