2016数学建模A题系泊系统设计
- 格式：doc
- 大小：1.14 MB
- 文档页数：26
下载文档原格式
合集下载
2016大学生建模A题提示——知识2
1. 某型传输节点选用 II 型电焊锚链 22.05m， 选用的重物球的质量为 1200kg。
现将该型传输节点布放在水深 18m、海床平坦、海水密度为 1.025× 103kg/m3 的海 域。若海水静止，分别计算海面风速为 12m/s 和 24m/s 时钢桶和各节钢管的倾斜 角度、锚链形状、浮标的吃水深度和游动区域。 分析:
2016 高教社杯全国大学生数学建模竞赛题目
A题 系泊系统的设计
对系缆力的计算，目前主要有三种模型：悬链线模型（我们下面说的第三种静力学分析） 、 以多体动力学理论为基础的集中质量一弹簧模型（我们下面说的第二种，需要 matlab 做常 微分方程数值解）以及细长杆模型（我们下面说的第一种，力学有限元分析） ） 。查阅参考文 献《深海系泊系统动力特性研究进展》 ，请大家自行选择各类方法。
为简化起见, 按平浮处理，风引起的水平力 Fx
Fx 0.625v2 S , h 0.625 2r h h v 2
浮力 F f 为
Ff g r 2 h
其中 h 为正浮吃水深度。 则对浮标的方程有
Fx T1 sin 1 , Ff T1 cos 1 G0 Fx T1 sin 1 , Ff G0 T1 cos 1
T4 sin 4 T5 sin 5 , T4 cos 4 T5 cos 5 Gg T4 sin 4 T5 sin 5 , T4 cos 4 Gg T5 cos 5
最钢筒对第 4 钢管的拉力为 T5 ，与垂直方向的倾斜角度为 5 。 对钢筒继续分析
(5)
22.05*cos6 1*cos5 1*cos4 1*cos3 1*cos2 1*cos1 h 18
(7)
2016国赛A题国家一等奖论文
x0 , y0
T1 Ti i
D l0
§6 模型的建立与求解
5.1 问题一的分析与求解 5.1.1. 模型的分析 问题一要求我们在给定的一些参数下，假设海水静止，分别计算海面风速为 12m/s 和 24m/s 时钢桶、各节钢管、锚链等的一些指标。首先，我们对整个系泊系统建立直角 坐标系，然后对整个系统做受力分析。设计算法流程，先初始化参数 x0 , y0 ，然后计 算每个物体的 Ti ,i 和 xi , yi ，在通过与海水深度比较，不断修正 y0 和相应的 xn ，使整 体达到最优[3]。 5.1.2. 模型的建立与求解 （1）构建整体坐标系 以锚垂直于海平面向上为 y 轴的正方向，以海面风向为 x 轴，建立二维平面直角坐 标系 xoy 。根据假设条件，浮标系统整体如图 2 所示
图 3 浮标受力分析图
由浮标质量得出，得出其所受重力 G1 m1 g ；浮标所受的浮力（当浮标的吃水深度 D 不断变化时排开水体积用积分表示） ： F1 g ( ) 2 h ；由近海风荷载的近似公式可得 2 2 浮标所受的风力： Fw 0.625D(h0 h)vw ；考虑到浮标最终处于静力平衡状态，由静力 学平衡方程有： F1 G1 T1 sin 1
关键词：系泊系统，动力系统，多目标优化，GA 算法
1
§1 问题的重述
1.1 研究问题的背景是什么？ 1.1.1 总背景介绍 伴随着世界经济的快速发展， 人们更是逐步加强对海洋领域的探索。为收集海洋环 境的数据资料，人们开始应用浮标系统，同时在开发利用时，都离不开观测设备，如海 底观测站，水下探测器等[1][2]。然而这些设备无一例外的需要系泊系统定位。近浅海观 测网的传输节点由浮标系统、 系泊系统和水声通讯系统组成，简化的某型号输节点的系 泊系统可以如图 1 所示。传统的浮标系统都是由简单的锚—锚链—浮标构成。而这里， 我们研究的浮标系统在锚与浮标之间有一个钢桶（用于安装水声通讯系统） 。钢桶与电 焊锚链链接处悬挂了重物球，是为了控制钢桶的倾斜角度，钢桶的倾斜角度越大，设备 的工作效果较差。 而且钢桶与浮标之间是通过四节相同的钢管连接的。钢管与钢管之间 的连接是可以有偏转角度的。
2016年数学建模竞赛A题优秀论文
2016年数学建模竞赛A题优秀论文基于力学分析的系泊系统设计摘要关于系泊系统的设计问题，需要对稳态下的各个物体进行受力分析和力矩分析，建立力学分析模型来求解问题。
针对问题1，先对稳态下的各个物体进行受力分析和力矩分析，建立满足受力平衡和力矩平衡的力学模型。
再以浮标的吃水深度为搜索变量，采用二分法，计算海水深度为18m时所对应的吃水深度和各物体的倾角。
利用MATLAB软件求解可得，风速为12m/s时，钢桶与竖直方向的夹角为1.2319°，钢管与竖直方向的夹角依次为1.2064°,1.2064°,1.2148°,1.2233°。
浮标的吃水深度和游动半径分别为0.6715m,14.6552m。
风速为24m/s时，钢桶夹角为4.6763°，钢管夹角依次为4.5360°,4.5836°,4.6141°,4.6450°；浮标的吃水深度和游动半径分别为0.6857m，17.7614m。
针对问题2，可利用问题1中建立的数学模型，利用MATLAB进行求解，可得风速为36m/s时，钢桶夹角9.6592°；钢管夹角依次为9.4814°，9.4814°，9.5399°，9.5992°；浮标的吃水深度和游动半径分别为0.7086m，18.4906m；最后一节锚链与水平面的夹角为20.9997°故以钢桶夹角小于5°和锚链夹角小于16°为约束条件，逐步增加重物球的质量，采用二分法向水深18m进行逼近。
当重物球的质量为2280kg时，浮标的吃水深度为0.9848m；钢桶夹角为4.4737°；锚链夹角为15.9748°；为使通讯设备的工作效果增强，重物球的质量可以在2280kg的基础上进行适当增加。
针对问题3，可在问题1的受力分析时加入水流力的作用，以最大风速36m/s，最大水流速度1.5m/s为设计指标，通过控制单一变量的方式可确定链条的型号为Ⅴ型的电焊锚链。
2016年数学建模国赛A题一等奖论文
系泊系统的设计
摘要
近海系泊系统作为气象监控、海洋探测的主要载体工具，对工程的实际应用 有一定的积极作用[1]，研究系泊系统在不同环境状况下的内在关系，进而给出适 应不同情况的设计方案，并编写相应的应用软件，有着不能忽视的现实意义[2]。
针对问题一，在整个系泊系统处于最终平衡状态下，从系统的上部钢管开始 受力分析计算，建立不同方向上力的平衡方程和以下部链结点为取距中心的力矩 平衡方程，求得钢管倾斜角度以及下部单元间相互作用拉力，进而计算出钢管的 相对位置改变量。继续分析下部单元的受力情况，建立相同的平衡方程组并求解， 通过反复迭代计算，建立以浮标吃水深度为自变量的迭代代数模型，可求得河道 底部的链环倾斜角度以及整个系泊系统的垂悬高度。进而利用粒子群算法优化上 部浮标的吃水深度，并经过多次迭代优化，最终得到水深 18 米并且风速为 12m/s 和 24m/s 时，浮标吃水深度分别为 0.7348 米和 0.7489 米，同时算出各节钢管的 倾斜角度和各单元的位置坐标（附录及支撑材料），以及浮标游动区域半径 14.2005 米和 17.3203 米。结合理想状态下的锚链悬链线方程拟合位置坐标数据 得出良好的锚链形状曲线方程（式 1.16-1.17），并利用 CAD 软件绘制了所得结 果下的系泊系统 3-维立体分布示意图（图 10）。
在系泊系统中，锚的质量为600kg ，锚链选用无档普通链环。锚与锚链末端 链接，要求链接处的切线方向与海床的夹角不超过 16 度，否则锚会被拖行，致 使节点移位丢失。钢管共 4 节，每节长度 1m ，直径为 50mm ，每节钢管的质量 为10kg。钢桶上接第 4 节钢管，下接电焊锚链。钢桶竖直时，水声通讯设备的 工作效果最佳，钢桶的倾斜角度超过 5 度时，设备的工作效果较差。为了控制钢 球桶的倾斜角度，钢桶与电焊锚链接处可悬挂重物球。
摘要
近海系泊系统作为气象监控、海洋探测的主要载体工具，对工程的实际应用 有一定的积极作用[1]，研究系泊系统在不同环境状况下的内在关系，进而给出适 应不同情况的设计方案，并编写相应的应用软件，有着不能忽视的现实意义[2]。
针对问题一，在整个系泊系统处于最终平衡状态下，从系统的上部钢管开始 受力分析计算，建立不同方向上力的平衡方程和以下部链结点为取距中心的力矩 平衡方程，求得钢管倾斜角度以及下部单元间相互作用拉力，进而计算出钢管的 相对位置改变量。继续分析下部单元的受力情况，建立相同的平衡方程组并求解， 通过反复迭代计算，建立以浮标吃水深度为自变量的迭代代数模型，可求得河道 底部的链环倾斜角度以及整个系泊系统的垂悬高度。进而利用粒子群算法优化上 部浮标的吃水深度，并经过多次迭代优化，最终得到水深 18 米并且风速为 12m/s 和 24m/s 时，浮标吃水深度分别为 0.7348 米和 0.7489 米，同时算出各节钢管的 倾斜角度和各单元的位置坐标（附录及支撑材料），以及浮标游动区域半径 14.2005 米和 17.3203 米。结合理想状态下的锚链悬链线方程拟合位置坐标数据 得出良好的锚链形状曲线方程（式 1.16-1.17），并利用 CAD 软件绘制了所得结 果下的系泊系统 3-维立体分布示意图（图 10）。
在系泊系统中，锚的质量为600kg ，锚链选用无档普通链环。锚与锚链末端 链接，要求链接处的切线方向与海床的夹角不超过 16 度，否则锚会被拖行，致 使节点移位丢失。钢管共 4 节，每节长度 1m ，直径为 50mm ，每节钢管的质量 为10kg。钢桶上接第 4 节钢管，下接电焊锚链。钢桶竖直时，水声通讯设备的 工作效果最佳，钢桶的倾斜角度超过 5 度时，设备的工作效果较差。为了控制钢 球桶的倾斜角度，钢桶与电焊锚链接处可悬挂重物球。
2016年数学建模竞赛A题优秀论文
1.某型传输节点选用 II 型电焊锚链 22.05m，选用的重物球的质量为 1200kg。 现将该型传输节点布放在水深 18m、海床平坦、海水密度为 1.025×103kg/m3 的海 域。在海水静止时，分别计算海面风速为 12m/s 和 24m/s 时钢桶和各节钢管的倾 斜角度、锚链形状、浮标的吃水深度和游动区域。
将(1)式代入得：
dy mg T1 sin 1
dx
T1 cos1
(2)
对于锚链，m=σs ，其中 s 是 AB 锚链的长度，σ是锚链的线密度，即单位长
度锚链的质量[1]。代入(2)式得：
dy sg T1 sin 1
(3)
dx
T1 cos1
根据勾股定理可以得到弧长公式：
ds
1
dy dx
dp dx
T1
cos1
g
1 p2
然后对 x 和 p 分离变量并对两端进行积分得到：
dp
1 p2
T1
g cos 1
dx
即：sinh 1
p
g T1
x
C1
(4)
其中 C1 可以由 x=0,y=0 时的值确定，原点 A 处 p y ' tan 1 ，可得 C1 为：
当海面风速一定且海水静止时，钢桶和各节钢管的倾斜角度、锚链形状、浮 标的吃水深度和游动区域，与锚链线的方程、系泊系统各部分之间的受力平衡和 力矩平衡的约束密切相关。由于传输节点各部分相互影响，根据力学相关知识， 可以按照锚链→钢桶和重物球→钢管→浮标的顺序依次进行受力分析，从而得到 各部分受力平衡时的定量解析式，通过这些表达式可以确定钢桶和各节钢管的倾 斜角度、锚链形状。由于吃水深度与浮标受力直接相关，还可以确定浮标的吃水 深度。对于浮标的游动区域，可以由稳定后系泊系统各个部分在水平方向投影的 总长度来计算游动区域的最大半径。
将(1)式代入得：
dy mg T1 sin 1
dx
T1 cos1
(2)
对于锚链，m=σs ，其中 s 是 AB 锚链的长度，σ是锚链的线密度，即单位长
度锚链的质量[1]。代入(2)式得：
dy sg T1 sin 1
(3)
dx
T1 cos1
根据勾股定理可以得到弧长公式：
ds
1
dy dx
dp dx
T1
cos1
g
1 p2
然后对 x 和 p 分离变量并对两端进行积分得到：
dp
1 p2
T1
g cos 1
dx
即：sinh 1
p
g T1
x
C1
(4)
其中 C1 可以由 x=0,y=0 时的值确定，原点 A 处 p y ' tan 1 ，可得 C1 为：
当海面风速一定且海水静止时，钢桶和各节钢管的倾斜角度、锚链形状、浮 标的吃水深度和游动区域，与锚链线的方程、系泊系统各部分之间的受力平衡和 力矩平衡的约束密切相关。由于传输节点各部分相互影响，根据力学相关知识， 可以按照锚链→钢桶和重物球→钢管→浮标的顺序依次进行受力分析，从而得到 各部分受力平衡时的定量解析式，通过这些表达式可以确定钢桶和各节钢管的倾 斜角度、锚链形状。由于吃水深度与浮标受力直接相关，还可以确定浮标的吃水 深度。对于浮标的游动区域，可以由稳定后系泊系统各个部分在水平方向投影的 总长度来计算游动区域的最大半径。
高教社杯全国大学生数学建模竞赛题目A.B之令狐文艳创作
2016年高教社杯全国大学生数学建模竞赛题目令狐文艳（请先阅读“全国大学生数学建模竞赛论文格式规范”）A题系泊系统的设计近浅海观测网的传输节点由浮标系统、系泊系统和水声通讯系统组成（如图1所示）。
某型传输节点的浮标系统可简化为底面直径2m、高2m的圆柱体，浮标的质量为1000kg。
系泊系统由钢管、钢桶、重物球、电焊锚链和特制的抗拖移锚组成。
锚的质量为600kg，锚链选用无档普通链环，近浅海观测网的常用型号及其参数在附表中列出。
钢管共4节，每节长度1m，直径为50mm，每节钢管的质量为10kg。
要求锚链末端与锚的链接处的切线方向与海床的夹角不超过16度，否则锚会被拖行，致使节点移位丢失。
水声通讯系统安装在一个长1m、外径30cm的密封圆柱形钢桶内，设备和钢桶总质量为100kg。
钢桶上接第4节钢管，下接电焊锚链。
钢桶竖直时，水声通讯设备的工作效果最佳。
若钢桶倾斜，则影响设备的工作效果。
钢桶的倾斜角度（钢桶与竖直线的夹角）超过5度时，设备的工作效果较差。
为了控制钢桶的倾斜角度，钢桶与电焊锚链链接处可悬挂重物球。
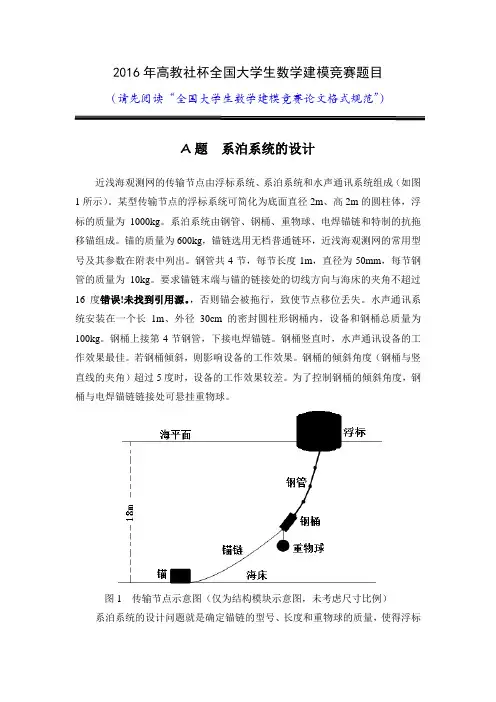
图1 传输节点示意图（仅为结构模块示意图，未考虑尺寸比例）系泊系统的设计问题就是确定锚链的型号、长度和重物球的质量，使得浮标的吃水深度和游动区域及钢桶的倾斜角度尽可能小。
问题1某型传输节点选用II型电焊锚链22.05m，选用的重物球的质量为1200kg。
现将该型传输节点布放在水深18m、海床平坦、海水密度为 1.025×103kg/m3的海域。
若海水静止，分别计算海面风速为12m/s和24m/s时钢桶和各节钢管的倾斜角度、锚链形状、浮标的吃水深度和游动区域。
问题2在问题1的假设下，计算海面风速为36m/s时钢桶和各节钢管的倾斜角度、锚链形状和浮标的游动区域。
请调节重物球的质量，使得钢桶的倾斜角度不超过5度，锚链在锚点与海床的夹角不超过16度。
问题 3 由于潮汐等因素的影响，布放海域的实测水深介于16m~20m之间。
2016全国大学生数学建模A题
2016年高教社杯全国大学生数学建模竞赛题目（请先阅读“全国大学生数学建模竞赛论文格式规范”）A题系泊系统的设计近浅海观测网的传输节点由浮标系统、系泊系统和水声通讯系统组成（如图1所示）。
某型传输节点的浮标系统可简化为底面直径2m、高2m的圆柱体，浮标的质量为1000kg。
系泊系统由钢管、钢桶、重物球、电焊锚链和特制的抗拖移锚组成。
锚的质量为600kg，锚链选用无档普通链环，近浅海观测网的常用型号及其参数在附表中列出。
钢管共4节，每节长度1m，直径为50mm，每节钢管的质量为10kg。
要求锚链末端与锚的链接处的切线方向与海床的夹角不超过16度错误！未找到引用源。
，否则锚会被拖行，致使节点移位丢失。
水声通讯系统安装在一个长1m、外径30cm的密封圆柱形钢桶内，设备和钢桶总质量为100kg。
钢桶上接第4节钢管，下接电焊锚链。
钢桶竖直时，水声通讯设备的工作效果最佳。
若钢桶倾斜，则影响设备的工作效果。
钢桶的倾斜角度（钢桶与竖直线的夹角）超过5度时，设备的工作效果较差。
为了控制钢桶的倾斜角度，钢桶与电焊锚链链接处可悬挂重物球。
图1 传输节点示意图（仅为结构模块示意图，未考虑尺寸比例）系泊系统的设计问题就是确定锚链的型号、长度和重物球的质量，使得浮标的吃水深度和游动区域及钢桶的倾斜角度尽可能小。
问题1某型传输节点选用II型电焊锚链22.05m，选用的重物球的质量为1200kg。
现将该型传输节点布放在水深18m、海床平坦、海水密度为1.025×103kg/m3的海域。
若海水静止，分别计算海面风速为12m/s和24m/s时钢桶和各节钢管的倾斜角度、锚链形状、浮标的吃水深度和游动区域。
问题2在问题1的假设下，计算海面风速为36m/s时钢桶和各节钢管的倾斜角度、锚链形状和浮标的游动区域。
请调节重物球的质量，使得钢桶的倾斜角度不超过5度，锚链在锚点与海床的夹角不超过16度。
问题3 由于潮汐等因素的影响，布放海域的实测水深介于16m~20m之间。
2016年全国大学生数学建模竞赛A题
2016年全国大学生数学建模竞赛A题2016年高教社杯全国大学生数学建模竞赛题目 ,请先阅读“全国大学生数学建模竞赛论文格式规范”,A题系泊系统的设计近浅海观测网的传输节点由浮标系统、系泊系统和水声通讯系统组成(如图1所示)。
某型传输节点的浮标系统可简化为底面直径2m、高2m的圆柱体，浮标的质量为1000kg。
系泊系统由钢管、钢桶、重物球、电焊锚链和特制的抗拖移锚组成。
锚的质量为600kg，锚链选用无档普通链环，近浅海观测网的常用型号及其参数在附表中列出。
钢管共4节，每节长度1m，直径为50mm，每节钢管的质量为10kg。
要求锚链末端与锚的链接处的切线方向与海床的夹角不超过16度，否则锚会被拖行，致使节点移位丢失。
水声通讯系统安装在一个长1m、外00kg。
钢桶上接第4节钢径30cm的密封圆柱形钢桶内，设备和钢桶总质量为1 管，下接电焊锚链。
钢桶竖直时，水声通讯设备的工作效果最佳。
若钢桶倾斜，则影响设备的工作效果。
钢桶的倾斜角度(钢桶与竖直线的夹角)超过5度时，设备的工作效果较差。
为了控制钢桶的倾斜角度，钢桶与电焊锚链链接处可悬挂重物球。
图1 传输节点示意图(仅为结构模块示意图，未考虑尺寸比例)系泊系统的设计问题就是确定锚链的型号、长度和重物球的质量，使得浮标的吃水深度和游动区域及钢桶的倾斜角度尽可能小。
问题1 某型传输节点选用II型电焊锚链22.05m，选用的重物球的质量为1200kg。
现将该型传输节点布放在水深18m、海床平坦、海水密度为1.025×103kg/m3的海域。
若海水静止，分别计算海面风速为12m/s和24m/s时钢桶和各节钢管的倾斜角度、锚链形状、浮标的吃水深度和游动区域。
问题2 在问题1的假设下，计算海面风速为36m/s时钢桶和各节钢管的倾斜角度、锚链形状和浮标的游动区域。
请调节重物球的质量，使得钢桶的倾斜角度不超过5度，锚链在锚点与海床的夹角不超过16度。
问题3 由于潮汐等因素的影响，布放海域的实测水深介于16m~20m之间。
2016年全国数学建模竞赛A题国家一等奖
针对问题一我们采用集中质量法将系统中的各个物体视为一个质点，对各个 物体建立静力平衡方程，在水深 18m 时给定浮标在海水中所受浮力，从而根据我 们建立的平衡方程求出各物体的倾斜角度，再根据几何关系求出海域的模拟深度， 通过不断修正浮标的浮力使得海域的模拟深度等于 18m，最终求得风速分别为
12m/s 和 24m/s 时浮标的吃水深度 h0 为 0.7397m 和 0.74883m，同时给出不同风
深度无法计算得出，需要给定浮力初始值 F0 ，从而得到T0 和1 。
钢管受力分析 将钢管看作一个质点，对每节钢管一一受力分析，如图 2 所示，由于每节钢
管规格一致，即质量、长度和直径相同，所有每节钢管重力和所受浮力相等。每
节钢管受到的力有钢管自身重力 Ggg 、浮力 Fgg 、上一节钢管拉力Ti,i1 和下一节钢
成负相关，即重物球质量越大， 和 越小，故在 5o, 16o, h0 2 条件下，
可以通过不断调节重物球的质量，找到重物球的最小质量和最大质量。 问题三的分析：
对问题三第一个子问题的分析： 系泊系统的设计问题就是要确定锚链的型号、长度和重物球的质量，使得浮 标的吃水深度和游动区域及钢桶的倾斜角度尽可能小。 沿用问题一的算法，增加一个与风力方向相同的水流力，近海水水流力可以
速下钢桶和各节钢管的倾斜角度及浮标的最远位置（浮标的游动区域视为一个圆 面）。考虑到锚链由 210 节链环构成，通过对每节链环进行受力分析确定了每节 链环的位置，从而给出了链环的形状图像。在求解过程中由于拉力具有不确定性， 我们通过两次角度代换使得程序可以顺利地运行。
针对问题二我们沿用了问题一的算法，求得风速为 36m/s 时钢桶和各节钢管
3.4 假设近浅海观测网的传输节点位于同一平面。 3.5 假设在海水流动情况下，仅考虑水流力对浮标、钢管和钢桶的影响，对 锚链和重物球的影响忽略不计。 3.6 假设在海水流动情况下，锚受到的水流力不影响锚链末端与锚的链接处 的切线方向与海床的夹角。 3.7 假设链环在拉力作用下形状不发生改变。
12m/s 和 24m/s 时浮标的吃水深度 h0 为 0.7397m 和 0.74883m，同时给出不同风
深度无法计算得出，需要给定浮力初始值 F0 ，从而得到T0 和1 。
钢管受力分析 将钢管看作一个质点，对每节钢管一一受力分析，如图 2 所示，由于每节钢
管规格一致，即质量、长度和直径相同，所有每节钢管重力和所受浮力相等。每
节钢管受到的力有钢管自身重力 Ggg 、浮力 Fgg 、上一节钢管拉力Ti,i1 和下一节钢
成负相关，即重物球质量越大， 和 越小，故在 5o, 16o, h0 2 条件下，
可以通过不断调节重物球的质量，找到重物球的最小质量和最大质量。 问题三的分析：
对问题三第一个子问题的分析： 系泊系统的设计问题就是要确定锚链的型号、长度和重物球的质量，使得浮 标的吃水深度和游动区域及钢桶的倾斜角度尽可能小。 沿用问题一的算法，增加一个与风力方向相同的水流力，近海水水流力可以
速下钢桶和各节钢管的倾斜角度及浮标的最远位置（浮标的游动区域视为一个圆 面）。考虑到锚链由 210 节链环构成，通过对每节链环进行受力分析确定了每节 链环的位置，从而给出了链环的形状图像。在求解过程中由于拉力具有不确定性， 我们通过两次角度代换使得程序可以顺利地运行。
针对问题二我们沿用了问题一的算法，求得风速为 36m/s 时钢桶和各节钢管
3.4 假设近浅海观测网的传输节点位于同一平面。 3.5 假设在海水流动情况下，仅考虑水流力对浮标、钢管和钢桶的影响，对 锚链和重物球的影响忽略不计。 3.6 假设在海水流动情况下，锚受到的水流力不影响锚链末端与锚的链接处 的切线方向与海床的夹角。 3.7 假设链环在拉力作用下形状不发生改变。
2016全国大学生数学建模竞赛A题论文
系泊系统的设计摘要本文为系泊系统的设计问题，根据题目要求建立了数学模型，计算出系泊系统在不同条件下的具体参数，并利用模型对系泊系统进行优化分析，使其能运用到更广的领域。
针对问题一，首先分析了锚链的形状，利用微积分原理求出锚链的静态方程，用Matlab 画出锚链形状，得出锚链的形状所符合悬链线方程。
然后把钢管、钢桶看成一个整体，并忽略钢管和钢桶倾斜引起的锚链上端高度的变化，分析出锚链的长度和锚链末端与海平面的夹角对吃水深度的影响，又对钢桶、钢管和浮标进行了受力和力矩分析。
最后建立了数学模型，计算出风速为12m/s 和24m/s 时，钢桶和各节钢管的倾斜角度(见表2)，浮标吃水深度分别为0.737m 、0.752m ，浮标的浮动区域（此浮动区域是以锚为圆心的圆）面积分别为、，锚链的形状如图(5-11)、(5-12)所示。
针对问题二，由问题一中建立的系泊系统的模型，计算风速为36m/s 时钢桶和各节钢管的倾斜角度、锚链形状和浮标的游动区域。
得到了钢桶和各节钢管的倾斜角度如(表3)，浮标吃水深度：0.787m ，以及游动区域面积：1229.39m 。
由于重物球的质量变化影响锚点与海床的夹角，可以通过调节重物球的质量控制锚点与海床的夹角。
分析得出当锚点与海床的夹角处于临界点（即16度）时，重物球的最小质量为1756.8kg ；当浮标刚好没入水中时，重物球的最大质量为5335.8kg 。
针对问题三，以钢桶、钢管的倾斜角度、锚链形状、浮标的吃水深度和游动区域为目标函数，分析动态优化问题。
与问题一、二不同的是：此问题给定了水深、海水速度、风速的取值范围，属于模型动态变化问题。
所以对模型进行了动态分析，求得钢桶、钢管的倾斜角度、锚链形状、浮标的吃水深度和游动区域的取值范围，进而分析水深、海水速度、风速对结果的影响，这有利于系泊系统的调整和应用。
本文所建立的模型对相关问题在理论上作了证明，虽然对部分模型进行了简化，但是实用性很强，而且易于推广，能够扩展到其他系泊系统。
数学建模a题系泊系统设计完整版
数学建模a题系泊系统设计集团标准化办公室：[VV986T-J682P28-JP266L8-68PNN]系泊系统的设计摘要本题要求观测近海观测网的组成，建立模型对其中系泊系统进行设计，在不同风速和水流的情况下确定锚链，重物球，钢管及浮标等的状态，从而使通讯设备的工作效果最佳。
求解的具体流程如下：针对问题一，分别对系统中的受力物体在水平方向和竖直方向上的力进行分析，找出锚链对锚无拉力时的临界风速，运用力矩平衡求出钢管与钢桶的倾斜角度。
对于锚链，将其等效为悬链线模型，根据风速不同判断锚链的状态，从而求出结果。
⁄时能够正常工针对问题二，需要调节重物球的质量，使通讯设备在36m m作。
为了确定重物球的质量，首先将实际风速与临界风速进行比较，判断此时系统中各物体的状态，与题目中已知数据进行比较。
在钢桶倾斜角度达到临界角度时，计算锚链与海床的夹角并于题中数据进行比较，计算重物球的质量。
在浮标完全没入海面时，计算相应条件下重物球的质量，从而确定满足条件的重物球的质量范围。
针对问题三，要求在不同条件下，求出系泊系统中各物体的状态。
以型号I 锚链为例，当水流方向与风速方向相同时，系统条件最差，分析在不同水深条件下的系泊系统设计。
由题中已知条件确定系统设计的限制条件，对系统各物体进行受力分析，以使整体结果最小，即可得出最优的系泊系统设计。
关键词：悬链线多目标非线性规划一、问题重述近浅海观测网的传输节点由浮标系统、系泊系统和水声通讯系统组成（如图1所示）。
某型传输节点的浮标系统可简化为底面直径2m、高2m的圆柱体，浮标的质量为1000kg。
系泊系统由钢管、钢桶、重物球、电焊锚链和特制的抗拖移锚组成。
锚的质量为600kg，锚链选用无档普通链环，近浅海观测网的常用型号及其参数在附表中列出。
钢管共4节，每节长度1m，直径为50mm，每节钢管的质量为10kg。
要求锚链末端与锚的链接处的切线方向与海床的夹角不超过16度，否则锚会被拖行，致使节点移位丢失。
2016数学建模A题官方答案提示
2016高教社杯全国大学生数学建模竞赛A题评阅要点[说明]本要点仅供参考，各赛区评阅组应根据对题目的理解及学生的解答，自主地进行评阅。
“系泊系统的设计”评阅要点本问题要求学生分析浮标、钢管、钢桶、重物球和锚链的受力情况，建立计算锚链形状、钢桶和钢管的倾斜角度、浮标的吃水深度和游动区域的数学模型。
在此基础上，确定锚链的型号、长度和重物球的质量，给出不同情况下锚链形状、锚链与海床的夹角、钢桶和钢管的倾斜角度、浮标的吃水深度和游动区域的表达式和具体数值。
评阅应该以模型为主，数值结果为辅。
问题1 要求学生对给定的锚链型号、长度和重物球的质量，分别计算出当海面风力为12m/s和24m/s的情况时锚链的形状、在锚点锚链与海床的夹角、钢桶和钢管的倾斜角度、浮标的吃水深度和游动区域。
（参考结果：当海面风力为12m/s时，有6.2m左右的锚链拖地，钢桶的倾斜角度1.2度左右，浮标的吃水深度0.7m左右，游动区域的半径14.7m左右;在海面风力为24m/s时，锚链与海床在锚点的夹角4.5度左右，钢桶的倾斜角度4.6度左右，浮标的吃水深度0.7m左右，游动区域的半径17.8m左右）问题2 对题目中给定的锚链型号、长度和重物球的质量，当海面风力为36m/s时，钢桶的倾斜角度、锚链在锚点与海床的夹角都不满足要求。
需要增加重物球的质量进行调整，论文中要给出调整后重物球的质量、在这个质量下锚链与海床的夹角、钢桶的倾斜角度（参考结果：满足要求的重物球的质量不会小于2160kg）。
问题3 要求学生根据模型在最大风速可达36m/s、海水最大速度可达1.5m/s、海水深度在16m到20m之间变化的情况下给出锚链的型号、长度、重物球的质量，使得在不同情况下锚链与海床的夹角不大于16度、钢桶的倾斜角度不超过5度，且浮标的吃水深度和游动区域较小。
并基于该设计，给出一些典型情况下钢管的倾角、钢桶的倾角、在锚点锚链与海床的夹角、浮标的吃水深度和游动区域。
2016年“高教社杯”全国大学生数学建模竞赛题目
说明近海风荷载可通过近似公式 Ｆ＝０．６２５×Ｓｖ２（Ｎ）计算，其中，Ｓ 为物体 在 风 向 法 平 面 的 投 影 面 积（ｍ２），ｖ 为风速（ｍ／ｓ）。近海水流力可通过近似公式 Ｆ＝３７４×Ｓｖ２（Ｎ）计 算，其 中，Ｓ 为 物 体 在 水 流 速 度法平面的投影面积（ｍ２），ｖ 为水流速度（ｍ／ｓ）。
注 ：长 度 是 指 每 节 链 环 的 长 度 。
· ２３ ·
·竞赛论坛·
２０１６ 年 “高 教 社 杯 ”全 国 大 学 生 数 学 建 模 竞 赛 题 目
２０１６ ，国务院发布《关 于 进 一 步 加 强 城 市 规 划 建 设 管 理 工 作 的 若 干 意 见 》，其 中 第 １６ 条关于推广街区制，原则上不再建设封闭住宅小区，已建成的住宅小区 和 单 位 大 院 要 逐 步 开 放 等 意 见， 引起了广泛的关注和讨论。
系 泊 系 统 的 设 计 问 题 就 是 确 定 锚 链 的 型 号 、长 度 和 重 物 球 的 质 量 ，使 得 浮 标 的 吃 水 深 度 和 游 动 区 域 及钢桶的倾斜角度尽可能小。
问 题 １ 某 型 传 输 节 点 选 用ＩＩ型 电 焊 锚 链２２．０５ｍ，选 用 的 重 物 球 的 质 量 为１ ２００ｋｇ。 现 将 该 型 传 输节点布放在水深１８ｍ、海床 平 坦、海 水 密 度 为 １．０２５×１０３ ｋｇ／ｍ３ 的 海 域。 若 海 水 静 止，分 别 计 算 海 面 风 速 为 １２ ｍ／ｓ和 ２４ ｍ／ｓ时 钢 桶 和 各 节 钢 管 的 倾 斜 角 度 、锚 链 形 状 、浮 标 的 吃 水 深 度 和 游 动 区 域 。
城 市 规 划 和 交 通 管 理 部 门 希 望 你 们 建 立 数 学 模 型 ，就 小 区 开 放 对 周 边 道 路 通 行 的 影 响 进 行 研 究 ，为 科 学 决 策 提 供 定 量 依 据 ，为 此 ，请 你 们 尝 试 解 决 以 下 问 题 ：
注 ：长 度 是 指 每 节 链 环 的 长 度 。
· ２３ ·
·竞赛论坛·
２０１６ 年 “高 教 社 杯 ”全 国 大 学 生 数 学 建 模 竞 赛 题 目
２０１６ ，国务院发布《关 于 进 一 步 加 强 城 市 规 划 建 设 管 理 工 作 的 若 干 意 见 》，其 中 第 １６ 条关于推广街区制，原则上不再建设封闭住宅小区，已建成的住宅小区 和 单 位 大 院 要 逐 步 开 放 等 意 见， 引起了广泛的关注和讨论。
系 泊 系 统 的 设 计 问 题 就 是 确 定 锚 链 的 型 号 、长 度 和 重 物 球 的 质 量 ，使 得 浮 标 的 吃 水 深 度 和 游 动 区 域 及钢桶的倾斜角度尽可能小。
问 题 １ 某 型 传 输 节 点 选 用ＩＩ型 电 焊 锚 链２２．０５ｍ，选 用 的 重 物 球 的 质 量 为１ ２００ｋｇ。 现 将 该 型 传 输节点布放在水深１８ｍ、海床 平 坦、海 水 密 度 为 １．０２５×１０３ ｋｇ／ｍ３ 的 海 域。 若 海 水 静 止，分 别 计 算 海 面 风 速 为 １２ ｍ／ｓ和 ２４ ｍ／ｓ时 钢 桶 和 各 节 钢 管 的 倾 斜 角 度 、锚 链 形 状 、浮 标 的 吃 水 深 度 和 游 动 区 域 。
城 市 规 划 和 交 通 管 理 部 门 希 望 你 们 建 立 数 学 模 型 ，就 小 区 开 放 对 周 边 道 路 通 行 的 影 响 进 行 研 究 ，为 科 学 决 策 提 供 定 量 依 据 ，为 此 ，请 你 们 尝 试 解 决 以 下 问 题 ：
系泊系统的设计和探究
赛区评阅编号（由赛区组委会填写）：2016年高教社杯全国大学生数学建模竞赛承诺书我们仔细阅读了《全国大学生数学建模竞赛章程》和《全国大学生数学建模竞赛参赛规则》（以下简称为“竞赛章程和参赛规则”，可从全国大学生数学建模竞赛网站下载）。
我们完全明白，在竞赛开始后参赛队员不能以任何方式（包括电话、电子邮件、网上咨询等）与队外的任何人（包括指导教师）研究、讨论与赛题有关的问题。
我们知道，抄袭别人的成果是违反竞赛章程和参赛规则的，如果引用别人的成果或资料（包括网上资料），必须按照规定的参考文献的表述方式列出，并在正文引用处予以标注。
在网上交流和下载他人的论文是严重违规违纪行为。
我们以中国大学生名誉和诚信郑重承诺，严格遵守竞赛章程和参赛规则，以保证竞赛的公正、公平性。
如有违反竞赛章程和参赛规则的行为，我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会，可将我们的论文以任何形式进行公开展示（包括进行网上公示，在书籍、期刊和其他媒体进行正式或非正式发表等）。
我们参赛选择的题号（从A/B/C/D中选择一项填写）：我们的报名参赛队号（12位数字全国统一编号）：参赛学校（完整的学校全称，不含院系名）：参赛队员(打印并签名) ：1.2.3.指导教师或指导教师组负责人(打印并签名)：（指导教师签名意味着对参赛队的行为和论文的真实性负责）日期：年月日（请勿改动此页内容和格式。
此承诺书打印签名后作为纸质论文的封面，注意电子版论文中不得出现此页。
以上内容请仔细核对，如填写错误，论文可能被取消评奖资格。
）赛区评阅编号（由赛区组委会填写）：2016年高教社杯全国大学生数学建模竞赛编号专用页送全国评阅统一编号（赛区组委会填写）：全国评阅随机编号（全国组委会填写）：（请勿改动此页内容和格式。
此编号专用页仅供赛区和全国评阅使用，参赛队打印后装订到纸质论文的第二页上。
注意电子版论文中不得出现此页。
）系泊系统的设计和探究摘要本文利用牛顿力学定律，力矩平衡原理、非线性规划、循环遍历法等方法对系泊系统进行了设计与探究。
2016数学建模国赛
4
为浮标游动范围。最后对结果进行灵敏度分析，通过在极小范围内改变风速，看结 果
是否有较大的变动来验证结果的稳定性。
。 图 1 问题一分析流程图 对于问题二，要求计算风速为 36m / s 时钢桶和各节钢管的倾斜角度、锚链形状 和浮标的游动区域，并建立使钢桶的倾斜角度不超过 5 度、锚链在锚点与海床的夹 角不超过 16 度的重物球质量计算模型。对于第一个问题，可建立计算锚链在锚点 与海床夹角的模型。将最后一节链节与海床的夹角视为锚链与海床夹角，在链节两 端设坐标，结合问题一的受力分析建立模型，根据题中数据进行求解。以链节两端 坐标的斜率大小来判断是否满足锚链在锚点与海床的夹角不超过 16 度的条件，且 计算锚链与锚连接处坐标的解即为所需结果。对于第二个问题，可建立重物球质量 计算模型。需满足的条件一为钢桶的倾斜角度不超过 5 度，二为浮标不得完全沉入 水中，三为锚链在锚点与海床的夹角不超过 16 度。对前两个条件，可用问题一建 立的计算模型将临界值带入并求解出重物球质量范围；对于第三个条件，可用前面 建立的锚链在锚点与海床夹角计算模型代入临界值求解出。将得出的三个范围取交 集，得到最终结果。最后分别对钢管倾斜角度、浮标吃水深度、锚链在锚点与海床 的夹角与重物球质量的正反相关性进行分析，验证临界值取值的正误，若取值正确， 则结果可信。 对于问题三，要求给出考虑风力、水流力和水深情况下的系泊系统设计。可建 立多目标规划模型来求解问题，首先根据问题一对浮标、钢管、钢桶、锚链进行受 力分析，钢管和钢桶因为受力情况相似且受力平衡，故可看作一个整体根据虚位移 原理进行分析。然后分析系统的约束条件，由题中信息可知设计的系泊系统需满足 锚链末端与锚连接处的切线方向与海床的夹角不超过 16 度，根据问题二中锚链在
F r WF 0
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
系泊系统的设计摘要对于问题一，建立模型一，已知题目给出的锚链长度与其单位长度的质量，得到悬链共210环。
对各节锚链，钢桶，四节钢管受力分析得出静力平衡方程，使用分段外推法，可以得到静力平衡下的迭代方程。
其中锚对锚链的拉力大小方向为输入变量，迭代的输出变量为浮标的位置和对钢管的拉力，在给定的风速下，输入和输出满足关系2)2(25.1cos 水v h T -=α，αθcos cos 11T T =，通过多层搜索算法得出最符合的输入输出值，即可得到给定风速下浮标的吃水深度，浮标拉力、锚链与海床夹角。
利用MATLAB 软件编程求解模型得到：风力12m/s 时，钢桶与竖直方向上的角度1.9863度，从下往上四节钢管与竖直方向夹角为1.9652度、1.9592度、1.9532度、1.9472度，浮标吃水0.7173m ，以锚为圆心浮标的游动区域16.5125m ，锚链末端切线与海床的夹角3.8268度。
风力24m/s 时，锚链形状，钢桶与竖直方向上的夹角3.9835度，从下往上四节钢管与竖直方向夹角为3.9420度、3.9301度、3.9183度、3.9066度，浮标吃水0.7244m ，以锚为圆心浮标的游动区域18.3175m 。
锚链末端切线与海床夹角15.9175度。
对于问题二的第一小问，使用模型一求解，当风速36m/s 时，锚链末端切线与海床夹角26.3339度，浮标吃水0.7482m ，浮标游动区域为以锚为圆心半径为18.9578m 的圆形区域，从下往上四节钢管与竖直方向倾斜角度为8.4463度、8.4225度、8.3989度、8.3753度，钢桶与竖直方向倾斜角度为8.5294度。
为满足问题二的要求，在模型一的基础上把重物球质量作为变量，建立模型二，将钢桶倾斜角小于5度和锚链前端夹角小于16度当做两个约束条件，通过MATLAB 编程求解得到满足约束条件要求的重物球质量取值范围为3700kg 到5320kg 。
对于问题三，首先取不同水深、水速、风速三种情况，建立模型三，即在模型一的基础上增加水流对系统产生的影响。
在三种情况下，找到合适的锚链型号、锚链长度，重物球质量，对吃水深度、游动区域、钢桶的倾斜角三个目标进行优化达到最小。
通过MATLAB 编程实现该模型三得到结果：选用Ⅲ型锚链，锚链长度为27.24m ，重物球质量为2580kg 。
关键词：平面静力系分析 多层搜索算法 遗传算法 逐步外推法 多目标优化一、问题重述近浅海观测网的传输节点由三部分组成：浮标系统、系泊系统和水声通讯系统，如下图所示：浮标系统可简化为一个圆柱体，质量为1000kg 。
系泊系统由五部分组成：钢管、钢桶、重物球、电焊锚链和特制的抗拖移锚。
锚的质量为600kg ，常用型号及其参数在附表中列出。
钢管共4节，每节质量为10kg 。
锚链末端与锚的链接处的切线方向与海床的夹角不超过︒16。
水声通讯系统安装在圆柱形钢桶内，设备和钢桶总质量为100kg 。
钢桶上接第4节钢管，下接电焊锚链，钢桶的倾斜角度不超过︒5。
为控制钢桶的倾斜角度，钢桶与锚链链接处可悬挂重物球。
传输节点示意图系泊系统的设计问题就是确定锚链的型号、长度和重物球的质量，使得浮标的吃水深度和游动区域及钢桶的倾斜角度尽可能小。
1.某型传输节点选用锚链型号II ，长度22.05m ，选用的重物球的质量为1200kg 。
现将该型传输节点布放在水深18m 、海床平坦、海水密度为33m /kg 10025.1⨯的海域。
假设海水静止，分别计算海面风速为12m/s 和24m/s 时钢桶和各节钢管的倾斜角度、锚链形状、浮标的吃水深度和游动区域。
2.在问题1的假设下，计算海面风速为36m/s 时钢桶和各节钢管的倾斜角度、锚链形状和浮标的游动区域。
请调节重物球的质量，使得钢桶的倾斜角度不超过︒5，锚链在锚点与海床的夹角不超过︒16。
3.由于潮汐等因素的影响，布放海域的实测水深介于20m -16m 之间。
布放点的海水速度最大为1.5m/s 、风速最大为36m/s 。
请给出考虑风力、水流力和水深情况下的系泊系统设计，分析不同情况下钢桶、钢管的倾斜角度、锚链形状、浮标的吃水深度和游动区域。
注：近海风荷载的近似公式为)(v 625.02N S F ⨯=，S 为物体在风向法平面的投影面积)m (2，v 为风速)(m/s 。
近海水流力的近似公式为)(v 3742N S F ⨯=，其中S 为物体在水流速度法平面的投影面积)m (2，v 为水流速度)(m/s 。
附表锚链型号和参数表型号长度(mm) 单位长度的质量(kg/m)I 78 3.2II 105 7III 120 12.5IV 150 19.5V 180 28.12表注：长度是指每节链环的长度。
二、问题分析对于问题一，所选取锚链的长度和型号是给定的，所以其锚链的节数、每一节的长度、每一节的质量都是已知的，该问中选用II型的锚链，根据题目中的附表求得锚链分为210节，每节重0.735kg。
根据题目所给图示可知该系泊系统的构成是：在海底的锚连接锚链的下端，在锚链的上端也就是钢桶的下端节点处挂有重物球，钢桶的上端连接4个钢管，钢管的上端连接浮标。
可以假设链环之间、锚链和其他结构的连接处、钢管之间的连接为铰接，且所有结构都是质量分布均匀的，故每个链环和钢桶和钢管可以抽象为体积不同质量不同的铰接圆柱体，在独立分析出每个圆柱体所受浮力来之后，可以再把各圆柱体抽象为有质量的铰接直杆。
对与锚连接的第一个链环进行受力分析如图1、图2、图3、图4所示：图1 图2图3 图4对于该链环，假设和锚连接的节点的力与该链环方向一致，需要满足力平衡与力矩平衡。
列出所有杆的平衡方程，可以通过方程迭代求解出在不同拉力1T作用时的对应的浮标的位置，利用浮标位置和风力、拉力的关系式，可以再通过优化算法得到满足关系式的最优解分别求解风速为12m/s和24m/s的情况下的。
对于问题二，可以继续利用在问题一中建立的模型求解出风速在36m/s的情况下各个需要求的量。
接着在问题一模型的基础上进行修改，将重物球的质量改为变量当做模型二，把该问题中对钢桶倾斜角小于5度和锚链前端夹角小于16度的要求当做两个约束条件来限制重物球质量的范围，把在充分大范围内按一定精度取值的重物球质量带入模型二中，得到一系列对应的钢桶倾斜角和锚链前端夹角值，取两者都符合约束条件的值对应的一组质量值，该组值的最小值和最大值即为可调节重物球质量的下限和上限。
对于问题三，由于海水的速度可能是由于风力的影响产生的，所以可以认为海水速度和风速是相同方向的。
考虑到水里的部分都需要受到水流力的影响所以在受力分析时需要添加水平方向的作用力，如图5、图6所示：图5 图6由于锚链的体积忽略，故锚链的部分没有水流力的影响，对于其他部分可写出每个杆的力平衡方程，力矩平衡方程。
由于水深、水流速、风速都是在一定范围内的变量，所以要寻找合适的锚链型号和链长度以及合适的重物球质量，来使得吃水深度、钢桶倾斜角、和游动区域尽可能小。
该问题属于多目标优化问题，其中优化的目标为吃水深度、钢桶倾斜角、游动区域求最小；变量有水深、水流速、风速、锚链型号、链长度，其中的水深、水流速、锚链要分别取不同的情况，每个优化目标在不同情况下得到值的和最小所对应的设计方案即为最优方案。
三、模型假设1.假设重物球的体积可以忽略2.假设浮标系统在水中的倾斜可以忽略3.假设锚链是不可压缩或伸长的4.假设锚链在水中的体积可以忽略5.假设各连接点都是铰连接方式6.假设忽略波浪力的作用四、符号说明v水的流速水v风速风ρ海水密度海h浮标自身吃水深度sh海深度海l钢管长度管l钢桶长度桶V钢管体积管V钢桶体积桶h浮标高度浮V浮标体积浮h浮标吃水m钢桶质量桶m钢管质量管m重物球质量重m每节锚链质量lx第n个节点横坐标ny第n个节点纵坐标ng重力加速度l单节链的长度链T锚对链的拉力1θ锚链末端与海床的夹角1T浮标对链的拉力α浮标拉力和海平面夹角θ钢桶与竖直线的夹角桶x最大游动区域半径m ax五、模型建立与求解5.1问题一5.1.1模型一的建立首先对锚链进行受力分析，如图7所示图7拉力1T 是沿杆方向的拉力，重力作用于杆的中心产生力矩，拉力2T 需要平衡拉力1T 和重力产生的力矩，才能使所有杆满足力平衡和力矩平衡：0,0==∑∑yn xn F F0,0==∑∑yn xn M M其中n 为所有杆个数，这里根据题目里提供的数据，其锚链的节数、每一节的长度、每一节的质量都是已知的，该问中选用II 型的锚链，根据题目中的附表求得锚链分为210节，整个抽象杆除此之外还有一节钢桶和四节钢杆组成。
因此215=n 。
对于前209个杆满足(5.2)式的迭代关系：1111111111sin cos 00θθθθ=====T T T T y x y x （5.1）)1()1(1)1()1(arctan 21+++++=+==n x n y n l yn n y xnn x T T g m T T T T θ （5.2） 其中（5.1）式作为初始的条件。
在接入重物球段也就是210个杆的迭代表达式不同于（5.2）为： q l yn n y m g m T T ++=+21)1( 钢桶的为：g m T T t yn n y 21)1(+=+ 钢管的为：g m T T g yn n y 21)1(+=+以上各部分都满足（5.3）式n n n nn n l y y l x x θθsin cos 11+=+=++ （5.3）通过（5.3）迭代求解出每个1θ和1T 对应的最终的节点位置即浮标下底面中心的坐标),(216216y x 和该点的作用力),(216216y x T T ，可以将以上迭代过程省略，写成),(],,,[11216216216216T f T T y x y x θ= （5.4）对整个铰接杆结构受力分析可以得到水平方向上不受外力作用，故由于受力平衡得到：αθcos cos 11T T = （5.5）在忽略浮标倾斜的情况下，浮标对杆的拉力的水平分量大小等于浮标受到的风力2)2(25.1cos 水v h T -=α （5.6）其中g T h h s 海πραsin += （5.7） h y -=18216 （5.8）这里需要完成：求一组),(11T θ可以满足（5.5）、（5.6）、（5.7）、（5.8）四式，联立可得到三个方程αθαπραθcos cos )2025.1(cos )sin 2(25.1cos 112216211T T v y T v gT h T s =-=--=风风海 （5.9）这里需要完成：求一组),(11T θ可以满足（5.9）式。
利用优化的思想该问题可以转化为⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧-+--+---αθαπραθcos cos )2025.1(cos )sin 2(25.1cos min 11221621T T v y T v g T h T s 风风海 （5.10）有约束⎪⎩⎪⎨⎧≤≤≤≤100000900..11T t s θ （5.11）（5.10）中各个量可以通过下面式子求得),(],,,[11216216216216T f T T y x y x θ=5.1.2模型一的求解对于模型一所建立的优化模型，有多种求解方法，考虑到各种优化算法的效率以及准确度。