微分几何13空间曲线

《微分几何》课程教学大纲一、课程信息课程名称：微分几何Differentia1Geometry课程代码：06S1022B课程类别：专业选修课适用专业：数学与应用数学专业（师范类）课程学时：45学时（理论35,实践10）课程学分：2.5学分修读学期：第6学期先修课程：数学分析、高等代数、解析几何、常微分方程二、课程目标微分几何是数学与应用数学专业的选修课程，是运用微积分的理论研究空间的几何性质的数学分支学科。

古典微分几何研究三维空间中的曲线和曲面，而现代微分几何开始研究更一般的空间一一流形。

微分几何与拓扑学等其它数学分支有紧密的联系，对物理学的发展也有重要影响，爱因斯坦的广义相对论就以微分几何中的黎曼几何作为其重要的数学基础。

本课程的前导课程为解析几何、高等代数、数学分析和常微分方程。

本课程旨在介绍微分几何的基本思想方法和理论，让学生了解它的研究对象、研究方法和技巧，了解一些重要概念及其几何意义，经典理论及其模型，掌握重要几何量的计算，通过重要例题的演示，让学生学会综合利用数学分析、解析几何、微分方程等的基本知识解决微分几何问题，使学生掌握三维欧氏空间中的曲线和曲面的局部微分理论和方法，培养学生分析三维欧氏空间的曲线和曲面的局部性态的能力以及对微分几何这门学科的兴趣。

（一）具体目标通过本课程的学习，使学生达到以下目标：1.了解现代几何学的发展背景，熟悉微分几何研究的基本方法和技巧，理解从欧式空间到一般几何对象的基本思想，对中学的几何课程有更好的理解，具有一定的批判精神及创新能力，具有分析问题和解决问题的能力。

【支撑毕业要求3、4、7]2.掌握向量函数的相关概念和计算；掌握一般曲线的参数表示及切线、法平面、密切平面等概念；掌握曲线的曲率、挠率及伏雷内公式；理解曲线的局部结构及空间曲线论的基本定理；了解一般螺线的概念;综合运用微积分、解析几何的知识解决微分几何的问题，具备一定的计算能力。

【支撑毕业要求3、4]3.掌握曲面的参数表示及相关概念；掌握曲面的第一基本形式及其应用，理解等距变换及曲面的内蕴性质；掌握曲面的第二基本形式及各种曲率的概念和计算；理解直纹面、可展曲面的概念；了解曲面论的基本定理；理解曲面上的测地线及其性质，了解高斯-波涅公式及其应用。

曲线与曲面的微分几何 pdf
微分几何是一种数学理论，它研究几何曲面和曲线在空间中的结构以及它们建立起来的空间之间的关系。

曲线和曲面在微分几何中被看作被不同变化量——尤其是微分——指定的对象。

微分几何把曲面和曲线看成是由一组微分变换定义的几何结构，而不是传统的几何定义，这是由微积分和几何的结合产生的一种新的数学理论。

在这种理论中，当需要研究曲线和曲面的形状，运行行为或特性的时候，我们必须用微分变换来描述它们。

微分几何可以用于对曲线和曲面的确切表达和运算，以及描述曲线和曲面上物体的机械性质。

它还可以用来分析复杂的几何结构，帮助科学家们建立准确的物理模型，进而了解大自然中复杂的空间模型。

另外，微分几何还可以用于构建有关曲线和曲面的微分方程的计算，以及提供衡量曲线和曲面之间的距离和方位角的方法。

这可以用来分析曲线和曲面的属性，比如曲率、弯曲、收缩等，进而了解大自然的丰富复杂性。

此外，微分几何还可以用于几何建模，模型可以用来模拟复杂的实际世界中几何曲线和曲面。

这可以帮助我们研究由曲线和曲面构成的物体在空间里的行为特性，从而更好地解决人类技术中的实际问题。

总之，微分几何是由微积分和几何的结合产生的一种新的几何理论，它用来研究空间中曲线和曲面的结构以及它们建立起来的空间之间的关系。

它可以应用于几何建模、物理模型建立、衡量曲面和曲线之间的距离和方位角以及构建微分方程，以及描述曲线与曲面上物体的机械性质等等。

《微分几何》知识点总结微分几何是数学的一个分支，研究曲线、曲面及高维空间中的几何性质和变换。

下面是一些关键知识点的总结：1. 切空间：切空间描述了曲线或曲面在某一点上的局部性质。

对于曲线，切向量是切线的方向；对于曲面，切空间是与曲面相切的平面。

2. 参数化曲线和曲面：参数化是将曲线或曲面表示为参数的函数形式。

通过参数化，我们可以在数学上描述曲线和曲面，并进行分析。

3. 曲率：曲率描述了曲线或曲面在某一点附近的弯曲程度。

曲线的曲率由曲率向量表示，曲面的曲率由主曲率和法向量表示。

4. 流形：流形是一个具有局部坐标系的空间，可以用一组坐标来描述其中的点。

流形可以是一维曲线、二维曲面或更高维的空间。

5. 流形上的度量：度量是流形上定义的内积结构。

度量可以用来计算距离、角度和曲率等几何量。

6. 流形上的切向量和切空间：在流形上，切向量和切空间与欧几里得空间中的相似。

切向量是切平面上的向量，切空间是与流形在某点的切平面对应的向量空间。

7. 平均曲率流：平均曲率流描述了曲线或曲面根据其曲率的时间变化。

它常用于模型匹配、图像处理和几何建模等领域。

8. 黎曼流形：黎曼流形是一种拥有黎曼度量的流形。

黎曼度量允许我们定义切向量的长度和角度。

9. 流形上的测地线：测地线是流形上的特殊曲线，沿该曲线运动的物体会保持速度恒定。

测地线在广义相对论、地理学和航天飞行等领域中具有重要应用。

10. 张量场：张量场是定义在流形上的张量函数。

张量场可以用于描述力、电磁场和应力等物理量在空间中的分布。

这些是微分几何中的一些关键知识点。

通过研究这些概念和方法，我们可以更好地理解和分析曲线、曲面和高维空间中的几何性质。

空间曲线本节内容：研究空间曲线的基本理论，研究刻画空间曲线在某一点邻近的弯曲程度和离开平面程度的量——曲率和挠率，以及曲线在一点邻近的近似形状。

复习内容：切线、切向量；()r t 对自然参数的导矢是单位向量；()r t 具有固定长()()r t r t '⇔⊥ ；单位向量()r t 对于t 的旋转速度等于其微商的模。

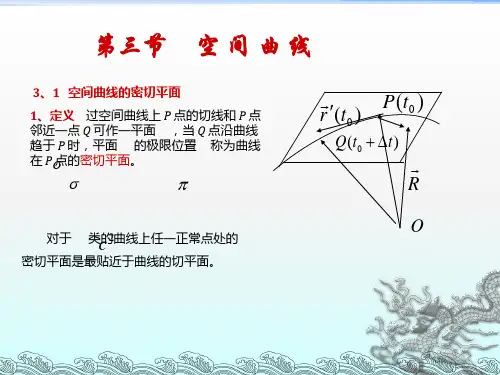
一 空间曲线的密切平面、副法线1 密切平面、副法线的定义：过曲线上P 点的切线和P 点的邻近一点Q 可作一平面σ，当Q 点沿着曲线趋于P 点时平面σ的极限位置π 称为曲线在P点的密切平面。

密切平面在P 点的法线称为曲线在P 点的副法线。

2 密切平面、副法线的方程设曲线(c)为2C 类曲线，P 点的径矢00(),()r t Q r t t +∆ 点的径矢 2000001()()()(())(),lim 02t r t t r t r t t r t t εε∆→'''+∆-=∆++∆= PQ= 。

20001()()(())()2r t r t r t t ε''''⨯⨯+∆ PQ=‖00()(())r t r t ε'''⨯+ ，当Q P →时， 000,0,()()t r t r t ε'''∆→→→⨯这个矢积。

如果00()()0r t r t '''⨯≠ ，则该矢量为密切平面法线上的一个非零矢量，它和P 点完全确定了密切平面，方程是：000(()()())0r t r t r t ρ'''-= ，，副法线方程：000()()())r t r t r t ρλ'''=⨯+( 副法线的标准方程是：000()()(),x x t y y t z z t X Y Z---== 00{,,}()()X Y Z r t r t '''=⨯ 其中。

说明：1．任意参数t , 绘曲线。

曲线方程可以取自题库，或自由输入。

起点或终点可以自动调整。

2．改变为离起点的弧长s为参数，方程相应变换为新的方程。

起点或终点s参数也可以自动调整。

3．活动标架应以弧长s 为参数。

可先给定固定的某s，用按键来逐步求出并显示标架：三个坐标向量，三个坐标平面与两个特征函数。

s，κ(s)，ρ(s)显示于输出栏。

κ(s)，ρ(s)的图形也相应显示于相应窗口。

按键可以弹出窗口，显示公式与评注。

4．让s 从起点到终点，动起来。

5．把κ(s)，ρ(s)加进第二屏的题库中，备生成图形后与之对比。

文字描述与程序要求微分几何知识结构网络曲线论参量向量表示，即与坐标系，又与参数有关。

换参数与坐标系则换表达式。

条件约束：正则。

即三阶以上连续可微。

活动标架：运动公式：本质特征：与坐标系，又与参数无关。

存在唯一定理，决定曲线形状。

三维空间曲线参量r (t) = [ x (t), y(t), z (t) ] , t0 ≤t ≤T换参数程序：s (t) = ∫|r ‘(t ) | dt, t = s –1 (t )换坐标系程序：活动标架：切向量α(s) α(s) = r ‘(t) / | r ‘(t)| 弧长参数则自动归一。

法向量β(s) β(s)=α‘(s) /|α‘(s)| 向量微商，一定正交。

从法向量γ(s) γ(s) =α(s) X β(s) 画曲线及其活动标架。

α(s) β(s) 张成密切平面。

β(s) γ(s) 张成主法平面。

γ(s) α(s) 张成从法平面。

要画曲线在三个坐标平面上的投影。

本质特征：κ(s) = |α‘(s)| 曲率，未必单位长ρ(s) = |γ‘(s)| 挠率，存在唯一定理，决定曲线形状要画曲线的特征曲线。

运动公式：局部关系d r /ds = α(s)dα(s)/ds =κ(s) β(s)dβ(s)/ds =κdα(s)/ds + ρdγ(s)/dsdγ(s)/ds = -ρ(s) β(s) 解方程组的数值计算程序。

空间曲线曲率中心轨迹的曲率与挠率在几何学中，空间曲线的曲率与挠率是非常重要且有趣的概念。

通过研究曲率和挠率，我们能够更好地理解曲线的形状和性质，从而深入探讨空间曲线的运动规律和变化过程。

本文将从简单到复杂的方式，逐步探讨空间曲线曲率中心轨迹的曲率与挠率。

1. 曲率与挠率的定义空间曲线的曲率描述了曲线在某一点处的弯曲程度，是一个标量。

而挠率描述了曲线扭曲的程度，是一个矢量。

在三维空间中，曲线的运动轨迹往往具有复杂的形态，曲率和挠率正是用来描述这种复杂性的重要概念。

2. 曲率与挠率的计算曲率和挠率的计算是非常复杂的数学问题，通常需要运用微分几何学和向量分析的知识来进行推导和计算。

在计算过程中，需要考虑曲线的参数方程、切线和曲率、正切矢量等多个因素，以确定曲线在某一点的曲率和挠率值。

通过精确的数学计算，我们能够准确地理解曲线的形状和特性。

3. 曲率中心轨迹的特性曲率中心轨迹是指在空间曲线上，曲率中心点构成的轨迹。

通过对曲率中心轨迹的研究，我们能够发现曲线的整体特性和变化规律，从而更好地理解曲线的几何性质。

曲率中心轨迹的形状和曲率对于空间曲线的运动和变化有着重要的指导意义。

4. 个人观点和理解对于空间曲线曲率中心轨迹的曲率与挠率，我个人认为其深刻地揭示了曲线运动的奥秘和规律，是一项极具挑战性和价值的数学研究。

通过深入研究曲率与挠率，我们可以更好地理解曲线的形状和特性，为曲线的运动和变化提供重要的数学支持和指导。

空间曲线曲率中心轨迹的研究不仅具有学术价值，还对实际问题的探讨和解决具有重要的意义。

总结通过本文对空间曲线曲率中心轨迹的曲率与挠率的探讨，我们可以看出这一主题的广度和深度。

曲率与挠率的应用涵盖了微分几何学、向量分析、曲线运动学等多个领域，具有重要的理论和实际意义。

通过不断深入研究和探讨，我们能够更好地理解曲线的运动规律和变化特性，为相关领域的发展和应用提供重要的理论和技术支持。

希望本文能够对读者有所启发，引起对空间曲线曲率中心轨迹的曲率与挠率的深入思考和探讨。