107024_组合与组合数公式_韩庆文

1．2．2组合第一课时 组合与组合数公式教学目标：1.理解组合与组合数的定义，明确组合与排列的联系与区别，能判断一个问题是排列问题还是组合问题2．会用公式和性质处理简单的计算问题。

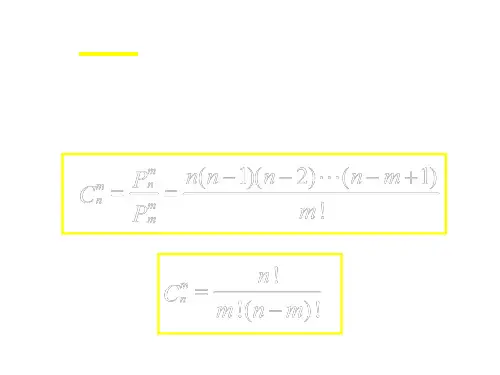
教学重点：理解组合与组合数的定义教学难点：会用选择恰当的公式计算和证明 授课类型：新授课 教学过程：一、复习引入：复习排列数的定义：从n 个不同元素中，任取m （m n ≤）个元素的所有排列的个数叫做从n 个元素中取出m 元素的排列数，用符号mn A 表示探究：问题1：从甲、乙、丙3名同学中选出2名去参加某天的一项活动，其中1名同学参加上午的活动，1名同学参加下午的活动，有多少种不同的选法？问题2：从甲、乙、丙3名同学中选出2名去参加一项活动，有多少种不同的选法？ 师引导学生观察：示例1中不但要求选出2名同学，而且还要按照一定的顺序“排列”，而示例2只要求选出2名同学，是与顺序无关的引出课题：组合．．． 二、讲解新课：类比排列给出组合定义1组合的概念：一般地，从n 个不同元素中取出m ()m n ≤个元素并成一组，叫做从n 个不同元素中取出m 个元素的一个组合学生活动：在课本划出定义并找出关键点说明：⑴不同元素；⑵“只取不排”——无序性；⑶()m n ≤ 学生活动：小组讨论1.比较排列和组合定义找出两者的区别与联系2.什么是相同的排列与组合 例1．判断下列问题是组合还是排列(1)一个小组有7名学生，现抽调5人参加劳动； (2)从5名同学中选4名组成代表团参加对外交流；(3)从5名同学中选4名组成代表团去4个单位参加对外交流；2．组合数的概念：从n 个不同元素中取出m ()m n ≤个元素的所有组合的个数，叫做从n 个不同元素中取出m 个元素的组合数．．．．用符号mn C 表示． 3．组合数公式的推导：（1）回顾引例问题找到排列数与组合数的关系（2）从4个不同元素,,,a b c d 中取出3个元素的组合数34C 是多少呢？启发：由于排列是先组合再排列．．．．．．．．．，而从4个不同元素中取出3个元素的排列数34A 可以求得，故我们可以考察一下34C 和34A 的关系，如下：组 合 排列dcbcdb bdc dbc cbd bcd bcd dca cda adc dac cad acd acd dba bda adb dab bad abd abd cba bca acb cab bac abc abc ,,,,,,,,,,,,,,,,,,,,→→→→ 由此可知,每一个组合都对应着6个不同的排列，因此，求从4个不同元素中取出3个元素的排列数34A ，可以分如下两步：① 考虑从4个不同元素中取出3个元素的组合，共有34C 个；② 对每一个组合的3个不同元素进行全排列，各有33A 种方法．由分步计数原理得：34A ＝⋅34C 33A ． （2）推广：一般地，求从n 个不同元素中取出m 个元素的排列数mn A ，可以分如下两步： ① 先求从n 个不同元素中取出m 个元素的组合数m n C ；② 求每一个组合中m 个元素全排列数m m A ，根据分步计数原理得：m n A ＝m n C m mA ⋅． （3）组合数的公式：(1)(2)(1)!m m n nm m A n n n n m C A m ---+==或)!(!!m n m n C mn -=,,(n m N m n ≤∈*且学生活动：记忆公式规定: 01n C =.三、讲解范例：例2．计算710C ．解法1：710109876547!C ⨯⨯⨯⨯⨯⨯=＝120．解法2：71010!10987!3!3!C ⨯⨯==＝120． 师板书两个公式计算，比较难易度，引导学生选择恰当的公式学生活动：熟记公式，完成针对练习课堂练习1：计算师由特殊例子引导学生总结性质1组合数的性质1：mn nm n C C -=． 课堂练习2：完成市本112页自我测评A 组1、6（1） 师提问学生口答并强调易错点组合数的性质2：m n C 1+＝m n C +1-m nC ． 学生活动：学生板演证明性质2成立证明：)]!1([)!1(!)!(!!1---+-=+-m n m n m n m n C C m n m n )!1(!!)1(!+-++-=m n m m n m n n )!1(!!)1(+-++-=m n m n m m n )!1(!)!1(+-+=m n m n m n C 1+= ∴m n C 1+＝m n C +1-m nC ． 说明：①公式特征：下标相同而上标差1的两个组合数之和，等于下标比原下标多1而上标与大的相同的一个组合数；②此性质的作用：恒等变形，简化运算 学生活动：熟记性质完成针对练习 四、课堂小结：学生思考总结：1、本节课重点和难点分别是什么？2、本节课讲解了几类题型 五、课后作业：完成市本第一课时C37)1(C)2(25C C 24362)3(-。

组合数的计算公式组合数是一类有趣的数字，可以帮助我们解决许多有关组合的问题。

它也有着广泛的应用，是重要的数学工具。

组合数的计算公式作为一种重要的算法，可以帮助我们计算组合数。

首先，我们来看看组合数的定义。

组合数表示从一组候选项中选出n个元素的组合数，其中每个元素有k个可用的选择，并且顺序无关。

它可以表示为：C(n,k)=n!/(k! * (n-k!)）。

其次，我们来讨论组合数计算公式的运用。

组合数的计算公式可以用来计算从一组候选项中选取特定数量的组合的个数。

它可以帮助我们解决问题，比如：有多少种从一组N个数字中选出K个数字的方式？此外，组合数计算公式也可以用来解决组合问题。

它可以帮助我们计算从一组N个数中选出K个数字的组合，并且可以用来解决关于特定组合事项的问题，比如：从一篮子苹果中，怎样可以选出3个，不改变它们原有的排列方式？组合数的计算公式也有着广泛的应用。

它可以用来计算不同形式的组合，比如两者的组合，三者的组合，四者的组合或更多。

它可以用来计算复杂的组合情况，如多组权重的组合，或组合问题的复杂重叠情况。

此外，它也可以用于计算组合期权价值，以及组合投资组合的收益率。

最后，组合数计算公式有着多种变体。

可以采用不同的方法来计算不同形式的组合，这些方法包括：加法原理、乘法原理、排列组合原理、哥德巴赫原理等。

除此之外，还可以采用数学归纳法来证明组合的计算公式的有效性。

总之，组合数计算公式是一种重要的算法，可以用来计算组合、解决组合问题，也有着广泛的应用。

它有着多种变体，可以采用不同的方式来计算组合，也可以用数学归纳法来证明其有效性。

综上所述，组合数计算公式具有实际上的价值，可以帮助我们解决复杂组合问题，从而实现更有效的计算结果。

《组合数的性质》讲义一、组合数的定义在数学中，组合数表示从 n 个不同元素中选取 k 个元素的组合方式的数量，记作 C(n, k)。

其计算公式为：C(n, k) ＝ n! ／ k!（n k)！，其中 n! 表示 n 的阶乘，即 n! ＝ n ×（n 1) ×（n 2) × ··· × 2 × 1 。

二、组合数的基本性质1、对称性组合数具有对称性，即 C(n, k) ＝ C(n, n k) 。

这意味着从 n 个元素中选取 k 个元素的组合数与从 n 个元素中选取 n k 个元素的组合数是相等的。

例如，从 5 个元素中选取 2 个元素的组合数 C(5, 2) 与从 5 个元素中选取 3 个元素的组合数 C(5, 3) 是相等的。

我们可以通过组合数的计算公式来证明这一性质。

C(5, 2) ＝ 5! ／（2! × 3!）＝ 10 ，C(5, 3) ＝ 5! ／（3! × 2!）＝ 10 ，两者相等。

这种对称性在解决组合问题时，可以灵活地选择计算量较小的一种方式进行计算。

2、递推性质组合数还具有递推性质，即 C(n, k) ＝ C(n 1, k 1) ＋ C(n 1, k) 。

这个性质可以通过实际的组合情况来理解。

假设我们要从 n 个元素中选取 k 个元素，我们可以分为两种情况：第一种情况，包含第 n 个元素。

那么在剩下的 n 1 个元素中选取 k1 个元素，组合数为 C(n 1, k 1) 。

第二种情况，不包含第 n 个元素。

那么就在剩下的 n 1 个元素中选取 k 个元素，组合数为 C(n 1, k) 。

将这两种情况的组合数相加，就得到了从 n 个元素中选取 k 个元素的组合数 C(n, k) 。

利用这个递推性质，可以通过较小规模的组合数逐步计算出较大规模的组合数，从而简化计算过程。

3、加法性质C(m ＋ n, r) ＝∑（i ＝ 0 到 r) C(m, i) × C(n, r i) 。

第一课时组合与组合数公式[对应学生用书P10][例1](1)从a，b，c，d四名学生中选两名学生完成一件工作，有多少种不同的安排方法？(2)从a，b，c，d四名学生中选两名学生完成两件不同的工作，有多少种不同的安排方法？(3)a，b，c，d四支足球队之间进行单循环比赛，共需赛多少场？(4)a，b，c，d四支足球队争夺冠、亚军，有多少种不同的结果？在上述问题中，哪些是组合问题，哪些是排列问题？[思路点拨] 要分清是组合还是排列问题，只要确定取出的这些元素是否与顺序有关．[精解详析] (1)两名学生完成的是同一件工作，没有顺序，是组合问题；(2)两名学生完成两件不同的工作，有顺序，是排列问题；(3)单循环比赛要求每两支球队之间只打一场比赛，没有顺序，是组合问题；(4)冠亚军是有顺序的，是排列问题．[一点通] 区分一个问题是排列问题还是组合问题，关键是看它有无“顺序”，有顺序就是排列问题，无顺序就是组合问题．要判定它是否有顺序的方法是先将元素取出来，看交换元素的顺序对结果有无影响，有影响就是“有序”，也就是排列问题；没有影响就是“无序”，也就是组合问题．1．判断下列问题是组合问题，还是排列问题．(1)设集合A＝{a，b，c，d}，则集合A的含有3个元素的子集有多少个？(2)从1,2,3,4四个数字中，任选两个做加法，其结果有多少种不同的可能？(3)从1,2,3,4四个数字中，任选两个做除法，其结果有多少种不同的可能？(4)会场有50个座位，要求选出3个座位有多少种方法？若选出3个座位安排3个客人入座，又有多少种方法？(5)把4本相同的数学书分给5个学生，每人至多得一本，有多少种分配方法？(6)4个人去干5种不同的工作，每人干一种，有多少种分工方法？解：(1)组合问题，因为集合中取出元素具有“无序性”．(2)组合问题，由于加法运算满足交换律，所以选出的两个元素做加法时，与两个元素的位置无关．(3)排列问题，两个元素做除法时，谁作除数，谁作被除数不一样，此时与位置有关． (4)第一问是组合问题，第二问是排列问题，“入座”问题同“排队”，与顺序有关． (5)组合问题，由于4本数学书是相同的，不同的分配方法取决于从5个学生中选择哪4个人，这和顺序无关．(6)排列问题，因为5种工作是不同的，一种分工方法就是从5种不同的工作中选出4种，按一定的顺序分配给4个人，它与顺序有关．[例2] 1073100200(3)C 38－n3n ＋C 3n21＋n .[思路点拨] 用组合数公式和组合数的性质解决． [精解详析] (1)原式＝C 410－A 37 ＝10×9×8×74×3×2×1－7×6×5＝210－210＝0.(2)C 98100＋C 199200＝C 2100＋C 1200＝100×992＋200＝4 950＋200＝5 150.(3)∵⎩⎪⎨⎪⎧38－n ≤3n ，3n ≤21＋n ，∴9.5≤n ≤10.5.∵n ∈N ＋，∴n ＝10.∴C 38－n3n ＋C 3n21＋n ＝C 2830＋C 3031＝C 230＋C 131 ＝30×292×1＋31＝466. [一点通] (1)对于组合数的有关运算，除了利用组合数公式外，还要注意利用组合数的两个性质，对式子进行适当的变形，选择最恰当的公式计算．(2)有关组合数的证明问题，一般先依据组合数的性质化简，再用组合数的阶乘形式证明．2．若C 2n ＝28，则n 的值为( ) A ．9 B ．8 C ．7D ．6解析：∵C 2n ＝n ！2！n －！＝n n －2＝28，∴n (n －1)＝56，即n ＝8. 答案：B3．若C 4n ，C 5n ，C 6n 成等差数列，则C 12n 的值为________． 解析：由已知，得2C 5n ＝C 4n ＋C 6n ， 所以2·n ！5！n －！＝n ！4！n －！＋n ！6！n －！， 整理，得n 2－21n ＋98＝0，解得n ＝7或n ＝14. 要求C 12n 的值，故n ≥12，所以n ＝14， 于是C 1214＝C 214＝14×132×1＝91.答案：914．证明：C mn ＝n mC m －1n －1. 证明：∵n m·C m －1n －1＝n m·n －！m －！n －－m －！＝n ！[mm －！n －m ！＝n ！m ！n －m ！＝C mn ，∴C mn ＝n mC m －1n －1成立.[例3] (12分) (1)从口袋内取出3个球，共有多少种取法？(2)从口袋内取出3个球，使其中含有1个黑球，有多少种取法？ (3)从口袋内取出3个球，使其中不含黑球，有多少种取法？[思路点拨] 先判断是不是组合问题，再用组合数公式写出结果，最后求值． [精解详析] (1)从口袋内的8个球中取出3个球，取法种数是C 38＝8×7×63×2×1＝分)(2)从口袋内取出3个球有1个是黑球，于是还要从7个白球中再取出2个，取法种数是C 11C 27＝7×62×1＝21.分)(3)由于所取出的3个球中不含黑球，也就是要从7个白球中取出3个球，取法种数是C 37＝7×6×53×2×1＝35.分)[一点通] 解简单的组合应用题，要首先判断它是不是组合问题，即取出的元素是“合成一组”还是“排成一列”，其次要看这件事是分类完成还是分步完成．5．某施工小组有男工7名，女工3名，现要选1名女工和2名男工去支援另一施工队，不同的选法有( )A ．C 310种 B ．A 310种 C ．A 27A 13种D ．C 27C 13种解析：每个被选的人员无角色差异，是组合问题．分两步完成： 第一步，选女工，有C 13种选法； 第二步，选男工，有C 27种选法． 故有C 13C 27种不同选法． 答案：D6．10个人分成甲、乙两组，甲组4人，乙组6人，则不同的分组种数为________．(用数字作答)解析：从10个人中选4人作为甲组，剩下的6人为乙组，共有C 410＝210种分组方法． 答案：2107．现有10名教师，其中男教师6名，女教师4名． (1)现要从中选2名去参加会议，有多少种不同的选法？(2)现要从中选出男、女教师各2名去参加会议，有多少种不同的选法？ 解：(1)从10名教师中选2名去参加会议的选法有C 210＝45种．(2)从6名男教师中选2名有C 26种选法，从4名女教师中选2名有C 24种选法．根据分步乘法计数原理，共有选法C 26C 24＝90种．1．“组合”与“组合数”是两个不同的概念，组合是m 个元素形成的一个整体，不是数，组合数是形成的不同组合的个数，是数量．2．对于有关组合数的计算、证明、解方程或不等式时，一是要注意组合数本身的有意义的未知数的取值范围．二是掌握组合数性质，在计算C mn 时，若m ＞n2，通常使用C m n ＝C n －mn 转化；求多个组合数的和时，要注意观察上、下标的特征，灵活运用C mn ＋1＝C mn ＋C m －1n .[对应课时跟踪训练四1．给出下面几个问题：①10人相互通一次电话，共通多少次电话？②从10个人中选出3个作为代表去开会，有多少种选法？ ③从10个人中选出3个不同学科的课代表，有多少种选法？ ④由1,2,3组成无重复数字的两位数． 其中是组合问题的有( ) A ．①③ B ．②④ C ．①②D ．①②④解析：①是组合问题，因为甲与乙通了一次电话，也就是乙与甲通了一次电话，没有顺序的区别；②是组合问题，因为三个代表之间没有顺序的区别；③是排列问题，因为三个人担任哪一科的课代表是有顺序区别的；而④中选出的元素还需排列，有顺序问题是排列．所以①②是组合问题．答案：C2．若A 3n ＝12C 2n ，则n 等于( ) A ．8 B ．5或6 C ．3或4D ．4解析：∵A 3n ＝12C 2n ，∴n (n －1)(n －2)＝12×n n －2.解得n ＝8.答案：A3．下列四个式子中正确的个数是( ) (1)C m n＝A mn m ！；(2)A m n ＝n A m －1n －1；(3)C m n ÷C m ＋1n ＝m ＋1n －m ；(4)C m ＋1n ＋1＝n ＋1m ＋1C m n . A ．1个 B ．2个 C ．3个D ．4个解析：因为C m n＝n ！m ！n －m ！＝1m ！·n ！n －m ！＝A mnm ！，故(1)正确；因为n A m －1n －1＝n ·n －！n －m ！＝n ！n －m ！＝A mn ，故(2)正确；因为C mn ÷C m ＋1n ＝n ！m ！n －m ÷n ！m ＋！n －m －！＝n ！m ！n －m ！×m ＋！n －m －！n ！＝m ＋1n －m， 故(3)正确． 因为Cm ＋1n ＋1＝n ＋！m ＋！n －m ！，n ＋1m ＋1Cmn＝n ＋1m ＋1·n ！m ！n －m ！＝n ＋！m ＋！n －m ！，所以C m ＋1n ＋1＝n ＋1m ＋1C m n ，故(4)正确．答案：D4．若C 7n ＋1－C 7n ＝C 8n ，则n 等于( ) A ．12 B ．13 C ．14D ．15解析：C 7n ＋1－C 7n ＝C 8n ，即C 7n ＋1＝C 8n ＋C 7n ＝C 8n ＋1， 所以n ＋1＝7＋8，即n ＝14. 答案：C5．从2,3,5,7四个数中任取两个不同的数相乘，有m 个不同的积，任取两个不同的数相除，有n 个不同的商，则m ∶n ＝________.解析：∵m ＝C 24，n ＝A 24，∴m ∶n ＝12.答案：126．方程C x 28＝C 3x －828的解为________．解析：当x ＝3x －8，解得x ＝4；当28－x ＝3x －8，解得x ＝9. 答案：4或97．计算：(1)C 58＋C 98100C 77； (2)C 05＋C 15＋C 25＋C 35＋C 45＋C 55.解：(1)原式＝C 38＋C 2100×1＝8×7×63×2×1＋100×992×1＝56＋4 950＝5 006.(2)原式＝2(C 05＋C 15＋C 25)＝2(C 16＋C 25)＝2×⎝ ⎛⎭⎪⎫6＋5×42×1＝32. 8．在一次数学竞赛中，某学校有12人通过了初试，学校要从中选出5人去参加市级培训，在下列条件下，有多少种不同的选法？(1)任意选5人；(2)甲、乙、丙三人必须参加； (3)甲、乙、丙三人不能参加； (4)甲、乙、丙三人只能有1人参加． 解：(1)C 512＝792种不同的选法．(2)甲、乙、丙三人必须参加，只需从另外的9人中选2人，共有C 29＝36种不同的选法． (3)甲、乙、丙三人不能参加，只需从另外的9人中选5人，共有C 59＝126种不同的选法．(4)甲、乙、丙三人只能有1人参加，分两步：第一步从甲、乙、丙中选1人，有C 13＝3种选法；第二步从另外的9人中选4人有C 49种选法．共有C 13C 49＝378种不同的选法．。