非周期信号的频域分析2
- 格式：ppt
- 大小：1.09 MB
- 文档页数：33
下载文档原格式
合集下载
实验四非周期信号频域分析
实验四 非周期信号频域分析1 实验目的(1) 掌握傅里叶变换的分析方法及其物理意义。
(2) 掌握各种典型的连续时间非周期信号的频谱特征以及傅里叶变换的主要性质。
(3) 学习掌握利用MA TLAB 语言编写计算CTFT 的仿真程序，并能利用这些程序对一些典型信号进行频谱分析，验证CTFT 的若干重要性质。
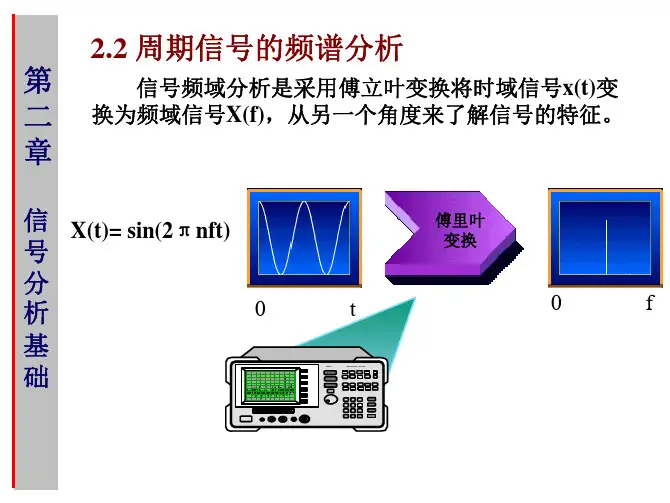
2 实验原理及方法2.1连续时间信号傅里叶变换——CTFT傅里叶变换在信号分析中具有非常重要的意义，它主要是用来进行信号的频谱分析的。
傅里叶变换和其逆变换定义如下：⎰∞∞--=dt e t x j X t j ωω)()( 4-1 ⎰∞∞-=ωωπωd e j X t x t j )(21)( 4-2连续时间傅里叶变换主要用来描述连续时间非周期信号的频谱。
任意非周期信号，如果满足狄里克利条件，它可以被看作是由无穷多个不同频率(这些频率都是非常的接近)的周期复指数信号e j ωt 的线性组合构成的，每个频率所对应的周期复指数信号e j ωt 称为频率分量，其相对幅度为对应频率的|X(j ω)|之值，其相位为对应频率的X(j ω)的相位。
X(j ω)通常为关于ω的复函数，可以按照复数的极坐标表示方法表示为：X(j ω)=| X(j ω)|e j ∠ X(j ω)其中，| X(j ω)|称为x(t)的幅度谱， ∠X(j ω)称为x(t)的相位谱。
给定一个连续时间非周期信号x(t)，它的频谱是连续且非周期的。
对于连续时间周期信号，也可以用傅里叶变换来表示其频谱，其特点是，连续时间周期信号的傅里叶变换是由冲激序列构成的，是离散的——这是连续时间周期信号的傅里叶变换的基本特征。
2.2 用MA TLAB 实现CTFT 及其逆变换2.2.1 用MATLAB 实现CTFT 的计算MA TLAB 进行傅里叶变换有两种方法，一种利用符号运算的方法计算，另一种是数值计算，本实验采用数值计算的方法。
严格来说，用数值计算的方法计算连续时间信号的傅里叶变换需要有个限定条件，即信号是时限信号，也就是当时间|t|大于某个给定时间时其值衰减为零或接近于零，这个条件与前面提到的为什么不能用无限多个谐波分量来合成周期信号的道理是一样的。
第三章第二节离散信号频域分析
若 Y (k ) X 1 (k ) X 2 (k )
则 y (n ) IDFS [Y (k )] x1 (m) x2 (n m)
m 0
N 1
x2 (m) x1 (n m)
m 0
N 1
证： y(n) IDFS[ X 1 (k ) X 2 (k )]
j
2
j j e 2 e 2
e
3 j 2
sin 2 sin / 2
求x n 的8点DFT N 8
X k X e j
3 j k 2 4
2 k 8
e
2 sin 2 k 8 1 2 sin k 2 8 sin k 2 sin k 8
若 则有
2．周期序列的移位 设
则 如果m>N，则m=m1+Nm2
3．周期卷积 设 和 DFS系数分别为
都是周期为N的周期序列，它们的
令
则
上式表示的是两个周期序列的卷积，称为周期卷积。 周期为N的两个序列的周期卷积的离散傅里叶级数等于 它们各自离散傅里叶级数的乘积。
周期卷积的计算：
周期卷积中的序列 和 对m都是周 期为N的周期序列，它们的乘积对m也是以N为周期的， 周期卷积仅在 一个周期内求和。 相乘和相加运 算仅在m=0到N-1的区间内进行。计算出 n=0到N-1(一个周期)的结果后，再将其进行周期延拓， 就得到周期卷积 。 周期卷积满足交换律
j
2 nk N
一个域的离散造成另一个域的周期延拓， 因此离散傅里叶变换的时域和频域都是 离散的和周期的。
离散时间、连续频率—序列的傅里叶变换
则 y (n ) IDFS [Y (k )] x1 (m) x2 (n m)
m 0
N 1
x2 (m) x1 (n m)
m 0
N 1
证： y(n) IDFS[ X 1 (k ) X 2 (k )]
j
2
j j e 2 e 2
e
3 j 2
sin 2 sin / 2
求x n 的8点DFT N 8
X k X e j
3 j k 2 4
2 k 8
e
2 sin 2 k 8 1 2 sin k 2 8 sin k 2 sin k 8
若 则有
2．周期序列的移位 设
则 如果m>N，则m=m1+Nm2
3．周期卷积 设 和 DFS系数分别为
都是周期为N的周期序列，它们的
令
则
上式表示的是两个周期序列的卷积，称为周期卷积。 周期为N的两个序列的周期卷积的离散傅里叶级数等于 它们各自离散傅里叶级数的乘积。
周期卷积的计算：
周期卷积中的序列 和 对m都是周 期为N的周期序列，它们的乘积对m也是以N为周期的， 周期卷积仅在 一个周期内求和。 相乘和相加运 算仅在m=0到N-1的区间内进行。计算出 n=0到N-1(一个周期)的结果后，再将其进行周期延拓， 就得到周期卷积 。 周期卷积满足交换律
j
2 nk N
一个域的离散造成另一个域的周期延拓， 因此离散傅里叶变换的时域和频域都是 离散的和周期的。
离散时间、连续频率—序列的傅里叶变换
2.5信号的频域分析(非周期信号)2.6傅立叶变换的性质
能 量 谱
由此最后得
E = ∫ x2 (t )dt =
−∞ ∞
1 ∞ 2 X(ω) dω 2π ∫−∞
(16)
式（15）亦称巴塞伐尔方程或 能量等式。它表示，一个非周 期信号x(t)在时域中的能量可由 它在频域中连续频谱的能量来 表示。 式（15）亦可写成
E= 1 ∞ 2 X(ω) dω 2π ∫−∞ 1 ∞ 2 = ∫ X(ω) dω = ∫ S(ω)dω
证明： 由欧拉公式
X (ω) = ∫ x(t)e
−∞
∞ −∞
∞
− jωt
dt
∞ −∞
X (ω) = ∫ x(t) cosωtdt − j∫ x(t) sin ωtdt
= Re X (ω) + j Im X (ω)
若x(t)为实函数
Re X (ω) = Re X (−ω) Im X (ω) = − Im X (−ω)
x(t) = Arect
(t − t0 )
T
图2.30 具有时移t0的矩形脉冲
X( f ) = AT sin c(πfT) sin c(πfT) > 0 − 2πt0 f , ϕ( f ) = − 2πt0 f ±π , sin c(πfT) < 0
测试技术
2.6傅里叶变换的性质 2.6傅里叶变换的性质
∫
∞
−∞
x(t) dt < ∞
但上述条件并非必要条件 必要条件。因为当引入广义函数概 必要条件 念之后，许多原本不满足绝对可积条件的函数也能进行傅 里叶变换。 若将上述变换公式中的角频率ω用频率f来替代，则由 于ω=2πf，式（5）和（6）分别变为
X( f ) = ∫ x(t)e− j 2πft dt
非周期信号(方波,锯齿波,三角波)的合成分解以及频谱分析的MATLAB实现
MATLAB 在数学类科技应用软件中在数值计算方面首屈一指。MATLAB 可以进行矩 阵运算、绘制函数和数据、实现算法、创建用户界面、连接其他编程语言的程序等， 主要应用于工程计算、控制设计、信号处理与通讯、图像处理、信号检测、金融建模 设计与分析等领域。
1.2 主要功能
1.数值分析 2.数值和符号计算 3.工程与科学绘图 4.控制系统的设计与仿真 5.数字图像处理 6.数字信号处理 7.通讯系统设计与仿真 8.财务与金融工程
2
连续周期信号的傅立叶级数分析及其 MATLAB 实现
２ 连续周期信号的傅立叶级数
频域分析法即傅里叶分析法，它是变换域分析法的基石。其中，傅里叶级数 是变换域分析法的理论基础，傅里叶变换作为频域分析法的重要数学工具，具有 明确的物理意义，在不同的领域得到广泛的应用。
2.1 连续时间周期信号的分解
以高等数学的知识，任何周期为 T 的周期函数，在满足狄里赫利条件时，则 该周期信号可以展开成傅里叶级数。傅里叶级数有三角形式和指数形式两种。
(3-2)
2
2
3
MATLAB 实现程序：
n=7;
6
连续周期信号的傅立叶级数分析及其 MATLAB 实现
T0=2;A=2; T1=2; tn_i=1; for tn=0:0.01:T1*T0
y_t(tn_i)=A* rem (tn,T0)/T0; t_t(tn_i)=tn; tn_i=tn_i+1; end; t=0:0.01:T1*T0; x=A/2; pi=3.1415926; w0=2*pi/T0; for i=1:n fw(i)=i*w0; a(i)=-A/(pi*i); y(i,:)=a(i)*sin(fw(i)*t); x=x+y(i,:); end; subplot(1,3,1); plot(t_t,[y_t;x]); title('锯齿波、锯齿波合成图') subplot(1,3,2); plot(t,[x; y]); title('0-n 次谐波及合成图') subplot(1,3,3); stem(fw,a); title('锯齿波频谱图') 生成图形：
1.2 主要功能
1.数值分析 2.数值和符号计算 3.工程与科学绘图 4.控制系统的设计与仿真 5.数字图像处理 6.数字信号处理 7.通讯系统设计与仿真 8.财务与金融工程
2
连续周期信号的傅立叶级数分析及其 MATLAB 实现
２ 连续周期信号的傅立叶级数
频域分析法即傅里叶分析法，它是变换域分析法的基石。其中，傅里叶级数 是变换域分析法的理论基础，傅里叶变换作为频域分析法的重要数学工具，具有 明确的物理意义，在不同的领域得到广泛的应用。
2.1 连续时间周期信号的分解
以高等数学的知识，任何周期为 T 的周期函数，在满足狄里赫利条件时，则 该周期信号可以展开成傅里叶级数。傅里叶级数有三角形式和指数形式两种。
(3-2)
2
2
3
MATLAB 实现程序：
n=7;
6
连续周期信号的傅立叶级数分析及其 MATLAB 实现
T0=2;A=2; T1=2; tn_i=1; for tn=0:0.01:T1*T0
y_t(tn_i)=A* rem (tn,T0)/T0; t_t(tn_i)=tn; tn_i=tn_i+1; end; t=0:0.01:T1*T0; x=A/2; pi=3.1415926; w0=2*pi/T0; for i=1:n fw(i)=i*w0; a(i)=-A/(pi*i); y(i,:)=a(i)*sin(fw(i)*t); x=x+y(i,:); end; subplot(1,3,1); plot(t_t,[y_t;x]); title('锯齿波、锯齿波合成图') subplot(1,3,2); plot(t,[x; y]); title('0-n 次谐波及合成图') subplot(1,3,3); stem(fw,a); title('锯齿波频谱图') 生成图形：
离散非周期信号的频谱
离散非周期信号的频谱频谱是任何信号的一个非常重要的特性，它决定了信号中能量的分布。
离散非周期信号的频谱研究一直是信号处理的重要领域之一。
本文将介绍离散非周期信号的频谱特性和分析方法，并以实际应用为例进行说明。
一、离散非周期信号的频谱特性频谱是一种信号分析方法，可用来确定信号中能量的分布，以便更好地描述信号的特性。
离散非周期信号指的是，信号永远不能重复，有时也叫离散调制信号。
离散非周期信号特别适合用傅立叶变换分析，其频谱具有特殊的结构，表现为频率峰峰值（频域谱线中的峰值）的带状构造。
这种带状结构是由信号的离散性造成的，因此，它决定了信号的能量集中在一定频率和其附近的带宽中。
理论上，对于离散非周期信号，频率峰值带状结构可以无限放大，这说明了离散非周期信号具有较大的带宽，因此，有关离散非周期信号频谱的研究非常有价值。
二、离散非周期信号的频谱分析方法离散非周期频谱分析通常采用傅立叶变换。
傅立叶变换可以将时域上的离散信号转换为频域上的离散信号，从而可以研究离散非周期信号的频谱特性。
傅立叶变换的另一个优点是，它可以将时域的正弦信号转换为频域的峰峰值形式。
另外，通过幅度谱和相位谱，可以更清楚地分析信号的频率特性，从而可以更轻松地分析信号中能量的分布情况。
三、实际应用离散非周期信号频谱的实际应用十分广泛，在通信、声学和多媒体中都有应用。
例如，图像处理的最终结果是一个离散非周期信号，它的傅立叶变换可以帮助我们更加准确地确定图像中能量的分布。
同样，在语音信号处理中，人类语音的本质也是一个离散非周期信号，可以利用傅立叶变换更加准确地分析语音特性，从而提高语音识别和合成的效果。
最后，离散非周期信号频谱在多媒体中也有重要作用，可以用来更准确地表示多媒体信号，帮助我们更好地处理多媒体信号。
综上所述，离散非周期信号的频谱分析是信号处理的重要内容，它的研究与实际应用都有很多价值。
不仅可以用来理论研究，还可以用来实际应用，并在各种领域中得到广泛应用。
非周期信号的频谱
(2) 若f(t)为t的奇函数，即f(-t)=-f(t)，则f(t)的频 谱函数F(jω)为ω的虚函数，且为ω的奇函数。
与周期信号类似，也可将非周期信号的傅里叶变
换表示式改写成三角函数的形式，即
.
6
f(t)21
F(j)ejtd
21
F(j)ej[t()]d
2 1 F (j)co ts [()d ]
2
0
2
t
实偶
4
2
0
2
4
实偶
图 3.4-1 门函数及其频谱
一般而言，信号的频谱函数需要用幅度谱 F( j)和相位
谱 ( )两个图形才能将它完全表示出来。但如果频谱
函数是实函数或虚函数，那么只用一条曲线即可。
F(j) 为负代表相位为 ，
0
.
F(为j正) 代表相位为 。
11
由图可见，第一个零值的角频率为 2 （频率 1 ）。
为了描述非周期信号的频谱特性，引入频谱密度的 概念。
令
F(j)T l i m 1F /n TT l i m FnT
称 F(j)为频谱密.度函数。
2
如何求频谱密度函数？ F(j)T l i m 1F /n TT l i m FnT
由式
f(t) Fnejnt
n
，Fn
1 T
T
2 T
2
f(t)ej ntd t可得
可知
'(t)ejtd tdejt j
dt t 0
即 ℱ 'tj
同理可得 ℱ [(n)(t). ](j)n
23
例3.4-6 求单位直流信号的频谱
f(t)1 - t
显然，该信号不满足绝对可积条件，但其傅里叶变换
2 信号分析基础(频谱分析)
(2.69)
傅 里 叶 变 换 与 非 周 期 信 号 的 分 解
式2.68称为 x t 的傅立叶变换，称式2.69为 X 的 傅立叶逆变换，两者称为傅立叶变换对，可记为
x t X
IFT
FT
2 f 代入傅立叶积分式中，则式2.68, 2.69变为
X f x t e j 2 ft dt
Im[X ( f )] ( f ) arctgRe[ X ( f )]
x (t ) 1 X ( )e jt d 2 X ( ) x (t )e jt dt
X f 连续幅值谱
f
连续相位谱
X 频谱密度函数
2.2 周期信号的频谱分析 第 二 章
信号频域分析是采用傅立叶变换将时域信号x(t)变 换为频域信号X(f)，从另一个角度来了解信号的特征。
信 X(t)= sin(2πnft) 号 分 0 析 基 础
傅里叶 变换
t
8563A
SPECTRUM ANALYZER 9 kHz - 26.5 GHz
0
f
频域分析的概念 周 期 信 号 的 频 谱 分 析
傅 里 叶 变 换 与 非 周 期 信 号 的 分 解
T0 T0 , 设有一个周期信号x(t)在区间 2 2
以傅立叶级数表示为
x t
n
ce
n
jn0t
1 式中 cn T0
T0 2 T 0 2
x t e
jn0t
dt
将其代入上式则得
n n
幅频谱 相频谱
频谱图的概念 周 期 信 号 的 频 谱 分 析
信号与系统课程第06讲 非周期信号的分解——傅里叶变换
信号与系统——非周期信号的分解—傅里叶变换
1
第06 讲
上一页 返 回
2019/10/8
信号与系统——非周期信号的分解—傅里叶变换
本章主要内容
4.1 引言 4.2 傅里叶级数 4.3 周期信号的频谱 4.4 非周期信号的频谱 4.5 傅里叶变换的性质 4.6 能量谱和功率谱 4.7 周期信号的傅里叶变换
上一页 返 回
2 2019/10/8
信号与系统——非周期信号的分解—傅里叶变换
4.1 引言 4.2 傅里叶级数 4.3 周期信号的频谱
4.4 非周期信号的频谱
4.5 傅里叶变换的性质 4.6 能量谱和功率谱 4.7 周期信号的傅里叶变换
上一页 返 回
3 2019/10/8
信号与系统——非周期信号的分解—傅里叶变换
1
0
+ j 0 j +
F ( j ) = 1
2 +2
(
)
=
−
arctan
2
o
( )
o
− 2
上一页
2019/10/8
信号与系统——非周期信号的分解—傅里叶变换
12
双边指数信号
f (t ) = e− t − t
0
e− t (t)
f (t)e− j t dt =
−
0 e( − j )t dt +
当T→∞时，有 → d , n → , →
上一页
2019/10/8
信号与系统——非周期信号的分解—傅里叶变换
7
∵
F( j) = lim 2Fn ，则
T →
F( j)
lim
T →
Fn
1
第06 讲
上一页 返 回
2019/10/8
信号与系统——非周期信号的分解—傅里叶变换
本章主要内容
4.1 引言 4.2 傅里叶级数 4.3 周期信号的频谱 4.4 非周期信号的频谱 4.5 傅里叶变换的性质 4.6 能量谱和功率谱 4.7 周期信号的傅里叶变换
上一页 返 回
2 2019/10/8
信号与系统——非周期信号的分解—傅里叶变换
4.1 引言 4.2 傅里叶级数 4.3 周期信号的频谱
4.4 非周期信号的频谱
4.5 傅里叶变换的性质 4.6 能量谱和功率谱 4.7 周期信号的傅里叶变换
上一页 返 回
3 2019/10/8
信号与系统——非周期信号的分解—傅里叶变换
1
0
+ j 0 j +
F ( j ) = 1
2 +2
(
)
=
−
arctan
2
o
( )
o
− 2
上一页
2019/10/8
信号与系统——非周期信号的分解—傅里叶变换
12
双边指数信号
f (t ) = e− t − t
0
e− t (t)
f (t)e− j t dt =
−
0 e( − j )t dt +
当T→∞时，有 → d , n → , →
上一页
2019/10/8
信号与系统——非周期信号的分解—傅里叶变换
7
∵
F( j) = lim 2Fn ，则
T →
F( j)
lim
T →
Fn
非周期信号的频谱
F(j)称为 f(t) 的傅里叶变换或频谱密度函数，简称频谱；
f(t) 称为F(j) 的傅里叶反变换或原函数。
也可简记为： F ( j )
f (t)
f (t)
1 F ( j)
或者： f (t ) F ( j )
频谱密度函数
F ( j ) 一般为复函数，可写为
F ( j) F ( j) ej () F ( ) e j ()
0,
2
A e j tdt
2
A e j t 2
j
2A sin 2
A Sa( )
2
2
t
2
t
2
8.矩形脉冲信号的频谱
f (t ) A
2π
F( j)
A
t 2 0 2
0 2π 4π
Ag (t)
A
Sa( )
2
傅里叶变换对 F ( j ) f ( t ) e j t d t
T
Fn
2Fn 1
Fn f1
T
2 T
f ( t ) e j n 1t d t
2
其中， Fn 或 Fn 表示单位频带上的频谱值，即频谱密度。
1
f1
对上式取极限 T ，各变量将相应改为 T
虽然 记作
Fn 0
F ( j)
，但
T
F
n 趋于一有限函数
1
2
T
d
n 1 n
F ( j )
et t 0
f (t) e t t 0
为 0的实数
F ( j) 0 eate jtdt eate jtdt j
2
0
2 a2
F (j) 2 2 a2
非周期信号的频谱分析
X
4．傅里叶变换对
F(
j )
f
(t)ej t
dt
F
f
(t)
正变换
f
(t)
1
2
F
j
e j
t
d
F
1 F
j
反变换
简写
f t F j
记做：
F f (t) F( j) F 1 F( j) f (t)
二、傅里叶反变换的物理意义——信号分解
f (t) 1 F j e j t d F j d e j t
π
2
O
π2
O π 2
注意：只有α＞0时傅里叶变换才存在， α＜0时f(t)不
满足绝对可积条件
8．升余弦脉冲信号（自学）
f
t
E 2
1
cos
π
t
0 t
f t
E
E
2
F j f t ejt d t
O
2
E 2
1
cos π t
e jt
dt
t
2
E
ejt d t E
2
(t)
Sa 2
(
w 2
)
1 f2τ△ (t)
注意对比两 者不同
F j
－τ 0 τ
t
2π O 2π 4π
X
第
五.非周期信号频谱的特点
34 页
1.连续性
特例：直流和阶跃信号的频谱含冲激。
2.收敛性
第 13 页
4）与周期信号傅立叶级数展开的收敛条件比较
f (t) d t （有限值或收敛）
T
傅里叶变换存在的条件与傅立叶级数展开的收敛条 件一样。 信号绝对可积； 任何有限区间里，只有有限个最大值和最小值； 任何有限区间里，有有限个不连续点，且不连续点有值。
《信号、系统与数字信号处理》第二章 连续时间信号与系统的频域分析
0 21
/4
/2
(b)相位图
图2.1-2例2.1-2的频谱图
二、指数形式的傅里叶级数
利用欧拉公式将三角形式的傅里叶级数，表示为 复指数形式的傅氏级数
其中
f t F n1 e jn1t
n
F n1
1 T
t0 T t0
f t e jn1tdt
F n1 是复常数，通常简写为 Fn 。
21t
5
4
2
sin
1t
1 2
sin
31t
解：将 f t 整理为标准形式
f
(t)
1
2cos 1t来自4cos 21t
5
4
1 2
cos
31t
2
1
2
cos
1t
4
cos
21t
4
1 2
cos
31t
2
振幅谱与相位谱如图2-1所示。
cn
2
1
1
1/2
0 1 21 31
(a) 振幅图
n
/4
31
第二章 连续时间信号与系统的频域分析 ——Fourier变换
2. 1 周期信号的傅里叶级数分析 2. 2 非周期信号的频谱--傅里叶变换 2. 3 傅里叶变换的性质及定理 2. 4 系统的频域分析方法 2. 5 无失真传输系统与滤波
LTI系统分析的一个基本任务，是求解系统对任意 激励信号的响应，基本方法是将信号分解为多个基本信 号元。
一、三角形式傅里叶级数
周期信号: f t f t nT
其中
T
是信号的最小重复时间间隔，f1
1 是信号的基波频率。 T
若 f t 满足狄里赫利条件，则 f t 可以展开为三角形
离散非周期信号的频域表示
主讲人：陈后金
电子信息工程学院
离散非周期信号的频域分析
※ 离散非周期信号的频域表示 ※ 离散非周期信号的频谱
1. 离散非周期信号的频域表示
满足一定收敛条件的非周期序列 x[k] 可用虚指数序列表示为
x[k] 1
X (ej )ejkd
2π 2π
加权系数X (ej )称为离散非周期信号x[k] 的频谱。
离散非周期信号的频域分析
谢谢
本课程所引用的一些素材为主讲老师多年的教学积累，来源 于多种媒体及同事、同行、朋友的交流，难以一一注明出处，特 此说明并表示感谢！
2 x[k]
1
1 0 1
k
4 X (ej )
…
…
0
1. 离散非周期信号的频域表示
IDTFT
x[k] 1
X (ej )ejkd
2π 2π
DTFT
X (ej ) x[k]e jk
k
X (ej ) 称为离散非周期信号x[k] 的频谱。
x[k]DTFTX (ej )
DTFT的收敛性
定义X(ej)的部分和
N
X N (ej ) x[k]e j k
k N
若 x[k] 绝对可和
k
则
lim
N
X (ej ) X N (ej ) 0
若序列满足绝对可和，则序列存在DTFT。（充分条件）
2.离散非周期信号的频谱
X(ej ) 特点：
（1）X(ej )是 的连续函数
（2）X(ej )是周期为2的周期函数
X [ej( ] x[k]e j( k
解：
X (ej ) [k]e jk 1
k
[k]
X(ej)
1
电子信息工程学院
离散非周期信号的频域分析
※ 离散非周期信号的频域表示 ※ 离散非周期信号的频谱
1. 离散非周期信号的频域表示
满足一定收敛条件的非周期序列 x[k] 可用虚指数序列表示为
x[k] 1
X (ej )ejkd
2π 2π
加权系数X (ej )称为离散非周期信号x[k] 的频谱。
离散非周期信号的频域分析
谢谢
本课程所引用的一些素材为主讲老师多年的教学积累，来源 于多种媒体及同事、同行、朋友的交流，难以一一注明出处，特 此说明并表示感谢！
2 x[k]
1
1 0 1
k
4 X (ej )
…
…
0
1. 离散非周期信号的频域表示
IDTFT
x[k] 1
X (ej )ejkd
2π 2π
DTFT
X (ej ) x[k]e jk
k
X (ej ) 称为离散非周期信号x[k] 的频谱。
x[k]DTFTX (ej )
DTFT的收敛性
定义X(ej)的部分和
N
X N (ej ) x[k]e j k
k N
若 x[k] 绝对可和
k
则
lim
N
X (ej ) X N (ej ) 0
若序列满足绝对可和，则序列存在DTFT。（充分条件）
2.离散非周期信号的频谱
X(ej ) 特点：
（1）X(ej )是 的连续函数
（2）X(ej )是周期为2的周期函数
X [ej( ] x[k]e j( k
解：
X (ej ) [k]e jk 1
k
[k]
X(ej)
1
信号与系统第三章(2)
F n ⋅ 2 πδ (ω − n ω
) )
= 2π
n = −∞
∑
∞
F n ⋅ δ (ω − n ω
0
即周期信号的傅里叶变换为
F (ω ) = 2π ∑ Fn ⋅ δ (ω − nω 0 )
−∞
∞
上式表明：周期信号的频谱函数，是由无限多个冲激组 上式表明：周期信号的频谱函数， 成，这些冲激位于基频整数倍的频率 nω0处，每一冲激的 强度即为 2π Fn 。
3.5.1 单位冲激 δ (t )
由根据傅里叶变换的定义式， 由根据傅里叶变换的定义式，并且考虑到冲激函 数的抽（取）样性质，得 数的抽（ 样性质，
F (ω ) = ∫ δ (t )e
−∞
∞
− jωt
dt = ∫ δ (t )dt = 1
−∞
∞
结论:
1、单位冲激信号在整个频率范围内具有恒定的频 、单位冲激信号在整个频率范围内具有恒定的频 恒定的 谱函数,为常数1,即冲激信号包含相对幅度相等的所 谱函数 为常数 即冲激信号包含相对幅度相等的所 有频率分量,相位都为 相位都为0. 有频率分量 相位都为 2、信号的持续时间与其频带宽度成反比。 反比。 、信号的持续时间与其频带宽度成反比
−∞ ∞ − jωt
dt = ∫ τ e
2 − 2
− jωt
dt =
e
−e − jω
j
ωτ
2
3.5.7 虚指数函数
利用傅里叶反变换定义和冲激函数的抽样性质， 利用傅里叶反变换定义和冲激函数的抽样性质，可得
1 F [δ (ω − ω 0 )] = 2π
−1
∫ δ (ω − ω )e
−∞ 0
∞
非周期信号的频谱
3.3.2 常用非周期信号的傅立叶变换
• 直流信号1可表示为： P110例3.4-6
f (t) 1 t
F( j)
1
e
jt
dt
（直接积分无法进行）
由傅立叶逆变换的定义式有： (t) 1
1
e
jt
d
令：t
2 () 1 1 e jt dt
2
冲激信号是偶函数： () () 1 1 e jt dt
F( j) F( j) e j() a() jb()
| F( j) | a2() b2()
() arctg b() a()
是ω的偶函数 是ω的奇函数
F( j) F( j) () ()
a( j) a( j) b() b()
3.3.1 傅立叶变换
• 关于连续谱的说明 具有离散频谱的信号，其能量集中在一些谐波分量中。
具有连续频谱的信号，其能量分布在所有的频率中， 每一频率分量包含的能量则为无穷小量。
• 几个重要结论：
当 f (t) 是实函数时：
3.3.1 傅立叶变换
(1) 若 f(t)为t的偶函数，即 f(t) = f(-t)，
则 f(t)的频谱函数 F(jω) 为ω的实函数， 且为ω的偶函数。
(2) 若f(t)为t的奇函数，即 f(-t) = -f(t)， 则f(t)的频谱函数 F(jω) 为ω的虚函数，且为ω的奇函数。
2
f (t) Fne jn1t
T
n
Fn T
2 T
f (t)e jn1t dt
2
周期信号趋于非周期信号。
• 当 T 时： 谱线无限密集，1 d
幅度 Fn 趋于无穷小， n1
令：F
1.3信号分析基础(非周期信号频域分析)2011修改 (2)
w dw ， 由于： T ，
所以：
非周期信号的频谱
x(t )
浙江工业大学
n
Cn e jn0t , (n 0,1,2,...)
1 x(t ) x(t )e jwt dt e jwt dw 2
x(t ) X ( jf ) e j 2ft df
( jf ) arctg
Im[X ( jf )] Re[ X ( jf )]
X f -f 连续幅值谱
f
-f
连续相位谱
非周期信号的频谱
浙江工业大学
例：方波信号的复频谱
1.求取复系数Cn
x(t ) C0 C n e jnw0t C n e jnw0t
T0 / 2
T0 / 2
x(t )e jn0t dt
当T0→∞时， ①积分区间由[-T0/2,T0/2]变为(-∞,∞)； ② ω0=2π/T0 →0， →离散频率nω0→连续变量ω。
T0
lim Cn T0 x(t )e
jt
dt
浙江工业大学
非周期信号： 周期T0 →∞的周期信号 周期信号x(t)，周期为T0，则其频谱是离散谱，而相邻谐波之间的 频率间隔为∆ω=ω0=2π/T0。 当T0→∞，则ω0=∆ω→0， 信号频谱谱线间隔∆ω=ω0→0，无限缩小， 相邻谐波分量无限接近， 离散参数nω0可用连续变量ω来代替， 离散频谱变成了连续频谱， A( ) 求和运算可用积分运算来取得， 所以非周期信号的频谱是连续的。
1
(t )dt lim S (t )dt 1
所以：
非周期信号的频谱
x(t )
浙江工业大学
n
Cn e jn0t , (n 0,1,2,...)
1 x(t ) x(t )e jwt dt e jwt dw 2
x(t ) X ( jf ) e j 2ft df
( jf ) arctg
Im[X ( jf )] Re[ X ( jf )]
X f -f 连续幅值谱
f
-f
连续相位谱
非周期信号的频谱
浙江工业大学
例：方波信号的复频谱
1.求取复系数Cn
x(t ) C0 C n e jnw0t C n e jnw0t
T0 / 2
T0 / 2
x(t )e jn0t dt
当T0→∞时， ①积分区间由[-T0/2,T0/2]变为(-∞,∞)； ② ω0=2π/T0 →0， →离散频率nω0→连续变量ω。
T0
lim Cn T0 x(t )e
jt
dt
浙江工业大学
非周期信号： 周期T0 →∞的周期信号 周期信号x(t)，周期为T0，则其频谱是离散谱，而相邻谐波之间的 频率间隔为∆ω=ω0=2π/T0。 当T0→∞，则ω0=∆ω→0， 信号频谱谱线间隔∆ω=ω0→0，无限缩小， 相邻谐波分量无限接近， 离散参数nω0可用连续变量ω来代替， 离散频谱变成了连续频谱， A( ) 求和运算可用积分运算来取得， 所以非周期信号的频谱是连续的。
1
(t )dt lim S (t )dt 1
瞬变非周期信号的频谱分析
瞬变非周期信号的频谱分析1.傅立叶变换当周期信号的周期趋于无穷大时，该信号就成为非周期信号了。
周期信号频谱谱线的频率间隔为△ω=ω0=2π/T ，由于T为无穷大时，其频率间隔Δω为无穷小,所以非周期信号的频谱是连续的。
非周期信号的幅值谱表示单位频宽上的幅值，精确地讲Ｘ（Ｆ）是频谱密度函数。
2.傅立叶变换的主要性质奇偶虚实性：x(t)为实偶函数，X(f)是实偶函数x(t)为实奇函数，X(f)是虚奇函数线性叠加性：假如f1(t)←→F1(jω),f2(t)←→F2(jω)则对于任何常数a1、a2有：a1f1(t)+a2f2(t)←→a1f1(jω)+a2f2(jω)对称性：时间尺度转变特性：时间尺度压缩，频谱的频带加宽，幅值降低；时间尺度扩大，频谱变窄，幅值增高。
时移和频移特性：时域的延时对应频谱在频域内的相位滞后。
卷积特性：该部分内容请同学自己阅读教材。
微分和积分特性：知道震惊系统的位移、速度、或加速度中任一个参数，应用微分、积分特性就可以获得其他参数的频谱。
3.几种典型信号的频谱矩形窗函数的频谱：时域有限区间内有值的信号，频谱可延长至无限频率。
在时域中若截取信号的一段记录长度，则相当于原信号和矩形窗函数之乘积，因而所得到的频谱将是原信号频域函数和sinc函数的卷积，它将是连续的、频率无限延长的频谱。
单位脉冲函数及其频谱：在极短时间内激发一个矩形脉冲（三角、钟形、双边指数），其面积为1。
当激发时间趋于0时，矩形脉冲的极限就称为单位脉冲函数。
单位脉冲函数的筛选性质：具有采样性质。
单位脉冲函数与其他函数的卷积：就是简洁地将x(t)在发生脉冲函数的坐标位置上（以此为坐标原点）重新构图。
δ(t)的频谱：具有无限宽广的频谱，在全部的频段上都是等强度，是抱负的白噪声。
周期性单位脉冲序列的频谱：若时域中脉冲间隔为T，则频域中也为脉冲间隔，间隔为1/T；时域中脉冲幅值为1，频域中幅值为1/T。
时域只要是周期性的，频谱就是离散的。
4-4信号的频域分析-非周期信号频域分析
式中t0为任意实数
✓ 证明： F[ f (t t0 )] f (t t0 )ejt dt
令x = tt0，则dx = dt，代入上式可得
F[
f
(t
t0
)]
f (x)ej(t0 x)dx
F ( j) e jt0
信号在时域中的时移，对应频谱函数在频域 中产生的附加相移，而幅度频谱保持不变。 8
f
(t)
d
d
e jt
d
[(
jt)
f
(t )]e
jt
dt
将上式两边同乘以j得
j
dF( j) d
[t
f
(t)]
e jt
dt
23
例4 试求单位斜坡信号tu(t)的频谱。
解： 已知单位阶跃信号傅里叶变换为:
F[u(t)] π () 1 j
故利用频域微分特性可得:
F[tu(t)] j d [π () 1 ] π () 1
又因为
F
t
f1
(
)d
F[
f
(t)
f
()]
F(
j)
2f
() ()
整理即得结果.
22
9. 频域微分特性
若 f (t) F F ( j)
则t f (t) F j dF( j) d
t n f (t) F jn dF n ( j) d n
证明： F(j) f (t)ejt dt
dF( j) d
30
12. 非周期信号的能量谱密度
帕什瓦尔能量守恒定理：
f
2 (t)dt
1 2π
|
F( j) |2
d
定义单位角频率的信号能量为能量频谱密度
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
当f(t)为实偶函数时，有
F(j) = F*(j) ， F(j)是的实偶函数
当f(t)为实奇函数时，有
F(j) = F*(j) ， F(j)是的虚奇函数
3. 时移特性
若f (t) F F ( j) 则f (t t0 ) F F ( j) e jt0
式中t0为任意实数
证明： F[ f (t t0 )] = f (t t0 )ejt dt
令x = tt0，则dx = dt，代入上式可得
F[
f
(t
t0
)]
=
f (x)ej(t0 x)dx
= F ( j) e jt0
信号在时域中的时移，对应频谱函数在频域 中产生的附加相移，而幅度频谱保持不变。
j)
=
A
Sa(
)
2
应用频移特性可得
F[ f (t) cos 0t]
=
1 2
F[
j(
0
)]
1 2
F[
j(
0
)]
= A {Sa ( 0 ) Sa ( 0 ) }22 Nhomakorabea2
例 试求矩形脉冲信号f(t)与余弦信号cos0 t相
乘后信号的频谱函数。
解:
f (t)
例 试求图示延时矩形脉冲信号f1(t)的频
谱函数F1(j)。
f1 (t )
A
f (t)
A
0
T
t
0
t
2
2
解： 无延时且宽度为 的矩形脉冲信号f(t) 如图，
其对应的频谱函数为
F( j) = A Sa( )
2
因为 f1(t) = f (t T ) 故，由延时特性可得
F1 ( j) = F ( j)e jT
证明：
F[ f1(t) f2 (t)] = [ f1( ) f2 (t )d ]ejt dt = f1( )[ f2 (t )ejt dt]d
= f1( )F2 ( j)ej d = F1 ( j) F2 ( j)
|F(j)| = |F(j)| ， () = ()
FR ( j) = FR ( j), FI ( j) = FI ( j)
2. 共轭对称特性
若 f (t) F F ( j)
则 f * (t) F F * ( j) f * (t) F F * ( j)
同理
F[
f
(t) sin 0t] =
1 2j
F[
f
(t)e j0t
]
1 2j
F[
f
(t)e j0t
]
=
j 2
F[
j(
0
)]
j 2
F[ j(
0
)]
例 试求矩形脉冲信号f(t)与余弦信号cos0 t相
乘后信号的频谱函数。
解: 已知宽度为的矩形脉冲信号对应的频谱函数为
F
(
=
f (t)e j(0 )t dt
= F[ j( 0 )]
6. 频移特性（调制定理）
F[ f
(t) cos 0t]
=
1 2
F[
f
(t)e j0t
]
1 2
F[ f
(t )e j0t
]
=
1 2
F[ j(
0
)]
1 2
F[ j(
0
)]
信号f(t)与余弦信号cos0 t相乘后，其频谱是将 原来信号频谱向左右搬移0，幅度减半。
2. 共轭对称特性
若 f (t) F F ( j)
则 f * (t) F F * ( j) f * (t) F F * ( j) F(j)为复数，可以表示为
F ( j) = F ( j) e j() = FR ( j) jFI ( j) 当f(t)为实函数时，有
4π 2π 2π 4π
f () A
0
2
2
6. 频移特性（调制定理）
若
f (t) F F ( j)
则
f (t) e j0t F F[ j( 0 )]
式中0为任意实数
证明：由傅里叶变换定义有
F[ f (t) e j0t ] = f (t)e j0t ejt dt
= A Sa( )ejT
2
4. 展缩特性
若f (t) F F ( j)
则f (at) F 1 F ( j )
aa
证明:
F[
f
(at)]
=
f (at)ejt dt
令 x = at，则 dx = adt ，代入上式可得
F[ f (at)] =
1 a
t
44
0
F ( ) A
2 0 2
1 F(1)
22
1 A
2
4
0
4
5. 互易对称特性
若f (t) F F ( j)
f (t)
A
则F ( jt) F 2πf ()
F(j) A
0
t
2
2
F(jt)/2
A
t
4π 2π 2π 4π
傅立叶变换的基本性质
1. 线性特性 2. 共轭对称特性 3. 对称互易特性 4. 展缩特性 5. 时移特性 6. 频移特性
7. 时域卷积特性 8. 频域卷积特性 9. 时域微分特性 10. 积分特性 11. 频域微分特性 12. 能量定理
1. 线性特性
若f1 (t) F F1 ( j)； f 2 (t) F F2 ( j)， 则af1 (t) bf 2 (t) F aF1 ( j) bF2 ( j) 其中a和b均为常数。
j x
f (x)e a dx =
1
F(j)
aa
时域压缩，则频域展宽；展宽时域，则频域压缩。
4. 展缩特性 若f (t) F F( j) 则f (at) F 1 F( j ) aa
f (1 t) 2
2F (2 ) 2 A
t
0
f (t)
t
2
2
f (2t)
A
A
F ( j)
A
/2 0
/2
t
f (t) cos0t
A
/2
/2
t
0
0
F[ f (t) cos(0t)]
A/2
0
0
7. 时域卷积特性
若f1 (t) F F1 ( j)
f 2 (t) F F2 ( j)
则f1 (t) f 2 (t) F F1 ( j) F2 ( j)
F(j) = F*(j) ， F(j)是的实偶函数
当f(t)为实奇函数时，有
F(j) = F*(j) ， F(j)是的虚奇函数
3. 时移特性
若f (t) F F ( j) 则f (t t0 ) F F ( j) e jt0
式中t0为任意实数
证明： F[ f (t t0 )] = f (t t0 )ejt dt
令x = tt0，则dx = dt，代入上式可得
F[
f
(t
t0
)]
=
f (x)ej(t0 x)dx
= F ( j) e jt0
信号在时域中的时移，对应频谱函数在频域 中产生的附加相移，而幅度频谱保持不变。
j)
=
A
Sa(
)
2
应用频移特性可得
F[ f (t) cos 0t]
=
1 2
F[
j(
0
)]
1 2
F[
j(
0
)]
= A {Sa ( 0 ) Sa ( 0 ) }22 Nhomakorabea2
例 试求矩形脉冲信号f(t)与余弦信号cos0 t相
乘后信号的频谱函数。
解:
f (t)
例 试求图示延时矩形脉冲信号f1(t)的频
谱函数F1(j)。
f1 (t )
A
f (t)
A
0
T
t
0
t
2
2
解： 无延时且宽度为 的矩形脉冲信号f(t) 如图，
其对应的频谱函数为
F( j) = A Sa( )
2
因为 f1(t) = f (t T ) 故，由延时特性可得
F1 ( j) = F ( j)e jT
证明：
F[ f1(t) f2 (t)] = [ f1( ) f2 (t )d ]ejt dt = f1( )[ f2 (t )ejt dt]d
= f1( )F2 ( j)ej d = F1 ( j) F2 ( j)
|F(j)| = |F(j)| ， () = ()
FR ( j) = FR ( j), FI ( j) = FI ( j)
2. 共轭对称特性
若 f (t) F F ( j)
则 f * (t) F F * ( j) f * (t) F F * ( j)
同理
F[
f
(t) sin 0t] =
1 2j
F[
f
(t)e j0t
]
1 2j
F[
f
(t)e j0t
]
=
j 2
F[
j(
0
)]
j 2
F[ j(
0
)]
例 试求矩形脉冲信号f(t)与余弦信号cos0 t相
乘后信号的频谱函数。
解: 已知宽度为的矩形脉冲信号对应的频谱函数为
F
(
=
f (t)e j(0 )t dt
= F[ j( 0 )]
6. 频移特性（调制定理）
F[ f
(t) cos 0t]
=
1 2
F[
f
(t)e j0t
]
1 2
F[ f
(t )e j0t
]
=
1 2
F[ j(
0
)]
1 2
F[ j(
0
)]
信号f(t)与余弦信号cos0 t相乘后，其频谱是将 原来信号频谱向左右搬移0，幅度减半。
2. 共轭对称特性
若 f (t) F F ( j)
则 f * (t) F F * ( j) f * (t) F F * ( j) F(j)为复数，可以表示为
F ( j) = F ( j) e j() = FR ( j) jFI ( j) 当f(t)为实函数时，有
4π 2π 2π 4π
f () A
0
2
2
6. 频移特性（调制定理）
若
f (t) F F ( j)
则
f (t) e j0t F F[ j( 0 )]
式中0为任意实数
证明：由傅里叶变换定义有
F[ f (t) e j0t ] = f (t)e j0t ejt dt
= A Sa( )ejT
2
4. 展缩特性
若f (t) F F ( j)
则f (at) F 1 F ( j )
aa
证明:
F[
f
(at)]
=
f (at)ejt dt
令 x = at，则 dx = adt ，代入上式可得
F[ f (at)] =
1 a
t
44
0
F ( ) A
2 0 2
1 F(1)
22
1 A
2
4
0
4
5. 互易对称特性
若f (t) F F ( j)
f (t)
A
则F ( jt) F 2πf ()
F(j) A
0
t
2
2
F(jt)/2
A
t
4π 2π 2π 4π
傅立叶变换的基本性质
1. 线性特性 2. 共轭对称特性 3. 对称互易特性 4. 展缩特性 5. 时移特性 6. 频移特性
7. 时域卷积特性 8. 频域卷积特性 9. 时域微分特性 10. 积分特性 11. 频域微分特性 12. 能量定理
1. 线性特性
若f1 (t) F F1 ( j)； f 2 (t) F F2 ( j)， 则af1 (t) bf 2 (t) F aF1 ( j) bF2 ( j) 其中a和b均为常数。
j x
f (x)e a dx =
1
F(j)
aa
时域压缩，则频域展宽；展宽时域，则频域压缩。
4. 展缩特性 若f (t) F F( j) 则f (at) F 1 F( j ) aa
f (1 t) 2
2F (2 ) 2 A
t
0
f (t)
t
2
2
f (2t)
A
A
F ( j)
A
/2 0
/2
t
f (t) cos0t
A
/2
/2
t
0
0
F[ f (t) cos(0t)]
A/2
0
0
7. 时域卷积特性
若f1 (t) F F1 ( j)
f 2 (t) F F2 ( j)
则f1 (t) f 2 (t) F F1 ( j) F2 ( j)