第二章 编程坐标系与数值计算
- 格式：ppt
- 大小：626.00 KB
- 文档页数：22
下载文档原格式
合集下载
解释说明编程坐标系
解释说明编程坐标系编程坐标系是一种用来描述和定位图形或对象在二维或三维空间中位置的系统。
它是计算机图形学和计算机编程中非常重要的概念，对于开发各种应用程序和游戏有着广泛的应用。
编程坐标系能够帮助开发者准确地控制和操作图形或对象的位置、旋转、缩放等属性，从而实现各种视觉效果和交互功能。
在二维空间中，编程坐标系一般采用笛卡尔坐标系，也就是直角坐标系。
它由两个坐标轴组成，通常为水平的x轴和垂直的y轴。
原点(0,0)表示坐标系的起始位置，x轴表示水平方向的位置，y轴表示垂直方向的位置。
通过指定坐标点的x和y值，开发者可以确定图形或对象在平面上的位置。
在三维空间中，编程坐标系一般使用笛卡尔坐标系的扩展，也就是三维笛卡尔坐标系。
它由三个坐标轴组成，分别为水平的x轴、垂直的y轴和垂直于平面的z轴。
原点(0,0,0)表示坐标系的起始位置，x、y和z轴分别表示三个方向上的位置。
通过指定坐标点的x、y和z 值，开发者可以确定图形或对象在空间中的位置。
在编程中，开发者可以使用不同的编程语言和工具来操作编程坐标系。
例如，在网页开发中，可以使用HTML5的Canvas元素和JavaScript来操作二维坐标系。
可以使用CSS3的3D转换和变换属性来操作三维坐标系。
还可以使用计算机图形学库如OpenGL或Unity来进行更复杂的图形操作和计算。
同时，为了方便开发者的使用，编程坐标系通常还提供了一些函数和方法来操作图形或对象的位置和属性。
比如，在二维坐标系中，可以使用translate()函数来移动图形的位置，rotate()函数来旋转图形，scale()函数来缩放图形的大小。
在三维坐标系中，也有类似的函数和方法供开发者使用。
总之，编程坐标系是计算机图形学和计算机编程中的基础概念，它可以帮助开发者准确地操作图形或对象的位置和属性，实现各种视觉效果和交互功能。
掌握编程坐标系的概念和使用方法，对于开发者来说是非常有指导意义的，可以帮助他们更好地实现自己的编程目标。
第二章 数控编程基础
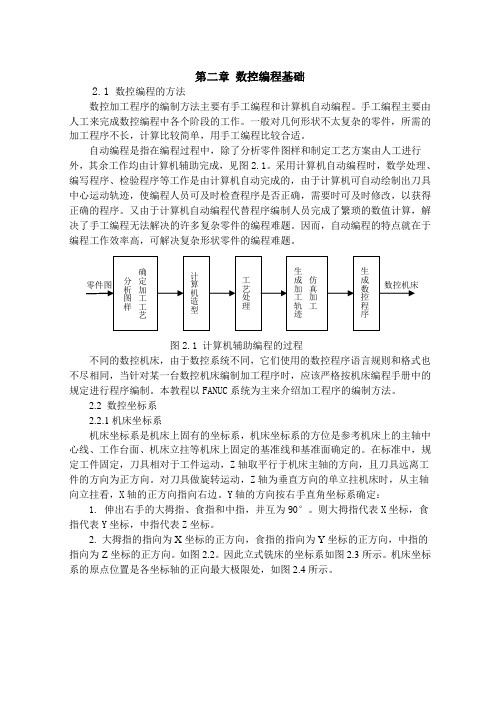
第二章数控编程基础2.1 数控编程的方法数控加工程序的编制方法主要有手工编程和计算机自动编程。
手工编程主要由人工来完成数控编程中各个阶段的工作。
一般对几何形状不太复杂的零件，所需的加工程序不长，计算比较简单，用手工编程比较合适。
自动编程是指在编程过程中，除了分析零件图样和制定工艺方案由人工进行外，其余工作均由计算机辅助完成，见图2.1。
采用计算机自动编程时，数学处理、编写程序、检验程序等工作是由计算机自动完成的，由于计算机可自动绘制出刀具中心运动轨迹，使编程人员可及时检查程序是否正确，需要时可及时修改，以获得正确的程序。
又由于计算机自动编程代替程序编制人员完成了繁琐的数值计算，解决了手工编程无法解决的许多复杂零件的编程难题。
因而，自动编程的特点就在于编程工作效率高，可解决复杂形状零件的编程难题。
图2.1 计算机辅助编程的过程不同的数控机床，由于数控系统不同，它们使用的数控程序语言规则和格式也不尽相同，当针对某一台数控机床编制加工程序时，应该严格按机床编程手册中的规定进行程序编制。
本教程以FANUC系统为主来介绍加工程序的编制方法。
2.2 数控坐标系2.2.1机床坐标系机床坐标系是机床上固有的坐标系，机床坐标系的方位是参考机床上的主轴中心线、工作台面、机床立拄等机床上固定的基准线和基准面确定的。
在标准中，规定工件固定，刀具相对于工件运动，Z轴取平行于机床主轴的方向，且刀具远离工件的方向为正方向。
对刀具做旋转运动，Z轴为垂直方向的单立拄机床时，从主轴向立拄看，X轴的正方向指向右边。
Y轴的方向按右手直角坐标系确定：1. 伸出右手的大拇指、食指和中指，并互为90°。
则大拇指代表X坐标，食指代表Y坐标，中指代表Z坐标。
2. 大拇指的指向为X坐标的正方向，食指的指向为Y坐标的正方向，中指的指向为Z坐标的正方向。
如图2.2。
因此立式铣床的坐标系如图2.3所示。
机床坐标系的原点位置是各坐标轴的正向最大极限处，如图2.4所示。
第二章_数控加工编程基础
2.2 编程的基础知识
2.辅助功能M代码 M指令构成：
地址码M后跟2位数字组成，从M00-M99共100种。
(1) M00—程序停止。
(2) M01—计划（任选）停止。 程序运行前，在操作面板上按下“任选停止” 键时，
才执行M01指令，主轴停转、进给停止、冷却液关 断、程序停止执行。若“任选停止”处于无效状态 时，M01指令不起作用。利用启动按钮才能再次自 动运转，继续执行下一个程序段。
零件图纸
图纸工艺分析 确定工艺过程
数值计算
修
编写程序
改
制备控制介质
校验和试切 错误
4、制备控制介质
将程序单上的内容，经转 换记录在控制介质上，作为 数控系统的输入信息。 注意：若程序较简单，也可 直接通过键盘输入。
零件图纸
图纸工艺分析 确定工艺过程
数值计算
修
编写程序
改
制备控制介质
校验和试切 错误
5、程序的校验和试切
轴转动的圆进给坐标轴分别 用A、B、C表示。
坐标轴正向：由右手螺旋 法则而定。
右手直角笛卡尔坐标系
数控机2.床2的进编给程运动的是基相对础运动知。Y识
具体规定：
①坐标系是假定工件 不动，刀具相对于 工件做进给运动的 坐标系。
+B
X、Y、Z
Y
+A X
Z +C
②以增大工件与刀具
之间距离的方向为 坐标轴的正方向。 Z
a. 在刀具旋转的机床上（铣床、钻床、镗床）
Z轴水平时（卧式），则从刀具(主轴)向工件看时， X坐标的正方向指向右边。
＋X
Z轴垂直时（立式），对单立柱机床，面向刀具主轴 向立柱看时， X轴的正方向指向右边
MATLAB数值计算教程
MATLAB数值计算教程第一章：MATLAB入门1.1 MATLAB简介MATLAB（Matrix Laboratory）是一款强大的数值计算软件，广泛用于工程、科学和金融领域。
它的特点是简单易用、高效快速，并且拥有丰富的工具箱和函数库。
1.2 MATLAB环境搭建要使用MATLAB进行数值计算，首先需要安装MATLAB软件，并进行必要的配置。
通过官方网站下载安装程序，根据提示进行安装即可。
安装完成后，打开MATLAB环境，即可开始使用。
1.3 MATLAB基本操作在MATLAB环境中，可以通过命令行窗口输入和执行命令，也可以使用脚本文件进行批量处理。
常用的基本操作包括变量赋值、算术运算、函数调用等。
例如，使用"="符号赋值变量，使用"+"、"-"、"*"、"/"等符号进行算术运算。
第二章：向量和矩阵操作2.1 向量操作在MATLAB中，向量是一种特殊的矩阵，可以通过一组有序的元素构成。
向量可以进行基本的算术运算，如加法、减法、乘法、除法，还可以进行向量的点积、叉积等操作。
可以使用内置函数和运算符来实现。
2.2 矩阵操作矩阵是MATLAB中最常用的数据结构之一，使用矩阵可以进行多个向量的组合和运算。
可以进行矩阵的加法、减法、乘法、除法等操作，也可以进行矩阵的转置、求逆、求特征值等操作。
MATLAB提供了大量的函数和工具箱来支持矩阵的操作。
第三章：数值计算方法3.1 数值积分数值积分是一种用数值方法计算定积分的方法。
在MATLAB 中，可以使用内置函数来进行数值积分，如trapz函数和quad函数。
也可以使用Simpson法则、复合辛普森法等方法实现数值积分。
3.2 数值微分数值微分是一种用数值方法计算导数的方法。
在MATLAB中，可以使用内置函数进行数值微分，如diff函数和gradient函数。
参考答案-《数控机床编程与操作(第四版 数控车床分册)习题册》-A02-3584
（缺少半径 R 值）
……
N150 GOTO 15；
（检索不到 N15 程序段）
N160 G00 X100.0 Y100.0； （程序中的 Y 坐标应改为 Z 坐标）
N170 M05；
N180 M99；
（主程序用 M30 结束）
4．
绝对坐标
增量坐标
坐标点
…
…
…
G00 X0 Z0；
G00 X0 Z0；
O点
…
…
坐标点 … O点 A点 B点 C点 …
第六节 基础编程综合实例
1．
执行的 起点坐标 终点坐标 圆弧半径
程序段
mm
(X、Y)
(X、Y)
号
N50 100.0,100.0 52.0,2.0
N60
52.0,2.0 20.0,2.0
N70
20.0,2.0 20.0,-15.0
进给速度
mm/min
1500 1500 1500
4
C 点相对于 A 点的增量坐标 U 15.0 W 15.0 。 五、简答及计算题 1．相对于每一脉冲信号的机床运动部件的位移量称为脉冲当量，又称最小 设定单位。 2．所谓指令分组，就是将系统中不能同时执行的指令分为一组，并以编程 号区别。 3．56.52m/min。 4．约 1194r/min。
5
G03：表示逆时针圆弧插补。
X Z ：为圆弧的终点坐标值，其值可以是绝对坐标，也可以是增量坐标。
在增量方式下，其值为圆弧终点坐标相对于圆弧起点的增量值。
R 为圆弧半径。在 SIEMENS 系统中，圆弧半径用符号“CR=”表示。
I J K 为圆弧的圆心相对其起点并分别在 X、Y 和 Z 坐标轴上的增量值。
数控加工基本知识
在一次装夹中，尽可能用一把刀加工出可能加工的所有部 位，然后再换刀。专用数控机床和加工中心上常用此法。
2）粗精加工分序法 根据零件的形状、尺寸精度等因素，将零件的粗精加 工分开进行。先粗加工、半精加工，而后精加工。粗精加 工最好间隔一段时间。 3）加工部位分序法
对于加工内容较多、零件轮廓的表面结构差异较大的 零件，可按其结构特点将加工部位分成几个部分，如内型、 外型、平面、曲面等。在一道工序中完成所有相同型面的 加工，然后再在另一道工序中加工其他型面。 4）零件装夹分序法 以一次安装作为一道工序。 总之，加工零件时，其加工工序的划分要视加工零件的具 体情况具体分析。
2）X坐标
X坐标平行于工件的装夹平面，位于水平面内。 a）如果工件做旋转运动，则刀具离开工件的方向为X轴正方向。 b）如果刀具做旋转运动，则分为2种情况： ① Z坐标水平时，观察者沿刀具主轴向工件看 时，+X运动方向 指向右方。 ②Z坐标垂直时，观察者面对刀具主轴向立柱看时，+X运动方向 指向右方。
2）加工工艺分析 加工工艺分析的目的是制定工艺方案，包括：确定工件 的定位基准，夹具的选择及装夹；确定所选用的刀具，安 排合理的走刀路线，选用合理的切削量、进给速度和主轴 转速等切削参数；确定加工过程中是否需要提供冷却液， 是否需要换刀，何时换刀等。在安排工序时，要根据数控 加工的特点按照工序集中的原则，尽可能在一次装夹中完 成所有的加工内容。
2、工步的划分 工步的划分主要从加工精度和效率两方面考虑。合理 的加工工艺，不仅要保证加工出符合图纸要求的零件，而 且要使机床的功能得到充分发挥，因此往往要将一道工序 分为多个工步来加工。 1）按粗加工、精加工分 某一表面的尺寸精度要求较高时，按粗加工、半精加工、 精加工一次完成；位置精度要求较高时，全部加工表面按 粗、精加工分开进行。
2）粗精加工分序法 根据零件的形状、尺寸精度等因素，将零件的粗精加 工分开进行。先粗加工、半精加工，而后精加工。粗精加 工最好间隔一段时间。 3）加工部位分序法
对于加工内容较多、零件轮廓的表面结构差异较大的 零件，可按其结构特点将加工部位分成几个部分，如内型、 外型、平面、曲面等。在一道工序中完成所有相同型面的 加工，然后再在另一道工序中加工其他型面。 4）零件装夹分序法 以一次安装作为一道工序。 总之，加工零件时，其加工工序的划分要视加工零件的具 体情况具体分析。
2）X坐标
X坐标平行于工件的装夹平面，位于水平面内。 a）如果工件做旋转运动，则刀具离开工件的方向为X轴正方向。 b）如果刀具做旋转运动，则分为2种情况： ① Z坐标水平时，观察者沿刀具主轴向工件看 时，+X运动方向 指向右方。 ②Z坐标垂直时，观察者面对刀具主轴向立柱看时，+X运动方向 指向右方。
2）加工工艺分析 加工工艺分析的目的是制定工艺方案，包括：确定工件 的定位基准，夹具的选择及装夹；确定所选用的刀具，安 排合理的走刀路线，选用合理的切削量、进给速度和主轴 转速等切削参数；确定加工过程中是否需要提供冷却液， 是否需要换刀，何时换刀等。在安排工序时，要根据数控 加工的特点按照工序集中的原则，尽可能在一次装夹中完 成所有的加工内容。
2、工步的划分 工步的划分主要从加工精度和效率两方面考虑。合理 的加工工艺，不仅要保证加工出符合图纸要求的零件，而 且要使机床的功能得到充分发挥，因此往往要将一道工序 分为多个工步来加工。 1）按粗加工、精加工分 某一表面的尺寸精度要求较高时，按粗加工、半精加工、 精加工一次完成；位置精度要求较高时，全部加工表面按 粗、精加工分开进行。
数控编程数字知识点总结
数控编程数字知识点总结一、数学知识点1. 数学坐标系：数控编程中常用的坐标系包括直角坐标系和极坐标系。
直角坐标系是以x、y、z轴作为基准，极坐标系是以半径和角度作为坐标系。
掌握坐标系的转换和运算是进行数控编程的基础。
2. 几何知识：数控编程需要对机械加工中的图形和尺寸有所了解，掌握几何学的知识可以帮助程序员有效地进行加工路径的规划和分析。
3. 数值计算：在数控编程中需要进行各种数值计算，如坐标位置计算、插补算法等。
熟练掌握数值计算方法对于编写高效的数控程序至关重要。
4. 三角函数：在数控编程中经常用到三角函数，如正弦、余弦、正切等，在进行坐标变换和路径规划时会用到这些数学函数。
5. 插值算法：数控编程中的插值算法包括线性插补、圆弧插补、螺旋线插补等，这些算法需要依靠数学计算来实现，并且对于不同的机床和加工要求有不同的应用方法。
二、机床加工知识点1. 机床坐标系：不同类型的机床有不同的坐标系设定，掌握各种类型机床的坐标系设定对于正确编写数控程序是至关重要的。
2. 加工工艺参数：数控编程需要了解工件材料的特性、工艺要求、刀具选择等加工参数，这些知识对于编写合理的加工程序起着至关重要的作用。
3. 刀具路径规划：在数控编程中需要根据刀具的形状、工艺要求等规划刀具的路径，这需要对机床加工特性有一定的了解。
4. 数控程序格式：数控编程需要将编写好的程序转化成机床可执行的代码格式，了解常见数控程序格式对于正确编写程序是必不可少的。
5. 运动控制原理：在数控编程中需要了解机床的运动控制原理，包括各轴的运动控制方式、坐标系转换等。
三、数控编程语言知识点1. G代码和M代码：G代码是数控编程中描述加工路径的命令代码，M代码是描述机床辅助功能的命令代码，了解G代码和M代码的语法和应用是进行数控编程的基础。
2. 宏变量和系统变量：数控编程中常用的宏变量和系统变量可以帮助程序员在编程过程中自动生成代码，提高编程效率。
3. 子程序和循环：在数控编程中常常需要编写子程序和循环，对于复杂的加工过程，采用子程序和循环可以简化程序编写和管理。
数控第二章
第二章 数控编程基础知识
（6）圆弧插补指令（G02、G03)
指令格式：①用I、J、K指定圆心位置 G02（G03） X__Y__Z__I__J__K__F__；
②用R指定圆心位置 G02（G03） X__Y__Z__R__F__； 功能：以F给定的进给速度，在平面内从当前位置沿圆弧轨迹运动到终点位置。
（2）工件坐标系设定（G92、G50） 指令格式：G92(或G50) X__Y__Z__；
功能：G50和G92是用来设置刀具的对刀点在编程坐标系里的位置的。 G50用于车床 G92用于铣床或车床
第二章 数控编程基础知识
说明： ①X、Y、Z表示编程原点与对刀点的距离。 ②应在刀具的其它运动指令之前使用G92和G50，先设定编程坐标系。 ③系统执行该指令后，刀具并不运动，系统会根据指令中的X、Y、Z 推算出编程原点。
第二章 数控编程基础知识
（6）分配数控加工中的容差，规定编程误差，处理数控机床上的部分工艺指令。 （7）编制加工工艺文件
二、 数控加工工艺分析与设计
数控加工工艺的实质： 就是在分析零件精度和表面粗糙度的基础上，对数控加工的方法、装夹 方式、切削加工进给路线、刀具使用以及切削用量等工艺内容进行正确 合理的选择。
那么，两个坐标系是如何转换的？
对刀点
机床坐标系
编程坐标系
因此，数控机床坐标系统可概述为两系一点。
第二章 数控编程基础知识
四、数控编程的特征点
1.刀位点：刀位点相对运动的轨迹即加工路线，也称编程轨迹。 车刀：刀尖或刀尖圆弧中心 铣刀：刀具端面中心或球心
2.对刀点：是指在加工零件时，刀具相对工件运动的起点。 也称为程序起始点或起刀点。
包括内容
零件轮廓中几何元素的基点 插补线段的节点 刀具中心位置 辅助计算
（6）圆弧插补指令（G02、G03)
指令格式：①用I、J、K指定圆心位置 G02（G03） X__Y__Z__I__J__K__F__；
②用R指定圆心位置 G02（G03） X__Y__Z__R__F__； 功能：以F给定的进给速度，在平面内从当前位置沿圆弧轨迹运动到终点位置。
（2）工件坐标系设定（G92、G50） 指令格式：G92(或G50) X__Y__Z__；
功能：G50和G92是用来设置刀具的对刀点在编程坐标系里的位置的。 G50用于车床 G92用于铣床或车床
第二章 数控编程基础知识
说明： ①X、Y、Z表示编程原点与对刀点的距离。 ②应在刀具的其它运动指令之前使用G92和G50，先设定编程坐标系。 ③系统执行该指令后，刀具并不运动，系统会根据指令中的X、Y、Z 推算出编程原点。
第二章 数控编程基础知识
（6）分配数控加工中的容差，规定编程误差，处理数控机床上的部分工艺指令。 （7）编制加工工艺文件
二、 数控加工工艺分析与设计
数控加工工艺的实质： 就是在分析零件精度和表面粗糙度的基础上，对数控加工的方法、装夹 方式、切削加工进给路线、刀具使用以及切削用量等工艺内容进行正确 合理的选择。
那么，两个坐标系是如何转换的？
对刀点
机床坐标系
编程坐标系
因此，数控机床坐标系统可概述为两系一点。
第二章 数控编程基础知识
四、数控编程的特征点
1.刀位点：刀位点相对运动的轨迹即加工路线，也称编程轨迹。 车刀：刀尖或刀尖圆弧中心 铣刀：刀具端面中心或球心
2.对刀点：是指在加工零件时，刀具相对工件运动的起点。 也称为程序起始点或起刀点。
包括内容
零件轮廓中几何元素的基点 插补线段的节点 刀具中心位置 辅助计算
数控编程数值计算
x xa2 y ya2 2
T
P a
O
② 求圆与曲线旳公切线PT旳斜率k：
k yT yP xT xP
Y=f(x) X
继续
等误差法节点计算(7-6) Y
⑵ 等误差法节点计算
因直线PT为圆弧与曲线
T
旳公切线，且点P(xP，yP)、 P
点T(xT，yT)分别在圆和曲线
a
上，故有：
O
yT yP xPxa xT xP yP ya yT yP f xT xT xP xP xa2 yP ya2 2
结束
直线、圆弧平面轮廓旳基点计算(6-1)
一种零件旳轮
廓曲线可能由不同
旳几何元素构成，
R
如直线、圆弧、非
圆曲线等。基点就
C
是构成零件轮廓旳
B
各相邻几何元素旳
交点或切点，如右
D
图所示。显然，相 邻基点间只能是一 种几何元素。
A
O
a
E
直线、圆弧平面轮廓旳基点计算(6-2)
因为一般数控机床都有具有直线和圆弧插补 功能，故对由直线和圆弧构成旳平面轮廓，都能 够经过调用数控系统旳直线或圆弧插补功能来加 工。此时，需计算出零件上旳全部基点坐标。零 件轮廓上旳基点可根据零件图上旳尺寸标注或经 过较简朴旳计算间接求得。
O为曲线旳曲率中心,连接fO和gO
h
g′
f
gห้องสมุดไป่ตู้
O Rmin
y=f(x)
X
因为δ很小，能够将曲线fg′g看成是半径为Rmin旳一段 圆弧。故有：
(h/2)2=Rmin2-(Rmin-δ)2 =2×Rmin×δ-δ2 ∴ h≈(8Rminδ)1/2
继续
等步长法节点计算(7-3)
T
P a
O
② 求圆与曲线旳公切线PT旳斜率k：
k yT yP xT xP
Y=f(x) X
继续
等误差法节点计算(7-6) Y
⑵ 等误差法节点计算
因直线PT为圆弧与曲线
T
旳公切线，且点P(xP，yP)、 P
点T(xT，yT)分别在圆和曲线
a
上，故有：
O
yT yP xPxa xT xP yP ya yT yP f xT xT xP xP xa2 yP ya2 2
结束
直线、圆弧平面轮廓旳基点计算(6-1)
一种零件旳轮
廓曲线可能由不同
旳几何元素构成，
R
如直线、圆弧、非
圆曲线等。基点就
C
是构成零件轮廓旳
B
各相邻几何元素旳
交点或切点，如右
D
图所示。显然，相 邻基点间只能是一 种几何元素。
A
O
a
E
直线、圆弧平面轮廓旳基点计算(6-2)
因为一般数控机床都有具有直线和圆弧插补 功能，故对由直线和圆弧构成旳平面轮廓，都能 够经过调用数控系统旳直线或圆弧插补功能来加 工。此时，需计算出零件上旳全部基点坐标。零 件轮廓上旳基点可根据零件图上旳尺寸标注或经 过较简朴旳计算间接求得。
O为曲线旳曲率中心,连接fO和gO
h
g′
f
gห้องสมุดไป่ตู้
O Rmin
y=f(x)
X
因为δ很小，能够将曲线fg′g看成是半径为Rmin旳一段 圆弧。故有：
(h/2)2=Rmin2-(Rmin-δ)2 =2×Rmin×δ-δ2 ∴ h≈(8Rminδ)1/2
继续
等步长法节点计算(7-3)
实际应用中的坐标系及其相关计算
实际应用中的坐标系及其相关计算在数学中，坐标系是一个重要的概念，它在实际应用中有着广泛的应用。
无论是在几何学、物理学、经济学还是其他学科中，我们都可以看到坐标系的身影。
通过坐标系，我们可以准确地描述和计算各种实际问题，使得我们能够更好地理解和解决这些问题。
一、直角坐标系直角坐标系是最常见的坐标系之一。
它由两条相互垂直的坐标轴组成，通常称为x轴和y轴。
在直角坐标系中，我们可以用有序数对(x, y)来表示一个点的位置。
其中，x代表点在x轴上的位置，y代表点在y轴上的位置。
例如，点A的坐标为(2, 3)，表示它在x轴上的位置是2，在y轴上的位置是3。
在实际应用中，直角坐标系可以帮助我们解决很多问题。
例如，在几何学中，我们可以通过直角坐标系计算两点之间的距离。
假设有两个点A(2, 3)和B(5, 7)，我们可以使用勾股定理来计算它们之间的距离。
根据勾股定理，我们有：AB² = (5-2)² + (7-3)²= 3² + 4²= 9 + 16= 25因此，AB的距离等于5。
二、极坐标系除了直角坐标系，还有一种常用的坐标系是极坐标系。
极坐标系由一个原点O和一个极轴组成，极轴通常与x轴重合。
在极坐标系中，我们用有序数对(r, θ)来表示一个点的位置。
其中，r代表点到原点O的距离，θ代表点与极轴正方向的夹角。
极坐标系在实际应用中也有很多用途。
例如，在物理学中，我们可以使用极坐标系描述一个物体的运动轨迹。
假设一个物体以恒定的速度沿着一个圆形轨道运动，我们可以使用极坐标系来描述它的位置。
设物体到原点O的距离为r，物体与极轴正方向的夹角为θ。
根据物体的运动规律，我们可以得到它的位置关系：r = r₀θ = ωt其中，r₀为物体的初始距离，ω为物体的角速度，t为时间。
通过这些关系，我们可以计算出物体在任意时刻的位置。
三、三维坐标系除了二维的直角坐标系和极坐标系，还有一种常用的坐标系是三维坐标系。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第二章 数控车床加工工艺设计
上节回顾一、
1、遵循右手笛卡儿直角坐标系 2、永远假设工件是静止的，刀具相 对于工件运动。 3、刀具远离工件的方向为正方向。
第二章 数控车床加工工艺设计
上节回顾二、
1、先确定Z轴。 a、传递主要切削力的主轴为Z轴。 b、若没有主轴，则Z轴垂直于工件装夹面。 c、若有多个主轴，选择一个垂直于工件装夹面的主轴为Z轴。
第二章 数控车床加工工艺设计
【实例】 在CK6150型数控车床上加工一个轴类零件，零件图2-7所示， 其中ø80的外径不加工(可用于装夹)。
图2-7 轴类零件加工实例 (1)确定工件的装夹方式及加工工艺路线 由于这个工件是一个实心轴， 并且轴的长度不很长，所以采用工件的左端面和ø80外圆作为定位基准。 使用普通三爪自定心卡盘夹紧工件，取卡盘的端面中心为工件坐标系的 原点，如图2-7所示。 加工顺序为：①倒角粗车M36×4螺纹外圆、ø50外圆，R35圆弧面
３）编程原点要尽量与设计基准或工艺基准统一，以利于保 证加工精度。
第二章 数控车床加工工艺设计
2.3.1确定编程坐标系，选择编程原点 原点选择要尽量满足编程简单，尺寸换算少，引
起的加工误差小等条件。
一般情况下，以坐标式尺寸标注的零件，程序原 点应选在尺寸标注的基准点；对称零件或以同心圆 为主的零件，程序原点应选在对称中心线或圆心上。
2、再确定X轴。（X轴始终水平，且平行于工件装夹面） a、没有回转刀具和工件，X轴平行于主要切削方向。（牛头刨） b、有回转工件，X轴是径向的，且平行于横滑座。（车、磨） c、有刀具回转的机床，分以下三类： Z轴水平，由刀具主轴向工件看，X轴水平向右。 Z轴垂直，由刀具主轴向立柱看，X轴水平向右。 龙门机床，由刀具主轴向左侧立柱看，X轴水平向右。
5）轴套类零件安排走刀路线的原则是轴向走刀、径向进刀，循 环切除余量的循环终点在粗加工起点附近，这样可以减少走刀 次数，避免不必要的空走刀，节省加工时间。
6）轮盘类零件安排走刀路线的原则是径向走刀、轴向进刀，循 环去除余量的循环终点在加工起点。编制轮盘类零件的加工程 序时，与轴套类零件相反，是从大直径端开始顺序向前。
第二章 数控车床加工工艺设计
由于数控车床加工的零件都是回转体，径向尺寸都是关 于轴线对称的，所以，车削件的X坐标原点应取在零件加工 面的回转中心，即零件的轴线上， Z坐标原点可以选在工件 的右端面或左端面，对于左右对称的零件，还可以选在对称 中心。Z坐标原点放在右端面有利于对刀，当刀具离开工件 时，Z坐标为正值；当刀具进入工件加工时，Z坐标为负值， 有利于程序检查。
①外圆车刀02号坐标 x＝2×(170－35)＝270 Z＝450－5－(40－25)＝430
②切槽刀04号坐标 x＝2×(170－30)＝280 Z＝450－(40－25)＝435 ③螺纹车刀06号坐标 x＝2×(170－25)＝290 Z＝450+5－(40－25)＝440
第二章 数控车床加工工艺设计
3、最后确定Y轴。按右手笛卡儿直角坐标系确定。
第二章 数控车床加工工艺设计
2.3 编程坐标系与数值计算
确定编程坐标系的原点最根本的原则有以下三条：
１）编程原点的选择要便于坐标计算。尽量选择能直观地确 定零件基点坐标值的一些特殊点为坐标原点，可以简化计算 的工作量，也便于程序检查。
２）编程原点的选择要便于加工中的对刀。因为对刀的目的 是要确定编程原点在工件毛坯上的位置，即找出该点在机床 坐标系中的坐标值，使图样上的编程坐标系转化为加工中的 工件坐标系。
第二章 数控车床加工工艺设计
2.3.4 相对坐标与绝对坐标计算的应用 坐标的表示方法有两种：绝对方式和相对方式。绝对坐标指的是坐标的 计算以坐标原点为起点。而相对坐标指的是坐标的计算以刀具运动的上 一点为起点。
【实例】 如图2-5所示的零件，假设刀具按ABCDE的顺序走刀，则用绝对
方式表示的各点坐标为：
选择绝对坐标系与相对坐标系的应用特点：
1）采用绝对坐标系计算时各计算坐标点位置间不会 产生累积误差，但有些数控系统需进行两种坐标尺 寸方式之间的数值换算。
2）增量坐标系运算简便且直接，并与数控装置以增 量值进行数字控制的方式相一致，当采用平面解析 几何计算法以外的各种常用计算法解得的各基点坐 标，可以不经换算而直接用于加工程序段。
这是一个比较复杂的工件，包括了外圆、内孔、端面、环槽、外 锥螺纹、C轴定位和铣削等加工内容，在带有三轴控制的数控车 削中心上完成该零件的加工，可以按照外圆、端面、毛坯等加工 路线方法去设计，读者可自行设计加工路线。
编程坐标原点的选择也会影响坐标计算的难易，如果零 件轮廓中包含有椭圆、抛物线等曲线，则应把坐标原点放在 其对称中心上，可以简化曲线的方程，使计算变得简单。
第二章 数控车床加工工艺设计
2.3.2基点坐标的计算
1）基点的含义 构成零件轮廓的不同几何素线的交点或切点称为
基点。基点可以直接作为其运动轨迹的起点或终点。 显然，基点坐标是编程中需要的重要数据。
A（16，100）；B（32，80）；C（32，60）；D(40，40)；E（40，0）
用相对坐标表示的各点坐标为（假设刀具从A点起刀）： A（0，0）；B（16，－20）；C（0，－20）；D（8，－20）；E（0，－
40）。即相对坐标计算的是后一点在各坐标方向上与前一点的增量。
第二章 数控车床加工工艺设计
第二章 数控车床加工工艺设计
2）基点坐标直接计算的内容
基点直接计算的方法比较简单，一般可根据零件图样所 给的已知条件用人工完成。即依据零件图样上给定的尺寸运 用代数、三角、几何或解析几何的有关知识，直接计算出数 值。在计算时，要注意小数点后的位数要留够，以保证足够 的精度 。现以下图所示的零件为例，说明当零件由直线和 圆弧两种曲线组成时，基点坐标的计算方法。（以直径编程 为例，X坐标用点所在圆的直径表示
在数控车床上加工轴类零件的方法，遵循“先粗后精”、“由大到小” 等基本原则。先对工件整体进行粗加工，然后进行半精车、精车。如果 在半精车与精车之间不安排热处理工序，则半精车和精车就可以在一次 装夹中完成。 在车削时，先从工件的最大直径处开始车削，然后依次往小直径处进行 加工。在数控机床上精车轴类工件时，往往从工件的最右端开始连续不 间断地完成整个工件的切削。
第二章 数控车床加工工艺设计
Z=－82.641，半径为30，则圆的方程为：
(X－20）2+(Z+82.641)2=302………………⑴
直线BC的斜率为k=tg120°=－1.732，经过点B，则直线BC的
方程为：
X－20=1.732(Z+48)………………………..⑵
由⑴、⑵两式联立方程组即可求得：
2．圆锥面的加工路线 加工圆锥面有两种进给路线，一种如图2-11 a） 所示，切削路线与锥面始终平行，另一种如图2-11 b)所示，切削锥 度由小逐渐接近最终锥度。图a加工质量较好，但编程计算较多， 图b编程简单，但加工质量较差。
a）加工质量较好
b）加工质量较差
图2-11 圆锥面的加工路线
3．圆弧面的加工路线 加工圆弧面通常有同心圆、三角形、矩形等方 式的加工路线，如图2-12，不同形式的切削路线有不同的特点。图 2-12 a）编程计算较为复杂，精加工时切削余量较大；图2-12b）切 削时受力较均匀，编程较方便；图2-12c）编程计算量大，精加工 刀具受力不均匀。
X=35 Z=－56.6603 则C点坐标为：XC=70，ZC=－56.660。
注意列方程时，X坐标用半径表示，解出答案后，表示点编 程坐标时用直径表示。
第二章 数控车床加工工艺设计
2.3.3 节点坐标的计算
逼近线段与被加工曲线的交点就称为节点
１）节点的定义
当采用不具备非圆曲线插补功能的数控机床加工非圆曲线轮廓的零 件时，在加工程序的编制工作中，常用多个直线段或圆弧去近似代 替非圆曲线，这称为拟合处理。拟合线段的交点或切点称为节点。
7）铸锻件毛坯形状与加工后零件形状相似，留有—定的加工余 量。一般采用逐渐接近最终形状的循环切削加工方法加工。
第二章 数控车床加工工艺设计
2.4.2 常用加工路线的确定方法
1．圆柱表面的加工路线 1）轴类零件（长L与直径D之比L：D≥1的零件）：采用沿Z坐标方向切削 加工，X方向进刀、退刀的矩形循环进给路线。
２）节点坐标的计算
节点坐标的计算难度和工作量都较大，故常通过计算机完成，必要 时也可由人工计算,常用的有直线逼近法（等间距法、等步长法、和 等误差法）和圆弧逼近法。
计算节点坐标时除要列出插补线段方程和被加工曲线的方程外，还 要考虑到插补误差的问题。因现代计算机软件发展很快，节点计算 用人工进行的可能性不大，故本书不介绍插补节点的计算。
2）盘类零件（长L与直径D之比L：D≤1的零件） 采用沿 X坐标方向切削加工，Z方向进刀、退刀的矩形循环进 给路线。如图2-9所示。
图2-9 盘类零件常用加工路线 3）余量分布较均匀的铸件、锻件的加工路线 按零件
形状逐渐接近最终尺寸的“剥皮”式进给路线，如图 2-10所示。
第二章 数控车床加工工艺设计
2）寻求最短加工路线（包括空行程路线和切削加工 路线），减少空刀时间以提高加工效率。
3）选择加工路线时应使工件加工时变形最小，对横 截面积小的细长零件或薄壁零件应采用分几次走刀 或对称去余量法安排进给路线。
第二章 数控车床加工工艺设计
4）数控车削加工过程一般要经过循环切除余量、粗加工和精 加工三道工序，应根据毛坯类型和工件形状确立循环切除余量 的方式，以达到减少循环走刀次数、提高加工效率的目的。
第二章 数控车床加工工艺设计
最终完工的精加工轮廓的进给路线 在安排精加工进给路线时，零件的完工轮廓应由最后一刀连续切削完成，
并且加工刀具的进、退刀位置不要在连续的轮廓中安排切入和切出或 换刀、停顿，以免因切削力突然变化造成弹性变形，致使在已加工面 上产生刀痕缺陷 三、加工路线优化，减少空行程，灵活移动起刀点 在采用矩形循环方式加工阶梯轴时，每循环的起刀点位置不是固定在一点， 而是随加工的位置往前移动，以减少回程时走空刀的时间。如图2-13 所示
上节回顾一、
1、遵循右手笛卡儿直角坐标系 2、永远假设工件是静止的，刀具相 对于工件运动。 3、刀具远离工件的方向为正方向。
第二章 数控车床加工工艺设计
上节回顾二、
1、先确定Z轴。 a、传递主要切削力的主轴为Z轴。 b、若没有主轴，则Z轴垂直于工件装夹面。 c、若有多个主轴，选择一个垂直于工件装夹面的主轴为Z轴。
第二章 数控车床加工工艺设计
【实例】 在CK6150型数控车床上加工一个轴类零件，零件图2-7所示， 其中ø80的外径不加工(可用于装夹)。
图2-7 轴类零件加工实例 (1)确定工件的装夹方式及加工工艺路线 由于这个工件是一个实心轴， 并且轴的长度不很长，所以采用工件的左端面和ø80外圆作为定位基准。 使用普通三爪自定心卡盘夹紧工件，取卡盘的端面中心为工件坐标系的 原点，如图2-7所示。 加工顺序为：①倒角粗车M36×4螺纹外圆、ø50外圆，R35圆弧面
３）编程原点要尽量与设计基准或工艺基准统一，以利于保 证加工精度。
第二章 数控车床加工工艺设计
2.3.1确定编程坐标系，选择编程原点 原点选择要尽量满足编程简单，尺寸换算少，引
起的加工误差小等条件。
一般情况下，以坐标式尺寸标注的零件，程序原 点应选在尺寸标注的基准点；对称零件或以同心圆 为主的零件，程序原点应选在对称中心线或圆心上。
2、再确定X轴。（X轴始终水平，且平行于工件装夹面） a、没有回转刀具和工件，X轴平行于主要切削方向。（牛头刨） b、有回转工件，X轴是径向的，且平行于横滑座。（车、磨） c、有刀具回转的机床，分以下三类： Z轴水平，由刀具主轴向工件看，X轴水平向右。 Z轴垂直，由刀具主轴向立柱看，X轴水平向右。 龙门机床，由刀具主轴向左侧立柱看，X轴水平向右。
5）轴套类零件安排走刀路线的原则是轴向走刀、径向进刀，循 环切除余量的循环终点在粗加工起点附近，这样可以减少走刀 次数，避免不必要的空走刀，节省加工时间。
6）轮盘类零件安排走刀路线的原则是径向走刀、轴向进刀，循 环去除余量的循环终点在加工起点。编制轮盘类零件的加工程 序时，与轴套类零件相反，是从大直径端开始顺序向前。
第二章 数控车床加工工艺设计
由于数控车床加工的零件都是回转体，径向尺寸都是关 于轴线对称的，所以，车削件的X坐标原点应取在零件加工 面的回转中心，即零件的轴线上， Z坐标原点可以选在工件 的右端面或左端面，对于左右对称的零件，还可以选在对称 中心。Z坐标原点放在右端面有利于对刀，当刀具离开工件 时，Z坐标为正值；当刀具进入工件加工时，Z坐标为负值， 有利于程序检查。
①外圆车刀02号坐标 x＝2×(170－35)＝270 Z＝450－5－(40－25)＝430
②切槽刀04号坐标 x＝2×(170－30)＝280 Z＝450－(40－25)＝435 ③螺纹车刀06号坐标 x＝2×(170－25)＝290 Z＝450+5－(40－25)＝440
第二章 数控车床加工工艺设计
3、最后确定Y轴。按右手笛卡儿直角坐标系确定。
第二章 数控车床加工工艺设计
2.3 编程坐标系与数值计算
确定编程坐标系的原点最根本的原则有以下三条：
１）编程原点的选择要便于坐标计算。尽量选择能直观地确 定零件基点坐标值的一些特殊点为坐标原点，可以简化计算 的工作量，也便于程序检查。
２）编程原点的选择要便于加工中的对刀。因为对刀的目的 是要确定编程原点在工件毛坯上的位置，即找出该点在机床 坐标系中的坐标值，使图样上的编程坐标系转化为加工中的 工件坐标系。
第二章 数控车床加工工艺设计
2.3.4 相对坐标与绝对坐标计算的应用 坐标的表示方法有两种：绝对方式和相对方式。绝对坐标指的是坐标的 计算以坐标原点为起点。而相对坐标指的是坐标的计算以刀具运动的上 一点为起点。
【实例】 如图2-5所示的零件，假设刀具按ABCDE的顺序走刀，则用绝对
方式表示的各点坐标为：
选择绝对坐标系与相对坐标系的应用特点：
1）采用绝对坐标系计算时各计算坐标点位置间不会 产生累积误差，但有些数控系统需进行两种坐标尺 寸方式之间的数值换算。
2）增量坐标系运算简便且直接，并与数控装置以增 量值进行数字控制的方式相一致，当采用平面解析 几何计算法以外的各种常用计算法解得的各基点坐 标，可以不经换算而直接用于加工程序段。
这是一个比较复杂的工件，包括了外圆、内孔、端面、环槽、外 锥螺纹、C轴定位和铣削等加工内容，在带有三轴控制的数控车 削中心上完成该零件的加工，可以按照外圆、端面、毛坯等加工 路线方法去设计，读者可自行设计加工路线。
编程坐标原点的选择也会影响坐标计算的难易，如果零 件轮廓中包含有椭圆、抛物线等曲线，则应把坐标原点放在 其对称中心上，可以简化曲线的方程，使计算变得简单。
第二章 数控车床加工工艺设计
2.3.2基点坐标的计算
1）基点的含义 构成零件轮廓的不同几何素线的交点或切点称为
基点。基点可以直接作为其运动轨迹的起点或终点。 显然，基点坐标是编程中需要的重要数据。
A（16，100）；B（32，80）；C（32，60）；D(40，40)；E（40，0）
用相对坐标表示的各点坐标为（假设刀具从A点起刀）： A（0，0）；B（16，－20）；C（0，－20）；D（8，－20）；E（0，－
40）。即相对坐标计算的是后一点在各坐标方向上与前一点的增量。
第二章 数控车床加工工艺设计
第二章 数控车床加工工艺设计
2）基点坐标直接计算的内容
基点直接计算的方法比较简单，一般可根据零件图样所 给的已知条件用人工完成。即依据零件图样上给定的尺寸运 用代数、三角、几何或解析几何的有关知识，直接计算出数 值。在计算时，要注意小数点后的位数要留够，以保证足够 的精度 。现以下图所示的零件为例，说明当零件由直线和 圆弧两种曲线组成时，基点坐标的计算方法。（以直径编程 为例，X坐标用点所在圆的直径表示
在数控车床上加工轴类零件的方法，遵循“先粗后精”、“由大到小” 等基本原则。先对工件整体进行粗加工，然后进行半精车、精车。如果 在半精车与精车之间不安排热处理工序，则半精车和精车就可以在一次 装夹中完成。 在车削时，先从工件的最大直径处开始车削，然后依次往小直径处进行 加工。在数控机床上精车轴类工件时，往往从工件的最右端开始连续不 间断地完成整个工件的切削。
第二章 数控车床加工工艺设计
Z=－82.641，半径为30，则圆的方程为：
(X－20）2+(Z+82.641)2=302………………⑴
直线BC的斜率为k=tg120°=－1.732，经过点B，则直线BC的
方程为：
X－20=1.732(Z+48)………………………..⑵
由⑴、⑵两式联立方程组即可求得：
2．圆锥面的加工路线 加工圆锥面有两种进给路线，一种如图2-11 a） 所示，切削路线与锥面始终平行，另一种如图2-11 b)所示，切削锥 度由小逐渐接近最终锥度。图a加工质量较好，但编程计算较多， 图b编程简单，但加工质量较差。
a）加工质量较好
b）加工质量较差
图2-11 圆锥面的加工路线
3．圆弧面的加工路线 加工圆弧面通常有同心圆、三角形、矩形等方 式的加工路线，如图2-12，不同形式的切削路线有不同的特点。图 2-12 a）编程计算较为复杂，精加工时切削余量较大；图2-12b）切 削时受力较均匀，编程较方便；图2-12c）编程计算量大，精加工 刀具受力不均匀。
X=35 Z=－56.6603 则C点坐标为：XC=70，ZC=－56.660。
注意列方程时，X坐标用半径表示，解出答案后，表示点编 程坐标时用直径表示。
第二章 数控车床加工工艺设计
2.3.3 节点坐标的计算
逼近线段与被加工曲线的交点就称为节点
１）节点的定义
当采用不具备非圆曲线插补功能的数控机床加工非圆曲线轮廓的零 件时，在加工程序的编制工作中，常用多个直线段或圆弧去近似代 替非圆曲线，这称为拟合处理。拟合线段的交点或切点称为节点。
7）铸锻件毛坯形状与加工后零件形状相似，留有—定的加工余 量。一般采用逐渐接近最终形状的循环切削加工方法加工。
第二章 数控车床加工工艺设计
2.4.2 常用加工路线的确定方法
1．圆柱表面的加工路线 1）轴类零件（长L与直径D之比L：D≥1的零件）：采用沿Z坐标方向切削 加工，X方向进刀、退刀的矩形循环进给路线。
２）节点坐标的计算
节点坐标的计算难度和工作量都较大，故常通过计算机完成，必要 时也可由人工计算,常用的有直线逼近法（等间距法、等步长法、和 等误差法）和圆弧逼近法。
计算节点坐标时除要列出插补线段方程和被加工曲线的方程外，还 要考虑到插补误差的问题。因现代计算机软件发展很快，节点计算 用人工进行的可能性不大，故本书不介绍插补节点的计算。
2）盘类零件（长L与直径D之比L：D≤1的零件） 采用沿 X坐标方向切削加工，Z方向进刀、退刀的矩形循环进 给路线。如图2-9所示。
图2-9 盘类零件常用加工路线 3）余量分布较均匀的铸件、锻件的加工路线 按零件
形状逐渐接近最终尺寸的“剥皮”式进给路线，如图 2-10所示。
第二章 数控车床加工工艺设计
2）寻求最短加工路线（包括空行程路线和切削加工 路线），减少空刀时间以提高加工效率。
3）选择加工路线时应使工件加工时变形最小，对横 截面积小的细长零件或薄壁零件应采用分几次走刀 或对称去余量法安排进给路线。
第二章 数控车床加工工艺设计
4）数控车削加工过程一般要经过循环切除余量、粗加工和精 加工三道工序，应根据毛坯类型和工件形状确立循环切除余量 的方式，以达到减少循环走刀次数、提高加工效率的目的。
第二章 数控车床加工工艺设计
最终完工的精加工轮廓的进给路线 在安排精加工进给路线时，零件的完工轮廓应由最后一刀连续切削完成，
并且加工刀具的进、退刀位置不要在连续的轮廓中安排切入和切出或 换刀、停顿，以免因切削力突然变化造成弹性变形，致使在已加工面 上产生刀痕缺陷 三、加工路线优化，减少空行程，灵活移动起刀点 在采用矩形循环方式加工阶梯轴时，每循环的起刀点位置不是固定在一点， 而是随加工的位置往前移动，以减少回程时走空刀的时间。如图2-13 所示