江苏省靖江市2011-2012学年八年级(上)期末数学试题(含答案)

一、选择题（本大题共有8小题，每小题2分，共16分．） 1．如果b a <，下列各式中不．一定．．正确．．的是A ． 11-<-b aB ．b a 33->-C ．b a 11< D ． 44b a < 2．如图，A 、B 是数轴上的亮点，在线段AB 上任取一点C ，则点C 到表示－1的点的距离不大于．．．2的概率是（ ） A ．21 B ．32 C ．43 D ．54(第2题) 3．下列各式中，正确的是A ．22b b a a =B ．22a b a b a b +=++C ．22y y x y x y =++D ．11x y x y=--+-4．如图，数轴上有点O 、A 、B 、C 、D 五点，根据图中个点所表示的数，判断18在数轴上对应的点的位置会落在下列哪一条线段上（ ） A ．OA B ．AB C ．BC D ．CD5．反比例函数y =1―2mx（m 为常数），当0<x 时，y 随x 的增大而增大，则m 的取值范围是 A ．0<mB ．21<m C ．21>m D ．21≥m 6．小刚身高1.7 m ，测得他站立在阳光下的影长为0. 85 m ，紧接着他把手臂竖直举起，测得影长为1.1 m ，那么小刚举起手臂超出头顶 A ．0.5 m B ．0. 55 m C ．0.6 m D ．2.2 m 7．下面命题的逆命题是真命题的是A ．菱形的对角线互相垂直B ．全等三角形是相似三角形C ．等腰三角形的两个底角相等D ．如果ac 2>bc 2，那么a >b8．下列轴对称图形中，只用一把无刻度的直尺（该直尺不能作垂线）不能．．画出对称轴的是 A ．菱形B ．矩形C ．等腰梯形D ．正五边形二、填空题（本大题共有10小题， 每题2分，共20分．）9．当x 满足 ▲ 时，代数式2-x x 有意义；当x 满足 ▲ 时，分式x 2―9x ―3值为0.10．若最简根式1+x 和y3是同类根式，则 x ＋y ＝_ ▲ ____11．若整数m 满足条件2)1(+m ＝1+m 且m ＜52，则m 的值是 ▲ ．12．不等式()22-x ≤2-x 的非负整数解．．．．．为 ▲ . 13．已知a 、b 、c 三条线段，其中2,8a c ==，若线段b 是线段a 、c 的比例中项，则b ＝ ▲ 。

一、选择题（每题3分，共30分）1. 下列各数中，有理数是（）A. √-1B. πC. 2.5D. √92. 已知a、b是实数，且a + b = 0，则a、b互为（）A. 相等B. 相反数C. 绝对值相等D. 无关3. 下列各图中，相似三角形是（）A.B.C.D.4. 下列函数中，是反比例函数的是（）A. y = 2x + 1B. y = x²C. y = 3/xD. y = 2x³5. 已知等腰三角形的底边长为10cm，腰长为8cm，则该三角形的周长是（）A. 16cmB. 18cmC. 26cmD. 32cm6. 若a、b、c是等差数列，且a + b + c = 9，a + c = 7，则b的值为（）A. 2B. 3C. 4D. 57. 下列各式中，能表示平面图形是圆的是（）A. x² + y² = 4B. x² - y² = 1C. x² + y² = 0D. x² + y² = 28. 下列各式中，能表示x轴上的点的是（）A. y = 0B. x = 0C. y = 2xD. y = -x9. 若直角三角形的两条直角边分别为3cm和4cm，则该三角形的斜边长是（）A. 5cmB. 7cmC. 8cmD. 9cm10. 下列各式中，能表示平行四边形面积的是（）A. S = abB. S = ahC. S = abhD. S = ah²二、填空题（每题3分，共30分）11. 已知方程2x - 3 = 5，解得x = _______。

12. 若∠A = 45°，则∠B的度数为_______。

13. 下列各数中，绝对值最小的是_______。

14. 下列各数中，有理数是_______。

15. 已知等差数列的首项为2，公差为3，则第5项的值为_______。

16. 若x² - 4x + 3 = 0，则x的值为_______。

2011—2012学年第一学期期末考试试卷初二数学下列各小题均有4个选项，其中只有一个．．选项是正确的，请你把正确答案的字母序号填在下表中相应题号的下面 1．若分式21x -的值为0，则x 的值为 A ．1B ．1-C ．1±D ．22x 的取值范围是A ．1x >B ．1x ≥C ．1x <D ．1x ≤ 3．已知三角形的两边长分别为3cm 和8cm ，则此三角形的第三边的长可能是 A ．4cmB ．5cmC ．6cmD ．13cm4．如图，AC ∥BD ，AD 与BC 相交于O ，4530A B ∠=∠=，，那么AOB ∠等于 A ．75° B ．60° C ．45° D ．30°5．下列判断中，你认为正确的是 AB ．π是有理数 第4题C xD 26．在某次国际乒乓球单打比赛中，甲、乙两名中国选手进入最后决赛，那么下列事件为必然事件的是A ．冠军属于中国选手B ．冠军属于外国选手C ．冠军属于中国选手甲D ．冠军属于中国选手乙7．下列运算中正确的是A ．623x x x = B ．1x y x y -+=-+C ．22222a ab b a b a b a b +++=--D ．11x xy y+=+8．如图，在Rt △ABC 中，∠C =90︒，AB=4，BC =2, D 为AB 的中点，则△ACD 的面积是 AB．C ．2D ．49．2011年雨季，一场大雨导致一条全长为550米的污水排放管道被冲毁．为了尽量减少施工对城市交通所造成的影响，实际施工时，每天的工效比原计划增加10%，结果提前5天完成这一任务，问原计划每天铺设多少米管道？设原计划每天铺设x 米管道，所列方程正确的是A ．5505505(110%)x x -=+B ．5505505(110%)x x -=+ C ．5505505(110%)x x-=-D ．5505505(110%)x x-=-10.如图，D 是AB 边上的中点，将ABC ∆沿过D 的直线折叠，使点A 落在BC 上F 处，若50B ∠=︒，则BDF ∠度数是 第10题A ．60°B ．70°C ．80°D ．不确定 二、填空题（本题共15分，每小题3分） 11．如图，在ABC △中，∠C 是直角，AD 平分∠BAC 交BC 于点D .如果AB =8，CD =2那么△ABD 的面积 等于 ．12．计算：222233yx y x-÷= ． 第11题 13．如图，ABC △是等边三角形，点D 是BC 边上任意一点，DE AB ⊥于点E ，DF AC ⊥于点F ．若4BC =， 则BE CF +=_____________． 14.如果11m m-=-，那么2m m += . 15．一般的，形如1x a x+=（a 是已知数）的分式方程有两个解，通常用1x ，2x 表示. 请你观察下列方程及其解的特征：（1）12x x +=的解为121x x ==；（2）152x x +=的解为12122x x ==，； （3）1103x x +=的解为12133x x ==，；…… ……解答下列问题：（1）猜想：方程1265x x +=的解为1x = ，2x = ； （2）猜想：关于x 的方程1x x += 的解为121(0)x a x a a==≠，.CBAF E B C D A第13题三、计算题（本题共15分，每小题5分）16．. 解：17．22⎤-⎦.解：18.2222+224a a a a a a +⎛⎫∙ ⎪+-+⎝⎭． 解：四、解答题（本题共10分，每小题5分）19. 已知：如图，在△ABC 中，∠B=∠C ．求证：AB =AC .小红和小聪在解答此题时，他们对各自所作的辅助线叙述如下： 小红：“过点A 作AD ⊥BC 于点D ”；小聪：“作BC 的垂直平分线AD ，垂足为D ”.(1) 请你判断小红和小聪的辅助线作法是否正确； (2) 根据正确的辅助线作法，写出证明过程． 解：（1）判断： ； （2）证明：20．如图，在ABC △中，AB=AC ，D 是AB 的中点，点P 是线段CD 上不与端点重合的 任意一点，连接AP 交BC 于点E ，连接BP 交AC 于点F ．求证：（1）CAE CBF =∠∠； （2）AE BF =. 证明（1）（2）五、解答题（本题共15分，每小题5分） 21．已知20x y -=， 求22y 1x y x y÷-- 的值． 解：22. 解分式方程： 223124x x x --=+-． 解：23.列方程或方程组解应用题：随着人们环保意识的增强，环保产品进入千家万户.今年1月小明家将天燃气热水器换成了太阳能热水器．去年12月份小明家的燃气费是96元，从今年1月份起天燃气价格每立方米上涨25%，小明家2月份的用气量比去年12月份少10立方米，2月份的燃气费是90元．问小明家2月份用气多少立方米? 解：六、解答题（本题共9分，其中24小题4分，25小题小题5分）24. 如图，ABC △中，90ACB ∠=°，将ABC △沿着一条直线折叠后，使点A 与点C 重合（图②）．（1）在图①中画出折痕所在的直线l ．设直线l 与AB AC ，分别相交于点D E ，，连结CD ．（画图工具不限，不要求写画法） （2）请你找出完成问题（1）后所得到的图形中的等腰三角形．（用字母表示，不要求证明） 解：（2）25. 已知：如图，ABC △中，45ACB ∠=︒，AD ⊥BC 于D ，CF 交AD 于点F ，连接BF 并延长交AC 于点E ，BAD FCD ∠=∠． 求证：（1）△ABD ≌△CFD ；（2）BE ⊥AC ． 证明：(1)（2）①A B ②B 折叠后七、解答题（本题6分）26．已知ABC △，以AC 为边在ABC △外作等腰ACD △， 其中AC =AD .（1）如图1，若2DAC ABC ∠=∠，△ACB ≌△DAC ， 则ABC ∠= °；（2）如图2，若30ABC ∠=︒，ACD △是等边三角形， AB =3，BC =4. 求BD 的长. 解：（2）答案及评分参考一 、选择题（本题共30分，每小题3分）11. 8, 12.392x -, 13. 2, 14. 1 ,15.1215,5x x ==（2分）；21a a +（1分）三、计算下列各题（本题共20分，每小题5分） 16．解： 1=3452⨯⨯⨯==分分.................................................................5分222(13)(62)..........................................288⎤-⎦=+--=++=分分....................................4=分分2222222+224(2)2(2)(2)=.......................3(2)(2)(2)(2)422+4(2)................................................4(2)(2)4 (2)a a a a a a a a a a a a a a a a a a a a a a a a a a +⎛⎫∙ ⎪+-+⎝⎭⎡⎤-+++∙⎢⎥+-+-+⎣⎦-++=∙+-+=-分分....................................................................5分四、解答题（本大题共2个小题，每小题5分，共10分） 19. 解：（1）判断：小红的辅助线作法正确 ；………….1分 （2）证明：∵AD ⊥BC ，∴ ∠ADB=∠ADC =90°.…………………………2分 ∵ ∠B=∠C ，AD =AD . ………………………………………3分 ∴ △ABD ≌△ACD .………………………………4分 ∴ AB =AC . ……………………………………..5分 20．证明（1） ∵ AB=AC ，D 是AB 的中点，∴ CD 平分∠ACB ………………………………………1分 ∴ ACP BCP ∠=∠ ∵ CP CP =，∴ △ACP ≌△BCP ………………………………2分 ∴ CAE CBF ∠=∠…………………………………3分 （2） ∵BCF ACE ∠=∠， CBF CAE ∠=∠，BC AC =，∴ △ACE ≌△BCF …………………………………………………………………4分 ∴ BF AE =. ………………………………………………………………………5分 五、解答题（本大题共15分，每小题5分） 21．解：原式=()()）（y x y x y x y-⋅-+………………………………………………………2分 =yx y+………………………………………………………………………3分 ∵ 20x y -=， ∴ x =2y∴y x y +=312=+y y y ………………………………………………………………5分 22. 解分式方程：223124x x x --=+-． 解：22(2)(4)3x x ---=．.................................................................................................2分45x -=-．………………………………………………………………3分54x =．………………………………………………………………..4分经检验，54x =是原方程的解．……………………………………………………….5分23.解：解：设小明家2月份用气x 立方米，则去年12月份用气(x +10) 立方米．-------1分 根据题意，得%251096109690⨯+=+-x x x ．………………………………………….2分 解这个方程，得x ＝30 ．…………………………………………………………………..3分 经检验，x ＝30是所列方程的根．………….……………………………………………….4分 答：小明家2月份用气30立方米． …………………………………………………….5分 六、解答题（本大题共9分，其中24小题4分，25小题小题5分） 24. 解：（1）如图所示： 2分 （2）ADC △，BDC △为等腰三角形． 4分25，∴ ∠ADC=∠FDB=90°.∵ 45ACB ∠=︒，∴ 45ACB DAC ∠=∠=︒……………………..1分∴ AD=CD. ………………………………………2分 ∵ BAD FCD ∠=∠，∴ △ABD ≌△CFD ………………………………3分(2) ∴ BD=FD. ………………………………………………………………………4分 ∵ ∠FDB=90°，∴ 45FBD BFD ∠=∠=︒. ∵ 45ACB ∠=︒， ∴ 90BEC ∠=︒.∴ BE ⊥AC ．……………………………………………………………………………5分 七、解答题（本题6分）26. 解：（1）45；…….………………………………………………………………………..2分 （2）如图2，以A 为顶点AB 为边在ABC △外作BAE ∠=60°， 并在AE 上取AE =AB ，连结BE 和CE .∵ ACD △是等边三角形, ∴AD =AC ，DAC ∠=60°. ∵ BAE ∠=60°,∴ DAC ∠+BAC ∠=BAE ∠+BAC ∠.即EAC ∠=BAD ∠. ∴EAC △≌BAD △. …….…………………………….3分∴ EC =BD.∵ BAE ∠=60°，AE =AB=3, ∴ AEB △是等边三角形，∴ =60EBA ∠︒，EB =3.………………………………………………………………….4分∵ 30ABC ∠=︒, ∴ 90EBC ∠=︒.∵ 90EBC ∠=︒，EB =3，BC =4,∴ EC =5…………………………………………………………………………………5分 ∴ BD =5. ……………………………………………………………………………….6分A AEBCD2图。

2011～2012学年度第一学期期末考试八年级数学试卷一．选择题（3分X 12—36分）下列各题均有四个备这备案，其中只有一个正确答案，将你认为正确的答案一在答题卷中1．有意义，则a的取值范围是2．下列图案中，为轴对称图形的是3，在五个实数中，无理数的个数有A．4个B．3个C．2个D．1个4．下图分别给出了变量x与y之间的对应关系，其中y不是x的函数是5．一次函数y=2x-3的图象大致为6．如自，直线y=mx+n与直线y=kx+b交于点P（-1，1），则关于x的不等式。

mx＋n≥kx ＋b的解集为A．x≥1 B．x≥-1C．x≤l D．x≤-17．甲、乙两人从学校沿相同路线前往距离学校10km的培训中心参加学习,图中后ι甲ι分别表示甲、乙两人前往目的地所走的路程S（km）随时间t（分）变化的函数图象．以乙下说法：①乙比甲提前12分钟到达；②乙只用10分钟到达培训中心。

③甲出发18分钟后乙才出发。

其中正确的有A.3个B．2个C．1个D．0个8．如图，AD⊥BC，BD=CD，且点C在AE的垂直平分线上，那么下列结论错误的是A．AB＝AC B．BC＝CE C．AB十BD＝DE D．∠B=2∠E9．如图，把R t△ABC放在直角坐标系内，其中∠CAB＝90°，点C、B的坐标分别为（1，4）、（4，0），将△ABC沿x轴向右平移，当点C落在直线y=2x-6上时，线段BC扫过的面积为A．4 B．8 C．1610．如图是相同长度的小棒换成的一组有规律的图案，图案（1）需要4根，小样，图案（2）需要10根小棒……，按此规律摆下去，第6个图案需要小棒的根数为．11．如图，在△ABC中，点E是BC上一点，点D是AE上一点，下列条件。

①DE⊥BC；②∠BDE＝∠CDE；③BE＝EC．共有3对组合条件：①②；①③；②③.其中能推出AB＝AC的组合条件有A．3对B．2对C．1对D．0对12．如图，△ABD、△BDC都是等边三角形，点E、F分别在AB、AD上，且AE＝DF，连接BF与DE交于点G，下列结论：≌△①△AED≌△DFH ; ②∠BGE=600; ③ GC=GE+GB④若AF=2AE, 则S△GE B－S△DFG=1/3S△BDC其中正确的结论是A①②③B．①②④C．③④D．①②③④二．填空题（3分 ×4＝12分）13．9的平方根为；化简的值为；与最接近的整数为。

2012-2013学年度靖江市第一学期期末调研试卷八年级数学一、选择题：本大题共8小题, 每小题2分，共16分．在每小题给出的四个选项中，只有 一个是符合题目要求的，请将答案直接填在．．．．．．．．试卷．．相应的位置上．．．．．．． 1．下列各数中是无理数的是 【 】 A ． 3 B.722 C.38 D. 316 2. 9的平方根是 【 】 A.－3 B. 3 C.±3 D.±33.下列一次函数中，y 的值随着x 值的增大而减小的是 【 】 A. y ＝x B. y ＝x －1 C.y ＝x ＋1 D. y ＝－x4.若一组数据n x x x x x ,,.,,4321⋅⋅⋅的平均数为2008，那么5,5,5,54321++++x x x x , …,5+n x 这组数据的平均数是 【 】 A ．2009 B.2013 C.2015 D.20165.若实数a 满足a a -=||，则||2a a -一定等于 【 】 A. -2a B. 2a C. -a D. 06.在同一坐标系中，对于以下几个函数: ①y=－x －1;②y=x+1;③y=－x+1;④y=－2(x+1)的图象有四种说法: ⑴过点(－1，0)的是①和③; ⑵②和④的交点在y 轴上; ⑶互相平行的是①和③; ⑷关于x 轴对称的是②和③.那么正确说法的个数是 【 】 A.1个 B.2个 C.3个 D.4个7.如图，直线EF 过平行四边形ABCD 对角线的交点O ，分别交AB 、CD 于E 、F ，那么阴 影部分的面积是平行四边形ABCD 面积的 【 】 A. 12B ．31 C ．41 D ．518.如图，在△ABC 中，AB ＝3，AC ＝4，BC ＝5，P 为边BC 上一动点，PE ⊥AB 于E ， PF ⊥AC 于F ，M 为EF 中点，则AM 的最小值为 【 】 A ． 1 B ．1.2 C ． 1.3 D ．1.5二、填空题：本大题共10小题, 每小题2分，共20分．把答案直接填在试卷相对应的位 置上．9.科学家发现某病毒的长度约为0.000001595mm ，用科学记数法表示的结果为 mm ．（保留3个有效数字）10.点P （－2，3）关于x 轴的对称点的坐标是__ _____.11.若等腰三角形中有一个角等于50°，则这个等腰三角形的顶角的度数为___ _____． 12.已知：如图，在△ABC 中，BC ＝6 , AD 是BC 边上的高，D 为垂足，将△ABC 折叠使点A 与点D 重合，则折痕EF 的长为 ．第8题A E F MB P C第7题A13.已知直线y ＝3x －1，把其沿y 轴向下平移3个单位后的直线所对应的函数解析式是 ．14.有甲、乙两班，甲班有m 个人，乙班有n 个人.在一次考试中甲班平均分是a 分，乙班 平均分是b 分.则甲乙两班在这次考试中的总平均分是________________．15.有一个最多能称10千克的弹簧秤，称重发现，弹簧的长度与物体重量满足一定的关系，如下表.16.DG ，若AB =2，BC =1，则AG 的长是_____ _____．17.如图，在等边ΔABC 中，AC =8，点O 在AC 上，且AO =3，点P 是AB 上一动点，连结OP ，将线段OP 绕点O 逆时针旋转60°得到线段OD ．要使点D 恰好落在BC 上，则AP 的长是 ．18. 如图，以矩形OABC 的顶点O 为原点，OA 所在的直线为x 轴，OC 所在的直线为y 轴，建立平面直角坐标系．已知OA ＝3，OC ＝2，点E 是AB 的中点，在OA 上取一点D ，将△BDA 沿BD 翻折，使点A 落在BC 边上的点F 处．若在y 轴上存在点P ，且满足FE=FP ，则P 点坐标为 ．三、解答题：本大题共8小题，共64分．把解答过程写在试卷相对应的位置上．解答时应写出必要的计算过程，推演步骤或文字说明, 作图时用2B 铅笔． 19. （每小题4分，共12分） (1) 计算：4127-253++；⑵解方程组： ⎪⎩⎪⎨⎧+=+=+54711532y x y x ; (3)解方程：(2x –1)2–16=0.20.（满分6分）某校八年级（1）班50名学生参加数学考试，全班学生的成绩统计如下表：请根据表中提供的信息解答下列问题：（1）该班学生考试成绩的众数是 ； （2）该班学生考试成绩的中位数是 ； （3）该班王明同学在这次考试中的成绩是85分，能不能说王明同学的成绩处于全班中等偏上水平？ ．（填能或不能，并说明理由）21. （满分6分）“种粮补贴”惠农政策的出台，大大激发了农民的种粮积极性，某粮食生产专业户去年计划生产小麦和玉米共18吨，实际生产了20吨，其中小麦超产12％，玉米超产10％，该专业户去年实际生产小麦、玉米各多少吨？22.（满分6分）如图，在△ABC 中，AB=AC,点D 、E 分别在AB 、AC 上，BE 、CD 相交于点O. (1)若BD=CE,试说明OB=OC.(2)若BC=10，BC 边上的中线AM=12,试求AC 的长.23.（满分7分）已知函数y=kx+b 的图象经过点A(- 3, - 2)及点B(1, 6).O MEDCAB(1) 求此一次函数解析式,并画图象;(2) 求此函数图象与坐标轴围成的三角形的面积.24.（满分8分）如图，已知E是平行四边形ABCD中BC边的中点，连接AE并延长AE交DC 的延长线于点F．（1）求证：△ABE≌△FCE．（2）连接AC、BF，若∠AEC=2∠ABC，求证：四边形ABFC为矩形．25.（满分9分）小伟和小剑沿同一条路同时从学校出发到图书馆查阅资料，学校与图书馆的路程是4千米，小伟骑自行车，小剑步行，当小伟从原路回到学校时，小剑刚好到达图书 馆，图中折线O －A －B －C 和线段OD 分别表示两人离学校的路程y （千米）与所经过的时 间x （分钟）之间的函数关系，请根据图象回答下列问题： （1）小伟在图书馆查阅资料的时间为 分钟，小聪返回学校的速度为 千米/分钟．（2）请你求出小剑离开学校的路程y (千米)与所经过的时间x(分钟)之间的函数关系； （3）当小伟与小剑迎面相遇时，他们离学校的路程是多少千米？26.（满分10分）在平面直角坐标中，边长为2的正方形OABC 的两顶点A 、C 分别在y 轴、x 轴的正半轴上，点O 在原点.现将正方形OABC 绕O 点顺时针旋转，当A 点第一次落在直线y=x 上时停止旋转，旋转过程中，AB 边交直线y=x 于点M,BC 边交x 轴于点N （如图）.（1）当A点第一次落在直线y=x上时停止旋转，求边OA在旋转过程中所扫过的面积；（2）旋转过程中，当MN和AC平行时，求正方形OABC旋转的度数；（3）设△MBN的周长为p，在旋转正方形OABC的过程中，p值是否有变化？请证明你的结论.八年级数学参考答案一、选择题：DCDB AACBx二、填空题：9.1.60×10-610.（－2，-3） 11. 50°或80° 12. 3 13. y ＝3x －4 14.nm bnam ++15. 13.5 16. 215- 17. 5 18.（0，4）,（0，0） 三、解答题：．19. (1) 原式=5+(-3)+12 ……………3分 =52……………4分 ⑵解：23151475x y x y +=⎧⎪⎨++=⎪⎩L L L L ①②;由①得253y x =-……………2分 代入 ②解得x=6 ……………3分 ∴⎩⎨⎧==16y x ……………4分(3)解：由方程得:(2x –1)2=16 ∴2x -1=±4……………2分 ∴x 1=25或x 2=23- ……………4分 20. （1）87 ……………2分（2）86 ……………2分（3）不能, 因为全班平均成绩为85.06, 故王明同学的成绩处于全班中等……………2分 21. 解：设原计划生产小麦x 吨，生产玉米y 吨， 根据题意，得1812102018.x y x y +=⎧⎨+=-⎩，％％ ……………………2分 解得108.x y =⎧⎨=⎩， ……………………4分10(112)11.2⨯+=％（吨），8(110)8.8⨯+=％（吨）． 答：该专业户去年实际生产小麦11.2吨，玉米8.8吨． ……………………6分 22. （1）∵AC AB = ∴ACB ABC ∠=∠ 又 ∵CB BC CE BD ==, ∴⊿≅DBC ⊿ECB ————————————2分 ∴EBC DCB ∠=∠∴OC OB = —————————————3分 (2)由等腰三角形“三线合一”可得BC AM ⊥且BC CM 21==5 ———————4分 在Rt ⊿AMC 中135122222=+=+=CM AM AC ————6分23. 解:(1)将A(－３，－２),B(1,6)代入b kx y +=得⎩⎨⎧=+-=+-623b k b k 解得⎩⎨⎧==42b k …………2分 所以所求的解析式为:42+=x y ……3分 图象略 …………………………………5分 (2)S=44221=⨯⨯ ……………………7分 24. 证明：（1）∵四边形ABCD 为平行四边形， ∴AB∥DC，∴∠ABE=∠ECF， 又∵E 为BC 的中点，∴BE=CE ， ……………………2分 在△ABE 和△FCE 中， ∵， ……………………3分∴△ABE ≌△FCE （ASA ）； ……………………4分 （2）∵△ABE≌△FCE， ∴AB=CF，又AB∥CF，∴四边形ABFC 为平行四边形， ∴BE=EC，AE=EF ，又∵∠AEC=2∠ABC，且∠AEC 为△ABE 的外角， ∴∠AEC=∠ABC+∠EAB，∴∠ABC=∠EAB， ……………………6分 ∴AE=BE，∴AE+EF=BE+EC，即AF=BC ，则四边形ABFC 为矩形． ……………………8分 25.（是多少千米？解：（1）15，154……………………2分 （2）由图像可知，y 是x 的正比例函数设所求函数的解析式为y kx =（0≠k ）代入（45，4）得：k 454= 解得：454=k ……………………4分 ∴y 与x 的函数关系式445y x =（045x ≤≤）……………5分（不写取值范围不扣分）（3）由图像可知，小聪在3045x ≤≤的时段内，y 是x 的一次函数，设函数解析式为y mx n =+（0≠m ）代入（30，4），（45，0）得：⎩⎨⎧=+=+045430n m n m解得：⎪⎩⎪⎨⎧=-=12154n m ……………………6分∴41215y x =-+（3045x ≤≤）……………………7分 令44121545x x -+=，解得1354x =……………………8分 当1354x =时，41353454y =⨯=答：当小伟与小剑迎面相遇时，他们离学校的路程是3千米．……………………9分 26.（1）解：∵A 点第一次落在直线y x =上时停止旋转，∴OA 旋转了045.∴OA 在旋转过程中所扫过的面积为24523602ππ⨯=.……………………2分 （2）解：∵MN ∥AC ，∴45BMN BAC ∠=∠=︒,45BNM BCA ∠=∠=︒. ∴BMN BNM ∠=∠.∴BM BN =.又∵BA BC =，∴AM CN =. 又∵OA OC =,OAM OCN ∠=∠,∴OAM OCN ∆≅∆. ∴AOM CON ∠=∠.∴1(90452AOM ∠=︒-︒)=22.5︒. ∴旋转过程中，当MN 和AC 平行时，正方形OABC 旋转的度数为45︒-22.5︒=22.5︒. ……………………6分 （3）答：p 值无变化. ……………………7分 证明：延长BA 交y 轴于E 点，则045AOE AOM ∠=-∠，000904545CON AOM AOM ∠=--∠=-∠，∴AOE CON ∠=∠.又∵OA OC =，0001809090OAE OCN ∠=-==∠.∴OAE OCN ∆≅∆. ∴,OE ON AE CN ==. 又∵045MOE MON ∠=∠=,OM OM =, ∴OME OMN ∆≅∆.∴MN ME AM AE ==+.∴MN AM CN =+，∴4p MN BN BM AM CN BN BM AB BC =++=+++=+=.………………10分 ∴在旋转正方形OABC 的过程中，p 值无变化.（第29题）x。

20112012学年度第一学期期末考试题(卷)八年2011—2012学年度第一学期期末考试题（卷）八年级数学A 卷（100分）一．选择题（本大题共30分，每小题3分，共10小题；请把最佳的一个选项填在题中括号内） 1.下列运算中，结果正确的是( ) A .aa a=÷33B ．422)(ab ab = C ．523)(a a = D ．2a a a =⋅2.下列图形中，是轴对称图形．．．．．的是（ ） 3.下列各曲线中，不能表示y 是x 的函数的是（ ）A B CD 4. 估计2+15的运算结果应在（ ）Ａ．3到4之间 Ｂ．4到5之间 Ｃ．5到6之间 Ｄ．6到7之间5.下列计算错误的是（ ） A.b a a b a 3215)3)(5(=-- B.232412)13)(4(x x x x--=+-A B C D O xy O xy O xy O xyABCDE12C.273)2)(13(2++=++x xx x D.243531155ab b a c b a -=÷- 6.下列计算正确的是（ ） A.2)1)(2(2--=-+x xx x B.222)(b a b a +=+C.22))((b ab a b a -=-+ D.xy x x xxy -=÷+-6)6(27. 图中全等的三角形是 （ ）A.Ⅰ和ⅡB.Ⅱ和ⅣC.Ⅱ和Ⅲ D.Ⅰ和Ⅲ 8.Rt 90ABC C BAC∠∠o 在△中，＝，的角平分线AD 交BC 于点D ，2CD ＝，则点D 到AB 的距离是（ ）A ．1B ．2C ．3D ．49．已知一次函数y=kx+b 的图象如图所示,则k 、b 的符号是( )A.k>0,b>0 C.k<0,b>0 10．如图，∠1=∠2，∠C=∠D ，AC 、BD 交于E 点，下列结论中不正确的是（ ）yA ．∠DAE=∠CBEB ．ΔDEA 不全等于ΔCEBC ．CE=DED ．ΔEAB 是等腰三角形 二．填空题（本大题共30分，每小题3分，共10小题；请把最佳答案填在题中横线上）11.点（2，3）关于y 轴对称的点的坐标为_________．12.把直线121-=x y 向上平移21个单位,可得到函数_______________.13.若直线y=kx 平行直线y=5x+3，则k=_____. 14.比较大小：－３ －1015.16的算术平方根是 .16. 函数2y x =-中自变量x的取值范围是_______________.17. 在Rt △ABC 中，∠C ＝90°，∠B ＝60°，AB ＝12，则BC ＝ .18. 若函数mx m y )1(-=是正比例函数，则m 的值是 .19. 如图，△ABC 中边AB 的垂直平分线分别交BC 、AB 于点D 、E ，AE=3cm ，△ADC•的周长为9cm ，则△ABC 的周长是 .20. 大家一定知道杨辉三角（Ⅰ），观察下列等式（Ⅱ）根据前面各式规律，则5()a b += ．三．解答题（本大题共40分，共6小题；请写出必要的演算、推理、解答过程） 21．化简（每题4分，共8分） （1）33+23+308)14.3(16-+--π（2）（3x —2）2—（2x+4）（2x —4）22. 分解因式(每题4分，共8分) (1) 22363ay axy ax ++ (2) 3x 3 —12x1222332234432234()()2()33()464a b a ba b a ab b a b a a b ab b a b a a b a b ab b +=++=+++=++++=++++Ⅱ11 123．（5分）已知一次函数的图像经过点（—2，－2）和点（2，4）， 求这个一次函数的解析式.24．（6分）已知：如图，CAE ∠是ABC ∆的外角，12∠=∠，AD ∥BC. 求证：AB AC =25．（6分）已知:如图,AB=AD,AC=AE,∠BAD=∠CAE. 求证:BC=DE.26．（7分）甲骑自行车、AB DC E _2_1EA DCB乙骑摩托车沿相同路线由A地到B地，行驶过程中路程与时间的函数关系的图象如图7. 根据图象解决下列问题：(1) 谁先出发？先出发多少时间？谁先到达终点？先到多少时间？(2) 分别求出甲、乙两人的行驶速度；(3) 在什么时间段内，两人均行驶在途中(不包括起点和终点)？在这一时间段内: ①什么时间甲在乙的前面；②什么时间甲与乙相遇；③什么时间甲在乙后面.B卷（50分）四．解答题（本大题共50分，共6小题；请写出必要的演算、推理、解答过程）27.（8分）运用乘法公式计算：2)+b+a+-+．+-cb)(a((c)bca28．（8分）如图在AFD∆中，点A，E，F，C在∆和CEB同一条直线上,有下面四个论断：（1）AD =CB ，（2）AE =CF ，（3）D∠，（4）AD //BC .请用其B∠=中三个作为条件，余下一个作为结论，编一道数学问题，并写出解答过程.29．（8分）如图，∆ABC中BD、CD平分∠ABC、∠ACB，过D作直线平行于BC，交AB、AC于E、F，求证:EF=BE+CF.30. （8分）如图，已知直线1:23l y x =+，直线2:5ly x =-+，直线1l 、2l分别交x 轴于B 、C 两点，1l 、2l 相交于点A ．(1) 求A 、B 、C 三点坐标； (2) 求△ABC 的面积．31．（8分）探索： 11)(1(2-=+-x x x ）1)1)(1(32-=++-x x x x 1)1)(1(423-=+++-x x x x x1)1)(1(5234-=++++-x x x x x x．．．．．． (1)试求122222223456++++++的值;(2)判断1222222200620072008++++++Λ的值的个位数是几？32．（10分）抗震救灾中，某县粮食局为了保证库存粮食的安全，决定将甲、乙两个仓库的粮食，全部转移到具有较强抗震功能的A 、B 两仓库。

图2 DA图1m E DCBA 2011-2012学年度上学期期末考试八年级数学试题一、选择题(本大题共12小题, 每小题3分, 共36分)1、计算4的结果是（）A.2B.±2C.-2D.42、函数 y =31-x 的自变量x 的取值范围是（ ）Ａ．x ＞-3 Ｂ．x ＜3 Ｃ．x ≠3 Ｄ．x ≠-33、下列不是一次函数的是（ ） A ．y=x 1-x B. y=21x －1 C. y=21-x D. y=2x 4、 下面哪个点不在函数y=－x +3的图象上（ ） A ．（-1，2） B ．（0，3） C ．（3，0） D ．（1，2） 5、点（4，5）关于y 轴的对称点的坐标是（ ） A ．（-4，5） B ．（4，-5） C ．（-4，-5） D ．（4，5）6、如图1, 直线ｍ是多边形ABCDE 的对称轴，其中∠Ａ＝130°，∠ABC ＝110°,那么∠BCD 的度数等于（ ） A ．50° B ．60° C ．70° D ．80°7如图2，已知∠1=∠2，AC=AD ，增加下列条件之一：①AB=AE ；②BC=ED ； ③∠C =∠D ；④∠B =∠E ．其中能使△ABC ≌△AED 的条件有（ ） A ．1个 B ．2个 C ．3个 D ．4个 8、下列各式由左边到右边的变形中，是因式分解的为（ ）A ．ay ax y x a +=+)(B ．4)4(442+-=+-x x x xC ．)12(22-=-x x x xD ．x x x x x 3)4)(4(3162+-+=+-9、已知一次函数(1)y a x b =-+的图象如图3所示，那么a 的取值范围是( ) A.1a > B.1a < C.0a > D.0a <10、如图4，李老师骑自行车上班，最初以某一速度匀速行进，中途由于自行车发生故障，停下修车耽误了几分钟，为了按时到校，李老师加快了速度，仍保持匀速行进，结果准时到校.在课堂上，李老师请学生画出他行进的路程y （千米）与行进时间t （小时）的函数图象的示意图，同学们画出的图象如图所示，你认为正确的是（ ）图3图411、如图5，△ABC 是等边三角形，D 是BC 中点，DE ⊥AC 于E ，若CE =1,则AB =（ ）A ．2B ．．3 D ．412、如图6，Rt △ACB 中，∠ACB =90°，∠ABC 的角平分线BE 和∠BAC 的外角平分线AD 相交于点P ，分别交AC 和BC 的延长线于E ,D . 过P 作PF ⊥AD 交AC 的延长线于点H ，交BC 的延长线于点F ，连结AF 交DH 于点G .则下列结论：①∠APB =45°；②PF=P A ；③BD-AH=AB ；④DG=AP+GH .其中正确的是（ ）A ．①②③B ．①②④C ．②③④D ．①②③④二、填空题（共4小题，每小题3分，共12分）13、计算： ⎪⎭⎫⎝⎛-⋅23313x x =________；24(2)a --=________；()532x x ÷= ． 14、a 的算术平方根为8，则a 的立方根是__________。

2011—2012学年度上期期末质量监测八年级数学试题（考试时间：120分钟 满分：150分）一、选择题：（本大题10个小题，每小题4分，共40分）在每个小题的下面，都给出了代号为A 、B 、C 、D 的四个答案，其中只有一个是正确的，请将正确答案的代号填在题后的括号中．1．－2倒数是（ ） A ．2- B ．21-C ．21D ．22．8的立方根是（ ）A ．±4B ．4C ．±2D ．2 3．在下列长度的各组线段中，能组成直角三角形的是（ ） A ．5，6，7 B ．1，4，9 C ．3，4，5D ．5，11，124．下列四个图形中，不能通过基本图形平移得到的是（ ）5，6中，有理数的个数（ ）A ．0个B ．1个C ．2个D ．3个 6．化简)23(+³（3－2）正确的是（ ）A ．－1B ．1 C ． －2 D ．2D ．7．如图，以两条直线1l 、2l 的交点坐标为解的方程组是（ ） A ．11x y x y -=⎧⎨2-=⎩，B ．121x y x y -=-⎧⎨-=-⎩，C ．121x y x y -=-⎧⎨-=⎩，D ．121x y x y -=⎧⎨-=-⎩，8．如图，P 是等边三角形ABC 内的一点，若将P AC 绕点A 逆时针旋转到△P′AB ， 则∠P AP′ 的度数为（ ）A ．︒30B ． ︒45C ． ︒60D ．︒909．如图，某电信部门为了鼓励固定电话消费，推出新的优惠套餐：月租费10元；每月拔打市内电话在120分钟内时，每分钟收费0.2元，超过120分钟的每分钟收费0.1元；不足1分钟时按1分钟计费．则某用户一个月的市内电话费用y （元）与拔打时间t （分钟）的函数关系用图象表示正确的是（ ）10．如图，△ABC 和△ADE 都是等腰直角三角形，∠BAC=∠DAE =90°， 四边形ACDE是平行四边形，连结CE 交AD 于点F ，连结BD 交 CE 于点G ， 连结BE . 下列结论中：① CE =BD ； ② △ADC 是等腰直角三角形； ③ ∠ADB =∠AEB ； ④ CD =EF .一定正确的结论有（ ）A ．①②③B ． ①②④C ．①③④D ．②③④7题图10题图A BCDEFGA ．B ．C ．D ．8题图二、填空题：（本大题6个小题，每小题4分，共24分） 请将正确答案直接填写在题中的横线上．11．4的平方根是_______． 12. 化简：327-= _______．13．如图，直线m 是一次函数y=kx+b 的图象，则k 的值是 _______．14．如图是举世闻名的三星堆考古中发掘出的一个梯形残缺玉片，其中AD//BC ，∠A=115°，∠D=110°． 则∠B 、∠C 的度数分别是_______．15．解古算题：今有甲、乙二人持钱不知其数，甲得乙半而钱六十；乙得甲太 半（32）而亦钱六十，则甲、乙持钱分别为__ ____．16．如图，方格纸中每个方格都是边长为1的正方形，点A 、B是方格纸中的两个格点（即正方形的顶点），A 、B 两点的坐 标分别为A （0，1）、B （1，3），则以A 、B 、C 、D 为四个格 点为顶点的平行四边形的面积是4，则满足条件的点C 、D 的坐标分别是____ _____．三、解答题：（本大题4个小题，每小题6分，共24分）解答 时每小题必须给出必要的演算过程或推理步骤．17．计算：()()161321120121--+--⎪⎭⎫ ⎝⎛+︒--π．14题图110°115° CDBA18．写出图中多边形ABCDEF 各个顶点的坐标．19．计算：32)2145051183(÷-+20．如图，□ ABCD 的两条对角线AC 、BD 相交于点O ，AB =5，AO =2，OB=１，四边ABCD 会是菱形吗？请说明理由.DBACEFCA20题图四、解答题：（本大题4个小题，每小题10分，共40分）解答时每小题必须给出必要的演算过程或推理步骤．21．某商厦张贴巨幅广告，称他们这次“真心回报顾客”活动共设奖金20万元，最高奖每份1万元，平均每份200元．一顾客抽到一张奖券，奖金数为10元．她调查了周围兑奖的顾客，没有一个超过50元的，她气愤地要求商厦经理评理，经理解释“不（1）求这次活动奖金的平均数、中位数、众数；（2）你认为商厦说“平均每份奖金200元”是否欺骗了顾客？以后遇到开奖的问题你会更关心什么？22．动手操作：如图，在矩形纸片ABCD中，AB=3，AD=5．如图所示折叠纸片，使点A 落在BC边上的A/处，折痕为PQ，当点A/在BC边上移动时，折痕的端点P、Q也随之移动．若限定点P、Q分别在AB、AD边上移动．求：（1）当点Q与点D重合时，A/C的长是多少？（2）点A/在BC边上可移动的最大距离是多少？22题图23．（1）解方程组：⎩⎨⎧⨯=⋅+⋅=+;200%35%45%5,200y x y x（2）编一道应用题，使得其中的未知数满足（1）中的方程组．当然，在编拟应用题时，你可以根据实际背景适当改变上面方程中的数据但不能改变方程的形式．24． 如图，四边形ABCD 是正方形，点E 、K 分别在BC 、AB 上，点G 在BA 的延长线上，且CE =BK =AG .（1）请探究DE 与DG 有怎样的数量关系和位置关系？并说明理由．（2）以线段DE 、DG 为边作平行四边形DEFG ，连接KF （要求：在已知图中作出相应简图），猜想四边形CEFK 是怎样的特殊四边形，并说明理由．G EDCBA24题图五、解答题：（本大题2个小题，25题10分，26题12分， 共22分）解答时每小题必须给出必要的演算过程或推理步骤．25．一辆客车从甲地开往乙地，一辆出租车从乙地开往甲地，两车同时出发，设客车离甲地的距离为1y （km ），出租车离甲地的距离为2y （km ），客车行驶时间为x （h ），1y 、2y 与x 的函数关系图象如图12所示．（1）根据图象，求出1y ，2y 关于x 的函数关系式．（2）若设两车间的距离为S （km ），请写出S 关于x 的函数关系式．（3）甲、乙两地间有A 、B 两个加油站，相距200km ，若客车进入A 站加油时，出租车恰好进入B 站加油．求A 加油站到甲地的距离．25题图26．平面直角坐标系中边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上，点O在原点．如图，将正方形OABC绕O点顺时针旋转，当A点第一次落在直线y x=于点M，BC边交x轴于=上时停止旋转，旋转过程中，AB边交直线y x点N．（1）求此时OA旋转的度数；（2）旋转过程中，当MN与AC平行时，求正方形OABC旋转的度数；△的周长为p，在正方形OABC旋转的过程中，p值是否有变化？（3）设MBN请证明你的结论．O南岸区2011—2012学年度上期期末质量监测八年级数学试题参考答案及评分意见一．BDCCB ACCBA二．11．±2； 12．32； 13．2； 14．65°、70°；15． 甲持钱45、乙持钱30； 16．（0,5）（-1,3）或（3,3）（2,1）或（-1,3）（2,1）． 三．17．解：原式=1+2-3+1-4…………………………………………………………（5分） =-3……………………………………………………………………（6分） 18．解;A （-4,4）、B （-7,0）、C （-4,-4）、D （0,-4）、E （3,0）、F （0,4） （每个点各一分，共6分） 19．解：原式=()3222229÷-+……………………………………………（3分）=28³241…………………………………………………………………（5分）=2．……………………………………………………………………………（6分） 20．解： 四边形ABCD 会是菱形，理由如下： ………………………………（1分） ∵在△AOB 中，AB =5，AO =2，OB=１，∴AO 2+ OB 2=22+1=5． …………（2分） 又∵AB 2=（5）2=5，∴AO 2+ OB 2= AB 2．…………………………………………（3分）∴根据勾股定理的逆定理，得∠AOB=90°．…………………………………………（4分）∴AC ⊥BD ．……………………………………………………………………………（5分）∵四边形ABCD 是平行四边形，∴四边形ABCD 会是菱形． ……………………（6分） 四．21．解：（1）这次活动奖金的平均数是x =2001000200000550350871031055050350100087600010100003==++++⨯+⨯+⨯+⨯+⨯…（5分） 这次活动奖金的中位数是10、众数是10. ……………………………………………（7分） （2）因为这次活动奖金的平均数是200，所以商厦说“平均每份奖金200元”没有欺骗顾客，但中位数是10、众数也是10，这就是说多数顾客得奖为10元．以后遇到开奖的问题应更关心中位数和众数．………………………………………………………（10分）22．解：（1）当Q 点与D 重合时，如图①，∵四边形ABCD 是矩形，AD=5，AB=3，∴BC=AD=5，DC=AB=3, ∠C=90°．…………（3分） 由折叠知'1A D=AD=5，…………………………（4分） 在Rt △'1A CD 中，根据勾股定理，得21221D A DC C A '=+' 22121DC D A C A -'='2235-=16=．………………………………………………………………………（5分） ∵C A '1＞0，∴C A '1=16=4．………………………………………………（6分） （2）'1A 在BC 上最左边时点Q 点与D 重合，此时，由（1）得，'1A C=4;……（7分） 当点P 与B 重合时，图②中的'2A 在BC 上最右边．………………………………（8分） 此时，由折叠知： '2A B =AB=3，则A 2C =5 -3 =2; ………………………………（9分）A '应在'1A '2A 之间移动，所以A '在BC 边上可移动的最大距离为C '1A --C '2A =4 -2 =2．……………………………………（10分）23．（1）解：由②得：14009=+y x ．③ ………………………………………（2分） ③－①得：12008=y ．………………………………………………………………（3分）y =150．…………………………………………………………………（4分） 将y =150，代入①得：50=x ．……………………………………（5分）∴原方程组的解为：⎩⎨⎧==.150,50y x ……………………………………（6分） （2）所编应用题为：答案不唯一．如：一、二班共有200名学生，他们在半期数学考试中的优生率为35％，如果一班学生的优生率为5％，二班学生的优生率为45％．那么一、八年级数学质量监测试题 11二班学生的学生数各是多少？（200、35％、5％、45％四个数据各一分．）……（10分）24．解：（1）DE=DG ，DE ⊥DG ．理由如下：………………………………（1分）∵四边形ABCD 是正方形，∴DC=DA ，∠DCE=∠DAG=90°．又∵CE=AG ，∴△DCE ≌△GDA ．∴DE=DG ，∠EDC=∠GDA ．……（4分） 又∵∠ADE+∠EDC=∠ADC=90°，∴∠ADE+∠GDA=90°，∴DE ⊥DG ．…（5分）（2）画图如图． 四边形CEFK 为平行四边形．理由如下：……（6分）∵四边形ABCD ，∴AB ∥CD ，AB=CD ．∵BK=AG ，∴GK=AK+ AG =AK+BK=AB ．即 GK=CD. ……………………………………（7分）又∵K 在AB 上，点G 在BA 的延长线上，∴GK ∥CD ．∴四边形CKGD 是平行四边形．∴DG=CK ，DG ∥CK ．…………………………（8分）又∵四边形DEFG 都是正方形，∴EF=DG ，EF ∥DG ．∴CK =EF ，CK ∥EF ．…………………………（9分）∴四边形CEFK 为平行四边形．………………（10分）25．解：（1）设 x k y 11= ∵图象过(10,600)∴110600k =． ∴601=k ． ∴ ()100601≤≤=x x y ．………（1分）设b x k y +=22，∵图象过(0,600), (6,0)，∴⎩⎨⎧=+=)2(06)1(,600b k b 将600=b 代入（2）得 600k =-．∴ ()606001002≤≤+-=x x y ．………………………………………… （3分） （2）⎩⎨⎧+-==60010060x y x y 解得：⎪⎩⎪⎨⎧==225415y x ∴ M ⎪⎭⎫ ⎝⎛225,415……………（4分）∴①当4150≤≤x 时，S 1=12y y -=x x 60600100-+-=600160+-x ； ……（5分） ②当6415≤≤x 时，S 2=21y y -=()60010060+--x x 600160-=x ；……（6分） ③当106≤≤x 时S 3x 60= ……………（7分）（3）当4150≤≤x 时，200=S ，∴200600160=+-x ． 解之，得()h x 25160400==．∴)(1502560km y =⨯= ……………（8分）八年级数学质量监测试题 12 当6415≤≤x 时，200=S ，∴200600160=-x ．解之，得()h x 5=，∴)(300560km y =⨯=………………………………（9分） ∴当106≤≤x 时，20060=x ，310=x ． ∵106≤≤x ， ∴310=x （舍去）. 综上所述：A 加油站到甲地的距离为km 150或km 300…………………（10分）26．解：延长BA 交y 轴于E 点，（1）∵直线x y =是一、三象限的角平分线，∴∠MOE=∠MON=21³90°=45°． ∴A 点第一次落在直线y=x 上时停止旋转时，OA 旋转了45°；………………（2分）（2）∵四边形ABCO 是正方形，∴∠B=∠OAB=∠OCB=∠AO C=90°，OA = OC ，且∠BAC=∠BCA=45°． ∵MN ∥AC, ∴∠BMN =∠BAC = 450, ∠BNM =∠BCA=45°，∠BMN =∠BNM. ∴BM = BN .…………………………………………………………（4分） 又∵ BA = BC, ∴BA －BM=BC －BN ，即 AM = CN.又∵∠OAM =∠OCN =900，OA = OC ，∴△OAM ≌△OCN. …（6分）∴∠AOM= ∠CON.∴∠AOM=∠CON=21（∠AOC －∠MON ） =21（90°－45°）=22.5°， ∴当MN 和AC 平行时，正方形OABC 旋转的度数为22.5°……………………（7分）（3）p 值无变化，理由如下：∵由旋转的性质得：∠AOE= ∠CON ．………………………………………………（8分） 又∵∠ OAE+∠OAB=180°，∠OAB=90°，∴∠ OAE=90°．∴∠ OAE =∠OCN = 90°,．又∵OA = OC ，∴△OAE ≌△OCN.…………………………………………………（9分） ∴OE=ON, AE=CN ．又∵∠MOE=∠MON=45°，OM= OM ，∴△OME ≌△OMN ，………………（10分） ∴MN= ME= AM+ AE ．∴MN= AM+ CN ．∴p =MN+BN+BM=AM+CN+BN+ BM= AB+ BC=4．.................................（11分） ∴在正方形OABC 旋转的过程中p 值无变化． (12)八年级数学质量监测试题13。

一、选择题（每题5分，共25分）1. 下列各数中，有理数是（）A. √2B. πC. 0.1010010001…D. √-12. 如果a > 0，b < 0，那么下列不等式中正确的是（）A. a + b > 0B. a - b > 0C. a - b < 0D. a + b < 03. 已知x² - 5x + 6 = 0，则x的值为（）A. 2B. 3C. 2或3D. 无法确定4. 一个长方形的长是6cm，宽是4cm，它的周长是（）A. 20cmB. 24cmC. 18cmD. 22cm5. 在直角三角形ABC中，∠C = 90°，∠A = 30°，那么∠B的度数是（）A. 60°B. 90°C. 120°D. 150°二、填空题（每题5分，共25分）6. （-3）×（-5）= _______7. （-2）² = _______8. （-3）×（-3）×（-3）= _______9. 3x² - 4x + 1 = 0的解为：x = _______10. 2a - 3b + 5 = 0，如果a = 4，那么b = _______三、解答题（每题15分，共60分）11. （1）计算：(-2)⁴ - 3×(-3)² + 4×(-1)³（2）化简：2(3x - 4) - 5(2x + 3)12. （1）解方程：2x - 5 = 3x + 1（2）解方程：x² - 6x + 9 = 013. （1）计算长方形的长为8cm，宽为6cm，求这个长方形的周长和面积。

（2）计算等腰三角形的底边长为10cm，腰长为8cm，求这个三角形的面积。

14. （1）已知直角三角形ABC中，∠A= 30°，∠B = 60°，斜边AB = 10cm，求AC和BC的长度。

2011-2012学年度第一学期八年级数学期末考试试题（考试时间：120分钟 总分：100分）一、选择题（每小题3分，共24分，下列各题所用的四个选项中，有且只有一个是正确的） 1.B 2.D 3.C 4.D 5.B 6.A 7.B 8.C 二、填空题（每空3分，共30分）9.百，2 10.7 11. AC ＝BD 或∠ABC ＝90°等 12.1 13.⎩⎨⎧=-=32y x 14.120 15.1016.y=2x+5 17.（-3，3） 18.103三、解答题：（本大题共10小题，共96分） 19. 由题意得2x -y =16 y =-8 ∴ x =4∴-2xy =-2×4×（-8）=64 ∴-2xy 的平方根是±8. 20. （1）把点（2，m ）代入x y 21=得，m=1 （2）把点（－1，－5）、（2，1）代入y ＝kx ＋b 得， ⎩⎨⎧=+-=+-125b k b k 解得，⎩⎨⎧-==32b k∴ 一次函数的解析式为：32-=x y （3）如图，直线32-=x y 与x 轴交于点B （23，0） 与直线x y 21=相交于点A （2，1） ∴ OB=23 ∴ S △OA B =431232121=⨯⨯=⋅A y OB 22.（1）△ADG 是直角三角形，∵AF 、DE 是∠BAD 、∠ADC 的平分线， ∴∠FAD=21∠BAD ，∠ADE=21∠ADC ， ∵四边形ABCD 是平行四边形，∴∠BAD+∠ADC=180°， ∴∠FAD+∠ADE=90°， ∴∠AGD=90°，∴△ADG 是直角三角形．（2）∵四边形ABCD 是平行四边形，∴AD ∥BC ，AD=BC=6，AB=CD=4， ∴∠FAD=∠AFB ， ∵∠FAD=∠BAF ， ∴∠BAF=∠AFB ， ∴AB=BF=4， ∴CF=6-4=2．23. 由题意可知，将木块展开，长为2+0.2×2=2.4米；宽为1米． 于是最短路径为：2214.2+=2.6米．故答案为：2.6．22.（1）观察表格，可知这组样本数据的平均数是0311321631741250x -⨯+⨯+⨯+⨯+⨯==，∴这组样本数据的平均数为2.∵在这组数据中，3出现了17次，出现的次数最多， ∴这组数据的众数是3.∵将这组样本数据从小到大的顺序排列，其中处于中间的两个数都是2有2222+= ∴这组数据的中位数为2.（2）∵在50名学生中，读书多于2册的学生有18名，有1830050⨯=108. 24.⑴连结AB ，作线段AB 的垂直平分线，交过点B 的水平线于点P.⑵作点B 关于x 轴的对称点B ′(-1，-1)，连结AB ′交x 轴于点Q ， 设直线AB ′的函数关系式为y=kx+b(k ≠0)，将A 、B ′的坐标代入，得4133y x =+ 令y=0，得x= 14-， 所以点Q 的坐标为(14-，0) 25. 画图形如下：（1） （2） （3） 26. （1）证明：连结AD∵△ABC 是等腰直角三角形，D 是BC 的中点 ∴AD⊥BC，AD = BD = DC ，∠DAQ =∠B 又∵BP = AQ ∴△BPD≌△AQD∴PD = QD，∠ADQ =∠BDP ∵∠BDP +∠ADP = 90°∴∠ADQ +∠ADP =∠PDQ =90° ∴△PDQ 为等腰直角三角形．（2）当P 点运动到AB 的中点时，四边形APDQ 是正方形． 由（1）知△ABD 为等腰直角三角形．当P 点运动到AB 的中点时，DP⊥AB，即∠APD =90° 又∵∠A =90°，∠PDQ =90° ∴四边形APDQ 为矩形 又∵DP = AP = AB∴四边形APDQ 是正方形．27. （1）小颖的理由：依次连接矩形各边的中点所得到的四边形是菱形，小明的理由：∵ABCD 是矩形， ∴AD ∥BC ，则∠DAC=∠ACB ，又∵∠CAE=∠CAD ，∠ACF=∠ACB ， ∴∠CAE=∠CAD=∠ACF=∠ACB ， ∴AE=EC=CF=FA ，∴四边形AECF 是菱形． （2）方案一：S 菱形=S 矩形-4S △AEH =12×5-4× 12×6× 52=30（cm ）2， 方案二：设BE=x ，则CE=12-x ，∴ AE 2=BE 2+AB 2=x 2+25由AECF 是菱形，则AE 2=CE 2∴x 2+25=（12-x ）2，∴ x=24119， S 菱形=S 矩形-2S △ABE = 12×5-2×12×5×24119≈35.21（cm ）2. 28.：（1）晚0.5，两城相距300km ；（2）①设直线BC 的解析式为s=kt+b ， ∵B （0.5，300），C （3.5，0）， ∴ {3.5k+b=00.5k+b=300， 解得 {k=-100b=350， ∴s=-100t+350；②设第二列动车组列车MN的解析式为s=k1t+b1，∵M（1，0），N（3，300），∴{k1+b1=03k1+b1=300，解得{k1=150b1=150，∴s=150t-150，由①可知直线BC的解析式为s=-100t+350，∴150t-150=-100t+350，解得t=2，∴2-1=1．答：第二列动车组列车出发后1小时与普通列车相遇．。

2011-2012学年度第一学期八年级数学期末考试试题（考试时间：120分钟 总分：150分）一、选择题（每小题3分，共24分，下列各题所用的四个选项中，有且只有一个是正确的） 1．下列平面图形中，既是轴对称图形，又是中心对称图形的是（▲ ）A. B. C. D. 2．下列各式中正确的是（ ）A ．416±=B ．9273-=-C ．3)3(2-=- D ．211412= 3.在0.51525354…、49100、0.2、1π、7、13111、327中，无理数的个数是（▲） A ． 2 B ． 3 C ． 4 D ． 53．下列每一组数据中的三个数值分别为三角形的三边长，不能．．构成直角三角形的是(▲) A.3、4、5 B.6、8、10 C.3、2、5 D.5、12、13 4．下列说法中正确的是（▲）A ．对角线相等的四边形是菱形B ．对角线互相垂直的四边形是菱形C ．对角线相等的平行四边形是菱形D ．对角线互相垂直的平行四边形是菱形5. 有9名同学参加歌咏比赛，他们的预赛成绩各不相同，现取其中前4名参加决赛，小红同学在知道自己成绩的情况下，要判断自己能否进入决赛，还需要知道这9名同学成绩的（▲） A ．众数 B ．中位数 C ．平均数 D ．加权平均数6. 两条直线y=ax+b 与y=bx+a 在同一直角坐标系中的图象位置可能是(▲）A. B. C. D.7. 如图，两条笔直的公路l1、l2相交于点O ，村庄C 的村民在公路的旁边建三个加工厂 A 、B 、D ，已知AB=BC=CD=DA=5公里，村庄C 到公路l 1的距离为4公里，则村庄C 到公路l 2的距离是（▲）A.3公里B.4公里C.5公里D.6公里 8. 药品研究所开发一种抗菌新药，经过多年的动物实验之后，首次用于临床人体试验，测得成人服药后，血液中药物浓度y(微克/毫升)与服药后时间x(时)之间的函数关系如图所示，则当1≤x ≤6时，y 的取值范围是(▲）A.116438≤≤y B.81164≤≤y C.838≤≤y D.168≤≤y第7题二、填空题（每空3分，共30分）9．由四舍五入法得到的近似数 8.8×103精确到 ▲ 位，有 ▲ 个有效数字． 10. 若将三个数-3，7，11表示在数轴上，其中能被如图所示的墨迹覆盖的数是_____▲___．11.如图，在□ABCD 中，对角线AC 与BD 相交于点O ，在不添加任何辅助线和字母的情况下，请添加一个条件，使得□ABCD 变为矩形，需要添加的条件是 ▲ ．（写出一个即可）12.已知一组数据1，2，0，x ，-1，1的平均数是1，则这组数据的中位数是_____▲ __.13. 两条直线y=k 1x+b 1和y=k 2x+b 2相交于点A(－2，3)，则方程组⎩⎨⎧+=+=2211b x k y b x k y 的解是 .14. 一个等腰梯形的周长是40cm ，高是12cm ，并且腰长与中位线相等，该梯形的面积为___▲ _cm 2.15. 如图，矩形OBCD 的顶点C 的坐标为（1，3），则BD= ▲ ．16. 如图，将直线OA 向上平移一个单位，再向左平移2个单位，得到一次函数的图象，那么这个一次函数的关系式为：____▲ ____.17. 如图，如果所在的位置坐标为（-1，-2），所在的位置坐标为（2，-2），则所在位置坐标为 ▲ .18. 如图，已知等边三角形ABC 的边长为10，点P 、Q 分别为边AB 、AC 上的一个动点，点P 从点B 出发以1cm/s 的速度向点A 运动，点Q 从点C 出发以2cm/s 的速度向点A 运动，连接PQ ，以Q 为旋转中心，将线段PQ 按逆时针方向旋转60°得线段QD ，若点P 、Q 同时出发，则当运动 ▲ s 时，点D 恰好落在BC 边上． 三、解答题：（本大题共10小题，共96分） 19．（8分）已知2x -y 的平方根为±4，-2是y 的立方根，求-2xy 的平方根． 20. （10分）已知一次函数y=kx+b 的图像经过点（－1，－5），且与正比例函数12y x =的图像第8题 A BCDO第11题 第15题 o x 1 y 2 A 第16题第17题第18题PD C BAQ相交于点（2，m ）. （1）求m 的值；（2）求一次函数y=kx+b 的解析式；（3）求这两个函数图像与x 轴所围成的三角形面积.21. （10分） 如图，在□ABCD 中，∠ADC 与∠BAD 的平分线分别交AB 于E 、F ． （1）探究△ADG 的形状并说明理由．（2）若AB ＝4，AD ＝6，问CF 的长是多少？22. （8分）在一个长为2米，宽为1米的矩形草地上，如图放着一根长方体的木块，它的棱长和场地的宽平行且大于AD ，木块的正视图是边长为0.2米的正方形，一只蚂蚁要从点A 处到达点C 处的最短路程是多少米.23. （8分）在我市开展的“好书伴我成长”读书活动中，某中学为了解八年级300名学生读书情况，随机调查了八年级50名学生读书的册数，统计数据如下表所示：册数 0 1 2 3 4 人数31316171（Ⅰ）求这50个样本数据的平均数、众数和中位数；（Ⅱ）根据样本数据，估计该校八年级300名学生在本次活动中读书多于2册的人数.24. （10分）如图，在直角坐标系中，点A （2，3），点B(-1，1)（1）有一小球从点B 水平向右匀速滚去，同时一个机器人从点A 以同样的速度直线前进去拦截小球，请你在图中画出机器人最快截住小球的位置点P.(作图要求：尺规作图，保留作图痕迹) （2）在x 轴上找一点Q ，使AQ+BQ 的值最小，并求出此时点Q 的坐标。

2011-2012学年八年级（上）期末数学试卷一、选择题（共6小题，每小题3分，满分18分）1．有下列几种说法：①1的平方根是1；②无论x取任何实数，式子都有意义；③无理数是无限小数；④是分数，其中正确的个数是（）2．（3分）下列运算正确的是（）3．（3分）（2008•宝安区二模）在线段、平行四边形、菱形、正方形、梯形、等边三角形中既是轴对称图形又是中心对称图形的有（）4．（3分）如图数轴上的点A、C分别表示﹣1和1，BC⊥AC且BC=1，以A为圆心，AB为半径作弧交数轴于点D，则点D表示的数是（）﹣1 +15.（2012•西城区模拟）正方形具备而菱形不具备的性质是（）6．（2006•枣庄）在下列图形中，沿着虚线将长方形剪成两部分，那么由这两部分既能拼成三角形，又能拼成平行四边形和梯形的可能是（）二、填空题（共9小题，每小题3分，满分27分）7．（3分）的平方根是_________．8．（3分）已知a m=2，a n=3，则a2n﹣m=_________．9．（3分）分解因式：（a﹣b）2﹣4（a﹣b）+4=_________．10．已知a、b均为实数且+（ab﹣7）2=0，则a2+b2=_________．11．（3分）在平行四边形ABCD中，对角线AC与BD相交于点O，若AC=6，BD=8，则边AB的取值范围是_________．12．（3分）如图，四边形ABCD是正方形，点E是CD上一点，点F是CB延长线上一点，且DE=BF，通过观察与思考可以知道△AFB可以看作是_________绕_________，顺时针旋转_________得到△AEF 是_________三角形．13．菱形的对角线长分别是6cm和8cm，则菱形的周长是_________．14．（3分）如图，在边长为6cm的菱形中∠DAB=60°，E为AC上一动点，当E运动到某个位置时，BE+DE有最小值，这个最小值是_________．15．（3分）（2008•随州）如图，梯形ABCD中，AD∥BC，AB=DC，∠ABC=72°，现平行移动腰AB至DE后，再将△DCE沿DE折叠，得△DC′E，则∠EDC′的度数是_________度．三、解答题（共8小题，满分75分）16．（8分）分解因式（1）2x5﹣32x；（2）（x﹣y）2+4xy．17．（10分）化简求值．（1）[（x+y）（x﹣y）﹣（x﹣y）2+2y（x﹣y）]÷（﹣2y），其中x=﹣，y=2．（2）已知x2﹣2x﹣2=0，求（x﹣1）2+（x+3）（x﹣3）+（x﹣3）（x﹣1）的值．18．（9分）有一块铁皮零件，AB=4cm，BC=3cm，CD=12cm，AD=13cm．按照规定标准，这个零件中∠B=90°，求这块铁皮零件的面积．19．（9分）（2006•陕西）观察下面网格中的图形，解答下列问题：（1）将网格中左图沿水平方向向右平移，使点A移至点A′处，作出平移后的图形：（2）（1）中作出的图形与右边原有的图形，组成一个新的图形，这个新图形是中心对称图形，还是轴对称图形？20．（9分）如图，在四边形ABCD中，∠B=∠D=90°，∠AEC=∠BAD，则AE与DC的位置有什么关系？并说明理由．21．（9分）如图所示，P是正方形ABCD的边CD上任意一点，PE⊥BD 于E，PF⊥AC于F，则PE+PF=1，求正方形ABCD的面积．22．（10分）如图，△ABC中，D为AB的中点，E为AC上一点，过D作DF∥BE交AC于O，EF∥AB．（1）猜想：OD与OF之间的关系是_________．（2）证明你的猜想．23．（11分）如图，在等腰梯形ABCD中，AD∥BC，AB=DC=5，AD=6，BC=12，动点P从A点出发以每秒1个单位的速度向终点D运动，动点Q 从C点出发以每秒2个单位的速度向终点B运动，两点同时出发，设运动时间为t．（1）梯形ABCD的面积是_________．（2）①当t为多少秒时，四边形ABQP是平行四边形？②当t为多少秒时，四边形ABQP是梯形？（3）当t=3秒时通过计算判断四边形ABQP是否是直角梯形？参考答案:1.B2.D3.C4.C5.C6.C（a﹣b﹣2）2．7.正负根号3. 8.10. 11 11. 1＜AB＜712. △AED点A，90°等腰直角13. 20 14. 6cm15. 3616. 解：（1）原式=2x（x4﹣16），=2x（x2﹣4）（x2+4），=2x（x﹣2）（x+2）（x2+4）；（2）原式=x2﹣2xy+y2+4xy，=（x+y）2．17.解：（1）原式=（x﹣y）[（x+y）﹣（x﹣y）+2y]÷（﹣2y）=2y﹣2x，当x=﹣，y=2时，原式=2×2﹣2×（﹣）=5；（2）原式=x2﹣2x+1+x2﹣9+x2﹣4x+3=3x2﹣6x﹣5，原式=3（x2﹣2x）﹣5=3×2﹣5=1．18.解：在Rt△ABC中，AB=4cm，BC=3cm，∴AC2=25．即AC2+CD2=AD2．∴△ACD为直角三角形，∴3×4×+5×12×=6+30=36cm2．19.20. 解：AE∥DC，理由是：∵四边形ABCD的内角和为360°，∠B=∠D=90°，∴∠BAD+∠C=180°，又∵∠AEC=∠BAD，∴∠AEC+∠C=180°，∴AE∥DC．21. 解：∵正方形ABCD，PE⊥BD于E，PF⊥AC于F，∴四边形OEPF为矩形，三角形PFC为等腰直角三角形，∴PE=OF，PF=CF，∴PE+PF=OF+CF=OC=1，∴OA=1，BD=2，∴正方形ABCD的面积=△ABD的面积+△BCD的面积=×2×1+×2×1=2，所以正方形ABCD的面积为2．22. 解：（1）OD=OF；（2）∵EF∥AB，DF∥BE，∴四边形BDFE是平行四边形，∴BD=EF，∵D是AB的中点，∴AD=BD，∴EF=AD，∵EF∥AB，∴∠ADO=∠EFO，∠DAO=∠FEO，∴，∴△ADO≌△EFO，∴OD=OF．23. 解：（1）由题意得，AB=DC=5，AD=6，BC=12，∴BE=（BC﹣AD）=3，在RT△ABE中，AE==4，∴S梯形ABCD=（AD+BC）×AE=36．（2）由题意得，AP，BQ=BC﹣2t=12﹣2t，①AP=BQ即可满足四边形ABQP是平行四边形，即t=12﹣2t，∴t=4秒．即：t为4秒时，四边形ABQP是平行四边形；②要使四边形ABQP是梯形，只需满足AP≠BQ即可，这时t≠4；即t不为4秒时，四边形ABQP是梯形；（3）当t=3秒时，AP=t=3，BQ=12﹣2t=6，此时，P为AD的中点，Q为BC中点，∵AB=DC=5，∴此时PQ所在直线是梯形ABCD的对称轴，∴PQ⊥BC，PQ⊥AD，又AP∥BQ∴ABQP是直角梯形．。

2011～2012学年度第一学期期末考试八年级数学试卷命题人：徐晓兰 审核人：赵志林说明：1．本试卷共4页，满分120分。

考试时间120分钟；2．考生必须在答卷纸上指定区域内作答，在本试卷上和其他位置作答一律无效.． 一、填空题 (共12小题，每小题2分，计24分)1．计算：38-＝ ▲ ．2．点A （—2，4）关于y 轴对称的点的坐标是 ▲ ． 3．写出一．个．在函数2y x =图象上的点的坐标_____▲ _____． 4．观察手机号码133********的11个数字，这些数字的中位数是 ▲ ． 5．一个正比例函数的图象经过点（2，－3），它的表达式为______▲ ________. 6．如图，等腰三角形ABC 中，已知AB ＝AC ，∠A ＝30°，AB 的垂直平分线交AC 于D ，则∠CBD的度数为 ▲ °.7．如图，矩形ABCD 中，AE ⊥BD 于E ，AD =4cm,∠DAE ＝2∠BAE ，则DE = ▲ cm ． 8．已知梯形ABCD 的面积为24cm 2，高DE =4cm ，则该梯形的中位线长是 ▲ cm ． 9．已知一次函数2(2)4y m x m =-+-，当m ＝ ▲ 时，它的图象过原点．10．在直角坐标系中，一次函数334y x =+图象与坐标轴围成的三角形的周长为 ▲ ．11．如图所示，两个全等菱形的边长为1厘米，一只蚂蚁由A 点开始按ABCDEFCGA 的顺序沿菱形的边循环运动，行走2012厘米后停下，则这只蚂蚁停在 ▲ 点．12．如图，在△ABC 中，∠BAC =150º，AD ⊥BC 于D ，且AB +BD =DC ，那么∠C = ▲ °．二、选择题（共6小题，每小题3分，计18分）13．无理数3-的相反数是………………………………………（ ▲ ）A ．3-B ．3C ．31 D ．31-14．5个整数从小到大排列，中位数是4，这组数据唯一的众数是6，则这5个整数可能的最大和是（ ▲） A ． 21 B ． 22 C ． 23 D ．2415．一次函数20122012y x =-的图象不经过的象限是 …………………………（ ▲ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限ADCB E第7题 第6题 AC DE 第8题 CAF DEB G第11题 BAC第12题C BA第20题 16．如图，ABC ∆是边长为3的等边三角形，DCE ∆与ABC ∆呈轴对称，已知点B 、C 、E 在同一条直线上，连接BD ，则BD 的长为……………………………………（ ▲ ） A ．3 B ．4 C ．6 D ．2317．如图，矩形OBCD 的顶点C 的坐标为（1，3），则线段BD 的长等于…………（ ▲ ）A ．7B ．22C ．23D ．1018．如图1，在矩形MNPQ 中，动点R 从点N 出发，沿N →P →Q →M 方向运动至点M 处停止．设点R 运动的路程为x ，MNR △的面积为y ，如果y 关于x 的函数图象如图2所示，则当9x =时，点R 应运动到……………………………………（ ▲ ）A ．N 处B ．P 处C ．Q 处D ．M 处三、解答题：（共10题，计78分） 19．（每小题4分，共8分）求各式中的实数x .（1）(x － 3 )2=25 （2）27)5(3=+x20．（本题6分）在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）ABC 的顶点A ，C 的坐标分别为（4-，5），（1-，3）． ⑴请在如图所示的网格平面内作出平面直角坐标系；⑵请作出△ABC 关于y 轴对称的△A′B′C′；⑶写出点B′的坐标．21．（本题8分）已知一次函数y=kx+4的图象经过点（－3，－2），（1）求这个函数表达式；（2）建立适当坐标系，画出该函数的图象． （3）判断（－4， 4）是否在此函数的图象上；（4）把这条直线向下平移4个单位长度后的函数关系式是___▲____． EDCBA 第16题第17题第18题 QM（图1）（图2）4 9 yxO22．（本题8分）如图，在梯形ABCD 中，AB ∥CD ，BD ⊥AD ，BC =CD ，∠A =60°，CD =3cm . (1)求∠CBD 的度数； (2)求下底AB 的长.23．（本题8分）已知：如图，在ABCD 中，AE 是BC 边上的高，将ABE △沿BC 方向平移，使点E 与点C 重合，得GFC △． （1）求证：BE DG =；（2）若60B ∠=°，当AB 与BC 满足什么数量关系时， 四边形ABFG 是菱形？证明你的结论．24．（本题8分）镇江市教育局举办初中生演讲比赛，每校派一名学生参赛，某校有A 、B 、C 三名学生竞选，他们的笔试成绩和口试成绩（单位：分）分别用两种方式进行了统计，如表和图①：(1)请将表和图①中的空缺部分补充完整；(2)竞选的最后一个程序是由本校的300名学生代表进行投票，三名候选人的得票情况如图②（没有弃权票，每名学生只能推荐一人），请计算每人的得票数；(3)若每票计1分，学校里将笔试、口试、得票三项测试得分按4：3：3的比例确定最后成绩，请计算三名学生的最后成绩，并根据成绩判断谁能当选． 25．（本题8分）如图，Rt △ABC 中，∠C ＝90°，AC ＝4，BC ＝3，以△ABC 的一边为边画等腰三角形，使它的第三个顶点在△ABC 的其它边上．请在图①、图②、图③、图④中分别画出一个符合条件的等腰三角形，且四个图形中的等腰三角形各不相同，并在图中表明所画等腰三角形哪两条边相等（要求尺规作图并保留痕迹）．第25题图③ B C A 图④B C A 图①B C A 图②B C A ADGCBFE23题A BCD60°22题26．（满分8分）已知某种水果的批发单价与批发量的函数关系如图所示． （1）请说明图中①、②两段函数图象的实际意义．（2）写出批发该种水果的资金金额w （元）与批发量m （kg ）之间的函数关系式；在下图的坐标系中画出该函数图象；指出金额在什么范围内，以同样的资金可以批发到较多数量的该种水果．27．（满分8分）如图，在△ABC 中，点O 是AC 边上的一个动点（点O 不与A 、C 两点重合），过点O 作直线MN ∥BC ，直线MN 与∠BCA 的平分线相交于点E ，与∠DCA （△ABC 的外角）的平分线相交于点F ．(1)OE 与OF 相等吗？为什么？(2)探究：当点O 运动到何处时，四边形AECF 是矩形？并证明你的结论．(3)在(2)中，当∠ACB 等于多少时，四边形AECF 为正方形．(不要求说理由)28．（满分8分）如图1，在平面直角坐标系中，直线AB 与x 轴交于点A ，与y 轴交于点B ，与直线OC ：y x =交于点C ． ⑴ 若直线AB 解析式为212y x =-+，①求点C 的坐标；②求△OBC 的面积．⑵ 如图2，作AOC ∠的平分线ON ，若AB ⊥ON ，垂足为E ，△OAC 的面积为6，且OA ＝4，P 、Q 分别为线段OA 、OE 上的动点，连结AQ 与PQ ，试探索：AQ ＋PQ 是否存在最小值？ 若存在，求出这个最小值；若不存在，说明理由．O M N A ByOCx图1图2APQ ByOC xE N。

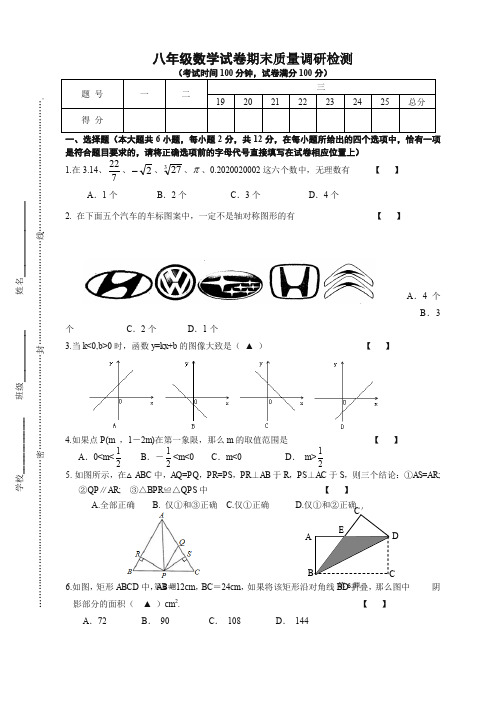
学校_____________ 班级_________姓名_____________……………………………………………密……………………………封………………………………线……………………………………….八年级数学试卷期末质量调研检测（考试时间100分钟，试卷满分100分）题 号 一 二 三19 20 21 22 23 24 25 总分 得 分一、选择题（本大题共6小题，每小题2分，共12分，在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号直接填写在试卷相应位置上） 1.在3.14、722、2-、327、π、0.2020020002这六个数中，无理数有 【 】 A ．1个 B ．2个 C ．3个 D ．4个2. 在下面五个汽车的车标图案中，一定不是轴对称图形的有 【 】A ．4个B ．3个 C ．2个D ．1个3.当k <0,b >0时，函数y =kx +b 的图像大致是（ ▲ ） 【 】4.如果点P (m ，1－2m )在第一象限，那么m 的取值范围是 【 】A ．0<m <12B ．－12<m <0C ．m <0D ． m >125. 如图所示，在△ABC 中，AQ =PQ ，PR =PS ，PR ⊥AB 于R ，PS ⊥AC 于S ，则三个结论：①AS =AR ;②QP ∥AR ; ③△BPR ≌△QPS 中 【 】A.全部正确B. 仅①和③正确C.仅①正确D.仅①和②正确6.如图，矩形ABCD 中，AB ＝12cm ，BC ＝24cm ，如果将该矩形沿对角线BD 折叠，那么图中 阴影部分的面积（ ▲ ）cm 2. 【 】 A ．72 B ． 90 C ． 108 D ． 144EC ′A BCD第5题 第6题二、填空题（本大题共10小题，每小题2分，共20分．不需写出解答过程，请把答案直接填写在试卷相应位置．．．．上） 7.比较大小：56 65.8.已知点（－1，y 1）,（2，y 2）都在直线y =－2x +6上，则y 1与 y 2大小关系是 .9.某市今年预计完成国内生产总值（GDP ）达3 466 000 000 000元，用四舍五入法取近似值，精确到10 000 000 000元并用科学记数法表示为 元．10.函数y =－3x +2的图像上存在点P ，使得P •到x •轴的距离等于3，•则点P •的坐标为 ．11.如图，已知Rt △ABC 中，∠ACB =90°，D 是AB 的中点，CD =2cm ，则AB = cm .12.一等腰三角形的的腰长为 15，底边长为18，则它底边上的高为cm ．13.从A 地到B 地的距离为60千米，一辆摩托车以平均每小时30千米的速度从A 地出发到 B 地，则摩托车距B 地的距离s （千米）与行驶时间t （时）的函数表达式为 ． 14.如图，南北向的公路上有一点A , 东西向的公路上有一点B ,若要在南北向的公路上确定点 P , 使得△PAB 是等腰三角形, 则这样的点P 最多能确定 个.15.如图，已知函数y=3x+b 和y=ax －3的图像交于点P (－2，－5)，则根据图像可得不等式 ax －3<3x +b <0的解集是 .16.如图所示，在边长为2的正三角形ABC 中，E 、F 、G 分别为AB 、AC 、BC 的中点，点P 为线段EF 上一个动点，连接BP 、GP ，则△PBG 的周长的最小值是 .三、解答题（本大题共9小题，共68分．请在试卷指定区域内作答，解答时应写出必要的文字说明、证明过程或演算步骤．．．．．．．．．．．．．．. 17.求下列各式中x 的值：（每小题3分，共6分）⑴9x 2－121＝0； ⑵ 64(x ＋1)3＝125．18.计算：（每小题4分，共8分） (1)223(6)27(5)-+-(2)()535136-+--19.（每小题8分）已知函数y =(1－2m )x +m +1，求当m 为何值时．D B C A第16题图 第11题图 第15题图 第14题图⑴y 随x 的增大而增大? ⑵图象经过第一、二、四象限? ⑶图象经过第一、三象限? ⑷图象与y 轴的交点在x 轴的上方?20.（每小题6分）如图，在平面直角坐标系中，A (－1，5)，B (－3，1)，C (－6，3)． (1)在图中作出△ABC 关于y 轴的对称图形△A 1B 1C 1； (2)写出△ABC 关于x 轴的对称图形△A2B 2C 2 顶点A 2、B 2、C 2的坐标．21.（每小题7分）已知一次函数y =kx +b 的图象经过点（﹣1，﹣5），且与正比例函数x y 21的图象相交于点（2 ，a ）．⑴求一次函数y =kx +b 的表达式；⑵在同一坐标系中，画出这两个函数的图象， 并求这两条直线与y 轴围成的三角形的面积．22.（每小题8分）如图所示，在四边形ABCD 中，AD ∥BC ，E 为CD 的中点，连接AE 、BE ，BE ⊥AE ，延长AE 交BC 的延长线于点F ． 求证：⑴FC =AD ；⑵AB =BC +AD ．23.（每小题8分）如图，直线y ＝－43x ＋8与x 轴、y 轴分别相交于点A 、B ，设M 是OB 上一点，若将△ABM 沿AM 折叠，使点B 恰好落在x 轴上的点B '处．求： (1)点B '的坐标；(2)直线AM 所对应的函数关系式．24.（每小题9分）已知在等腰△ABC 中，AB ＝AC ，在射线CA 上截取线段CE ，在射线AB 上截取线段BD ，连结DE ，DE 所在直线交直线BC 于点M .请探究：⑴如图①，当点E 在线段AC 上，点D 在AB 延长线上时，若BD ＝CE ，请判断线段MD 和线段ME 的数量关系，并证明你的结论；⑵如图②，当点E 在CA 的延长线上，点D 在AB 的延长线上时，若BD ＝CE ，则⑴中的结论还成立吗？如果成立，请证明；如果不成立，说明理由.⑶如图③，当点E 在CA 的延长线上，点D 在线段AB 上（点D 不与A 、B 重合），DE 所在直线与直线BC 交于点M ，若CE ＝2BD ，请你判断线段MD 与线段ME 的数量关系，并说明理由.ABC E MD图①A BCEM 图②25.（每小题8分）小聪和小明沿同一条路同时从学校出发到图书馆查阅资料，学校与图书馆的路程是4千米，小聪骑自行车，小明步行，当小聪从原路回到学校时，小明刚好到达图书馆，图中折线O －A －B －C 和线段OD 分别表示两人离学校的路程s （千米）与所经过的时间t （分钟）之间的函数关系，请根据图象回答下列问题：⑴小聪在图书馆查阅资料的时间为________分钟，小聪返回学校的速度为_____千米/分钟. ⑵请你求出小明离开学校的路程s （千米）与所经过的时间t （分钟）之间的函数关系; ⑶当小聪与小明迎面相遇时，他们离学校的路程是多少千米？s （千米） t （分钟）ABDC 304515O2 4 小聪 小明参考答案一、选择题BCCA DB二、填空题7. > 8. y 1> y 2 9.3.47×1012 10.⎪⎭⎫⎝⎛-3,31或⎪⎭⎫ ⎝⎛-3,35 11.4 12.12 13.s =60－30t (0≦t ≦2) (没有t 范围不给分) 14.4 15.212-<<-x 16.3 三、解答题17.求下列各式中x 的值：⑴9x 2－121＝0； ⑵ 64(x ＋1)3＝125．9x 2＝121 (x ＋1)3＝125/64x 2＝121/9 ………… 1分 x ＋1 =5/4………… 2分x =±11/3 ………… 3分 x =1/4 ………… 3分18.计算：(1)223(6)27(5)-+- (2)()535136-+--＝6＋3－5 …………3分 ＝3－5＋1－6 ………… 3分 ＝4 …………4分 ＝－2－5 ………… 4分19.(1)∵y 随x 的增大而增大 ∴1－2m >0 ∴m <21…………2分 (2)∵图象经过第一、二、四象限 ∴⎩⎨⎧>+<0102-1m m ∴m >21…………4分(3)∵图象经过第一、三象限 ∴⎩⎨⎧=+>0102-1m m ∴m = －1 …………6分(4)∵图象与y 轴的交点在x 轴的上方 ∴m +1>0 ∴m > －1 …………8分 20.⑴图略 …………3分⑵A 2(－1,－5) 、B 2(－3,－1)、C 2(－6,－3) …………6分 21.（1）∵正比例函数x y 21=经过点（2，a ） ∴a =12×2=1 … … … … 1分∵一次函数y =kx +b 的图象经过点（﹣1，﹣5）与（2，1）∴⎩⎨⎧=+-=+1b 2k5b -k … … … … … … … … … … … …2分∴ 解得⎩⎨⎧-==3b2k∴y =2x ﹣3 … … … … … … … … … … … … 4分（3）画图略 … … … … … … … … … … … … 6分 S =2321⨯⨯=3 … … … … … … … … … … … … 7分 22.证明：（1）∵ AD ∥BC （已知），∴ ∠ADC =∠ECF （两直线平行，内错角相等）.∵ E 是CD 的中点（已知），∴ DE =EC （中点的定义）．∵ 在△ADE 与△FCE 中，∠ADC =∠ECF ，DE =EC ，∠AED =∠CEF ， ∴ △ADE ≌△FCE （ASA ）， … … … … … … … … … … … 3分 ∴ FC =AD （全等三角形的性质）． … … … … … … … … … … … 4分（2）∵ △ADE ≌△FCE ，∴ AE =EF ，AD =CF （全等三角形的对应边相等）. 又BE ⊥AE ，∴ BE 是线段AF 的垂直平分线， … … … … … … … … … … … 6分 ∴ AB =BF =BC +CF . ∵ AD =CF （已证），∴ AB =BC +AD （等量代换）． … … … … … … … … … … …8分 23.(1)当x =0时，y =8 B (0，8)当y =0时，x =6 A (6，0) … … … … … … … … … … …2分 ∴AO =6，BO =9∴AB '=AB =10 ∴BB 'O =4∴B '(－4，0) … … … … … … … … … … …3分 (2) ∵△ABM 沿AM 折叠∴B 'M =BM设OM =x ,则B 'M =BM =8－x , x 2＋42＝(8－x )2x ＝3∴M (0，3) … … … … … … … … … … …5分 设直线AM 所对应的函数关系式y =kx +b∴6k +b =0 又∵b =3解得k =－0.5 … … … … … … … … … … …7分 ∴y = －0.5x +3 … … … … … … … … … … …8分 24.解：（1）DM ＝EM ；证明：过点E 作EF ∥AB 交BC 于点F ， ∵AB ＝AC ，∴∠ABC ＝∠C ；又∵EF ∥AB ，∴∠ABC ＝∠EFC ，∴∠ EFC ＝∠C ， ∴EF ＝EC ．又∵BD ＝EC ，∴EF ＝BD ． 又∵EF ∥AB ，∴∠ADM ＝∠MEF ．在△DBM 和△EFM 中，∠BDE ＝∠FEM ，∠BMD ＝∠FME ，BD ＝EF ∴△DBM ≌△EFM ，∴DM ＝EM ． ……………..3分 （2）成立；证明：过点E 作EF ∥AB 交CB 的延长线于点F ， ∵AB ＝AC ，∴∠ABC ＝∠C ；又∵EF ∥AB ，∴∠ABC ＝∠EFC ， ∴∠EFC ＝∠C ，∴EF ＝EC ． 又∵BD ＝EC ，∴EF ＝BD ．又∵EF ∥AB ，∴∠ADM ＝∠MEF ．在△DBM 和△EFM 中，∠BDE ＝∠FEM ，∠BMD ＝∠FME ，BD ＝EF ∴△DBM ≌△EFM ；∴DM ＝EM ； … … … … … … … … … … …7分 ⑶过点E 作EF ∥AB 交CB 的延长线于点F ，过D 作DN ∥FC 交EF 于N , 由（2）可知EC =EF ∴EC :BD =EF :BD =2:1∴四边形FBDN 为平行四边形 ∴NF =NE ∴N 是EF 的中点 ∴D 是EM 的中点∴EM =2DM … … … … … … … … … … …9分 25.解：（1）15，154… … … … … … … … … … …2分（2）由图像可知，s 是t 的正比例函数 设所求函数的解析式为kt s =（0≠k ） 代入（45，4）得：k 454= 解得：454=k ∴s 与t 的函数关系式t s 454=（450≤≤t ） … … … … … … …4分 （3）由图像可知，小聪在4530≤≤t 的时段内s 是t 的一次函数，设函数解析式为n mt s +=（0≠m ）代入（30，4），（45，0）得：⎩⎨⎧=+=+045430n m n m解得：⎪⎩⎪⎨⎧=-=12154n m∴12154+-=t s （4530≤≤t ） … … … … … … … … … … …6分 令t t 45412154=+-，解得4135=t 当4135=t 时，34135454=⨯=S 答：当小聪与小明迎面相遇时，他们离学校的路程是3千米. … … … … … …8分。

一、选择题（每题5分，共25分）1. 下列各数中，有理数是（）A. √9B. √-9C. √0D. √22. 已知a > b，下列不等式中正确的是（）A. a + b > 2bB. a - b < 2aC. a - b > 2bD. a + b < 2a3. 若方程2x - 3 = 0的解为x，则x的值是（）A. 1.5B. 2C. 3D. 44. 下列各式中，同类项是（）A. 3a^2bB. 4ab^2C. 5a^2D. 6ab5. 在直角坐标系中，点A（2，3）关于原点的对称点是（）A.（-2，-3）B.（2，-3）C.（-2，3）D.（3，-2）二、填空题（每题5分，共25分）6. 若a = -3，则|a|的值为______。

7. 已知x + 2 = 5，则x的值为______。

8. 在△ABC中，∠A = 60°，∠B = 45°，则∠C的度数是______。

9. 2x^2 - 5x + 3的因式分解结果是______。

10. 若函数f(x) = 2x + 3，则f(-1)的值为______。

三、解答题（共50分）11. （10分）计算下列各式的值：（1）-3x^2 + 5x - 2，当x = -2时的值；（2）3x^2 - 4x + 1，当x = 1/2时的值。

12. （10分）解下列方程：（1）2x - 5 = 3x + 1；（2）5x^2 - 2x - 3 = 0。

13. （15分）在直角坐标系中，已知点A（-2，3），点B（4，-1），求：（1）点A关于x轴的对称点A'的坐标；（2）直线AB的斜率；（3）点B关于直线y = x的对称点B'的坐标。

14. （15分）已知二次函数f(x) = ax^2 + bx + c（a ≠ 0），若f(1) = 4，f(-1) = 0，且a + b + c = 3，求：（1）a、b、c的值；（2）函数f(x)的图像与x轴的交点坐标。

2011—2012学年度上学期期末考试八年级数学试卷姓名：学号：得分：一、选择题（每小题3分，共30分） 请将你认为正确的答案代号填在下表中1．对称现象无处不在，请你观察下面的四个图形，它们体现了中华民族的传统文化，其中，可以看作是轴对称图形的有 A ．1个B ．2个C ．3个D ．4个2．如图，D 、E 、F 分别是等边△ABC 各边上的点，且AD ＝BE ＝CF ，则△DEF 的形状是 A ．等边三角形 B ．腰和底边不相等的等腰三角形 C ．直角三角形 D ．不等边三角形 3．如果2(x －2)3＝643，则x 等于A ．21 B ．27 C ．21或27 D ．以上答案都不对4．下列多项式中不含因式(x －1)的是 A ．x 3－x 2－x ＋1 B ．x 2＋y －xy －x C ．x 2－2x －y 2＋1 D ．(x 2＋3x )2－(2x ＋2)25．估算324+的值 A ．在5和6之间B ．在6和7之间C ．在7和8之间D ．在8和9之间6．下列可使两个直角三角形全等的条件是 A ．一条边对应相等 B ．斜边和一直角边对应相等 C ．一个锐角对应相等 D ．两个锐角对应相等7．化简()()()()13131313842++++得A ．()2813+B ．()2813-C ．1316-D ．()132116-8．如图，∠B 、∠C 的平分线相交于F ，过点F 作DE ∥BC ，交 AB 于D ，交AC 于E ，那么下列结论正确的是 ①△BDF 、△CEF 都是等腰三角形； ②DE ＝BD ＋CE ； ③△ADE 的周长为AB ＋AC ； ④BD ＝CE ；A ．③④B ．①②C ．①②③D ．②③④9．图中的三角形是有规律地从里到外逐层排列的。

设y 为第n 层 （n 为正整数）三角形的个数，则下列函数关系式中正确的是 A ．y ＝4n －4 B ．y ＝4n C ．y ＝4n ＋4D ．y ＝n 210．父亲节，学校“文苑”专栏登出了某同学回忆父亲的小诗：“同辞家门赴车站，别时叮咛语千万，学子满载信心去，老父怀抱希望还。