数学---山东省菏泽市郓城高级中学2017届高三上学期期中考试试题(文)

高三数学测试题2(文史类)一、选择题：本大题共10个小题，每小题5分．共50分． 1.已知集合}2|1||{≤-=x x M ⎭⎬⎫⎩⎨⎧≥+=115|x x N ，则N M 等于（ ）A.[]3,1-B. (]3,1-C.[]4,1-D. (]4,1-2. 已知i 为虚数单位，R a ∈，若ia i+-2为纯虚数，则复数i a z 2)12(++=的模等于（ ） A ．2 B ．3 C ．6 D ．11 3．已知函数()1,0,,0.xx x f x a x -≤⎧=⎨>⎩若()()11f f =-，则实数a 的值等于（ ）A ．1B ．2C ．3D ．44. 命题“若220a b +=，则0a =且0b =”的逆否命题是（ ）A ．若220a b +≠，则0a ≠且0b ≠B ．若220a b +≠，则0a ≠或0b ≠C ．若0a ≠且0b ≠，则220a b +≠D ．若0a ≠或0b ≠，则220a b +≠5.某三棱锥的三视图如图所示，则该三棱锥的体积为（ ） A ．23 B ．16C ．1 D ．136. 下列说法中正确的个数为（ ）①若样本数据12,,,n x x x 的平均数5x =，则样本数据1221,21,,21n x x x +++ 的平均数为10②将一组数据中的每个数据都减去同一个数后， 平均数与方差均没有变化③采用系统抽样法从某班按学号抽取5名同学参加活动，学号为5,16,27,38,49的同学均被选出，则该班学生人数可能为60 A ．0B ．1C ． 2D ．37.函数()()sin ln 1f x x x =⋅+的图象大致为（ ）8.函数()sin()3f x x πω=+的图象向右平移3π个单位后与原函数的图象关于x 轴对称，则ω的最小正值是 （ ）A ． 12B ．1C ．2D ．39.已知12,F F 为椭圆22221(0)x y a b a b+=>>的左、右焦点，以原点O 为圆心，半焦距为半径的圆与椭圆相交于四个点，设位于y 轴右侧的两个交点为,B A ，若1ABF 为等边三角形，则椭圆的离心率为（ ）1B. 1C.12D. 10. 设函数[],0(),(1),0x x x f x f x x -≥⎧=⎨+<⎩其中][x 表示不超过x 的最大整数，如[ 1.2]-=-2，]2.1[=1，]1[=1，若直线(0)y kx k k =+>与函数y=)(x f 的图象恰有三个不同的交点，则k 的取值范围是 （）A ．]31,41(B ．]41,0(C ．]31,41[D ．)31,41[ 二、填空题：本大题共5小题，每小题5分，共25分.11. 执行如图所示的程序框图，若输入K=5，则输出的S 是12 .设x ，y 满足约束条件110x y x y x +≤⎧⎪-≤⎨⎪≥⎩,则目标函数2z x y=-的取值范围为 ．13.在区间[]1,2上随机取一个数r ，则使得圆222x y r +=与直线20x y ++=存在公共点的概率为14.四边形ABCD 中，BD AC ⊥且3,2==BD AC ，⋅的最小值为 15.给出以下四个结论：①函数()211x f x x -=+的对称中心是()1,2-； ②若关于x 的方程()100,1x k x x-+=∈在没有实数根，则k 的取值范围是2k ≥；③在ABC ∆中，“cos cos b A a B =”是“ABC ∆为等边三角形”的必要不充分条件④若将函数()sin 23f x x π⎛⎫=- ⎪⎝⎭的图象向右平移()0ϕϕ>个单位后变为偶函数，则ϕ的最小值是12π.其中正确的结论是____. 三、解答题：本大题共6小题，共75分，解答应写出文字说明，证明过程或演算步骤. 16.（本题满分12分）已知函数()2sin cos sin sin 44f x x x x x x ππ⎛⎫⎛⎫=+++- ⎪ ⎪⎝⎭⎝⎭.（I ）求()f x 的最小正周期和单调增区间； （Ⅱ）若()0002x x x f x π⎛⎫=≤≤ ⎪⎝⎭为的一个零点，求0cos 2x 的值.17.(本题满分12分)某市为了了解今年高中毕业生的体能状况，从某校高中毕业班中抽取一个班进行铅球测试，成绩在8.0米(精确到0.1米)以上的为合格．数据分成6组画出频率分布直方图的一部分(如图)，已知从左到右前5个小组的频率分别为0.04，0.10，0.14，0.28，0.30 .第6小组的频数是7.（Ⅰ）求这次铅球测试成绩合格的人数；（Ⅱ）若参加测试的学生中9人成绩优秀，现要从成绩优秀的学生中，随机选出2人参加“毕业运动会”，已知学生a 、b 的成绩均为优秀，求两人a 、b 至少有1人入选的概率.18.(本题满分12分)如图，AB 为圆O 的直径，点E 、F 在圆O 上，且//AB EF ，矩形ABCD 所在的平面和圆O 所在的平面互相垂直，且2AB =，1AD EF ==.（I ）求证：AF ⊥平面CBF ；（Ⅱ）设FC 的中点为M ，求证：//OM 平面DAF ； （III ）设平面CBF 将几何体EFABCD 分成的两个锥体的体积分别为F ABCD V -，F CBE V -，求:F ABCD F CBE V V --．19. （本小题满分12分）已知正项数列{}n a 的前n 项和为n S ，且21111,n n n a S S a ++=+=，数列{}n b 满足1131n a n n b b b +⋅==，且.（I ）求数列{}n a ，{}n b 的通项公式；（II ）记21412n n n n T a b a b a b -=++⋅⋅⋅+，求n T .20.（本小题满分13分）已知函数()ln ,f x ax x a R =+∈.（I ）讨论()f x 的单调性；（II ）若()()g x f x ax =-⎤⎦，且对任意()11xx g x x λ'≥-≥+恒成立，求实数λ的取值范围.21.（本小题满分14分）在平面直角坐标系xOy 中，椭圆()2222:10x y C a b a b+=>>的左、右焦点分别为12F F 、，且离心率是12，过坐标原点O 的任一直线交椭圆C 于M ，N 两点，且224NF MF +=.（I ）求椭圆C 的方程；（II ）若直线:l y kx m =+与椭圆C 交于不同的两点A 、B ，且与圆221x y +=相切.（i ）求证：221m k =+；（ii ）求OA OB ⋅ 的最小值.高三数学测试题2(文史类)答案一、BCBDD AADBD二、18 []-1,2 134- ①_③_④三、16.解：（I ）()2sin cos sin sin 44f x x x x x x ππ⎛⎫⎛⎫=+++- ⎪ ⎪⎝⎭⎝⎭()()21sin 2sin cos sin cos 2x x x x x x =++- 1cos 2112cos 22cos 2222x x x x x -=-=-+12sin 262x π⎛⎫=-+ ⎪⎝⎭ -3分 ()f x 的最小正周期为π……………. 4分222,,26263k x k k x k k Z πππππππππ-≤-≤+∴-≤≤+∈函数()f x 的单调递增区间是[,],63k k k Z ππππ-+∈ ……………6分 （II ）()000112sin 20sin 26264f x x x ππ⎛⎫⎛⎫=-+=∴-=- ⎪ ⎪⎝⎭⎝⎭……..------8分 00050,220266666x x x ππππππ≤≤-≤-≤∴-≤-<0cos 26x π⎛⎫-== ⎪⎝⎭分0000cos 2cos 2cos 2cos sin 2sin 666666x x x x ππππππ⎛⎫⎛⎫⎛⎫=-+=--- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭11142428=+⨯=--12分 17.解：（Ⅰ）第6小组的频率为1－(0.04＋0.10＋0.14＋0.28＋0.30)＝0.14，∴此次测试总人数为7500.14=(人). ∴第4、5、6组成绩均合格，人数为(0.28＋0.30＋0.14)×50＝36(人)． --4分 （Ⅱ）设成绩优秀的9人分别为,,,,,,,,,a b c d e f g h k 则选出的2人所有可能的情况为：,,,,,,,;ab ac ad ae af ag ah ak ,,,,,,;bc bd be bf bg bh bk ,,,,,;cd ce cf cg ch ck ,,,,;de df dg dh dk ,,,;ef eg eh ek ,,;fg fh fk ,;gh gk hk . 共36种，其中a 、b 到少有1人入选的情况有15种，∴a 、b 两人至少有1人入选的概率为155.3612P ==--12分 18.解：（1）证明： 平面⊥ABCD 平面ABEF ,AB CB ⊥,平面 ABCD 平面ABEF =AB ， ⊥∴CB 平面ABEF ，⊂AF 平面ABEF ，CB AF ⊥∴ , 又AB 为圆O 的直径，BF AF ⊥∴，⊥∴AF 平面CBF . ---------4分（2）设DF 的中点为N ，则MN //CD 21，又AO //CD 21，则MN//AO ，MNAO 为平行四边形，//OM ∴AN ，又⊂AN 平面DAF ，⊄OM 平面DAF ，//OM ∴平面DAF . --------8分（3）过点F 作AB FG ⊥于G ， 平面⊥ABCD 平面ABEF ，⊥∴FG 平面ABCD ，FG FG S V ABCD ABCD F 3231=⋅=∴-，⊥CB 平面ABEF ，CB S V V BFE BFE C CBE F ⋅==∴∆--31FG CB FG EF 612131=⋅⋅⋅=，ABCD F V -∴1:4:=-CBE F V ． ------------------12分。

2016-2017学年山东省菏泽一中高三(上）第一次月考数学试卷(文科）一、选择题（本大题共10个小题;每小题5分,共50分．在每小题给出的4个选项中,只有一项符合题目要求.）1．设全集U={1，2，3，4,5}，集合A=｛2,3,4}，B=｛2，5}，则B∪（∁U A）=（）A．｛5}B．｛1，2,5｝C．{1，2,3，4，5}D．∅2．已知函数f（x)=，则f(f（)）=（）A．B．C．D．3．下列四种说法中，错误的个数是（）①A=｛0，1｝的子集有3个；②“若am2＜bm2，则a＜b"的逆命题为真；③“命题p∨q为真”是“命题p∧q为真”的必要不充分条件;④命题“∀x∈R，均有x2﹣3x﹣2≥0”的否定是：“∃x∈R，使得x2﹣3x﹣2≤0”A．0个B．1个C．2个D．3个4．设函数f(x）=,则满足f（x）≤2的x的取值范围是（)A．［﹣1,2]B．[0，2］C．[1，+∞）D．［0，+∞）5．下列函数中，既是偶函数又在（0，+∞）单调递增的函数是(）A．y=3x B．y=|x|+1 C．y=﹣x2+1 D．y=6．若a=log23,b=log32，2，c=log2,则a，b,c的大小关系是（)A．a＜b＜c B．b＜c＜a C．c＜b＜a D．c＜a＜b7．若f（x）为奇函数且在（0，+∞）上递增,又f（2）=0,则的解集是（）A．(﹣2，0）∪(0，2）B．（﹣∞，2）∪(0，2）C．（﹣2，0)∪（2，+∞) D．（﹣∞，﹣2）∪（2,+∞）8．已知命题p：关于x的函数y=x2﹣3ax+4在[1,+∞）上是增函数，命题q：y=（2a﹣1)x为减函数，若p且q为真命题，则a的取值范围是（)A．B．C．D．9．函数f（x）=的零点个数为（）A．0 B．1 C．2 D．310．已知函数f(x)=，满足对任意的x1≠x2都有＜0成立，则a的取值范围是（）A．（0,］B．（0，1）C．［，1）D．（0，3)二、填空题（本大题共5小题，每小题5分，共25分,请将答案填在答题纸上）11．命题“对任意的x∈R,x3﹣x2+1≤1"的否定是．12．函数f（x）对于任意实数x满足条件f（x+2）=，若f（1)=﹣5，则f[f(5）］=．13．若，则实数a的取值范围是．14．已知函数y=f(x)满足f(x+1）=f（x﹣1），且x∈[﹣1，1]时,f(x)=x2，则函数y=f（x）与y=log3|x｜的图象的交点的个数是．15．若存在负实数使得方程2x﹣a=成立，则实数a的取值范围是．三、解答题:本大题共6小题,共75分，解答应写出文字说明，证明过程或演算步骤。

山东省菏泽市2018届高三上学期期中考试数学（文）试题（B）第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知集合，则（）A. B. C. D.【答案】B【解析】由题意得：∴故选：B点睛：在进行集合的运算时要尽可能地借助Venn图和数轴使抽象问题直观化．一般地，集合元素离散时用Venn图表示；集合元素连续时用数轴表示，用数轴表示时要注意端点值的取舍．2. 函数的定义域为（）A. B. C. D.【答案】A【解析】由题意可得：，解得：∴定义域为：故选：A3. 若，且，则的值为（）A. 2B.C. 1D.【答案】A【解析】易得：∵，∴，∴，即故选：A4. 已知，则（）A. B. C. D.【答案】D【解析】，选D.5. 下列函数中，既是偶函数又在区间上为增函数的是（）A. B. C. D.【答案】D【解析】对于A，为非奇非偶函数，在区间上为增函数，错误；对于B，为偶函数，在区间上为减函数，错误；对于C，为奇函数，在区间上为增函数，错误；对于D，偶函数，在区间上为增函数，正确；故选;D6. 中，角所对的边为，已知，则角等于（）A. B. C. 或 D. 以上都不对【答案】A【解析】试题分析：在中，，由正弦定理，得：，又故选A．考点：正弦定理．7. 将函数的图象向左平移个单位，所得的图象对应的函数解析式是（）A. B. C. D.【答案】C【解析】的图象向左平移单位得到的图象，即将函数的图象向左平移个单位，所得的图象所对应的函数解析式是，故选C.8. 函数的一个零点落在区间（）A. B. C. D.【答案】B所以零点一定在（1，2）内.选B考点：函数的零点9. 在中，则“”是“”的（）A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件【答案】C【解析】由题意等价于,根据正弦定理可得,即,则中，“” 是“”的充要条件,故选C.10. 命题“且”的否定形式是（）A. 且B. 且C. 或D. 或【答案】C【解析】命题“且”的否定形式是或故选：C11. 若函数的图象与轴没有交点，则实数的取值范围是（）A. 或B. 或C. 或D. 或【答案】A【解析】∵函数的图象与轴没有交点∴无解，即，又，∴，解得：或故选：A点睛：已知函数有零点求参数取值范围常用的方法和思路(1)直接法：直接根据题设条件构建关于参数的不等式，再通过解不等式确定参数范围；(2)分离参数法：先将参数分离，转化成求函数值域问题加以解决；(3)数形结合法：先对解析式变形，在同一平面直角坐标系中，画出函数的图象，然后数形结合求解．12. 已知函数是函数的导函数，，对任意实数都有，设则不等式的解集为（）A. B. C. D.【答案】B【解析】,又,∴,即在定义域上单调递减。

2016—2017学年度上学期高三期中考试语文试题 （时间：150分钟 满分：150分 用黑色笔书写)第Ⅰ卷（选择题,共36分) 一、（15分，每题3分）阅读下面文段，完成1~3小题。

昨夜做了一场梦，梦见自己一（甲)青衣，漫步．．在长安街头.走过十里长街，用指尖轻抚斑驳．．的城墙，眼前的烟雨都幻化．．成了朦胧．．的诗篇， .醒来，已是月挂中天,窗外的高楼向我陈述美梦一场的无奈。

我忽然份外．．思念故事里的长安，想去看看那个让我魂牵梦绕的地方。

梦里长安,若为女子，定是容色倾城，恰似牡丹，娇媚华贵;若为男儿,定是温文如玉,犹如翠竹，风流倜傥．．。

长安之于我,是一处江湖。

容许我打马走过十里长街，容许我煮茶一盏坐至天明，亦容许我（乙）半卷诗书但看江湖恩怨.我时常幻想，千年后的长安街头, ，提一壶酒，满腹惆怅．．都寄寓．．其中，然后（丙）明月对饮，来一场不醉不归。

1。

文中加点词语的书写有错误的一项是( )A 。

漫步 斑驳 B.朦胧 份外C 。

幻化 倜傥D 。

惆怅 寄寓2.依次填入甲、乙、丙三处的词语，最恰当的一项是( ）A 。

袭 读 赏 B.身 枕 邀C 。

袭 枕 邀D 。

身 读 赏3。

在文中两处横线上依次填入语句，衔接最恰当的一项是 ( ) A 。

千年来的等待与缠绵向我诉说 是否也会有一个失意之人B 。

向我诉说着千年来的等待与缠绵 是否有人会失意C 。

千年来的等待与缠绵向我诉说 是否有人会失意D 。

向我诉说着千年来的等待与缠绵 是否也会有一个失意之人4.下列各句中，加点的成语使用恰当的一句是（ ）A ．现在一些大学生制作简历时，多彩色打印，铜版纸印刷，贴艺术照,不惜工本，然而那些华而不实的简历即使投到用人单位也不过是泥牛入海．．．．，起不到实际的求职作用。

B ．我呸！你是招聘教师，又不是选美，凭什么女的要长得人面桃．．．花．，男的要身高一米七五？C ．一个人要勇敢改过,不断修正自己的行为，努力成为一个高尚的人。

2017-2018学年山东省菏泽市高三（上）期中数学试卷（文科）（B卷）一、选择题（共12小题，每小题5分，满分60分）1．（5分）已知集合A={﹣2，0，2}，B={x|x2﹣x﹣2=0}，则A∩B=（）A．∅B．{2}C．{0}D．{﹣2}2．（5分）函数f（x）=的定义域为（）A．（0，1） B．[0，1） C．（﹣∞，1）D．（0，+∞）3．（5分）若f（x）=，且f（f（e））=10，则m的值为（）A．2 B．﹣1 C．1 D．﹣24．（5分）已知cosx=，则cos2x=（）A．﹣ B．C．﹣ D．5．（5分）下列函数中，既是偶函数又在区间（0，1）上为增函数的是（）A．y=e x B．y=x﹣2C．y=sinx D．y=ln|x|6．（5分）在△ABC中，角A、B、C所对的边分别为a、b、c，已知a=3，b=，A=，则角B等于（）A．B． C．或D．以上都不对7．（5分）将函数的图象向左平移个单位，所得的图象所对应的函数解析式是（）A．y=sin2x B．y=cos2x C． D．8．（5分）函数f（x）=﹣+log2x的一个零点落在下列哪个区间（）A．（0，1） B．（1，2） C．（2，3） D．（3，4）9．（5分）在△ABC中，“A＞B“是“tanA＞tanB的（）A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件10．（5分）命题“∀n∈N，f（n）∈N且f（n）＞n”的否定形式是（）A．∀n∈N，f（n）∉N且f（n）≤n B．∀n∈N，f（n）∉N且f（n）＞nC．∃n0∈N，f（n0）∉N或f（n0）≤n0D．∃n0∈N，f（n0）∉N且f（n0）＞n0 11．（5分）若函数f（x）=（）|x﹣1|+m的图象与x轴没有交点，则实数m的取值范围是（）A．m≥0或m＜﹣1 B．m＞0或m＜﹣1 C．m＞1或m≤0 D．m＞1或m＜0 12．（5分）已知函数f′（x）是函数f（x）的导函数，f（1）=，对任意实数都有f（x）﹣f′（x）＞0，设F（x）=，则不等式F（x）＜的解集为（）A．（﹣∞，1）B．（1，+∞）C．（1．e） D．（e，+∞）二、填空题（共4小题，每小题5分，满分20分）13．（5分）已知α是锐角，且cos（α+）=，则sin（﹣α）=．14．（5分）已知函数f（x）是定义在R上的周期为2的奇函数，当0＜x＜1时，f（x）=9x，则=．15．（5分）已知函数f（x）=e x﹣mx+1的图象为曲线C，若曲线C存在与直线y=ex 垂直的切线，则实数m的取值范围为．16．（5分）已知函数f（x）=sinx+cosx，则下列命题正确的是（填上你认为正确的所有命题的序号）①函数f（x）的最大值为2；②函数f（x）的图象关于点（，0）对称；③函数f（x）的图象关于直线x=对称；④函数f（x）在[，π]上单调递减．三、解答题（共6小题，满分70分）17．（10分）已知p：|x﹣a|＜3（a为常数）；q：代数式有意义．（1）若a=1，求使“p∧q”为真命题的实数x的取值范围；（2）若p是q成立的充分不必要条件，求实数a的取值范围．18．（12分）在△ABC中，内角A，B，C的对边长分别为a，b，c，且（2b﹣c）cosA=acosC．（1）求角A的大小；（2）若a=3，b=2c，求△ABC的面积．19．（12分）已知函数f（x）=（sinx+cosx）2+cos2x（1）求f（x）最小正周期；（2）求f（x）在区间上的最大值和最小值．20．（12分）已知函数f（x）=x2﹣3lnx．（1）求f（x）在（1，f（1））处的切线方程；（2）试判断f（x）在区间（1，e）上有没有两个零点？若有则判断零点的个数．21．（12分）在某次水下科研考察活动中，需要潜水员潜入水深为60米的水底进行作业，根据以往经验，潜水员下潜的平均速度为v（米/单位时间），每单位时间的用氧量为（）3+1（升），在水底作业10个单位时间，每单位时间用氧量为0.9（升）返回水面的平均速度为（米/单位时间），每单位时间用氧量我1.5（升），记该潜水员在此次考察活动中的总用氧量为y（升）．（1）求y关于v的函数关系；（2）求当下潜速度v取什么值时，总用氧量最少．22．（12分）已知函数f（x）=（x2+mx）e x（其中e为自然对数的底数）．（1）当m=﹣2时，求函数f（x）的单调递增区间；（2）若函数f（x）在区间[1，3]上单调递减，求m的取值范围．2017-2018学年山东省菏泽市高三（上）期中数学试卷（文科）（B卷）参考答案与试题解析一、选择题（共12小题，每小题5分，满分60分）1．（5分）已知集合A={﹣2，0，2}，B={x|x2﹣x﹣2=0}，则A∩B=（）A．∅B．{2}C．{0}D．{﹣2}【解答】解：∵A={﹣2，0，2}，B={x|x2﹣x﹣2=0}={﹣1，2}，∴A∩B={2}．故选：B．2．（5分）函数f（x）=的定义域为（）A．（0，1） B．[0，1） C．（﹣∞，1）D．（0，+∞）【解答】解：由题意得：，解得：0＜x＜1，故函数的定义域是（0，1），故选：A．3．（5分）若f（x）=，且f（f（e））=10，则m的值为（）A．2 B．﹣1 C．1 D．﹣2【解答】解：∵f（x）=，且f（f（e））=10，∴f（e）=lne=1，f（f（e））=f（1）=2+m3=10，解得m=2．故选：A．4．（5分）已知cosx=，则cos2x=（）A．﹣ B．C．﹣ D．【解答】解：∵根据余弦函数的倍角公式cos2x=2cos2x﹣1，且cosx=，∴cos2x=2×﹣1=．故选：D．5．（5分）下列函数中，既是偶函数又在区间（0，1）上为增函数的是（）A．y=e x B．y=x﹣2C．y=sinx D．y=ln|x|【解答】解：函数y=e x在区间（0，1）上单调递增，但是非奇非偶函数，不满足题意；函数y=x﹣2|在区间（0，1）上单调递减，且是偶函数，不满足题意；函数y=sinx|在区间（0，1）上单调递增，但是奇函数，不满足题意；函数y=ln|x|在区间（0，1）上单调递增，且是偶函数，满足题意；故选：D．6．（5分）在△ABC中，角A、B、C所对的边分别为a、b、c，已知a=3，b=，A=，则角B等于（）A．B． C．或D．以上都不对【解答】解：由正弦定理可得：=，解得sinB=．∵a＞b，∴A＞B，因此B为锐角．∴B=．故选：A．7．（5分）将函数的图象向左平移个单位，所得的图象所对应的函数解析式是（）A．y=sin2x B．y=cos2x C． D．【解答】解：将函数的图象向左平移个单位，所得的图象所对应的函数解析式为y=sin[2（x+）+]=sin（2x+）的图象，故选：C．8．（5分）函数f（x）=﹣+log2x的一个零点落在下列哪个区间（）A．（0，1） B．（1，2） C．（2，3） D．（3，4）【解答】解：根据函数的实根存在定理得到f（1）•f（2）＜0．故选：B．9．（5分）在△ABC中，“A＞B“是“tanA＞tanB的（）A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件【解答】解：当A=，B=时，满足A＞B，但是tanA=﹣，tanB=，tanA ＜tanB，所以△ABC中，“A＞B”推不出“tanA＞tanB”；当tanA＞tanB，取A=，B=，满足tanA＞tanB，推不出A＞B，∴“A＞B”是“tanA＞tanB”的既不充分也不必要条件，故选：D．10．（5分）命题“∀n∈N，f（n）∈N且f（n）＞n”的否定形式是（）A．∀n∈N，f（n）∉N且f（n）≤n B．∀n∈N，f（n）∉N且f（n）＞nC．∃n0∈N，f（n0）∉N或f（n0）≤n0D．∃n0∈N，f（n0）∉N且f（n0）＞n0【解答】解：由全称命题的否定为特称命题可知：命题“∀n∈N，f（n）∈N且f（n）＞n”的否定形式是∃n0∈N，f（n0）∉N或f（n0）≤n0，故选：C．11．（5分）若函数f（x）=（）|x﹣1|+m的图象与x轴没有交点，则实数m的取值范围是（）A．m≥0或m＜﹣1 B．m＞0或m＜﹣1 C．m＞1或m≤0 D．m＞1或m＜0【解答】解：∵y=（）|x﹣1|≤（）0=1，即y=（）|x﹣1|∈（0，1），∴函数f（x）=（）|x﹣1|+m的值域为：（m，m+1），若函数f（x）=（）|x﹣1|+m的图象与x轴没有交点，则m≥0，或m+1≤0，解得：m≥0或m＜﹣1，故选：A．12．（5分）已知函数f′（x）是函数f（x）的导函数，f（1）=，对任意实数都有f（x）﹣f′（x）＞0，设F（x）=，则不等式F（x）＜的解集为（）A．（﹣∞，1）B．（1，+∞）C．（1．e） D．（e，+∞）【解答】解：根据题意，F（x）=，其导数F′（x）===，又由f（x）﹣f′（x）＞0，则有F′（x）==＜0，即函数在R上为减函数，又由f（1）=，则F（1）==，不等式F（x）⇔F（x）＜F（1），则有x＞1，则不等式的解集为（1，+∞）；故选：B．二、填空题（共4小题，每小题5分，满分20分）13．（5分）已知α是锐角，且cos（α+）=，则sin（﹣α）=．【解答】解：α是锐角，且cos（α+）=，则sin（﹣α）=sin[﹣（α+）]=cos （α+）=，故答案为：．14．（5分）已知函数f（x）是定义在R上的周期为2的奇函数，当0＜x＜1时，f（x）=9x，则=﹣3．【解答】解：因为f（x）是周期为2的函数，所以f（x）=f（x+2）．因为f（x）是奇函数，所以f（0）=0，所以f（2）=f（0）=0．∵当0＜x＜1时，f（x）=9x，∴f（）=3，则==﹣f（）=﹣3，∴=﹣3．故答案为：﹣3．15．（5分）已知函数f（x）=e x﹣mx+1的图象为曲线C，若曲线C存在与直线y=ex 垂直的切线，则实数m的取值范围为（，+∞）．【解答】解：函数f（x）=e x﹣mx+1的导数为f′（x）=e x﹣m，若曲线C存在与直线y=ex垂直的切线，即有e x﹣m=﹣有解，即m=e x+，由e x＞0，则m＞，则实数m的范围为（，+∞），故答案为：（，+∞）．16．（5分）已知函数f（x）=sinx+cosx，则下列命题正确的是①③④（填上你认为正确的所有命题的序号）①函数f（x）的最大值为2；②函数f（x）的图象关于点（，0）对称；③函数f（x）的图象关于直线x=对称；④函数f（x）在[，π]上单调递减．【解答】解：函数f（x）=sinx+cosx=2sin（x+），∴x+=2kπ+，k∈Z时，函数f（x）取得最大值2，①正确；x=时，f（）=2sin（+）=≠0，∴函数f（x）的图象不关于点（，0）对称，②错误；x=时，f（）=2sin（+）=2为最大值，∴函数f（x）的图象关于直线x=对称，③正确；x∈[，π]时，x+∈[，]，且＜，∴函数f（x）=2sin（x+）在[，π]上单调递减，④正确；综上，正确的命题序号是①③④．故答案为：①③④．三、解答题（共6小题，满分70分）17．（10分）已知p：|x﹣a|＜3（a为常数）；q：代数式有意义．（1）若a=1，求使“p∧q”为真命题的实数x的取值范围；（2）若p是q成立的充分不必要条件，求实数a的取值范围．【解答】解：p：|x﹣a|＜3等价于：﹣3＜x﹣a＜3即a﹣3＜x＜a+3；q：代数式有意义等价于：，即﹣1≤x＜6 …（2分）（1）a=1时，p即为﹣2＜x＜4若“p∧q”为真命题，则，得：﹣1≤x＜4故a=1时，使“p∧q”为真命题的实数x的取值范围是[﹣1，4），…（5分）（2）记集合A={x|a﹣3＜x＜a+3}，B={x|﹣1≤x＜6}若p是q成立的充分不必要条件，则A⊂B，…（7分）因此：，∴2≤a≤3，故实数a的取值范围是[2，3]．…（10分）18．（12分）在△ABC中，内角A，B，C的对边长分别为a，b，c，且（2b﹣c）cosA=acosC．（1）求角A的大小；（2）若a=3，b=2c，求△ABC的面积．【解答】解：（1）（2b﹣c）cosA=acosC，∴2sinBcosA=sinAcosC+sinCcosA，即2sinB•cosA=sin（A+C），∴2sinBcosA=sinB，∵0＜B＜π，∴sinB≠0．∴cosA=，∵0＜A＜π，∴A=．（2）由余弦定理得：cosA===，解得c=，∴b=2．∴S=bcsinA=×2××=．△ABC19．（12分）已知函数f（x）=（sinx+cosx）2+cos2x（1）求f（x）最小正周期；（2）求f（x）在区间上的最大值和最小值．【解答】解：，（1）函数的最小正周期T=．（2）∵，∴∴，即时，∴，即时，f（x）min=0．故得f（x）在区间上的最大值为，最小值为0．20．（12分）已知函数f（x）=x2﹣3lnx．（1）求f（x）在（1，f（1））处的切线方程；（2）试判断f（x）在区间（1，e）上有没有两个零点？若有则判断零点的个数．【解答】（12分）解：（1）由已知得，有f′（1）=﹣2，…（3分）∴在（1，f（1））处的切线方程为：，化简得4x+2y﹣5=0…（5分）（2）由（1）知，因为（x＞0），令f′（x）=0，得…（7分）所以当时，有f′（x）＜0，则是函数f（x）的单调递减区间；、当时，有f′（x）＞0，则是函数f（x）的单调递增区间．…（9分）当x∈（1，e）时，函数f（x）在上单调递减，在上单调递增；又因为，，所以f（x）在区间（1，e）上有两个零点．…（12分）21．（12分）在某次水下科研考察活动中，需要潜水员潜入水深为60米的水底进行作业，根据以往经验，潜水员下潜的平均速度为v（米/单位时间），每单位时间的用氧量为（）3+1（升），在水底作业10个单位时间，每单位时间用氧量为0.9（升）返回水面的平均速度为（米/单位时间），每单位时间用氧量我1.5（升），记该潜水员在此次考察活动中的总用氧量为y（升）．（1）求y关于v的函数关系；（2）求当下潜速度v取什么值时，总用氧量最少．【解答】（12分）解：（1）由题意，下潜用时（单位时间），用氧量为（升），水底作业时的用氧量为10×0.9=9（升），返回水面用时（单位时间），用氧量为（升），∴总用氧量．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（5分）（2）总用氧量．可得，令y'=0得，在时，y'＜0，在时，y'＞0，﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（9分）∴函数在上单调递减，在上单调递增，∴此时，时总用氧量最少，22．（12分）已知函数f（x）=（x2+mx）e x（其中e为自然对数的底数）．（1）当m=﹣2时，求函数f （x ）的单调递增区间；（2）若函数f （x ）在区间[1，3]上单调递减，求m 的取值范围． 【解答】解：（1）当m=﹣2时，f （x ）=（x 2﹣2x ）e x ， f′（x ）=（x 2﹣2）e x ， 令f′（x ）≥0，解得：x ≥或x ≤﹣，∴f （x ）在（﹣∞，﹣），（，+∞）递增；（2）∵f′（x ）=[x 2+（m +2）x +m ]e x ， 由题意得f′（x ）≤0对于x ∈[1，3]恒成立， ∴x 2+（m +2）x +m ≤0，即m ≤﹣=﹣（x +1）+， 令g （x ）=﹣（x +1）+，则g′（x ）=﹣1﹣＜0恒成立， ∴g （x ）在区间[1，3]递减，g （x ）min =g （3）=﹣，∴m 的范围是（﹣∞，﹣]．赠送—高中数学知识点二次函数（1）一元二次方程20(0)ax bx c a ++=≠根的分布一元二次方程根的分布是二次函数中的重要内容，这部分知识在初中代数中虽有所涉及，但尚不够系统和完整，且解决的方法偏重于二次方程根的判别式和根与系数关系定理（韦达定理）的运用，下面结合二次函数图象的性质，系统地来分析一元二次方程实根的分布．设一元二次方程20(0)ax bx c a ++=≠的两实根为12,x x ，且12x x ≤．令2()f x ax bx c =++，从以下四个方面来分析此类问题：①开口方向：a ②对称轴位置：2bx a=-③判别式：∆ ④端点函数值符号． ①k ＜x 1≤x 2 ⇔②x 1≤x 2＜k ⇔③x 1＜k ＜x 2 ⇔ af (k )＜0)(<k f xy1x 2x 0>a O∙kx y1x 2x O∙k<a 0)(>k f④k 1＜x 1≤x 2＜k 2 ⇔xy1x 2x 0>a O ∙∙1k2k 0)(1>k f 0)(2>k f ab x 2-=xy1x 2x O∙<a 1k ∙2k 0)(1<k f 0)(2<k f ab x 2-=⑤有且仅有一个根x 1（或x 2）满足k 1＜x 1（或x 2）＜k 2⇔ f (k 1)f (k 2)<0，并同时考虑f (k 1)=0或f (k 2)=0这两种情况是否也符合⑥k 1＜x 1＜k 2≤p 1＜x 2＜p 2 ⇔ 此结论可直接由⑤推出．（5）二次函数2()(0)f x ax bx c a =++≠在闭区间[,]p q 上的最值设()f x 在区间[,]p q 上的最大值为M ，最小值为m ，令01()2x p q =+． （Ⅰ）当0a >时（开口向上） ①若2b p a -<，则()m f p = ②若2b p q a ≤-≤，则()2b m f a =- ③若2b q a->，则()m f q =①若02b x a -≤，则()M f q = ②02b x a->，则()M f p =(Ⅱ)当0a <时(开口向下) ①若2b p a -<，则()M f p = ②若2b p q a ≤-≤，则()2b M f a =- ③若2b q a->，则()M f q =x>O-=f(p) f (q)()2b f a-x>O-=f (p)f (q)()2b f a-xx>O-=f (p) f (q)()2b f a-0x x>O -=f(p) f(q) ()2b f a-0x xfxfx①若02b x a -≤，则()m f q = ②02b x a->，则()m f p =．x<O-=f (p)f(q)()2bf a-0xx<O-=f (p)f (q)()2b f a-0x。

山东省日照市2017届高三数学上学期期中试题 文本试卷分第I 卷和第Ⅱ卷两部分，共5页。

满分150分。

考试120分钟。

考试结束后，将本试卷和答题卡一并交回。

注意事项：1．答题前，考生务必用0.5毫米黑色签字笔将姓名、座号、考生号、县区和科类填写在答题卡和试卷规定的位置上。

2．第I 卷每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。

3．第Ⅱ卷必须用0.5毫米黑色签字笔作答，答案必须写在答题卡各题目指定区域内相应的位置；如需改动，先划掉原来的答案，然后再写上新的答案；不能使用涂改液、胶带纸、修正带。

不按以上要求作答的答案无效。

4．填空题请直接填写答案，解答题应写出文字说明、证明过程或演算步骤。

第I 卷(共50分)一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.已知角α的终边经过点()1,2P -，则tan 2πα⎛⎫+ ⎪⎝⎭的值是 A.2B. 2-C.12D. 12-2.设n S 是等差数列{}n a 的前n 项和，若13553,=a a a S ++=则 A.5B.7C.9D.113.设函数()()2lg 1f x x =-，集合A 为函数()f x 的定义域，集合(],0B =-∞则图中阴影部分表示的集合为 A. []1,0-B. ()1,0-C.()[),10,1-∞-⋃D.(](),10,1-∞-⋃4.已知函数()f x 的图象是连续不断的，给出(),x f x 对应值如下表：函数()f x 在区间[]1,6上的零点至少有 A.2个B.3个C.4个D.5个5.如图，2,,,AB BC OA a OB b OC c ====，则下列等式中成立的是 A. 3c a b =-B. 3c b a =-C. 3122c b a =- D. 3122c a b =- 6.若21sin 2cos 16362ππαα⎛⎫⎛⎫-=+-= ⎪ ⎪⎝⎭⎝⎭，则 A.13B. 13-C.79D. 79-7.若01x y <<<，则A. 33y x< B. log 3log 3x y <C. 22log log x y >D. 1122x y⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭8.已知()6,1,2,a b b a b ==-=则,a b 值为 A.6π B.4π C.3π D.2π 9.下列说法正确的是A.“220x x +->”是“1x >”的充分不必要条件 B.“若22am bm <，则a b <”的逆否命题为真命题C.命题“x R ∃∈，使得2210x -<”的否定是“x R ∀∈，均有2210x ->” D.命题“若tan 14x x π==，则”的逆命题为真命题10.设向量()()1212,,,a a a b b b ==，定义一种向量运算()1122,a b a b a b ⊗=，已知向量()12,,,0sin 23m n P x y y x π⎛⎫⎛⎫''=== ⎪ ⎪⎝⎭⎝⎭，点，在的图象上运动.点(),Q x y 是函数()y f x =图象上的动点，且满足OQ m OP n =⊗+（其中O 为坐标原点），则函数()y f x =的值域是 A. 11,22⎡⎤-⎢⎥⎣⎦B. 11,22⎛⎫-⎪⎝⎭C.[]1,1-D.()1,1-第II 卷（共100分）二、填空题：本大题共5小题，每小题，共25分.11.设向量()(),1,4,,a x b x a b ==，若方向相反，则实数x 的值是_________.12.若函数()()()2,4,23,4,x x f x f f x x ⎧≥⎪==⎨+<⎪⎩则_________.13.已知函数()f x 是(),-∞+∞上的偶函数，若对于0,x ≥都有()()2f x f x +=，且当[)0,2x ∈时，()()2log 1f x x =+，则()2017f -=____________.14.已知变量,x y 满足约束条件240,2,40,x y y x y k -+≤⎧⎪≥⎨⎪-+≥⎩且目标函数3z x y =+的最小值为1-，则实数k=_________.15.如图所示的数阵中，用(),A m n 表示第m 行的第n 个数，依此规律，则()9,2A =________.三、解答题：本大题共6小题，共75分. （16）（本小题满分12分）已知命题p ：函数()212log 2y x x a =++的值域R ，命题q ：函数()250,a y x-=+∞在上是减函数.若p q ∧⌝为真命题，求实数a 的取值范围. （17）（本小题满分12分） 已知函数()cos sin 6f x x x π⎛⎫=++ ⎪⎝⎭.（I ）利用“五点法”，列表并画出()533f x ππ⎡⎤-⎢⎥⎣⎦在，上的图象； ,,a b c（II ）ABC∆分别是中角A,B,C 的对边.若()33,,1a f A b ===，求ABC ∆的面积.(18）（本小题满分12分）设等差数列{}n a 的前n 项和为n S ，且12n n n S na a c =+-（c 是常数，n N *∈），26a =. （I ）求c 的值及数列{}n a 的通项公式； （II ）设122n n n a b +-=，求数列{}n b 的前n 项和为n T . （19）（本小题满分12分）已知函数()y f x =，若在定义域内存在0x ，使得()()00f x f x -=-成立，则称0x 为函数()f x 的局部对称点.（I ）若0a R a ∈≠且，求函数()2f x ax x a =+-的“局部对称点”；（II ）若函数()12423xx f x m m +=-⋅+-在R 上有局部对称点，求实数m 的取值范围.（20）（本小题满分13分）在创城活动中，海曲市园林公司设计如图所示的环状绿化景观带.已知该景观带的内圈由两条平行线段（图中的AB ，CD ）和两个半圆构成，设计要求AB 长为x ()80x ≥. （I ）若内圈周长为400米，则x 取何值时，矩形ABCD 的面积最大？ （II ）若景观带的内圈所围成区域的面积为22500πm 2，则x 取何值时，内圈周长最小？（21）（本小题满分14分）已知函数()()()31,ln h x ax a R g x x =-∈=.（I ）若()()()3f x h x xg x =+图象过点()1,1-时，()f x 求的单调区间；（II ）函数()()()3211132F x a x x g a h x ⎛⎫=-+-- ⎪⎝⎭，当103a e >（e 为自然对数的底数）时，函数()F x 过点()1,A m 的切线()F x 切于点()()00,B x F x①试将m 表示成0x 的表达式. ②若切线至少有2条，求实数m 的值.二○一六年高三校际联合检测 文科数学（A ）答题卡姓 名_________________ 座号 准考证号▄请在各题目的答题区域内作答，超出答题区域的答案无效请在各题目的答题区域内作答，超出答题区域的答案无效请在各题目的答题区域内作答，超出答题区域的答案无效考生必填姓名座号考生务必将姓名、座号用0.5毫米的黑色签字笔认真填写在书写框内，座号的每个书写框只能填写一个阿拉伯数字，填写样例：若座号02，填写为□0□2三、（17）请在各题目的答题区域内作答，超出答题区域的答案无效请在各题目的答题区域内作答，超出答题区域的答案无效二○一六年高三校际联合检测 文科数学（A ）答题卡姓 名_________________ 座号 准考证号请在各题目的答题区域内作答，超出答题区域的答案无效请在各题目的答题区域内作答，超出答题区域的答案无效请在各题目的答题区域内作答，超出答题区域的答案无效二〇一六年高三校际联合检测文科数学参考答案及评分标准2016.11一、选择题：本大题共10小题，每小题5分，共50分.BADBC ADCBA（1）答案B ．解：由三角定义2tan 21y x α===--，故tan(π)tan αα+==2-，故选B. （2）答案A ．解：由等差数列{a n }的性质及1353a a a ++=得333a =，所以31a =，所以()155355 5.2a a S a +===故选A ． （3）答案D ．解：由012>-x ，得11<<-x ，所以)1,1(-=A ，阴影部分表示的集合为交集B A 在并集B A 中的补集，即为(](),10,1-∞-，故选D.（4）答案B ．解：由图可知，()(2)0,30f f ><，0)5(,0)4(<>f f ，由零点存在定理知在区间(2,3)上至少有一个零点，同理可以判断出在区间)4,3(、(4,5)上各至少有一个零点，所以在区间[]1,6上的零点至少有三个.（5）答案C ．解析：由2AB BC =得2()AO OB BO OC +=+,即23OC OA OB =-+,即3122=-c b a ．（6）答案A ．解：若π1sin 63α⎛⎫-=⎪⎝⎭，则2π2cos 162⎛⎫+-= ⎪⎝⎭απππcos sin 323⎡⎤⎛⎫⎛⎫+=-+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ααπ1sin 63⎛⎫=-= ⎪⎝⎭α，故选A ．（7）答案D ．解：根据指数函数的单调性，可得33y x>，11()()22xy>，根据对数函数的单调性，可得log 3log 3x y >，22log log x y <，故选D ．（8）答案C ．解：由2)(=-⋅b a b ，得2||2=-⋅b a b ，所以3||22=+=⋅b a b ，从而21163||||,cos =⨯=⋅>=<b a b a b a ，又]π,0[,>∈<b a ，3π,>=∴<b a ．（9）答案B ．解：选项A ，220x x +->，解得2x <-或1x >，故“220x x +->”是“1x >”的必要不充分条件，故A 错误；选项B ，“若22am bm <，则a b <”的逆否命题为“若a b ≥，则22am bm ≥”为真命题，故B 正确；选项C ，命题“x ∃∈R ，使得2210x -<”的否定是“x ∀∈R ，均有2210x -≥”，故C 错误； 选项D ，命题“若π4x =，则tan 1x =”的逆命题“若tan 1x =，则π4x =”，因为tan 1x =，则ππ()4x k k =+∈Z ”，故D 错误，故选B.（10）答案A ．解：)sin 21,3π2()0,3π()sin 21,2(x x x x OP OQ '+'=+''=+⊗=n m , 所以⎪⎩⎪⎨⎧'=+'=,sin 21,3π2x y x x 消去x '，得)6π21sin(21-=x y ，易知y ＝f (x )的值域是]21,21[-. 二、填空题：本大题共5小题，每小题5分，共25分.（11）2±；（12）32；（13）1；（14）9；（15）.3019（11）答案2±．解：由题意，得2140x -⨯=，解得：2x =±． （12）答案32．解：322)5()32()2(5===+=f f f ．（13）答案1．解析：由已知函数是偶函数，且0x ≥时，都有(2()f x f x +=），所以2(2017)(2017)(1)log 2 1.f f f -====（14）答案9．解：由题意作出平面区域如图，结合图象可知， 当过点)2,(x A 时，目标函数y x z +=3取得最小值1-， 故123-=+x ，解得，1-=x ，故)2,1(-A ， 故0241=+⨯--k ，故.9=k （15）答案3019．解：由已知归纳可得，第n 行的第一个数 和最后一个数均为)2)(1(2++n n ，其它数字等于上一行该数字“肩膀“上两个数字的和，所以).2,2()1,2()2,3();2,6()1,6()2,7();2,7()1,7()2,8();2,8()1,8()2,9(A A A A A A A A A A A A +=+=+=+=故)2,2()]1,2()1,6()1,7()1,8([)2,9(A A A A A A +++++= ， 所以3019)10131(261)1092302202122(61)2,9(=-+=⨯+++++=A ． 三、解答题：本大题共6小题，共75分. （16）（本小题满分12分）解：对于命题p ：因其定义域为R ，故220x x a ++>恒成立， 所以440a ∆=-<，∴1a >．…………………………3分对于命题q ：因其在()0,+∞上是减函数，故250a -<，则52a <．……6分 ∵p q ∧⌝为真命题，∴p 真q 假，则1,52a a >⎧⎪⎨≥⎪⎩，则52a ≥， …………………………10分 故实数a 的取值范围为5[,)2+∞．…………………………12分（17）（本小题满分12分） 解：（Ⅰ）x x x f sin )6πcos()(++= =x x x sin 6πsin sin 6πcoscos +- x x sin 21cos 23+=)3πsin(+=x ，…………………………2分 利用“五点法”列表如下，x +3π2π π23π 2πx 3π-6π 32π 67π 35π y1﹣1……………………………………… 4分画出)(x f 在]35π,3π[-上的图象，如图所示：… 6分（Ⅱ）由（Ⅰ）23)3πsin()(=+=A A f ，在△ABC 中，π0<<A ，可知3π=A ． 由正弦定理可知B bA a sin sin =，即B sin 13πsin 3=，所以21sin =B ， ……9分 又3π20<<B ，6π=∴B ，∴23132121,2π=⨯⨯==∴=ab S C ．因此△ABC 面积是23． ……………………………………… 12分（18）（本小题满分12分）解：（Ⅰ）由已知12n n n S na a c =+-. 所以当1n =时，11112S a a c =+-,解得12a c =.………………………2分当2n =时，222S a a c =+-, 即1222a a a a c +=+-. 解得23a c =，所以36c =.解得2c =. ………………………4分 则14a =，数列{}n a 的公差212d a a =-=. ………………………5分所以1(1)22n a a n d n =+-=+． ………………………6分 （Ⅱ）因为112222222n n n n n a n nb ++-+-===,………………………8分所以231232222n n nT =++++， ① 2341112322222n n nT +=++++， ② ①－②，得2341111111111222222222n n n n n n nT ++=+++++-=--，所以222n n nT +=-.………………………12分（19）（本小题满分12分）解：（Ⅰ）由2()f x ax x a =+-，得2()f x ax x a -=--，代入()()f x f x -=-，得220ax x a ax x a +-+--=，即()200ax a a -=≠，1±=∴x ，所以函数2()f x ax x a =+-的局部对称点是1±； .............5分 （Ⅱ）因为12()423x x f x m m --+-=-⋅+-，由()()f x f x -=-得()1212423423x x x x m m m m --++-⋅+-=--⋅+-，于是()()()244222230x x x x m m --+-++-=*在R 上有解，………………8分令()22,2xxt t -=+≥，则2442x x t -+=-，∴方程()*变为222280t mt m -+-=在区间[)2,+∞内有解，令()22228g t t mt m =-+-，由题意需满足以下条件：()20g ≤或()()224840,2,20,m m m g ⎧∆=--≥⎪≥⎨⎪≥⎩解得1313m -≤≤+1322m ≤≤综上1322m -≤≤ ..................................12分 （20）（本小题满分13分）解：（Ⅰ）设半圆的半径为r ，由题意得20080<≤x ，且2+2π400x r =，即+π200x r =，矩形ABCD 的面积为222π200002(π)()ππ2πx r S rx x r +==⋅=≤， 当且仅当π=100x r =时，矩形的面积取得最大值20000πm 2；……………………6分（Ⅱ）设半圆的半径为r ，由题意可得222500π+2=πr xr ，可得225002=ππx r r -， 即有内圈周长22500=22π=ππc x r r r ++，…………………………9分 由80x ≥，可得22500π160πr r-≥，解得0<π90r ≤，设222225002250022500()=π()=π=π(1)<0,πππf r r f r r r r'+--， 即有()f r 在90(0]π，上递减，即有π=90r ，即=80m x 时，周长c 取得最小值340m ．………………………13分（21）（本小题满分14分）解：（Ⅰ）由已知3()()3()13ln f x h x xg x ax x x =+=-+，又)(x f 过点)1,1(-，所以0a =．()3ln 1f x x x ∴=-，且定义域为(0,)+∞，()3ln 33(ln 1)f x x x '=+=+，故()3ln 1f x x x =-在1(0,)e 上是减函数，在1(,)e+∞上是增函数．……………4分（Ⅱ）函数3211()()()()132F x a x x g a h x =-+--3211()ln 32F x x x a =-+，①由已知切点为3200011(,ln )32B x x x a -+，a x x x F ln )(2+-='，a x x x F ln )(0200+-='，则B 处的切线方程为3220000011(ln )(ln )()32y x x a x x a x x --+=-+-，将A 点坐标代入得3220000011(ln )(ln )(1)32m x x a x x a x --+=-+-，所以3200021(1ln )ln .()32m x a x x a =-++*…………………………8分 ②据题意，原命题等价于关于0x 的方程()*至少有2个不同的解. 设3221()(1ln )ln 32φx x a x x a =-++， 2()2(2ln )ln (1)(2ln )φx x a x a x x a '=-++=--，因为103e a >，所以15ln 123a >>， 当(,1)x ∈-∞和1(ln ,)2a +∞时，()0x '>ϕ，()x ϕ为增函数；高三数学上学期期中试题文21 / 21 当x ∈1(1,ln )2a 时，()0x '<ϕ，()x ϕ为减函数． 所以()x ϕ的极大值为2111(1)1ln ln ln 3223φa a a =--+=-， ()x ϕ的极小值为32211111(ln )ln ln (1ln )ln 212422φa a a a a =-++3211ln ln 244a a =-+， 设10ln ,3a t t =>， 则原命题等价于32321111ln ,23231111ln ln 244244m a t m a a t t ⎧≤-=-⎪⎪⎨⎪≥-+=-+⎪⎩对103t >恒成立，………12分 所以由1123m t ≤-对103t >恒成立，得43m ≤； ⑴ 记3211()244s t t t =-+，)411(212181)(2t t t t t s -=+-='，所以103t >时，)(t s 的最大值为4(4)3s =，由3211244m t t ≥-+对103t >恒成立，得43m ≥． ⑵ 由⑴⑵得，34=m ． 综上，当103e a >，实数m 的值为43时，函数)(x F 过点),1(m A 的切线至少有2条． ………………………………………14分。

郓城一中高三第一次检测性考试数学试题一、选择题（本大题共10小题,共50分)1. 命题“∃x∈R,使x2+ax-4a＜0为假命题”是“-16≤a≤0”的（）A。

充要条件 B.充分不必要条件C。

必要不充分条件 D.既不充分又不必要条件集合2。

.命题p：存在实数m，使方程x2+mx+1=0有实数根，则“非p”形式的命题是（）A.存在实数m，使方程210x mx++=没有实数根B.不存在实数m，使方程210x mx++=没有实数根C.对任意实数m，使方程210x mx++=没有实数根D.至多有一个实数m，使方程210x mx++=没有实数根3。

.已知命题:函数在R上为增函数,：函数在R 上为减函数,则在命题和中,真命题是（）A。

B。

C。

D。

4. 函数的定义域为（）A. B.C。

D。

5.函数1()lnf x xx⎛⎫=-⎪⎝⎭的图象是（）A. B。

C。

D.6。

函数在上为减函数，则的取值范围是（）A 。

B. C 。

D 。

7. 定义在上的函数满足：，，是的导函数，则不等式（其中为自然对数的底数)的解集为( ） A 。

B.C 。

D 。

8. 设集合A=10,2⎡⎫⎪⎢⎣⎭,B=1,12⎡⎤⎢⎥⎣⎦，函数()1,x A 2(),21,x x f x x B ⎧+∈⎪=⎨⎪-∈⎩若x 0∈A ，且f ［f （x 0）]∈A,则x 0的取值范围是（ ） A.10,4⎛⎤ ⎥⎝⎦B.11,42⎡⎤⎢⎥⎣⎦C 。

11,42⎛⎫⎪⎝⎭D.30,8⎡⎤⎢⎥⎣⎦9。

定义在R 上的函数y=f （x ）的图象关于点3,04⎛⎫-⎪⎝⎭成中心对称，对任意的实数x 都有()32f x f x ⎛⎫=-+ ⎪⎝⎭，且f(—1）=1,f(0)=—2,则f （1）+f(2）+f(3)+…+f(2014）的值为（ ） A 。

2 B 。

-2 C.—1 D.1 10. 函数的定义域为D,若对于任意,当时都有，则称函数在D 上为非减函数,设函数在［0,1]上为非减函数,且满足以下三个条件：①;②；③，则等于（ ）A. B. C.1 D 。

2016—2017学年山东省菏泽市高三(上）期中数学试卷（B卷）一、选择题：本大题共10小题，每小题5分,共50分，在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知全集U=｛a，b,c，d，e，f｝，集合A={a，b，e}，B=｛b，d，f｝，则（∁U A）∪B 为（)A．｛a，e｝B．｛c｝C．｛d,f} D．｛b，c，d，f｝2．已知p：∀x∈R,x2﹣x+1＞0，q：∃x∈（0，+∞），sinx＞1，则下列命题为真命题的是() A．p∧q B．￢p∨q C．p∨￢q D．￢p∧￢q3．已知a,b∈R,条件p：“a＞b＞0”,条件q：“2a＞2b+1"，则p是q的（）A．充分不必要条件B．必要不充分条件C．充分必要条件 D．既不充分也不必要条件4．已知函数f（x）=，若f（f（0)）=3a，则实数a等于（）A．4 B．2 C．D．5．函数f（x）=+lg（x+2）的定义域为（)A．（﹣2,3）B．（﹣2，3] C．（﹣2，+∞) D．［﹣2，3]6．下列函数中，既是偶函数又在（0,+∞）上单调递减的函数是（）A．y=2x3B．y=｜x|+1 C．y=﹣x2+4 D．y=2｜x｜7．函数的零点所在的区间是（)A． B．（1,2）C．（2，e）D．(e，3）8．已知函数f(x）=x﹣ln｜x｜,则f（x)的图象大致为（）A．B．C．D．9．若tanα=3，则sin2α=（）A．B．﹣C．﹣D．10．将函数y=sin（2x﹣）的图象向左平移个单位，所得函数图象的一个对称中心为（)A．B．C．D．二、填空题：本大题共5个小题，每小题5分，共25分。

11．已知函数f（x）=2cos(ωx+）的最小正周期是π，则f(）=．12．设函数f（x）对任意实数x满足f(x)=﹣f(x+2）,且当0≤x≤2时,f(x）=x（x﹣2)，则f （﹣2017)=．13．已知函数f（x)=x3﹣ax2﹣3x，若f（x)在区间［1，+∞)上是增函数，实数a的取值范围是．14．已知α，β∈（，π）,sin（α+β）=﹣，sin（β﹣）=，则cos（α+）=．15．下列几个命题:①方程x2+（a﹣3）x+a=0若有一个正实根和一个负实根，则a＜0；②函数y=+是偶函数也是奇函数;③函数f(x）的值域是［﹣2，2],则函数f（x+1）的值域为［﹣3，1］；④一条曲线y=|3﹣x2|和直线y=a（a∈R）的公共点个数是m，则m的值可能是1．其中错误的有．三、解答题:本大题共6小题,共75分。

2016-2017学年度上学期高三期中数学（理）试卷考试时间：120分钟注意事项：1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上,在试卷上答题无效.第I 卷（共50分）一、选择题:本大题共十小题，每小题5分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知全集R U =，集合}31|{≤<=x x A ，}2|{>=x x B ，则B C A U 等于（ ） A ．{|12}x x <≤ B ．{|12}x x ≤< C ．{|12}x x ≤≤ D ．{|13}x x ≤≤ 2．下列函数中，与函数||x e y -=的奇偶性相同，且在)0,(-∞上单调性也相同的是 （ ） A ．xy 1-= B ．||ln x y = C ．33-=x y D ．22+-=x y3．已知函数y f x =+()1定义域是[]-23，，则y f x =-()21的定义域是 （ ） A.[]052， B.[]-14， C.[]-55， D.[]-37，4．若“40≤≤x ”是“0)]2()[(≤+--a x a x ”的必要不充分条件，则实数a 的取值范围是（ ） A ．)2,0( B ．]2,0[ C ．]0,2[- D ．)0,2(- 5．下列四种说法中，①命题“存在2,0x R x x ∈->”的否定是“对于任意2,0x R x x ∈-<”； ②命题“p 且q 为真”是“p 或q 为真”的必要不充分条件；③已知幂函数()f x x α=的图象经过点，则(4)f 的值等于12；④已知向量(3,4)a =-，(2,1)b =，则向量a 在向量b 方向上的投影是25. 说法正确的个数是（ ） A ．1 B ．2 C ．3 D ．46．已知函数⎪⎩⎪⎨⎧≤---=)1()1(,5)(2x ＞x a x ax x x f 是R 上的增函数，则a 的取值范围是（ ）A.3-≤a ＜0B.3-≤a ≤2-C.a ≤2-D.a ＜07．函数x xx xe e y e e --+=-的图像大致为（ ）A B C D8．已知函数()cos()3f x x π=+，则要得到其导函数'()y f x =的图象，只需将函数()y f x =的图象（ ） A ． 向右平移2π个单位B ．向左平移2π个单位C ．向右平移23π个单位D ．左平移23π个单位9．设函数)(x f 在R 上可导，其导函数为)(x f '，且函数)()1(x f x y '-=的图像如图所示，则下列结论中一定成立的是（ ）A ． 函数)(x f 有极大值)2(f 和极小值)1(fB ． B ．函数)(x f 有极大值)2(-f 和极小值)1(fC ．函数)(x f 有极大值)2(f 和极小值)2(-fD ．函数)(x f 有极大值)2(-f 和极小值)2(f10．定义在R 上的函数()f x 满足：()1()f x f x '>-，(0)6f =，()f x '是()f x 的导函数，则不等式()5xxe f x e >+（其中e 为自然对数的底数）的解集为（ ） A ．()0,+∞ B ．()(),03,-∞+∞U C ．()(),01,-∞+∞U D ．()3,+∞第II 卷（共100分）A二、填空题:本大题共5小题,每小题5分,共25分.11．已知命题:0p m <，命题2:,10q x R x mx ∀∈++>成立，若“q p ∧”为真命题，则实数m 的取值范围是_ _ ． 12．若函数321()(23)13f x ax ax a x =-+-+在R 上存在极值，则实数a 的取值范围是______． 13．过点(1,1)A 作曲线2(0)y x x =≥的切线,设该切线与曲线及x 轴所围图形的面积为,S 则S =． 14．在ABC ∆中，角A 、B 、C 的对边分别为,,a b c，且满足).c BA BC cCB CA -⋅=⋅则角B 的大小为；15．对于函数⎪⎩⎪⎨⎧+∞∈-∈=),,2(),2(21],2,0[,sin )(x x f x x x f π，有下列5个结论：①任取1x ，],0[2+∞∈x ，都有2|)()(|21≤-x f x f ； ②函数)(x f y =在]5,4[上单调递增；③))(2(2)(*N k k x kf x f ∈+=，对一切),0[+∞∈x 恒成立； ④函数)1ln()(--=x x f y 有3个零点；⑤若关于x 的方程)0()(<=m m x f 有且只有两个不同的实根1x ，2x ，则321=+x x . 则其中所有正确结论的序号是.三、解答题:解答应写出必要的文字说明,证明过程或演算步骤. 16．（本题12分）已知集合312x A xx -⎧⎫=≥⎨⎬⎩⎭,集合1228x B x ⎧⎫=<<⎨⎬⎩⎭．（1）求A B ⋂；（2）若集合{}21C x a x a =≤≤+，且()A B C ⋂⊇，求实数a 的取值范围．17．（本题12分）已知函数x x x x f 2cos 2cos sin 32)(-⋅=)(R x ∈.（Ⅰ）求函数)(x f 的最小正周期及单调递减区间；（Ⅱ）若⎥⎦⎤⎢⎣⎡∈2,0πx ，求)(x f 的值域.18．（本题12分）在△ABC 中，a ，b ，c 分别为内角A ，B ，C 的对边, 面积C S cos ab 23= （1）求角C 的大小；（2）设函数2cos 2cos 2sin 3)(2x x x x f +=，求)(B f 的最大值,及取得最大值时角B 的值．19．（本题12分）在淘宝网上，某店铺专卖孝感某种特产．由以往的经验表明，不考虑其他因素，该特产每日的销售量y （单位：千克）与销售价格x （单位：元/千克，51≤<x ）满足：当31≤<x 时，1)3(2-+-=x bx a y ，为常数）（b a ,；当53≤<x 时，70490y x =-+．已知当销售价格为2元/千克时，每日可售出该特产600千克；当销售价格为3元/千克时，每日可售出150千克．（1）求b a ,的值，并确定y 关于x 的函数解析式；（2）若该特产的销售成本为1元/千克，试确定销售价格x 的值，使店铺每日销售该特产所获利润)(x f 最大（x 精确到0．1元/千克）． 20．（本题13分）（10分）已知函数)(ln )(R a x a x x f ∈-= (1)当2=a 时,求曲线)(x f y =在点))1(,1(f A 处的切线方程; (2)求函数)(x f y =的极值.21．（本题14分）（本小题满分12分)已知函数kx x f =)(，xxx g ln )(= （1）求函数xxx g ln )(=的单调递增区间； （2）若不等式)()(x g x f ≥在区间（0,)+∞上恒成立，求k 的取值范围； （3）求证：e nn 21ln 33ln 22ln 444<+++参考答案（理）1．A.【解析】}2|{>=x x B ,{}2|≤=∴x x B C U ,则{}21|≤<=x x B C A U . 考点：集合的运算.2．D.【解析】因为)()(x f eex f xx=-=-=--，所以||x y e =-是偶函数，且在(0)-∞，上单调递增，与之相同的只有D 选项，因为A 选项是奇函数，不合题意；B 选项是在(0)-∞，上单调递减；C 选项为非奇非偶函数，不合题意，故选D. 考点：函数的单调性与奇偶性.3．A 【解析】设1+=x t ,由∈x []-23，,则41≤≤-t ,则有4121≤-≤-x ,所以∈x []052，. 考点：对函数定义域的理解。

2016-2017学年山东省菏泽一中高三（上）第二次月考数学试卷（文科）（宏志部）一、选择题（本题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．设集合U=R，A={x|y=ln（1﹣x）}，B={x|x2﹣3x≥0}，则A∩∁U B=（）A．{x|0＜x＜1}B．{x|1＜x＜3}C．{x|0＜x＜3}D．{x|x＜1}2．已知，则f（3）=（）A．B．C．log32 D．log233．下列说法中，正确的是（）A．“∃x0∈R，x02﹣x0≤0”的否定是“∃x∈R，x2﹣x＞0”B．已知p，q为命题，则“p∨q为真”是“p∧q为真”的必要不充分条件C．命题“若x2＜1，则﹣1＜x＜1”的逆否命题是“若x＞1或x＜﹣1，则x2＞1”D．命题“若a＞2，则a+的最小值为2”为真命题4．等比数列{a n}的前n项和为S n，已知a2a5=2a3，且a4与2a7的等差中项为，则S5=（）A．29 B．31 C．33 D．365．若α∈（0，π），且3cos2α=sin（﹣α），则sin2α的值为（）A．1或﹣B．C．1 D．6．已知函数，当x=a时，y取得最小值b，则a+b=（）A．﹣3 B．2 C．3 D．87．若函数f（x）=（k﹣1）a x﹣a﹣x（a＞0，a≠1）在R上既是奇函数，又是减函数，则g （x）=log a（x+k）的图象是（）A．B．C．D．8．已知f（x）为R上的可导函数，且对x∈R，均有f（x）＞f′（x），则有（）A．e2016f（﹣2016）＜f（0），fB．e2016f（﹣2016）＞f（0），fC．e2016f（﹣2016）＜f（0），fD．e2016f（﹣2016）＞f（0），f9．已知在三角形ABC中，AB=AC，BC=4，∠BAC=120°，=3，若P是BC边上的动点，则•的取值范围是（）A．[﹣1，3] B．C．D．10．设f（x）和g（x）是定义在同一区间[a，b]上的两个函数，若对任意的x∈[a，b]，都有|f（x）﹣g（x）|≤1，则称f（x）和g（x）在[a，b]上是“密切函数”，[a，b]称为“密切区间”，设f（x）=x2﹣3x+4与g（x）=2x﹣3在[a，b]上是“密切函数”，则它的“密切区间”可以是（）A．[1，4]B．[2，3]C．[3，4]D．[2，4]二、填空题：（本大题共5小题，每小题5分，共25分．）11．若tanα=3，则的值等于．12．已知f（x）是定义域为R的函数，且满足f（x+2）=﹣，当2≤x≤3时，f（x）=x+，则f（﹣）=．13．若向量=（x，2x），=（﹣3x，2），且的夹角为钝角，则x的取值范围是．14．过点P（1，）作圆x2+y2=1的两条切线，切点分别为A，B，则=．15．已知函数f（x）=，若存在实数a，b，c，d，满足f（a）=f （b）=f（c）=f（d），其中d＞c＞b＞a＞0，则abcd的取值范围是．三、解答题：本大题共6个小题.共75分.解答应写出文字说明，证明过程或演算步骤. 16．已知等差数列{a n}中，a3a7=﹣16，a4+a6=0，求{a n}前n项和s n．17．已知集合A={x|（x﹣6）（x﹣2a﹣5）＞0}，集合B={x|[（a2+2）﹣x]•（2a﹣x）＜0}．（Ⅰ）若a=5，求集合A∩B；（Ⅱ）已知a＞．且“x∈A”是“”的必要不充分条件，求实数a的取值范围．18．已知向量（x∈R）函数f（x）=（Ⅰ）求f（x）的最小正周期；（Ⅱ）若函数y=f（x）的图象向右平移个单位，再向上平移个单位，得到函数y=g（x）的图象，求y=g（x）在[0，]上的最大值．19．为了在夏季降温和冬季供暖时减少能源损耗，房屋的屋顶和外墙需要建造隔热层．某幢建筑物要建造可使用20年的隔热层，每厘米厚的隔热层建造成本为6万元．该建筑物每年的能源消耗费用C（单位：万元）与隔热层厚度x（单位：cm）满足关系：C（x）=（0≤x≤10），若不建隔热层，每年能源消耗费用为8万元．设f（x）为隔热层建造费用与20年的能源消耗费用之和．（Ⅰ）求k的值及f（x）的表达式．（Ⅱ）隔热层修建多厚时，总费用f（x）达到最小，并求最小值．20．已知数列{a n}是等差数列，{b n}是等比数列，且a1=b1=2，b4=54，a1+a2+a3=b2+b3．（1）求数列{a n}和{b n}的通项公式；（2）数列{c n}满足c n=a n b n，求数列{c n}的前n项和S n．21．设函数f（x）=x2+ax﹣lnx，a∈R，（Ⅰ）当a=1时，求函数f（x）的极值；（Ⅱ）当a＞1时，讨论函数f（x）的单调性；（Ⅲ）若对任意a∈（3，4）及任意x1，x2∈[1，2]，恒有|成立，求实数m的取值范围．2016-2017学年山东省菏泽一中高三（上）第二次月考数学试卷（文科）（宏志部）参考答案与试题解析一、选择题（本题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．设集合U=R，A={x|y=ln（1﹣x）}，B={x|x2﹣3x≥0}，则A∩∁U B=（）A．{x|0＜x＜1}B．{x|1＜x＜3}C．{x|0＜x＜3}D．{x|x＜1}【考点】交、并、补集的混合运算．【分析】求出A中x的范围确定出A，求出B中不等式的解集确定出B，找出A与B补集的交集即可．【解答】解：由A中y=ln（1﹣x），得到1﹣x＞0，即x＜1，∴A={x|x＜1}，由B中不等式变形得：x（x﹣3）≥0，解得：x≤0或x≥3，即B={x|x≤0或x≥3}，∴∁U B={x|0＜x＜3}，则A∩∁U B={x|0＜x＜1}，故选：A．2．已知，则f（3）=（）A．B．C．log32 D．log23【考点】函数的值．【分析】设2x=t，则x=log2t．从而f（t）=，由此能求出f（3）．【解答】解：∵，设2x=t，则x=log2t．∴f（t）=，∴f（3）==log32．故选：C．3．下列说法中，正确的是（）A．“∃x0∈R，x02﹣x0≤0”的否定是“∃x∈R，x2﹣x＞0”B．已知p，q为命题，则“p∨q为真”是“p∧q为真”的必要不充分条件C．命题“若x2＜1，则﹣1＜x＜1”的逆否命题是“若x＞1或x＜﹣1，则x2＞1”D．命题“若a＞2，则a+的最小值为2”为真命题【考点】命题的真假判断与应用．【分析】对四个命题分别进行判断，即可得出结论．【解答】解：对于A，“∃x0∈R，x02﹣x0≤0”的否定是“∀x∈R，x2﹣x＞0”，故错误；对于B，“p∧q为真”则p．q均为真，所以“p∨q为真”；“p∨q为真”，则p，q至少有一个为真，所以“p∧q为真”，故正确；对于C，命题“若x2＜1，则﹣1＜x＜1”的逆否命题是：“若x≥1或x≤﹣1，则x2≥1”，故错误；对于D，若a＞2，则a+=a﹣2++2≥4，故a+的最小值为4，是假命题．故选：B．4．等比数列{a n}的前n项和为S n，已知a2a5=2a3，且a4与2a7的等差中项为，则S5=（）A．29 B．31 C．33 D．36【考点】等比数列的前n项和．【分析】利用a2•a3=2a1，且a4与2a7的等差中项为，求出数列的首项与公比，再利用等比数列的求和公式，即可得出结论．【解答】解：∵数列{a n}是等比数列，a2•a3=2a1=a1q•=a1•a4，∴a4=2．∵a4与2a7的等差中项为，∴a4 +2a7 =，故有a7 =．∴q3==，∴q=，∴a1==16．∴S5==31．故选：B．5．若α∈（0，π），且3cos2α=sin（﹣α），则sin2α的值为（）A．1或﹣B．C．1 D．【考点】二倍角的正弦．【分析】利用二倍角的余弦函数公式，两角差的正弦函数公式化简已知等式可得cosα﹣sinα=0，或3（cosα+sinα）=，分类讨论，即可得解sin2α的值．【解答】解：∵3cos2α=sin（﹣α），∴3（cos2α﹣sin2α）=3（cosα+sinα）（cosα﹣sinα）=（cosα﹣sinα），∴cosα﹣sinα=0，或3（cosα+sinα）=，∴当cosα﹣sinα=0时，可得：sin（α﹣）=0，由于α∈（0，π），可得：α﹣∈（﹣，），可得：α=，则sin2α=sin=1；当3（cosα+sinα）=时，可得：cosα+sinα=，两边平方可得：1+sin2α=，解得：sin2α=﹣．故选：A．6．已知函数，当x=a时，y取得最小值b，则a+b=（）A．﹣3 B．2 C．3 D．8【考点】基本不等式．【分析】将，转化为y=（x+1+）﹣5，再利用基本不等式求解即可．【解答】解：∵x＞﹣1，∴x+1＞0，∴=（x+1）+﹣5≥2﹣5=1，当且仅当x=2时取等号．∴a=2，b=1，∴a+b=3．故选C．7．若函数f（x）=（k﹣1）a x﹣a﹣x（a＞0，a≠1）在R上既是奇函数，又是减函数，则g （x）=log a（x+k）的图象是（）A．B．C．D．【考点】奇偶性与单调性的综合；对数函数的图象与性质．【分析】根据函数是一个奇函数，函数在原点出有定义，得到函数的图象一定过原点，求出k的值，根据函数是一个减函数，看出底数的范围，得到结果．【解答】解：∵函数f（x）=（k﹣1）a x﹣a﹣x（a＞0，a≠1）在R上是奇函数，∴f（0）=0∴k=2，又∵f（x）=a x﹣a﹣x为减函数，所以1＞a＞0，所以g（x）=log a（x+2）定义域为x＞﹣2，且递减，故选：A8．已知f（x）为R上的可导函数，且对x∈R，均有f（x）＞f′（x），则有（）A．e2016f（﹣2016）＜f（0），fB．e2016f（﹣2016）＞f（0），fC．e2016f（﹣2016）＜f（0），fD．e2016f（﹣2016）＞f（0），f【考点】导数的运算．【分析】设函数h（x）=，求得h′（x）＜0，可得h（x）在R上单调递减，可得h，h（﹣2016）＞h（0），再进一步化简，可得结论．【解答】解：设函数h（x）=，∵∀x∈R，均有f（x）＞f′（x），则h′（x）=＜0，∴h（x）在R上单调递减，∴h，h（﹣2016）＞h（0）∴e2016f（﹣2016）＞f（0），f，故选：D．9．已知在三角形ABC中，AB=AC，BC=4，∠BAC=120°，=3，若P是BC边上的动点，则•的取值范围是（）A．[﹣1，3] B．C．D．【考点】平面向量数量积的运算．【分析】利用余弦定理求得AB、AC的值，再根据E是线段BC较靠近点C的一个四等分点，利用两个向量的加减法的法则，以及其几何意义，两个向量数量积的运算求得•=，λ∈[0，1]，从而求得它的取值范围．【解答】解：设AB=AC=x，则由BC=4，∠BAC=120°，利用余弦定理可得16=x2+x2﹣2x•xcos120°，∴x=．∴=x•x•cos120°=﹣．∵=3，∴E是线段BC较靠近点C的一个四等分点，若P是BC边上的动点，则=λ，λ∈[0，1]，∴•=（+）•（+）=（+λ）•（+）=[（1﹣λ）+λ]•（+）=•+（+）+=•+•（﹣）+•=，故当λ=0时，•取得最小值为﹣，当λ=1时，•取得最大值为，故选：C．10．设f（x）和g（x）是定义在同一区间[a，b]上的两个函数，若对任意的x∈[a，b]，都有|f（x）﹣g（x）|≤1，则称f（x）和g（x）在[a，b]上是“密切函数”，[a，b]称为“密切区间”，设f（x）=x2﹣3x+4与g（x）=2x﹣3在[a，b]上是“密切函数”，则它的“密切区间”可以是（）A．[1，4]B．[2，3]C．[3，4]D．[2，4]【考点】函数的值域．【分析】根据“密切函数”的定义列出绝对值不等式|x2﹣3x+4﹣（2x﹣3）|≤1，求出解集即可得到它的“密切区间”．【解答】解：因为f（x）与g（x）在[a，b]上是“密切函数”，则|f（x）﹣g（x）|≤1即|x2﹣3x+4﹣（2x﹣3）|≤1即|x2﹣5x+7|≤1，化简得﹣1≤x2﹣5x+7≤1，因为x2﹣5x+7的△＜0即与x轴没有交点，由开口向上得到x2﹣5x+7＞0＞﹣1恒成立；所以由x2﹣5x+7≤1解得2≤x≤3，所以它的“密切区间”是[2，3]故选B二、填空题：（本大题共5小题，每小题5分，共25分．）11．若tanα=3，则的值等于6．【考点】二倍角的正弦；同角三角函数间的基本关系．【分析】由于tanα=3，将化简为2tanα，问题解决了．【解答】解：∵tanα=3，==2tanα=6，故答案为：6．12．已知f（x）是定义域为R的函数，且满足f（x+2）=﹣，当2≤x≤3时，f（x）=x+，则f（﹣）=3．【考点】函数的值．【分析】由已知得f（x+4）=﹣=f（x），从而f（﹣）=f（），由此能求出结果．【解答】解：∵f（x）是定义域为R的函数，且满足f（x+2）=﹣，∴f（x+4）=﹣=f（x），∵当2≤x≤3时，f（x）=x+，∴f（﹣）=f（）==3．故答案为：3．13．若向量=（x，2x），=（﹣3x，2），且的夹角为钝角，则x的取值范围是（﹣∞，﹣）∪（﹣，0）∪（，+∝）．【考点】数量积表示两个向量的夹角．【分析】本题考查的知识点是平面向量数量积表示两个向量的夹角，=（x，2x），=（﹣3x，2），且的夹角为钝角，结合数量积表示两个向量的夹角，我们可以得到一个关于x的不等式，解不等式即可得到x的取值范围，但要注意，与反向的排除．【解答】解：∵的夹角θ为钝角又∵向量=（x，2x），=（﹣3x，2），∴cosθ==＜0即﹣3x2+4x＜0解x＜0，或x＞又∵当x=﹣时，与反向，不满足条件故满足条件的x的取值范围是（﹣∞，﹣）∪（﹣，0）∪（，+∝）故答案为：（﹣∞，﹣）∪（﹣，0）∪（，+∝）14．过点P（1，）作圆x2+y2=1的两条切线，切点分别为A，B，则=．【考点】平面向量数量积的运算；直线与圆相交的性质．【分析】根据直线与圆相切的性质可求PA=PB，及∠∠APB，然后代入向量数量积的定义可求．【解答】解：连接OA，OB，PO则OA=OB=1，PO=，2，OA⊥PA，OB⊥PB，Rt△PAO中，OA=1，PO=2，PA=∴∠OPA=30°，∠BPA=2∠OPA=60°∴===故答案为：15．已知函数f（x）=，若存在实数a，b，c，d，满足f（a）=f（b）=f（c）=f（d），其中d＞c＞b＞a＞0，则abcd的取值范围是（21，24）．【考点】对数函数图象与性质的综合应用．【分析】由题意可得﹣log3a=log3b=c2﹣c+8=d2﹣d+8，可得log3（ab）=0，ab=1．结合函数f（x）的图象，在区间[3，+∞）时，令f（x）=1可得c=3、d=7、cd=21．令f（x）=0可得c=4 d=6、cd=24．由此求得abcd的范围．【解答】解：由题意可得﹣log3a=log3b=c2﹣c+8=d2﹣d+8，可得log3（ab）=0，故ab=1．结合函数f（x）的图象，在区间[3，+∞）上，令f（x）=1可得c=3、d=7、cd=21．令f（x）=0可得c=4、d=6、cd=24．故有21＜abcd＜24，故答案为（21，24）．三、解答题：本大题共6个小题.共75分.解答应写出文字说明，证明过程或演算步骤. 16．已知等差数列{a n}中，a3a7=﹣16，a4+a6=0，求{a n}前n项和s n．【考点】等差数列的前n项和；等差数列的通项公式．【分析】利用等差数列的通项公式，结合已知条件列出关于a1，d的方程组，求出a1、d，进而代入等差数列的前n项和公式求解即可．【解答】解：设{a n}的公差为d，则，即，解得，因此S n=﹣8n+n（n﹣1）=n（n﹣9），或S n=8n﹣n（n﹣1）=﹣n（n﹣9）．17．已知集合A={x|（x﹣6）（x﹣2a﹣5）＞0}，集合B={x|[（a2+2）﹣x]•（2a﹣x）＜0}．（Ⅰ）若a=5，求集合A∩B；（Ⅱ）已知a＞．且“x∈A”是“”的必要不充分条件，求实数a的取值范围．【考点】必要条件、充分条件与充要条件的判断；交集及其运算．【分析】（Ⅰ）分别求出关于A、B的不等式，求出A、B的交集即可；（Ⅱ）求出关于A的不等式，根据集合的包含关系求出a的范围即可．【解答】解：（Ⅰ）当a=5时，A={x|（x﹣6）（x﹣15）＞0}={x|x＞15或x＜6}…B={x|（27﹣x）（10﹣x）＜0}={x|10＜x＜27}．…∴A∩B={x|15＜x＜27}．…（Ⅱ）∵，∴2a+5＞6，∴A={x|x＜6或x＞2a+5}…又a2+2＞2a，∴B={x|2a＜x＜a2+2}．…∵“x∈A”是“”的必要不充分条件，∴B⊆A，∴，解之得：．…18．已知向量（x∈R）函数f（x）=（Ⅰ）求f（x）的最小正周期；（Ⅱ）若函数y=f（x）的图象向右平移个单位，再向上平移个单位，得到函数y=g（x）的图象，求y=g（x）在[0，]上的最大值．【考点】平面向量数量积的运算；函数最值的应用；函数y=Asin（ωx+φ）的图象变换．【分析】（Ⅰ）根据向量的数量积和二倍角公式，两角和的正弦公式，诱导公式，和最小正周期的定义即可求出．（Ⅱ）根据图象的平移得到g（x）=cos（2x﹣）+，再根据正弦函数的性质即可求出最大值．【解答】解：（Ⅰ）向量（x∈R），函数f（x）==sinxcosx﹣cosxcos（π+x）=sin2x+cos2x+（cos2x+1）=sin（2x+）+，∴f（x）的最小正周期，T==π，（Ⅱ）∵函数y=f（x）的图象向右平移个单位，再向上平移个单位，得到函数y=g （x）的图象，∴g（x）=sin[2（x﹣）+]++=sin（2x﹣）+，∵x∈[0，]，∴（2x﹣）∈[﹣，]，∴g（x）在[0，]上单调递增，∴g（x）max=g（）=．19．为了在夏季降温和冬季供暖时减少能源损耗，房屋的屋顶和外墙需要建造隔热层．某幢建筑物要建造可使用20年的隔热层，每厘米厚的隔热层建造成本为6万元．该建筑物每年的能源消耗费用C（单位：万元）与隔热层厚度x（单位：cm）满足关系：C（x）=（0≤x≤10），若不建隔热层，每年能源消耗费用为8万元．设f（x）为隔热层建造费用与20年的能源消耗费用之和．（Ⅰ）求k的值及f（x）的表达式．（Ⅱ）隔热层修建多厚时，总费用f（x）达到最小，并求最小值．【考点】函数模型的选择与应用；利用导数求闭区间上函数的最值．【分析】（I）由建筑物每年的能源消耗费用C（单位：万元）与隔热层厚度x（单位：cm）满足关系：C（x）=，若不建隔热层，每年能源消耗费用为8万元．我们可得C（0）=8，得k=40，进而得到．建造费用为C1（x）=6x，则根据隔热层建造费用与20年的能源消耗费用之和为f（x），我们不难得到f（x）的表达式．（II）由（1）中所求的f（x）的表达式，我们利用导数法，求出函数f（x）的单调性，然后根据函数单调性易求出总费用f（x）的最小值．【解答】解：（Ⅰ）设隔热层厚度为x cm，由题设，每年能源消耗费用为．再由C（0）=8，得k=40，因此．而建造费用为C1（x）=6x，最后得隔热层建造费用与20年的能源消耗费用之和为（Ⅱ），令f'（x）=0，即．解得x=5，（舍去）．当0＜x＜5时，f′（x）＜0，当5＜x＜10时，f′（x）＞0，故x=5是f（x）的最小值点，对应的最小值为．当隔热层修建5cm厚时，总费用达到最小值为70万元．20．已知数列{a n}是等差数列，{b n}是等比数列，且a1=b1=2，b4=54，a1+a2+a3=b2+b3．（1）求数列{a n}和{b n}的通项公式；（2）数列{c n}满足c n=a n b n，求数列{c n}的前n项和S n．【考点】等差数列与等比数列的综合；数列的求和．【分析】（1）利用等比数列的通项公式，可求确定公比，从而可求{b n}的通项公式，利用a1+a2+a3=b2+b3，可得数列的公差，从而可求数列{a n}的通项公式；（2）利用错位相减法可求数列{c n}的前n项和S n．【解答】解：（1）设{a n}的公差为d，{b n}的公比为q由=54，得，从而q=3因此又a1+a2+a3=3a2=b2+b3=6+18=24，∴a2=8从而d=a2﹣a1=6，故a n=a1+（n﹣1）•6=6n﹣4（2）令两式相减得=﹣（3n﹣2）•3n=∴，又．21．设函数f（x）=x2+ax﹣lnx，a∈R，（Ⅰ）当a=1时，求函数f（x）的极值；（Ⅱ）当a＞1时，讨论函数f（x）的单调性；（Ⅲ）若对任意a∈（3，4）及任意x1，x2∈[1，2]，恒有|成立，求实数m的取值范围．【考点】利用导数研究函数的单调性；利用导数研究函数的极值．【分析】（Ⅰ）确定函数的定义域为（0，+∞），求导函数，确定函数的单调性，即可求得函数f （x）的极值；（Ⅱ）求导函数，并分解，再进行分类讨论，利用f′（x）＜0，确定函数单调减区间；f′（x）＞0，确定函数的单调增区间；（Ⅲ）确定f（x）在[1，2]上单调递减，可得f（x）的最大值与最小值，进而利用分离参数法，经整理得，由3＜a＜4，从而可求实数m的取值范围．【解答】解：（Ⅰ）函数的定义域为（0，+∞）．当a=1时，，…当0＜x＜1时，f′（x）＜0；f（x）单调递减；…当x＞1时，f′（x）＞0．f（x）单调递增…=f（1）=1，无极大值．…∴f（x）极小值（Ⅱ）==…当，即a=2时，，f（x）在定义域上是减函数；…当，即a＞2时，令f′（x）＜0，得或x＞1；令f′（x）＞0，得．．…当，即1＜a＜2时，令f′（x）＜0，得0＜x＜1或；令f′（x）＞0，得．…综上，当a=2时，f（x）在（0，+∞）上是减函数；当a＞2时，f（x）在和（1，+∞）单调递减，在上单调递增；1＜a＜2时，f（x）在（0，1）和单调递减，在上单调递增；…（Ⅲ）由（Ⅱ）知，当a∈（3，4）时，f（x）在[1，2]上单减，f（1）是最大值，f（2）是最小值．∴…∴，而a＞0经整理得，…由3＜a＜4得，所以．…2017年1月4日。

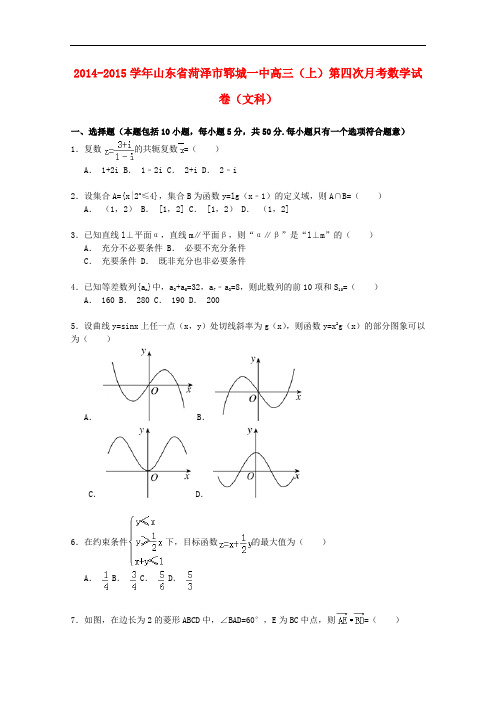
2014-2015学年山东省菏泽市郓城一中高三（上）第四次月考数学试卷（文科）一、选择题（本题包括10小题，每小题5分，共50分.每小题只有一个选项符合题意）1．复数的共轭复数=（）A． 1+2i B． 1﹣2i C． 2+i D． 2﹣i2．设集合A={x|2x≤4}，集合B为函数y=lg（x﹣1）的定义域，则A∩B=（） A．（1，2） B． [1，2] C． [1，2） D．（1，2]3．已知直线l⊥平面α，直线m∥平面β，则“α∥β”是“l⊥m”的（） A．充分不必要条件 B．必要不充分条件C．充要条件 D．既非充分也非必要条件4．已知等差数列{a n}中，a3+a5=32，a7﹣a3=8，则此数列的前10项和S10=（） A． 160 B． 280 C． 190 D． 2005．设曲线y=sinx上任一点（x，y）处切线斜率为g（x），则函数y=x2g（x）的部分图象可以为（）A． B．C． D．6．在约束条件下，目标函数的最大值为（）A． B． C． D．7．如图，在边长为2的菱形ABCD中，∠BAD=60°，E为BC中点，则=（）A．﹣3 B． 0 C．﹣1 D． 18．定义=a1a4﹣a2a3，若函数f（x）=，则将f（x）的图象向右平移个单位所得曲线的一条对称轴方程是（）A． x= B． x= C． x= D． x=π9．一个几何体的三视图如图所示，其中的长度单位为cm，则该几何体的体积为（）cm3．A． 18 B． 48 C． 45 D． 5410．已知函数f（x）对定义域R内的任意x都有f（x）=f（4﹣x），且当x≠2时其导函数f′（x）满足xf′（x）＞2f′（x），若2＜a＜4则（）A． f（2a）＜f（3）＜f（log2a） B． f（3）＜f（log2a）＜f（2a）C． f（log2a）＜f（3）＜f（2a） D． f（log2a）＜f（2a）＜f（3）二、填空题：本大题共5小题，每小题5分，共25分．11．已知||=1，||=2，且+=与垂直，则向量与的夹角大小是．12．函数y=a2﹣x（a＞0且a≠1）的图象过定点A，若点A的坐标满足方程mx+ny=1（m，n＞0），则+的最小值为．13．现有一根n节的竹竿，自上而下每节的长度依次构成等差数列，最上面一节长为10cm，最下面的三节长度之和为114cm，第6节的长度是首节与末节长度的等比中项，则n= ．14．设y=f（t）是某港口水的深度y（米）关于时间t（时）的函数，其中0≤t≤24．下表t 0 3 6 9 12 15 18 21 24y 5.0 7.5 5.0 2.5 5.0 7.5 5.0 2.5 5.0经长期观察，函数y=f（t）的图象可以近似地看成函数y=h+Asin（ωx+ϕ）的图象．最能近似表示表中数据间对应关系的函数是．15．定义在R上的偶函数f（x），且对任意实数x都有f（x﹣2）=f（x），当x∈[0，1]时，f （x）=x2，若在区间[﹣1，3]内，函数g（x）=f（x）﹣kx﹣k有4个零点，则实数k的取值范围是．三、解答题：本大题共6小题，共75分.16．不等式（1﹣a）x2﹣4x+6＞0的解集是{x|﹣3＜x＜1}．（1）解不等式2x2+（2﹣a）x﹣a＞0；（2）b为何值时，（a﹣3+b）x2+bx+3≥0的解集为R？17．已知函数．其图象的两个相邻对称中心的距离为，且过点．（I）函数f（x）的表达式；（Ⅱ）在△ABC中．a、b、c分别是角A、B、C的对边，，，角C为锐角．且满，求c的值．18．如图，在四棱锥S﹣ABCD中，底面ABCD是正方形，SA⊥底面ABCD，SA=AB，点M是SD的中点，AN⊥SC，且交SC于点N．（Ⅰ）求证：SB∥平面ACM；（Ⅱ）求证：平面SAC⊥平面AMN；（Ⅲ）求二面角D﹣AC﹣M的余弦值．19．设数列{a n}满足：a1=5，a n+1+4a n=5，（n∈N*）（I）是否存在实数t，使{a n+t}是等比数列？（Ⅱ）设数列b n=|a n|，求{b n}的前2014项和S2014．20．某化工厂引进一条先进生产线生产某种化工产品，其生产的总成本y（万元）与年产量x（吨）之间的函数关系式可以近似地表示为y=﹣48x+8000，已知此生产线年产量最大为210吨．（1）求年产量为多少吨时，生产每吨产品的平均成本最低，并求最低成本；（2）若每吨产品平均出厂价为40万元，那么当年产量为多少吨时，可以获得最大利润？最大利润是多少？21．设函数f（x）=x﹣﹣alnx（a∈R）．（Ⅰ）当a=3时，求f（x）的极值；（Ⅱ）讨论函数f（x）的单调性．2014-2015学年山东省菏泽市郓城一中高三（上）第四次月考数学试卷（文科）参考答案与试题解析一、选择题（本题包括10小题，每小题5分，共50分.每小题只有一个选项符合题意）1．复数的共轭复数=（）A． 1+2i B． 1﹣2i C． 2+i D． 2﹣i考点：复数代数形式的乘除运算．专题：计算题．分析：利用两个复数代数形式的乘除法法则求得z，即可求得它的共轭复数．解答：解：∵复数===1+2i，∴它的共轭复数=1﹣2i，故选B．点评：本题主要考查复数的基本概念，两个复数代数形式的乘除法，虚数单位i的幂运算性质，属于基础题．2．设集合A={x|2x≤4}，集合B为函数y=lg（x﹣1）的定义域，则A∩B=（） A．（1，2） B． [1，2] C． [1，2） D．（1，2]考点：其他不等式的解法；交集及其运算．专题：计算题；不等式的解法及应用．分析：通过指数不等式求出集合A，求解函数的定义域求出集合B，然后求解交集即可．解答：解：因为集合A={x|2x≤4}={x|x≤2}，集合B为函数y=lg（x﹣1）的定义域为：{x|x ＞1}，则A∩B={x|x≤2}∩{x|x＞1}={x|1＜x≤2}．故选D．点评：本题考查指数不等式的求法，函数的定义域的求法集合的交集的运算，考查计算能力．3．已知直线l⊥平面α，直线m∥平面β，则“α∥β”是“l⊥m”的（） A．充分不必要条件 B．必要不充分条件C．充要条件 D．既非充分也非必要条件考点：必要条件、充分条件与充要条件的判断．专题：空间位置关系与距离．分析：结合面面平行性质定理，利用充分条件和必要条件的定义进行判断．解答：解：若α∥β，∵直线l⊥平面α，∴直线l⊥β，∵m∥β，∴l⊥m成立．若l⊥m，当m∥β时，则l与β的位置关系不确定，∴无法得到α∥β．∴“α∥β”是“l⊥m”的充分不必要条件．点评：本题主要考查充分条件和必要条件的判断，利用空间直线和平面的位置关系是解决本题的关键．4．已知等差数列{a n}中，a3+a5=32，a7﹣a3=8，则此数列的前10项和S10=（）A． 160 B． 280 C． 190 D． 200考点：等差数列的前n项和．专题：等差数列与等比数列．分析：由已知数据易得数列的首项和公差，代入求和公式计算可得．解答：解：∵等差数列{a n}中，a3+a5=32，a7﹣a3=8，∴2a4=a3+a5=32，公差d=，解得a4=16，d=2，∴a1=16﹣3×2=10，∴数列的前10项和S10=10×10+×2=190故选：C点评：本题考查等差数列的求和公式，求出数列的首项和公差是解决问题的关键，属基础题．5．设曲线y=sinx上任一点（x，y）处切线斜率为g（x），则函数y=x2g（x）的部分图象可以为（）A． B．C． D．考点：利用导数研究曲线上某点切线方程；函数的图象．专题：函数的性质及应用．分析：先根据导数几何意义得到曲线y=sinx上任一点（x，y）处切线斜率g（x），再研究函数y=x2g（x）的奇偶性，再根据在某点处的函数值的符号进一步进行判定．解答：解：曲线y=sinx上任一点（x，y）处切线斜率为g（x），∴g（x）=cosx，则函数y=x2g（x）=x2•cosx，设f（x）=x2•cosx，则f（﹣x）=f（x），cos（﹣x）=cosx，∴y=f（x）为偶函数，其图象关于y轴对称，排除A、B．令x=0，得f（0）=0．排除D．点评：本题主要考查了导数的运算，以及考查学生识别函数的图象的能力，属于基础题．6．在约束条件下，目标函数的最大值为（）A． B． C． D．考点：简单线性规划．专题：计算题；不等式的解法及应用．分析：作出题中不等式组表示的平面区域，得如图的△AB0及其内部，再将目标函数z=x+y 对应的直线进行平移，可得当x=，y=时，z取得最大值，得到本题答案．解答：解：作出不等式组表示的平面区域，得到如图的△AB0及其内部，其中A（，），B（，），O（0，O）设z=F（x，y）=x+y，将直线l：z=x+y进行平移，可得当l经过点A时，目标函数z达到最大值∴z最大值=F（，）=故选：C点评：本题给出二元一次不等式组，求目标函数z=x+y的最大值，着重考查了二元一次不等式组表示的平面区域和简单的线性规划等知识，属于基础题．7．如图，在边长为2的菱形ABCD中，∠BAD=60°，E为BC中点，则=（）A．﹣3 B． 0 C．﹣1 D． 1考点：平面向量数量积的运算．专题：平面向量及应用．分析：利用向量的运算法则和数量积的计算公式即可得出．解答：解：∵在边长为2的菱形ABCD中，∠BAD=60°，∴==2．又E为BC中点，∴．∴=====﹣1，故选C．点评：熟练掌握向量的运算法则和数量积的计算公式是解题的关键．8．定义=a1a4﹣a2a3，若函数f（x）=，则将f（x）的图象向右平移个单位所得曲线的一条对称轴方程是（）A． x= B． x= C． x= D． x=π考点：函数y=Asin（ωx+φ）的图象变换．专题：三角函数的图像与性质．分析：根据新定义求得平移后所得函数的解析式为y=﹣2cos2x，令 2x=kπ，k∈z，求得x 的值，可得所得曲线的对称轴方程，从而得出结论．解答：解：由于函数f（x）==sin2x﹣cos2x=2sin（2x﹣），则将f（x）的图象向右平移个单位所得曲线的解析式为y=2sin2[（x﹣）﹣]=2sin（2x﹣），令 2x﹣=kπ+，k∈z，求得 x=+，k∈z，结合所给的选项，只有A满足条件，故选：A．点评：本题主要考查新定义，函数y=Asin（ωx+φ）的图象变换规律，属于基础题．9．一个几何体的三视图如图所示，其中的长度单位为cm，则该几何体的体积为（）cm3．A． 18 B． 48 C． 45 D． 54考点：由三视图求面积、体积．专题：空间位置关系与距离．分析：由三视图可知：该几何体是高为4的直棱柱，底面为一个直角梯形，上下边长分别为4，5，其高为3．据此即可得出体积．解答：解：由三视图可知：该几何体是高为4的直棱柱，底面为一个直角梯形，上下边长分别为4，5，其高为3．V==54．故选D．点评：由三视图正确恢复原几何体及掌握直棱柱的体积计算公式是解题的关键．10．已知函数f（x）对定义域R内的任意x都有f（x）=f（4﹣x），且当x≠2时其导函数f′（x）满足xf′（x）＞2f′（x），若2＜a＜4则（）A． f（2a）＜f（3）＜f（log2a） B． f（3）＜f（log2a）＜f（2a）C． f（log2a）＜f（3）＜f（2a） D． f（log2a）＜f（2a）＜f（3）考点：抽象函数及其应用；导数的运算．专题：计算题；函数的性质及应用．分析：由f（x）=f（4﹣x），可知函数f（x）关于直线x=2对称，由xf′（x）＞2f′（x），可知f（x）在（﹣∞，2）与（2，+∞）上的单调性，从而可得答案．解答：解：∵函数f（x）对定义域R内的任意x都有f（x）=f（4﹣x），∴f（x）关于直线x=2对称；又当x≠2时其导函数f′（x）满足xf′（x）＞2f′（x）⇔f′（x）（x﹣2）＞0，∴当x＞2时，f′（x）＞0，f（x）在（2，+∞）上的单调递增；同理可得，当x＜2时，f（x）在（﹣∞，2）单调递减；∵2＜a＜4，∴1＜log2a＜2，∴2＜4﹣log2a＜3，又4＜2a＜16，f（log2a）=f（4﹣log2a），f（x）在（2，+∞）上的单调递增；∴f（log2a）＜f（3）＜f（2a）．故选C．点评：本题考查抽象函数及其应用，考查导数的性质，判断f（x）在（﹣∞，2）与（2，+∞）上的单调性是关键，属于中档题．二、填空题：本大题共5小题，每小题5分，共25分．11．已知||=1，||=2，且+=与垂直，则向量与的夹角大小是．考点：数量积表示两个向量的夹角．专题：平面向量及应用．分析：由题意可得=1，=4，（）•=0，故有=﹣1．设与的夹角等于θ，再由cosθ==﹣．结合0≤θ≤π，可得θ的值．解答：解：由题意可得=1，=4，（）•=+=1+=0，∴=﹣1．设与的夹角等于θ，则cosθ===﹣．再由0≤θ≤π，可得θ=，故答案为．点评：本题本题主要考查两个向量的数量积的定义，两个向量的夹角公式的应用，属于中档题．12．函数y=a2﹣x（a＞0且a≠1）的图象过定点A，若点A的坐标满足方程mx+ny=1（m，n＞0），则+的最小值为3+2．考点：基本不等式；指数函数的图像与性质．专题：不等式的解法及应用．分析：函数y=a2﹣x（a＞0且a≠1）的图象过定点A（2，1），又点A的坐标满足方程mx+ny=1（m，n＞0），可得2m+n=1．再利用“乘1法”与基本不等式的性质即可得出．解答：解：∵函数y=a2﹣x（a＞0且a≠1）的图象过定点A（2，1），又点A的坐标满足方程mx+ny=1（m，n＞0），∴2m+n=1．则+=（2m+n）=3+=3+2，当且仅当n=m=﹣1时取等号．∴+的最小值为3+2．故答案为：3+2．点评：本题考查了指数函数的运算性质、“乘1法”与基本不等式的性质，考查了推理能力与计算能力，属于基础题．13．现有一根n节的竹竿，自上而下每节的长度依次构成等差数列，最上面一节长为10cm，最下面的三节长度之和为114cm，第6节的长度是首节与末节长度的等比中项，则n= 16 ．考点：等差数列的通项公式；等比数列的通项公式．专题：等差数列与等比数列．分析：把已知问题用一个等差数列表示，然后利用等差数列的通项公式和等比中项即可得出．解答：解：设此根n节的竹竿的自上而下每节的长度依次构成等差数列为{a n}，公差为d．由题意可知：a1=10，a n﹣2+a n﹣1+a n=114，．联立可得，解得因此n=16．故答案为16．点评：熟练掌握等差数列的通项公式和等比中项是解题的关键．14．设y=f（t）是某港口水的深度y（米）关于时间t（时）的函数，其中0≤t≤24．下表是该港口某一天从0时至24时记录的时间t与水深y的关系：t 0 3 6 9 12 15 18 21 24y 5.0 7.5 5.0 2.5 5.0 7.5 5.0 2.5 5.0经长期观察，函数y=f（t）的图象可以近似地看成函数y=h+Asin（ωx+ϕ）的图象．最能近似表示表中数据间对应关系的函数是y=5.0+2.5sin t ．考点：在实际问题中建立三角函数模型．专题：计算题；三角函数的图像与性质．分析：根据函数的最大最小值的差，算出2A=7.5﹣2.5=5，从而得到A=2.5，可得h=7.5﹣2.5=5.0．由函数的两个最大值之间的差为12，结合周期公式算出ω=，最后根据f（3）=7.5为函数的最大值，可算出ϕ=0，由此即可解出所求函数关系式．解答：解：根据题意，得∵f（3）=f（15）=7.5，为函数的最大值；f（9）=f（21）=2.5，为函数的最小值∴函数的周期T=15﹣3=12，可得=12，得ω=2A=7.5﹣2.5=5，可得A=2.5，h=7.5﹣2.5=5.0f（3）=5.0+2.5sin（×3+ϕ）=7.5，可得+ϕ=+2kπ（k∈Z）取k=0，得ϕ=0因此，所求函数的关系式为y=5.0+2.5sin t故答案为：y=5.0+2.5sin t点评：本题给出实际应用问题，求其中的近似表示表中数据间对应关系的函数表达式．着重考查了三角函数的图象与性质和函数解析式的求法等知识，属于中档题．15．定义在R上的偶函数f（x），且对任意实数x都有f（x﹣2）=f（x），当x∈[0，1]时，f （x）=x2，若在区间[﹣1，3]内，函数g（x）=f（x）﹣kx﹣k有4个零点，则实数k的取值范围是（0，] ．考点：函数的周期性；函数奇偶性的性质；根的存在性及根的个数判断．专题：函数的性质及应用．分析：由题意可得函数是周期等于2的函数，当x∈[0，1]时，f（x）=x2，可得当x∈[﹣1，0]时，f（x）=x2．再由函数g（x）=f（x）﹣kx﹣k有4个零点，可得函数f（x）的图象和直线y=kx+k=k（x+1）有4个交点，数形结合可得则实数k的取值范围．解答：解：由函数满足对任意实数x都有f（x﹣2）=f（x），可得函数是周期等于2的函数．再根据f（x）是偶函数，当x∈[0，1]时，f（x）=x2，可得当x∈[﹣1，0]时，f（x）=x2．函数g（x）=f（x）﹣kx﹣k有4个零点，可得函数f（x）的图象和直线y=kx+k=k（x+1）有4个交点，如图所示：则由题意可得，A（﹣1，0）、D（3，1），且 0＜k≤k AD=，则实数k的取值范围是（0，]．点评：本题主要考查函数的奇偶性和周期性的应用，函数的零点和方程的根的关系，体现了转化和数形结合的数学思想，属于中档题．三、解答题：本大题共6小题，共75分.16．不等式（1﹣a）x2﹣4x+6＞0的解集是{x|﹣3＜x＜1}．（1）解不等式2x2+（2﹣a）x﹣a＞0；（2）b为何值时，（a﹣3+b）x2+bx+3≥0的解集为R？考点：一元二次不等式的解法．专题：计算题．分析：先由根与系数的关系得出﹣3+1=，a=3．（1）依照一元二次不等式的解法求解（2）分当b=0时，b≠0时分别求解，结合二次函数的图象与性质．解答：解：（1﹣a）x2﹣4x+6＞0的解集是{x|﹣3＜x＜1}．由根与系数的关系得出﹣3+1=，a=3．（1）不等式2x2+（2﹣a）x﹣a＞0即为2x2﹣x﹣3＞0；解集为{x|x＜﹣1或x＞}．（2）（a﹣3+b）x2+bx+3≥0的解集为R，即bx2+bx+3≥0的解集为R当b=0时，3≥0成立；b≠0时，须，解得0＜b≤12综上所述，0≤b≤12．点评：本题考查一元二次不等式的解法，要将二次函数的图象与性质结合起来，数形结合．17．已知函数．其图象的两个相邻对称中心的距离为，且过点．（I）函数f（x）的表达式；（Ⅱ）在△ABC中．a、b、c分别是角A、B、C的对边，，，角C为锐角．且满，求c的值．考点：二倍角的余弦；两角和与差的正弦函数；二倍角的正弦；函数y=Asin（ωx+φ）的图象变换；余弦定理．专题：计算题；综合题；三角函数的图像与性质；解三角形．分析：（I）由二倍角的三角函数公式和辅助角公式，化简得f（x）=sin（ωx+φ﹣）+，结合图象的两个相邻对称中心的距离为和点在函数图象上，建立关于ω、φ的关系式，解之即可得到函数f（x）的达式；（II）将代入函数表达式，解出sinC=，结合C为锐角，算出cosC=．根据面积正弦定理公式，由S△ABC=2算出b=6，最后由余弦定理代入题中的数据即可求出边c的值．解答：解：（I）∵=sin（ωx+φ），=[1﹣cos（ωx+φ）]∴=sin（ωx+φ）+[1﹣cos（ωx+φ）]=sin（ωx+φ﹣）+∵函数图象的两个相邻对称中心的距离为，∴函数的周期T==π，得ω=2∵点是函数图象上的点，∴f（）=sin（2×+φ+）+=1，解之得cosφ=∵φ∈（0，），∴φ=因此，函数f（x）的达式为f（x）=sin（2x+）+；（II）f（﹣）=sin（C﹣+）+=，解之得sinC=∵0＜C＜，∴cosC==又∵a=，S△ABC=2∴×a×b×sinC=2，即××b×=2，解之得b=6根据余弦定理，得c2=a2+b2﹣2abcosC=5+36﹣2××6×=21∴c=，即得c的值为．点评：本题给出三角函数式，根据函数的图象特征求函数表达式，并依此解三角形ABC的边c的长，着重考查了三角恒等变换、正余弦定理和三角函数的图象与性质等知识，属于基础题．18．如图，在四棱锥S﹣ABCD中，底面ABCD是正方形，SA⊥底面ABCD，SA=AB，点M是SD的中点，AN⊥SC，且交SC于点N．（Ⅰ）求证：SB∥平面ACM；（Ⅱ）求证：平面SAC⊥平面AMN；（Ⅲ）求二面角D﹣AC﹣M的余弦值．考点：二面角的平面角及求法；直线与平面平行的判定；平面与平面垂直的判定．专题：空间位置关系与距离；空间角．分析：（Ⅰ）连结BD交AC于E，连结ME，由△DSB的中位线定理，得ME∥SB，由此能证明SB∥平面ACM．（Ⅱ）法一：由DC⊥SA，DC⊥DA，得DC⊥平面SAD，从而AM⊥DC，由等腰三角形性质得AM⊥SD，从而AM⊥平面SDC，进而SC⊥AM，由SC⊥AN，能证明平面SAC⊥平面AMN．法二：以A为坐标原点，建立空间直角坐标系O﹣xyz，利用向量法能证明平面SAC⊥平面AMN．（Ⅲ）法一：取AD中点F，则MF∥SA．作FQ⊥AC于Q，连结MQ，由已知得∠FQM为二面角D ﹣AC﹣M的平面角，由此能求出二面角D﹣AC﹣M的余弦值．法二：分别求出平面ABCD的一个法向量和平面ACM的一个法向量，由此利用向量法能求出二面角D﹣AC﹣M的余弦值．解答：（选修2一1第109页例4改编）（Ⅰ）证明：连结BD交AC于E，连结ME，∵ABCD是正方形，∴E是BD的中点．∵M是SD的中点，∴ME是△DSB的中位线．∴ME∥SB．…（2分）又ME⊂平面ACM，SB⊄平面ACM，∴SB∥平面ACM．…（4分）（Ⅱ）证法一：由条件有DC⊥SA，DC⊥DA，∴DC⊥平面SAD，且AM⊂平面SAD，∴AM⊥DC．又∵SA=AD，M是SD的中点，∴AM⊥SD．∴AM⊥平面SDC．SC⊂平面SDC，∴SC⊥AM．…（6分）由已知SC⊥AN，∴SC⊥平面AMN．又SC⊂平面SAC，∴平面SAC⊥平面AMN．…（8分）（Ⅱ）证法二：如图，以A为坐标原点，建立空间直角坐标系O﹣xyz，由SA=AB，可设AB=AD=AS=1，则．∵，，∴，∴，即有SC⊥AM…（6分）又SC⊥AN且AN∩AM=A．∴SC⊥平面AMN．又SC⊂平面SAC，∴平面SAC⊥平面AMN．…（8分）（Ⅲ）解法一：取AD中点F，则MF∥SA．作FQ⊥AC于Q，连结MQ．∵SA⊥底面ABCD，∴MF⊥底面ABCD．∴FQ为MQ在平面ABCD内的射影．∵FQ⊥AC，∴MQ⊥AC．∴∠FQM为二面角D﹣AC﹣M的平面角．…（10分）设SA=AB=a，在Rt△MFQ中，，∴．∴二面角D﹣AC﹣M的余弦值为．…（12分）（Ⅲ）解法二：∵SA⊥底面ABCD，∴是平面ABCD的一个法向量，．设平面ACM的法向量为，，则即，∴令x=﹣1，则．…（10分），由作图可知二面角D﹣AC﹣M为锐二面角∴二面角D﹣AC﹣M的余弦值为．…（12分）点评：本题考查直线与平面平行的证明，考查平面与平面垂直的证明，考查二面角的余弦值的求法，涉及到线线、线面、面面平行与垂直的性质的应用，考查向量法的合理运用，考查空间思维能力的培养，是中档题．19．设数列{a n}满足：a1=5，a n+1+4a n=5，（n∈N*）（I）是否存在实数t，使{a n+t}是等比数列？（Ⅱ）设数列b n=|a n|，求{b n}的前2014项和S2014．考点：数列的求和；数列递推式．专题：等差数列与等比数列．分析：（Ⅰ）由已知得a n+1=﹣4a n+5，令a n+1+t=﹣4（a n+t），得t=﹣1，从而求出存在这样的实数t=﹣1，使{a n+t}是等比数列．（Ⅱ）由a n﹣1=4•（﹣4）n﹣1．得b n=|a n|=，由此能求出{b n}的前2014项和S2014．解答：解：（Ⅰ）由a n+1+4a n=5，得a n+1=﹣4a n+5，令a n+1+t=﹣4（a n+t），…（2分）得a n+1=﹣4a n﹣5t，则﹣5t=5，解得t=﹣1，…（4分）从而a n+1﹣1=﹣4（a n﹣1）．又a1﹣1=4，∴{a n﹣1}是首项为4，公比为﹣4的等比数列，∴存在这样的实数t=﹣1，使{a n+t}是等比数列．…（6分）（Ⅱ）由（Ⅰ）得a n﹣1=4•（﹣4）n﹣1．∴b n=|a n|=，（8分）∴S2015=（1+4）+（42﹣1）+（1+43）+…+（42014﹣1）=4+42+43+…+42014==．…（12分）点评：本题考查是否存在使得数列为等比数列的实数的判断与求法，考查数列的前2014项和的求法，是中档题，解题时要注意等比数列的性质的合理运用．20．某化工厂引进一条先进生产线生产某种化工产品，其生产的总成本y（万元）与年产量x （吨）之间的函数关系式可以近似地表示为y=﹣48x+8000，已知此生产线年产量最大为210吨．（1）求年产量为多少吨时，生产每吨产品的平均成本最低，并求最低成本；（2）若每吨产品平均出厂价为40万元，那么当年产量为多少吨时，可以获得最大利润？最大利润是多少？考点：函数模型的选择与应用．专题：计算题．分析：（1）利用总成本除以年产量表示出平均成本；利用基本不等式求出平均成本的最小值．（2）利用收入减去总成本表示出年利润；通过配方求出二次函数的对称轴；由于开口向下，对称轴处取得最大值．解答：解：（1）设每吨的平均成本为W（万元/T），则（0＜x＜210），（4分）当且仅当，x=200（T）时每吨平均成本最低，且最低成本为32万元．（6分）（2）设年利润为u（万元），则=．（11分）所以当年产量为210吨时，最大年利润1660万元．（12分）点评：本题考查将实际问题的最值问题转化为函数的最值问题、考查利用基本不等式求函数的最值需满足：一正、二定、三相等、考查求二次函数的最值关键看对称轴．21．设函数f（x）=x﹣﹣alnx（a∈R）．（Ⅰ）当a=3时，求f（x）的极值；（Ⅱ）讨论函数f（x）的单调性．考点：函数在某点取得极值的条件；利用导数研究函数的单调性．专题：综合题；分类讨论；导数的综合应用．分析：（Ⅰ）先求出函数的定义域，当a=3时在定义域内解不等式f′（x）＞0，f′（x）＜0即可；（Ⅱ）f′（x）=，令g（x）=x2﹣ax+2，其判别式△=a2﹣8，按△≤0时，△＞0时两种情况解不等式f′（x）＞0，f′（x）＜0，△＞0时再按根与0的大小讨论，即共分三种情况进行讨论解不等式即可；解答：解：（Ⅰ）函数的定义域为（0，+∞），当a=3时，f′（x）=1+﹣=，令f′（x）=0，解得x=1或x=2，当0＜x＜1或x＞2时，f′（x）＞0，当1＜x＜2时，f′（x）＜0，所以当x=1时f（x）取得极大值f（1）=﹣1，当x=2时f（x）取得极小值f（2）=1﹣3ln2；（Ⅱ）f′（x）=1+﹣=，令g（x）=x2﹣ax+2，其判别式△=a2﹣8，①当|a|时，△≤0时，f′（x）≥0，故f（x）在（0，+∞）上单调递增；②当a＜﹣2时，△＞0时，g（x）=0的两根都小于0，所以在（0，+∞）上f′（x）＞0，故f（x）在（0，+∞）上单调递增；③当a＞2时，△＞0，g（x）=0的两根为：x1=，x2=，且都大于0，当0＜x＜x1或x＞x2时f′（x）＞0，当x1＜x＜x2时f′（x）＜0，故f（x）在（0，）和（，+∞）上递增，在（，）上递减，综上，当a时f（x）（0，+∞）上单调递增；当a＞时，f（x）在（0，）和（，+∞）上递增，在（，）上递减；点评：本题考查利用导数研究函数的极值、函数的单调性，考查分类讨论思想，考查学生分析解决问题的能力．。

本试卷共4页，分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，共 150分，考试时间120分钟.第Ⅰ卷 (选择题 共60分) 注意事项:1. 答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上. 2．每题选出答案后，用2B 铅笔把答题卡对应题目的答案标号涂黑.（特别强调：为方便本次阅卷，每位考生在认真填涂 “数学”答题卡的前提下，再将Ⅰ卷选择题答案重涂在另一答题卡上.）如需改动，用橡皮擦干净后，再改涂在其它答案标号.一、选择题:本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1. 复数11+-i i （i 为虚数单位）等于 A ．1 B.—1 C.i D.i - 2. 设集合{1,2,3,4,5},{1,2,3},{2,5},()U U A B A B ===则=A ．{1，3}B ．{2}C ．{2，3}D ．{3}3. 等差数列{}n a 的前n 项和为n S ，若371112a a a ++=，则13S 等于A ．52B ．54C ．56D ．584. 在ABC ∆中，若60,3,42A BC AC =︒==B 的大小为A ．30°B ．45°C ．135°D ．45°或135°5. 设函数1()ln (0)3f x x x x =->，则()y f x = A.在区间1(,1),(1,)e e内均有零点.B.在区间(1,),(,3)e e 内均有零点.C.在区间2(,3),(3,)e e 内均无零点.D.在区间内2(1,),(3,)e e 内均有零点.6.设向量)2,1(=→a ，)1,(xb =→，当向量→→+b a 2与→→-b a 2平行时，则→→⋅b a 等于 A ．2 B ．1 C ．25D ．277．若不等式|1|x a -<成立的充分条件是04x <<，则实数a 的取值范围是A ．[)3,+∞B ．(],3-∞C ．[)1,+∞D ．(],1-∞8. 函数1lg|1|y x =+的大致图象为9. 将函数sin(2)3y x π=-的图象先向左平移6π，然后将得到的图象上所有点的横坐标变为原来的2倍（纵坐标不变），则所得到的图象对应函数解析式为A ．cos y x =-B ．sin 4y x =C ．sin()6y x π=-D ．sin y x =10. 考察下列命题：①命题“若lg 0,x =则1x =”的否命题为“若lg 0,1x x ≠≠则；” ②若“p q ∧”为假命题，则p 、q 均为假命题；③命题p ：x R ∃∈，使得sin 1x >；则p ⌝：x R ∀∈，均有sin 1x ≤； ④“),0(,)1()(,342+∞⋅-=∈∃+-且在是幂函数使m mx m x f m R 上递减”则真命题的个数为A ．1B ．2C ．3D ．4 11.已知(3)4,1()log ,1a a x a x f x x x --⎧=⎨≥⎩＜，是（-∞，+∞）上的增函数，那么a 的取值范围是A ．(1，+∞) B.(-∞,3) C.[53，3) D.(1,3)12. 已知定义在R 上的函数)(x f y =满足下列三个条件：①对任意的R x ∈都有);()2(x f x f -=+②对于任意的2021≤<≤x x ，都有),()(21x f x f <③)2(+=x f y 的图象关于y 轴对称，则下列结论中，正确的是A ．)7()5.6()5.4(f f f <<B ． )5.6()7()5.4(f f f <<C ．)5.6()5.4()7(f f f <<D ． )5.4()5.6()7(f f f <<第Ⅱ卷 (非选择题 共90分)注意事项:1. 第Ⅱ卷包括填空题和解答题共两个大题.2．第Ⅱ卷所有题目的答案考生需用黑色签字笔答在 “数学”答题卡指定的位置. 二、填空题：本大题共4个小题，每小题4分，共16分. 13. 当0a >且1a ≠时，函数2()5x f x a+=+的图象必过定点 .14. 已知⎪⎩⎪⎨⎧≥-<=-,3),6(log 3,3)(231x x x e x f x 则))3((f f 的值为 . 15. 已知直线1y x =+与曲线ln()y x a =+相切，则a 的值为 .16. 设ABC ∆中，(1,2)AB =，(,2)(0)AC x x x =->，若ABC ∆的周长为x 的值为 .三、解答题:本大题共6小题，共74分.解答应写出文字说明，证明过程或演算步骤. 17. （本小题满分12分）已知函数.cos 3cos sin )(2x x x x f +=（Ⅰ）求)(x f 的最小正周期； （Ⅱ）求)(x f 在区间]2,6[ππ-上的最大值和最小值． 18.（本小题满分12分）记函数2()lg(2)f x x x =--的定义域为集合A，函数()g x =B .（Ⅰ）求AB ；（Ⅱ）若{}22440,0C x x x p p =++-<>，且()C A B ⊆，求实数p 的取值范围.19. （本小题满分12分）已知ABC ∆的角A 、B 、C 所对的边分别是,,a b c ，设向量(,)m a b =, (sin ,sin )n B A =,(2,2)p b a =--（Ⅰ）若m ∥n ，求证：ABC ∆为等腰三角形； （Ⅱ）若m ⊥p ，边长2c =，3C π=，求ABC ∆的面积.20. （本小题满分12分）若二次函数2()f x x bx c =++满足(2)(2)f f =-，且函数的()f x 的一个零点为1. (Ⅰ) 求函数()f x 的解析式；（Ⅱ）对任意的1,2x ⎡⎫∈+∞⎪⎢⎣⎭，224()(1)44m f x f x m +-≥-恒成立，求实数m 的取值范围.21.（本小题满分12分）经市场调查，某旅游城市在过去的一个月内（以30天计），第t 天(130,)t t N *≤≤∈的旅游人数()f t (万人)近似地满足()f t =4+1t,而人均消费()g t (元)近似地满足()12020g t t =--.(Ⅰ)求该城市的旅游日收益()w t （万元）与时间t (130,)t t N *≤≤∈的函数关系式； (Ⅱ)求该城市旅游日收益的最小值. 22.（本小题满分14分） 已知函数()ln .f x x x = (Ⅰ)求函数()f x 的极值点；(Ⅱ)若直线l 过点(0,1)-且与曲线()y f x =相切，求直线l 的方程；(Ⅲ)设函数()()(1),g x f x a x =--,a R ∈求函数()g x 在[1]e ，上的最小值.( 2.71828e =)高三数学（文科）参考答案及评分标准 一、选择题:本大题共12小题，每小题5分，共60分.CAABD CADDC DB二、填空题：本大题共4个小题，每小题4分，共16分. 13. (2,6)- 14. 3 15. 2 16. 3011三、解答题:本大题共6小题，共74分.17. 解：（Ⅰ）x x x x f 2cos 3cos sin )(+=)12(cos 23cos sin 221++⋅=x x x 232cos 232sin 21++=x x 23)32sin(++=πx ∴函数)(x f 的最小正周期ππ==22T ． …………………6分 （Ⅱ）∵26ππ≤≤-x ，34320ππ≤+≤x ，∴,1)32sin(23≤+≤-πx …………………9分∴20sin(2)13222x π≤++≤+= ∴ )(x f 在区间]2,6[ππ-上的最大值为232+，最小值为0． ……………12分 18.解：（Ⅰ）依题意，得{}{}22012A x x x x x x =-->=<->或{}{}3033B x x x x =-≥=-≤≤{}3123A B x x x ∴=-≤<-<≤或 …………………6分（Ⅱ）{}022p C x p x p >∴=--<<-+又()C AB ⊆ 2321p p --≥-⎧∴⎨-+≤-⎩01p ∴<≤ …………………12分19. 证明：(Ⅰ) ∵m ∥n ， ∴sin sin a A b B =，由正弦定理可知，22a ba b R R ⋅=⋅，其中R 是ABC ∆外接圆的半径， ∴a b =.因此，ABC ∆为等腰三角形. …………………6分（Ⅱ）由题意可知，0m p ⋅=，即(2)(2)0,.a b b a a b ab -+-=∴+= 由余弦定理可知，2224()3,a b ab a b ab =+-=+-即2()340ab ab --=4ab ∴=，(1ab =舍去)∴11sin 4sin 223S ab C π==⋅⋅=…………………12分20.解：(Ⅰ) ∵(2)(2)f f =-且(1)0f =∴0,1b c ==- ∴2()1f x x =- ………………………4分（Ⅱ）由题意知：22224(1)(1)1440m x x m -+--+-≥在1[,)2x ∈+∞上恒成立，整理得2211124m x x ≥+-在1[,)2x ∈+∞上恒成立， ………………………6分 令()g x =22111115()24416x x x +-=+-∵1[,)2x ∈+∞ ∴(]10,2x ∈ ………………………8分当12x =时，函数()g x 得最大值194， ………………………10分 所以2194m ≥，解得2m ≤-或2m ≥. ………………………12分21．（Ⅰ）解：()()()()2012014--⎪⎭⎫ ⎝⎛+==t t t g t f t W (4)分=()()⎪⎪⎩⎪⎪⎨⎧≤<-+≤≤++302041405592011004401t t t t t t (6)分（Ⅱ）当[]20,1∈t ，441100424011004140=⋅+≥++tt t t （t=5时取最小值）……9分当(]3020，，∈t ，因为()t tt W 4140559-+=递减， 所以t=30时，W(t)有最小值W(30)= 32443， (11)分所以[]30,1∈t 时，W(t)的最小值为441万元 ………12分22 .解：（Ⅰ）()x x x f ,1ln +='＞0 …………1分而()x f '＞0⇔lnx+1＞0⇔x ＞()x f e',1＜0⇔1ln +x ＜0⇔0＜x ＜,1e所以()x f 在⎪⎭⎫ ⎝⎛e 1,0上单调递减，在⎪⎭⎫ ⎝⎛+∞,1e 上单调递增 . …………3分 所以ex 1=是函数()x f 的极小值点，极大值点不存在. …………………4分（Ⅱ）设切点坐标为()00,y x ，则,ln 000x x y =切线的斜率为,1ln 0+x所以切线l 的方程为()().1ln ln 0000x x x x x y -+=- …………5分 又切线l 过点()1,0-，所以有()().01ln ln 10000x x x x -+=--解得.0,100==y x 所以直线l 的方程为.1-=x y ………6分 （Ⅲ）()()1ln --=x a x x x g ，则().1ln a x x g -+=' ()x g '＜0a x -+⇔1ln ＜0⇔0＜x ＜()x g ea '-,1＞0x ⇔＞,1-a e 所以()x g 在()1,0-a e 上单调递减，在()+∞-,1a e 上单调递增. ………………8分 当,11≤-a e即1≤a 时，()x g 在[]e ,1上单调递增，所以()x g 在[]e ,1上的最小值为().01=g ……9分当1＜1-a e＜e ，即1＜a ＜2时，()x g 在[)1,1-a e上单调递减，在(]e ea ,1-上单调递增.()x g 在[]e ,1上的最小值为().11---=a a e a e g ………11分当,1-≤a e e即2≥a 时，()x g 在[]e ,1上单调递减，所以()x g 在[]e ,1上的最小值为().ae a e e g -+= ……12分综上，当1≤a 时，()x g 的最小值为0；当1＜a ＜2时，()x g 的最小值为1--a ea ；当2≥a 时，()x g 的最小值为.ae e a -+ ………14分。

2016-2017学年山东省菏泽一中高三（上）期中数学试卷（理科）一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．设集合M={﹣1，0，1，2}，N={x|x2﹣x﹣2＜0}，则M∩N=（）A．{0，1}B．{﹣1，0}C．{1，2}D．{﹣1，2}2．设命题p：∃x＜0，x2≥1，则¬p为（）A．∀x≥0，x2＜1 B．∀x＜0，x2＜1 C．∃x≥0，x2＜1 D．∃x＜0，x2＜13．要得到函数y=sin2x的图象，只要将函数y=sin（2x﹣）的图象（）A．向左平移单位B．向右平移单位C．向左平移单位D．向右平移单位4．函数的定义域为（）A．[0，+∞）B．（﹣∞，2]C．[0，2]D．[0，2）5．若变量x，y满足条件，则目标函数z=2x+y的最小值为（）A．﹣3 B．﹣2 C．﹣1 D．16．中国古代数学著作《算法统宗》中有这样一个问题：“三百七十八里关，初行健步不为难，次日脚痛减一半，六朝才得到其关，要见次日行里数，请公仔细算相还．”其大意为：“有一个人走了378里路，第一天健步行走，从第二天起因脚痛每天走的路程为前一天的一半，走了6天后到达目的地．”问此人第4天和第5天共走了（）A．60里B．48里C．36里D．24里7．函数的图象大致是（）A．B．C．D ．8．函数f （x ）的图象关于y 轴对称，且对任意x ∈R 都有f （x +3）=﹣f （x ），若当x ∈（，）时，f （x ）=（）x ，则fA ．﹣B ．C ．﹣4D ．49．如图，在▱ABCD 中，M ，N 分别为AB ，AD 上的点，且=，=，连接AC ，MN 交于P 点，若=λ，则λ的值为（ ）A ．B ．C ．D ．10．函数f （x ）=（kx +4）lnx ﹣x （x ＞1），若f （x ）＞0的解集为（s ，t ），且（s ，t ）中只有一个整数，则实数k 的取值范围为（ ）A ．（﹣2，﹣）B ．（﹣2，﹣]C ．（﹣，﹣1]D ．（﹣，﹣1）二、填空题（每题5分，满分25分，将答案填在答题纸上） 11．定积分的值为 ．12．不等式|x ﹣2|﹣|2x ﹣1|＞0的解集为 ．13．已知cos （α﹣）=，α∈（0，），则= ．14．一艘海警船从港口A 出发，以每小时40海里的速度沿南偏东40°方向直线航行，30分钟到达B 处，这时候接到从C 处发出的一求救信号，已知C 在B 的北偏东65°，港口A 的东偏南20°处，那么B ，C 两点的距离是 海里．15．设函数f （x ）=，若函数g （x ）=[f （x ）]2+bf （x ）+c有三个零点x 1，x 2，x 3，则x 1x 2+x 2x 3+x 1x 3= ．三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）16．设函数f（x）=sinωx•cosωx﹣（ω＞0）的图象上相邻最高点与最低点距离为．（1）求ω的值；（2）若函数y=f（x+φ）（0＜φ＜）是奇函数，求函数g（x）=cos（2x﹣φ）在区间[0，2π]上的单调减区间．17．已知在△ABC中，a，b，c是角A，B，C的对边，向量与向量共线．（1）求角C的值；（2）若，求的最小值．18．已知m∈R，设p：对∀x∈[﹣1，1]，x2﹣2x﹣4m2+8m﹣2≥0恒成立；q：∃x∈[1，2]，成立．如果“p∨q”为真，“p∧q”为假，求m 的取值范围．19．已知数列{a n}的前n项和为S n，a1=1，且点P（a n，S n）（其中n≥1且n∈N*）在直线4x﹣3y﹣1=0上，数列是首项为﹣1，公差为﹣2的等差数列．（1）求数列{a n}，{b n}的通项公式；（2）设，求数列{c n}的前n项和T n．20．在某次水下科研考察活动中，需要潜水员潜入水深为60米的水底进行作业，根据以往经验，潜水员下潜的平均速度为v（米/单位时间），每单位时间的用氧量为（升），在水底作业10个单位时间，每单位时间用氧量为0.9（升），返回水面的平均速度为（米/单位时间），每单位时间用氧量为1.5（升），记该潜水员在此次考察活动中的总用氧量为y（升）．（1）求y关于v的函数关系式；（2）若c≤v≤15（c＞0），求当下潜速度v取什么值时，总用氧量最少．21．已知函数f（x）=．（1）求曲线y=f（x）在点（1，f（1））处的切线方程；（2）若x＞0且x≠1，f（x）﹣．（i）求实数t的最大值；（ii）证明不等式：lnn＜（n∈N*且n≥2）．2016-2017学年山东省菏泽一中高三（上）期中数学试卷（理科）参考答案与试题解析一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．设集合M={﹣1，0，1，2}，N={x|x2﹣x﹣2＜0}，则M∩N=（）A．{0，1}B．{﹣1，0}C．{1，2}D．{﹣1，2}【考点】交集及其运算．【分析】求出N中不等式的解集确定出N，找出M与N的交集即可．【解答】解：由N中的不等式解得：﹣1＜x＜2，即N=（﹣1，2），∵M={﹣1，0，1，2}，∴M∩N={0，1}．故选：A2．设命题p：∃x＜0，x2≥1，则¬p为（）A．∀x≥0，x2＜1 B．∀x＜0，x2＜1 C．∃x≥0，x2＜1 D．∃x＜0，x2＜1【考点】命题的否定．【分析】根据含有量词的命题的否定进行判断即可．【解答】解：特称命题的否定是全称命题，∴¬p：∀x∈R，都有x2＜1．故选：B．3．要得到函数y=sin2x的图象，只要将函数y=sin（2x﹣）的图象（）A．向左平移单位B．向右平移单位C．向左平移单位D．向右平移单位【考点】函数y=Asin（ωx+φ）的图象变换．【分析】根据函数y=Asin（ωx+∅）的图象变换规律得出结论．【解答】解：将函数y=sin（2x﹣）的图象向左平移个单位，可得函数y=sin[2（x+）﹣]=sin2x的图象，故选C．4．函数的定义域为（）A．[0，+∞）B．（﹣∞，2]C．[0，2]D．[0，2）【考点】函数的定义域及其求法．【分析】直接由根式内部的对数式大于等于0，分式的分母不等于0，列出不等式组，求解即可得答案．【解答】解：由，解得0≤x＜2．∴函数的定义域为：[0，2）．故选：D．5．若变量x，y满足条件，则目标函数z=2x+y的最小值为（）A．﹣3 B．﹣2 C．﹣1 D．1【考点】简单线性规划．【分析】画出平面区域，利用目标函数等于直线在y轴的截距得到最最优解位置，求得z的最小值．【解答】解：变量x，y满足的平面区域如图：目标函数z=2x+y变形为y=﹣2x+z，当此直线经过图中A时z最小，由得到A（﹣1，﹣1），所以z=2×（﹣1）﹣1=﹣3；故选：A．6．中国古代数学著作《算法统宗》中有这样一个问题：“三百七十八里关，初行健步不为难，次日脚痛减一半，六朝才得到其关，要见次日行里数，请公仔细算相还．”其大意为：“有一个人走了378里路，第一天健步行走，从第二天起因脚痛每天走的路程为前一天的一半，走了6天后到达目的地．”问此人第4天和第5天共走了（）A．60里B．48里C．36里D．24里【考点】函数模型的选择与应用．【分析】由题意可知，每天走的路程里数构成以为公比的等比数列，由S6=378求得首项，再由等比数列的通项公式求得该人第4天和第5天共走的路程【解答】解：记每天走的路程里数为{a n}，可知{a n}是公比q=的等比数列，由S6=378，得S6=，解得：a1=192，∴，此人第4天和第5天共走了24+12=36里．故选：C．7．函数的图象大致是（）A．B．C．D．【考点】函数的图象．【分析】求出函数的零点个数，图象所过象限及极限值，利用排除法，可得答案．【解答】解：令函数=0，则x=0，或x=，即函数有两个零点，故排除B；当0＜x＜时，函数值为负，图象出现在第四象限，故排除C；由=0，可排除D，故选：A8．函数f（x）的图象关于y轴对称，且对任意x∈R都有f（x+3）=﹣f（x），若当x∈（，）时，f（x）=（）x，则fA．﹣ B．C．﹣4 D．4【考点】函数的值．【分析】推导出f（x+6）=﹣f（x+3）=f（x），当x∈（，）时，f（x）=（）x，从而f=f（﹣1）=﹣f（2），由此能求出结果．【解答】解：∵函数f（x）的图象关于y轴对称，且对任意x∈R都有f（x+3）=﹣f（x），∴f（x+6）=﹣f（x+3）=f（x），∵当x∈（，）时，f（x）=（）x，∴f=f（﹣1）=﹣f（2）=﹣（）2=﹣．故选：A．9．如图，在▱ABCD中，M，N分别为AB，AD上的点，且=，=，连接AC，MN交于P点，若=λ，则λ的值为（）A．B．C．D．【考点】平面向量的基本定理及其意义．【分析】=，=，∴=λ=λ（=，三点M，N，P共线．，即可求得λ．【解答】解：∵=，=，∴=λ=λ（=，∵三点M，N，P共线．∴，则λ=．故选：D．10．函数f（x）=（kx+4）lnx﹣x（x＞1），若f（x）＞0的解集为（s，t），且（s，t）中只有一个整数，则实数k的取值范围为（）A．（﹣2，﹣）B．（﹣2，﹣]C．（﹣，﹣1]D．（﹣，﹣1）【考点】利用导数研究函数的单调性．【分析】令f（x）＞0，得到kx+4＞，令g（x）=，集合函数图象求出k 的范围即可．【解答】解：令f（x）＞0，得：kx+4＞，令g（x）=，则g′（x）=，令g′（x）＞0，解得：x＞e，令g′（x）＜0，解得：1＜x＜e，故g（x）在（1，e）递增，在（e，+∞）递减，画出函数草图，如图示：，结合图象，解得：﹣2＜k≤﹣，故选：B．二、填空题（每题5分，满分25分，将答案填在答题纸上）11．定积分的值为e+1．【考点】定积分．【分析】找出被积函数的原函数，代入积分上限和下限计算即可．【解答】解：原式==e+1；故答案为：e+1．12．不等式|x﹣2|﹣|2x﹣1|＞0的解集为（﹣1，1）．【考点】绝对值不等式的解法．【分析】通过讨论x的范围求出各个区间上的x的范围，取并集即可．【解答】解：x≥2时，x﹣2﹣2x+1＞0，解得：x＜﹣1，不合题意，＜x＜2时，2﹣x﹣2x+1＞0，解得：x＜1，x≤时，2﹣x+2x﹣1＞0，解得：x＞﹣1，故不等式的解集是（﹣1，1）；故答案为：（﹣1，1）．13．已知cos（α﹣）=，α∈（0，），则=﹣．【考点】三角函数的化简求值．【分析】利用诱导公式和二倍角公式进行化简求值．【解答】解：∵α∈（0，），∴α﹣∈（﹣，0），∵cos（α﹣）=，∴sin（α﹣）=﹣=，==﹣=﹣2sin（）=﹣．故答案是：﹣．14．一艘海警船从港口A出发，以每小时40海里的速度沿南偏东40°方向直线航行，30分钟到达B处，这时候接到从C处发出的一求救信号，已知C在B的北偏东65°，港口A的东偏南20°处，那么B，C两点的距离是10海里．【考点】解三角形的实际应用．【分析】根据题意画出图象确定∠BAC、∠ABC的值，进而可得到∠ACB的值，根据正弦定理可得到BC的值【解答】解：如图，由已知可得，∠BAC=30°，∠ABC=105°，AB=20，从而∠ACB=45°．在△ABC中，由正弦定理可得BC=×sin30°=10．故答案为：；15．设函数f（x）=，若函数g（x）=[f（x）]2+bf（x）+c有三个零点x1，x2，x3，则x1x2+x2x3+x1x3=3﹣a4．【考点】根的存在性及根的个数判断．【分析】设f（x）=t，根据f（x）的函数图象得出方程f（x）=t的根的个数，从而得出f（x）=1，故而可求出f（x）=1的三个解，得出答案．【解答】解：不妨设a＞1（或0＜a＜1），作出f（x）的函数图象如图所示：设f（x）=t，由图象可知：当t=1时，方程f（x）=t有3解，当t≠1时，方程f（x）=t有2解，∵函数g（x）=[f（x）]2+bf（x）+c有三个零点，∴关于t的方程t2+bt+c=0有且只有一解t=1，∴f（x）=1，∴x1，x2，x3是f（x）=1的三个解，不妨设x1＜x2＜x3，则x2=1，令log a|x﹣1|﹣1=1得x=1±a2，∴x1=1﹣a2，x3=1+a2．∴x1x2+x2x3+x1x3=1+a2+1﹣a2+1﹣a4=3﹣a4．故答案为：3﹣a4．三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）16．设函数f（x）=sinωx•cosωx﹣（ω＞0）的图象上相邻最高点与最低点距离为．（1）求ω的值；（2）若函数y=f（x+φ）（0＜φ＜）是奇函数，求函数g（x）=cos（2x﹣φ）在区间[0，2π]上的单调减区间．【考点】由y=Asin（ωx+φ）的部分图象确定其解析式；三角函数中的恒等变换应用；正弦函数的图象．【分析】（1）由已知利用三角函数恒等变换的应用化简函数解析式可得f（x）=sin（2ωx﹣），设T为f（x）的最小值周期，由题意得，结合f（x）max=1，可求T的值，利用周期公式可求ω的值．（2）由题意可求f（x+φ）=sin（x+φ﹣）是奇函数，则sin（φ﹣）=0，结合0＜φ＜，可求φ，进而可求函数g（x）的解析式，利用余弦函数的图象和性质可求其单调递减区间，结合范围x∈[0，2π]，即可得解．【解答】解：（1）∵=，设T为f（x）的最小值周期，由f（x）图象上相邻最高点与最低点的距离为，得，∵f（x）max=1，∴，整理可得T=2π，又∵ω＞0，T==2π，∴ω=．（2）由（1）可得f（x）=sin（x﹣），∴f（x+φ）=sin（x+φ﹣），∵y=f（x+φ）是奇函数，则sin（φ﹣）=0，又∵0＜φ＜，∴φ=，∴g（x）=cos（2x﹣φ）=cos（2x﹣），令，则，∴单调递减区间是，又∵x∈[0，2π]，∴当k=0时，递减区间为；当k=1时，递减区间为，∴函数g（x）在[0，2π]上的单调递减区间是，．17．已知在△ABC中，a，b，c是角A，B，C的对边，向量与向量共线．（1）求角C的值；（2）若，求的最小值．【考点】平面向量数量积的运算．【分析】（1）利用两个向量的数量积公式，两个向量共线的性质，正弦定理、余弦定理，求得cosC的值，可得C的值．（2）利用两个向量的数量积的定义求得||||的值，利用以及基本不等式，求得的最小值．【解答】解：（1）向量与向量共线．∴（a﹣b）•sin（A+C）=（a﹣c）（sinA+sinC），由正弦定理可得（a﹣b）•b=（a ﹣c）（a+c），∴c2=a2+b2﹣ab，∴，∵0＜C＜π，∴．（2）∵，∴，∴，∴，∵，∴，∴，（当且仅当时，取“=”），∴的最小值为．18．已知m∈R，设p：对∀x∈[﹣1，1]，x2﹣2x﹣4m2+8m﹣2≥0恒成立；q：∃x∈[1，2]，成立．如果“p∨q”为真，“p∧q”为假，求m 的取值范围．【考点】命题的真假判断与应用；复合命题的真假；函数的最值及其几何意义；函数恒成立问题．【分析】如果“p∨q”为真，“p∧q”为假，则p与q一真一假，进而可得m的取值范围．【解答】解：若p为真：对∀x∈[﹣1，1]，4m2﹣8m≤x2﹣2x﹣2恒成立，设f（x）=x2﹣2x﹣2，配方得f（x）=（x﹣1）2﹣3，∴f（x）在[﹣1，1]上的最小值为﹣3，∴4m2﹣8m≤﹣3，解得，∴p为真时，；若q为真：∃x∈[1，2]，x2﹣mx+1＞2成立，∴成立，设，易知g（x）在[1，2]上是增函数，∴g（x）的最大值为，∴，∵“p∨q”为真，“p∧q”为假，∴p与q一真一假，当p真q假时，，∴，当p假q真时，，∴，综上所述，m的取值范围为或．19．已知数列{a n}的前n项和为S n，a1=1，且点P（a n，S n）（其中n≥1且n∈N*）在直线4x﹣3y﹣1=0上，数列是首项为﹣1，公差为﹣2的等差数列．（1）求数列{a n}，{b n}的通项公式；（2）设，求数列{c n}的前n项和T n．【考点】数列的求和；数列递推式．【分析】（1）利用点在直线上，得到递推关系式，判断数列是等比数列，然后求出通项公式．（2）化简数列的通项公式，利用裂项法求和即可．【解答】（1）解：由点P（a n，S n）在直线4x﹣3y﹣1=0上，∴4a n﹣3S n﹣1=0即3S n=4a n﹣1，又3S n﹣1=4a n﹣1﹣1（n≥2），两式相减得a n=4a n ，﹣1∴，∴{a n}是以4为公比的等比数列，又a1=1，∴，∵是以为首项，以﹣2为公差的等差数列，∴，∴．（2）由（1）知，，∴，∴，以上两式相减得，==+，∴T n=．20．在某次水下科研考察活动中，需要潜水员潜入水深为60米的水底进行作业，根据以往经验，潜水员下潜的平均速度为v（米/单位时间），每单位时间的用氧量为（升），在水底作业10个单位时间，每单位时间用氧量为0.9（升），返回水面的平均速度为（米/单位时间），每单位时间用氧量为1.5（升），记该潜水员在此次考察活动中的总用氧量为y（升）．（1）求y关于v的函数关系式；（2）若c≤v≤15（c＞0），求当下潜速度v取什么值时，总用氧量最少．【考点】函数模型的选择与应用．【分析】（1）分别计算潜入水底用时、用氧量；水底作业时用氧量；返回水面用时、用氧量，即可得到总用氧量的函数；（2）利用基本不等式可得，时取等号，再结合c≤v≤15（c＞0），即可求得确定下潜速度v，使总的用氧量最少．【解答】解：（1）由题意，下潜用时（单位时间），用氧量为（升），水底作业时的用氧量为10×0.9=9（升），返回水面用时（单位时间），用氧量为（升），∴总用氧量（v＞0）．（2），令y'=0得，在时，y'＜0，函数单调递减，在时，y'＞0，函数单调递增，∴当时，函数在上递减，在上递增，∴此时时用氧量最少．当时，[c，15]上递增，此时v=c时，总用氧量最少．21．已知函数f（x）=．（1）求曲线y=f（x）在点（1，f（1））处的切线方程；（2）若x＞0且x≠1，f（x）﹣．（i）求实数t的最大值；（ii）证明不等式：lnn＜（n∈N*且n≥2）．【考点】利用导数研究曲线上某点切线方程．【分析】（1）利用导数的几何意义求曲线y=f（x）在点（1，f（1））处的切线方程；（2）（i）分类讨论，利用函数的单调性，即可求实数t的最大值；（ii）当x＞1时整理得，令，则，即可证明不等式．【解答】解：（1）由题意x∈（0，+∞）且，∴，又，∴f（x）在点（1，f（1））处的切线方程为，即x﹣2y﹣1=0．（2）（i）由题意知，设，则=，设，则，当t≥0时，∵x＞0，∴h'（x）＞0，∴h（x）在（0，+∞）上单调递增，又h（1）=0，∴x∈（0，1）时，h（x）＜0，又，∴g（x）＜0不符合题意．当t＜0时，设ϕ（x）=tx2+2x+t，①若△=4﹣4t2≤0即t≤1时，ϕ（x）≤0恒成立，即h'（x）≤0在（0，+∞）恒成立，∴h（x）在（0，+∞）上单调递减，又h（1）=0，∴x∈（0，1）时，h（x）＞0，，g（x）＞0，x∈（1，+∞）时，h（x）＜0，，g（x）＞0，符合题意．②若△=4﹣4t2＞0即﹣1＜t＜0时，ϕ（x）的对称轴，∴ϕ（x）在上单调递增，∴时，ϕ（x）＞ϕ（1）=2+2t＞0，∴h'（x）＞0，∴h（x）在上单调递增，∴h （x ）＞h （1）=0，而，∴g （x ）＜0，不符合题意．综上所述t ≤﹣1，∴t 的最大值为﹣1．（ii ）由（i ）知t=﹣1时，，当x ＞1时整理得，令，则，∴，∴，∴，即．2017年4月2日。

山东省菏泽市郓城高级中学2017届高三上学期期中考试物理试题说明：本试卷满分100分，试题分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，考试时间100分钟。

一、选择题（本题共12小题，每小题4分．在每小题给出的四个选项中，第1～7题只有一项符合题目要求；第8～12题有多项符合题目要求．全部选对的得4分，选对但不全的得2分，有选错的得0分）1．关于物理学思想方法，下列说法中叙述错误的是（）A．在不需要考虑物体本身的大小和形状时，用质点来代替物体的方法是理想模型法B．伽利略在研究自由落体运动时采用了微小量放大的方法C．在定义“速度”、“加速度”等物理量时，应用了比值的方法D．验证力的平行四边形定则的实验中，主要是应用了“等效替换”的思想2.下列说法正确的是（）A．做圆周运动的物体所受合力的方向必定指向圆心B．某人骑自行车以恒定的速率驶过一段弯路，自行车的运动是匀速运动C．做匀变速曲线运动的物体，单位时间内速率的变化量总是不变D．做平抛运动的物体，一段时间的平均速度方向为该段时间内物体的初位置指向末位置的方向3．某物块从固定斜面底端以一定的初速度沿斜面上滑，其速度大小随时间变化的关系如图所示，下列说法错误的是()A．在0.5 s时离斜面底端最远B．沿斜面上滑的最大距离为2 mC．在1.5 s时回到斜面底端D．上滑时加速度大小是下滑时加速度大小的4倍4．在2016年里约奥运会女子蹦床比赛中，我国运动员李丹荣获铜牌给中国代表队带来了荣耀。

比赛中李丹从最高点开始下落到运动至最低点的过程中，下列说法正确的是（）A．李丹下落到刚与蹦床接触时速度最大B．李丹下落到最低点时加速度为零C．从开始接触蹦床到最低点的过程中，李丹加速度的最大值为gD ．到最低点的时刻，李丹的加速度最大5. 如图所示，转动轴垂直于光滑平面，交点O 的上方h 处固定细绳的一端，细绳的另一端拴接一质量为m 的小球B ，绳长AB ＝l >h ，小球可随转动轴转动并在光滑水平面上做匀速圆周运动．要使球不离开水平面，转动轴的转速的最大值是( ) A.12πg l B ．πgh C.12πg h D ．2πl g 6．如图所示，离地面高2m 处有甲、乙两个物体，甲以初速度水平射出，同时乙以初速度沿倾角为的光滑斜面滑下，已知重力加速度，若甲、乙同时到达地面，则的大小是（）A ．B ．C ．D ．7．如图所示，一内壁光滑、质量为m 、半径为r 的环形细圆管，用硬杆竖直固定在天花板上．有一质量为m 的小球(可看做质点)在圆管中运动．小球以速率v 0经过圆管最低点时，杆对圆管的作用力大小为( ) A ．m v 20r B ．mg ＋m v 20r C ．2mg ＋m v 20r D ．2mg －m v 20r8．如图所示，水平转台上放着A 、B 、C 三个物体，质量分别为2m 、m 、m ，离转轴的距离分别为R 、R 、2R ，与转台间的动摩擦因数相同，转台旋转时，下列说法中正确的是( )A ．若三个物体均未滑动，C 物体的向心加速度最大B ．若三个物体均未滑动，B 物体受的摩擦力最大C ．转速增加，A 物体比B 物体先滑动D ．转速增加，C 物体先滑动9．如图所示，物体在沿粗糙斜面向上的拉力F 作用下处于静止状态．当F 逐渐增大到物体即将相对于斜面向上运动的过程中，斜面对物体的作用力可能（ ）A ．逐渐增大B ．逐渐减小C ．先增大后减小D ．先减小后增大10．如图所示，一竖直放置、内壁粗糙的圆锥筒绕其中心轴线旋转，角速度为ω0（ω0﹥0），内壁上有一小物块始终与圆锥筒 保持相对静止，则下列说法正确的是（ ）A ．物块可能受两个力作用B ．物块受到的支持力一定大于重力C ．当角速度从ω0增大时，物块受到的支持力可能减小D ．当角速度从ω0增大时，物块受到的摩擦力可能一直增大11．10月17日7时30分在神州十一号飞船发射后，经多次轨道控制，调整至距地面393公里的预定轨道上，使其正式进入与“天宫二号”对接准备阶段。

（考试时间：100分钟满分：100分）可能用到的相对原子质量：Na 23 CI 35.5 O 16 Mg 24 N 14第I卷选择题（共48分）一、选择题（单项选择，本题包括16小题，每小题3分，共48分）1．下列叙述正确的是( )A．NaCl的摩尔质量是58.5g B．64g氧气中含有2mol氧C．58.5gNaCl中含有lmolNaCl分子 D．0.lmolCO2含有6.02×1022个CO2分子【答案】D【解析】试题分析：NaCl的摩尔质量是58.5g/mol，A项与题意不符；64g氧气中含有2mol氧分子，4摩尔氧原子，B项与题意不符； NaCl中不含有NaCl分子，只含有钠离子和氯离子，C项与题意不符；0.lmol二氧化碳含有6.02×1022个CO2分子，D项与题意相符。

考点：物质的量及相关概念的理解2．下图是某同学用500 mL容量瓶配制0.10 mol·L－1NaOH溶液的过程该同学的错误步骤有（）A．1处 B．2处 C．3处 D．4处【答案】C【解析】试题分析：第①步不能把NaOH放在称量纸上称量；第④步玻璃棒应接触容量瓶内壁刻度线以下的部分；第⑤步定容时应平视刻度线。

考点：溶液的配置操作3．N A表示阿伏加德罗常数的值，下列说法正确的是（）A．标准状况下，22.4L四氯化碳的分子数约为N AB．2.4g金属镁变为镁离子时失去的电子数为0.1N AC．16gO2和O3的混合气体中所含的原子数为N AD．1mo1·L-1的A1C13溶液中，C1-离子的数目为3 N A【答案】C【解析】试题分析：A、标准状况下四氯化碳不是气态，不能利用气体摩尔体积计算分子数，A错误；B2.4g金属镁是0.1mol，变为镁离子时失去的电子数为0.2N A，B错误；C、16gO2和O3的混合气体中所含的原子的物质的量是16g/16g/mol=1mol，其氧原子数为N A，C正确；D、1mol/L的A1C13溶液中的C1-离子的数目为3mol/L，不能确定溶液体积，则不能计算数目，D错误。