盐城市神州路小学2014~2015学年度第二学期

2014/2015学年度第二学期高二年级期终考试英语试题第一部分听力（共两节，满分20分）做题时，先将答案标在试卷上。

录音内容结束后，你将有两分钟的时间将试卷上的答案转涂到答题卡上。

第一节（共5小题：每小题1分，满分5分）听下面5段对话，每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1. When will Paul and Susan leave?A. Next Monday.B. They haven’t decided yet.C. Next Tuesday.2. Why did John fail to go to the party yesterday evening?A. He had to work.B. He caught a cold.C. He had to study.3. How old is Jack?A. He must be over ten years old.B. He must be less than ten years old.C. He must be ten years old.4. What will Jim probably do?A. He will repair his car.B. He will use the woman’s car.C. He will visit his parents.5. What does the man advise the woman to do?A. Read the newspaper.B. Go to the cinema.C. Watch the film at home.第二节（共15小题：每小题1分，满分15分）听下面5段对话或独白。

每段对话或独白后有几个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

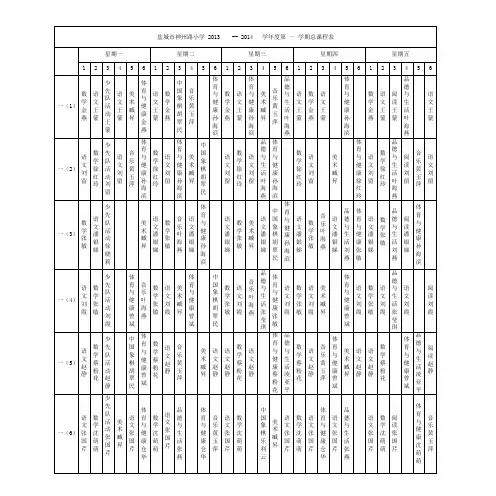
备注：每学期少先队活动中有2节为版图意识宣传教育课盐城市神州路小学一（1）班备注：每学期少先队活动中有2节为版图意识宣传教育课盐城市神州路小学一（2）班备注：每学期少先队活动中有2节为版图意识宣传教育课盐城市神州路小学一（3）班备注：每学期少先队活动中有2节为版图意识宣传教育课盐城市神州路小学一（4）班备注：每学期少先队活动中有2节为版图意识宣传教育课盐城市神州路小学一（5）班备注：每学期少先队活动中有2节为版图意识宣传教育课盐城市神州路小学一（6）班备注：每学期少先队活动中有2节为版图意识宣传教育课盐城市神州路小学一（7）班备注：每学期少先队活动中有2节为版图意识宣传教育课盐城市神州路小学一（8）班备注：每学期少先队活动中有2节为版图意识宣传教育课盐城市神州路小学一（9）班备注：每学期少先队活动中有2节为版图意识宣传教育课盐城市神州路小学一（10）班备注：每学期少先队活动中有2节为版图意识宣传教育课盐城市神州路小学一（11）班备注：每学期少先队活动中有2节为版图意识宣传教育课盐城市神州路小学一（12）班备注：每学期少先队活动中有2节为版图意识宣传教育课盐城市神州路小学二（1）班备注：每学期少先队活动中有2节为版图意识宣传教育课盐城市神州路小学二（2）班备注：每学期少先队活动中有2节为版图意识宣传教育课备注：每学期少先队活动中有2节为版图意识宣传教育课盐城市神州路小学二（4）班备注：每学期少先队活动中有2节为版图意识宣传教育课盐城市神州路小学二（5）班备注：每学期少先队活动中有2节为版图意识宣传教育课备注：每学期少先队活动中有2节为版图意识宣传教育课盐城市神州路小学二（7）班备注：每学期少先队活动中有2节为版图意识宣传教育课盐城市神州路小学二（8）班备注：每学期少先队活动中有2节为版图意识宣传教育课备注：每学期少先队活动中有2节为版图意识宣传教育课盐城市神州路小学二（10）班备注：每学期少先队活动中有2节为版图意识宣传教育课盐城市神州路小学二（11）班备注：每学期少先队活动中有2节为版图意识宣传教育课备注：每学期少先队活动中有2节为版图意识宣传教育课盐城市神州路小学三（1）班备注：每学期少先队活动中有2节为版图意识宣传教育课盐城市神州路小学三（2）班备注：每学期少先队活动中有2节为版图意识宣传教育课备注：每学期少先队活动中有2节为版图意识宣传教育课盐城市神州路小学四（1）班备注：每学期少先队活动中有2节为版图意识宣传教育课盐城市神州路小学五（1）班备注：每学期少先队活动中有2节为版图意识宣传教育课备注：每学期少先队活动中有2节为版图意识宣传教育课。

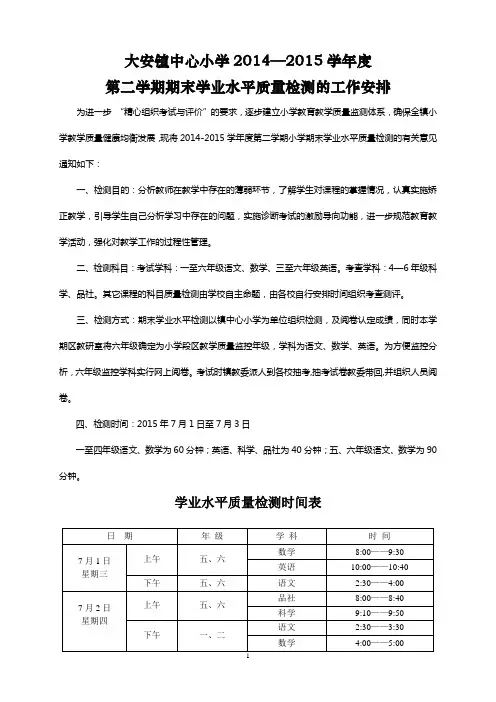
大安镇中心小学2014—2015学年度第二学期期末学业水平质量检测的工作安排为进一步“精心组织考试与评价”的要求，逐步建立小学教育教学质量监测体系，确保全镇小学教学质量健康均衡发展，现将2014-2015学年度第二学期小学期末学业水平质量检测的有关意见通知如下：一、检测目的：分析教师在教学中存在的薄弱环节，了解学生对课程的掌握情况，认真实施矫正教学，引导学生自己分析学习中存在的问题，实施诊断考试的激励导向功能，进一步规范教育教学活动，强化对教学工作的过程性管理。

二、检测科目：考试学科：一至六年级语文、数学、三至六年级英语。

考查学科：4—6年级科学、品社。

其它课程的科目质量检测由学校自主命题，由各校自行安排时间组织考查测评。

三、检测方式：期末学业水平检测以镇中心小学为单位组织检测，及阅卷认定成绩，同时本学期区教研室将六年级确定为小学段区教学质量监控年级，学科为语文、数学、英语。

为方便监控分析，六年级监控学科实行网上阅卷。

考试时镇教委派人到各校抽考,抽考试卷教委带回,并组织人员阅卷。

四、检测时间：2015年7月1日至7月3日一至四年级语文、数学为60分钟；英语、科学、品社为40分钟；五、六年级语文、数学为90分钟。

学业水平质量检测时间表日期年级学科时间7月1日星期三上午五、六数学8:00——9:30英语10:00——10:40 下午五、六语文2:30——4:007月2日星期四上午五、六品社8:00——8:40科学9:10——9:50 下午一、二语文2:30——3:30数学4:00——5:007月3日星期五上午三、四数学8:00——9:00英语9:30——10:10品社（四）10:40——11:20下午三、四语文2:30——3:30科学（四）4:00——4:40五、注意事项：1.各监测点负责安排监测场，书写门标（各班班主任书写考生座号，六年级座号要包括三项内容，即姓名、座号、考生号，其它年级只写姓名和座号）备好放录设备，备齐密封用品，提前半小时考勤，严格操作，不得随意变更监测时间及科目。

2014/2015学年度第二学期高二年级期终考试数 学 答 案一、填空题：1 2．(,0),34x x x ∀∈-∞≥都有3． 40 4．125． 14 6．()1,+∞7． 48．221312x y -=9．1()3AG AB AC AD =++10．（理科）1（文科）56π11．（理科）24 （文科）充要12．7+13． 2,13⎛⎫ ⎪⎝⎭14．11(,)22e - 二、解答题：15．（理科）解：（1）随机任取2条网线共有10种不同的情况．21324336,(6)1010P x ++=+=∴===，...................................................................................2' 4347,(7)10P x +=∴==，............................................................................................................4' 1448,(8)10P x +=∴==，............................................................................................................6'34184(6)101010105P x ∴≥=++==．...............................................................................................8'（2）21235,(5)105P x +====，..............................................................................................10'∴线路通过信息量的数学期望是1341()5678 6.45101010E x =⨯+⨯+⨯+⨯=．..................................................................................13'答：（1）线路信息畅通的概率是45； （2）线路通过信息量的数学期望是6.4．..................14'15．（文科）解：非q 为假命题，则q 为真命题；...................................................................................3'p q 且为假命题，则p 为假命题，......................................................................................................6'即12,x x Z -<∈且，得212x -<-<，解得13,x x Z -<<∈，.....................................................................................................................12' 0,1,2x ∴=或． .............................................................................................................................14'16．（理科）解：（1）如图所示，以A 为原点，建立空间直角坐标系A xyz -，则(0,0,0)A ，(2,0,0)B ，(0,4,0)D ，(0,0,2)P ，(2,4,0)C ，(1,2,1)M ，......................................................................................................................2'(1,2,1),(0,4,2)AM PD ==-，cos ,106AM PD AM PD AM PD⋅∴<>===∴异面直线AM 与PD ． .........................................................................7' （2）设BPC 平面的法向量为(,,)x y z =m ，(0,4,0),(2,0,2)BC BP ==-，并且,BC BP ⊥⊥m m ，40220y x z =⎧∴⎨-+=⎩，令1x =得1z =，0y =，∴MBD 平面的一个法向量为(1,0,1)=m ．......................................................................................9' 设DPC 平面的法向量为(,,)a b c =n ，(2,0,0),(0,4,2)DC DP ==-，并且,DC DP ⊥⊥n n ，20420a b c =⎧∴⎨-+=⎩，令1b =得2c =，0a =，∴MBD 平面的一个法向量为(0,1,2)=n ． .....................................................................................11'∴cos ,⋅<>===⋅m nm n |m |n ，.......................................................................................13' ∴二面角B PC D --的余弦值为.........................................................................................14' 16．（文科）解：（1）22()cos sin cos 12cos 21f x x x x x x x =-++=++=2sin(2)16x π++． ..........................................................................................5' 因此()f x 的最小正周期为π，最小值为1-．..................................................................................7'（2）由()2f α=得2sin(2)16πα++=2，即1sin(2)62πα+=．......................................................9'而由,42ππα⎡⎤∈⎢⎥⎣⎦得272,636παππ⎡⎤+∈⎢⎥⎣⎦．故5266παπ+=，解得3πα=．....................................................................................................14'17．（理科）解：当1n =时，132n -⋅<23n +；当2n =时，132n -⋅<23n +； 当3n =时，132n -⋅=23n +；当4n =时，132n -⋅>23n +；当5n =时，132n -⋅>23n +；..............................................................................................................5' 猜想：当4n ≥时，132n -⋅>23n +．.................................................................................................7' 证明：当4n =时，132n -⋅>23n +成立； 假设当(4n k k =≥）时，132k -⋅>23k +成立， 则1n k =+时，左式=32k ⋅=1232k ⋅⋅－>223k +（），右式=213k ++（）， 因为223k +（）－213k ++[()]=222k k -+=211k +（－）>0， 所以，左式>右式，即当1n k =+时，不等式也成立.综上所述：当4n ≥时，132n -⋅>23n +．..........................................................................................14' 17．（文科）证明：假设12x y +<和12y x +<都不成立，即12x y +≥， 12yx+≥..............................2' 又,x y 都是正数，∴12x y +≥，12y x +≥两式相加得到 2()2()x y x y ++≥+，. ............................................................................................8' 2x y ∴+≤．与已知2x y +>矛盾，所以假设不成立，...........................................................................................12' 即12x y +<和12yx+<中至少有一个成立．......................................................................................14'18．解（1）①当MN 在三角形区域内滑动时即x ∈//,MN AB ABC ∆是等腰三角形，060MNC ∠= 连接EC 交MN 于P 点，则PC=x ，x，MN x ABC ∆的面积1()||)2S f x MN x ==2x x =+.....................................................................................4'②当MN在半圆形区域滑动即1)x ∈时MN =所以2()(1)x x x S f x x x ⎧+∈⎪==⎨⎪∈⎩......................................................8'（2）x ∈时，2()S f x x ==+的对称轴为x =所以2max ()f x f ==+=................................................................................11'1)x ∈时，()(f x x =12≤=当且仅当1)2x =取等号，..................................................................................15'又12>所以三角形EMN 的面积最大值为12...............................................................................16' 19．解：记c =（1）当点P 在椭圆的短轴端点位置时，12PF F ∆则有a ，得e =． 所以，此时椭圆的离心率为2．......................4' （2）点00(,)P x y 在椭圆22221x y a b +=上，得2200221x y a b+=．把00(,)x y 代入方程00221x y x y a b+=，得2200221x y a b +=，所以点00(,)P x y 在直线00221x y x y a b+=上，...............................................................................6' 联列方程组2222002211x y a b x y x y a b ⎧+=⎪⎪⎨⎪+=⎪⎩，消去y 可得222220020a x a x x a x -+=， 解得0x x =，即方程组只有唯一解． 所以，直线00221x y x y a b+=为椭圆在点P 处的切线方程．......................................................10' （3）由题可设11(,)S x y 、22(,)T x y 、23(,)a R y c．由（2）结论可知，切线SR 的方程为11221x y x y a b +=① 切线TR 的方程为22221x y x y a b +=②.....................................................12'把23(,)aR y c 分别代入方程①、②，可得11321x y y c b+=③和22321x y y c b +=④ 由③、④两式，消去3y ，可得1221x c y x c y -=-()()， 即有12210)0)x c y x c y --=--()(()(， 所以，点11(,)S x y 、22(,)T x y 、2(,0)F c 三点共线，所以，直线ST 经过定点，定点坐标为2F ．..........................................................16'（图2）（图1）20．解：（1）若2t =，则329()612f x x x x =-++， 所以，2'()396f x x x =-+，令'()0f x =，得1,2x =；令'()0f x <，得12x <<，所以，()f x 在区间（1，2）内递减，在区间（－∞，1）,（2，+∞）内递增，得()f x 的极大值为7(1)2f =．............................................................................................................4' （2）函数323(1)()312t f x x x tx +=-++． 得2'()33(1)33(1)()f x x t x t x x t =-++=--，0t >．令'()0f x =，得1,x t =；....................................................................................................................6' ①当2t ≥时，可以判定()f x 在区间（0，1）内递增，在区间（1，2）内递减， 此时，不存在0(0,2)x ∈使得0()()f x f x 是在[0，2]上的最小值；②当12t <<时，可以判定()f x 在区间（0，1）、（t ，2）内递增，在区间（1，t ）内递减， 欲存在0(0,2)x ∈使得0()()f x f x 是在[0，2]上的最小值，则必须有()(0)f t f ≤，即3223(1)3112t t t t +-++≤，解得3t ≥，不合题意，舍去． ③当01t <<时，可以判定()f x 在区间（0， t ）、（1，2）内递增，在区间（t ，1）内递减，欲存在0(0,2)x ∈使得0()()f x f x 是在[0，2]上的最小值，则必须有(1)(0)f f ≤，即3112t +≤，解得13t ≤，所以，103t <≤． ④当1t =时，可以判定()f x 在区间（0，2）内递增，不存在0(0,2)x ∈使得0()()f x f x 是在[0，2]上的最小值．综上所述，得t 的取值范围为1(0,]3．...........................................................................................10'（3）若()xf x xe m ≤-（e 为自然对数的底数）对任意的[0,)x ∈+∞恒成立，即 3223(1)3(1)31[3]122x x t t m xe x x tx x e x x t ++≤-+--=-+--对任意的0x ≥恒成立，.....11' 令23()32(1)x g x t e x x t +-+-=，由于m 的最大值为1－， 所以23((30)1)2x t e x x t g x +-+-≥=恒成立．...............................................................................12' 由(0)130g t =-≥可得103t <≤，当103t <≤时，3(1)2'()2x g x t e x =+-+，再设3(1))2'(2()x h x g x t e x +=+=-，得'()20xh x e =-=，解得ln2x =． ()h x 在区间（0，ln2）内递减，在区间（ln2，+∞）内递增，()h x 的最小值为3(1)(ln 2)22ln 22t h +=+-，可以判定(ln 2)0h >，即'()0g x >，所以()g x 在区间[0，+∞）内递增，则有()g x 在区间[0，+∞）内的最小值(0)130g t =-≥，得13t ≤．所以，t 的取值范围是1(0,]3．.....................................................................................................16'。

2014～2015学年度第二学期期中考试七年级语文试题考试时间：120分钟卷面总分：120分考试形式：闭卷命题：蒯晓晔审阅：张丽一、积累与运用（30分）1.默写填空。

（10分，每空1分）（1）曲径通幽处， ▲ 。

（常建《题破山寺后禅院》）（2）桃李不言， ▲ 。

（司马迁《史记·李将军列传》）（3）亡羊补牢， ▲ 。

（《战国策·楚策四》）（4） ▲ ，不知其可。

（《论语》）（5） ▲ ，可笑不自量。

（韩愈《调张籍》）（6）油蛉在这里低唱， ▲ 。

（鲁迅《从百草园到三味书屋》）（7）《鹧鸪》中的“ ▲ ， ▲ ”两句，让人仿佛置身于湖边古庙，聆听鹧鸪声声哀鸣。

（8）《孤雁》中的“ ▲ ， ▲ ” 描写了一只悲伤而执著的孤雁：它不饮不啄，只是一个劲儿飞着、叫着，追寻它的同伴。

2.给加点字注音或根据拼音写汉字。

（4分）在浩荡的大江之滨，坐落着我国著名的古都——南京，许多叱咤（▲ ）风云的著名人物长眠于此。

伟大的革命先驱孙中山先生的陵墓就位于南京东郊的钟山南lù（ ▲ ）。

陵园的设计者独jù（ ▲）匠心，把陵园设计成钟形，既与钟山吻合，又与“中山”谐音，且钟具有“示警”与“自由”的涵义。

整个中山陵充满了安详宁静、庄严肃mù（▲ ）的气氛。

3.下面句子中加点成语使用不正确的一项是（2分） （ ▲ ）A.贝聿铭年轻时就以他惊人的天才和不懈的努力，在美国建筑界崭露头角。

B.樱花节期间，天气晴好，到大洋湾赏花的游人络绎不绝。

C.她蹑手蹑脚地撕开信封，将里面的百元大钞捏出来，塞到衣服布袋里，然后将信件递给他。

D.季羡林先生学富五车，著作等身，是世人敬仰的“学界泰斗”。

4.下列各句中没有语病的一项是（2分） （ ▲ ）A.大纵湖的仲夏时节是旅游休闲的好去处。

B.能否取得好的成绩，关键就在于要勇于克服困难，充满自信。

C.如今，年轻人喜欢上网购物，一些老年人也加入到“淘宝一族”的行列。

钓渭镇朱家滩小学2014—2015学年度第二学期教育教学工作总结本学期，我校紧紧围绕“管理求规范，质量求提高，环境求优化”的工作思路，以提高教育教学质量为终极目标，以减负增效为重点，以规范、务实、精细、创新为工作要求，立足实际求发展，与时俱进创一流，积极打造和谐、奋进的学习型校园，实现了各项工作齐头并进，为学校科学、持续发展奠定了坚实的基础。

一、立足阵地，德育工作力求再提升。

1、加强师德建设，提高师表形象。

首先，健全师德师风学习机制。

采取自学和集中学相结合，组织教师学习《教育法》、《义务教育法》、《中小学教师职业道德规范》等法律法规。

坚持群众路线有关文件学习，要求全体教师边学习，边摘记、写体会，通过各项活动的开展，教师的政治、法律意识、师德修养不断提高，做到为人师表、以身立教、以身示教。

其次，开展各种教育活动，弘扬高尚师德。

一是引导全体教师，根据自身实际，从党性承诺、岗位承诺、先进示范承诺三方面作出公开承诺，并将每位教师的承诺书办成专栏，展示校园，接受学生家长监督；二是坚持师德月考核，月总结，月公布，将考核结果纳入绩效工资奖惩；三是开展向宝鸡市慈善总会“一日捐”慈善活动，为社会献爱心；四是通过开展志愿者认领岗位，坚持服务社区活动。

2、狠抓常规教育，促进规范管理。

本学期我们狠抓学生的思想道德建设，凸显“育人为本”，促进规范管理。

一是抓好行为规范教育，充分利用班队课组织学生认真学习《小学生守则》、《小学生日常行为规范》以及校纪校规，坚持开展每日经常性检查，并通过具体的强化训练，充分发挥学校“校园监督员”的主体作用，做到及时反馈、纠正学生的行为习惯，定期召开班主任会进行分析、总结、研讨，使良好的行为习惯内化为学生的自觉行动；二是结合学雷锋日开展讲雷锋的故事，寻找身边的雷锋，为学校、社区定期服务，此项活动在宝鸡高新教育网和宝鸡教育网报道三次；三八妇女节开展感恩母爱主题征文；清明节倡议“缅怀先辈，文明祭祖”活动；六一儿童节开展“放飞梦想美好成长文艺汇演”活动，朱家滩村委会大力支持，为师生送来节日礼物。

2014/2015学年度第二学期高二年级期终考试数 学 试 题注意事项：1．本试卷考试时间为120分钟，试卷满分160分，考试形式闭卷． 2．本试卷中所有试题必须作答在答题卡上规定的位置，否则不给分．3．答题前，务必将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在试卷及答题卡上． 一、填空题：本大题共14小题，每小题5分，共计70分.请把答案填写在答题卡相应位置上. 1．已知复数12z i =+（i 为虚数单位），则||z = ▲ ． 2．命题“(,0)x ∃∈-∞，使得34x x <”的否定是 ▲ ．3．某学校高三有1800名学生，高二有1500名学生，高一有1200名学生，现采用分层抽样的方法抽取一个容量为150的样本，则应在高一抽取 ▲ 人．4．若在集合{1，2，3，4}和集合{5，6，7}中各随机取一个数相加，则和为奇数的概率为 ▲ ． 5．下面是一个算法的伪代码，输出结果是 ▲ ．6．函数()ln f x x x =-的单调递增区间是 ▲ ．7．若变量,x y 满足约束条件：2020350x y x y x y -≥⎧⎪+≥⎨⎪+-≤⎩，则2x y +的最大值为 ▲ ．8．若双曲线C 经过点(2，2)，且与双曲线2214y x -=具有相同渐近线，则双曲线C 的标准方程为▲ ．9．在△ABC 中，若D 为BC 的中点，则有1()2AD AB AC =+，将此结论类比到四面体中，在四面体 A -BCD 中，若G 为△BCD 的重心，则可得一个类比结论： ▲ ．10．（理科学生做）已知0m >，若6260126(1)mx a a x a x a x +=+++⋅⋅⋅+，且123663a a a a +++⋅⋅⋅+=，则实数m = ▲ ．（文科学生做）将函数()2sin(2)f x x ϕ=+的图像向右平移6π个单位后，得到的函数图像关于y 轴对称，则ϕ的最小正值为 ▲ ．11．（理科学生做）6把椅子摆成一排，3人随机就座，任何两人不相邻的坐法种数为 ▲ ． （文科学生做）设U 为全集，A 、B 是U 的子集，则“存在集合C 使得A ⊆C ，B ⊆UC ”是“A ∩B＝φ”的 ▲ 条件．（选填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”） 12．若log 4(3a ＋4b )＝log则a ＋b 的最小值是 ▲ ． 13．中心在原点、焦点在x 轴上的椭圆与双曲线有公共焦点，左右焦点分别为1F 、2F ，且它们在第一象限的交点为P ，12PF F △是以2PF 为底边的等腰三角形．若210PF =，双曲线离心率的取值范围为()1,2，则椭圆离心率的取值范围是 ▲ ．14．已知函数21()ln (22)(0)4f x x ax a x a a=++-+>，若存在三个不相等的正实数123,,x x x ，使得312123()()()3f x f x f x x x x ===成立，则a 的取值范围是 ▲ ． 二、解答题：本大题共6小题，共计90分.请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤． 15．（本小题满分14分）（理科学生做）如图，,A B 两点之间有5条网线并联，它们能通过的信息量分别为2、3、3、4、4．现从中随机任取2条网线．（1）设选取的2条网线由A 到B 通过的信息总量为x ，当6x ≥时，则保证信息畅通． 求线路信息畅通的概率；（2）求选取的2条网线可通过信息总量的数学期望．（文科学生做）已知命题:12p x -≥和命题:q x Z ∈．若“p q 且”与“非q ”同时为假命题，求实数x 的值．第15题（理）图第13题图（理科学生做）如图，已知四棱锥P ABCD -中，底面ABCD 为矩形，侧棱PA ABCD ⊥底面，2PA AB ==，4AD =，M 为侧棱PC 的中点．（1）求异面直线AM 与PD 所成角的余弦值； （2）求二面角B PC D --的余弦值．（文科学生做）已知函数22()cos sin cos 1f x x x x x =-++，x R ∈. （1）求()f x 的最小正周期及()f x 的最小值；（2）若()2f α=，且,42ππα⎡⎤∈⎢⎥⎣⎦，求α的值．17．（本小题满分14分）（理科学生做）若n 为正整数，试比较132n -⋅与23n +的大小，分别取1,2,3,4,5n =加以试验，根据试验结果猜测一个一般性结论，并用数学归纳法证明． （文科学生做）设,x y 都是正数，且2x y +>，试用反证法证明：12x y +<和12yx+<中至少有一个成立.18．（本小题满分16分）某仓库为了保持库内温度，四周墙上装有如图所示的通风设施，该设施的下部是等边三角形ABC ，其中AB =2米，上部是半圆，点E 为AB 的中点．△EMN 是通风窗，（其余部分不通风）MN 是可以沿设施的边框上下滑动且保持与AB 平行的伸缩杆（MN 和AB 不重合）． （1）设MN 与C 之间的距离为x 米，试将△EMN 的面积S 表示成x 的函数()S f x =； （2）当MN 与C 之间的距离为多少时，△EMN 面积最大？并求出最大值．第16题（理）图DB第18题图（图1）（图2）已知点00(,)P x y 为椭圆22221(0)x y a b a b+=>>上的任意一点（长轴的端点除外），1F 、2F 分别为左、右焦点，其中a ，b 为常数．（1）若点P 在椭圆的短轴端点位置时，12PF F ∆为直角三角形，求椭圆的离心率. （2）求证：直线00221x y x y a b+=为椭圆在点P 处的切线方程； （3）过椭圆的右准线上任意一点R 作椭圆的两条切线，切点分别为S 、T ．请判断直线ST 是否经过定点？若经过定点，求出定点坐标，若不经过定点，请说明理由．20．（本小题满分16分）设函数323(1)()312t f x x x tx +=-++（0t >）． （1）若2t =，求函数()f x 的极大值；（2）若存在0(0,2)x ∈，使得0()()f x f x 是在区间[0，2]上的最小值，求实数t 的取值范围； （3）若()x f x xe m ≤-（e 2.718≈）对任意的[0,)x ∈+∞恒成立时m 的最大值为1－，求实数t 的取值范围．2014/2015学年度第二学期高二年级期终考试数 学 答 案一、填空题： 12．(,0),34x x x ∀∈-∞≥都有 （图2）（图1）第19题图3． 40 4．125． 14 6．()1,+∞7． 48．221312x y -=9．1()3AG AB AC AD =++10．（理科）1（文科）56π 11．（理科）24 （文科）充要12．7+13． 2,13⎛⎫ ⎪⎝⎭14．11()22e 二、解答题：15．（理科）解：（1）随机任取2条网线共有10种不同的情况．21324336,(6)1010P x ++=+=∴===，...................................................................................2' 4347,(7)10P x +=∴==，............................................................................................................4' 1448,(8)10P x +=∴==，............................................................................................................6'34184(6)101010105P x ∴≥=++==．...............................................................................................8'（2）21235,(5)105P x +====，..............................................................................................10'∴线路通过信息量的数学期望是1341()5678 6.45101010E x =⨯+⨯+⨯+⨯=． (1)3'答：（1）线路信息畅通的概率是45； （2）线路通过信息量的数学期望是6.4．..................14' 15．（文科）解：非q 为假命题，则q 为真命题；...................................................................................3'p q 且为假命题，则p 为假命题，......................................................................................................6' 即12,x x Z -<∈且，得212x -<-<，解得13,x x Z -<<∈，.....................................................................................................................12'0,1,2x ∴=或． .............................................................................................................................14' 16．（理科）解：（1）如图所示，以A 为原点，建立空间直角坐标系A xyz -，则(0,0,0)A ，(2,0,0)B ，(0,4,0)D ，(0,0,2)P ，(2,4,0)C ，(1,2,1)M ，......................................................................................................................2'(1,2,1),(0,4,2)AM PD ==-，0cos ,6AM PD AM PD AM PD⋅+∴<>===，∴异面直线AM 与PD ． .........................................................................7' （2）设BPC 平面的法向量为(,,)x y z =m ，(0,4,0),(2,0,2)BC BP ==-，并且,BC BP ⊥⊥m m ， 40220y x z =⎧∴⎨-+=⎩，令1x =得1z =，0y =，∴MBD平面的一个法向量为(1,0,1)=m ．......................................................................................9' 设DPC 平面的法向量为(,,)a b c =n ，(2,0,0),(0,4,2)DC DP ==-，并且,DC DP ⊥⊥n n ，20420a b c =⎧∴⎨-+=⎩，令1b =得2c =，0a =，∴MBD平面的一个法向量为(0,1,2)=n ． .....................................................................................11' ∴cos ,⋅<>===⋅m n m n |m |n ，.......................................................................................13'∴二面角B PCD --的余弦值为.........................................................................................14'16．（文科）解：（1）22()cos sin cos 12cos 21f x x x x x x x =-++=++=2sin(2)16x π++． ..........................................................................................5'因此()f x 的最小正周期为π，最小值为1-．..................................................................................7' （2）由()2f α=得2sin(2)16πα++=2，即1sin(2)62πα+=．......................................................9' 而由,42ππα⎡⎤∈⎢⎥⎣⎦得272,636παππ⎡⎤+∈⎢⎥⎣⎦．故5266παπ+=，解得3πα=．....................................................................................................14' 17．（理科）解：当1n =时，132n -⋅<23n +；当2n =时，132n -⋅<23n +； 当3n =时，132n -⋅=23n +； 当4n =时，132n -⋅>23n +；当5n =时，132n -⋅>23n +；..............................................................................................................5' 猜想：当4n ≥时，132n -⋅>23n +．.................................................................................................7' 证明：当4n =时，132n -⋅>23n +成立；假设当(4n k k =≥）时，132k -⋅>23k +成立， 则1n k =+时，左式=32k ⋅=1232k ⋅⋅－>223k +（），右式=213k ++（），因为223k +（）－213k ++[()]=222k k -+=211k +（－）>0，所以，左式>右式，即当1n k =+时，不等式也成立.综上所述：当4n ≥时，132n -⋅>23n +．..........................................................................................14' 17．（文科）证明：假设12x y +<和12y x +<都不成立，即12x y +≥， 12yx+≥..............................2'又,x y 都是正数，∴12x y +≥，12y x +≥两式相加得到2()2()x y x y ++≥+，. ............................................................................................8' 2x y ∴+≤． 与已知2x y +>矛盾，所以假设不成立，...........................................................................................12' 即12xy+<和12yx+<中至少有一个成立．......................................................................................14'18．解（1）①当MN 在三角形区域内滑动时即x ∈//,MN AB ABC ∆是等腰三角形，060MNC ∠= 连接EC 交MN 于P 点，则PC=x ，，MN = ABC ∆的面积1()||)2S f x MN x ==23x x =-+.....................................................................................4'②当MN在半圆形区域滑动即1)x ∈+时MN =..........................................................................................................................6' 所以23()(1)x x x S f x x x ⎧-+∈⎪==⎨⎪∈⎩......................................................8'（2）x ∈时，2()S f x x ==+的对称轴为x =所以2max ()f x f ===................................................................................11'当且仅当1)2x =取等号，..................................................................................15'又12>所以三角形EMN的面积最大值为12...............................................................................16' 19．解：记c =（1）当点P 在椭圆的短轴端点位置时，12PF F ∆则有a ，得e =． 所以，此时椭圆的离心率为2．......................4' （2）点00(,)P x y 在椭圆22221x y a b +=上，得2200221x y a b+=．把00(,)x y 代入方程00221x y x y a b+=，得2200221x y a b +=，所以点00(,)P x y 在直线00221x y x y a b+=上，...............................................................................6'联列方程组2222002211x y a b x y x y a b ⎧+=⎪⎪⎨⎪+=⎪⎩，消去y 可得222220020a x a x x a x -+=， 解得0x x =，即方程组只有唯一解． 所以，直线00221x y x y a b +=为椭圆在点P 处的切线方程．......................................................10' （3）由题可设11(,)S x y 、22(,)T x y 、23(,)a R y c．由（2）结论可知，切线SR 的方程为11221x y x y a b +=① 切线TR的方程为22221x y x y +=②.....................................................12'把23(,)a R y c 分别代入方程①、②，可得11321x y y c b+=③和22321x y y c b +=④ 由③、④两式，消去3y ，可得1221x c y x c y -=-()()，即有12210)0)x c y x c y --=--()(()(，（图2）（图1）所以，点11(,)S x y 、22(,)T x y 、2(,0)F c 三点共线， 所以，直线ST经过定点，定点坐标为2F ．..........................................................16'20．解：（1）若2t =，则329()612f x x x x =-++， 所以，2'()396f x x x =-+，令'()0f x =，得1,2x =；令'()0f x <，得12x <<，所以，()f x 在区间（1，2）内递减，在区间（－∞，1）,（2，+∞）内递增，得()f x 的极大值为7(1)2f =．............................................................................................................4' （2）函数323(1)()312t f x x x tx +=-++． 得2'()33(1)33(1)()f x x t x t x x t =-++=--，0t >．令'()0f x =，得1,x t =；....................................................................................................................6' ①当2t ≥时，可以判定()f x 在区间（0，1）内递增，在区间（1，2）内递减， 此时，不存在0(0,2)x ∈使得0()()f x f x 是在[0，2]上的最小值；②当12t <<时，可以判定()f x 在区间（0，1）、（t ，2）内递增，在区间（1，t ）内递减， 欲存在0(0,2)x ∈使得0()()f x f x 是在[0，2]上的最小值， 则必须有()(0)f t f ≤，即3223(1)3112t t t t +-++≤，解得3t ≥，不合题意，舍去． ③当01t <<时，可以判定()f x 在区间（0， t ）、（1，2）内递增，在区间（t ，1）内递减， 欲存在0(0,2)x ∈使得0()()f x f x 是在[0，2]上的最小值， 则必须有(1)(0)f f ≤，即3112t +≤，解得13t ≤，所以，103t <≤． ④当1t =时，可以判定()f x 在区间（0，2）内递增， 不存在0(0,2)x ∈使得0()()f x f x 是在[0，2]上的最小值．综上所述，得t 的取值范围为1(0,]3．...........................................................................................10'（3）若()xf x xe m ≤-（e 为自然对数的底数）对任意的[0,)x ∈+∞恒成立，即 3223(1)3(1)31[3]122x x t t m xe x x tx x e x x t ++≤-+--=-+--对任意的0x ≥恒成立，.....11'令23()32(1)x g x t e x x t +-+-=，由于m 的最大值为1－， 所以23((30)1)2x t e x x t g x +-+-≥=恒成立．...............................................................................12'由(0)130g t =-≥可得103t <≤，当103t <≤时，3(1)2'()2x g x t e x =+-+， 再设3(1))2'(2()x h x g x t e x +=+=-，得'()20xh x e =-=，解得ln 2x =．()h x 在区间（0，ln2）内递减，在区间（ln2，+∞）内递增，()h x 的最小值为3(1)(ln 2)22ln 22t h +=+-，可以判定(ln 2)0h >，即'()0g x >，所以()g x 在区间[0，+∞）内递增，则有()g x 在区间[0，+∞）内的最小值(0)130g t =-≥，得13t ≤．所以，t 的取值范围是1(0,]3．.....................................................................................................16'。

上兴隆庄小学2014-2015学年第二学期学校教学工作计划一、指导思想。

为全面实施素质教育，不断深化教育教学改革，努力办好人民满意的学校，牢固树立“教学是中心，质量是生命”的意识，我校教学工作将立足我校教育发展的实际，以素质教育和教育现代化工作为目标，以课程改革为中心，以提高课堂教学效率为重点，以提高师资整体素质为核心，以强化教学过程的精细化管理为突破口，促进全校教师专业化发展，有效提高我校教育教学质量。

不断更新教学观念，改变教师的教学行为和学生的学习方式，全面提高教学质量，提出新举措，开创新局面，力争新突破。

二、主要工作。

1、努力实施新课程改革，以课改为核心，牵动学校整体教学改革，提高全员的课改意识，做好课改实施阶段性的总结，争创课改启动实施的示范校。

2、要大兴教学研究之风，认真做好现有科研课题、教研课题的实验研究工作，同时，做好已结题实验成果的推广使用工作，组织教师开展立足课堂，面向学生、服务教学实际的校本教研，努力构建学习型教师组织。

3、探索常规教学改革。

以作文教学、教学能力培养、英语口语交际等为突破口，强化教师落实课程改革的“三维度”目标，切实提高教学质量。

4、加强校本培训，加快校本课程的开发进程，培训中做到理论学习与基本功训练有机结合，做到信息技术掌握与课堂教学实践相结合，做到发现问题与教学反思相结合。

使培训工作制度化、内容化、科学化。

5、实施青年教师培养工程，通过学习、实践、研讨等形式，不断发现能人，培养能人，鼓励能人，搭建平台，训练培养一批青年教师，使其牢固树立名师意识，打造名师带名校效应。

6、强化质量意识，认真做好阶段性检测，及教学质量分析，逐步规范学生作业，教师批改等常规性工作，探索新课改下的评价改革。

7、在各科教学中注重加强环保教育，以课堂渗透为主，并辅以综合实践活动，培养学生环保意识。

8、加强艺体卫工作，培养全面发展的人才。

改善学校体育环境。

三、具体工作。

１、加强师资培训，转变观念与新课程同行，不断提高专业素质。

盐城市一小 2015 年春六年级数学期中试卷盐城市第一小学教育集团 2014—2015 学年度第二学期六年级数学课堂练习命题人：祁正茂审核人：陈小洋 等第____________卷首语：一转眼半个学期过去了，相信这半个学期你一定有很多收获吧。

这份练习会让你对自己的学习有一个全面的把握，相信只要你仔细审题，认真答题，一定会取得满意的成绩，加油，你一定行！一、认真辨析。

(每空 1 分，共 19 分)1. 5.1 立方米＝（）立方分米（）升＝2080 毫升0.5 公顷=（）平方米2015 立方分米=（ ）升（ ）毫升2．一台压路机的前轮宽 3 米，直径是 1 米，前轮滚动一周，压过路面的面积是()平方米。

3．一个比例的两个外项互为倒数，如果其中一个内项为 0.2，另一个内项是（）。

4．一个圆锥的体积比与它等底等高的圆柱的体积少 20 立方厘米,那么这个圆锥的体积是()立方厘米，圆柱的体积是()立方厘米。

5．在一个比例式中，两个比的比值都是 2，两个外项都是 10，这个比例式写作（）。

6. 六(1)班男生人数是女生的43 ，女生人数是总人数的(() )。

如果六(1)班的总人数在 40～50 人之间，那么六(1)班男生有（ ）人。

7. 如右图，是从一个圆柱的前面和上面看到的图形，那么这个圆柱的表面积是（ ）平方厘米。

8.把直径是 2 厘米的圆按 2:1 的比放大，放大后圆的周长是（ ）厘米，放大后圆的面积与放大前圆的面积比是（）。

9. 一幅地图，它的线段比例尺是，把它改写成数值比例尺是（），已知 AB 两地的图上距离是 8 厘米，那么 AB 两地的实际距离是（）千米。

10.将 1 米长的圆柱体木棍锯下 4 分米长的一段后，表面积减少 25.12 平方分米，原来这根木棍的体积是（ ）立方分米。

11. 右图是实验小学六年级男生喜欢的球类运动统计图，已知喜欢乒乓球的有 80人，那么喜欢足球的有（ ）人。

12.把一个圆柱的底面平均分成若干个扇形，然后切开拼成一个近似的长方体（如图），已知圆柱底面周长比长方体底面周长少 20 厘米，长方体高 5 厘米，圆柱体的体积是（ ）立方厘米。

洪州镇中心小学关于2014—2015学年度第二学期期末教学质量检测的通知各校点：接县教育和科技局通知，现将2014—2015学年度第二学期期末教学质量检测的有关事宜通知如下，请遵照执行。

一、检测目的为全面贯彻课程（教学）计划，引导各校认真执行学科课程标准，落实基础，培养能力，促进学校加强教学常规管理和增强教育质量意识，调动广大师生的积极性，提高教学效率，从而提高教学质量。

二、检测重点学期教学质量检测为水平考试，检测着重体现学科课程标准和教材的基本要求，重点考查基础知识、基本方法，适当考查运用知识的能力。

三、检测内容范围及答卷方式小学各年级各学科按本年级现行使用的教材和课程标准进行命题。

其中中心小学英语学科各年级都进行听力测试，占全卷分值20%（听力测试统一提供音频材料）。

各科检测的内容及范围见附件一。

小学一至六年级在试卷上答题，可直接用试卷扫描。

四、命题制卷：小学由州教育局命题制卷。

五、检测时间小学：六年级7月1—2日，一、二年级7月2日，三、四、五年级7月3—4日。

具体安排见附件二。

六、考点安排1.小学六年级集中检测，我镇设1个考点。

洪州中学考点：洪州镇中心小学和村小2.小学一至五年级以校为单位设置考点。

七、考场设置与布置1.小学一至六年级按30人设置考场，单人、单桌、单行，不足30人的按实际人数设为1个考场。

2.考场由所在学校负责布置，各考场均要张贴考场号和学生考号，考场号与学生考号标识由考点学校制作打印。

八、考号编排1.村小一至五年级学生考号由所在校点编排。

2.镇中心小学一至六年（含村小六年级）学生考号由教研室统一编排。

九、监考安排与要求1.六年级检测由考点中学教师监考。

2.村级小学及教学点检测由中心校安排循环交叉监考（另行安排通知）。

3.中心小学一至五年级检测由教研室安排循环交叉监考。

十、条形码粘贴与答题要求1.小学一至五年级每考完一科后，由监考教师统一在学生试卷上粘贴条形码。

答题时，要求学生务必将自己的姓名、考号填写在试卷或答题卡规定的位置上。

资料概述与简介 2014/2015学年度第二学期高二年级期终考试 语文试题 （满分160分，时间150分钟） 一、语言文字运用（15分） 1．依次填入下列句中横线处的词语，最恰当的一组是（3分） 才能和思想是一个人的立身之本像石缝里的一棵小树被扭曲挤压成不了旗杆却也可成一条遒劲的龙头拐杖别是一种价值A．即使平分秋色 B．虽然各有千秋 C．即使各有千秋 D．虽然平分秋色 2．下列句中，没有语病的一项是（3分）A．B．C．D．近年来，的消费观念、消费水平和消费方式都有了明显的提高和转变，不应漠视这些变化。

3．下列句所用修辞手法与其他几项不同的一项是（3分） A．天空老张着那灰色的幔，没有一点点漏洞。

午后三点钟光景，忽然天空那灰色的幔裂了一条缝！(《雷雨前》) B．整个灶头几乎没有直线，那么多即兴式的弧线使灶头既端庄秀气，像一位穿着蓝印花布的农家少妇。

(金曾豪《家里的灶头》) C．冬天，有多少人放下一年的事情，像我一样用自己冰冷的手，从头到尾地抚摸自己的一生。

(刘亮程《寒风吹彻》) D．只要你自己心灵上不长疮瘢，眼不盲，耳不塞，这无形迹的最高等教育便永远是你的名分。

(徐志摩《山居闲话》) 4．在下文方格处填入语句，恰当的一项是（3分） A．最爱湖东行不足，绿杨阴里白沙堤 B．寺古僧闲云作伴，山深世远月为朋 C．日日扁舟藕花里，有心长做济南人 D．四面荷花三面柳，一城山色半城湖 5．在下面一段文字横线处填入语句，衔接最恰当的一项是（3分） …… ①每一棵树都是真正的皇家大乐队的成员。

②因为歌唱，树木和森林的生命焕发出无限光彩。

③树——乐队的成员在白天黑夜持续歌唱，表达对自然创世之美对万物生命的浩大礼赞。

④它们的歌唱，仿佛是大地裸露出地面的斑驳多节的粗野喉咙的歌唱。

⑤森林是隐藏在大地的一整列阵容完整的皇家大乐队。

A．B．C．D． 二、文言文阅读（19分） 阅读下面的文言文，完成6～9题。

孝景三年，吴楚反。

2014—2015学年度第二学期小学老师教学工作总结2014—2015学年度第二学期小学老师教学工作总结海口市滨海第九小学; 王;;渝光阴似箭，这个学期即将结束，本人在学校领导及同事们的关心与帮助下圆满的完成了学校安排的各项教学工作及班主任工作，在思想觉悟方面有了更进一步的提高，本年度的工作总结主要有以下几项：1、思想政治表现、品德素质修养及职业道德。

本人能够认真贯彻党的基本路线方针政策，以党员的标准严格要求自己，按时完成党交给的各项任务，通过报纸、杂志、书籍积极学习政治理论；遵纪守法，认真学习法律知识；爱岗敬业，具有强烈的责任感和事业心，积极主动认真的学习专业知识，工作态度端正，认真负责。

2、教学工作。

积极学习各种理论知识，以充实自己，以便在工作中以坚实的理论作为指导，更好地进行教育教学。

我坚持经常看英语报、去书店看相关书籍、浏览互联网上相关的网站等，还经常搜集一些优秀的教案课件学习；按时参加科组里组织的教研听课、评课活动，除此以外，还争取机会出外听课，从中学习别人的长处，领悟其中的教学艺术。

平时还虚心请教组里面的其他老师。

本学期担任一(3)的副班主任工作，担任一年级一（3）、一（4）、一（5）3个班级和四年级四（7）、四（8）班的的英语课程的教学工作，从本学期开学以来，认真备课、上课、听课、评课，做好课后辅导工作，广泛涉猎各种知识，形成比较完整的知识结构，严格要求学生，尊重学生，发扬教学民主，使学生学有所得，不断提高，从而不断提高自己的教学水平和思想觉悟，并顺利完成教育教学任务。

我特别关注班里听说能力强的学生，从中发现英语小能手，在课堂给予他们更多的机会去练习口语。

一个学期马上结束了，感觉蛮辛苦的，但看到学生们有了进步，也得到了成长，我感到很欣慰。

总结本学期的工作，发现自己有了一定的成绩和进步，但在某些方面还存在着不足之处。

比如有创造性的工作思路还不是很多，个别工作做的还不够完善，这些都有待于在今后的教育、教学工作中加以改进、提高。

2014—2015学年度第二学期五①班主任半期工作总结府谷县庙沟门中心小学刘婧一、班级情况分析本班共有学生45人。

通过5年的努力，大部分同学的学习主动性强，上课能认真听讲，积极举手发言，课后按时完成作业，自觉遵守课堂常规，有良好的行为习惯和学习习惯。

班干部工作能力强，工作主动，在他们的大力协助下，班级的各项工作都开展得有声有色，基本形成良好的班风。

但本班学生呈两极分化，后进生所占的比例还比较大，对班级各项工作都造成一定的负面影响。

特别是进入5年级后，学生的心理发生了很大的变化，主要表现为：1、自主意识增强，对事物的认识有一定的是非观念，对教师和家长教育有抵触情绪，情绪不稳定，课堂上学习不专心，喜欢三五成群地结队外出。

培养学生良好的个性心理，加强自我教育也是一项长期而艰难的任务。

针对以上情况，半期以来我主要做了以下几个方面的工作：（一）抓好常规管理。

“没有规矩，不成方圆”，我班的学生虽然大部分学生思想单纯，积极上进，但他们毕竟只是孩子，在许多方面还不知约束自己，或不知怎样约束自己，还需要教师的督促、引导。

为此，我首先做好以“安全”为首的常规教育工作。

开学初期，就地取材组织学生认真学习《中小学教育安全指导纲要》《中华人民共和国突发事件应对法》和《道路交通安全法》，组织观看《道路交通安全法》讲座，随时特别强调“安全第一”观念，让每一个学生都牢固树立起“安全问题重于泰山的重要意识。

其次，我根据学校常规教育安排，组织学生认真学习《小学生守则》《小学生日常行为规范》《花垣小学师生礼仪常规》等有关规则，使每个学生明确应该怎样做一个合格的小学生，从而自觉地用有关规则约束自己。

再次，鼓励班干部自主工作，大胆工作，放手放手，早自习、放学、布置作业和有关工作都由班干部完成，有意培养他们的组织能力、管理能力。

同时激发每一个学生的主人翁意识，树立对自己责任的思想，做好自己的份内事，整理好自己的学习用品，收拾自己的书包，认真完成每一次作业，做好每一次的值日等，充分调动他们的积极性、创造性，营造出班级就是家的良好意识和氛围，从而形成“人人管我，我管人人”的班级责任感。

盐城市秦南小学 2014/2015学年度第二学期六年级数学学业检测试卷一、填空。

（17分）1．地球的表面陆地面积是149000000平方千米，把这个数改写成用“亿”作单位的数是（ ）亿平方千米；海洋面积是361000000平方千米，把这个数省略“亿”后面的尾数约是（ ）亿平方千米。

2．一个比例里，两个外项正好互为倒数，其中一个内项是32，另一个内项是（ ）。

3．在一个直角三角形中，三个内角度数的比是3 ：2：5 ,则最小的一个内角是（ ）度。

4． 3.4时=（ ）时（ ）分 7升50毫升=（ ）升5．在有余数的除法中，除数是a,商是8，余数是b ，那么用含有字母的式子表示出被除数是（ ）。

6．观察右图,用“>”或“<”填空.(1)a ____b (2)c ____0 7．一个蛋糕重4千克，把它平均分给10个小朋友，每人分得这个蛋糕的（ ），每份重（ ） 千克。

9．一次数学测验全班平均95分，小明考了98分，张老师记作+3分。

小亮考了91分，那么张老师记作（ ）分。

10．张亮做了一个底面周长为25.12厘米，高为20厘米的圆柱体模型，他的同学李强做了一个底面半径为4厘米，高为20厘米的圆锥体模型。

那么，李强做的模型的体积是张亮做的模型体积的（ ）。

11．不同蔬菜中钙和磷含量的比是不同的。

如下表，（ ）蔬菜的钙磷含量比最低。

.12．甲数的等于乙数的，甲乙两数的最简整数比是（ ），如果甲数是30，那么乙数是（ ）。

二、判断对错。

（5分）1．如果数a 是2的倍数，则a+1必定是奇数。

（ ）2.等腰三角形所在底边上的高就是它的对称轴。

（ ）3.小红坐在教室的第5列第6行，用对表示小红的位置是（6，5）。

（ ）4. 在100克盐水中含有1克盐，盐与盐水的比是1:100。

（ ）5. 1900年的第一季度有91天。

（ ）三、选择。

将正确答案的序号填在括号里。

（6分）1.李红向下面每一个靶掷一块石头（四个靶大小相等，均为等分），她最有可能击中哪个靶的阴影部分？（ ）A B C D2.图中每个小正方形面积为1个单位。

盐城市秦南小学 2014/2015学年度第二学期四年级英语学业检测试卷一、单项选择（30分）( )1. —I can ’t swim. —I can ’t swim ________.A.tooB. twoC. either( )2. —Have a ________, Bobby. —Yeah! I can fly.A. A.Look atB. lookC. try( )3.Look at dogs under the tree. They’re very cute.A. theyB. thatC. those( )4. —How many ________ do you have? w W w .x K b 1.c o M —________.A. mango; TwoB. mangoes; TwoC. mangoes; Too( )5. —Here ’s ________ egg for you.—Thank you. What ________ big egg! w W w .x K b 1.c o MA.an; aB. an; anC. a; a( )6. This is our snowman. His nose ____ small. His eyes ____ big. A. is; isB. are; areC. is; are( )7. – Where is your aunt? -- _______ in the living room. A. I ’m B. She ’s C. He ’s ( )8. --Do you have ______ apple? -- No. I have ______ oranges. A. an, an B. an, some C. an, any ( )9. I ’d like to drink two of . 新-课 -标- 第-一-网A. cups; coffeesB. cups ; coffeeC. cup; coffee ( )10. -Where the cakes ? -- in the fridge.A. is ; They ’reB.are ; They ’reC. is ; It ’s ( )11. Where ______ my pens? X|k | | 1 . c |O |mA. isB. areC. am( )12.A: Your school bag is nice. B: __________A. Yes.B. No, it isn’t.C. Thank you.( )13. A:_________would you like? B: _________like some noodles. A.What’s ; I B What ; I’d C How ; I’d ( )14.I’m hungry. I’d like ________.A some tea B. a sandwich C. some coffee学校_________ ___ 班级____________ 姓名______________ 学号______________ ………………………装…………………………………………订……………………………………线…………………………………( )15. Do you have_______toy animals?A someB anyC a( )16. Whose classroom is this? It’s__________ classroom.A. weB. usC. our( )17.His father is very _______.A. bigB.tallC.long( )18.____ you like a pie? Yes,pleaseA. DoB. WouldC. do( )19. —Can you play football?— Yes, I ______.X k B 1 c o mA. doB. canC. can’t( )20. —_______ _______ crayons do you have?— Twelve.A. How manyB. How niceC. How much二、从右栏中找出左栏相应的答句。