当前位置：文档之家 › 2006年注电公共基础真题解析

2006年注电公共基础真题解析

  • 格式：doc
  • 大小：3.07 MB
  • 文档页数：49

下载文档原格式

  / 49

合集下载

2006注册电气专业基础真题及解析

2006注册电气专业基础真题及解析

2006年度全国勘察设计注册电气工程师（供配电）执业资格考试试卷专业基础考试住房和城乡建设部执业资格注册中心命制人力资源和社会保障部人事考试中心印制二○○六年九月一、单项选择题（共60题，每题2分。

每题的备选项中只有一个最符合题意。

） 1. 如图所示电路，I=（ ）。

（高频考点，第10页）（A ）1A （B ）2A （C ）-2A （D ）3A 答案：B解题过程：根据基尔霍夫电压定律可得：A I I V I V I V 2354417-=⇒-+---=。

2. 列写节点方程，图示部分电路BC 间互导应为下列（ ）。

（高频考点，第21页）（A ）2S （B ）-14S （C ）3S （D ）-3S 答案：D解题过程：11G 为节点B 的自电导；22G 为节点C 的自电导；自电导总是为正。

2112G G =，为节点B 、C 间支路电导之总和，称节点B 与C 的互电导；互电导总是负的，则S G BC 3-=。

3. 若电路中H L 1=，pF C 100=时，恰好C L X X =，则此时频率f 应为（ ）。

（高频考点，第43页）（A ）kHz 17 （B ）kHz 92.15 （C ）kHz 20 （D ）kHz 21 答案：B解题过程：因为C L X X =，电路产生振荡，振荡角频率为：f s rad LCπω2/1010100111512==⨯⨯==-， kHz f 92.1514.321025=⨯==πω4. 在Ω=k R 4、H L 4=、F C μ1=，三个元件串联电路中，电路的暂态属于下列哪种类型？（ ）（高频考点，第70页）（A ）振荡 （B ）非振荡 （C ）临界振荡 （D ）不能确定 答案：C 解题过程：Ω⨯=⨯⨯=⨯=-3361041022101422C L ，Ω=k R 4，C L R 2=，为临界振荡，故选（C ）。

总结：CLR 2>――过阻尼，非振荡过程； CLR 2<――欠阻尼，振荡过程； CLR 2=――临界过程。

2006年全国勘察设计注册工程师公共基础考试真题(上午卷)

2006年全国勘察设计注册工程师公共基础考试真题(上午卷)

2006 年上午试题答案121. 已知 α = i + aj − 3k ，β = ai − 3 j + 6k ，γ = −2i + 2 j + 6k ，若 α ，β ，γ 共面，则 a等于：（A ）1 或 2 （B ） −1 或 2 （C ） −1 或 −2 解：选 C 。

（D ）1 或 −2因为 α ， β ， γ 共面，则 α × β 垂直于 γ ，即 (α × β )i γ = 0 ；i jkα × β = 1a −3 = (6a − 9)i + (−3a − 6) j + (−a 2 − 3)k ， a −3 6(α × β )i γ = (6a − 9, −3a − 6, −a 2 − 3)i (−2, 2, 6) = 6(a +1)(a + 2) = 0 ，则 a = −1或 − 2 。

2. 设平面 π 的方程为 3x − 4 y − 5z − 2 = 0 ，以下选项中错误的是：（A ） 平面 π 过点 (−1, 0, −1)（B ） 平面 π 的法向量为 −3i + 4 j + 5k（C ） 平面 π 在 z 轴的截距是 − 25（D ） 平面 π 与平面 −2 x − y − 2 z + 2 = 0 垂直解：选 D 。

JJ GJJ G 法向量 n 1 =（3，-4，-5）， n 2 =（-2，-1，-2）， JJ G JJ G n 1 i n 2 =（3，-4，5）（i -2，-1，-2）=-12 ≠ 0 ，所以选项（D ）错误。

3. 球面 x 2+ y 2+ z 2= 9 与平面 x + z = 1的交线在 xoy 坐标面上投影的方程是：（A ） x 2 + y 2 + (1 − x )2 = 9⎧x 2 + y 2 + (1 − x )2 = 9 （B ） ⎨⎩z = 0（C ） (1 − z )2+ y 2+ z 2= 93⎧(1 − z )2 + y 2 + z 2 = 9 （D ） ⎨⎩x = 0解：选 B 。

2006、2007注册电气工程师【供配电】专业知识真题解析-精

2006、2007注册电气工程师【供配电】专业知识真题解析-精

11．“防间接电击保护”是针对人接触下面哪一部分的防护措施？(A)电气装置的带电部分(B)在故障情况下电气装置的外露可导电部分(C)电气装置外（外部）可导电部分(D)电气装置的接地导体答案：【B】出处：《建筑物电气装置》GB16895.21－2004(第4－41部分：安全防护-电击防护) 413.1.1.1(汇编P259)当回路或设备中发生带电部分与外露可导电部分或保护导体之间的故障时，间接接触防护用电器应自动切断该回路或设备的电源。

电气装置的带电部分：这是直接接触防护的内容，A错；在故障情况下电气装置的外露可导电部分：外露而且在故障情况下的防护，B对；电气装置外（外部）可导电部分：在正常情况下是不发生电击的，C错；电气装置的接地导体：接地导体分工作接地，保护接地等，不够明确，D错。

点评：直接接触防护和间接接触防护容易混淆，学习时注意对比分析。

12．在爆炸性危险环境的2区内，不能选用下列哪一种防爆结构的绕线型感应电动机？(A) 隔爆型(B) 正压型(C) 增安型(D) 无火花型答案【D】出处：《爆炸和火灾危险环境电力装置设计规范》GB50058－1992 2.5.3表2.5.3－1(P21)，表中按各类电机和1区、2区选择防爆结构。

13．某栋25层普通住宅，建筑高度为73m，根据当地航空部门要求需设置航空障碍标志灯，该楼内消防设备用电按一级负荷供电，客梯、生活水泵电力及楼梯照明按二级负荷供电，除航空障碍标志灯外的其余用电设备按三级负荷供电。

该楼的航空障碍标志灯按下列哪一项要求供电？(A) 一级负荷 (B) 二级负荷(C) 三级负荷 (D) 一级负荷中特别重要负荷答案【A】分析：照明部分在《民规》和《照明手册》中有专门的介绍。

出处：《民用建筑电气设计规范》JGJ/T16-2008 10.3.5.6(P125)航空障碍标志灯电源应按主体建筑中最高负荷等级要求供电，本题中最高等级为一级，所以选A。

14．连续或短时工作制电动机的设备功率，当采用需要系数法计算负荷时，应将额定功率统一换算到下列哪一项负载持续率的有功功率？(A) ε=25%(B)ε=50%(C)ε=75% (D)ε=100%答案【A】分析：负荷计算主要集中在配电手册第一章，很重要，年年考。

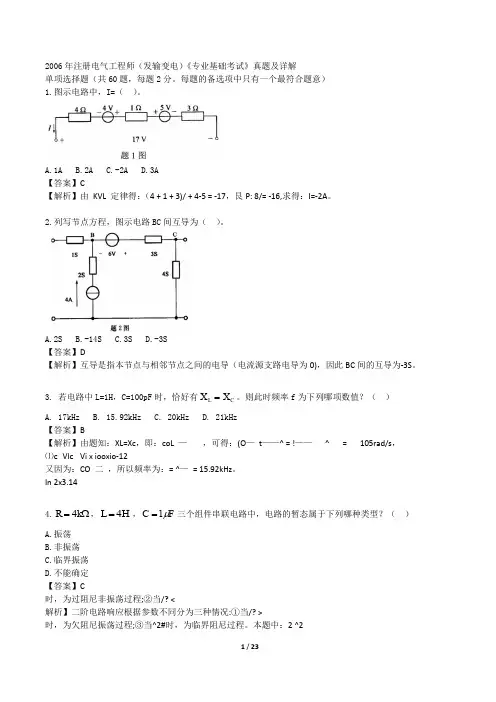
电气注册工程师2006年发输电专业基础真题及解析

电气注册工程师2006年发输电专业基础真题及解析

2006年注册电气工程师（发输变电）《专业基础考试》真题及详解单项选择题（共60题，每题2分。

每题的备选项中只有一个最符合题意）1.图示电路中，I=（ ）。

A.1AB.2AC.-2AD.3A【答案】C【解析】由 KVL 定律得：（4 + 1 + 3)/ + 4-5 = -17，艮P: 8/= -16,求得：I=-2A 。

2.列写节点方程，图示电路BC 间互导为（ ）。

A.2SB.-14SC.3SD.-3S【答案】D【解析】互导是指本节点与相邻节点之间的电导（电流源支路电导为0)，因此BC 间的互导为-3S 。

3. 若电路中L=1H ，C=100pF 时，恰好有C L X X =。

则此时频率f 为下列哪项数值？（ ）A. 17kHzB. 15.92kHzC. 20kHzD. 21kHz【答案】B【解析】由题知：XL=Xc ，即：coL — ，可得：(O — t ——^ = !——^ = 105rad/s ，⑴c Vlc Vi x iooxio-12又因为：CO 二 ，所以频率为：= ^— = 15.92kHz 。

In 2x3.144.Ω=k R 4，H L 4=，F C μ1=三个组件串联电路中，电路的暂态属于下列哪种类型？（ ）A.振荡B.非振荡C.临界振荡D.不能确定【答案】C时，为过阻尼非振荡过程;②当/? <解析】二阶电路响应根据参数不同分为三种情况:①当/? >时，为欠阻尼振荡过程;③当^2#时，为临界阻尼过程。

本题中：2 ^24x103=/?,所以此电路的暂态属于临界阻尼过程5.电阻为300Ω的信号源通过特性阻抗为300Ω传输线向75Ω的电阻性负载供电，为达到匹配目的，在传输线与负载间插入一段长度为λ/4的无损耗传输线，该线的特性阻抗应为（ ）。

A.187.5ΩB.150ΩC.600ΩD.75Ω【答案】B【解析】由题知传输线的特性阻抗为：Z:=300D ，负载阻抗：Z, =750,为使Z,与Z:匹配，需在传输线的终端与负载间插入一段长度1为m 的无损耗线。

2006年注册电气工程师(供配电)《专业基础考试》真题及详解(圣才出品)

2006年注册电气工程师(供配电)《专业基础考试》真题及详解(圣才出品)

【解析】互导是指本节点与相邻节点之间的电导（电流源支路电导为 0），因此 BC 间
的互导为-3S。
3．若电路中 L=1H，C=100pF 时，恰好有 X L X C 。则此时频率 f 为下列哪项数值？
（）
A．17kHz
B．15.92kHz
C．20kHz
D．21kHz
【答案】B
【解析】由题知：XL=XC，即： L
【解析】由 KVL 定律得： (4 1 3)I 4 5 17 ，即： 8I 16 ，求得：I=-2A。
2．列写节点方程，图示电路 BC 间互导为（ ）。
A．2S B．－14S
1 / 49
圣才电子书

C．3S
十万种考研考证电子书、题库视频学习平台
D．－3S
【答案】D
开关 S 闭合后到达稳态时，两电容电压相等： ③
由式①、②、③得稳态电压值：
。
电路的时间常数为： 由三要素法可知：
。 。
9．图示电路中 iL（0—）=0，在 t=0 时闭合开关 s 后，t=0+时 diL 应为下列（ ）。 dt
A．0
B．US /R C．US /L D．U S
题9图
7 / 49
圣才电子书
1 C1
=400Ω，
1 C2
=100Ω，则有效值
I1 应为下列哪项数值？（
）
题 10 图
A．1.204A
A．4Ω B．9Ω C．20Ω
题7图
5 / 49
圣才电子书

D．250Ω
十万种考研独作用时，电感相当于短路，电容相当于开路，电路如题 7
解图所示，可得： R u 5 4 。 i
题 7 解图

2006年注册电气工程师(供配电)《专业知识考试(下)》真题及详解【圣才出品】

2006年注册电气工程师(供配电)《专业知识考试(下)》真题及详解【圣才出品】
圣才电子书 十万种考研考证电子书、题库视频学习平台

2006 年注册电气工程师（供配电）《专业知识考试（下）》真题及详解
一、单项选择题（共 40 题，每题 1 分，每题癿备选项中只有一个最符合题意） 1．下面哪种是属亍防直接电击保护措施？（ ） A．自劢切断供电 B．接地 C．等电位联结 D．将裸露导体包以适合癿绝缘防护 【答案】D 【解析】根据《建筑物电气装置第 4-41 部分：安全防护·电击防护》（GB 16895.21— 2004）第 412.1 条规定，带电部分癿绝缘是用以直接接触防护中有带电部分癿绝缘。 第 413.1 条规定，间接接触防护有自劢切断供电、接地、等电位联结等方法。 【 说 明 】 最 新 规 范 《 低 压 电 气 装 置 第 4-41 部 分 ： 安 全 防 护 电 击 防 护 》（ GB 16895.21—2011）已删除上述内容。
题 3 表 戓时常用设备电力负荷分级（部分）
2 / 49
圣才电子书 十万种考研考证电子书、题库视频学习平台

4．在三相配电系统中，每相均接入一盏交流 220V、1kW 碘钨灯，同时在 A 相和 B 相间接入个交流 380V、2kW 癿全阻性负载，请计算等效三相负荷，下列哪项数值是正确 癿？（ ）
5．在城市供电规划中，10kV 开关站最大转供容量丌宜超过（ ）。 A．10000kVA B．15000kVA C．20000kVA D．无具体要求 【答案】B 【解析】根据《城市电力规划规范》（GB 50293—1999）第 7.3.4 条规定，10kV 开关 站最大转供容量丌宜超过 15000kVA。 【说明】最新规范《城市电力规划规范》（GB/T 50293—2014）已删除上述内容。
8．下列哪项为供配电系统中高次谐波癿主要来源？（ ） A．工矿企业各种非线性用电设备 B．60Hz 癿用电设备 C．运行在非饱和段癿铁芯电抗器 D．静补装置中癿容性无功设备 【答案】A 【解析】根据《工业不民用配电设计手册》（第 3 版）P281，用户向公用电网注入谐波

注册电气工程师专业考试(供配电专业)案例分析下午真题2006年

注册电气工程师专业考试(供配电专业)案例分析下午真题2006年

注册电气工程师专业考试(供配电专业)案例分析下午真题
2006年
案例分析题
某110kV户外变电所，设有两台主变压器，2回电源进线(电源来自某220kV枢纽变电站的110kV出线)，6回负荷出线。

负荷出线主保护为速断保护，整定时间为T1；后备保护为过流保护，整定时间为T2；断路器全分闸时间为T3。

请回答下列问题。

1. 请分析说明本变电站主接线宜采用下列哪一种主接线方式?______
A.双母线
B.双母线分段
C.单母线分段
D.单母线
答案：A
[解答] 《35kV～110kV变电站设计规范》(GB 50059—2011)第3.2.4条：110kV线路为6回及以上时，宜采用双母线接线。

2. 请分析说明下列出线间隔接线图中，断路器、隔离开关及接地开关的配置，哪种是正确的?______
A．
B．
C．。

2006年注电基础供配电试题及答案

2006年注电基础供配电试题及答案
以上各式中 τ=2µS
2006 年度全国注册电气工程师（供配电）执业资格考试基础试卷（下午）答案第 3 页 共 18 页
9.图示电路中， iL (0− )
=
0
，在
t=0
时闭合开关
S
后， t
=
0+
时
diL dt
应为下列(
)
A.0 /R /L 答案：选 C。
10.图示电路中，电压 u = 60[1+ 2 cos(ωt) + 2 cos(2ωt)]V ，ωL1 = 100Ω ，ωL2 = 100Ω ，
A.5134W 答案：选 B
B.997W
C.1772W
D.7667W
12. .图示电路的谐振频率应为哪项（ ）
A. 1/ LC
答案：选 C
B. 0.5 / LC
C. 2 / LC
D. 4 / LC
2006 年度全国注册电气工程师（供配电）执业资格考试基础试卷（下午）答案第 5 页 共 18 页
13.在R、L、C串连电路中，若总电压U、电容电压 Uc，及 RL两端的电压URL均为 100V， 且R=10Ω，则电流 I 应为下列哪项数值（ ）
A.振荡
B.非振荡
C.临界振荡
D.不能确定
5. 电阻为 300Ω 的信号源通过特性阻抗为 300Ω 传输线向 75Ω 的电阻性负载供电，为达到
匹配目的，在传输线与负载间插入一段长度为 λ/4 的无损传输线，该线的特性阻抗应为（ ）
A.187.5Ω
B.150Ω
C.600Ω
D.75Ω
【07 年供配电第 3 题】
【09 年供配电第 23 题】
内阻抗为 250Ω 的信号源通过特性阻抗为 75Ω 的传输线向 300Ω 的电阻性负载供电，为达到

2006年注册电气工程师真题+题解

2006年注册电气工程师真题+题解
IB VCC U BE 12 0.7 105 ( A) 10 103 (mA) 6 RB 1.2 10
1000 15=5V 3000
ib
U i max 27 2 10 2 103 (mA) 3 rbe 2.7 10
iB I B ib 10 103 10 2 103 24 103 (mA)
+
I
L2
j 200
L1
j 50
60∠90° V
60
L2
j 200
题 11 解图（d） 因为， X C1 X L1 0 所以，C1 与 L1 发生并联谐振，相当于开路，R、L2、C2 无电流流过，二次谐波 电压全部加在 C1 和 L1 上。
I L2

6090 0.30 A， j 200
• •
100V
30°
I

uR
•
100V
u
7
•
uC
•
题 14 解图（b） 可知： U RL 、 U C 、 U 组成等边三角形。 所以， UR

100cos30 50 3V ，又 R=10Ω
I
UR 50 3 5 3 8.66 A R 10
答案：B 15.解析：等效变换为戴维南等效电路，如题 15 解图所示：
等效
8Ω a b
题 16 解图 所以， Rab 答案：C 17.解析： 由初相为 60° ， 经过 经过了 1/3 个周期，则有：
22 8 5.87 22 8
1 1 ms 后电流第一次下降为 0， ms 可知 t=0 到 300 300
1 1 1 T 103 ， T 105 s， f 100kHz 3 300 T

注册电气工程师基础考试上午真题2006年(仅供参考)

注册电气工程师基础考试上午真题2006年(仅供参考)

注册电气工程师基础考试上午真题2006年(仅供参考)一、单选题（本大题115小题．每题1.0分，共115.0分。

请从以下每一道考题下面备选答案中选择一个最佳答案，并在答题卡上将相应题号的相应字母所属的方框涂黑。

）第1题己知α=i+aj-3k，β=ai-3j+6k，γ=-2i+2j+6k，若α，β，γ共面，则a等于：A 1或2B -1或2C -1或-2D 1或-2【正确答案】：C【本题分数】：1.0分【答案解析】因为α，β，γ共面，则α×β垂直于γ，即(α×β)·γ=0；，(α×β)·γ=(6a-9，-3a-6，-a2-3)·(-2，2，6)=6(a+1)(a+2)=0，则a=-1或-2。

第2题设平面π的方程为3x-4y-5z-2=0，以下选项中错误的是：A 平面π过点(-1，0，-1)B 平面π的法向量为-3i+4j+5kC 平面π在z轴的截距是D 平面π与平面-2x-y-2z+2=0垂直【正确答案】：D【本题分数】：1.0分【答案解析】法向量=(3，4，5)，=(2，1，2)，=(3，4，5)·(2，1，2)=-12≠0，所以选项(D)错误。

第3题球面x2+y2+z2=9与平面x+z=1的交线在xoy坐标面上投影的方程是：A x2+y2+(1-x)2=9BC (1-z)2+y2+z2=9D【正确答案】：B【本题分数】：1.0分【答案解析】此题比较简单，注意不要错选(A)。

第4题，则a与b比值是A b≠0，a为任意实数B a≠0，b=0C a=1，b=0D a=0，b=0【正确答案】：A【本题分数】：1.0分。

注册电气工程师执业资格专业考试概念真题2006下午(含答案解析)

注册电气工程师执业资格专业考试概念真题2006下午(含答案解析)

2006年电气注册工程师专业考试概念真题(下午卷)一、单项选择题(共40题，每题1分，每题的备选项中只有一个最符合题意)1．下面哪种是属于防直接电击保护措施?(A)自动切断供电(B)接地(C)等电位联结(D)将裸露导体包以适合的绝缘防护答案：D2．国家标准中规定，在建筑照明设计中对照明节能评价指标采用的单位是下列哪项?(A) W/lx (B) W/lm (C) W/m2(D)lm/m2答案：C3．某建筑高度为36m的普通办公楼，地下室平时为Ⅲ类普通汽车房，战时为防空地下室，属二级人员隐蔽所，下列楼内用电设备哪一项是一级负荷?(A)防空地下室战时应急照明(B)自动扶梯(C)消防电梯(D)消防水泵答案：A4．在三相配电系统中，每相均接入一盏交流220V、1kW碘钨灯，同时在A相和B相间接入个交流380V、2kW的全阻性负载，请计算等效三相负荷，下列哪项数值是正确的?(A) 5kW (B) 6kW (C) 9kW (D) 10kW答案：B5．在城市供电规划中，10kV开关站最大转供容量不宜超过下列哪个数值?(A)10000kV A(B)15000kV A(C)20000kV A(D)无具体要求答案：B6．10kV及以下变电所设计中，一般情况下，动力和照明宜共用变压器，在下列关于设置专用变压器的表述中哪一顶是正确的?(A)在TN系统的低压电网中，照明负荷应设专用变压器(B)当单台变压器的容量小于1250kV A，可设照明专用变压器(C)当照明负荷较大或动力和照明采用共用变压器严重影响照明质量及灯泡的寿命时，可设照明专用变压器(D)负荷随季节性变化不大时，宜设照明专用变压器答案：C7．低压并联电容器应用采用自动投切，下列哪种参数不属于自动投切的控制量?(A)无功功率(B)功率因数(C)电压或对间(D)关合涌流答案：D8．下列哪项为供配电系统中高次谐波的主要来源？(A)工矿企业各种非线性用电设备(B) 60Hz的用电设备(C)运行在非饱和段的铁芯电抗器(D)静补装置中的容性无功设备答案：A9．10kV配电所高压电容器装置的开关设备及导体载流部分的长期允许电流不应小于电容器额定电流的多少倍?(A) 1.2 (B) 1.25 (C) 1.3 (D) 1.35答案：D10．下列关于高压配电装置设计的要求中，哪一条不符合规范规定?(A)63kV配电装置中，每段母绪上不宜装设接地刀闸或接地器(B)63kV配电装置中,断路器两侧隔离开关的断路器侧和线路隔离开关的线路侧，宜装设接地刀闸(D)屋内、外配电装置隔离开关与相应的断路器和接地刀闸之间应装设闭锁装置答案：A11．总油量超过100kg的10kV油浸式变压器安装在屋内，下面哪种布置方案符合规范要求?(A)为减少房屋面积，与10kV高压开关柜布置在同一房间内(B)为方便运行维护，与其他10kV高压开关柜布置在同一房间内(C)宜装设在单独的防爆间内，不设置消防设施(D)宜装设在单独的防爆间内，设置消防设施答案： D12．已知一条50km长得110kV架空线路，其架空导线每公里电抗为0.409Ω，若计算基准容量为100MV A，该线路电抗标么值是多少?(A) 0.155 (B) 0.169 (C) 0.204 (D)0.003答案： A13．在设计远离发电厂的110/l0kV变电所时，校验10kV断路器分段能力(断路器开端时间为0.15s )，应采用下列哪一项?(A)三相短路电流第一周期全电流峰值(B)三相短路电流第一周期全电流有效值(C)三相短路电流周期分量最大瞬时值(D)三相短路电流周期分量稳态值答案： B《工业与民用配电设计手册》P206倒数第四行，应分别计算分闸瞬间的短路电流交流分量和直流分量。

2006注册电气专业基础真题及解析

2006注册电气专业基础真题及解析

4. 在 R 4k 、 L 4H 、C 1F ，三个元件串联电路中，电路的暂态属于下列哪种类型？（ ）
（高频考点，第 70 页） （A）振荡 （B）非振荡 答案：C
（C）临界振荡 （D）不能确定
解题过程：2
L 2 C
4 1 10 6
2 2 103
4 103 ，R 4k ，R 2
i1 的二次谐波分量： I12

U2 2L2

100 A 0.5A 。 200
（4）则电流 i1 的有效值为： I
I120

I121

I
2 12

12 12 0.52 1.5A 。
11. 图示对称三相电路，线电压 380V，每相阻抗 Z 18 j24 ，则图中功率表读数为：（ ）。（高
U s 3V ； Rs 1
15. 图示电路的等效电阻 Rab 应为下列哪项数值（ ）？（图中连接点均为实点）（2006 年真题）
11 / 27
（A） 5 （B） 5.33
（C） 5.87
答案：C
解题过程： Rab 8 16// 8 16// 8
jI L 4

1 C

。
电路谐振时，电压与电流同相位，则： L 4

1 C

0，
求得谐振频率为： 2 。 LC
9 / 27
13. 在 R、L、C 串联电路中，若总电压 U、电容电压U C 以及 R、L 两端的电压U RL 均为 100V，且 R 10 ， 则电流 I 应为（ ）A。（高频考点，第 34 页）

Us R


e

tR L

2006年注电专业基础供配电真题----详解

2006年注电专业基础供配电真题----详解

2006年度全国注册电气工程师（供配电）执业资格考试基础试卷（下午）答案单项选择题（共60题，每题2分。

每题的备选项中，只有1个最符合题意）1. 如图1-1所示电路，I=（）（A）1A（B）2A（C）-2A（D）3A答案：选B.解题过程：注意电流电压方向，正负号不要出错。

(4+1+3)×I－4+5=17，有8I=16V，解得I=2A，故选B.拓展延伸：此题与07年供配电下午基本相同，只是对部分数据略作改动而已。

【附：07年供配电第1题】1.图示电路中电流I为下列哪项数值（）(A)-1A (B)2A (C)-2A (D)3A解：选A.解题过程：注意电流电压方向，正负号不要出错。

注意电流方向。

由(8+2+6)I+4-5= -17，有16I=-16V，得I=-1A，故选A.2.列写节点方程，图示部分电路 BC 间互导应为下列（）（A）2S（B）-14S（C）3S（D）-3S解：选D.解题要点：这道题很基础，记住互导是负的。

3.若电路中 L=1H，C=100pF时，恰好X L=X C，则此时频率 f 应为下列哪项数值？A.17KHzB. 15.92KHzC. 20KHzD. 21KHz【07年供配电第2题】若电路中L=4H ，C=25pF 时恰好有X L =X C ，则此时频率f 为下列哪项数值？(A) 15.92kHz (B) 16kHz(C) 24kHz (D) 36kHz解：选A 。

510/s rad ω===，510f 15.92kHz 22 3.14ωπ===×。

4. 在4R K =Ω，L=4H ，C=1µF 三个元件串连电路中，电路的暂态属于下列那种类型？ A.振荡 B.非振荡 C.临界振荡 D.不能确定5. 电阻为300Ω的信号源通过特性阻抗为300Ω传输线向75Ω的电阻性负载供电，为达到匹配目的，在传输线与负载间插入一段长度为λ/4的无损传输线，该线的特性阻抗应为（ ） A.187.5Ω B.150Ω C.600Ω D.75Ω【07年供配电第3题】电阻为300Ω的信号源通过特性阻抗为36Ω的传输线向25Ω的电阻性负载馈电，为达到匹配的目的，在传输线与负载间插入一段λ/4的无损耗传输线，该线的特性阻抗应为： （A ）30Ω （B ）150Ω（C ）20Ω （D ）70Ω 解：选A 。

2006年注电公共基础真题解析

2006年注电公共基础真题解析

2006年度全国勘察设计注册电气工程师（发输电）执业资格考试试卷公共基础考试住房和城乡建设部执业资格注册中心命制人力资源和社会保障部人事考试中心印制二○○六年九月一、单项选择题（共120题，每题1分。

每题的备选项中只有一个最符合题意。

）1.已知k aj i 3-+=α，k j ai 63+-=β，k j i 622++-=γ，若α，β，γ共面，则a 等于：（）。

（A）1或2（B）-1或2（C）-1或-2（D）1或-2答案：C。

解析：若α，β，γ共面，则下列行列式的值为零。

()()()01262361218661218612186226331222=++-=++-=---=--+---=---a a a a a a a a a a a 求解该方程得21--=或a 。

2.设平面π的方程为02543=---z y x ，以下选项中错误的是：（）。

（2006年真题）（A）平面π过点（-1,0，-1）（B）平面π的法向量为k j i 543++-（C）平面π在z 轴的截距是52-（D）平面π与平面0222=+---z y x 垂直答案：D 解析：选项（A），把点（-1,0，-1）代入方程02543=---z y x ，()()()025*******=-+-=--⨯-++⨯-，正确。

选项（B），我怎么感觉平面π的法向量应该为k j i 543--呀？选项（C），把0=x ，0=y 代入02543=---z y x ，得52-=z ，正确。

选项（D），()()()()()0810********≠=++-=-⨯-+-⨯-+-⨯，两平面不垂直，错误。

3.球面9222=++z y x 与平面1=+z x 的交线在xoy 坐标面上投影的方程是：（）。

（A）()91222=-++x y x （B）()⎩⎨⎧==-++091222z x y x （C）()91222=++-z y z （D）()⎩⎨⎧==++-091222x z y z 答案：B解析：联立9222=++z y x 和1=+z x ，消去z ，得投影柱面方程()91222=-++x y x ，再与0=z 联立，就得到投影曲线的方程。

2006年注电公共基础真题及解析

2006年注电公共基础真题及解析

2006年度全国勘察设计注册电气工程师（发输电）执业资格考试试卷公共基础考试住房和城乡建设部执业资格注册中心命制人力资源和社会保障部人事考试中心印制二○○六年九月一、单项选择题（共120题，每题1分。

每题的备选项中只有一个最符合题意。

）1. 已知k aj i 3-+=α，k j ai 63+-=β，k j i 622++-=γ，若α，β，γ共面，则a 等于：（ ）。

（A ）1或2 （B ）-1或2 （C ）-1或-2 （D ）1或-2 答案：C 。

解析：若α，β，γ共面，则下列行列式的值为零。

()()()01262361218661218612186226331222=++-=++-=---=--+---=---a a a a a a a a a a a 求解该方程得21--=或a 。

2. 设平面π的方程为02543=---z y x ，以下选项中错误的是：（ ）。

（2006年真题） （A ）平面π过点（-1,0，-1） （B ）平面π的法向量为k j i 543++- （C ）平面π在z 轴的截距是52-（D ）平面π与平面0222=+---z y x 垂直 解析：选项（A ），把点（-1,0，-1）代入方程02543=---z y x ，()()()025*******=-+-=--⨯-++⨯-，正确。

选项（B ），我怎么感觉平面π的法向量应该为k j i 543--呀？选项（C ），把0=x ，0=y 代入02543=---z y x ，得52-=z ，正确。

选项（D ），()()()()()0810********≠=++-=-⨯-+-⨯-+-⨯，两平面不垂直，错误。

3. 球面9222=++z y x 与平面1=+z x 的交线在xoy 坐标面上投影的方程是：（ ）。

（A ）()91222=-++x y x （B ）()⎩⎨⎧==-++091222z x y x（C ）()91222=++-z y z （D ）()⎩⎨⎧==++-091222x z y z 答案：B解析：联立9222=++z y x 和1=+z x ，消去z ，得投影柱面方程()91222=-++x y x ，再与0=z 联立，就得到投影曲线的方程。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

一、單項選擇題（共120題，每題1分。

每題的備選項中只有一個最符合題意。

）1. 已知k aj i 3-+=α，k j ai 63+-=β，k j i 622++-=γ，若α，β，γ共面，則a 等於：（ ）。

（A ）1或2 （B ）-1或2 （C ）-1或-2 （D ）1或-2 答案：C 。

解析：若α，β，γ共面，則下列行列式的值為零。

()()()01262361218661218612186226331222=++-=++-=---=--+---=---a a a a a a a a a a a 求解該方程得21--=或a 。

2. 設平面π的方程為02543=---z y x ，以下選項中錯誤的是：（ ）。

（2006年真題） （A ）平面π過點（-1,0，-1） （B ）平面π的法向量為k j i 543++- （C ）平面π在z 軸的截距是52-（D ）平面π與平面0222=+---z y x 垂直 答案：D 解析：選項（A ），把點（-1,0，-1）代入方程02543=---z y x ，()()()025*******=-+-=--⨯-++⨯-，正確。

選項（B ），我怎麼感覺平面π的法向量應該為k j i 543--呀？ 選項（C ），把0=x ，0=y 代入02543=---z y x ，得52-=z ，正確。

選項（D ），()()()()()0810********≠=++-=-⨯-+-⨯-+-⨯，兩平面不垂直，錯誤。

3. 球面9222=++z y x 與平面1=+z x 的交線在xoy 座標面上投影的方程是：（ ）。

（A ）()91222=-++x y x （B ）()⎩⎨⎧==-++091222z x y x（C ）()91222=++-z y z （D ）()⎩⎨⎧==++-091222x z y z 答案：B解析：聯立9222=++z y x 和1=+z x ，消去z ，得投影柱面方程()91222=-++x y x ，再與0=z 聯立，就得到投影曲線的方程。

4. ∞=⎪⎪⎭⎫⎝⎛+++-∞→213lim 22bx x ax x ，則a 與b 比值是：（ ）。

（A ）0≠b ，a 為任意實數 （B ）0≠a ，0=b （C ）1=a ，0=b （D ）0=a ，0=b 答案：A 解析過程：()()()∞=+-+++=+++++-=⎪⎪⎭⎫ ⎝⎛+++-∞→∞→∞→112lim 11213lim 213lim 223222222x bx x a bx x x x bx ax bx x ax x x x 。

只要0≠b ，極限均趨向於無窮大。

主要考點：極限的基本計算性質，當∞→x 時，只要分子的最高次冪大於分母的最高次冪，極限一定是無窮大。

5. 函數22x a x y -=在x 點的導數是：（ ）。

（A ）22222x a x a -- （B ）2221x a - （C ）222x a x -- （D ）22x a -答案：A解析：利用兩個函數乘積求導公式以及複合函數求導法則，有：222222222222222222/222xa x a xa x x a xa x x a xa x x x a y --=---=---=--+-=。

6. 已知函數2,x y x xy f =⎪⎪⎭⎫ ⎝⎛，則()()y y x f x y x f ∂∂+∂∂,,等於：（ ）。

（A ）y x 22+ （B ）y x + （C ）y x 22- （D ）y x -解析：令xy u =，yxv =，由這兩式可解得uv x =2，於是有()uv v u f =,，即()xy y x f =,， 所以()y x y x f =∂∂,，()x y y x f =∂∂,，()()y x yy x f x y x f +=∂∂+∂∂,,。

7. 設()x f 在()+∞∞-,上是奇函數，在()+∞∞-,上()0/<x f ，()0//>x f ，則在()0,∞-上必有：（ ）。

（A ）()0/>x f ，()0//>x f （B ）()0/<x f ，()0//<x f （C ）()0/<x f ，()0//>x f （D ）()0/>x f ，()0//<x f答案：B 解析過程：函數()x f 在()+∞∞-,上是奇函數，其圖形關於原點對稱，由於在()+∞,0內有()0/<x f ，()0//>x f ，()x f 單調減少，其圖形為凹的；故在()0,∞-內，()x f 應單調減少，且圖形為凸的，所以有()0/<x f ，()0//<x f 。

8. 曲面221y x z --=在點⎪⎭⎫⎝⎛21,21,21處的切平面方程是：（ ）。

（A ）023=-++z y x （B ）023=+--z y x （C ）023=-+-z y x （D ）023=++-z y x答案：A解析：切平面的法向量為x f x 2/=，y f y 2/=，1/=z f ，切平面方程的點法式方程為：0212121221212=⎪⎭⎫⎝⎛-+⎪⎭⎫ ⎝⎛-⨯+⎪⎭⎫ ⎝⎛-⨯z y x ， 計算得：0212121=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-z y x ，即：023=-++z y x 。

9. dx x x ⎰-23等於：（ ）。

（A ）c x +-231（B ）()c x +--232331（C ）c x +-23 （D ）()c x +-223答案：B解析：用第一類換元及冪函數積分公式，有：()()()c x c x x d x dx x x +--=+-⨯-=---=-⎰⎰232232222331332213321310. 若()02302=+⎰kx x ，()0≠k ，則k 等於：（ ）。

（A ）1 （B ）-1 （C ）23 （D ）21答案：B解析：由()()()012322302302=+⋅=+=+=+⎰k k k k x x x x k k，得()01≠-=k k 。

11. 設()()420-=⎰x f dt t f x，且()20=f ，則()x f 是（ ）。

（A ）2xe （B ）12+x e （C ）22x e （D ）221xe答案：C解析：對()()420-=⎰x f dt t f x兩邊關於x 求導，得：()()02/=-x f x f ，()()x f x f21/=，這是可分離變數微分方程，求解得()2xCe x f =，再由()20=f ，得2=C 。

12. 設()y x f ,是連續函數，則()dy y x f dx x⎰⎰01,等於：（ ）。

（A ）()dx y x f dy x ⎰⎰10, （B ）()dx y x f dy x⎰⎰010,（C ）()dx y x f dy ⎰⎰1010, （D ）()dx y x f dy y⎰⎰110,答案：A解析：積分區域D 如圖所示，將積分區域D 看成X-型區域，則1:≤≤x y D ，10≤≤y ， 故有()()dx y x f dy dy y x f dx yx⎰⎰⎰⎰=111,,。

13. 設L 為連接（0,0）點與（1,1）點的拋物線2x y =，則對弧長的曲線積分⎰Lxds 等於：（ ）。

（A ）()155121- （B ）1255 （C ）()15532- （D ）3510 答案：A解析：這是第一類曲線積分，使用曲線積分化定積分公式，有：()()()()155121151214132814141412141212312321221122-=⎪⎪⎭⎫ ⎝⎛-=+⨯=++⨯=+=+=⎰⎰⎰⎰x x d x dx x x dx x x xds L14. 已知级数()∑∞=+-1122n n n u u 是收敛的，则下列结论成立的是：（ ）。

（A ）∑∞=1n n u 必收敛 （B ）∑∞=1n n u 未必收敛 （C ）0lim =∞→n n u （D ）∑∞=1n n u 发散答案：B解析：可舉例加以說明，取級數∑∞=11n ，級數()∑∞=-111n 收斂，但級數∑∞=11n 發散，故選項（A ）和（C ）都不成立；再取級數∑∞=121n n ，()()()∑∑∞=∞=-+=⎥⎦⎤⎢⎣⎡--1221221241421121n n n n n n n 收斂，而∑∞=121n n 也收斂，故選項（D ）不成立。

15. 級數()∑∞=-01n n n x 在1<x 內收斂於函數：（ ）。

（A ）x -11 （B ）x +11 （C ）x x -1 （D ）xx+1 答案：B解析過程：由於() ++-+-=-∑∞=432011x x x x x n n n，可知這是公比為x -，首項為1的等比級數，當1<x 時級數收斂，且和為()xx +=--1111。

16. 微分方程()()011=--+dy x dx y 的通解是：（ ）。

（A ）c xy=-+11 （B ）()211x c y -=+ （C ）()()c y x =+-11 （D ）c xy=++11 （c 為任意常數） 答案：C解析：這是可分離變數微分方程，分離變數得：()()()()x d x y d y dx x dy y dy x dx y ---=++-=+=--+1111111111011 兩邊取積分，得：()()()()()()C y x C x y C x y =+-=-+++--=+111ln 1ln 1ln 1ln17. 微分方程21/=+y xy 滿足初始條件01==x y 的特解是：（ ）。