七年级数学上册 暑假班预习讲义 第十三讲 整式的加减复习(新版)新人教版

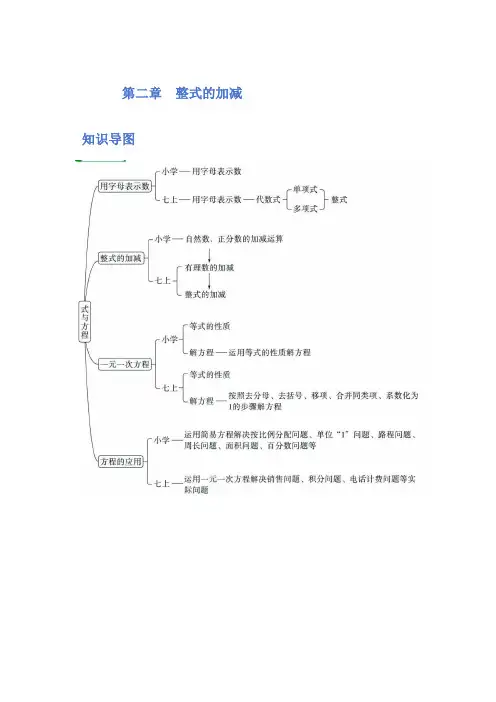
第二章整式的加减知识导图教材知识衔接小学七上1.用字母表示数: 用任意一个字母, 都可以表示我们学过的整数、小数、分数和百分数. 用学母表示数, 既可以把数量关系简明地表达出来, 同时也可以表示运算的结果.2.2. 用字母表示数的书写: 在含有字母的式子中, 字母中间的乘号可以写作“. ”, 也可以省略不写. 1. 代数式: 像m+1,2a+10,3v,st等式子,它们都是用运算符号把数字和字母连接而成的, 这样的式子叫做代数式. 单独一个数或一个字母也是代数式.2. 用字母表示数的书写: 在含有字母的式子中如果出现乘号, 通常将乘号写作“·”或省略不写,如100×t写成100⋅t或100t一. 用字母表示数的常见类型1. 单项式用字母表示数例如: 凡凡今年a岁了,林林比凡凡大 3 岁,则林林今年(a+3)岁了用字母表示数量关系如路程(s)、速度(v)、时间(t)三者之间的关系为: s=vt,v=st,t=sv用字母表示运算定律和运算性质加法交换律: a+b=b+a; 乘法分配律: (a+b)c=ac+bc 或(a−b)c=ac−bc; 减法的性质: a−b−c=a−(b+c)用字母表示计算公式三角形中底(a)、高(ℎ)、面积(S),则字母公式为: S=12aℎ; 长方形中长(a)、宽(b)、周始(C)、面积(S),则字母公式为⋮(C) =2(a+b),S=ab初高2. 单项式定义多项式几个单项式的和叫做多项式多项式的项多项式里,每个单项式叫做多项式的项,不含字母的项叫做常数项多项式 的次数 多项式里,次数最高项的次数,叫做这个多项式的次数点拨: 知识点一样, 都是用字母表示数, 只是七上更深入地学习了用字母表示的式子, 也就是代数式, 并引入了单项式和多项式、整式的概念, 进一步理解用字母表示数的意义.〖经典例题〗例1. 下列各式中，哪些是单项式？哪些是多项式？哪些都不是? （1）7-3 （2）n m + （3）x （4）11（5）m +21 （6）52=x （7）x >3 （8）ba例2. 下列各式中符合代数式书写规则的是（ ）A. m ab ÷5B.ab 211C.5⋅aD.)(34y x -例3. 根据下列语句列代数式。

《整式的加减》全章复习与巩固（基础）知识讲解【学习目标】1．理解并掌握单项式与多项式的相关概念；2．理解整式加减的基础是去括号和合并同类项，并会用整式的加减运算法则，熟练进行整式的加减运算、求值；3．深刻体会本章体现的主要的数学思想----整体思想．【知识网络】【要点梳理】要点一、整式的相关概念1．单项式：由数或字母的积组成的代数式叫做单项式，单独的一个数或一个字母也是单项式．要点诠释：（1）单项式的系数是指单项式中的数字因数．（2）单项式的次数是指单项式中所有字母的指数和．2．多项式：几个单项式的和叫做多项式．在多项式中，每个单项式叫做多项式的项．要点诠释：（1）在多项式中，不含字母的项叫做常数项．（2）多项式中次数最高的项的次数，就是这个多项式的次数．（3）多项式的次数是n次，有m个单项式，我们就把这个多项式称为n次m项式．3. 多项式的降幂与升幂排列：把一个多项式按某一个字母的指数从大到小的顺序排列起来，叫做把这个多项式按这个字母降幂排列．另外，把一个多项式按某一个字母的指数从小到大的顺序排列起来，叫做把这个多项式按这个字母升幂排列．要点诠释：（1）利用加法交换律重新排列时，各项应连同它的符号一起移动位置；（2）含有多个字母时，只按给定的字母进行降幂或升幂排列．4．整式：单项式和多项式统称为整式．要点二、整式的加减1．同类项：所含字母相同，并且相同字母的指数也相同的项叫做同类项．所有的常数项都是同类项．要点诠释：辨别同类项要把准“两相同，两无关”：（1）“两相同”是指：①所含字母相同；②相同字母的指数相同；（2）“两无关”是指：①与系数无关；②与字母的排列顺序无关．2．合并同类项：把多项式中的同类项合并成一项，叫做合并同类项．要点诠释：合并同类项时，只是系数相加减，所得结果作为系数，字母及字母的指数保持不变．3．去括号法则：括号前面是“+”，把括号和它前面的“+”去掉后，原括号里各项的符号都不改变；括号前面是“-”，把括号和它前面的“-”号去掉后，原括号里各项的符号都要改变．4．添括号法则：添括号后，括号前面是“+”，括号内各项的符号都不改变；添括号后，括号前面是“-”，括号内各项的符号都要改变．5．整式的加减运算法则：几个整式相加减，通常用括号把每一个整式括起来，再用加、减号连接，然后去括号，合并同类项． 【典型例题】类型一、整式的相关概念1．指出下列各式中的整式、单项式和多项式，是单项式的请指出系数和次数，是多项式的请说出是几次几项式． (1)3a - (2)5 (3)2b a - (4)2x y - (5)3xy (6)xπ(7)5m n + (8)1+a% (9)1()2a b h + 【答案与解析】解：整式：(1)、(2)、(4)、(5)、(6)、(7)、(8)、(9)单项式：(2)、(5)、(6)，其中：5的系数是5，次数是0；3xy 的系数是3，次数是2；x π的系数是1π，次数是1.多项式：(1)、(4)、(7)、(8)、(9)，其中：3a -是一次二项式；2x y -是一次二项式；5m n+是一次二项式；1+a%是一次二项式； 1()2a b h +是二次二项式。

第十三讲：整式的加减单元达标卷姓名：_________日期：_________一、选择题：〔每题3分，共30分〕1、 在代数式3,5,,1,32,5,212z y x y xyz y x a y x -+-+--π中有〔 〕 A. 5个整式B. 4个单项式，3个多项式C. 6个整式，4个单项式D. 6个整式，单项式与多项式个数相同 2、 以下说法正确的选项是〔 〕A. 2xy -是单项式B. ab 没有系数C. 81-是一次一项式 D. 3不是单项式 3、 以下各组式子是同类项的是〔 〕A.y x 23与23xyB.abc 51与ac 51C.xy 2-与ab 3-D.xy 与xy -4、 以下计算正确的选项是〔 〕A.xy y x 532=+B.b a b a ba 2222-=+-C.532222a a a =+D.13422=-a a5、 减去x 3-得432+-x x 的式子为〔 〕A.43+xB.432++x xC.462+-x xD. x x 62- 6、 如果单项式22+m y x 与y x n 的和仍然是一个单项式，那么m 、n 的值是〔 〕A.2,2==n mB.2,1=-=n mC. 2,2=-=n mD. 1,2-==n m 7、 以下各题去括号所得结果正确的选项是〔 〕A.z y x x z y x x 2)2(22++-=+--B.132)132(+-+=-+--y x x y x xC.153)]1(5[3+--=---x x x x x xD.21)2()1(22---=---x x x x 8、 与多项式3223423a b a ab b -+-相等的是〔 〕A.)42(33223a b a ab b +--B. )42(33223a b a ab b ++-C. )42(33223a b a ab b -+--D. )42(33223a b a ab b -+-9、 假设A 是一个七次多项式，B 也是一个七次多项式，那么A+B 一定是〔 〕A.十四次多项式B.七次多项式C.不高于七次多项式或单项式D.六次多项式10、当x 分别取2和﹣2时，多项式5235-+x x 的值〔 〕A.互为相反数B.互为倒数C.异号不等D.相等 二、填空题：〔每题3分，共18分〕11、多项式：x x 3122+-是_________次_________项式。

《整式的加减》全章复习与巩固（提高）知识讲解【学习目标】1．理解并掌握单项式与多项式的相关概念；2．理解整式加减的基础是去括号和合并同类项，并会用整式的加减运算法则，熟练进行整式的加减运算、求值；3．深刻体会本章体现的主要的数学思想----整体思想．【知识网络】【要点梳理】要点一、整式的相关概念1．单项式：由数或字母的积组成的代数式叫做单项式，单独的一个数或一个字母也是单项式．要点诠释：（1）单项式的系数是指单项式中的数字因数．（2）单项式的次数是指单项式中所有字母的指数和．2．多项式：几个单项式的和叫做多项式．在多项式中，每个单项式叫做多项式的项．要点诠释：（1）在多项式中，不含字母的项叫做常数项．（2）多项式中次数最高的项的次数，就是这个多项式的次数．（3）多项式的次数是n次，有m个单项式，我们就把这个多项式称为n次m项式．3. 多项式的降幂与升幂排列：把一个多项式按某一个字母的指数从大到小的顺序排列起来，叫做把这个多项式按这个字母降幂排列．另外，把一个多项式按某一个字母的指数从小到大的顺序排列起来，叫做把这个多项式按这个字母升幂排列．要点诠释：（1）利用加法交换律重新排列时，各项应连同它的符号一起移动位置；（2）含有多个字母时，只按给定的字母进行降幂或升幂排列．4．整式：单项式和多项式统称为整式．要点二、整式的加减1．同类项：所含字母相同，并且相同字母的指数也相同的项叫做同类项．所有的常数项都是同类项．要点诠释：辨别同类项要把准“两相同，两无关”：（1）“两相同”是指：①所含字母相同；②相同字母的指数相同；（2）“两无关”是指：①与系数无关；②与字母的排列顺序无关．2．合并同类项：把多项式中的同类项合并成一项，叫做合并同类项．要点诠释：合并同类项时，只是系数相加减，所得结果作为系数，字母及字母的指数保持不变．3．去括号法则：括号前面是“+”，把括号和它前面的“+”去掉后，原括号里各项的符号都不改变；括号前面是“-”，把括号和它前面的“-”号去掉后，原括号里各项的符号都要改变．4．添括号法则：添括号后，括号前面是“+”，括号内各项的符号都不改变；添括号后，括号前面是“-”，括号内各项的符号都要改变．5．整式的加减运算法则：几个整式相加减，通常用括号把每一个整式括起来，再用加、减号连接，然后去括号，合并同类项．【典型例题】类型一、整式的相关概念1．（2016春•新泰市期中）下列说法正确的是（ ）A ．1﹣xy 是单项式B ．ab 没有系数C ．﹣5是一次一项式D ．﹣a 2b+ab ﹣abc 2是四次三项式【思路点拨】根据多项式是几个单项式的和，数字因数是单项式的系数，字母指数和是单项式的次数，多项式中次数最高的单项式的次数是多项式的次数，每个单项式是多项式的项，可得答案．【答案】D ．【解析】解：A 、1﹣xy 是多项式，故A 错误；B 、ab 的系数是1，故B 错误；C 、﹣5是单项式，故C 错误；D 、﹣a 2b+ab ﹣abc 2是四次三项式，故D 正确；故选：D ．【总结升华】本题考查了单项式，单项式的系数，多项式，多项式的次数等基本概念，关键是对这些基本概念一定要熟悉．举一反三：【变式1】（2014•佛山）多项式2a 2b ﹣ab 2﹣ab 的项数及次数分别是（ ）A ．3，3B ．3，2C ．2，3D ．2，2【答案】A2a 2b ﹣ab 2﹣ab 是三次三项式，故次数是3，项数是3．【变式2】若多项式31(4)5(2)n m x x x n m -++---+是关于x 的二次三项式，则________m =，________n =，这个二次三项式为 .【答案】4,3,-259x x -- 类型二、同类项及合并同类项2．若315212135m n m n x y x y --+-与是同类项，求出m, n 的值，并把这两个单项式相加. 【答案与解析】 解：因为312121535m n m n x y x y --+-与是同类项，所以315,21 1.m n -=⎧⎨-=⎩ 解得2,1.m n =⎧⎨=⎩当2m =且1n =时，55553152121424214()()35353515m n m n x y x y x y x y x y x y --++-=-=-=. 【总结升华】同类项的定义中强调，除所含字母相同外，相同字母．．．．的指数也要相同.其中，常数项也是同类项.合并同类项时，若不是同类项，则不需合并.举一反三：【变式】合并同类项．(1)2222344522x xy y x xy y -+-+-； (2)3232399111552424xy x y xy x y xy x y --+---． 【答案】(1)原式＝22(35)(42)(42)x xy y -+-++- 22222x xy y =--+(2)原式3232391191554422xy x y x y x y ⎛⎫⎛⎫=--+-+-- ⎪ ⎪⎝⎭⎝⎭32345x y x y =---．类型三、去（添）括号3．化简2211()22x x x x ⎡⎤--+⎢⎥⎣⎦． 【答案与解析】 解：原式＝2211()24x x x x -++22111244x x x x =-++25144x x =-． 【总结升华】根据多重括号的去括号法则，可由里向外，也可由外向里逐层推进，在计算过程中要注意符号的变化．若括号前是“-”号，在去括号时，括号里各项都应变号，若括号前有数字因数，应把数字因数乘到括号里，再去括号．举一反三：【变式1】下列去括号正确的是( )．A ．2222(2)2a a b b a a b b --+=--+B ．2222(2)()2x y x y x y x y -+--+=-++-C ．2223(5)235x x x x --=-+D ．3232[4(13)]431a a a a a a ---+-=-++-【答案】D【变式2】先化简代数式22211(351)5333a a a a a ⎧⎫⎡⎤---+--⎨⎬⎢⎥⎣⎦⎩⎭，然后选取一个使原式有意义的a 的值代入求值． 【答案】22211(351)5333a a a a a ⎧⎫⎡⎤---+--⎨⎬⎢⎥⎣⎦⎩⎭22211[(3515)]333a a a a a =---+-- 222116[(34)]333a a a a =----222116(34)333a a a a =--++ 22816(4)333a a a =--++228164333a a a =+--2814433a a =--． 当0a =时，原式＝0-0-4＝-4．【变式3】(1) (x ＋y )2－10x －10y ＋25＝(x ＋y )2－10(______)＋25;(2) (a －b ＋c －d )(a ＋b －c －d )＝[(a －d )＋(______)][(a －d )－(______)]．【答案】（1）x ＋y ; （2）－b ＋c ，－b ＋c 类型四、整式的加减4. （2015春•无锡校级期中）已知x=2015，求代数式（2x+3）（3x+2）﹣6x （x+3）+5x+16的值”时，马小虎把“2015”看成了“2051”，但是他的运算结果却是正确的，这是为什么？请你说明原因．【答案与解析】解：原式=6x 2+4x+9x+6﹣6x 2﹣18x+16=22，结果不含x ，故原式化简后与x 的取值无关，则马小虎把“2015”看成了“2051”，但是他的运算结果却是正确的【总结升华】原式利用多项式乘以多项式，以及单项式乘以多项式法则计算，去括号合并得到最简结果，根据结果不含x ，即可得证．此题考查了整式的加减﹣化简求值，熟练掌握运算法则是解本题的关键．举一反三：【变式】已知A ＝x 2＋2y 2－z 2，B ＝－4x 2＋3y 2＋2z 2，且A ＋B ＋C ＝0，则多项式C 为( )．A ．5x 2－y 2－z 2B ．3x 2－5y 2－z 2C ．3x 2－y 2－3z 2D ．3x 2－5y 2＋z 2【答案】B 类型五、化简求值5.（2016春•盐城校级月考）先化简，再求值：3x 2y ﹣[2x 2﹣（xy 2﹣3x 2y ）﹣4xy 2]，其中|x|=2，y=，且xy ＜0．【思路点拨】原式去括号合并得到最简结果，利用绝对值的代数意义求出x 的值，代入原式计算即可得到结果．【答案与解析】解：原式=3x 2y ﹣2x 2+xy 2﹣3x 2y+4xy 2=5xy 2﹣2x 2，∵|x|=2，y=，且xy ＜0，∴x=﹣2，y=，则原式=﹣﹣8=﹣．【总结升华】化简求值题一般采用“一化二代三计算”，此类题最后结果的书写格式一般为：当x=…时，原式=….举一反三： 【变式】已知26a b a b -=+，求代数式2(2)3()2a b a b a b a b -+++-的值． 【答案】 设2a b p a b-=+，则12a b a b p +=-，原式32p p =+． 又因为p ＝6，所以原式31261262=⨯+=． 类型六、综合应用6. 对于任意有理数x ，比较多项式2452x x -+与2352x x --的值的大小．【答案与解析】解：22222(452)(352)4523524x x x x x x x x x -+---=-+-++=+∵240x +>∴无论x 为何值，2452x x -+＞2352x x --．【总结升华】本题考查整式的加减，解决此类题目的关键是熟记去括号法则，熟练运用合并同类项的法则，这是各地中考的常考点．举一反三：【高清课堂：整式的加减单元复习388396 经典例题5】【变式】设22232A x xy y x y =-+-+, 224623B x xy y x y =-++-. 若22(3)0x a y -++=且2B A a -=，求a .【答案】∵ 22(3)0x a y -++=，20x a -≥， 2(3)0y +≥ ∴ 20,30.x a y -=⎧⎨+=⎩即 2,3.x a y =⎧⎨=-⎩ ∴ 222(2)3(2)(3)(3)22(3)A a a a =--+--+-228189268163a a a a a =++--=++224(2)6(2)(3)2(3)32(3)B a a a =--+⨯-+-- 2216361863164221a a a a a =++++=++ ∵ 2164221,2216326,B a a A a a ⎧=++⎪⎨⎪-=---⎩ 且2B A a -=， ∴21015B A a -=+∴1015a a +=915a =-, 53a =-.。

《整式的加减》全章复习与巩固（基础）知识讲解【知识网络】【要点梳理】要点一、整式的相关概念1．单项式：由数或字母的积组成的代数式叫做单项式，单独的一个数或一个字母也是单项式．要点诠释：（1）单项式的系数是指单项式中的数字因数．（2）单项式的次数是指单项式中所有字母的指数和．2．多项式：几个单项式的和叫做多项式．在多项式中，每个单项式叫做多项式的项．要点诠释：（1）在多项式中，不含字母的项叫做常数项．（2）多项式中次数最高的项的次数，就是这个多项式的次数．（3）多项式的次数是n次，有m个单项式，我们就把这个多项式称为n次m项式．3. 多项式的降幂与升幂排列：把一个多项式按某一个字母的指数从大到小的顺序排列起来，叫做把这个多项式按这个字母降幂排列．另外，把一个多项式按某一个字母的指数从小到大的顺序排列起来，叫做把这个多项式按这个字母升幂排列．要点诠释：（1）利用加法交换律重新排列时，各项应连同它的符号一起移动位置；（2）含有多个字母时，只按给定的字母进行降幂或升幂排列．4．整式：单项式和多项式统称为整式．要点二、整式的加减1．同类项：所含字母相同，并且相同字母的指数也相同的项叫做同类项．所有的常数项都是同类项．要点诠释：辨别同类项要把准“两相同，两无关”：（1）“两相同”是指：①所含字母相同；②相同字母的指数相同；（2）“两无关”是指：①与系数无关；②与字母的排列顺序无关．2．合并同类项：把多项式中的同类项合并成一项，叫做合并同类项．要点诠释：合并同类项时，只是系数相加减，所得结果作为系数，字母及字母的指数保持不变．3．去括号法则：括号前面是“+”，把括号和它前面的“+”去掉后，原括号里各项的符号都不改变；括号前面是“-”，把括号和它前面的“-”号去掉后，原括号里各项的符号都要改变．4．添括号法则：添括号后，括号前面是“+”，括号内各项的符号都不改变；添括号后，括号前面是“-”，括号内各项的符号都要改变．5．整式的加减运算法则：几个整式相加减，通常用括号把每一个整式括起来，再用加、减号连接，然后去括号，合并同类项．【典型例题】类型一、整式的相关概念1．指出下列各式中的整式、单项式和多项式，是单项式的请指出系数和次数，是多项式的请说出是几次几项式．(1)3a - (2)5 (3)2b a - (4)2x y - (5)3xy (6)x π(7)5m n + (8)1+a% (9)1()2a b h +举一反三：【变式1】(1)3xy -的次数与系数的和是________；(2)已知单项式26x y 的系数是等于单项式52m x y -的次数，则m ＝________；(3)若nma b 是关于a 、b 的一个五次单项式，且系数为9，则-m+n ＝________．【变式2】多项式432231y y y y -+-+是________次________项式，常数项是________，三次项是________．【变式3】把多项式321325x x x --+按x 的降幂排列是________．类型二、同类项及合并同类项2．（2015•遵义）如果单项式﹣xy b+1与x a ﹣2y 3是同类项，那么（a ﹣b ）2015= ．举一反三：【变式】若47a x y 与579b x y -是同类项，则a ＝________，b ＝________．类型三、去（添）括号3． 计算 22232(12)[5(436)]x x x x x -----+举一反三：【变式1】下列式子中去括号错误的是( )．A ．5x －(x －2y ＋5z )＝5x －x ＋2y －5zB ．2a 2＋(－3a －b )－(3c －2d )＝2a 2－3a －b －3c ＋2dC ．3x 2－3(x ＋6)＝3x 2－3x －6D ．－(x －2y )－(－x 2＋y 2)＝－x ＋2y ＋x 2－y 2【变式2】化简：-2a+(2a -1)的结果是( )．A ．-4a -1B ．4a -1C ．1D ．-1类型四、整式的加减4. 求比多项式22523a a ab b --+少25a ab -的多项式．举一反三：【变式】计算：11(812)3(22)32a a b c c b ---+-+类型五、化简求值5. （1）直接化简代入已知12x =，1y =-，求225(23)2(43)x y x x x y ---的值．（2）条件求值(烟台)若523m x y +与3n x y 的和是单项式，则n m =________．（3）整体代入已知x 2-2y ＝1，那么2x 2-4y+3＝________．举一反三：【变式1】（2015•娄底）已知a 2+2a=1，则代数式2a 2+4a ﹣1的值为（）A ．0B ．1C ．﹣1D ．﹣2【变式2】已知25m n -+=，求25(2)6360m n n m -+--的值.类型六、综合应用6. 已知多项式 是否存在m ，使此多项式与x 无关？若不存在，说明理由；若存在，求出m 的值.【巩固练习】一、选择题1．已知a 与b 互为相反数，且x 与y 互为倒数，那么|a+b|-2xy 的值为( )．A ．2B ．-2C ．-1D ．无法确定2．（2015•厦门）已知一个单项式的系数是2，次数是3，则这个单项式可以是（ ）A ．﹣2xy 2B ． 3x 2C ． 2xy 3D ． 2x 33．有下列式子：12x yz +，2b ，2323x x --，abc ，0，y x ，x ，a b ab+，对于这些式子下列结论正确的是( )．A ．有4个单项式，2个多项式B ．有5个单项式，3个多项式C ．有7个整式D ．有3个单项式，2个多项式4．对于式子421.210x y -⨯，下列说法正确的是( )．A ．不是单项式B ．是单项式，系数为-1.2×10，次数是7C ．是单项式，系数为-1.2×104，次数是3D ．是单项式，系数为-1.2，次数是35．下面计算正确的是（ ）．A ．32x －2x =3B ．32a ＋23a =55aC ．3＋x =3xD ．－0.25ab ＋41ba =0()()22222mx -x +3x +1-5x -4y +3x6．2a -(5b -c+3d -e )＝2a □5b □c □3d □e ，方格内所填的符号依次是( )．A ．+，-，+，-B ．-，-，+，-C ．-，+，-，+D ．-，+，-，-7．某工厂现有工人a 人，若现有工人数比两年前减少了35%，则该工厂两年前工人数为( )．A ．135%a +B ．(1+35%)aC ．135%a - D ．(1-35%)a 8．若2237y y ++的值为8，则2469y y +-的值是( )．A ．2B ．-17C ．-7D ．7二、填空题9．比x 的15％大2的数是________．10．（2015•岳阳）单项式﹣x 2y 3的次数是 ．11．22372x y x -++是________次________项式，最高次项的系数是________． 12．化简：2a -(2a -1)＝________．13．如果24a ab +=，21ab b +=-，那么22a b -=________．14．一个多项式减去3x 等于2535x x --，则这个多项式为________．15．若单项式22m n x y +-与单项式323m y x 的和是单项式，那么3m n -= ．16．如图所示，外圆半径是R 厘米，内圆半径是r 厘米，四个小圆的半径都是2厘米，则图中阴影部分的面积是________平方厘米．三、解答题17．（2014秋•镇江校级期末）合并同类项①3a ﹣2b ﹣5a+2b ②（2m+3n ﹣5）﹣（2m ﹣n ﹣5）③2（x 2y+3xy 2）﹣3（2xy 2﹣4x 2y ）18.已知：2263A x x =+-，213B x x =--，2451C x x =--，当32x =-时，求代数式32A B C -+的值.。

《整式的加减》全章复习与巩固（提高）知识讲解责编：胡老师【学习目标】1．理解并掌握单项式与多项式的相关概念；2．理解整式加减的基础是去括号和合并同类项，并会用整式的加减运算法则，熟练进行整式的加减运算、求值；3．深刻体会本章体现的主要的数学思想----整体思想．【知识网络】【要点梳理】要点一、整式的相关概念1．单项式：由数或字母的积组成的代数式叫做单项式，单独的一个数或一个字母也是单项式．要点诠释：（1）单项式的系数是指单项式中的数字因数．（2）单项式的次数是指单项式中所有字母的指数和．2．多项式：几个单项式的和叫做多项式．在多项式中，每个单项式叫做多项式的项．要点诠释：（1）在多项式中，不含字母的项叫做常数项．（2）多项式中次数最高的项的次数，就是这个多项式的次数．（3）多项式的次数是n次，有m个单项式，我们就把这个多项式称为n次m项式．3. 多项式的降幂与升幂排列：把一个多项式按某一个字母的指数从大到小的顺序排列起来，叫做把这个多项式按这个字母降幂排列．另外，把一个多项式按某一个字母的指数从小到大的顺序排列起来，叫做把这个多项式按这个字母升幂排列．要点诠释：（1）利用加法交换律重新排列时，各项应连同它的符号一起移动位置；（2）含有多个字母时，只按给定的字母进行降幂或升幂排列．4．整式：单项式和多项式统称为整式．要点二、整式的加减1．同类项：所含字母相同，并且相同字母的指数也相同的项叫做同类项．所有的常数项都是同类项．要点诠释：辨别同类项要把准“两相同，两无关”：（1）“两相同”是指：①所含字母相同；②相同字母的指数相同；（2）“两无关”是指：①与系数无关；②与字母的排列顺序无关．2．合并同类项：把多项式中的同类项合并成一项，叫做合并同类项．要点诠释：合并同类项时，只是系数相加减，所得结果作为系数，字母及字母的指数保持不变．3．去括号法则：括号前面是“+”，把括号和它前面的“+”去掉后，原括号里各项的符号都不改变；括号前面是“-”，把括号和它前面的“-”号去掉后，原括号里各项的符号都要改变．4．添括号法则：添括号后，括号前面是“+”，括号内各项的符号都不改变；添括号后，括号前面是“-”，括号内各项的符号都要改变．5．整式的加减运算法则：几个整式相加减，通常用括号把每一个整式括起来，再用加、减号连接，然后去括号，合并同类项． 【典型例题】类型一、整式的相关概念1．指出下列各式中的整式、单项式和多项式，是单项式的请指出系数和次数，是多项式的请说出是几次几项式． (1)3a - (2)5 (3)2b a - (4)2x y - (5)3xy (6)x π(7)5m n + (8)1+a%(9)1()2a b h + 【答案与解析】解：整式：(1)、(2)、(4)、(5)、(6)、(7)、(8)、(9)单项式：(2)、(5)、(6)，其中：5的系数是5，次数是0；3xy 的系数是3，次数是2；xπ的系数是1π，次数是1.多项式：(1)、(4)、(7)、(8)、(9)，其中：3a -是一次二项式；2x y -是一次二项式；5m n +是一次二项式；1+a%是一次二项式； 1()2a b h +是二次二项式。

七年级上册人教版数学整式的加减
七年级上册人教版数学中，整式的加减是一个重要的知识点。

整式是由常数、变量、加、减、乘等运算符号组成的代数式。

整式的加减主要涉及到合并同类项和去括号等运算。

合并同类项是指将整式中的同类项（即变量部分相同的项）合并成一个项，其系数是这些同类项系数的和或差。

例如，对于整式3x + 2x，我们可以将其合并为5x。

去括号则是整式加减中的另一个重要运算。

在整式中去括号时，需要注意括号前的符号。

如果括号前是正号，去括号后各项的符号不变；如果括号前是负号，去括号后各项的符号都要改变。

例如，对于整式2(x + y)，去括号后得到2x + 2y；而对于整式-3(x - y)，去括号后得到-3x + 3y。

在进行整式的加减运算时，还需要注意运算的顺序。

通常，我们按照先乘除后加减的顺序进行运算，并且要注意括号内的运算优先进行。

以下是一个整式加减的例子：
给定整式A = 3x^2 + 2xy - 5y^2 和B = -2x^2 + xy + 4y^2，求A + B。

解：
A +
B = (3x^2 + 2xy - 5y^2) + (-2x^2 + xy + 4y^2)
= 3x^2 - 2x^2 + 2xy + xy - 5y^2 + 4y^2
= x^2 + 3xy - y^2
通过合并同类项，我们得到了整式A + B 的结果。

整式的加减运算在实际问题中有广泛的应用，例如在物理、化学等领域中，我们经常需要用到整式来表示各种量之间的关系，并通过整式的加减运算来求解问题。

因此，掌握整式的加减运算是非常重要的。

七年级数学上册暑假班预习讲义第十三讲整式的加减复习（无答案）（新版）新人教版编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（七年级数学上册暑假班预习讲义第十三讲整式的加减复习（无答案）（新版）新人教版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为七年级数学上册暑假班预习讲义第十三讲整式的加减复习（无答案）（新版）新人教版的全部内容。

第十三讲:整式的加减复习姓名:_________日期：_________1．若a－b＝2，b－c＝－3，则a－c等于( ）A．1 B．－1 C．5 D．－53．计算：（1) 2（x－y）＋3y＝____；（2)(3a2＋b2－5ab)＋(4ab－b2＋7a2)＝____________________；（3）－（m－2n）－(－m＋n)＝____；(4)（7a2－7ab－6）＋(2－4a2)＝____．4．已知长方形的周长为4a＋2b，其一边长为a－b，则另一边长为________．5．计算：（1）(－6x2＋5xy）－12xy－(2x2－9xy）；（2）3a－［－2b＋(4a－3b)]．6．先化简，再求值：（x2－2x3＋1）－（－1＋2x3＋2x2)，其中x＝2。

类型之一字母表示数1．某企业今年3月份产值为a万元，4月份比3月份减少了10%，5月份比4月份增加了15％，则5月份的产值是( )A．（a－10％）(a＋15％）万元B．(1－90%)(1＋85％)a万元C．（1－10％）（1＋15％）a万元D．(1－10%＋15％）a万元2．今年“五一”假期，张老师一家四口开着一辆轿车去长春市净月潭森林公园度假．若门票每人a元，进入园区的轿车每辆收费20元,则张老师一家开轿车进净月潭森林公园园区所需的费用是___元(用含a的代数式表示)．3．体育委员带了500元钱去买体育用品，已知一个足球a元，一个篮球b元,则代数式500－3a－2b表示的意义为_________________________________．4．定义新运算“⊗",规定:a⊗b＝错误!a－4b,则12⊗(－1）＝____．类型之二整式的概念5．在式子ab5c，－4x,－错误!abc，π，错误!，x＋错误!，0,－错误!，a2－b2中,单项式与多项式各有（)A．5个，1个 B．5个,2个 C．4个，1个 D．4个,2个6．下列说法中，正确的是( )A．－错误!x2yz的系数是错误! B．错误!ab2c的次数是2C．－5x2与0。

第十三讲：整式的加减单元达标卷姓名：_________日期：_________一、选择题：（每题3分，共30分）1、 在代数式3,5,,1,32,5,212z y x y xyz y x a y x -+-+--π中有（ ） A. 5个整式B. 4个单项式，3个多项式C. 6个整式，4个单项式D. 6个整式，单项式与多项式个数相同 2、 下列说法正确的是（ ）A. 2xy -是单项式B. ab 没有系数C. 81-是一次一项式 D. 3不是单项式 3、 下列各组式子是同类项的是（ ） A.y x 23与23xy B.abc 51与ac 51C.xy 2-与ab 3-D.xy 与xy -4、 下列计算正确的是（ ）A.xy y x 532=+B.b a b a ba 2222-=+-C.532222a a a =+D.13422=-a a5、 减去x 3-得432+-x x 的式子为（ ）A.43+xB.432++x xC.462+-x xD. x x 62- 6、 如果单项式22+m y x 与y x n 的和仍然是一个单项式，则m 、n 的值是（ ）A.2,2==n mB.2,1=-=n mC. 2,2=-=n mD. 1,2-==n m 7、 下列各题去括号所得结果正确的是（ ）A.z y x x z y x x 2)2(22++-=+--B.132)132(+-+=-+--y x x y x xC.153)]1(5[3+--=---x x x x x xD.21)2()1(22---=---x x x x 8、 与多项式3223423a b a ab b -+-相等的是（ ）A.)42(33223a b a ab b +--B. )42(33223a b a ab b ++-C. )42(33223a b a ab b -+--D. )42(33223a b a ab b -+-9、 若A 是一个七次多项式，B 也是一个七次多项式，则A+B 一定是（ ）A.十四次多项式B.七次多项式C.不高于七次多项式或单项式D.六次多项式10、当x 分别取2和﹣2时，多项式5235-+x x 的值（ ）A.互为相反数B.互为倒数C.异号不等D.相等 二、填空题：（每题3分，共18分）11、多项式：x x 3122+-是_________次_________项式。