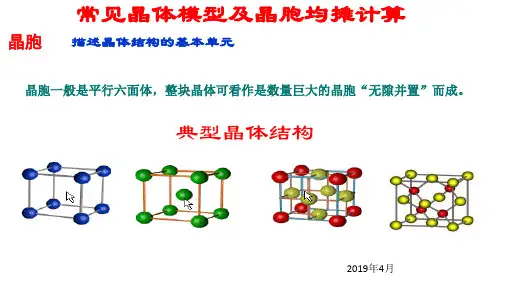
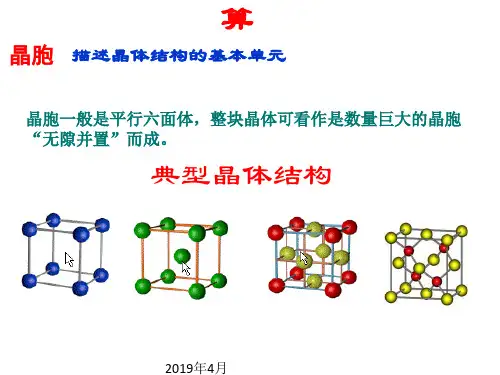
《晶胞计算专题》

1.回答下列问题(1)金属铜晶胞为面心立方最密堆积, 边长为acm。

又知铜的密度为ρ g·cm－3, 阿伏加德罗常数为_______。

(2)下图是CaF2晶体的晶胞示意图, 回答下列问题：①Ca2＋的配位数是______, F－的配位数是_______。

②该晶胞中含有的Ca2＋数目是____, F－数目是_____, ③CaF2晶体的密度为ag·cm－3, 则晶胞的体积是_______(只要求列出算式)。

2.某些金属晶体(Cu、Ag、Au)的原子按面心立方的形式紧密堆积, 即在晶体结构中可以划出一块正立方体的结构单元, 金属原子处于正立方体的八个顶点和六个侧面上, 试计算这类金属晶体中原子的空间利用率。

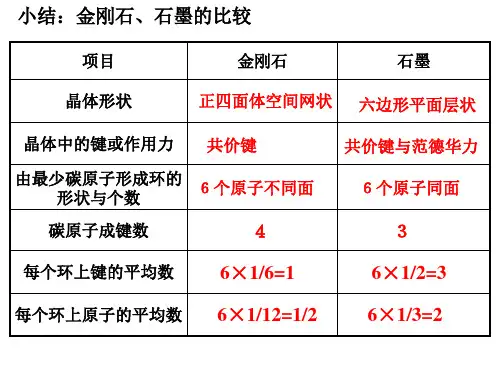
（2）（3）3、单晶硅的晶体结构与金刚石一种晶体结构相似, 都属立方晶系晶胞, 如图：（1）将键联的原子看成是紧靠着的球体, 试计算晶体硅的空间利用率（计算结果保留三位有效数字, 下同）。

（2）已知Si—Si键的键长为234 pm, 试计算单晶硅的密度是多少g/cm3。

4、金晶体的最小重复单元(也称晶胞)是面心立方体, 如图所示, 即在立方体的8个顶点各有一个金原子, 各个面的中心有一个金原子, 每个金原子被相邻的晶胞所共有。

金原子的直径为d, 用NA表示阿伏加德罗常数, M表示金的摩尔质量。

请回答下列问题：(1)金属晶体每个晶胞中含有________个金原子。

(2)欲计算一个晶胞的体积, 除假定金原子是刚性小球外, 还应假定_______________。

(3)一个晶胞的体积是____________。

(4)金晶体的密度是____________。

5.1986年, 在瑞士苏黎世工作的两位科学家发现一种性能良好的金属氧化物超导体, 使超导工作取得突破性进展, 为此两位科学家获得了1987年的诺贝尔物理学奖, 实验测定表明, 其晶胞结构如图所示。

（4）（5）（6）（1）根据所示晶胞结构, 推算晶体中Y、Cu、Ba和O的原子个数比, 确定其化学式。

高中化学晶胞的相关计算专项训练知识归纳总结含答案一、晶胞的相关计算1．2Mg Si 具有反萤石结构，晶胞结构如图所示，其晶胞参数为0.635nm 。

下列叙述错误的是（ ）A ．Si 的配位数为8B ．紧邻的两个Mg 原子的距离为0.6352nm C ．紧邻的两个Si 原子间的距离为20.635⨯nm D ．2Mg Si 的密度计算式为()337A 76g cm 0.63510N --⋅⨯2．2020年，自修复材料、自适应材料、新型传感材料等智能材料技术将大量涌现，为生物医疗、国防军事以及航空航天等领域发展提供支撑。

（1）我国科研工作者基于丁二酮肟氨酯基团的多重反应性，研制了一种强韧、自愈的超级防护材料，其中的分子机制如图所示。

Cu 在元素周期表中位于_____区，M 层中核外电子能量最高的电子云在空间有_____个伸展方向。

C 、N 、O 第一电离能由大到小的顺序为_____________（2）氧化石墨烯基水凝胶是一类新型复合材料，对氧化石墨烯进行还原可得到还原氧化石墨烯，二者的结构如图所示：还原石墨烯中碳原子的杂化形式是______，上图中氧化石墨烯转化为还原石墨烯时，1号C 与其相邻 C原子间键能的变化是_____________（填“变大”、“变小”或“不变”），二者当中在水溶液中溶解度更大的是____________ （填物质名称），原因为__________________（3）砷化硼是近期受到广泛关注一种III—V半导体材料。

砷化硼为立方晶系晶体，该晶胞中原子的分数坐标为：B：（0，0，0）；（，，0）；（，0，）；（0，，）；……As：（，，）；（，，）；（，，）；（，，）请在图中画出砷化硼晶胞的俯视图．．．．．．．．．．．___________，已知晶体密度为dg/cm3，As半径为a pm，假设As、B原子相切，则B原子的半径为_________pm（写计算表达式）。

3．补铁剂常用于防治缺铁性贫血，其有效成分般为硫酸亚铁、琥珀酸亚铁、富马酸亚铁和乳酸亚铁等。

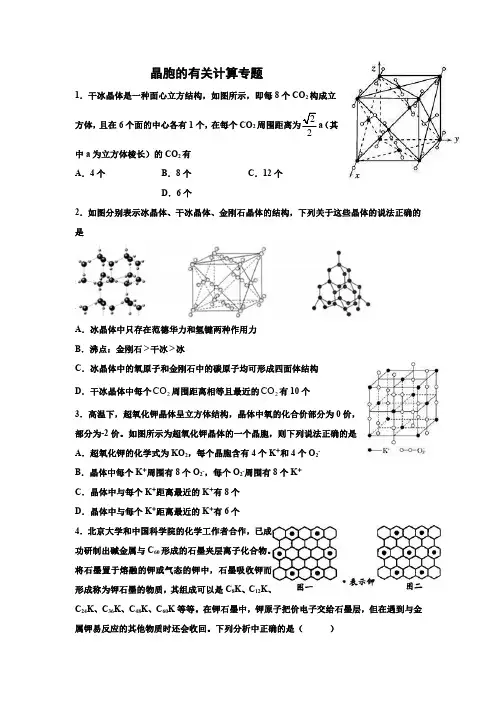
晶胞的有关计算专题1．干冰晶体是一种面心立方结构，如图所示，即每8个CO 2构成立方体，且在6个面的中心各有1个，在每个CO 2周围距离为22a （其中a 为立方体棱长）的CO 2有A ．4个B ．8个C ．12个D ．6个2．如图分别表示冰晶体、干冰晶体、金刚石晶体的结构，下列关于这些晶体的说法正确的是A ．冰晶体中只存在范德华力和氢键两种作用力B ．沸点：金刚石>干冰>冰C ．冰晶体中的氧原子和金刚石中的碳原子均可形成四面体结构D ．干冰晶体中每个2CO 周围距离相等且最近的2CO 有10个3．高温下，超氧化钾晶体呈立方体结构，晶体中氧的化合价部分为0价，部分为-2价。

如图所示为超氧化钾晶体的一个晶胞，则下列说法正确的是A ．超氧化钾的化学式为KO 2，每个晶胞含有4个K ＋和4个O 2-B ．晶体中每个K ＋周围有8个O 2-，每个O 2-周围有8个K＋C ．晶体中与每个K ＋距离最近的K ＋有8个D ．晶体中与每个K ＋距离最近的K ＋有6个4．北京大学和中国科学院的化学工作者合作，已成功研制出碱金属与C 60形成的石墨夹层离子化合物。

将石墨置于熔融的钾或气态的钾中，石墨吸收钾而形成称为钾石墨的物质，其组成可以是C 8K 、C 12K 、C 24K 、C 36K 、C 48K 、C 60K 等等。

在钾石墨中，钾原子把价电子交给石墨层，但在遇到与金属钾易反应的其他物质时还会收回。

下列分析中正确的是（）A ．题干中所举出的6种钾石墨，属于同素异形体B ．若某钾石墨的原于分布如图一所示，则它所表示的是C 24KC ．若某钾石墨的原子分布如图二所示，则它所表示的是C 12KD ．另有一种灰色的钾石墨C 32K ，其中K 的分布也类似图中的中心六边形，则最近两个K 原子之间的距离为石墨键长的4倍5．下列叙述不正确的是A ．金刚石、SiC 、NaF 、NaCl 、2H O 、2H S 晶体的熔点依次降低B ．CaO 晶体结构与NaCl 晶体结构相似，CaO 晶体中2Ca +的配位数为6，且这些最邻近的2O -围成正八面体C ．设NaCl 的摩尔质量为1Mg mol -⋅，NaCl 的密度为3ρg cm -⋅，阿伏加德罗常数为A N 1mol -，在NaCl 晶体中，两个距离最近的Cl -3AM2cm2ρN D ．X 、Y 可形成立方晶体结构的化合物，其晶胞中X 占据所有棱的中心，Y 位于顶角位置，则该晶体的化学式为3XY 6．如图所示，直线交点处的圆圈为NaCl 晶体中Na ＋或Cl －所处的位置。

晶胞计算专题优秀课件一、引言晶胞计算（also known as晶体结构预测、晶格计算或晶体成像计算）是一种用于预测固体材料的晶体结构的方法。

晶胞计算使用原子坐标和生成能量来优化晶格，并预测出稳定的晶体结构。

本课件将介绍晶胞计算的基本原理和方法。

二、晶胞计算的原理1.单位胞单位胞是最基本的晶体结构单元，它通过周期性排列来描述整个晶体的结构。

在晶胞计算中，通过优化晶胞的参数和原子坐标来获得最稳定的晶体结构。

2.势能函数晶胞计算使用势能函数来描述晶体的稳定性。

势能函数通常由两部分组成：晶格势能和原子间相互作用势能。

通过优化势能函数，可以得到晶体的最低稳定态。

3.优化算法晶胞计算使用优化算法来晶格参数和原子坐标的最优解。

常用的算法包括梯度下降法和遗传算法等。

三、晶胞计算的方法1.第一性原理方法第一性原理方法是一种基于量子力学的方法，通过求解薛定谔方程来预测材料的性质。

常用的第一性原理方法包括密度泛函理论（DFT）和蒙特卡洛方法等。

2.经验势方法经验势方法是一种基于经验公式的方法，通过对已知晶体结构进行统计分析来预测新材料的结构。

经验势方法常用的模型包括伦敦分子力场（Lennard-Jones potential）和Brenner势能等。

3.动力学方法动力学方法是一种基于分子动力学模拟的方法，通过模拟原子在晶体中的运动来预测晶格的稳定态。

常用的动力学方法包括蒙特卡洛模拟和分子动力学模拟等。

四、晶胞计算的应用1.新材料的设计晶胞计算可以用于设计新材料的晶体结构和性能。

通过预测材料的结构和稳定性，可以帮助研发人员选择最佳的材料组合。

2.功能性材料的研究晶胞计算可以用于研究功能性材料的晶体结构和性能。

例如，可以通过计算材料的电子结构来预测其导电性和光学性质。

3.材料的相变研究晶胞计算可以用于研究材料的相变过程。

通过模拟材料在不同温度和压力下的结构变化，可以预测材料的相变点和相变机制。

五、总结晶胞计算是一种重要的预测材料性质和晶体结构的方法。

晶胞计算晶胞计算是晶体考查的重要知识点之一，也是考查学生分析问题、解决问题能力的较好素材。

晶体结构的计算常常涉及如下数据：晶体密度、N A 、M 、晶体体积、微粒间距离、微粒半径、夹角等，密度的表达式往往是列等式的依据。

解决这类题，一是要掌握晶体“均摊法”的原理，二是要有扎实的立体几何知识，三是要熟悉常见晶体的结构特征，并能融会贯通，举一反三。

有关晶胞各物理量的关系：1、晶胞质量＝晶胞占有的微粒的质量＝晶胞占有的微粒数×MN A 。

2、空间利用率＝晶胞占有的微粒体积晶胞体积。

3、金属晶体中体心立方堆积、面心立方堆积中的几组公式(设棱长为a )(1)面对角线长＝2a 。

(2)体对角线长＝3a 。

(3)体心立方堆积4r ＝3a (r 为原子半径)。

(4)面心立方堆积4r ＝2a (r 为原子半径)。

对于立方晶胞，可简化成下面的公式进行各物理量的计算：a 3×ρ×N A ＝n ×M ，a 表示晶胞的棱长，ρ表示密度，N A 表示阿伏加德罗常数的值，n 表示1 mol 晶胞中所含晶体的物质的量，M 表示摩尔质量，a 3×ρ×N A 表示1 mol 晶胞的质量。

1、【2012全国1】（6）ZnS 在荧光体、光导体材料、涂料、颜料等行业中应用广泛。

立方ZnS 晶体结构如下图所示，其晶胞边长为540．0 pm ．密度为 （列式并计算），a 位置S 2-离子与b 位置Zn 2+离子之间的距离 pm （列示表示）44.1 2、【2013全国1】（6）在硅酸盐中，SiO 4- 4四面体（如下图（a ））通过共用顶角氧离子可形成岛状、链状、层状、骨架网状四大类结构型式。

图（b ）为一种无限长单链结构的多硅酸根，其中Si 原子的杂化形式为 ，Si 与O 的原子数之比为 ，化学式为 。

（6）sp 3 1∶3[SiO 3]2n- n (或SiO 2-3)3、【2014全国1】（4）铝单质为面心立方晶体，其晶胞参数a ＝0．405nm ，晶胞中铝原子的配位数为 。