工程流体力学课后习题答案
- 格式:docx
- 大小:2.28 MB
- 文档页数:85

第一章 流体及其主要物理性质1-1.轻柴油在温度15ºC 时相对密度为0.83,求它的密度和重度。
解:4ºC 时33/9800/1000mN m kg ==水水γρ 相对密度:水水γγρρ==d所以,33/8134980083.083.0/830100083.083.0mN m kg =⨯===⨯==水水γγρρ 1-2. 甘油在温度0ºC 时密度为1.26g/cm 3,求以国际单位表示的密度和重度。
解:33/1000/1m kg cmg = g ργ=333/123488.91260/1260/26.1m N g m kg cm g =⨯==⇒==ργρ1-3. 水的体积弹性系数为1.96×109N/m 2,问压强改变多少时,它的体积相对压缩1%?解:dpVdV Pa E p p-==ββ)(1MPa Pa E E VVVV p p6.191096.101.07=⨯==∆=∆=∆β 1-4.容积4m 3的水,温度不变,当压强增加105N/m 2时容积减少1000cm 3,求该水的体积压缩系数βp 和体积弹性系数E 。
解:1956105.2104101000---⨯=⨯--=∆∆-=Pa p V V p β Pa E p89104105.211⨯=⨯==-β 1-5.用200L 汽油桶装相对密度为0.70的汽油,罐装时液面上压强为1个大气压,封闭后由于温度变化升高了20ºC ,此时汽油的蒸气压为0.18大气压。
若汽油的膨胀系数为0.0006ºC -1,弹性系数为14000kg/cm 2。
试计算由于压力及温度变化所增减的体积?问灌桶时每桶最多不超过多少公斤为宜?解:E =E ’·g =14000×9.8×104PaΔp =0.18atdp pV dT T V dV ∂∂+∂∂=00V T V T V V T T ββ=∂∂⇒∂∂=00V pVp V V p p ββ-=∂∂⇒∂∂-= 所以,dp V dT V dp pVdT T V dV p T 00ββ-=∂∂+∂∂= 从初始状态积分到最终状态得:LL L V p p E V T T V V dpV dT V dV T p pp T T T VV 4.21057.24.2200108.914000108.918.020*******.0)(1)(34400000000≈⨯-=⨯⨯⨯⨯⨯-⨯⨯=---=--=-⎰⎰⎰βββ即()kg V V M 32.13810004.220010007.0=-⨯⨯=∆-=ρ另解:设灌桶时每桶最多不超过V 升,则200=++p t dV dV VV dt V dV t t 2000061.0⨯=⋅⋅=βV dp V dV p p 18.0140001⨯-=⋅⋅-=β(1大气压=1Kg/cm 2) V =197.6升 dV t =2.41升 dV p =2.52×10-3升G =0.1976×700=138Kg =1352.4N 1-6.石油相对密度0.9,粘度28cP ,求运动粘度为多少m 2/s? 解:s Pa P sPa s mPa P cP ⋅=⋅=⋅==--1.0110110132()c S t St s m 3131.0/101.310009.01028253==⨯=⨯⨯==--ρμν1-7.相对密度0.89的石油,温度20ºC 时的运动粘度为40cSt ,求动力粘度为多少? 解:89.0==水ρρd ν=40cSt =0.4St =0.4×10-4m 2/sμ=νρ=0.4×10-4×890=3.56×10-2 Pa ·s 1-8.图示一平板在油面上作水平运动,已知运动速度u=1m/s ,板与固定边界的距离δ=1,油的动力粘度μ=1.147Pa ·s ,由平板所带动的油层的运动速度呈直线分布,求作用在平板单位面积上的粘性阻力为多少?解:233/10147.11011147.1m N dy du ⨯=⨯⨯==-μτ 1-9.如图所示活塞油缸,其直径D =12cm ,活塞直径d =11.96cm ,活塞长度L =14cm ,油的μ=0.65P ,当活塞移动速度为0.5m/s 时,试求拉回活塞所需的力F=?解:A =πdL , μ=0.65P =0.065 Pa ·s , Δu =0.5m/s , Δy=(D-d)/2()N dy du AF 55.821096.11125.010141096.1114.3065.0222=⨯-⨯⨯⨯⨯⨯⨯==---μ第二章流体静力学2-1. 如图所示的U形管中装有水银与水,试求:(1)A、C两点的绝对压力及表压各为多少?(2)A、B两点的高度差为多少?解:①p A表=γh水=0.3mH2O=0.03at=0.3×9800Pa=2940Pap A绝=p a+p A表=(10+0.3)mH2O=1.03at=10.3×9800Pa=100940Pa p C表=γhg h hg+p A表=0.1×13.6m H2O+0.3mH2O=1.66mH2O=0.166at=1.66×9800Pa=16268Pap C绝=p a+p C表=(10+1.66)mH2O=11.66 mH2O=1.166at=11.66×9800Pa=114268Pa② 30c mH2O=13.6h cmH2O h=30/13.6cm=2.2cm题2-2 题2-32-2. 水银压力计装置如图。

第1章 绪论【1-1】500cm 3的某种液体,在天平上称得其质量为0.453kg ,试求其密度和相对密度。
【解】液体的密度3340.4530.90610 kg/m 510m V ρ-===⨯⨯ 相对密度330.906100.9061.010w ρδρ⨯===⨯ 【1-2】体积为5m 3的水,在温度不变的条件下,当压强从98000Pa 增加到4.9×105Pa 时,体积减少1L 。
求水的压缩系数和弹性系数。
【解】由压缩系数公式10-1510.001 5.110 Pa 5(4.91098000)p dV V dP β-=-==⨯⨯⨯- 910111.9610 Pa 5.110pE β-===⨯⨯ 【1-3】温度为20℃,流量为60m 3/h 的水流入加热器,如果水的体积膨胀系数βt =0.00055K -1,问加热到80℃后从加热器中流出时的体积流量变为多少? 【解】根据膨胀系数1t dV V dtβ=则2113600.00055(8020)6061.98 m /ht Q Q dt Q β=+=⨯⨯-+= 【1-4】用200升汽油桶装相对密度0.70的汽油。
罐装时液面上压强为98000Pa 。
封闭后由于温度变化升高了20℃,此时汽油的蒸汽压力为17640Pa 。
若汽油的膨胀系数为0.0006K -1,弹性系数为13.72×106Pa ,(1)试计算由于压力温度变化所增加的体积,(2)问灌装时汽油的体积最多不应超过桶体积的百分之多少?【解】(1)由1β=-=P pdV Vdp E可得,由于压力改变而减少的体积为6200176400.257L 13.7210⨯∆=-===⨯P p VdP V dV E 由于温度变化而增加的体积,可由1β=tt dV V dT得 0.000620020 2.40L β∆===⨯⨯=t t t V dV VdT(2)因为∆∆tp V V ,相比之下可以忽略由压力变化引起的体积改变,则由 200L β+=t V V dT得1198.8%200110.000620β===++⨯t V dT 【1-5】图中表示浮在油面上的平板,其水平运动速度为u =1m/s ,δ=10mm ,油品的粘度μ=0.9807Pa ·s ,求作用在平板单位面积上的阻力。
![工程流体力学课后习题答案1-3章[精.选]](https://uimg.taocdn.com/5662d7957cd184254a353515.webp)
第1章 绪论【1-1】500cm 3的某种液体,在天平上称得其质量为0.453kg ,试求其密度和相对密度。
【解】液体的密度3340.4530.90610 kg/m 510m V ρ-===⨯⨯相对密度 330.906100.9061.010w ρδρ⨯===⨯【1-2】体积为5m 3的水,在温度不变的条件下,当压强从98000Pa 增加到4.9×105Pa 时,体积减少1L 。
求水的压缩系数和弹性系数。
【解】由压缩系数公式10-1510.001 5.110 Pa 5(4.91098000)p dV V dP β-=-==⨯⨯⨯- 910111.9610 Pa 5.110pE β-===⨯⨯ 【1-3】温度为20℃,流量为60m 3/h 的水流入加热器,如果水的体积膨胀系数βt =0.00055K -1,问加热到80℃后从加热器中流出时的体积流量变为多少?【解】根据膨胀系数1t dVV dtβ=则2113600.00055(8020)6061.98 m /ht Q Q dt Q β=+=⨯⨯-+= 【1-4】用200升汽油桶装相对密度0.70的汽油。
罐装时液面上压强为98000Pa 。
封闭后由于温度变化升高了20℃,此时汽油的蒸汽压力为17640Pa 。
若汽油的膨胀系数为0.0006K -1,弹性系数为13.72×106Pa ,(1)试计算由于压力温度变化所增加的体积,(2)问灌装时汽油的体积最多不应超过桶体积的百分之多少?【解】(1)由1β=-=P p dV Vdp E可得,由于压力改变而减少的体积为6200176400.257L 13.7210⨯∆=-===⨯P p VdP V dV E由于温度变化而增加的体积,可由1β=tt dV V dT得 0.000620020 2.40L β∆===⨯⨯=t t t V dV VdT(2)因为∆∆t p V V ?,相比之下可以忽略由压力变化引起的体积改变,则 由 200L β+=t V V dT 得 1198.8%200110.000620β===++⨯t V dT 【1-5】图中表示浮在油面上的平板,其水平运动速度为u =1m/s ,δ=10mm ,油品的粘度μ=0.9807Pa ·s ,求作用在平板单位面积上的阻力。

第一章 绪论1-1.20℃的水2.5m 3,当温度升至80℃时,其体积增加多少? [解] 温度变化前后质量守恒,即2211V V ρρ= 又20℃时,水的密度31/23.998m kg =ρ 80℃时,水的密度32/83.971m kg =ρ 321125679.2m V V ==∴ρρ 则增加的体积为3120679.0m V V V =-=∆1-2.当空气温度从0℃增加至20℃时,运动粘度ν增加15%,重度γ减少10%,问此时动力粘度μ增加多少(百分数)? [解] 原原ρννρμ)1.01()15.01(-+==原原原μρν035.1035.1==035.0035.1=-=-原原原原原μμμμμμ此时动力粘度μ增加了3.5%1-3.有一矩形断面的宽渠道,其水流速度分布为μρ/)5.0(002.02y hy g u -=,式中ρ、μ分别为水的密度和动力粘度,h 为水深。
试求m h 5.0=时渠底(y =0)处的切应力。
[解] μρ/)(002.0y h g dydu-=)(002.0y h g dydu-==∴ρμτ 当h =0.5m ,y =0时)05.0(807.91000002.0-⨯⨯=τPa 807.9=1-4.一底面积为45×50cm 2,高为1cm 的木块,质量为5kg ,沿涂有润滑油的斜面向下作等速运动,木块运动速度u=1m/s ,油层厚1cm ,斜坡角22.620 (见图示),求油的粘度。
[解] 木块重量沿斜坡分力F 与切力T 平衡时,等速下滑yu AT mg d d sin μθ== 001.0145.04.062.22sin 8.95sin ⨯⨯⨯⨯==δθμu A mg s Pa 1047.0⋅=μ1-5.已知液体中流速沿y 方向分布如图示三种情况,试根据牛顿内摩擦定律yud d μτ=,定性绘出切应力沿y 方向的分布图。
[解]1-6.为导线表面红绝缘,将导线从充满绝缘涂料的模具中拉过。

第一章 流体及其主要物理性质1-1.轻柴油在温度15ºC 时相对密度为0.83,求它的密度和重度。
解:4ºC 时所以,33/8134980083.083.0/830100083.083.0mN m kg =⨯===⨯==水水γγρρ1-2.甘油在温度0ºC 时密度为1.26g/cm3,求以国际单位表示的密度和重度。
333/123488.91260/1260/26.1m N g m kg cm g =⨯==⇒==ργρ 1-3.水的体积弹性系数为1.96×109N/m 2,问压强改变多少时,它的体积相对压缩1%?MPa Pa E E VVVV p p6.191096.101.07=⨯==∆=∆=∆β 1-4.容积4m 3的水,温度不变,当压强增加105N/m 2时容积减少1000cm 3,求该水的体积压缩系数βp 和体积弹性系数E 。
解:1956105.2104101000---⨯=⨯--=∆∆-=Pa p V V p β Pa E p89104105.211⨯=⨯==-β 1-5. 用200L 汽油桶装相对密度为0.70的汽油,罐装时液面上压强为1个大气压,封闭后由于温度变化升高了20ºC ,此时汽油的蒸气压为0.18大气压。
若汽油的膨胀系数为0.0006ºC -1,弹性系数为14000kg/cm 2。
试计算由于压力及温度变化所增减的体积?问灌桶时每桶最多不超过多少公斤为宜?解:E =E ’·g =14000×9.8×104PaΔp =0.18atdp pVdT T V dV ∂∂+∂∂=00V TVT V V T T ββ=∂∂⇒∂∂=00V p V p V V p p ββ-=∂∂⇒∂∂-= 所以,dp V dT V dp pVdT T V dV p T 00ββ-=∂∂+∂∂=从初始状态积分到最终状态得:LL L V p p E V T T V V dpV dT V dV T p pp T T T VV 4.21057.24.2200108.914000108.918.020*******.0)(1)(34400000000≈⨯-=⨯⨯⨯⨯⨯-⨯⨯=---=--=-⎰⎰⎰βββ即()kg V V M 32.13810004.220010007.0=-⨯⨯=∆-=ρ另解:设灌桶时每桶最多不超过V 升,则200=++p t dV dV VV dt V dV t t 2000061.0⨯=⋅⋅=βV dp V dV p p 18.0140001⨯-=⋅⋅-=β(1大气压=1Kg/cm 2) V =197.6升 dV t =2.41升 dV p =2.52×10-3升G =0.1976×700=138Kg =1352.4N 1-6.石油相对密度0.9,粘度28cP ,求运动粘度为多少m 2/s?解:s Pa P sPa s mPa P cP ⋅=⋅=⋅==--1.0110110132()cSt St s m 3131.0/101.310009.01028253==⨯=⨯⨯==--ρμν 1-7.相对密度0.89的石油,温度20ºC 时的运动粘度为40cSt ,求动力粘度为多少? 解:89.0==水ρρd ν=40cSt =0.4St =0.4×10-4m 2/s μ=νρ=0.4×10-4×890=3.56×10-2 Pa ·s 1-8.图示一平板在油面上作水平运动,已知运动速度u=1m/s ,板与固定边界的距离δ=1,油的动力粘度μ=1.147Pa ·s ,由平板所带动的油层的运动速度呈直线分布,求作用在平板单位面积上的粘性阻力为多少?解:233/10147.11011147.1m N dy du ⨯=⨯⨯==-μτ 1-9.如图所示活塞油缸,其直径D =12cm ,活塞直径d =11.96cm ,活塞长度L =14cm ,油的μ=0.65P ,当活塞移动速度为0.5m/s 时,试求拉回活塞所需的力F=?解:A =πdL , μ=0.65P =0.065 Pa ·s , Δu =0.5m/s , Δy=(D-d)/2()N dy du AF 55.821096.11125.010141096.1114.3065.0222=⨯-⨯⨯⨯⨯⨯⨯==---μ第二章 流体静力学2-1. 如图所示的U 形管中装有水银与水,试求:(1)A 、C 两点的绝对压力及表压各为多少? (2)A 、B 两点的高度差为多少?解:① p A 表=γh 水=0.3mH 2O =0.03at =0.3×9800Pa =2940Pap A 绝=p a + p A 表=(10+0.3)mH 2O =1.03at =10.3×9800Pa=100940Pap C 表=γhg h hg + p A 表=0.1×13.6m H 2O+0.3mH 2O =1.66mH 2O =0.166at=1.66×9800Pa =16268Pap C 绝=p a + p C 表=(10+1.66)mH 2O =11.66 mH 2O =1.166at =11.66×9800Pa =114268Pa ② 30c mH 2O =13.6h cmH 2O ⇒h =30/13.6cm=2.2cm题2-2 题2-32-2.水银压力计装置如图。

⼯程流体⼒学课后习题答案第⼀章绪论1-1.20℃的⽔,当温度升⾄80℃时,其体积增加多少 [解] 温度变化前后质量守恒,即2211V V ρρ= ⼜20℃时,⽔的密度31/23.998m kg =ρ 80℃时,⽔的密度32/83.971m kg =ρ 321125679.2m V V ==∴ρρ则增加的体积为3120679.0m V V V =-=?1-2.当空⽓温度从0℃增加⾄20℃时,运动粘度ν增加15%,重度γ减少10%,问此时动⼒粘度µ增加多少(百分数) [解] 原原ρννρµ)1.01()15.01(-+==Θ原原原µρν035.1035.1==035.0035.1=-=-原原原原原µµµµµµΘ此时动⼒粘度µ增加了%1-3.有⼀矩形断⾯的宽渠道,其⽔流速度分布为µρ/)5.0(002.02y hy g u -=,式中ρ、µ分别为⽔的密度和动⼒粘度,h 为⽔深。
试求m h 5.0=时渠底(y =0)处的切应⼒。
[解] µρ/)(002.0y h g dydu-=Θ)(002.0y h g dydu-==∴ρµτ当h =,y =0时)05.0(807.91000002.0-??=τPa 807.9=1-4.⼀底⾯积为45×50cm 2,⾼为1cm 的⽊块,质量为5kg ,沿涂有润滑油的斜⾯向下作等速运动,⽊块运动速度u=1m/s ,油层厚1cm ,斜坡⾓(见图⽰),求油的粘度。
[解] ⽊块重量沿斜坡分⼒F 与切⼒T 平衡时,等速下滑yuATd sinµθ= = 001 .0145 .0 4.0 62 .22 sin 8.9 5 sin==δθµuA mg s Pa 1047 .0?1-5.已知液体中流速沿y⽅向分布如图⽰三种情况,试根据⽜顿内摩擦定律yuddµτ=,定性绘出切应⼒沿y⽅向的分布图。
第2章 流体静力学2.1 解:相对压强:gh p ρ=333/0204.1051/100510.13008.93090m kg m kg gh p =⨯=⨯==ρ 2.2 解:设小活塞顶部所受的来自杠杆的压力为F ,则小活塞给杠杆的反力亦为F ,对杠杆列力矩平衡方程:Fa b a T =+)(a b a T F )(+=小活塞底部的压强为:22)(44ad b a T d F p ππ+==根据帕斯卡原理,p 将等值的传递到液体当中各点,大活塞底部亦如此。
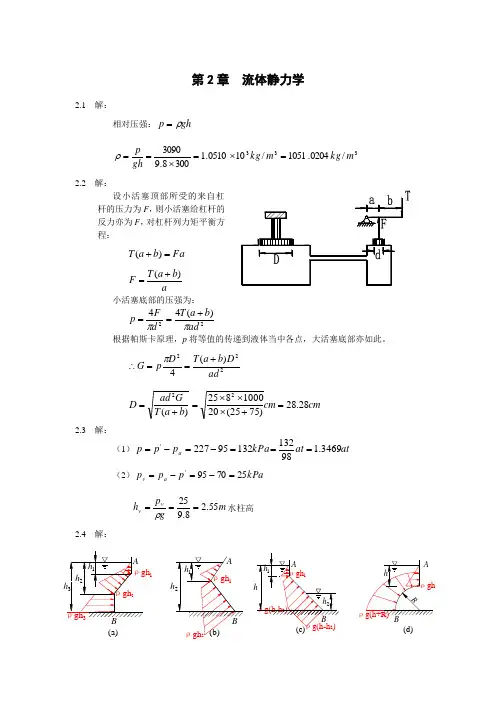
222)(4ad D b a T D p G +==∴π cm cm b a T Gad D 28.28)7525(201000825)(22=+⨯⨯⨯=+=2.3 解:(1)at at kPa p p p a 3469.19813213295227'===-=-= (2)kPa p p p a v 257095'=-=-=m g p h v v 55.28.925===ρ水柱高 2.4 解:ρgh 2 ρgh 1ρgh 3ρgh 2ρgh 1h 2h 1 h 1 h 2h 3 (b)(a)BAA Bρg(h-h 2)ρg(h+R)ρghρg(h-h 2) ρgh 1Rhh 2h 1h(d)(c)B AAB2.5 解:1-1为等压面:gh p gH p a ρρ+=+0kPa m N m N m N H h g p p a 94.100/100940/)2.15.1(8.91000/108.9)('22240==-⨯⨯+⨯=-+=ρ kPa p 94.20=2.6 解: kPa gL p c 45.230sin 5.08.9sin =⨯⨯==αρ 2.7 解:如图所示,过1、2、3点的水平面是等压面。
)()()(322341121z z g z z g gh p z z g gh p B B A A ---++=--+ρρρρρ[])()()()(32212341z z g z z z z g h h g p p A B B A ---+-+-=-ρρρ[])()()()(3221234141z z g z z z z g z z g ---+-+-=ρρρ[]{}310)3262(8.0)1862()3253(6.13)5318(8.9-⨯---+-+-⨯=Pa 8085=2.8 解:gh gh p gh p p B B A A ρρρ+-=- ()gh h h g p p p B A B A ρρ+-=-=()[]gh h g p ρρ++-1=()[]31036.08.96.13136.08.9-⨯⨯⨯++-=34.6528kPa2.9 解:如图所示,A 、B 、C 点水平面是等压面。

第一章 流体及其主要物理性质1-1.轻柴油在温度15ºC 时相对密度为0.83,求它的密度和重度。
解:4ºC 时33/9800/1000mN m kg ==水水γρ 相对密度:水水γγρρ==d所以,33/8134980083.083.0/830100083.083.0mN m kg =⨯===⨯==水水γγρρ 1-2. 甘油在温度0ºC 时密度为1.26g/cm 3,求以国际单位表示的密度和重度。
解:33/1000/1m kg cmg = g ργ=333/123488.91260/1260/26.1m N g m kg cm g =⨯==⇒==ργρ1-3. 水的体积弹性系数为1.96×109N/m 2,问压强改变多少时,它的体积相对压缩1%?解:dpVdV Pa E p p-==ββ)(1MPa Pa E E VVVV p p6.191096.101.07=⨯==∆=∆=∆β 1-4.容积4m 3的水,温度不变,当压强增加105N/m 2时容积减少1000cm 3,求该水的体积压缩系数βp 和体积弹性系数E 。
解:1956105.2104101000---⨯=⨯--=∆∆-=Pa p V V p β Pa E p89104105.211⨯=⨯==-β 1-5.用200L 汽油桶装相对密度为0.70的汽油,罐装时液面上压强为1个大气压,封闭后由于温度变化升高了20ºC ,此时汽油的蒸气压为0.18大气压。
若汽油的膨胀系数为0.0006ºC -1,弹性系数为14000kg/cm 2。
试计算由于压力及温度变化所增减的体积?问灌桶时每桶最多不超过多少公斤为宜?解:E =E ’·g =14000×9.8×104PaΔp =0.18atdp pV dT T V dV ∂∂+∂∂=00V T V T V V T T ββ=∂∂⇒∂∂=00V pVp V V p p ββ-=∂∂⇒∂∂-= 所以,dp V dT V dp pVdT T V dV p T 00ββ-=∂∂+∂∂= 从初始状态积分到最终状态得:LL L V p p E V T T V V dpV dT V dV T p pp T T T VV 4.21057.24.2200108.914000108.918.020*******.0)(1)(34400000000≈⨯-=⨯⨯⨯⨯⨯-⨯⨯=---=--=-⎰⎰⎰βββ即()kg V V M 32.13810004.220010007.0=-⨯⨯=∆-=ρ另解:设灌桶时每桶最多不超过V 升,则200=++p t dV dV VV dt V dV t t 2000061.0⨯=⋅⋅=βV dp V dV p p 18.0140001⨯-=⋅⋅-=β(1大气压=1Kg/cm 2) V =197.6升 dV t =2.41升 dV p =2.52×10-3升G =0.1976×700=138Kg =1352.4N 1-6.石油相对密度0.9,粘度28cP ,求运动粘度为多少m 2/s? 解:s Pa P sPa s mPa P cP ⋅=⋅=⋅==--1.0110110132()c S t St s m 3131.0/101.310009.01028253==⨯=⨯⨯==--ρμν1-7.相对密度0.89的石油,温度20ºC 时的运动粘度为40cSt ,求动力粘度为多少? 解:89.0==水ρρd ν=40cSt =0.4St =0.4×10-4m 2/sμ=νρ=0.4×10-4×890=3.56×10-2 Pa ·s 1-8.图示一平板在油面上作水平运动,已知运动速度u=1m/s ,板与固定边界的距离δ=1,油的动力粘度μ=1.147Pa ·s ,由平板所带动的油层的运动速度呈直线分布,求作用在平板单位面积上的粘性阻力为多少?解:233/10147.11011147.1m N dy du ⨯=⨯⨯==-μτ 1-9.如图所示活塞油缸,其直径D =12cm ,活塞直径d =11.96cm ,活塞长度L =14cm ,油的μ=0.65P ,当活塞移动速度为0.5m/s 时,试求拉回活塞所需的力F=?解:A =πdL , μ=0.65P =0.065 Pa ·s , Δu =0.5m/s , Δy=(D-d)/2()N dy du AF 55.821096.11125.010141096.1114.3065.0222=⨯-⨯⨯⨯⨯⨯⨯==---μ第二章流体静力学2-1. 如图所示的U形管中装有水银与水,试求:(1)A、C两点的绝对压力及表压各为多少?(2)A、B两点的高度差为多少?解:①p A表=γh水=0.3mH2O=0.03at=0.3×9800Pa=2940Pap A绝=p a+p A表=(10+0.3)mH2O=1.03at=10.3×9800Pa=100940Pa p C表=γhg h hg+p A表=0.1×13.6m H2O+0.3mH2O=1.66mH2O=0.166at=1.66×9800Pa=16268Pap C绝=p a+p C表=(10+1.66)mH2O=11.66 mH2O=1.166at=11.66×9800Pa=114268Pa② 30c mH2O=13.6h cmH2O h=30/13.6cm=2.2cm题2-2 题2-32-2. 水银压力计装置如图。

第一章 绪论1-1.20℃的水2.5m 3,当温度升至80℃时,其体积增加多少? [解] 温度变化前后质量守恒,即2211V V ρρ= 又20℃时,水的密度31/23.998m kg =ρ 80℃时,水的密度32/83.971m kg =ρ 321125679.2m V V ==∴ρρ 则增加的体积为3120679.0m V V V =-=∆1-2.当空气温度从0℃增加至20℃时,运动粘度ν增加15%,重度γ减少10%,问此时动力粘度μ增加多少(百分数)? [解] 原原ρννρμ)1.01()15.01(-+==Θ原原原μρν035.1035.1==035.0035.1=-=-原原原原原μμμμμμΘ此时动力粘度μ增加了3.5%1-3.有一矩形断面的宽渠道,其水流速度分布为μρ/)5.0(002.02y hy g u -=,式中ρ、μ分别为水的密度和动力粘度,h 为水深。
试求m h 5.0=时渠底(y =0)处的切应力。
[解] μρ/)(002.0y h g dydu-=Θ)(002.0y h g dydu-==∴ρμτ 当h =0.5m ,y =0时)05.0(807.91000002.0-⨯⨯=τPa 807.9=1-4.一底面积为45×50cm 2,高为1cm 的木块,质量为5kg ,沿涂有润滑油的斜面向下作等速运动,木块运动速度u=1m/s ,油层厚1cm ,斜坡角22.620 (见图示),求油的粘度。
[解] 木块重量沿斜坡分力F 与切力T 平衡时,等速下滑yuATmgddsinμθ==001.0145.04.062.22sin8.95sin⨯⨯⨯⨯==δθμuAmgsPa1047.0⋅=μ1-5.已知液体中流速沿y方向分布如图示三种情况,试根据牛顿内摩擦定律yuddμτ=,定性绘出切应力沿y方向的分布图。
[解]1-6.为导线表面红绝缘,将导线从充满绝缘涂料的模具中拉过。
已知导线直径0.9mm,长度20mm,涂料的粘度μ=0.02Pa.s。

第一章 绪论1-1.20℃的水2.5m 3,当温度升至80℃时,其体积增加多少? [解] 温度变化前后质量守恒,即2211V V ρρ= 又20℃时,水的密度31/23.998m kg =ρ 80℃时,水的密度32/83.971m kg =ρ 321125679.2m V V ==∴ρρ 则增加的体积为3120679.0m V V V =-=∆1-2.当空气温度从0℃增加至20℃时,运动粘度ν增加15%,重度γ减少10%,问此时动力粘度μ增加多少(百分数)? [解] 原原ρννρμ)1.01()15.01(-+==原原原μρν035.1035.1==035.0035.1=-=-原原原原原μμμμμμ此时动力粘度μ增加了3.5%1-3.有一矩形断面的宽渠道,其水流速度分布为μρ/)5.0(002.02y hy g u -=,式中ρ、μ分别为水的密度和动力粘度,h 为水深。
试求m h 5.0=时渠底(y =0)处的切应力。
[解] μρ/)(002.0y h g dydu-=)(002.0y h g dydu-==∴ρμτ 当h =0.5m ,y =0时)05.0(807.91000002.0-⨯⨯=τPa 807.9=1-4.一底面积为45×50cm 2,高为1cm 的木块,质量为5kg ,沿涂有润滑油的斜面向下作等速运动,木块运动速度u=1m/s ,油层厚1cm ,斜坡角22.620 (见图示),求油的粘度。
[解] 木块重量沿斜坡分力F 与切力T 平衡时,等速下滑yu AT mg d d sin μθ== 001.0145.04.062.22sin 8.95sin ⨯⨯⨯⨯==δθμu A mg s Pa 1047.0⋅=μ1-5.已知液体中流速沿y 方向分布如图示三种情况,试根据牛顿内摩擦定律yud d μτ=,定性绘出切应力沿y 方向的分布图。
[解]1-6.为导线表面红绝缘,将导线从充满绝缘涂料的模具中拉过。

第一章 流体及其主要物理性质1-1.轻柴油在温度15ºC 时相对密度为0.83,求它的密度和重度。
解:4ºC 时所以,33/8134980083.083.0/830100083.083.0mN m kg =⨯===⨯==水水γγρρ1-2.甘油在温度0ºC 时密度为1.26g/cm3,求以国际单位表示的密度和重度。
333/123488.91260/1260/26.1m N g m kg cm g =⨯==⇒==ργρ 1-3.水的体积弹性系数为1.96×109N/m 2,问压强改变多少时,它的体积相对压缩1%?M P aPa E E VVVV p p6.191096.101.07=⨯==∆=∆=∆β 1-4.容积4m 3的水,温度不变,当压强增加105N/m 2时容积减少1000cm 3,求该水的体积压缩系数βp 和体积弹性系数E 。
解:1956105.2104101000---⨯=⨯--=∆∆-=Pa p V V p β Pa E p89104105.211⨯=⨯==-β 1-5石油相对密度0.9,粘度28cP ,求运动粘度为多少m 2/s?()c S t St s m 3131.0/101.310009.01028253==⨯=⨯⨯==--ρμν1-6 相对密度0.89的石油,温度20ºC 时的运动粘度为40cSt ,求动力粘度为多少? 解:89.0==水ρρd ν=40cSt =0.4St =0.4×10-4m 2/s μ=νρ=0.4×10-4×890=3.56×10-2 Pa ·s1-7 图示一平板在油面上作水平运动,已知运动速度u=1m/s ,板与固定边界的距离δ=1mm ,油的动力粘度μ=1.147Pa ·s ,由平板所带动的油层的运动速度呈直线分布,求作用在平板单位面积上的粘性阻力为多少?解:233/10147.11011147.1m N dy du ⨯=⨯⨯==-μτ 1-8 如图所示活塞油缸,其直径D =12cm ,活塞直径d =11.96cm ,活塞长度L =14cm ,油的μ=0.65P ,当活塞移动速度为0.5m/s 时,试求拉回活塞所需的力F=?解:A =πdL , μ=0.65P =0.065 Pa ·s , Δu =0.5m/s , Δy=(D-d)/2()N dy du AF 55.821096.11125.010141096.1114.3065.0222=⨯-⨯⨯⨯⨯⨯⨯==---μ第二章 流体静力学2-1. 如图所示的U 形管中装有水银与水,试求:(1)A 、C 两点的绝对压力及表压各为多少? (2)A 、B 两点的高度差为多少?解:① p A 表=γh 水=0.3mH 2O =0.03at =0.3×9800Pa =2940Pap A 绝=p a + p A 表=(10+0.3)mH 2O =1.03at =10.3×9800Pa=100940Pap C 表=γhgh hg + p A 表=0.1×13.6m H 2O+0.3mH 2O =1.66mH 2O =0.166at=1.66×9800Pa =16268Pap C 绝=p a + p C 表=(10+1.66)mH 2O =11.66 mH 2O =1.166at =11.66×9800Pa =114268Pa ② 30c mH 2O =13.6h cmH 2O ⇒h =30/13.6cm=2.2cm题2-22-2 今有U 形管,内装水和四氯化碳(CCl 4),如图所示。
第1章 绪论【1-1】500cm 3的某种液体,在天平上称得其质量为0.453kg ,试求其密度和相对密度。
【解】液体的密度3340.4530.90610 kg/m 510m V ρ-===⨯⨯ 相对密度330.906100.9061.010w ρδρ⨯===⨯ 【1-2】体积为5m 3的水,在温度不变的条件下,当压强从98000Pa 增加到4.9×105Pa 时,体积减少1L 。
求水的压缩系数和弹性系数。
【解】由压缩系数公式10-1510.001 5.110 Pa 5(4.91098000)p dV V dP β-=-==⨯⨯⨯- 910111.9610 Pa 5.110pE β-===⨯⨯ 【1-3】温度为20℃,流量为60m 3/h 的水流入加热器,如果水的体积膨胀系数βt =0.00055K -1,问加热到80℃后从加热器中流出时的体积流量变为多少? 【解】根据膨胀系数1t dV V dtβ=则2113600.00055(8020)6061.98 m /ht Q Q dt Q β=+=⨯⨯-+= 【1-4】用200升汽油桶装相对密度0.70的汽油。
罐装时液面上压强为98000Pa 。
封闭后由于温度变化升高了20℃,此时汽油的蒸汽压力为17640Pa 。
若汽油的膨胀系数为0.0006K -1,弹性系数为13.72×106Pa ,(1)试计算由于压力温度变化所增加的体积,(2)问灌装时汽油的体积最多不应超过桶体积的百分之多少?【解】(1)由1β=-=P pdV Vdp E可得,由于压力改变而减少的体积为6200176400.257L 13.7210⨯∆=-===⨯P p VdP V dV E 由于温度变化而增加的体积,可由1β=tt dV V dT得 0.000620020 2.40L β∆===⨯⨯=t t t V dV VdT(2)因为∆∆tp V V ,相比之下可以忽略由压力变化引起的体积改变,则由 200L β+=t V V dT得1198.8%200110.000620β===++⨯t V dT 【1-5】图中表示浮在油面上的平板,其水平运动速度为u =1m/s ,δ=10mm ,油品的粘度μ=0.9807Pa ·s ,求作用在平板单位面积上的阻力。
第一章 绪论1-1.20℃的水2.5m 3,当温度升至80℃时,其体积增加多少? [解] 温度变化前后质量守恒,即2211V V ρρ= 又20℃时,水的密度31/23.998m kg =ρ 80℃时,水的密度32/83.971m kg =ρ 321125679.2m V V ==∴ρρ 则增加的体积为3120679.0m V V V =-=∆1-2.当空气温度从0℃增加至20℃时,运动粘度ν增加15%,重度γ减少10%,问此时动力粘度μ增加多少(百分数)? [解] 原原ρννρμ)1.01()15.01(-+==Θ原原原μρν035.1035.1==035.0035.1=-=-原原原原原μμμμμμΘ此时动力粘度μ增加了3.5%1-3.有一矩形断面的宽渠道,其水流速度分布为μρ/)5.0(002.02y hy g u -=,式中ρ、μ分别为水的密度和动力粘度,h 为水深。
试求m h 5.0=时渠底(y =0)处的切应力。
[解] μρ/)(002.0y h g dydu-=Θ)(002.0y h g dydu-==∴ρμτ 当h =0.5m ,y =0时)05.0(807.91000002.0-⨯⨯=τPa 807.9=1-4.一底面积为45×50cm 2,高为1cm 的木块,质量为5kg ,沿涂有润滑油的斜面向下作等速运动,木块运动速度u=1m/s ,油层厚1cm ,斜坡角22.620 (见图示),求油的粘度。
[解] 木块重量沿斜坡分力F 与切力T 平衡时,等速下滑yu AT mg d d sin μθ== 001.0145.04.062.22sin 8.95sin ⨯⨯⨯⨯==δθμu A mg s Pa 1047.0⋅=μ1-5.已知液体中流速沿y 方向分布如图示三种情况,试根据牛顿内摩擦定律yud d μτ=,定性绘出切应力沿y 方向的分布图。
[解]1-6.为导线表面红绝缘,将导线从充满绝缘涂料的模具中拉过。
(完整版)工程流体力学习题及答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第1章 绪论选择题【1.1】 按连续介质的概念,流体质点是指:(a )流体的分子;(b )流体内的固体颗粒;(c )几何的点;(d )几何尺寸同流动空间相比是极小量,又含有大量分子的微元体。
解:流体质点是指体积小到可以看作一个几何点,但它又含有大量的分子,且具有诸如速度、密度及压强等物理量的流体微团。
(d )【1.2】 与牛顿内摩擦定律直接相关的因素是:(a )切应力和压强;(b )切应力和剪切变形速度;(c )切应力和剪切变形;(d )切应力和流速。
解:牛顿内摩擦定律是d d v y τμ=,而且速度梯度d d v y 是流体微团的剪切变形速度d d t γ,故d d t γτμ=。
(b )【1.3】流体运动黏度υ的国际单位是:(a )m 2/s ;(b )N/m 2;(c )kg/m ;(d )N·s/m 2。
解:流体的运动黏度υ的国际单位是/s m 2。
(a )【1.4】理想流体的特征是:(a )黏度是常数;(b )不可压缩;(c )无黏性;(d )符合RTp=ρ。
解:不考虑黏性的流体称为理想流体。
(c )【1.5】当水的压强增加一个大气压时,水的密度增大约为:(a )1/20 000;(b )1/1 000;(c )1/4 000;(d )1/2 000。
解:当水的压强增加一个大气压时,其密度增大约95d 1d 0.51011020 000k p ρρ-==⨯⨯⨯=。
(a )【1.6】 从力学的角度分析,一般流体和固体的区别在于流体:(a )能承受拉力,平衡时不能承受切应力;(b )不能承受拉力,平衡时能承受切应力;(c )不能承受拉力,平衡时不能承受切应力;(d )能承受拉力,平衡时也能承受切应力。
解:流体的特性是既不能承受拉力,同时具有很大的流动性,即平衡时不能承受切应力。
工程流体力学练习题第一章1-1解:设:柴油的密度为ρ,重度为γ;40C 水的密度为ρ0,重度为γ0。
则在同一地点的相对密度和比重为:ρρ=d ,0γγ=c ;30/830100083.0m kg d =⨯=⨯=ρρ30/81348.9100083.0m N c =⨯⨯=⨯=γγ1-2解:336/1260101026.1m kg =⨯⨯=-ρ;3/123488.91260m N g =⨯==ργ1-3解:269/106.191096.101.0m N E V V VVp p V Vp p p⨯=⨯⨯=∆-=∆-=∆⇒∆∆-=ββ1-4解:N m pVVp/105.21041010002956--⨯=⨯=∆∆-=β299/104.0105.211m N E pp ⨯=⨯==-β1-5解:1)求体积膨涨量和桶内压强受温度增加的影响,200升汽油的体积膨涨量为:()l T V V T T 4.2202000006.00=⨯⨯=∆=∆β由于容器封闭,体积不变,从而因体积膨涨量使容器内压强升高,体积压缩量等于体积膨涨量。
故:26400/1027.16108.9140004.22004.2mN E V V V V V V p p TT pTT⨯=⨯⨯⨯+=∆+∆-=∆+∆-=∆β2)在保证液面压强增量0.18个大气压下,求桶内最大能装的汽油质量。
设装的汽油体积为V ,那么:体积膨涨量为:T V V T T ∆=∆β;体积压缩量为:()()T V E p V VE p V T pT pp ∆+∆=∆+∆=∆β1因此,温度升高和压强升高联合作用的结果,应满足:()()⎪⎪⎭⎫ ⎝⎛∆-∆+=∆-∆+=p T pT E p T V V T V V 1110ββ()())(63.197108.9140001018.01200006.012001145l E p T V V p T =⎪⎪⎭⎫⎝⎛⨯⨯⨯-⨯⨯+=⎪⎪⎭⎫ ⎝⎛∆-∆+=β()kg V m 34.1381063.19710007.03=⨯⨯⨯==-ρ1-6解:石油的动力粘度:s pa .028.01.010028=⨯=μ石油的运动粘度:s m /1011.39.01000028.025-⨯=⨯==ρμν1-7解:石油的运动粘度:s m St /1044.01004025-⨯===ν石油的动力粘度:s pa .0356.0104100089.05=⨯⨯⨯==-ρνμ1-8解:2/1147001.01147.1m N u=⨯==δμτ1-9解:()()2/5.1621196.012.0215.0065.021m N d D u u=-⨯=-==μδμτN L d F 54.85.16214.01196.014.3=⨯⨯⨯=⨯⨯⨯=τπ第二章2-4解:设:测压管中空气的压强为p 2,水银的密度为1ρ,水的密度为2ρ。
第一章 流体及其主要物理性质1-1.轻柴油在温度15ºC 时相对密度为0.83,求它的密度和重度。
解:4ºC 时所以,33/8134980083.083.0/830100083.083.0mN m kg =⨯===⨯==水水γγρρ1-2.甘油在温度0ºC 时密度为1.26g/cm3,求以国际单位表示的密度和重度。
333/123488.91260/1260/26.1m N g m kg cm g =⨯==⇒==ργρ 1-3.水的体积弹性系数为1.96×109N/m 2,问压强改变多少时,它的体积相对压缩1%?MPa Pa E E VVVV p p6.191096.101.07=⨯==∆=∆=∆β 1-4.容积4m 3的水,温度不变,当压强增加105N/m 2时容积减少1000cm 3,求该水的体积压缩系数βp 和体积弹性系数E 。
解:1956105.2104101000---⨯=⨯--=∆∆-=Pa p V V p β Pa E p89104105.211⨯=⨯==-β 1-5石油相对密度0.9,粘度28cP ,求运动粘度为多少m 2/s?()cSt St s m 3131.0/101.310009.01028253==⨯=⨯⨯==--ρμν 1-6 相对密度0.89的石油,温度20ºC 时的运动粘度为40cSt ,求动力粘度为多少? 解:89.0==水ρρd ν=40cSt =0.4St =0.4×10-4m 2/s μ=νρ=0.4×10-4×890=3.56×10-2 Pa ·s1-7 图示一平板在油面上作水平运动,已知运动速度u=1m/s ,板与固定边界的距离δ=1mm ,油的动力粘度μ=1.147Pa ·s ,由平板所带动的油层的运动速度呈直线分布,求作用在平板单位面积上的粘性阻力为多少?解:233/10147.11011147.1m N dy du ⨯=⨯⨯==-μτ 1-8 如图所示活塞油缸,其直径D =12cm ,活塞直径d =11.96cm ,活塞长度L =14cm ,油的μ=0.65P ,当活塞移动速度为0.5m/s 时,试求拉回活塞所需的力F=?解:A =πdL , μ=0.65P =0.065 Pa ·s , Δu =0.5m/s , Δy=(D-d)/2()N dy du AF 55.821096.11125.010141096.1114.3065.0222=⨯-⨯⨯⨯⨯⨯⨯==---μ第二章 流体静力学2-1. 如图所示的U 形管中装有水银与水,试求:(1)A 、C 两点的绝对压力及表压各为多少? (2)A 、B 两点的高度差为多少?解:① p A 表=γh 水=0.3mH 2O =0.03at =0.3×9800Pa =2940Pap A 绝=p a + p A 表=(10+0.3)mH 2O =1.03at =10.3×9800Pa=100940Pap C 表=γhg h hg + p A 表=0.1×13.6m H 2O+0.3mH 2O =1.66mH 2O =0.166at=1.66×9800Pa =16268Pap C 绝=p a + p C 表=(10+1.66)mH 2O =11.66 mH 2O =1.166at =11.66×9800Pa =114268Pa ② 30c mH 2O =13.6h cmH 2O ⇒h =30/13.6cm=2.2cm题2-22-2 今有U 形管,内装水和四氯化碳(CCl 4),如图所示。
工程流体力学(第二版)习题与解答1 2p p 2 1 V 第 1 章 流体的力学性质1-1 用压缩机压缩初始温度为 20℃的空气,绝对压力从 1 个标准大气压升高到 6 个标准大气压。
试计算等温压缩、绝热压缩、以及压缩终温为 78℃这三种情况下,空气的体积 减小率∆V = (V 1 - V 2 )/V 1 各为多少?解:根据气体压缩过程方程: pV k = const ,有(V /V ) = ( p / p )1/ k ,所以2112(V -V ) V ⎛ p ⎫1/ k ∆ = 1 2 = 1 - 2= 1 - 1 ⎪VV V p 1 1 ⎝ 2 ⎭ 等温过程 k =1,所以∆V = 1 - p 1 / p 2 = 1 -1/ 6 =83.33%绝热过程 k =1.4,所以 ∆ = 1 - ( p / p )1/1.4= 1 - (1/ 6)1/1.4 =72.19% 压缩终温为 78℃时,利用理想气体状态方程可得∆ = 1 - V 2 = 1 - p 1T 2 = 1 - 1⨯ 78=80.03% V 1 p 2T 1 6 ⨯ 201-2 图 1-12 所示为压力表校验器,器内充满体积压缩系数 β = 4.75 ⨯10-10 m 2/N 的油, 用手轮旋进活塞达到设定压力。
已知活塞直径 D =10mm ,活塞杆螺距 t =2mm ,在 1 标准大气压时的充油体积为 V 0=200cm 3。
设活塞周边密封良好,问手轮转动多少转,才能达到 200 标准大气压的油压(1 标准大气压=101330Pa )。
解:根据体积压缩系数定义积分可得:β = - 1 d V → V = V exp[-β ( p - p )]pV d pp因为 ntπ D 24 = V 0 - V = V 0 ⎩⎣1 - e x p - β p ( p - p 0 ) ⎤⎦所以n = 4 V ⎡1 - e - β ( p - p )⎤ = 12.14 rpmπ D 2t 0 ⎣⎦0.05mm1kN20°图 1-12 习题 1-2 附图图 1-13 习题 1-3 附图1-3 如图 1-13 所示,一个底边为200mm ⨯ 200mm 、重量为 1kN 的滑块在 20°斜面的油膜上滑动,油膜厚度 0.05mm ,油的粘度μ= 7 ⨯10-2 Pa·s 。
设油膜内速度为线性分布,试求滑块的平衡速度u T 。
V30 ⎝ ⎭解:设油膜内速度呈线性分布,平衡时油膜内的速度梯度可计算为d u = d y u T - 0 0.05 ⨯10-3= 20000u T1/s 由牛顿剪切定理可得滑块表面处流体受到的切应力τ 为τ = μ d u= 7 ⨯10-2 ⨯ 20000u =1400 u Pad y T T滑块受到的切应力与τ 的大小相等方向相反,且滑块受到的摩擦力与滑块重力沿斜面分量平衡,所以A τ = mg sin θ → 0.2 ⨯ 0.2 ⨯1400u T = 1000sin 20 → u T ≈ 6.11m/s1-4 有一直径 d =150mm 的轴在轴承中转动,转速 n =400 r/min ,轴承宽度 L = 300mm , 轴与轴承间隙δ = 0.25mm ,其间充满润滑油膜,油的粘度为 μ = 0.049 Pa ⋅ s 。
假定润滑油膜内速度为线性分布,试求转动轴的功率 N (注:N =转轴表面积 A ⨯表面切应力τ ⨯表面线速度v θ )。
解:根据牛顿剪切定律有τ = μ d v θ = μ ωd /2 - 0 =μωd , M = A τ R = π dL μωd d = πμd 3L ω d r δ 2δ πμd 3 L ω2 2δ πμd 3 L ⎛ n π ⎫22 4δ由此得轴功率为: N = M ω = 4δ = 4δ⎪ =273.47W⎝ ⎭1-5 如图 1-14 所示,已知圆形管道中流体层流流动时的速度分布为:⎛ r 2 ⎫u = 2u m 1 - R 2 ⎪其中 u m 为管内流体的平均速度。
(1)设流体粘度为 μ ,求管中流体的剪切应力τ 的分布公式;(2)如长度为 L 的水平管道两端的压力降为∆p (进口压力-出口压力),求压力降∆p 的表达式。
解:(1)根据牛顿剪切定律有τ = μd u= -4μu d r rm R2由上式可知,壁面切应力为τ 0 = -4μu m / R ,负号表示τ 0 方向与 z 相反; (2)由流体水平方向力平衡有: π R 2 ∆p + τ π DL = 0 ,将τ 表达式代入得0 0∆p =8μu m L R 21-6 图 1-15 所示为两平行圆盘,直径为 D ,间隙中液膜厚度为δ ,液体动力粘性系数为 μ ,若下盘固定,上盘以角速度ω 旋转,求所需力矩 M 的表达式。
=AτR解:固定圆盘表面液体速度为零,转动圆盘表面半径r 处液体周向线速度速度vθs=rω;设液膜速度沿厚度方向线性分布,则切应力分布为τ=μ∂vθ =μvθs - 0 =μrω∂δδδR 2ππμωD4所需力矩M 为:M =⎰⎰τr(r d r dθ) =0 032δr =R /2yb b'd yt= 0 t=d tαα-dαa a'u ( y)ox 图1-15 习题1-6 附图图1-16 习题1-7 附图1-7如图1-16 所示,流体沿x 轴方向作层状流动,在y 轴方向有速度梯度。
在t=0 时,任取高度为d y 的矩形流体面考察,该矩形流体面底边坐标为y,对应的流体速度为u( y) ;经过d t 时间段后,矩形流体面变成如图所示的平行四边形,原来的α角变为α- dα,其剪切变形速率定义为dα/d t (单位时间内因剪切变形产生的角度变化)。
试推导表明:流体的剪切变形速率就等于流体的速度梯度,即dα=d ud t d y解:因为a 点速度为u,所以b 点速度为u+d ud y ;由此得a - a'、b - b'的距离为:d yaa'=u d t ,bb'= (u+d ud y)d td y所以dα≈ tan dα=bb'-aa'=d ud t 即dα=d ud y d y d t d yLR δ1n δ2δ 1-8 图 1-17 所示为旋转粘度测定仪。
该测定仪由内外两圆筒组成,外筒以转速 n (r/min )旋转,通过内外筒之间的油液,将力矩传递至内筒;内筒上下两端用平板封闭,上端固定悬挂于一金属丝下,通过测定金属丝扭转角度确定金属丝所受扭矩为 M 。
若内外筒之间的间隙为δ1 ,底面间隙为δ2 , 筒高为 L ,求油液动力粘性系数的计算式。
解:半径 R 的筒体表面磨擦扭矩为μ R ω 2π R 3 L ⎛ n π ⎫M 1 = A τ R = 2π RL δ R = μ δ 30 ⎪1 1 ⎝ ⎭筒体端部表面摩擦扭矩(相当于圆盘摩擦)为R 2πR Rr ω π μω R 4M 2 = ⎰ ⎰ τ r (r d r d θ ) = 2π ⎰τ r 2d r = 2π ⎰ μ 0 0 0 02由总扭矩 M = M 1 + M 2 解出油液动力粘性系数为r 2d r = 2δ2 μ = 2δ1δ2 M ⎛ 30 ⎫π R 3 (4L δ + R δ π ⎪2 1) ⎝ n⎭1-9 空气中水滴直径为 0.3mm 时,其内部压力比外部大多少?解:查附录表 C-1,水在常温空气中的表面张力系数σ =0.073N/m ,所以⎛ 1 1 ⎫ 2σ 2 ⨯ 0.073 ∆p = σ R + R ⎪ = R = 0.15 ⨯10-3= 973Pa⎝ 1 2 ⎭1-10 图 1-18 所示为插入水银中的两平行玻璃板,板间距δ =1mm ,水银在空气中的表面张力σ =0.514N/m ,与玻璃的接触角θ =140°,水银密度ρ =13600kg/m 3。
试求玻璃板内外水银液面的高度差 h 。
解:对于两平板间的液膜,如图所示,液面下侧压力 p 0 + ρ gh ,液面上侧压力为 p 0 ,取垂直书面方向为单位厚度,写出液膜竖直方向力平衡方程有p 0δ + 2σ cos(π - θ ) = ( p 0 + ρ gh )δ由此得两平壁间的液膜爬升高度为 h = 2σ cos θ = - 5.9 ⨯10-3 m= -5.9mmδρ g1-11 如图 1-19 所示,一平壁浸入体积很大的水中。
由于存在表面张力,在靠近壁面的地方水的表面成为弯曲面,弯曲液面垂直于 x-y 平面。
假定弯曲面曲率半径 r 可以表示成1/ r= d 2 y /d x 2 ,接触角θ 和表面张力系数σ 已知。
试确定平壁附近水面的形状和最大高度 h 。
1mmhθ图 1-18 习题 1-10 附图图 1-17 习题 1-8 附图yhθoxσyxp 0h p θGσp 0图 1-19 习题 1-11 附图水平液面以上流体受力分析解:根据弯曲表面张力压差公式,任意 x 处自由表面内外压力差为∆p = p - p = σ ( 1 + 1)R 1 R 2其中 p i 是 x 处自由表面内的压力, R 1 、 R 2 是 x 处自由表面两个正交法截线的半径。
因为 x 轴为水平液面,所以根据静力学原理,x 轴对应的水平面上压力为 p 0 ;设任意 x 处弯曲液面与水平液面的距离为 y ,根据静力学关系有p 0 = p i + ρ gy 即 ∆p = p 0 - p i = ρ gy所以ρ gy =σ ( R 1+ 1)R 2根据本题附图可知,如果取弯曲面曲线(x-y 平面内)曲率半径:1/ R 1 = d y / d x ,则 2 2与其正交的曲率半径 R 2 →∞ (因为自由液面⊥x-y 平面),于是有d y 2σd x 2- ρ gy = 0 → y = C 1e + C 2e由边界条件: x →∞ : y = 0 ,x =0:y =h ,可得C 1 = 0 , C 2 = h ,所以y = h exp (- ρ g /σ x)其中的 h 可根据边界条件: x = 0 , y ' = -1/ tan θ ,表示为h = (1/ tan θ ) 或,取 z 方向为单位厚度,由 y 方向力平衡可得∞σ cos θ = G → σ cos θ = ⎰ρ g y d x →h = cos θ 或,取 z 方向为单位厚度,由 x 方向力平衡可得hhσ sin θ + hp 0 = ⎰ p d y + σ → σ sin θ + hp 0 = ⎰ ( p 0 - ρ g y )d y + σh即σ sin θ = -⎰ ρ g y d y + σ 0→ h = ρ g x σ-ρ g x σρ g /σρ g /σ2(1-sin θ ) ρg /σ 1 0 i0 1 2 1 2 1-12 如图 1-20 所示,一圆形管内装有理想塑性流体,其剪切应力与变形速率的关系由式(1-18)所描述。