2018-2019闵行外国语高一下期中考试试卷

2019-2020学年上海市闵行区七宝中学高一（下）期中数学试卷试题数：21，总分：01.（填空题，3分）若cosα=- √32，则cos2α=___ ．2.（填空题，3分）已知sinα= 13，α∈（π2，π），则cosα=___ ．3.（填空题，3分）已知{a n}是等比数列，首项为3，公比为12，则前4项的和为___ ．4.（填空题，3分）若tanα=3，则sin2α=___ ．5.（填空题，3分）等差数列{a n}的前n项和为S n，a4=1，则S7=___ ．6.（填空题，3分）已知扇形的圆心角为2π3，半径为5，则扇形的面积S=___ ．7.（填空题，3分）在数列{a n}中，a2=5，a n+1-a n=2n（n∈N*），则数列{a n}的通项a n=___ ．8.（填空题，3分）我国南宋著名数学家秦九韶发现了从三角形三边求三角形面积的“三斜公式”，设△ABC内角A、B、C的对边分别为a、b、c，面积为S，则“三斜求积”公式为S=√1 4[a2c2−(a2+c2−b22)2]，若c2sinA=4sinC，B= π3，则用“三斜求积”公式求得△ABC的面积为___ ．9.（填空题，3分）函数y=sin(2x+π3)的图象向右平移π3个单位后与函数f（x）的图象重合，则下列结论中正确的是___ ．① f（x）的一个周期为-2π；② f（x）的图象关于x=- 7π12对称；③ x= 7π6是f（x）的一个零点；④ f（x）在(−π12，5π12)单调递减．10.（填空题，3分）已知函数f（x）=3sinx+4cosx，x1，x2∈[0，π]，则f（x1）-f（x2）的最大值是___ ．11.（填空题，3分）在锐角△ABC中，内角A，B，C对的边分别为a，b，c．若a2+b（b- √3 a）=1，c=1，则√3 a-b的取值范围为___ ．12.（填空题，3分）已知数列{a n}满足a1=4，a n=2a n-1+2n（n≥2，n∈N*），若不等式2n2-n-3＜（5-λ）a n对任意n∈N*恒成立，则实数λ的取值范围是___ ．13.（单选题，3分）函数y=2sin πx6，x∈R的最小正周期为（）A.12B.6C. π12D. π614.（单选题，3分）已知k∈Z，下列各组角中，终边相同的是（）A.2kπ与kπB.2kπ+π与4kπ±πC.kπ+ π6与2kπ± π6D. kπ2与kπ± π215.（单选题，3分）已知函数f（x）= √3sinωx+cosωx（ω＞0）在[0，π]上有两个零点，则ω的取值范围为（）A.（116，176）B.[ 116，176）C.（53，83）D.[ 53，83）16.（单选题，3分）有一个三人报数游戏：首先A报数字1，然后B报下两个数字2，3，接下来C报下三个数字4，5，6，然后轮到A报下四个数字7，8，9，10，依次循环，直到报出10000，则A报出的第2020个数字为（）A.5979B.5980C.5981D.以上都不对17.（问答题，0分）在△ABC中，三个内角A、B、C所对的边分别为a、b、c，且a2+c2-b2=ac．（1）求B；（2）若a+c=6，三角形的面积S△ABC=2 √3，求b．18.（问答题，0分）已知S n为{a n}的前n项和，{b n}是等比数列且各项均为正数，且S n=3 2n2+12n，b1=2，b2+b3= 32．（1）求{a n}和{b n}的通项公式；（2）记c n=a n•b n，求数列{c n}的前n项和T n．，现要在其中圈19.（问答题，0分）如图，有一块扇形草地OMN，已知半径为R，∠MON= π2̂上，且线段AB平行于线段出一块矩形场地ABCD作为儿童乐园使用，其中点A、B在弧MNMN．̂的一个三等分点，求矩形ABCD的面积S；（1）若点A为弧MN̂上何处时，矩形ABCD的面积S最大？最大值为多少？（2）设∠AOB=θ，求A在MN20.（问答题，0分）设正项数列{a n}的前n项和为S n，首项为1，q为非零正常数，数列{lg（a n）}是公差为lgq的等差数列．（1）求数列{S n}的通项公式；}是递增数列；（2）求证：数列{S nS n+1（3）是否存在正常数c，使得{lg（c-S n）}为等差数列？若存在，求出c的值和此时q的取值范围；若不存在，说明理由．21.（问答题，0分）数列{a n}满足a n a n+1a n+2=a n+a n+1+a n+2（a n a n+1≠1，n∈N*），且a1=1，）的形式表示．a2=2，若a n=Asin（ωx+φ）+c（A≠0，ω＞0，|φ|＜π2（1）求a3的值；（2）证明3为数列{a n}的一个周期，并用正整数k表示ω；（3）求{a n}的通项公式．2019-2020学年上海市闵行区七宝中学高一（下）期中数学试卷参考答案与试题解析试题数：21，总分：01.（填空题，3分）若cosα=- √32，则cos2α=___ ．【正确答案】：[1] 12【解析】：由已知利用二倍角的余弦函数公式即可计算求值得解．【解答】：解：∵cosα=- √32，∴cos2α=2cos2α-1=2× (−√32)2-1= 12．故答案为：12．【点评】：本题主要考查了二倍角的余弦函数公式在三角函数化简求值中的应用，属于基础题．2.（填空题，3分）已知sinα= 13，α∈（π2，π），则cosα=___ ．【正确答案】：[1]- 2√23【解析】：由sinα的值，及α的范围，判断出cosα为负数，利用同角三角函数间基本关系求出cosα的值即可．【解答】：解：∵sinα= 13，α∈（π2，π），∴cosα＜0，则cosα=- √1−sin2α =- 2√23，故答案为：- 2√23【点评】：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．3.（填空题，3分）已知{a n}是等比数列，首项为3，公比为12，则前4项的和为___ ．【正确答案】：[1] 458【解析】：利用等比数列前n 项和公式能求出等比数列前4项的和．【解答】：解：{a n }是等比数列，首项为3，公比为 12， 则前4项的和为S 4= 3(1−124)1−12= 458 ．故答案为： 458 ．【点评】：本题考查等比数列的前4项和的求法，考查等比数列的性质等基础知识，考查运算求解能力，是基础题．4.（填空题，3分）若tanα=3，则sin2α=___ ． 【正确答案】：[1] 35【解析】：利用同角三角函数的基本关系以及二倍角的正弦公式，把要求的式子化为 2tanα1+tan 2α ，把已知条件代入运算求得结果．【解答】：解：∵tanα=3， ∴sin2α=2sinαcosα= 2sinαcosαsin 2α+cos 2α = 2tanα1+tan 2α = 2×31+32 = 35． 故答案为： 35 ．【点评】：本题主要考查同角三角函数的基本关系的应用，二倍角的正弦公式的应用，属于基础题．5.（填空题，3分）等差数列{a n }的前n 项和为S n ，a 4=1，则S 7=___ ． 【正确答案】：[1]7【解析】：先由等差数列的性质可得a 1+a 7=2a 4，再根据等差数列的求和公式代入即可．【解答】：解：根据题意，等差数列{a n }中，a 1+a 7=2a 4， 则S 7=a 1+a 72×7=7a 4=7， 故答案为7．【点评】：本题考查等差数列的前n 项和公式，以及等差数列的性质应用，属于基础题． 6.（填空题，3分）已知扇形的圆心角为 2π3 ，半径为5，则扇形的面积S=___ ． 【正确答案】：[1]25π3【解析】：利用S= 12lr=12αr2，即可求得结论．【解答】：解：∵扇形的圆心角为2π3，半径为5，∴S= 12lr=12αr2 = 12×2π3×25 = 25π3故答案为：25π3【点评】：本题考查扇形面积的计算，考查学生的计算能力，属于基础题．7.（填空题，3分）在数列{a n}中，a2=5，a n+1-a n=2n（n∈N*），则数列{a n}的通项a n=___ ．【正确答案】：[1]2n+1【解析】：直接利用递推关系式和累加法求出数列的通项公式．【解答】：解：由题意可得：{a n−a n−1=2n−1a n−1−a n−2=2n−2…a2−a1=2，利用累加法，得：a n−a1=2(2n−1−1)2−1=2n−2，a1=3，于是：a n=2n+1．故答案为：2n+1【点评】：本题考查的知识要点：数列的通项公式的求法及应用，累加法在求数列通项公式中的应用，主要考查学生的运算能力和转化能力，属于基础题型．8.（填空题，3分）我国南宋著名数学家秦九韶发现了从三角形三边求三角形面积的“三斜公式”，设△ABC内角A、B、C的对边分别为a、b、c，面积为S，则“三斜求积”公式为S=√1 4[a2c2−(a2+c2−b22)2]，若c2sinA=4sinC，B= π3，则用“三斜求积”公式求得△ABC的面积为___ ．【正确答案】：[1] √3【解析】：根据已知利用正弦定理可得ac=4，根据余弦定理可得a2+c2-b2=4，利用三斜公式即可求解．【解答】：解：根据正弦定理，由c2sinA=4sinC，得ac=4，则由B= π3，得：a2+c2-b2=4，则△ABC的面积S= √14(16−4) = √3．故答案为：√3．【点评】：本题主要考查了正弦定理，余弦定理在解三角形中的应用，考查了转化思想，属于基础题．9.（填空题，3分）函数y=sin(2x+π3)的图象向右平移π3个单位后与函数f（x）的图象重合，则下列结论中正确的是___ ．① f（x）的一个周期为-2π；② f（x）的图象关于x=- 7π12对称；③ x= 7π6是f（x）的一个零点；④ f（x）在(−π12，5π12)单调递减．【正确答案】：[1] ① ② ③【解析】：推导出f（x）=sin[2（x- π3）+ π3]=sin（2x- π3），由此能求出结果．【解答】：解：∵函数y=sin（2x+ π3）的图象向右平移π3个单位后与函数f（x）的图象重合，∴f（x）=sin[2（x- π3）+ π3]=sin（2x- π3），∴f（x）的一个周期为-2π，故① 正确；y=f（x）的对称轴满足：2x- π3=kπ+ π2，k∈Z，∴当k=-2时，y=f（x）的图象关于x=- 7π12对称，故② 正确；由f（x）=sin（2x- π3）=0，得x= π6+ kπ2，∴x= 7π6是f（x）的一个零点，故③ 正确；当x∈（- π12，5π12）时，2x- π3∈（- π2，π2），∴f（x）在（- π12，5π12）上单调递增，故④ 错误．故答案为：① ② ③ ．【点评】：本题考查命题真假的判断，考查三角函数的平移变换、三角函数的性质等基础知识，考查运算求解能力，考查化归与转化思想，属于中档题．10.（填空题，3分）已知函数f（x）=3sinx+4cosx，x1，x2∈[0，π]，则f（x1）-f（x2）的最大值是___ ．【正确答案】：[1]9【解析】：本题先将函数f（x）转化成正弦函数的形式，然后结合正弦函数的图象判断出函数f（x）在区间[0，π]上的最大值和最小值，从而得出结果．【解答】：解：由题意，可知：f（x）=3sinx+4cosx=5•（35 sinx+ 45cosx）=5sin（x+θ），其中s inθ= 45，cosθ= 35．∵sinθ= 45，可知sin π4= √22≤45≤1=sinπ2，∴ π4≤θ≤π2对于函数f（x）=5sin（x+θ），可知：sinx向左平移θ个单位得到sin（x+θ），再将sin（x+θ）的图象沿y轴伸长到原来的5倍得到5sin（x+θ）．由题意，可知求f（x1）-f（x2）的最大值就是求函数f（x）=5sin（x+θ）在区间[0，π]上的最大值与最小值之差．又函数f（x）=5sin（x+θ）在区间[0，π]上的图象如下：由图象可知，在区间[0，π]上，当x= π2−θ时，f（x）取最大值5，当x=π时，f（x）取最小值5sin（π+θ）=-5sinθ=-4．∴在区间[0，π]上，f（x1）-f（x2）的最大值是5-（-4）=9．故答案为：9．【点评】：本题考查了三角函数的转化以及函数图象的变换知识，本题要特别注意细节点不能粗心大意．属中档题．11.（填空题，3分）在锐角△ABC 中，内角A ，B ，C 对的边分别为a ，b ，c ．若a 2+b （b- √3 a ）=1，c=1，则 √3 a-b 的取值范围为___ ． 【正确答案】：[1]（1， √3 ）【解析】：先根据余弦定理求得角C ，结合正弦定理把 √3 a-b 转化为2（ √3 sinA-sinB ），再结合AB 之间的关系求出角A 的范围，与正弦函数相结合即可求得结论．【解答】：解：因为在锐角△ABC 中，内角A ，B ，C 对的边分别为a ，b ，c ． ∵a 2+b （b- √3 a ）=1，c=1⇒a 2+b 2- √3 ab=c 2⇒2cosC= √3 ⇒cosC= √32 ⇒C=30°， ∴ csinC = asinA = bsinB = 1sin30° =2； ∴a=2sinA ，b=2sinB ；∴ √3 a-b=2（ √3 sinA-sinB ）=2[ √3 sinA-sin （150°-A ）]=2[ √3 sinA-（ 12 cosA+ √32 sinA ）]=2（ √32sinA- 12cosA ）=2sin （A-30°）； ∵0°＜A ＜90°，0°＜B ＜90°，A+B=150°； ∴60°＜A ＜90°；∴30°＜A-30°＜60°⇒2sin （A-30°）∈（1， √3 ）； 故 √3 a-b∈（1， √3 ）； 故答案为：（1， √3 ）．【点评】：本题主要考查了正弦定理和余弦定理的运用．考查了学生对三角函数基础知识的综合运用．12.（填空题，3分）已知数列{a n }满足a 1=4，a n =2a n-1+2n （n≥2，n∈N *），若不等式2n 2-n-3＜（5-λ）a n 对任意n∈N*恒成立，则实数λ的取值范围是___ ． 【正确答案】：[1] (−∞，378) 【解析】：首先利用构造新数列法的应用求出数列的通项公式，进一步利用函数的恒成立问题的应用和函数的导数的应用求出结果．【解答】：解：数列{a n }满足a 1=4，a n =2a n-1+2n （n≥2，n ∈N *），则： a n 2n −a n−12n−1=1 （常数），所以数列{ a n2n }是以 421=2 为首项，1为公差的等差数列． 所以 an 2n =2+(n −1)=n +1 ，整理得 a n =(n +1)•2n ，不等式2n 2-n-3＜（5-λ）a n 对任意n∈N *恒成立，所以5−λ＞(n+1)(2n−3)(n+1)•2n = 2n−32n，所以λ＜5−2n−32n对任意的n∈N*恒成立，所以设f（n）= 2n−32n ，故f′(n)=2−(2n−3)ln22n，当n=1，2时，f′（n）＞0，当n≥3时，f′（n）＜0，所以f（2）= 14，f（3）= 38．所以λ＜5−38=378．故答案为：（- ∞，378）．【点评】：本题考查的知识要点：数列的通项公式的求法及应用，恒成立问题的应用，函数的导数的应用，主要考查学生的运算能力和转换能力及思维能力，属于中档题型．13.（单选题，3分）函数y=2sin πx6，x∈R的最小正周期为（）A.12B.6C. π12D. π6【正确答案】：A【解析】：由题意利用函数y=Asin（ωx+φ）的周期为2πω，得出结论．【解答】：解：函数y=2sin πx6，x∈R的最小正周期为2ππ6=12，故选：A．【点评】：本题主要考查函数y=Asin（ωx+φ）的周期性，利用了函数y=Asin（ωx+φ）的周期为2πω，属于基础题．14.（单选题，3分）已知k∈Z，下列各组角中，终边相同的是（）A.2kπ与kπB.2kπ+π与4kπ±πC.kπ+ π6与2kπ± π6D. kπ2与kπ± π2【正确答案】：B【解析】：分别写出选项中所表示的终边所在的角的集合，逐一核对即可．【解答】：解：2kπ（k∈Z）表示终边在x轴非负半轴上的角的集合，kπ（k∈Z）表示终边在x 轴上的角的集合，两组角终边不同；2kπ+π与4kπ±π（k∈Z）都表示终边在x轴非正半轴上的角的集合，两组角终边相同；kπ+ π6（k∈Z）表示终边与π6和7π6终边相同的角的集合，2kπ± π6（k∈Z）表示终边与π6和- π6终边相同的角的集合，两组角终边不同；kπ2（k∈Z）表示终边在坐标轴上的角的集合，kπ± π2（k∈Z）表示终边在y轴上的角的集合，两组角终边不同；故选：B．【点评】：本题考查了终边相同的角的概念，属于基础题．15.（单选题，3分）已知函数f（x）= √3sinωx+cosωx（ω＞0）在[0，π]上有两个零点，则ω的取值范围为（）A.（116，176）B.[ 116，176）C.（53，83）D.[ 53，83）【正确答案】：B【解析】：利用辅助角公式化积，由x的范围得到ωx+π6∈[ π6，ωπ+π6]，再由函数f（x）在[0，π]上有两个零点，可得2π≤ωπ+ π6＜3π，由此求得ω的取值范围．【解答】：解：f（x）= √3sinωx+cosωx= 2sin(ωx+π6)，∵x∈[0，π]，∴ ωx+π6∈[ π6，ωπ+π6]，要使函数f（x）在[0，π]上有两个零点，则2π≤ωπ+ π6＜3π，解得：116≤ω＜176．∴ω的取值范围为[ 116，176）．故选：B．【点评】：本题考查对三角函数的化简能力和三角函数的图象和性质的运用，利用三角函数公式将函数进行化简是解决本题的关键．属于中档题．16.（单选题，3分）有一个三人报数游戏：首先A报数字1，然后B报下两个数字2，3，接下来C报下三个数字4，5，6，然后轮到A报下四个数字7，8，9，10，依次循环，直到报出10000，则A报出的第2020个数字为（）A.5979B.5980C.5981D.以上都不对【正确答案】：B【解析】：首先分析出A第n次报数的个数为3n-2，进一步求出3人以公报的次数，进一步利用前n项和公式的应用求出结果．【解答】：解：由题意可得：A第n次报数的个数为3n-2，则A第n次报完数后共报的个数为T n=n[1+(3n−2)]2=n(3n−1)2．再代入正整数n，使得T n≥2020，解得：n的最小值为37，得T37=2035．而A第37次报时，3人总共报了36×3+1=109次，当A第109次报完数3人总的报数个数为S n=1+2+3+⋯+109=109×(109+1)2=5995．即A报出的第2035个数字为5995，故A报出的第2020个数字为5980．故选：B．【点评】：本题考查的知识要点：数列的通项公式，数列的前n项和公式，主要考查学生的运算能力和转换能力及思维能力，属于中档题．17.（问答题，0分）在△ABC中，三个内角A、B、C所对的边分别为a、b、c，且a2+c2-b2=ac．（1）求B；（2）若a+c=6，三角形的面积S△ABC=2 √3，求b．【正确答案】：【解析】：（1）由已知结合余弦定理可求cosB，进而可求B；（2）由已知结合三角形的面积公式可求ac，进而可求．【解答】：解：（1）因为a2+c2-b2=ac．由余弦定理可得，cosB= a 2+c2−b22ac= 12，因为B为三角形的内角，所以B=π3；（2）∵a+c=6，三角形的面积S△ABC= 12acsin13π = √34ac =2 √3，∴ac=8，∵a2+c2-b2=ac，∴（a+c）2-b2=3ac，∴36-b2=24，∴b=2 √3【点评】：本题主要考查了余弦定理，三角形的面积公式的简单应用，属于中档试题．18.（问答题，0分）已知S n为{a n}的前n项和，{b n}是等比数列且各项均为正数，且S n=3 2n2+12n，b1=2，b2+b3= 32．（1）求{a n}和{b n}的通项公式；（2）记c n=a n•b n，求数列{c n}的前n项和T n．【正确答案】：【解析】：（1）先由a n=S n-S n-1求得a n，再检验n=1时是否适合，从而求得a n．设等比数列{b n}的公比为q，由题意列出q的方程，求得q，进而求得b n；（2）由（1）求得c n，再利用错位相减法求其前n项和T n．【解答】：解：（1）∵S n = 32n 2+12 n ，∴当n≥2时，有a n =S n -S n-1= 32n 2+12 n-3(n−1)22−12(n −1) =3n-1，又当n=1时，有S 1= 32+12=2=a 1也适合，∴a n =3n-1．设等比数列{b n }的公比为q ，由题意得： {q ＞0b 1=2b 1(q +q 2)=32，解得q= 12 ，故 b n =(12)n−2；（2）由（1）得c n =（3n-1）•（ 12）n-2，∴T n =2×（ 12 ）-1+5×（ 12 ）0+8×（ 12 ）1+…+（3n-1）×（ 12）n-2 ① ， 又 12T n =2×（ 12 ）0+5×（ 12 ）1+8×（ 12 ）2+…+（3n-1）×（ 12 ）n-1 ② ，由 ① - ② 得： 12T n =4+3[1+ 12 +（ 12 ）2+…+（ 12 ）n-2]-（3n-1）×（ 12 ）n-1=4+3× 1−(12)n−11−12 +（1-3n ）×（ 12 ）n-1=10-（3n+5）•（ 12 ）n-1 ∴ T n =20−3n+52n−2．【点评】：本题主要考查数列通项公式的求法及错位相减法在数列求和中的应用，属于基础题． 19.（问答题，0分）如图，有一块扇形草地OMN ，已知半径为R ，∠MON= π2 ，现要在其中圈出一块矩形场地ABCD 作为儿童乐园使用，其中点A 、B 在弧 MN ̂ 上，且线段AB 平行于线段MN ．（1）若点A 为弧 MN̂ 的一个三等分点，求矩形ABCD 的面积S ； （2）设∠AOB=θ，求A 在 MN̂ 上何处时，矩形ABCD 的面积S 最大？最大值为多少？【正确答案】：【解析】：（1）作OH⊥AB 于点H ，交线段CD 于点E ，连接OA 、OB ，求出AB ，EH ，可得矩形ABCD 的面积S ；（2）设∠AOB=θ（0＜θ＜ π2 ），求出AB ，EH ，可得矩形ABCD 的面积S ，再求最大值．【解答】：解：（1）如图，作OH⊥AB 于点H ，交线段CD 于点E ，连接OA 、OB ， ∴∠AOB= π6 ，∴AB=2Rsin π12 ，OH=Rcos π12 ， OE=DE= 12 AB=Rsin π12 ，∴EH=OH -OE=R （cos π12 -sin π12 ）， S=AB •EH=2R 2（sin π12 cos π12 -sin 2 π12 ）= √3−12R 2，（2）设∠AOB=θ（0＜θ＜ π2 ），则AB=2Rsin θ2 ，OH=Rcos θ2 ，oe= 12 AB=Rcos θ2 ，OE= 12 AB=Rsin θ2 ， ∴EH=OH -OE=R （cos θ2 -sin θ2 ），S=AB•EH=R 2（2sin θ2 cos θ2 -2sin 2 θ2 ）=R 2（sinθ+cosθ-1）=R 2[ √2 sin （θ+ π4 ）-1]， ∵0＜θ＜ π2 ， ∴ π4＜θ+ π4＜ 3π4 ， ∴θ+ π4 = π2 即θ= π4 时，S max =（ √2 -1）R 2，此时A 在弧MN 的四等分点处． 答：当A 在弧MN 的四等分点处时，S max =（ √2 -1）R 2．【点评】：本题考查扇形的面积公式，考查三角函数的性质，比较基础．20.（问答题，0分）设正项数列{a n }的前n 项和为S n ，首项为1，q 为非零正常数，数列{lg （a n ）}是公差为lgq 的等差数列． （1）求数列{S n }的通项公式；（2）求证：数列 {S nSn+1} 是递增数列；（3）是否存在正常数c ，使得{lg （c-S n ）}为等差数列？若存在，求出c 的值和此时q 的取值范围；若不存在，说明理由．【正确答案】：【解析】：（1）根据题意得a 1=1，根据题意可得lg （a n ）=lg （a 1）+（n-1）lgq=lg1+（n-1）lgq=lgq n-1，即a n =q n-1，分当q=1时，当q≠1时，两种情况写出S n （2）当q=1时，S n =n ， S nSn+1=1- 1n+1 随着n 的增大而增大，当q ＞0，q≠1时， S nSn+1- Sn+1S n+2=1−q n 1−q n+1 - 1−q n+11−q n+2 = −q n (1−q )2(1−q n+1)(1−q n+2) ＜0，可得数列 {S nS n+1} 是递增数列； （3）假设存在正常数c 使得{lg （c-S n ）}为等差数列，若{lg （c-S n ）}为等差数列，可得q≠1，lg （c- 11−q + q n1−q ）=lg q n1−q =nlgq-lg （1-q ）为等差数列， 即可求出c= 11−q（0＜q ＜1）．【解答】：解：（1）根据题意得a 1=1， 因为数列{lg （a n ）}是公差为lgq 的等差数列，所以lg （a n ）=lg （a 1）+（n-1）lgq=lg1+（n-1）lgq=lgq n-1， 所以a n =q n-1， 当q=1时，S n =n ， 当q≠1时，S n = 1×(1−q n )1−q = 1−q n1−q ，所以 S n ={nq =11−q n1−qq ＞0且q ≠1．（2）证明：当q=1时，S n =n ， 所以 S nSn+1= n n+1 =1- 1n+1 随着n 的增大而增大，当q ＞0，q≠1时， S n = 1−q n1−q ，S n S n+1= 1−q n1−q n+1 ，由S nS n+1 - S n+1S n+2= 1−q n1−q n+1- 1−q n+11−q n+2= −q n(1−q)2(1−q n+1)(1−q n+2)＜0，可得数列{S nS n+1}是递增数列；（3）假设存在正常数c使得{lg（c-S n）}为等差数列，所以C n=lg（c-S n）=lg（c- 1−q n1−q），数列{C n}是等差数列，即C1=lg（C-1），C2=lg（c- 1−q21−q）=lg（c-1-q），C3=lg（c- 1−q31−q）=lg（c-1-q2-q），（c-1-q）2=（c-1）（c-1-q2-q），解得c= 11−q，因此c＞0，所以0＜q＜1，此时C n=lg（11−q - 1−q n1−a）=lg q n1−q，因为C n+1-C n=lg q n+11−q -lg q n1−q=lgq，所以数列{C n}是等差数列，因此存在正常数c= 11−q，使得{lg（c-S n）}为等差数列，且0＜q＜1．【点评】：本题考查了等差数列，等比数列的性质、考查了推理能力与计算能力，属于基础题．21.（问答题，0分）数列{a n}满足a n a n+1a n+2=a n+a n+1+a n+2（a n a n+1≠1，n∈N*），且a1=1，a2=2，若a n=Asin（ωx+φ）+c（A≠0，ω＞0，|φ|＜π2）的形式表示．（1）求a3的值；（2）证明3为数列{a n}的一个周期，并用正整数k表示ω；（3）求{a n}的通项公式．【正确答案】：【解析】：（1）代值计算即可，（2）分别令n=1，2，3，即可证明，根据周期公式即可求出，（3）分别由a1=1，a2=2，a3=3，可得1=Asin（2π3+φ）+c，2=-Asin（π3+φ）+c，3=Asinφ+c，解得即可求出．【解答】：解：（1）当a 1=1，a 2=2，a 1a 2a 3=a 1+a 2+a 3，解得a 3=3； （2）当n=2时，6a 4=2+3+a 4，解得a 4=1， 当n=3时，3a 5=1+3+a 5，解得a 5=2， …，可得a n+3=a n ，当a 1=1，a 2=2，a 3=3； 故3为数列{a n }的一个周期， 则2kπω=3，k∈N*，则 ω=2kπ3(k ∈N ∗) ；（3）由（2）可得a n =Asin （ 2π3 n+φ）+c ，则1=Asin （ 2π3 +φ）+c ，2=-Asin （ π3 +φ）+c ，3=Asinφ+c ， 即1=A• √32 cosφ-A• 12 sinφ+c ， ① 2=-A• √32 cosφ-A• 12 sinφ+c ， ② 由 ① + ② ，可得3=-Asinφ+2c ， ∴c=2，Asinφ=1，① - ② ，可得-1=A• √3 cosφ， 则tanφ=- √3 ， ∵|φ|＜ π2 ， ∴φ=- π3 ， ∴A=-2√33， 故 a n =−2√33sin (2π3n −π3)+2 ．【点评】：本题考查了数列的递推公式和三角函数的解析式，考查了运算能力和转化能力，属于中档题．。

2018-2019学年上海市闵行区七宝中学高一下学期期末数学试题一、单选题1．已知{}n a 、{}n b 都是公差不为0的等差数列，且lim 2nn na b →∞=，12n n S a a a =++⋯+，则22lim nn nS nb →∞的值为（ ） A ．2B ．-1C ．1D ．不存在【答案】C【解析】首先根据lim 2n n n a b →∞=求出数列{}n a 、{}n b 公差之间的关系，再代入22lim nn nSnb →∞即可。

【详解】因为{}n a 和{}n b 都是公差不为零的等差数列，所以设()()11121?1n n b b n d a a n d =+-=+- 故()()11121limlim 21nn n n a n d a b b n d →∞→∞+-==+-，可得122d d =又因为()112112n n n d a a a na -+++=+和()21121n b b n d =+-代入则()()1112122122lim lim 21212n n n nn n d na S d nb nb n n d d →∞→∞⎛⎫-+ ⎪=⨯== ⎪+- ⎪ ⎪⎝⎭． 故选：C ． 【点睛】本题主要考查了极限的问题以及等差数列的通项属于基础题。

2．设{}n a 是公比为()01q q <<的无穷等比数列，若{}n a 的前四项之和等于第五项起以后所有项之和，则数列21{}n a -是（ ） A ．公比为12的等比数列B ．公比为2的等比数列C ．公比为2或2-的等比数列D的等比数列【答案】B【解析】根据题意可得42n S S =，带入等比数列前n 和即可解决。

【详解】根据题意，若{}n a 的前四项之和等于第五项起以后所有项之和， 则42n S S =，又由{}n a 是公比为()01q q <<的无穷等比数列，则()4111211a q a q q-=--，变形可得412q =，则q =，数列{}21n a -为{}n a 的奇数项组成的数列，则数列{}21n a -为公比为2q =列； 故选：B ． 【点睛】本题主要考查了利用等比数列前n 项和计算公比，属于基础题。

上海市浦东新区2018-2019学年高一下学期期中联考数学试卷注意事项：1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上第I 卷（选择题）一、选择题A. 第一象限的角都是锐角B. 小于π2的角是锐角 C. 2019°是第三象限的角 D. 2019°是第四象限的角2.“sinα=sinβ”是“α=β”的________条件A. 充分非必要B. 必要非充分C. 充要D. 既非充分又非必要3.若ΔABC 的三内角分别为A,B,C ，满足sin2A =sin2B ，则ΔABC 的形状为（ ）A. 等腰三角形B. 直角三角形C. 等边三角形D. 等腰或直角三角形4.设MP 与OM 分别是角11π12的正弦线和余弦线，则A. MP ＜OM ＜0B. MP ＜0＜OMC. OM ＜MP ＜0D. OM ＜0＜MP第II 卷（非选择题）二、解答题20cm,当它的圆心角为多大时,该扇形的面积最大?并求面积的最大值。

6.已知tanθ=a (a >1)，求sin (π4+θ)sin (π2−θ)⋅tan2θ的值。

7.修建铁路时要在一个大山体上开挖一隧道，需要测量隧道口D 、E 之间的距离，测量人员在山的一侧选取点C ，因有障碍物，无法测得CE 、CD 的距离，现测得CA=482.80米，CB=631.50米，∠ACB=56.3°，又测得A 、B 两点到隧道口的距离分别是80.13米、40.24米(A 、D 、E 、B 在同一条直线上)，求隧道DE 的长(精确到1米)。

8.已知tanx=17,siny =√1010，x ，y ∈(0，π2)，求x +2y 的值.9.在△ABC 中，已知边a=2√3，角B=45°，面积S △ABC =3+√3.求:(1)边c；三、填空题10.与2终边相同的角的集合是________.11.若tanθ＜0且sinθ＜0，则θ是第_______象限的角.12.已知角α的终边经过点P(-3,4)，则sinα+cosα=________.13.已知cosα=45，且α是第四象限的角，则cscα=_______,14.若sinx+cosx=12，则sin2x=_______.15.把sinα+√3cosα化成Asin(α+φ)(A>0)的形式___________(注:φ不唯一).16.若cosα=−35，α∈(π2，π)，则sin(α+π6)=_______.17.log2(sin2α+sec2α+12−1cot2α)=_______.=__________.18.化简：cos(2π−α)cot(3π+α)tan(−α−π)sin(π−α)cot(5π−α)19.若α∈(π2，π)且sinα=1213，则sin2α=_________.20.已知cosα=−23且π＜α＜3π2，则sinα2=______.21.在△ABC中，a=4，A=30°，请给出一个b值_______，使该三角形有两解.参考答案1.C【解析】1.根据象限角的定义依次判断即可.对于A. 第一象限的角都是锐角是错误的，比如3650就是第一象限角，但是不是锐角；对于B. 小于π2的角是锐角也是错误的，比如负角，小于π2，但不是锐角；对于C. 2019°=5×3600+2190,2190是第三象限角，故正确；对于D ，由C 知是错误的.故答案为：C. 2.B【解析】2. 因为sinα=sinβ根据正弦函数的性质得到α=β+2kπ，或者α+β=π+2kπ,k ∈z ，反之一定成立，再根据充分必要条件的判断，得到结果.因为sinα=sinβ，故得到α=β+2kπ，或者α+β=π+2kπ,k ∈z ,推不出α=β.反之，若α=β，则sinα=sinβ.故sinα=sinβ是“α=β”的必要非充分条件.故答案为：B. 3.D【解析】3.根据三角形内角范围得到2A ∈(0,2π),2B ∈(0,2π)，再结合三角函数正弦图像得到结果.在△ABC 中，内角A 、B 满足sin2A =sin2B ,2A ∈(0,2π),2B ∈(0,2π)，根据正弦函数的图像的性质得到2A =2B 或2A +2B =π⇒A +B =π2.故三角形是等腰三角形或者直角三角形. 故答案为：D. 4.D【解析】4.根据三角函数线的定义得结果即可.根据三角函数线的定义得到，钝角的余弦线是负的，正弦线是正的，故得到OM ＜0＜MP. 故答案为：D.5.当圆心角为2弧度时，面积最大，最大值为25cm 2【解析】5.首先根据扇形的弧长与半径的关系，建立等式，然后根据面积公式转化成关于r 的二次函数，通过解二次函数最值求结果． 设扇形的半径为r ，弧长为l ， ∵l ＝20﹣2r ，∴S =12lr =12（20﹣2r ）•r ＝﹣r 2+10r ＝﹣（r ﹣5）2+25∴当半径r ＝5cm 时，扇形的面积最大为25cm 2， 此时，α=l r=2（rad ）．故当圆心角为2弧度时，面积最大，最大值为25cm 2. 6.√2a1−a【解析】6.利用两角和与差的正弦函数，以及二倍角的正切，化简sin(π4+θ)sin(π2−θ)⋅tan2θ，代入tanθ＝a ，求出结果即可． 原式=√22cosθ+√22sinθcosθ⋅2tanθ1−tan 2θ=√22(1+tanθ)⋅2tanθ1−tan 2θ=√2a 1−a．即：sin(π4+θ)sin(π2−θ)⋅tan2θ=√2a1−a ．7.421米【解析】7.结合题意和示意图，根据余弦定理得到AB 长，进而得到结果.根据题意以及图像得到：在三角形ABC中，∠ACB=56.30,由余弦定理得到AB2=AC2+BC2−2AC⋅BC⋅cos∠ACB=482.802+631.502−2×482.80×631.50×cos56.30=293557.0525∴AB≈541.81,ED=AB−AD−BE≈421（米）所以，隧道长度约为421米.8.π4【解析】8.根据两角的正弦值，以及x，y∈(0，π2)得到两个角的较为精确的范围x,y∈(0,π6)，通过同角三角函数关系得到tany=13，由二倍角公式得到tan2y=34<1,2y∈(0,π4)，从而得到结果.∵tanx=17<12,siny=√1010<12,x,y∈(0,π2)∴x,y∈(0,π6)∴cosy=√1−sin2y=3√1010∴tany=sinycosy =13∴tan2y=2tany1−tan2y =34<1∴2y∈(0,π4)∴x+2y∈(0,512π)由tan(x+2y)=tanx+tan2y1−tanxtan2y=1.∴x+2y=π4.9.（1）√2+√6；（2）75∘【解析】9.（1）根据题意，由三角形的面积公式，代入数值得到结果；（2）由余弦定理得到b= 2√2，再由余弦定理得到A=600，由三角形三角和为π，得到结果.（1）由S△=12acsinB⇒3+√3=12×2√3⋅c⋅sin450解得c=√2+√6.(2)由余弦定理得到b2=a2+c2−2accosB,所以得到b 2=(2√3)2+(√2+√6)2−2⋅2√3(√2+√6)cos450解得b=2√2再由余弦定理得到cosA=b 2+c 2−a 22bc=12⇒A =600C =75010.{α|α=π2+2kπ,k ∈Z }【解析】10.与π2终边相同的角的集合是终边落在y 轴正半轴的角构成的，写出来即可.与π2终边相同的角的集合是终边落在y 轴正半轴的角构成的，即{α|α=π2+2kπ,k ∈Z }. 故答案为：{α|α=π2+2kπ,k ∈Z }. 11.四【解析】11.若tanθ＜0则角在第二和第四象限，若sin θ＜0则角在第三或第四象限，取两者交集即可. 若tanθ＜0则角在第二和第四象限，若sin θ＜0则角在第三或第四象限，同时成立，则角在第四象限. 故答案为：四. 12.15【解析】12.根据三角函数的定义可得到相应的三角函数值.已知角α的终边经过点P(-3,4),根据三角函数定义得到sinα=45,cos =−35,故得到结果为：15. 故答案为：15. 13.−53【解析】13.根据同角三角函数的基本关系得到sinα=−35,进而得到结果.已知cos α=45，且α是第四象限的角,根据sin 2α+cos 2α=1得到sinα=−35,cscα=1sinα=−53.故答案为：−53. 14.−34【解析】14.将式子两侧平方得到结果. 若sinx+cosx =12,将两边平方得到1+2sinxcosx =1+sin2x =14,sin2x =−34.故答案为：−34.15.2sin (α+π3)【解析】15.根据特殊角的三角函数值，以及两角和的正弦公式得到结果.sinα+√3cosα=2(12sinα+√32cosα)=2sin (α+π3)故答案为：2sin (α+π3)16.4√3−310【解析】16.根据题干以及同角三角函数关系得到sinα=45,再结合两角和的正弦公式得到结果。

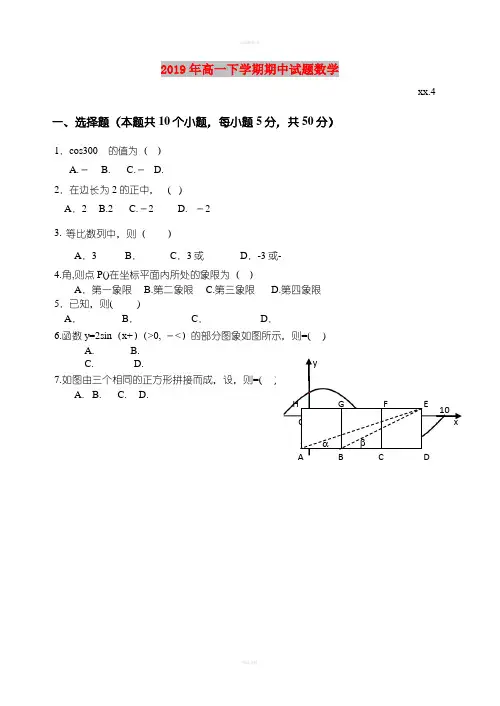
2019年高一下学期期中试题数学xx.4一、选择题（本题共10个小题，每小题5分，共50分）1．cos300的值为（ ） A.－ B. C.－ D. 2．在边长为2的正中， ( ) A ．2 B.2 C.－2 D. －2 3. 等比数列中，则（ ）A ．3B ．C ．3或D ．-3或- 4.角,则点P()在坐标平面内所处的象限为（ ）A ．第一象限 B.第二象限 C.第三象限 D.第四象限 5．已知，则( )A ．B ．C ．D ．6.函数y=2sin （x+）（>0, －<）的部分图象如图所示，则=( )A. B.C. D. 7.如图由三个相同的正方形拼接而成，设，则=( ) A. B. C. D.y xO10 H F G α β8.设函数，则下列结论正确的是：A.的图象关于点中心对称B.在上单调递增C.把的图象向左平移个单位后关于y 轴对称D.的最小正周期为 9. 在等比数列中，若，则=( ) A. B. C. D.10.若△ABC 的内角A 、B 、C 所对的边a 、b 、c,若角A 、B 、C 依次成等差数列，且，则△ABC 的面积为A ．B ．C ．D ．二、填空题（本大题共4小题，每小题5分，共20分）11. = ▲ .12．等差数列中，有，则= ▲ 。

13. 向量、的坐标分别是(1,2)、(3,-4),则在上的射影= ▲ .14．观察下面的行列数阵的排列规律：⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------12321.....................215431143212321n n n nn n n n n n记位于第行第列的数为。

当n=8时，= ▲ ;(2分) 当n=xx 时，= ▲ .(3分)三、解答题（本题共6小题，共80分。

解答应写出文字说明、证明过程或演算步骤）15. （本小题满分12分）（6分+6分）在直角坐标系中，A (3，0)，B(0，3)，C（1）若,求的值；（2）与能否共线？说明理由。

等于第 1 页，共 12 页2018-2019 学年重庆外国语学校高一（下）期中数学试卷选择题（本大题共 12小题，共 60.0 分）数列 1， ，，， ， 的一个通项公式可能是 A. 已知 ， A.B. C.， a ， b ， ，则下列不等式成立的是D.B . 中，B . 已知等差数列 A. 64 在 中， ， ， A.B.在 中，若 ， A.等腰三角形 B.钝角三角形 D.， ，则 的值是31 C.C. 30，则 b 等于D.15 二次不等式 的解集为 C. 则 必定是 C.直角三角形 ，则 D. D.A. B. 5C. 已知 中，角 A ，B ，C 的对边为 面积为 3，则 A.已知等比数列 a ，b ， B. C. 中，各项都是正数，且 锐角三角形 ab 的值为 D.6 c ，且 ， ， 的 ，， D.成等差数列，则 等于A.6 等差数列 中， ， ，当其前 n 项和取得最大值时， A.16 B.8 某校运动会开幕式上举行升旗仪式， 排测得旗杆顶部的仰角分别为 B. 7 C.8 D. 9 C. 9 D.17 在坡度为的看台上， 同一列上的第一和最后 ， 和 ，第一排和最后一排的距离为 如图所示 ，则旗杆的高度为A. 10m数列 满足 ，且对于任意的 都有D.，则1. 2.3. 4.5. 6.7.8.9. 10.11.B.C.12.已知数列的前n 项和为，且满足，，，若不等式对任意的正整数n恒成立，则整数m的最大值为A. 3B. 4C. 5D. 6二、填空题（本大题共4 小题，共20.0 分）13.在等比数列中，已知，则_________________________14.在中，，，，则解的情况是____________________________________ 填“无解”“一解”或“两解”15.在数列中，已知，则__________________________________ ．16.在中，a，b，c分别为内角A，B，C 的对边，其面积为S，若，则周长的最大值为____________ ．三、解答题（本大题共6 小题，共70.0 分）17.已知数列是公差不为0 的等差数列，首项，且，，成等比数列．求数列的通项公式；设数列满足，求数列的前n 项和18.设函数．若，解不等式；若，解关于x 的不等式．19.在中，内角A，B，C所对的边分别为a，b，c 已知．Ⅰ 求角C 的大小Ⅱ 若，的面积为，求的周长．20. 已知数列 的前 n 项的和为 ，且 ，其中 ．求数列 的通项公式； 若数列 满足 ，求数列的前 n 项和 ，并证明 ．若 ，求 的大小； 若 ，且 ，求 AD 的长．已知数列 满足 ， 设 ，求证是等比数列；求数列 的通项公式；设 ，数列 的前 n 项和为 ，求 的范围．21. 如图， D 是直角 斜边 BC 上一点， ．22.1.答案： B解析： 【分析】 本题考查了不完全归纳法求数列的通项公式，做题时要认真观察，找到规律，属于基础 题．根据数列前几项找规律，求出数列的通项公式，【解答】 解：数列 1， ， ， ， 中， 分子是连续整数，分母是连续奇数， 故数列 1， ， 故选 B ．2.答案： B解析： 解： ，，故选： B ． 由不等式的性质直接可以判断选项 B 正确 本题考查不等式性质的运用，属于基础题．3.答案： D解析： 【分析】 本题考查了等差数列的性质，属于基础题． 对等差数列 ，有 成立，代入数值计算即可． 【解答】 解：因为 是等差数列， 所以所以 ． 故选 D ．4.答案： A解析： 【分析】 本题考查正弦定理的应用，三角形的解法，是基础题． 利用三角形的内角和求出 C ，然后利用正弦定理求解即可． 【解答】解： 中， ， ， ，故选： A ．5.答案： A答案与解析的一个通项公式可能是，由正弦定理可得：解析：解：，由余弦定理可得，，整理可得，，为等腰三角形．故选：A．由已知结合余弦定理即可得到b，c 之间的关系，从而可判断．本题主要考查了余弦定理在求解三角形中的简单应用，属于基础题．6. D解析：解：不等式的解集为，，原不等式等价于，由韦达定理知，，，，．故选：D ．先对原不等式进行等价变形，进而利用韦达定理求得和的值，进而求得aba和b，则的值可求得．本题主要考查了一元二次不等式的解法，注意和一元二次方程的相关问题解决．7.答案：C解析：解：，，．的面积为3，，解得．则，解得．故选：C．利用三角形面积计算公式及其余弦定理即可得出．本题考查了三角形面积计算公式及其余弦考查了推理能力与计算能力，属于中档定理，题．8.答案：D解析：解：，，成等差数列，，，，舍去．故选：D ．根据所给的三项成等差数列，写出关系式，得到公比的值，把要求的代数式整理成只含 有首项和公比的形式，进一步化简计算得到结果．本题主要考查了等差数列和等比数列的性质， 考查了学生综合分析的能力和对基础知识 的理解，是基础题．9.答案： B，当其前 n 项和取得最大值时， ． 故选： B ． 本题考查了等差数列的通项公式求和公式及其性质， 中档题．10.答案： B解析： 解：如图， 依题意知 ，，在 中， ，即旗杆的高度为 30m ． 故选： B ．作图，分别求得 ， 和 ，然后利用正弦定理求得 AC ，最后在直角 三角形 ACD 中求得AD本题主要考查了解三角形的实际应用． 结合了正弦定理等基础知识， 考查了学生分析和 推理的能力，属于中档题．11.答案： D解析： 解： 数列 满足 ，且对于任意的 都有 ， ，解析： 解： ，利用等差数列的通项公式求和公式及其性质可得：进而得出结论．考查了推理能力与计算能力， 属于由正弦定理知． ．． ．故选： D ．数列 满足 ，且对于任意的 都有 ，可得，利用 ，可得再利用裂项求和方法即可得出．本题考查了数列递推关系、等差数列的通项公式与求和公式、累加求和方法、裂项求和 方法，考查了推理能力与计算能力，属于中档题．12.答案： B解析：解： ， ， ， 可得时， ，由 可得 ， 即有 ； 不等式 ， 当 时， 不成立， 即为 ，即为， 设 ， ， 可得 ， 即有 为 的最大值，且为 ，即有 ，即 ，可得 m 的最大值为 4． 故选： B ．将 n 换为 ，两式相减，运用数列的递推式和等差数列的定义和通项公式，可得； ，设断单调性，可得 的最大值，解不等式可得所求最大值．本题考查整数的最大值的求法，考查等差数列、等比数列的性质等基础知识，考查运算 求解能力，是中档题．13.答案： 4解析： 解：根据题意，在等比数列 中， 已知 ，则 ，则 ， 则； 故答案为： 4．根据题意，由等比数列的性质可得 ，则 ，又由 ，即可得答 案． 本题考查等比数列的性质，关键是掌握等比中项的性质，属于基础题．14.答案： 无解解析： 解：由正弦定理得： 即 ，解得 ， 因为， ，故角 B 无解． 即此三角形解的情况是无解． 故答案为：无解．．由 a ， b 及 sinA 的值，利用正弦定理即可求出 sinB 的值，求解即可．，判即有 ，此题考查学生灵活运用正弦定理化简求值，掌握正弦函数的图象与性质，是一道基础题．15.答案：解析：解：在数列中，已知，当时，，所以数列的等差数列，则．所以．故答案为：．推出数列是等差数列，求出通项公式，然后求解即可．本题考查数列的递推关系式的应用，通项公式的求法，是基本知识的考查．16.答案：6解析：解：，，，．由余弦定理可得：，可得，即，当且仅当时取等号．周长的最大值为．故答案为：6．由，利用三角形面积计算公式、余弦定理可得A ，再利用余弦定理、结合基本不等式的性质即可得出．本题考查了三角形面积计算公式、余弦定理、基本不等式的性质，考查了推理能力与计算能力，属于中档题．17.答案：解：设数列的公差为d，由题意，即：，解得：，或舍去，所以：．由可知，，，．解析：直接利用已知条件求出数列的通项公式．利用分组法求出数列的和．本题考查的知识要点：数列的通项公式的求法及应用，利用分组法求出数列的和．18.答案：解：，当时，即为，即，解得故不等式的解集为；由可知，，当时，不等式的解集为；当时，不等式的解集为空集；当时，不等式的解集为．解析：将代入，直接计算即可；可知，然后分类讨论即可求解不等式．本题主要考查一元二次不等式的解法，考查分类讨论思想，属于基础题．19.答案：解：Ⅰ ．由正弦定理可得：，，可得：，，．Ⅱ ，，的面积为，解得：，由余弦定理可得：，解得：，的周长．解析：Ⅰ 由正弦定理可得，结合，可求，结合范围，可求C 的值．Ⅱ 由已知利用三角形面积公式可求 ，根据余弦定理可解得 ，即可 解得 的周长． 本题主要考查了正弦定理，三角形面积公式，余弦定理在解三角形中的综合应用，属于 中档题．20.答案： 解：在中，由 时， ，得 ，当 时， ， 由 ， ， 两式相减得 ，即 是首项为 ，公比为 的等比数列， 所以 ， ；求得 ，运用数列的错位相减法求和，以及等比数列的求和公式，计算可得所求和，再由不等式的性质，即可得证． 本题考查数列的递推式的运用： 求通项公式， 考查等比数列的通项公式和求和公式的运 用，以及数列的错位相减法求和，考查化简运算能力和推理能力，属于中档题．21.答案： Ⅰ ， ， ，在 中，由正弦定理可得：，，或 ，又，；Ⅱ，，解运用数列的递推式： 时， ，当 时， ，结 ．合等比数列的定义和通项公式，即可得到所求通项公式；两式相减得：所以证明： ， 则在 中，由勾股定理可得： ，可得： ，， ， ，令 ，由余弦定理：在 中， ，在 中， ，， 解得： ，可得： ．解析： 本题主要考查了正弦定理，余弦定理，勾股定理在解三角形中的应用，考查了计 算能力和转化思想，属于中档题．Ⅰ 由已知可求 ，在 中，由正弦定理可得 ，即 可解得 ．Ⅱ 由已知在 中，由勾股定理可得 ， ， ，令22.答案： 证明：依题意，由 ，可得两边取以 5 为底的对数，可得，即 ．，数列 是以 1 为首项， 2 为公比的等比数列． 解：由 知， ， 即，，，可得：，由余弦定理即可解得 AD的值．，．解：由 知，解析：第题将递推式进行转化变形可得再两边取以5 为底的对数进行计算可证得数列是等比数列；第题先根据第题的结论计算出数列的通项公式，进一步可计算出数列的通项公式；第题先将数列的表达式进行变形之后运用裂项相消法计算前n 项和，然后根据逐步推导并进行不等式运算可得的范围．本题主要考查数列由递推公式求通项公式，裂项相消法计算前n项和．考查了转化和化归思想，整体思想，以及不等式的运算能力，逻辑思维能力和数学运算能力．本题属中档题．。

2018-2019学年上海市闵行区七宝中学高一（下）期末数学试卷.填空题公式为b -a 的最小值为2 2 211. (3 分)△ ABC 中，sin A < sin B+sin C - sinBsinC ,贝U A 的取值范围为2 212.（ 3分）关于x 的方程x - 4 arctan （ cosx ） + n ?a = 0只有一个实数根，则实数a =3 13. (3 分)等差数列｛a n ｝前 n 项和为 S n ,已知(a 2- 2) +2013 (a 2- 2) = sin3-2) +2013 (a 2013 - 2)= cos14. （ 3分）数列｛a n ｝的前n 项和为S n,若数列｛a n ｝的各项按如下规律排列： 1. (3 分)方程cosx = sin —的解为x =2. (3 分)设｛a n ｝为等差数列，若 a i +a 5+a 9= n 贝V a 2+a 8=3. (3 分) 求值:4. (3 分)函数 y = arccos (sinx ), 5. (3 分)设数列｛a n ｝的前n 项和Si ,若a i =- 1, S n 0 ( n N *),则｛a n ｝的通项 6. (3 分) 利用数学归纳法证明不等式“ 1 >-(n > 2, n N * )” 的过程 中，由 “ n = k ”变项7. (3 分) 若 f (x )= 2sinx - 1 在区间[a , b] (a , b R 且a v b ）上至少含有 30个零点，则 9. （3分）设数列｛a n ｝的通项公式为a n ' (a 〔+a 2+ …+a n )= （3分）已知数列｛a n ｝中，其前n 项和为S n , 为正奇数 ,为正偶数 ，则S 9 = 10. （3分）对于正项数列｛a n ｝，定义 为｛a n ｝的“光阴”值，现知 某数列的“光阴”值为 ，则数列｛a n ｝的通项公式为 ,(a 2013，则 S2Q 14=，…有如下运算和结论:, , ,,第1页（共14页）①a24②数列a i, a2+a3, a4+a5+a6, a7+a8+a9+a io,…是等比数列；③数列a i, a2+a3, a4+a5+a6, a7+a8+a9+a io,…的前n 项和为T n ------------------- ;④若存在正整数k,使S k V 10, S k+i> 10,则a k其中正确的结论是________ .（将你认为正确的结论序号都填上）二.选择题15. （3分）已知｛a n｝、｛b n｝都是公差不为0的等差数列，且一2, S n= a i+a2+…+a n,贝U ---------- 的值为（）A . 2B . - 1 C. 1 D .不存在16. （3分）设｛a n｝是公比为q （0V |q|v 1 ）的无穷等比数列，若｛a n｝的前四项之和等于第五项起以后所有项之和，则数列｛a2n-1｝是（）A .公比为-的等比数列B .公比为一的等比数列C .公比为一或一的等比数列D .公比为r或=的等比数列17. （3分）函数V V-图象的一条对称轴在 -，-内，则满足此条件的一个$值为（）A . —B . - C. 一D.—18. （3分）若数列｛a n｝的前n项和为S n,则下列命题：（1）若数列｛a n｝是递增数列，则数列｛S n｝也是递增数列；（2）数列｛ $｝是递增数列的充要条件是数列｛a n｝的各项均为正数；（3 ）若｛a n｝是等差数列（公差d M 0）,贝y S1?S2…S<= 0的充要条件是a1?a2…a k= 0.（4）若｛a n｝是等比数列，则S1?S2…S k= 0 （k> 2, k N）的充要条件是a n+a n+1 = 0. 其中，正确命题的个数是（）A . 0个B . 1个C. 2个 D . 3个三.解答题第2页（共14页）219. 已知函数f (x )= x + (2 - n ) x - 2n 的图象与x 轴正半轴的交点为 A (a n , 0) , n = 1 , 2, 3,…(1)求数列｛a n ｝的通项公式;正整数n ,都有b n+i > b n ?若存在，求出 入的值，若不存在，请说明理由.2 220.已知函数 f (x )= 2 sinxcosx+3sin x+cos x - 2, x R ;(1)求函数f (乂)在(0, n)上的单调递增区间;(2)在厶ABC 中，内角A 、B 、C 所对边的长分别是 a , b , c ,若f (A )=2，求△ ABC 的面积S MBC 的值;21.已知函数f (x )= 2sin (3X ),其中常数 3>0.(H) 令3 = 2，将函数y = f (x )的图象向左平移一个单位，再向上平移 到函数y = g (x )的图象.对任意 a R ，求y = g (x )在区间［a , a+10 n 上的零点个数的所有可能.(1 )求 a 2、a 3、a 4；(2) 求证：数列｛b n ｝为等比数列，并求其通项公式;(3) 求禾口 T n = a 2+a 4+ …+a 2n ；23.已知｛a n ｝ , ｛b n ｝为两非零有理数列(即对任意的 i N , a i , b i 均为有理数)，｛d n ｝为一无 理数列(即对任意的i N * , d i 为无理数).2 2 *(1)已知b n =- 2a n ,并且(a n +b n d n - a n d n ) (1+d n )= 0对任意的n N 恒成立，试求 ｛d n ｝的通项公式.3 * 2 2(2 )若｛d n ｝为有理数列，试证明：对任意的 n N , ( a n +b n d n - a n d n ) (1 + d n )= 1恒成 立的充要条件为(2 )令为正整数)，问是否存在非零整数 入，使得对任意 (I)令3= 1,判断函数-的奇偶性，并说明理由.1个单位，得 22.已知数列｛a n ｝满足：a i = 1, a n+i,为正奇数，b n = a 2n - 2; ,为正偶数，试计算b n.(3) 已知sin2 B — (0v 0< —), d n第3页(共14页)。

高一下学期数学期中考试试卷【一】第Ⅰ卷（选择题，共60分）一、选择题：本大题共有12小题,每小题5分,共60分；在每小题给出的四个选项中，有且只有一项是符合题目要求的。

1．数列1，－4，9，－16，25，…的一个通项公式为()A．B．C．D．2．计算的值等于()A．B．C．D．3．已知数列成等比数列,则=()A．B．C．D．4．等于()A．－1B．1C．22D．－225．如图,三点在地面同一直线上,从地面上C,D两点望山顶A，测得它们的仰角分别为45°和30°,已知CD＝200米,点C位于BD上,则山高AB等于()A．米B．米C．米D．200米6．若为锐角，且满足，，则的值为()A．B．C．D．7．《莱茵德纸草书》是世界上最古老的数学着作之一.书中有一道这样的题目：把100个面包分给5个人，使每人所得成等差数列，且使较大的三份之和的是较小的两份之和，则最小1份为()A．B．C．D．8．在中，＝(分别为角的对边)，则的形状为()A．直角三角形B．等边三角形C．等腰三角形或直角三角形D．等腰直角三角形9．已知△中，,,分别是、的等差中项与等比中项，则△的面积等于()A．B．C．或D．或10．若，且，则的值为()A．B．C．D．11.设等差数列满足，公差，当且仅当时，数列的前项和取得值，求该数列首项的取值范围()A．B．C．D．12．在锐角三角形中，,,分别是角,,的对边,,则的取值范围为()A．B．C．D．第Ⅱ卷（非选择题，共90分）二、填空题：本大题共4小题，每小题5分。

13．已知函数,则的值为.14．等差数列的前项和为,若,则等于.15．已知内角的对边分别是,若,，则的面积为.16．已知数列满足：,若，且数列是单调递增数列，则实数的取值范围为.三、解答题：本大题共6小题,共70分；解答应写出文字说明、证明过程或演算步骤.17．(本题满分10分)已知公差不为零的等差数列中，，且成等比数列.（1）求数列的通项公式；（2）设,求数列的前项和.18．(本题满分12分)（1）设为锐角，且,求的值；（2）化简求值：.19．(本题满分12分)已知函数（1）求函数的最小正周期和函数的单调递增区间；（2）已知中,角的对边分别为,若,求.20．（本小题满分12分）已知数列前项和（1）求数列的通项公式；（2）若，求数列的前项和.21．（本小题满分12分）的内角的对边分别为,且（1）证明：成等比数列；（2）若角的平分线交于点,且,求.22．（本小题满分12分）已知数列满足，,数列满足,,对任意都有（1）求数列、的通项公式；（2）令.求证:.【答案】一．选择题：本大题共有12小题,每小题5分,共60分.12.【解析】由条件根据余弦定理得：是锐角，.即又是锐角三角形，，即,.二、填空题：本大题共4小题，每小题5分.16.【解析】：由得，，易知，则，可得，则，由得>，则恒成立，的最小值为3，则的取值范围为.三、解答题：本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. 17．(本题满分10分)解：（1）设数列公差为d,……………………………………………1分成等比数列…………………………………2分∴（舍）或,…………………………………………………3分∴………………………………………………………………………5分（2）令………………………………6分………………………………7分……………………………………8分……………………………………9分…………………………………10分18．(本题满分12分)解：（1）为锐角，………………………………1分为锐角，………………………………2分………………………………3分…………………………………………4分………………………………………………5分……………………………………………………6分（2）原式=………………………………………………7分…………………………………………………8分……………………………………………………10分………………………………………………12分19．(本题满分12分)解：（1）…………………………………………1分=…………………………………………3分的最小正周期……………………………4分要使函数的单调递增………………………………………5分故函数的单调递增区间………………6分（2）…………………………………7分………………………………………8分………………………………………………9分在中，由正弦定理得：，即………………………10分,即…………………………………12分20．(本题满分12分)解：（1）数列前项和为当时,…………………………………………………………………1分……………………………………………………………………3分当时,，不满足…………………4分∴的通项公式为………………………………6分（2）当时,=………………………8分当时,………………………………………………9分……………………10分………………………………………………………………11分……………………………………………………………………12分21．(本题满分12分)解：（1）因为，所以化简可得……………………………………………………1分由正弦定理得，，又因a、b、c均不为0………………………………3分故成等比数列.…………………………………………………………4分（2）由，得，又因为是角平分线，所以，即，化简得，，即.…………………………………………………………6分由（1）知，，解得，……………………………………7分再由得，（为中边上的高），即，又因为，所以.…………………………8分在中由余弦定理可得，，…………10分在中由余弦定理可得，，即，求得.……………12分（说明：角平分线定理得到同样得分）（2）另解：同解法一算出.在中由余弦定理可得，，……………10分在中由余弦定理可得，，即，求得.……………12分(说明：本题还有其它解法，阅卷老师根据实际情况参照上述评分标准给分。

2018-2019学年上海外国语大学闵行外国语、莘庄高中联考高一（上）期中数学试卷一、选择题（本大题共4小题，共16.0分）1.下列四组函数中，函数f（x）与g（x）表示同一个函数的是（）A. ，B. ，C. ，D. ，2.若x＞y＞1，则下列下列四个数中最小的数是（）A. B. C. D.3.已知a，b为实数，则“a+b＞4”是“a，b中至少有一个大于2”的（）A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分又不必要条件4.设集合A={x|x2+2x-3＞0}，集合B={x|x2-2ax-1≤0，a＞0}．若A∩B中恰含有一个整数，则实数a的取值范围是（）A. B. C. D.二、填空题（本大题共12小题，共48.0分）5.满足A⊆{0，1}的集合A共有______个．6.已知集合，，用列举法表示集合A=______7.已知函数，，则f（x）•g（x）=______8.函数的定义域为______．9.若关于x的不等式ax2+x+b＞0的解集是（-1，2），则a+b=______．10.已知全集U=R，集合A={x|x＜a}，B═{x|-1＜x＜2}，且A∪∁U B=R，则实数a的取值范围是______．11.已知集合：A={x|x2=1}，B={x|ax=1}，且A∩B=B，则实数a的取值集合为______．12.关于x的不等式ax-b＞0的解集是（-∞，1），则关于x的不等式≥0的解集为______．13.若命题甲的否命题为“若a≠3且b≠4，则a+b≠7”，则命题甲的逆命题为______14.若函数的图象全部在x轴下方，则实数m的取值范围是______15.已知函数f（x）=其中m＞0，若不存在实数b，使得关于x的方程f（x）=b有三个不同的根，则m的取值范围是______．16.设a，b R，a＜b，函数g（x）=|x+t|（x R），（其中表示对于x R，当t[a，b]时，表达式|x+t|的最大值），则g（x）的最小值为______三、解答题（本大题共5小题，共56.0分）17.当k为何值时，关于x的方程3（x+1）=k（x-2）的解分别是．（1）（2）非正数18.设α：x2-4x+3≤0，β：m+1≤x≤2m+4．（1）α是β的充分条件，求实数m的取值范围；（2）记A={x|{x2-4x+3≤0}，B={x|m+1≤x≤2m+4}，且∁R A∩B=B，求实数m的取值范围19.10辆货车从A站匀速驶往相距2000千米的B站，其时速都是v千米/小时，为安全起见，要求：每辆车时速不得超过100千米/小时，每辆货车间隔kv2千米（k为常数，货车长度忽略不计）．将第一辆货车由A出发到最后一辆货车到达B站所需时间t表示为v的函数f（v）．（1）求t=f（v），并写出v的取值范围；（2）若k=请问，当v取何值时，t有最小值？并求出最小值．20.已知二次函数f（x）满足f（x+1）-f（x）=4x且f（0）=1．（1）求f（x）的解析式；（2）设a R，解关于x的不等式：f（x）＞2x2+ax+2a；（3）记A={x|f（x）≤|x|，x R}，若对于任意x A，函数h（x）=+2m的值恒为负数，求实数m的取值范围．21.若实数x，y，m满足|x-m|＞|y-m|，则称x比y远离m．（1）若2比3x-4远离1，求x的取值范围；（2）对任意两个不相等的实数a，b证明比（）2远离ab；（3）设函数f（x）的定义域为D，值域为E，任取x D，f（x）是g（x）=x2-2x-3和h（x）=2x+2中远离0的那个值，写出f（x）的解析式，并写出其定义域与值域．答案和解析1.【答案】C【解析】解：A．不是同一函数，定义域不同，f（x）定义域为R，g（x）定义域为[0，+∞）；B．不是同一函数，定义域不同，f（x）定义域为R，g（x）定义域为{x|x≠0}；C．是同一函数，g（x）==x=f（x）；D．不是同一函数，对应法则即解析式不同，g（x）==|x|．故选：C．通过求函数的定义域以及化简函数解析式即可找出表示同一函数的选项．考查确定函数的两要素：定义域和对应法则，以及求函数的定义域，以及对于函数解析式的化简．2.【答案】B【解析】解：∵x＞y＞1，∴＜＜，∴最小．故选：B．利用不等式的性质、基本不等式的性质即可得出．本题考查了不等式的性质、基本不等式的性质，考查了推理能力与计算能力，属于中档题．3.【答案】A【解析】解：“a+b＞4”⇒“a，b中至少有一个大于2”，反之不成立．∴“a+b＞4”是“a，b中至少有一个大于2”的充分不必要条件．故选：A．“a+b＞4”⇒“a，b中至少有一个大于2”，反之不成立．即可判断出关系．本题考查了不等式的性质、简易逻辑的判定方法，考查了推理能力与计算能力，属于基础题．4.【答案】B【解析】解：由x2+2x-3＞0，得：x＜-3或x＞1．由x2-2ax-1≤0，得：．所以，A={x|x2+2x-3＞0}={x|x＜-3或x＞1}，B={x|x2-2ax-1≤0，a＞0}={x|}．因为a＞0，所以a+1＞，则且小于0．由A∩B中恰含有一个整数，所以．即，也就是．解①得：a，解②得：a．所以，满足A∩B中恰含有一个整数的实数a的取值范围是．故选：B．先求解一元二次不等式化简集合A，B，然后分析集合B的左端点的大致位置，结合A∩B中恰含有一个整数得集合B的右端点的范围，列出无理不等式组后进行求解．本题考查了交集及其运算，考查了数学转化思想，训练了无理不等式的解法，求解无理不等式是该题的一个难点．此题属中档题．5.【答案】4【解析】解：∵满足A⊆{0，1}，∴满足条件的集合A共有：22=4（个）．故答案为：4．利用子集定义直接求解．本题考查集合的子集个数的求法，考查子集定义等基础知识，考查运算求解能力，是基础题．6.【答案】{1，2，4}【解析】解：∵集合，∴A={1，2，4}．故答案为：{1，2，4}．利用列举法能求出结果．本题考查集合的求法，考查列举法等基础知识，考查运算求解能力，是基础题．7.【答案】x（x≠0）【解析】解：f（x）•g（x）=x2=x，（x≠0），故答案为：x （x≠0）．f（x）•g（x）=x2=x，（x≠0），本题考查了函数解析式的求解方法．属基础题．8.【答案】[0，2）∪（2，3]【解析】解：由，解得0≤x≤3，且x≠2．∴函数的定义域为[0，2）∪（2，3]．故答案为：[0，2）∪（2，3]．由根式内部的代数式大于等于0，分式的分母不为0联立不等式组得答案．本题考查函数的定义域及其求法，考查一元二次不等式的解法，是基础题．9.【答案】1【解析】解：关于x的不等式ax2+x+b＞0的解集是（-1，2），∴-1，2是方程ax2+x+b=0的两个根，∴-1+2=-，-1×2=，解得a=-1，b=2；∴a+b=-1+2=1．故答案为：1．根据一元二次不等式的解集得出对应方程的两个根，再由根与系数的关系求出a，b即可．本题考查了一元二次不等式对应方程的关系，解题的关键是根据不等式的解集得出不等式相应方程的根，再由根与系数的关系求参数的值．10.【答案】a≥2【解析】解：∵全集U=R，B={x|-1＜x＜2}，∴∁U B={x|x≤-1或x≥2}，∵A={x|x＜a}，A∪（∁U B）=R，∴a≥2，则a的取值范围为a≥2．故答案为：a≥2由全集R及B，求出B的补集，根据A与B补集的并集为R，确定出a的范围即可．此题考查了交、并、补集的混合运算，熟练掌握各自的定义是解本题的关键．11.【答案】{-1，0，1}【解析】解：∵A={x|x2=1}={-1，1}，B={x|ax=1}={}，且A∩B=B，∴B⊆A，∴B=∅或B={-1}，或B={1}，∴不存在，或=-1或，解得a=0或a=-1或a=1．∴实数a的取值集合为{-1，0，1}．故答案为：{-1，0，1}．由已知得B⊆A，从而B=∅或B={-1}，或B={1}，进而不存在，或=-1或，由此能求出实数a的取值集合．本题考查集合的求法，是基础题，解题时要认真审题，注意交集的性质的合理运用．12.【答案】[-1，2）【解析】解：∵关于x的不等式ax-b＞0的解集是（-∞，1），∴a＜0，=1，则关于x的不等式≥0，即≤0，求得-1≤x＜2，故答案为：[-1，2）．由题意可得a＜0，=1，则关于x的不等式即≤0，由此求得x的范围．本题主要考查一元一次不等式、分式不等式的解法，体现了等价转化的数学思想，属于基础题．13.【答案】若a+b=7，则a=3或a=4【解析】解：命题甲的否命题为“若a≠3且b≠4，则a+b≠7”，则甲的原命题为：“若a=3或b=4，则a+b=7”，则命题甲的逆命题为：若a+b=7，则a=3或a=4故答案为：若a+b=7，则a=3或a=4先求出甲的原命题，再求出逆命题即可．本题主要考查四种命题的关系，比较基础．注意否命题和命题的否定的区别．14.【答案】（-3，0]【解析】解：根据题意，函数的图象全部在x轴下方，即＜0恒成立，当m=0时，y=-＜0，符合题意；当m≠0时，为二次函数，则有，解可得：-3＜m＜0，综合可得：m的取值范围为（-3，0]；故答案为：（-3，0]．根据题意，函数的图象全部在x轴下方，即＜0恒成立，分m=0与m≠0两种情况讨论，求出m的取值范围，综合即可得答案．本题考查函数的恒成立问题，涉及二次函数的性质，注意m的值可以为0，属于综合题．15.【答案】（0，1）∪（2，+∞）【解析】解：当m＞0时，f（x）=的图象如图：∵x＞m时，f（x）=x2-2mx+4m=（x-m）2+4m-m2＞4m-m2，∴要使得关于x的方程f（x）=b有三个不同的根，必须4m-m2＜m+2（m＞0），即m2-3m+2＞0（m＞0），解得0＜m＜1或m＞2，∴m的取值范围是（0，1）∪（2，+∞），故答案为：（0，1）∪（2，+∞）．作出函数f（x）的图象，依题意，可得4m-m2＜m+2（m＞0），求解得答案．本题考查根的存在性及根的个数判断，数形结合思想的运用是关键，属于中档题．16.【答案】（b-a）【解析】解：设f（t）=|x+t|，t[a，b]，可得t=-x为对称轴，当-x≥b，即x≤-b，[a，b]为减区间，则g（x）=-a-x；当a＜-x＜b即-b＜x＜-a，若-≤x＜-a，即f（a）≤f（b），可得g（x）=f（b）=b+x；当-b＜x＜-，f（a）＞f（b），可得g（x）=f（a）=-a-x；当-x≤a即x≥-a时，区间[a，b]为增区间，可得g（x）=f（b）=b+x．则g（x）=，当x≤-b，g（x）≥b-a；-≤x＜-a时，g（x）≥（b-a）；当-b＜x＜-，g（x）＞（b-a）；x≥-a时，g（x）≥b-a．则g（x）的最小值为（b-a）．故答案为：（b-a）．求得f（t）=|x+t|，t[a，b]的对称轴，讨论对称轴与区间的关系，结合单调性可得最大值g（x），再由一次函数的单调性，可得最小值．本题考查函数的最值的求法，注意运用分类讨论思想方法，以及单调性的运用，考查运算能力，属于中档题．17.【答案】解：（1）∵x=，∴3（+1）=k（-2），解得：k=-3；（2）由3（x+1）=k（x-2）得：x=，依题意有：≤0，解得：-≤k＜3．故（1）当k=-3时，关于x的方程3（x+1）=k（x-2）的解是；（2）当-≤k＜3时，关于x的方程3（x+1）=k（x-2）的解是非正数．【解析】（1）将x=代入方程解得k=-3；（2）由已知方程解出x=，再由x≤0可解出k的范围．本题考查了函数的零点与方程的根的关系．属基础题．18.【答案】解：（1）α：x2-4x+3≤0，可得：1≤x≤3；β：m+1≤x≤2m+4．∵α是β的充分条件，∴ ，解得；即实数m的取值范围为[，0]；（2）B={x|m+1≤x≤2m+4}，由A={x|{x2-4x+3≤0}={x|1≤x≤3}，可得∁R A={x|1＞x或x＞3}，∵∁R A∩B=B，∴B⊆{x|1＞x或x＞3}，①当B=∅时，2m+4＜m+1，可得m＜-3；②当B≠∅时，则m+1≤2m+4，可得m≥-3．由B⊆{x|1＞x或x＞3}，则m+1＞3或2m+4＜1，解得：m＞2或m＜；可得：-3≤m＜；综合可得：实数m的取值范围（-∞，）．【解析】（1）根据α是β的充分条件，即α是β的子集，可得实数m的取值范围；（2）由A={x|{x2-4x+3≤0}={x|1≤x≤3}，可得∁R A，在根据∁R A∩B=B，即可求解实数m的取值范围；此题考查了交集、补集及其运算，熟练掌握交集、补集的定义是解本题的关键．19.【答案】解：（1）由题意可得：t=f（v）=，0＜v≤100，v的单位是千米/小时．（2）k=，可得t=+≥5×=，当且仅当v=60千米/小时取等号，即t取得最小值小时．答：（1）t=，0＜v，0＜v≤100，v的单位是千米/小时．（2）k=，当且仅当v=60千米/小时，即t取得最小值小时．【解析】（1）由题意可得最后一辆货车需要行驶的路程为2000+9kv2，即可得出关系，0＜v≤100，v的单位是千米/小时．（2）k=，可得t=+，利用基本不等式的性质即可得出．本题考查了路程与速度的关系、基本不等式的性质，考查了推理能力与计算能力，属于中档题．20.【答案】解：（1）根据题意，设二次函数f（x）=ax2+bx+c（a≠0），又由f（0）=1，则c=1，若f（x+1）-f（x）=4x，有a（x+1）2+b（x+1）+1-（ax2+bx+1）=4，则有2ax+a+b=4x，即a=2，b=-2；故f（x）=2x2-2x+1；（2）根据题意，不等式f（x）＞2x2+ax+2a即2x2-2x+1＞2x2+ax+2a，变形可得：（a+2）x＜1-2a，当a=-2时，不等式为0＜5，其解集为R；当a＞-2时，a+2＞0，则不等式的解集为{x|x＜}；当a＜-2时，a+2＜0，则不等式的解集为{x|x＞}；则当a=-2时，不等式的解集为R；当a＞-2时，不等式的解集为{x|x＜}；当a＜-2时，不等式的解集为{x|x＞}；（3）根据题意，f（x）≤|x|即-x≤2x2-2x+1≤x，解可得：≤x≤1，则A=[，1]，若对于任意x A，函数h（x）=+2m的值恒为负数，则h（x）=2x+-2+m＜0在[，1]上恒成立，即2x+＜2-m在[，1]上恒成立，设g（x）=2x+，在区间[，]上递减，[，1]上递增；且g（）=g（1）=3，则g（x）在[，1]上的最大值为3，若2x+＜2-m在[，1]上恒成立，必有2-m＞3，解可得m＜-1，即m的取值范围为（-∞，-1）．【解析】（1）根据题意，设二次函数f（x）=ax2+bx+c，由f（0）=1，则c=1，又由f（x+1）-f（x）=4x，则有a（x+1）2+b（x+1）+1-（ax2+bx+1）=4，即2ax+a+b=4x，分析可得a、b 的值，即可得函数的解析式；（2）根据题意，不等式f（x）＞2x2+ax+2a变形可得：（a+2）x＜1-2a，分类讨论a 的取值范围，求出不等式的解集，综合即可得答案；（3）先解不等式-x≤2x2-2x+1≤x可得集合A，函数h（x）=+2m的值恒为负数，则h（x）=2x+-2+m＜0在[，1]上恒成立，即2x+＜2-m在[，1]上恒成立，设g（x）=2x+，分析g（x）在区间[，1]上的最大值，则有2-m＞3，解可得m的取值范围，即可得答案．本题考查函数的恒成立问题，涉及二次函数的解析式的计算，关键是求出函数的解析式，属于综合题．21.【答案】解：根据题意得：（1）＞∴＜1解得＜x＜2；（2）证明：==；=∵a≠b∴＞∴比远离ab；（3）令x2-2x-3=2x+2=0得x=-1令x2-2x-3=2x+2得x=-1或x=5∴f（x）=＜＜定义域为R值域[-4，+∞）．【解析】（1）运用基本不等式的知识可解决；（2）绝对值不等式的解法可解决此问题；（3）函数的解析式．本题考查不等式的知识和绝对值不等式的解法．。

2018-2019学年重庆市外国语中学高一下学期期中考试英语试卷第Ⅰ卷第一部分：听力（共两节，满分30分）第一节（共5小题；每小题1.5分，满分7.5分）1. What does the woman want to do?A. Change the channel.B. Go to a movie.C. Watch a TV program.2. What will the woman do next?A. Watch TV.B. Use the bathroom.C. Clean the living room.3. What time is it now?A. 8:00.B. 7:30.C. 7:15.4. How does the man feel about the interview?A. Worried.B. Surprised.C. Confident.5. What are the speakers mainly talking about?A. Shopping online.B. Saving money.C. Decorating a bathroom.第二节（共15小题；每小题1.5分，满分22.5分）听第6段材料,回答第6至7题。

6. Who will probably pay a visit to the company?A. Some customers.B. Some tourists.C. Some reporters.7. Where will the woman meet the visitors?A. In her office.B. At a restaurant.C. At the factory.听第7段材料,回答第8至9题。

8. Who is the woman talking to?A. Her friend.B. A travel agent.C. A teacher.9. What is true about Williamsburg?A. It’s a v ery young city.B. It is in the south.C. Its buildings and gardens are all modern.听第8段材料，回答第10至12题10. Where is the woman’s husband now?A. In London.B. In Beijing.C. In Paris.11. Why did the woman come to Beijing？A. To study space technology.B. To travel around.C. To attend an international meeting.12. How often does the man come to Beijing?A. Every year.B. Twice a month.C. Every other year.听第9段材料，回答第13至16题。

成都外国语学校2018－2019学年度下期期中考试高一数学试卷(理)一、选择题：本大题共12小题，每小题5分共60分，在每小题所给出的四个选项中，只有一项是符合题目要求的，并将正确选项的序号填涂在答题卷。

1.一个三角形的三个内角的度数成等差数列，则的度数为（）A. B. C. D.【答案】C【解析】【分析】结合等差数列的等差中项的性质，以及三角形内角和，即可求出角.【详解】由题意可知，又，则，解得，故选.【点睛】主要考查了等差中项的性质，以及三角形内角和，属于基础题.2.数列的一个通项公式是( )A.B.C.D.【答案】C【解析】数列的一个通项公式是即为故选C.3.下面关于等比数列和公比叙述正确的是（　）A. 为递增数列B. 为递增函数C. 为递减数列D. 为递增函数列且为递增函数【答案】D【解析】【分析】通过举反例即可将项分别排除，确定正确答案.【详解】项：若，则的各项为……，显然是递减数列，不正确.项：等比数列的各项为……，是递增数列，，该选项不正确.项：若，则的各项为……，显然是递增数列，不正确.利用排除法即可知，只有项正确.【点睛】主要考查了等比数列的单调性问题，属于基础题.4.在△ABC中角所对的边分别为以下叙述或变形中错误的是( )A. B.C. D.【答案】B【解析】【分析】结合正弦定理即可判断项正确；利用诱导公式即可判断项不正确；利用等比性质即可判断项正确；利用正弦函数单调性，诱导公式以及大边对大角即可判断项正确.【详解】项：由正弦定理，则，则由，答案正确.项：因为当时，则或，则或，所以不一定能得到，故B不正确，答案选B.项：由正弦定理，结合分数的等比性质即可得.项：因为当时，由正弦函数单调性可得，当时，由正弦函数单调性以及诱导公式可得，所以当时，可得；由正弦定理，当时，可得，即，从而可得，该结论正确.【点睛】主要考查了正弦定理的理解，等比性质，正弦函数单调性以及三角形的相关结论如大边对大角，属于基础题.5.在△ABC中，若2cosB•sinA=sinC，则△ABC的形状一定是（ ）A. 等腰直角三角形B. 直角三角形C. 等腰三角形D. 等边三角形【答案】C【解析】∵2sin A cos B＝sin（A＋B）＋sin（A－B），且2sin A cos B＝sin C，∴sin（A－B）＝0．∴A＝B．6.已知α、β为锐角，cosα＝，tan(α−β)＝−，则tanβ＝ ( )A. B. 3 C. D.【答案】B【解析】【分析】利用角的关系，再利用两角差的正切公式即可求出的值.【详解】因为，且为锐角，则，所以，因为，所以故选B.【点睛】主要考查了两角差的正切公式，同角三角函数的平方关系，属于中档题.对于给值求值问题，关键是寻找已知角（条件中的角）与未知角（问题中的角）的关系，用已知角表示未知角，从而将问题转化为求已知角的三角函数值，再利用两角和与差的三角函数公式、二倍角公式以及诱导公式即可求出.7.设是等差数列，Sn是其前n项的和，且S5＜S6，S6＝S7＞S8，则下列结论错误的是（）A. d＜0B. a7＝0C. S9＞S5D. S6与S7均为Sn的最大值【答案】C【解析】试题分析：根据题设条件且S5＜S6，S6=S7＞S8，则可判断A的正确性；∵且S5＜S6，S6=S7＞S8，则a7=0，可判断B正确；∵在等差数列中S n等差数列的前n项和公式存在最大值可判断数列的单调性，这样可判断D的正确性；利用数列的前n项和定义与等差数列的性质，来判断D的正确性解：∵S5＜S6，S6=S7＞S8，则A正确；∵S6=S7，∴a7=0，∴B正确；∵S5＜S6，S6=S7＞S8，则a6＞0，a7=0，a8＜0，∴d＜0，A正确∵a6+a7+a8+a9=2（a7+a8）＜0，∴S9＜S5，C错误．故选C考点：命题的真假, 等差数列的前n项和公式点评：本题借助考查命题的真假判断，考查等差数列的前n项和公式及等差数列的性质．在等差数列中S n 存在最大值的条件是：a1＞0，d＜0．一般两种解决问题的思路：项分析法与和分析法8.在中，已知则此三角形有几个解 ( )A. 0B. 1C. 2D. 不确定【答案】B【解析】【分析】利用三角形多解问题判断方法即可判断.【详解】因为，所以三角形只有一个解，故选B.【点睛】主要考查了三角形多解问题，属于基础题.对于三角形多解问题，判断方法如下：已知，且为锐角，则（1）如果，无解；（2）如果，有一解且；（3）如果，有两解（一个锐角，一个钝角）；（4）如果，有一解且为锐角.已知，且为钝角，则（1）如果，无解；（2）如果，则有一解且为锐角.9.在中，角、、所对的边分别为、、，若，且，则下列关系一定不成立的是（）A. B. C. D.【答案】B【解析】试题分析：由余弦定理，得，∴，∵，由正弦定理，得，∴或．当时，为直角三角形，且，所以C，D可能成立；当时，，所以∴，即A可能成立，因此一定不成立的是选项B．考点：正弦定理与余弦定理的应用．10.已知，且，则（）A. B. C. D.【答案】C【解析】试题分析：由得：解方程组：得：或因为，所以所以不合题意，舍去所以，所以，故选C.考点：同角三角函数的基本关系和两角差的三角函数公式.11.某学生家长为缴纳该学生上大学时的教育费，于2018年8月20号从银行贷款a元，为还清这笔贷款，该家长从2019年起每年的8月20号便去银行偿还相同的金额，计划恰好在贷款的m年后还清，若银行按年利率为p的复利计息（复利：即将一年后的贷款利息也纳入本金计算新的利息），则该学生家长每年的偿还金额是（）A. B.C. D.【答案】D【解析】【分析】根据题意建立方程，再结合等比数列求和公式，即可求出的值.【详解】设每年偿还的金额为，则，所以，解得故选D.【点睛】主要考查了等比数列求和，方程的求解，以及数学应用能力，属于中档题.这类型题的关键在于结合生活实际，读懂题意，合理地转化为数学问题，再进行求解.12.两位同学课余玩一种类似于古代印度的“梵塔游戏”：有3个柱子甲、乙、丙，甲柱上有个盘子，最上面的两个盘子大小相同，从第二个盘子往下大小不等，大的在下，小的在上（如图）.把这个盘子从甲柱全部移到乙柱游戏结束，在移动的过程中每次只能移动一个盘子，甲、乙、丙柱都可以利用，且3个柱子上的盘子始终保持小的盘子不能放在大的盘子之下.设游戏结束需要移动的最少次数为，则当时，和满足（）A. B. C. D.【答案】C【解析】【分析】通过写出几项，寻找规律，即可得到和满足的递推公式.【详解】若甲柱有个盘，甲柱上的盘从上往下设为，其中，，当时，将移到乙柱，只移动1次；当时，将移到乙柱，将移到乙柱，移动2次；当时，将移到丙柱，将移到丙柱，将移到乙柱，再将移到乙柱，将移到乙柱，；当时，将上面的3个移到丙柱，共次，然后将移到乙柱，再将丙柱的3个移到乙柱，共次，所以次；当时，将上面的4个移到丙柱，共次，然后将移到乙柱，再将丙柱的4个移到乙柱，共次，所以次；……以此类推，可知，故选.【点睛】主要考查了数列递推公式的求解，属于中档题.这类型题的关键是写出几项，寻找规律，从而得到对应的递推公式.二、填空题(本大题共4个小题，每小题5分，共20分)13.在中角所对的边分别为，若则___________【答案】【解析】,；由正弦定理，得，解得.考点：正弦定理.14.设为数列的前项和，已知，则___________【答案】【解析】【分析】利用与的关系，将转化为，化简即可证明为等差数列，从而利用公式求出.【详解】因为当时，，则，当时，，化简得，所以是以为首项，2为公差的等差数列，所以，即【点睛】主要考查了与的关系，以及等差数列的通项公式，属于中档题.这类型题的关键在于利用与的关系进行转化，有两个转化方向：（1）将转化为；（2）将转化为.15.已知非零平面向量满足，且与的夹角为，则的最大值为____________【答案】2【解析】【分析】运用平面向量夹角公式，结合向量的相关运算，即可将的最值求解.【详解】设与夹角为，则由题意，，化简得，，解得，而由与夹角为，可知，当时，显然，因为，不符合；，符合.当时，不符合，，符合；则，则当时，取得最大值.【点睛】主要考查了平面向量的夹角公式，数量积，辅助角公式，函数与方程思想，属于难题.对于范围型问题，主要有三种思路：（1）通过建立关于目标变量的一元函数，运用函数相关结论求出最值.（2）通过运用基本不等式求解目标变量的最值；（3）通过建立约束条件以及目标函数，运用数形结合的方法求出目标变量的最值.16.已知的三个内角的对边分别为，满足，且，则的值为__________【答案】【解析】【分析】利用题目的条件，结合正弦定理将边化角，然后通过三角恒等变换，即可得关于的等式，再结合，消去即可求出.【详解】因为，结合正弦定理可得：...又因为，代入上式得：.因为，则得，代入化简得，又因为所以.【点睛】主要考查了已知恒等式解三角形问题，正弦定理的应用，以及三角恒等变换，属于难题.对于已知恒等式解三角形问题，主要有两个方向进行求解：（1）利用正余弦定理将角化边，利用边的代数变换求解三角形；（2）利用正余弦定理将边化角，再利用三角恒等变换求解三角形.三、解答题(本大题共6个小题，共70分)：解答应写出文字说明，证明过程或演算步骤17.已知函数(1)求的最小正周期；(2)求在区间上的最大值和最小值．【答案】,最大值为,最小值为．【解析】试题分析：逆用二倍角公式将化成的形式，利用周期公式求其周期，再利用正弦函数的图像与性质进行求解.试题解析：2分，4分5分因为，所以，6分当时，即时，的最大值为，7分当时，即时，的最小值为.考点：1.三角恒等变换；2.三角恒等的图像与性质.18.已知sinα＋cosα＝，，，(1)求sin2α和tan2α的值；(2)求cos(α＋2β)的值．【答案】(1) sin2α＝，tan2α＝，（2）cos(α＋2β)＝－【解析】分析：（1）把已知条件两边平方，然后利用同角三角函数间的关系及二倍角的正弦函数公式化简可得sin 2α的值，根据2α的范围利用同角三角函数间的关系求出cos 2α即可得到tan 2α的值；（2）根据β的范围求出的范围，由sin （）的值利用同角三角函数间的关系求出cos （）的值，然后利用二倍角的正弦函数公式及同角三角函数间的关系分别求出sin2β和cos2β的值，根据第一问分别求出sinα和cos α的值，把所求的式子利用两角和的余弦函数公式化简后，将每个三角函数值代入即可求出．详解：(1)由题意得(sinα＋cosα)2＝，即1＋sin2α＝，∴sin2α＝.又2α∈(0，)，∴cos2α＝＝，∴tan2α＝＝.(2)∵β∈(，)，β－∈(0，)，∴cos(β－)＝，于是sin2(β－)＝2sin(β－)cos(β－)＝.又sin2(β－)＝－cos2β，∴cos2β＝－.又2β∈(，π)，∴sin2β＝.又cos 2α＝＝，∴cosα＝，sinα＝(α∈(0，))．∴cos(α＋2β)＝cosαcos2β－sinαsin2β＝×(－)－×＝－.点睛：本题重点考查学生灵活运用二倍角的正弦函数公式、同角三角函数间的基本关系及两角和的余弦函数公式化简求值，解题的关键是注意角的取值范围，属于中档题．19.设正项等比数列中，，且的等差中项为.（1）求数列的通项公式；（2）若，数列的前项和为，数列满足，记为数列的前项和，求.【答案】（1）；（2）.【解析】（1）设等比数列的公比为，由题意，得，解得，所以.（2）由（1）得，∴，∴，∴.【思路点拨】（1）根据等比数列的公式得到求得基本量，进而得到通项；（2）根据第一问得到，，从而得到，再裂项求和即可.20.已知各项均为正数的等差数列的前三项的和为27，且满足，数列的前项和为，且对一切正整数，点都在函数的图象上.(1)求数列和的通项公式；(2)设，求数列的前项和为；【答案】（1），；（2）【解析】【分析】（1）利用等差数列的性质，结合题意即可求出和，然后利用等差数列通项公式求解通项.再利用与的关系，即可求出.（2）利用错位相减法，即可求出数列的前项和为.【详解】（1）设等差数列的公差为，且由题则又则，所以又……①当时，当时……②由有当时也满足上式所以（2）……③……④由③-④有则【点睛】主要考查了等差数列的性质运用，通项公式的求解，与的关系以及错位相减法，属于中档题.利用与的关系求通项的步骤：（1）令，求出；（2）当时，求出；（3）检验是否符合.对于（为等差数列，为等比数列，为其公比）的前项和可以用错位相减法，基本步骤为：（1）写；（2）错位：；（3）相减：（4）化简求出.21.数列的前项和为（1）若为等差数列，求证：；（2）若，求证：为等差数列.【答案】（1）见解析；（2）见解析【解析】【分析】（1）利用倒序相加法即可证明.（2）利用与的关系分别求出与，然后作差，化简即可证明其满足，即可证明为等差数列.【详解】（1）证明：已知数列为等差数列，设其公差为，有则于是……①又……②由①②相加有即（2）证明：由，有当时，，所以， ③，④④－③并整理，得，即所以数列是等差数列．【点睛】主要考查了倒序相加法，以及等差数列的证明，属于中档题.等差数列的证明常常运用以下两种方法：（1）定义法，通过证明（为常数，）即可；（2）等差中项法：通过证明其满足即可.22.在中，是的内角，向量，且（1）求角；（2）求的面积.【答案】（1）；（2）【解析】【分析】（1）利用向量数量积的坐标运算，两角和的余弦公式以及诱导公式即可求出角.（2）利用即可求出的值，再由可得，结合余弦定理即可求出，再运用余弦定理即可求出，从而求出的面积.【详解】（1）又中所以，有，所以（2）在中，设角、、所对的边分别为、、又由余弦定理有所以代入中有联立解得所以【点睛】主要考查了平面向量的数量积运算，两角和的余弦公式，诱导公式以及余弦定理的应用，属于中档题.三角函数与平面向量的综合题型，关键是利用向量的相关运算将问题转化为三角函数问题，再运用相关公式进行三角恒等变换，从而将问题求解.。

上海市闵行中学2018-2019学年高一数学文模拟试卷含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 函数，（）在一个周期内的图象如右图所示，此函数的解析式为( )A. B.C. D.参考答案：A略2. 已知△ABC的重心为O，AC=6，BC=7，AB=8，则A．B．C．D．参考答案：C略3. 由元素1，2，3组成的集合可记为( )．A．{x＝1，2，3} B．{1，2，3}C．{ x│x∈N，x＜4} D．{6的质因数}参考答案：B4. 若弧长为4的弧所对的圆心角是2 ，则这条弧所在的圆的半径等于（）A．8 B．4 C．2 D．1参考答案：C略5. 若对于任意都有，则函数的图象的对称中心为（）A. B.C. D.参考答案：D∵对任意x∈R，都有f（x）+2f（–x）=3cos x–sin x①，用–x代替x，得f（–x）+2f（x）= 3cos（–x）–sin（–x），即f（–x）+2f（x）=3cos x+sin x②；①②联立，解得f（x）=sin x+cos x，所以函数y=f（2x）–cos2x=sin2x+cos2x–cos2x=sin2x，图象的对称中心为（，0），k∈Z，故选D．6. 已知，，则的最小值为（）A.－1B. 1C. 4D. 7参考答案：B【分析】转化，由即得解【详解】由题意：故故故选：B【点睛】本题考查了利用数量积研究向量的模长，考查了学生转化划归，数学运算的能力，属于基础题.7. 已知锐角的面积为，，则角的大小为（）A. 75°B. 60°C. 45°D.30°参考答案：B略8. 下列四组函数中，表示同一函数的是()A．y＝x－1与y＝B．y＝与y＝C．y＝4lg x与y＝2lg x2D．y＝lg x－2与y＝lg参考答案：D9. 一个算法的程序框图如图所示，若该程序输出的结果是，则判断框中应填入的条件是A． B．C． D．参考答案：D略10. 若且，则（）A. B. C. 3 D. 4参考答案：A略二、填空题:本大题共7小题,每小题4分,共28分11. 已知,则参考答案：略12. 在△ABC中，a=7，b=4，则△ABC的最小角为弧度．参考答案：【考点】HR：余弦定理．【分析】由三角形中大边对大角可知，边c所对的角C最小，然后利用余弦定理的推论求得cosC，则答案可求．【解答】解：∵在△ABC中，a=7，b=4，∴由大边对大角可知，边c所对的角C最小，由余弦定理可得：cosC===．∵0＜C＜π，∴C=．故答案为：．13. 若=，=，则=_________参考答案：解析：14. 用过球心的平面将一个球分成两个半球，则一个半球的表面积与原来整球的表面积之比为。

2019-2020学年上海市闵行区七宝中学高一第二学期期中数学试卷一、填空题（共12小题）.1．若cosα＝﹣，则cos2α＝．2．已知sinα＝，α∈（，π），则cosα＝．3．已知{a n}是等比数列，首项为3，公比为，则前4项的和为．4．若tanα＝3，则sin2α＝．5．等差数列{a n}的前n项和为S n，a4＝1，则S7＝．6．已知扇形的圆心角为，半径为5，则扇形的面积S＝．7．在数列{a n}中，a2＝5，a n+1﹣a n＝2n（n∈N*），则数列{a n}的通项a n＝．8．我国南宋著名数学家秦九韶发现了从三角形三边求三角形面积的“三斜公式”，设△ABC 内角A、B、C的对边分别为a、b、c，面积为S，则“三斜求积”公式为S＝，若c2sin A＝4sin C，B＝，则用“三斜求积”公式求得△ABC的面积为．9．函数的图象向右平移个单位后与函数f（x）的图象重合，则下列结论中正确的是．①f（x）的一个周期为﹣2π；②f（x）的图象关于x＝﹣对称；③x＝是f（x）的一个零点；④f（x）在单调递减．10．已知函数f（x）＝3sin x+4cos x，x1，x2∈[0，π]，则f（x1）﹣f（x2）的最大值是．11．在锐角△ABC中，内角A，B，C对的边分别为a，b，c．若a2+b（b﹣a）＝1，c ＝1，则a﹣b的取值范围为．12．已知数列{a n}满足a1＝4，a n＝2a n﹣1+2n（n≥2，n∈N*），若不等式2n2﹣n﹣3＜（5﹣λ）a n对任意n∈N*恒成立，则实数λ的取值范围是．二.选择题13．函数y＝2sin，x∈R的最小正周期为（）A．12B．6C．D．14．已知k∈Z，下列各组角中，终边相同的是（）A．2kπ与kπB．2kπ+π与4kπ±πC．kπ+与2kπ±D．与kπ±15．已知函数f（x）＝sinωx+cosωx（ω＞0）在[0，π]上有两个零点，则ω的取值范围为（）A．（，）B．[，）C．（，）D．[）16．有一个三人报数游戏：首先A报数字1，然后B报下两个数字2，3，接下来C报下三个数字4，5，6，然后轮到A报下四个数字7，8，9，10，依次循环，直到报出10000，则A报出的第2020个数字为（）A．5979B．5980C．5981D．以上都不对三.解答题17．在△ABC中，三个内角A、B、C所对的边分别为a、b、c，且a2+c2﹣b2＝ac．（1）求B；（2）若a+c＝6，三角形的面积S△ABC＝2，求b．18．已知S n为{a n}的前n项和，{b n}是等比数列且各项均为正数，且S n＝n，b1＝2，b2+b3＝．（1）求{a n}和{b n}的通项公式；（2）记c n＝a n•b n，求数列{c n}的前n项和T n．19．如图，有一块扇形草地OMN，已知半径为R，∠MON＝，现要在其中圈出一块矩形场地ABCD作为儿童乐园使用，其中点A、B在弧上，且线段AB平行于线段MN．（1）若点A为弧的一个三等分点，求矩形ABCD的面积S；（2）设∠AOB＝θ，求A在上何处时，矩形ABCD的面积S最大？最大值为多少？20．设正项数列{a n}的前n项和为S n，首项为1，q为非零正常数，数列{lg（a n）}是公差为lgq的等差数列．（1）求数列{S n}的通项公式；（2）求证：数列是递增数列；（3）是否存在正常数c，使得{lg（c﹣S n）}为等差数列？若存在，求出c的值和此时q 的取值范围；若不存在，说明理由．21．数列{a n}满足a n a n+1a n+2＝a n+a n+1+a n+2（a n a n+1≠1，n∈N*），且a1＝1，a2＝2，若a n＝A sin（ωx+φ）+c（A≠0，ω＞0，|φ|＜）的形式表示．（1）求a3的值；（2）证明3为数列{a n}的一个周期，并用正整数k表示ω；（3）求{a n}的通项公式．参考答案一.填空题（共12小题）.1．若cosα＝﹣，则cos2α＝．【分析】由已知利用二倍角的余弦函数公式即可计算求值得解．解：∵cosα＝﹣，∴cos2α＝2cos2α﹣1＝2×﹣1＝．故答案为：．2．已知sinα＝，α∈（，π），则cosα＝﹣．【分析】由sinα的值，及α的范围，判断出cosα为负数，利用同角三角函数间基本关系求出cosα的值即可．解：∵sinα＝，α∈（，π），∴cosα＜0，则cosα＝﹣＝﹣，故答案为：﹣3．已知{a n}是等比数列，首项为3，公比为，则前4项的和为．【分析】利用等比数列前n项和公式能求出等比数列前4项的和．解：{a n}是等比数列，首项为3，公比为，则前4项的和为S4＝＝．故答案为：．4．若tanα＝3，则sin2α＝．【分析】利用同角三角函数的基本关系以及二倍角的正弦公式，把要求的式子化为，把已知条件代入运算求得结果．解：∵tanα＝3，∴sin2α＝2sinαcosα＝＝＝＝．故答案为：．5．等差数列{a n}的前n项和为S n，a4＝1，则S7＝7．【分析】先由等差数列的性质可得a1+a7＝2a4，再根据等差数列的求和公式代入即可．解：根据题意，等差数列{a n}中，a1+a7＝2a4，则S7＝×7＝7a4＝7，故答案为7．6．已知扇形的圆心角为，半径为5，则扇形的面积S＝．【分析】利用S＝，即可求得结论．解：∵扇形的圆心角为，半径为5，∴S＝＝＝故答案为：7．在数列{a n}中，a2＝5，a n+1﹣a n＝2n（n∈N*），则数列{a n}的通项a n＝2n+1．【分析】直接利用递推关系式和累加法求出数列的通项公式．解：由题意可得：，利用累加法，得：，a1＝3，于是：．故答案为：2n+18．我国南宋著名数学家秦九韶发现了从三角形三边求三角形面积的“三斜公式”，设△ABC内角A、B、C的对边分别为a、b、c，面积为S，则“三斜求积”公式为S＝，若c2sin A＝4sin C，B＝，则用“三斜求积”公式求得△ABC的面积为．【分析】根据已知利用正弦定理可得ac＝4，根据余弦定理可得a2+c2﹣b2＝4，利用三斜公式即可求解．解：根据正弦定理，由c2sin A＝4sin C，得ac＝4，则由B＝，得：a2+c2﹣b2＝4，则△ABC的面积S＝＝．故答案为：．9．函数的图象向右平移个单位后与函数f（x）的图象重合，则下列结论中正确的是①②③．①f（x）的一个周期为﹣2π；②f（x）的图象关于x＝﹣对称；③x＝是f（x）的一个零点；④f（x）在单调递减．【分析】推导出f（x）＝sin[2（x﹣）+]＝sin（2x﹣），由此能求出结果．解：∵函数y＝sin（2x+）的图象向右平移个单位后与函数f（x）的图象重合，∴f（x）＝sin[2（x﹣）+]＝sin（2x﹣），∴f（x）的一个周期为﹣2π，故①正确；y＝f（x）的对称轴满足：2x﹣＝kπ+，k∈Z，∴当k＝﹣2时，y＝f（x）的图象关于x＝﹣对称，故②正确；由f（x）＝sin（2x﹣）＝0，得x＝+，∴x＝是f（x）的一个零点，故③正确；当x∈（﹣，）时，2x﹣∈（﹣，），∴f（x）在（﹣，）上单调递增，故④错误．故答案为：①②③．10．已知函数f（x）＝3sin x+4cos x，x1，x2∈[0，π]，则f（x1）﹣f（x2）的最大值是9．【分析】本题先将函数f（x）转化成正弦函数的形式，然后结合正弦函数的图象判断出函数f（x）在区间[0，π]上的最大值和最小值，从而得出结果．解：由题意，可知：f（x）＝3sin x+4cos x＝5•（sin x+cos x）＝5sin（x+θ），其中sinθ＝，cosθ＝．∵sinθ＝，可知sin＝，∴对于函数f（x）＝5sin（x+θ），可知：sin x向左平移θ个单位得到sin（x+θ），再将sin（x+θ）的图象沿y轴伸长到原来的5倍得到5sin（x+θ）．由题意，可知求f（x1）﹣f（x2）的最大值就是求函数f（x）＝5sin（x+θ）在区间[0，π]上的最大值与最小值之差．又函数f（x）＝5sin（x+θ）在区间[0，π]上的图象如下：由图象可知，在区间[0，π]上，当x＝时，f（x）取最大值5，当x＝π时，f（x）取最小值5sin（π+θ）＝﹣5sinθ＝﹣4．∴在区间[0，π]上，f（x1）﹣f（x2）的最大值是5﹣（﹣4）＝9．故答案为：9．11．在锐角△ABC中，内角A，B，C对的边分别为a，b，c．若a2+b（b﹣a）＝1，c ＝1，则a﹣b的取值范围为（1，）．【分析】先根据余弦定理求得角C，结合正弦定理把a﹣b转化为2（sin A﹣sin B），再结合AB之间的关系求出角A的范围，与正弦函数相结合即可求得结论．解：因为在锐角△ABC中，内角A，B，C对的边分别为a，b，c．∵a2+b（b﹣a）＝1，c＝1⇒a2+b2﹣ab＝c2⇒2cos C＝⇒cos C＝⇒C＝30°，∴＝＝＝＝2；∴a＝2sin A，b＝2sin B；∴a﹣b＝2（sin A﹣sin B）＝2[sin A﹣sin（150°﹣A）]＝2[sin A﹣（cos A+sin A）]＝2（sin A﹣cos A）＝2sin（A﹣30°）；∵0°＜A＜90°，0°＜B＜90°，A+B＝150°；∴60°＜A＜90°；∴30°＜A﹣30°＜60°⇒2sin（A﹣30°）∈（1，）；故a﹣b∈（1，）；故答案为：（1，）．12．已知数列{a n}满足a1＝4，a n＝2a n﹣1+2n（n≥2，n∈N*），若不等式2n2﹣n﹣3＜（5﹣λ）a n对任意n∈N*恒成立，则实数λ的取值范围是．【分析】首先利用构造新数列法的应用求出数列的通项公式，进一步利用函数的恒成立问题的应用和函数的导数的应用求出结果．解：数列{a n}满足a1＝4，a n＝2a n﹣1+2n（n≥2，n∈N*），则：（常数），所以数列{}是以为首项，1为公差的等差数列．所以，整理得，不等式2n2﹣n﹣3＜（5﹣λ）a n对任意n∈N*恒成立，所以＝，所以对任意的n∈N*恒成立，所以设f（n）＝，故，当n＝1，2时，f′（n）＞0，当n≥3时，f′（n）＜0，所以f（2）＝，f（3）＝．所以．故答案为：（﹣）．二.选择题13．函数y＝2sin，x∈R的最小正周期为（）A．12B．6C．D．【分析】由题意利用函数y＝A sin（ωx+φ）的周期为，得出结论．解：函数y＝2sin，x∈R的最小正周期为＝12，故选：A．14．已知k∈Z，下列各组角中，终边相同的是（）A．2kπ与kπB．2kπ+π与4kπ±πC．kπ+与2kπ±D．与kπ±【分析】分别写出选项中所表示的终边所在的角的集合，逐一核对即可．解：2kπ（k∈Z）表示终边在x轴非负半轴上的角的集合，kπ（k∈Z）表示终边在x轴上的角的集合，两组角终边不同；2kπ+π与4kπ±π（k∈Z）都表示终边在x轴非正半轴上的角的集合，两组角终边相同；kπ+（k∈Z）表示终边与和终边相同的角的集合，2kπ±（k∈Z）表示终边与和﹣终边相同的角的集合，两组角终边不同；（k∈Z）表示终边在坐标轴上的角的集合，kπ±（k∈Z）表示终边在y轴上的角的集合，两组角终边不同；故选：B．15．已知函数f（x）＝sinωx+cosωx（ω＞0）在[0，π]上有两个零点，则ω的取值范围为（）A．（，）B．[，）C．（，）D．[）【分析】利用辅助角公式化积，由x的范围得到∈[，]，再由函数f（x）在[0，π]上有两个零点，可得2π≤ωπ+＜3π，由此求得ω的取值范围．解：f（x）＝sinωx+cosωx＝，∵x∈[0，π]，∴∈[，]，要使函数f（x）在[0，π]上有两个零点，则2π≤ωπ+＜3π，解得：≤ω＜．∴ω的取值范围为[，）．故选：B．16．有一个三人报数游戏：首先A报数字1，然后B报下两个数字2，3，接下来C报下三个数字4，5，6，然后轮到A报下四个数字7，8，9，10，依次循环，直到报出10000，则A报出的第2020个数字为（）A．5979B．5980C．5981D．以上都不对【分析】首先分析出A第n次报数的个数为3n﹣2，进一步求出3人以公报的次数，进一步利用前n项和公式的应用求出结果．解：由题意可得：A第n次报数的个数为3n﹣2，则A第n次报完数后共报的个数为．再代入正整数n，使得T n≥2020，解得：n的最小值为37，得T37＝2035．而A第37次报时，3人总共报了36×3+1＝109次，当A第109次报完数3人总的报数个数为．即A报出的第2035个数字为5995，故A报出的第2020个数字为5980．故选：B．三.解答题17．在△ABC中，三个内角A、B、C所对的边分别为a、b、c，且a2+c2﹣b2＝ac．（1）求B；（2）若a+c＝6，三角形的面积S△ABC＝2，求b．【分析】（1）由已知结合余弦定理可求cos B，进而可求B；（2）由已知结合三角形的面积公式可求ac，进而可求．解：（1）因为a2+c2﹣b2＝ac．由余弦定理可得，cos B＝＝，因为B为三角形的内角，所以；（2）∵a+c＝6，三角形的面积S△ABC＝＝＝2，∴ac＝8，∵a2+c2﹣b2＝ac，∴（a+c）2﹣b2＝3ac，∴36﹣b2＝24，∴b＝218．已知S n为{a n}的前n项和，{b n}是等比数列且各项均为正数，且S n＝n，b1＝2，b2+b3＝．（1）求{a n}和{b n}的通项公式；（2）记c n＝a n•b n，求数列{c n}的前n项和T n．【分析】（1）先由a n＝S n﹣S n﹣1求得a n，再检验n＝1时是否适合，从而求得a n．设等比数列{b n}的公比为q，由题意列出q的方程，求得q，进而求得b n；（2）由（1）求得c n，再利用错位相减法求其前n项和T n．解：（1）∵S n＝n，∴当n≥2时，有a n＝S n﹣S n﹣1＝n﹣＝3n﹣1，又当n＝1时，有S1＝＝2＝a1也适合，∴a n＝3n ﹣1．设等比数列{b n}的公比为q，由题意得：，解得q＝，故；（2）由（1）得c n＝（3n﹣1）•（）n﹣2，∴T n＝2×（）﹣1+5×（）0+8×（）1+…+（3n﹣1）×（）n﹣2①，又＝2×（）0+5×（）1+8×（）2+…+（3n﹣1）×（）n﹣1②，由①﹣②得：＝4+3[1++（）2+…+（）n﹣2]﹣（3n﹣1）×（）n﹣1＝4+3×+（1﹣3n）×（）n﹣1＝10﹣（3n+5）•（）n﹣1∴．19．如图，有一块扇形草地OMN，已知半径为R，∠MON＝，现要在其中圈出一块矩形场地ABCD作为儿童乐园使用，其中点A、B在弧上，且线段AB平行于线段MN．（1）若点A为弧的一个三等分点，求矩形ABCD的面积S；（2）设∠AOB＝θ，求A在上何处时，矩形ABCD的面积S最大？最大值为多少？【分析】（1）作OH⊥AB于点H，交线段CD于点E，连接OA、OB，求出AB，EH，可得矩形ABCD的面积S；（2）设∠AOB＝θ（0＜θ＜），求出AB，EH，可得矩形ABCD的面积S，再求最大值．解：（1）如图，作OH⊥AB于点H，交线段CD于点E，连接OA、OB，∴∠AOB＝，∴AB＝2R sin，OH＝R cos，OE＝DE＝AB＝R sin，∴EH＝OH﹣OE＝R（cos﹣sin），S＝AB•EH＝2R2（sin cos﹣sin2）＝，（2）设∠AOB＝θ（0＜θ＜），则AB＝2R sin，OH＝R cos，oe＝AB＝R cos，OE＝AB＝R sin，∴EH＝OH﹣OE＝R（cos﹣sin），S＝AB•EH＝R2（2sin cos﹣2sin2）＝R2（sinθ+cosθ﹣1）＝R2[sin（θ+）﹣1]，∵0＜θ＜，∴＜θ+＜，∴θ+＝即θ＝时，S max＝（﹣1）R2，此时A在弧MN的四等分点处．答：当A在弧MN的四等分点处时，S max＝（﹣1）R2．20．设正项数列{a n}的前n项和为S n，首项为1，q为非零正常数，数列{lg（a n）}是公差为lgq的等差数列．（1）求数列{S n}的通项公式；（2）求证：数列是递增数列；（3）是否存在正常数c，使得{lg（c﹣S n）}为等差数列？若存在，求出c的值和此时q 的取值范围；若不存在，说明理由．【分析】（1）根据题意得a1＝1，根据题意可得lg（a n）＝lg（a1）+（n﹣1）lgq＝lg1+（n﹣1）lgq＝lgq n﹣1，即a n＝q n﹣1，分当q＝1时，当q≠1时，两种情况写出S n（2）当q＝1时，S n＝n，＝1﹣随着n的增大而增大，当q＞0，q≠1时，﹣＝﹣＝＜0，可得数列是递增数列；（3）假设存在正常数c使得{lg（c﹣S n）}为等差数列，若{lg（c﹣S n）}为等差数列，可得q≠1，lg（c﹣+）＝lg＝nlgq﹣lg（1﹣q）为等差数列，即可求出c＝（0＜q＜1）．解：（1）根据题意得a1＝1，因为数列{lg（a n）}是公差为lgq的等差数列，所以lg（a n）＝lg（a1）+（n﹣1）lgq＝lg1+（n﹣1）lgq＝lgq n﹣1，所以a n＝q n﹣1，当q＝1时，S n＝n，当q≠1时，S n＝＝，所以．（2）证明：当q＝1时，S n＝n，所以＝＝1﹣随着n的增大而增大，当q＞0，q≠1时，S n＝，＝，由﹣＝﹣＝＜0，可得数列是递增数列；（3）假设存在正常数c使得{lg（c﹣S n）}为等差数列，当q＝1时，S n＝n，q≠1，S n＝，{lg（c﹣S n）}为等差数列，可得q≠1，lg（c﹣+）＝lg＝nlgq﹣lg（1﹣q）为等差数列，则有c＝（0＜q＜1）．21．数列{a n}满足a n a n+1a n+2＝a n+a n+1+a n+2（a n a n+1≠1，n∈N*），且a1＝1，a2＝2，若a n＝A sin（ωx+φ）+c（A≠0，ω＞0，|φ|＜）的形式表示．（1）求a3的值；（2）证明3为数列{a n}的一个周期，并用正整数k表示ω；（3）求{a n}的通项公式．【分析】（1）代值计算即可，（2）分别令n＝1，2，3，即可证明，根据周期公式即可求出，（3）分别由a1＝1，a2＝2，a3＝3，可得1＝A sin（+φ）+c，2＝﹣A sin（+φ）+c，3＝A sinφ+c，解得即可求出．解：（1）当a1＝1，a2＝2，a1a2a3＝a1+a2+a3，解得a3＝3；（2）当n＝2时，6a4＝2+3+a4，解得a4＝1，当n＝3时，3a5＝1+3+a5，解得a5＝2，…，可得a n+3＝a n，当a1＝1，a2＝2，a3＝3；故3为数列{a n}的一个周期，则＝3，k∈N*，则；（3）由（2）可得a n＝A sin（n+φ）+c，则1＝A sin（+φ）+c，2＝﹣A sin（+φ）+c，3＝A sinφ+c，即1＝A•cosφ﹣A•sinφ+c，①2＝﹣A•cosφ﹣A•sinφ+c，②由①+②，可得3＝﹣A sinφ+2c，∴c＝2，A sinφ＝1，①﹣②，可得﹣1＝A•cosφ，则tanφ＝﹣，∵|φ|＜，∴φ＝﹣，∴A＝﹣，故．。