平行线与相交线经典例题汇总

平行与相交专项练习30题(有答案)ok平行与相交专项练30题（有答案）1．下列对于线的描述，说法正确的是（）A．不相交的两条直线是平行线B．两条直线相交成直角时，这两条直线互相垂直C．过直线外一点，能画无数条平行线D．有一条直线长6分米2．从直线外一点画已知直线的平行线，可以画（）条．A．1B．2C．无数3．下面的图形中，（）只有2组平行线．A．B．C．D．4．如果在同一平面内画两条直线，它们都和第三条直线相交成直角，那么这两条直线（A．互相垂直B．互相平行C．不垂直也不平行5．下列各句话中有（）句是错误的．（1）两条直线相交，这两条直线互相垂直．（2）两条直线的交点，叫做这两条直线的垂足．（3）平行线之间的线段到处相等．（4）两条直线都与另一条直线相交，这两条直线一定平行．A．1B．2C．3D．46．在同一平面内，若把两根小棒都摆成和第三根小棒垂直，那么这两根小棒（）A．相互平行B．相互垂直C．相交7．同一平面内的两条直线最多有（）个交点．A．B．1C．28．一张长方形纸对折两次后展开，折痕（）A．相互平行B．相互垂直C．可能相互垂直，也可能相互平行9．在两条平行线之间画垂直线段，第一条长7厘米，第二条长（）A．大于7厘米B．小于7厘米C．等于7厘米10．关于平行线的说法正确的是（）A．不相交的两条线段B．不相交的两条直线C．在同一平面内，不相交的两条直线11．直线a、b、c在同一平面里，a与b相互垂直，b与c 相互垂直，那么a与c相互（A．.垂直B．平行C．平行或垂直12．有两条直线都与同一条直线平行，则这两条直线一定（）平行与相交----1））A．相互垂直B．相互平行C．相交13．在同一个平面上垂直于同一条直线的两条直线一定（）A．互相垂直B．互相平行C．两种都有可能D．A、B两种都不可能．14．在同一平面内，两条直线可能_________，也可能_________，互相垂直是一种特殊的_________．15．指出左图形中各有几组互相平行的线段，并写在括号里，（_________）．16．在同一平面内不相交的两条直线叫做_________，也可以说这两条直_________．在同一平面内的两条直线的位置关系有_________、_________两种情况．17．语文课本的封面，相对的两条边是相互_________的，相邻的两条边是相互_________的．18．点到直线的所有线段中，_________最短．19．平行线之间的垂直线段不但相互_________，并且长度_________．20．在同一平面内，两条不重合的直线的位置干系有_________、_________．21．上面有一排字母：TEFNKHXZ有互相垂直线段的字母是_________；有互相平行线段的字母是_________；既有互相垂直，又有互相平行的线段的字母是_________．22．如图，能找到_________组相互垂直的线段．23．两条直线不相交，就说这两条直线相互平行．_________．24．图中有几组相互垂直的线段？_________组．25．当两条直线相交成直角时，这两条直线相互平行．_________．26．在一张纸上画若干条直线后发现，凡是不平行的，就一定会相交．_________．平行与相交----227．在同一平面内，两条直线的位置干系可分红哪两类？相交或垂直_________相交或平行_________平行或垂直_________．28．过直线外一点只能画一条直线的垂线．_________．29．小猪要过河，它走下面的哪条路最近？这条路有什么特点？30．点A是大象的家，XXX表示河．大象要去河岸边饮水，请设想一条使大象饮水近来的线路图．平行与相交----3参考答案：1．A、不相交的两条直线是平行线，说法错误，前提是：在同一平面内；B、根据互相垂直的含义：两条直线相交成直角时，这两条直线互相垂直，说法正确；C、过直线外一点，能画无数条平行线，说法错误，应为一条平行线；D、因为直线无限长，所以有一条直线长6分米，说法错误；故选：B．2.按照平行的性质得：过直线外一点画直线的平行线，可以画一条直线与直线平行，应选：A．3．A、是正六边形，有3组平行线；B、没有平行线；C、有2组平行线；D、是正八边形，有4组平行线；故选：C．4．如图：在同一平面内，p⊥d，k⊥d，所以XXX，故选：B．5．（1）两条直线相交，这两条直线互相垂直，说法错误，应为：两条直线相交成直角时，这两条直线就互相垂直；（2）两条直线的交点，叫做这两条直线的垂足，说法错误；因为两条直线相交成直角，这两条直线就互相垂直，交点叫做垂足；（3）平行线之间的线段处处相等，说法错误，应为：平行线之间的距离处处相等；（4）根据垂直的性质可知：两条直线都与另一条直线相交，这两条直线一定平行，说法错误，前提必须在同一个平面内；故选：D．6．如图所示，，a和b都垂直于c，则a和b平行；应选：A．7．同一平面内的两条直线最多有1个交点．应选：B．8．由阐发可知：把一张长方形的纸对折两次后，折痕的干系是可能相互平行，也可能相互垂直；应选：C．9．由阐发可知：两条平行线中可以画无数条垂线段，这些线段的长度都相等，所以在两条平行线之间画垂直线段，第一条长7厘米，第二条也长7厘米；应选：C．10．因为在同一平面内，两条不相交的直线是平行线，故A、B错误；应选：C．11．由垂直和平行的特征和性质可知：直线a、b、c在同一平面里，a与b相互垂直，b与c相互垂直，那么a与c互相平行；故选：B．12．根据平行的性质可得：有两条直线都与同一条直线平行，则这两条直线一定互相平行；故选：B13．由垂直的性质可得：在同一个平面内垂直于同一条直线的两条直线一定互相平行；故选：B．14．在同一平面内，两条直线可能相交，也可能平行，互相垂直是一种特殊的相交．15．指出左图形中各有几组互相平行的线段，并写在括号里，（9组）．如图：平行与相交----4图中的平行线段有：AD∥EF，BD∥EF，DE∥FB，DE∥FC，DF∥AE，DF∥EC，DE∥BC，DF∥AC，EF∥AB；共有9对；故谜底为：9组16．在同一平面内不相交的两条直线叫做平行线，也能够说这两条直线相互平行．在同一平面内的两条直线的位置干系有相交、平行两种情形．由阐发得出：在同一平面内不相交的两条直线叫做平行线，也可以说这两条直线互相平行，在同一平面内的两条直线的位置关系有相交、平行两种情况．故答案为：平行线；线互相平行；相交；平行17．语文课本的封面，相对的两条边是相互平行的，相邻的两条边是相互垂直的．18．点到直线的所有线段中，垂线段最短．19．平行线之间的垂直线段不但相互平行，并且长度相等．20．在同一平面内，两条不重合的直线的位置干系有相交、平行．21．上面有一排字母：XXX有相互垂直线段的字母是T、E、H；有相互平行线段的字母是E、N、Z、H；既有相互垂直，又有相互平行的线段的字母是E、H．22．如图，能找到8组相互垂直的线段．23.两条直线如果永不相交，这两条直线一定互相平行，说法错误，前提是必须在同一平面内；故答案为：错误．24．图中有几组互相垂直的线段？6组．25．当两条直线相交成直角时，这两条直线相互平行．错误．26．在一张纸上画若干条直线后发现，凡是不平行的，就一定会相交．正确．由分析可知：在一张纸上画若干条直线后发现，凡是不平行的，就必然会相交；故答案为：正确．27．在同一平面内，两条直线的位置关系可分成哪两类？相交或垂直×相交或平行√平行或垂直×．28．过直线外一点只能画一条已知直线的垂线．正确．29．如图：PC近来，这条路垂直于河对岸的路．30．如图所示：根据垂直线段最短的性质，红色的垂线段就是使大象饮水最近的线路，。

初一数学相交线与平行线28道典型题（含答案和解析及考点）1、若直线AB,CD相交于O，∠AOC与∠BOD的和为200°，则∠AOD的度数为．答案：80°.解析：∵∠AOC=∠BOD，∠AOC与∠BOD的和为200°.∴∠AOC=100°.∵∠AOD与∠AOC互补.∴∠AOD=80°.考点：几何初步——相交线与平行线——对顶角、邻补角.2、已知OA⊥OB，∠AOC∶∠AOB=2∶3，则∠BOC= ．答案：30°或150°.解析：当OC在∠AOB内部时，∠BOC=30°；当OC在∠AOB外部时，∠BOC=150°.考点：几何初步——相交线与平行线——对顶角、邻补角——垂线.3、若直线a与直线b相交于点A，则直线b上到直线a距离等于2cm的点的个数是（）．A.0B.1C.2D.3答案：C.解析: 直线b的交点两侧各有一点到直线a的距离等于2cm.考点：几何初步——相交线与平行线——点到直线的距离.4、如图所示，在平面内，两条直线l1、l2相交于点O，对于平面内任意一点M，若p、q分别是点M到直线l1、l2的距离，则称（p,q）为点M的“距离坐标”．根据上述规定，“距离坐标”是（2,1）的点共有个．答案：4.解析：因为两条直线相交有四个角，因此每一个角内就有一个到直线l1、l2的距离分别是2、1，的点，即距离坐标是（2,1）的点，因而共有4个．考点：几何初步——相交线与平行线——点到直线的距离.5、若∠1和∠2是同旁内角，若∠1=50°，则∠2的度数为（ ）． A.45° B.135° C.45°或135° D. 不能确定 答案：D.解析：若∠1和∠2是同旁内角，若∠1=50°，则∠2的度数为不能确定． 考点：几何初步——相交线与平行线——三线八角.6、平面上n 条直线最少能将平面分为__________部分，最多能将平面分为__________部分． A. 最少能将平面分成n+1部分；最多分为n2+n+22.B. 最少能将平面分成n+2部分；最多分为n2+n−22.C. 最少能将平面分成n+1部分；最多分为n2+n−22. D. 最少能将平面分成n+2部分；最多分为n2−n+22.答案：A.解析：1条直线将平面分成2部分.2条直线最少将平面分成3部分，最多将平面分成4部分，其中4=1+1+2. 3条直线最少将平面分成4部分，最多将平面分成7部分，其中7=1+1+2+3. 4条直线最少将平面分成5部分，最多将平面分成11部分，其中11=1+1+2+3+4. ……n 条直线最少将平面分成n+1部分，最多将平面分成n2+n+22部分，其中n2+n+22=1+1+2+3+…+n .综上，n 条直线最少能将平面分成n+1部分,对多能将平面分成n2+n+22部分．考点：几何初步——相交线与平行线——相交线.7、如图，已知∠1=∠2，要使∠3=∠4，则需（ ）．A. ∠1=∠2B. ∠2=∠4C. ∠1=∠4D. AB ∥CD答案：D.解析：假设∠3=∠4，即∠BEF=∠CFE.由内错角相等，两直线平行，可得AB∥CD.故已知∠1=∠2，要使∠3=∠4，只要AB∥CD.考点：几何初步——相交线与平行线——平行线公理及推论.8、如图①是长方形纸带，将纸带沿EF折叠成图②，再沿BF折叠成图③．（1）若图①中的∠DEF=20°，则图②中的∠CFE度数是．（2）若图①中的∠DEF=α，则图③中的∠CFE度数是．（用含有α的式子表示）答案：（1）160°.（2）180°-3α.解析：（1）在图①中：∵AD∥BC.∴∠BFE=∠DEF=20°.∴∠CFE=160°.在图②中，根据折叠性质，∠CFE大小不变.∴∠CFE=160°.（2）在图①中，∠CFE=180°-∠BFE=180°-α.在图②中，∠CFB=∠CFE-∠BFE=180°-α.根据折叠性质，图③中∠CFB与图②中∠CFB相等.在图③中，∠CFE=∠CFB-∠BFE=180°-3α.∴图③中的∠CFE度数是180°-3α.考点：几何初步——角——角的计算与证明.相交线与平行线——平行线的性质.几何变换——图形的对称——翻折变换（折叠问题）——轴对称基础——轴对称的性质.9、已知：如图，∠D=110°，∠EFD=70°，∠1=∠2.求证：∠3=∠B.证明：∵∠D=110°，∠EFD=70°，（已知）.∴∠D+∠EFD=180°.∴_____∥ _____．（）.又∵∠1=∠2，（已知）.∴_____∥ _____．（）.∴_____∥ _____．（）.∴∠3=∠B．（）.答案：答案见解析．解析：∵∠D=110°，∠EFD=70°，（已知）.∴∠D+∠EFD=180°.∴AD∥EF．（同旁内角互补，两直线平行）.又∵∠1=∠2，（已知）.∴AD∥BC．（内错角相等，两直线平行）.∴EF∥BC．（平行于同一直线的两直线平行）.∴∠3=∠B．（两直线平行，同位角相等）.考点：几何初步——相交线与平行线——平行线的判定——平行线的性质.10、车库的电动门栏杆如图所示，BA垂直于地面AE于A，CD平行于地面AE，则∠ABC+∠BCD的大小是（）．A.150°B.180°C.270°D.360°答案：C.解析：过B作CD的平行线BF，则CD∥BF∥AE.∴∠DCB+∠CBF=180°，∠ABF=90°.∴∠ABC+∠BCD=∠DCB+∠CBD+∠ABF=180°+90°=270°.考点：几何初步——角——角的计算与证明.相交线与平行线——平行线的性质.11、如图，一条公路修到湖边时，需拐弯绕湖而过；如果第一次拐角∠A是120°，第二次拐角∠B是150°，第三次拐角是∠C，这时的道路恰好和第一次拐弯之前的道路平行，则∠C是．答案：150°.解析：如图，作BE∥AD.∴∠1=∠A=120°.∴∠2=∠ABC=∠1=150°-120°=30°.∵AD∥CF.∴BE∥CF.∴∠C+∠2=180°.∴∠C=180°-30°=150°.考点：几何初步——相交线与平行线——平行线公理及推论——平行线的性质.12、如图所示，若AB∥CD，则角α，β，γ的关系为（）．A.α+β+γ=360°B.α-β+γ=180°C.α+β+γ=180°D.α+β-γ=180°答案：D.解析：过β角的顶点为E，作EF∥AB，α+β-γ=180°.考点：几何初步——相交线与平行线平行线的判定——平行线的性质——平行有关的几何模型.13、如图AB∥CD∥EF，CG平分∠ACE，∠A=140°，∠E=110°，则∠DCG=（）.A.13°B.14°C.15°D.16°答案：C.解析：∵EF∥CD，∴∠ECD=180°-∠E=70°.同理∠ACD=40°.∴∠ACE=110°.∵CG平分∠ACE.∴∠ECG=55°.∴∠DCG=∠ECD-∠ECG=70°-55°=15°.考点：几何初步——相交线与平行线——平行线——平行线的性质——平行有关的几何模型.14、如图，AB∥EF∥CD，EG平分∠BEF，∠B+∠BED+∠D=192°，∠B-∠D=24°，求∠GEF的度数.A.15°B.20°C.25°D.30°答案：D.解析：由AB∥EF∥CD,可知∠BED=∠B+∠D.已知∠B+∠BED+∠D=192°．∴2∠B+2∠D=192°，∠B+∠D=96°.又∠B-∠D=24°，于是可得关于∠B、∠D的方程组：{∠B+∠D=96°∠B−∠D=24°.解得∠B=60°．由AB∥EF知∠BEF=∠B=60°.因为EG平分∠BEF，所以∠GEF=12∠BEF=30°.考点：几何初步——相交线与平行线——平行线——平行有关的几何模型.15、把命题“在同一平面内，垂直于同一直线的两直线互相平行”改写成“如果……，那么……”的形式：.答案：“在同一平面内，如果两条直线都垂直于同一直线，那么这两直线互相平行”.解析：略.考点：命题与证明——命题与定理.16、下列命题中，假命题是（）．A. 如果两条直线都与第三条直线平行，那么这两条直线也互相平行.B. 两条直线被第三条直线所截，同旁内角互补.C. 两直线平行，内错角相等.D. 在同一平面内，过一点有且只有一条直线与已知直线垂直.答案：B.解析：两条直线被第三条直线所截，同旁内角不一定互补，只有两直线平行时，同旁内角互补．考点：命题与证明——命题与定理.17、已知：如图，AE⊥BC,FG⊥BC，∠1=∠2，∠D=∠3+60°，∠CBD=70°.（1）求证：AB∥CD.（2）求∠C的度数．答案：（1）证明见解析．（2）∠C=25°.解析：（1）∵AE⊥BC,FG⊥BC.∴AE∥FG.∴∠2=∠A.∵∠1=∠2.∴∠1=∠A.∴AB∥CD.（2）∵AB∥CD.∴∠C=∠3.∵∠D=∠3+60°，∠CBD=70°，∠C+∠D+∠CBD=180°.∴∠C+∠C+60°+70°=180°.∴∠C=25°.考点：几何初步——相交线与平行线——平行线的判定——平行线的性质.18、已知：如图，在△ABC中，BD⊥AC于点D，E为BC上一点，过E点作EF⊥AC，垂足为F，过点D作DH∥BC交AB于点H．（1）请你补全图形．（2）求证：∠BDH=∠CEF.答案：（1）画图见解析．（2）证明见解析．解析：（1）补全图形.（2）∵BD⊥AC，EF⊥AC.∴BD∥EF.∴∠CEF=∠CBD.∵DH∥BC.∴∠BDH=∠CBD.∴∠BDH=∠CEF.考点：几何初步——相交线与平行线——平行线的判定——平行线的性质.尺规作图——过一点作已知直线的垂线——过一点作已知直线的平行线.19、已知，如图，AB∥CD，∠1=∠B，∠2=∠D．求证：BE⊥DE.答案：证明见解析．解析：过E点作EF∥AB，则∠B=∠3.又∵∠1=∠B.∴∠1=∠3.∵AB∥EF，AD∥CD.∴EF∥CD.∴∠A=∠D.又∵∠2=∠D.∴∠2=∠4.∵∠1+∠2+∠3+∠4=180°.∴∠3+∠4=90°，即∠BED=90°.∴BE⊥ED.考点：几何初步——角——角的计算与证明.相交线与平行线——平行线的判定——平行线的性质.20、如图，已知CD∥EF，∠1+∠2=∠ABC.求证：AB∥GF.答案：证明见解析．解析：延长CD、GF交于点H，∠1=∠H.故∠2+∠H=∠ABC.易得AB∥GF.考点：几何初步——相交线与平行线——平行线的判定——平行线的性质.21、如图，已知点A，E，B在同一条直线上，设∠CED=x，∠C+∠D=y.（1）若AB∥CD，试用含x的式子表示y，并写出x的取值范围．（2）若x=90°，且∠AEC与∠D互余，求证：AB∥CD.答案：（1）y=180°-x，其中x的取值范围是（0＜x＜180）.（2）证明见解析．解析：（1）∵AB∥CD.∴∠AEC=∠C，∠BED=∠D.∵∠C+∠D=y.∴∠AEC+∠BED=y.∵∠CED=x，∠AEC+∠CED+∠BED=180°.∴x+y=180°.∴y=180°-x，其中x的取值范围是（0＜x＜180）.（2）∵x=90°，即∠CED=90°.∴∠AEC+∠BED=90°.∵∠AEC与∠D互余.∴∠AEC+∠D=90°.∴∠BED=∠D.∴AB∥CD.考点：函数——函数基础知识——函数自变量的取值范围.几何初步——角——余角和补角——角的计算与证明.相交线与平行线——平行线的判定——平行线的性质.22、阅读材料：材料1：如图（a）所示，科学实验证明：平面镜反射光线的规律是：射到平面镜上的光线和反射出的光线与平面镜所夹的角相等．即∠1=∠2.材料2：如图（b）所示，已知△ABC，过点A作AD∥BC，则∠DAC=∠C，又∵AD∥BC，∴∠DAC+∠BAC+∠B=180°，∴∠BAC+∠B+∠C=180°．即三角形内角和为180°.根据上述结论，解决下列问题：（1）如图（c）所示，一束光线m射到平面镜a上，被a反射到平面镜b上，又被b镜反射，若b反射出的光线n平行于m，且∠1=50°，则∠2= ，∠3= .（2）在（1）中，若∠1=40°，则∠3= ，若∠1=55°，则∠3= .（3）由（1）（2）请你猜想：当∠3= 时，任何射到平面镜a上的光线m经过平面镜a和b的两次反射后，入射光线m与反射光线n总是平行，请说明理由．答案：（1）1．100°.2．90°.（2）1．90°.2．90°.（3）90°.解析：（1）∵∠1=50°.∴∠4=∠1=50°.∴∠6=180°-50°-50°=80°.∵m∥n.∴∠2+∠6=180°.∴∠2=100°.∴∠5=∠7=40°.∴∠3=180°-50°-40°=90°.故答案为：100°，90°.（2）∵∠1=40°.∴∠4=∠1=40°.∴∠6=180°-40°-40°=100°.∵m∥n.∴∠2+∠6=180°.∴∠2=80°.∴∠5=∠7=50°.∴∠3=180°-50°-40°=90°.∵∠1=55°.∴∠4=∠1=55°.∴∠6=180°-55°-55°=70°.∵m∥n.∴∠2+∠6=180°.∴∠2=110°.∴∠5=∠7=35°.∴∠3=180°-55°-35°=90°.（3）当∠3=90°时，m∥n.理由是：∵∠3=90°.∴∠4+∠5=180°-90°=90°.∵∠4=∠1，∠7=∠5.∴∠1+∠7+∠4+∠5=2×90°=180°.∴∠2+∠6=180°-（∠1+∠4）+180°-（∠5+∠7）=180°.∴m∥n.故答案为：90°.考点：几何初步——相交线与平行线——平行线的判定——平行线的性质.23、如图，直线AC∥BD，连接AB，直线AC,BD及线段AB把平面分成①、②、③、④四个部分，规定：线上各点不属于任何部分．当动点P落在某个部分时，连接PA,PB，构成∠PAC，∠APB，∠PBD三个角．（提示：有公共端点的两条重合的射线所组成的角是0°角）（1）如图1，当动点P落在第①部分时，求证：∠APB=∠PAC+∠PBD.，（2）如图2，当动点P落在第②部分时，∠APB=∠PAC+∠PBD是否成立？（请画出图形并直接回答成立或不成立）（3）如图3，当动点P落在第③部分时，探究∠PAC，∠APB，∠PBD之间的关系，请画出图形并直接写出相应的结论．答案：（1）证明见解析．（2）不成立．（3）证明见解析．解析：（1）过点P作直线AC的平行线，易知∠1=∠PAC，∠2=∠PBD.又∵∠APB=∠1+∠2，∴∠APB=∠PAC+∠PBD．（2）不成立．（3）①当动点P在射线BA的右侧时（如图4）.结论是∠PBD =∠PAC+∠APB.②当动点P在射线BA上（如图5）.结论是∠PBD =∠PAC+∠APB或∠PAC =∠PBD +∠APB或∠APB=0°，∠PAC=∠PBD.③当动点P在射线BA的左侧时（如图6）.结论是∠PAC =∠PBD +∠APB.考点：几何初步——相交线与平行线——平行线的判定——平行线的性质——平行有关的几何模型.24、如图所示，在下列条件中：①∠1=∠2；②∠BAD=∠BCD；③∠3=∠4且∠ABC=∠ADC；④∠BAD+∠ABC=180°；⑤∠ABD=∠ACD；⑥∠ABC+∠BCD=180°．能判定AB∥CD的共有（）个．A.2B.3C.4D.5答案：A.解析：由平行的判定知③⑥可以判定AB∥CD.考点：几何初步——相交线与平行线——平行线的判定.25、有下列四个命题：①如果两条直线都与第三条直线平行，那么这两条直线也互相平行.②两条直线被第三条直线所截，同旁内角互补.③在同一平面内，如果两条直线都与第三条直线垂直，那么这两条直线也互相垂直.④在同一平面内，过一点有且只有一条直线与已知直线垂直.其中所有正确的命题是（）．A. ①②B. ①④C. ②③D. ③④答案：B.解析：①④正确；②两条直线被第三条直线所截，同旁内角不一定互补，需要两条直线平行；③在同一平面内，如果两条直线都与第三条直线垂直，那么这两条直线互相平行． 考点：几何初步——相交线与平行线——平行线公理及推论——平行线的判定——平行线的性质.26、如图，DB ∥FG ∥EC ，∠ABD=60°，∠ACE=30°，AP 平分∠BAC ，求∠PAG 的度数.A.11°B.12°C.13°D.14°答案：B.解析：由DB ∥FG ∥EC.可得∠BAC=∠BAG+∠CAG=∠DBA+∠ACE=60°+36°=96°.由AP 平分∠BAC 得∠CAP=12∠BAC=12×96°=48°. 由FG ∥EC 得∠GAC=∠ACE=36°.∴∠PAG=48°-36°=12°.考点：几何初步——相交线与平行线——平行线——平行有关的几何模型.27、如图，AB ∥CD ，且∠BAP=60°-α，∠APC=45°+α，∠PCD=30°-α，则α=（ ）．A.10°B.15°C.20°D.30°答案：B.解析：得∠APC=∠BAP+∠DCP .∴45°+α=60°-α+30°-α.解得：α=15°.考点：几何初步——相交线与平行线——平行线的性质.28、已知，如图，AB∥CD，直线α交AB、CD分别于点E、F，点M在线段EF点上，P是直线CD 上的一个动点，（点P不与F重合）.（1）当点P在射线FC上移动时，∠FMP、∠FPM和∠AEF之间的数量关系是：.（2）当点P在射线FD上移动时，∠FMP、∠FPM和∠AEF之间的数量关系是：. 答案：（1）∠FMP+∠FPM=∠AEF.（2）∠FMP+∠FPM+∠AEF=180°.解析：（1）当点P在射线FC上移动时.∵AB∥CD.∴∠AEF+∠CFE=180°.又∵∠FMP+∠FPM+∠CFE=180°.∴∠FMP+∠FPM=∠AEF.（2）当点P在射线FD上移动时.∵AB∥CD.∴∠AEF=∠MFD.又∵∠FMP+∠FPM+∠CFE=180°.∴∠FMP+∠FPM+∠AEF=180°.考点：几何初步——相交线与平行线——平行线的性质.。

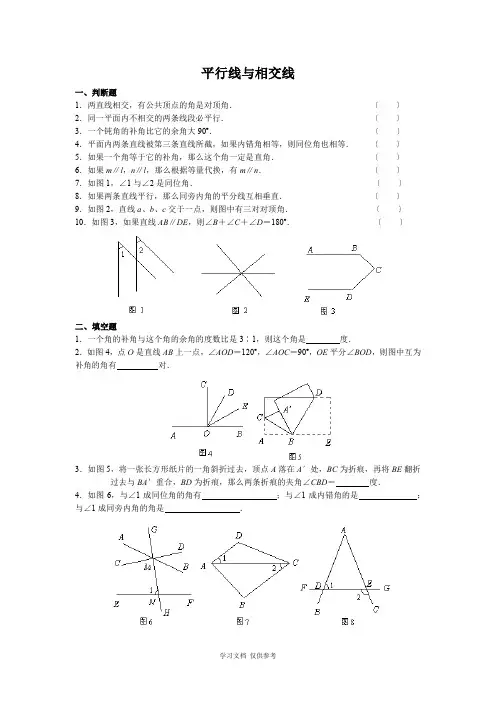
平行线与相交线一、判断题1．两直线相交，有公共顶点的角是对顶角．〔〕2．同一平面内不相交的两条线段必平行．〔〕3．一个钝角的补角比它的余角大90º．〔〕4．平面内两条直线被第三条直线所截，如果内错角相等，则同位角也相等．〔〕5．如果一个角等于它的补角，那么这个角一定是直角．〔〕6．如果m∥l，n∥l，那么根据等量代换，有m∥n．〔〕7．如图1，∠1与∠2是同位角．〔〕8．如果两条直线平行，那么同旁内角的平分线互相垂直．〔〕9．如图2，直线a、b、c交于一点，则图中有三对对顶角．〔〕10．如图3，如果直线AB∥DE，则∠B＋∠C＋∠D＝180º．〔〕二、填空题1．一个角的补角与这个角的余角的度数比是3∶1，则这个角是度．2．如图4，点O是直线AB上一点，∠AOD＝120º，∠AOC＝90º，OE平分∠BOD，则图中互为补角的角有对．3．如图5，将一张长方形纸片的一角斜折过去，顶点A落在A′处，BC为折痕，再将BE翻折过去与BA′重合，BD为折痕，那么两条折痕的夹角∠CBD＝度．4．如图6，与∠1成同位角的角有；与∠1成内错角的是；与∠1成同旁内角的角是．5．如图7，∠1＝∠2，∠DAB ＝85º，则∠B ＝ 度．6．如图8，已知∠1＋∠2＝180º，则图中与∠1相等的角共有 个．7．如图9，直线a 、b 都与直线c 相交，给出以下条件：①∠1＝∠2；②∠3＝∠6；③∠1＝∠8； ∠5＋∠8＝180º，其中能判断a ∥b 的条件是： 〔把你认为正确的序号填在空格内〕8．假设要把一个平面恰好分成5个部分，需要 条直线，这些直线的位置关系是 ．三、选择题1．以下说法中，正确的选项是〔 〕 〔A 〕锐角小于它的补角 〔B 〕锐角大于它的补角 〔C 〕钝角小于它的补角 〔D 〕锐角小于的余角2．如图10，假设∠AOB ＝180º，∠1是锐角，则∠1的余角是〔 〕〔A 〕21∠2－∠1 〔B 〕21∠2－23∠1 〔C 〕21〔∠2－∠1〕 〔D 〕31〔∠2＋∠1〕3．如图11，是同位角位置关系的是〔 〕〔A 〕∠3和∠4 〔B 〕∠1和∠4 〔C 〕∠2和∠4 〔D 〕∠1和∠2 4．假设两个角的一边在同一直线上，另一边互相平行，则这两个角〔 〕 〔A 〕相等 〔B 〕互补 〔C 〕相等或互补 〔D 〕都是直角 5．假设一个角等于它余角的2倍，则该角是它补角的〔 〕 〔A 〕21 〔B 〕31 〔C 〕51 〔D 〕61 6．如图12，四条直线相交，∠1和∠2互余，∠3是∠1的余角的补角，且∠3＝116º，则∠4等于〔 〕〔A 〕116º 〔B 〕126º 〔C 〕164º 〔D 〕154º7．同一平面内有三条直线a 、b 、c ，满足a ∥b ，b 与c 垂直，那么a 与c 的位置关系是〔 〕 〔A 〕垂直 〔B 〕平行 〔C 〕相交但不垂直 〔D 〕不能确定8．如图13，AB ∥EF ∥DC ，EG ∥DB ，则图中与∠1相等的角〔∠1除外〕有〔 〕 〔A 〕6个 〔B 〕5个 〔C 〕4个 〔D 〕3个9．如图14，一只小猴顺着一根斜放的竹竿往上爬，眼睛一直盯着挂在上端的帽子．在小猴爬行的过程中，视线与水平方向所成角〔 〕〔A 〕逐渐变大 〔B 〕逐渐变小 〔C 〕没有变化 〔D 〕无法确定 10．以下判断正确的选项是〔 〕〔A 〕相等的角是对顶角 〔B 〕互为补角的两个角一定是一个锐角和一个钝角 〔C 〕内错角相等 〔D 〕等角的补角相等 四、解答以下各题1．一个角的补角与它余角的2倍的差是平角的31，求这个角的度数．2．如图15，已知直线AB 和CD 相交于O ，∠AOE ＝∠EOC ，且∠AOE ＝28º．求∠BOD 、∠DOE 的度数．3．如图16，补全下面的思维过程，并说明这一步的理由． 〔1〕∠B ＝∠1 〔2〕BC ∥EF ↓ ↓∥ 理由： ∠2 ＝ 理由：五、完成以下推理过程1．已知：如图17，AB ⊥BC 于B ，CD ⊥BC 于C ，∠1＝∠2．求证：BE ∥CF ．证明：∵ AB ⊥BC ，CD ⊥BC 〔已知〕∴ ∠1＋∠3＝90º，∠2＋∠4＝90º〔 〕 ∴ ∠1与∠3互余，∠2与∠4互余又∵ ∠1＝∠2〔 〕 ∵ ∠3＝∠4〔 〕 ∴ BE ∥CF 〔 〕2．已知：如图18，AB ∥CD ，∠1＝∠2，求证：∠B ＝∠D ．证明：∵ ∠1＝∠2〔已知〕 ∴ ∥ 〔 〕∴ ∠BAD ＋∠B ＝ 〔 〕又∵ AB ∥CD 〔已知〕 ∴ ＋ ＝180º〔 〕 ∴ ∠B ＝∠D 〔 〕六、作图题如图19，已知∠BAC 及BA 上一点P ，求作直线MN ，使MN 经过点P ，且MN ∥AC ． 〔要求：使用尺规正确作图，保留作图痕迹〕七、计算与说理1．已知：如图20，∠ABC ＝50º，∠ACB ＝60º，∠ABC 、∠ACB 的平分线交于点O ，过点O 作EF ∥BC 交AB 于E ，交AC 于F ．求∠BOC 的度数．2．如图21，AB ∥DE ，∠1＝∠ACB ，∠CAB ＝21∠BAD ，试说明AD ∥BC ．6．假设两个角的两边分别平行，而一个角30°，则另一角的度数是____________________. 7、命题“同角的补角相等”改写成“如果……， 那么……”的形式可写成 ______________________________. 二、选择题(6×3)8、命题：①对顶角相等；②垂直于同一条直线的两直线平行；③相等的角是对顶角；④同位角相等。

平行线与相交线的计算题平行线与相交线是几何学中的重要概念，它们在我们的日常生活中有着广泛的应用。

本文将向你介绍一些有关平行线与相交线的计算题，帮助你更好地理解和应用这些概念。

1. 平行线的计算题在平行线的计算题中，我们通常需要求解平行线之间的距离或者找到符合特定条件的平行线。

例题1：已知平行线l1和l2，其中l1过点A（2，4），l2过点B（-1，3），求解l1与l2之间的距离。

解析：首先，我们可以根据已知条件得到l1和l2的斜率分别为k1和k2。

由于平行线具有相同的斜率，我们可以通过求解斜率的方式得到l1和l2的方程。

已知l1过点A（2，4），l2过点B（-1，3），因此l1的方程为y -4 = k1(x - 2)，l2的方程为y - 3 = k2(x - (-1))。

进一步化简方程，我们可以得到k1和k2的值，然后计算出l1和l2之间的距离。

例题2：已知直线l过点A（1，2），l的斜率为k，求解与直线l平行且过点A的直线方程。

解析：根据已知条件，我们可以得到l的斜率为k，过点A（1，2）。

那么与l平行且经过点A的直线方程可以表示为y - 2 = k(x - 1)。

综上所述，平行线的计算题通常涉及到求解直线的方程、距离等问题。

2. 相交线的计算题在相交线的计算题中，我们需要根据已知条件找到交点的坐标或者求解相交线的方程。

例题1：已知直线l1过点A（1，2），l2过点B（-1，3），求解l1和l2的交点坐标。

解析：我们可以首先得到l1和l2的方程，然后通过求解这两条直线的交点来求解。

l1的方程为y - 2 = k1(x - 1)，l2的方程为y - 3 = k2(x - (-1))。

将l1和l2的方程联立，解方程组，可以求解出交点的坐标。

例题2：已知直线l过点A（1，2），l的斜率为k，求解与直线l相交且过点A的直线方程。

解析：根据已知条件，我们可以得到l的斜率为k，过点A（1，2）。

那么与l相交且经过点A的直线方程可以表示为y - 2 = -1/k(x - 1)。

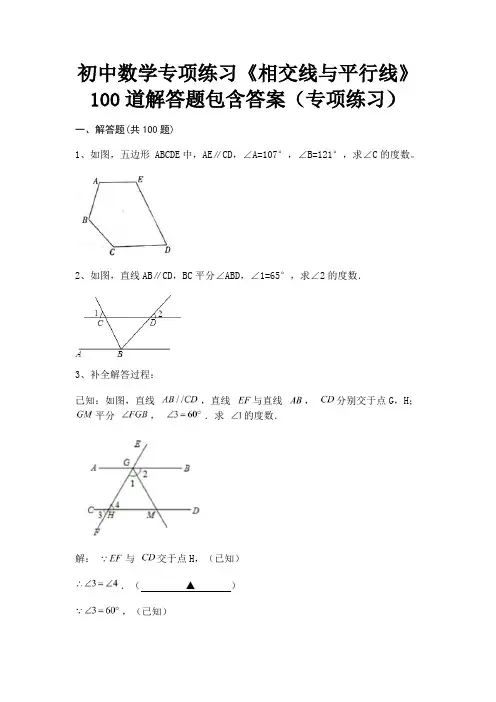
初中数学专项练习《相交线与平行线》100道解答题包含答案（专项练习）一、解答题(共100题)1、如图，五边形 ABCDE中，AE∥CD，∠A=107°，∠B=121°，求∠C的度数。

2、如图，直线AB∥CD，BC平分∠ABD，∠1=65°，求∠2的度数．3、补全解答过程：已知：如图，直线，直线与直线，分别交于点G，H；平分，．求的度数．解：与交于点H，（已知）．（▲），（已知）．（▲），与，交于点G，H，（已知）（▲）▲平分，（已知）▲．（角平分线的定义）4、如图所示，直线AB∥CD，∠1＝75°，求∠2的度数。

5、如图，AB与CD相交于O，OE平分∠AOC，OF⊥AB于O，OG⊥OE于O，若∠BOD=40°，求∠AOE和∠FOG的度数．6、如图，已知点B，E，C，F在同一条直线上，BE=CF，AB∥DE，∠A=∠D．求证：AB=DE．7、如图，已知，，，.AB 与DE平行吗？为什么？8、已知：如图，△ABC中，∠ABC=45°，CD⊥AB于D，BE⊥AC于E，BE与CD 相交于点F．求证：BF=AC．9、把下面的说理过程补充完整：已知：如图，BC//EF，BC＝EF，AF＝DC线段AB和线段DE平行吗？请说明理由．答：AB//DE理由：∵AF＝DC（已知）∴AF+FC＝DC+ ▲∴AC＝DF（▲）（填推理的依据）∵BC//EF（已知）∴∠BCA＝∠▲（两直线平行，内错角相等）又∵BC＝EF（已知）∴ （▲）（填推理的依据）∴∠A＝∠▲（全等三角形的对应角相等）∴AB//▲（内错角相等，两直线平行）10、小明在踢足球时把一块梯形ABCD的玻璃的下半部分打碎了，若量得上半部分∠A=123 ，∠D=105 ，你能知道下半部分的两个角∠B和∠C的度数吗？请说明理由.11、如图，BE∥CG，∠1＝∠2，求证：BD∥CF12、如图，EF∥BC，AC平分∠BAF，∠B=80°．求∠C的度数．13、如图，已知AB∥CD，∠B=40°，CN是∠BCE的平分线，CM⊥CN，求∠BCM 的度数．14、如图，有两堵围墙，有人想测量地面上两堵围墙内所形成的∠AOB的度数，但人又不能进入围墙，只能站在墙外，请问该如何测量？15、已知：如图，∠1=∠2，∠3=∠E，求证：∠A=∠CBE．16、如图，在直角△ABC 中，∠ACB=90°，CD 是高，∠1=35°，求∠2，∠B 与∠A 的度数．17、在平行四边形ABCD中, ∠A＋∠C＝160°，求∠A，∠C，∠B，∠D的度数．18、已知：如图，AB∥CD，直线EF分别交AB、CD于点E、F，EG平分∠BEF，若∠EFD=72°，则∠EGC等于多少度？19、如图，AF=BE，AC∥BD，CE∥DF，则(1)AC=_____，CE=______，(2)证明(1)中的结论。

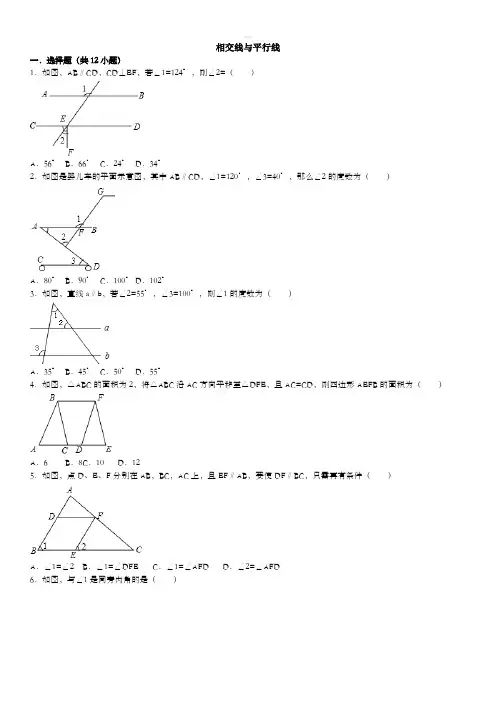
相交线与平行线一．选择题（共12小题）1．如图，AB∥CD，CD⊥EF，若∠1=124°，则∠2=（）A．56°B．66°C．24°D．34°2．如图是婴儿车的平面示意图，其中AB∥CD，∠1=120°，∠3=40°，那么∠2的度数为（）A．80°B．90°C．100° D．102°3．如图，直线a∥b，若∠2=55°，∠3=100°，则∠1的度数为（）A．35°B．45°C．50°D．55°4．如图，△ABC的面积为2，将△ABC沿AC方向平移至△DFE，且AC=CD，则四边形AEFB的面积为（）A．6 B．8 C．10 D．125．如图，点D、E、F分别在AB，BC，AC上，且EF∥AB，要使DF∥BC，只需再有条件（）A．∠1=∠2 B．∠1=∠DFE C．∠1=∠AFD D．∠2=∠AFD6．如图，与∠1是同旁内角的是（）A．∠2 B．∠3 C．∠4 D．∠57．如图，在下列条件中，不能判定直线a与b平行的是（）A．∠1=∠2 B．∠2=∠3 C．∠3=∠5 D．∠3+∠4=180°8．如图，直线a、b被直线c所截，下列条件能使a∥b的是（）A．∠1=∠6 B．∠2=∠6 C．∠1=∠3 D．∠5=∠79．如图，将一副三角板叠放在一起，使直角的顶点重合于点O，AB∥OC，DC与OB交于点E，则∠DEO的度数为（）A．85°B．70°C．75°D．60°10．如图，AB∥CD，AE平分∠CAB交CD于点E，若∠C=50°，则∠AED=（）A．65°B．115° C．125° D．130°11．如图，AB∥CD，DA⊥AC，垂足为A，若∠ADC=35°，则∠1的度数为（）A．65°B．55°C．45°D．35°12．如图，直线a∥b，∠1=85°，∠2=35°，则∠3=（）A．85°B．60°C．50°D．35°二．填空题（共12小题）13．如图，已知BD∥AC，∠1=65°，∠A=40°，则∠2的大小是．14．如图，将长方形ABCD沿AE折叠，使点D落在BC边上的点F，若∠BFA=34°，则∠DAE= 度．15．如图，m∥n，直角三角板ABC的直角顶点C在两直线之间，两直角边与两直线相交所形成的锐角分别为α、β，则α+β=．16．如图，四边形ABCD中，∠BAD=∠ADC=90°，AB=AD=，CD=，点P是四边形ABCD四条边上的一个动点，若P到BD的距离为，则满足条件的点P有个．17．如图，将一副三角板和一张对边平行的纸条按下列方式摆放，两个三角板的一直角边重合，含30°角的直角三角板的斜边与纸条一边重合，含45°角的三角板的一个顶点在纸条的另一边上，则∠1的度数是．18．如图，直线AB∥CD，BC平分∠ABD，若∠1=54°，则∠2= ．19．如图，直线AB∥CD，CA平分∠BCD，若∠1=50°，则∠2= ．20．如图，已知AB∥CD，BC∥DE．若∠A=20°，∠C=120°，则∠AED的度数是．21．如图，直线a∥b，直线c与直线a、b分别相交于A、B两点，若∠1=60°，则∠2= ．22．如图，AB∥CD，直线EF分别交AB、CD于M，N两点，将一个含有45°角的直角三角尺按如图所示的方式摆放，若∠EMB=75°，则∠PNM等于度．23．如图，△ABC中，BC=5cm，将△ABC沿BC方向平移至△A′B′C′的对应位置时，A′B′恰好经过AC的中点O，则△ABC平移的距离为cm．24．如图，是赛车跑道的一段示意图，其中AB∥DE，测得∠B=140°，∠D=120°，则∠C的度数为度．三．解答题（共16小题）25．如图，一个由4条线段构成的“鱼”形图案，其中∠1=50°，∠2=50°，∠3=130°，找出图中的平行线，并说明理由．26．如图，已知AC∥ED，AB∥FD，∠A=65°，求：∠EDF的度数．27．如图，已知AB∥CD，若∠C=40°，∠E=20°，求∠A的度数．28．如图，在△ABC中，∠B+∠C=110°，AD平分∠BAC，交BC于点D，DE∥AB，交AC于点E，求∠ADE的度数．29．如图，直线a∥b，BC平分∠ABD，DE⊥BC，若∠1=70°，求∠2的度数．30．如图，E为AC上一点，EF∥AB交AF于点F，且AE=EF．求证：∠BAC=2∠1．31．如图，直线AB、CD相交于点O，OE平分∠BOD，∠AOC=76°，∠DOF=90°，求∠EOF的度数．32．如图，直线AB，CD相交于O点，OM⊥AB于O．（1）若∠1=∠2，求∠NOD；（2）若∠BOC=4∠1，求∠AOC与∠MOD．33．如图，两直线AB、CD相交于点O，OE平分∠BOD，∠AOC：∠AOD=7：11．（1）求∠COE的度数．（2）若射线OF⊥OE，请在图中画出OF，并求∠COF的度数．34．如图，四边形ABCD中，∠A=∠C=90°，BE平分∠ABC，DF平分∠ADC，则BE与DF有何位置关系？试说明理由．35．将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起（其中，∠A=60°，∠D=30°；∠E=∠B=45°）：（1）①若∠DCE=45°，则∠ACB的度数为；②若∠ACB=140°，求∠DCE的度数；（2）由（1）猜想∠ACB与∠DCE的数量关系，并说明理由．（3）当∠ACE＜180°且点E在直线AC的上方时，这两块三角尺是否存在一组边互相平行？若存在，请直接写出∠ACE 角度所有可能的值（不必说明理由）；若不存在，请说明理由．36．已知：如图，∠C=∠1，∠2和∠D互余，BE⊥FD于点G．求证：AB∥CD．37．已知：如图所示，∠ABD和∠BDC的平分线交于E，BE交CD于点F，∠1+∠2=90°．（1）求证：AB∥CD；（2）试探究∠2与∠3的数量关系．38．如图，∠1+∠2=180°，∠A=∠C，DA平分∠BDF．（1）AE与FC会平行吗？说明理由；（2）AD与BC的位置关系如何？为什么？（3）BC平分∠DBE吗？为什么．39．如图，一条直线分别与直线BE、直线CE、直线BF、直线CF相交于点A，G，H，D且∠1=∠2，∠B=∠C （1）找出图中相互平行的线，说说它们之间为什么是平行的；（2）证明：∠A=∠D．40．将△ABC纸片沿DE折叠，其中∠B=∠C．（1）如图1，点C落在BC边上的点F处，AB与DF是否平行？请说明理由；（2）如图2，点C落在四边形ABCD内部的点G处，探索∠B与∠1+∠2之间的数量关系，并说明理由．相交线与平行线提高题与常考题和培优题(含解析)参考答案与试题解析一．选择题（共12小题）1．（2017•新城区校级模拟）如图，AB∥CD，CD⊥EF，若∠1=124°，则∠2=（）A．56°B．66°C．24°D．34°【分析】先根据平行线的性质，得出∠CEH=124°，再根据CD⊥EF，即可得出∠2的度数．【解答】解：∵AB∥CD，∠1=124°，∴∠CEH=124°，∴∠CEG=56°，又∵CD⊥EF，∴∠2=90°﹣∠CEG=34°．故选：D．【点评】本题主要考查了平行线的性质与垂线的定义，解题时注意：两直线平行，同位角相等．2．（2017•禹州市一模）如图是婴儿车的平面示意图，其中AB∥CD，∠1=120°，∠3=40°，那么∠2的度数为（）A．80°B．90°C．100°D．102°【分析】根据平行线性质求出∠A，根据三角形外角性质得出∠2=∠1﹣∠A，代入求出即可．【解答】解：∵AB∥CD，∴∠A=∠3=40°，∵∠1=120°，∴∠2=∠1﹣∠A=80°，故选A．【点评】本题考查了平行线性质和三角形外角性质的应用，关键是求出∠A的度数和得出∠2=∠1﹣∠A．3．（2017•莒县模拟）如图，直线a∥b，若∠2=55°，∠3=100°，则∠1的度数为（）A．35°B．45°C．50°D．55°【分析】根据两直线平行，同位角相等可得∠4=∠2，再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解．【解答】解：如图，∵直线a∥b，∴∠4=∠2=55°，∴∠1=∠3﹣∠4=100°﹣55°=45°．故选B．【点评】本题考查了平行线的性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，熟记性质并准确识图是解题的关键．4．（2017•莒县模拟）如图，△ABC的面积为2，将△ABC沿AC方向平移至△DFE，且AC=CD，则四边形AEFB的面积为（）A．6 B．8 C．10 D．12【分析】直接利用平移的性质结合三角形面积求法得出答案．【解答】解：∵将△ABC沿AC方向平移至△DFE，且AC=CD，∴A点移动的距离是2AC，则BF=AD，连接FC，则S△BFC=2S△ABC，S△ABC=S△FDC=S△FDE=2，∴四边形AEFB的面积为：10．故选：C．【点评】此题主要考查了平移的性质以及三角形面积求法，正确得出三角形之间面积关系是解题关键．5．（2017春•杭州月考）如图，点D、E、F分别在AB，BC，AC上，且EF∥AB，要使DF∥BC，只需再有条件（）A．∠1=∠2 B．∠1=∠DFE C．∠1=∠AFD D．∠2=∠AFD【分析】由平行线的性质得出∠1=∠2，再由∠1=∠DFE，得出∠2=∠DFE，由内错角相等，两直线平行即可得出DF∥BC．【解答】解：要使DF∥BC，只需再有条件∠1=∠DFE；理由如下：∵EF∥AB，∴∠1=∠2，∵∠1=∠DFE，∴∠2=∠DFE，∴DF∥BC；故选：B．【点评】本题考查了平行线的判定与性质；熟练掌握平行线的判定与性质，并能进行推理论证是解决问题的关键．6．（2016•柳州）如图，与∠1是同旁内角的是（）A．∠2 B．∠3 C．∠4 D．∠5【分析】根据同位角、内错角、同旁内角、对顶角的定义逐个判断即可．【解答】解：A、∠1和∠2是对顶角，不是同旁内角，故本选项错误；B、∠1和∠3是同位角，不是同旁内角，故本选项错误；C、∠1和∠4是内错角，不是同旁内角，故本选项错误；D、∠1和∠5是同旁内角，故本选项正确；故选D．【点评】本题考查了同位角、内错角、同旁内角、对顶角的定义的应用，能熟记同位角、内错角、同旁内角、对顶角的定义是解此题的关键，注意：数形结合思想的应用．7．（2016•来宾）如图，在下列条件中，不能判定直线a与b平行的是（）A．∠1=∠2 B．∠2=∠3 C．∠3=∠5 D．∠3+∠4=180°【分析】直接用平行线的判定直接判断．【解答】解：A、∵∠1与∠2是直线a，b被c所截的一组同位角，∴∠1=∠2，可以得到a∥b，∴不符合题意，B、∵∠2与∠3是直线a，b被c所截的一组内错角，∴∠2=∠3，可以得到a∥b，∴不符合题意，C、∵∠3与∠5既不是直线a，b被任何一条直线所截的一组同位角，内错角，∴∠3=∠5，不能得到a∥b，∴符合题意，D、∵∠3与∠4是直线a，b被c所截的一组同旁内角，∴∠3+∠4=180°，可以得到a∥b，∴不符合题意，故选C【点评】此题是平行线的判定，解本题的关键是熟练掌握平行线的判定定理．8．（2016•百色）如图，直线a、b被直线c所截，下列条件能使a∥b的是（）A．∠1=∠6 B．∠2=∠6 C．∠1=∠3 D．∠5=∠7【分析】利用平行线的判定方法判断即可．【解答】解：∵∠2=∠6（已知），∴a∥b（同位角相等，两直线平行），则能使a∥b的条件是∠2=∠6，故选B【点评】此题考查了平行线的判定，熟练掌握平行线的判定方法是解本题的关键．9．（2016•营口）如图，将一副三角板叠放在一起，使直角的顶点重合于点O，AB∥OC，DC与OB 交于点E，则∠DEO的度数为（）A．85°B．70°C．75°D．60°【分析】由平行线的性质求出∠AOC=120°，再求出∠BOC=30°，然后根据三角形的外角性质即可得出结论．【解答】解：∵AB∥OC，∠A=60°，∴∠A+∠AOC=180°，∴∠AOC=120°，∴∠BOC=120°﹣90°=30°，∴∠DEO=∠C+∠BOC=45°+30°=75°；故选：C．【点评】本题主要考查了平行线的性质、三角形的外角性质；熟练掌握平行线的性质和三角形的外角性质是解决问题的关键．10．（2016•陕西）如图，AB∥CD，AE平分∠CAB交CD于点E，若∠C=50°，则∠AED=（）A．65°B．115°C．125°D．130°【分析】根据平行线性质求出∠CAB的度数，根据角平分线求出∠EAB的度数，根据平行线性质求出∠AED的度数即可．【解答】解：∵AB∥CD，∴∠C+∠CAB=180°，∵∠C=50°，∴∠CAB=180°﹣50°=130°，∵AE平分∠CAB，∴∠EAB=65°，∵AB∥CD，∴∠EAB+∠AED=180°，∴∠AED=180°﹣65°=115°，故选B．【点评】本题考查了角平分线定义和平行线性质的应用，注意：平行线的性质有：①两条平行线被第三条直线所截，同位角相等，②两条平行线被第三条直线所截，内错角相等，③两条平行线被第三条直线所截，同旁内角互补．11．（2016•威海）如图，AB∥CD，DA⊥AC，垂足为A，若∠ADC=35°，则∠1的度数为（）A．65°B．55°C．45°D．35°【分析】利用已知条件易求∠ACD的度数，再根据两线平行同位角相等即可求出∠1的度数．【解答】解：∵DA⊥AC，垂足为A，∴∠CAD=90°，∵∠ADC=35°，∴∠ACD=55°，∵AB∥CD，∴∠1=∠ACD=55°，故选B．【点评】本题主要考查了平行线的性质，垂直的定义等知识点，熟记平行线的性质定理是解题关键．12．（2016•毕节市）如图，直线a∥b，∠1=85°，∠2=35°，则∠3=（）A．85°B．60°C．50°D．35°【分析】先利用三角形的外角定理求出∠4的度数，再利用平行线的性质得∠3=∠4=50°．【解答】解：在△ABC中，∵∠1=85°，∠2=35°，∴∠4=85°﹣35°=50°，∵a∥b，∴∠3=∠4=50°，故选C．【点评】本题考查了平行线的性质和三角形的外角定理，比较简单；运用了三角形的一个外角等于与它不相邻的两个内角的和，及两直线平行，内错角相等；本题的解法有多种，也可以利用直线b下方的三角形和对顶角相等来求解．二．填空题（共12小题）13．（2017•辽宁模拟）如图，已知BD∥AC，∠1=65°，∠A=40°，则∠2的大小是75°．【分析】由BD与AC平行，利用两直线平行同位角相等求出∠C的度数，再利用三角形内角和定理求出所求角度数即可．【解答】解：∵BD∥AC，∠1=65°，∴∠C=∠1=65°，在△ABC中，∠A=40°，∠C=65°，∴∠2=75°，故答案为：75°【点评】此题考查了平行线的性质，以及三角形内角和定理，熟练掌握平行线的性质是解本题的关键．14．（2017春•萧山区月考）如图，将长方形ABCD沿AE折叠，使点D落在BC边上的点F，若∠BFA=34°，则∠DAE= 17 度．【分析】首先根据平行线的性质得到∠DAF的度数，再根据对折的知识即可求出∠DAE的度数．【解答】解：∵四边形ABCD是矩形，∴AD∥BC．∴∠BFA=∠DAF，∵∠BFA=34°，∴∠DAF=34°，∵△AFE是△ADE沿直线AE对折得到，∴∠DAE=∠FAE，∴∠DAE=∠DAF=17°，故答案为17．【点评】本题主要考查了平行线的性质，解题的关键是根据平行线的性质求出∠DAF的度数，此题难度不大．15．（2017•河北一模）如图，m∥n，直角三角板ABC的直角顶点C在两直线之间，两直角边与两直线相交所形成的锐角分别为α、β，则α+β=90°．【分析】根据平行线的性质即可得到结论．【解答】解：过C作CE∥m，∵m∥n，∴CE∥n，∴∠1=∠α，∠2=∠β，∵∠1+∠2=90°，∴∠α+∠β=90°，故答案为：90°．【点评】本题考查了平行线的性质，熟练掌握平行线的性质即可得到结论．16．（2016•凉山州）如图，四边形ABCD中，∠BAD=∠ADC=90°，AB=AD=，CD=，点P 是四边形ABCD四条边上的一个动点，若P到BD的距离为，则满足条件的点P有 2 个．【分析】首先作出AB、AD边上的点P（点A）到BD的垂线段AE，即点P到BD的最长距离，作出BC、CD的点P（点C）到BD的垂线段CF，即点P到BD的最长距离，由已知计算出AE、CF 的长为，比较得出答案．【解答】解：过点A作AE⊥BD于E，过点C作CF⊥BD于F，∵∠BAD=∠ADC=90°，AB=AD=，CD=2，∴∠ABD=∠ADB=45°，∴∠CDF=90°﹣∠ADB=45°，∵sin∠ABD=，∴AE=AB•sin∠ABD=3•sin45°=3＞，CF=2＜，所以在AB和AD边上有符合P到BD的距离为的点2个，故答案为：2．【点评】本题考查了解直角三角形和点到直线的距离，解题的关键是先求出各边上点到BD的最大距离比较得出答案．17．（2016•菏泽）如图，将一副三角板和一张对边平行的纸条按下列方式摆放，两个三角板的一直角边重合，含30°角的直角三角板的斜边与纸条一边重合，含45°角的三角板的一个顶点在纸条的另一边上，则∠1的度数是15°．【分析】过A点作AB∥a，利用平行线的性质得AB∥b，所以∠1=∠2，∠3=∠4=30°，加上∠2+∠3=45°，易得∠1=15°．【解答】解：如图，过A点作AB∥a，∴∠1=∠2，∵a∥b，∴AB∥b，∴∠3=∠4=30°，而∠2+∠3=45°，∴∠2=15°，∴∠1=15°．故答案为15°．【点评】本题考查了平行线的性质：两直线平行，内错角相等．18．（2016•连云港）如图，直线AB∥CD，BC平分∠ABD，若∠1=54°，则∠2= 72°．【分析】由AB∥CD，根据平行线的性质找出∠ABC=∠1，由BC平分∠ABD，根据角平分线的定义即可得出∠CBD=∠ABC，再结合三角形的内角和为180°以及对顶角相等即可得出结论．【解答】解：∵AB∥CD，∠1=54°，∴∠ABC=∠1=54°，又∵BC平分∠ABD，∴∠CBD=∠ABC=54°．∵∠CBD+∠BDC+∠DCB=180°，∠1=∠DCB，∠2=∠BDC，∴∠2=180°﹣∠1﹣∠CBD=180°﹣54°﹣54°=72°．故答案为：72°．【点评】本题考查了平行线的性质、角平分线的定义以及三角形内角和定理，解题的关键是找出各角的关系．本题属于基础题，难度不大，解决该题型题目时，根据平行线的性质找出相等（或互补）的角是关键．19．（2016•青海）如图，直线AB∥CD，CA平分∠BCD，若∠1=50°，则∠2= 65°．【分析】先根据平行线的性质得∠ABC+∠BCD=180°，根据对顶角相等得∠ABC=∠1=50°，则∠BCD=130°，再利用角平分线定义得到∠ACD=∠BCD=65°，然后根据平行线的性质得到∠2的度数．【解答】解：∵AB∥CD，∴∠ABC+∠BCD=180°，而∠ABC=∠1=50°，∴∠BCD=130°，∵CA平分∠BCD，∴∠ACD=∠BCD=65°，∵AB∥CD，∴∠2=∠ACD=65°．故答案为65°．【点评】本题考查了平行线性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．20．（2016•金华）如图，已知AB∥CD，BC∥DE．若∠A=20°，∠C=120°，则∠AED的度数是80°．【分析】延长DE交AB于F，根据平行线的性质得到∠AFE=∠B，∠B+∠C=180°，根据三角形的外角的性质即可得到结论．【解答】解：延长DE交AB于F，∵AB∥CD，BC∥DE，∴∠AFE=∠B，∠B+∠C=180°，∴∠AFE=∠B=60°，∴∠AED=∠A+∠AFE=80°，故答案为：80°．【点评】本题考查了平行线的性质，三角形的外角的性质，熟练掌握平行线的性质是解题的关键．21．（2016•云南）如图，直线a∥b，直线c与直线a、b分别相交于A、B两点，若∠1=60°，则∠2= 60°．【分析】先根据平行线的性质求出∠3的度数，再由对顶角的定义即可得出结论．【解答】解：∵直线a∥b，∠1=60°，∴∠1=∠3=60°．∵∠2与∠3是对顶角，∴∠2=∠3=60°．故答案为：60°．【点评】本题考查的是平行线的性质，用到的知识点为：两直线平行，同位角相等．22．（2016•吉林）如图，AB∥CD，直线EF分别交AB、CD于M，N两点，将一个含有45°角的直角三角尺按如图所示的方式摆放，若∠EMB=75°，则∠PNM等于30 度．【分析】根据平行线的性质得到∠DNM=∠BME=75°，由等腰直角三角形的性质得到∠PND=45°，即可得到结论．【解答】解：∵AB∥CD，∴∠DNM=∠BME=75°，∵∠PND=45°，∴∠PNM=∠DNM﹣∠DNP=30°，故答案为：30．【点评】本题考查了平行线的性质，等腰直角三角形的性质，熟练掌握平行线的性质是解题的关键．23．（2016•泰州）如图，△ABC中，BC=5cm，将△ABC沿BC方向平移至△A′B′C′的对应位置时，A′B′恰好经过AC的中点O，则△ABC平移的距离为 2.5 cm．【分析】根据平移的性质：对应线段平行，以及三角形中位线定理可得B′是BC的中点，求出BB′即为所求．【解答】解：∵将△ABC沿BC方向平移至△A′B′C′的对应位置，∴A′B′∥AB，∵O是AC的中点，∴B′是BC的中点，∴BB′=5÷2=2.5（cm）．故△ABC平移的距离为2.5cm．故答案为：2.5．【点评】考查了平移的性质，平移的基本性质：①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等．24．（2016•都匀市一模）如图，是赛车跑道的一段示意图，其中AB∥DE，测得∠B=140°，∠D=120°，则∠C的度数为100 度．【分析】过点C作CF∥AB，由平行线性质可得∠B，∠D，∠BCF，∠DCF的关系，进而求得∠C．【解答】解：如图所示：过点C作CF∥AB．∵AB∥DE，∴DE∥CF；∴∠BCF=180°﹣∠B=40°，∠DCF=180°﹣∠D=60°；∴∠C=∠BCF+∠DCF=100°．故答案为：100．【点评】本题运用了两直线平行，同旁内角互补的性质，需要作辅助线求解，难度中等．三．解答题（共16小题）25．（2016•淄博）如图，一个由4条线段构成的“鱼”形图案，其中∠1=50°，∠2=50°，∠3=130°，找出图中的平行线，并说明理由．【分析】根据同位角相等，两直线平行证明OB∥AC，根据同旁内角互补，两直线平行证明OA∥BC．【解答】解：OA∥BC，OB∥AC．∵∠1=50°，∠2=50°，∴∠1=∠2，∴OB∥AC，∵∠2=50°，∠3=130°，∴∠2+∠3=180°，∴OA∥BC．【点评】本题考查的是平行线的判定，掌握平行线的判定定理：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行是解题的关键．26．（2016•槐荫区二模）如图，已知AC∥ED，AB∥FD，∠A=65°，求：∠EDF的度数．【分析】根据平行线的性质，即可解答．【解答】解：∵AC∥ED，∴∠BED=∠A=65°，∵AB∥FD，∴∠EDF=∠BED=65°．【点评】本题考查了平行线的性质，解决本题的关键是熟记平行线的性质．27．（2016•厦门校级一模）如图，已知AB∥CD，若∠C=40°，∠E=20°，求∠A的度数．【分析】根据两直线平行，同位角相等可得∠1=∠C，再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解．【解答】解：如图，∵AB∥CD，∴∠1=∠C=40°，∴∠A=∠1﹣∠E=40°﹣20°=20°．【点评】本题考查了平行线的性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，熟记各性质是解题的关键．28．（2016•江西模拟）如图，在△ABC中，∠B+∠C=110°，AD平分∠BAC，交BC于点D，DE∥AB，交AC于点E，求∠ADE的度数．【分析】根据三角形内角和定理求出∠BAC，根据角平分线定义求出∠BAD，根据平行线的性质得出∠ADE=∠BAD即可．【解答】解：∵在△ABC中，∠B+∠C=110°，∴∠BAC=180°﹣∠B﹣∠C=70°，∵AD是△ABC的角平分线，∴∠BAD=∠BAC=35°，∵DE∥AB，∴∠ADE=∠BAD=35°．【点评】本题考查了平行线的性质，三角形内角和定理，角平分线定义的应用，注意：两直线平行，内错角相等．29．（2016•江西模拟）如图，直线a∥b，BC平分∠ABD，DE⊥BC，若∠1=70°，求∠2的度数．【分析】根据平行线的性质得到∠1=∠ABD=70°，由角平分线的定义得到∠EBD=ABD=35°，根据三角形的内角和即可得到结论．【解答】解：∵直线a∥b，∴∠1=∠ABD=70°，∵BC平分∠ABD，∴∠EBD=ABD=35°，∵DE⊥BC，∴∠2=90°﹣∠EBD=55°．【点评】本题考查了平行线的性质，角平分线的定义，三角形的内角和，熟练掌握平行线的性质是解题的关键．30．（2016•朝阳区一模）如图，E为AC上一点，EF∥AB交AF于点F，且AE=EF．求证：∠BAC=2∠1．【分析】根据平行线的性质得到∠1=∠FAB，由等腰三角形的性质得到∠EAF=∠EFA，根据邻补角和对顶角的定义即可得到结论．【解答】证明：∵EF∥AB，∴∠1=∠FAB，∵AE=EF，∴∠EAF=∠EFA，∵∠1=∠EFA，∴∠EAF=∠1，∴∠BAC=2∠1．【点评】本题考查了平行线的性质，邻补角的定义，熟练掌握平行线的性质是解题的关键．31．（2016秋•宜兴市期末）如图，直线AB、CD相交于点O，OE平分∠BOD，∠AOC=76°，∠DOF=90°，求∠EOF的度数．【分析】根据对顶角相等可得∠BOD=∠AOC，再根据角平分线的定义求出∠DOE，然后根据∠EOF=∠DOF﹣∠DOE代入数据计算即可得解．【解答】解：由对顶角相等得，∠BOD=∠AOC=76°，∵OE平分∠BOD，∴∠DOE=∠BOD=38°，∵∠DOF=90°，∴∠EOF=∠DOF﹣∠DOE=90°﹣38°=52°．【点评】本题考查了对顶角相等，角平分线的定义，熟记性质与概念并准确识图是解题的关键．32．（2016春•西华县期末）如图，直线AB，CD相交于O点，OM⊥AB于O．（1）若∠1=∠2，求∠NOD；（2）若∠BOC=4∠1，求∠AOC与∠MOD．【分析】（1）由已知条件和观察图形可知∠1与∠AOC互余，再根据平角的定义求解；（2）利用已知的∠BOC=4∠1，结合图形以及对顶角的性质求∠AOC与∠MOD．【解答】解：（1）因为OM⊥AB，所以∠1+∠AOC=90°．又∠1=∠2，所以∠2+∠AOC=90°，所以∠NOD=180°﹣（∠2+∠AOC）=180°﹣90°=90°．（2）由已知∠BOC=4∠1，即90°+∠1=4∠1，可得∠1=30°，所以∠AOC=90°﹣30°=60°，所以由对顶角相等得∠BOD=60°，故∠MOD=90°+∠BOD=150°．【点评】本题利用垂直的定义，对顶角的性质和平角的定义计算，要注意领会由垂直得直角这一要点．33．（2016春•双城市期末）如图，两直线AB、CD相交于点O，OE平分∠BOD，∠AOC：∠AOD=7：11．（1）求∠COE的度数．（2）若射线OF⊥OE，请在图中画出OF，并求∠COF的度数．【分析】（1）根据∠AOC+∠AOD=180°可得∠AOC和∠AOD的度数，根据对顶角相等可得∠BOD=70°，再利用角平分线定义可得∠DOE=35°，再根据邻补角定义可得∠COE的度数；（2）分两种情况画图，进而求出∠COF的度数．【解答】解：（1）∠AOC：∠AOD=7：11，∠AOC+∠AOD=180°，∴∠AOC=70°，∠AOD=110°，∵∠BOD=∠AOC，∴∠BOD=70°，∵OE平分∠BOD，∴∠DOE=35°，∴∠COE=180°﹣∠DOE=145°；（2）分两种情况，如图1，∵OF⊥OE，∴∠EOF=90°，∴∠COF=∠COE﹣∠EOF=145°﹣90°=55°，如图2，∠COF=∠360°﹣∠COE﹣∠EOF=125°．【点评】此题主要考查了垂线、邻补角、对顶角，关键是掌握对顶角相等，邻补角互补．34．（2016春•太仓市期末）如图，四边形ABCD中，∠A=∠C=90°，BE平分∠ABC，DF平分∠ADC，则BE与DF有何位置关系？试说明理由．【分析】根据四边形的内角和定理和∠A=∠C=90°，得∠ABC+∠ADC=180°；根据角平分线定义、等角的余角相等易证明和BE与DF两条直线有关的一对同位角相等，从而证明两条直线平行．【解答】解：BE∥DF．理由如下：∵∠A=∠C=90°（已知），∴∠ABC+∠ADC=180°（四边形的内角和等于360°）．∵BE平分∠ABC，DF平分∠ADC，∴∠1=∠2=∠ABC，∠3=∠4=∠ADC（角平分线的定义）．∴∠1+∠3=（∠ABC+∠ADC）=×180°=90°（等式的性质）．又∠1+∠AEB=90°（三角形的内角和等于180°），∴∠3=∠AEB（同角的余角相等）．∴BE∥DF（同位角相等，两直线平行）．【点评】此题运用了四边形的内角和定理、角平分线定义、等角的余角相等和平行线的判定，难度中等．35．（2016春•周口期末）将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起（其中，∠A=60°，∠D=30°；∠E=∠B=45°）：（1）①若∠DCE=45°，则∠ACB的度数为135°；②若∠ACB=140°，求∠DCE的度数；（2）由（1）猜想∠ACB与∠DCE的数量关系，并说明理由．（3）当∠ACE＜180°且点E在直线AC的上方时，这两块三角尺是否存在一组边互相平行？若存在，请直接写出∠ACE角度所有可能的值（不必说明理由）；若不存在，请说明理由．【分析】（1）①首先计算出∠DCB的度数，再用∠ACD+∠DCB即可；②首先计算出∠DCB的度数，再计算出∠DCE即可；（2）根据（1）中的计算结果可得∠ACB+∠DCE=180°，再根据图中的角的和差关系进行推理即可；（3）根据平行线的判定方法可得．【解答】解：（1）①∵∠ECB=90°，∠DCE=45°，∴∠DCB=90°﹣45°=45°，∴∠ACB=∠ACD+∠DCB=90°+45°=135°，故答案为：135°；②∵∠ACB=140°，∠ACD=90°，∴∠DCB=140°﹣90°=50°，∴∠DCE=90°﹣50°=40°；（2）∠ACB+∠DCE=180°，∵∠ACB=∠ACD+∠DCB=90°+∠DCB，∴∠ACB+∠DCE=90°+∠DCB+∠DCE=90°+90°=180°；（3）存在，当∠ACE=30°时，AD∥BC，当∠ACE=∠E=45°时，AC∥BE，当∠ACE=120°时，AD∥CE，当∠ACE=135°时，BE∥CD，当∠ACE=165°时，BE∥AD．【点评】此题主要考查了角的计算，以及平行线的判定，关键是理清图中角的和差关系．36．（2016秋•郓城县期末）已知：如图，∠C=∠1，∠2和∠D互余，BE⊥FD于点G．求证：AB∥CD．【分析】首先由BE⊥FD，得∠1和∠D互余，再由已知，∠C=∠1，∠2和∠D互余，所以得∠C=∠2，从而证得AB∥CD．【解答】证明：∵BE⊥FD，∴∠EGD=90°，∴∠1+∠D=90°，又∠2和∠D互余，即∠2+∠D=90°，∴∠1=∠2，又已知∠C=∠1，∴∠C=∠2，∴AB∥CD．【点评】此题考查的知识点是平行线的判定，关键是由BE⊥FD及三角形内角和定理得出∠1和∠D 互余．37．（2016春•广州校级期末）已知：如图所示，∠ABD和∠BDC的平分线交于E，BE交CD于点F，∠1+∠2=90°．（1）求证：AB∥CD；（2）试探究∠2与∠3的数量关系．【分析】（1）已知BE、DE平分∠ABD、∠BDC，且∠1+∠2=90°，可得∠ABD+∠BDC=180°，根据同旁内角互补，可得两直线平行．（2）已知∠1+∠2=90°，即∠BED=90°；那么∠3+∠FDE=90°，将等角代换，即可得出∠3与∠2的数量关系．【解答】证明：（1）∵BE、DE平分∠ABD、∠BDC，∴∠1=∠ABD，∠2=∠BDC；∵∠1+∠2=90°，∴∠ABD+∠BDC=180°；∴AB∥CD；（同旁内角互补，两直线平行）解：（2）∵DE平分∠BDC，∴∠2=∠FDE；∵∠1+∠2=90°，∴∠BED=∠DEF=90°；∴∠3+∠FDE=90°；∴∠2+∠3=90°．【点评】此题主要考查了角平分线的性质以及平行线的判定，难度不大．38．（2016秋•内江期末）如图，∠1+∠2=180°，∠A=∠C，DA平分∠BDF．（1）AE与FC会平行吗？说明理由；（2）AD与BC的位置关系如何？为什么？（3）BC平分∠DBE吗？为什么．【分析】（1）证明∠1=∠CDB，利用同位角相等，两直线平行即可证得；（2）平行，根据平行线的性质可以证得∠A=∠CBE，然后利用平行线的判定方法即可证得；（3）∠EBC=∠CBD，根据平行线的性质即可证得．【解答】解：（1）平行．理由如下：∵∠1+∠2=180°，∠2+∠CDB=180°（邻补角定义），∴∠1=∠CDB，∴AE∥FC（同位角相等两直线平行）；（2）平行．理由如下：∵AE∥CF，∴∠C=∠CBE（两直线平行，内错角相等），又∵∠A=∠C，∴∠A=∠CBE，∴AD∥BC（同位角相等，两直线平行）；（3）平分．理由如下：∵DA平分∠BDF，∴∠FDA=∠ADB，∵AE∥CF，AD∥BC，∴∠FDA=∠A=∠CBE，∠ADB=∠CBD，∴∠EBC=∠CBD，∴BC平分∠DBE．【点评】本题考查了平行线的判定与性质，解答此题的关键是注意平行线的性质和判定定理的综合运用．39．（2016秋•双柏县期末）如图，一条直线分别与直线BE、直线CE、直线BF、直线CF相交于点A，G，H，D且∠1=∠2，∠B=∠C（1）找出图中相互平行的线，说说它们之间为什么是平行的；（2）证明：∠A=∠D．【分析】（1）根据同位角相等，两直线平行可得CE∥FB，进而可得∠C=∠BFD，再由条件∠B=∠C 可得∠B=∠BFD，从而可根据内错角相等，两直线平行得AB∥CD；（2）根据（1）可得AB∥CD，再根据两直线平行，内错角相等可得∠A=∠D．【解答】（1）解：∵∠1=∠2，∴CE∥FB，∴∠C=∠BFD，∵∠B=∠C，∴∠B=∠BFD，∴AB∥CD；（2）证明：由（1）可得AB∥CD，∴∠A=∠D．【点评】此题主要考查了平行线的判定和性质，关键是掌握平行线的判定定理和性质定理．40．（2016春•邳州市期末）将△ABC纸片沿DE折叠，其中∠B=∠C．（1）如图1，点C落在BC边上的点F处，AB与DF是否平行？请说明理由；（2）如图2，点C落在四边形ABCD内部的点G处，探索∠B与∠1+∠2之间的数量关系，并说明理由．【分析】（1）AB与DF平行．根据翻折可得出∠DFC=∠C，结合∠B=∠C即可得出∠B=∠DFC，从而证出AB∥DF；（2）连接GC，由翻折可得出∠DGE=∠ACB，再根据三角形外角的性质得出∠1=∠DGC+∠DCG，∠2=∠EGC+∠ECG，通过角的运算即可得出∠1+∠2=2∠B．【解答】解：（1）AB与DF平行．理由如下：由翻折，得∠DFC=∠C．又∵∠B=∠C，∴∠B=∠DFC，∴AB∥DF．（2）连接GC，如图所示．由翻折，得∠DGE=∠ACB．∵∠1=∠DGC+∠DCG，∠2=∠EGC+∠ECG，∴∠1+∠2=∠DGC+∠DCG+∠EGC+∠ECG=（∠DGC+∠EGC）+（∠DCG+∠ECG）=∠DGE+∠DCE=2∠ACB．∵∠B=∠ACB，∴∠1+∠2=2∠B．【点评】本题考查了平行线的判定以及翻折得性质，解题的关键是：（1）找出∠B=∠DFC；（2）根据三角形外角的性质利用角的计算求出∠1+∠2=2∠B．本题属于基础题，难度不大，解决该题型题目时，找出相等（或互补）的角是关键．。

相交线与平行线
一．选择题（共3小题）
1．在同一平面内，有8条互不重合的直线，l1，l2，l3…l8，若l1⊥l2，l2∥l3，l3⊥l4，l4∥l5…以此类推，则l1和l8的位置关系是（ ）
A．平行B．垂直C．平行或垂直D．无法确定
2．如图，直线AB、CD相交于O，OE⊥AB，OF⊥CD，则与∠1互为余角的有（ ）
26．几何推理，看图填空：
（1）∵∠3=∠4（已知）
∴∥（）
（2）∵∠DBE=∠CAB（已知）
∴∥（）
（3）∵∠ADF+=180°（已知）
∴AD∥BF（）
27．如图，直线AB、CD相交于点O，OE平分∠BOD．
（1）若∠AOC=68°，∠DOF=90°，求∠EOF的度数．
（2）若OF平分∠COE，∠BOF=30°，求∠AOC的度数．
7．将一副学生用三角板按如图所示的方式放置．若AE∥BC，则∠AFD的度数是．
评卷人
得分
三．解答题（共43小题）
8．已知：直线EF分别与直线AB，CD相交于点F，E，EM平∠FED，AB∥CD，H，P分别为直线AB和线段EF上的点．
（1）如图1，HM平分∠BHP，若HP⊥EF，求∠M的度数．
（2）如图2，EN平分∠HEF交AB于点N，NQ⊥EM于点Q，当H在直线AB上运动（不与点F重合）时，探究∠FHE与∠ENQ的关系，并证明你的结论．
（3）若点P在图（3）位置时，写出∠1、∠2、∠3之间的关系并给予证明．
15．如图，已知AB∥PN∥CD．
（1）试探索∠ABC，∠BCP和∠CPN之间的数量关系，并说明理由；
（2）若∠ABC=42°，∠CPN=155°，求∠BCP的度数．
16．如图，AD∥BC，∠EAD=∠C，∠FEC=∠BAE，∠EFC=50°

相交线与平行线一．选择题（共3小题）1．在同一平面内，有8条互不重合的直线，l1，l2，l3…l8，若l1⊥l2，l2∥l3，l3⊥l4，l4∥l5…以此类推，则l1和l8的位置关系是（）A．平行B．垂直C．平行或垂直 D．无法确定2．如图，直线AB、CD相交于O，OE⊥AB，OF⊥CD，则与∠1互为余角的有（）A．3个B．2个C．1个D．0个3．如图所示，同位角共有（）A．6对B．8对C．10对D．12对二．填空题（共4小题）4．一块长方体橡皮被刀切了3次，最多能被分成块．5．如图，P点坐标为（3，3），l1⊥l2，l1、l2分别交x轴和y轴于A点和B点，则四边形OAPB的面积为．6．如图，直线l1∥l2，∠1=20°，则∠2+∠3= ．7．将一副学生用三角板按如图所示的方式放置．若AE∥BC，则∠AFD的度数是．三．解答题（共43小题）8．已知：直线EF分别与直线AB，CD相交于点F，E，EM平∠FED，AB∥CD，H，P分别为直线AB 和线段EF上的点．（1）如图1，HM平分∠BHP，若HP⊥EF，求∠M的度数．（2）如图2，EN平分∠HEF交AB于点N，NQ⊥EM于点Q，当H在直线AB上运动（不与点F重合）时，探究∠FHE与∠ENQ的关系，并证明你的结论．9．我们知道，两条直线相交，有且只有一个交点，三条直线相交，最多只有三个交点，那么，四条直线相交，最多有多少个交点？一般地，n条直线最多有多少个交点？说明理由．10．如图，直线AB，CD相交于点O，OA平分∠EOC．（1）若∠EOC=70°，求∠BOD的度数．（2）若∠EOC：∠EOD=4：5，求∠BOD的度数．11．如图，直线EF，CD相交于点0，OA⊥OB，且OC平分∠AOF，（1）若∠AOE=40°，求∠BOD的度数；（2）若∠AOE=α，求∠BOD的度数；（用含α的代数式表示）（3）从（1）（2）的结果中能看出∠AOE和∠BOD有何关系？112．如图1，已知MN∥PQ，B在MN上，C在PQ上，A在B的左侧，D在C的右侧，DE平分∠ADC，BE平分∠ABC，直线DE、BE交于点E，∠CBN=100°．（1）若∠ADQ=130°，求∠BED的度数；（2）将线段AD沿DC方向平移，使得点D在点C的左侧，其他条件不变，若∠ADQ=n°，求∠BED 的度数（用含n的代数式表示）．13．如图，将含有45°角的三角板ABC的直角顶点C放在直线m上，若∠1=26°（1）求∠2的度数（2）若∠3=19°，试判断直线n和m的位置关系，并说明理由．14．如图，已知直线l1∥l2，l3、l4和l1、l2分别交于点A、B、C、D，点P 在直线l3或l4上且不与点A、B、C、D重合．记∠AEP=∠1，∠PFB=∠2，∠EPF=∠3．（1）若点P在图（1）位置时，求证：∠3=∠1+∠2；（2）若点P在图（2）位置时，请直接写出∠1、∠2、∠3之间的关系；（3）若点P在图（3）位置时，写出∠1、∠2、∠3之间的关系并给予证明．15．如图，已知AB∥PN∥CD．（1）试探索∠ABC，∠BCP和∠CPN之间的数量关系，并说明理由；（2）若∠ABC=42°，∠CPN=155°，求∠BCP的度数．16．如图，AD∥BC，∠EAD=∠C，∠FEC=∠BAE，∠EFC=50°（1）求证：AE∥CD；（2）求∠B的度数．17．探究题：（1）如图1，若AB∥CD，则∠B+∠D=∠E，你能说明理由吗？（2）反之，若∠B+∠D=∠E，直线AB与直线CD有什么位置关系？简要说明理由．（3）若将点E移至图2的位置，此时∠B、∠D、∠E之间有什么关系？直接写出结论．（4）若将点E移至图3的位置，此时∠B、∠D、∠E之间有什么关系？直接写出结论．（5）在图4中，AB∥CD，∠E+∠G与∠B+∠F+∠D之间有何关系？直接写出结论．18．如图1，AB∥CD，在AB、CD内有一条折线EPF．（1）求证：∠AEP+∠CFP=∠EPF．（2）如图2，已知∠BEP的平分线与∠DFP的平分线相交于点Q，试探索∠EPF与∠EQF之间的关系．（3）如图3，已知∠BEQ=∠BEP，∠DFQ=∠DFP，则∠P与∠Q有什么关系，说明理由．（4）已知∠BEQ=∠BEP，∠DFQ=∠DFP，有∠P与∠Q的关系为．（直接写结论）19．如图所示，L1，L2，L3交于点O，∠1=∠2，∠3：∠1=8：1，求∠4的度数．试卷第2页，总6页20．如图，一个由4条线段构成的“鱼”形图案，其中∠1=50°，∠2=50°，∠3=130°，找出图中的平行线，并说明理由．21．如图，直线AB、CD相交于点O，OE平分∠BOD．（1）若∠AOC=70°，∠DOF=90°，求∠EOF的度数；（2）若OF平分∠COE，∠BOF=15°，若设∠AOE=x°．①则∠EOF= ．（用含x的代数式表示）②求∠AOC的度数．22．如图，直线AB、CD相交于点O，已知∠AOC=75°，OE把∠BOD分成两个角，且∠BOE：∠EOD=2：3．（1）求∠EOB的度数；（2）若OF平分∠AOE，问：OA是∠COF的角平分线吗？试说明理由．23．如图，直线AB、CD相交于点O，∠AOC=72°，射线OE在∠BOD的内部，∠DOE=2∠BOE．（1）求∠BOE和∠AOE的度数；（2）若射线OF与OE互相垂直，请直接写出∠DOF的度数．24．如图，直线AB，CD相交于点O，OA平分∠EOC，且∠EOC：∠EOD=2：3．（1）求∠BOD的度数；（2）如图2，点F在OC上，直线GH经过点F，FM平分∠OFG，且∠MFH﹣∠BOD=90°，求证：OE ∥GH．25．如图，直线AB．CD相交于点O，OE平分∠BOC，∠COF=90°．（1）若∠BOE=70°，求∠AOF的度数；（2）若∠BOD：∠BOE=1：2，求∠AOF的度数．26．几何推理，看图填空：（1）∵∠3=∠4（已知）∴∥（）（2）∵∠DBE=∠CAB（已知）∴∥（）（3）∵∠ADF+=180°（已知）∴AD∥BF（）27．如图，直线AB、CD相交于点O，OE平分∠BOD．（1）若∠AOC=68°，∠DOF=90°，求∠EOF的度数．（2）若OF平分∠COE，∠BOF=30°，求∠AOC的度数．28．将一副三角板拼成如图所示的图形，∠DCE的平分线CF交DE于点F．3（1）求证：CF∥AB．（2）求∠DFC的度数．29．看图填空，并在括号内注明说理依据．如图，已知AC⊥AE，BD⊥BF，∠1=35°，∠2=35°，AC与BD平行吗？AE与BF平行吗？解：因为∠1=35°，∠2=35°（已知），所以∠1=∠2．所以∥（）．又因为AC⊥AE（已知），所以∠EAC=90°．（）所以∠EAB=∠EAC+∠1=125°．同理可得，∠FBG=∠FBD+∠2= °．所以∠EAB=∠FBG（）．所以∥（同位角相等，两直线平行）．30．已知如图所示，∠B=∠C，点B、A、E在同一条直线上，∠EAC=∠B+∠C，且AD平分∠EAC，试说明AD∥BC的理由．31．如图，直线AB、CD相交于点O，OE把∠BOD分成两部分；（1）直接写出图中∠AOC的对顶角为，∠BOE的邻补角为；（2）若∠AOC=70°，且∠BOE：∠EOD=2：3，求∠AOE的度数．32．如图，已知AB∥CD，现将一直角三角形PMN放入图中，其中∠P=90°，PM交AB于点E，PN 交CD于点F（1）当△PMN所放位置如图①所示时，则∠PFD与∠AEM的数量关系为；（2）当△PMN所放位置如图②所示时，求证：∠PFD﹣∠AEM=90°；（3）在（2）的条件下，若MN与CD交于点O，且∠DON=30°，∠PEB=15°，求∠N的度数．33．阅读下面的推理过程，在括号内填上推理的依据，如图：因为∠1+∠2=180°，∠2+∠4=180°（已知）所以∠1=∠4，（）所以a∥c．（）又因为∠2+∠3=180°（已知）∠3=∠6（）所以∠2+∠6=180°，（）所以a∥b．（）所以b∥c．（）试卷第4页，总6页34．已知：如图，AB∥CD，FG∥HD，∠B=100°，FE为∠CEB的平分线，求∠EDH的度数．35．已知：如图，AB∥CD，FE⊥AB于G，∠EMD=134°，求∠GEM的度数．36．如图，∠B和∠D的两边分别平行．（1）在图1 中，∠B和∠D的数量关系是，在图2中，∠B和∠D的数量关系是；（2）用一句话归纳的命题为：；并请选择图1或图2中一种情况说明理由；（3）应用：若两个角的两边分别互相平行，其中一个角是另一个角的2倍，求这两个角的度数．37．已知AD∥BC，AB∥CD，E为射线BC上一点，AE平分∠BAD．（1）如图1，当点E在线段BC上时，求证：∠BAE=∠BEA．（2）如图2，当点E在线段BC延长线上时，连接DE，若∠ADE=3∠CDE，∠AED=60°．①求证：∠ABC=∠ADC；②求∠CED的度数．38．如图，已知a∥b，ABCDE是夹在直线a，b之间的一条折线，试研究∠1、∠2、∠3、∠4、∠5的大小之间有怎样的等量关系？请说明理由．39．如图，AB∥DC，增加折线条数，相应角的个数也会增多，∠B，∠E，∠F，∠G，∠D之间又会有何关系？40．已知直线AB∥CD，（1）如图1，点E在直线BD上的左侧，直接写出∠ABE，∠CDE和∠BED之间的数量关系是．（2）如图2，点E在直线BD的左侧，BF，DF分别平分∠ABE，∠CDE，直接写出∠BFD和∠BED的数量关系是．（3）如图3，点E在直线BD的右侧BF，DF仍平分∠ABE，∠CDE，那么∠BFD和∠BED有怎样的数量关系？请说明理由．41．（1）如图，直线a，b，c两两相交，∠3=2∠1，∠2=155°，求∠4的度数．（2）如图，直线AB、CD相交于点O，OE平分∠BOD，OF平分∠COE，∠AOD：∠BOE=4：1，求∠AOF 的度数．42．如图，已知CD⊥DA，DA⊥AB，∠1=∠2．试说明DF∥AE．请你完成下列填空，把解答过程补充完整．解：∵CD⊥DA，DA⊥AB，∴∠CDA=90°，∠DAB=90°．（）∴∠CDA=∠DAB．（等量代换）又∠1=∠2，从而∠CDA﹣∠1=∠DAB﹣．（等式的性质）即∠3= ．5∴DF∥AE．（）．43．如图1，AB∥CD，EOF是直线AB、CD间的一条折线．（1）说明：∠O=∠BEO+∠DFO．（2）如果将折一次改为折二次，如图2，则∠BEO、∠O、∠P、∠PFC会满足怎样的关系，证明你的结论．（3）若将折线继续折下去，折三次，折四次…折n次，又会得到怎样的结论？请写出你的结论．44．如图，已知∠1=60°，∠2=60°，∠MAE=45°，∠FEG=15°，EG平分∠AEC，∠NCE=75°．求证：（1）AB∥EF．（2）AB∥ND．45．如图，∠E=∠1，∠3+∠ABC=180°，BE是∠ABC的角平分线．求证：DF∥AB．46．已知，直线AB∥CD，E为AB、CD间的一点，连结EA、EC．（1）如图①，若∠A=30°，∠C=40°，则∠AEC= ．（2）如图②，若∠A=100°，∠C=120°，则∠AEC= ．（3）如图③，请直接写出∠A，∠C与∠AEC之间关系是．47．如图，已知AB∥CD，EF⊥AB于点G，若∠1=30°，试求∠F的度数．48．生活中到处都存在着数学知识，只要同学们学会用数学的眼光观察生活，就会有许多意想不到的收获，如图两幅图都是由同一副三角板拼凑得到的：（1）请你计算出图1中的∠ABC的度数．（2）图2中AE∥BC，请你计算出∠AFD的度数．49．如图，将一张矩形纸片ABCD沿EF对折，延长DE交BF于点G，若∠EFG=50°，求∠1，∠2的度数．50．如图所示，在长方体中．（1）图中和AB平行的线段有哪些？（2）图中和AB垂直的直线有哪些？试卷第6页，总6页本卷由系统自动生成，请仔细校对后使用，答案仅供参考。

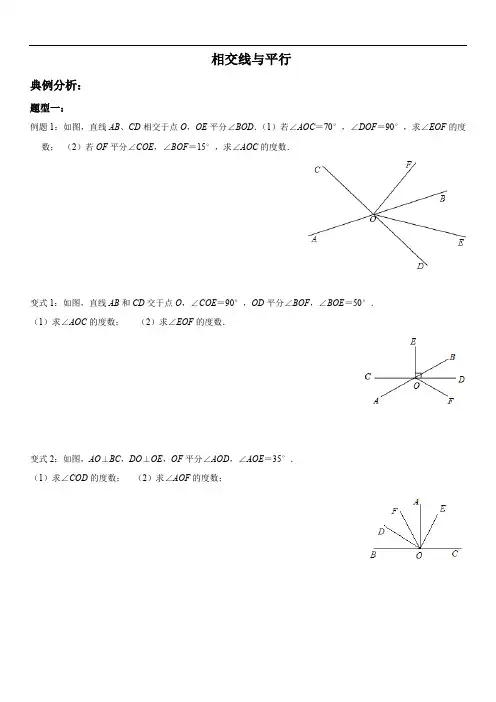
相交线与平行典例分析：题型一：例题1：如图，直线AB、CD相交于点O，OE平分∠BOD．（1）若∠AOC＝70°，∠DOF＝90°，求∠EOF的度数；（2）若OF平分∠COE，∠BOF＝15°，求∠AOC的度数．变式1：如图，直线AB和CD交于点O，∠COE＝90°，OD平分∠BOF，∠BOE＝50°．（1）求∠AOC的度数；（2）求∠EOF的度数．变式2：如图，AO⊥BC，DO⊥OE，OF平分∠AOD，∠AOE＝35°．（1）求∠COD的度数；（2）求∠AOF的度数；变式3：直线AB、CD相交于点O，OE、OF是两条射线．（1）如图1，若∠EOF＝90°，且OD平分∠AOE，∠BOF＝60°，求∠AOD的度数；（2）如图2，若OE平分∠BOD，∠AOC＝68°，∠DOF＝90°，求∠EOF的度数；（3）如图3，若OF平分∠COE，∠BOF＝15°，若设∠AOE＝x，求∠AOC的度数．（用含x的式子表示）题型二：例题2．如图，直线AB与CD相交于点O，∠AOM＝90°．（1）如图1，若OC平分∠AOM，求∠AOD的度数；（2）如图2，若∠BOC＝4∠NOB，且OM平分∠NOC，求∠MON的度数．变式1：如图，直线AB，CD相交于O点，OM⊥AB于O．（1）若∠1＝∠2，求∠NOD；（2）若∠BOC＝4∠1，求∠AOC与∠MOD．变式2：如图，直线AB、CD相交于O点，∠AOC与∠AOD的度数比为4：5，OE⊥AB，OF平分∠DOB，求∠EOF 的度数．变式3：如图，直线AB、CD相交于点O，OE把∠BOD分成两部分；（1）直接写出图中∠AOC的对顶角为，∠BOE的邻补角为；（2）若∠AOC＝70°，且∠BOE：∠EOD＝2：3，求∠AOE的度数．题型三：例题3：如图，将一块含30°角的直角三角尺放在一个矩形中，三个顶点分别在矩形的三条边上，如果∠1＝25°，那么∠2的度数是（）A．25°B．35°C．45°D．55°变式1：如图，已知a∥b，将含30°角的三角尺如图放置，∠1＝110°，则∠2的度数为（）A．40°B．45°C．50°D．60°变式2：如图，直尺的一条边经过一个含45角的直角顶点直尺的一组对边分别与直角三角尺的两边相交，若∠1＝30°，则∠2的度数是（）A．30°B．45°C．60°D．75°变式3：如图，将一块含有30°角的直角三角板的两个顶点放在长方形直尺的一组对边上，如果∠1＝30°，那么A．30°B．40°C．50°D．60°变式4：如图所示，将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上，若∠1＝35°，则∠2的度数（）A．10°B．25°C．30°D．35°变式5：．直角三角板与两边平行的纸条如图所示放置，下列结论不一定正确的是（）A．∠1＝∠2B．∠3＝∠4C．∠2+∠4＝90°D．∠1＝∠4题型四：例题4：如图1是长方形纸带，∠DEF＝15°，将纸带沿EF折叠成图2，再沿BF折叠成图3，则图3中∠CFE度数是多少（）A．160°B．150°C．135°D．110°变式1：图1是矩形纸片，∠SAB＝20°，将纸片沿AB折叠成图2，则∠ACN的度数是（）A．40°B．45°C．50°D．60°变式2：如图，将一张长方形纸片ABCD沿EF折叠，点D、C分别落在D′、C′的位置处，若∠1＝56°，则∠A．56°B．62°C．68°D．124°变式3：如图，将矩形ABCD沿GH折叠，点C落在点Q处，点D落在AB边上的点E处，若∠AGE＝32°，则∠GHC等于（）A．112°B．110°C．108°D．106°变式4：如图所示，将矩形纸片ABCD折叠，使点D与点B重合，点C落在点C′处，折痕为EF，若∠ABE＝20°，那么∠EFC′的度数为（）A．115°B．120°C．125°D．130°变式5：如图，图1是AD∥BC的一张纸条，按图1→图2→图3，把这一纸条先沿EF折叠并压平，再沿BF折叠并压平，若图3中∠CFE＝18°，则图2中∠AEF的度数为（）A．120°B．108°C．126°D．114°题型五：例题5：如图，已知AB∥CD，∠α＝．变式1：如图所示，AB∥EF，∠B＝35°，∠E＝25°，则∠C+∠D的值为．变式2：珠江流域某江段江水流向经过B、C、D三点拐弯后与原来相同，如图，若∠ABC＝120°，∠BCD＝80°，则∠CDE＝度．变式3：如图，AB∥CD，∠P＝90°，设∠A＝α、∠E＝β、∠D＝γ，则α、β、γ满足的关系是（）A．β+γ﹣α＝90°B．α+β+γ＝90°C．α+β﹣γ＝90° D．α+β+γ＝180°变式4：如图，已知AB∥DE，∠ABC＝50°，∠CDE＝150°，则∠BCD的值为变式5：11．如图，AB∥CD，有图中α，β，γ三角之间的关系是题型六：例题6：如图，已知AB∥CD，分别探究下面四个图形中∠P和∠A、∠C的关系，并从所得的四个关系中任选一个加以说明，证明所探究的结论的正确性．结论（1）（2）（3）（4）．我选择结论．说明理由．变式1：（1）如图1，a∥b，则∠1+∠2＝（2）如图2，AB∥CD，则∠1+∠2+∠3＝，并说明理由（3）如图3，a∥b，则∠1+∠2+∠3+∠4＝（4）如图4，a∥b，根据以上结论，试探究∠1+∠2+∠3+∠4+…+∠n＝（直接写出你的结论，无需说明理由）变式2：如图，已知直线l1∥l2，l3、l4和l1、l2分别交于点A、B、C、D，点P在直线l3或l4上且不与点A、B、C、D重合．记∠AEP＝∠1，∠PFB＝∠2，∠EPF＝∠3．（1）若点P在图（1）位置时，求证：∠3＝∠1+∠2；（2）若点P在图（2）位置时，请直接写出∠1、∠2、∠3之间的关系；（3）若点P在图（3）位置时，写出∠1、∠2、∠3之间的关系并给予证明．变式3：（1）如图甲，AB∥CD，试问∠2与∠1+∠3的关系是什么，为什么？（2）如图乙，AB∥CD，试问∠2+∠4与∠1+∠3+∠5一样大吗？为什么？（3）如图丙，AB∥CD，试问∠2+∠4+∠6与∠1+∠3+∠5+∠7哪个大？为什么？你能将它们推广到一般情况吗？请写出你的结论．题型七：例7．如图，AD∥BC，∠BAD＝∠BCD，AE，CF分别是∠BAD，∠BCD的角平分线，由此判断AE∥CF，请说明理由．变式1．如图，四边形ABCD中，∠A＝∠C＝90°，BE，DF分别是∠ABC，∠ADC的平分线．（1）∠1与∠2有什么关系，为什么？（2）BE与DF有什么关系？请说明理由．变式2．如图，四边形ABCD中，∠A＝∠C＝90°，BE平分∠ABC，DF平分∠BCD（1）BE与DF平行吗？请说明理由．（2）若（1）中“∠A＝∠C＝90°”改为∠A＝∠C，上述结论还成立吗？请说明理由．题型八：例8．已知：如图，CB⊥AB，CE平分∠BCD，DE平分∠CDA，∠1+∠2＝90°，求证：DA⊥AB．变式1．如图，DE平分∠ADC，CE平分∠BCD，且∠1+∠2＝90°．试判断AD与BC的位置关系，并说明理由．题型九：例9．问题情景：如图1，AB∥CD，∠P AB＝130°，∠PCD＝120°，求∠APC的度数．问题迁移：（2）如图3，AD∥BC，当点P在A、B两点之间运动时，∠ADP＝∠α，∠BCP＝∠β，求∠CPD与∠α、∠β之间有何数量关系？请说明理由．（3）在（2）的条件下，如果点P在A、B两点外侧运动时（点P与点A、B、O三点不重合），请你直接写出∠CPD 与∠α、∠β之间的数量关系．变式1．已知：如图，直线a∥b，直线c与直线a、b分别相交于C、D两点，直线d与直线a、b分别相交于A、B 两点，点P在直线AB上运动（不与A、B两点重合）．（1）如图1，当点P在线段AB上运动时，总有：∠CPD＝∠PCA+∠PDB，请说明理由；（2）如图2，当点P在线段AB的延长线上运动时，∠CPD、∠PCA、∠PDB之间有怎样的数量关系，并说明理由；（3）如图3，当点P在线段BA的延长线上运动时，∠CPD、∠PCA、∠PDB之间又有怎样的数量关系（只需直接给出结论）？课后巩固：1．已知，OA⊥OC，且∠AOB：∠AOC＝2：3，则∠BOC的度数为（）A．30°B．150°C．30°或150°D．90°2．如图，AB∥CD∥EF，∠ABE＝70°，∠DCE＝144°，则∠BEC的度数为（）A．34°B．36°C．44°D．46°3．如图，将三角尺的直角顶点放在直尺的一边上，∠1＝30°，∠2＝50°，则∠3的度数等于（）A．20°B．30°C．50°D．80°4．观察下列图形，并阅读，图形下面的相关字．两条直线相交最多有1个交点三条直线相交最多有3个交点四条直线相交最多有6个交点则n条直线最多有个交点．第2题图第3题图第4题图5．如图，图1是AD∥BC的一张纸条，按图1→图2→图3，把这一纸条先沿EF折叠并压平，再沿BF折叠并压平，若图3中∠CFE＝18°，则图2中∠AEF的度数为6．如图，AB∥CD，则∠A、∠C、∠E、∠F满足的数量关系是（）A．∠A＝∠C+∠E+∠F B．∠A+∠E﹣∠C﹣∠F＝180°C．∠A﹣∠E+∠C+∠F＝90°D．∠A+∠E+∠C+∠F＝360°7．如图，AB∥CD，DE⊥BE，BF、DF分别为∠ABE、∠CDE的角平分线，则∠BFD＝（）A．110°B．120°C．125°D．135°第6题图第7题图8．如图所示，某住宅小区内有一长方形地块，想在长方形地块内修筑同样宽的两条”之”字路，余下部分绿化，道路的宽为2米，则绿化的面积为m2．9．如图，将△ABE向右平移2cm得到△DCF，AE、DC交于点G．如果△ABE的周长是16cm，那么△ADG与△CEG的周长之和是cm．10．如图，将等腰直角△ABC沿斜边BC方向平移得到△A1B1C1．若AB＝3，图中阴影部分面积为2，则BB1＝．11．如图所示，把直角梯形ABCD沿AD方向平移到梯形EFGH，HG＝24cm，WG＝8cm，WC＝6cm，求阴影部分的面积为cm2．第8题图第9题图第10题图第11题图。

相交线与平行线专项训练及解析答案一、选择题1．下列四个命题：①对顶角相等；②内错角相等；③平行于同一条直线的两条直线互相平行；④如果一个角的两边分别平行于另一个角的两边，那么这两个角相等．其中真命题的个数是( )A．1个B．2个C．3个D．4个【答案】B【解析】解：①符合对顶角的性质，故本小题正确；②两直线平行，内错角相等，故本小题错误；③符合平行线的判定定理，故本小题正确；④如果一个角的两边分别平行于另一个角的两边，那么这两个角相等或互补，故本小题错误．故选B．2．如图，若AB∥CD，则∠α、∠β、∠γ之间关系是（）A．∠α+∠β+∠γ=180°B．∠α+∠β﹣∠γ=360°C．∠α﹣∠β+∠γ=180°D．∠α+∠β﹣∠γ=180°【答案】D【解析】试题解析：如图，作EF∥AB，∵AB∥CD，∴EF∥CD，∵EF∥AB，∴∠α+∠AEF=180°，∵EF∥CD，∴∠γ=∠DEF，而∠AEF+∠DEF=∠β，∴∠α+∠β=180°+∠γ，即∠α+∠β-∠γ=180°．故选：D ．3．如图，已知ABC ∆，若AC BC ⊥，CD AB ⊥，12∠=∠，下列结论：①//AC DE ；②3A ∠=∠；③3EDB ∠=∠；④2∠与3∠互补；⑤1B ∠=∠，其中正确的有（ ）A ．2个B ．3个C ．4个D ．5个【答案】C【解析】【分析】 根据平行线的判定得出AC ∥DE ，根据垂直定义得出∠ACB=∠CDB=∠CDA=90°，再根据三角形内角和定理求出即可．【详解】∵∠1=∠2，∴AC ∥DE ，故①正确；∵AC ⊥BC ，CD ⊥AB ，∴∠ACB=∠CDB=90°，∴∠A+∠B=90°，∠3+∠B=90°，∴∠A=∠3，故②正确；∵AC ∥DE ，AC ⊥BC ，∴DE ⊥BC ，∴∠DEC=∠CDB=90°，∴∠3+∠2=90°（∠2和∠3互余），∠2+∠EDB=90°，∴∠3=∠EDB ，故③正确，④错误；∵AC ⊥BC ，CD ⊥AB ，∴∠ACB=∠CDA=90°，∴∠A+∠B=90°，∠1+∠A=90°，∴∠1=∠B ，故⑤正确；即正确的个数是4个，故选：C ．【点睛】此题考查平行线的判定和性质，三角形内角和定理，垂直定义，能综合运用知识点进行推理是解题的关键．4．如图，已知正五边形ABCDE ，AF ∥CD ，交DB 的延长线于点F ，则∠DFA 的度数是（ ）A ．28°B ．30°C ．38°D ．36°【答案】D【解析】【分析】根据两直线平行，内错角相等，得到∠DFA=∠CDB ，根据三角形的内角和求出∠CDB 的度数从而得到∠DFA 的度数.【详解】 解：∠C=(52)1801085︒-⨯=，且CD=CB ， ∴∠CDB=∠CBD ∵由三角形的内角和∠C+∠CDB+∠CBD=180°∴∠CDB+∠CBD=180°-∠C =180°-108°=72°∴∠CDB==∠CBD=72362︒︒= 又∵AF ∥CD∴∠DFA=∠CDB=36°（两直线平行，内错角相等）故选D【点睛】本题主要考查多边形的基本概念和三角形的基本概念，正n 边形的内角读数为(2)180n n-⨯.5．下列结论中：①若a=b a b ；②在同一平面内，若a ⊥b ，b//c ，则a ⊥c ；③直线外一点到直线的垂线段叫点到直线的距离；33( ) A ．1个B ．2个C ．3个D ．4个【答案】B【解析】【分析】【详解】解：①若a=b 0≥a b②在同一平面内，若a ⊥b,b//c ，则a ⊥c ，正确③直线外一点到直线的垂线段的长度叫点到直线的距离 33正确的个数有②④两个6．如图，下列推理错误的是( )A．因为∠1＝∠2，所以c∥d B．因为∠3＝∠4，所以c∥dC．因为∠1＝∠3，所以a∥b D．因为∠1＝∠4，所以a∥b【答案】C【解析】分析：由平行线的判定方法得出A、B、C正确，D错误；即可得出结论．详解：根据内错角相等，两直线平行，可知因为∠1＝∠2，所以c∥d，故正确；根据同位角相等，两直线平行，可知因为∠3＝∠4，所以c∥d，故正确；因为∠1和∠3的位置不符合平行线的判定，故不正确；根据内错角相等，两直线平行，可知因为∠1＝∠4，所以a∥b，故正确.故选：C.点睛：本题考查了平行线的判定方法；熟练掌握平行线的判定方法，并能进行推理论证是解决问题的关键．7．如图所示，b∥c，a⊥b，∠1=130°，则∠2=（）．A．30°B．40°C．50°D．60°【答案】B【解析】【分析】证明∠3=90°，利用三角形的外角的性质求出∠4即可解决问题．【详解】如图，反向延长射线a交c于点M，∵b∥c，a⊥b，∴∠3=90°，∵∠1=90°+∠4，∴130°=90°+∠4，∴∠4=40°，∴∠2=∠4=40°，故选B．【点睛】本题考查平行线的性质，垂线的性质，三角形的外角的性质等知识，解题的关键是熟练掌握基本知识8．下列五个命题：①如果两个数的绝对值相等，那么这两个数的平方相等；②内错角相等；③在同一平面内，垂直于同一条直线的两条直线互相平行；④两个无理数的和一定是无理数；⑤坐标平面内的点与有序数对是一一对应的．其中真命题的个数是（）A．2个B．3个C．4个D．5个【答案】B【解析】【分析】根据平面直角坐标系的概念，在两直线平行的条件下，内错角相等，两个无理数的和可以是无理数也可以是有理数，进行判断即可.【详解】①正确；②在两直线平行的条件下，内错角相等，②错误；③正确；④反例：两个无理数π和-π，和是0，④错误；⑤坐标平面内的点与有序数对是一一对应的，正确；故选：B．【点睛】本题考查实数，平面内直线的位置；牢记概念和性质，能够灵活理解概念性质是解题的关键．9．下列命题是真命题的是（）A．同位角相等B．对顶角互补C．如果两个角的两边互相平行，那么这两个角相等D ．如果点P 的横坐标和纵坐标互为相反数，那么点P 在直线y x =-的图像上．【答案】D【解析】【分析】根据平行线的性质定理对A 、C 进行判断；利用对顶角的性质对B 进行判断；根据直角坐标系下点坐标特点对D 进行判断．【详解】A ．两直线平行，同位角相等，故A 是假命题；B ．对顶角相等，故B 是假命题；C ．如果两个角的两边互相平行，那么这两个角相等或互补，故C 是假命题；D ．如果点的横坐标和纵坐标互为相反数，那么点P 在直线y x =-的图像上，故D 是真命题故选：D【点睛】本题考查了真命题与假命题，正确的命题称为真命题，错误的命题称为假命题．利用了平行线性质、对顶角性质、直角坐标系中点坐标特点等知识点．10．如图，11,,33AB EF ABP ABC EFP EFC ∠=∠∠=∠∥，已知60FCD ∠=︒，则P ∠的度数为（ ）A ．60︒B ．80︒C ．90︒D ．100︒【答案】B【解析】【分析】 延长BC 、EF 交于点G ，根据平行线的性质得180ABG BGE +=︒∠∠，再根据三角形外角的性质和平角的性质得60180120EFC FCD BGE BGE BCF FCD =+=︒+=︒-=︒∠∠∠∠，∠∠，最后根据四边形内角和定理求解即可．【详解】延长BC 、EF 交于点G∵//AB EF∴180ABG BGE +=︒∠∠∵60FCD ∠=︒∴60180120EFC FCD BGE BGE BCF FCD =+=︒+=︒-=︒∠∠∠∠，∠∠∵11,33ABP ABC EFP EFC ∠=∠∠=∠ ∴360P PBC BCF PFC =︒---∠∠∠∠2236012033ABG EFC =︒---︒∠∠ ()223606012033ABG BGE =︒--︒+-︒∠∠ 223604012033ABG BGE =︒--︒--︒∠∠ ()22003ABG BGE =︒-+∠∠ 22001803=︒-⨯︒ 80=︒故答案为：B ．【点睛】本题考查了平行线的角度问题，掌握平行线的性质、三角形外角的性质、平角的性质、四边形内角和定理是解题的关键．11．下列图形中线段PQ 的长度表示点P 到直线a 的距离的是（ ）A ．B ．C ．D ．【答案】C【解析】【分析】 根据点到直线的距离的定义，可得答案．【详解】由题意得PQ ⊥a ，P 到a 的距离是PQ 垂线段的长，故选C ．【点睛】本题考查了点到直线的距离，点到直线的距离是解题关键．12．如图，在△ABC中，AB＝AC，∠A＝36°，D、E两点分别在边AC、BC上，BD平分∠ABC，DE∥AB．图中的等腰三角形共有（）A．3个B．4个C．5个D．6个【答案】C【解析】【分析】已知条件，根据三角形内角和等于180，角的平分线的性质求得各个角的度数，然后利用等腰三角形的判定进行判断即可．【详解】解：∵AB＝AC，∠A＝36°，∴∠ABC＝∠C＝72°，∵BD平分∠ABC，∴∠ABD＝∠DBC＝36°，∴∠BDC＝180°﹣36°﹣72°＝72°，∵DE∥AB，∴∠EDB＝∠ABD＝36°，∴∠EDC＝72°﹣36°＝36°，∴∠DEC＝180°﹣72°﹣36°＝72°，∴∠A＝∠ABD，∠DBE＝∠BDE，∠DEC＝∠C，∠BDC＝∠C，∠ABC＝∠C，∴△ABC、△ABD、△DEB、△BDC、△DEC都是等腰三角形，共5个，故选C．【点睛】本题考查了等腰三角形判定和性质、角平分线的性质、平行线的性质，由已知条件利用相关的性质求得各个角相等是解题的关键．13．如图，∠BCD ＝95°，AB ∥DE ，则∠α与∠β满足（ ）A ．∠α+∠β＝95°B ．∠β﹣∠α＝95°C ．∠α+∠β＝85°D ．∠β﹣∠α＝85°【答案】D【解析】【分析】 过点C 作CF ∥AB ，然后利用两直线平行，内错角相等；两直线平行，同旁内角互补进行推理证明即可.【详解】解：过点C 作CF ∥AB∵AB ∥DE ，CF ∥AB∴AB ∥DE ∥CF∴∠BCF=∠α∠DCF+∠β=180°∴∠BCD ＝∠BCF +∠DCF∴∠α+180°-∠β=95°∴∠β﹣∠α＝85°故选：D【点睛】本题考查平行线的性质，熟练掌握平行线的性质进行推理证明是本题的解题关键.14．如图，直线//a b ，将一块含45︒角的直角三角尺（90︒∠=C ）按所示摆放．若180︒∠=，则2∠的大小是（ ）A ．80︒B ．75︒C ．55︒D ．35︒【答案】C【解析】【分析】 先根据//a b 得到31∠=∠，再通过对顶角的性质得到34,25∠=∠∠=∠，最后利用三角形的内角和即可求出答案.【详解】解：给图中各角标上序号，如图所示：∵//a b∴3180︒∠=∠=（两直线平行，同位角相等），又∵34,25∠=∠∠=∠（对顶角相等），∴251804180804555A ∠=∠=︒-∠-∠=︒-︒-︒=︒.故C 为答案.【点睛】本题主要考查了直线平行的性质（两直线平行，同位角相等）、对顶角的性质（对顶角相等），熟练掌握直线平行的性质是解题的关键.15．如图，1B ∠=∠，2C ∠=∠，则下列结论正确的个数有（ ）①//AD BC ；②B D ∠=∠；③//AB CD ；④2180B ∠+∠=︒A ．4个B ．3个C ．2个D ．1个 【答案】A【解析】【分析】根据∠1=∠B可判断AD∥BC，再结合∠2=∠C可判断AB∥CD，其余选项也可判断.【详解】∵∠1=∠B∴AD∥BC，①正确；∴∠2+∠B=180°，④正确；∵∠2=∠C∴∠C+∠B=180°∴AB∥CD，③正确∴∠1=∠D，∴∠D=∠B，②正确故选：A【点睛】本题考查平行的证明和性质，解题关键是利用AD∥BC推导出∠B+∠2=180°，为证AB∥DC 作准备.16．如图，DE∥BC，BE平分∠ABC，若∠1=70°，则∠CBE的度数为（）A．20°B．35°C．55°D．70°【答案】B【解析】【分析】根据平行线的性质可得∠1=∠ABC=70°，再根据角平分线的定义可得答案．【详解】∵DE∥BC，∴∠1=∠ABC=70°，∵BE平分∠ABC，∴1352CBE ABC∠=∠=︒，故选：B．【点睛】此题主要考查了平行线的性质，以及角平分线的定义，解题的关键是掌握两直线平行，内错角相等．17．下列说法中错误的个数是( )(1)过一点有且只有一条直线与已知直线平行；(2)过一点有且只有一条直线与已知直线垂直；(3)不相交的两条直线叫做平行线；(4)有公共顶点且有一条公共边的两个互补的角互为邻补角．A．1个B．2个C．3个D．4个【答案】C【解析】（1）应强调过直线外一点，故错误；（2）正确；（3）不相交的两条直线叫做平行线，没有说明是否是在同一平面内，所以错误；（4）有公共顶点且有一条公共边的两个角不一定互为邻补角，角平分线的两个角也满足，但可以不是,故错误.错误的有3个，故选C.18．如图，小慧从A处出发沿北偏东60°方向行走至B处，又沿北偏西20°方向行走至C 处，此时需要将方向调整到与出发时一致，则方向的调整应为（）A．左转80°B．右转80°C．左转100°D．右转100°【答案】B【解析】【分析】如图，延长AB到D，过C作CE//AD，由题意可得∠A=60°，∠1=20°，根据平行线的性质可得∠A=∠2，∠3=∠1+∠2，进而可得答案.【详解】如图，延长AB到D，过C作CE//AD，∵此时需要将方向调整到与出发时一致，∴此时沿CE方向行走，∵从A处出发沿北偏东60°方向行走至B处，又沿北偏西20°方向行走至C处，∴∠A=60°，∠1=20°，AM∥BN，CE∥AB，∴∠A=∠2=60°，∠1+∠2=∠3∴∠3=∠1+∠2=20°+60°=80°，∴应右转80°.故选B.【点睛】本题考查了方向角有关的知识及平行线的性质，解答时要注意以北方为参照方向，进行角度调整.19．如图a 是长方形纸带，∠DEF=20°，将纸带沿EF 折叠成图b ，再沿BF 折叠成图c ，则图c 中的∠CFE 的度数是（ ）A ．110°B ．120°C ．140°D ．150° 【答案】B【解析】【详解】解：∵AD ∥BC ，∴∠DEF=∠EFB=20°， 图b 中∠GFC=180°-2∠EFG=140°，在图c 中∠CFE=∠GFC-∠EFG=120°，故选B ．20．如图，在矩形ABCD 中，6AB =，8BC =，若P 是BD 上的一个动点，则PB PC PD ++的最小值是（ ）A ．16B ．15.2C ．15D ．14.8【答案】D【解析】【分析】 根据题意，当PC ⊥BD 时，PB PC PD ++有最小值，由勾股定理求出BD 的长度，由三角形的面积公式求出PC 的长度，即可求出最小值.【详解】解：如图，当PC ⊥BD 时，PB PC PD BD PC ++=+有最小值，在矩形ABCD 中，∠A=∠BCD=90°，AB=CD=6，AD=BC=8，由勾股定理，得226810BD +=，∴=10PB PD BD +=，在△BCD 中，由三角形的面积公式，得11=22BD PC BC CD ••， 即1110=8622PC ⨯⨯⨯⨯， 解得： 4.8PC =， ∴PB PC PD ++的最小值是：10 4.814.8PB PC PD BD PC ++=+=+=； 故选：D.【点睛】本题考查了勾股定理解直角三角形，最短路径问题，垂线段最短，以及三角形的面积公式，解题的关键是熟练掌握勾股定理，正确确定点P 的位置，得到PC 最短.。

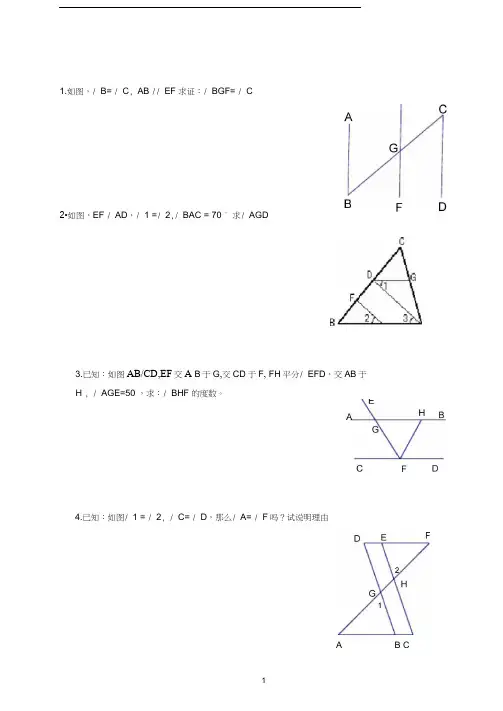
1.如图，/ B= / C, AB // EF 求证：/ BGF= / C2•如图，EF / AD，/ 1 =/ 2,/ BAC = 70 ° 求/ AGD3.已知：如图AB/CD,EF交A B于G,交CD于F, FH平分/ EFD，交AB于H , / AGE=50°，求：/ BHF 的度数。

4.已知：如图/ 1 = / 2, / C= / D，那么/ A= / F吗？试说明理由A B C5•已知：如图，AB//CD，试解决下列问题:(1) / 1 + Z 2= ___ ;(2) / 1 + Z 2+Z 3= __ 一；(3) / 1 + Z 2+Z 3+Z 4= _ __ __；(4) 试探究Z 1+Z 2+Z 3 +Z 4+ - + Z n= _____________________________6.如图11, E、F分别在AB、CD上，1 垂足为。

，求证：AB//CD .C图117 如图AC // BD , AB//CD , 1交CF于点O，试说明：AE CF .F , AED , 2与C互余且EC AF ,&如图，AEB NFP , M C ,判断A 与P 的大小关系，并说明理由9 •如图，AD 是CAB 的角平分线，DE//AB , DF // AC , EF 交AD 于点0.请问：(1)DO 是 EDF 的角平分线吗？如果是，请给予证明；如果不是，请说明 理由.(2)若将结论与AD 是CAB 的角平分线、DE//AB 、DF //AC 中的任一条件 交换，？所得命题正确吗？10. 如图，AD 是/ EAC 的平分线，AD // BC ,/ B = 30 :你能算出/ EAD 、/ DAC 、/ C的度数吗?11. 如图,/ 1= / 2 , / 3=105°, 求 / 4 的度数。

12. ______________________________ 如图，EF // AD ，/ 1 = / 2,Z BAC = 70 °将求/ AGD 的过程填写完整。

第一章：平行线与相交线考点1：余角、补角、对顶角一、考点讲解：1．余角：如果两个角的和是直角，那么称这两个角互为余角．2．补角：如果两个角的和是平角，那．么称这两个角互为补角．3．对顶角：如果两个角有公共顶点，并且它们的两边互为反向延长线，这样的两个角叫做对顶角．4．互为余角的有关性质：①∠1＋∠2=90°，则∠1、∠2互余．反过来，若∠1，∠2互余．则∠1+∠2=90○．②同角或等角的余角相等，如果∠l十∠2=90○，∠1+∠3= 90○，则∠2= ∠3．5．互为补角的有关性质：①若∠A +∠B=180○则∠A、∠B互补，反过来，若∠A、∠B 互补，则∠A+∠B＝180○．②同角或等角的补角相等．如果∠A ＋∠C=18 0○，∠A+∠B=18 0°，则∠B=∠C．6．对顶角的性质：对顶角相等．二、经典考题剖析：【考题1－1】（2004、厦门，2分）已知：∠A= 30○，则∠A的补角是________度．解：150○点拨：此题考查了互为补角的性质．【考题1－2】（2004、青海，3分）如图l－2－1，直线AB，CD相交于点O，OE⊥AB 于点O，OF平分∠AOE，∠1＝15○30’，则下列结论中不正确的是（）A．∠2 =45○B．∠1=∠3C．∠AOD与∠1互为补角D．∠1的余角等于75○30′解：D 点拨：此题考查了互为余角，互为补角和对顶角之间的综合运用知识．三、针对性训练：(30 分钟) (答案：220 ) 1．_______的余角相等，_______的补角相等．2．∠1和∠2互余，∠2和∠3互补，∠1=63○，∠3=__3．下列说法中正确的是（）A．两个互补的角中必有一个是钝角B．一个角的补角一定比这个角大C．互补的两个角中至少有一个角大于或等于直角D．相等的角一定互余4．轮船航行到C处测得小岛A的方向为北偏东32○，那么从A处观测到C处的方向为（）A．南偏西32○B．东偏南32○C．南偏西58○D．东偏南58○5．若∠l=2∠2，且∠1+∠2=90○则∠1=___，∠2=___．6．一个角的余角比它的补角的九分之二多1°，求这个角的度数．7．∠1和∠2互余，∠2和∠3互补，∠3=153○，∠l=_8．如图l－2－2，AB⊥CD，AC⊥BC，图中与∠CAB互余的角有（）A．0个B．l个C．2个D．3个9．如果一个角的补角是150○，那么这个角的余角是____________10．已知∠A和∠B互余，∠A与∠C互补，∠B与∠C的和等于周角的13，求∠A+∠B+∠C的度数．11．如图如图1―2―3，已知∠AOC与∠B都是直角，∠BOC=59○．（1）求∠AOD的度数；（2）求∠AOB和∠DOC的度数；（3）∠A OB与∠DOC有何大小关系；（4）若不知道∠BOC的具体度数，其他条件不变，这种关系仍然成立吗？考点2：同位角、内错角、同旁内角的认识及平行线的性质一、考点讲解：1．同一平面内两条直线的位置关系是：相交或平行．2．“三线八角”的识另：三线八角指的是两条直线被第三条直线所截而成的八个角．正确认识这八个角要抓住：同位角位置相同，即“同旁”和“同规”；内错角要抓住“内部，两旁”；同旁内角要抓住“内部、同旁”．3．平行线的性质：（1）两条平行线被第三条直线所截，同位角相等，内错角相等，同旁内角互补．（2）过直线外一点有且只有一条直线和已知直线平行．（3）两条平行线之间的距离是指在一条直线上任意找一点向另一条直线作垂线，垂线段的长度就是两条平行线之间的距离.二、经典考题剖析：【考题2－1】（2004贵阳，3分）如图1―2―4，直线a ∥b，则∠A CB＝________解：78○点拨：过点C作CD平行于a，因为a∥b，所以CD∥b．则∠A C D＝2 8○，∠DCB=5 0○．所以∠ACB＝78○．【考题2－2】（2004、开福，6分）如图1―2―5，AB∥CD，直线EF分别交A B、CD于点E、F，EG平分∠B EF，交CD于点G，∠1=5 0○求∠2的度数．解：65○点拨：由AB∥CD，得∠BEF＝180○－∠1=130○，∠BEG=∠2．又因为EG平分∠BEF，所以∠2=∠BEG=12∠BEF=65°（根据平行线的性质）三、针对性训练：( 40分钟) (答案：220 ) 1．如图1－2－6，AB∥CD，AC⊥BC，图中与∠CAB互余的角有（）A．l个B．2个C．3个D．4个2．下列说法中正确的个数是（）（1）在同一平面内不相交的两条直线必平行；（2）在同一平面内不平行的两条直线必相交；（3）两条直线被第三条直线所截，所得的同位角相等；（4）两条平行线被第三条直线所截，一对内错角的平分线互相平行。

相交线与平行线100题一．选择题（共45小题）1．（2014•铜仁地区）下列图形中，∠1与∠2是对顶角的是（）A．B．C．D．2．（2012春•鼓楼区校级期中）平面内有两两相交的三条直线，若最多有m个交点，最少有n个交点，则m+n等于（）A．1B．2C．3D．43．下列说法正确的是（）（1）如果∠1+∠2+∠3=180°，那么∠1与∠2与∠3互为补角；（2）如果∠A+∠B=90°，那么∠A是余角；（3）互为补角的两个角的平分线互相垂直；（4）有公共顶点且又相等的角是对顶角；（5）如果两个角相等，那么它们的余角也相等．A．1个B．2个C．3个D．4个4．（2014•河南）如图，直线AB，CD相交于点O，射线OM平分∠AOC，ON⊥OM，若∠AOM=35°，则∠CON 的度数为（）A．35°B．45°C．55°D．65°5．如图，直线AB、CD相交于点O，∠DOE=90°，则∠AOE与∠DOB的关系是（）A．对顶角B．互补的两个角C．互余的两个角D．一对相等的角6．如图，直线l1，l2，l3相交于一点，则下列答案中，全对的一组是（）A．∠1=90°，∠2=30°，∠3=∠4=60°B．∠1=∠3=90°，∠2=∠4=30°C．∠1=∠3=90°，∠2=∠4=60°D．∠1=∠3=90°，∠2=60°，∠4=30°7．（2014•上海）如图，已知直线a、b被直线c所截，那么∠1的同位角是（）A．∠2B．∠3C．∠4D．∠58．如图，已知AB⊥MN于E，下列条件中不能得到CD⊥MN的是（）A．CD∥AB B．∠CFE=∠AEM C．∠CFE+∠AEF=180°D．∠CFE+∠CFN=180°9．（2014•汕尾）如图，能判定EB∥AC的条件是（）A．∠C=∠ABE B．∠A=∠EBD C．∠C=∠ABC D．∠A=∠ABE 10．（2009秋•翠屏区期末）已知如图，∠A=135°，∠B=45°，在下面的说法中，一定正确的是（）A．AD∥BC B．AB∥CD C．∠C=135°，∠D=45°D．∠C=45°，∠D=135°11．（2007春•西城区期末）下列命题中，错误的是（）A．对顶角的角平分线互为反向延长线B．在同一平面内，垂直于同一直线的两条直线互相平行C．如果一个角的两边与另一个角的两边分别平行，那么这两个角相等或互补D．同时垂直于两条平行线，并且夹在这两条平行线间的线段叫做这两条平行线的距离12．（2011秋•岳阳楼区校级期末）下列说法中正确的有（）①同位角相等．②凡直角都相等．③一个角的余角一定比它的补角小．④在直线、射线和线段中，直线最长．⑤两点之间的线段的长度就是这两点间的距离．⑥如果一个角的两边分别平行于另一个角的两边，则这两个角一定相等．A．0个B．1个C．2个D．3个13．（2011春•灌南县校级期末）如图，下列推理正确的是（）A．∵MA∥NB，∴∠1=∠3B．∵∠2=∠4，∴MC∥ND C．∵∠1=∠3，∴MA∥NB D．∵MC∥ND，∴∠1=∠3 14．（2012春•金台区期末）如图，AB⊥BC，BC⊥CD，∠EBC=∠BCF，则∠ABE与∠FCD的关系是（）A．同位角且相等B．不是同位角但相等C．是同位角但不相等D．不是同位角也不相等15．（2013春•下城区期末）如图，AB∥EF∥DC，EG∥DB，则图中与∠1相等的角（∠1除外）共有（）A．6个B．5个C．4个D．3个16．（2015•河北一模）如图，在五边形ABCDE中，AB∥DE，若△ABE的面积为5，则△ABD的面积为（）A．4B．5C．10D．无法判断17．（2014•安顺）如图，∠AOB的两边OA，OB均为平面反光镜，∠AOB=40°．在射线OB上有一点P，从P点射出一束光线经OA上的Q点反射后，反射光线QR恰好与OB平行，则∠QPB的度数是（）A．60°B．80°C．100°D．120°18．（2014•龙岩）如图，直线a，b被直线c所截，a∥b，∠1=∠2，若∠3=40°，则∠4等于（）A．40°B．50°C．70°D．80°19．（2014•荆州）如图，AB∥ED，AG平分∠BAC，∠ECF=70°，则∠FAG的度数是（）A．155°B．145°C．110°D．35°20．（2011秋•射洪县校级期末）如图，已知l1∥l2，AB∥CD，CE⊥l2于点E，FG⊥l2于点G，则下列说法中错误的是（）A．AB=CDB．CE=FGC．A、B两点间距离就是线段AB的长度D．l1与l2两平行线间的距离就是线段CD的长度21．（2009春•常州期末）如图，∠1=120°，∠2=60°，∠3=65°，则∠4等于（）A．40°B．50°C．65°D．115°22．（2009秋•长春校级期末）如图，已知∠1=∠2，∠3=60°，则∠4=（）A．80°B．70°C．60°D．50°23．（2014春•乳山市期末）如图，AC⊥CD于C，ED⊥CD于D，AB∥EF，∠CAE=25°，∠BAE=10°，则∠DEF=（）A．30°B．35°C．40°D．45°24．（2013春•下城区期末）如图，∠1=100°，∠2=100°，且∠3：∠1=6：5，则∠4的度数为（）A．100°B．110°C．120°D．130°25．（2005春•武昌区期末）如图，∠1与∠3互余，∠2与∠3的余角互补，∠4=115°，则∠3为（）A．45°B．60°C．65°D．70°26．（2014春•苏州期末）如图，已知AB∥CD，∠1=∠2，∠E=50°，则∠F=（）A．40°B．50°C．60°D．70°27．（2008秋•江苏校级期末）如图，AB∥CD，EG、EM、FM分别平分∠AEF，∠BEF，∠EFD，则图中与∠DFM 相等的角（不含它本身）的个数为（）A．5B．6C．7D．828．（2008春•江岸区期末）如图，AB∥CD，∠D=∠E，∠B=110°，则∠D为（）A．70°B．60°C．55°D．45°29．（2014春•宜宾校级期末）如图，矩形纸片ABCD中，沿折痕EF折叠，得∠EFG=40°，∠AEG的度数为（）A．98°B．99°C．100°D．101°30．如图所示，AD∥BC，∠BCD=50°，∠B=80°，CA平分∠BCD，则∠CAD与∠BAC的度数分别为（）A．25°，75°B．75°，25°C．20°，50°D．25°，65°31．如图，已知AB∥CD，直线EF交AB于E，交CD于F，∠1=∠2，则下列判断不正确的是（）A．FN∥EM B．∠MEB=∠NFC C．∠1+∠AEF=180°D．∠AEM=∠DFN 32．（2006春•襄城区期末）如图，AB∥CD，OE平分∠AOC，OE⊥OF，∠C=60°，则∠BOF的度数为（）A．15°B．30°C．60°D．90°33．（2013•台湾）附图中直线L、N分别截过∠A的两边，且L∥N．根据图中标示的角，判断下列各角的度数关系，何者正确？（）A．∠2+∠5＞180°B．∠2+∠3＜180°C．∠1+∠6＞180°D．∠3+∠4＜180°34．（2014春•招远市期末）如图，直线l1，l2分别截射线AB，AC，若l1∥l2，则下列各角度数关系正确的是（）A．∠5+∠1=180°B．∠4+∠2＞180°C．∠6+∠3＜180°D．∠4+∠6＜180°35．（2009春•成华区期末）如图，已知AB∥EF，则∠B+∠C+∠D+∠E的度数为（）A．270°B．360°C．450°D．540°36．（2011春•抚州校级期末）如图，AB∥CD，∠BED=110°，BF平分∠ABE，DF平分∠CDE，则∠BFD=（）A．110°B．115°C．125°D．130°37．（2013春•太仓市期末）如图，已知AB∥CD，则∠a、∠B和∠y之间的关系为（）A．α+β﹣γ=180°B．α+γ=βC．α+β+γ=360°D．α+β﹣2γ=180°38．（2013秋•永州期末）如图，AB∥CD，用含α，β，γ的式子表示θ，则θ=（）A．180°+α+β﹣γB．180°+γ﹣α﹣βC．β+γ﹣αD．α+γ﹣β39．（2014•鄂州）如图，直线a∥b，直角三角形如图放置，∠DCB=90°．若∠1+∠B=70°，则∠2的度数为（）A．20°B．40°C．30°D．25°40．（2014•长沙二模）如图，AB∥EF，BC⊥CD于C，∠ABC=30°，∠DEF=45°，则∠CDE等于（）A．105°B．75°C．135°D．115°41．（2014春•武昌区期末）如图，AB∥EF，则∠A，∠C，∠D，∠E满足的数量关系是（）A．∠A+∠C+∠D+∠E=360°B．∠A+∠D=∠C+∠EC．∠A﹣∠C+∠D+∠E=180°D．∠E﹣∠C+∠D﹣∠A=90°42．（2013秋•招远市期末）如图，AB∥EF∥CD，连接BD，ED，则下列等式中正确的是（）A．∠1﹣∠2+∠3=180°B．∠1+∠2﹣∠3=180°C．∠2+∠3﹣∠1=180°D．∠1+∠2+∠3=180°43．（2013春•石景山区期末）如图，AF是∠BAC的平分线，EF∥AC交AB于点E，若∠1=155°，则∠BEF的度数为（）A．50°B．12.5°C．25°D．15°44．（2014春•招远市期末）如图，一条公路修到湖边时，需拐弯绕湖而过，第一次拐的角∠A=110°，第二次拐的角∠B=150°，第三次拐的角是∠C，这时的道路恰好和第一次拐弯之前的道路平行，则∠C的度数为（）A．120°B．130°C．140°D．150°45．（2014春•海淀区期末）如图，AB∥CD，∠BAC与∠DCA的平分线相交于点G，EG⊥AC于点E，F为AC上的一点，且FA=FG=FC，GH⊥CD于H．下列说法正确的是（）①AG⊥CG；②∠BAG=∠CGE；③S△AFG=S△GFC；④若∠EGH：∠ECH=2：7，则∠EGF=50°．A．①③④B．②③C．①②③D．①②③④二．填空题（共45小题）46．（2014春•新泰市期末）如图，已知直线CD、EF相交于点O，OA⊥OB，且OC平分∠AOF，∠BOE=2∠AOE．则∠BOD=．47．（2013春•黄山期末）如图，已知直线AD、BE、CF相交于O，OG⊥AD，且∠BOC=35°，∠FOG=30°，则∠DOE=．48．（2013秋•昌平区期末）如图，直线AB，CD相交于点O，∠AOC=60°，∠1=2∠2，则∠2=°，∠AOE=°．49．（2014春•霸州市期末）如图，直线AB、CD相交于点O，OE⊥AB，O为垂足，如果∠EOD=38°，则∠AOC =度，∠COB=度．50．（2013•河北模拟）如图，直线AB与直线CD相交于点O，射线OP平分∠AOD，若∠BOC=130°，则∠COP 的度数为．51．（2010秋•江阴市期末）已知直线AB和CD相交于O点，OE⊥AB，∠1=55°，则∠BOD=度；若OF平分∠DOB，则∠EOF的度数是度．52．（2011秋•大兴区期末）如图，三条直线相交于一点，按从小到大的顺序排列∠1，∠2，∠3为．53．（2014春•武昌区期末）如图，已知∠α与∠β共顶点O，∠α+∠β＜180°，∠α=∠β．若∠β的邻补角等于∠α，则∠β=度．54．（2011•平塘县校级模拟）如图，要从小河引水到村庄A，请设计并作出一最佳路线，理由是．55．看图填空：（1）∠1和∠4是角；（2）∠1和∠3是角；（3）∠2和∠D是角；（4）∠3和∠D是角；（5）∠4和∠D是角；（6）∠4和∠B是角．56．如图所示，AB与BC被AD所截得的内错角是；DE与AC被AD所截得的内错角是；∠1与∠4是直线被直线截得的角，图中同位角有对．57．（2011秋•岳阳楼区校级期末）如图所示，其中共有对对顶角．58．（2014春•富顺县校级期末）如图所示，同位角一共有对，内错角一共有对，同旁内角一共有有对．59．（2004秋•奉贤区期末）如图：a∥b，图中的∠1，∠2，∠3，∠4，∠5，∠6，∠7中同位角有对．60．如图，DH∥EO∥BC，EF∥CD，则与∠BFE相等的角，不包括∠BFE有个．61．如果两条平行直线被第三条直线所截，一对同旁内角的度数之比为3：6，那么这两个角分别等于和．62．（2014春•东城区期末）如图，直线a，b被直线c所截，现给出四个条件：①∠1=∠5；②∠2=∠7；③∠2+∠8=180°；④∠4=∠7．其中能说明a∥b的条件序号为．63．（2014•湘潭）如图，直线a、b被直线c所截，若满足，则a、b平行．64．（2011•开县校级模拟）如图，BC∥DE，∠1=105°，∠AED=65°，则∠A=．65．（2014春•丰城市校级期中）如图∠1=82°，∠2=98°，∠3=80°，则∠4=度．66．（2014•温州）如图，直线AB，CD被BC所截，若AB∥CD，∠1=45°，∠2=35°，则∠3=度．67．（2014春•兴业县期末）如图，已知AB∥CD∥EF，则∠x、∠y、∠z三者之间的关系是．68．（2011秋•东营期末）如图，若AB∥DE，BC∥FE，∠E+∠B=度．69．（2009•沙坪坝区校级模拟）如图，EF∥GH，点A在EF上，AP，AQ分别交GH于点B、C，且AP⊥AQ，∠PBG=35°，则∠FAC=．70．（2012•温州模拟）如图，AB∥CD，CD∥EF，∠A=110°，∠E=30°，则∠ACE=．71．（2012•开县校级模拟）如图，直线a∥b，直线m分别交a、b于A、B两点，CB⊥m，垂足为B，若∠1=25°，则∠2=．72．（2014•广东模拟）将三角板ABC按如图放置，使其三个顶点分别落在三条平行直线上，其中∠CAB=90°，且CF恰好平分∠ACB．若∠CBA=30°，则∠DAC的度数是．73．如图，如果AB∥EF，BC∥DE，那么∠E和∠B满足的关系．74．如图，直线a∥b，∠1=72°，∠2=130°，那么∠3+∠4=．75．（2009•荆州校级模拟）如图，a∥b，∠1=105°，∠2=140°，则∠3的度数是．76．（2012•湛江模拟）如图所示，AB平行CD，AE与CE相交于点E，∠BAE=30°，∠DCE=40°．∠1=，∠2=．77．（2014•孝南区校级模拟）如图，已知直线AB∥CD，FH平分∠EFD，FG⊥FH，∠AEF=62°，则∠GFC=度．78．（2011•北京模拟）如图，已知AB∥CD，BE平分∠ABC，∠CDE=140°，则∠C=．79．（2013•深圳模拟）如图，AB∥CD，∠CFE=112°，ED平分∠BEF，交CD于D，则∠EDF=度．80．（2012•河南模拟）如图直线a与直线b平行，则|x﹣y|的值是．81．（2013秋•云阳县期末）如图，已知AB，CD，EF互相平行，且∠ABE=70°，∠ECD=150°，则∠BEC=°．82．如图，AB∥EF，设∠C=90°，那么x，y，z的关系是．83．（2009•荆州二模）如图，直线MN∥PQ，∠ABM=30°，∠D=40°，∠EFQ=70°，则∠C+∠E=．84．（2011•鸠江区校级自主招生）如图，DC∥AB，∠BAE=∠BCD，AE⊥DE，∠D=130°，则∠B=度．85．（2009•琼海模拟）如图，∠1=∠2，要判断AB∥DF，需要增加条件．86．（2013秋•翠屏区校级期末）将一直角三角形与两边平行的纸条如图所示放置，下列结论①∠1=∠2，②∠3=∠4，③∠2+∠4=90°，④∠4+∠5=180°，其中正确的有（填序号）．87．（2012•诸城市校级模拟）如图，直线AE∥BD，点C在BD上，若AE=5，BD=8，△ABD的面积为16，则△ACE 的面积为．88．（2012春•盐都区期末）如图，将一个长方形纸条折成如图的形状，若已知∠1=130°，则∠2=度．89．（2014•鹿城区校级二模）如图，在四边形纸片ABCD中，∠A=100°，∠C=40°，现将其右下角向内翻折得△FGE，折痕为EF，恰使GF∥CD，GE∥AD，则∠B=度．90．如图（1）是长方形纸条，将纸条沿EF折叠成图（2），再沿AF折叠成图（3），已知图（3）中的∠CFE=120°，则图（1）中∠DEF的度数是．三．解答题（共10小题）91．（2014•益阳）如图，EF∥BC，AC平分∠BAF，∠B=80°．求∠C的度数．92．如图，请分别根据已知条件进行推理，得出结论，并在括号内注明理由．（1）∵∠2=∠3（已知），∴∥（）（2）∵∠2=∠5（已知），∴∥（）（3）∵∠2+∠1=180°（已知），∴∥（）（4）∵∠5=∠3（已知），∴∥（）（5）∵∠4+∠6=180°（已知），∴∥（）（6）∵AB∥CD，AB∥EF（已知），∴∥（）93．如图，∠PCN=45°，直线CP与CN分别交AQ、EF于点B、D，∠ABC=20°，∠CDE=25°，试说明：AQ∥EF．94．如图，若∠ABC+∠CDE﹣∠C=180°，试证明：AB∥DE．95．如图所示，两平面镜OM、ON的夹角为∠θ，入射光线AB沿着与镜面ON平行的方向照射到镜面OM上，经过两次反射后的反射光线CD平行于镜面OM，求∠θ的度数．96．如图，已知∠3+∠DCB=180°，∠1=∠2，∠CME：∠GEM=4：5，求∠CME的度数．97．如图，已知BD∥AC，CE∥BA，且D、A、E在同一条直线上，设∠BAC=x，∠D+∠E=y．（1）试用x的一次式表示y；（2）当x=90°，且∠D=2∠E时，DB与EC具有怎样的位置关系？98．（1）阅读填空：如图1，AB∥DE，试问∠B、∠E、∠BCE有什么关系．解：∠B+∠E=∠BCE过点C作CF∥AB，则∠B=∠1【】又∵AB∥DE，AB∥CF，∴CF∥DE∴∠E=∠2【】∴∠B+∠E=∠1+∠2，即∠B+∠E=∠BCE．（2）应用解答：观察上面图形与结论，解决下面的问题：如图2，∠DAB+∠B+∠BCE=360°，作∠BCF=∠BCG，CF与∠BAH的平分线交于F，若∠F的余角等于2∠B的补角，求∠BAH的度数．（3）拓展深化：如图3，在前面的条件下，若点P是AB上一点，Q是GE上任一点，QR平分∠PQR，PM∥QR，PN平分∠APQ，下列结论：①∠APQ+∠NPM的值不变；②∠NPM的度数不变，可以证明，只有一个是正确的，请你做出正确的选择并求值．99．（2014•赤峰）如图1，E是直线AB，CD内部一点，AB∥CD，连接EA，ED．（1）探究猜想：①若∠A=30°，∠D=40°，则∠AED等于多少度？②若∠A=20°，∠D=60°，则∠AED等于多少度？③猜想图1中∠AED，∠EAB，∠EDC的关系并证明你的结论．（2）拓展应用：如图2，射线FE与矩形ABCD的边AB交于点E，与边CD交于点F，①②③④分别是被射线FE隔开的4个区域（不含边界，其中区域③、④位于直线AB上方，P是位于以上四个区域上的点，猜想：∠PEB，∠PFC，∠EPF 的关系（不要求证明）．100．（2007•福州）如图，直线AC∥BD，连接AB，直线AC、BD及线段AB把平面分成①、②、③、④四个部分，规定：线上各点不属于任何部分．当动点P落在某个部分时，连接PA，PB，构成∠PAC，∠APB，∠PBD 三个角．（提示：有公共端点的两条重合的射线所组成的角是0°角）（1）当动点P落在第①部分时，求证：∠APB=∠PAC+∠PBD；（2）当动点P落在第②部分时，∠APB=∠PAC+∠PBD是否成立？（直接回答成立或不成立）（3）当动点P落在第③部分时，全面探究∠PAC，∠APB，∠PBD之间的关系，并写出动点P的具体位置和相应的结论．选择其中一种结论加以证明．相交线与平行线100题参考答案与试题解析一．选择题（共45小题）1．（2014•铜仁地区）下列图形中，∠1与∠2是对顶角的是（）A．B．C．D．解答：解：利用对顶角的定义可得出：符合条件的只有C，故选：C．2．（2012春•鼓楼区校级期中）平面内有两两相交的三条直线，若最多有m个交点，最少有n个交点，则m+n等于（）A．1B．2C．3D．4解答：解：平面内两两相交的三条直线，最多有3个交点，最少有1个交点，即m=3，n=1，∴m+n=4．故选D．3．下列说法正确的是（）（1）如果∠1+∠2+∠3=180°，那么∠1与∠2与∠3互为补角；（2）如果∠A+∠B=90°，那么∠A是余角；（3）互为补角的两个角的平分线互相垂直；（4）有公共顶点且又相等的角是对顶角；（5）如果两个角相等，那么它们的余角也相等．A．1个B．2个C．3个D．4个解答：解：（1）互为补角的应是两个角而不是三个，故错误；（2）没说明∠A是∠B的余角，故错误；（3）互为邻补角的两个角的平分线互相垂直，故错误；（4）根据对顶角的定义可判断此命题错误．（5）相等角的余角相等，故正确．综上可得（5）正确．故选A．4．（2014•河南）如图，直线AB，CD相交于点O，射线OM平分∠AOC，ON⊥OM，若∠AOM=35°，则∠CON 的度数为（）A．35°B．45°C．55°D．65°解答：解：∵射线OM平分∠AOC，∠AOM=35°，∴∠MOC=35°，∵ON⊥OM，∴∠MON=90°，∴∠CON=∠MON﹣∠MOC=90°﹣35°=55°．故选：C．5．如图，直线AB、CD相交于点O，∠DOE=90°，则∠AOE与∠DOB的关系是（）A．对顶角B．互补的两个角C．互余的两个角D．一对相等的角解答：解：∵∠DOE=90°，∴∠EOC=90°，即∠AOC+∠AOE=90°，∵∠AOC=∠DOB，∴∠DOB+∠AOE=90°，即∠AOE与∠DOB互余．故选C．6．如图，直线l1，l2，l3相交于一点，则下列答案中，全对的一组是（）A．∠1=90°，∠2=30°，∠3=∠4=60°B．∠1=∠3=90°，∠2=∠4=30°C．∠1=∠3=90°，∠2=∠4=60°D．∠1=∠3=90°，∠2=60°，∠4=30°解答：解：根据对顶角相等，可知∠2=60°∠4=30°．由平角的定义知，∠3=180°﹣∠2﹣∠4=90°，所以∠1=∠3=90°．故选D．7．（2014•上海）如图，已知直线a、b被直线c所截，那么∠1的同位角是（）A．∠2B．∠3C．∠4D．∠5解答：解：∠1的同位角是∠5，故选：D．8．如图，已知AB⊥MN于E，下列条件中不能得到CD⊥MN的是（）A．CD∥AB B．∠CFE=∠AEM C．∠CFE+∠AEF=180°D．∠CFE+∠CFN=180°解答：解：A、∵CD∥AB，AB⊥MN，∴CD⊥MN．B、∵∠CFE=∠AEM，∴CD∥AB（同位角相等，两直线平行）．∵AB⊥MN，∴CD⊥MN．C、∵∠CFE+∠AEF=180°，∴CD∥AB，（同旁内角互补两直线平行）∵AB⊥MN，∴CD⊥MN．D、∵∠CFE与∠CFN是邻补角，当然有∠CFE+∠CFN=180°，不能得到CD⊥MN．故选D．9．（2014•汕尾）如图，能判定EB∥AC的条件是（）A．∠C=∠ABE B．∠A=∠EBD C．∠C=∠ABC D．∠A=∠ABE解答：解：A、∠C=∠ABE不能判断出EB∥AC，故A选项不符合题意；B、∠A=∠EBD不能判断出EB∥AC，故B选项不符合题意；C、∠C=∠ABC只能判断出AB=AC，不能判断出EB∥AC，故C选项不符合题意；D、∠A=∠ABE，根据内错角相等，两直线平行，可以得出EB∥AC，故D选项符合题意．故选：D．10．（2009秋•翠屏区期末）已知如图，∠A=135°，∠B=45°，在下面的说法中，一定正确的是（）A．AD∥BC B．AB∥CD C．∠C=135°，∠D=45°D．∠C=45°，∠D=135°解答解：∵∠A=135°，∠B=45°，∴∠A+∠B=135°+45°=180°，∴AD∥BC．故选：A．11．（2007春•西城区期末）下列命题中，错误的是（）A．对顶角的角平分线互为反向延长线B．在同一平面内，垂直于同一直线的两条直线互相平行C．如果一个角的两边与另一个角的两边分别平行，那么这两个角相等或互补D．同时垂直于两条平行线，并且夹在这两条平行线间的线段叫做这两条平行线的距离解答：解：A、对顶角的角平分线成180°的角，它们互为反向延长，所以A选项的说法正确；B、在同一平面内，垂直于同一直线的两条直线互相平行，所以B选项的说法正确；C、如果一个角的两边与另一个角的两边分别平行，那么这两个角相等或互补，所以C选项的说法正确；D、同时垂直于两条平行线，并且夹在这两条平行线间的线段长叫做这两条平行线的距离，所以D选项的说法错误．故选D．12．（2011秋•岳阳楼区校级期末）下列说法中正确的有（）①同位角相等．②凡直角都相等．③一个角的余角一定比它的补角小．④在直线、射线和线段中，直线最长．⑤两点之间的线段的长度就是这两点间的距离．⑥如果一个角的两边分别平行于另一个角的两边，则这两个角一定相等．A．0个B．1个C．2个D．3个解答：解：①只有两直线平行，同位角才相等，故本小题错误；②凡直角都相等，正确；③根据定义，一个角的余角比补角小90°，所以一个角的余角一定比它的补角小，正确；④在直线、射线和线段中，只有线段有长短，直线是向两方无限延伸的，没有长度，故本小题错误；⑤两点之间的线段的长度就是这两点间的距离，正确；⑥如果一个角的两边分别平行于另一个角的两边，则这两个角相等或互补，故本小题错误；所以，正确的有②③⑤共3个．故选D．13．（2011春•灌南县校级期末）如图，下列推理正确的是（）A．∵MA∥NB，∴∠1=∠3B．∵∠2=∠4，∴MC∥ND C．∵∠1=∠3，∴MA∥NB D．∵MC∥ND，∴∠1=∠3解答：解：A、由MA∥NB，能够得到∠1+∠2=∠3+∠4（两直线平行，同位角相等），若∠1，∠2的大小不确定，则不能判定∠1=∠3；故A错误．B、因为∠2=∠4，则MC∥ND（同位角相等，两直线平行）；故B正确．C、由∠1=∠3，不能判定MA∥NB，因为∠1、∠3不是NB、MA两直线截得的同位角；故C错误．D、由MC∥ND，可得∠2=∠4，而不能得到∠1=∠3；故D错误．故选B．14．（2012春•金台区期末）如图，AB⊥BC，BC⊥CD，∠EBC=∠BCF，则∠ABE与∠FCD的关系是（）A．同位角且相等B．不是同位角但相等C．是同位角但不相等D．不是同位角也不相等解答：解：∵AB⊥BC，BC⊥CD，∴∠ABC=∠DCB=90°，∵∠EBC=∠BCF，∴∠ABE=∠FCD．故选：B．15．（2013春•下城区期末）如图，AB∥EF∥DC，EG∥DB，则图中与∠1相等的角（∠1除外）共有（）A．6个B．5个C．4个D．3个解答：解：如图，∵EG∥DB，∴∠1=∠2，∠1=∠3，∵AB∥EF∥DC，∴∠2=∠4，∠3=∠5=∠6，∴与∠1相等的角有∠2、∠3、∠4、∠5、∠6共5个．故选B．16．（2015•河北一模）如图，在五边形ABCDE中，AB∥DE，若△ABE的面积为5，则△ABD的面积为（）A．4B．5C．10D．无法判断解答：解：∵在五边形ABCDE中，AB∥DE，∴点E、点D到直线AB上的垂线段相等，即在△ABE与△ABD中，边AB上的高线相等，∴△ABE与△ABD是同底等高的两个三角形，S△ABE =S△ABD=5．故选：B．17．（2014•安顺）如图，∠AOB的两边OA，OB均为平面反光镜，∠AOB=40°．在射线OB上有一点P，从P点射出一束光线经OA上的Q点反射后，反射光线QR恰好与OB平行，则∠QPB的度数是（）A．60°B．80°C．100°D．120°解答：解：∵QR∥OB，∴∠AQR=∠AOB=40°，∠PQR+∠QPB=180°；∵∠AQR=∠PQO，∠AQR+∠PQO+∠RQP=180°（平角定义），∴∠PQR=180°﹣2∠AQR=100°，∴∠QPB=180°﹣100°=80°．故选：B．18．（2014•龙岩）如图，直线a，b被直线c所截，a∥b，∠1=∠2，若∠3=40°，则∠4等于（）A．40°B．50°C．70°D．80°解答：解：∵∠1=∠2，∠3=40°，∴∠1=×（180°﹣∠3）=×（180°﹣40°）=70°，∵a∥b，∴∠4=∠1=70°．故选：C．19．（2014•荆州）如图，AB∥ED，AG平分∠BAC，∠ECF=70°，则∠FAG的度数是（）A．155°B．145°C．110°D．35°解答：解：如图，∵AB∥ED，∠ECF=70°，∴∠BAC=∠ECF=70°，∴∠FAB=180°﹣∠BAC=110°．又∵AG平分∠BAC，∴∠BAG=∠BAC=35°，∴∠FAG=∠FAB+∠BAG=145°．故选：B．20．（2011秋•射洪县校级期末）如图，已知l1∥l2，AB∥CD，CE⊥l2于点E，FG⊥l2于点G，则下列说法中错误的是（）A．AB=CDB．CE=FGC．A、B两点间距离就是线段AB的长度D．l1与l2两平行线间的距离就是线段CD的长度解答：解：A、∵l1∥l2，AB∥CD，∴四边形ABDC是平行四边形，∴AB=CD，故本选项正确；B、∵l1∥l2，CE⊥l2于点E，FG⊥l2于点G，∴边形CEGF是平行四边形，∴CE=FG，故本选项正确；C、∵AB是线段，∴A、B两点间距离就是线段AB的长度，故本选项正确；D、∵CE⊥l2于点E，∴l1与l2两平行线间的距离就是线段CE的长度，故本选项错误．故选D．21．（2009春•常州期末）如图，∠1=120°，∠2=60°，∠3=65°，则∠4等于（）A．40°B．50°C．65°D．115°解答：解：∵∠1=120°，∠2=60°，120°+60°=180°，∴这两个角所在的两条直线平行，∴∠4=∠3=65°．故本题选C．22．（2009秋•长春校级期末）如图，已知∠1=∠2，∠3=60°，则∠4=（）A．80°B．70°C．60°D．50°解答：解：∵∠1=∠2，2=∠5（对顶角相等）∴∠1=∠5，∴a∥b，（内错角相等，两直线平行）∴∠4=∠3=60°，故选C．23．（2014春•乳山市期末）如图，AC⊥CD于C，ED⊥CD于D，AB∥EF，∠CAE=25°，∠BAE=10°，则∠DEF=（）A．30°B．35°C．40°D．45°解答：解：∵AC⊥CD，ED⊥CD，∴∠C=∠D=90°，∴AC∥DE，∴∠CAE=∠DEF=25°，∵AB∥EF，∠BAE=10°，∴∠BAE=∠CEF=10°，∴∠DEF=∠DEA+∠CEA=25°+10°=35°，故选B．24．（2013春•下城区期末）如图，∠1=100°，∠2=100°，且∠3：∠1=6：5，则∠4的度数为（）A．100°B．110°C．120°D．130°解答：解：∵∠1=100°，∠3：∠1=6：5，∴∠3=120°．∵∠1=100°，∠2=100°，即∠1=∠2，∴a∥b，∴∠4=∠3=120°．故选C．25．（2005春•武昌区期末）如图，∠1与∠3互余，∠2与∠3的余角互补，∠4=115°，则∠3为（）A．45°B．60°C．65°D．70°解答：解：∵∠1与∠3互余，∠2与∠3的余角互补，∴∠1+∠3=90°，∠2+（90°﹣∠3）=180°，∴∠1+∠2=180°，∴l1∥l2，∴∠3+∠5=180°，又∵∠5=∠4=115°，∴∠3=180°﹣115°=65°．故选C．26．（2014春•苏州期末）如图，已知AB∥CD，∠1=∠2，∠E=50°，则∠F=（）A．40°B．50°C．60°D．70°解答：解：∵AB∥CD，∴∠ABC=∠BCD，∵∠1=∠2，∴∠EBC=∠BCF，∴EB∥CF，∴∠F=∠E=50°．故选B．27．（2008秋•江苏校级期末）如图，AB∥CD，EG、EM、FM分别平分∠AEF，∠BEF，∠EFD，则图中与∠DFM 相等的角（不含它本身）的个数为（）A．5B．6C．7D．8解答：解：∵FM平分∠EFD，∴∠EFM=∠DFM=∠CFE，∵EG平分∠AEF，∴∠AEG=∠GEF=∠AEF，∵EM平分∠BEF，∴∠BEM=∠FEM=∠BEF，∴∠GEF+∠FEM=（∠AEF+∠BEF）=90°，即∠GEM=90°，∠FEM+∠EFM=（∠BEF+∠CFE），∵AB∥CD，∴∠EGF=∠AEG，∠CFE=∠AEF∴∠FEM+∠EFM=（∠BEF+∠CFE）=（BEF+∠AEF）=90°，∴在△EMF中，∠EMF=90°，∴∠GEM=∠EMF，∴EG∥FM，∴与∠DFM相等的角有：∠EFM、∠GEF、∠EGF、∠AEG以及∠GEF、∠EGF、∠AEG三个角的对顶角．故选C．28．（2008春•江岸区期末）如图，AB∥CD，∠D=∠E，∠B=110°，则∠D为（）A．70°B．60°C．55°D．45°解答：解：∵AB∥CD，∴∠BFD=∠B=110°．又∵∠D=∠E，∴∠D=110°÷2=55°．故选C29．（2014春•宜宾校级期末）如图，矩形纸片ABCD中，沿折痕EF折叠，得∠EFG=40°，∠AEG的度数为（）A．98°B．99°C．100°D．101°解答：解：∵在矩形ABCD中，AD∥BC，∴∠DEF=∠EFG=40°由对称性可知∠GEF=∠DEF=40°．∴∠AEG=180°﹣∠GEF﹣∠DEF=100°．故选C．30．如图所示，AD∥BC，∠BCD=50°，∠B=80°，CA平分∠BCD，则∠CAD与∠BAC的度数分别为（）A．25°，75°B．75°，25°C．20°，50°D．25°，65°解答：解：∵∠BCD=50°，CA平分∠BCD，∴∠BCA=∠BCD=25°，∵AD∥BC，∴∠CAD=∠BCA=25°；∵∠B=80°，∴∠BAC=180°﹣∠B﹣∠BCA=75°．故选：A．31．如图，已知AB∥CD，直线EF交AB于E，交CD于F，∠1=∠2，则下列判断不正确的是（）A．FN∥EM B．∠MEB=∠NFC C．∠1+∠AEF=180°D．∠AEM=∠DFN解答：解：A、由∠1=∠2可得FN∥EM；故结论正确；B、由AB∥CD可得∠BED=∠CFE，由A证得的结论可推得：∠MEB=∠NFC；故结论正确；C、由AB∥CD可得∠AEF+∠CFE=180°，故原结论错误；D、由AB∥CD可得∠AEF=∠DFE，由A证得的结论可推得：∠AEM=∠DFC；故结论正确．故选C．32．（2006春•襄城区期末）如图，AB∥CD，OE平分∠AOC，OE⊥OF，∠C=60°，则∠BOF的度数为（）A．15°B．30°C．60°D．90°解答：解：∵AB∥CD，∠C=60°，∴∠BOC=∠C=60°，∴∠AOC=180°﹣∠BOC=180°﹣60°=120°，∵OE平分∠AOC，∴∠BOC=∠AOC=×120°=60°，∵OE⊥OF，∴∠COF=90°﹣60°=30°，∴∠BOF=∠BOC﹣∠COF=60°﹣30°=30°．故选B．33．（2013•台湾）附图中直线L、N分别截过∠A的两边，且L∥N．根据图中标示的角，判断下列各角的度数关系，何者正确？（）A．∠2+∠5＞180°B．∠2+∠3＜180°C．∠1+∠6＞180°D．∠3+∠4＜180°解答：解：根据三角形的外角性质，∠3=∠1+∠A，∵∠1+∠2=180°，∴∠2+∠3=∠2+∠1+∠A＞180°，故B选项错误；∵L∥N，∴∠3=∠5，∴∠2+∠5=∠2+∠1+∠A＞180°，故A选项正确；C、∵∠6=180°﹣∠5，∴∠1+∠6=∠3﹣∠A+180°﹣∠5=180°﹣∠A＜180°，故本选项错误；D、∵L∥N，∴∠3+∠4=180°，故本选项错误．故选A．34．（2014春•招远市期末）如图，直线l1，l2分别截射线AB，AC，若l1∥l2，则下列各角度数关系正确的是（）A．∠5+∠1=180°B．∠4+∠2＞180°C．∠6+∠3＜180°D．∠4+∠6＜180°解答：解：∵l1∥l2，∠3=∠1，∴∠2=∠6，∠3+∠6=180°，即∠1+∠6=180°，选项C错误；而AB与AC不平行，故∠5≠∠6，即∠5+∠1≠180°，选项A错误；∠4+∠6≠180°，即∠4+∠2＞180°，选项B正确，选项D错误；故选B35．（2009春•成华区期末）如图，已知AB∥EF，则∠B+∠C+∠D+∠E的度数为（）A．270°B．360°C．450°D．540°解答：解：如图，分别过点C，D作AB的平行线CG，DH，则∠B+∠BCG=180°，∠GCD+∠HDC=180°，∠HDE+∠DEF=180°，∴∠B+∠BCG+∠GCD+∠HDC+∠HDE+∠DEF=180°×3=540°，∴∠B+∠BCD+∠CDE+∠E=540°．故选D．36．（2011春•抚州校级期末）如图，AB∥CD，∠BED=110°，BF平分∠ABE，DF平分∠CDE，则∠BFD=（）A．110°B．115°C．125°D．130°解答：解：过点E作EM∥AB，过点F作FN∥AB，∵AB∥CD，∴EM∥AB∥CD∥FN，∴∠ABE+∠BEM=180°，∠CDE+∠DEM=180°，∴∠ABE+∠BED+∠CDE=360°，∵∠BED=110°，∴∠ABE+∠CDE=250°，∵BF平分∠ABE，DF平分∠CDE，∴∠ABF=∠ABE，∠CDF=∠CDE，∴∠ABF+∠CDF=（∠ABE+∠CDE）=125°，∵∠DFN=∠CDF，∠BFN=∠ABF，∴∠BFD=∠BFN+∠DFN=∠ABF+∠CDF=125°．故选C．37．（2013春•太仓市期末）如图，已知AB∥CD，则∠a、∠B和∠y之间的关系为（）A．α+β﹣γ=180°B．α+γ=βC．α+β+γ=360°D．α+β﹣2γ=180°解答：解：过点E作EF∥AB∴∠α+∠AEF=180°（两直线平行，同旁内角互补）∵AB∥CD（已知）∴EF∥CD．∴∠FED=∠EDC（两直线平行，内错角相等）∵∠β=∠AEF+∠FED又∵∠γ=∠EDC（已知）∴∠α+∠β﹣∠γ=180°．故选A．38．（2013秋•永州期末）如图，AB∥CD，用含α，β，γ的式子表示θ，则θ=（）A．180°+α+β﹣γB．180°+γ﹣α﹣βC．β+γ﹣αD．α+γ﹣β解答：解：过点E作EM∥AB，过点F作FN∥AB，∵AB∥CD，∴AB∥EM∥FN∥CD，∴∠AEM=α，∠CFN=β，∠FEM+∠EFN=180°，∴∠EFN=γ﹣β，∴∠FEM=180°﹣∠EFN=180°﹣γ+β，∴θ=∠AEM+∠FEM=α+（180°﹣γ+β）=180°+α+β﹣γ．故选A．39．（2014•鄂州）如图，直线a∥b，直角三角形如图放置，∠DCB=90°．若∠1+∠B=70°，则∠2的度数为（）A．20°B．40°C．30°D．25°解答：解：由三角形的外角性质，∠3=∠1+∠B=70°，∵a∥b，∠DCB=90°，∴∠2=180°﹣∠3﹣90°=180°﹣70°﹣90°=20°．故选：A．40．（2014•长沙二模）如图，AB∥EF，BC⊥CD于C，∠ABC=30°，∠DEF=45°，则∠CDE等于（）A．105°B．75°C．135°D．115°解答：解：作CM∥AB，DN∥AB，由AB∥EF，得到AB∥CM∥DN∥EF，∴∠ABC=∠BCM=30°，∠DEF=∠GDE=45°，∠MCD=∠CDG，∵BC⊥CD，∴∠BCD=90°，∴∠MCD=∠CDG=60°，∴∠CDE=∠CDG+∠GDE=105°．故选A41．（2014春•武昌区期末）如图，AB∥EF，则∠A，∠C，∠D，∠E满足的数量关系是（）A．∠A+∠C+∠D+∠E=360°B．∠A+∠D=∠C+∠EC．∠A﹣∠C+∠D+∠E=180°D．∠E﹣∠C+∠D﹣∠A=90°解答：解：如图，过点C作CG∥AB，过点D作DH∥EF，则∠A=∠ACG，∠EDH=180°﹣∠E，∵AB∥EF，∴CG∥DH，∴∠CDH=∠DCG，∴∠C=∠ACG+∠CDH=∠A+∠D﹣（180°﹣∠E），∴∠A﹣∠C+∠D+∠E=180°．故选C．42．（2013秋•招远市期末）如图，AB∥EF∥CD，连接BD，ED，则下列等式中正确的是（）A．∠1﹣∠2+∠3=180°B．∠1+∠2﹣∠3=180°C．∠2+∠3﹣∠1=180°D．∠1+∠2+∠3=180°解答：解：如图，延长CD，∵EF∥CD，∴∠4=180°﹣∠3，∵AB∥CD，∴∠1=∠2+∠4，∴∠1=∠2+180°﹣∠3，整理得，∠1﹣∠2+∠3=180°．故选A．43．（2013春•石景山区期末）如图，AF是∠BAC的平分线，EF∥AC交AB于点E，若∠1=155°，则∠BEF的度数为（）A．50°B．12.5°C．25°D．15°解答：解：∵∠AFE=180°﹣∠1=180°﹣155°=25°，又∵EF∥AC，∴∠CAF=∠AFE=25°，∵AF是∠BAC的平分线，∴∠BAC=2∠CAF=50°，∵EF∥AC，∴∠BEF=∠BAC=50°．故选A．44．（2014春•招远市期末）如图，一条公路修到湖边时，需拐弯绕湖而过，第一次拐的角∠A=110°，第二次拐的角∠B=150°，第三次拐的角是∠C，这时的道路恰好和第一次拐弯之前的道路平行，则∠C的度数为（）A．120°B．130°C．140°D．150°解答：解：延长FC，AB，交于点E，如图所示，∵AD∥CE，∴∠A=∠E=110°，∵∠ABC为△BCE的外角，∴∠BCE=∠ABC﹣∠E=40°，∴∠BCF=140°．故选C45．（2014春•海淀区期末）如图，AB∥CD，∠BAC与∠DCA的平分线相交于点G，EG⊥AC于点E，F为AC上的一点，且FA=FG=FC，GH⊥CD于H．下列说法正确的是（）①AG⊥CG；②∠BAG=∠CGE；③S△AFG=S△GFC；④若∠EGH：∠ECH=2：7，则∠EGF=50°．A．①③④B．②③C．①②③D．①②③④解答：解：①中，∵AB∥CD，∴∠BAC+∠ACD=180°，∵∠BAC与∠DCA的平分线相交于点G，∴∠GAC+∠GCA=∠BAC+∠ACD=×180°=90°，∵∠GAC+∠GCA+AGC=∠180°，∴AG⊥CG；②中，根据等角的余角相等，得∠CGE=∠GAC，故∠BAG=∠CGE；③中，根据三角形的面积公式，∵AF=CF，∴S△AFG =S△CFG；④中，根据题意，得：在四边形GECH中，∠EGH+∠ECH=180°．又∵∠EGH：∠ECH=2：7，∴∠EGH=180°×=40°，∠ECH=180°×=140°．∵CG平分∠ECH，∴∠FCG=∠ECH=70°，根据直角三角形的两个锐角互余，得∠EGC=20°．∵FG=FC，∴∠FGC=∠FCG=70°，∴∠EGF=50°．故上述四个都是正确的．故选D．二．填空题（共45小题）46．（2014春•新泰市期末）如图，已知直线CD、EF相交于点O，OA⊥OB，且OC平分∠AOF，∠BOE=2∠AOE．则∠BOD=15°．解答：解：∵OA⊥OB，∠BOE=2∠AOE．∴∠AOE=30°，∴∠AOF=180°﹣∠AOE=180°﹣30°=150°，∵OC平分∠AOF，∴∠AOC=75°，∴∠BOD=180°﹣∠BOA﹣∠AOC=180°﹣90°﹣75°=15°故答案为：15°．47．（2013春•黄山期末）如图，已知直线AD、BE、CF相交于O，OG⊥AD，且∠BOC=35°，∠FOG=30°，则∠DOE= 25°．解答：解：∵OG⊥AD，∴∠GOD=90°，∵∠EOF=∠BOC=35°，又∵∠FOG=30°，∴∠DOE=∠GOD﹣∠EOF﹣∠GOF=90°﹣35°﹣30°=25°，故答案为：25°．48．（2013秋•昌平区期末）如图，直线AB，CD相交于点O，∠AOC=60°，∠1=2∠2，则∠2=20°，∠AOE= 140°．解答：解：∵∠AOC与∠BOD是对顶角，∴∠BOD=∠AOC=60°，∵∠1=2∠2，∠1+∠2=60°，∴∠2=20°；∵∠AOC+∠BOD=180°，∴∠BOD=180°﹣∠AOC=120°，∵∠AOE=∠AOD+∠EOD=120°+20°=140°，故答案为：20，140．49．（2014春•霸州市期末）如图，直线AB、CD相交于点O，OE⊥AB，O为垂足，如果∠EOD=38°，则∠AOC= 52度，∠COB=128度．解答：解：∵OE⊥AB，∴∠EOB=90°，又∠EOD=38°，∴∠DOB=90°﹣38°=52°，∵∠AOC=∠DOB，∴∠AOC=52°，∵∠COB与∠AOC互补，∴∠COB=180°﹣52°=128°．故答案为：52；128．50．（2013•河北模拟）如图，直线AB与直线CD相交于点O，射线OP平分∠AOD，若∠BOC=130°，则∠COP 的度数为115°．解答：解：∵∠BOC=130°，∴∠AOD=∠BOC=130°，∵OP平分∠AOD，∴∠POD=∠AOD=×130°=65°，∴∠COP=180°﹣∠POD=180°﹣65°=115°．故答案为：115°．51．（2010秋•江阴市期末）已知直线AB和CD相交于O点，OE⊥AB，∠1=55°，则∠BOD=35度；若OF平分∠DOB，则∠EOF的度数是107.5度．解答：解：∵OE⊥AB，∠1=55°，∴∠AOC=90°﹣∠1=90°﹣55°=35°，又∵∠BOD=∠AOC，∴∠BOD=35°；∵OE⊥AB，∴∠EOB=90°，又∵OF平分∠DOB，∴∠BOF=∠DOB=×35°=17.5°，∠EOF=∠EOB+∠BOF=90°+17.5°=107.5°．故答案分别为：35°；107.5°．52．（2011秋•大兴区期末）如图，三条直线相交于一点，按从小到大的顺序排列∠1，∠2，∠3为∠1＜∠3＜∠2．解答：解：根据图形，∠1=180°﹣60°﹣70°=180°﹣130°=50°，根据对顶角相等，∠2=70°，∠3=60°，所以∠1＜∠3＜∠2．故答案为：∠1＜∠3＜∠2．53．（2014春•武昌区期末）如图，已知∠α与∠β共顶点O，∠α+∠β＜180°，∠α=∠β．若∠β的邻补角等于∠α，则∠β=120度．解答：解：设∠α=x，则∠β=3x，根据题意得：解得：，解得：x=40°，∴∠β=3x=120°，故答案为：120．54．（2011•平塘县校级模拟）如图，要从小河引水到村庄A，请设计并作出一最佳路线，理由是垂线段最短．解答：解：根据垂线段定理，连接直线外一点与直线上所有点的连线中，垂线段最短，∴过点A作河岸的垂线段，理由是垂线段最短．55．看图填空：（1）∠1和∠4是邻补角；（2）∠1和∠3是对顶角；（3）∠2和∠D是内错角；（4）∠3和∠D是同旁内角；（5）∠4和∠D是同位角；（6）∠4和∠B是同位角．解答：解：（1）∠1和∠4是邻补角，故答案为：邻补；（2）∠1和∠3是对顶角，故答案为：对顶；（3）∠2和∠D是内错角，故答案为：内错；（4）∠3和∠D是同旁内角，故答案为：同旁内；（5）∠4和∠D是同位角，故答案为：同位；（6）∠4和∠B是同位角，故答案为：同位．56．如图所示，AB与BC被AD所截得的内错角是∠1与∠3；；DE与AC被AD所截得的内错角是∠2与∠4；∠1与∠4是直线AE、ED被直线AD截得的角，图中同位角有6对．解答：解：，AB与BC被AD所截得的内错角是∠1与∠3；DE与AC被AD所截得的内错角是∠2与∠4；∠1与∠4是直线AE、ED被直线AD截得的角，图中同位角有4对，故答案为：∠1与∠3，∠2与∠4，AE、ED，AD，6．57．（2011秋•岳阳楼区校级期末）如图所示，其中共有4对对顶角．解答：解：如图，在顶点H处有2对对顶角，在顶点C处有2对对顶角，所以，共有2+2=4对对顶角．故答案为：4．58．（2014春•富顺县校级期末）如图所示，同位角一共有6对，内错角一共有4对，同旁内角一共有有4对．解答：解：同位角一共有6对，分别是∠1和∠5，∠2和∠6，∠3和∠7，∠4和∠8，∠7和∠9，∠4和∠9；内错角一共有4对，分别是∠1和∠7，∠4和∠6，∠5和∠9，∠2和∠9；同旁内角一共有4对，分别是∠1和∠6，∠1和∠9，∠4和∠7，∠6和∠9．故答案为：6，4，4．59．（2004秋•奉贤区期末）如图：a∥b，图中的∠1，∠2，∠3，∠4，∠5，∠6，∠7中同位角有3对．解答：解：观察图形可知：∠1的同位角是∠4，∠3的同位角是，5，∠7的同位角是∠6，∴图中同位角有3个．故答案为：3．60．如图，DH∥EO∥BC，EF∥CD，则与∠BFE相等的角，不包括∠BFE有5个．。

平行线与相交线经典题一、经典题示例1. 已知直线a，b被直线c所截，∠1与∠2是同位角，若∠1 = 50°，求∠2的度数。

这题很简单啦，因为两直线平行，同位角相等嘛。

可这里没说a和b平行哦，所以∠2的度数是不能确定的呢。

2. 如图，AB∥CD，直线EF分别交AB、CD于点E、F，EG平分∠BEF，若∠1 = 72°，求∠2的度数。

首先我们知道AB∥CD，所以∠1+∠BEF = 180°（两直线平行，同旁内角互补）。

因为∠1 = 72°，所以∠BEF = 180° - 72° = 108°。

又因为EG平分∠BEF，所以∠BEG = 1/2∠BEF = 54°。

而∠2 = ∠BEG（两直线平行，内错角相等），所以∠2 = 54°。

二、较难题型1. 有两条直线l1和l2，l1上有A、B两点，l2上有C、D两点，连接AC、BD，若∠CAB和∠ABD的平分线相交于点E，∠CAB = 100°，∠ABD = 120°，求∠AEB的度数。

这题有点绕呢。

我们可以先根据三角形内角和定理来做。

因为AE平分∠CAB，所以∠EAB = 1/2∠CAB = 50°。

同理，∠EBA = 1/2∠ABD = 60°。

在△AEB中，根据三角形内角和为180°，可得∠AEB = 180° - 50° - 60° = 70°。

2. 已知直线a∥b，直线c与a、b相交，点A在直线a上，点B在直线b上，点M在直线c上，且AM⊥c，BM与c的夹角为30°，求∠AMB的度数。

这题要分情况讨论哦。

当点M在a、b之间时，∠AMB = 90°+30° = 120°；当点M不在a、b之间时，∠AMB = 90° - 30° = 60°。