微课-21认识无理数(2)

即99x=492．
∴x= 164
33
课堂小结
1．本节课你学习了什么？ 2．本节课你有哪些收获？ 3．通过今天的学习，你想进一步探究的问题是什么？
课堂小结
1．无理数的定义． 2．理解无理数定义时要注意的问题：
再见
D．无理数
3．设面积为3的正方形的边长为x，那么关于x的说法正确的 是（ D ）
A．x是有理数
B．x取0和1之间的实数
C．x不存在
D．x取1和2之间的实数
随堂练习
4.把下列各数填入相应集合.
0.351
-
2 3
••
4.96
3.14159
-5.232332…， π
3
1.2334567891011…(由相继的正整数组成).
A.0
B. 1.010010001
C.π
22
D. 7
典型例题
例2.如图所示的是面积分别为1、2、3、4、5、6、7、8、 9的正方形，边长是有理数的正方形有 3 个,边长是无理
数的正方形有 6 个.
典型例题
例3.下列各数中，哪些是有理数？哪些是无理数？
1
0.4583 3.7 ，-π，－ 7
，18，
认识无理数
无理数常见的形式主要有三种： ①一般的无限不循环小数，如1.414 213 56…是无理数． 看似循环而实质不循环的小数，如0.101 001 000 1…(相邻两个1之 间0的个数逐次增加1)是无理数． ②圆周率π以及含π的数，如π，2π，π＋5，都是无理数． ③开方开不尽的数(下一节学到).
认识无理数
有理数与无理数的主要区别： ①无理数是无限不循环小数，有理数是有限小数或无限循环小数. ②任何一个有理数都可以化为分数的形式，而无理数不能.

（2）★ π是无限不循环小数，是无理数
二、探究新知
有限小数
小数
无限小数
无限循环小数 有理数 无限不循环小数 无理数
★无理数一定是无限小数 无限小数不一定是无理数
三、典例讲解
1. 下列结论正确的是 （ B ） A. 无限小数是无理数 B. 无限不循环小数是无理数 C. 有理数就是有限小数 D. 无理数就是开方开不尽的数
数依次加 1)，0.
正数集合：{
…}；
负数集合：{
…}；
有理数集合：{
…}；
无理数集合：{
…}．
解：正数集合：{0.236，0.37·，18，0.403 400 340 003 4…(4 和 3 之间 0 的个数依次加 1)，…}； 负数集合：{－π2，－112，－0.021 021 021…，…}； 有理数集合：{0.236，0.37·，－112，18，－0.021 021 021…，0，…}； 无理数集合：{－π2，0．403 400 340 003 4…(4 和 3 之间 0 的个数 依次加 1)，…}．
3 3.0；4 0.8; 3 0.375;
5
8
5 0.55555555......; 9
8 0.17777777......; 45
2 0.181818......; 11
分数化成小数，有几种形式？
有限小数
分数
无限循环小数

二、探究新知
有理数
整数
分数
有限小数 无限循环小数
即任何有限小数或无限循环小数都是有理数.
a b
=1.41421356…
=2.23606797…
无限不循环小数
无限不循环小数称为无理数
二、探究新知

第二章实数
1.认识无理数（2）
学习目标
1 掌握无理数的定义，比较无理数与有理数的区别，并 能辨别出一个数是无理数还是有理数； 2 探索无理数是无限不循环小数．
复习巩固
1 . 整数 和 分数 统称为有理数. 2 .若x2=10,则x 不是 分数， 不是 整数，
所以x 不是 有理数.
认识无理数
面积为2的正方形的边长a究竟是多少呢？
••
••
解：设 x= 4.96 则100x=496. 96
••
••
∴ 100x-x=492. 96 -4.96
即99x=492．
∴x= 164
33
1．无理数的定义
课堂小结
课堂小结
2．无理数与有理数的区别
再见
认识无理数
无理数常见的形式主要有三种： ①一般的无限不循环小数，如1.414 213 56…是无理数 看似循环但是不循环的小数，如0.101 001 000 1…(相邻两个1之间0 的个数逐次增加1)是无理数． ②圆周率π以及含π的数，如π，2π，π＋5，都是无理数． ③开方开不尽的数(下一节学到).
(4)有理数是有限小数.
（× ）
随堂练习
2．面积为6的长方形，长是宽的3倍，则宽为（ D ）
A．整数 B．分数 C．有理数
D．无理数
3．设面积为3的正方形的边长为x，那么关于x的说法正确的 是（ D ）
A．x是有理数
B．x取0和1之间的实数
C．x不存在
D．x取1和2之间的实数
随堂练习
4.把下列各数填入相应集合.
数的正方形有 6 个.
典型例题
例3.下列各数中，哪些是有理数？哪些是无理数？
0.4583

创设情境 探究新知 应用新知 巩固新知 课堂小结 布置作业
归纳
定义
像0.585无88限588不858循888环5…小（数相邻称两为个无5之理间数8的.个数逐次加1）
π=3.14159265，1.41421356…，－2.2360679…
等这些数判的断小一数位个数数都是是无不限是的无，，理又数不，是循关环键的就，而是看它能不 能写成无限不循环的小数.
合作探究
(2) a的整数部分是几？十分位是几？百分位呢？千分位呢？
借助计算器探索，用表格的形式整理.
a 1.5 1.4 1.45
1.44 1.43 1.42 1.41
1.415 1.414 1.4145
1.4144 1.4143
a的平方 2.25 1.96 2.1025 2.0736 2.0449 2.0164 1.9881
2.002225 1.999396
2.00081025 2.00052736 2.00024449
创设情境 探究新知 应用新知 巩固新知 课堂小结 布置作业
合作探究
(2) a的整数部分是几？十分位是几？百分位呢？千分位呢？ 借助计算器探索，用表格的形式整理.
边长a
面积S
1< a <2
1< S <4
创设情境 探究新知 应用新知 巩固新知 课堂小结 布置作业
归纳
无理数的常见形式
主要有三种： ①无限不循环小数，如1.414 213 56…是无理数． 像看π0.=5似38.518循4815环589828而6558，8实818质.54…1不4（21相循35邻环6…两的，个－小5之2数.间238，6的06如个79数0….逐10次1加010）1 000 1…(相邻 等两这些个数1的之小间数0位的数个都是数无逐限次的，增，加又1不)是是循无环理的数，而． ②圆周率π以及含π的数，如π，2π，π＋5都是无理数． ③开方开不尽的数(下一节学到).

.理论介绍：首先，我们要了解无理数的基本概念。无理数是不能表示为两个整数比的数，如π、√2等。无理数在数学和科学领域具有重要地位，它们帮助我们更准确地描述世界。
2.案例分析：接下来，我们来看一个具体的案例。通过分析√2为什么是无理数，了解无理数在实际中的应用，以及它如何帮助我们解决问题。
3.成果展示：每个小组将向全班展示他们的讨论成果和实验操作的结果。
（四）学生小组讨论（用时10分钟）
1.讨论主题：学生将围绕“无理数在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法，并与其他小组成员进行交流。
2.引导与启发：在讨论过程中，我将作为一个引导者，帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考。
举例：解释为什么√2是无理数，可以通过反证法来证明，假设√2是有理数，可以表示为两个整数之比，然后通过一系列数学推导，得出矛盾，从而证明√2是无理数。在运算方面，讲解如何计算√2与√3的和、差、积、商，并提供具体例题，让学生通过实际操作掌握运算方法。在联系实际问题时，可以设计测量不规则图形面积等题目，让学生将无理数应用于实际问题求解。
3.重点难点解析：在讲授过程中，我会特别强调无理数的定义和表示这两个重点。对于难点部分，我会通过举例和比较来帮助大家理解如何判断一个数是否为无理数。
（三）实践活动（用时10分钟）
1.分组讨论：学生们将分成若干小组，每组讨论一个与无理数相关的实际问题，如无理数在生活中的应用。
2.实验操作：为了加深理解，我们将进行一个简单的实验操作，如测量不同图形的边长和面积，演示无理数的基本原理。
3.成果分享：每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上，以便全班都能看到。

第六页，共十八页。
解：如圈里所示．
第七页，共十八页。
探究 ：已知直角三角形的两直角边长分别为 9 cm 和 5 cm，斜边长是 x cm.
(1)估计 x 在哪两个整数之间？ (2)如果把 x 的结果精确到十分位，估计 x 的值；如 果精确到百分位呢？
第八页，共十八页。
解 ： (1) 根 据 条 件 ， 得 x2 ＝ 92 ＋ 52 ＝ 106 ， 因 为 100<106<121，即 102<x2<112，所以 10<x<11，即 x 在 10 和 11 之间．
解：正方形面积 S1＝122＝144 是有理数，圆的面积 S2＝57π6是无理数，57π6>5746＝144，S2>S1.
规律：当周长一定时，围成圆形的面积比正方形面 积大．
第十七页，共十八页。
第二章 实数(shìshù)

内容(nèiróng)总结
第十八页，共十八页。
知识点 ：无理数的概念
2. 如果一个圆的半径是 2，那么该圆的周长是( B )
A．一个有理数
B．一个无理数
C．一个分数
D．一个整数
第五页，共十八页。
3. 下列各数中，哪些是有理数？哪些是无理数？ 0．351，－32，4.9·6·，3.14159，－5.232332…(相邻两 个 2 之间依次多一个 3)，0.123456789101112…(由相继的 正整数组成)． 把结果填入下列相应的圈里．
A．23
B． 3
C．0
D．－1.010101
第十二页，共十八页。
3. 如图是面积分别为 1，2，3，4，5，6，7，8，9 的正方形，其中边长是有理数的正方形有__3__个，边长 是无理数的正方形有__6__个．

2.引导与启发：在讨论过程中，我将作为一个引导者，帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考，如无理数在科技发展中的作用。
3.成果分享：每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上，以便全班都能看到。
（五）总结回顾（用时5分钟）
今天的学习，我们了解了无理数的基本概念、重要性和应用。同时，我们也通过实践活动和小组讨论加深了对无理数的理解。我希望大家能够掌握这些知识点，并在日常生活中灵活运用。最后，如果有任何疑问或不明白的地方，请随时向我提问。
3.重点难点解析：在讲授过程中，我会特别强调无理数的定义和表示方法这两个重点。对于难点部分，我会通过构造正方形对角线长度√2的例子，以及π在圆的周长中的应用，来帮助大家理解。
（三）实践活动（用时10分钟）
1.分组讨论：学生们将分成若干小组，每组讨论一个与无理数相关的实际问题，如√3在等边三角形中的应用。
2.1.2认识无理数（教案）
一、教学内容
本节课选自《数学》八年级上册第二章“数的开方”中的2.1.2节“认识无理数”。教学内容主要包括以下两个方面：
1.无理数的定义：引导学生理解无理数的概念，掌握无理数是无限不循环小数的特性，并能识别常见的无理数。
2.无理数的表示：学习无理数的表示方法，包括根号表示法（如√2、√3等）和无限不循环小数表示法（如π、e等），了解无理数与有理数的区别和联系。
然而，在讲解无理数的表示方法时，我发现有些学生对根号表示法还不够熟悉，对无限不循环小数的理解也有些困难。这可能是因为我对这些概念的解释不够清晰，或者例子不够丰富。在以后的教学中，我需要准备更多生动、具体的例子，帮助学生更好地理解这些表示方法。
在实践活动环节，学生们分组讨论和实验操作的过程比我预期的要顺利。他们能够将所学的无理数知识应用到实际问题中，这让我感到很欣慰。但同时，我也注意到有些学生在操作过程中遇到了困难，可能是由于他们对无理数的理解还不够深入。针对这个问题，我计划在下一节课中增加一些针对性的练习，让学生在实践中进一步巩固对无理数的理解。

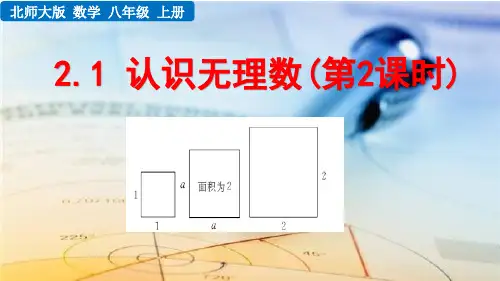
探究新知
2.1 认识无理数/
想一想 用上面的方法估计面积为5的正方形的边长b的值. 边长b会不会算到某一位时，它的平方恰好等于5？
如果b算到某一位时，它的平方恰好等于5，即b是一 个有限小数，那么它的平方一定是一个有限小数，而不可 能是5，所以b不可能是有限小数.
事实上，b=2.236 067 978…它是一个无限不循环小数. 同样,对于体积为2的正方体,借用计算器,可以得到它
课堂检测
2.1 认识无理数/
拓广探索题
小明买了一盒饮料，盒子的尺寸为5×4×3(单位：cm)， 现在小明要将这盒饮料分别倒在两个同样大小的正方体容器内， 问这两个正方体容器的棱长是有理数还是无理数？请说说你的理 由．若是无理数，请你利用计算器探索这个正方体的棱长至少为 多少？(精确到十分位)
课堂检测
课堂小结
2.1 认识无理数/
有理数：有限小数或无限 循环小数
整数 分数
数
无理数：无限不循环小数
课后作业
作业 内容
2.1 认识无理数/
教材作业 从课后习题中选取 自主安排 配套练习册练习
(3)无理数都是无限小数; （ √ ）
(4)有理数是有限小数. （ × ）
课堂检测
2.1 认识无理数/
基础巩固题
2.以下各正方形的边长是无理数的是（ C ）
A.面积为25的正方形；
B.面积为245的正方形； C.面积为8的正方形； D.面积为1.44的正方形.
课堂检测
2.1 认识无理数/
基础巩固题
课堂检测
1 认识无理数
2.1 认识无理数/
能力提升题
如图,在方格纸中,假设每个小正方形的面积为2,则图中 的四条线段中长度为有理数的线段是 CD,EF. 解析:设小正方形的边长为x,则x2=2. 因为AB2=x2+(3x)2=10x2=20,所以AB的长不是有理数. 因为CD2=(2x)2+(2x)2=8x2=16,CD=4,即CD的长是有理数. 因为EF2=x2+x2=2x2=4,EF=2,即EF的长是有理数. 因为GH2=x2+(2x)2=5x2=10,所以GH的长不是有理数.

（3）无理数在实际问题中的应用：将无理数知识应用于实际问题，学生可能感到困惑。
突破方法：设计贴近生活的实际问题，引导学生将无理数知识应用于解题过程，提高应用能力。
四、教学流程
（一）导入新课（用时5分钟）
同学们，今天我们将要学习的是《认识无理数》这一章节。在开始之前，我想先问大家一个问题：“你们在日常生活中是否遇到过无法用整数或分数表示的长度、面积或体积？”（如：一张纸的对角线长度）这个问题与我们将要学习的内容密切相关。通过这个问题，我希望能够引起大家的兴趣和好奇心，让我们一同探索无理数的奥秘。
2.实验操作：为了加深理解，我们将进行一个简单的实验操作，如测量并计算正方形对角线的长度，演示无理数的基本原理。
3.成果展示：每个小组将向全班展示他们的讨论成果和实验操作的结果。
（四）学生小组讨论（用时10分钟）
1.讨论主题：学生将围绕“无理数在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法，并与其他小组成员进行交流。
3.重点难点解析：在讲授过程中，我会特别强调无理数的定义和性质、无理数的表示方法这两个重点。对于难点部分，如无理数的无限不循环性质，我会通过举例和比较来帮助大家理解。
（三）实践活动（用时10分钟）
1.分组讨论：学生们将分成若干小组，每组讨论一个与无理数相关的实际问题，如：生活中哪些地方会用到无理数？
二、核心素养目标
本节课的核心素养目标主要包括以下几个方面：一是培养学生数学抽象能力，通过无理数的学习，让学生理解数学概念背后的抽象意义，提升数学思维水平；二是发展学生逻辑推理能力，使学生能够运用所学知识对无理数的性质、运算规律进行推理和证明；三是提高学生数学建模能力，学会将实际问题中的无理数问题转化为数学模型，进行求解；四是增强学生数学运算能力，熟练掌握无理数的四则运算，并能解决实际问题；五是培养学生数学应用意识，将所学无理数知识应用于解决生活实际问题，体会数学在生活中的价值。通过本节课的学习，旨在全面提升学生的数学学科核心素养，为学生的终身发展奠定基础。

(1)使它的一边为有理数，另两边边长不是有 理数；
(2)使它的三边边长都是有理数．
课堂检测
下列说法：①有理数都是有限小数；
能力提升题
解：答案不唯一．如图所示：
首先通过拼图把几个小正方形拼成一个大正方形，然后利用面积发现非有理数
解：(1)如图1所示． 面积为 的正方形
D.
(2)设该正方形的边长为b，则b应满足什么条件？b是有理数吗？
B.
下列说法：①有理数都是有限小数；
即两个相同最简分数的乘积仍是分数.
有理数包b不可能是分数.
下列说法：①有理数都是有限小数；
通过拼图活动和勾股定理的应用感受无理数产生的实际背景和引入的必要性．
把边长是1的两个正方形纸片重新剪裁成一个大的正方形，则大正方形的面积是______，它的边长_____有理数（填写“是”或“不是”）
利用勾股定理发现非有理数
非有理数的识别
（2020·威海模拟）下列正方形的边长不是有理数的是（ ）
(2)如图2所示． ②有限小数都是有理数；
②没有两个相同的分数相乘得5，故b不可能是分数. h不可能是整数，也不可能是分数.
整数
B.
面积为 的正方形
D.
4
C.
EF2＝18,18不能写成一个整数或分数的平方，所以EF表示的数是非有理数．
利用勾股定理识别非有理数
所以a一定不是分数.
在等式a2=2中，a既不是整数，也 不是分数，那么一定不是有理数.
探究新知
归纳总结
有理数包括：整数和分数. 如果一个数既不是整数也不是分数， 那么这个数不是有理数. 在a2=2中，a不是有理数.
探究新知
素养考点 1 非有理数的识别 例 如图，有一个由五个边长为1的小正方形组成的图形，我