当前位置：文档之家 › 图论作业(1)

图论作业(1)

  • 格式：doc
  • 大小：60.00 KB
  • 文档页数：7

下载文档原格式

  / 7

合集下载

图论大作业

图论大作业

《图论及其应用》大作业指导老师郝荣霞知行1503 徐鹏宇 152912002.1.9证明：若G是森林且恰有2k个奇点，则在G中有k条边不重的路P1,P2......P K,使得E(G)=E(P1) E(P2) ...... E(P K)。

证明：对奇点数k使用数学归纳法。

①当k=1时，G是森林，且有且只有2个奇点⇒G只能为一颗树，且G的所有奇度顶点为两个1度顶点⇒G是一条路⇒满足题设②假设当k=t时，结论成立。

接下来考虑k=t + 1时的情况。

在G中一个分支中取两个叶子点u与v，令P是连接该两个顶点的唯一路。

由于P上除u，v以外的点均被P经过两次，即G-P后除u，v以外的点奇偶性不变。

⇒则G–P是有2t个奇度顶点的森林⇒由归纳假设知，G–P可以分解为t条边不重合的路之并，即E(G-P)=E(P1) E(P2) ...... E(P t)。

⇒则G可分解为t+1条边不重合的路之并，即E(G)=E(P1) E(P2) ...... E(P t) E(P)。

⇒即证。

2.4.4证明：若e 是K n 的边，则τ（K n -e ）=（n-2）n n-3证明：由定理2.9：τ（K n ）=n n-2由于τ（K n -e ）=τ（K n ）-τ（含有e 的生成树棵树）现在需要求含有e 的生成树棵树，τ（含有e 的生成树棵树）=)1(21n 1-n 2-n n n ）（=2n n-3τ（K n -e ）=τ（K n ）-τ（含有e 的生成树棵树）=（n-2）n n-33.2.4证明：不是块的连通图至少有两个块，其中每个恰有一个割点。

证明：设G 为不是块的连通图，由于G 连通且不是块⇒G 有割点①当G 只有1个割点v 时，延割点分开，G1，G2内无割点，且连通，由块的定义知⇒G1,G2是块，且分别含一个割点v 。

②当G 含有2个及2个以上割点时，取相距距离最远的两个割点u 和v ，此时分G 为三部分G1,G2,G3。

电子科技大学-图论第一次作业-

电子科技大学-图论第一次作业-
.
课本习题一：
4. 证明下面两图同构。
v1
u1
v2
v6
v10 v5
v7
v8 v9
v3
v4 (a)
u6 u5
u2
u8
u10
u3
u7
u9
u4
(b)
证明:作映射 f : vi ↔ ui (i=1,2….10)
容易证明，对vi v j E ((a)),有 f (v i vj,),,ui,uj,,E,((b))
中不
3.设 G 是阶大于 2 的连通图，证明下列命题等价：
（1）
G 是块
（2）
G 无环且任意一个点和任意一条边都位于同一
个圈上；
（3）
G 无环且任意三个不同点都位于同一条路上。
： 是块，任取 的一点 ，一边 ，在 边插入一点 ，使得 成为两条边，由此 得到新图 ，显然 的是阶数大于 的块，由定理 4， 中的 u,v 位于同一个 圈上，于是 中 u 与边 都位于同一个圈上。
件下的不同构的情形，则从上面穷举出的情况可以看出四个顶点的非同构简单图
有 11 个。
11.证明：序列（7,6,5,4,3,3,2）和（6,6,5,4,3,3,1）
不是图序列。
证明：由于 7 个顶点的简单图的最大度不会超过 6，因此序列（7,6,5,4,3,3,2）不
是图序列；
（6,6,5,4,3,3,1）是图序列
(G1) 2 最小边割{（6,5），（8,5）} {（6,7），（8,7）}{（6,9），（8,9）}
1j 10 ) 由图的同构定义知，图(a)与(b)是同构的。
5.证明：四个顶点的非同构简单图有 11 个。
证明：设四个顶点中边的个数为 m，则有：

图论1

图论1

d<u,v> + d<v,w> ≥ d<u,w> 《定义》：在简单有向图中,若图中任何一 定义》 对结点间,至少有一点到另一结点是可达 的，则称此图是单侧连通的；如果两结 点均是互相可达的，则称是强连通的。 如果在图中略去边的方向,将它看成无向 图后，图是连通的，则称此图为弱连通 的. 强连通⇒单侧连通⇒弱连通
(10)闭路（自回路）： 闭路（自回路）：图中起始且终止于同一结 闭路 ）： 点的边 (闭路的箭头方向是没有意义的 )例：
(11)多重边（平行边）： 多重边（平行边）：二个结点之间 多重边 ）： 方向相同的二条（多条）边 例：
多重图，非多重 《定义》：含有多重边的图称为多重图 定义》 多重图 图称为线图 线图。 线图 简单图： 简单图。 简单图：无自回路的线图称为简单图。由定义可 简单图 见，简单图是没有自回路和多重边的图。 例：
图论不断发展，它在解决运筹学，网络理 论，信息论，控制论，博奕论以及计算 机科学等各个领域的问题时，显示出越 来越大的效果。 对于这样一门应用广泛的学科，其包含的 内容是丰富的，本篇我们只准备介绍基 本的概念和定理，为今后有关学科及课 程的学习和研究提供方便。 第七章 图论
§1图的基本概念
1.基本名词和定义 1.基本名词和定义 定义》 《定义》一个图G是一个三元组<V(G),E(G), ΦG>, 其中V(G)为有限非空结点（或叫顶点）集合, E(G)是边的集合， ΦG是从边集E到结点偶对集 合上的函数。 (1). V(G) ={V1,V2,…,Vn}为有限非空集合, Vi称为结点,简称V是点集。 (2). E(G)={e1,…,em}为有限的边集合,ei称为边。 。 每个边ei都有V中的结点对与之相对应,称E为边集。 。 即每条边是连结V中的某两个点的。

图论作业(1)

图论作业(1)

第三章1.证明： 必要性：v 是连通图G 的割边， 则， 至少有两个连通分支。

设其中一个连通分支顶点集合为V1,另外连通分支顶点集合为V2,即V1与V2构成V 的划分。

对于任意的u ∈V1, v ∈V2，如果割边e 不在某一条（u ，v ）路上，那么，该路也是连接G-e 中的u 与v 的路，这与u,v 处于G-v 的不同分支矛盾。

“充分性”若e 不是图G 的割边，那么G-v 连通，因此在G-v 中存在u,v 路，当然也是G 中一条没有经过边e 的u,v 路。

矛盾。

7.证明： v 是单图G 的割点，则G-v 至少两个连通分支。

现任取 , 如果x,y 在G-v 的同一分支中，令u 是与x,y 处于不同分支的点，那么，通过u ，可说明，x 与y 在G-v 的补图中连通。

若x,y 在G-v 的不同分支中，则它们在G-v 的补图中邻接。

所以，若v 是G 的割点，则v 不是其补图的割点。

9.连通图G 的一个子图B 称为是G 的一个块，如果(1), 它本身是块；(2), 若没有真包含B 的G 的块存在。

又由于对于阶数至少是3的()()G e G ωω->图G是块当且仅当G无环并且任意两点都位于同一圈上。

根据题意，对于阶数至少是3的图G，由于G没有偶圈，所以G的每个块的点可以在奇圈上，如果不在奇圈上，则块只能是K2，否则如果不是K2的话，该子图将存在割点，该子图就不是块。

得证。

16.（1）（2）（3）第四章3. （1）既是欧拉闭迹又是哈密尔顿圈（2）（3）（4）7.由于图没有奇度顶点，所以是欧拉图，又定理1可得，图G的边集可以划分为圈C1，C2，。

Cm，所以E（G）可以表示成C1，C2.。

Cm的并。

10.若图不是二连通，则存在割点，由于哈密尔顿图不存在割点，因而G是非哈密尔顿图。

若G是具有二分类（X,Y）的偶图，且|X|不等于|Y|，设X中所有点为x1，x2.。

xm，Y中的所有点为y1，y2.。

yn，若存在哈密尔顿图，则在哈密尔顿圈中必然存在X中的点与Y中的点相互交替出现，但是|X|不等于|Y|，则必然出现某两个点同属于|X|或者|Y|，但是G是偶图，属于同一集合的这样的两个点不可以相连，所以存在哈密尔顿圈矛盾，因而不存在哈密尔顿圈。

习题参考解答(图论部分)

习题参考解答(图论部分)

习题十1. 设G 是一个(n ，m)简单图。

证明：，等号成立当且仅当G 是完全图。

证明：（1）先证结论：因为G 是简单图，所以G 的结点度上限 max(d(v)) ≤ n-1, G 图的总点度上限为 max(Σ(d(v)) ≤ n ﹒max(d(v)) ≤ n(n-1) 。

根据握手定理，G 图边的上限为 max(m) ≤ n(n-1)/2,所以。

（2） =〉G 是完全图 因为G 具有上限边数，假设有结点的点度小于n-1,那么G 的总度数就小于上限值，边数就小于上限值，与条件矛盾。

所以，G 的每个结点的点度都为n-1，G 为完全图。

G 是完全图 =〉 因为G 是完全图，所以每个结点的点度为n-1, 总度数为n(n-1)，根据握手定理，图G 的边数 。

■2. 设G 是一个（n ，n +1）的无向图，证明G 中存在顶点u ，d （u ）≥3。

证明：反证法，假设,则G 的总点度上限为max(Σ(d(u)) ≤2 n ，根据握手定理，图边的上限为max(m) ≤ 2n/2=n 。

与题设m = n+1，矛盾。

因此，G 中存在顶点u ，d （u ）≥3。

■3．确定下面的序列中哪些是图的序列，若是图的序列，画出一个对应的图来: （1）（3，2，0，1，5）； （2）（6，3，3，2，2） （3）（4，4，2，2，4）； （4）（7，6，8，3，9，5）解：除序列（1）不是图序列外，其余的都是图序列。

因为在（1）中，总和为奇数，不满足图总度数为偶数的握手定理。

可以按如下方法构造满足要求的图：序列中每个数字ai 对应一个点，如果序列数字是偶数，那么就在对应的点上画ai/2个环，如果序列是奇数，那么在对应的点上画(ai-1)/2个环。

最后，将奇数序列对应的点两两一组，添加连线即可。

下面以（2）为例说明：(6 , 3, 3, 2, 2 ) 对应图G 的点集合V= { v 1,v 2,v 3,v 4,v 5}每个结点对应的环数(6/2, (3-1)/2, (3-1)/2, 2/2,2/2) = (3,1,1,1,1)将奇数3，3 对应的结点v 2,v 3一组，画一条连线其他序列可以类式作图，当然大家也可以画图其它不同的图形。

图论习题课

图论习题课
21
三、简答题(每小题5分，共20分)
2. 给出集合X={1,2,3,4,5,6}上的一个等价关系 R （3分）
并给出他们的等价类
（2分）
22
三、简答题(每小题5分，共20分)
3.集合A={3, 4, 12, 24, 36}, A在整除关系“|” 下构成一个偏序集（A, |），
请画出偏序集（A, |）的哈斯图。（5分）
3
习题
6(P209).在一个有n个人的宴会上，每个人至少有m 个朋友（2m n）。试证：有不少于m+1个人，使 得他们按某种方法坐在一张圆桌旁，每人的左右均是他 的朋友。
证明: 把n个人作为n个顶点，是朋友的顶点间连边构成图 图GG的每个顶点的度数都大于等于m 原题的意思是每个顶点的度数都不小于m的图必有长 度至少为m+1的圈。
是 m=
10(P228n).证明具有奇数个顶点的偶图不是哈密顿 图？
9
习题
1(P216).若图G不是连通图,则GC是连通图, 证明：
由于G不连通，假设G有两个分支，V1和V2，分别有m 和n个顶点。
在GC V1和V2任意两点间都有边； 对于任意顶点u和v,假如u和v在G中位于两个分支中， u和v在GC中必有边相连; 否则假设都位于V1中，设w是V2中顶点， u和v在GC 中都与w邻接，因次u与v之间有路。
......
31
17
考试题型
一、选择题 20分 二、判断题 10分 三、简答题 40分 四、证明题 15分 五、计算题 15分
18
一、填空题（每小题2分，共20分）
1. 集合的 表述方法能够引起悖论。
2. 自反关系在关系图中的特ห้องสมุดไป่ตู้是 。

图论习题

图论习题

第三章 平面图
7.若G的顶点数不少于11个，则G c 不是平面图 证明：ε (G ) + ε (G c ) = v(v − 1) 2 , 又ε (G ) ≤ 3v(G ) − 6 则ε (G c ) ≥ 1 （v 2 − 7v + 12） 2 当v ≥ 11时，ε (G c ) > 3v(G c ) − 6, 从而G c 不是平面图
第四章 匹配理论及其应用
• 2.树上是否可能有两个不同的完备匹配？为什么？ • 解：不可能。
设M1，M 2为两个不同的完备匹配，则M1 ⊕ M 2 ≠ φ 且T[M1 ⊕ M 2 ]中的每个顶点的度为2. 由例1.9可知，T中包含圈。这与T为树矛盾。
第五章 着色理论
• 1.求n顶轮的边色数 • hints：n-1
' '
第五章 着色理论
第一条边颜色不变，其余边两色互换。 直至vl −1处无i h 色，多i l -1色； 得出矛盾：v l -1v l 着i h 色; vl 处i h = i l 色出现至少三次； 从而G中i h 和i l -1色边的导出子图中含v l的分支不可能是奇圈， 从而得出矛盾。
第五章 着色理论
• 8. 4名老师4个班级上课问题。 • 计算，一天应分几节课？若每天8节课，需几 间教室？ • hints： ∆(G ) = 16, ε (G ) = 48
16 = 4 一天分4节课 5 48 = 2 需2间教室 5*8
若 13. δ是单图G顶的最小次数，证明；若δ > 1则存在δ − 1边着色， 使与每顶关联的边种有δ − 1种颜色。 h int s : 反证法：设C = (E1 , E 2 ,..., E δ −1 )为G的(δ − 1) − 最佳边着色 构造点列：v1 , v2 ,..., vh , vh +1 ,....., vl ,.... v1处无i 0色，v j v j +1着i j色，且在v j点处i j 色重复出现，仅一个i j-1色；h = i l i 着色调整：v j v j +1着i j-1色( j = 1,2,..., h) 奇圈，颜色互换：E( Eih ∪ Eik )(k = h + 1, h + 2,..., l − 2),

中科院研究生院图论讲义习题1

中科院研究生院图论讲义习题1

第一章习题1. 对任何简单图G ，(1) 证明：(1)()2G υυε−≤；(2)(1)()2G υυε−=当且仅当G K ν≅。

2. 证明：(1),()m n K mn ε=；(2) 若G 是完全二部图，则2()4G υε≤。

3. 图G 有21条边，12个3度顶点，其余顶点的度均为2，求图G 的阶数。

4. 证明：任何简单图必有至少两个顶点具有相等的度。

5. 设G 是简单图，求G 的所有不同的生成子图的个数（包括G 本身和空图）。

6. 证明：任何图中，奇度顶点的个数总是偶数（包括0）。

并由此证明：在任一次聚会上握过奇数次手的人必为偶数个。

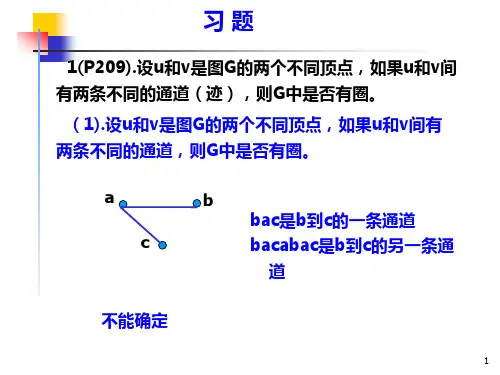
7. 证明或反证：如果u 和v 是图G 中仅有的具有奇数度的顶点，则G 包含一条u , v 路。

8. 证明：若4υ≥且1+=νε，则存在)(G V v ∈使得3)(≥v d 。

由此证明： n 个球队比赛（4n ≥），已赛完n +1场，则必定有一个球队已参加过至少3场比赛。

9. 在一个运动联盟中，将所有运动队组织成两个赛区，每个赛区有13个队，能否恰当安排比赛使得每个队在其所在赛区中进行9场比赛而与另一个赛区中的运动队进行4场比赛？10. 在平面上有n 个点12{,,,}n S x x x =⋅⋅⋅，其中任两个点之间的距离至少是1。

证明在这n 个点中，距离为1 的点对数不超过3n 。

11. 某次会议有n 人参加，其中有些人互相认识，但每两个互相认识的人，都没有共同的熟人，每两个互不认识的人都恰好有两个共同的熟人。

证明每一个参加者都有同样数目的熟人。

12. 在一个化学实验室里，有n 个药箱，其中每两个不同的药箱恰有一种相同的化学品，而且每种化学品恰好在两个药箱中出现，问：（1）每个药箱有几种化学品？（2）这n 个药箱中共有几种不同的化学品？13. 在一次舞会中，A 、B 两国留学生各(2)n n >人，A 国每个学生都与B 国一些(不是所有)学生跳过舞，B 国每个学生至少与A 国一个学生跳过舞。

图论大作业

图论大作业

《图论及其应用》大作业指导老师郝荣霞知行1503 徐鹏宇 152912002.1.9证明：若G是森林且恰有2k个奇点，则在G中有k条边不重的路P1,P2......P K,使得E(G)=E(P1) E(P2) ...... E(P K)。

证明：对奇点数k使用数学归纳法。

①当k=1时，G是森林，且有且只有2个奇点⇒G只能为一颗树，且G的所有奇度顶点为两个1度顶点⇒G是一条路⇒满足题设②假设当k=t时，结论成立。

接下来考虑k=t + 1时的情况。

在G中一个分支中取两个叶子点u与v，令P是连接该两个顶点的唯一路。

由于P上除u，v以外的点均被P经过两次，即G-P后除u，v以外的点奇偶性不变。

⇒则G–P是有2t个奇度顶点的森林⇒由归纳假设知，G–P可以分解为t条边不重合的路之并，即E(G-P)=E(P1) E(P2) ...... E(P t)。

⇒则G可分解为t+1条边不重合的路之并，即E(G)=E(P1) E(P2) ...... E(P t) E(P)。

⇒即证。

2.4.4证明：若e 是K n 的边，则τ（K n -e ）=（n-2）n n-3证明：由定理2.9：τ（K n ）=n n-2由于τ（K n -e ）=τ（K n ）-τ（含有e 的生成树棵树）现在需要求含有e 的生成树棵树，τ（含有e 的生成树棵树）=)1(21n 1-n 2-n n n ）（=2n n-3τ（K n -e ）=τ（K n ）-τ（含有e 的生成树棵树）=（n-2）n n-33.2.4证明：不是块的连通图至少有两个块，其中每个恰有一个割点。

证明：设G 为不是块的连通图，由于G 连通且不是块⇒G 有割点①当G 只有1个割点v 时，延割点分开，G1，G2内无割点，且连通，由块的定义知⇒G1,G2是块，且分别含一个割点v 。

②当G 含有2个及2个以上割点时，取相距距离最远的两个割点u 和v ，此时分G 为三部分G1,G2,G3。

图论习题参考答案

图论习题参考答案

二、应用题题0：（1996年全国数学联赛）有n（n≥6）个人聚会，已知每个人至少认识其中的[n/2]个人，而对任意的[n/2]个人，或者其中有两个人相互认识，或者余下的n-[n/2]个人中有两个人相互认识。

证明这n个人中必有3个人互相认识。

注：[n/2]表示不超过n/2的最大整数。

证明将n个人用n个顶点表示，如其中的两个人互相认识，就在相应的两个顶点之间连一条边，得图G。

由条件可知，G是具有n个顶点的简单图，并且有（1）对每个顶点x，)(xN G≥[n/2]；（2）对V的任一个子集S，只要S＝[n/2]，S中有两个顶点相邻或V-S中有两个顶点相邻。

需要证明G中有三个顶点两两相邻。

反证，若G中不存在三个两两相邻的顶点。

在G中取两个相邻的顶点x1和y1,记N G(x1)＝{y1,y2,……,y t}和N G(y1)={x1,x2,……,x k},则N G(x1)和N G(y1)不相交，并且N G(x1)（N G(y1)）中没有相邻的顶点对。

情况一；n=2r：此时[n/2]＝r，由（1）和上述假设，t=k=r且N G(y1)＝V-N G(x1)，但N G(x1)中没有相邻的顶点对，由（2），N G(y1)中有相邻的顶点对，矛盾。

情况二；n=2r+1: 此时[n /2]＝r ，由于N G (x 1)和N G (y 1)不相交，t ≥r,k ≥r,所以r+1≥t,r+1≥k 。

若t=r+1,则k=r ，即N G (y 1)=r ，N G (x 1)＝V-N G (y 1)，由（2），N G (x 1)或N G (y 1)中有相邻的顶点对，矛盾。

故k ≠r+1，同理t ≠r+1。

所以t=r,k=r 。

记w ∈V- N G (x 1) ∪N G (y 1),由（2），w 分别与N G (x 1)和N G (y 1)中一个顶点相邻，设wx i0∈E, wy j0∈E 。

若x i0y j0∈E ，则w ，x i0, y j0两两相邻，矛盾。

图论作业1

图论作业1

4. 证明：任何一个人群中至少有两个人认识的朋友数相同。
5. 证明：若 k 正则二部图具有二分类 V=V 1 UV 2 ，则|V 1 |=|V 2 |。
2/2
1/2
ห้องสมุดไป่ตู้
班级
姓名
学号
三、解答题 1. 设无向图 G 有 10 条边，3 度与 4 度顶点各 2 个，其余顶点度数均小于 3，问 G 中至少有 几个顶点？在最少顶点数的情况下，写出 G 的度序列，该度序列是一个图序列吗？
2. 设 G 与其补图的边数分别为 m 1 和 m 2 ，求 G 的阶数。
3. 设 G 为 n 阶简单无向图，n>2 且 n 为奇数，G 与其补图中度数为奇数的顶点个数是否相 等？并给出理由。
1 2 1 1 1
1 1 3 0 2
2 1 0 2 0
0 1 2 ， 0 2
则图 G 的边数为 。 5. 设 G 是 n 阶简单图，且不含完全子图 K 3 ，则其边数一定不会超过 。 6. 设 n 阶图 G 是具有 k 个分支的森林，则其边数为 。 7. 一棵树有 n i 个度数为 i 的结点，i=2,3,…,k，则它有 个度数为 1 的顶点。 8. K 5 的生成树的棵数为 。 二、选择题 1．关于图的度序列，下列命题错误的是( ) (A) 同构的两个图的度序列相同； (B) 非负整数序列(d 1 , d 2 ,…,d n )是图的度序列当且仅当 d 1 +d 2 +…+d n 是偶数； (C) 如果非负整数序列(d 1 , d 2 ,…,d n )是一棵树的度序列且 n≥2，那么序列中至少有两个 1； (D) 如果非负整数序列(d 1 , d 2 ,…,d n )是简单图的度序列， 那么在同构意义下只能确定一个图。 2. 对于序列(7, 5, 4, 3, 3, 2)，下列说法正确的是( ) (A) 是简单图的度序列; (B) 是非简单图的度序列; (C) 不是任意图的度序列; (D) 是图的唯一度序列。 3. 下列说法错误的是( ) (A) 若一个图中存在闭途径，则一定存在圈； (B) 偶图中不存在奇圈； (C) 无向图的顶点之间的连通关系一定是等价关系； (D) 存在非平凡简单图 ，使得每个顶点的度数互不相同。 4. 关于简单图的邻接矩阵 A，下列说法错误的是( ) (A) 矩阵 A 的行和等于该行对应顶点的度数； (B) 矩阵 A 的所有元素之和等于该图边数的 2 倍； (C) 不同构的两个图，它们的邻接谱一定不同； (D) 非连通图的邻接矩阵一定可以表示为准对角矩阵形式。 5. 图 G=(n, m)一定是树的是( ) (A) 连通图； (B) 无回路但添加一条边后有回路的图； (C) 每对顶点间都有路的图； (D) 连通且 m=n-1。

图论习题

图论习题
4 n
2 2 1 4 A 4 1 1 2 3 9 B 8
）
6
2
．已知在传输中，a、b、c、d、e、f 、g、h 出现的频率分别为 25%、15%、15%、10%、10%、9%、6%、10%， 编一个传输它们的最佳前缀码。
3
．有向图 D 如下图所示，用邻接矩阵法求 D 中长度为 3 的通路数和长度为 3 的回路数。
5. D=<V,E>
1 2 3 4 + 1 4 2 4 n n,m n
设图
三．判断题 1. 任一图 G 的△(G)必小于其结点数。 （ ） 2. 在 n 个结点的简单图 G 中，若 n 为奇数，则 G 与 G 的度为奇数的结点数相同。 （ ） 3. K 有 10 个生成子图。 （ ） 4. 图 G 和 G’同构当且仅当 G 和 G’的结点和边分别存在一一对应关系。 （ ） 5. 具有 3 个结点的有向完全图，含 4 条边的不同构的子图有 4 个。 （ ） 6. 3 个(4,2)无向简单图中，至少有 2 个同构。 （ ） 7. 若无向图中恰有 2 个度为奇数的结点，则这两个结点必连通。 （ ） 8. 在有向图中，结点间的可达关系是等价的。 （ ） （ ） 9. 若图 G 不连通，则 G 必连通。 10. 若图 G 的边 e 不包含在图 G 的某简单回路中，则 e 是 G 的割边。 （ ） 11. 若无向连通图中无回路，则其每条边均为割边。 （ ） 12. 若有向图 D 强连通，则 D 必为欧拉图。 （ ） 13. 若有向图 D 是欧拉图，则 D 必为强连通图。 （ ） 14. K 是哈密尔顿图。 （ ） 15. 任一(n,m)平面图，若 n≥3，则 m≤3n-6。 （ ） 16. 设 G=<V,E>，|V|≥11，则 G 或 G 是非平面图。 （ ） 17. 极大平面图必连通。 （ ） 18. 设 G=<V,E>为连通的简单平面图，若|V|≥3，则所有结点 v，有 deg(v) ≤5。 （ ） 19. 任何树都至少有两片树叶。 （ ） 20. 任何图 G=<V,E>都至少有一颗生成树。 （ ） 21. 图 G 是（m，n）连通图，要求 G 的一颗生成树，则要删去 G 中的 m-n 条边。 （ ） 22. 一个有向图 G 若仅有一个节点入度为 0，其余节点的入度全为 1，则 G 一定是有向树。 （ 23.{000,001,01,10,11}是一个前缀码。 （ ） （ ） 24.T 为完全 m 元树，有 t 片树叶，i 个分支点，则有关系式(m-1)i=t-1。 四．综合题 1. 求下面带权图中从 A 到 B 的最短路径，要求用图示给出求解过程，并计算它们的权值。

图论及其应用 第一章答案

图论及其应用 第一章答案

)2214(题后两个算法不作要求题，除第图的基本概念<1.>若G 是简单图，证明：()()2V G E G ⎛⎫≤ ⎪⎝⎭。

证明：()()1()()()1v Gd v V G d v V G V G ∈≤-∴≤-∑（当且仅当G 是完全图时取等号） 又11()()()()122v G E G d v V G V G ∈=≤-∑ ()()2V G E G ⎛⎫∴≤ ⎪⎝⎭。

<2.>设G 是(,)p q 简单图，且12p q -⎛⎫>⎪⎝⎭。

求证G 为连通图。

证明：反证法，假设G 为非连通图。

设G 有两个连通分支1G 和2G ，且112212()1,()1,V G p V G p p p p =≥=≥+= 则1212()()22p p E G E G q ⎛⎫⎛⎫+=≤+⎪ ⎪⎝⎭⎝⎭而1211221(1)(1)(1)(2)222222p p p p p p p p p -⎛⎫⎛⎫⎛⎫----+-=+-⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭2222221212121222()2()222p p p p p p p p p p +-+-+-+++-==12(1)(1)0p p =--≤（因为121,1p p ≥≥），矛盾。

<3.>超图H 是有序二元组((),())V H E H ，其中()V H 是顶点非空有限集合，()E H 是()V H 的非空子集簇，且()()i i E E H E V H ∈=。

其中，()E H 中的元素i E 称为超图的边，没有相同边的超图称为简单超图。

证明：若H 是简单超图，则21υε≤-，其中,υε分别是H 的顶点数和边数。

证明：()V H υ=，有一条边的子集个数为1υ⎛⎫ ⎪⎝⎭，有i 条边的子集个数为,1,,.i n i υ⎛⎫= ⎪⎝⎭又02,211i i υυυυυυυ=⎛⎫⎛⎫⎛⎫=∴++=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∑ 。

<4.>若G 是二部图，则2()()4V G E G ≤。

图论参考答案

图论参考答案

图论参考答案图论参考答案图论作为一门数学分支，研究的是图的性质与关系。

图由节点（顶点）和连接节点的边组成，它可以用来解决许多实际问题，如网络规划、社交网络分析等。

本文将从图的基本概念、图的表示方法、图的遍历算法以及图的应用等方面进行探讨。

一、图的基本概念图由节点和边构成，节点表示对象，边表示节点之间的关系。

图可以分为有向图和无向图两种类型。

在有向图中，边有方向，表示从一个节点到另一个节点的箭头；而在无向图中，边没有方向，表示节点之间的双向关系。

图中的节点可以用来表示不同的实体，如人、地点、物品等。

而边则表示节点之间的关系，可以是实体之间的联系、交互或者依赖关系等。

图的度是指与节点相连的边的数量。

在无向图中，节点的度等于与之相连的边的数量；而在有向图中，节点的度分为入度和出度，入度表示指向该节点的边的数量，出度表示从该节点出发的边的数量。

二、图的表示方法图可以使用邻接矩阵和邻接表两种方式进行表示。

邻接矩阵是一个二维数组，其中的元素表示节点之间的关系。

如果节点i和节点j之间有边相连，则邻接矩阵中的第i行第j列的元素为1；否则为0。

邻接矩阵的优点是可以快速判断两个节点之间是否有边相连，但是对于稀疏图来说，会浪费大量的空间。

邻接表是一种链表的形式，其中每个节点都有一个指针指向与之相连的节点。

邻接表的优点是可以有效地节省空间，适用于稀疏图。

但是在判断两个节点之间是否有边相连时，需要遍历链表，效率较低。

三、图的遍历算法图的遍历算法是指以某个节点为起点，按照一定的规则依次访问图中的所有节点。

深度优先搜索（DFS）是一种常用的图遍历算法。

它的思想是从起始节点开始，沿着一条路径一直访问到最后一个节点，然后回溯到上一个节点，继续访问其他路径。

DFS可以用递归或者栈来实现。

广度优先搜索（BFS）是另一种常用的图遍历算法。

它的思想是从起始节点开始，先访问所有与起始节点直接相连的节点，然后再依次访问与这些节点相连的节点。

图论及其应用1-3章习题答案(电子科大) (1)

图论及其应用1-3章习题答案(电子科大) (1)

学号：201321010808 姓名：马涛习题14．证明图1-28中的两图是同构的证明 将图1-28的两图顶点标号为如下的(a)与(b)图作映射f : f(v i )→u i (1≤ i ≤ 10)容易证明，对∀v i v j ∈E((a)),有f(v i v j )=u i u j ∈E((b)) (1≤ i ≤ 10, 1≤j ≤ 10 ) 由图的同构定义知，图1-27的两个图是同构的。

6．设G 是具有m 条边的n 阶简单图。

证明：m =⎪⎪⎭⎫⎝⎛2n 当且仅当G 是完全图。

证明 必要性 若G 为非完全图，则∃ v ∈V(G),有d(v)< n-1 ⇒ ∑ d(v) < n(n-1) ⇒ 2m <n(n-1)⇒ m < n(n-1)/2=⎪⎪⎭⎫⎝⎛2n , 与已知矛盾！充分性 若G 为完全图，则 2m=∑ d(v) =n(n-1) ⇒ m= ⎪⎪⎭⎫⎝⎛2n 。

9.证明：若k 正则偶图具有二分类V = V 1∪V 2，则 | V 1| = |V 2|。

(a)v 1v 2 v 3 v 4v 5 v 6v 7v 8 v 9v 10 u 1 u 2u 3u 4u 5 u 6 u 7 u 8 u 9 u 10 (b)证明 由于G 为k 正则偶图，所以，k | V 1 | =m = k | V 2 | ⇒ ∣V 1∣= ∣V 2 ∣。

12.证明：若δ≥2，则G 包含圈。

证明 只就连通图证明即可。

设V(G)=｛v 1,v 2,…,v n ｝,对于G 中的路v 1v 2…v k ,若v k 与v 1邻接，则构成一个圈。

若v i1v i2…v in 是一条路，由于δ≥ 2，因此，对v in ，存在点v ik 与之邻接，则v ik ⋯v in v ik 构成一个圈 。

17.证明：若G 不连通，则G 连通。

证明 对)(,_G V v u ∈∀,若u 与v 属于G 的不同连通分支，显然u 与v 在_G 中连通；若u 与v 属于g 的同一连通分支，设w 为G 的另一个连通分支中的一个顶点，则u 与w ，v 与w 分别在_G 中连通，因此，u 与v 在_G 中连通。

图论期末考试题库及答案

图论期末考试题库及答案

图论期末考试题库及答案一、单项选择题1. 图论的创始人是（）。

A. 欧拉B. 莱布尼茨C. 牛顿D. 高斯答案：A2. 在图论中，一个图的顶点集合为空，但边集合不为空的图称为（）。

A. 空图B. 完全图C. 树D. 多重图答案：A3. 如果一个图的任意两个顶点之间都存在一条路径，则称该图为（）。

A. 连通图B. 强连通图C. 弱连通图D. 无环图答案：A4. 在图论中，一个图的边的集合可以划分为若干个不相交的路径，使得图中的每个顶点恰好属于其中一条路径，这样的图称为（）。

A. 欧拉图B. 哈密顿图C. 树答案：C5. 图论中，一个图的边的集合可以划分为若干个不相交的回路，使得图中的每个顶点恰好属于其中一条回路，这样的图称为（）。

A. 欧拉图B. 哈密顿图C. 树D. 环答案：A二、多项选择题1. 下列哪些是图论中的基本术语（）。

A. 顶点B. 边D. 权重答案：ABCD2. 在图论中，以下哪些图是无向图（）。

A. 完全图B. 树C. 多重图D. 有向图答案：ABC3. 图论中，以下哪些图是连通图（）。

A. 完全图B. 树C. 多重图D. 空图答案：ABC三、填空题1. 图论中，一个图的顶点集合为V，边集合为E，那么图可以表示为G=（）。

答案：(V, E)2. 如果一个图的任意两个顶点之间都存在一条路径，则称该图为（）。

答案：连通图3. 在图论中，一个图的边的集合可以划分为若干个不相交的路径，使得图中的每个顶点恰好属于其中一条路径，这样的图称为（）。

答案：树四、简答题1. 请解释什么是图论中的“完全图”？答案：完全图是指图中每一对不同的顶点之间都恰好有一条边相连的图。

在完全图Kn中，n个顶点两两相连，共有n(n-1)/2条边。

2. 请解释什么是图论中的“欧拉路径”和“欧拉回路”？答案：欧拉路径是指图中存在一条路径，该路径恰好经过每条边一次。

欧拉回路是指图中存在一条回路，该回路恰好经过每条边一次。

五、计算题1. 给定一个图G=(V, E)，其中V={A, B, C, D, E}，E={(A, B), (B, C), (C, D), (D, E), (E, A), (A, C)}，请判断该图是否为连通图，并说明理由。

22趣味的图论问题(1)

22趣味的图论问题(1)
上面的等式右边是一个偶数，左边是奇顶点的总个数， 所以奇顶点的个数为偶数。
2、图的连通性 在图G中，一个由不同的边组成的序列e1、e2、……、er，如 果其中ei是连接顶点vi与vi+1的边( i=1、2、3、……、r) 我们称这个序列为从v1到vr+1的链，数r叫做链长，顶点 v1 与vr+1叫做链的端点。 如果图G是简单图，这个链可以记为（e1、e2、……、er） 如右图，其中的边e1、e2、e3、e4、e5、e6 e e e e e e 就组成一个链。 如果一个链的两个端点vi与vi+1重 合，我们称这个链为一个圈。
e1 e3 e4 e5 e2 e6
初 等 数 学 专 题 研 究
在链的定义中，并不要求顶点v1、v2、……、vr、 vr+1 互不相 同，如果出现在这条链中的顶点互不相同，这样的链叫做初级 链。一条链的首尾两个端点重合时，这样的初级链叫初级圈。
下面的图就是不连通的
初
这样一个图G能否“一笔画”等价于这个图是否是一个链 （不回到出发点）或一个圈（回到出发点） 3、“一笔画”问题的解决 定理2：有限图连通G是一条链（即可以一笔画成）的充分必 要条件是G的奇顶点的个数等于0或2。并且当且仅当奇顶点 个数为0时，连通图G是一个圈（孤立点也可以看成圈）。
趣味的图论问题（ 第二十二讲 趣味的图论问题（一） 一、基本概念
初 等
1、什么是图？
数 学
v2 v1 v3 v5 v4
v10 v8 v6
专
v9
题 研 究
v7
返回
趣味的图论问题 一、基本概念 1、什么是图？ 前面的图形就是图论中的研究对象——图。它有若干个不同 的点v1、v2、……，我们称之为顶点，或简称为点。这些顶 点中有一些是用直线段或曲线段连接的，我们称这些直线段 或曲线段为边。 上图中v1与v2之间有两条边，v2与v3之间有一条边，v2与v4 之间没有边，……等等。 上图中v1与v1本身也有边相连，这样的边叫环。 图

运筹学基础-图论方法(1)

运筹学基础-图论方法(1)

回路：若起始点和终点是同一个点的路称为回路。 连通图：一个图中，任意两个顶点至少存在一条链，则称这样的图 为连通图。否则称为不连通的。
图的名词和基本概念
次：与一个点相关联的边的数目称为次, 如v1 的次为2， v5的次 为3，次为奇数的点称为奇点，次为偶数的点称为偶点，次为0 的点称为孤立点，如v6 悬挂节点: 次为1的点称为悬挂节点: v1 e1 e 5 v3 e2 v5 e7 e4 e6 e3 v4 v6 v2
1 1
利用EXCEL求起点到终点的最短路径 利用EXCEL求起点到终点的最短路径
第三步： 第三步：定义最小路线运行方案
最小路线物运行方案
v1 v2 v3 v4 v5 v6 v1 v2 v3 v4 v5 v6 v7
流入 结点流 结点流限制 0 0 0 0 0 0 0 0 0 0 0 0 0 0
v7
流出
100 600
3
500
600
5
400 1100
7 2
900
此为最小树杈，最小线路长度为2400 此为最小树杈，最小线路长度为2400
练习：求最小树杈 v3 5 6 v1 5 v2 2 v4 1 7 3 4 4 v6 v5
破圈法答案
v3 6 v1 5 v2 1
5 7 3
v5 4 v6 4 v4
2
避圈法答案
弧：若点与点之间的连线有方向，称为弧，由此构成的图为有向图。 环：如果边的两个端点相重，称该边为环，如e10；如果两个端点之 间的边多于一条, 称为具有多重边，如[v2, v4] ,无环，无多重边的图为 简单图。
图的名词和基本概念
v1 e4 v3 e1 v5 e5 e3 e6 e9 e2 e7 v4 e10 v2 e8 v6 e1 e5 v5 e7 e6 e3 v6 v1 e2 v2 e9 e10 e8 v7

图论习题答案1

图论习题答案1

图论习题课作业1，3，6，8，10By jgy•作业1：第一章：1,2,4,12,20,29,35•作业3：第二章：14,28,30第三章：1,5,7,8•作业6：第五章：18,33•作业8：第六章：6,12,17•作业10：第七章10 第八章5,6,8作业1|E(G)|,2|E(G)|2G υυ⎛⎫≤ ⎪⎝⎭⎛⎫⎪⎝⎭1.1 举出两个可以化成图论模型的实际问题略1.2 证明其中是单图证明：（思路）根据单图无环无重边的特点，所以 最大的情形为任意两个顶点间有一条边相连，即极 端情况为。

•1.20证明每顶皆二次的连通图是圈•证明：（思路）易证每顶皆二次的连通图中有圈。

设图中最大圈为H，假设除H外还有其他顶点集U，任取u k，因为连通，u k 与H中任意顶均有一条道路，存在H中一顶h j与u k相邻，则h j为三次。

•1.29 证明二分图的子图是二分图•方法一：•定理1.2 图G是二分图当且仅当G中无奇圈•反证：设二分图为G，子图为S，假设S非二分图，由定理1.2知S中有奇圈，则G中有奇圈，这与G是二分图矛盾。

•方法二：•（思路）定义：V(G) = X U Y, X n Y=空, 且X中任二顶不相邻，且Y中任二顶不相邻。

•证明：•(a)第一个序列考虑度数7,第二个序列考虑6,6,2•(b)将顶点v分成两部分v’和v’’•v’ = {v|v= vi , 1≤ i≤ k},•v’’ = {v|v= vi , k< I ≤ n}•以v’点为顶的原图的导出子图度数之和小于•然后考虑剩下的点贡献给这k个点的度数之和最大可能为•2.14 画出带权0.2 0.17 0.13 0.1 0.1 0.08 0.06 0.06 0.07 0.03的huffman 树•排序：①0.03 0.06 0.06 0.07 0.08 0.1 0.1 0.13 0.17 0.2•②0.06 0.07 0.08 0.090.1 0.1 0.13 0.17 0.2•③0.08 0.090.1 0.1 0.130.13 0.17 0.2•④0.1 0.10.130.13 0.170.17 0.2•⑤0.130.13 0.170.17 0.20.2•⑥0.170.17 0.20.2 0.26•⑦0.20.20.26 0.34•⑧0.26 0.34 0.4•⑨0.4 0.60.030.060.090.030.060.090.060.070.130.030.060.090.060.070.130.170.08①③②0.030.060.090.060.070.130.170.080.10.10.20.130.26Huffman 树为0.170.340.20.40.61•2.28证明T是顶数至少为2的树，则T是二分图•证明1：•定理1.2 图G是二分图当且仅当G中无奇圈•T是树，所以T中无奇圈，由‘图G是二分图当且仅当G中无奇圈’知T是二分图。

哈工大图论习题

哈工大图论习题

哈⼯⼤图论习题1．画出具有4个顶点的所有⽆向图(同构的只算⼀个)。

2．画出具有3个顶点的所有有向图(同构的只算⼀个)。

3．画出具有4个、6个、8个顶点的三次图。

4．某次宴会上，许多⼈互相握⼿。

证明：握过奇数次⼿的⼈数为偶数(注意，0是偶数)。

5．证明：哥尼斯堡七桥问题⽆解。

6．设u与v是图G的两个不同顶点。

若u与v间有两条不同的通道(迹)，则G中是否有回路？7．证明：⼀个连通的(p，q)图中q ≥p-1。

8．设G是⼀个(p，q)图，δ(G)≥[p/2]，试证G是连通的。

9．证明：在⼀个连通图中，两条最长的路有⼀个公共的顶点。

10．在⼀个有n个⼈的宴会上，每个⼈⾄少有m个朋友(2≤m≤n)。

试证：有不少于m+1个⼈，使得他们按某种⽅法坐在⼀张圆桌旁，每⼈的左、右均是他的朋友。

11．⼀个图G是连通的，当且仅当将V划分成两个⾮空⼦集V1和V2时，G总有⼀条联结V1的⼀个顶点与V2的⼀个顶点的边。

12．设G是图。

证明：若δ(G)≥ 2，则G包含长⾄少是δ(G)+1的回路。

13．设G是⼀个(p，q)图，证明：(a)q≥p，则G中有回路；(b)若q≥p+4，则G包含两个边不重的回路。

14．证明：若图G不是连通图，则G c 是连通图。

15．设G是个(p，q)图，试证：(a)δ(G)·δ(G C)≤[(p-1)/2]([(p+1)/2]+1)，若p≡0，1，2(mod 4)(b) δ(G)·δ(G C)≤[(p-3)/2]·[(p+1)/2]，若p≡3(mod 4)16．证明：每⼀个⾃补图有4n或4n+1个顶点。

17．构造⼀个有2n个顶点⽽没有三⾓形的三次图，其中n≥3。

18.给出⼀个10个顶点的⾮哈密顿图的例⼦，使得每⼀对不邻接的顶点u和v，均有degu+degv≥919．试求Kp中不同的哈密顿回路的个数。

20．试证：图四中的图不是哈密顿图。

21．完全偶图Km，n为哈密顿图的充分必要条件是什么？22．菱形12⾯体的表⾯上有⽆哈密顿回路？23．设G是⼀个p(p≥3)个顶点的图。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第三章
1.证明： 必要性：
v 是连通图G 的割边， 则
， 至少有两个连通
分支。

设其中一个连通分支顶点集合为V1,另外连通分支顶点集合为V2,即V1与V2构成V 的划分。

对于任意的u ∈V1, v ∈V2，如果割边e 不在某一条（u ，v ）路上，那么，该路也是连接G-e 中的u 与v 的路，这与u,v 处于G-v 的不同分支矛盾。

“充分性”
若e 不是图G 的割边，那么G-v 连通，因此在G-v 中存在u,v 路，当然也是G 中一条没有经过边e 的u,v 路。

矛盾。

7.证明： v 是单图G 的割点，则G-v 至少两个连通分支。

现任取 , 如果x,y 在G-v 的同一分支中，令u 是与x,y 处于不同分支的点，那么，通过u ，可说明，x 与y 在G-v 的补图中连通。

若x,y 在G-v 的不同分支中，则它们在G-v 的补图中邻接。

所以，若v 是G 的割点，则v 不是其补图的割点。

9.连通图G 的一个子图B 称为是G 的一个块，如果(1), 它本身是块；(2), 若没有真包含B 的G 的块存在。

又由于对于阶数至少是3的
()()G e G ωω->
图G是块当且仅当G无环并且任意两点都位于同一圈上。

根据题意，对于阶数至少是3的图G，由于G没有偶圈，所以G的每个块的点可以在奇圈上，如果不在奇圈上，则块只能是K2，否则如果不是K2的话，该子图将存在割点，该子图就不是块。

得证。

16.（1）
（2）
（3）
第四章3. （1）既是欧拉闭迹又是哈密尔顿圈
（2）
（3）
（4）
7.由于图没有奇度顶点，所以是欧拉图，又定理1可得，图G的边集可以划分为圈C1，C2，。

Cm，所以E（G）可以表示成C1，C2.。

Cm的并。

10.若图不是二连通，则存在割点，由于哈密尔顿图不存在割点，因而G是非哈密尔顿图。

若G是具有二分类（X,Y）的偶图，且|X|不等于|Y|，设X中所有点为x1，x2.。

xm，Y中的所有点为y1，y2.。

yn，若存在哈密尔顿图，则在哈密尔顿圈中必然存在X中的点与Y中的点相互交替出现，但是|X|不等于|Y|，则必然出现某两个点同属于|X|或者|Y|，但是G是偶图，属于同一集合的这样的两个点不可以相连，所以存在哈密尔顿圈矛盾，因而不存在哈密尔顿圈。

12. 证明：在G之外加上一个新点v,把它和G的其余各点连接得图G1
G1的度序列为：(d1+1,d2+1,…,dn+1, n)
由条件：不存在小于(n+1)/2的正整数m,使得dm+1≦m,且dn-m+1+1<n-m+1=(n+1)-m。

于是由度序列判定定理知：G1是H图，得G有H路。

第五章
1.（1）证明一：
证明每个k方体都是k正则偶图。

事实上，由k方体的构造：k方体有2k个顶点，每个顶点可以用长度为k的二进制码来表示，两个顶点连线当且仅当代表两个顶点的二进制码只有一位坐标不同。

如果我们划分k方体的2k个顶点，把坐标之和为偶数的顶点归入X，否则归入Y。

显然，X中顶点互不邻接，Y中顶点也如此。

所以k方体是偶图。

又不难知道k方体的每个顶点度数为k,所以k方体是k正则偶图。

由推论：k方体存在完美匹配。

（2）我们用归纳法求K2n和Kn,n中不同的完美匹配的个数。

K2n的任意一个顶点有2n-1种不同的方法被匹配。

所以K2n的不同
完美匹配个数等于(2n-1)K2n-2,如此推下去，可以归纳出K2n的不同完美匹配个数为：(2n-1)!!
同样的推导方法可归纳出K n, n的不同完美匹配个数为：n!
2. 证明：若不然，设M1与M2是树T的两个不同的完美匹配，那么M1ΔM2≠Φ,且T[M1ΔM2]每个非空部分顶点度数为2，即它存在圈，于是推出T中有圈，矛盾。

6.证明：由习题5第一题知：K2n的不同完美匹配的个数为(2n-1)!!。

所以，K2n的一因子分解数目为(2n-1)!!
7.将K9进行2因子分解，四个圈为
C1=p9 p1 p8 p2 p7 p3 p6 p4 p5 p9
C2=p9 p2 p1 p3 p8 p4 p7 p5 p6 p9
C3=p9 p3 p2 p4 p1 p5 p8 p6 p7 p9
C4=p9 p4 p3 p5 p2 p6 p1 p7 p8 p9
13. 最小权值和是30
19. 证明：K4n+1= K 2(2n)+1 , 所以，可以分解为2n个边不重的2
因子之和。

而任意2个2因子可以并成一个4因子。

所以，共可以并成n个4因子。

即K4n+1可以分解为n个4因子的和。