2020东莞中考

2020年东莞市初中毕业生水平考试《数学》参考答案一、选择题：1-5CBDCA 6-10CBDAD二、填空题： 11.3 12.10 13.3 14.110°15.5 16.7 17.64（填62亦可） 三、解答题（一）18.解：原式122212=--+⨯-4=-19.解：原式2(1)1(1)(1)x x x x -=⋅--1x =当23x =时，原式323==20.解：（1）如图，EF 为AB 的垂直平分线；（2）∵EF 为AB 的垂直平分线∴152AE AB ==，90AEF ∠=︒∵在Rt ABC ∆中，8AC =，10AB =∴221086BC =-=∵90C AEF ∠=∠=︒，A A ∠=∠∴AFE ABC ∆∆∽∴AE EFAC BC =，即586EF=∴154EF = 四、解答题（二） 21.解：（1）108°（2）（3）∴机会均等的结果有AB 、AC 、AD 、BA 、BC 、BD 、CA 、CB 、CD 、DA 、DB 、DC 等共12种情况，其中所选的项目恰好是A 和B 的情况有2种；∴P （所选的项目恰好是A 和B ）21126==. 22.解：（1）设乙厂每天能生产口罩x 万只，则甲厂每天能生产口罩1.5x 万只，依题意，得：606051.5x x-=， 解得：4x =，经检验，4x =是原方程的解，且符合题意，∴甲厂每天可以生产口罩：1.546⨯=（万只）.答：甲、乙厂每天分别可以生产6万和4万只口罩.（3）设应安排两个工厂工作y 天才能完成任务，依题意，得：()64100y +≥，解得：10y ≥.答：至少应安排两个工厂工作10天才能完成任务.23.（1）证明：过点O 作OM BC ⊥，交AD 于点M ，∴MC MB =，90OMA ∠=︒，∵OA OD =，OM AD ⊥，∴MA MD =∴MA MB MD MC -=-，即AB CD =.又∵OA OD =，OB OC =，∴()OAB ODC SSS ∆∆≌.（2）解：连OE ，设半径OE r =，∵O 与AE 相切于点E ，∴90OEA ∠=︒，又∵90EAD ∠=︒，90OMA ∠=︒，∴四边形AEOM 为矩形，∴4OM AE ==，OE AM r ==，在Rt OBM ∆中，222BM OM OB +=，即222(2)4r r -+=，∴5r =.即O 的半径为5.五、解答题（三）24.（1）证明：∵ED 为AC 平移所得，∴//AC ED ，AC ED =，∴四边形ACDE 为平行四边形，∴AE CD =，在Rt ABC ∆中，点E 为斜边AB 的中点，∴AE CE BE ==，∴CD BE =.（2）证明：∵四边形ACDE 为平行四边形，∴//AE CD ，即//CD BE ，又∵CD BE =，∴四边形BECD 为平行四边形，又∵CE BE =，∴四边形BECD 为菱形.（3）解：在菱形BECD 中，点M 为DE 的中点，又10DE AC ==， ∴152ME DE ==， ∵//AC DE ，∴18090CEM ACB ∠=︒-∠=︒，ACE CEM ∠=∠，∴在Rt CME ∆中，5cos 13ME CEM CE ∠==， 即5cos 13ME ACE CE ∠==， ∴135135CE =⨯=， 在平行四边形ACDE 中，点N 为CE 的中点， ∴1 6.52MN CE ==. 25.解：（1）∵对称轴12(1)b x =-=-⨯-， ∴2b =-，∴223y x x =--+ 当0y =时，2230x x --+=，解得13x =-，21x =，即(3,0)A -，(1,0)B ，∴1(3)4AB =--=.（2）经过点(3,0)A -和(0,3)C 的直线AC 关系式为3y x =+，∴点D 的坐标为(,3)m m +.在抛物线上的点E 的坐标为()2,23m m m --+，∴()2223(3)3DE m m m m m =--+-+=--， ∴111222ACE S DE F DE OF DE OA ∆=⋅⋅+⋅⋅=⋅⋅ ()2213933222m m m m =⋅--⋅=--，当9323222m-=-=-⎛⎫⨯- ⎪⎝⎭时，ACES∆的最大值是233932722228⎛⎫⎛⎫-⨯--⨯-=⎪ ⎪⎝⎭⎝⎭，∴点D的坐标为33,322⎛⎫--+⎪⎝⎭，即33,22⎛⎫-⎪⎝⎭（3）连EF，情况一：如图，当//CE AF时，ADF CDE∆∆∽，当3y=时，2233x x--+=，解得1x=，22x=-，∴点E的横坐标为－2，即点D的横坐标为－2，∴2m=-情况二：∵点(3,0)A-和(0,3)C，∴OA OC=，即45OAC∠=︒.如图，当ADF EDC∆∆∽时，45OAC CED∠=∠=︒，90AFD DCE∠=∠=︒，即EDC∆为等腰直角三角形，过点C作CG DE⊥，即点CG为等腰Rt EDC∆的中线，∴22mDE CG==-，3DF m=+，∴EF DE DF=+，即22323m m m m--+=-++，解得1m=，0m=（舍去）综述所述，当1m=-或－2时，ADF∆与CDE∆相似.【若缺失公式、图片现象属于系统读取不成功，文档内容齐全完整，请放心下载。

2020年广东省东莞市中考数学试卷一、选择题（本大题10小题，每小题3分，共30分）在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑．1．（3分）9的相反数是（ ）A ．﹣9B ．9C ．19D ．−192．（3分）一组数据2，4，3，5，2的中位数是（ ）A ．5B ．3.5C ．3D ．2.53．（3分）在平面直角坐标系中，点（3，2）关于x 轴对称的点的坐标为（ ）A ．（﹣3，2）B ．（﹣2，3）C ．（2，﹣3）D ．（3，﹣2）4．（3分）若一个多边形的内角和是540°，则该多边形的边数为（ ）A ．4B ．5C ．6D ．75．（3分）若式子√2x −4在实数范围内有意义，则x 的取值范围是（ ）A ．x ≠2B ．x ≥2C ．x ≤2D ．x ≠﹣26．（3分）已知△ABC 的周长为16，点D ，E ，F 分别为△ABC 三条边的中点，则△DEF 的周长为（ ）A ．8B ．2√2C ．16D ．47．（3分）把函数y ＝（x ﹣1）2+2图象向右平移1个单位长度，平移后图象的函数解析式为（ ）A ．y ＝x 2+2B ．y ＝（x ﹣1）2+1C ．y ＝（x ﹣2）2+2D ．y ＝（x ﹣1）2+38．（3分）不等式组{2−3x ≥−1，x −1≥−2(x +2)的解集为（ ） A ．无解 B ．x ≤1 C ．x ≥﹣1 D ．﹣1≤x ≤19．（3分）如图，在正方形ABCD 中，AB ＝3，点E ，F 分别在边AB ，CD 上，∠EFD ＝60°．若将四边形EBCF 沿EF 折叠，点B ′恰好落在AD 边上，则BE 的长度为（ ）A ．1B ．√2C ．√3D ．2 10．（3分）如图，抛物线y ＝ax 2+bx +c 的对称轴是直线x ＝1，下列结论：①abc ＞0；②b 2﹣4ac ＞0；③8a +c ＜0；④5a +b +2c ＞0，正确的有（ ）A ．4个B ．3个C ．2个D ．1个二、填空题（本大题7小题，每小题4分，共28分）请将下列各题的正确答案填写在答题卡相应的位置上．11．（4分）分解因式：xy ﹣x ＝ ．12．（4分）如果单项式3x m y 与﹣5x 3y n 是同类项，那么m +n ＝ ．13．（4分）若√a −2+|b +1|＝0，则（a +b ）2020＝ ．14．（4分）已知x ＝5﹣y ，xy ＝2，计算3x +3y ﹣4xy 的值为 ．15．（4分）如图，在菱形ABCD 中，∠A ＝30°，取大于12AB 的长为半径，分别以点A ，B 为圆心作弧相交于两点，过此两点的直线交AD 边于点E （作图痕迹如图所示），连接BE ，BD ．则∠EBD 的度数为 ．16．（4分）如图，从一块半径为1m 的圆形铁皮上剪出一个圆周角为120°的扇形ABC ，如果将剪下来的扇形围成一个圆锥，则该圆锥的底面圆的半径为 m ．17．（4分）有一架竖直靠在直角墙面的梯子正在下滑，一只猫紧紧盯住位于梯子正中间的老鼠，等待与老鼠距离最小时扑捉．把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点，模型如图，∠ABC ＝90°，点M ，N 分别在射线BA ，BC 上，MN 长度始终保持不变，MN＝4，E为MN的中点，点D到BA，BC的距离分别为4和2．在此滑动过程中，猫与老鼠的距离DE的最小值为．三、解答题（一）（本大题3小题，每小题6分，共18分）18．（6分）先化简，再求值：（x+y）2+（x+y）（x﹣y）﹣2x2，其中x=√2，y=√3．19．（6分）某中学开展主题为“垃圾分类知多少”的调查活动，调查问卷设置了“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级，要求每名学生必选且只能选其中一个等级，随机抽取了120名学生的有效问卷，数据整理如表：等级非常了解比较了解基本了解不太了解人数（人）247218x （1）求x的值；（2）若该校有学生1800人，请根据抽样调查结果估算该校“非常了解”和“比较了解”垃圾分类知识的学生共有多少人？20．（6分）如图，在△ABC中，点D，E分别是AB、AC边上的点，BD＝CE，∠ABE＝∠ACD，BE与CD相交于点F．求证：△ABC是等腰三角形．四、解答题（二）（本大题3小题，每小题8分，共24分）21．（8分）已知关于x，y的方程组{ax+2√3y=−10√3，x+y=4与{x−y=2，x+by=15的解相同．（1）求a，b的值；（2）若一个三角形的一条边的长为2√6，另外两条边的长是关于x的方程x2+ax+b＝0的解．试判断该三角形的形状，并说明理由．22．（8分）如图1，在四边形ABCD 中，AD ∥BC ，∠DAB ＝90°，AB 是⊙O 的直径，CO平分∠BCD ．（1）求证：直线CD 与⊙O 相切；（2）如图2，记（1）中的切点为E ，P 为优弧AÊ上一点，AD ＝1，BC ＝2．求tan ∠APE 的值．23．（8分）某社区拟建A ，B 两类摊位以搞活“地摊经济”，每个A 类摊位的占地面积比每个B 类摊位的占地面积多2平方米．建A 类摊位每平方米的费用为40元，建B 类摊位每平方米的费用为30元．用60平方米建A 类摊位的个数恰好是用同样面积建B 类摊位个数的35． （1）求每个A ，B 类摊位占地面积各为多少平方米？（2）该社区拟建A ，B 两类摊位共90个，且B 类摊位的数量不少于A 类摊位数量的3倍．求建造这90个摊位的最大费用．五、解答题（三）（本大题2小题，每小题10分，共20分）24．（10分）如图，点B是反比例函数y=8x（x＞0）图象上一点，过点B分别向坐标轴作垂线，垂足为A，C．反比例函数y=kx（x＞0）的图象经过OB的中点M，与AB，BC分别相交于点D，E．连接DE并延长交x轴于点F，点G与点O关于点C对称，连接BF，BG．（1）填空：k＝；（2）求△BDF的面积；（3）求证：四边形BDFG为平行四边形．25．（10分）如图，抛物线y=3+√36x2+bx+c与x轴交于A，B两点，点A，B分别位于原点的左、右两侧，BO＝3AO＝3，过点B的直线与y轴正半轴和抛物线的交点分别为C，D，BC=√3CD．（1）求b，c的值；（2）求直线BD的函数解析式；（3）点P在抛物线的对称轴上且在x轴下方，点Q在射线BA上．当△ABD与△BPQ 相似时，请直接写出所有满足条件的点Q的坐标．2020年广东省东莞市中考数学试卷参考答案与试题解析一、选择题（本大题10小题，每小题3分，共30分）在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑．1．（3分）9的相反数是（ ）A ．﹣9B ．9C ．19D ．−19【解答】解：9的相反数是﹣9，故选：A ．2．（3分）一组数据2，4，3，5，2的中位数是（ ）A ．5B ．3.5C ．3D ．2.5【解答】解：将数据由小到大排列得：2，2，3，4，5，∵数据个数为奇数，最中间的数是3，∴这组数据的中位数是3．故选：C ．3．（3分）在平面直角坐标系中，点（3，2）关于x 轴对称的点的坐标为（ ）A ．（﹣3，2）B ．（﹣2，3）C ．（2，﹣3）D ．（3，﹣2）【解答】解：点（3，2）关于x 轴对称的点的坐标为（3，﹣2）．故选：D ．4．（3分）若一个多边形的内角和是540°，则该多边形的边数为（ ）A ．4B ．5C ．6D ．7【解答】解：设多边形的边数是n ，则（n ﹣2）•180°＝540°，解得n ＝5．故选：B ．5．（3分）若式子√2x −4在实数范围内有意义，则x 的取值范围是（ ）A ．x ≠2B ．x ≥2C ．x ≤2D ．x ≠﹣2【解答】解：∵√2x −4在实数范围内有意义，∴2x ﹣4≥0，解得：x ≥2，∴x 的取值范围是：x ≥2．故选：B ．6．（3分）已知△ABC 的周长为16，点D ，E ，F 分别为△ABC 三条边的中点，则△DEF 的周长为（ ）A ．8B ．2√2C ．16D ．4【解答】解：∵D 、E 、F 分别为△ABC 三边的中点，∴DE 、DF 、EF 都是△ABC 的中位线，∴DF =12AC ，DE =12BC ，EF =12AC ，故△DEF 的周长＝DE +DF +EF =12（BC +AB +AC ）=12×16＝8． 故选：A ．7．（3分）把函数y ＝（x ﹣1）2+2图象向右平移1个单位长度，平移后图象的函数解析式为（ ）A ．y ＝x 2+2B ．y ＝（x ﹣1）2+1C ．y ＝（x ﹣2）2+2D ．y ＝（x ﹣1）2+3【解答】解：二次函数y ＝（x ﹣1）2+2的图象的顶点坐标为（1，2），∴向右平移1个单位长度后的函数图象的顶点坐标为（2，2），∴所得的图象解析式为y ＝（x ﹣2）2+2．故选：C ．8．（3分）不等式组{2−3x ≥−1，x −1≥−2(x +2)的解集为（ ） A ．无解 B ．x ≤1 C ．x ≥﹣1 D ．﹣1≤x ≤1【解答】解：解不等式2﹣3x ≥﹣1，得：x ≤1，解不等式x ﹣1≥﹣2（x +2），得：x ≥﹣1，则不等式组的解集为﹣1≤x ≤1，故选：D ．9．（3分）如图，在正方形ABCD 中，AB ＝3，点E ，F 分别在边AB ，CD 上，∠EFD ＝60°．若将四边形EBCF 沿EF 折叠，点B ′恰好落在AD 边上，则BE 的长度为（ ）A．1B．√2C．√3D．2【解答】解：∵四边形ABCD是正方形，∴AB∥CD，∠A＝90°，∴∠EFD＝∠BEF＝60°，∵将四边形EBCF沿EF折叠，点B'恰好落在AD边上，∴∠BEF＝∠FEB'＝60°，BE＝B'E，∴∠AEB'＝180°﹣∠BEF﹣∠FEB'＝60°，∴B'E＝2AE，设BE＝x，则B'E＝x，AE＝3﹣x，∴2（3﹣x）＝x，解得x＝2．故选：D．10．（3分）如图，抛物线y＝ax2+bx+c的对称轴是直线x＝1，下列结论：①abc＞0；②b2﹣4ac＞0；③8a+c＜0；④5a+b+2c＞0，正确的有（）A．4个B．3个C．2个D．1个【解答】解：由抛物线的开口向下可得：a＜0，根据抛物线的对称轴在y轴右边可得：a，b异号，所以b＞0，根据抛物线与y轴的交点在正半轴可得：c＞0，∴abc＜0，故①错误；∵抛物线与x轴有两个交点，∴b2﹣4ac＞0，故②正确；∵直线x＝1是抛物线y＝ax2+bx+c（a≠0）的对称轴，所以−b2a=1，可得b＝﹣2a，由图象可知，当x＝﹣2时，y＜0，即4a﹣2b+c＜0，∴4a﹣2×（﹣2a）+c＜0，即8a+c＜0，故③正确；由图象可知，当x＝2时，y＝4a+2b+c＞0；当x＝﹣1时，y＝a﹣b+c＞0，两式相加得，5a+b+2c＞0，故④正确；∴结论正确的是②③④3个，故选：B．二、填空题（本大题7小题，每小题4分，共28分）请将下列各题的正确答案填写在答题卡相应的位置上．11．（4分）分解因式：xy﹣x＝x（y﹣1）．【解答】解：xy﹣x＝x（y﹣1）．故答案为：x（y﹣1）．12．（4分）如果单项式3x m y与﹣5x3y n是同类项，那么m+n＝4．【解答】解：∵单项式3x m y与﹣5x3y n是同类项，∴m＝3，n＝1，∴m+n＝3+1＝4．故答案为：4．13．（4分）若√a−2+|b+1|＝0，则（a+b）2020＝1．【解答】解：∵√a−2≥，|b+1|≥0，√a−2+|b+1|＝0，∴a﹣2＝0，a＝2，b+1＝0，b＝﹣1，∴（a+b）2020＝1．故答案为：1．14．（4分）已知x＝5﹣y，xy＝2，计算3x+3y﹣4xy的值为7．【解答】解：∵x＝5﹣y，∴x+y＝5，当x+y＝5，xy＝2时，原式＝3（x+y）﹣4xy＝3×5﹣4×2 ＝15﹣8 ＝7， 故答案为：7．15．（4分）如图，在菱形ABCD 中，∠A ＝30°，取大于12AB 的长为半径，分别以点A ，B为圆心作弧相交于两点，过此两点的直线交AD 边于点E （作图痕迹如图所示），连接BE ，BD ．则∠EBD 的度数为 45° ．【解答】解：∵四边形ABCD 是菱形， ∴AD ＝AB ，∴∠ABD ＝∠ADB =12（180°﹣∠A ）＝75°， 由作图可知，EA ＝EB ， ∴∠ABE ＝∠A ＝30°，∴∠EBD ＝∠ABD ﹣∠ABE ＝75°﹣30°＝45°， 故答案为45°．16．（4分）如图，从一块半径为1m 的圆形铁皮上剪出一个圆周角为120°的扇形ABC ，如果将剪下来的扇形围成一个圆锥，则该圆锥的底面圆的半径为13m ．【解答】解：如图，连接OA ，OB ，OC ，则OB ＝OA ＝OC ＝1m ，因此阴影扇形的半径为1m ，圆心角的度数为120°， 则扇形的弧长为：120π×1180m ，而扇形的弧长相当于围成圆锥的底面周长，因此有： 2πr =120π×1180， 解得，r =13（m ）， 故答案为：13．17．（4分）有一架竖直靠在直角墙面的梯子正在下滑，一只猫紧紧盯住位于梯子正中间的老鼠，等待与老鼠距离最小时扑捉．把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点，模型如图，∠ABC ＝90°，点M ，N 分别在射线BA ，BC 上，MN 长度始终保持不变，MN ＝4，E 为MN 的中点，点D 到BA ，BC 的距离分别为4和2．在此滑动过程中，猫与老鼠的距离DE 的最小值为 2√5−2 ．【解答】解：如图，连接BE ，BD ．由题意BD=√22+42=2√5，∵∠MBN＝90°，MN＝4，EM＝NE，∴BE=12MN＝2，∴点E的运动轨迹是以B为圆心，2为半径的弧，∴当点E落在线段BD上时，DE的值最小，∴DE的最小值为2√5−2．（也可以用DE≥BD﹣BE，即DE≥2√5−2确定最小值）故答案为2√5−2．三、解答题（一）（本大题3小题，每小题6分，共18分）18．（6分）先化简，再求值：（x+y）2+（x+y）（x﹣y）﹣2x2，其中x=√2，y=√3．【解答】解：（x+y）2+（x+y）（x﹣y）﹣2x2，＝x2+2xy+y2+x2﹣y2﹣2x2＝2xy，当x=√2，y=√3时，原式＝2×√2×√3=2√6．19．（6分）某中学开展主题为“垃圾分类知多少”的调查活动，调查问卷设置了“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级，要求每名学生必选且只能选其中一个等级，随机抽取了120名学生的有效问卷，数据整理如表：等级非常了解比较了解基本了解不太了解人数（人）247218x （1）求x的值；（2）若该校有学生1800人，请根据抽样调查结果估算该校“非常了解”和“比较了解”垃圾分类知识的学生共有多少人？【解答】解：（1）x＝120﹣（24+72+18）＝6；（2）1800×24+72120=1440（人），答：根据抽样调查结果估算该校“非常了解”和“比较了解”垃圾分类知识的学生共有1440人．20．（6分）如图，在△ABC中，点D，E分别是AB、AC边上的点，BD＝CE，∠ABE＝∠ACD，BE与CD相交于点F．求证：△ABC是等腰三角形．【解答】证明：∵∠ABE ＝∠ACD ， ∴∠DBF ＝∠ECF ，在△BDF 和△CEF 中，{∠DBF =∠ECF∠BFD =∠CFE BD =CE ，∴△BDF ≌△CEF （AAS ）， ∴BF ＝CF ，DF ＝EF ， ∴∠FBC ＝∠FCB ， ∴∠ABC ＝∠ACB ， ∴AB ＝AC ，即△ABC 是等腰三角形．四、解答题（二）（本大题3小题，每小题8分，共24分） 21．（8分）已知关于x ，y 的方程组{ax +2√3y =−10√3，x +y =4与{x −y =2，x +by =15的解相同．（1）求a ，b 的值；（2）若一个三角形的一条边的长为2√6，另外两条边的长是关于x 的方程x 2+ax +b ＝0的解．试判断该三角形的形状，并说明理由．【解答】解：（1）由题意得，关于x ，y 的方程组的相同解，就是方程组{x +y =4x −y =2的解，解得，{x =3y =1，代入原方程组得，a ＝﹣4√3，b ＝12；（2）该三角形是等腰直角三角形，理由如下：当a ＝﹣4√3，b ＝12时，关于x 的方程x 2+ax +b ＝0就变为x 2﹣4√3x +12＝0， 解得，x 1＝x 2＝2√3，又∵（2√3）2+（2√3）2＝（2√6）2，∴以2√3、2√3、2√6为边的三角形是等腰直角三角形．22．（8分）如图1，在四边形ABCD 中，AD ∥BC ，∠DAB ＝90°，AB 是⊙O 的直径，CO平分∠BCD．（1）求证：直线CD与⊙O相切；（2）如图2，记（1）中的切点为E，P为优弧AÊ上一点，AD＝1，BC＝2．求tan∠APE 的值．【解答】（1）证明：作OE⊥CD于E，如图1所示：则∠OEC＝90°，∵AD∥BC，∠DAB＝90°，∴∠OBC＝180°﹣∠DAB＝90°，∴∠OEC＝∠OBC，∵CO平分∠BCD，∴∠OCE＝∠OCB，在△OCE和△OCB中，{∠OEC=∠OBC ∠OCE=∠OCB OC=OC，∴△OCE≌△OCB（AAS），∴OE＝OB，又∵OE⊥CD，∴直线CD与⊙O相切；（2）解：作DF⊥BC于F，连接BE，如图2所示：则四边形ABFD是矩形，∴AB＝DF，BF＝AD＝1，∴CF＝BC﹣BF＝2﹣1＝1，∵AD∥BC，∠DAB＝90°，∴AD⊥AB，BC⊥AB，∴AD、BC是⊙O的切线，由（1）得：CD 是⊙O 的切线， ∴ED ＝AD ＝1，EC ＝BC ＝2， ∴CD ＝ED +EC ＝3，∴DF =√CD 2−CF 2=√32−12=2√2， ∴AB ＝DF ＝2√2， ∴OB =√2， ∵CO 平分∠BCD ， ∴CO ⊥BE ，∴∠BCH +∠CBH ＝∠CBH +∠ABE ＝90°， ∴∠ABE ＝∠BCH ， ∵∠APE ＝∠ABE ， ∴∠APE ＝∠BCH ，∴tan ∠APE ＝tan ∠BCH =OBBC =√22．23．（8分）某社区拟建A ，B 两类摊位以搞活“地摊经济”，每个A 类摊位的占地面积比每个B 类摊位的占地面积多2平方米．建A 类摊位每平方米的费用为40元，建B 类摊位每平方米的费用为30元．用60平方米建A 类摊位的个数恰好是用同样面积建B 类摊位个数的35．（1）求每个A ，B 类摊位占地面积各为多少平方米？（2）该社区拟建A，B两类摊位共90个，且B类摊位的数量不少于A类摊位数量的3倍．求建造这90个摊位的最大费用．【解答】解：（1）设每个B类摊位的占地面积为x平方米，则每个A类摊位占地面积为（x+2）平方米，根据题意得：60x+2=60x⋅35，解得：x＝3，经检验x＝3是原方程的解，所以3+2＝5，答：每个A类摊位占地面积为5平方米，每个B类摊位的占地面积为3平方米；（2）解法一：设建A摊位a个，建造这90个摊位的费用为y元，则建B摊位（90﹣a）个，由题意得：y＝5a×40+3×30（90﹣a）＝110a+8100，∵110＞0，∴y随a的增大而增大，∵90﹣a≥3a，解得a≤22.5，∵a为整数，∴当a取最大值22时，费用最大，此时最大费用为：110×22+8100＝10520；解法二：设建A摊位a（a为整数）个，则建B摊位（90﹣a）个，由题意得：90﹣a≥3a，解得a≤22.5，∵建A类摊位每平方米的费用为40元，建B类摊位每平方米的费用为30元，∴要想使建造这90个摊位有最大费用，所以要多建造A类摊位，即a取最大值22时，费用最大，此时最大费用为：22×40×5+30×（90﹣22）×3＝10520，答：建造这90个摊位的最大费用是10520元．五、解答题（三）（本大题2小题，每小题10分，共20分）24．（10分）如图，点B 是反比例函数y =8x（x ＞0）图象上一点，过点B 分别向坐标轴作垂线，垂足为A ，C ．反比例函数y =kx （x ＞0）的图象经过OB 的中点M ，与AB ，BC 分别相交于点D ，E ．连接DE 并延长交x 轴于点F ，点G 与点O 关于点C 对称，连接BF ，BG ．（1）填空：k ＝ 2 ； （2）求△BDF 的面积；（3）求证：四边形BDFG 为平行四边形．【解答】解：（1）设点B （s ，t ），st ＝8，则点M （12s ，12t ），则k =12s •12t =14st ＝2， 故答案为2；（2）连接OD ，则△BDF 的面积＝△OBD 的面积＝S △BOA ﹣S △OAD =12×8−12×2＝3；（3）设点D （m ，2m），则点B （4m ，2m），∵点G 与点O 关于点C 对称，故点G （8m ，0）， 则点E （4m ，12m），设直线DE 的表达式为：y ＝px +n ，将点D 、E 的坐标代入上式得{2m =mp +n 12m=4mp +n 并解得{p =−12m 2n =52m， 直线DE 的表达式为：y =−12m2x +52m ，令y ＝0，则x ＝5m ，故点F （5m ，0）， 故FG ＝8m ﹣5m ＝3m ，而BD ＝4m ﹣m ＝3m ＝FG ， 又∵FG ∥BD ，故四边形BDFG 为平行四边形． 25．（10分）如图，抛物线y =3+√36x 2+bx +c 与x 轴交于A ，B 两点，点A ，B 分别位于原点的左、右两侧，BO ＝3AO ＝3，过点B 的直线与y 轴正半轴和抛物线的交点分别为C ，D ，BC =√3CD ． （1）求b ，c 的值；（2）求直线BD 的函数解析式；（3）点P 在抛物线的对称轴上且在x 轴下方，点Q 在射线BA 上．当△ABD 与△BPQ 相似时，请直接写出所有满足条件的点Q 的坐标．【解答】解：（1）∵BO ＝3AO ＝3， ∴点B （3，0），点A （﹣1，0）， ∴抛物线解析式为：y =3+√36（x +1）（x ﹣3）=3+√36x 2−3+√33x −3+√32， ∴b =−3+√33，c =−3+√32； （2）如图1，过点D 作DE ⊥AB 于E ，∴CO ∥DE ，∴BC CD =BO OE ，∵BC =√3CD ，BO ＝3，∴√3=3OE， ∴OE =√3，∴点D 横坐标为−√3，∴点D 坐标为（−√3，√3+1），设直线BD 的函数解析式为：y ＝kx +m ，由题意可得：{√3+1=−√3k +m 0=3k +m， 解得：{k =−√33m =√3，∴直线BD 的函数解析式为y =−√33x +√3；（3）∵点B （3，0），点A （﹣1，0），点D （−√3，√3+1）， ∴AB ＝4，AD ＝2√2，BD ＝2√3+2，对称轴为直线x ＝1， ∵直线BD ：y =−√33x +√3与y 轴交于点C ， ∴点C （0，√3），∴OC =√3，∵tan ∠CBO =CO BO =√33，∴∠CBO ＝30°，如图2，过点A 作AK ⊥BD 于K ，∴AK =12AB ＝2，∴DK =√AD2−AK 2=√8−4=2，∴DK ＝AK ，∴∠ADB ＝45°，如图，设对称轴与x 轴的交点为N ，即点N （1，0），若∠CBO ＝∠PBO ＝30°，∴BN =√3PN ＝2，BP ＝2PN ，∴PN =2√33，BP =4√33， 当△BAD ∽△BPQ ，∴BP BA =BQ BD ，∴BQ =4√33×(2√3+2)4=2+2√33， ∴点Q （1−2√33，0）；当△BAD ∽△BQP ，∴BP BD =BQ AB ，∴BQ=4√33×42√3+2=4−4√33，∴点Q（﹣1+4√33，0）；若∠PBO＝∠ADB＝45°，∴BN＝PN＝2，BP=√2BN＝2√2，当△DAB∽△BPQ，∴BPAD =BQ BD，∴√22√2=2√3+2，∴BQ＝2√3+2∴点Q（1﹣2√3，0）；当△BAD∽△PQB，∴BPBD =BQAD，∴BQ=2√2×2√22√3+2=2√3−2，∴点Q（5﹣2√3，0）；综上所述：满足条件的点Q的坐标为（1−2√33，0）或（﹣1+4√33，0）或（1﹣2√3，0）或（5﹣2√3，0）．。

一、补录条件（一）公办普通高中考生如需填报有补录计划的公办普通高中，须同时符合下列条件：1.具有东莞户籍。

2.学业考试成绩在500分或以上。

3.信息技术会考科目合格。

4.在常规录取阶段未被普通高中录取（已被普通高中录取，但没有按规定时间注册的考生，作自动放弃就读普通高中处理，不得再参与补录）。

（二）民办普通高中考生如需填报有补录计划的民办普通高中，须同时符合下列条件：1.具有东莞户籍或符合报考普通高中认定条件的随迁子女。

2.学业考试成绩在500分或以上。

3.信息技术会考科目合格。

4.在常规录取阶段未被普通高中录取（已被普通高中录取，但没有按规定时间注册的考生，作自动放弃就读普通高中处理，不得再参与补录）。

二、工作安排8 月12日：市中招办统一公布补录招生计划和录取最低控制分数线。

考生可以回原毕业学校或登录东莞教育网或关注“东莞慧教育”微信公众号查询补录招生计划。

8月13日15:00前：各初中学校组织符合补录条件的考生在网上填报补录学校的志愿。

考生最多可以填报3个志愿，录取时按考生填报的志愿顺序进行，下一志愿的分数要比前一志愿的分数提高5分。

具体操作方法：考生使用准考证号及密码登录中考管理系统进行补填志愿。

8月13日：市中招办根据考生的学业考试成绩及志愿划定分数线并进行录取。

录取时，根据考生志愿、综合素质评价等级、考查科目等级和学业考试成绩总分及排位情况择优录取。

8月14日：市中招办公布普通高中补录结果。

补录考生于上午10:00后自行登录东莞中考管理系统打印录取通知书。

8月15日：普通高中补录学生注册。

已被学校补录录取，但没有按规定时间注册的考生作自动放弃就读普通高中和中等职业学校处理，不得再参与后续批次录取。

三、有关要求1.有补录计划的普通高中要按要求及时做好考生的注册工作。

2.各初中要做好符合补录条件考生补填志愿的宣传、指导及组织工作，并及时提醒被补录录取的考生按时上网打印录取通知书及到录取学校注册。

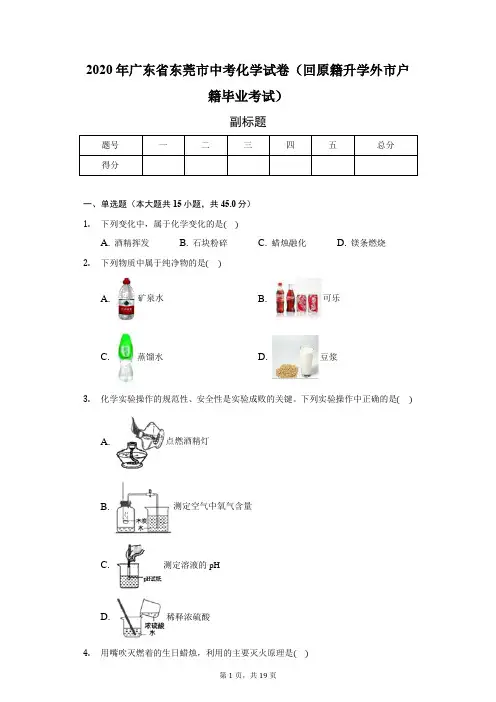
2020年广东省东莞市中考化学试卷（回原籍升学外市户籍毕业考试）副标题题号一二三四五总分得分一、单选题（本大题共15小题，共45.0分）1.下列变化中，属于化学变化的是()A. 酒精挥发B. 石块粉碎C. 蜡烛融化D. 镁条燃烧2.下列物质中属于纯净物的是()A. 矿泉水B. 可乐C. 蒸馏水D. 豆浆3.化学实验操作的规范性、安全性是实验成败的关键。

下列实验操作中正确的是()A. 点燃酒精灯B. 测定空气中氧气含量C. 测定溶液的pHD. 稀释浓硫酸4.用嘴吹灭燃着的生日蜡烛，利用的主要灭火原理是()A. 隔绝空气B. 降低可燃物的着火点C. 使可燃物温度降到着火点以下D. 消除可燃物5.下列有关抗击新型冠状病毒的说法中不正确的是()A. 各地运往武汉的新鲜瓜果、蔬菜中富含维生素，它属于人体必需的营养素B. 消毒的医用酒精溶质为乙醇(C2H5OH)，乙醇属于碱C. 喷洒84消毒液后，室内充满刺激性气味，是因为微粒在不断运动D. 医用口罩的制作原料主要是聚丙烯[(C3H6)n]，聚丙烯属于有机物6.下列化学用语书写正确的是()A. 五氧化二磷：P2O5B. 钙离子：Ca+2C. 2个氢原子：H2D. 铝元素：AL7.实验室用过氧化氢制氧气的实验中，应加入少量二氧化锰。

下列说法中正确的是()A. 只有二氧化锰能作过氧化氢分解的催化剂B. 二氧化锰只能作过氧化氢分解的催化剂C. 加入二氧化锰可以增加过氧化氢分解产生氧气的质量D. 二氧化锰能加快过氧化氢分解8.化学方程式2Mg+O2− 点燃 2MgO可读作()A. 镁加氧气等于氧化镁B. 2个镁加1个氧气等于2个氯化镁C. 镁和氧气在点燃条件下生成氧化镁D. 镁加氧气点燃等于氧化镁9.一些食物的pH近似值如下表，其中酸性最强的是()A. 葡萄汁B. 苹果汁C. 牛奶D. 鸡蛋清10.关于丁酸乙酯(C6H12O2)的叙述正确的是()A. 丁酸乙酯是由20个原子构成的B. 丁酸乙酯中碳、氢、氧元素的质量比为18：3：8C. 丁酸乙酯的相对分子质量为116gD. 一个丁酸乙酯分子是由6个碳原子、12 个氢原子和1个氧分子构成的11.K2FeO4是一种新型非氯高效消毒净水剂。

2020年广东省东莞市中考数学试卷一、选择题（本大题10小题，每小题3分，共30分）在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑．1．（3分）9的相反数是( )A ．9-B ．9C ．19D ．19- 2．（3分）一组数据2，4，3，5，2的中位数是( )A ．5B ．3.5C ．3D ．2.53．（3分）在平面直角坐标系中，点(3,2)关于x 轴对称的点的坐标为( )A ．(3,2)-B ．(2,3)-C ．(2,3)-D ．(3,2)-4．（3分）若一个多边形的内角和是540︒，则该多边形的边数为( )A ．4B ．5C ．6D ．75．（3在实数范围内有意义，则x 的取值范围是( )A ．2x ≠B ．2xC ．2xD ．2x ≠-6．（3分）已知ABC ∆的周长为16，点D ，E ，F 分别为ABC ∆三条边的中点，则DEF ∆的周长为( )A ．8B ．C ．16D ．47．（3分）把函数2(1)2y x =-+图象向右平移1个单位长度，平移后图象的函数解析式为( )A ．22y x =+B ．2(1)1y x =-+C ．2(2)2y x =-+D ．2(1)3y x =--8．（3分）不等式组231,12(2)x x x --⎧⎨--+⎩的解集为( ) A ．无解 B ．1x C ．1x - D ．11x -9．（3分）如图，在正方形ABCD 中，3AB =，点E ，F 分别在边AB ，CD 上，60EFD ∠=︒．若将四边形EBCF 沿EF 折叠，点B 恰好落在AD 边上，则BE 的长度为( )A ．1B ．2C ．3D ．210．（3分）如图，抛物线2y ax bx c =++的对称轴是1x =，下列结论：①0abc >；②240b ac ->；③80a c +<；④520a b c ++>，正确的有( )A ．4个B ．3个C ．2个D ．1个二、填空题（本大题7小题，每小题4分，共28分）请将下列各题的正确答案填写在答题卡相应的位置上．11．（4分）分解因式：xy x -= ．12．（4分）如果单项式3m x y 与35n x y -是同类项，那么m n += ．13．（4分）若2|1|0a b -++=，则2020()a b += ．14．（4分）已知5x y =-，2xy =，计算334x y xy +-的值为 ．15．（4分）如图，在菱形ABCD 中，30A ∠=︒，取大于12AB 的长为半径，分别以点A ，B 为圆心作弧相交于两点，过此两点的直线交AD 边于点E （作图痕迹如图所示），连接BE ，BD ．则EBD ∠的度数为 ．16．（4分）如图，从一块半径为1m 的圆形铁皮上剪出一个圆周角为120︒的扇形ABC ，如果将剪下来的扇形围成一个圆锥，则该圆锥的底面圆的半径为 m ．17．（4分）有一架竖直靠在直角墙面的梯子正在下滑，一只猫紧紧盯住位于梯子正中间的老鼠，等待与老鼠距离最小时扑捉．把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点，模型如图，90ABC ∠=︒，点M ，N 分别在射线BA ，BC 上，MN 长度始终保持不变，4MN =，E 为MN 的中点，点D 到BA ，BC 的距离分别为4和2．在此滑动过程中，猫与老鼠的距离DE 的最小值为 ．三、解答题（一）（本大题3小题，每小题6分，共18分）18．（6分）先化简，再求值：22()()()2x y x y x y x +++--，其中2x =3y =．19．（6分）某中学开展主题为“垃圾分类知多少”的调查活动，调查问卷设置了“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级，要求每名学生选且只能选其中一个等级，随机抽取了120名学生的有效问卷，数据整理如下： 等级非常了解 比较了解 基本了解 不太了解 人数（人)24 72 18 x（1）求x 的值；（2）若该校有学生1800人，请根据抽样调查结果估算该校“非常了解”和“比较了解”垃圾分类知识的学生共有多少人？20．（6分）如图，在ABC ∆中，点D ，E 分别是AB 、AC 边上的点，BD CE =，ABE ACD ∠=∠，BE 与CD 相交于点F ．求证：ABC ∆是等腰三角形．四、解答题（二）（本大题3小题，每小题8分，共24分）21．（8分）已知关于x，y的方程组23103,4ax yx y⎧+=-⎪⎨+=⎪⎩与2,15x yx by-=⎧⎨+=⎩的解相同．（1）求a，b的值；（2）若一个三角形的一条边的长为26，另外两条边的长是关于x的方程20x ax b++=的解．试判断该三角形的形状，并说明理由．22．（8分）如图1，在四边形ABCD中，//AD BC，90DAB∠=︒，AB是O的直径，CO 平分BCD∠．（1）求证：直线CD与O相切；（2）如图2，记（1）中的切点为E，P为优弧AE上一点，1AD=，2BC=．求tan APE∠的值．23．（8分）某社区拟建A，B两类摊位以搞活“地摊经济”，每个A类摊位的占地面积比每个B类摊位的占地面积多2平方米．建A类摊位每平方米的费用为40元，建B类摊位每平方米的费用为30元．用60平方米建A类摊位的个数恰好是用同样面积建B类摊位个数的35．（1）求每个A，B类摊位占地面积各为多少平方米？（2）该社区拟建A，B两类摊位共90个，且B类摊位的数量不少于A类摊位数量的3倍．求建造这90个摊位的最大费用．五、解答题（三）（本大题2小题，每小题10分，共20分）24．（10分）如图，点B 是反比例函数8(0)y x x=>图象上一点，过点B 分别向坐标轴作垂线，垂足为A ，C ．反比例函数(0)k y x x=>的图象经过OB 的中点M ，与AB ，BC 分别相交于点D ，E ．连接DE 并延长交x 轴于点F ，点G 与点O 关于点C 对称，连接BF ，BG ．（1）填空：k = ；（2）求BDF ∆的面积；（3）求证：四边形BDFG 为平行四边形．25．（10分）如图，抛物线2336y x bx c +=++与x 轴交于A ，B 两点，点A ，B 分别位于原点的左、右两侧，33BO AO ==，过点B 的直线与y 轴正半轴和抛物线的交点分别为C ，D ，3BC CD =．（1）求b ，c 的值；（2）求直线BD 的函数解析式；（3）点P 在抛物线的对称轴上且在x 轴下方，点Q 在射线BA 上．当ABD ∆与BPQ ∆相似时，请直接写出所有满足条件的点Q 的坐标．2020年广东省东莞市中考数学试卷参考答案与试题解析一、选择题（本大题10小题，每小题3分，共30分）在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑．1．（3分）9的相反数是( )A ．9-B ．9C ．19D ．19- 【分析】根据相反数的定义即可求解．【解答】解：9的相反数是9-，故选：A ．2．（3分）一组数据2，4，3，5，2的中位数是( )A ．5B ．3.5C ．3D ．2.5【分析】中位数是指一组数据从小到大排列之后，如果数据的总个数为奇数，则中间的数即为中位数；如果数据的总个数为偶数个，则中间两个数的平均数即为中位数．【解答】解：将数据由小到大排列得：2，2，3，4，5，数据个数为奇数，最中间的数是3，∴这组数据的中位数是3．故选：C ．3．（3分）在平面直角坐标系中，点(3,2)关于x 轴对称的点的坐标为( )A ．(3,2)-B ．(2,3)-C ．(2,3)-D ．(3,2)-【分析】根据“关于x 轴对称的点，横坐标相同，纵坐标互为相反数”解答即可．【解答】解：点(3,2)关于x 轴对称的点的坐标为(3,2)-．故选：D ．4．（3分）若一个多边形的内角和是540︒，则该多边形的边数为( )A ．4B ．5C ．6D ．7【分析】根据多边形的内角和公式(2)180n -︒列式进行计算即可求解．【解答】解：设多边形的边数是n ，则(2)180540n -︒=︒，解得5n =．故选：B ．5．（3分）若式子24x -在实数范围内有意义，则x 的取值范围是( )A ．2x ≠B ．2xC ．2xD ．2x ≠-【分析】根据二次根式中的被开方数是非负数，即可确定二次根式被开方数中字母的取值范围．【解答】解：24x -在实数范围内有意义，240x ∴-，解得：2x ，x ∴的取值范围是：2x ．故选：B ．6．（3分）已知ABC ∆的周长为16，点D ，E ，F 分别为ABC ∆三条边的中点，则DEF ∆的周长为( )A ．8B ．22C ．16D ．4【分析】根据中位线定理可得12DF AC =，12DE BC =，12EF AC =，继而结合ABC ∆的周长为16，可得出DEF ∆的周长．【解答】解：D 、E 、F 分别为ABC ∆三边的中点，DE ∴、DF 、EF 都是ABC ∆的中位线，12DF AC ∴=，12DE BC =，12EF AC =， 故DEF ∆的周长11()16822DE DF EF BC AB AC =++=++=⨯=． 故选：A ．7．（3分）把函数2(1)2y x =-+图象向右平移1个单位长度，平移后图象的函数解析式为( )A ．22y x =+B ．2(1)1y x =-+C ．2(2)2y x =-+D ．2(1)3y x =--【分析】先求出2(1)2y x =-+的顶点坐标，再根据向右平移横坐标加，求出平移后的二次函数图象顶点坐标，然后利用顶点式解析式写出即可．【解答】解：二次函数2(1)2y x =-+的图象的顶点坐标为(1,2)，∴向右平移1个单位长度后的函数图象的顶点坐标为(2,2)，∴所得的图象解析式为2(2)2y x =-+．故选：C ．8．（3分）不等式组231,12(2)x x x --⎧⎨--+⎩的解集为( ) A ．无解 B ．1x C ．1x - D ．11x -【分析】分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．【解答】解：解不等式231x --，得：1x ，解不等式12(2)x x --+，得：1x -，则不等式组的解集为11x -，故选：D ．9．（3分）如图，在正方形ABCD 中，3AB =，点E ，F 分别在边AB ，CD 上，60EFD ∠=︒．若将四边形EBCF 沿EF 折叠，点B 恰好落在AD 边上，则BE 的长度为( )A ．1B 2C 3D ．2【分析】由正方形的性质得出60EFD BEF ∠=∠=︒，由折叠的性质得出60BEF FEB '∠=∠=︒，BE B E '=，设BE x =，则B E x '=，3AE x =-，由直角三角形的性质可得：2(3)x x -=，解方程求出x 即可得出答案．【解答】解：四边形ABCD 是正方形，//AB CD ∴，90A ∠=︒，60EFD BEF ∴∠=∠=︒，将四边形EBCF 沿EF 折叠，点B 恰好落在AD 边上，60BEF FEB '∴∠=∠=︒，BE B E '=，18060AEB BEF FEB ''∴∠=︒-∠-∠=︒，2B E AE '∴=，设BE x =，则B E x '=，3AE x =-，2(3)x x ∴-=，解得2x =．故选：D ．10．（3分）如图，抛物线2y ax bx c =++的对称轴是1x =，下列结论：①0abc >；②240b ac ->；③80a c +<；④520a b c ++>，正确的有( )A ．4个B ．3个C ．2个D ．1个【分析】根据抛物线的开口方向、对称轴、与坐标轴的交点判定系数符号及运用一些特殊点解答问题．【解答】解：由抛物线的开口向下可得：0a <，根据抛物线的对称轴在y 轴右边可得：a ，b 异号，所以0b >，根据抛物线与y 轴的交点在正半轴可得：0c >，0abc ∴<，故①错误；抛物线与x 轴有两个交点，240b ac ∴->，故②正确；直线1x =是抛物线2(0)y ax bx c a =++≠的对称轴，所以12b a-=，可得2b a =-， 由图象可知，当2x =-时，0y <，即420a b c -+<，42(2)0a a c ∴-⨯-+<， 即80a c +<，故③正确；由图象可知，当2x =时，420y a b c =++>；当1x =-时，0y a b c =-+>，两式相加得，520a b c ++>，故④正确；∴结论正确的是②③④3个，故选：B ．二、填空题（本大题7小题，每小题4分，共28分）请将下列各题的正确答案填写在答题卡相应的位置上．11．（4分）分解因式：xy x -= (1)x y - ．【分析】直接提取公因式x ，进而分解因式得出答案．【解答】解：(1)xy x x y -=-．故答案为：(1)x y -．12．（4分）如果单项式3m x y 与35n x y -是同类项，那么m n += 4 ．【分析】根据同类项的定义（所含字母相同，相同字母的指数相同）可得3m =，1n =，再代入代数式计算即可．【解答】解：单项式3m x y 与35n x y -是同类项，3m ∴=，1n =，314m n ∴+=+=．故答案为：4．13．（4|1|0b +=，则2020()a b += 1 ．【分析】根据非负数的意义，求出a 、b 的值，代入计算即可．【解答】解：|1|0b +=，20a ∴-=且10b +=，解得，2a =，1b =-，20202020()(21)1a b ∴+=-=，故答案为：1．14．（4分）已知5x y =-，2xy =，计算334x y xy +-的值为 7 ．【分析】由5x y =-得出5x y +=，再将5x y +=、2xy =代入原式3()4x y xy =+-计算可得．【解答】解：5x y =-，5x y ∴+=，当5x y +=，2xy =时，原式3()4x y xy =+- 3542=⨯-⨯ 158=-7=，故答案为：7．15．（4分）如图，在菱形ABCD 中，30A ∠=︒，取大于12AB 的长为半径，分别以点A ，B 为圆心作弧相交于两点，过此两点的直线交AD 边于点E （作图痕迹如图所示），连接BE ，BD ．则EBD ∠的度数为 45︒ ．【分析】根据EBD ABD ABE ∠=∠-∠，求出ABD ∠，ABE ∠即可解决问题． 【解答】解：四边形ABCD 是菱形，AD AB ∴=，1(180)752ABD ADB A ∴∠=∠=︒-∠=︒，由作图可知，EA EB =， 30ABE A ∴∠=∠=︒，753045EBD ABD ABE ∴∠=∠-∠=︒-︒=︒，故答案为45︒．16．（4分）如图，从一块半径为1m 的圆形铁皮上剪出一个圆周角为120︒的扇形ABC ，如果将剪下来的扇形围成一个圆锥，则该圆锥的底面圆的半径为13m ．【分析】求出阴影扇形的弧长，进而可求出围成圆锥的底面半径．【解答】解：由题意得，阴影扇形的半径为1m ，圆心角的度数为120︒， 则扇形的弧长为：1201180π⨯， 而扇形的弧长相当于围成圆锥的底面周长，因此有： 12012180r ππ⨯=， 解得，13r =，故答案为：13．17．（4分）有一架竖直靠在直角墙面的梯子正在下滑，一只猫紧紧盯住位于梯子正中间的老鼠，等待与老鼠距离最小时扑捉．把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点，模型如图，90ABC ∠=︒，点M ，N 分别在射线BA ，BC 上，MN 长度始终保持不变，4MN =，E 为MN 的中点，点D 到BA ，BC 的距离分别为4和2．在此滑动过程中，猫与老鼠的距离DE 的最小值为 252- ．【分析】如图，连接BE ，BD ．求出BE ，BD ，根据DE BD BE -求解即可． 【解答】解：如图，连接BE ，BD ．由题意222425BD =+90MBN ∠=︒，4MN =，EM NE =， 122BE MN ∴==，∴点E 的运动轨迹是以B 为圆心，2为半径的弧， ∴当点E 落在线段BD 上时，DE 的值最小，DE ∴的最小值为2．故答案为2．三、解答题（一）（本大题3小题，每小题6分，共18分）18．（6分）先化简，再求值：22()()()2x y x y x y x +++--，其中x =y =． 【分析】根据整式的混合运算过程，先化简，再代入值求解即可． 【解答】解：22()()()2x y x y x y x +++--，2222222x xy y x y x =+++-- 2xy =，当x ，y =原式2==19．（6分）某中学开展主题为“垃圾分类知多少”的调查活动，调查问卷设置了“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级，要求每名学生选且只能选其中一个等级，随机抽取了120名学生的有效问卷，数据整理如下：（1）求x 的值；（2）若该校有学生1800人，请根据抽样调查结果估算该校“非常了解”和“比较了解”垃圾分类知识的学生共有多少人？【分析】（1）根据四个等级的人数之和为120求出x 的值；（2）用总人数乘以样本中“非常了解”和“比较了解”垃圾分类知识的学生占被调查人数的比例．【解答】解：（1）120(247218)6x =-++=； （2）2472180********+⨯=（人)， 答：根据抽样调查结果估算该校“非常了解”和“比较了解”垃圾分类知识的学生共有1440人．20．（6分）如图，在ABC ∆中，点D ，E 分别是AB 、AC 边上的点，BD CE =，ABE ACD ∠=∠，BE 与CD 相交于点F ．求证：ABC ∆是等腰三角形．【分析】先证()BDF CEF AAS ∆≅∆，得出BF CF =，DF EF =，则BE CD =，再证()ABE ACD AAS ∆≅∆，得出AB AC =即可．【解答】证明：ABE ACD ∠=∠， DBF ECF ∴∠=∠，在BDF ∆和CEF ∆中，DBF ECF BFD CFE BD CE ∠=∠⎧⎪∠=∠⎨⎪=⎩，()BDF CEF AAS ∴∆≅∆， BF CF ∴=，DF EF =， BF EF CF DF ∴+=+，即BE CD =，在ABE ∆和ACD ∆中，ABE ACD A A BE CD ∠=∠⎧⎪∠=∠⎨⎪=⎩，()ABE ACD AAS ∴∆≅∆， AB AC ∴=，ABC ∴∆是等腰三角形．四、解答题（二）（本大题3小题，每小题8分，共24分）21．（8分）已知关于x ，y 的方程组3103,4ax x y ⎧+=-⎪⎨+=⎪⎩与2,15x y x by -=⎧⎨+=⎩的解相同．（1）求a ，b 的值；（2）若一个三角形的一条边的长为26x 的方程20x ax b ++=的解．试判断该三角形的形状，并说明理由．【分析】（1）关于x ，y 的方程组23103,4ax x y ⎧+=-⎪⎨+=⎪⎩与2,15x y x by -=⎧⎨+=⎩的解相同．实际就是方程组42x y x y +=⎧⎨-=⎩的解，可求出方程组的解，进而确定a 、b 的值；（2）将a 、b 的值代入关于x 的方程20x ax b ++=，求出方程的解，再根据方程的两个解与26为边长，判断三角形的形状．【解答】解：（1）由题意得，关于x ，y 的方程组的相同解，就是程组42x y x y +=⎧⎨-=⎩的解，解得，31x y =⎧⎨=⎩，代入原方程组得，43a =-，12b =；（2）当43a =-，12b =时，关于x 的方程20x ax b ++=就变为2_43120x x -+=， 解得，1223x x ==， 又222(23)(23)(26)+=，∴以23、23、26为边的三角形是等腰直角三角形．22．（8分）如图1，在四边形ABCD 中，//AD BC ，90DAB ∠=︒，AB 是O 的直径，CO 平分BCD ∠．（1）求证：直线CD 与O 相切；（2）如图2，记（1）中的切点为E ，P 为优弧AE 上一点，1AD =，2BC =．求tan APE ∠的值．【分析】（1）证明：作OE CD ⊥于E ，证()OCE OCB AAS ∆≅∆，得出OE OB =，即可得出结论；（2）作DF BC ⊥于F ，连接BE ，则四边形ABFD 是矩形，得AB DF =，1BF AD ==，则1CF =，证AD 、BC 是O 的切线，由切线长定理得1ED AD ==，2EC BC ==，则3CD ED EC =+=，由勾股定理得DF =OB =，证ABE BCH ∠=∠，由圆周角定理得APE ABE ∠=∠，则APE BCH ∠=∠，由三角函数定义即可得出答案． 【解答】（1）证明：作OE CD ⊥于E ，如图1所示： 则90OEC ∠=︒，//AD BC ，90DAB ∠=︒， 18090OBC DAB ∴∠=︒-∠=︒， OEC OBC ∴∠=∠， CO 平分BCD ∠， OCE OCB ∴∠=∠，在OCE ∆和OCB ∆中，OEC OBCOCE OCB OC OC ∠=∠⎧⎪∠=∠⎨⎪=⎩，()OCE OCB AAS ∴∆≅∆， OE OB ∴=，又OE CD ⊥，∴直线CD 与O 相切；（2）解：作DF BC ⊥于F ，连接BE ，如图所示： 则四边形ABFD 是矩形，AB DF ∴=，1BF AD ==，211CF BC BF ∴=-=-=， //AD BC ，90DAB ∠=︒，AD AB ∴⊥，BC AB ⊥， AD ∴、BC 是O 的切线，由（1）得：CD 是O 的切线，1ED AD ∴==，2EC BC ==，3CD ED EC ∴=+=，DF ∴AB DF ∴==OB ∴=，CO 平分BCD ∠， CO BE ∴⊥，90BCH CBH CBH ABE ∴∠+∠=∠+∠=︒， ABE BCH ∴∠=∠，APE ABE ∠=∠，APE BCH ∴∠=∠，2tan tan 2OB APE BCH BC ∴∠=∠==．23．（8分）某社区拟建A ，B 两类摊位以搞活“地摊经济”，每个A 类摊位的占地面积比每个B 类摊位的占地面积多2平方米．建A 类摊位每平方米的费用为40元，建B 类摊位每平方米的费用为30元．用60平方米建A 类摊位的个数恰好是用同样面积建B 类摊位个数的35． （1）求每个A ，B 类摊位占地面积各为多少平方米？（2）该社区拟建A ，B 两类摊位共90个，且B 类摊位的数量不少于A 类摊位数量的3倍．求建造这90个摊位的最大费用．【分析】（1）设每个B 类摊位的占地面积为x 平方米，则每个A 类摊位占地面积为(2)x +平方米，根据用60平方米建A 类摊位的个数恰好是用同样面积建B 类摊位个数的35这个等量关系列出方程即可．（2）设建A 摊位a 个，则建B 摊位(90)a -个，结合“B 类摊位的数量不少于A 类摊位数量的3倍”列出不等式并解答．【解答】解：（1）设每个B 类摊位的占地面积为x 平方米，则每个A 类摊位占地面积为(2)x +平方米， 根据题意得：6060325x x =+， 解得：3x =，经检验3x =是原方程的解， 所以325+=，答：每个A 类摊位占地面积为5平方米，每个B 类摊位的占地面积为3平方米；（2）设建A 摊位a 个，则建B 摊位(90)a -个， 由题意得：903a a -， 解得22.5a ，建A 类摊位每平方米的费用为40元，建B 类摊位每平方米的费用为30元，∴要想使建造这90个摊位有最大费用，所以要多建造A 类摊位，即a 取最大值22时，费用最大，此时最大费用为：2240530(9022)310520⨯⨯+⨯-⨯=， 答：建造这90个摊位的最大费用是10520元．五、解答题（三）（本大题2小题，每小题10分，共20分）24．（10分）如图，点B 是反比例函数8(0)y x x =>图象上一点，过点B 分别向坐标轴作垂线，垂足为A ，C ．反比例函数(0)ky x x=>的图象经过OB 的中点M ，与AB ，BC 分别相交于点D ，E ．连接DE 并延长交x 轴于点F ，点G 与点O 关于点C 对称，连接BF ，BG ． （1）填空：k = 2 ； （2）求BDF ∆的面积；（3）求证：四边形BDFG 为平行四边形．【分析】（1）设点(,)B s t ，8st =，则点1(2M s ，1)2t ，则1112224k s t st ===；（2）BDF ∆的面积OBD =∆的面积BOA OAD S S ∆∆=-，即可求解； （3）确定直线DE 的表达式为：21522y x m m=-+，令0y =，则5x m =，故点(5,0)F m ，即可求解．【解答】解：（1）设点(,)B s t ，8st =，则点1(2M s ，1)2t ，则1112224k s t st ===，故答案为2；（2）BDF ∆的面积OBD =∆的面积1182322BOA OAD S S ∆∆=-=⨯-⨯=；（3）设点2(,)D m m ，则点2(4,)B m m，点G 与点O 关于点C 对称，故点(8,0)G m ， 则点1(4,)2E m m， 设直线DE 的表达式为：y sx n =+，将点D 、E 的坐标代入上式得2142ms n mms n m ⎧=+⎪⎪⎨⎪=+⎪⎩，解得21252k m b m ⎧=-⎪⎪⎨⎪=⎪⎩， 故直线DE 的表达式为：21522y x m m=-+，令0y =，则5x m =，故点(5,0)F m ， 故853FG m m m =-=，而43BD m m m FG =-==， 则//FG BD，故四边形BDFG 为平行四边形． 25．（10分）如图，抛物线2y bx c ++与x 轴交于A ，B 两点，点A ，B 分别位于原点的左、右两侧，33BO AO ==，过点B 的直线与y 轴正半轴和抛物线的交点分别为C ，D ，BC =．（1）求b ，c 的值；（2）求直线BD 的函数解析式；（3）点P 在抛物线的对称轴上且在x 轴下方，点Q 在射线BA 上．当ABD ∆与BPQ ∆相似时，请直接写出所有满足条件的点Q 的坐标．【分析】（1）先求出点A ，点B 坐标，代入交点式，可求抛物线解析式，即可求解； （2）过点D 作DE AB ⊥于E ，由平行线分线段成比例可求3OE =，可求点D 坐标，利用待定系数法可求解析式；（3）利用两点距离公式可求AD ，AB ，BD 的长，利用锐角三角函数和直角三角形的性质可求30ABD ∠=︒，45ADB ∠=︒，分30ABP ∠=︒或45ABP ∠=︒两种情况讨论，利用相似三角形的性质可求解．【解答】解：（1）33BO AO ==，∴点(3,0)B ，点(1,0)A -， ∴抛物线解析式为：233333333(1)(3)6632y x x x x ++++=+-=--， 333b +∴=-，332c +=-； （2）如图1，过点D 作DE AB ⊥于E ，//CO DE ∴，∴BC BO CD OE=，3BC =，3BO =，∴3OE=，OE ∴=，∴点D横坐标为 ∴点D坐标(1)， 设直线BD 的函数解析式为：y kx b =+，由题意可得：103b k b =+=+⎪⎩，解得：k b ⎧=⎪⎨⎪=⎩，∴直线BD的函数解析式为y =+； （3）点(3,0)B ，点(1,0)A -，点(D1)， 4AB ∴=，AD =2BD =，对称轴为直线1x =，直线:BD y =与y 轴交于点C ， ∴点C ，OC ∴tan CO CBO BO ∠==， 30CBO ∴∠=︒，如图2，过点A 作AK BD ⊥于K ，122AK AB ∴==， 22842DK AD AK ∴=-=-=， DK AK ∴=，45ADB ∴∠=︒，如图，设对称轴与x 轴的交点为N ，即点(1,0)N ，若30CBO PBO ∠=∠=︒， 32BN PN ∴=，2BP PN =， 23PN ∴，43BP = 当BAD BPQ ∆∆∽，∴BP BQ BA BD=， 43(232)23324BQ ∴==+ ∴点23(1Q -，0)； 当BAD BQP ∆∆∽，∴BP BQBD AB=，44BQ∴==，∴点(1Q-+，0)；若45PBO ADB∠=∠=︒，2BN PN∴==，BP==当BAD BPQ∆∆∽，∴BP BQ AD BD=，∴2BQ∴=∴点(1Q-0)；当BAD PQB∆∆∽，∴BP BQBD AD=，2 BQ∴==，∴点(5Q-，0)；综上所述：满足条件的点Q的坐标为(1，0)或(1-+，0)或(1-，0)或(5-0)．。

2020东莞中考
一是整体成绩。

试卷难度、改卷松紧等因素都会产生影响。

2019年中考由于试题难度下降，导致了分数线整体上浮了20分左右。

二是招生计划和考生人数。

假设招生计划增加不少，考生人数维持上一年水平不变，试卷难度也和上一年差不多，那么，分数线肯定下降。

三是志愿热度。

中考录取分数线是在录取工作之后划分的。

各学校分数线的高低反应了考生对各学校的关注度和认可度的差别，也可以通过分数线预估各学校生源质量整体情况。

对于学校来说，高考成绩优秀，口碑良好而被大家认可，自然会吸引更多优秀高分的孩子填报，分数居高不下。

从东莞市2020年各高中录取分数线来看，东莞各高中的整体格局并未改变。

东莞民办五大校与公办六大校牢牢占据第一阵营，短期内不会改变。

公办高中的竞争依旧激烈，优质公办高中的录取分数线会继续保持高位，甚至会继续提高。

今年在东莞参加中考考生仍有5.8万人，比上一年增加约0.88万人，中考参加人数正在逐年增加，招生数量也在逐年提高。

2020年普高率约为60.8%（35322/52000），与2019年（54.6%）相比，提高了6.2%。

这跟东莞正推进的扩容提质千日攻坚行动有着密切的关系。

今年以来，东莞正式启动教育扩容提质千日攻坚行动，加快推进基础教育阶段公办学校新建、改建、扩建工作，大幅增加公办中小学学位供给，扩大优质教育资源覆盖面。

广东省东莞市2020年语文中考试题基础（20分）1.根据课文默写古诗文。

（8分）（1）欲为圣明除弊事，____________。

（韩愈《左迁至蓝关示侄孙湘》（1分）（2）__________，化作春泥更护花。

（龚自珍《己亥杂诗》）（1分）（3）欧阳修在《醉翁亭记》中用“____________,_____________”描绘出两幅对比鲜明的画面，展现了朝暮景色的变化之美。

（2分）（4）请把王勃的《送杜少府之任蜀州》补充完整。

（4分）城阙辅三秦，风烟望五津。

与君离别意，同是宦游人。

___________,______________.___________,______________.2.根据拼音写出相应的词语。

（2分）（1）在实验开始时，我原和小鸭子一样pú fú（）在草中，后来我逐渐换成坐的姿势。

（2）风里带来些新翻的泥土的气息，混着青草味儿，还有各种花的香，都在微微润湿的空气里yùn ni àng（）。

（3）白求恩同志是个医生，他以医疗为职业，对技术jīng yì qíu jīng（）。

（4）富有创造力的人总是zī zī bù juàn（）地汲取知识，使自己学识渊博。

3.依次填人下面横线处的词语，恰当的一项是（）（3分）人格就像人身上的“暗物质"，看不见、摸不着却有不可______的力量，譬如磁力之于磁体，是一呼百应的号召力、_____的吸引力、_____的感染力。

A.忽视潜移默化凝心聚力B.轻视潜移默化凝心聚力C.忽视凝心聚力潜移默化D.轻视凝心聚力潜移默化4.下列对病句的修改不正确的一项是（）（3分）A.肯尼亚经济学家姆旺吉·瓦吉拉表示，70年来，在中国共产党的领导下，中国成就有目共睹，许多非洲国家都希望学习和借鉴中国的发展。

（在发展后加“经验”）B.热播电视剧《安家》以漫画式的笔触刻画出兼具职业特点和人物个性的角色，展现了房产中介的日常生活，表现了普通人买房过程中的喜怒哀乐。

-------------在------------------此------------------卷------------------上-------------------答-------------------题-------------------无------------------------------------绝密★启用前2020年广东省东莞市中考试卷语文基础（20分）一、1.根据课文默写古诗文。

（8分）（1）欲为圣明除弊事，________。

（韩愈《左迁至蓝关示侄孙湘》）（1分） （2）________，化作春泥更护花。

（龚自珍《己亥杂诗》）（1分）（3）欧阳修在《醉翁亭记》中用“________,________”描绘出两幅对比鲜明的画面，展现了朝暮景色的变化之美。

（2分）（4）请把王勃的《送杜少府之任蜀州》补充完整。

（4分）城阙辅三秦，风烟望五津。

与君离别意，同是宦游人。

________,________。

________,________。

2.根据拼音写出相应的词语。

（2分）（1）在实验开始时，我原和小鸭子一样pú fú________在草中，后来我逐渐换成坐的姿势。

（2）风里带来些新翻的泥土的气息，混着青草味儿，还有各种花的香，都在微微润湿的空气里yùn ni àn ɡ________。

（3）白求恩同志是个医生，他以医疗为职业，对技术j īn ɡyì q íu jīn ɡ________。

（4）富有创造力的人总是z ī z ī b ù ju àn________地汲取知识，使自己学识渊博。

3.依次填入下面横线处的词语，恰当的一项是（3分） （ ）人格就像人身上的“暗物质”，看不见、摸不着却有不可________的力量，警如磁力之于磁体，是一呼百应的号召力、________的吸引力、________的感染力。