下载文档原格式
统计作业指导书引言概述：统计学是一门研究数据采集、分析和解释的学科，它在各个领域都有广泛的应用。
在学习统计学的过程中，作业是不可或者缺的一部份。
本文将为您提供一份统计作业指导书，匡助您更好地完成统计学作业。
一、数据采集1.1 选择适当的数据源：在开始采集数据之前，确定数据的来源是非常重要的。
可以选择公开数据集、实地调查或者自己设计实验等方式来获取数据。
1.2 数据采集方法：根据研究目的和数据类型，选择合适的数据采集方法。
例如，可以使用问卷调查、观察、实验等方法来采集数据。
1.3 数据质量控制：在数据采集过程中，要注意数据的准确性和完整性。
可以通过重复测量、数据清洗和筛选等方法来保证数据的质量。
二、数据分析2.1 数据整理和描述统计：在进行数据分析之前，首先要对数据进行整理和描述统计。
包括计算数据的均值、中位数、标准差等统计指标，绘制直方图、散点图等图表来展示数据的分布情况。
2.2 探索性数据分析：通过图表和统计分析方法，对数据进行进一步的探索。
可以使用相关分析、回归分析、方差分析等方法来探索变量之间的关系。
2.3 假设检验和判断统计：根据研究目的，进行假设检验和判断统计。
可以使用t检验、方差分析、卡方检验等方法来验证研究假设，并对总体参数进行判断。
三、数据解释和报告3.1 结果解释：在数据分析完成后，要对结果进行解释。
解释应该清晰、准确地表达出数据的含义和结果的统计学意义。
3.2 结果展示：将数据分析的结果以图表、表格等形式进行展示，使读者能够更直观地理解数据和结果。
3.3 结果报告：根据具体要求，撰写数据分析的报告。
报告应包括研究目的、数据采集和分析方法、结果和结论等内容。
四、常见问题和解决方法4.1 数据异常值处理：在数据分析过程中，可能会遇到异常值的问题。
可以通过删除异常值、替换异常值或者使用鲁棒统计方法来处理异常值。
4.2 样本量不足问题：当样本量较小时，可能会影响结果的可靠性。
可以通过增加样本量、使用非参数统计方法或者进行摹拟分析来解决样本量不足的问题。
管理统计学课后习题答案第一章：统计学基础1. 描述统计与推断统计的区别是什么？- 描述统计关注的是对数据集的描述和总结，如均值、中位数、众数、方差等；而推断统计则使用样本数据来推断总体特征，包括参数估计和假设检验。
2. 什么是正态分布？- 正态分布是一种连续概率分布，其形状呈钟形曲线，具有对称性，其数学表达式为 \( N(\mu, \sigma^2) \)，其中 \( \mu \) 为均值，\( \sigma^2 \) 为方差。
第二章：数据收集与处理1. 抽样误差和非抽样误差的区别是什么？- 抽样误差是由于样本不能完全代表总体而产生的误差；非抽样误差则来源于数据收集和处理过程中的其他问题，如测量误差、数据录入错误等。
2. 描述数据清洗的步骤。
- 数据清洗通常包括：识别和处理缺失值、异常值检测与处理、数据标准化和归一化、数据整合等步骤。
第三章：描述性统计分析1. 计算给定数据集的均值和标准差。
- 均值是数据集中所有数值的总和除以数据点的数量。
标准差是衡量数据点偏离均值的程度，计算公式为 \( \sigma =\sqrt{\frac{1}{N}\sum_{i=1}^{N}(x_i - \mu)^2} \)。
2. 解释箱型图（Boxplot）的作用。
- 箱型图是一种图形表示方法，用于展示数据的分布情况，包括中位数、四分位数、异常值等，有助于快速识别数据的集中趋势和离散程度。
第四章：概率分布1. 什么是二项分布？- 二项分布是一种离散概率分布，用于描述在固定次数 \( n \) 的独立实验中，每次实验成功的概率为 \( p \) 时，成功次数的概率分布。
2. 正态分布的数学性质有哪些？- 正态分布具有许多重要性质，如对称性、均值等于中位数、68-95-99.7规则等。
第五章：参数估计1. 解释点估计和区间估计的区别。
- 点估计是用样本统计量来估计总体参数的单个值；区间估计是在一定置信水平下，给出总体参数可能落在的区间范围。
《管理统计学》作业参考答案统计推断（P147—148）5.解：设7.6:7.6:10>↔≤μμH H 11.3200/5.27.625.7/0=-=-=nS x U μ当α=0.01时,，所以拒绝原假设，即当α=0.01时，现今每个家33.201.0=>u U 庭每天看电视的平均时间较10年前显著增大。
6.解：设211210::μμμμ>↔≤H H 233.250140165.278224823801121=+-=+-=n n S yx t T当α=0.05时，，拒绝，故在置信水平为95%时可以认为第一分)88(05.0t t >0H 店的营业额高于第二分店的营业额。
当α=0.01时，，接受，故在置信水平为99%时还没有充分的把)88(05.0t t <0H 握说明第一分店的营业额高于第二分店的营业额。
9.解：这是一个成对比较问题设且，0:0:10>↔≤d d H H μμ3486.0,375.0==d d s x ()83311.19t 0.05=402.310/3486.0375.0/*===dd dn S x t 当α=0.05时，，拒绝原假设，即显著性水平为5%时可以判断人的)9(05.0*t t >情感更显著地表现在左脸上。
非参数检验1.（P 168）解：设消费额与分店位置无关，:0H 消费额与分店位置有关:1H 根据题意可以计算理论频数得列联表如下：由于，而()()84146.3)1(,111,2,2205.0==--==χb a b a 接受，即有95%的把握说明消费额与分店位置无关。
0H 84146.3)1(07788.2)(205.022=<=-=∑χχEE O回归分析和相关分析（P136）1.解：图中数据如下：xy nx bnyx b y a S S b y x n y x y y x x S y n y y y S x n x x x S n y x y x y xiixxxyii i i i n i i xy i i n i i yy i i n i i xx i i i i i i0535.49491.243势势9491.243103270535.4103765,0535.41.4505.1824势5.182437653271011249401))((5.900237651011426525)(1)(1.45032710111143)(1)(10,1426525,11143,124940,3765,3271222212222122+==⨯-=-=-=====⨯⨯-=-=--==⨯-=-=-==⨯-=-=-=======∧∧∧∧∧===∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑直线回归方程为：(1)相关系数906375.05.90021.4505.1824 =⨯==yyxx xyS S S r (2)当广告费为30万元时，该周销售额的区间估计为：()()()()()()0817.400,0265.3311.4507.32301011306.21722.14300535.49491.243)(11)2(1722.148/81.1606210/7.32,81.16065.9002906375.011,306.22102202/0222/05.0=-++⨯⨯±⨯+=⎪⎪⎭⎫ ⎝⎛-++-±+∈==-===⨯-=-==-∧∧xx yy S x x n n st x b a y RSS s x S r RSS t α(3)当广告费为42万时周平均销售额的95%置信区间为：()()8607.431,5315.3961.4507.3242101306.21722.14420535.49491.243)(1)2(2202/0=-+⨯⨯±⨯+= ⎝⎛⎪⎪⎭⎫-+-±+∈+∧∧xx S x x n n st x b a bx a α时间序列（P219）解：题中数据可整理如下：(1)、因此有：ty nt b ny t b y a t t n y t ty n S Sb n t ty y t tt t tttytt835.0595.94势势势595.9414105835.0141412835.01102510151414121051078014)(14,1015,10780,1412,105222+==⨯-=-=-==-⨯⨯-⨯=--=======∧∧∧∧∧∑∑∑∑∑∑∑∑∑∑∑方程为：直线(2)、对于加法模型，有S=y-T ，根据实际数据和直线趋势方程，得下表：把同一季节的因子作一平均，得季度平均值，如下表所示：因5.310+(-6.025)+(-9.440)+10.392=0.237，故修正因子，每05925.04237.0==L 个季节因子减去L 得修正后季节因子为：5.251，-6.084，-9.499，10.333。
目录实验一用Excel 搜集与整理数据⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1实验二用Excel 进行时间序列分析⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3实验三用Excel 进行指数分析⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6实验四用Excel 进行相关与回归分析⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯8实验五用Excel 进行预测⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯12主要参考文献⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯17实验一 用 Excel 整理数据实验目的和任务掌握用 EXCEL 进行数据的搜集整理和显示 实验仪器、设备及材料 计算机小麦的单位面积产量与降雨量和温度有一定关系。
为了解它们之间的关系形态，收集数据如下序号温度(℃)降雨量 (mm)产量 (kg/hm2)1 6 25 22502 8 40 34503 10 58 45004 13 68 57505 14 110 58006 16 98 7500 7211208250要求：绘制小麦产量与降雨量和温度的气泡图，并分析它们之间的关系图1第二步：选中某一单元格，单击插入菜单，选择图表选项，弹出图表向导对话框，再选择气泡图。
如图图2第三步： 单击下一步，再在子图表类型中选择一种类型，这里我们选用系统默认的方式。
然后单击下一步按钮，实验原理及步骤2：第一步：把数据输入到工作表中，如图 1 所示：开源数据对话框。
再选择系列按钮，在对话框中填入数据 X 、 Y 以及其对应值，如图 3 所示：实验二 用 Excel进行时间序列分析四、实验结论 从气泡图上可以看出，也在提高（气泡变大） 。
随着气温的增高， 降雨量也在增加； 随着气温好降雨量的增加， 小麦的产量图3第四步：单击完成按钮，即可得如图 4 所示的气泡图：图4、实验目的和任务用EXCEL进行时间序列分析、实验仪器、设备及材料计算机三、实验原理及步骤1、我国1990 年至2004 年人均GDP的情况如下：（2）计算长期趋势2、一家商场2003-2005 年各季度的销售额数据（单位：元万）如下表所示一）测定发展速度和平均发展速度图5第一步：在A列输入年份，在 B 列输入人均GDP。
第六章1. 解: 概率是衡量某一特定事件的机会或可能性的数量指标。
概率的统计定义:在相同条件下，重复做n 次试验，事件A 出现了m 次，当n 很大时，频 率m /n 稳定在某个数值p 的附近。
当n 趋近于∞时，频率m/n 趋近于p 值，则称p 为事件A 的概率，记为P （A ）= p 。
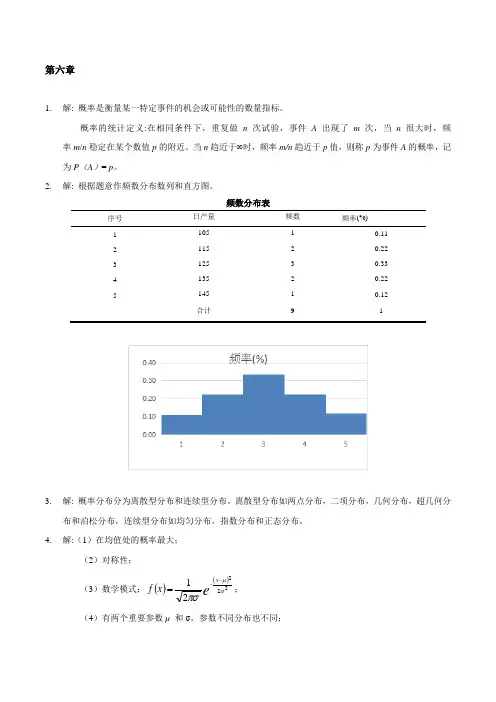
2. 解: 根据题意作频数分布数列和直方图。
频数分布表序号 日产量 频数 频率(%)1 105 1 0.112 115 2 0.223 125 3 0.334 135 2 0.22 5145 1 0.12合计913. 解: 概率分布分为离散型分布和连续型分布。
离散型分布如两点分布，二项分布，几何分布，超几何分布和泊松分布，连续型分布如均匀分布，指数分布和正态分布。
4. 解:（1）在均值处的概率最大；（2）对称性；（3）数学模式：()()ex x f 22221σμπσ--=；（4）有两个重要参数µ 和σ，参数不同分布也不同；（5）曲线对横轴是渐近的，区间与概率的关系：()()ασμσμ-=-=-1≤x ≤x t P t P5. 解:()⎪⎭⎫ ⎝⎛-Φ=⎪⎭⎫ ⎝⎛-≤=⎪⎭⎫⎝⎛-≤-=≤σμσμσμσμC C Z P C P C P x x 查《标准正态分布表》中Z =（C －μ）/σ的概率。
6. 解: 当Z=1，2，3时，标准正态分布下的概率分别为：()()()()%..ΦΦΦZ P 2768184134502112111=-⨯=-=--=≤ ()()()()%..ΦΦΦZ P 459519772502122222=-⨯=-=--=≤ ()()()()%..ΦΦΦZ P 739919986502132333=-⨯=-=--=≤7. 解: ()1346489701..Z -=-= ()39.26.4891002=-=Z查《正态分布表》得()()%..ΦZ Φ001901341=-= ()()%..ΦZ Φ1576993922==()()()%.Z ΦZ Φx P 1557991007012=-=≤≤8. 解: ()()()()%..ΦZ Φx P x P 842403921110011002=-=-=≤-=>9. 解: 都是离散型分布，二项分布的极限分布是泊松分布，可以证明，当p 很小（小于0.1），n 较大（大于总体0.1），可用泊松分布作为二项分布的近似，两种分布的结论几乎完全一致。
第十二章1.解：统计决策是解决为实现已确定的目标如何抉择行动方案，也即要回答“做什么”和“怎么做”的问题。
从而使统计在国民经济宏观调控和企业微观管理中发挥更大的作用。
自20世纪50年代瓦尔德发表《统计决策函数》以来，统计决策的理论和方法发展很快，应用日益广泛。
在竞争激烈、瞬息万变的市场经济中，学习和掌握科学的决策方法，对于提高经营管理的决策水平，减少决策失误，有十分重要的意义。
统计决策是根据已掌握的信息对实现的目标的未来行动所作出的决定。
决策的主体、目标、环境和行动方案构成了决策系统的四个基本因素。
在管理中，决策者经常会遇到各种决策问题，如确定型问题、不确定型问题和对抗型问题。
在决策中，就有确定型决策、不确定型决策和对抗型决策等决策类型。
无论哪种决策类型，都要经过确定决策目标、拟定决策方案、预测方案得失、选择最优方案和实施方案等五个基本决策程序。
一般来说，统计决策有广义和狭义之分，凡是应用统计方法进行的决策称为广义的统计决策。
狭义的统计决策是指不确定情况下的决策。
在不确定情况下进行决策需要具备以下四个条件：（1）决策人要求达到的一定目标，如利润最大，损失最小，质量最高，等等。
从不同的目的出发往往有不同的决策标准。
（2）存在两个或两个以上可供选择的方案，所有的方案构成一个方案的集合。
（3）存在不以决策人主观意志为转移的客观状态，或称为自然状态。
所有可能出现的自然状态构成状态空间。
（4）在不同情况下采取不同方案所产生的结果是可以计量的。
所有的结果构成一个结果空间。
凡符合这四个条件的决策，即称为狭义的统计决策。
统计决策面对着的是各种不确定性因素，因此，统计决策的最显著特点是运用概率进行判断和抉择。
在这个过程中，常用到决策、收益（损失）和风险三个重要的基本概念。
决策是对方案的选择，不同的方案带来的收益或损失不同，最佳方案是能够使平均风险达到最小的方案。
要作出正确的决策，必须遵循可行性、经济性和合理性三大原则。
管理统计学课后习题答案管理统计学课后习题答案统计学是一门研究数据收集、分析和解释的学科，对于管理者来说，掌握统计学知识是非常重要的。
通过统计学分析，管理者可以更好地了解企业的运营情况，做出科学的决策。
而课后习题则是巩固和应用这些知识的重要方式。
本文将通过一些实例，为大家提供一些管理统计学课后习题的答案。
1. 样本与总体的关系在统计学中，样本是从总体中抽取的一部分个体或观察值。
样本的特点是具有代表性，可以通过样本来推断总体的特征。
例如，某公司想要了解员工的平均工资水平，但是由于员工众多，无法对每个员工进行调查。
这时，可以通过抽取一部分员工作为样本，通过对样本的调查和分析，来推断总体的平均工资水平。
2. 描述统计与推断统计统计学分为描述统计和推断统计两个方面。
描述统计是通过对收集到的数据进行整理、汇总和分析，来描述数据的特征和分布情况。
例如，可以通过计算平均值、中位数、标准差等指标，来描述一个数据集的中心趋势和离散程度。
推断统计则是通过对样本数据进行分析，来对总体进行推断。
通过对样本的调查和分析，可以得到总体的估计值，并对总体特征进行推断。
例如，某公司想要了解全国消费者对某一产品的满意度，但是无法对所有消费者进行调查。
这时，可以通过抽取一部分消费者作为样本，通过对样本的调查和分析，来推断全国消费者对该产品的满意度。
3. 频数分布与频率分布在统计学中，频数分布是将数据按照一定的范围进行分类，并统计每个范围内的数据个数。
频数分布可以通过直方图来展示，可以直观地了解数据的分布情况。
例如，某公司想要了解员工的年龄分布情况，可以将员工的年龄按照一定的范围进行分类，并统计每个范围内的员工人数。
频率分布则是将频数除以总数，得到每个范围内的相对频率。
相对频率可以反映每个范围内数据的相对比例。
例如，某公司想要了解员工的年龄分布情况，并且希望知道每个年龄段的员工所占比例。
可以将员工的年龄按照一定的范围进行分类，并统计每个范围内的员工人数，然后除以总人数，得到每个范围内的相对频率。
一、实验目的通过本实验，使学生掌握管理统计学的基本概念、原理和方法，提高运用统计学方法分析和解决实际问题的能力。
同时，培养学生的团队协作精神和创新意识。
二、实验原理管理统计学是研究管理活动中数据的搜集、整理、分析和解释的统计学。
它主要涉及以下几个方面：1. 数据搜集：通过调查、观察、实验等方法，获取管理活动中的原始数据。
2. 数据整理：对搜集到的原始数据进行筛选、分类、编码等处理，使之系统化、条理化。
3. 数据分析：运用统计学方法，对整理后的数据进行描述性分析、推断性分析等。
4. 结果解释：根据分析结果，提出合理的建议和对策。
三、实验内容1. 数据搜集本实验以某企业为例，通过查阅相关资料，搜集该企业2019年的销售额、利润、员工人数等数据。
2. 数据整理将搜集到的数据输入Excel表格，并进行以下处理：（1）数据清洗：删除异常值和缺失值。
（2）数据分类：根据销售额、利润等指标，将企业分为不同类别。
（3）数据编码：对员工人数、部门等变量进行编码。
3. 数据分析（1）描述性分析对销售额、利润等指标进行描述性统计分析，包括计算均值、标准差、最大值、最小值等。
（2）推断性分析运用假设检验、方差分析等方法，分析不同类别企业之间的差异。
4. 结果解释根据分析结果，提出以下建议：（1）针对不同类别企业，制定有针对性的营销策略。
（2）优化企业内部管理，提高员工工作效率。
（3）加强企业创新能力，提升市场竞争力。
四、实验结果1. 描述性分析结果（1）销售额：平均销售额为100万元，标准差为20万元。
（2）利润：平均利润为10万元，标准差为2万元。
（3）员工人数：平均员工人数为50人，标准差为10人。
2. 推断性分析结果（1）不同类别企业销售额差异显著（p<0.05）。
（2）不同类别企业利润差异显著（p<0.05）。
五、实验结论通过本次实验，我们掌握了管理统计学的基本原理和方法，提高了运用统计学方法分析和解决实际问题的能力。
《管理统计学》作业参考答案统计推断（P147—148）5.解：设7.6:7.6:10>↔≤μμH H11.3200/5.27.625.7/0=-=-=nS x U μ当α=0.01时,33.201.0=>u U ，所以拒绝原假设，即当α=0.01时，现今每个家庭每天看电视的平均时间较10年前显著增大。
6.解：设211210::μμμμ>↔≤H H233.250140165.278224823801121=+-=+-=n n S y x t T当α=0.05时，)88(05.0t t >，拒绝0H ，故在置信水平为95%时可以认为第一分店的营业额高于第二分店的营业额。
当α=0.01时，)88(05.0t t <，接受0H ，故在置信水平为99%时还没有充分的把握说明第一分店的营业额高于第二分店的营业额。
9.解：这是一个成对比较问题设0:0:10>↔≤d d H H μμ且3486.0,375.0==d d s x ，()83311.19t 0.05=402.310/3486.0375.0/*===dd d n S x t当α=0.05时，)9(05.0*t t >，拒绝原假设，即显著性水平为5%时可以判断人的情感更显著地表现在左脸上。
非参数检验1.（P 168）解：设:0H 消费额与分店位置无关，:1H 消费额与分店位置有关根据题意可以计算理论频数得列联表如下：由于()()84146.3)1(,111,2,2205.0==--==χb a b a ，而接受0H ，即有95%的把握说明消费额与分店位置无关。
84146.3)1(07788.2)(205.022=<=-=∑χχEE O回归分析和相关分析（P136）1.解：图中数据如下：x y nx bnyx b y a S S b y x n y x y y x x S y n y y y S x n x x x S n y x y x y xiixxxy ii i i i n i i xy i i ni i yy i i ni i xx i i i i i i0535.49491.243因此9491.243103270535.4103765,0535.41.4505.1824故5.182437653271011249401))((5.900237651011426525)(1)(1.45032710111143)(1)(10,1426525,11143,124940,3765,327122*********2+==⨯-=-=-=====⨯⨯-=-=--==⨯-=-=-==⨯-=-=-=======∧∧∧∧∧===∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑直线回归方程为：(1)相关系数906375.05.90021.4505.1824 =⨯==yyxx xy S S S r(2)当广告费为30万元时，该周销售额的区间估计为：()()()()()()0817.400,0265.3311.4507.32301011306.21722.14300535.49491.243)(11)2(1722.148/81.1606210/7.32,81.16065.9002906375.011,306.22102202/0222/05.0=-++⨯⨯±⨯+=⎪⎪⎭⎫ ⎝⎛-++-±+∈==-===⨯-=-==-∧∧xx yy S x x n n st x b a y RSS s x S r RSS t α(3)当广告费为42万时周平均销售额的95%置信区间为：()()8607.431,5315.3961.4507.3242101306.21722.14420535.49491.243)(1)2(2202/0=-+⨯⨯±⨯+= ⎝⎛⎪⎪⎭⎫-+-±+∈+∧∧xx S x x n n st x b a bx a α时间序列（P219）解：题中数据可整理如下：(1)、因此有：ty n t b n y t b y a t t n y t ty n S Sb n t ty y t tttttty tt835.0595.94趋势故595.9414105835.0141412835.01102510151414121051078014)(14,1015,10780,1412,105222+==⨯-=-=-==-⨯⨯-⨯=--=======∧∧∧∧∧∑∑∑∑∑∑∑∑∑∑∑方程为：直线(2)、对于加法模型，有S=y-T ，根据实际数据和直线趋势方程，得下表：把同一季节的因子作一平均，得季度平均值，如下表所示：因5.310+(-6.025)+(-9.440)+10.392=0.237，故修正因子05925.04237.0==L ，每个季节因子减去L 得修正后季节因子为：5.251，-6.084，-9.499，10.333。
管理统计学_实验指导书实验⼀⽤Excel作频数分布表和图形⼀、实验⽬的1、学会应⽤Excel作频数分布表2、学会应⽤Excel作条形图⼆、实验仪器计算机，Excel软件三、实验内容与步骤（参考课本《管理统计学》P167 例2）例 2 ⼀家市场调查公司为研究不同品牌饮料的市场占有率，对随机抽取的⼀家超市进⾏了调查。
调查员在某天对50名顾客购买饮料的品牌进⾏了记录，如果⼀个顾客购买某⼀品牌的饮料，就将这⼀饮料的品牌名字记录下来。
下表是原始数据。
表1 原始数据实验步骤：1、打开EXCEL，菜单“⼯具”中查找“数据分析”，如果有此模块，请继续第2步；如果没有，请选择“加载宏”，加载如下模块——分析⼯具库、分析⼯具库（VBA）、规划求解。
然后继续第2步。
2、将不同品牌的饮料分别⽤⼀个数字代码表⽰，输⼊到Excel表格中3、选择“⼯具”下拉菜单，选择“数据分析”选项，在分析⼯具中选“直⽅图”4、出现对话框时，在输⼊⾥设定相应的“输⼊区域”和“接收区域”；在输出选项⾥，设定“输出区域”；选择“累积百分率”；选择“图表输出”；选择“确定”，得到结果。
四、实验后提交实验报告的格式（实验报告要求⼿写，不能打印）1、Excel作频数分布表和条形图的步骤2、柏拉图的作⽤是什么？查阅资料，简述其在⼯业⼯程领域的应⽤。
实验⼆⽤Excel计算描述统计量⼀、实验⽬的1、学会应⽤Excel计算描述统计量2、掌握常⽤描述统计量及计算公式⼆、实验仪器计算机，Excel软件三、实验步骤（可参考课本P172）1、打开⼯作表，在A列输⼊10个数2、选择“⼯具”下拉菜单，选择“数据分析”选项，在分析⼯具中选择“描述统计”3、当出现对话框时，在“输⼊区域”⽅框内输⼊A1:A10，在“输出”选项中选择“新⼯作表”，然后选择“汇总统计”，最后选择“确定”。
四、实验后提交实验报告的格式（实验报告要求⼿写，不能打印）1、回答你所输⼊的10个数据是？2、描述统计量的各个计算结果是？3、查阅资料，解释标准误差、峰值、偏倚度的意义和作⽤。
.=《管理统计学》实验指导书及实验报告王金玉编著沈阳航空工业学院经济管理学院班级学号姓名成绩实验一用Excel对数据的图表描述实验目的：掌握用EXCEL进行数据的搜集整理和显示实验步骤：用Excel进行数据的统计分组描述，可以获得相应数据分组的频数、频率以及向上向下累计频数、频率的情况，并能做出相应的直方图、折线图等描述数据分布特征的统计图形。
我们举例介绍一下数据的Excel图表描述的操作方法。
【例1-1】为了确定灯泡的使用寿命（小时），在一批灯泡中随机抽取100只进行测试，所得结果如下，数据进行适当的分组，编制频数分布表；（2）制作合适的统计图反映分布特征。
700 716 728 719 685 709 691 684 705 718706 715 712 722 691 708 690 692 707 701708 729 694 681 695 685 706 661 735 665668 710 693 697 674 658 698 666 696 698706 692 691 747 699 682 698 700 710 722694 690 736 689 696 651 673 749 708 727688 689 683 685 702 741 698 713 676 702701 671 718 707 683 717 733 712 683 692693 697 664 681 721 720 677 679 695 691713 699 725 726 704 729 703 696 717 688一、编制分布数列在Excel中有两类方法可以实现分布数列的编制：一是使用相关的函数，如Frequency函数；二是使用分析工具中的【直方图】工具。
本例中我们采用函数方法。
具体步骤如下：第一步：将表1-1中的数据输入或导入到Excel电子表格中，并输入相应的分组数据。
如图1-1所示。
图1-1图1-1中，C、J列均为原始输入数据，寿命数据在A2:A101（图中未完全显示出来）,J列的接受区域的各个数据（各组的上限值）是使用Frequency函数或【直方图】分析工具编制分布数列所必需的数据。
第二步：选定D5：D14，输入公式“=Frequency（A2:A101，J5：J14）”，然后按Ctrl+Shift+Enter组合键，即可计算出各组的频数。
该函数的第一个参数指定用于编制数列的原始数据，第二个参数指定每一组的上限。
在D15中输入公式“=sum （D5:D14）”计算出频数的合计。
第三步：计算频率。
在E5中输入公式“=D5/D$15*100”，然后将该公式复制到E6:E14即可。
D15存放的是频数的合计数。
第四步：计算向上累计频数。
在F5单元格中输入“=D5”，在F6单元格中输入公式“=D6+F5”，再将公式复制到F7:F14。
第五步：计算向下累计频数。
在H14中输入公式“=D14”，在H13单元格中输入公式“=H14+D13”，再将公式复制到H5:H12。
可以采用向上填充的方法复制公式，即选中H5:H13单元格区域，然后点击菜单【编辑】→【填充】→【向上填充】。
第六步：参照第三步，可以分别计算出向上累计频率和向下累计频率，如图1-1中G、I列所示。
二、用Excel作统计图Excel提供的统计图有多种，包括柱形图、条形图、折线图、饼图、散点图、面积图、环形图、雷达图、曲面图、气泡图、股价图、圆柱图、圆锥图等，各种图的作法大同小异。
根据上面所得的频数（频率）以及向上、向下累计频数（频率）表，可以做出相应的统计图来直观描述数据的统计特征。
第一步：做直方图。
点击菜单【插入】→【图表】，弹出图表向导对话框，选择图表类型【柱形图】，数据区域选择频数（或频率）所在的区域D5:D14，设定其余参数即可得到频数分布的柱形图，，若要把它变成直方图，可按如下操作：用鼠标左键单击任一直条，然后右键单击，在弹出的快捷菜单中选取数据系列格式，弹出数据系列格式对话框，在对话框中选择选项标签，把间距宽度改为0，按确定后即可得到直方图，如图1-2所示：图1-2第二步：做折线图。
右键单击直方图，在弹出菜单中选择【图表类型】，将其更改为折线图即可得到频数折线图，如图1-3所示。
图1-3第三步：做累计频数（频率）图。
此图以折线图形式显示为佳。
操作步骤与第一步相似，在图表类型中选择【折线图】，数据区域选择向上累计频数（频率）以及向下累计频数（频率）。
即可得到向上、向下累计频数（频率）图。
见图1-4。
图1-４根据所得的频数图表，我们可以看出此类灯泡的寿命平均约为７００小时，集中趋势比较明显，近似服从于正态分布。
实验二用Excel、SPSS做描述统计实验目的：用EXCEL计算描述统计量，从而求出有些参数的点估计。
实验步骤：EXCEL中用于计算描述统计量的方法有两种，函数方法和描述统计工具的方法。
一、用函数计算描述统计量常用的描述统计量有众数、中位数、算术平均数、调和平均数、几何平均数、极差、四分位差、标准差、方差、平均差、标准差系数、偏斜度和峰度等。
一般来说，在Excel中求这些统计量，未分组资料可用函数计算，已分组资料可用公式计算。
这里我们仅介绍如何用函数计算。
(一)众数【例2】：为了解某经济学院新毕业大学生的工资情况，随机抽取30人，月工资如下：156013401600141015901410161015701710155014901690138016801470 153015601250156013501560151015501460155015701980161015101440 用函数方法求众数，应先将30个人的工资数据输入A1：A30单元格，然后单击任一空单元格，输入“=MODE （A1：A30）”，回车后即可得众数为1560(二)中位数仍采用上面的例子，单击任一空单元格，输入“=MEDIAN（A1：A30）”，回车后得中位数为1550。
(三)算术平均数单击任一单元格，输入“=A VERAGE（A1：A30）”，回车后得算术平均数为1535。
(四)几何平均数单击任一单元格，输入“=GEOMEAN（A1：A30）”，回车后得几何平均数为1529.425。
(五)调和平均数单击任一单元格，输入“=HARMEAN（A1：A30）”，回车后得调和平均数为1523.971。
(六)四分位数在相邻的五个单元格，依次输入“=QUARTILE（A1：A30,0）”、“=QUARTILE（A1：A30,1）”、“=QUARTILE （A1：A30,2）”、“=QUARTILE（A1：A30,3）”、“=QUARTILE（A1：A30,4）”，可得这组数据的最小值、最大值以及中间的三个四分位点，按照输入公式的顺序得到这五个点为：1250、1462.5、1550、1585、1980。
(七)极差单击任一单元格，输入“=MAX（A1：A30）-MIN(A1：A30)”，回车后得极差为730。
(八)标准差单击任一单元格，输入“=STDEV（A1：A30）”，回车后得标准差为135.0287。
(九)平均差单击任一单元格，输入“=A VEDEV（A1：A30）”，回车后得平均差为93.66667。
(十)方差单击任一单元格，输入“=V AR（A1：A30）”，回车后得方差为18232.76。
(十一)偏斜度单击任一单元格，输入“=SKEW（A1：A30）”，回车后得偏斜度为0.832785。
(十二)峰度单击任一单元格，输入“=KURT（A1：A30）”，回车后得峰度值为3.257451。
二、描述统计工具箱的使用仍使用上面的例子，我们已经把数据输入到A1：A30单元格，然后按以下步骤操作：第一步：在工具菜单中选择数据分析选项，从其对话框中选择描述统计，按确定后打开描述统计对话框，如图13-14所示：第二步：在输入区域中输入$A$1:$A$30，在输出区域中选择$C$1，其他复选框可根据需要选定，选择汇总统计，可给出一系列描述统计量；选择平均数置信度，会给出用样本平均数估计总体平均数的置信区间；第K大值和第K小值会给出样本中第K个大值和第K个小值。
第三步：单击确定，可得输出结果，如图2-1所示：图2-2描述统计输出结果图2-1描述统计对话框上面的结果中，平均指样本均值；标准误差指样本平均数的标准差；中值即中位数；模式指众数；标准偏差指样本标准差，自由度为n-1；峰值即峰度系数；偏斜度即偏度系数；区域实际上是极差，或全距。
（可见中文版的翻译有问题）利用频数分布过程可以方便地对数据按组进行归类整理，形成各变量的不同水平（分组）的频数分布表和图形，以便对各变量的数据的特征和记录分布状况有一个概括的认识。
三、SPSS描述性统计分析描述统计分析过程通过平均值、算术和、标准差、最大值、最小值、方差、极值和均值标准误等统计量变量进行描述。
操作步骤（1）在数据窗中建好或打开一个数据文件。
（2）按Analyze→Descriptive Statistics→Descriptives打开Descriptives对话框。
（3）在左侧的源变量中选择一个或多个变量作为待分析变量移入Variable(s).框中。
（4）选中Save standardized values as variables 复选项，对所选择的每一个变量进行标准化产生相应的Z得分，作为新变量保存在数据窗中。
其变量名为相应变量名加前缀Z。
（5）单击Options 按钮，展开Options对话框，在对话框中可以指定其他统计量与输出结果显示的顺序基本统计量与Display order输出顺序栏的具体操作，参见5.1中Statisticst 和Format对话框中的选项。
（6）单击OK按钮提交系统执行。
四、SPSS作统计图与Excel比较而言，SPSS提供了更多的统计图。
例如，可以利用SPSS软件迅速做出箱形图。
使用SPSS做箱形图的操作步骤如下：（1）建立或打开了数据文件。
（2）按照Graphs→Boxplot的顺序打开【Boxplot】箱线图作图对话框。
（3）在对话框下侧的数据类型中选择待分析数据的类型—分组数据或者单组数据，单击右上侧的Define按钮，进入下一界面。
（4）若是单组变量，在左侧的源变量框中选择待描述的变量，单击向右箭头按钮使其进入右侧的Boxes Represent框中。
如是分组变量，比如是两组数据则选择第一列上连续输入第一组及第二组数，然后在第二列上输入1（第一列第一组数据的相应位置）或2（第一列第二组数据的相应位置），然后在左侧的源变量框中选择相应的变量（第一列），单击向右箭头按钮使其进入右侧的Variable框中，并从源变量框中选择对应的分组变量（第二列）移至Category Axis框中。
