§1.2中心投影和平行投影及空间几何体的三视图

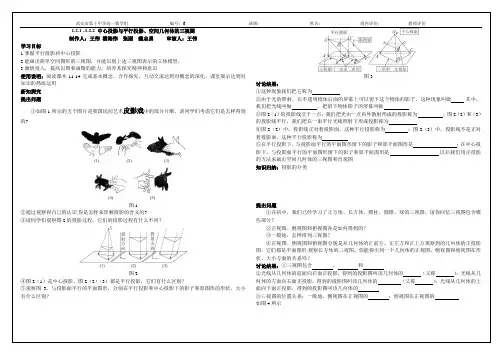
图1
你是怎样来理解投影的含义的?
的投影过程，它们的投影过程有什么不同？
图2
）是中心投影、图2（2）（3）都是平行投影，它们有什么区别？
，与投影面平行的平面图形，分别在平行投影和中心投影下的影子和原图形的形状、大小
图3
②由于光的照射，在不透明物体后面的屏幕上可以留下这个物体的影子，这种现象叫做
，把留下物体影子的屏幕叫做.
图4
的位置关系，即反映了物体的
(1) (2)
的位置关系，即反映了物体的
的位置关系，即反映了物体的
所示的矿泉水瓶的三视图.
引导学生认识这种容器的结构特征.矿泉水瓶是我们熟悉的一种容器，这种容器是简单的组合体，
其主要结构特征是从上往下分别是圆柱、圆台和圆柱
图6
7所示的几何体的三视图
图7
课堂小结。

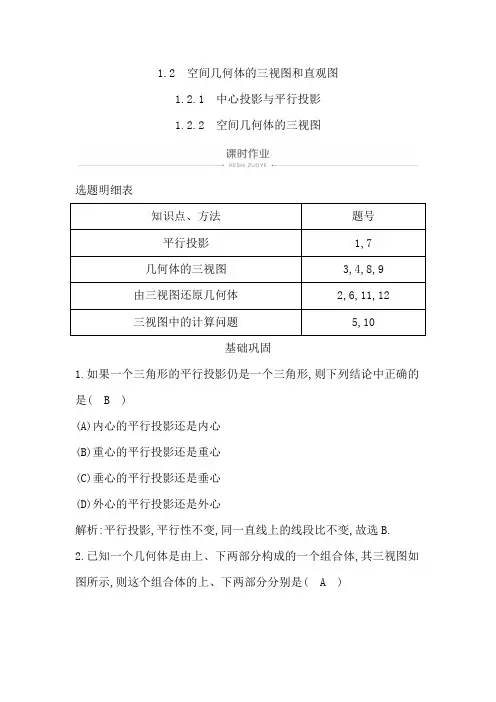
1.2 空间几何体的三视图和直观图1.2.1 中心投影与平行投影1.2.2 空间几何体的三视图选题明细表基础巩固1.如果一个三角形的平行投影仍是一个三角形,则下列结论中正确的是( B )(A)内心的平行投影还是内心(B)重心的平行投影还是重心(C)垂心的平行投影还是垂心(D)外心的平行投影还是外心解析:平行投影,平行性不变,同一直线上的线段比不变,故选B. 2.已知一个几何体是由上、下两部分构成的一个组合体,其三视图如图所示,则这个组合体的上、下两部分分别是( A )(A)上部是一个圆锥,下部是一个圆柱(B)上部是一个圆锥,下部是一个四棱柱(C)上部是一个三棱锥,下部是一个四棱柱(D)上部是一个三棱锥,下部是一个圆柱解析:由几何体的三视图可知,该组合体的上部是一个圆锥,下部是一个圆柱.3.一几何体的直观图如图,下列给出的四个俯视图中正确的是( B )解析:由直观图可知,该几何体由一个长方体和一个截角三棱柱组成.从上往下看,外层轮廓线是一个矩形,矩形内部有一条线段连接的两个三角形.故选B.4.由8个大小相同的正方体组成的几何体的正视图和俯视图如图所示,则这个几何体的侧视图是( A )解析:因为该组合体共有8个小正方体,由俯视图和正视图,可知该组合体共有两层,第一层有5个小正方体,第二层有3个小正方体,且全位于第二层的左边,所以侧视图应该是两层,每层两个,故选A.5.(2018·成都高二期末)某几何体的三视图如图所示,则该几何体的侧面积为( D )(A)4+2(B)2+4(C)2+2(D)4+4解析:由三视图得到几何体如图:正方体的棱长为2,该四棱锥P ABCD的侧面积是×2×2+×2×2+×2×2+×2×2=4+4;故选D.6.如图中的三视图表示的几何体是.解析:根据三视图的生成可知,该几何体为三棱柱.答案:三棱柱7.如图甲所示,在正方体ABCD A1B1C1D1中,E,F分别是AA1,C1D1的中点,G 是正方形BCC1B1的中心,则四边形AGFE在该正方体的各个面上的投影可能是图乙中的.解析:在平面ABCD和平面A1B1C1D1上的投影是图乙(1);在平面ADD1A1和平面BCC1B1上的投影是图乙(2);在平面ABB1A1和平面DCC1D1上的投影是图乙(3).答案:(1)(2)(3)8.如图,四棱锥的底面是正方形,顶点在底面上的射影是底面正方形的中心,试画出其三视图.解:所给四棱锥的三视图如图.能力提升9.如图几何体是由五个相同正方体叠成的,其三视图中的侧视图序号是( A )(A)(1) (B)(2) (C)(3) (D)(4)解析:几何体是由五个相同正方体叠成的,其三视图中的侧视图为(1).故选A.10.一四面体的三视图如图所示,则该四面体四个面中最大的面积是( D )(A)2 (B)2(C)(D)2解析: 由四面体的三视图知其直观图为如图所示的正方体中的四面体A-BCD,由三视图知正方体的棱长为2.所以S △ABD=×2×2=2,S △ADC=×2×2×=2,S △ABC=×2×2=2,S△BCD=×2×2=2.所以所求的最大面积为2.故选D.11.如图所示是一位同学画的一个实物的三视图,老师已判断正视图是正确的,问其他两个视图有无错误?如有,请纠正.解:由于正视图正确,观察可知侧视图少画了一条可见轮廓线,俯视图少画了四条可见轮廓线和一条不可见轮廓线,正确的三视图如图所示.探究创新12.一个物体由几块相同的小正方体组成,其三视图如图所示,试据图回答下列问题:(1)该物体有多少层?(2)该物体的最高部分位于哪里?(3)该物体一共由几个小正方体构成?解:(1)该物体一共有两层,从正视图和侧视图都可以看出来.(2)该物体最高部分位于左侧第一排和第二排.(3)从侧视图及俯视图可以看出,该物体前后一共三排,第一排左侧2个,右侧1个;第二排左侧2个,右侧没有;第三排左侧1个,右侧1个.该物体一共由7个小正方体构成.。

高中数学必修2第1页 解密佛山吉红勇老师扣扣：一0七669八11高中数学必修二1.21-1.2.2《中心投影与平行投影与空间几何体的三视图》【知识要点】1、中心投影与平行投影（重点）（1）平行投影的概念： （2）平行投影的性质：性质1．直线或线段的平行投影仍是直线或线段； 性质2．平行直线的平行投影是平行或重合的直线； 性质3．平行于投射面的线段，它的投影与这条线段平行且等长；性质4．与投射面平行的平面图形，它的投影与这个图形全等； 性质5．在同一直线或平行直线上，两条线段平行投影的比等于这两条线段的比．2、空间几何体的三视图①正投影：在平行投影中，如果投射线与投射面垂直，这样的平行投影叫做正投影． ②三视图：主视图： 俯视图： 左视图： ③三视图：将空间图形向这三个平面做正投影，然后把三个投影按右图所示的布局放在一个水平面内，这样构成的图形叫空间图形的三视图．④三视图的基本原则：“主左一样高，主俯一样长，俯左一样宽”． 3、简单组合体的三视图【范例析考点】考点一．中心投影与平行投影例1：正方体ABCD-A 1B 1C 1D 1中，E,F 分别是A 1A ，C 1C 的中点，则下列判断正确的有（1）四边形BFD 1E 在底面ABCD 内的投影是正方形； （2）四边形BFD 1E 在面A 1D 1DA 内的投影是菱形；（3）四边形BFD 1E 在面A 1D 1DA 内的投影与在面ABB 1A 1内的投影是全等的平行四边形. 【针对练习】1、下列说法正确的是（ ）A 水平放置的正方形的直观图可能是梯形B 两条相交直线的直观图可能是平行直线C 平行四边形的直观图仍然是平行四边形D 互相垂直的两条直线的直观图仍然互相垂直 2、两条相交直线的平行投影是（ ）A 两条相交直线B 一条直线C 一条折线D 两条相交直线或一条直线3、有下列结论：①角的水平放置的直观图一定是角②相等的角在直观图中仍然相等③相等的线段在直观图中仍然相等④若两条线段平行，则在直观图中对应的两条线段仍然平行 其中正确的是————————————4、①如果一个几何体的三视图是完全相同的，则这个几何体一定是正方体。

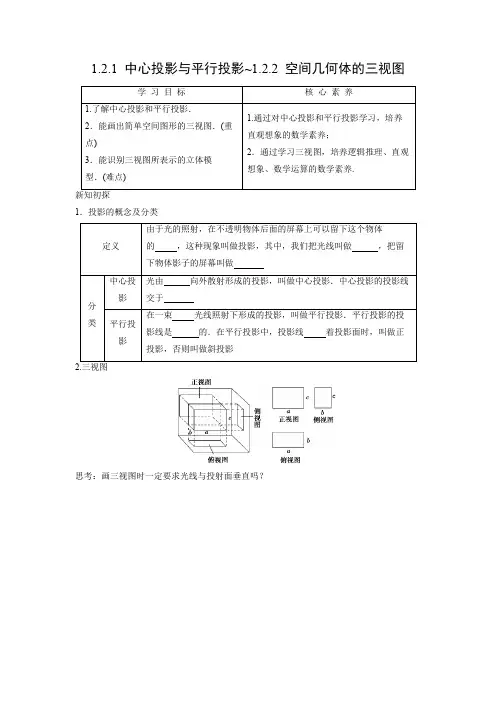
1.2.1 中心投影与平行投影~1.2.2 空间几何体的三视图1．投影的概念及分类思考：画三视图时一定要求光线与投射面垂直吗？初试身手1．哪个实例不是中心投影()A．工程图纸B．小孔成像C．相片D．人的视觉2．如图，小华拿一个矩形木框在阳光下玩，矩形木框在地面上形成的投影不可能是()A B C D3．有一个几何体的三视图如图所示，这个几何体应是一个________．4．水平放置的下列几何体，正视图是长方形的是________．(填序号)①②③④合作探究A．矩形的平行投影一定是矩形B．梯形的平行投影一定是梯形C．两条相交直线的投影可能平行D．一条线段的中点的平行投影仍是这条线段投影的中点(2)如图所示，在正方体ABCD­A1B1C1D1中，M、N分别是BB1、BC的中点，则图中阴影部分在平面ADD1A1上的正投影是()A B C D【规律方法】判断几何体投影形状的方法及画投影的方法：(1)判断一个几何体的投影是什么图形，先分清楚是平行投影还是中心投影，投影面的位置如何，再根据平行投影或中心投影的性质来判断．(2)画出一个图形在一个平面上的投影的关键是确定该图形的关键点，如顶点、端点等，方法是先画出这些关键点的投影，再依次连接各投影点即可得出此图形在该平面上的投影．跟踪训练1．已知△ABC，选定的投影面与△ABC所在平面平行，则经过中心投影后所得的△A′B′C′与△ABC()A．全等B．相似C．不相似D．以上都不对()(2)画出如图所示几何体的三视图：①②【规律方法】1．画组合体三视图的“四个步骤”(1)析：分析组合体的组成形式；(2)分：把组合体分解成简单几何体；(3)画：画分解后的简单几何体的三视图；(4)拼：将各个三视图拼合成组合体的三视图．2．画三视图时要注意的“两个问题”(1)务必做到“正侧一样高，正俯一样长，俯侧一样宽”．(2)把可见轮廓线画成实线，不可见轮廓线要画成虚线，重合的线只画一条．跟踪训练2．螺栓是棱柱和圆柱构成的组合体，如图，画出它的三视图．1．如何由三视图确定几何体的长、宽、高？2．如图所示的三视图，其几何体是什么？其正视图、侧视图中的三角形的腰是几何体的侧棱长吗？例3(1)若一个几何体的正视图和侧视图都是等腰三角形，俯视图是带圆心的圆，则这个几何体可能是()A．圆柱B．三棱柱C．圆锥D．球体(2)若某几何体的三视图如图所示，则这个几何体的直观图可以是()A B C D【规律方法】由三视图确定几何体一般分两步：第一步：通过正视图和侧视图确定是柱体、锥体还是台体．若正视图和侧视图为矩形，则原几何体为柱体；若正视图和侧视图为等腰三角形，则原几何体为锥体；若正视图和侧视图为等腰梯形，则原几何体为台体．第二步：通过俯视图确定是多面体还是旋转体．若俯视图为多边形，则原几何体为多面体；若俯视图为圆，则原几何体为旋转体．跟踪训练3．根据下列图中所给出的几何体的三视图，试画出它们的形状．①②课堂小结1．三视图的正视图、侧视图、俯视图是分别从几何体的正前方、正左方、正上方观察几何体画出的轮廓线，画几何体三视图的要求是正视图、俯视图长对正，正视图、侧视图高平齐，俯视图、侧视图宽相等，前后对应，画出的三视图要检验是否符合“长对正、高平齐、宽相等”的基本特征．2．画组合体的三视图的步骤特别提醒：画几何体的三视图时，能看见的轮廓线和棱用实线表示，看不见的轮廓线和棱用虚线表示．当堂达标1．中心投影的投影线()A．相互平行B．交于一点C．是异面直线D．在同一平面内2．如图网格纸的各小格都是正方形，粗实线画出的是一个几何体的三视图，则这个几何体是()A．三棱锥B．三棱柱C．四棱锥D．四棱柱3．一个正三棱柱(俯视图为正三角形)的三视图如图所示，则这个三棱柱的高和底面边长分别为________．4．画出如图所示的几何体的三视图．参考答案新知初探1．影子投影线投影面一点一点平行平行正对2.思考：[提示]正确．由画三视图的规则要求可知正确．初试身手1．【答案】A【解析】根据中心投影的概念可知A不是中心投影．2．【答案】A【解析】矩形的投影可以是线段，矩形，平行四边形，但不会是梯形．3．【答案】棱台【解析】从俯视图来看，上、下底面都是正方形，但大小不一样，可以判断是棱台．4．【答案】③④【解析】①③④的正视图均是长方形，②是等腰三角形．合作探究【解析】矩形的平行投影可能是线段、平行四边形或矩形，梯形的平行投影可能是线段或梯形，两条相交直线的投影还是相交直线．因此A、B、C均错，故D正确．(2)【答案】A【解析】由正投影的定义知，点M、N在平面ADD1A1上的正投影分别是AA1、DA的中点，D在平面ADD1A1上的投影还是D，因此A正确．跟踪训练1．【答案】B【解析】本题主要考查对中心投影的理解．根据题意画出图形，如图所示．由图易得OAOA′＝ABA′B′＝OBOB′＝BCB′C′＝OCOC′＝ACA′C′，则△ABC∽△A′B′C′.【解析】依题意，侧视图中棱的方向是从左上角到右下角．故选B.(2) [解]①此几何体的三视图如图③所示；②此几何体的三视图如图④所示．①④跟踪训练2．[解]它的三视图如图所示．类型3由三视图还原几何体1．[提示]由正视图可确定几何体的长、高；由俯视图可确定几何体的宽．2．[提示]由三视图可知，该几何体为正四棱锥，如图所示．正视图、侧视图中三角形的腰长不是四棱柱的侧棱长，应为四棱椎的侧面高线．【例3】【答案】(1) C【解析】正视图和侧视图都是等腰三角形，俯视图是带圆心的圆说明此几何体是圆锥．(2)【答案】D【解析】对于选项A，B，正视图均不符合要求；对于选项C，俯视图显然不符合要求．只有D符合要求．跟踪训练3．[解]由三视图的特征，结合柱、锥、台、球及简单组合体的三视图逆推．图①对应的几何体是一个正六棱锥，图②对应的几何体是一个三棱柱，则所对应的空间几何体的图形分别如下：当堂达标1．【答案】B【解析】由中心投影的定义知，中心投影的投影线交于一点，故选B.2．【答案】B【解析】由题意知，该几何体的三视图为一个三角形，两个四边形，经分析可知该几何体为三棱柱．3．【答案】2，4【解析】由正三棱柱三视图中的数据，知三棱柱的高为2，底面边长为23×23＝4.4．[解]该几何体的三视图如图所示．。