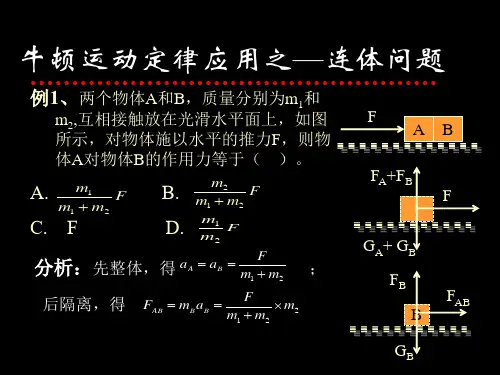
连接体问题 (公开课)
- 格式:ppt
- 大小:331.00 KB
- 文档页数:27

连接体问题分析策略:整体法与隔离法两个或两个以上物体相互连接参与运动的系统称为连接体。
以平衡态或非平衡态下连接体问题是高考备考的难点之一。
●案例探究[问题1]如图2-3所示,质量为M 的木箱放在水平面上,木箱中的立杆上套着一个质量为m 的小球,开始时小球在杆的顶端,由静止释放后,小球沿杆下滑的加速度为重力加速度的21,即a =21g ,则小球在下滑的过程中,木箱对地面的压力为多少? 解法一:(隔离法)取小球m 为研究对象,据牛顿第二定律得:mg -F f =ma ① 取木箱M 为研究对象,据物体平衡条件得:F N -F f ′-Mg =0②且F f =F f ′③由①②③式得: F N =22mM +g 由牛顿第三定律知,木箱对地面的压力大小为 F N ′=F N =22mM +g . 解法二:(整体法)对于“一动一静”连接体,也可选取整体为研究对象,依牛顿第二定律列式: (mg +Mg )-F N =ma +M ×0故木箱所受支持力:F N =22mM +g ,由牛顿第三定律知: 木箱对地面压力F N ′=F N =22mM +g .[问题2]一个质量为0.2 kg 的小球用细线吊在倾角θ=53°的斜面顶端,如图2-6,斜面静止时,球紧靠在斜面上,绳与斜面平行,不计摩擦,当斜面以10 m/s 2的加速度向右做加速运动时,求绳的拉力及斜面对小球的弹力.解:当加速度a较小时,小球与斜面体一起运动,此时小球受重力、图2-6图2-3绳拉力和斜面的支持力作用,绳平行于斜面,当加速度a 足够大时,小球将“飞离”斜面,此时小球受重力和绳的拉力作用,绳与水平方向的夹角未知,题目中要求a =10 m/s 2时绳的拉力及斜面的支持力,必须先求出小球离开斜面的临界加速度a 0.(此时,小球所受斜面支持力恰好为零)由mg cot θ=ma 0 所以a 0=g cot θ=7.5 m/s 2 因为a =10 m/s 2>a 0所以小球离开斜面N =0,小球受力情况如图2-7,则 Tc os α=ma , T sin α=mg 所以T =22)()(mg ma +=2.83 N, N =0.[问题3]如图2所示,三个物体的质量分别为m 1、m 2、m 3,带有定滑轮的物体m 3放在光滑的水平地面上,滑轮和所有接触处的摩擦及绳的质量不计,为使三物体无相对运动,则水平推力F 为多少?解:根据牛顿第二定律得对m 2研究,m 2研究竖直方向上没有加速度,力平衡,则得绳子的拉力大小为T=m 2g . 对m 1研究,a=T/m 2=m 2g/m 1对整体:F=(m 1+m 2+m 3)a =(m 1+m 2+m 3)・12m m g●相关练习:1.如图2-8所示,质量为M 的框架放在水平地面上,一轻弹簧上端固定一个质量为m 的小球,小球上下振动时,框架始终没有跳起.当框架对地面压力为零瞬间,小球的加速度大小为( )A.gB.m m M - gC.0D. mmM +g 1.答案:D2.如图2-11所示,半径为R 的光滑圆柱体,由支架固定于地面上,用一条质量可以忽略的细绳,将质量为m 1和m 2的两个可看作质点的小图2-8图2-7球连接,放在圆柱体上,两球和圆心O 在同一水平面上,在此位置将两物体由静止开始释放,问在什么条件下m 2能通过圆柱体的最高点且对圆柱体有压力? 2.解:选系统为研究对象,据机械能守恒定律得: m 1g42R π=m 2gR +21(m 1+m 2)v 2①选m 2为研究对象,在最高点据牛顿第二定律得:m 2g -N =m 2Rv 2(N 为m 2所受支持力)② 欲使m 2通过圆柱体最高点,则:N >0③联列①②③得:132-πm >m 1,且应m 1>m 2. 故条件为:132-πm >m 1>m 2. 3.如图所示,在光滑水平面上有两个并排放置的木块A 和B ,已知m A =0.5 kg ,m B =0.3 kg,有一质量为m C =0.1 kg 的小物块C 以20 m/s 的水平速度滑上A 表面,由于C 和A 、B 间有摩擦,C 滑到B 表面上时最终与B 以2.5 m/s 的共同速度运动,求:(1)木块A 的最后速度.(2)C 离开A 时C 的速度.3.解答:由于水平面是光滑的,A 、B 、C 三个物体 组成系统在水平方向上不受外力,故系统动量守恒, (1)当C 滑上A 至C 离开A 时A 、B 有共同的速度记为Vab,C 离开A 时,C 物体的速度记为Vc,则Mc×Vc0=McVc+(Ma+Mb)×Vab ① Mc×Vc0=MaVab+(Mc+Mb)×Vbc ②(2)C 离开A 时C 、B 组成的系统动量守恒。