下载文档原格式
区间估计
一、区间估计的Excel实现
1、总体方差已知，在某显著性水平下，均值区间估计。
某药材生产商需要对某仓库中的1000箱药材的平均重量进行估计。
已知药材重量的总体标准差为5千克，在随机抽取40箱样本称重后计算出每箱的平均值为52千克，求该仓库中每箱药材平均重量的区间估计（置信水平95%）
2.总体方差未知，大样本（n>=30）时的均值区间估计。
某药材生产商需要对其仓库中的1000箱药材的平均重量进行估计，药材重量的总体方差未知。
随机抽取50箱样本称重后
结果如下表所示。
求该仓库中每箱药材平均
重量在95%置信水平下的区间估计。
3.总体方差未知，小样本（n<30）下的均值区间估计。
T分布
tinv( )——求某自由度水平下，某显著性水平（注意录入的是a，而不是a/2!）下的t临界值。
某药材生产商需要对其仓库中的1000项药材的平均重量进行估计，药材重量的总体方差未知，随机抽取16箱样本称重后结果如下表所示，求该仓库中每箱药材平均重量在95%置信水平下的区间估计。
二、样本容量估计
已知样本方差、抽样误差，求样本容量。
教材55页，第5题
课堂练习：某市场调查公司接受客户委托，调查学生每月上网的时间，由于市场调查公司没做过此类调查，在正式调查前首先进行了一次预调查，抽取了20名学生进行访谈，结果如下表所示。
而客户要求偏差不超过0.5小时，试分别求在1%和5%的显著性水平下需要调查的学生的数量。
表1 20名学生每月上网时间（小时）
参考答案：a=0.01时，n=572人；a=0.05时, n=331人。
一、概述90置信区间是统计学中常用的概念，它用于对总体参数的区间估计。
计算90置信区间可以帮助我们对总体参数的范围有一个更准确的估计。
在实际应用中，经常需要使用Excel来进行90置信区间的计算。
本文将介绍如何使用Excel来计算90置信区间的公式。
二、计算公式在Excel中，计算90置信区间的公式可以通过使用STDEV.P函数和NORM.S.INV函数来实现。
我们需要计算样本数据的标准差，然后使用NORM.S.INV函数来计算标准正态分布的分位数。
根据90置信水平的要求，依据置信水平的两侧分别计算上下限值。
1. 计算样本数据的标准差在Excel中，我们可以使用STDEV.P函数来计算样本数据的标准差。
该函数的语法为：STDEV.P(number1, [number2], ...)，其中number1, number2等为样本数据。
通过该函数计算得到的标准差将作为后续计算90置信区间的基础数据。
2. 计算标准正态分布的分位数在Excel中，我们可以使用NORM.S.INV函数来计算标准正态分布的分位数。
该函数的语法为：NORM.S.INV(probability)，其中probability为所需分位数的概率值。
通过该函数计算得到的值将用于计算90置信区间的上下限。
3. 计算90置信区间的上下限值在Excel中，我们可以使用以下公式来计算90置信区间的上下限值：上限 = 样本均值 + NORM.S.INV(0.95) * 样本标准差 / SQRT(样本容量)下限 = 样本均值 - NORM.S.INV(0.95) * 样本标准差 / SQRT(样本容量)其中，样本均值为样本数据的平均值，样本标准差为样本数据的标准差，样本容量为样本数据的容量，NORM.S.INV(0.95)为90置信水平下的标准正态分布的分位数。
三、实例演示为了帮助读者更好地理解如何在Excel中计算90置信区间，下面通过一个实例演示来展示具体的计算步骤。
帮我通俗的解释下显著性水平和置信水平这两个概念通俗的理解是咋样的啊，显著水平的0.05和0.01是什么意思，越高越好还是越低越好？除了0.05和0.01外还有别的值么？置信度和置信区间又是什么意思？置信度越高越好么？回答:首先，置信水平和置信度应该是一样的，就是变量落在置信区间的可能性，“置信水平”就是相信变量在设定的置信区间的程度，是个0~1的数，用1-α表示。
置信区间，就是变量的一个范围，变量落在这个范围的可能性是就是1-α。
显著性水平就是变量落在置信区间以外的可能性，“显著”就是与设想的置信区间不一样，用α表示。
显然，显著性水平与置信水平的和为1。
显著性水平为0.05时，α=0.05，1-α=0.95如果置信区间为（-1，1），即代表变量x在（-1，1）之间的可能性为0.95。
0.05和0.01是比较常用的，但换个数也是可以的，计算方法还是不变。
总之，置信度越高，显著性水平越低，代表假设的可靠性越高，越好。
置信度计算现认为置信度在此算法中应该是用户指定一个即可。
“Ingeneral,due to the weak （logarit hmic）depende nce on T,small setting s for T(i.e.,less than 0.1)do not have a large effecton the overall windowsize”。
没找到较好的计算过程，先贴一段吧。
置信度：置信度，是指特定个体对待特定命题真实性相信的程度，也就是概率是对个人信念合理性的量度。
对概率的置信度解释表明，事件本身并没有什么概率，事件之所以指派有概率只是指派概率的人头脑中所具有的信念证据。
置信水平是指总体参数值落在样本统计值某一区内的概率；而置信区间是指在某一置信水平下，样本统计值与总体参数值间误差范围。
正态分布置信区间EXCEL计算公式1.确定样本数量、样本均值和样本标准差。
在Excel中，假设样本数量为n，样本均值为x̄，样本标准差为s。
你可以使用诸如COUNT、AVERAGE和STDEV.S等函数来计算这些值。
2.确定置信水平。
置信水平是一个概率，表示我们对总体参数的估计有多大的信心。
常用的置信水平有90%、95%和99%。
你需要将这个置信水平转换为与其对应的α值。
例如，对于95%的置信水平，α值为0.053.确定临界值。
根据样本数量和置信水平，你需要确定正态分布的临界值。
在Excel 中，可以使用函数NORM.S.INV来计算这个临界值。
公式如下：```临界值=NORM.S.INV(1-α/2,0,1)```其中，α/2表示α值的一半。
4.计算置信区间的下限值和上限值。
接下来，你可以使用以下公式来计算置信区间的下限值和上限值：```下限值=x̄-(临界值*s/√n)上限值=x̄+(临界值*s/√n)```下限值表示总体参数可能的最小值，上限值表示总体参数可能的最大值。
例如，假设样本数量为100，样本均值为50，样本标准差为10，置信水平为95%。
可以使用以下公式来计算置信区间：```临界值=NORM.S.INV(1-0.05/2,0,1)=1.96下限值=50-(1.96*10/√100)=47.04上限值=50+(1.96*10/√100)=52.96```因此，95%的置信区间为(47.04,52.96)。
以上就是在Excel中计算正态分布置信区间的公式和步骤。
使用这些公式，你可以根据样本数据和置信水平来估计总体参数的取值范围。
统计学中的显著性水平和置信区间统计学是一种研究数据收集、分析和解释的科学方法。
在统计学中，我们经常会遇到两个重要的概念：显著性水平和置信区间。
它们是帮助我们做出可靠统计推断的工具。
一、显著性水平显著性水平是指在进行统计推断时，我们所设置的判断标准。
通常用字母α来表示显著性水平。
它反映了当我们对假设进行检验时，犯错误的风险。
一般来说，常见的显著性水平有0.05和0.01。
在假设检验中，我们通常会对一个假设进行判断。
根据显著性水平的设置，将统计得到的结果与临界值进行比较，从而判断是否拒绝原假设。
如果统计得到的结果小于临界值，我们就可以认为结果是显著的，即假设成立的可能性较小；反之，如果统计结果大于临界值，我们就无法拒绝原假设，即假设存在较大的可能性。
举个例子来说，假设我们要研究某药物对疾病的疗效，我们将随机选择一组患者进行药物治疗，并将另一组患者作为对照组接受安慰剂。
最后，我们通过收集数据并进行统计分析，得到了一个p值，即观察到的差异出现的概率。
当我们设置显著性水平为0.05时，如果p值小于0.05，我们就可以拒绝原假设，即药物对疾病的疗效存在差异；反之，如果p值大于0.05，我们则无法拒绝原假设，即药物对疾病的疗效可能没有显著差异。
二、置信区间置信区间是统计推断中另一个重要的概念。
它是用来度量样本估计值与总体参数之间差异的范围。
通常用一个区间来表示，其中包含了样本估计值的可能取值范围。
在统计推断中，我们通常根据样本数据来估计总体参数，比如均值、比例等。
然而，由于样本的随机性，样本估计值很可能与总体参数存在差异。
为了获得更准确的估计结果，我们可以给出一个置信区间，该区间覆盖了总体参数的真实范围。
置信区间的计算依赖于样本的大小和可靠性程度。
一般来说，置信区间的宽度与置信水平成反比，即置信水平越高，置信区间越宽。
常见的置信水平有95%和99%。
以某电商平台的用户满意度为例，假设我们随机抽取了100名用户进行调查，得到了平均满意度为4.5分，并计算出了95%的置信区间为[4.2, 4.8]。
[试验]
用Excel的函数工具以及使用者自己输入公式等组合方式，可以构造出专门用于区间估计的Excel工作表格。
下面结合一个例子说明具体的操作步骤。
[例]
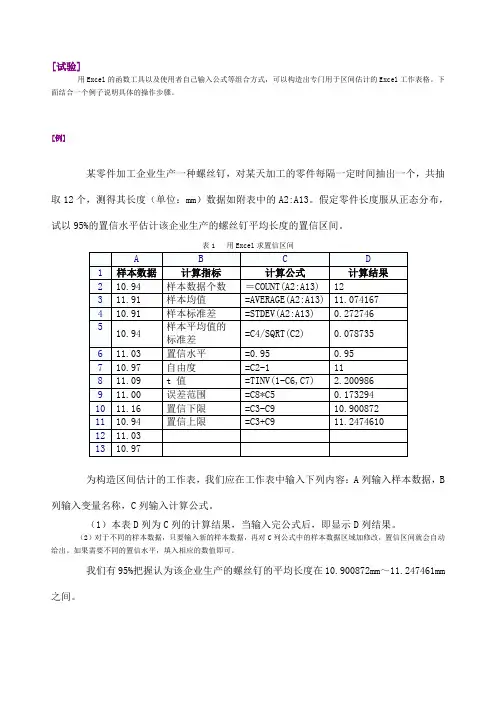
某零件加工企业生产一种螺丝钉，对某天加工的零件每隔一定时间抽出一个，共抽取12个，测得其长度（单位：mm）数据如附表中的A2:A13。
假定零件长度服从正态分布，试以95%的置信水平估计该企业生产的螺丝钉平均长度的置信区间。
表1 用Excel求置信区间
为构造区间估计的工作表，我们应在工作表中输入下列内容：A列输入样本数据，B列输入变量名称，C列输入计算公式。
（1）本表D列为C列的计算结果，当输入完公式后，即显示D列结果。
（2）对于不同的样本数据，只要输入新的样本数据，再对C列公式中的样本数据区域加修改，置信区间就会自动给出。
如果需要不同的置信水平，填入相应的数值即可。
我们有95%把握认为该企业生产的螺丝钉的平均长度在10.900872mm～11.247461mm之间。
帮我通俗的解释下显著性水平和置信水平这两个概念通俗的理解是咋样的啊，显著水平的0.05和0.01是什么意思，越高越好还是越低越好？除了0.05和0.01外还有别的值么？置信度和置信区间又是什么意思？置信度越高越好么？回答:首先，置信水平和置信度应该是一样的，就是变量落在置信区间的可能性，“置信水平”就是相信变量在设定的置信区间的程度，是个0~1的数，用1-α表示。
置信区间，就是变量的一个范围，变量落在这个范围的可能性是就是1-α。
显著性水平就是变量落在置信区间以外的可能性，“显著”就是与设想的置信区间不一样，用α表示。
显然，显著性水平与置信水平的和为1。
显著性水平为0.05时，α=0.05，1-α=0.95如果置信区间为（-1，1），即代表变量x在（-1，1）之间的可能性为0.95。
0.05和0.01是比较常用的，但换个数也是可以的，计算方法还是不变。
总之，置信度越高，显著性水平越低，代表假设的可靠性越高，越好。
置信度计算现认为置信度在此算法中应该是用户指定一个即可。
“Ingenera l,due to the weak （logari thmic）depend enceon T,smallsettin gs for T(i.e.,less than 0.1)do not have a largeeffect on the overal l windowsize”。
没找到较好的计算过程，先贴一段吧。
置信度：置信度，是指特定个体对待特定命题真实性相信的程度，也就是概率是对个人信念合理性的量度。
对概率的置信度解释表明，事件本身并没有什么概率，事件之所以指派有概率只是指派概率的人头脑中所具有的信念证据。
置信水平是指总体参数值落在样本统计值某一区内的概率；而置信区间是指在某一置信水平下，样本统计值与总体参数值间误差范围。
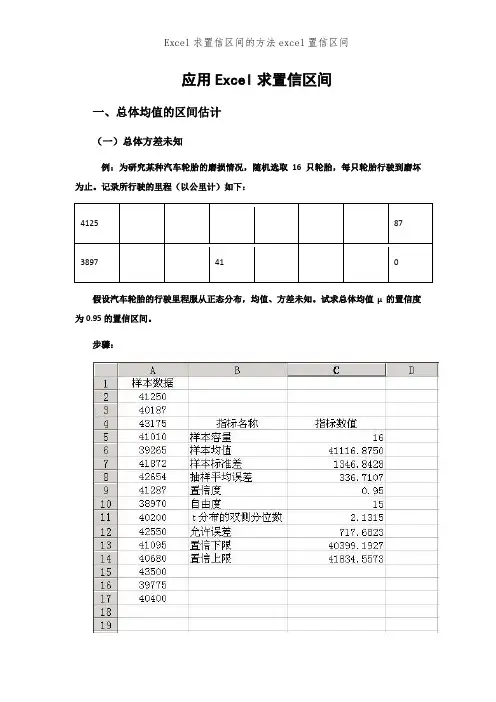
应用Excel求置信区间一、总体均值的区间估计（一）总体方差未知例：为研究某种汽车轮胎的磨损情况，随机选取16只轮胎，每只轮胎行驶到磨坏为止。
记录所行驶的里程（以公里计）如下：4125 87 3897 41 0假设汽车轮胎的行驶里程服从正态分布，均值、方差未知。
试求总体均值μ的置信度为0.95的置信区间。
步骤：1.在单元格A1中输入“样本数据”，在单元格B4中输入“指标名称”，在单元格C4中输入“指标数值”，并在单元格A2：A17中输入样本数据。
2.在单元格B5中输入“样本容量”，在单元格C5中输入“16”。
3.计算样本平均行驶里程。
在单元格B6中输入“样本均值”，在单元格C6中输入公式：“=AVERAGE（A2，A17）”，回车后得到的结果为41116.875。
4.计算样本标准差。
在单元格B7中输入“样本标准差”，在单元格C7中输入公式：“＝STDEV(A2，A17)”，回车后得到的结果为1346.842771。
5.计算抽样平均误差。
在单元格B8中输入“抽样平均误差”，在单元格C8中输入公式：“＝C7/SQRT(C5)” ，回车后得到的结果为336.7106928。
6.在单元格B9中输入“置信度”，在单元格C9中输入“0.95”。
7.在单元格B10中输入“自由度”，在单元格C10中输入“15”。
8.在单元格B11中输入“t分布的双侧分位数”，在单元格C11中输入公式：“ ＝TINV(1-C9，C10)”，回车后得到α＝0.05的t分布的双侧分位数t＝2.1315。
9.计算允许误差。
在单元格B12中输入“允许误差”，在单元格C12中输入公式：“＝C11*C8”，回车后得到的结果为717.6822943。
10.计算置信区间下限。
在单元格B13中输入“置信下限”，在单元格C13中输入置信区间下限公式：“＝C6－C12”，回车后得到的结果为40399.19271。
11.计算置信区间上限。
在单元格B14中输入“置信上限”，在单元格C14中输入置信区间上限公式：“＝C6＋C12”，回车后得到的结果为41834.55729。
帮我通俗的解释下显著性水平和置信水平这两个概念通俗的理解是咋样的啊，显著水平的0.05和0.01是什么意思，越高越好还是越低越好？除了0.05和0.01外还有别的值么？置信度和置信区间又是什么意思？置信度越高越好么？回答:首先，置信水平和置信度应该是一样的，就是变量落在置信区间的可能性，“置信水平”就是相信变量在设定的置信区间的程度，是个0~1的数，用1-α表示。
置信区间，就是变量的一个范围，变量落在这个范围的可能性是就是1-α。
显著性水平就是变量落在置信区间以外的可能性，“显著”就是与设想的置信区间不一样，用α表示。
显然，显著性水平与置信水平的和为1。
显著性水平为0.05时，α=0.05，1-α=0.95如果置信区间为（-1，1），即代表变量x在（-1，1）之间的可能性为0.95。
0.05和0.01是比较常用的，但换个数也是可以的，计算方法还是不变。
总之，置信度越高，显著性水平越低，代表假设的可靠性越高，越好。
置信度计算现认为置信度在此算法中应该是用户指定一个即可。
“In general,due to the weak （logarithmic）dependence on T,small settings for T(i.e.,less than 0.1)do not have a large effect on the overall window size”。
没找到较好的计算过程，先贴一段吧。
置信度：置信度，是指特定个体对待特定命题真实性相信的程度，也就是概率是对个人信念合理性的量度。
对概率的置信度解释表明，事件本身并没有什么概率，事件之所以指派有概率只是指派概率的人头脑中所具有的信念证据。
置信水平是指总体参数值落在样本统计值某一区内的概率；而置信区间是指在某一置信水平下，样本统计值与总体参数值间误差范围。
置信区间越大，置信水平越高。
置信度，也称为可靠度，或置信水平、置信系数，即在抽样对总体参数作出估计时，由于样本的随机性，其结论总是不确定的。
应用Excel求置信区间一、总体均值的区间估计（一）总体方差未知例：为研究某种汽车轮胎的磨损情况，随机选取16只轮胎，每只轮胎行驶到磨坏为止。
记录所行驶的里程（以公里计）如下：假设汽车轮胎的行驶里程服从正态分布，均值、方差未知。
试求总体均值μ的置信度为0.95的置信区间。
步骤：161.在单元格A1中输入“样本数据”，在单元格B4中输入“指标名称”，在单元格C4中输入“指标数值”，并在单元格A2：A17中输入样本数据。
2.在单元格B5中输入“样本容量”，在单元格C5中输入“16”。
3.计算样本平均行驶里程。
在单元格B6中输入“样本均值”，在单元格C6中输入公式：“=AVERAGE（A2，A17）”，回车后得到的结果为41116.875。
4.计算样本标准差。
在单元格B7中输入“样本标准差”，在单元格C7中输入公式：“＝STDEV(A2，A17)”，回车后得到的结果为1346.842771。
5.计算抽样平均误差。
在单元格B8中输入“抽样平均误差”，在单元格C8中输入公式：“＝C7/SQRT(C5)” ，回车后得到的结果为336.7106928。
6.在单元格B9中输入“置信度”，在单元格C9中输入“0.95”。
7.在单元格B10中输入“自由度”，在单元格C10中输入“15”。
8.在单元格B11中输入“t分布的双侧分位数”，在单元格C11中输入公式：“ ＝26TINV(1-C9，C10)”，回车后得到α＝0.05的t分布的双侧分位数t＝2.1315。
9.计算允许误差。
在单元格B12中输入“允许误差”，在单元格C12中输入公式：“＝C11*C8”，回车后得到的结果为717.6822943。
10.计算置信区间下限。
在单元格B13中输入“置信下限”，在单元格C13中输入置信区间下限公式：“＝C6－C12”，回车后得到的结果为40399.19271。
11.计算置信区间上限。
在单元格B14中输入“置信上限”，在单元格C14中输入置信区间上限公式：“＝C6＋C12”，回车后得到的结果为41834.55729。
帮我通俗的解释下显著性水平和置信水平这两个概念通俗的理解是咋样的啊，显著水平的0.05和0.01是什么意思，越高越好还是越低越好？除了0.05和0.01外还有别的值么？置信度和置信区间又是什么意思？置信度越高越好么？回答:首先，置信水平和置信度应该是一样的，就是变量落在置信区间的可能性，“置信水平”就是相信变量在设定的置信区间的程度，是个0~1的数，用1-α表示。
置信区间，就是变量的一个范围，变量落在这个范围的可能性是就是1-α。
显著性水平就是变量落在置信区间以外的可能性，“显著”就是与设想的置信区间不一样，用α表示。
显然，显著性水平与置信水平的和为1。
显著性水平为0.05时，α=0.05，1-α=0.95如果置信区间为（-1，1），即代表变量x在（-1，1）之间的可能性为0.95。
0.05和0.01是比较常用的，但换个数也是可以的，计算方法还是不变。
总之，置信度越高，显著性水平越低，代表假设的可靠性越高，越好。
置信度计算现认为置信度在此算法中应该是用户指定一个即可。
“In general,due to the weak （logarithmic）dependence on T,small settings for T(i.e.,less than 0.1)do not have a large effect on the overall window size”。
没找到较好的计算过程，先贴一段吧。
置信度：置信度，是指特定个体对待特定命题真实性相信的程度，也就是概率是对个人信念合理性的量度。
对概率的置信度解释表明，事件本身并没有什么概率，事件之所以指派有概率只是指派概率的人头脑中所具有的信念证据。
置信水平是指总体参数值落在样本统计值某一区内的概率；而置信区间是指在某一置信水平下，样本统计值与总体参数值间误差范围。
置信区间越大，置信水平越高。
置信度，也称为可靠度，或置信水平、置信系数，即在抽样对总体参数作出估计时，由于样本的随机性，其结论总是不确定的。
因此，采用一种概率的陈述方法，也就是数理统计中的区间估计法，即估计值与总体参数在一定允许的误差范围以内，其相应的概率有多大，这个相应的概率称作置信度。
一般情况下，置信度是表明抽样指标和总体指标的误差不超过一定范围的概率保证度，用F(t)来表示，在大样本(n>30)条件下，置信度F(t)是概率度t函数，概率度越大，置信度越越大。
假设我们指出测量结果的准确性有95％的可靠性，这个95％就称为置信度(P)，又称为置信水平，它是指人们对测量结果判断的可信程度。
置信水平(Confidence level)，是描述GIS中线元素与面元素的位置不确定性的重要指标之一。
置信水平表示区间估计的把握程度，置信区间的跨度是置信水平的正函数，即要求的把握程度越大，势必得到一个较宽的置信区间，这就相应降低了估计的准确程度.简单地从数学角度分析一下。
首先明确其统计模型的类型，加入把每个对象的感觉量化为分数的话，例如从0～100之间的某个数字，那么该统计的结果即3000个数值，应该近似服从于正态分布。
即，当结果受到若干个彼此影响力差不多的因素影响时，所得的大量结果服从正态分布。
如果调查不是上述那样简单，则基本思路是：先将结果量化为数值，再根据影响结果的因素的特征来分类，看它具体符合哪种分布类型。
具体的置信度设置：它应当是样本容量(例如上面的“3000”)和数值结果波动范围的函数。
也就是说，你得到的结果会在某个特定数值附近波动，你希望知道的是波动范围到底有多大。
简单的说，置信度随着所取范围增大而减小，例如假设平均值为50分，那么45～55之间的可能性显然比35～65之间小，也就是置信度低，而出现在0～100之间的置信度则是100％，因为全部范围就这么大。
另外，样本容量一般有利于提高置信度，即人数越多所得结果越可靠，不过在达到一定界限之后对于提高置信度贡献就很小了，所以一般取一定容量就足够了。
具体估算置信度时，利用所得到的结果(平均值和样本方差)计算出一个表征偏离程度的数，然后在任何一本概率统计的书后查表，表中给出的是偏离程度与置信百分数的对应关系。
基本上就是这个道理，更具体的涉及到操作层面的东西，恐怕还是要参考有关书籍，按图索骥会更稳妥些。
例如在10000个样本中，要得到95％的置信度，大概需要抽取至少600份样本。
确定调查样本量的计算公式，可以从统计教材中找到，例如：n=Z[(2×S)2/d]2其中：N：代表所需要样本量Z：置信水平的Z统计量，如95％置信水平的Z统计量为1.96S：总体的标准差d：置信区间的1/2，在实际应用中就是容许误差，或者调查误差但是总体标准差往往难以确定，所以按经验，这个总体数量，抽取600份左右。
当然，如果分层分类控制得好，也可以少一些样本。
置信度是区间估计里的概念，显著性水平是假设检验里的概念。
置信度是一个比较接近于1的数字，如0.9，0.95，0.99等，显著性水平是一个比较接近于0的数字，如0.01，0.05，0.1等。
置信水平是1-a，显著性水平是a，在区间估计商，只关注置信度或置信水平1-a，而显著性水平是假设检验中的概念。
置信度或置信水平是正确的概率，显著性水平是犯错误的概率，置信度可以直接理解为所做的估计有多大的把握，比如有95％的把握，观测值落在所给出的区间中可以这么说：置信度是人为规定的，是检验是否发生小概率的标准，显著性水平则是数据本身是否有差异，一般用P表示，P越小越好,例如，P＜0.05，说明差异显著。
期望两组数不同，但假设它们完全相同，概率是95％、98％(置信度)，但处理后的结果发现数在置信区间外，即发生了小概率事件，P＜0.05或P＜0.01，那么既然发生了小概率事件，则两组数据不同，选择置信度0.95和0.98是不同的，就要剔除一个离群数据，选择高置信度的结果就更可靠。
置信区间是一个期望轴，以Ｔ检验为例，以样本情况推断总体情况，如果总体多出现在置信区间外，则推翻原假设，差异显著的检验其实是想证明两数据不同，但只能假设相同推翻这个假设，才能证明它们不同。
[转载]置信区间与置信度置信区间或称置信间距，是指在某一置信度时，总体参数所在的区域距离或区域长度。
置信度又称显著性水平，意义阶段，信任系数等，是指估计总体参数落在某一区间时，可能犯错误的概率，用符号α表示。
例如．95置信区间是指总体参数落在该区间之内，估计正确的概率为95％，而出现错误的概率为5％(α＝．05)，由此可见：．95置信间距=．05显著性水平的置信间距，或．05置信度的置信间距。
．99置信间距=．01显著性水平的置信间距，或．01置信度的置信间距。
显著性水平在假设检验中，还指拒绝虚无假设时可能出现的犯错误的概率水平。
区间估计的原理与标准误区间估计是根据样本分布的理论，用样本分布的标准误(SE)计算区间长度，解释总体参数落入某置信区间可能的概率。
区间估计包括成功估计的概率大小及估计范围大小两个问题。
人们在解决实际问题时，总希望估计值的范围小一点，成功的概率大一些。
但在样本容量一定的情况下，二者不可兼得。
如果使估计正确的概率加大些，势必要将置信区间加长，若使正确估计的概率为1．00，即完全估计正确，则置信区间就会很长，也就等于没作估计了。
这就像在百分制的测验中你估计一个人的得分可能为0至100分之间一样。
反之，如果要使估计的区间变小，那就势必会使正确估计的概率降低。
统计分析中一般规定：正确估计的概率，也即置信水平为．95或．99，那么显著性水平则为．05或．01，这是依据．05或．01属于小概率事件，而小概率事件在一次抽样中是不可能出现的原理规定的。
区间估计的原理是样本分布理论。
即在进行区间估计值的计算及估计正确概率的解释上，是依据该样本统计量时分布规律样本分布的标准误(SE)。
也就是说，只有知道了样本统计量的分布规律和样本统计量分布的标准误才能计算总体参数可能落入的区间长度，才能对区间估计的概率进行解释，可见标准误及样本分布对于总体参数的区间估计是十分重要的。
样本分布可提供概率解释，而标准误的大小决定区间估计的长度，如果标准误越小可使置信区间的长度变短，而估计成功的概率仍可保持较高水平。
一般情况下，加大样本容量可使标准误变小。
平均数分布的概率下面以平均数的区间估计为例，说明如何根据平均数的样本分布及平均数分布的标准误，计算置信区间和解释成功估计的概率。
第五章已讲到，当总体方差已知时样本平均数的分布为正态分布或渐近正态分布。
样本平均数的平均数？，平均数的离散程度即平均数分布的标准差(简称标准误写作？或？)，根据正态分布，可以说：有68．26％的平均数落在μ±1标准误之间，有95％的平均数落在μ±1．96标准误之间，有99％的平均数落在μ±2．58标准误之间等等。
图6—1 平均数分布的概率或者说：μ±1标准误之间包含所有平均数的68．26％，μ±1.96标准误之间包含所有平均数的95％，μ±2.58标准误之间包含所有平均数的99％，等等。
只要符合正态分布，平均数的分布一定遵循按正态分布理论所计算出的概率。
平均数的区间估计可是在实际的研究中，只能得到一个样本的平均数，我们可将这个样本平均数看作无限多个样本平均数之中的一个。
当只知样本平均数( )，而不知总体平均数时，可根据平均数的样本分布进行推理。
如果有所有平均数的68．26％的平均数落在μ上下一个标准误之间，那么可以推理：所有平均数中有68．26％的平均数加上一个或减去一个标准误这一间距之内将包含总体参数μ，也就是说有68．26％的机会被包含在任何一个平均数±1标准误之间，或者说，估计μ在平均数±1标准误之间正确的概率为68．26％。
同样的道理可以说：μ在平均数±1.96标准误之间的正确概率为95％，μ在平均数±2．58标准误之间的正确概率为99％，以及其他任何可能的概率。
那为什么置信区间用平均数加、减一定数量的标准误来计算呢?这是因为样本平均数究竟μ落在的左侧还是右侧是不知道的，故用平均数±Zα／2标准误（Zα／2为样本分布的横坐标值），这一段距离表示置信区间。
如果能知平均数落在μ的左侧，那么平均数至平均数+1．96标准误这一区间内包含μ的可能为97．5％，若能确知平均数在μ之右侧，那么平均数至平均数+1．96标准误这一区间包含μ的可能亦为97．5％，这样不仅可以缩短置信区间的长度，还可提高正确估计的概率，但事实上这是做不到的。
见图6—2图6-2 平均数的区间估计置信度当推论出总体参数μ按一定的概率落在某一置信区间时，实际的均值究竟落在分布的哪个位置上并不能确知，它也有可能落在分布的两侧尾部，这时若说μ在平均值±Zα／2标准误之间便是错误的了，不过出现这种错误的可能概率可以根据样本分布进行计算：其概率为α。
