精品课时15.二次函数及其图像复习导学案

二次函数及其图像教案一、教学目标：1. 让学生理解二次函数的概念，掌握二次函数的一般形式；2. 培养学生利用配方法、顶点式求解二次函数的能力；3. 让学生熟悉二次函数的图像特点，理解二次函数图像与系数之间的关系；4. 培养学生解决实际问题的能力，提高学生对二次函数的应用意识。

二、教学内容：1. 二次函数的概念及一般形式；2. 配方法求解二次函数；3. 顶点式求解二次函数；4. 二次函数的图像特点；5. 二次函数图像与系数之间的关系。

三、教学重点与难点：1. 教学重点：二次函数的概念、一般形式，配方法、顶点式求解二次函数，二次函数的图像特点；2. 教学难点：配方法、顶点式求解二次函数的运用，二次函数图像与系数之间的关系。

四、教学方法：1. 采用问题驱动法，引导学生探究二次函数的性质；2. 利用数形结合法，让学生直观地理解二次函数的图像特点；3. 运用实例分析法，培养学生解决实际问题的能力。

五、教学过程：1. 导入新课：通过复习一次函数、正比例函数的图像，引导学生思考二次函数的概念及图像特点；2. 讲解二次函数的概念及一般形式，让学生掌握二次函数的基本知识；3. 运用配方法求解二次函数，让学生理解配方法的原理及步骤；4. 运用顶点式求解二次函数，让学生掌握顶点式的运用方法；5. 分析二次函数的图像特点，让学生了解二次函数图像的形状及对称性；6. 探讨二次函数图像与系数之间的关系，让学生理解系数对图像的影响；7. 运用实例分析，让学生解决实际问题，提高应用意识；8. 课堂小结，梳理本节课的主要知识点；9. 布置作业，巩固所学内容。

六、教学活动：1. 让学生通过数学软件或图形计算器绘制二次函数图像，观察图像与系数之间的关系；2. 组织小组讨论，让学生分享各自绘制二次函数图像的心得，探讨如何快速判断二次函数的图像特点；3. 安排课堂练习，让学生运用所学知识解决实际问题，如：抛物线射击、最大（小）值问题等。

“百搭体质”的抛物线----二次函数图像及其性质的应用一网打尽抛物线是一个数学名词,指平面上一个动点P与定点O和固定直线AB保持相等的距离移动时所成的轨迹.通俗地说,将一物体向上斜抛出去所经的路线就是抛物线.自然和社会生活中,随处可见到抛物线现象.枪炮射击中子弹、炮弹出膛后形成的轨迹就是一条抛物线.沙漠中刮风所形成的迎风坡凹进,背风坡凸出,两个翼角指向迎风方向,平面轮廓呈抛物线状的横向沙丘,被称做抛物线沙丘.儿时郊外抛石块、牧羊人和放鸭人抛出的赶羊、赶鸭的土疙瘩,也都形成了一条抛物线.以抛物线为载体，将初中数学的数形结合体现到极致，这是抛物线的特异功能。

仔细分析：1.求解析式；2.三角形的形状；3.距离最小值问题；4.相似问题；5.存在性问题：直角三角形、等腰三角形、平行四边形；6.面积问题；7.角的存在与倍分问题；8.动点问题等.一提多问，生发思维例已知：如图，抛物线y=x2+bx+c与x轴交于A、B两点，与y轴交于点C，OA=OC=3，顶点为D．（1）求此函数的关系式；（2）判断△ACD的形状，并说明理由；（3）求四边形ABCD的面积．（4）在对称轴上找一点P，使△BCP的周长最小，求出P点坐标及△BPC的周长。

（5）在AC下方的抛物线上有一点N,过点N作直线l∥y轴，交AC与点M,当点N坐标为多少时，线段MN的长度最大? 最大是多少?（6）在AC下方的抛物线上，是否存在一点N使△CAN面积最大？最大面积是多少？（7）在AC下方的抛物线上，是否存在一点N，使四边形ABCN面积最大，且最大面积是多少？（8）在y轴上是否存在一点E，使△ADE为直角三角形，若存在。

求出点E的坐标；若不存在，说明理由。

（9）在y轴上是否存在一点F，使△ADF为等腰三角形，若存在，求出点F的坐标；若不存在，说明理由。

（10）在抛物线上是否存在一点N,使S△ABN=S△ABC，若存在，求出点N的坐标；若不存在，说明理由。

二次函数及其图象◆【课前热身】1.向上发射一枚炮弹，经x 秒后的高度为y 公尺，且时间与高度关系为y =ax 2+bx .若此炮弹在第7秒与第14秒时的高度相等，则再下列哪一个时间的高度是最高的？（ ）A ． 第8秒B ． 第10秒C ．第12秒D ．第15秒 2.在平面直角坐标系中，将二次函数22x y =的图象向上平移2个单位，所得图象的解析式为（ ）A ．222-=x yB ．222+=x yC ．2)2(2-=x yD ．2)2(2+=x y 3.抛物线3)2(2+-=x y 的顶点坐标是（ ）A ．（2，3）B ．（－2，3）C ．（2，－3）D ．（－2，－3） 4.二次函数2(1)2y x =++的最小值是（ ）．A ．2B ．1C ．－3D ． 235.抛物线y=－2x 2－4x －5经过平移得到y=－2x 2，平移方法是（ ） A ．向左平移1个单位，再向下平移3个单位 B ．向左平移1个单位，再向上平移3个单位 C ．向右平移1个单位，再向下平移3个单位 D ．向右平移1个单位，再向上平移3个单位【参考答案】 1. B 2. B 3. A 4. A 5. D◆【考点聚焦】〖知识点〗二次函数、抛物线的顶点、对称轴和开口方向〖大纲要求〗1．理解二次函数的概念；2．会把二次函数的一般式化为顶点式，确定图象的顶点坐标、对称轴和开口方向，会用描点法画二次函数的图象；3．会平移二次函数y＝ax2(a≠0)的图象得到二次函数y＝a(ax＋m)2＋k的图象，了解特殊与一般相互联系和转化的思想；4．会用待定系数法求二次函数的解析式；5．利用二次函数的图象，了解二次函数的增减性，会求二次函数的图象与x轴的交点坐标和函数的最大值、最小值，了解二次函数与一元二次方程和不等式之间的联系.◆【备考兵法】〖考查重点与常见题型〗1．考查二次函数的定义、性质，有关试题常出现在选择题中，如：已知以x为自变量的二次函数y＝(m－2)x2＋m2－m－2额图象经过原点，则m的值是2．综合考查正比例、反比例、一次函数、二次函数的图象，习题的特点是在同一直角坐标系内考查两个函数的图象，试题类型为选择题，如：如图，如果函数y＝kx＋b的图象在第一、二、三象限内，那么函数y＝kx2＋bx－1的图象大致是（） y y y y1 1A B C D3．考查用待定系数法求二次函数的解析式，有关习题出现的频率很高，习题类型有中档解答题和选拔性的综合题，如：已知一条抛物线经过(0,3)，(4,6)两点，对称轴yxO为x ＝53，求这条抛物线的解析式.4． 考查用配方法求抛物线的顶点坐标、对称轴、二次函数的极值，有关试题为解答题，如：已知抛物线y ＝ax 2＋bx ＋c （a ≠0）与x 轴的两个交点的横坐标是－1、3，与y 轴交点的纵坐标是－32 （1）确定抛物线的解析式；（2）用配方法确定抛物线的开口方向、对称轴和顶点坐标.5．考查代数与几何的综合能力，常见的作为专项压轴题. 抛物线的平移抛物线的平移主要是移动顶点的位置，将y=ax 2沿着y 轴（上“＋”，下“－”）平移k （k>0）个单位得到函数y=ax 2±k ，将y=ax 2沿着x 轴（右“－”，左“＋”）平移h （h>0）个单位得到y=a （x ±h ）2．•在平移之前先将函数解析式化为顶点式，再来平移，若沿y•轴平移则直接在解析式的常数项后进行加减（上加下减），若沿x 轴平移则直接在含x 的括号内进行加减（右减左加）．◆【考点链接】1. 二次函数2()y a x h k =-+的图象和性质a ＞0a ＜0图 象开 口对 称 轴 顶点坐标最 值 当x ＝ 时，y 有最 值 当x ＝ ，y 有最 值增减性在对称轴左侧y 随x 的增大而y 随x 的增大而 在对称轴右侧 y 随x 的增大而y 随x 的增大而2. 二次函数c bx ax y ++=2用配方法可化成()k h x a y +-=2的形式，其中h ＝ ， k ＝ .3. 二次函数2()y a x h k =-+的图象和2ax y =图象的关系.4. 二次函数c bx ax y ++=2中c b a ,,的符号的确定. ◆【典例精析】例1 已知：二次函数为y=x 2－x+m ，（1）写出它的图象的开口方向，对称轴及顶点坐标；（2）m 为何值时，顶点在x 轴上方，（3）若抛物线与y 轴交于A ，过A 作AB ∥x 轴交抛物线于另一点B ，当S △AOB =4时，求此二次函数的解析式．【分析】（1）用配方法可以达到目的；（2）顶点在x 轴的上方，•即顶点的纵坐标为正；（3）AB ∥x 轴，A ，B 两点的纵坐标是相等的，从而可求出m 的值．【解答】（1）∵由已知y=x 2－x+m 中，二次项系数a=1>0，∴开口向上，又∵y=x 2－x+m=[x 2－x+（12）2]－ 14+m=（x －12）2+414m - ∴对称轴是直线x=12，顶点坐标为（12，414m -）．（2）∵顶点在x 轴上方， ∴顶点的纵坐标大于0，即414m ->0 ∴m>14 ∴m>14时，顶点在x 轴上方．（3）令x=0，则y=m ．即抛物线y=x 2－x+m 与y 轴交点的坐标是A （0，m ）． ∵AB ∥x 轴∴B 点的纵坐标为m ．当x 2－x+m=m 时，解得x 1=0，x 2=1． ∴A （0，m ），B （1，m ）在Rt △BAO 中，AB=1，OA=│m │． ∵S △AOB =12OA ·AB=4． ∴12│m │·1=4，∴m=±8 故所求二次函数的解析式为y=x 2－x+8或y=x 2－x －8．【点评】正确理解并掌握二次函数中常数a ，b ，c•的符号与函数性质及位置的关系是解答本题的关键之处．会用待定系数法求二次函数解析式例2(湖北武汉)如图，抛物线24y ax bx a =+-经过(10)A -，、(04)C ，两点，与x 轴交于另一点B ．（1）求抛物线的解析式；（2）已知点(1)D m m +，在第一象限的抛物线上，求点D 关于直线BC 对称的点的坐标； （3）在（2）的条件下，连接BD ，点P 为抛物线上一点，且45DBP ∠=°，求点P 的坐标．【分析】（1）中用待定系数法求出抛物线的解析式；（2）中考查象限，点关于直线的对称点求法；（3）中主要是做出正确的辅助线求解，进而求出点的坐标.【答案】解：（1）Q 抛物线24y ax bx a =+-经过(10)A -，，(04)C ，两点，404 4.a b a a --=⎧∴⎨-=⎩，解得13.a b =-⎧⎨=⎩，∴抛物线的解析式为234y x x =-++．yOABC（2）Q 点(1)D m m +，在抛物线上，2134m m m ∴+=-++， 即2230m m --=，1m ∴=-或3m =．Q 点D 在第一象限，∴点D 的坐标为(34)，．由（1）知45OA OB CBA =∴∠=，°． 设点D 关于直线BC 的对称点为点E ．(04)C Q ，，CD AB ∴∥，且3CD =，45ECB DCB ∴∠=∠=°，E ∴点在y 轴上，且3CE CD ==．1OE ∴=，(01)E ∴，． 即点D 关于直线BC 对称的点的坐标为（0，1）．（3）方法一：作PF AB ⊥于F ，DE BC ⊥于E ．由（1）有：445OB OC OBC ==∴∠=，°，45DBP CBD PBA ∠=∴∠=∠Q °，．(04)(34)C D Q ，，，，CD OB ∴∥且3CD =．yOABCDE yOA BC DEP F45DCE CBO ∴∠=∠=°，322DE CE ∴==． 4OB OC ==Q ，42BC ∴=，522BE BC CE ∴=-=， 3tan tan 5DE PBF CBD BE ∴∠=∠==． 设3PF t =，则5BF t =，54OF t ∴=-，(543)P t t ∴-+，．P Q 点在抛物线上，∴23(54)3(54)4t t t =--++-++，0t ∴=（舍去）或2225t =，266525P ⎛⎫∴- ⎪⎝⎭，． 方法二：过点D 作BD 的垂线交直线PB 于点Q ，过点D 作DH x ⊥轴于H ．过Q 点作QG DH ⊥于G ．45PBD QD DB ∠=∴=Q °，． QDG BDH ∴∠+∠90=°，又90DQG QDG ∠+∠=°，DQG BDH ∴∠=∠．QDG DBH ∴△≌△，4QG DH ∴==，1DG BH ==． 由（2）知(34)D ，，(13)Q ∴-，． (40)B Q ，，∴直线BP 的解析式为31255y x =-+．yOABC DPQGH解方程组23431255y x x y x ⎧=-++⎪⎨=-+⎪⎩，，得1140x y =⎧⎨=⎩，；222566.25x y ⎧=-⎪⎪⎨⎪=⎪⎩， ∴点P 的坐标为266525⎛⎫- ⎪⎝⎭，．◆【迎考精练】 一、选择题1.(上海市)抛物线22()y x m n =++（m n ，是常数）的顶点坐标是（ ）A ．()m n ，B ．()m n -，C ．()m n -，D ．()m n --，2.(陕西省)根据下表中的二次函数c bx ax y ++=2的自变量x 与函数y 的对应值，可判断二次函数的图像与x 轴（ ）x … －10 12…y … －1 47-－2 47- … A ．只有一个交点B ．有两个交点，且它们分别在y 轴两侧C ．有两个交点，且它们均在y 轴同侧D ．无交点3.（湖北荆门）函数y =ax ＋1与y =ax 2＋bx ＋1（a ≠0）的图象可能是（ ）4.（广东深圳）二次函数c bx ax y ++=2的图象如图2所示，若点A （1，y 1）、B （2，y 2）是它图象上的两点，则y 1与y 2的大小关系是（ ）A ．21y y <B ．21y y =C ．21y y >D ．不能确定B ．C ．D ．1111xo yyo x yo xxoy5.（湖北孝感）将函数2y x x =+的图象向右平移a (0)a >个单位，得到函数232y x x =-+的图象，则a 的值为 A ．1B ．2C ．3D ．46.（天津市）在平面直角坐标系中，先将抛物线22y x x =+-关于x 轴作轴对称变换，再将所得的抛物线关于y 轴作轴对称变换，那么经两次变换后所得的新抛物线的解析式为（ ）A ．22y x x =--+ B ．22y x x =-+-C.22y x x =-++ D ．22y x x =++7.（四川遂宁）把二次函数3412+--=x x y 用配方法化成()k h x a y +-=2的形式A.()22412+--=x yB. ()42412+-=x yC.()42412++-=x yD. 321212+⎪⎭⎫ ⎝⎛-=x y 8.(河北)某车的刹车距离y （m ）与开始刹车时的速度x （m/s ）之间满足二次函数2120y x =（x ＞0），若该车某次的刹车距离为5 m ，则开始刹车时的速度为（ ） A ．40 m/s B ．20 m/s C ．10 m/sD ．5 m/s二、填空题1.（北京市）若把代数式223x x --化为()2x m k -+的形式，其中,m k 为常数，则m k +=.2.（安徽）已知二次函数的图象经过原点及点（12-，14-），且图象与x 轴的另一交点到原点的距离为1，则该二次函数的解析式为 3.（湖南郴州）抛物线23(1)5y x =--+的顶点坐标为__________．4.（内蒙古包头）已知二次函数2y ax bx c =++的图象与x 轴交于点(20)-，、1(0)x ，，且112x <<，与y 轴的正半轴的交点在(02)，的下方．下列结论：①420a b c -+=；②0a b <<；③20a c +>；④210a b -+>．其中正确结论的个数是 个．5.（湖北襄樊）抛物线2y x bx c =-++的图象如图所示， 则此抛物线的解析式为 ．6.（湖北荆门）函数(2)(3)y x x =--取得最大值时，x =______． 三、解答题1.（湖南衡阳）已知二次函数的图象过坐标原点，它的顶点坐标是（1，－2），求这个二次函数的关系式．2.（湖南株洲）已知ABC ∆为直角三角形，90ACB ∠=︒，AC BC =,点A 、C 在x 轴上，点B 坐标为（3，m ）（0m >），线段AB 与y 轴相交于点D ，以P （1，0）为顶点的抛物线过点B 、D ．（1）求点A 的坐标（用m 表示）； （2）求抛物线的解析式；（3）设点Q 为抛物线上点P 至点B 之间的一动点，连结PQ 并延长交BC 于点E ，连结BQ 并延长交AC 于点F ，试证明：()FC AC EC +为定值．yxQPFEDC BAOyxO3x =15题3.（湖南常德）已知二次函数过点A （0，2-），B （1-，0），C （5948，）． （1）求此二次函数的解析式； （2）判断点M （1，12）是否在直线AC 上？ （3）过点M （1，12）作一条直线l 与二次函数的图象交于E 、F 两点（不同于A ，B ，C 三点），请自已给出E 点的坐标，并证明△BEF 是直角三角形．4. (陕西省) 如图，在平面直角坐标系中，OB ⊥OA ，且OB ＝2OA ，点A 的坐标是(－1，2)．（1）求点B 的坐标；（2）求过点A 、O 、B 的抛物线的表达式；（3）连接AB ，在（2）中的抛物线上求出点P ，使得S △ABP ＝S △ABO ．第3题5.(湖北黄冈)新星电子科技公司积极应对世界金融危机，及时调整投资方向，瞄准光伏产业，建成了太阳能光伏电池生产线．由于新产品开发初期成本高，且市场占有率不高等因素的影响，产品投产上市一年来，公司经历了由初期的亏损到后来逐步盈利的过程（公司对经营的盈亏情况每月最后一天结算1次）．公司累积获得的利润y（万元）与销售时间第x（月）之间的函数关系式（即前x个月的利润总和y与x之间的关系）对应的点都在如图所示的图象上．该图象从左至右，依次是线段OA、曲线AB和曲线BC，其中曲线AB为抛物线的一部分，点A为该抛物线的顶点，曲线BC为另一抛物线的一部分，且点A，B，C的横坐标分别为4，10，12（1）求该公司累积获得的利润y（万元）与时间第x（月）之间的函数关系式；（2）直接写出第x个月所获得S（万元）与时间x（月）之间的函数关系式（不需要写出计算过程）；（3）前12个月中，第几个月该公司所获得的利润最多？最多利润是多少万元？6.（内蒙古包头）某商场试销一种成本为每件60元的服装，规定试销期间销售单价不低于成本单价，且获利不得高于45%，经试销发现，销售量（件）与销售单价（元）符合一次函数，且时，；时，．（1）求一次函数的表达式；（2）若该商场获得利润为元，试写出利润与销售单价之间的关系式；销售单价定为多少元时，商场可获得最大利润，最大利润是多少元？（3）若该商场获得利润不低于500元，试确定销售单价的范围．7.（福建漳州）如图1，已知：抛物线与轴交于两点，与轴交于点C，经过B、C两点的直线是，连结．（1）B、C两点坐标分别为B（_____，_____）、C（_____，_____），抛物线的函数关系式为______________；（2）判断的形状，并说明理由；（3）若内部能否截出面积最大的矩形（顶点在各边上）？若能，求出在边上的矩形顶点的坐标；若不能，请说明理由．[抛物线的顶点坐标是]【参考答案】 选择题 1. B 2. B 3. C【解析】本题考查函数图象与性质，当0a >时，直线从左向右是上升的，抛物线开口向上，D 是错的，函数y =ax ＋1与y =ax 2＋bx ＋1（a ≠0）的图象必过（0，1），所以C 是正确的，故选C ． 4. C 5. B 6. C 7. D 8. C 填空题 1. -32. 2y x x =+，21133y x =-+ 3. （1，5） 4. 4【解析】本题考查二次函数图象的画法、识别理解，方程根与系数的关系筀等知识和数形结合能力.根据题意画大致图象如图所示，由2y ax bx c =++与X 轴的交点坐标为(-2,0)得()()2220a b c ⨯-+⨯-+=，即 420a b c -+=所以①正确；由图象开口向下知0a <，由2y ax bx c =++与X 轴的另一个交点坐标为()1,0x 且112x <<，则该抛物线的对称轴为()121222x b x a -+=-=>- 由a<0得b>a,所以结论②正确；由一元二次方程根与系数的关系知12.2cx x a=<-，结合a<0得20a c +>，所以③结论正确；由420a b c -+=得22c a b -=-，而0<c<2,，∴102c -<-< ∴-1<2a-b<0 ∴2a-b+1>0,所以结论④正确.点拨： 420a b c -+=是否成立，也就是判断当2x =-时，2y ax bx c =++的函数值是否为0；判断2y ax bx c =++中a 符号利用抛物线的开口方向来判断，开口向上a>0,开口向下a<0;判断a 、b 的小关系时，可利用对称轴2bx a =-的值的情况来判断；判断a 、c 的关系时，可利用由一元二次方程根与系数的关系12.cx x a=的值的范围来判断；2a-b+1的值情况可用420a b c -+=来判断. 5. 223y x x =-++【解析】本题考查二次函数的有关知识，由图象知该抛物线的对称轴是1x =，且过点（3，0），所以12930bb c ⎧-=⎪-⎨⎪-++=⎩，解得23b c =⎧⎨=⎩，所以抛物线的解析式为223y x x =-++，故填223y x x =-++ 6.52【解析】本题考查二次函数的最值问题，可以用配方法或二次函数顶点坐标公式求出当x 为何值时二次函数取得最大值，下面用配方法，22549(2)(3)5624y x x x x x ⎛⎫=--=-+-=--+ ⎪⎝⎭，所以当52x =时，函数(2)(3)y x x =--取得最大值，故填52解答题1. 解：设这个二次函数的关系式为得：解得：∴这个二次函数的关系式是，即2. （1）由(3,)B m 可知3OC =，BC m =，又△ABC 为等腰直角三角形，∴AC BC m ==，3OA m =-，所以点A 的坐标是（3,0m -）. （2）∵45ODA OAD ∠=∠=︒ ∴3OD OA m ==-，则点D 的坐标是（0,3m -）. 又抛物线顶点为(1,0)P ，且过点B 、D ，所以可设抛物线的解析式为：2(1)y a x =-，得：22(31)(01)3a m a m ⎧-=⎪⎨-=-⎪⎩ 解得14a m =⎧⎨=⎩ ∴抛物线的解析式为221y x x =-+ （3）过点Q 作QM AC ⊥于点M ，过点Q 作QN BC ⊥于点N ，设点Q 的坐标是2(,21)x x x -+，则2(1)QM CN x ==-，3MC QN x ==-.∵//QM CE ∴PQM ∆∽PEC ∆ ∴QM PMEC PC =即2(1)12x x EC --=，得2(1)EC x =- ∵//QN FC ∴BQN ∆∽BFC ∆ ∴QN BN FC BC =即234(1)4x x FC ---=，得41FC x =+ 又∵4AC = ∴444()[42(1)](22)2(1)8111FC AC EC x x x x x x +=+-=+=⋅+=+++ 即()FC AC EC +为定值8.3. （1）设二次函数的解析式为c bx ax y ++=2（0a ≠）， 把A （0，2-），B （1-，0），C （5948，）代入得2092558164c a b c a b c⎧⎪=-⎪=-+⎨⎪⎪=++⎩解得 a =2 ， b =0 ， c =－2， ∴222y x =-（2）设直线AC 的解析式为(0)y kx b k =+≠ ，把A （0，－2），C （5948，）代入得29584b k b =-⎧⎪⎨=+⎪⎩， 解得522k b ==-， ，∴522y x =- 当x =1时，511222y =⨯-= ∴M （1，12）在直线AC 上（3）设E 点坐标为（1322--，），则直线EM 的解析式为4536y x =- 由 2453622y x y x ⎧=-⎪⎨⎪=-⎩化简得2472036x x --=，即17()(2)023x x +-=，第3题∴F 点的坐标为（713618，）．过E 点作EH ⊥x 轴于H ，则H 的坐标为（102-，）． ∴3122EH BH ==， ∴2223110()()224BE =+=，类似地可得 22213131690845()()186324162BF =+==， 222401025001250()()186324162EF =+==， ∴2221084512504162162BE BF EF +=+==，∴△BEF 是直角三角形．4. 解：（1）过点A 作AF ⊥x 轴，垂足为点F ，过点B 作BE ⊥x 轴，垂足为点E ，则AF ＝2，OF ＝1．∵OA ⊥OB ，∴∠AOF+∠BOE ＝90°． 又 ∵∠BOE+∠OBE ＝90°，∴∠AOF ＝∠OBE ． ∴Rt △AFO ∽Rt △OEB ． ∴2===OAOBAF OE OF BE ． ∴BE ＝2，OE ＝4． ∴B(4，2)．（2）设过点A(－1，2)，B(4，2)，O(0，0)的抛物线为y=ax 2+bx+c ．∴⎪⎩⎪⎨⎧==++=+-.0,2416,2c c b a c b a 解之，得⎪⎪⎪⎩⎪⎪⎪⎨⎧=-==.0,23,21c b a∴所求抛物线的表达式为x x y 23212-=． （3）由题意，知AB ∥x 轴．设抛物线上符合条件的点P 到AB 的距离为d ，则S △ABP ＝AF AB d AB ⋅=⋅2121． ∴d ＝2．∴点P 的纵坐标只能是0或4． 令y ＝0，得023212=-x x ，解之，得x ＝0，或x ＝3． ∴符合条件的点P 1(0，0)，P 2(3，0)． 令y ＝4，得423212=-x x ，解之，得2413±=x ． ∴符合条件的点P 3(2413-，4)，P 4(2413+，4)． ∴综上，符合题意的点有四个： P 1(0，0)，P 2(3，0)，P 3(2413-，4)，P 4(2413+，4)． （评卷时，无P 1(0，0)不扣分）5.解：（1）当时，线段O A 的函数关系式为;当时，由于曲线AB 所在抛物线的顶点为A （4，－40），设其解析式为在中，令x=10，得；∴B （10，320）∵B （10，320）在该抛物线上 ∴解得∴当时，=综上可知，(2) 当时,当时,当时,(3) 10月份该公司所获得的利润最多,最多利润是110万元.6. 解：（1）根据题意得解得．所求一次函数的表达式为．（2），抛物线的开口向下，当时，随的增大而增大，而，当时，．当销售单价定为87元时，商场可获得最大利润，最大利润是891元．（3）由，得，整理得，，解得，．由图象可知，要使该商场获得利润不低于500元，销售单价应在70元到110元之间，而，所以，销售单价的范围是．7. （1）（4，0），．．（2）是直角三角形．证明：令，则．．．解法一：．．是直角三角形．解法二：，．．，．即．是直角三角形．（3）能．当矩形两个顶点在上时，如图1，交于．，．．解法一：设，则，，．=．当时，最大．．，．，．解法二：设，则．．当时，最大．．，．，．当矩形一个顶点在上时，与重合，如图2，，．．解法一：设，，．=．当时，最大．，．解法二：设，，，，．．=∴当时，最大，．．∴综上所述：当矩形两个顶点在上时，坐标分别为，（2，0）；当矩形一个顶点在上时，坐标为。

二次函数及其图像教案教学目标：1. 理解二次函数的概念和一般形式；2. 学会求解二次方程；3. 能够绘制二次函数的图像并理解其性质；4. 能够应用二次函数解决实际问题。

教学内容：第一章：二次函数的概念1.1 引入二次函数的概念1.2 二次函数的一般形式1.3 二次函数的图像特点第二章：求解二次方程2.1 引入二次方程的概念2.2 求解二次方程的公式2.3 求解二次方程的步骤第三章：绘制二次函数的图像3.1 绘制二次函数图像的方法3.2 二次函数图像的性质3.3 特殊情况下二次函数图像的特点第四章：二次函数的顶点4.1 顶点的概念4.2 顶点的求解方法4.3 顶点对二次函数图像的影响第五章：二次函数的单调性5.1 单调性的概念5.2 判断二次函数单调性的方法5.3 单调性对二次函数图像的影响教学方法：1. 采用讲授法，讲解二次函数的概念、一般形式、图像特点等内容；2. 采用案例分析法，通过具体例子讲解求解二次方程的步骤和方法；3. 采用实践操作法，引导学生动手绘制二次函数的图像，观察其性质；4. 采用小组讨论法，让学生分组讨论二次函数的顶点和单调性，并进行交流分享。

教学评价：1. 课堂问答：通过提问的方式检查学生对二次函数概念的理解程度；2. 练习题：布置相关的练习题，检查学生对二次方程求解方法的掌握情况；3. 图像绘制：让学生独立绘制二次函数的图像，并分析其性质，检查学生对图像特点的理解程度；4. 小组讨论：评价学生在小组讨论中的表现，检查学生对二次函数顶点和单调性的理解程度。

教学资源：1. 教学PPT：展示二次函数的概念、一般形式、图像特点等内容；2. 练习题：提供相关的练习题供学生练习；3. 图像绘制工具：如几何画板等，用于学生绘制二次函数的图像；4. 小组讨论材料：提供相关材料供学生在小组讨论中参考。

教学步骤：第一章：1.1 引入二次函数的概念：通过举例说明二次函数的定义；1.2 二次函数的一般形式：介绍一般形式的表达式；1.3 二次函数的图像特点：分析二次函数图像的开口方向、顶点位置等特点。

《二次函数》的复习教学设计复习教学设计：二次函数一、教学目标：1.理解二次函数的定义及其特点；2.掌握二次函数的图像、顶点、轴、对称轴等性质；3.能够根据二次函数的特点解决实际问题。

二、教学内容：1.二次函数的定义和基本形式；2.二次函数的图像和性质；3.二次函数的最值、零点及其应用。

三、教学步骤：步骤一：导入新知1.导入教学话题：“二次函数”，以回顾前几节课所学内容，引发学生对二次函数的认识和兴趣。

2.提问：“你能简单回忆一下二次函数是什么吗？”让学生简单复述二次函数的定义。

步骤二：概念及定义讲解1. 讲解二次函数的定义和基本形式，即f(x) = ax^2 + bx + c，其中a、b和c为实数。

2.引导学生理解a、b和c对二次函数图像的影响，如a决定了抛物线的开口方向和宽度，b决定了抛物线的位置偏移，c决定了抛物线与y轴的交点位置。

步骤三：图像及性质讲解1.讲解二次函数图像的性质，包括图像的开口方向、顶点、对称轴等。

2.通过示例分析，引导学生找出二次函数的顶点、对称轴及其它特征，让学生能够根据函数表达式确定图像的形状。

步骤四：实例分析及概念巩固1.给出一些具体的函数表达式，引导学生根据图像的特征进行分析，并求出对应的顶点、对称轴、开口方向等。

2.提问：“当a为正数时，抛物线的开口方向是向上还是向下？当a为负数时又怎样？”让学生总结出结论。

3.给出一些特殊情况的函数表达式，让学生分析并给出对应的图像和性质。

步骤五：最值、零点及应用讲解1.讲解二次函数的最值和零点，包括二次函数最值的判断和求解，以及二次函数零点的判断和求解。

2.引导学生通过实例分析，掌握解二次函数实际问题的方法和步骤。

3.给出一些实际问题，让学生通过建立等式或不等式解决，加深对二次函数的运用和理解。

步骤六：巩固练习1.布置相应的练习题，让学生通过计算和绘图巩固所学内容。

2.引导学生将练习题的解答和图像进行对比，分析解题方法和图像的关系。

精品“正版”资料系列，由本公司独创。

旨在将“人教版”、”苏教版“、”北师大版“、”华师大版“等涵盖几乎所有版本的教材教案、课件、导学案及同步练习和检测题分享给需要的朋友。

本资源创作于2020年8月，是当前最新版本的教材资源。

包含本课对应内容，是您备课、上课、课后练习以及寒暑假预习的最佳选择。

二次函数的图像归纳：二次函数y=ax 2+bx+c 的图像画法，可分三步：①用配方法把函数化为()k h x a y +-=2形式，②利用顶点式确定抛物线的开口方向、对称轴及顶点坐标，③利用对称点描点画图问题：对于二次函数的一般形式)0(2≠++=a c bx ax y ，怎样求对称轴、顶点坐标？()2222222222422244.24b c a a b b b c b ac b y ax bx c a x a x x a x a a a a a a b ac b a x a a +⎡⎤⎡⎤-⎛⎫⎛⎫⎛⎫=++=+=++-+=++⎢⎥⎢⎥⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦-⎛⎫=++ ⎪⎝⎭ 二次函数y ＝ax 2＋bx ＋c(a ≠0)的图像的性质是：1.对称轴是 ，顶点坐标是2.当a ＞0时，开口向 ，当x ＝ 时，函数有最 值为 ；当a ＜0时，开口向 当x ＝ 时，函数有最 值为 。

三.拓展提升1.抛物线y ＝－12x 2＋2x ＋4的顶点坐标是_______；对称轴是_______；2.二次函数y ＝ax 2＋4x ＋a 的最大值是3，求a 的值。

3、已知抛物线9)2(2++-=x a x y 的顶点在y 轴上，求a 的值?若顶点在x 轴上呢？4、已知二次函数图象的对称轴是x =-3，且函数有最大值为2，图象与x 轴的一个交点是（－1，0），求这个二次函数的解析式。

5、已知二次函数y ＝ax 2＋bx ＋c 图象如图所示，下列结论中： ①abc ＞0，②b ＝2a ；③a ＋b ＋c ＜0，④a －b ＋c ＞0，正确的个数是( ) A ．4个 B ．3个 C. 2个 D ．1个6、已知抛物线c bx x y ++=2的部分图象如右图所示，若y<0,则x 的取值范围是（ ） A ．-1<x<4 Ｂ．-1<x<3 Ｃ．x<-1或x>4 Ｄ．x<-1或x>3 四.当堂反馈1、下列抛物线，对称轴是x =21的是 ( ) A. 221x y =B. x x y 22+=C. 22++=x x yD. 22--=x x y 2、抛物线24y x x m =-+与x 轴只有一个交点，则m= 。

二次函数及其图像的复习教学设计教学目标：知识与技能目标1.理解二次函数的概念，掌握二次函数y＝ax2+bx+c(a≠0)的图象与性质；2.会用待定系数法求二次函数的解析式，能结合二次函数的图象掌握二次函数的性质。

3.发现二次函数的系数a,b,c,△的符号与图象之间的关系；a,b,c,△及相关代数式的符号；能力与程序性目标：通过具体实例，掌握函数的解决能力和分析能力教学重难点：1.能灵活的根据条件恰当地选取选择表达式，体会二次函数表达式之间的转化。

2.由抛物线确定a,b,c,△及相关代数式的符号；教学设计过程一．由于是第一轮复习，教师先归纳出知识点，让学生能回顾以前的知识。

(一）二次函数的概念和表达式的确定；a；y=ax2+bx+c（a≠0）①未知数的最高次数是2②表达式是整式③有两个未知数B;函数的表达式的确定根据不同的情况来设不同的形式1、一般式：已知抛物线上的三点，通常设解析式为_y=ax2+bx+c（a≠0）2,顶点式：已知抛物线顶点坐标（h, k），通常设抛物线解析式为y=a(x-h)2+k(a≠0)3,交点式:已知抛物线与x 轴的两个交点(x1,0)、 (x2,0),通常设解析式为y=a(x-x1)(x-x2)学生活动；在老师的归纳下，学生自主梳理知识，并及时巩固知识，讨论并完成下列习题1、已知二次函数的图象顶点是（-1，2），且经过（1，-3），那么这个二次函数的解析式是_______________。

(2)已知二次函数y=ax2+bx+c的最大值是2，图象顶点在直线y=x+1上，并且图象经过点（3，-6）。

求二次函数表达式。

(二)二次函数的图像与字母系数的确定由学生交流自学完成1.抛物线y=ax2+bx+c 的开口方向由决定：⇒开口向上⇒开口向下.2.抛物线y=ax2+bx+c与y轴的交点坐标是（）.c>o⇒与y轴的交点在；c<o⇒与y轴的交点在；c=o⇒抛物线过点3.抛物线y=ax2+bx+c的对称轴是直线 .b=0⇒对称轴是；0⇒对称轴在y轴的侧；a、b同号⇒－b2aa、b异号⇒－b0⇒对称轴在y轴的侧.2a4.若抛物线y=ax2+bx+c与x轴有交点，则交点的横坐标就是一元二次方程ax2+bx+c=0的根，因此抛物线y=ax2+bx+c与x轴的交点个数由决定.<⇒抛物线与x轴有两个交点；⇒抛物线与x轴有一个交点；⇒抛物线与x轴没有交点.5.a＋b＋c,a－b＋c与0的大小关系学生活动；课堂教学在师生、生生的互动氛围中，引导学生从感性认识到理性认知的过渡，培养、形成抽象思维的意识和能力，从而激发学生认识知识的运用；如图；抛物线y=ax2+bx+c的图像与y轴正半轴相交，其顶点坐标为（0.5,1），下列结论：①abc<0②a＋b=0③b2－4ac>0④a＋b＋c<0⑤4ac－b2=4a其中正确结论的序号是_教师进行点评，由于函数的重要性，学生必须学会应用，它是数形结合的一种表现，通过对开口方向以及对称轴位置，与坐标轴的交点。

新北师大版九年级数学下册《二次函数的图像与性质2》导学案环节一 知识连接（本节课关联知识点复习巩固）二次函数2x y =的函数图像为_________,开口______,顶点坐标为______对称轴为________二次函数2-x y =的函数图像为_________,开口______,顶点坐标为______对称轴为________ 环节二 教材精读（归纳出本节课需要掌握的知识点） 在同一直角坐标系中，画出函数222x 2y x 21y x y ===，，的图象．● 归纳：抛物线y ＝12 x 2，y ＝x 2，y ＝2x 2的二次项系数a_______0,开口_____顶点坐标都是__________；对称轴是_________；顶点是抛物线的最_________点（填“高”或“低”） ． ● 归纳：开口大小由_________决定.x … －4 －3 －2 －1 0 1 2 3 4 … y ＝12x 2……x … －2 －1.5 －1 －0.5 0 0.5 1 1.5 2 … y ＝2x 2……在同一直角坐标系中,画出二次函数y＝x2＋1,y＝x2－1的图象.x …－3 －2 －1 0 1 2 3 …y＝x2＋1 ……y＝x2－1 ……归纳1：可以发现,把抛物线y＝x2向______平移______个单位,就得到抛物线y＝x2＋1;把抛物线y＝x2向_______平移______个单位,就得到抛物线y＝x2－1.归纳2：开口方向顶点对称轴有最高(低)点最值y＝x2y＝x2－1y＝x2＋1课堂练习：1、抛物线y＝2x2向上平移3个单位,就得到抛物线__________________;2、抛物线y＝2x2向下平移4个单位,就得到抛物线__________________.3、因此,把抛物线y＝ax2向上平移k(k＞0)个单位,就得到抛物线_______________;4、把抛物线y＝ax2向下平移k(k＞0)个单位,就得到抛物线_______________.。

第二节 二次函数的图像与性质(第1课时)环节一 回顾旧知，导入新课。

1.一次函数的图像是 ，反比例函数的图像是 。

2.画函数图象的一般步骤是什么？， ， .环节二 小组合学，探究新知。

1.试画出二次函数y=x 2的图像。

（1.2.3组黑色笔完成）（1）列表（2）描点 （3）连线2. 试画出二次函数y=-x 2的图像。

（4.5.6组黑色笔完成）3. 在1中画出二次函数y ＝2x 2的图象（1.2.3组红色笔完成） 在2中画出二次函数y ＝-2x 2的图象（4.5.6组红色笔完成）环节三：归纳总结，提炼升华。

反思小结：1.当a>0时，a 越大，a ，抛物线开口 。

当a<0时，a 越小，a ，抛物线开口 。

综上：对于任意a ≠0，a越大， 抛物线开口 。

环节四:达标检测，反馈提高 A 组1．二次函数2x y =的函数图像为_________,开口______,顶点坐标为______对称轴为________ 二次函数2-x y =的函数图像为_________,开口______,顶点坐标为______对称轴为________2.判断正误（1）函数y = x2与y = －x2的图像都是抛物线（ ）； （2）函数y = x2与y = －x2的图像对称轴都是x 轴 （ ）； （3）函数y = x2与y = －x2的图像形状相同，开口方向相反（ ） （4）抛物线y = 3x2在x 轴的下方(除顶点外)（ ）（5）在抛物线y = -5x2左侧， y 随着x 的增大而增大（ ） 3.已知72)2(--=ax a y 是二次函数，且当0>x 时，y 随x 的增大而增大，则=a 。

4.设边长为x 的正方形的面积为y ，y 是x 的二次函数，该函数的图象是下列各图形中（ ）B 组：1．在函数y = x 2上有两点，（－1，y 1），（－3，y 2），那么y 1，y 2，0的大小关系是（ ）A .y 1 ＜ y 2 ＜0 B. y 2 ＜ y 1 ＜0 C. y 1 ＞ y 2 ＞0 D. y 2 ＞ y 1 ＞02、直线1+-=x y 与抛物线2x y =有（ ）A ．1个交点B . 2个交点C ．3个交点D ．没有交点3、如图边长为2的正方形ABCD 的中心在直 角坐标系的原点O ，AD ∥x 轴，抛物线y = x 2和 y = －x 2别经过A ，B ，C ，D 点，将正方形成几部 分，则图中阴影部分的面积为 ．探索乐趣 ：课下猜想并验证抛物线y = 3x2与y = 3x2+4之间有什么关系？它们是轴对称图形吗？开方方向，对称轴、定点坐标分别是什么？温馨提示：只有不断的思考,才会有新的发现;只有量的变化,才会有质的进步.赠送以下资料《二次函数的应用》中考题集锦10题已知抛物线222(0)y x mx m m =+-≠．（1）求证：该抛物线与x 轴有两个不同的交点；（2）过点(0)P n ，作y 轴的垂线交该抛物线于点A 和点B （点A 在点P 的左边），是否存在实数m n ，，使得2AP PB =？若存在，则求出m n ，满足的条件；若不存在，请说明理由．答案：解：（1）证法1：22229224m y x mx m x m ⎛⎫=+-=+- ⎪⎝⎭，当0m ≠时，抛物线顶点的纵坐标为2904m -<， ∴顶点总在x 轴的下方．而该抛物线的开口向上，∴该抛物线与x 轴有两个不同的交点．（或者，当0m ≠时，抛物线与y 轴的交点2(02)m -，在x 轴下方，而该抛物线的开口向上，∴该抛物线与x 轴有两个不同的交点．）证法2 ：22241(2)9m m m ∆=-⨯⨯-=，当0m ≠时，290m >，∴该抛物线与x 轴有两个不同的交点． （2）存在实数m n ，，使得2AP PB =．设点B 的坐标为()t n ，，由2AP PB =知，①当点B 在点P 的右边时，0t >，点A 的坐标为(2)t n -，，且2t t -，是关于x的方程222x mx m n +-=的两个实数根．2224(2)940m m n m n ∴∆=---=+>，即294n m >-．且(2)t t m +-=-（I ），2(2)t t m n -=--（II ）由（I ）得，t m =，即0m >．将t m=代入（II ）得，0n =．∴当0m >且0n =时，有2AP PB =．②当点B 在点P 的左边时，0t <，点A 的坐标为(2)t n ，，且2t t ，是关于x 的方程222x mx m n +-=的两个实数根． 2224(2)940m m n m n ∴∆=---=+>，即 294n m >-．且2t t m +=-（I ），222t t m n =--（II ）由（I ）得，3mt =-，即0m >． 将3m t =-代入（II ）得，2209n m =-且满足294n m >-． ∴当0m >且2209n m =-时，有2AP PB =第11题一人乘雪橇沿如图所示的斜坡笔直滑下，滑下的距离S （米）与时间t （秒）间的关系式为210S t t =+，若滑到坡底的时间为2秒，则此人下滑的高度为（ ）Ａ．24米 Ｂ．12米Ｃ．米 Ｄ．6米答案：Ｂ第12题我市英山县某茶厂种植“春蕊牌”绿茶，由历年来市场销售行情知道，从每年的3月25日起的180天内，绿茶市场销售单价y （元）与上市时间t （天）的关系可以近似地用如图（1）中的一条折线表示．绿茶的种植除了与气候、种植技术有关外，其种植的成本单价z （元）与上市时间t （天）的关系可以近似地用如图（2）的抛物线表示．（2）求出图（2）中表示的种植成本单价z （元）与上市时间t （天）（0t >）的函数关系式；（3）认定市场销售单价减去种植成本单价为纯收益单价，问何时上市的绿茶纯收益单价最大？ （说明：市场销售单价和种植成本单价的单位：元／500克．）答案：解：（1）依题意，可建立的函数关系式为：2160(0120)380(120150)220(150180)5t t y t t t ⎧-+<<⎪⎪=<⎨⎪⎪+⎩，，． ≤ ≤≤ （2）由题目已知条件可设2(110)20z a t =-+． 图象过点85(60)3，，2851(60110)203300a a ∴=-+∴=．． 21(110)20300z t ∴=-+ (0)t >．（3）设纯收益单价为W 元，则W =销售单价-成本单价． )图(1)图(2)(天)故22221160(110)20(0120)3300180(110)20(120150)3002120(110)20(150180)5300t t t W t t t t t ⎧-+---<<⎪⎪⎪=---<⎨⎪⎪+---⎪⎩，，． ≤ ≤≤ 化简得2221(10)100(0120)3001(110)60(120150)3001(170)56(150180)300t t W t t t t ⎧--+<<⎪⎪⎪=-+<⎨⎪⎪--+⎪⎩，，． ≤ ≤≤①当21(10)100(0120)300W t t =--+<<时，有10t =时，W 最大，最大值为100； ②当21(110)60(120150)300W t t =--+<≤时，由图象知，有120t =时，W 最大，最大值为2593；③当21(170)56(150180)300W t t =--+≤≤时，有170t =时，W 最大，最大值为56．综上所述，在10t =时，纯收益单价有最大值，最大值为100元．第13题如图，足球场上守门员在O 处开出一高球，球从离地面1米的A 处飞出（A 在y 轴上），运动员乙在距O 点6米的B 处发现球在自己头的正上方达到最高点M ，距地面约4米高，球落地后又一次弹起．据实验，足球在草坪上弹起后的抛物线与原来的抛物线形状相同，最大高度减少到原来最大高度的一半． （1）求足球开始飞出到第一次落地时，该抛物线的表达式． （2）足球第一次落地点C距守门员多少米？（取7=）（3）运动员乙要抢到第二个落点D，他应再向前跑多少米？（取5=）答案：解：（1）（3分）如图，设第一次落地时， 抛物线的表达式为2(6)4y a x =-+． 由已知：当0x =时1y =． 即1136412a a =+∴=-，． ∴表达式为21(6)412y x =--+．（或21112y x x =-++）（2）（3分）令210(6)4012y x =--+=，．212(6)4861360x x x ∴-===-<．≈，（舍去）． ∴足球第一次落地距守门员约13米．（3）（4分）解法一：如图，第二次足球弹出后的距离为CD根据题意：CD EF =（即相当于将抛物线AEMFC 向下平移了2个单位）212(6)412x ∴=--+解得1266x x =-=+1210CD x x ∴=-=． 1361017BD ∴=-+=（米）． 解法二：令21(6)4012x --+=．解得16x =-，2613x =+．∴点C 坐标为（13，0）．设抛物线CND 为21()212y x k =--+．将C 点坐标代入得：21(13)2012k --+=．解得：11313k =-（舍去），2667518k =+++=．21(18)212y x =--+ 令210(18)212y x ==--+，0．118x =-，21823x =+． 23617BD ∴=-=（米）． 解法三：由解法二知，18k =， 所以2(1813)10CD =-=， 所以(136)1017BD =-+=． 答：他应再向前跑17米．第14题荆州市“建设社会主义新农村”工作组到某县大棚蔬菜生产基地指导菜农修建大棚种植蔬菜．通过调查得知：平均修建每公顷大棚要用支架、农膜等材料费2.7万元；购置滴灌设备，这项费用（万元）与大棚面积（公顷）的平方成正比，比例系数为0.9；另外每公顷种植蔬菜需种子、化肥、农药等开支0.3万元．每公顷蔬菜年均可卖7.5万元． （1）基地的菜农共修建大棚x （公顷），当年收益（扣除修建和种植成本后）为y （万元），写出y 关于x的函数关系式．（2）若某菜农期望通过种植大棚蔬菜当年获得5万元收益，工作组应建议他修建多少公项大棚．（用分数表示即可）（3）除种子、化肥、农药投资只能当年受益外，其它设施3年内不需增加投资仍可继续使用．如果按3年计算，是否修建大棚面积越大收益越大？修建面积为多少时可以得到最大收益？请帮工作组为基地修建大棚提一项合理化建议．答案：（1）()227.5 2.70.90.30.9 4.5y x x x x x x =-++=-+． （2）当20.9 4.55x x -+=时，即2945500x x -+=，153x =，2103x =从投入、占地与当年收益三方面权衡，应建议修建53公顷大棚． （3）设3年内每年的平均收益为Z （万元）()()2227.50.90.30.30.3 6.30.310.533.075Z x x x x x x x =-++=-+=--+（10分）不是面积越大收益越大．当大棚面积为10.5公顷时可以得到最大收益．建议：①在大棚面积不超过10.5公顷时，可以扩大修建面积，这样会增加收益． ②大棚面积超过10.5公顷时，扩大面积会使收益下降．修建面积不宜盲目扩大．③当20.3 6.30x x -+=时，10x =，221x =．大棚面积超过21公顷时，不但不能收益，反而会亏本．（说其中一条即可）第15题一家用电器开发公司研制出一种新型电子产品，每件的生产成本为18元，按定价40元出售，每月可销售20万件．为了增加销量，公司决定采取降价的办法，经市场调研，每降价1元，月销售量可增加2万件．（1）求出月销售量y （万件）与销售单价x （元）之间的函数关系式（不必写x 的取值范围）； （2）求出月销售利润z （万元）（利润＝售价－成本价）与销售单价x （元）之间的函数关系式（不必写x 的取值范围）；（3）请你通过（2）中的函数关系式及其大致图象帮助公司确定产品的销售单价范围，使月销售利润不低于480万元．答案：略．第16题一座隧道的截面由抛物线和长方形构成，长方形的长为8m ，宽为2m ，隧道最高点P 位于AB 的中央且距地面6m ，建立如图所示的坐标系（1）求抛物线的解析式；（2）一辆货车高4m ，宽2m ，能否从该隧道内通过，为什么？（3）如果隧道内设双行道，那么这辆货车是否可以顺利通过，为什么？答案：（1）由题意可知抛物线经过点()()()024682A P B ，，，，，设抛物线的方程为2y ax bx c =++ 将A P D ，，三点的坐标代入抛物线方程． 解得抛物线方程为21224y x x =-++ （2）令4y =，则有212244x x -++=解得1244x x =+=-212x x -=>∴货车可以通过．（3）由（2）可知21122x x -=>∴货车可以通过．第17题如图，在矩形ABCD 中，2AB AD =，线段10EF =．在EF 上取一点M ，分别以EM MF ，为一边作矩形EMNH 、矩形MFGN ，使矩形MFGN ∽矩形ABCD ．令M N x=，当x 为何值时，矩形EMNH 的面积S 有最大值？最大值是多少？答案：解：矩形MFGN ∽矩形ABCD ，MN MFAD AB∴=． 2AB AD MN x ==，，2MF x ∴=．102EM EF MF x ∴=-=-． (102)S x x ∴=-2210x x =-+ 2525222x ⎛⎫=--+ ⎪⎝⎭．∴当52x =时，S 有最大值为252．第18题某企业信息部进行市场调研发现：信息一：如果单独投资A 种产品，则所获利润A y （万元）与投资金额x （万元）之间存在正比例函数关系：A y kx =，并且当投资5万元时，可获利润2万元．信息二：如果单独投资B 种产品，则所获利润B y （万元）与投资金额x （万元）之间存在二次函数关系：2B y ax bx =+，并且当投资2万元时，可获利润2.4万元；当投资4万元时，可获利润3.2万元．（1）请分别求出上述的正比例函数表达式与二次函数表达式；（2）如果企业同时对AB ，两种产品共投资10万元，请你设计一个能获得最大利润的投资方案，并求出按此方案能获得的最大利润是多少？答案：解：（1）当5x =时，12250.4y k k ===，，， 0.4A y x ∴=，当2x =时， 2.4B y =；当4x =时， 3.2B y =．2.4423.2164a ba b =+⎧∴⎨=+⎩解得0.21.6a b =-⎧⎨=⎩∴20.2 1.6B y x x =-+．（2）设投资B 种商品x 万元，则投资A 种商品(10)x -万元，获得利润W 万元，根据题意可得220.2 1.60.4(10)0.2 1.24W x x x x x =-++-=-++ 20.2(3) 5.8W x ∴=--+当投资B 种商品3万元时，可以获得最大利润5.8万元，所以投资A 种商品7万元，B 种商品3万元，这样投资可以获得最大利润5.8万元．第19题如图所示，图（1）是一座抛物线型拱桥在建造过程中装模时的设计示意图，拱高为30m ，支柱3350m A B =，5根支柱1122334455A B A B A B A B A B ，，，，之间的距离均为15m ，1515B B A A ∥，将抛物线放在图（2）所示的直角坐标系中．（1）直接写出图（2）中点135B B B ，，的坐标； （2）求图（2）中抛物线的函数表达式； （3）求图（1）中支柱2244A B A B ，的长度．答案：（1）1(30)B -，0，3(030)B ，，5(300)B ，； （2）设抛物线的表达式为(30)(30)y a x x =-+，把3(030)B ，代入得(030)(030)30y a =-+=．B A D MFB 图(1)图(2)l130a =-∴． ∵所求抛物线的表达式为：1(30)(30)30y x x =--+． （3）4B ∵点的横坐标为15， 4B ∴的纵坐标4145(1530)(1530)302y =--+=． 3350A B =∵，拱高为30，∴立柱44458520(m)22A B =+=． 由对称性知：224485(m)2A B A B ==。

新人教版九年级数学上册 二次函数总复习导学案知识点一、二次函数的概念和图像 1、 二次函数的概念：一般地，如果c b a c bx ax y ,,(2++=是常数，)0≠a ，那么y 叫做x 的二次函数. 强调：和一元二次方程类似，二次项系数0a ≠，而b c ，可以为零．二次函数的定义域是全体实数．2、二次函数2y ax bx c =++的结构特征：⑴ 等号左边是函数，右边是关于自变量x 的二次式，x 的最高次数是2． ⑵ a b c ，，是常数，a 是二次项系数，b 是一次项系数，c 是常数项． 3、二次函数的图像二次函数的图像是一条关于abx 2-=对称的曲线，这条曲线叫抛物线。

抛物线的主要特征：①有开口方向；②有对称轴；③有顶点。

4、二次函数图像的画法 五点法：（1）先根据函数解析式，求出顶点坐标，在平面直角坐标系中描出顶点M ，并用虚线画出对称轴（2）求抛物线c bx ax y ++=2与坐标轴的交点：当抛物线与x 轴有两个交点时，描出这两个交点A,B 及抛物线与y 轴的交点C ，再找到点C 的对称点D 。

将这五个点按从左到右的顺序连接起来，并向上或向下延伸，就得到二次函数的图像。

当抛物线与x 轴只有一个交点或无交点时，描出抛物线与y 轴的交点C 及对称点D 。

由C 、M 、D 三点可粗略地画出二次函数的草图。

如果需要画出比较精确的图像，可再描出一对对称点A 、B ，然后顺次连接五点，画出二次函数的图像。

画草图时应抓住以下几点：开口方向，对称轴，顶点，与 x 轴的交点，与 y 轴的交点.5、抛物线2y ax bx c =++的三要素：开口方向、对称轴、顶点.（1）a 的符号决定抛物线的开口方向：当0>a 时，开口向上；当0<a 时，开口向下；a 相等，抛物线的开口大小、形状相同.（2）对称轴：平行于y 轴（或重合）的直线记作2bx a=-.特别地，y 轴记作直线0=x . （3）顶点坐标坐标：），（ab ac a b 4422--6、二次函数)0,,(2≠++=a c b a c bx ax y 是常数，中，c b 、、a 的含义：a 表示开口方向：a >0时，抛物线开口向上a <0时，抛物线开口向下b 与对称轴有关：对称轴为x=ab2-c 表示抛物线与y 轴的交点坐标：（0，c ）7、几种特殊的二次函数的图像特征如下 函数解析式开口方向 对称轴顶点坐标2ax y = 当0>a 时 开口向上当0<a 时 开口向下0=x （y 轴） （0,0） k ax y +=20=x （y 轴） (0, k ) ()2h x a y -=h x =(h ,0) ()k h x a y +-=2h x =(h ,k )c bx ax y ++=2abx 2-= (ab ac a b 4422--，)案例分析：考点一、二次函数的定义例1函数2()y m n x mx n =-++是二次函数的条件是（ ） A ：m n 、为常数，且m ≠0。

《复习二次函数图像与系数的关系》导学案设计东城办中学张庆梅学习内容：复习二次函数y=ax2+bx+c(a≠0)的图像与系数的关系。

学习目标：1、能熟记二次函数的图像与系数的关系。

2、能熟练运用它们之间的关系解决相关问题。

(中考考点) 学习重点：目标1、2学习难点：目标2学法指导：充分自学----互助合作----展示纠错学习流程：一、学生组织复习二次函数的性质(温情提示:一定要总结全面,声音洪亮哦.)-----预设时间：5分钟（设计意图：二次函数的性质是这节课的基础，有效的复习可以为本节课打下基础，让学生组织又培养了学生的能力。

）二、自主学习：（相信自己，你是最棒的!）----预设时间：10分钟※ 1、完成下列表格，并熟记这些知识点。

字母的符号图像的特征a a >0a <0b b=0 ab>0 ab<0c c=0 c>0 c<0b2-4ac b2-4ac>0 b2-4ac=0 b2-4ac<0特殊关系 X=1时， y=X=-1时，y=教师进行巡视、抽查知识点；学生独立完成。

（设计意图：自学一定要集中本节课的重点，这个表格集中了本节的内容，条理清楚。

且这是复习课，学生完全有能力总结。

）2.针对练习：（提示:要求写出分析过程）①已知二次函数y=ax 2+bx+c(a ≠0)的图像如下图所示，对称轴是直线x=-½,下列结论正确的是（ ） A .abc > 0 B.a+b=0C. 2b+c> 0D. b 2-4ac>0②如图，二次函数y=ax 2+bx+c(a ≠0)的图像如图所示，则：ac 0 4ac-b 2 4a a+2b+c 0③已知二次函数y=ax 2+bx+c(a ≠0)的图像如下图所示,若ax 2+bx+c=k(K ≠0)有两个不相等的实数根，则k 的取值范围是 . 师追问:如果把题改为y=︱ax 2+bx+c ︴(a ≠0)， 其余条件不变，答案一样吗?（设计意图：对于本节的难点，题目 由易到难，有利于学生运用知识点去解决问题。

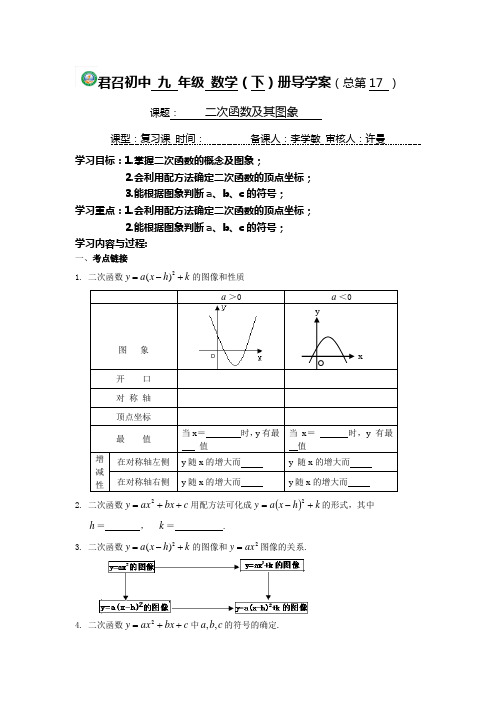
yxO君召初中 九 年级 数学（下）册导学案（总第17 ）课题： 二次函数及其图象课型：复习课 时间： 备课人：李学敏 审核人：许曼学习目标：1.掌握二次函数的概念及图象；2.会利用配方法确定二次函数的顶点坐标；3.能根据图象判断a 、b 、c 的符号； 学习重点：1.会利用配方法确定二次函数的顶点坐标； 2.能根据图象判断a 、b 、c 的符号； 学习内容与过程:一、考点链接1. 二次函数2()y a x h k =-+的图像和性质a ＞0a ＜0图 象 开 口 对 称 轴 顶点坐标最 值当x ＝ 时，y 有最 值 当x ＝ 时，y 有最 值增减性 在对称轴左侧 y 随x 的增大而y 随x 的增大而 在对称轴右侧 y 随x 的增大而y 随x 的增大而2. 二次函数c bx ax y ++=2用配方法可化成()k h x a y +-=2的形式，其中 h ＝ ， k ＝ .3. 二次函数2()y a x h k =-+的图像和2ax y =图像的关系.4. 二次函数c bx ax y ++=2中c b a ,,的符号的确定. 二、合作释疑OyxBAD C B A o y xo y x o y x o yx 例1如图，直线m x y +=和抛物线c bx x y ++=2都经过点A(1，0)，B(3，2)． ⑴ 求m 的值和抛物线的解析式；⑵ 求不等式m x c bx x +>++2的解集．(直接写出答案)三、问题点拨抛物线的平移，先化为顶点式然后平移顶点坐标四、中考演练1. 抛物线()22-=x y 的顶点坐标是 .2. 请写出一个开口向上，对称轴为直线x ＝2，且与y 轴的交点坐标为(0，3)的抛物线的解析式 .3.已知二次函数22y x x m =-++的部分图象如右图所示，则关于x 的一元二次方程220x x m -++=的解为 ．4. 函数2y ax =与(0,0)y ax b a b =+>>在同一坐标系中的大致图象是（ ）5.已知函数y=x 2-2x-2的图象如图1所示，根据其中提供的信息，可求得使 y ≥1成立的x 的取值范围是（ ） A ．-1≤x≤3B ．-3≤x≤1C ．x ≥-3D ．x ≤-1或x ≥36.二次函数c bx ax y ++=2（0≠a ）的图象如图所示，则下列结论： ①a ＞0； ②c ＞0； ③ b 2-4a c ＞0，其中正确的个数是( ) A. 0个 B. 1个 C. 2个 D. 3个（第5题） （第6题）。

（教案）二次函数图象和性质复习教案（共五篇）第一篇：(教案)二次函数图象和性质复习教案《二次函数的图象和性质》复习课教案海洲初级中学初三数学备课组内容来源：初中九年级《数学（上册）》教科书教学内容：二次函数图像与性质复习课时：两课时教学目标：1.根据二次函数的图象复习二次函数的性质，体会配方、平移的作用以及在解决相关问题的过程中进一步体会数形结合的数学思想。

2.会利用二次函数的图象判断a、b、c的取值情况。

3.在解决二次函数相关问题时，渗透解题的技巧和方法，培养学生的中考意识。

教材分析：二次函数是学生在中学阶段学习的第三种函数，是中考的重要考点之一，它与学生前面所学的一元二次方程有密切的联系，也是初中数学与高中数学的一个知识的交汇点。

本节课通过二次函数的图象和性质的复习，从特殊到一般，再由普遍的一般规律去指导具体的函数问题，加深学生对函数图象和性质之间的联系，构建知识网络体系，发展技能，归纳解题方法，让学生在练习中体会数形结合思想。

学情分析学生具有初步的、零散的关于二次函数的图象和性质的知识基础，但是还没有形成系统的知识体系，缺乏解决问题有效的、系统的方法，解决问题办法单一，较难想到运用函数的图象解决问题。

本节课针对班级学生特点采取小组合作进行教学，通过小组的交流、讨论和展示，提高学生学习的积极性和有效性。

通过本节课的学习使学生把函数的图象和性质紧密联系在一起，掌握解决一类问题的常用方法。

教学过程一、旧知回顾1、已知关于x的函数y=2、已知函数y=-2x-2,化为y=a+3x-4是二次函数，则a的取值范围是.+k的形式：此抛物线的开口向，对称轴为，顶点坐标；当x= 时，抛物线有最值，最值为；当x 时，y随x的增大而增大；当x 时，y随x的增大而减少。

3、二次函数y=-3的图象向右平移1个单位，再向上平移3个单位，所得到抛物线的解析式为4、若二次函数y=2x+m的图象与x轴有两个交点，则m的取值范围是5、抛物线的顶点在（-1，-2）且又过（-2，-1），求该抛物线的解析式。

二次函数的图像与性质导学案第二节二次函数的图像与性质环节一：回顾旧知，导入新课。

1.一次函数的图像是直线，反比例函数的图像是双曲线。

2.画函数图像的一般步骤是确定定义域和值域，列出函数表达式，选择合适的坐标系，计算出函数对应的点，然后用平滑的曲线将这些点连接起来。

环节二：小组合作，探究新知。

1.试画出二次函数 $y=x^2$ 的图像。

由 1、2、3 组用黑色笔完成以下步骤：1）列出函数表格：x$ | $2y=x$ | $y=2x^2$8$| $-16$ | $128$6$| $-12$ | $72$4$| $-8$。

| $32$2$| $-4$。

| $8$0$ | $0$。

| $0$2$ | $4$。

| $8$4$ | $8$。

| $32$6$ | $12$。

| $72$8$ | $16$。

| $128$2）描点3）连线2.试画出二次函数 $y=-x^2$ 的图像。

由 4、5、6 组用黑色笔完成以下步骤：1）列出函数表格：x$ | $y=-x^2$ | $y=-2x^2$8$| $-64$。

| $-128$6$| $-36$。

| $-72$4$| $-16$。

| $-32$2$| $-4$。

| $-8$0$ | $0$。

| $0$2$ | $-4$。

| $-8$4$ | $-16$。

| $-32$6$ | $-36$。

| $-72$8$ | $-64$。

| $-128$2）描点3）连线3.在第一题中画出二次函数 $y=2x^2$ 的图像。

由 1、2、3 组用红色笔完成。

4.在第二题中画出二次函数 $y=-2x^2$ 的图像。

由 4、5、6 组用红色笔完成。

环节三：归纳总结，提炼升华。

二次函数 $y=ax^2(a>0)$ 和 $y=ax^2(a<0)$ 的性质如下：对称轴：$x=0$。

顶点坐标：$(0,0)$。

位置：$y=ax^2$ 的图像上下平移 $|a|$ 个单位。

开口方向：$y=ax^2$ 的图像开口向上；$y=ax^2$ 的图像开口向下。

第二章二次函数（1）
一、知识梳理
1．二次函数的概念
一般地，形如(a，b，c是常数，)的函数，叫做二次函数．
[注意] (1)等号右边必须是整式；(2)自变量的最高次数是2；(3)当b＝0，c＝0时，y＝ax2是特殊的二次函数．
2．二次函数的图象
二次函数的图象是一条，它是轴对称图形，其对称轴平行于轴．
[注意] 二次函数y＝ax2＋bx＋c的图象的形状、大小、开口方向只与a有关．
3．二次函数的性质
4.二次函数图象的平移
一般地，平移二次函数y＝ax2的图象可得到二次函数y＝a(x－h)2＋k的图象．
[注意] 抓住顶点坐标的变化，熟记平移规律，左加右减，上加下减．
二、题型、技巧归纳
类型一二次函数的定义应用
例1 已知抛物线y＝(m＋1)xm2＋m的开口向下，求m的值．
[解析] 本题容易考虑不全面，只考虑m＋1＜0，而忽略抛物线是二次函数的图象，自变量x的次数为2.由抛物线开口向下得m＋1＜0且m2＋m＝2，即m＝－2.。