华师大版-数学-八年级上册-13.2三角形全等的判定4角边角第2课时角角边 同步练习

13.2三角形全等的判定1全等三角形(第1课时)一、基本目标全等三角形的概念，能运用符号语言表示两个三角形全等．二、重难点目标【教学重点】全等三角形的性质．【教学难点】掌握两个全等三角形的对应边、对应角的寻找规律，能迅速、正确指出两个全等三角形的对应元素．环节1自学提纲，生成问题【5 min阅读】阅读教材P59的内容，完成下面练习．【3 min反馈】1．全等用符号≌表示，读作全等于．2．△ABC全等于三角形△DEF，用式子表示为△ABC_≌△DEF_.3．若△ABC≌△DEF，∠A的对应角是∠D，∠B的对应角是∠E，则∠C的对应角是∠F；AB与DE是对应边，BC与EF是对应边，AC与DF是对应边．4．全等三角形的对应边相等，对应角相等．环节2合作探究，解决问题活动1小组讨论(师生互学)【例1】如图，若△BOD≌△COE，指出这两个全等三角形的对应边；若△ADO≌△AEO，指出这两个全等三角形的对应角．【互动探索】(引发学生思考)全等三角形的对应元素该如何找？【解答】∵△BOD≌△COE，∴△BOD与△COE的对应边为：BO与CO，OD与OE，BD与CE.∵△ADO≌△AEO，∴△ADO与△AEO的对应角为：∠DAO与∠EAO，∠ADO与∠AEO，∠AOD与∠AOE.【互动总结】(学生总结，老师点评)找全等三角形的对应元素的关键是准确分析图形．另外，记全等三角形时，对应顶点要写在对应的位置上，这样就可以比较容易地写出对应角和对应边了．【例2】如图，△ABC≌△DEF，∠A＝70°，∠B＝50°，BF＝4，EF＝7，求∠DEF的度数和CF的长．【互动探索】(引发学生思考)由△ABC≌△DEF，找出这两个三角形的对应角、边，即可解决问题．【解答】∵△ABC≌△DEF，∠A＝70°，∠B＝50°，BF＝4，EF＝7，∴∠DEF＝∠B＝50°，BC＝EF＝7，∴CF＝BC－BF＝7－4＝3.【互动总结】(学生总结，老师点评)全等三角形的对应边相等，对应角相等．活动2巩固练习(学生独学)1．已知图中的两个三角形全等，则∠α的度数是(D)A．72°B．60°C．58°D．50°2．如图，△ABC≌△DEF，BE＝3，AE＝2，则DE的长是(A)A．5 B．4C．3 D．23．如图，△ABC≌△FED，∠A＝30°，∠B＝80°，则∠EDF＝_70°.环节3课堂小结，当堂达标(学生总结，老师点评)请完成本课时对应练习！2全等三角形的判定条件(第2课时)一、基本目标1．理解影响两个三角形是否全等的元素(边、角)．2．理解两个三角形只有一组或两组对应相等的元素(边或角)，那么这两个三角形不一定全等．二、重难点目标【教学重点】通过探索得出：两个三角形只有一组或两组对应相等的元素(边或角)，这两个三角形不一定全等．【教学难点】通过探索得出三角形全等的判定条件是可以减少的．环节1自学提纲，生成问题【5 min阅读】阅读教材P59～P61的内容，完成下面练习．【3 min反馈】1．两个三角形完全重合，则这两个三角形全等．2．若两个三角形的三条边与三个角都分别对应相等，那么这两个三角形全等．3．一个三角形经过翻折、平移或旋转等变换得到的新三角形与原三角形全等．4．全等三角形的判定条件至少需要两个三角形有三个相等的元素．环节2合作探究，解决问题活动1小组讨论(师生互学)【例题】如图，Rt△ABC沿直角边BC所在的直线向右平移到△DEF处，下列结论中错误的是()A．AC＝DF B．∠DEF＝90°C．△ABC≌△DEF D．EC＝CF【互动探索】(引发学生思考)根据题意，得△ABC与△DEF具有怎样的关系？【分析】∵△DEF由Rt△ABC平移而成，∠ABC＝90°，∴△DEF≌△ABC，∴AC＝DF，∴∠DEF＝∠ABC＝90°，∴A、B、C正确．∵平移的距离及BC的长度不能确定，∴EC与CF的长短不能确定，∴D错误．【答案】D【互动总结】(学生总结，老师点评)一个三角形经过翻折、平移或旋转等变换得到的新三角形与原三角形全等．活动2巩固练习(学生独学)1．如图，△ABC≌△CDA，∠BAC＝95°，∠B＝45°，则∠CAD度数为(D)A．95°B．45°C．30°D．40°2．已知图中的两个三角形全等，则∠1等于(D)A．72°B．60°C．50°D．58°3．如图，△ABC为等边三角形，D是BC边上的一点，△ABD经过旋转后到达△ACE 的位置．(1)请说出旋转中心、旋转方向以及旋转角度；(2)请找出AB、AD旋转后的对应线段；(3)若∠BAD＝25°，求∠AEC度数．解：(1)由题意，得点A为旋转中心，旋转方向为顺时针，旋转角度为60°.(2)AB、AD旋转后的对应线段分别为AC、AE.(3)∵△ABC为等边三角形，∴∠B＝60°.又∵∠BAD＝25°，∴∠ADB＝180°－25°－60°＝95°.由题意知△ABD≌△ACE，∴∠AEC＝∠ADB＝95°.环节3课堂小结，当堂达标(学生总结，老师点评)请完成本课时对应练习！3边角边(第3课时)一、基本目标掌握三角形全等的“边角边”判定方法，并能进行简单的应用．二、重难点目标【教学重点】应用“边角边”证明两个三角形全等，进而得出线段或角相等．【教学难点】分析问题，寻找判定三角形全等的条件．环节1自学提纲，生成问题【5 min阅读】阅读教材P62～P65的内容，完成下面练习．【3 min反馈】1．两边及其夹角分别相等的两个三角形全等，可以简写成“边角边”或“S.A．S.”．2．有两边和一个角对应相等的两个三角形不一定全等．3．如图，AB与CD相交于点O，OA＝OC，OD＝OB，∠AOD＝_∠COB___，根据S.A．S.可得到△AOD≌△COB，从而得到AD＝CB.4．如图，已知BD ＝CD ，要根据“SAS ”判定△ABD ≌△ACD ，则还需添加的条件是_∠ADC ＝∠ADB_.环节2 合作探究，解决问题 活动1 小组讨论(师生互学)【例1】如图，A 、D 、F 、B 在同一直线上，AD ＝BF ，AE ＝BC ，且AE ∥BC .求证：△AEF ≌△BCD.【互动探索】(引发学生思考)由AD ＝BF 易得AF ＝BD .又AE ＝BC ，则要证△AEF ≌△BCD 还需什么条件？【证明】∵AE ∥BC ， ∴∠A ＝∠B . ∵AD ＝BF ， ∴AF ＝BD .在△AEF 和△BCD 中，∵⎩⎪⎨⎪⎧AE ＝BC ，∠A ＝∠B ，AF ＝BD ，∴△AEF ≌△BCD (S.A ．S.)．【互动总结】(学生总结，老师点评)判定两个三角形全等时，若有两边一角对应相等时，角必须是两边的夹角．【例2】如图，BC ∥EF ，BC ＝BE ，AB ＝FB ，∠1＝∠2.若∠1＝45°，求∠C 的度数．【互动探索】(引发学生思考)要求∠C 的度数，若△ABC ≌△FBE ，就可以得出∠C ＝∠BEF ，则由BC ∥EF 可得∠C ＝∠BEF ＝∠1，从而解决问题．【解答】∵∠1＝∠2， ∴∠ABC ＝∠FBE .在△ABC 和△FBE 中，∵⎩⎪⎨⎪⎧BC ＝BE ，∠ABC ＝∠FBE ，AB ＝FB ，∴△ABC ≌△FBE (S.A ．S.)， ∴∠C ＝∠BEF .又∵BC ∥EF ，∠1＝45°， ∴∠C ＝∠BEF ＝∠1＝45°.【互动总结】(学生总结，老师点评)(1)全等三角形是证明线段和角相等的重要工具；(2)学会挖掘题中的已知条件，如“公共边”“公共角”等．活动2 巩固练习(学生独学)1．如图，AB ＝AC ，AD ＝AE ，欲证△ABD ≌△ACE ，可补充条件( A)A ．∠1＝∠2B ．∠B ＝∠C C ．∠D ＝∠ED ．∠BAE ＝∠CAD2．下列条件中，不能证明△ABC ≌△ DEF 的是( C )A ．AB ＝DE ，∠B ＝∠E ，BC ＝EF B ．AB ＝DE ，∠A ＝∠D ，AC ＝DF C ．BC ＝EF ，∠B ＝∠E ，AC ＝DFD ．BC ＝EF ，∠C ＝∠F ，AC ＝DF3．如图，已知AB ＝AD ，若AC 平分∠BAD ，问AC 是否平分∠BCD ？为什么？解：AC 平分∠BCD .理由如下： ∵AC 平分∠BAD ， ∴∠BAC ＝∠DAC .在△ABC 和△ADC 中，∵⎩⎪⎨⎪⎧AB ＝AD ，∠BAC ＝∠DAC ，AC ＝AC ，∴△ABC ≌ADC (S.A ．S.)， ∴∠ACB ＝∠ACD ， ∴AC 平分∠BCD .活动3 拓展延伸(学生对学)【例3】如图，四边形ABCD 、DEFG 都是正方形，连结AE 、CG .求证： (1)AE ＝CG ； (2)AE ⊥CG.【互动探索】观察图形，证明 △ADE ≌△CDG ，就可以得出AE ＝CG ；结合全等三角形的性质和正方形的性质即可证得AE ⊥CG .【证明】(1)∵四边形ABCD 、DEFG 都是正方形， ∴AD ＝CD ，GD ＝ED .∵∠CDG ＝90°＋∠ADG ，∠ADE ＝90°＋∠ADG ， ∴∠CDG ＝∠ADE .在△ADE 和△CDG 中，∵ ⎩⎪⎨⎪⎧AD ＝CD ，∠ADE ＝∠CDG ，DE ＝DG∴△ADE ≌△CDG (S.A ．S.)， ∴AE ＝CG .(2)设AE 与DG 相交于点M ，AE 与CG 相交于N . 在△GMN 和△DME 中，由(1)得∠CGD ＝∠AED . 又∵∠GMN ＝∠DME ，∠DEM ＋∠DME ＝90°， ∴∠CGD ＋∠GMN ＝90°， ∴∠GNM ＝90°， ∴AE ⊥CG .【互动总结】(学生总结，老师点评)正方形的四条边相等，四个角都等于90°，利用正方形的性质结合全等三角形的判定与性质即可解决问题．环节3 课堂小结，当堂达标 (学生总结，老师点评)请完成本课时对应练习！4 角边角(第4课时)一、基本目标掌握三角形全等的判定方法：A ．S.A ．和A ．A ．S.并能解决实际问题． 二、重难点目标【教学重点】已知两角一边的三角形全等的探究．【教学难点】灵活运用三角形全等条件证明三角形全等．环节1自学提纲，生成问题【5 min阅读】阅读教材P66～P70的内容，完成下面练习．【3 min反馈】1．两角及其夹边分别相等的两个三角形全等，可以简写成“角边角”或“A.S.A.”．2．两角分别相等且其中一组等角的对边相等的两个三角形全等，可以简写成“角角边”或“A.A.S.”．3．能确定△ABC≌△DEF的条件是(D)A．AB＝DE，BC＝EF，∠A＝∠EB．AB＝DE，BC＝EF，∠C＝∠EC．∠A＝∠E，AB＝EF，∠B＝∠DD．∠A＝∠D，AB＝DE，∠B＝∠E4．如图所示，已知点F、E分别在AB、AC上，且AE＝AF，请你补充一个条件：∠B ＝∠C_，使得△ABE≌△ACF.(只需填写一种情况即可)教师点拨：此题答案不唯一，还可以填AB＝AC或∠AEB＝∠AFC.环节2合作探究，解决问题活动1小组讨论(师生互学)【例1】如图，AD∥BC，BE∥DF，AE＝CF，求证：△ADF≌△CBE.【互动探索】(引发学生思考)由AE＝CF，易得AF＝CE.要证ADF≌△CBE还需哪些条件？【证明】∵AD ∥BC ，BE ∥DF ， ∴∠A ＝∠C ，∠DF A ＝∠BEC . ∵AE ＝CF ，∴AE ＋EF ＝CF ＋EF ，即AF ＝CE . 在△ADF 和△CBE 中， ∵⎩⎪⎨⎪⎧∠A ＝∠C ，AF ＝CE ，∠DF A ＝∠BEC ，∴△ADF ≌△CBE (A .S.A ．)．【互动总结】(学生总结，老师点评)在“A .S.A ．”中，包含“边”和“角”两种元素，是两角夹一边，且“边”必须是“两角的夹边”，而不是两角及一角的对边，应用时要注意区分．【例2】如图，在△ABC 中，AD ⊥BC 交于点D ，BE ⊥AC 于点E ，AD 与BE 交于点F .若BF ＝AC ，求证：△ADC ≌△BDF.【互动探索】(引发学生思考)观察图形，要证△ADC ≌△BDF ，只需证∠DAC ＝∠DBF .又在Rt △ADC 与Rt △BDF 中，利用“等角的余角相等”即可得∠DAC ＝∠DBF .【证明】∵AD ⊥BC ，BE ⊥AC ， ∴∠ADC ＝∠BDF ＝∠BEA ＝90°.∵∠AFE ＝∠BFD ，∠DAC ＋∠AEF ＝90°，∠BFD ＋∠DBF ＝90°， ∴∠DAC ＝∠DBF .在△ADC 和△BDF 中，∵ ⎩⎪⎨⎪⎧∠DAC ＝∠DBF ，∠ADC ＝∠BDF ，AC ＝BF ，∴△ADC ≌△BDF (A .A .S.)．【互动总结】(学生总结，老师点评)(1)在解决三角形全等的问题中，要注意挖掘题中的隐含条件，如：对顶角、公共边、公共角等．(2)有直角三角形就有互余的角，利用“同角(等角)的余角相等”是证角相等的常用方法．活动2 巩固练习(学生独学) 1．完成教材P70“练习”第1～2题． 略2．如图，点B 在线段AD 上，BC ∥DE ，AB ＝ED ，BC ＝DB .求证：∠A ＝∠E.证明：∵BC ∥DE ， ∴∠ABC ＝∠BDE .在△ABC 和△EDB 中，∵⎩⎪⎨⎪⎧AB ＝DE ，∠ABC ＝∠BDE ，BC ＝BD ，∴△ABC ≌△EDB (S.A ．S.)， ∴∠A ＝∠E .环节3 课堂小结，当堂达标 (学生总结，老师点评)请完成本课时对应练习！5 边边边(第5课时)一、基本目标会运用“边边边”证明三角形全等． 二、重难点目标 【教学重点】掌握“边边边”判定两个三角形全等． 【教学难点】探索三角形全等条件的过程．环节1 自学提纲，生成问题 【5 min 阅读】阅读教材P71～P72的内容，完成下面练习． 【3 min 反馈】1．三边分别相等的两个三角形全等，可以简写成“边边边”或“S.S.S.”． 2．在△ABC 、△DEF 中，若AB ＝DE ，BC ＝EF ，AC ＝DF ，则△ABC ≌△EFG . 3．已知AB ＝3，BC ＝4，CA ＝6，EF ＝3，FG ＝4，要使△ABC ≌△EFG ，则EG ＝6. 4．如图是用直尺和圆规作一个角等于已知角的示意图，则说明∠A ′O ′B ′＝∠AOB 的依据是S.S.S..环节2 合作探究，解决问题 活动1 小组讨论(师生互学)【例1】如图，AB ＝AD ，CB ＝CD ，求证：△ABC ≌△ADC.【互动探索】(引发学生思考)要证△ABC ≌△ADC ，只需看这两个三角形的三边是否相等． 【证明】在△ABC 和△ADC 中，∵⎩⎪⎨⎪⎧AB ＝AD ，CB ＝CD ，AC ＝AC ，∴△ABC ≌△ADC (S.S.S.)．【互动总结】(学生总结，老师点评)注意运用“S.S.S.”证三角形全等时的证明格式；在证明过程中善于挖掘“公共边”这个隐含条件．【例2】如图，AB ＝DE ，AC ＝DF ，点E 、C 在直线BF 上，且BE ＝CF .求证：△ABC ≌△DEF.【互动探索】(引发学生思考)已知两个三角形有两组对边相等，同一直线上的一组边相等，可考虑用“S.S.S.”证明△ABC ≌△DEF .【证明】∵BE ＝CF ，∴EC ＋BE ＝EC ＋CF ，即BC ＝EF . 在△ABC 和△DEF 中，∵⎩⎪⎨⎪⎧BC ＝EF ，AB ＝DE ，AC ＝DF ，∴△ABC ≌△DEF (S.S.S.)．【互动总结】(学生总结，老师点评)判定两个三角形全等，先根据已知条件或易证的结论确定判定三角形全等的方法，然后根据判定方法看缺什么条件，再去证什么条件．【例3】如图，AB ＝AD ，DC ＝BC ，∠B 与∠D 相等吗？为什么？【互动探索】(引发学生思考)要判断角相等，可考虑用三角形全等证明，需添加辅助线AC 构造三角形．【解答】∠B ＝∠D .理由如下： 连结AC .在△ADC 和△ABC 中，∵⎩⎪⎨⎪⎧AD ＝AB ，AC ＝AC ，DC ＝BC ，∴△ADC ≌△ABC (S.S.S.)， ∴∠B ＝∠D .【互动总结】(学生总结，老师点评)要证∠B 与∠D 相等，可证这两个角所在的三角形全等，但现有条件并不满足，可以考虑添加辅助线证明．活动2 巩固练习(学生独学)1．如图，线段AD 与BC 交于点O ，且AC ＝BD ，AD ＝BC ，则下面的结论中不正确的是( C)A ．△ABC ≌△BADB ．∠CAB ＝∠DBAC ．OB ＝OCD ．∠C ＝∠D2．工人师傅常用角尺平分一个任意角，做法如下：如图，∠AOB 是一个任意角，在边OA 、OB 上分别取OM ＝ON ，移动角尺，使角尺两边相同的刻度分别与M 、N 重合，过角尺顶点C 作射线OC .由做法得△MOC ≌△NOC 的依据是S.S.S..3．如图，AC 与BD 交于点O ，AD ＝CB ，E 、F 是BD 上两点，且AE ＝CF ，DE ＝BF . 求证：(1)∠D ＝∠B ； (2)AE ∥CF.证明：(1)在△ADE 和△CBF 中，∵⎩⎪⎨⎪⎧AE ＝CF ，AD ＝BC ，DE ＝BF ，∴△ADE ≌△CBF (S.S.S.)， ∴∠D ＝∠B .(2)∵△ADE ≌△CBF ， ∴∠AED ＝∠CFB .∵∠AED＋∠AEO＝180°，∠CFB＋∠CFO＝180°，∴∠AEO＝∠CFO，∴AE∥CF.环节3课堂小结，当堂达标(学生总结，老师点评)请完成本课时对应练习！6斜边直角边(第6课时)一、基本目标掌握直角三角形全等的判定方法——斜边、直角边(或H.L.)．二、重难点目标【教学重点】直角三角形全等的判定定理的理解和应用．【教学难点】利用直角三角形全等的判定定理解决问题．环节1自学提纲，生成问题【5 min阅读】阅读教材P73～P75的内容，完成下面练习．【3 min反馈】1．如果两个直角三角形的两条直角边对应相等，那么两个直角三角形全等的依据是(B)A．A.A.S. B．S.A.S.C．H.L. D．S.S.S.2．斜边和一条直角边分别相等的两个直角三角形全等，简写成“斜边直角边”或“H.L.”．3．判定两个直角三角形全等的方法有S.S.S.、A.S.A ．、A.A.S.、S.A.S.、H.L.. 环节2 合作探究，解决问题 活动1 小组讨论(师生互学)【例1】如图，AB ⊥BC ，AD ⊥DC ，AB ＝AD ，求证：∠1＝∠2.【互动探索】(引发学生思考)可以通过证△ABC ≌△ADC 得到∠1＝∠2.结合已知条件，可以利用“H.L.”得到Rt △ABC ≌Rt △ADC .【证明】∵AB ⊥BC ，AD ⊥DC ， ∴∠B ＝∠D ＝90°，∴△ABC 和△ACD 均为直角三角形．在Rt △ABC 和Rt △ADC 中， ∵⎩⎪⎨⎪⎧AB ＝AD ，AC ＝AC ，∴Rt △ABC ≌Rt △ADC (H.L.)， ∴∠1＝∠2.【互动总结】(学生总结，老师点评)用“H.L.”证明三角形全等的前提是已知两个直角三角形，即在证明格式上表明“Rt △”．【例2】如图，AC ＝BD ，AD ⊥AC ，BC ⊥BD .求证：AD ＝BC .【互动探索】(引发学生思考)观察图形，不能直接通过证△AOD 与△BOC 得到结论，需作辅助线CD ，用“H.L.”证明Rt △ADC ≌Rt △BCD ，从而得到AD ＝BC .【证明】连结CD .∵AD ⊥AC ，BC ⊥BD ， ∴∠A ＝∠B ＝90°.在Rt △ADC 和Rt △BCD 中，∵⎩⎪⎨⎪⎧AC ＝BD ，DC ＝CD ，∴Rt △ADC ≌Rt △BCD ， ∴AD ＝BC .活动2 巩固练习(学生独学)1．下列条件不能判定两个直角三角形全等的是( B ) A ．斜边和一直角边对应相等 B ．两个锐角对应相等 C ．一锐角和斜边对应相等 D ．两条直角边对应相等2．如图，在Rt △ABC 中，∠BAC ＝90°，AB ＝AC ，分别过点B 、C 作过点A 的直线的垂线BD 、CE .若BD ＝4 cm ，CE ＝3 cm ，则DE ＝__7___cm.3．如图，点C 、E 、B 、F 在一条直线上，AB ⊥CF 于点B ，DE ⊥CF 于点E ，AC ＝DF ，AB ＝DE .求证：CE ＝BF .证明：∵AB ⊥CF ，DE ⊥CF ， ∴∠ABC ＝∠DEF ＝90°.在Rt △ABC 和Rt △DEF 中，∵⎩⎪⎨⎪⎧AC ＝DF ，AB ＝DE ，∴Rt △ABC ≌Rt △DEF (H.L.)， ∴BC ＝EF ，∴BC －BE ＝EF －BE ，即CE ＝BF . 活动3 拓展延伸(学生对学)【例3】如图，已知AD 、AF 分别是两个钝角△ABC 和△ABE 的高，如果AD ＝AF ，AC ＝AE .求证：BC ＝BE .【互动探索】要证BC ＝BE ，可以通过三角形全等解决，本题应该通过证明哪对三角形全等来解决呢？【证明】∵AD 、AF 分别是两个钝角△ABC 和△ABE 的高，且AD ＝AF ，AC ＝AE ， ∴Rt △ADC ≌Rt △AFE (H.L.)， ∴CD ＝EF .在Rt △ABD 和Rt △ABF 中，∵⎩⎪⎨⎪⎧AD ＝AF ，AB ＝AB ， ∴Rt △ABD ≌Rt △ABF (H.L.)， ∴BD ＝BF ，∴BD －CD ＝BF －EF ，即BC ＝BE .【互动总结】(学生总结，老师点评)证明线段相等可以通过证明三角形全等解决．在一个问题中，有时我们需要多次证明全等来创造已知条件，从而得到结论．环节3 课堂小结，当堂达标 (学生总结，老师点评)请完成本课时对应练习！。

第二页，共19页。
(角边角 (biān jiǎo))
第三页，共19页。
(角角边)
如图，已知两个(liǎnɡ ɡè)角和一条线段 ，以这两个(liǎnɡ ɡè)角为内角，以这条 线段为这两个(liǎnɡ ɡè)角的夹边，画一 个三角形．
M
N C
600
400
A
4cm
B
步骤(bùzhòu)：
图 19。2。7
A
A′口答：BC NhomakorabeaB′
C′
1.两个直角三角形中，斜边和一锐角对应(duìyìng)相等，这两个直角 三角形全等吗？为什么？
答：全等，根据(gēnjù)A.A.S.
2.两个直角三角形中，有一条直角边和一锐角(ruìjiǎo)对应相等，这 两个直角三角形全等吗？为什么？
答：全等，根据A.S.A.
第十页，共19页。
第十六页，共19页。
D
已知，如图，∠1=∠2，∠C=∠D
求证(qiúzhèng)：AC=AD。
证明：在△ABD和△ABC中 ∵∠1=∠2 （已知）
1
A2
B
∠D=∠C（已知）
AB=AB（公共(gōnggòng)边）
C
∴△ABD≌△ABC （AAS）
∴AC=AD （全等三角形对应边相等）
第十七页，共19页。
如图：△ABC是等腰三角形，AD、 BE分别(fēnbié)是∠A、∠B的角 平分线，△ABD和△BAE全等吗？ 试说明理由.
若改为(：ɡǎAiD、wéBiE)分：别AD(、fēBnEb分ié别) 是两腰上上的的高中，线△，A△BDA和BD△和BAE △全等BA吗E全？等试吗说？明试理说由明. 理由.
结 论 有两角和它们中的一边(yībiān)对应相等的

13.2.4 角边角（ASA）学习目标：1、理解并掌握“角边角”定理，能够运用“角边角”定理解决实际问题；2、会应用“角边角”定理构造全等三角形，体验解决问题方法的多样性，提高应用意识与创新意识。

重点：角边角定理的探究过程。

难点：角边角定理在实际中的应用。

一、复习回顾1、什么叫做全等三角形，如何识别两个三角形全等？所学过的识别两个三角形全等的方法有？2、叙述S.A.S.的内容。

当两个三角形的两条边及其中一边的对角分别对应相等时，两个三角形一定全等吗？二、探究：1、已知：如图，要得到△ABC≌△ABD,已经隐含有条件是_________根据所给的判定方法，在下列横线上写出还需要的两个条件：（1）____________________________________。

（SAS）（2）____________________________________。

（SAS）2、如图，已知两个角和一条线段，以这两个角为内角，以这条线段为这两个角的夹边，画一个三角形．把你画的三角形与其他同学画的三角形进行比较，所有的三角形都全等吗？换两个角和一条线段，试试看，是否有同样的结论．总结：三角形全等的又一种识别方法：两角一边。

判定：如果两个三角形的两个角及其夹边分别对应相等，那么这两个三角形全等．简记为 (A.S.A.)定理：如果两个三角形中有两个角和其中一个角的对边分别对应相等，那么这两个三角形全等．简记为A.A.S.（或角角边）．练习：如图，要证明△ACE≌△BDF,根据给定的条件和指明的依据，将应当添设的条件填在横线上。

（1）AC∥BD，CE=DF，______________________________(S.A.S.)(2) AC=BD， AC∥BD_______________________________(A.S.A.)(3) CE=DF，_______________________________________(A.S.A.)(4)∠C= ∠D，_______________________________________(A.S.A.)三、完成例题例1：如图，已知∠ABC＝∠DCB，∠ACB＝∠DBC，求证：△ABC≌△DCB；AB=DC．四、巩固（1）两个直角三角形中，斜边和一锐角对应相等，这两个直角三角形全等吗？为什么？（2）两个直角三角形中，有一条直角边和一锐角对应相等，这两个直角三角形全等吗？为什么？五、小结ASA判定定理内容：AAS判定定理内容：六、检测1、如图，∠ABC=∠DCB，∠ACB=∠DCB，试说明△ABC≌△DCB.2、已知：如图，∠DAB=∠CAB，∠DBE=∠CBE。

用符号语言表达为：
B E ∵BC EF C F
在△ABC和△DEF中，
A
D
B
\
C
E
\
F
练习
∴ △ABC≌△DEF (A.S.A.)
例1、已知：点D在AB上，点E在AC上，BE和 CD相交于点O，AB=AC，∠B=∠C。 求证： △ABE≌△ACD
A
证明：在△ABE和△ACD中 ∠A=∠A（公共角） ∵ AB=AC（已知）
C
A
O
B
D
探究2
在△ABC和△DEF中，∠A=∠D，∠B=∠E ， BC=EF，△ABC与△DEF全等吗？能利用角边 角条件证明你的结论吗？
A D
C E B
F
探究反映的规律是：
有两角和其中一个角的对边分别对应相等的 两个三角形全等(简写成“角角边”或 “A.A.S.”）
用数学符号表示
在△ABC和△A`B`C`中 ∠A=∠A` A
例2.如图，已知AB=AC，∠ADB= ∠AEC，求证：△ABD≌△ACE
证明：∵ AB=AC， ∴ ∠B= ∠C（等边对等角） ∵ ∠ADB= ∠AEC， AB=AC，
A
∴ △ABD≌△ACE（A.A.S.）
B
D
E
C
练习：
1.如图,AB⊥BC, AD⊥DC, ∠1=∠2.求证AB=AD
2：如图，已知∠ABC＝∠D， ∠ACB＝∠CBD判断图中的 两个三角形是否全等， 并说明理由．
不全等。因为虽然有两组内角相等， 且BC＝BC，但BC不都是两个三角形两 组内角的夹边，所以不全等。
作业：
1.如图已知∠ABC＝∠DCB， ∠ACB＝ ∠DBC， 求证：△ABC≌△DCB， AB=DC

(1)公共边相等；
(2)相等线段加(减)相等线段，其和(差)仍相等，即
等式的性质； (3)第三边代换，即等量代换； (4)全等三角形对应边相等．
类比这些方法，你 会总结证明两个角 相等的方法吗？
例题
【例2】求证:全等三角形对应边上的高相等.
已知：如图，△ABC≌△A′B′C′ ，AD、A′D′分
别是△ABC的BC边和△A′B′C′的B′C′边上的高. 求证: AD = A′D′.
求证：△ABC≌△A′B′C′.
C
C′
证明：∵ ∠A = ∠A′，∠B = ∠B′(已知)，
∠A′+∠B′+∠C′ = 180°
(三角形内角和等于180°)， A
B A′
B′Байду номын сангаас
∴ ∠A+∠B+∠C′ = 180°(等量代换).
又∵ ∠A+∠B+∠C = 180°(三角形内角和等于180°)，
∴∠C = ∠C′(等式的性质).
例题
【例1】如图，在△ABC中，D是边BC的中点,
过点C 画直线CE, 使CE // AB, 交AD的延长线
于点 E. 求证AD = ED.
证明：∵ CE // AB(已知)， ∴ ∠ABD = ∠ECD，∠BAD = ∠CED (两直线平行，内错角相等). 在△ABD与△ECD中，
【例1】如图，在△ABC中，D是边BC的中点,
过点C 画直线CE, 使CE // AB, 交AD的延长线
于点 E. 求证AD = ED.
∵∠ABD = ∠ECD， ∠BAD = ∠CED(已证)， BD = CD(已知)，
∴△ABD≌△ECD (A.A.S.)， ∴AD = ED(全等三角形的对应边相等).

＝，
＝ ,
＝.
∴△ABC≌△DFE(SSS).
讲授新课
变式2 若将上题中的三角形继续向左平移(如图)，若AB＝DC，
AC＝DB，问：△ABC≌△DCB 吗？
D
A
B
E
C
F
解:全等.
在△ABC和△DCB中，
＝，
＝ ,
＝.
∴△ABC≌△DCB(SSS).
讲授新课
（简写为“边边边”或“S.S.S.”）
A
几何语言：
在△ABC和△ DEF中，
AB=DE，
B
C
D
BC=EF，
CA=FD，
∴ △ABC ≌△ DEF（S.S.S.）.
E
F
讲授新课
典例精析
【例1】如图，在四边形 ABCD 中，AD = CB，AB = CD.
求证: ∠B = ∠D.
证明：在△ABC 和△CDA 中，
在△ABE和△CDF中，
AE=CF，∠A=∠C，AB=DC.
∴△ABE≌△CDF(SAS).
∴BE=DF.
当堂检测
8. 如图，点 B、E、C、F 在同一条直线上，AB = DE，AC = DF ，
BE = CF．求证:∠A = ∠D.并找出图中相互平行的线段，说明
你的理由.
证明:∵BE＝CF，∴BE＋CE＝FC＋EC，
b
3 cm
2.以点A为圆心,以线段b(3cm)的长为半
径画圆弧;以点B为圆心,以线段a(4cm)
的长为半径画圆弧;两弧交于点C.
c
4.5 cm
C
a
b
3.连结AC、BC.
△ABC即为所求.
c
A
B

问：通过实验可以发现什么事实？
探究反映的规律是：
有两角和它们夹边对应 相等的两个三角形全等 (简写成“角边角”或“ASA”） 。
用数学符号表示
证明：在△ABE和△A’CD中
∠A=∠A’ （已知 ） AB=A’C（已 ） ∠B=∠C（已知 ）
A
A'
∴ △ABE≌△A’CD（ASA）
ED
B
C
例题讲解：
复习 1.什么是全等三角形？
2.判定两个三角形全等要具备什 么条件?
三边对应相等的两个三角形全等。
边边边：SSS
有两边和它们夹角对应相等的两个三角形全等
。
边角边：SAS
创设情景,实例引入
怎么办？可以帮帮我吗？
一张教学用的三角形硬纸板不小心被撕坏了， 如图，你能制作一张与原来同样大小的新教具？能恢 复原来三角形的原貌吗？
D A
CE
F
B
两个角和其中一个
角的对边对应相等的 两个三角形全等(简写 成“角角边”或 “AAS”）。
1.如图，应填什么就有 △ADC≌ △BOD
∠A=∠B（已知）
（已知）
∠C=∠D （已知）
B
∴△ADC≌△BOD（
）
C
O D
A
2.已知，如图，∠1=∠2，∠C=∠D 求证：AC=AD
证明：
D
1
A2
B
C
3.已知，如图，∠1=∠2，∠C=∠D
求证：AC=AD
证明： 在△ABD和△ABC中
D
∠1=∠2
（已知）
∠D=∠C（已知）
AB=AB（公共边）
1
∴△ABD≌△ABC （AAS）
A2
B

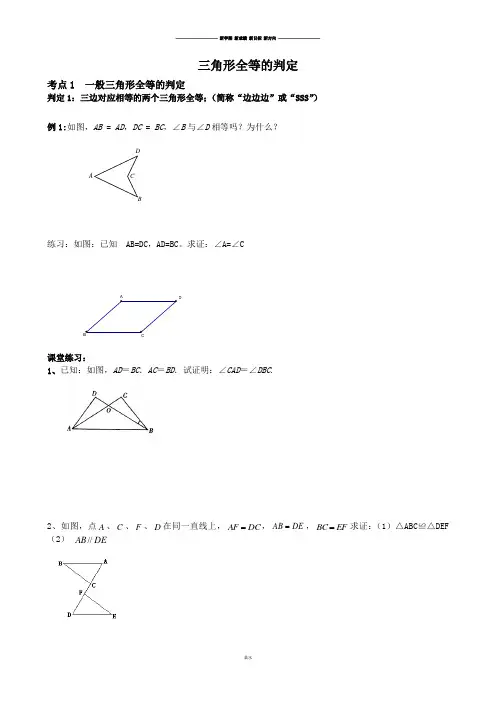
三角形全等的判定考点1 一般三角形全等的判定判定1：三边对应相等的两个三角形全等；（简称“边边边”或“SSS”）例1:如图，AB = AD，DC = BC，∠B与∠D相等吗？为什么？练习：如图：已知 AB=DC，AD=BC。

求证：∠A=∠C课堂练习：1、已知：如图，AD＝BC．AC＝BD．试证明：∠CAD＝∠DBC.2、如图，点A、C、F、D在同一直线上，DCAF=，DEAB=，EFBC=求证：（1）△ABC≌△DEF （2）DEAB//A DABCDA B3、如图，AC 与BD 交于点O ，CB AD =，E 、F 是BD 上两点，且CF AE =，BF DE =．求证：⑴B D ∠=∠；⑵CF AE //培优：如图，已知AC ，BD 相交于O ，且AB=DC ，AC=DB ，证明：△ABO ≌△DOC判定2：两边和它们的夹角对应相等的两个三角形全等；（简称“边角边”或“SAS ”）（注：“角”必须是“两边的夹角”）课堂练习：例2、已知EF 是AB 上的两点，AE =BF ，AC ∥BD ，且AC =DB ，求证：CF =DE ．1、已知：如图AB=AC,AD=AE,∠BAC=∠DAE求证： （1）△ABD ≌△ACE（2）BD=CE（3）∠B= ∠C2、已知CE=CB，∠1=∠2，AC=DC，求证：△ABC≌△DEC；3、如图，ABC∆都是等边三角形，连接BE、AD交于O.∆和ECD求证：⑴BEAD=⑵︒AOB∠60=4、如图，平行四边形ABCD中，E是CA延长线上的点，F是AC延长线上的点，且AE=CF，说明：∠E=∠F培优：如图，D是ABC∆中边BC的中点，ACDAB=.ABD∠∠，且AC=求证：△AEB≌△AECDBEAO判定3：两角和它们的夹边对应相等的两个三角形全等；（简称“角边角”或“ASA”）（注：“边”必须是“两角的夹边”）例1：已知：点D在AB上，点E在AC上，BE和CD相交于点O，AB=AC，∠B=∠C。

原创新课堂
原创新课堂
9．(宜昌中考)如图，在方格纸中，以AB为一边作△ABP，使之与△ABC全等，从P1，P2，P3，P4四个 点中找出符合条件的点P，则点P有( C ) A．1个 B．2个 C．3个 D．4个
10．如图，CA＝CB，AD＝BD，M，N分别是CA，CB的中点，若DM＝5 cm，则DN＝( C ) A．3 cm B．4 cm C．5 cm D．6 cm
6．如图，点A，E，F，D在同一直线上，若AB∥CD，AB＝CD，AE＝FD，则图中的全等三角形有( C ) A．1对 B．2对 C．3对 D．4对
7．(娄底中考)如图，已知AB＝BC，要使△ABD≌△CBD，还需添加一个条件，你添加的条件是 _____∠_A_B_D__＝__∠_C_B_D_或__A_D__＝__C_D___．(只需写一个，不添加辅助线)
原创新课堂
AB＝CD， 解：(1)证明：连结 AD.在△BAD 和△CDA 中，∵ DB＝AC，∴△BAD
AD＝DA，
≌△CDA(S.S.S.)，∴∠B＝∠C(全等三角形对应角相等) (2)作辅助
线的意图是构造全等三角形
原创新课堂
4．(2017·福建)如图，点B，E，C，F在一条直线上，AB＝DE，AC＝DF，BE＝CF.求证：∠A＝∠D.
AB＝DE， 证明：∵BE＝CF，∴BC＝EF.在△ABC 和△DEF 中，∵ AC＝DF，∴
BC＝EF， △ABC≌△DEF(S.S.S.)，∴∠A＝∠D
原创新课堂
5．给出下列四组条件：①AB＝DE，BC＝EF，AC＝DF；②AB＝DE，∠B＝∠E，BC＝EF；③∠B＝∠E， BC＝EF，∠C＝∠F；④AB＝DE，AC＝DF，∠B＝∠E.其中能使△ABC≌△DEF的条件共有( C ) A．1组 B．2组 C．3组 D．4组

D
E
∠C=∠B， ∴△ACD≌△ABE（ASA）.
B
C
∴AD=AE.
新课讲解
典例分析
例 2 如图，在△ABC和△DEF中，∠A=∠D，∠B=∠E，BC=EF. 求证：△AABC≌△DEF.
证明：在△ABC和△DEF中，
∠A=∠D， BC=EF，
B
C
D
∠B=∠E，
∴△ABC≌△DEF（ASA）.
E
F
你是不是这样证明的，错在哪里？
新课讲解
典例分析
例 2 如图，在△ABC和△DEF中，∠A=∠D，∠B=∠E，BC=EF. 求证：△AABC≌△DEF.
分析：BC，EF不是已知两对角的夹边， 在三角形中，知道两个角的关系，利用三 B 角形内角和定理可以求得第三个角之间的 关系.通过转化来构造“ASA”的判定条件.
E
C D
F
新课讲解
例 如图，在△ABC和△DEF中，∠A=∠D，∠B=∠E，BC=EF. 求证：△ABC≌△DEF.
证明：在△ABC和△DEF中，
A
∵∠A=∠D，∠B=∠E，
∠C=180°-∠A-∠B，∠F=180°-∠D-∠E， ∴∠C=∠F. 在△ABC和△DEF中，
∠B=∠E，
B
DC
E
F
BC=EF，
∴△AEB≌△ADC（AAS）. ∴AB=AC.
新课讲解
思考 有两个角和一条边分别对应相等的两个三角形是否一定全等？ 如果两个三角形中，有两个角和一条边分别相等，那么这两 个三角形是全等三角形.
思考 “ASA”和“AAS”之间有什么关系？
在证明两个三角形全等过程中，“ASA”和“AAS”两个判定 是可以相互转化的.

基于课程标准、中招视野、两类结构”的教案设计课题：全等三角形的判定——角边角课型：新授课一、学习目标确定的依据1、课程标准掌握基本事实：两角及其夹边分别相等的两个三角形全等。

2、教材分析本节课是初中数学华师版八年级下册第13章三角形全等的判定第四节内容，它是学生在认识三角形的基础上，在了解全等图形和全等三角形之后学习的，是后继学习探索相似形条件的基础，并且是用于说明线段相等、角相等的重要依据。

本节课的内容对学生学习几何说理来说具有具足轻重的作用。

3、中招考点全等三角形在中考试题中一直占有重要的地位，属于必考内容，单独考查的多以选择题、填空题为主，解答题中单独成题较少，多结合其他知识综合考查，主要解决问题有：1.利用三角形全等证明线段相等；2.利用三角形全等求角的度数；3.利用三角形全等证明线段的大小、位置关系（平行、垂直等）。

4、学情分析由于这个时期的学生好动、注意力利分散、喜爱发表见解，所以一方面要运用直观生动的形象激发学生的学习兴趣，另一方面要不断创造条件和机会，让学生展示自我，充分发挥其主动性，学会思考，体现其主体地位。

二、学习目标1、能说出角边角以及角角边的含义。

2、会运用角边角以及角角边来判定两个三角形全等。

三、评价任务1、向同桌说出ASA的判定条件，能明确其使用时的注意事项（即“夹角”）。

2、能灵活应用ASA,AAS解决三角形全等的边、角问题。

四、教学过程_______________________.C第4题图学习目标：会运用角角边来判定两个三角形全等。

自学指导2：♦自学范围：课本第67—68页。

♦自学时间：3分钟♦自学方法：独立看书，独立思考。

♦自学要求：1、能说出角角边的含义。

2、会运用角角边来判定两个三角形全等。

3、完成自学检测。

自学检测2：1、两角分别相等且其中一组等角的对边相等的两个三角形全等，简记为_____（或_____）。

2 、(1)两个直角三角形中，斜边和一锐角对应相等，这两个直角三角形全等吗？为什么？(2)两个直角三角形中，有一条直角边和一锐角对应相等，这两个直角三角形全等吗？为什么？3、如图，已知AB=AC，∠ADB= ∠AEC，求证：△ABD≌△ACE要点归纳2两角分别相等且其中一组等角的对边相等的两个三角全等，简记为角角边（或A.A.S. ）。

13.2.2三角形全等的判定—边角边(S.A.S)公开课教案一、背景介绍与教学资料本教材强调直观和操作，在观察中学会分析，在操作中体验变换。

教材的编排淡化概念的识记，强调图形性质的探索。

全等三角形的判定是今后证明线段相等和角相等的重要工具，是学习后续课程的必要基础。

在教学呈现方式上，改变了“结论——例题——练习”的陈述模式，而采用“问题——探索——发现”等多种研究模式。

在直观感知、操作确认的基础上，适当地进行数学说理，将两者有机地结合起来，让学生体验说理的必要性，用自己的语言说明理由，学会初步说理。

二、教学设计教学内容分析本节课的主要内容是探索三角形全等的条件“边角边”以及利用“S.A.S”判定基本事实证明三角形全等。

学生通过自己实验，经历探索三角形全等条件的过程，体会利用操作、归纳获得数学结论的方法。

由于本节课是学生探索三角形全等的条件的第一课时，所以对学生来讲是一次知识的飞跃，也为下面几节课的探索做铺垫。

教学目标：1、知识与技能：探索、领会“S.A.S”判定两个三角形全等的方法2、过程与方法：经历探索三角形全等的判定方法的过程，能灵活地运用三角形全等的条件，进行有条理的思考和简单推理，并能利用三角形的全等解决实际问题，体会数学与实际生活的联系。

3、情感态度与价值观：培养学生合理的推理能力，感悟三角形全等的应用价值，体会数学与实际生活的联系。

重难点与关键：1、重点：会用“边角边”证明两个三角形全等。

2、会正确运用“S.A.S”判定基本事实，在实践观察中正确选择判定三角形的方法。

同时通过作图，论证S.S.A不能证明两个三角形一定全等。

既是难点也是关键点。

教学方法：采用“问题----操作---结论—运用”的教学方法，让学生有一个直观的感受。

教学过程：一、创设情境。

1、因铺设电线的需要，要在池塘两侧A、B处各埋设一根电线杆（如图），因无法直接量出A、B两点的距离，现有一足够的米尺。

怎样测出A、B两杆之间的距离呢？。

3．【易错题】如图所示，AC 是∠BAD 的平分线，CA 是∠BCD 的平分线，则判定△ABC≌△ADC 的依据可以是( D )
A．AAA B．ASA C．AAS D．ASA 或 AAS
4．如图，点 B，F，C，E 在同一条直线上，AB∥ED，AC∥FD， 那么添加下列一个条件后，仍无法判定△ABC≌△DEF 的是 ( C) A．AB＝DE B．AC＝DF C．∠A＝∠D D．BF＝EC
【答案】A.A.S.
13．【中考·宜宾】如图，已知∠1＝∠2，∠B＝∠D.
求证：CB＝CD. 证明：∵∠1＝∠2，∴∠ACB＝∠ACD.
在△ABC 与△ADC 中， ∠B＝∠D， ∠ACB＝∠ACD， AC＝AC， ∴△ABC≌△ADC(A.A.S.)，∴CB＝CD.
14．【中考·温州】如图，在△ABC 中，AD 是 BC 边上的中线，E 是 AB 边上一点，过点 C 作 CF∥AB 交 ED 的延长线于点 F.
A．A.S.A. B．A.A.S. C．S.A.S. D．无法证明
2．如图，在∠AOB 的两边上截取 OC＝OD，连结 AD，BC 交于 点 P，若∠A＝∠B，则下列结论正确的是( D ) ①△AOD≌△BOC；②△APC≌△BPD； ③OC＋PC＝OD＋PD. A．① ＝90°，AC＝BC，AD 平分∠CAB 交 BC 于点 D，DE⊥AB，垂足为点 E，AB＝12 cm，则△DEB 的周长为___1_2____cm.
11．【中考·临沂】如图，∠ACB＝90°，AC＝BC，AD⊥CE， BE⊥CE，垂足分别是点 D，E，AD＝3，BE＝1，则 DE 的 长是( B ) A．32 B．2 C．2 2 D． 10
15．【中考·漳州】如图，BD 是平行四边形 ABCD 的对角线，过点 A 作 AE⊥BD，垂足为 E，过点 C 作 CF⊥BD，垂足为 F.

∠ = ∠,
如图,在△ABC和△DEF中, ∠ = ∠,
= ,
DEF
∴△ABC≌△______(A.A.S.).
A.S.A.S.
B.A.S.A.
C.A.A.S.
D.以上都正确
重点 典例研析
重点1 判定三角形全等的基本事实:角边角(几何直观、推理能力、应用意识)
【典例1】(教材再开发·P67例3拓展)如图,要测量水池宽AB,可从点A出发在地面上
画一条线段AC,使AC⊥AB,再从点C观测,在BA的延长线上测得一点D,使∠ACD=
∠ACB,这时量得AD=100 m,求水池宽AB.
【自主解答】∵AC⊥AB,∴∠CAB=∠CAD=90°,
∠ = ∠
在△ACB和△ACD中,
,
=
∠ = ∠
∴△ACB≌△ACD(A.S.A.),
4.角边角
基础 主干落实
重点 典例研析
素养 当堂测评
课时学习目标
素养目标达成
1.掌握三角形全等的“角边角”的基本事实,并运用其解 几何直观、推理能力、应
决简单的推理证明问题
2.经过推理证明并掌握三角形全等的“角角边”的判定
方法,并运用其解决简单的推理证明问题
用意识
几何直观、推理能力
基础 主干落实
∠ = ∠,
∠ = ∠,
在△ABC和△CDE中,
= ,
∴△ABC≌△CDE(A.A.S.).
【举一反三】
(2024·重庆期末)如图,在△ABC与△CDE中,AC=CE,AB∥DE,∠ACB=∠CED,
4
若BD=2,DE=6,则AB的长为_______.
素养 当堂测评
1.(4分·几何直观、推理能力)如图,已知∠D=∠A,∠1=∠2,那么要得到△ABC≌