小学一年级【经典例题】立体图形计数

1．下图中，共有多少个小正方体？A.3B.4C.5D.6来源：2014·乐乐课堂·练习难度：简单类型：选择题答案：C2．下图中，共有多少个小正方体？A.3B.4C.5D.6来源：2014·乐乐课堂·练习难度：简单类型：选择题答案：D3．下图中，共有多少个小正方体？A.6B.7C.8D.9来源：2014·乐乐课堂·练习难度：简单类型：选择题答案：B4．下图中，共有多少个小正方体？A.5B.6C.7D.8来源：2014·乐乐课堂·练习难度：简单类型：选择题答案：D5．下图中，共有多少个小正方体？A.9B.8C.7D.6来源：2014·乐乐课堂·练习难度：简单类型：选择题答案：A6．下图中，共有多少个小正方体？A.7B.8C.9D.10来源：2014·乐乐课堂·练习难度：简单类型：选择题答案：D7．下图中，共有多少个小正方体？A.10B.11C.12D.13来源：2014·乐乐课堂·练习难度：简单类型：选择题答案：D8．下图中，共有多少个小正方体？A.21B.22C.23D.24来源：2014·乐乐课堂·练习难度：简单类型：选择题答案：D9．下图中，共有多少个小正方体？A.15B.16C.17D.18来源：2014·乐乐课堂·练习难度：简单类型：选择题答案：B10．下图中，共有多少个小正方体？A.10B.11C.12D.13来源：2014·乐乐课堂·练习难度：简单类型：选择题答案：A首页上一页1234下一页尾页11．下图中，共有多少个小正方体？A.11B.12C.13D.14来源：2014·乐乐课堂·练习难度：简单类型：选择题答案：D12．下图中，共有多少个小正方体？A.15B.16C.17D.18来源：2014·乐乐课堂·练习难度：简单类型：选择题答案：C13．下面的大正方体是由几个小正方体组成的？A.4B.6C.8D.10来源：2014·乐乐课堂·练习难度：简单类型：选择题答案：C14．下面的大正方体是由几个小正方体组成的？A.19B.22C.25D.27来源：2014·乐乐课堂·练习难度：简单类型：选择题答案：D15．下面的大正方体是由几个小正方体组成的？A.68B.64C.60D.56来源：2014·乐乐课堂·练习难度：简单类型：选择题答案：B16．如果要把下面的立体图形补全成为一个完整的大正方体，那至少需要再添加几个小正方体呢？A.1B.2C.3D.4来源：2014·乐乐课堂·练习难度：简单类型：选择题答案：B17．如果要把下面的立体图形补全成为一个完整的大正方体，那至少需要再添加几个小正方体呢？A.5B.6C.7D.8来源：2014·乐乐课堂·练习难度：简单类型：选择题答案：A18．如果要把下面的立体图形补全成为一个完整的大正方体，那至少需要再添加几个小正方体呢？A.4B.5C.6D.7来源：2014·乐乐课堂·练习难度：简单类型：选择题答案：D19．如果要把下面的立体图形补全成为一个完整的大正方体，那至少需要再添加几个小正方体呢？A.14B.15C.16D.17来源：2014·乐乐课堂·练习难度：简单类型：选择题答案：B20．如果要把下面的立体图形补全成为一个完整的大正方体，那至少需要再添加几个小正方体呢？A.14B.15C.16D.17来源：2014·乐乐课堂·练习难度：简单类型：选择题答案：A首页上一页1234下一页尾页21．如果要把下面的立体图形补全成为一个完整的大正方体，那至少需要再添加几个小正方体呢？A.17B.16C.15D.14来源：2014·乐乐课堂·练习难度：简单类型：选择题答案：C22．如果要把下面的立体图形补全成为一个完整的大正方体，那至少需要再添加几个小正方体呢？A.3B.4C.5D.6来源：2014·乐乐课堂·练习难度：简单类型：选择题答案：C23．如果要把下面的立体图形补全成为一个完整的大正方体，那至少需要再添加几个小正方体呢？A.14B.15C.16D.17来源：2014·乐乐课堂·练习难度：中等类型：选择题答案：C24．如果要把下面的立体图形补全成为一个完整的大正方体，那至少需要再添加几个小正方体呢？A.16B.17C.18D.19来源：2014·乐乐课堂·练习难度：中等类型：选择题答案：B25．如图所示，将大正方体中的红色部分挖穿，那得挖走多少个小正方体呢？A.1B.2C.3D.4来源：2014·乐乐课堂·练习难度：简单类型：选择题答案：B26．如图所示，将大正方体中的红色部分挖穿，那得挖走多少个小正方体呢？A.1B.2C.3D.4来源：2014·乐乐课堂·练习难度：简单类型：选择题答案：C27．如图所示，将大正方体中的红色部分挖穿，那得挖走多少个小正方体呢？A.1B.2C.3D.4来源：2014·乐乐课堂·练习难度：简单类型：选择题答案：D28．如图所示，将大正方体中的红色部分挖穿，那得挖走多少个小正方体呢？A.3B.6C.9D.12来源：2014·乐乐课堂·练习难度：简单类型：选择题答案：C29．如图所示，将大正方体中的红色部分挖穿，那得挖走多少个小正方体呢？A.2B.4C.6D.8来源：2014·乐乐课堂·练习难度：简单类型：选择题答案：C30．如图所示，将大正方体中的红色部分挖穿，那得挖走多少个小正方体呢？A.16B.12C.8D.4来源：2014·乐乐课堂·练习难度：简单类型：选择题答案：B首页上一页1234下一页尾页31．如图所示，将立体图形中的红色部分挖穿，那得挖走多少个小正方体呢？A.3B.4C.5D.6来源：2014·乐乐课堂·练习难度：简单类型：选择题答案：A32．如图所示，将立体图形中的红色部分挖穿，那得挖走多少个小正方体呢？A.1B.2C.3D.4来源：2014·乐乐课堂·练习难度：简单类型：选择题答案：D33．如图所示，将立体图形中的红色部分挖穿，那得挖走多少个小正方体呢？A.1B.3C.4D.5来源：2014·乐乐课堂·练习难度：简单类型：选择题答案：D34．如图所示，将立体图形中的红色部分挖穿，那得挖走多少个小正方体呢？A.2B.3C.4D.6来源：2014·乐乐课堂·练习难度：简单类型：选择题答案：D35．如图所示，将立体图形中的红色部分挖穿，那得挖走多少个小正方体呢？A.2B.4C.6D.8来源：2014·乐乐课堂·练习难度：简单类型：选择题答案：D36．如图所示，将立体图形中的红色部分挖穿，那得挖走多少个小正方体呢？A.2B.5C.8D.10来源：2014·乐乐课堂·练习难度：简单类型：选择题答案：D首页上一页1234下一页尾页。

第十一讲立体图形计数前续知识点：一年级第一讲；XX模块第X讲后续知识点：X年级第X讲；XX模块第X讲墨莫墨莫卡莉娅小高把相应的人物换成红字标明的人物．还记得我们都学习过哪些立体图形吗？正方体、长方体、圆柱体、球体……数不胜数．今天我们来学习一下立体图形的计数．在地球上，一个小正方体可以在没有任何支撑的情况下悬浮在空中吗？答案当然是不可以！聪明的你赶快来看一看，下面题目中的立体图形到底由几个小正方体组成的呢？例题1数一数，它们分别由几个小正方体组成？【提示】有没有看不见的正方体？练习1数一数，它们分别由几个小正方体组成？数正方体有许多方法，其中我们可以一层一层的分层数，试试看．例题2左边方框中的立体图形和右边哪个立体图形中的小正方体个数相同呢？【提示】数一数，分别有几个小正方体！练习2左边方框中的立体图形和右边哪个立体图形中的小正方体个数相同呢？分层数的方法不仅简单快捷，而且清晰明了，不容易数重数漏．结合找规律的方法，我们更能轻松数出立体图形的个数．例题3数一数，下面这个“宝塔”由多少个小正方体组成？A BC DA B【提示】找一找，每层之间有什么规律？练习3数一数，下面这个“楼梯”由多少个小正方体组成？例题4要想把下面左边的立体图形补全成为一个完整的大正方体，至少需要再加几个小正方体呢？【提示】左边的立体图形由几个小正方体组成的？右边的呢？练习4要想把下面左边的立体图形补全成为一个完整的大正方体，至少需要再加几个小正方体呢？例题5要想把下面的立体图形补全成为一个完整的大正方体，至少需要再加几个小正方体呢？【提示】补全后的大正方体是什么样的呢？例题6如图所示，将大正方体中的“L”形挖穿，你能数出现在这个立体图形有多少个小正方体吗？【提示】挖穿了几层？课外阅读长方体和正方体的故事长方体是一个聪明的小男孩儿，他生活在一个数学图形的古老部落．长老们说他们一直拥有自然女神的庇护，自然女神总是不定期地出现在他们部落，每一次，她都只见一个有缘人，如果这个有缘人能够通过她的考验，她就会满足这个有缘人的一个合理的愿望．有一天，长方体去小河边玩，已经有一些伙伴在河边嬉戏，有三角形，正方形，圆等等……长方体刚走到附近就听到三角形喊救命，原来是平行四边形掉到河里去，长方体奋不顾身地跳进了河里，拼死救人．最后长方体把平行四边形救出来了．大家都很感谢长方体．长方体坐在草原上看风景，自然女神出现了．自然女神说：“你已经通过了我的考验，告诉我，你有什么愿望？”长方体说：“我没有什么愿望．”自然女神说：“既然你不说，那我就自作主张替你做决定了．”自然女神知道长方体一个人玩，没有伙伴，就创造了正方体，正方体和长方体一样聪明，而且，正方体和长方体还十分相似，有许多共同的特点．长方体很喜欢这个新伙伴．长方体对自然女神说；“我很喜欢正方体，他有许多和我相似的地方，像我的影子，但又和我完全不一样，有自己的个性．”自然女神说：“你喜欢就好，其实，正方体是另一个特殊的你．比你自己还要特别的你．以后，你自然会明白的．”作业1. 数一数，它们分别由几个小正方体组成？2. 左边方框中的立体图形和右边哪个立体图形中的小正方体个数相同呢？3. 数一数，下面这个“楼梯”由多少个小正方体组成？C B4. 要想把下面左边的立体图形补全成为一个完整的大正方体，至少需要再加几个小正方体呢？5. 如图所示，将大正方体中的“T”字形挖穿，现在这个图形中有几个小正方体？第十一讲 立体图形计数1. 例题1答案：5；5；9；10详解：先数出能看到的正方体个数，再数出看不见的正方体个数，相加即可．2. 例题2答案：A详解：左边方框中的立体图形的小正方体个数为10个，A 的小正方体个数为10个，B 的小正方体个数为9个，C 的小正方体个数为8个，D 的小正方体的个数为11个．3. 例题3答案：35详解：每层的小正方体个数分别为1、3、6、10、15，加起来的和为35．规律是每层分别在上一层的基础上增加2、3、4、5个小正方体．4. 例题4答案：2；17详解：第一个图中完整的大正方体中的小正方体个数为8个，左边立体图形中的小正方体个数为6个，还需要862-=（个）．第二个图中完整的大正方体中的小正方体个数为27个，左边立体图形中的小正方体个数为10个，还需要271017-=（个）．5. 例题5答案：48详解：符合要求的完整的大正方体至少需要64个小正方体组成，现在有16个小正方体，还需要再加小正方体641648-=（个）． 6. 例题6答案：52详解：完整的大正方体一共有1616161664+++=个)小正方体，“镂空”部分有333312+++= (个)小正方体，所以还剩下641252-= (个)小正方体．7. 练习1答案：5；4；6；8简答：第三个中有1个看不见的正方体，第四个中有3个看不见的正方体．8. 练习2答案：D简答：左边方框中的立体图形的小正方体的个数为7个，D 的小正方体的个数也为7个．9. 练习3答案：60简答：每层小正方体的个数分别为4、8、12、16、20，加起来的和为60．10. 练习4答案：3；13简答：第一个图中完整的大正方体中的小正方体个数为8个，左边立体图形中的小正方体个数为5个，还需要853-=（个）．第二个图中完整的大正方体中的小正方体个数为27个，左边立体图形中的小正方体个数为4个，还需要271413-=（个）．11. 作业1答案：6；8；9；10简答：观察这两层小正方体，分别数出每一层小正方体的个数，注意“看不见”的小正方体．也可分别数出每列的小正方体个数，加在一起即可．12. 作业2答案：A简答：左边方框中小正方体的个数是10个，而右边各立体图形的小正方体个数分别为：A .10个；B .13个；C .9个；D .9个．13. 作业3答案：20简答：从顶层开始数，最顶层为2个，第二层为4个，第三层为6个，第四层为8个，所以小正方体的个数为246820+++=（个）．14. 作业4答案：9简答：左边的立体图形中小正方体的个数为36918++=（个），完整的大正方体中小正方体的个数为99927++=（个）．还需要小正方体27189-=（个）．15. 作业5答案：44简答：方法一：整个大正方体中小正方体的个数为1616161664+++=（个），“T ”字形中小正方体的个数为555520+++=（个）或4444420++++=（个），所以现在有小正方体642044-=（个）． 方法二：每层剩下的小正方体有11个，共有4层，所以现在有小正方体：1111111144+++=（个）．。

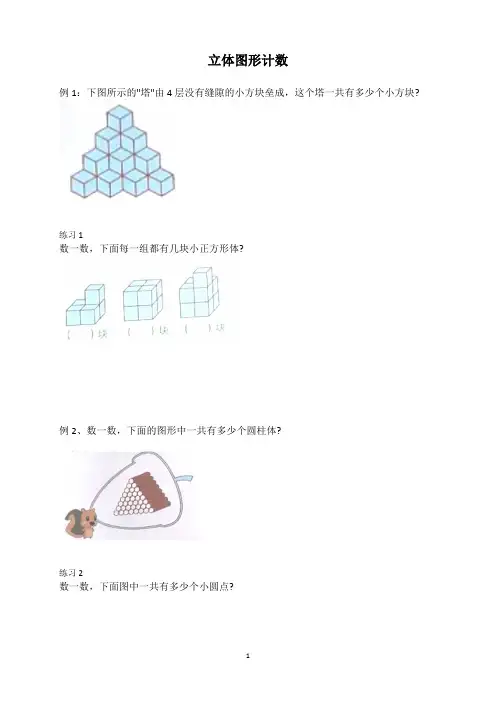
小学一年级数的立体几何练习题试卷主题：小学一年级数的立体几何练习题（本试卷共四节，包含选择题和填空题，请同学们认真作答）第一节选择题1. 下面哪一个物体是一个立方体？A. 圆柱体B. 球体C. 立方体D. 锥体2. 请在下面图片中圈出一个圆柱体。

（图片描述：一组物体中包括圆柱体、立方体、球体和四面体）3. 请问下面哪个物体的底面是一个正方形？A. 圆柱体B. 球体C. 立方体D. 锥体4. 请画出一个正方体，并标出它的底面。

5. 请在下面的图片中找到一个球体，并用黄色涂抹出来。

（图片描述：一组物体中包括圆柱体、立方体、四面体和球体）第二节填空题1. 请用直线将下面的两组图形连起来，并写出它们各自的名称。

（图片描述：上面一行有一个正方形、一个圆、一个三角形和一个长方形。

下面一行有一个立方体、一个圆柱体、一个球体和一个棱柱体）2. 请用红色圈出下面每个物体的顶点，并写出它们各自的名称。

A. 球体B. 圆柱体C. 立方体3. 立方体有多少个面？立方体有______个面。

4. 长方体有多少个顶点？长方体有______个顶点。

5. 请写出下面每个物体的名称，并注明它们所具有的面和顶点数。

A. 正方体B. 棱柱体C. 球体第三节综合题1. 请根据下面的描述，在图中找到相应的物体并填写名称。

物体A：有三个面，一个面是圆形，有一个顶点。

物体B：有五个面，它的底面是正方形，有八个顶点。

物体C：有四个面，它有两个圆形面，一个顶点。

（图片描述：一个大方格中有多个小格子，最上面一行从左到右依次有一个球体、一个正方体和一个长方体）2. 请写出下面物体的名称，并注明它们分别具有几个面和几个顶点。

A. 圆柱体B. 正方体第四节应用题1. 请你想象下面的场景：在操场上摆放了5个立方体，每个立方体的边长都是2米。

请计算这5个立方体的总体积。

（提示：立方体的体积计算公式为：体积 = 边长 x 边长 x 边长）2. 小明家里有一个长方体蛋糕，蛋糕的长、宽、高分别是8厘米、4厘米和6厘米。

一年级奥数——数立体图形23455.数一数下面的图形各由几个小正方体组成，并画出从它们的正面看到的形状．6.用正方体摆成下图，数一数一共有几个小正方体，其中几个能看见，几个看不见？一共（ ）个 一共（ ）个一共（ ）个看见（ ）个 看见（ ）个 看见（ ）个看不见（ ）个 看不见（ ）个看不见（）个7.数一数下面每个立体图形各有几个小正方体．8.数一数，下面的立体图形是由几个小正方体搭成的？9.给下列图形，再添加（）个小正方体，就能组成一个大正方体.10.数一数下面物体中各有几个小正方体．67（ ）个 （ ）个11.数一数下面物体中各有几个小正方体．（ ）个 （ ）个12.数一数，下图中一共有（ ）个正方体. A.6个 B.7个 C.8个课后自我提升：1.数一数下图分别有几个图形？8（ ）个正方形 （ ）个长方形（ ）个三角形2.数一数，下图有几个三角形？（ ）个 （ ）个 3.摆一摆，数一数．下面每个图形分别是由几个小正方体组成的.4.数一数，填一填（1）按层数：下面一层有 个正方体，中间一层有 个正方体，上面一层有 个正方体．（2）按前后排数：前排有个正方体，后排有个正方体．（3）一共有个正方体．5.数一数下列物体是由几个小正方体拼成的.（）个（）个（）个6.数一数下面物体中各有几个小正方体．（）个（）个（）个97.数一数下面物体中各有几个小正方体．（）个（）个10参考答案：课堂共同练习：5 6 10 5、4、7 5、8、7 6题略 5、9、813、10、10 3个 8、10 20、30 C课后自我提升5、6、10 5、8 5、5、5、5、6 5、3、1、3、6、9．7、9、9 1、8、27 20、301112。

一年级数学10道奥数练习题立体图形找规律计算解决问题附
答案
一直觉得奥数属于兴趣特长类的学习，比较适合数学方面有天赋和爱好的孩子。

如果孩子乐于钻研，奥数其实是很有趣的，而且特别锻炼孩子的思维。

答案解析——
2.用一个平底锅烙饼，每次最多只能烙2个，烙熟一个需要2分钟（正面反面各需用时1分钟),若烙熟3个至少需要用时几分钟？
答案解析——
3.图形认知——
答案解析——
4.立体图形——
答案解析——
5、立体图形认知——
答案解析——
6.一共多少人在一起玩游戏。

答案解析——
7.计算——
答案解析——
8.计算——
9.计算——
答案解析——
10.卡片组成数——
答案解析——
奥数题算是兴趣训练，如果孩子对数学感兴趣，并在这方面有特长，可以每天做一道奥数题活动活动脑子。

一年级第二讲图形的计数------------------------------------------作者------------------------------------------日期第二讲图形的计数本讲内容是让孩子们学会用计算的方法来数图形，在计算过程中结合第一讲速算巧算的方法来巩固和练习我们以往所学过的知识。

一、知识点(一) 平面图形的计数1、数线段与角的个数(打枪法、编号法)2、数三角形、正方形、长方形，圆形等（编号法、分层法）(二) 立体图形的计数1、数方块：⑴分层数（从上到下再求和）⑵按列数（刀切法）注意：每层数量=看见的+上层数量( 1)、数规整图形：观察规律，算是表达（牢记巧算速算的方法）(2)、数有缺口的图形方法：（1）分层数（2）补（补全图形去多余）（3）拆（拆成规整图形来计算）二、例题讲解与练习【习题1】你来数一数!( )个正方形 ( )个三角形 ( )个正方体【解析】：⑴、由小到大分类数,含有1个小方块的正方形个,编号法含有 2 个小方块的正方形 3 个共8+3=11(个);⑵、编号法,含有1个号的三角形1、2、 3、4、5 共5 个，含有3个号的三角形163、164、264、265、365 共5 个（5 角星每个小角对应新组成的5 个大三角形），所以三角形共5+5=10 （个）；(3)共1+5+6=12 （个）【习题2】数一数下面一共有多少个小圆点？【解析】: 不同的角度来观察，我们所选用的方法不同（方法不唯一），从上往下数第一层1个点，依次往下每一层都比上一层多一个一点，2、3、4、5、6、7、8、9，所以圆点的总数为1+2+3+4+5+6+7+8+9=45(个)【习题3】如下图所示，一单层砖墙下雨时塌了一处，请你数一数，需要多少块砖才能把墙补好？【解析】：细心观察的小朋友会发现整幅图里只有最后一层墙面的砖是全的，所以每层都与最后一层来比较（用缺补的思想把残缺的墙补全然后列算式），我们发现要补得砖的块数为：2+2+1+2+2+1=10 （块）。

第十一讲立体图形计数1.例题1答案：5；5；9；10详解：先数出能看到的正方体个数，再数出看不见的正方体个数，相加即可．2.例题2答案：A详解：左边方框中的立体图形的小正方体个数为10个，A的小正方体个数为10个，B的小正方体个数为9个，C的小正方体个数为8个，D的小正方体的个数为11个．3.例题3答案：35详解：每层的小正方体个数分别为1、3、6、10、15，加起来的和为35．规律是每层分别在上一层的基础上增加2、3、4、5个小正方体．4.例题4答案：2；17详解：第一个图中完整的大正方体中的小正方体个数为8个，左边立体图形中的小正方体个数为6个，还需要862-=（个）．第二个图中完整的大正方体中的小正方体个数为27个，左边立体图形中的小正方体个数为10个，还需要271017-=（个）．5.例题5答案：48详解：符合要求的完整的大正方体至少需要64个小正方体组成，现在有16个小正方体，还需要再加小正方体641648-=（个）．6.例题6答案：52详解：完整的大正方体一共有1616161664+++=+++=个)小正方体，“镂空”部分有333312(个)小正方体，所以还剩下641252-=(个)小正方体．7.练习1答案：5；4；6；8简答：第三个中有1个看不见的正方体，第四个中有3个看不见的正方体．8.练习2答案：D简答：左边方框中的立体图形的小正方体的个数为7个，D的小正方体的个数也为7个．9.练习3答案：60简答：每层小正方体的个数分别为4、8、12、16、20，加起来的和为60．10.练习4答案：3；13简答：第一个图中完整的大正方体中的小正方体个数为8个，左边立体图形中的小正方体个数-=（个）．第二个图中完整的大正方体中的小正方体个数为27个，左边立为5个，还需要853-=（个）．体图形中的小正方体个数为4个，还需要27141311.作业1答案：6；8；9；10简答：观察这两层小正方体，分别数出每一层小正方体的个数，注意“看不见”的小正方体．也可分别数出每列的小正方体个数，加在一起即可．12.作业2答案：A简答：左边方框中小正方体的个数是10个，而右边各立体图形的小正方体个数分别为：A.10个；B.13个；C.9个；D.9个．13.作业3答案：20简答：从顶层开始数，最顶层为2个，第二层为4个，第三层为6个，第四层为8个，所以小正方体的个数为246820+++=（个）．14.作业4答案：9简答：左边的立体图形中小正方体的个数为36918++=（个），完整的大正方体中小正方体的个数为99927++=（个）．还需要小正方体27189-=（个）．15.作业5答案：44简答：方法一：整个大正方体中小正方体的个数为1616161664+++=（个），“T”字形中小正方体的个数为555520++++=（个），所以现在有小正方体+++=（个）或4444420-=（个）．642044+++=（个）．方法二：每层剩下的小正方体有11个，共有4层，所以现在有小正方体：1111111144。

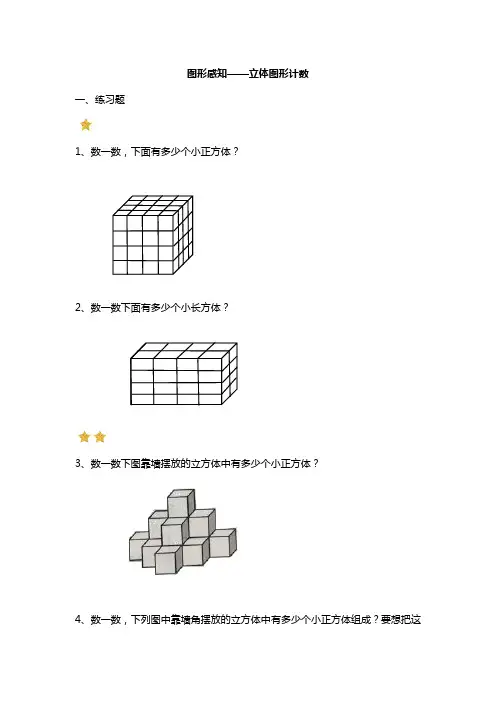
图形感知——立体图形计数一、练习题1、数一数，下面有多少个小正方体？2、数一数下面有多少个小长方体？3、数一数下图靠墙摆放的立方体中有多少个小正方体？4、数一数，下列图中靠墙角摆放的立方体中有多少个小正方体组成？要想把这个不规则立方体填补成规则的正方体，至少需要增加多少个小正方体？5、下图是一个大正方体，从上到下有地方被打通，前面又几乎完全被遮住了，请你数一数，这个大正方体一共有多少个小正方体。

（蓝色部分从上到下是被打通的）二、答案1、答案解析：数立方体个数，可分层数。

这是一个4层的正方体，每一层的个数都是相同的。

从上往下，第一层的小正方体，每行有4个，共4行，所以，第一层共有4×4=16（个），4层共有16×4=64（个）。

2、答案解析：数立方体个数，可分层数。

这个长方体共4层，每层个数相同。

从上往下，第一层有2×4=8（个）小长方体，因此，图中共有4×8=32（个）小长方体。

3、答案解析：方法一：数立方体个数，可分层数。

从上往下：第一层：1个第二层：比第一层多3个，共1+3=4（个）第三层：比第二层多5个，共4+5=9（个）共1+4+9=14（个）方法二：数立方体个数，可分列数。

从左到右：第1列：1个，第2列：比第1列多2个，共1+2=3（个）第3列：比第2列多3个，共3+3=6（个）第4列：与第2列相同，有3个第5列：1个。

共1+3+6+3+1=14（个）4、答案解析：（1）数立方体个数，可分层数。

从上往下：第一层：1个第二层：比第1层多2个，1+2=3（个）第三层：比第2层多2个，3+2=5（个）共：1+3+5=9（个）（2）从图中可知，如果填补成规则的正方体，至少是3×3×3的正方体。

一个规则的正方体，至少有：3×3×3=27（个）已有：9个至少需增加：27-9=18（个）。

5、答案解析：首先，从图上可看出，这是一个4层的正方体，每层有4×4=16个小正方体，共16×4=64（个）正方体；其次，蓝色部分是被打通的，被拆除的小正方体共4×2=8个；因此，剩下的小正方体共有64-8=56（个）。