单自由度模态分析理论共54页

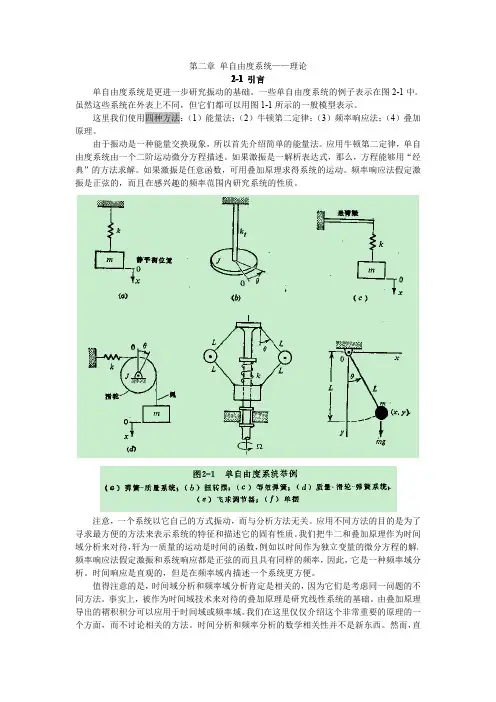
第二章单自由度系统——理论2-1引言单自由度系统是更进一步研究振动的基础。

一些单自由度系统的例子表示在图2-1中。

虽然这些系统在外表上不同，但它们都可以用图1-1所示的一般模型表示。

这里我们使用四种方法：（1）能量法；（2）牛顿第二定律；（3）频率响应法；（4）叠加原理。

由于振动是一种能量交换现象，所以首先介绍简单的能量法。

应用牛顿第二定律，单自由度系统由一个二阶运动微分方程描述。

如果激振是一解析表达式，那么，方程能够用“经典”的方法求解。

如果激振是任意函数，可用叠加原理求得系统的运动。

频率响应法假定激振是正弦的，而且在感兴趣的频率范围内研究系统的性质。

注意，一个系统以它自己的方式振动，而与分析方法无关。

应用不同方法的目的是为了寻求最方便的方法来表示系统的特征和描述它的固有性质。

我们把牛二和叠加原理作为时间域分析来对待，轩为一质量的运动是时间的函数，例如以时间作为独立变量的微分方程的解。

频率响应法假定激振和系统响应都是正弦的而且具有同样的频率，因此，它是一种频率域分析。

时间响应是直观的，但是在频率域内描述一个系统更方便。

值得注意的是，时间域分析和频率域分析肯定是相关的，因为它们是考虑同一问题的不同方法。

事实上，被作为时间域技术来对待的叠加原理是研究线性系统的基础。

由叠加原理导出的褶积积分可以应用于时间域或频率域。

我们在这里仅仅介绍这个非常重要的原理的一个方面，而不讨论相关的方法。

时间分析和频率分析的数学相关性并不是新东西。

然而，直到最近几年来，电子计算机、测试设备和试验技术的进步，它才在实际中得到应用。

2-2自由度一个振动系统的自由度个数是确定这个系统状态所必需的独立的空间坐标个数。

我们定义状态为这个系统的所有质量的几何位置。

如这些质量的相互关系只需要一个空间坐标就完全确定，那么就说这个系统具有一个自由度。

对于空间一个刚体的完全确定需要六个坐标，即三个确定直线运动的坐标和三个确定旋转运动的坐标。

要点二
非线性模态分析的研 究
目前，大多数模态分析研究都集中在 线性系统上。然而，在许多工程应用 中，非线性因素对结构振动的影响是 不可忽视的。因此，未来可以进一步 研究非线性模态分析方法，以更准确 地描述这些非线性效应。
要点三
智能材料和结构的应 用
随着智能材料和结构的发展，它们在 许多领域的应用越来越广泛。这些材 料和结构具有独特的动态特性，需要 新的模态分析方法来描述。因此，未 来的研究可以探索适用于智能材料和 结构的模态分析方法。
背景
随着工程结构的日益复杂化，模态分析在结构健康监测、振 动控制、地震工程等领域的应用越来越广泛。单自由度模态 分析作为模态分析的基础，为多自由度模态分析提供了理论 支持。
模态分析的定义
模态
模态是结构的固有振动特性，包 括频率、阻尼比和振型。
模态分析
模态分析是通过试验或数值方法 识别结构的模态参数的过程。
模态振型之间具有正交性， 即不同模态的振动不会相 互干扰。
选择性
在实际工程中，可以根据需要 选择特定的模态进行分析，以 简化计算和提高分析效率。
Part
03
单自由度系统的01
激振器激励
STEP 02
自由衰减振动
通过激振器对系统施加激励 ，使其产生振动响应，然后 采集响应信号进行分析。
04
单自由度系统的模态特性分析
模态正交性分析
模态正交性是指在模态空间中，不同的模态之间相互独立， 没有耦合关系。在单自由度系统中，模态正交性表现为各模 态振型函数的正交性，即它们的内积为零。
模态正交性的意义在于，它使得各模态之间互不干扰，各自 独立地响应外部激励，从而使得系统的响应可以通过叠加各 模态的响应得到。

精心整理模态分析指的是以振动理论为基础、以模态参数为目标的分析方法。

首先建立结构的物理参数模型，即以质量、阻尼、刚度为参数的关于位移的振动微分方程；其次是研究其特征值问题，求得特征对（特征值和特征矢量），进而得到模态参数模型，即系统的模态频率、模态22¨330m 0z k 2k k z 000m 0k k z 0z +--=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎣⎦⎢⎥⎣⎦（9） 定义主振型由于是无阻尼系统，因此系统守恒，系统存在振动主振型。

主振型意味着各物理坐标振动的相位角不是同相（相差0o ）就是反相位（相差180o ），即同时达到平衡位置和最大位置。

主振型定义如下：()i i j ωt+i i sin ωt+=Im(e )φφi mi mi z =z z （10）其中为第i 阶频率下，各自有度的位移矢量，为第i 个特征矢量，表示第i 阶固有频率下的振型，i ω为第i 阶频率下的第i 个特征值，i φ为（去除项化简得以矩阵的形式展开得：2i 2i mi 2i k-ωm -k 0-k 2k-ωm -k z =00-k k-ωm ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦（15）有非零解，则2i 2i 2i k-ωm -k 0-k 2k-ωm -k =00-k k-ωm ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦（16）即()234222ω-m ω+4km ω-3k m =0（17）阶固有频率，每一个特征根对应一个特征矢量，表示对应模态下该由式3i i 21=z k 如果设定了1z 值，则就可以求出三个特征根值下，2z 和3z 相对于1z 的位移。

假设m=k=1， 一阶模态，1ω=0：21z =1z ，31z =1z ，即；二阶模态，223kω=m ：21z=0z，31z=-1z，即；三阶模态，23kω=m ：21z=-2z，31z=1z，即。

运动方程的解耦图错误！未指定顺序。

运动方程解耦过程在进行坐标变换之前需对刚度矩阵和质量矩阵进行归一化。

模态分析指的是以振动理论为基础、以模态参数为目标的分析方法..首先建立结构的物理参数模型;即以质量、阻尼、刚度为参数的关于位移的振动微分方程；其次是研究其特征值问题;求得特征对特征值和特征矢量;进而得到模态参数模型;即系统的模态频率、模态矢量、模态阻尼比、模态质量、模态刚度等参数..特征根问题以图3所示的三自由度无阻尼系统为例;设123m =m =m =m ;123k =k =k =k ;图 1 三自由度系统其齐次运动方程为： 8其中分别为系统的质量矩阵和刚度矩阵;123m 00m 00m=0m 0=0m 000m 00m ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦;11212221k -k 0k -k 0k=-k k +k -k =-k 2k -k 0-k k 0-k k ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦;则运动方程展开式为：¨11¨22¨33z m 00k k 0z 00m 0z k 2k k z 000m 0k k z 0z ⎡⎤⎢⎥-⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥+--=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎣⎦⎢⎥⎣⎦9定义主振型由于是无阻尼系统;因此系统守恒;系统存在振动主振型..主振型意味着各物理坐标振动的相位角不是同相相差0o 就是反相位相差180o ;即同时达到平衡位置和最大位置..主振型定义如下：()i ij ωt+i i sin ωt+=Im(e)φφi mi mi z =z z 10其中为第i 阶频率下;各自有度的位移矢量;为第i 个特征矢量;表示第i 阶固有频率下的振型;i ω为第i 阶频率下的第i 个特征值;i φ为初始相位..对于三自由度系统;在第i 阶频率下;等式可以写成1m1i 2m2i i i 3m3i z z z =z sin(ωt+)z z φ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦11mki z 表示第k 个自由度在第i 阶模态下的模态矩阵..特征值对式10二次求导;得2i i i =-ωsin(ω+)φ¨i mi z z 12代入齐次运动方程得13去除项化简得14以矩阵的形式展开得：2i 2i mi 2i k-ωm -k 0-k 2k-ωm -k z =00-k k-ωm ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦15 有非零解;则2i 2i 2i k-ωm -k 0-k 2k-ωm -k =00-k k-ωm ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦16即()234222ω-m ω+4km ω-3k m =0 17方程解如下：1ω=0;23k ω=m ±;3kω=m±..三个解对应该系统的前三阶固有频率;每一个特征根对应一个特征矢量;表示对应模态下该系统的振型..特征矢量由式得矩阵展开形式：2i m1i 2i m2i 2i m3i k-ωm -k 0z -k 2k-ωm -k z =00-k k-ωm z ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦ 18 展开第一行和第二行;忽略下脚标m 和i;得()()2i1221i3k-ωm z -kz =0-kz 2k-ωm kz+-= 19得22i 124223ii21z k-ωm =z k z m ω-3km ω+k =z k 20如果设定了1z 值;则就可以求出三个特征根值下;2z 和3z 相对于1z 的位移..假设m=k=1;一阶模态;1ω=0：21z =1z ;31z =1z ;即；二阶模态;223k ω=m ：21z =0z ;31z =-1z ;即；三阶模态;23kω=m ：21z =-2z ;31z =1z ;即..模态矩阵所谓模态矩阵就是指各列由各阶模态特征矢量构成的矩阵;如图4所示..图 2 模态矩阵对于前面提到的三自由度系统;模态矩阵如下：运动方程的解耦对于一个复杂的系统;在物理坐标系统中建立的运动方程之间存在耦合关系;因此求解起来比较麻烦;因此需要进行坐标系转化;将耦合的运动方程变为非耦合的运动方程;再将求得的结果转化为物理坐标系下的结果;运动方程解耦过程如下图5：图 3 运动方程解耦过程在进行坐标变换之前需对刚度矩阵和质量矩阵进行归一化..任意上面的三自由度系统为例;由式得2122 对式21左乘得23 又因为因为系统对称所以;;则：24 对式24右乘25 则式23—式25得26 当时;则27 当;即;则可以为任何值;令28 则对质量矩阵和刚度矩阵的归一化结果如下：2930特征矢量的归一化由于特征矢量只是位移之比;而不是绝对振幅;因此可以对其进行归一化处理..令;其中3132对于对角质量矩阵33则三自由度系统：343m 2m 6m 326=003m 6m m 363m2m6m 326n z 35 则归一化的质量矩阵为100010001⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦Tn n n m =z mz 36 同理归一化后的刚度矩阵为000k =010m003⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦n k 37可以看出归一化后的刚度矩阵对角线上的各项就是各阶模态固有频率的平方..运动方程解耦将物理坐标系下的运动方程¨11¨22¨33z m 00k -k 0z 0 0m 0z +-k 2k -k z =000m 0-k k z 0z ⎡⎤⎢⎥⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎢⎥⎣⎦按照前面介绍的归一化方法转化为主坐标系下的运动方程;其结果如下：¨p1p1¨p2p2¨p3p30z 00z 0k 00z +-k z =0m 00z 03k z 0-km 001101⎡⎤⎡⎤⎢⎥⎢⎥⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦38 可以看出在主坐标系中的运动方程之间没有耦合关系;分别单独描述各阶模态的运动特性..初始条件和激励的坐标转换物理坐标系中的非齐次运动方程为..mz+kz =F 39做如下变形..T -1T -1Tnn nn n n n z mz z z+z kz z z =z F 40 其中T n n z mz ;Tn n z kz 就是前面介绍的质量和刚度矩阵的对角化.. 令Tp n n m =z mz ;主坐标质量矩阵；Tp n n k =z kz ;主坐标刚度矩阵； ....-1p nz z =z ;主坐标系加速度矢量；-1n p z z =z ;主坐标系位移矢量； T n p z F =F ;主坐标系激励矢量..同样的关系也适用于初始位移和速度：-1op n o ..-1op n o z =z z z =z z 42两种坐标系的对比物理坐标系主坐标系物理坐标系中的运动方程的变量是速度和位移;在主坐标系中的变量是各阶振动模态下的位移和速度..由主坐标系转变为物理坐标系前面介绍了物理坐标系与主坐标系之间的关系为-1n p z z =z 43对式41左乘n z ;变为=-1n n n p z z z =z z z 44同理p =..n z z z 45非参数模型传递函数传递函数由系统的本质特性所决定;与系统的输入输出无关..知道了系统的传递函数就可以根据输入求输出或根据输出求输入..以图2的单自由度粘性阻尼系统为例;图 4 单自由度系统则该系统的运动方程为：...m z +c z +kz=F 1其中m 为质量;c 为阻尼系数;k 为刚度系数;z;分别为位移、速度和加速度..对二阶微分方程进行拉普拉斯变换;其中二阶导数项的拉普拉斯变换为：2假设初始位移和速度都为零;则3则经过拉普拉斯变换后的运动方程为：4求解拉氏方程得传递函数：22z(s)11/m==c k F(s)ms +cs+k s +s+m m5 其中定义2n kω=m为非阻尼系统的固有频率;rad/sec ；cr c 2km =阻尼值;ζ为阻尼比;一般为阻尼与临界阻尼的比值;cr c =c ζ;则n c 2ω=mζ.. 则传递函数又可以写成：22n nz(s)1/m=F(s)s +2ωs+ωζ 6 频响函数FRF用“j ω”代替s;得系统的频响函数;其中j 是虚数项：()()22n n 22n n z(j ω)1/m=F(j ω)j ω+2ζωj ω+ω1/m=-ω+2ζωωj+ω 7其中n kω=m ;=2kmζ则频响函数可以写成2z(j ω)1=F(j ω)-m ω+j ωc+k8 质量、阻尼、刚度对FRF 的影响刚度增大导致共振频率的增大;并且降低FRF 在低频段的幅值..增加阻尼会使共振频率略微减小;但它的主要作用是减小频响函数在共振点的幅值;同时使相位的改变较为平缓..如果阻尼为零;在共振点振动振幅将趋于无穷大;相位会突变180o ..增大质量会降低共振频率;同时也降低FRF 在高频段的幅值..。

汽车振动分析之单自由度汽车振动是指汽车行驶过程中，由于路面不平、车身和悬挂系统的振动传递等因素引起的振动现象。

汽车振动对车辆性能和乘坐舒适度有很大影响，因此对汽车振动进行分析和研究具有重要意义。

在汽车振动分析中，单自由度是一种常用的方法。

单自由度是指将整个车身视为一个自由度的振动系统。

通过对车身进行建模，分析和计算出车身在不同工况下的振动特性，可以得到车身的共振频率、加速度和振幅等参数，为汽车设计和改进提供依据。

在单自由度振动系统中，主要有四个关键参数需要确定：质量、阻尼、刚度和外力。

质量是指车身的质量及其分布情况，通常可以通过质量补偿法或试验方法进行测量。

阻尼是指车身受到的阻尼力，包括震动吸收器的阻尼和内部摩擦阻尼等。

刚度是指车身对应的刚度系数，用来描述车身对外力的反应能力。

外力可以是路面的不平度、车轮的不平衡力、发动机的振动力等。

在进行单自由度振动分析时，可以采用模型简化和计算机仿真的方法。

通过建立合适的数学模型，可以得到车身的振动方程，并通过求解方程得到车身的振动响应。

在模型简化过程中，通常采用等效刚度法将车身简化为一个理想的弹簧-质量-阻尼系统。

通过调整刚度和阻尼参数的数值，可以模拟出不同车身的振动特性。

在振动分析过程中，可以通过求解振动方程得到车身的固有频率和振动模态。

固有频率是指汽车振动系统在自由振动状态下，振动频率不随外力的作用而改变的特征频率。

振动模态是指在固有频率下，车身各部分振动的空间分布特征。

通过分析固有频率和振动模态，可以找出对车辆乘坐舒适度影响最大的频率段和振动模态，从而进行有目的的改进和优化。

除了固有频率和振动模态，还可以通过求解振动方程得到车身的加速度和振幅等振动参数。

加速度是指车身振动速度变化率，是评价车辆乘坐舒适度的重要指标之一、振幅是指车身在振动过程中的最大位移变化，也是车辆乘坐舒适度的重要指标之一、通过分析和计算这些振动参数，可以评估车身在不同工况下的振动性能，并对车身进行优化设计。

1 1 2 H ( ) k (1 2 )2 4 2 2
R
H I ( )
1 2 k (1 2 )2 4 2 2
• 对于任一，根据上式可计算得到对应的一对HR()、 HI()值，从而得到复平面上的一条矢量。 从0变到∞， 矢端将画出变化过程的轨迹，该轨迹近似为一个圆。（ Nyquist图）
ms qs cs qs ks qs { s }T { f (t )}
• • • • • ms——第s阶模态质量 ks——第s阶模态刚度 cs——第s阶模态阻尼系数 cs ms ks qs——第s阶模态坐标 jt 令 { f (t )} {F }e jt ，则 qs Qs e
• 令 r

r
{X }
r 1
n
kr 1 2 j 2 r
{ r }{ r }T {F }
• 令 Yr
1 kr 1 2 j 2 r
• 频响函数
{X } n [H ] Yr {r }{r }T {F } r 1
N N
线性系统的输入与输出关系
• 根据傅里叶变换时域卷积性质，在时域的卷积在频域应为乘积
x(t ) h(t ) * f (t )
单位力作用下 的系统时域与 频域的响应
X () H () F ()
不同激励下频响函数表达式
• 简谐激励下，频响函数定义为系统的稳态响应幅值与激励的幅值 之比
X H( )F
• 周期激励f(t)（周期为T）作用下，稳态位移响应为周期T的函数 x(t)，都可写为傅里叶级数的形式
f (t ) F (k )e jk0t k 1 T jk0 t F ( ) 2 dt T f (t )e k 2 T

一、步进式正弦激励法
步进式正弦激励法是一种测量频响函数 的经典方法。在预先选定的频率范围内，从 最低频到最高频选定足够数目的离散频率值， 每次用一个频率给出激励信号，测出该激励 的稳定响应，再步进到下一个频率，进行同 样的测量。直到所有预先设定的离散点全都 步进完毕。
对于复杂的空间结构，一般情况下将表 现为三维空间变形。这就要求在结构上一个 几何点测量三个方向的响应。在这种情况下， 测量点数和几何点数并不相等。所有测点均 应在测量之前在结构上编号注明。
三、试验频段的选择
试验频段的选择应考虑机械或机构在正 常运行条件下激振力的频率范围。通常认为， 远离振源频带的模态对结构实际振动响应的 贡献较小，甚至认为低频激励激出的响应不 含高阶模态的贡献。实际上，高频模态的贡 献的大小除了与激励频带有关外，还与激振 力的分布状态有关。因此，试验频段应适当 高于振源频段。
五、激振器的支承
1. 当激振器外壳刚性固接于地面时，由 于支承刚度很大，可使激振系统的固有频率
远高于结构的弹性振动频率b>>s，适于用
来激振固有频率较低的结构。
2. 若将激振器外壳通过软弹簧接地，或
采用悬吊支承时，将有b<<s，适用于激振 固有频率较高的结构；为了尽量降低b，可
将重物附加在激振器上，以增加激振系统的 质量。
m1=20m2， 1:2=1 : 20，则二自由度系统
的第二阶固有频率与试件固有频率仅相差 1.2%，可近似为试件接地状态。
近似接地支承方法及等效二自由度系统
二 测点及测量方法的安排 测点位置、测点数量及测量方向的选定 应考虑以下两方面的要求： (1) 能够明确显示在试验频段内的所有模 态的变形特征及各模态间的变形区别; (2) 保证所关心的结构点(如在总装时要与 其他部件连接的点)都在所选的测量点之中。

（3）当 ＞1时，称为过阻尼（Over damped），
结构体系称为过阻尼体系。
对于钢结构： 0.01 左右
钢筋混凝土结构： 0.03 左右 0.05 左右
2021/4/6
脉动（微振） 地震（中小强度）
19/73
n
2021/4/6 8/73
3.1 无阻尼自由振动
体系无阻尼自由振动的解：
u
(t
)
u
(0)
cos
nt
u(0)
n
sin
nt
其中：
n
k m
无阻尼振动是一个简谐运动(Simple harmonic motion)
n ——自振频率（Natural frequency）。 2021/4/6 9/73
3.1 无阻尼自由振动
结构动力学
第3章 单自由度体系
2021/4/6 1/73
单自由度体系：SDOF（Single－Degree－of－Freedom）System 结构的运动状态仅需要一个几何参数即可以确定
分析单自由度体系的意义：
一、单自由度系统包括了结构动力分析中涉及的大部分物理量及 基本概念。 二、很多实际的动力问题可以直接按单自由度体系进行分析计算。
2m
n2
0
体系产生往复的振动。
使：( c )2
2m
n2
0
成立的阻尼c称为临界阻尼。
c 临界2021阻/4/6 尼记为 cr：
ccr 2mn 2 km 17/73
3.2.1 临界阻尼和阻尼比 ccr 2mn 2 km
临界阻尼：体系自由振动反应中不出现往复振动所需
的最小阻尼值。
临界阻尼是完全由结构的刚度和质量决定的常数。

单自由度及多自由度系统 模态分析
结构振动分析基本理论
• 振动分析的“理论路线”
空间模型 模态模型 响应模型
（质量、阻尼、 刚度）
（固有频率， 模态振型）
（频率响应、 脉冲响应）
• 空间模型——用于描述结构的物理特性，即质量、刚度和阻尼特性。 • 模态模型——一系列固有频率及相应的模态阻尼系数和模态振型。 • 响应模型——一系列响应函数组成 • 在理论分析中，首先从空间模型开始最终到响应模型。 • 在实验分析中，首先从响应特性开始，最终推求空间模型。
• 将0i代入：
([ K ] [ 2 ][M ])[] {0}
• 解得n个线性无关非零矢量i的比例解，通常选择一定方法进行归 一化，称为模态振型（特征方程的特征向量）
[] [{1},{2 }, {n }]
• 模态振型具有正交性
i j 0, {i } [ M ]{ j } mi , i j i j 0, T {i } [ K ]{ j } ki , i j
单自由度系统脉冲响应函数
• 单自由度系统，承受单位脉冲荷载(t)时，响应为h(t)——单位脉 冲响应函数（脉冲响应函数）
mx cx kx (t )
单自由度系统脉冲响应函数
mx cx kx (t )
• 该式的解为
1 t e sin D t , t 0 x(t ) h(t ) mD 0, t 0
线性系统的输入与输出关系
• 根据傅里叶变换时域卷积性质，在时域的卷积在频域应为乘积
x(t ) h(t ) * f (t )
单位力作用下 的系统时域与 频域的响应
X ( ) H ( ) F ( )
不同激励下频响函数表达式

速 50
度
导
纳
（ 虚
0
部
） -50
20 频 率(Hz)
40
0
加速度导纳图
20
40
频 率（Hz）
（3）、尼奎斯特图即矢量端图，是被工程广泛使用并能有 效地显示共振区细部的方法。如图所示。
Im
Re
Im
Im
Re
a 位移导纳
b 速度导纳
具有结构阻尼单自由度系统的尼奎斯特图
Re c 加速度导纳
图中表示了单自由度粘性阻尼系统的尼奎斯特形式的 频响函数图。这种图的特点是将离开共振区的点彼此靠的 很近，这样就突出了共振区，故尼奎斯特图对试验模态具 有很大的吸引力。
[ms2 (1 jg)k]x(s) f (s)
因此传递函数及频响函数分别为
H (s)
ms2
1 (1
jg )k
H ()
(1
1 jg )k
m2
（1—16） (1—17） （1—18）
将上式写为实部与虚部，
H ()
1 k
12
(1
2
)2
g2
j
g
(1 2 )2
g2
（1—19）
出曲线图（如图）。
(a)无阻尼单自由度系统的对数—对数 导纳图
-60 -80
速 -100 度 -120 导 纳 （0
DB
=1
m/ N）
100kg
1000kg
-20
加
-40 -60
速 -80
度 -100
导
纳
（0
DB
=1
m/N）
10kg 100kg 1000kg
kg j2

单自由度弹簧振子模态分析指导老师：马培勇学生姓名：周葵学号：2012216560班级：过程装备与控制工程一班目录一、课题研究背景_____________________________________________________________ 1二、课题主要研究内容和方法___________________________________________________ 3三、创建三维建模_____________________________________________________________ 3四、模型参数Ansys分析 _______________________________________________________ 4五、添加弹簧后的模型_________________________________________________________ 4六、模型的振形与固有频率Ansys分析 ___________________________________________ 5七、公式验算_________________________________________________________________ 5八、总结_____________________________________________________________________ 6一、课题研究背景弹簧是一种利用弹性来工作的机械零件。

用弹性材料制成的零件在外力作用下发生形变，除去外力后又恢复原状。

亦作“弹簧”。

一般用弹簧钢制成。

弹簧的种类复杂多样，按形状分，主要有螺旋弹簧、涡卷弹簧、板弹簧、异型弹簧等。

按受力性质，弹簧可分为拉伸弹簧、压缩弹簧、扭转弹簧和弯曲弹簧，按形状可分为碟形弹簧、环形弹簧、板弹簧、螺旋弹簧、截锥涡卷弹簧以及扭杆弹簧等，按制作过程可以分为冷卷弹簧和热卷弹簧。

+ +
(C1 (C2
+ +
C2 C3
)x&1(t) - C2x&2 (t) )x&2 (t) - C2x&1(t)
+ +
(K1 (K2
+ K2 )x1(t) - K2x2 (t) + K3 )x2 (t) - K2x1(t)
= =
f1 (t) f2 (t)
第三节 多自由度振动系统举例
一 系统方程
写出矩阵形式：

\
eλ1 t


\
e∧t
\

=



O
0

eλN t

eλ*1 t

0
O

e
λ*N
t

第四节 多自由度系统相关模态概念
一 无阻尼系统
阻尼矩阵[C]为零矩阵的系统
系统阻尼因子σ r = 0 ，全为纯虚数极点 λ1 = jω,L , λ*N = − jωN
系统方程：

P2 + Pα Pβ+1
[M]
+
[K
]{x}
=
{0}
比例阻尼系统频响函数
\
或 [H( jω)] = [ψ]

[ ] ∑ { } { } H(jω)
=
N
j2ωr Qr
ψ
r
ψ
T
r
r =1
(σ
2
r
+
ω
2
r
-
ω
2
)
-
2σ
r

单自由度系统模态计算一、引言单自由度系统是结构动力学中一个重要的研究对象，它可以用来描述许多实际工程中的振动问题。

在计算单自由度系统的模态时，我们需要了解什么是模态、模态计算的目的以及常用的计算方法。

二、什么是模态模态是指一个振动系统在固有频率下的振动形态。

对于单自由度系统来说，它的振动主要由一个自由度（通常是一个质点的位移）决定，而模态则是描述这个振动的特征。

每个模态都有一个固有频率和振型。

三、模态计算的目的模态计算的目的是确定单自由度系统的固有频率和振型。

固有频率是系统在没有外力作用下自由振动时的频率，而振型则是系统在该频率下的振动形态。

通过模态计算，可以帮助我们了解系统的振动特性，进而进行动力设计和振动控制。

四、常用的模态计算方法常见的模态计算方法包括解析法和数值计算法。

解析法主要是通过对系统的微分方程进行求解，得到固有频率和振型的解析解。

数值计算法则是利用计算机进行数值模拟，通过数值求解的方法来计算固有频率和振型。

1. 解析法解析法主要有两种常见的方法，即初始条件法和特征值法。

初始条件法是通过给定初始条件，求解系统的微分方程，得到固有频率和振型的解析解。

特征值法则是将系统的微分方程转化为特征值问题，通过求解特征值和特征向量来得到固有频率和振型。

2. 数值计算法数值计算法主要包括有限元法和模态超级位置法。

有限元法是一种常用的工程计算方法，通过将系统离散化为有限个子结构，然后求解子结构的固有频率和振型，最后组合得到整个系统的固有频率和振型。

模态超级位置法则是通过对系统的响应进行频谱分析，得到系统的固有频率和振型。

五、总结通过模态计算，我们可以了解单自由度系统的固有频率和振型，从而更好地理解和分析系统的振动特性。

在实际工程中，模态计算是进行结构动力学分析和振动控制的重要手段。

不同的计算方法可以根据具体情况选择，以获得准确和可靠的结果。

因此，掌握单自由度系统模态计算的方法和原理是非常重要的。

通过本文的介绍，希望读者对单自由度系统模态计算有一个初步的了解，并能够在实际工程中灵活应用。

无量纲形式
B 1 2 2 2 B0 (1 ) (2 )
振幅放大因子 动力放大系数
在不同的ξ值时，放大因子β，相位角θ与频率比λ的关 系图如下
Your site here
LOGO
λ
幅频响应曲 线
相频响应曲 线
Your site here
LOGO
B 1 B0 (1 2 ) 2 (2 ) 2
2.阻尼使系统振动的振幅按几何级数衰减。 相邻两个振幅之比为
Ai enTd Ai 1
式中η —减幅系数； n—衰减系数。 工程上，为应用方便起见，常用对数减幅系数δ 代替减 幅系数η ，即
ln nTd
Your site here
LOGO
综上所述，有阻尼系统是否作自由振动的条件为
x2 (t )
B0 sin(t ) (1 ) (2 )
2 2 2
Your site here
LOGO
简谐激励下的强迫振动稳态响应解为：
x 2 (t )
B0 sin( t )
2 2
(1 ) (2 )
2
强迫振动稳态响应的基本特点：
1、系统在简谐激励的作用下，其强迫振动稳态响应是简谐振动， 振动的频率与激励频率相同。 2、强迫振动稳态响应的相位比激励的相位滞后
激振力方向改变太快，振动物 体由于惯性来不及跟随。系统 的振幅B主要取决于系统的惯性 。 称为惯性控制区。
相位差 θ 接近 π ，即在高频范围 内位移与激振力接近反向
Your site here
LOGO
B 1 B0 (1 2 ) 2 (2 ) 2
3、频率比
p
1 B B0

模态之单自由度理论与CAE
模态是结构系统的固有振动特性。

线性系统的自由振动被解耦合为N个正交的单自由度振动系统，对应系统的N个模态。

每一个模态具有特定的固有频率、阻尼比和模态振型。

系统的模态可通过理论计算、试验或计算分析得到。

本文通过理论计算与CAE结合，更加体会到CAE工具的便捷及易懂。

一、理论分析
振动系统的组成三要素：质量，刚度，阻尼，振动系统的运动方程（力平衡给出方程）为：
图1 单自由度阻尼强迫振动系统
若系统无外界激励且略去阻尼，则系统运动方程为：
图2 单自由度无阻尼自由振动系统
通过求解可得到系统的固有频率为：
式中f为系统的固有频率，m为系统的质量，k为系统的刚度。

二、CAE分析
假设该单自由无阻尼振动系统的质量m为1.0kg，系统的刚度k 为100N/mm，在Hypermesh界面建立该振动模型如下所示：图3 单自由度无阻尼CAE振动模型
图4 单自由度无阻尼CAE模态振型
通过CAE计算，得到该系统的固有频率为50.33Hz，由理论公式计算得到固有频率为50.35Hz，即理论与CAE相吻合。

三、小结
通过CAE建立相对应的理论振动模型，可验证CAE的正确，且反哺理论的博大精深，这对于从事CAE的人员来说，更能增加信心，也能增强学习的热情，和对枯燥无味CAE仿真的热爱。

单自由度模态分析理论
11、用道德的示范来造就一个人，显然比用法律来约束他更有价值。—— 希腊
12、法律是无私的，对谁都一视同仁。在每件事上，她都不徇私情。—— 托马斯
13、公正的法律限制不了好的自由，因为好人不会去做法律不允许的事 情。——弗劳德
14、法律是为了保护无辜而制定的。——爱略特 15、像房子一样，法律和法律都是相互依存的。。——非洲 2、最困难的事情就是认识自己。——希腊 3、有勇气承担命运这才是英雄好汉。——黑塞 4、与肝胆人共事，无字句处读书。——周恩来 5、阅读使人充实，会谈使人敏捷，写作使人精确。——培根