哈尔滨工业大学《代数与几何》期末试题和答案

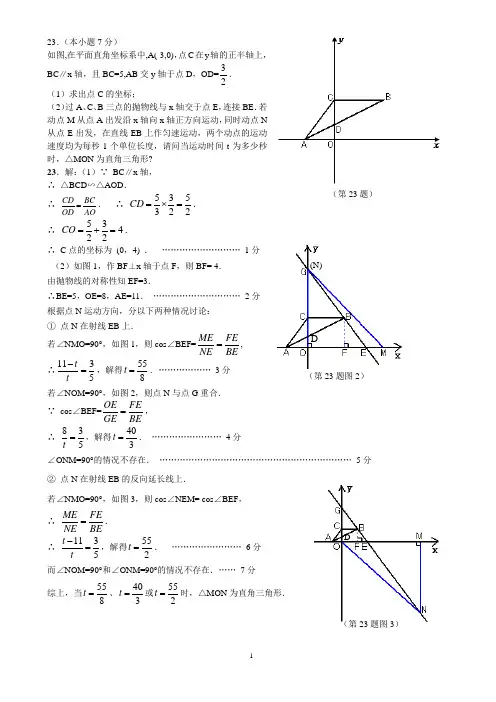
23．（本小题7分）如图,在平面直角坐标系中,A(-3,0)，点C 在y 轴的正半轴上，BC ∥x 轴，且BC=5,AB 交y 轴于点D ，OD=23． （1）求出点C 的坐标； （2）过A 、C 、B 三点的抛物线与x 轴交于点E ，连接BE ．若动点M 从点A 出发沿x 轴向x 轴正方向运动，同时动点N 从点E 出发，在直线EB 上作匀速运动，两个动点的运动速度均为每秒1个单位长度，请问当运动时间t 为多少秒时，△MON 为直角三角形? 23．解：（1）∵ BC ∥x 轴， ∴ △BCD ∽△AOD ．∴ CD BC OD AO=． ∴ 535322CD =⨯=．∴ 53422CO =+=． ∴ C 点的坐标为 (0，4) ． ……………………… 1分 （2）如图1，作BF ⊥x 轴于点F ，则BF= 4． 由抛物线的对称性知EF=3．∴BE=5，OE=8，AE=11． ………………………… 2分 根据点N 运动方向，分以下两种情况讨论： ① 点N 在射线EB 上．若∠NMO=90°，如图1，则cos ∠BEF=ME FENE BE=, ∴1135t t -=，解得558t =．……………… 3分 若∠NOM=90°，如图2，则点N 与点G 重合．∵ cos ∠BEF=OE FEGE BE=， ∴ 835t =，解得403t =． …………………… 4分∠ONM=90°的情况不存在． ………………………………………………………… 5分 ② 点N 在射线EB 的反向延长线上．若∠NMO=90°，如图3，则cos ∠NEM= cos ∠BEF ，∴ME FENE BE =． ∴ 1135t t -=，解得552t =． …………………… 6分 而∠NOM=90°和∠ONM=90°的情况不存在．…… 7分 综上，当558t =、403t =或552t =时，△MON 为直角三角形．（第23题图2）D(N)（第23题图3）D（第23题）25.（7分）已知，抛物线22y ax bx =+-与x 轴的两个交点分别为A （1,0），B （4，0），与y 轴的交点为C ． （1）求出抛物线的解析式及点C 的坐标；（2）点P 是在直线x=4右侧的抛物线上的一动点，过P 作PM x ⊥轴，垂足为M ，是否存在P 点，使得以A ，P ，M 为顶点的三角形与△OCB 相似？若存在，请求出符合条件的点P 的坐标；若不存在，请说明理由． 25．（7分）解：（1）据题意，有0164202a b a b =+-⎧⎨=+-⎩，　． 解得 1252a b ⎧=-⎪⎪⎨⎪=⎪⎩，　． ∴抛物线的解析式为：215222y x x =-+-．点C 的坐标为：（0，-2）． ………………………（2）答：存在点P （x ，215222x x -+-），使以A ，P ，M ∵∠COB =∠AMP =90°，∴①当OC OBMP MA =时，△OCB ∽△MAP ． ②当OC OB MA MP=时，△OCB ∽△MP A ． ①OC MP OB MA =，∴215222241x x x -+=-． 解得：x 1=8，x 2=1（舍）． ②OC MA OB MP =，∴221154222x x x -=-+． 解得：x 3=5，x 4=1（舍）．综合①，②知，满足条件的点P 为：P 1（8，-14），P 2（5，-2）． ……………………… 7分24. 在△ABC 中，∠A =∠B =30°，AB=．把△ABC 放在平面直角坐标系中，使AB 的中点位于坐标原点O (如图)，△ABC 可以绕点O 作任意角度的旋转．(1) 当点BB 的横坐标；(2) 如果抛物线2y ax bx c =++(a ≠0)的对称轴经过点C ，请你探究：当a =，12b =-，c =A ，B 两点是否都在这条抛物线上？并说明理由。

1 b 则f x− ， a a
−1
∈G 。
n k， 所以 n rk ， 由已知 (n, r ) = 1 ， 则有： 所以 k = n ， 即 a r 的阶为 n ， 从而 (a r ) = G 。
另证：由 (n, r ) = 1 ⇒ ∃k1 , k 2 ∈ Z ， k1 ⋅ n + k 2 ⋅ r = 1 ，则有： a 1 = a k1 ⋅n + k 2 ⋅r = a k1 ⋅n a k 2 ⋅r = ea k 2 ⋅r = (a r ) k 2 ，即 a = (a r ) k 2 ，即 G 的生成元 a 可由 a r 生 成，故有： (a r ) = G 。 12.5.5 证明： 设 a r 的阶为 k ， 则 (a r ) k = e ， 即 a rk = e 。 又 an = e ， 所以 n | rk ， 又 ( r , n) = d ，
f ( x ∗ y ) = ψ ϕ ( x ∗ y ) = ψ (ϕ ( x ∗ y )) = ψ (ϕ ( x) • ϕ ( y )) = ψ (ϕ ( x))∆ψ (ϕ ( y )) = ψ ϕ ( x)∆ψ ϕ ( y ) = f ( x) f ( y )
所以 f = ψ ϕ 为 S1 → S 3 的同态，即两个同态的合成还是同态。
1）封闭性：对 ∀f , g ∈ G ，设 f ( x) = ax + b ， g ( x) = cx + d ， a ≠ 0, c ≠ 0 ， 则 f g ( x) = f ( g ( x)) = f (cx + d ) = a (cx + d ) + b = (ac) x + ad + b ，所以 f g ∈ G 2）结合律：映射的复合满足结合律。 3）单位元： I R ( x) = x 4）逆元： 显然对 ∀f ∈ G ， 由 f 为双射， 故 f 可逆， 且 f −1 ( x) = 12.5.3 证明：由 a r ∈ G ，则 (a r ) ⊆ G 。设 a r 的阶为 k ，即 (a r ) k = e 。 因为 (a r ) n = (a n ) r = e r = e ，所以 k n 。又由 (a r ) k = e ⇒ a rk = e ，而 a n = e ，

m1 n1 p1 = = m2 n2 p2
19
直线与平面
直线 与平面 Ax+By+Cz=D 垂直
A B C = = m n p
x − x0 y − y0 z − z0 = = m n p
平行 mA+nB+pC=0 直线在平面上 mA+nB+pC=0，Ax0+By0+Cz0=D
20
第四章 n维向量
31
特征值与特征向量的性质
1．n阶方阵A的n个特征值之和等于A的n个对 角线元素之和，即 λ1+ λ2+… +λn= a11+ a22 +… + ann 称a11+ a22 +… + ann为方阵A的迹，记为tr(A) 2．A的n个特征值之积等于A的行列式，即 λ1λ2…λn=|A| n 阶方阵A可逆当且仅当 A的n个特征值 全不为零
16
距离
点（x0, y0, z0）到平面Ax+By+Cz=D
d= | Ax0 + By0 + Cz0 − D | A + B +C
2 2 2
异面直线间距离
s1 × s 2 d = P1 P2 • | s1 × s 2 |
17
位置关系
平面π1：A1x+B1y+C1z=D1与 平面π2：A2x+B2y+C2z=D2 垂直 A1A2+B1B2+C1C2=0 平行
28
非齐次增广矩阵 2．利用初等行变换将其化成行阶梯形，根据系数矩 阵与增广矩阵的秩讨论其解 3．继续利用初等行变换将其化成行最简阶梯形 4．确定自由未知数(非特异列对应的未知数作为自 由未知数，其个数为n-R(A))，写出同解方程组(将 自由未知数项移至方程右边) 5．对自由未知数取值(可取任意数，仅取一组）， 求得方程组的特解 6. 对自由未知数取值（取n-r个n-r维线性无关的向 量），求出方程组的导出组的基础解系 7. 写出方程组的通解

2021/4/22
3
2、 矩阵加法的运算规律
1 A B B A; 2 A B C A B C .
记-A=(-aij),成为矩阵A的负矩阵
3 A A 0, A B A B (aij bij )
2021/4/22
4
二、数与矩阵相乘
1、定义
数与矩阵A的乘积记作A或A , 规定为
A 2 0, 0 2
B 1 1, 1 1
则有 AB 2 2, 2 2
BA 2 2
2 2 AB BA. 此时称矩阵A、B可交换。
2021/4/22
16
例4
设
A
0 2
0 1
,
B
1 1
1 1
,
C
2 1
1 1
则AB
AC
0 3
0 3
注意4 矩阵不满足消去律，即：
a11
A
A
a21
a12
a22
a1n
a2n
.
am1 am1 amn
2021/4/22
5
2、数乘矩阵的运算规律 （设 A、B为 m n 矩阵， ,为数）
1 A A;
2 A A A;
3 A B A B.
矩阵相加与数乘矩阵合起来,统称为矩阵的线 性运算.
2021/4/22
1 3 1 1 2 3 10
2021/4/22
23
2、方阵的行列式
定义 由 n 阶方阵 A 的元素所构成的行列式， 叫做方阵 A 的行列式，记作 A 或 det A.
例 A 2 6
3 8
则A2
3 2.
68
运算性质 1 AT A;
2 A n A;

得 A 的特征值为 1 1, 2 1, 3 10 .
（3）对1 2 1时，解 (1 E A)X 0.
即
1 2 2 1 2 2
2
4
4
0
0
0
2 4 4 0 0 0
x1 2x2 2x3
所以得同解方程组为
x2
x2
x3 x3
2
2
得基础解系为
解：将交叉项 xi x的j 系数 2即平均分配给 xi x及j xj xi ( xi xj xj xi ) 的二次型的系数矩阵 A为
1
. 1
1
2
A 1 1 2
1
2
0
2
例２ 将二次型 f x1x2 x3x4 写成矩阵形式. 解：f 是一个四元二次型，先写出二次型的矩阵
0
1
A
可逆线性变换中可逆矩阵 C 不只是可逆，还是正交矩阵. 这个正交阵的存在是由实对称矩阵的性质决定的，值得注 意的是这种方法仅限于实二次型.
定理8.1 对 n元实二次型 f X T AX ， 正交线性变换： （不惟一）X PY ，使二次型 f 化为标准形. f 1y12 2 y22 n yn2, 1, 2, , n是 A 的 n 个特征值.
设
x2
c21 y1
c22 y2
c2n yn
xn cn1 y1 cn2 y2 cnn yn
x1
y1
c11 c12
c1n
令X
x2
,
Y
y2
,
C
c21
c22
c2
n
xn
yn
cn1 cn2
cnn
（1）
（1）可变为X CY .ห้องสมุดไป่ตู้但不惟一.

逆矩阵的概念及运算性质.
逆矩阵 A1 存在 A 0.
逆矩阵的计算方法
1待定系数法;
2利用公式A1
A ;
A
3初等变换法下一章介绍.
思考题
若A可逆,那么矩阵方程AX B是否有唯一解 X A1B? 矩阵方程YA B 是否有唯一解 Y BA1 ?
答：是的。这是由于A-1的唯一性决定的。
可得 B EB CAB CAB CE C.
所以A的逆矩阵是唯一的,即 B C A1.
定理1
矩阵 A 可逆的充要条件是 A 0 ，且 A1 1 A , A
其中A为矩阵A的伴随矩阵.
证明 若A可逆， 即有A1使AA1 E .
故 A A1 E 1, 所以 A 0.
反之，当|A|≠0时，因
例1 下列矩阵A、B是否可逆？若可逆，求出其逆阵
2 1
A
5
3 ,
2 3 1
B
1
3
5 .
1 5 3
解 因|A|＝１≠０， 故A可逆。
又因为A11=3，A12=-5，A21=-1，A22=2
A1
1 A
A
3 5
1
2
2 3 1 由于 B 1 3 5
0,
153
故B不可逆.
二阶可逆阵的逆阵公式为
3 0 1
3 5
1 2
1 0
0
12 2
3 5
1 2
2 10 10
1 4. 4
例4 设方阵A满足方程A2 A 2E 0,证明: A, A 2E都可逆,并求它们的逆矩阵.
证明 由A2 A 2E 0,
A1
得AA E 2E A A E E
2 A A E 1 A 0, 故A可逆.

高等代数期末考试题库及答案解析第一部分：选择题（共10题，每题2分，总分20分）1.高等代数是一门研究什么的数学学科？a.研究高等数学b.研究代数学c.研究线性代数d.研究数论–答案：b2.什么是矩阵的秩？a.矩阵中非零行的个数b.矩阵中非零列的个数c.矩阵中线性无关的行向量或列向量的最大个数d.矩阵的行数与列数的乘积3.给定一个方阵A，如果存在非零向量x使得Ax=0，那么矩阵A的秩为多少？a.0b.1c.方阵A的行数d.方阵A的列数–答案：a4.什么是特征值和特征向量？a.矩阵A与它的转置矩阵的乘积b.矩阵A的负特征值和负特征向量的乘积c.矩阵A与它的逆矩阵的乘积d.矩阵A与一个非零向量的乘积等于该向量的常数倍，并且这个向量成为特征向量，该常数成为特征值。

5.什么是行列式？a.矩阵A所有元素的和b.矩阵A中所有元素的乘积c.矩阵A的转置矩阵与它自身的乘积d.矩阵A的行列式是一个标量，表示矩阵A所表示的线性变换的倍数比例。

–答案：d6.什么是矩阵的逆？a.矩阵的行向量与列向量交换位置b.矩阵A的转置矩阵c.存在一个矩阵B，使得矩阵AB=BA=I（单位矩阵）d.矩阵的所有元素取倒数7.给定一个2x2矩阵A，当且仅当什么时候矩阵A可逆？a.矩阵A的行列式为0b.矩阵A的行列式不为0c.矩阵A的特征值为0d.矩阵A的特征值不为0–答案：b8.什么是矩阵的转置？a.矩阵的行与列互换b.矩阵的行与行互换c.矩阵的列与列互换d.矩阵的所有元素取相反数–答案：a9.对于矩阵A和B，满足AB=BA，则矩阵A和B是否可逆？a.可逆b.不可逆c.只有A可逆d.只有B可逆–答案：b10.什么是矩阵的秩-零空间定理？a.矩阵中非零行的个数加上零行的个数等于行数b.矩阵中非零列的个数加上零列的个数等于列数c.矩阵的秩加上矩阵的零空间的维数等于列数d.矩阵的秩加上矩阵的零空间的维数等于行数–答案：c第二部分：计算题（共4题，每题15分，总分60分）1.计算矩阵的秩： A = \[1, 2, 3; 4, 5, 6; 7, 8, 9\]–答案：矩阵A的秩为22.计算特征值和特征向量： A = \[1, 2; 3, 4\]–答案：矩阵A的特征值为5和-1，对应的特征向量分别为\[1; 1\]和\[-2; 1\]3.计算行列式： A = \[3, 1, 4; 1, 5, 9; 2, 6, 5\]–答案：矩阵A的行列式为-364.计算逆矩阵： A = \[1, 2; 3, 4\]–答案：矩阵A的逆矩阵为\[-2, 1/2; 3/2, -1/2\]第三部分：证明题（共2题，每题25分，总分50分）1.证明：当矩阵A为可逆矩阵时，有出现在矩阵A的行列式中的每个元素，将该元素与其对应的代数余子式相乘之后的结果，再求和得到的值等于矩阵A的行列式的值。

哈尔滨工业大学高等数学期末考试试题和答案高等数学期末考试试题（4）一、填空题：（本题共5小题，每小题4分，满分20分，把答案直接填在题中横线上）1、已知向量a r 、b r满足0a b +=r r r ，2a =r ，2b =r ，则a b ⋅=r r．2、设ln()z x xy =，则32zx y ∂=∂∂．3、曲面229x y z ++=在点(1,2,4)处的切平面方程为．4、设()f x 是周期为2π的周期函数，它在[,)ππ-上的表达式为()f x x =，则()f x 的傅里叶级数在3x =处收敛于，在x π=处收敛于 ．5、设L 为连接(1,0)与(0,1)两点的直线段，则()Lx y ds +=⎰．※以下各题在答题纸上作答，答题时必须写出详细的解答过程，并在每张答题纸写上：姓名、学号、班级．二、解下列各题：（本题共5小题，每小题7分，满分35分）1、 求曲线2222222393x y z z x y⎧++=⎪⎨=+⎪⎩在点0M (1,1,2)-处的切线及法平面方程． 2、 求由曲面2222z x y =+及226z x y =--所围成的立体体积．3、 判定级数11(1)lnn n n n∞=+-∑是否收敛？如果是收敛的，是绝对收敛还是条件收敛？4、设(,)sin x z f xy y y =+，其中f 具有二阶连续偏导数，求2,z zx x y∂∂∂∂∂．5、计算曲面积分,dSz∑⎰⎰其中∑是球面2222x y z a ++=被平面(0)z h h a =<<截出的顶部．三、（本题满分9分）抛物面22z x y =+被平面1x y z ++=截成一椭圆，求这椭圆上的点到原点的距离的最大值与最小值．四、（本题满分10分）计算曲线积分(sin )(cos )x x Le y m dx e y mx dy -+-⎰，其中m 为常数，L 为由点(,0)A a 至原点(0,0)O 的上半圆周22(0)x y ax a +=>．五、（本题满分10分）求幂级数13nn n x n∞=⋅∑的收敛域及和函数．六、（本题满分10分）计算曲面积分332223(1)I x dydz y dzdx z dxdy ∑=++-⎰⎰，其中∑为曲面221(0)z x y z =--≥的上侧．七、（本题满分6分）设()f x 为连续函数，(0)f a =，222()[()]tF t z f x y z dv Ω=+++⎰⎰⎰，其中t Ω是由曲面z =与z = 30()lim t F t t+→．2012高等数学期末考试试题【A 卷】参考解答与评分标准 2009年6月一、填空题【每小题4分，共20分】 1、4-； 2、21y-；3、2414x y z ++=； 4、3，0； 5、二、试解下列各题【每小题7分，共35分】1、解：方程两边对x 求导，得323dydz y z x dx dx dy dz y z xdxdx ⎧+=-⎪⎪⎨⎪-=-⎪⎩， 从而54dy x dx y =-，74dz x dx z = (4)该曲线在()1,1,2-处的切向量为571(1,,)(8,10,7).488T ==u r (5)故所求的切线方程为1128107x y z -+-==....................【6】 法平面方程为 ()()()81101720x y z -+++-= 即 810712x y z ++=.. (7)２、解：2222226z x y z x y⎧=+⇒⎨=--⎩222x y +=，该立体Ω在xOy 面上的投影区域为22:2xy D x y +≤． (2)故所求的体积为V dv Ω=⎰⎰⎰222620202(63)6d d dz d πρρθρπρρπ-==-=⎰⎰ (7)３、解：由11lim lim ln(1)lim ln(1)10nn n n n n u n n n →∞→∞→∞=+=+=>，知级数1n n u ∞=∑发散…………………【3】又111||ln(1)ln(1)||1n n u u n n +=+>+=+,1lim ||lim ln(1)0n n n u n→∞→∞=+=.故所给级数收敛且条件收敛．【7】 ４、解：121211()0z f y f yf f x y y∂''''=⋅+⋅+=+∂， …………………………………【3】 2111122212222211[()][()]z x xf y f x f f f x f x y y y y y ∂''''''''''=+⋅+⋅--+⋅+⋅-∂∂111222231.x f xyf f f y y''''''=+--【7】５、解：∑的方程为z =∑在xOy 面上的投影区域为2222{(,)|}xy D x y x y a h =+≤-．=…..………【３】故22222200xy D dS adxdy d a d z a x y a πρρθρ∑==---⎰⎰⎰⎰⎰22012ln()2ln 2aa a a hπρπ⎡=--=⎢⎥⎣⎦..【7】三、【9分】解：设(,,)M x y z 为该椭圆上的任一点，则点M到原点的距离为d =【1】令22222(,,)()(1)L x y z x y z z x y x y z λμ=+++--+++-，则由22220220201x y z L x x L y y L z z x yx y z λμλμλμ=-+=⎧⎪=-+=⎪⎪=++=⎨⎪=+⎪++=⎪⎩，解得12x y -==，2z =121111(,2(2222M M -+-+--- (7)又由题意知，距离的最大值和最小值一定存在，所以距离的最大值与最小值分别在这两点处取得．故max 2min 1||||d OM d OM ==== (9)四、【10分】 解：记L 与直线段OA 所围成的闭区域为D ，则由格林公式，得22(sin )(cos )8x x DL OAI e y m dx e y mx dy m d ma πσ+=-+-=-=-⎰⎰⎰Ñ． (5)而10(sin )(cos )ax xOAI e y m dx e y mx dy m dx ma =-+-=-=-⎰⎰ (8)∴221(sin )(cos ).8x x Le y m dx e y mx dy I I ma ma π-+-=-=-⎰ ………………………【10】五、【10分】解：()1131limlim 3133n n n n n na n R a n ρ++→∞→∞===⇒=+，收敛区间为 (3,3)- (2)又当3x =时，级数成为11n n∞=∑，发散；当3x =-时，级数成为()11nn n ∞=-∑，收敛．......【4】 故该幂级数的收敛域为[)3,3- (5)令()13nn n x s x n ∞==∑（33x -≤<），则11111111()()33331/33n n n n n x x s x x x -∞∞-=='====--∑∑, (||3x <) ……【8】 于是()()000()()ln 3ln 3ln 33xxx dxs x s x dx x x x '===--=---⎰⎰，（33x -≤<） (10)六、【10分】解：取1∑为220(1)z x y =+≤的下侧，记∑与1∑所围成的空间闭区域为Ω，则由高斯公式，有()()133222222316I x dydz y dzdx z dxdy x y z dv ∑+∑Ω=++-=++⎰⎰⎰⎰⎰Ò (5)()2211262d d z dz πρθρρρπ-=+=⎰⎰⎰ (7)而()()221133221122313133x y I x dydz y dzdx z dxdy z dxdy dxdy π∑∑+≤=++-=-==⎰⎰⎰⎰⎰⎰….…【9】2123.I I I πππ∴=-=-=- (10)七、【6分】解：()()22240sin cos tF t d d r f r r dr ππθϕϕϕ⎡⎤=+⎣⎦⎰⎰⎰….… 【2】 ()3224400002sin cos sin t t d r dr d f r r dr πππϕϕϕϕϕ⎡⎤=+⎢⎥⎣⎦⎰⎰⎰⎰(()422028tt r f r dr π⎡⎤=+⎢⎥⎣⎦⎰….… 【4】 故()(3222320002()222lim lim lim ().333t t t t t f t F t f t a t t π+++→→→⎡⎤+-⎢⎥--⎣⎦=== 【6】。

00 00
x 1
0 0 x 1
00
x 1 0 0
0 0 (1)nn( x a1) 0 x
00
0 1
00 0x
证法二：按第一列展开，得
Dn=xDn-1+an 再根据上面的递推公式可得结果。
c1 xc2 xn1cn
证法三：Dn
0
1 0
0
x 1
00 00
0
00
0
0
an
例2 计算
1111
abcd D
a2 b2 c2 d 2
a4 b4 c4 d 4
解：构造
1111 1 abcd x
f (x) a2 b2 c2 d 2 x2
a3 b3 c3 d 3 x3
a4 b4 c4 d 4 x4
（这是一个范德蒙行列式）
=(x-a)(x-b)(x-c)(x-d)(d-a)(d-b)(d-c)(c-a)(c-b)(b-a) 另外f(x)按最后一列展开，可得
1
11
1
an
an1 an Dn1
an1 an (a1a2 an2 an1Dn2 )
方法三：升级法。看例1
11
1 11
1
解：原式= 0 1 a1
1
1
a1
0
01
1 an 1 0
an
1 aa c1

i
n 2
1 ai 1
ci
n 1
i1 i
1
1

0
a1
0
5. 行列式按行（列）展开
1 ) 余子式与代数余子式 ２）关于代数余子式的重要性质
a A n ki k 1

P9-3 设A 为可列集，B 是有A 的有限子集构成的集合，证明B 可列。

证：记C n n C A A C⎧⎫⊂⎪⎪=⎨⎬⎪⎪⎩⎭且只有个元素则1nn B A ∞== ，设12,(,,,),in i j k N F k k k k k i j ⎧⎫∈⎪⎪=⎨⎬≠≠⎪⎪⎩⎭且则F 是可列集，对n A 中的每个元{}12,,n k k k a a a 素，令其对应于F 中的元素{}12,n k k k ，则nA 与F 中的一个子集对等，故nA 也是可列集，故B 也是可列集P9-6 证明以有理数为圆心且以有理数为半径的区间全体是可列集。

证：设{}12,,Q r r = ，用ij I 表示以i r 为中心，以jr 为半径的区间，则{},ij I I i j N =∈，令{}(,),i j i jB r r r r Q Q Q =∈=⨯是可列集，做映射:,()(,),,ij i j I B I r r i j N ψψ→=∈则ψ为一一映射，因而I 与B 的一个子集对等，由于B 为可列集，故I 也为可列集。

P16-8、对于点列,n x R ∈若11,1,2,...,2n n nx x n +-≤=求证n x 是cauchy 列。

犹若1lim 0n n n x x -→∞-=，问n x 是否一定为Cauchy 列？证：1）先证{}n x 为Cauchy 列。

由于对,n p N ∀∈有11111111...111(12)1221(12)2n p n p n p n n p n n np n p n p i i i n i ni nx x x x x x x x x x ++-++-+++-+-+-==-+-=--+--≤-≤=≤-∑∑而11lim0,2n n -→∞=故0,ε∀>00,N ∃>当n N >时有112n ε-<因而对,p N ∀∈当0n N >时，有112n ε-<因而对,p N ∀∈当0n N >时，有112n p n n x x ε+--≤<因此{}n x 为Cauchy 列。

哈尔滨工业大学远程教育学院 学期代数与几何 试题纸（闭卷，时间：90分钟）（所有答案必须写在答题纸上）一、填空题（每小题4分，共20分）1．设⎪⎪⎪⎭⎫ ⎝⎛--=219010003A ，则A 的行列式|A |= ． 2．设⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=111111111111x x x x A ，且R (A )=1，则x= ． 3．设设矩阵三阶方阵A 的特征值为1，2，-3，则|A +3E |= ． 4．经过点M (1, 2, 3)且与直线11221-+=-=z y x 平行的直线方程为 ． 5．已知⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛-=231,211βα，设A =αβ ′，其中β ′为β的转置，则A =．二、选择题（每小题4分，共20分） 1．设n (n ≥2)阶方阵A 满足A 2=E ，其中E 表示n 阶单位矩阵，则 【 】（A ）A =A -1． （B ）|A |=1．（C ）A =E ． （D ）A =-E ．2．设向量组α, β, γ线性无关，则 【 】（A ）向量组α+β, α-β, γ线性无关． （B ）向量组α, β-γ, α+β-γ线性无关．（C ）向量组α+β, β+γ, α-γ线性无关． （D ）向量组α, β+γ, α+β+γ线性无关．3． 曲面xy =z 在R 3中表示的图形是 【 】（A ）椭圆面．（B ）单叶双曲面． （C ）马鞍面． （D ）锥面．4. 下列论断中正确的是 【 】（A ）相似矩阵有相同的特征值和特征向量．（B ）有相同特征值的两个同阶方阵相似．（C ）若两个矩阵相似，则它们相似于同一个对角矩阵．（D ）有相同特征值的任意两个同阶对角矩阵一定相似．5．设A m ×n 为齐次线性方程组AX =O 的系数矩阵，其秩为r ，则AX =O 有非零解的充要条件是 【 】（A ）r=n ． （B ）r<n ．（C ）r=m ． （D ）r<m ．三、（10分）求矩阵方程中的未知矩阵A⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛123654*********A 四、（10分）求经过点M (-1, -2, -3)，并垂直于平面x -2y +3z =1和2x +y -3z =2的交线的平面方程．五、（10分）设有向量组⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=023,110,111,022,11154321ααααα 求其秩及一极大无关组．六、（20分）利用正交线性变换将二次型f (x 1,x 2,x 3)=2x 12-x 22-x 32-4x 1x 2+4x 1x 3+8x 2x 3化成标准形，写出所做的正交线性变换及相应的标准形．七、（10分）设λ为方阵A 的一个特征值，证明：2λ为矩阵2A 的一个特征值．参考答案一、6，1，0，132211--=-=-z y x ，⎪⎪⎪⎭⎫ ⎝⎛----462231231 二、A ，A ，C ，D ，B 三、 解：⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛≠=⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛--111611110011001123654111011001123654110011001111011001,111011001,0111101100112365411101100111A A 可逆故由于四、解：已知平面的法向量分别为n 1=(1,-2,3), n 2=(2,1,-3),所以，所求平面的法向量应与已知平面法向量垂直，可取所求平面的法向量为n =n 1×n 1，即又所求平面过点M (-1,-2,-3)，从而所求平面的点法式方程为3(x +1)+9(y +2)+5(z +3)=0，即3x +9y +5z =-36k j i k j i n 593312321++=--=五、解：()⎪⎪⎪⎭⎫ ⎝⎛--→⎪⎪⎪⎭⎫ ⎝⎛-==11000202200110101101211213012154321行αααααA因此，R (A )=3, α1, α1, α4为原向量组的一个极大无关组。

哈尔滨工业大学2007级代数与几何期末考试试题哈尔滨工业大学2007级《代数与几何》期末试题（此卷满分50分）注：本试卷中=小、』、」分别表示」的秩，」的转置矩阵、」的伴随矩 阵；匸表示单位矩阵.、填空题（每小题2分，共10 分） _____1 •若矩阵」满足』1° ,则」的特征值只能是2 2 2________ 2 •在空间直角坐标系中方程''''_■- 的图形是_____ 4.若矩阵 心& 沙满足AH , F 是行满秩阵，贝U 」5.空间直角坐标系中曲线LJ = 0绕2轴旋转一周，所生成的旋转曲面的方 程为、选择题（每小题2分，共10分）1 .设」是再勢矩阵，贝昉程组 J'：二$有唯一解的充要条件是 【】（A ）二』“； （B ）二卫（C ）附）皿必；（D ）R （A ） = R （a 宀2 .设有'维列向量组（I ）也 匕,,，.厲；可由向量组（…线性表 示，则（A ）若（I ）线性无关，贝U （ II ）线性无关; 9）若（I ）线性相关，贝U （ II ）线性相关;向量组卩2113的秩为（0若（I ）线性无关，则一 _「； （ D ）若（II ）线性无关，贝U - _：.3 •设】：，则必有 【】（A ）』是正交阵； （B ）」是正定阵； （C ）」是对称阵； （D ）二」匚W 上"丨 4 •实二次型'正定的充要条件是【】 （A ） i!匸]； （B ） 一-： -’ 1 ； （C ） i! ■； [ ；（ D ） J 一 J .5 •设」,B 都是' 阶实对称矩阵，则下列结论正确的是 【】（A ）若A 与B 等价，贝U A 与B 相似；（B ）若A 与B 相似，则A 与B 合 同； （C ）若A 与B 合同，贝U A 与B 相似；（D ）若A 与B 等价，则A 与B 合 同• 三、（本题5分）已知列向量组仁E 是R 的基，◎二E _g 区二 S -仁'：■ ■也是艮的基，求由基》匕匕到基°乩戏的过渡矩阵，并求0 芒在基也乩■儿下的坐标.四、（本题5 分）五、（本题6 分）六、（本题6 分）<1 2 2?A =2x2D =5设矩阵 <2 2 1, 与相似，求■''. ，其中1〔〕卫1 1 0 0 0 01 131 2」，求百.已知三阶实对称矩阵A 的每行元素之和都等于2,且秩■ [ - 1.（1） 用正交变换将二次型一-咒丄丫化为标准形，并求所用的正交变换矩 阵.（2） 求」1其中m 是大于等于1的自然数. 七、 （本题5分）设」是：阶方阵，匸'』-：，试证：若存在自然数汇使』0,则」-0. 八、 （本题3分） 设实矩阵」⑴’，°让：G 是」的列向量组.实向量A A '"-是齐次线性方程组」乜Q 的基础解系.试证：向量组 此4…-・0心、:线性无关.参考答案、填空题2, E二 2’、选择题C. 3、D. 4、B. 5、B.q 0 01©码还)二(勺E 何1 T 1(1 0T 丿知由基 到基。

代数几何综合题1、如图，已知平面直角坐标系中三点A （2，0），B （0，2），P （x ，0）()x <0，连结BP ，过P 点作PC PB ⊥交过点A 的直线a 于点C （2，y ） （1）求y 与x 之间的函数关系式；（2）当x 取最大整数时，求BC 与PA 的交点Q 的坐标。

2．如图，从⊙O 外一点A 作⊙O 的切线AB 、AC ，切点分别为B 、C ，⊙O 的直径BD 为6，连结CD 、AO.(1)求证：CD ∥AO ；(2)设CD ＝x ，AO ＝y ，求y 与x 之间的函数关系式，并写出自变量x 的取值范围； (3)若AO ＋CD ＝11，求AB 的长.3．如图，A 、B 两点的坐标分别是(x 1，0)、(x 2，O)，其中x 1、x 2是关于x 的方程x 2+2x+m -3=O 的两根，且x 1<0<x 2． (1)求m 的取值范围；(2)设点C 在y 轴的正半轴上，∠ACB=90°，∠CAB=30°，求m 的值；(3)在上述条件下，若点D 在第二象限，△DAB ≌△CBA ，求出直线AD 的函数解析式.4.一张矩形纸片OABC 平放在平面直角坐标系内，O 为原点，点A 在x 的正半轴上，点C 在y 轴的正半轴上，OA ＝5，OC ＝4。

①求直线AC 的解析式；②若M 为AC 与BO 的交点，点M 在抛物线285y x kx=-+上，求k 的值；③将纸片沿CE 对折，点B 落在x 轴上的点D 处，试判断点D 是否在②的抛物线上，并说明理由。

1、已知抛物线)0(22>--=m m x x y 与y 轴的交于C 点，C 点关于抛物线对称轴的对称点为C ′。

（1）求抛物线的对称轴及C 、C ′的坐标（可用含m 的代数式表示）；（2）如果点Q 在抛物线的对称轴上，点P 在抛物线上，以点C 、C ′、P 、Q 为顶点的四边形是平行四边形，求Q 点和P 的坐标（可用含m 的代数式表示）； （3）在（2）的条件下，求出平行四边形的周长。

哈尔滨工业大学2007级代数与几何期末考试试题哈尔滨工业大学2007级《代数与几何》期末试题（此卷满分50分）注：本试卷中、、分别表示的秩，的转置矩阵、的伴随矩阵；表示单位矩阵.一、填空题（每小题2分，共10分）1．若矩阵满足，则的特征值只能是 .2．在空间直角坐标系中方程的图形是 .3．向量组的秩为4．若矩阵满足，是行满秩阵，则 .5．空间直角坐标系中曲线绕轴旋转一周，所生成的旋转曲面的方程为.二、选择题（每小题2分，共10分）1．设是矩阵，则方程组有唯一解的充要条件是【】（A）；（B）；（C）；（D）.2．设有维列向量组（I）; 可由向量组（II）线性表示，则【】（A）若（I）线性无关，则（II）线性无关；（B）若（I）线性相关，则（II）线性相关；（C）若（I）线性无关，则；（D）若（II）线性无关，则.3．设，则必有【】（A）是正交阵；（B）是正定阵；（C）是对称阵；（D）.4．实二次型正定的充要条件是【】（A）；（B）；（C）；（D）.5．设, B都是阶实对称矩阵，则下列结论正确的是【】（A）若A与B等价，则A与B相似；（B）若A与B相似，则A与B合同；（C）若A与B合同，则A与B相似；（D）若A与B等价，则A与B合同.三、（本题5分）已知列向量组是的基，也是的基，求由基到基的过渡矩阵，并求在基下的坐标.四、（本题5分）设矩阵与相似，求.五、（本题6分）已知，其中，求.六、（本题6分）已知三阶实对称矩阵A的每行元素之和都等于2，且秩.（1）用正交变换将二次型化为标准形，并求所用的正交变换矩阵.（2）求, 其中m是大于等于1的自然数.七、（本题5分）设是阶方阵，，试证：若存在自然数使，则.八、（本题3分）设实矩阵，，是的列向量组. 实向量是齐次线性方程组的基础解系. 试证：向量组线性无关.参考答案一、填空题1、2.2、双叶双曲面.3、4、.5、.二、选择题1、A.2、C.3、 D.4、B.5、B.三、解：由知由基到基的过渡矩阵为在基下的坐标为四、解：由与相似，知是的特征值，所以，. 进而，由此得解得.五、解：. 由，得，整理得. 由知可逆，且，故.六、解：（1）因的每行元素之和都等于2，所以是的属于特征值2的特征向量. 因，所以是A特征值, 对应于有两个线性无关的特征向量.设是A的属于特征值的特征向量. 因实对称知X与正交，即.解得是A的属于特征值的特征向量，规范正交化得.将的属于特征值2的特征向量规范正交化得.令，则P为正交矩阵，在正交变换下，.（2），七、证：因，所以存在可逆矩阵使其中.于是故从而.八、证法1：设（1）因是齐次线性方程组的基础解系，用在左边乘（1）式两边得，进而，故，再由知由（1）知，由是基础解系，从而线性无关，于是，故线性无关.证法2：设（1）因是齐次线性方程组的基础解系，所以于是.由知线性无关，故的证明同上.证法3：设（1）得关于的齐次线性方程组系数行列式的证明同上.。

北 京 交 通 大 学2009 -2010学年第一学期《几何与代数B 》期末考试试卷（B ）参考答案及评分标准一．填空题（本题满分30分，共10道小题，每道小题3分）1．设211111101x x -=，则=x ____1，-1_______________． 2．已知向量,,αβγ满足0,||3,||5,||7.αβγαβγ++====，则,αβ的夹角是3π. 3．设矩阵12112y A B x -⎡⎤⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦，，且BA AB =，则=x __0___，=y ____1___． 4．已知实二次型()222123123121323,,222f x x x x tx tx x x x x x x =++++-为是正定的，则常数t 的取值范围是 ___t>3________________．5．若向量组123(1,0,1),(,1,0),(1,,1)a a ααα==-=--的秩是2，则a =_0___． 6．若向量组12345,,,,ααααα的秩为3，且满足13524230,2ααααα+-==，则12345,,,,ααααα的一个最大无关组为_____123,,ααα________________．或125,,ααα 或134,,ααα或 145,,ααα 或 235,,ααα或 345,,ααα 7．若方程组123123123111ax x x x ax x x x ax ++=⎧⎪++=⎨⎪++=⎩无解，则a 的值为______-2_______．8. 直线1513:312x y z l -+-==-与直线222:13x y z l a++==-相交，则a 的值为__-1____。

9. 设3阶方阵A 的特征值为1,1,2-，则矩阵*1(3)A -的特征值为111,,663-- 。

10. 由xoy 平面上曲线 222100x y z ⎧-+=⎨=⎩ 围绕y 轴旋转一周所成曲面的方程是2222210.x y z -++=二.(10分) 计算5阶行列式52111112111112111112111112D -------=---。

学院： 专业：班级：姓名： 学号：,,s α线性表示，则下列结论中正确的 2,,s k k 使等式s s k α+成立。

存在一组全为零的数12,,,,s k k k 使等式11s s k α+成立； 2,,,s k k 使等式1s s k k βαα=+成立； 的线性表达式唯一。

的特征值为1,1,2,-则矩阵2A E ++的特征值为1,3,7; C. 1,1,2-; 1,0,3-.二、填空题（每小题3分，共15分）6．设(,1,2)ij A i j = 为行列式2131D =中元素ij a 的代数余子式， 则11122122A A A A =7．设4阶方阵520021000012011A ⎛⎫⎪ ⎪= ⎪- ⎪⎝⎭，则1A -=8．设线性方程组1231231232202020x x x x x x x x x λ-+=⎧⎪-+=⎨⎪+-=⎩有非零解，则λ=9．已知向量组123(3,2,0,1),(3,0,,0),(1,2,4,1)ααλα===--的秩为2，则λ=10．设n 阶方阵A 的特征值为12,,,n λλλ，则kA （k 为常数）的特征值为三、计算n 阶行列式（本题14分）11. 211112111112n D =四、证明题（每小题8分，共16分）12．已知对于n 阶方阵A ，存在自然数k ，使得0k A =，试证明矩阵E A -可逆，并写出其逆矩阵的表达式。

13. 设向量组12:,,,L A ααα和向量组12:,,,,S B βββ的秩分别为p 和q ，试证明：若A 可由B 线性表示，则p q ≤。

五、解矩阵方程（14分）14．设412221311A -⎛⎫ ⎪= ⎪ ⎪-⎝⎭，132231B -⎛⎫ ⎪= ⎪ ⎪-⎝⎭，求X 使AX B =.六、解答题（每小题10分，共20分）15. 设11,11A ⎛⎫= ⎪-⎝⎭121101B ⎛⎫= ⎪--⎝⎭， 求AB .16. 设()12340,4,2,(1,1,0),(2,4,3),(1,1,1)αααα===-=-，求该向量组的秩和一个最大无关组，并将其余向量表示成最大无关组的线性组合。

记作 C AB.
2021/4/22
4
运算规律 ( AB)C A(BC );
( AB) (A)B A(B), (其中为数);
A(B C ) AB AC , (B C )A BA CA; E m Amn Amn Amn E n .
注（1）矩阵乘法可乘的条件与乘后的结果； (2)矩阵乘法不具有交换律与消去律。
例4 设三阶矩阵A, B满足关系 :
2 2 3
A1 BA
6
A
BA,
且A
0
2
2
0 0 2
求B .
解 A1BA BA 6A
A1 E BA 6A E A B 6A
B 6 E A 1 A
2021/4/22
24
1 2 3
E
A
0
1
2
0 0 1
1 2 1
(E
A)1
按
PCBA
键
开关 键
传统机械按键设计要点： 1.合理的选择按键的类型， 尽量选择平头类的按键，以 防按键下陷。 2.开关按键和塑胶按键设计 间隙建议留0.05~0.1mm，以 防按键死键。 3.要考虑成型工艺，合理计 算累积公差，以防按键手感 不良。
2 9 5 2 8 6 .
4 14 9
15
例2 解矩阵方程
AX=B，XA=B，AXB=C， 其中A、B都是可逆阵。
2021/4/22
16
矩阵方程
AX B XA B AXB C
2021/4/22
解
X A1 B X BA1 X A1C B1
17
例3 解矩阵方程 1 1 5 X 3 2;
1 4 1 4
2
X
1 1