第9章习题解

第九章 欧氏空间1.设()ij a =A 是一个n 阶正定矩阵,而),,,(21n x x x Λ=α, ),,,(21n y y y Λ=β,在n R 中定义内积βαβα'A =),(,1) 证明在这个定义之下, n R 成一欧氏空间； 2) 求单位向量)0,,0,1(1Λ=ε, )0,,1,0(2Λ=ε, … , )1,,0,0(Λ=n ε，的度量矩阵；3) 具体写出这个空间中的柯西—布湿柯夫斯基不等式。

解 1)易见βαβα'A =),(是n R 上的一个二元实函数，且 (1) ),()(),(αβαβαββαβαβα='A ='A '=''A ='A =， (2) ),()()(),(αβαββαβαk k k k ='A ='A =，(3) ),(),()(),(γβγαγβγαγβαγβα+='A '+'A ='A +=+， (4) ∑='A =ji j i ijy x a,),(αααα，由于A 是正定矩阵，因此∑ji j i ijy x a,是正定而次型，从而0),(≥αα，且仅当0=α时有0),(=αα。

2)设单位向量)0,,0,1(1Λ=ε, )0,,1,0(2Λ=ε, … , )1,,0,0(Λ=n ε，的度量矩阵为)(ij b B =，则)0,1,,0(),()(ΛΛi j i ij b ==εε⎪⎪⎪⎪⎪⎭⎫⎝⎛nn n n n n a a aa a a a a a ΛM O MM ΛΛ212222211211)(010j ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛M M =ij a ，),,2,1,(n j i Λ=， 因此有B A =。

4) 由定义，知∑=ji ji ij y x a ,),(βα，α==β==故柯西—布湿柯夫斯基不等式为2.在4R 中,求βα,之间><βα,(内积按通常定义)，设: 1) )2,3,1,2(=α, )1,2,2,1(-=β， 2) )3,2,2,1(=α, )1,5,1,3(-=β， 3) )2,1,1,1(=α, )0,1,2,3(-=β。

第9章习题参考答案
9.1
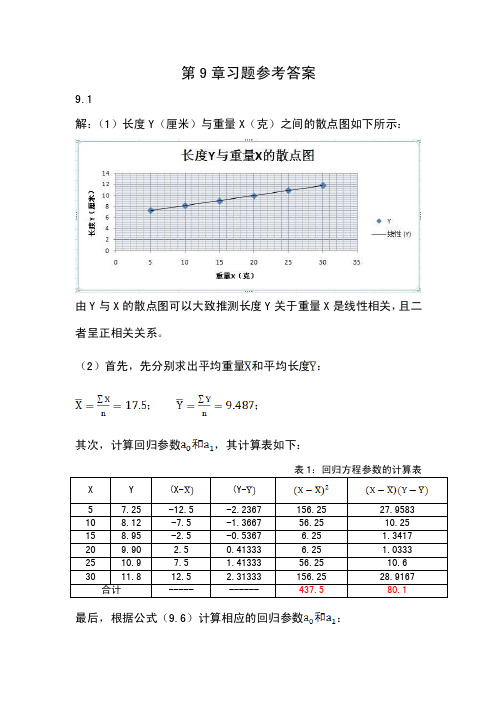
解：（1）长度Y（厘米）与重量X（克）之间的散点图如下所示：
由Y与X的散点图可以大致推测长度Y关于重量X是线性相关，且二者呈正相关关系。

（2）首先，先分别求出平均重量和平均长度：
；；
其次，计算回归参数，其计算表如下：
表1：回归方程参数的计算表
(X-(Y-
最后，根据公式（9.6）计算相应的回归参数：
；
所以，Y关于X的一元线性回归方程为：
9.5
解：总变差，回归平方和，残差平方和的计算如下：
表2：总变差，回归平方和，残差平方和的计算表
∴残差平方和：；
回归平方和：
9.6
解：由表2得：
判定系数
又∵习题9.1的散点图显示Y与X是呈正相关关系
∴相关系数
显著性检验：
（1）回归方程的显著性检验：
原假设H0：该回归方程不显著；备择假设H1：该回归方程显著
计算F统计量：
∵在α=0.05的显著性水平下，有4454.79＞F0.05(1,4)=7.71
∴拒绝原假设，认为该回归方程式显著的。

（2）回归参数的假设检验：
原假设H0：备择假设H1：
计算t统计量：;
[其中] ∵在α=0.05的显著性水平下，有15.98＞t0.05（4）=2.776
∴拒绝原假设，即认为自变量X对因变量Y有显著性影响。

(3)相关关系的显著性检验：
原假设H0：ρ=0；备择假设H1：ρ
计算t统计量：；
∵在α=0.05的显著性水平下，有66.64> t0.05（4）=2.776
∴拒绝原假设，认为总体相关系数不为0。

第9章 真空中的静电场9.1 两个电量都是q +的点电荷分别固定在真空中两点A B 、，相距2a 。

在它们连线的中垂线上放一个电量为q '的点电荷，q '到A B 、连线中点的距离为r 。

求q '所受的静电力，并讨论q '在A B 、连线的中垂线上哪一点受力最大？若q '在A B 、的中垂线上某一位置由静止释放，它将如何运动？分别就q '与q 同号和异号两种情况进行讨论。

解：()1222014qq F F a r πε'==+ ()1322022cos 2qq rF F arθπε'==+方向沿两点电荷连线垂直线远离它们方向。

令0dFdr= ()()()1222223220202a r a r dF qq dr a r πε⎡⎤+-'⎢⎥==⎢⎥+⎢⎥⎣⎦()2220a r -=r = 在q '为正电荷时，在中垂线某位置由静止释放时，q '将沿中垂线远离，作变加速速直线运动；若q '为负电荷，q '以AB 连线的中点为平衡位置作振动；若释放点为AB 连线中点，静止释放时，无论q '为正、负电荷均因受力为0而不运动。

9.2 在正方形的顶点上各放一个点电荷q 。

（1）证明放在正方形中心的任意点电荷受力为零。

（2）若在正方形中心放一个点电荷q '，使得顶点上每个点电荷受到的合力恰好为零，求q'与q的关系。

解：⑴设正方形边长为a，正方形上各点电荷对中心放置的点电荷的作用力大小均为：220011422qq qqFaaπεπε''==⎛⎫⎪⎝⎭q'所受到的四个力大小相等且对称，两相对顶点上的点电荷为一对平衡力，即q'受力为0。

⑵设正方形四个顶点上放置的点电荷q为正电荷，由于对称性，则可选一个顶点处理，其它点电荷对其的作用力大小为：1214qqFaπε=22142qqFaπε=32200112442qq qqFaaπεπε''==⎛⎫⎪⎝⎭各力的方向如图所示，要满足题意，中心点电荷q'应为负电荷。

9-1两个半径分别为R 和r 的同轴圆形线圈相距x ，且R >>r ，x >>R ．若大线圈通有电流I 而小线圈沿x 轴方向以速率v 运动，试求小线圈回路中产生的感应电动势的大小． 解：在轴线上的磁场()()22003322222IR IR B x R x R xμμ=≈>>+32202xr IR BS πμφ==v xr IR dt dx x r IR dt d 422042202332πμπμφε=--=-=9-2如图所示，有一弯成θ 角的金属架COD 放在磁场中，磁感强度B ϖ的方向垂直于金属架COD 所在平面．一导体杆MN 垂直于OD 边，并在金属架上以恒定速度v ϖ向右滑动，v ϖ与MN 垂直．设t =0时，x = 0．求当磁场分布均匀，且B ϖ不随时间改变，框架内的感应电动势i ε．解：12m B S B xy Φ=⋅=⋅,θtg x y ⋅=,vt x =22212/()/i d dt d Bv t tg dt Bv t tg εϕθθ=-=-=⋅，电动势方向：由M 指向N9-3 真空中，一无限长直导线，通有电流I ，一个与之共面的直角三角形线圈ABC 放置在此长直导线右侧。

已知AC 边长为b ，且与长直导线平行，BC 边长为a ，如图所示。

若线圈以垂直于导线方向的速度v 向右平移，当B 点与直导线的距离为d 时，求线圈ABC 内的感应电动势的大小和方向。

解：当线圈ABC 向右平移时，AB 和AC 边中会产生动生电动势。

当C 点与长直导线的距离为d 时，AC 边所在位置磁感应强度大小为：02()IB a d μπ=+AC 中产生的动生电动势大小为：xr IRx vC DOxMθBϖv ϖ02()AC AC IbvBl v a d μεπ==+，方向沿CA 方向如图所示，在AB 边上取微分元dl ，微分元dl 中的动生电动势为，()AB d v B dl ε=⨯⋅v v v其方向沿BA 方向。

题9-12解图第九章习题解答9-4 直角三角形ABC 如题图9-4所示，AB 为斜边，A 点上有一点荷91 1.810C q -=⨯，B点上有一点电荷92 4.810C q -=-⨯，已知BC =0.04m ，AC =0.03m ，求C 点电场强度E的大小和方向(cos37°≈0.8, sin37°≈0.6).（分析：运用点电荷场强公式及场强叠加原理求解。

） 解：如图所示C 点的电场强度为12E E E =+99411220 1.810910 1.810(N/C)(0.03)4π()q E AC ε-⨯⨯⨯===⨯ 99422220 4.810910 2.710(N/C)(0.04)4π()q E BC ε-⨯⨯⨯===⨯44103.2410(N/C)E ===⨯方向为：o 44217.33107.2108.1arctan E E arctan =⨯⨯==α 即方向与BC 边成33.7°。

9-12 一细棒被弯成半径为R 的半圆形,其上部均匀分布有电荷+Q ,下部均匀分布电荷-Q .如题图9-12所示,求圆心O 点处的电场强度。

（分析：微分取电荷元，运用点电荷场强公式及场强叠加原理积分求解。

将带电半圆环分割成无数个电荷元，运用点电荷场强公式表示电荷元场强。

将电荷元电场进行矢量分解，再进行对称性分析，然后积分求解。

） 解：把圆环分成无限多线元d l ，d l 所带电量为2d d πQq l R=，产生的场强为d E 。

则d E 的大小为： 232200d d d 2π2πQ l Q E R Rθεε== x y dE dE i dE j =+，且：d sin d x E E θ=， d c o s d y E E θ= 由于+Q 、-Q 带电量的对称性，x 轴上的分量相互抵消，则：0x E =题图9-12Cπ2222200cos d 2d 2cos d 22ππy y Q QE E E E R Rθθθεε=====⎰⎰⎰圆环在O 点产生的场强为： 220QE j R πε=-9-13 两平行无限大均匀带电平面上的面电荷密度分别为+б和-2б,如题图9-13所示,求: (1)图中三个区域的场强1E ，2E ，3E 的表达式；（2）若б=4.43×10-6C ·m -2，那么，1E ，2E ，3E各多大？（分析：首先确定场强正方向，然后利用无限大均匀带电平板场强及场强叠加原理求解。

第九章习题参考答案9-1对应于图9-la 逻辑图，若输入波形如图9-54所示，试分别画出原态为0和原 态为1对应时刻得Q 和◎波形。

3D 八图9-54逆9-1图解得到的波形如题9-1解图所示。

9-2逻辑图如图9-55所示，试分析它们的逻辑功能，分别画出逻辑符号，列出逻辑 真值表，说明它们是什么类型的触发器。

解 对于（a ）：由图可写出该触发器的输出与输入的逻辑关系式为：(9-1)原态为•丿京态为a) b)图9-55题9-2图下面按输入的不同组合，分析该触发器的逻辑功能。

(1) R n =1、S D =0若触发器原状态为0，由式(9-1)可得Q=0、Q =1 ；若触发器原状态为1，由式(9-1) 同样可得Q =0、Q = 1。

即不论触发器原状态如何，只要R D =1、S° =0，触发器将置成0态。

(2) R D=0、S°=l用同样分析可得知，无论触发器原状态是什么 > 新状态总为：Q =1・Q=0，即触发器被置成1态。

(3) R[)=Sj)=0按类似分析可知，触发器将保持原状态不变。

⑷= s° = 1两个“与非”门的输出端Q和Q全为0，这破坏了触发器的逻辑关系，在两个输入信号同时消失后，由于“或非”门延迟时间不可能完全相等，故不能确定触发器处于何种状态。

因此这种情况是不允许出现的。

逻辑真值表如表9-1所示，这是一类用或非门实现的基本RS触发器，逻辑符号如題9-2(a) 的逻辑符号所示。

对于(b)：此图与(a)图相比，只是多加了一个时钟脉冲信号，所以该逻辑电路在CP =1时的功能与(a)相同，真值表与表9-1相同；而在CP=0时相当于(a)中(3)的情况，触发器保持原状态不变。

逻辑符号见趣9-2 (b)逻辑符号。

这是一类同步RS触发器。

Q1000]表9」題9・2 (a)真值表00不变1 1 不定题9・2 (a)的逻辑符号9-3同步RS 触发器的原状态为1，R 、S 和CP 端的输入波形如图9-56所示，试画出 对应的Q 和。

第9章光学性能习题解答材料的光学性能一、名词解释1. 弹性散射解答：弹性散射：散射前后光的波长（或光子能量）不发生变化，只改变方向。

2.非弹性散射解答：非弹性散射：散射前后光的波长（或光子能量）发生变化，也改变方向。

3. 一般吸收解答：在某一波长范围内，材料对于通过它的各种波长的光波都做等量吸收（吸收系数不变），且吸收量很小，则称该材料具有一般吸收性。

一切物质都具有一般吸收性和选择吸收性两种特性。

4. 选择吸收解答：材料吸收某种波长的光能比较显著，则称该材料具有选择吸收性。

一切物质都具有一般吸收性和选择吸收性两种特性。

5.色散解答：折射率n随波长（或频率）而变化，这种变化率dn/dλ称为色散二、填空题1.大部分可见光没有被材料吸收，结果材料_____解答：（透明）。

2.假如PPT的背景是黑色的，不透明，表明PPT的背景_____。

解答：(吸收可见光)3.白色塑料袋，透明，表明白色塑料袋_____。

解答：（不吸收可见光）4.红色塑料袋，透明，表明红色塑料袋_____。

解答：（不吸收红光）5. 氦氖激光器中氦、氖气体的最佳分压比是_____。

解答：7:16. 根据激光输出方式的不同，激光器可分为_____________。

连续激光器和脉冲激光器三、简答题1. 请写出你所了解的光学的分类。

解答：几何光学，波动光学，量子光学。

线性光学，非线性光学。

2. 光具有波粒二象性，你将如何用公式表述光的波粒二象性？解答：1）公式：E=hυ P=hυ/C=h/λ2）公式的物理意义：(1) 能量、动量表征光的粒子性;(2) 波长、频率表征光的波动性;(3) 上述两个简单公式却将两种截然不同性质的物理量联系在了一起。

3、什么是色散现象?为什么会出现光的色散？解答：光在介质中的折射率(或介质的传播速度）随其波长（或频率）而变化的现象叫做光的色散现象。

光的色散的出现是由于不同波长的光经过介质时具有不同的速度，从而产生不同角度的折射而引起的。

第9章原子结构与元素周期律1．根据玻尔理论，计算氢原子第五个玻尔轨道半径（nm）及电子在此轨道上的能量。

解：(1)根据rn=a0n2r5=53pm×25= 53×10-3nm×25=1.325 nm(2) 根据En=－Ｂ/2 nE5= －13.6ev/52=－13.6ev/25=－0.544ev答: 第五个玻尔轨道半径为 1.325 nm，此轨道上的能量为－0.544ev。

2．计算氢原子电子由n=4能级跃迁到n=3能级时发射光的频率和波长。

解：（1）根据 E（辐射）=ΔE＝E4－E3 ＝ 2.179×１０-18 J（（1/3）2－（1/4）2）= 2.179×１０-18 J（1/9-1/16）=2.179×１０-18 J×0.0486=1.06X10-19J根据E（辐射）＝hνν= E（辐射）/h= 1.06×10-19J /6．626X10–34 = 1.60X1014 s-1（2）法1：根据E（辐射）＝hν= hC/λλ= hC/ E（辐射）= 6．626X10 –34 J.s×3×１０8 m.s-1/1.06×10-19J=1.88×10-6m。

法2：根据ν= C/λ，λ= C/ν=3×１０8 m.s-1/1.60X1014 s-1=1.88×10-6m。

答：频率为 1.60X1014 s-1，波长为 1.88×10-6m。

3．将锂在火焰上燃烧放出红光，波长=670.8nm，这是Li原子由电子组态1s22p1→1s22s1跃迁时产生的。

试计算该红光的频率、波数以及以KJ·mol-1为单位符号的能量。

解：（1）频率ν= C/λ=3×１０8 m.s-1/670.8nm×10-9 m/nm=4.47×1014 s-1；（2）波数ν=1/λ=1/670.8nm×10-9 m/nm=1.49×106 m-1(3) 能量E（辐射）＝hν=6．626X10 –34 J.s×4.47×1014 s-1=2.96×10-19 J2.96×10-19 J×6.023×1023mol-1×10-3KJ/J=178.28 KJ mol-1答: 频率为 4.47×1014 s-1,波数为 1.49×106 m-1，能量为178.28 KJ mol-1。

第9章 弯曲应力与弯曲变形 习题解答题9 – 1 试计算下列各截面图形对z 轴的惯性矩I z （单位为mm ）。

解：（a ）mm 317400250500350200400250250500350≈⨯-⨯⨯⨯-⨯⨯=c y()()49323mm 107314002502003171240025050035025031712500350⨯≈⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯-⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯=.I Z （b ）mm 431550400800500375550400400800500≈⨯-⨯⨯⨯-⨯⨯=c y()()410323mm 1054615504003754311255040080050040043112800500⨯≈⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯-⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯=.I Z （c ）()mm 3060202060506020102060=⨯+⨯⨯⨯+⨯⨯=c y()()46323mm103616020503012602020601030122060⨯=⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯+⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯=.Z I(a)(b) (c)题9-1图题9–2 悬臂梁受力及截面尺寸如图所示。

设q = 60kN/m ，F = 100kN 。

试求（1）梁1– 1截面上A 、B 两点的正应力。

（2）整个梁横截面上的最大正应力和最大切应力。

解：（1）求支反力kN 220100260=+⨯=A F （↑）m kN 32021001260⋅=⨯+⨯⨯=A M （ ） （2）画F S 、M 图（3）求1-1截面上A 、B 两点的正应力 m kN 1305016011001⋅=⨯⨯+⨯=.MF MA 点：MPa 254Pa 1025412150100550101306331=⨯≈⨯⨯⨯==...I y M zA t σB 点：MPa 162Pa 107816112150100*********331=⨯≈⨯⨯⨯==....I y M σzB c （4）求最大正应力和最大切应力M P a 853Pa 10385361501010320623max max =⨯≈⨯⨯==...W M σzM P a 22Pa 10221501010220232363max =⨯≈⨯⨯⋅=⋅=..A F τS 题9 - 3 简支梁受力如图所示。

第九章 欧氏空间1.设()ij a =A 是一个n 阶正定矩阵,而),,,(21n x x x =α, ),,,(21n y y y =β,在n R 中定义内积βαβα'A =),(,1) 证明在这个定义之下, n R 成一欧氏空间； 2) 求单位向量)0,,0,1(1 =ε, )0,,1,0(2 =ε, … , )1,,0,0( =n ε，的度量矩阵；3) 具体写出这个空间中的柯西—布湿柯夫斯基不等式。

解 1)易见βαβα'A =),(是n R 上的一个二元实函数，且 (1) ),()(),(αβαβαββαβαβα='A ='A '=''A ='A =， (2) ),()()(),(αβαββαβαk k k k ='A ='A =，(3) ),(),()(),(γβγαγβγαγβαγβα+='A '+'A ='A +=+， (4) ∑='A =ji j i ijy x a,),(αααα，由于A 是正定矩阵，因此∑ji j i ijy x a,是正定而次型，从而0),(≥αα，且仅当0=α时有0),(=αα。

2)设单位向量)0,,0,1(1 =ε, )0,,1,0(2 =ε, … , )1,,0,0( =n ε，的度量矩阵为)(ij b B =，则)0,1,,0(),()( i j i ij b ==εε⎪⎪⎪⎪⎪⎭⎫ ⎝⎛nn n n n n a a a a a aa a a212222211211)(010j ⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ =ij a ，),,2,1,(n j i =， 因此有B A =。

4) 由定义，知∑=ji ji ij y x a ,),(βα，α==β==故柯西—布湿柯夫斯基不等式为2.在4R 中,求βα,之间><βα,(内积按通常定义)，设: 1) )2,3,1,2(=α, )1,2,2,1(-=β， 2) )3,2,2,1(=α, )1,5,1,3(-=β， 3) )2,1,1,1(=α, )0,1,2,3(-=β。

第九章 习题及解答9-5 设文件A 按连续文件构造，并由四个逻辑记录组成 (每个逻辑记录的大小与磁盘块大小相等，均为512B) 。

若第一个逻辑记录存放在第100号磁盘块上，试画出此连续文件的结构。

答：连续文件的结构如下图：9-6 设文件B 按串联文件构造，并由四个逻辑记录组成 (其大小与磁盘块大小相等，均为512B)。

这四个逻辑记录分别存放在第100、157、66、67号磁盘块上，回答如下问题。

(1) 画出此串联文件文件的结构，(2) 若要读文件B 第1560字节处的信息，问要访问哪一个磁盘块? 为什么? (3) 读文件B 第1560字节处的信息需要进行多少次I/O 操作? 为什么? (1) 答：此串联文件结构如下图所示。

(2) 答：1560/512=3余24，因此文件第1560逻辑字节在r 3逻辑块上，该逻辑块被分配在67号磁盘块上。

(3) 答：要访问67号磁盘块，需要先找到文件目录，然后依次访问100、157和66号磁盘块，最后读取67号磁盘块。

因此若文件已打开 (文件目录信息已在内存中) 需要4次I/O 操作，文件未打开需要5次I/O 操作。

文件目录文件目录 r 1磁盘块号9-16什么是“重名”问题? 二级文件目录结构如何解决这一问题?答：重名是指不同用户对不同文件起了相同的名字。

在二级文件目录结构中，每个用户建立用户文件目录，系统建立主目录，登记所有用户目录的信息，用目录名加文件名唯一标识每个文件解决重名问题。

9-18 假设两个用户共享一个文件系统，用户甲要用到文件a、b、c、e，用户乙要用到文件a、d、e、f。

已知：用户甲的文件a与用户乙的文件a实际上不是同一文件；用户甲的文件c与用户乙的文件f实际上是同一文件；甲、乙两用户的文件e是同一文件。

试拟定一个文件组织方案，使得甲、乙两用户能共享该文件系统而不致造成混乱。

答：如下图所示。

用户甲的主目录名为jia，有四个文件，文件名为a、b、c、e。

习题9-11. 判定下列级数的收敛性：(1) 1n ∞=∑; (2) 113n n ∞=+∑; (3)1ln 1n n n ∞=+∑; (4) 1(1)2nn ∞=-∑;(5) 11n n n ∞=+∑; (6) 0(1)21n n nn ∞=-⋅+∑． 解：（1）11n n k S ===∑，则lim lim(11)nnnS n ，级数发散。

（2）由于14113n n nn，因此原级数是调和级数去掉前面三项所得的级数，而在一个级数中增加或删去有限项不改变级数的敛散性，所以原级数发散。

（3）11ln[ln ln(1)]ln1ln(1)ln(1)1nnnk k n S n n n n n ，则lim lim[ln(1)]nnnS n ，级数发散。

（4） 2 , 21, 1,2,3,; 0 , 2nn k S k nk因而lim n nS 不存在，级数发散。

（5）级数通项为1nn u n ，由于1lim10nn n，不满足级数收敛的必要条件，原级数发散。

（6）级数通项为(1)21n nnu n ，而lim n n S 不存在，级数发散。

2. 判别下列级数的收敛性，若收敛则求其和： (1) 11123n nn ∞=⎛⎫+ ⎪⎝⎭∑； (2) 11(1)(2)n n n n ∞=++∑; (3) 1πsin 2n n n ∞=⋅∑; (4)πcos 2n n ∞=∑．解：（1）因为111111111131111(1).23232232223nn n nk kkk n n n nk k k S 所以该级数的和为31113lim lim(),22232nn nnnSS 即1113.232nnk（2）由于1111[](1)(2)2(1)(1)(2)n n nn n n n，则111111111[][](1)(2)2(1)(1)(2)22(1)(2)nnnk kS k k kk kk kn n所以该级数的和为 1111limlim [],22(1)(2)4nnn SS n n即111.(1)(2)4n n n n（3）级数的通项为sin2nu n n，由于sin2lim sinlim()02222nnnn nn，不满足级数收敛的必要条件，所以原级数发散。

化⼯原理习题解第九章习题解第九章吸收9-1 总压为kPa 3.101、含3NH %5（体积分数）的混合⽓体，在C25下与浓度为3.71.1 m kmol 的氨⽔接触，试判别此过程的进⾏⽅向，并在c p 图上⽰意求取传质推动⼒的⽅法。

解氨—⽔平衡关系列在本章附录⼆中，需将题中组成化为其中的单位，以便⽐较。

⽓相氨分压 kPa p 065.505.03.101液相组成换算要⽤到密度，暂取3.990 m kg （参考例9-2，温度较⾼较⼩）。

对3.71.1 m kmol c 氨⽔，每⽴⽅⽶含氨kg 1.291771.1 ，含⽔kg 9.9601.29990 ；故kg 100⽔中含氨kg 03.3)9.960/1.26(100 。

与附录⼆⽐较，氨⽔组成为kg 3氨.1-100(⽔）kg ，C25下的平衡氨分压为kPa 13.3，⽐题给氨分压低，故知过程⽅向应为吸收。

（注：虽然氨⽔密度的估计稍有误差，但不影响过程⽅向。

作图从略）9-2 含%32CO （体积分数）的2CO —空⽓混合⽓，在填料塔中⽤⽔进⾏逆流吸收，操作压⼒为（绝）为kPa 200、温度为C 25，试求出塔的g 100⽔中最多可溶解多少克2CO ？其浓度⼜为多少？解出塔⽔的最⼤浓度系与逆流进塔的⽓体平衡，此时2CO 的分压kPa Py p 603.0200 ，查本章附录⼀，C 25下2CO 溶于⽔的亨利系数MPa E 166 。

按式（9-5），液相平衡组成为 153)(.1061.3101666 B A mol A mol E p x ⽽ 155max ).(1084.81061.3)1844()()(gS gA x M M x M M S A L A 即 123100.(1084.8 ）g gCO浓度 335max .1001.2)1061.3()18/1000()(m kmol x M sCx c s9-3 总压kPa 3.101、含%62CO （体积分数）的空⽓，在C20下与2CO 浓度为3.3 m kmol 的⽔溶液接触，试判别其传质⽅向。

第9章界面现象习题解答1、293K 时，水的表面张力为0.0728N ·m -1，汞的表面张力为0.483N ·m -1，汞-水的界面张力为0.375N ·m -1。

试判断水能否在汞的表面上铺展？汞能否在水的表面上铺展？解：（1）1lg m N 0352.0375.00728.0483.0-⋅=--=--=∆-=ls sg A A A G S S ＝0.0352N ·m -1＞0，能铺展开（2）1lg m N 7852.0375.0483.00728.0-⋅=--=--=∆-=ls sg A A A G S S ＝-0.7852N ·m -1＜0，不能铺展开答：（1）S ＝0.0352N ·m -1＞0，能铺展开（2）S ＝-0.7852N ·m -1＜0，不能铺展开2、在293.15K 及101.325kPa 下，半径为1×10-3m 的汞滴分散成半径为1×10-9m 的小汞滴，试求此过程系统的表面吉布斯函数变为若干？已知293.15K 汞的表面张力为0.470N ·m -1。

解：每个半径为m 1013-⨯的汞滴的表面积为252321m 10256.1)101(14.344--⨯=⨯⨯⨯==r A π每个半径为m 1019-⨯的汞滴的表面积为2172922m 10256.1)101(14.344--⨯=⨯⨯⨯==r A π将一滴半径为m 10131-⨯=r 的汞滴分散成半径为m 10192-⨯=r 的微粒时，微粒的个数n 为183********101101()(3434⨯=⨯⨯===--r r r n ππ故表面积增加变化25171812m 56.1210256.110256.1101=⨯-⨯⨯⨯=-=∆--A nA A 表面吉布斯函数变化2-1242,7.2810N m (4m 410m )0.914J T p s G A A ππ--∆=∆=⨯⋅⨯-⨯=J903.556.12470.0,=⨯=∆⋅=∆A A G p T 答：5.906J3、在293.15K 时，乙醚-水、乙醚-汞及水-汞的界面张力分别为0.0107N ·m -1、0.379N ·m -1及0.375N ·m -1，若在乙醚与汞的界面上滴一滴水，试求其润湿角。

第9章 水闸设计习题解答1.解：由《水闸设计规范》（SL265-2001）第7.3.2条规定可知，答案A 是正确的。

2.解：根据《水闸设计规范》（SL265-2001）附录A 式（A.0.1-1）计算闸孔总净宽。

堰上水深H=102.3-100=2.3（m ） 计入行近流速影响，0360.53(2626 2.3 1.52) 2.30.5Q v A ===++⨯⨯⨯⨯（m/s ） 则计入行近流速水头的堰上水深220010.532.3 2.31229.81v H H g α⨯=+=+=⨯（m ）由堰顶算起的下游水深h s =102.1-100=2.1（m ）， 由公式（A.0.1-6）计算淹没系数0.40.400 2.1 2.12.31(1) 2.31(1)0.8052.31 2.31s s h h H H σ=-=⨯⨯-= 则闸孔总净宽032QB σε==32360.805 1.00.365 2.31⨯⨯=7.9（m ）因此，选B 。

讨论: 本题0 2.10.910.92.31s h H ==>可按附录A 第A.0.2条计算，但计算结果相差甚大。

我算的08.95B =（m ）3. 解：由《水闸设计规范》（SL265-2001）第4.3.3条规定可知，答案B 是正确的。

4. 解：由《水闸设计规范》（SL265-2001）第4.3.6条规定可知，答案D 是正确的。

5. 解：根据《水闸设计规范》（SL265-2001）附录A 式（A.0.1-1）计算闸孔总净宽。

堰上水深H=102.3-100=2.3（m ） 计入行近流速影响，0360.53(2626 2.3 1.52) 2.30.5Q v A ===++⨯⨯⨯⨯（m/s ） 则计入行近流速水头的堰上水深220010.532.3 2.31229.81v H H g α⨯=+=+=⨯（m ）由堰顶算起的下游水深h s =102.1-100=2.1（m ）， 由公式（A.0.1-6）计算淹没系数0.40.400 2.1 2.12.31(1) 2.31(1)0.8052.31 2.31s s h h H H σ=-=⨯⨯-= 则闸孔总净宽032QB σε==32360.8050.950.385 2.3⨯⨯=7.91（m ）因此，选B 。

第9章 信号发生电路自测题填空题1．正弦波振荡电路属于 反馈电路，它主要由 、 、 和 组成。

其中， 的作用是选出满足振荡条件的某一频率的正弦波。

2．自激振荡电路从1AF >到1AF =的振荡建立过程中，减小的量是 。

3．RC 正弦波振荡电路、LC 正弦波振荡电路和石英晶体正弦波振荡电路是按组成 的元件不同来划分的。

若要求振荡电路的输出频率在10kHz 左右的音频范围时，常采用 元器件作选频网络，组成 正弦波振荡电路。

4．在正弦波振荡电路中，为了满足振荡条件，应引入 反馈；为了稳幅和减小非线性失真，可适当引入 反馈，若其太强，则 ，若其太弱，则 。

5．在 型晶体振荡电路中，晶体可等效为电阻；在 型晶体振荡电路中，晶体可等效为电感。

石英晶体振荡电路的振荡频率基本上取决于 。

6．当石英晶体作为正弦波振荡电路的一部分时，其工作频率范围是 。

7．集成运放组成的非正弦信号发生电路，一般由 、 和 几个基本部分组成。

8．非正弦波发生电路产生振荡的条件比较简单，只要反馈信号能使 的状态发生跳变，即能产生周期性的振荡。

9．方波和矩形波输出电压的幅值取决于比较器的 ；三角波和锯齿波输出电压的幅值取决于比较器的 。

答案：1．正、放大电路、反馈网络、选频网络、稳幅环节、选频网络。

2．放大倍数。

3．选频网络、RC 、RC 。

4．正、负、不易起振、容易产生非线性失真。

5．串联、并联、石英晶体本身的谐振频率。

6．s p f f f ≤≤。

7．开关元件、反馈网络、延迟环节。

8．比较器。

9．输出电压、阈值电压。

选择题1．为了满足振荡的相位平衡条件，反馈信号与输入信号的相位差应该等于 。

A ．o90； B ．o 180； C ．o 270； D ．o 360。

2．为了满足振荡的相位条件，RC 文氏电桥振荡电路中放大电路的输出信号与输入信号之间的相位差，合适的值是 。

A ．o 90；B ．o 180；C ．o 270；D ．o 360。

第九章 配位化合物参考答案P 108~1092 、解：①依题意，有： O H NH Ag 2232])([++++⋅Ag O H NH 232 初始： 0.1 1.0 0.0平衡时： 0.1-x 1.0+2x xθθ+=⋅⋅=++])([23223231])([][][NH Ag f K NH Ag Ag O H NH K 因为c([Ag(NH 3)2]＋)/K θ>500，且（[NH 3·H 2O]=1.0很大，所以0.1-x ≈0.1 ， 1.0+2x ≈1.0 7107.111.00.1⨯=⨯x 91088.5][-+⨯==x Ag②同理： θθ-=⋅=-+-])([2221])([][][CN Ag f K CN Ag Ag CN K 21100.111.00.1⨯=⨯y 22100.1][-+⨯==y Ag由计算可知，对于同类配合物，配合物的稳定常数越大，离解出的金属离子浓度越低。

4 、解：依题意，有： O H NH s AgBr 232)(⋅++-++232)(2NH Ag O H Br平衡时： x (1/187.77)/0.1 (1/187.77)/0.1 θθθ+⋅=⋅=+-])([232323][])([][NH Ag f SPAgBr K K NH NH Ag Br K θθ+⋅⋅==+-])([23323])([][][NH Ag f SPAgBr K K NH Ag Br x NH )/(26.18107.1100.5)77.187/10(7132L mol =⨯⨯⨯=- )/(37.18)10077.18710001(226.18)(23L mol O H NH c =⨯⨯⨯+=⋅>1.0mol/L 氨 水 故：Ag Br 不能溶解在1.0mol/L100ml 氨水中.。

同理： θθ-⋅⋅==---])([22])([][][CN Ag f SPAgBr K K CN Ag Br y CN 6211321038.2100.1100.5)77.187/10(--⨯=⨯⨯⨯=LKCN mol L mol CN c /0.1)/(106.0)10077.18710001(21038.2)(6<≈⨯⨯⨯+⨯=-- 故：Ag Br 能溶解在1.0mol/L 100mlKCN 溶液 中.。