八下数学反比例函数竞赛试卷k含答案

浙教版八年级数学下册《反比例函数》单元练习检测试卷及答案解析一、选择题1、下列函数中，不是反比例函数的是（ ）A ．B ．C ．D ．2、点A(－2，5)在反比例函数y ＝(k ≠0)的图象上，则k 的值是( )A ．10B ．5C ．－5D ．－103、已知函数y=（k ≠0），当x=时，y=8，则此函数的解析式为（ ）.A ．y=B ．y=C ．y=D ．y=4、下列函数中,图象经过点（1，-1）的反比例函数解析式是（ ）A ．B ．C ．D ．5、反比例函数在第一象限内的图象如图所示，点M 是图象上一点，MP ⊥x 轴，垂足为P.如果△MOP 的面积为1，那么k 的值是（ ）A ．1B ．2C ．4D ．6、已知点 A(x 1，y 1)，B(x 2，y 2 )是反比例函数的图象上的两点，若 x 1<0<x 2，则有（ ）A ．y 1<0<y 2B ．y 2<0<y 1C ．y 1<y 2<0D ．y 2<y 1<0 7、如果等腰三角形的底边长为。

底边上的高为，则它的面积为定植S 时，则与的函数关系式为（ ）A ．B ．xSy 2=C ．D ． Sx y =8、如图，已知点P 是双曲线y=（k ≠0）上一点，过点P 作PA ⊥x 轴于点A ，且S △PAO =2，则该双曲线的解析式为（ ）A．y=﹣B．y=﹣ C．y=D．y=二、填空题9、已知与成反比例，当时，，则当时，_________．10、点P在反比例函数（k≠0）的图象上，点Q（2,4）与点P关于y轴对称，则反比例函数的解析式为________．11、某厂有煤吨，求得这些煤能用的天数与每天用煤的吨数之间的函数关系为________________．12、已知反比例函数的图象经过A（-3,2）,那么此反比例函数的关系式为____________.13、若A(x1，y1)，B(x2，y2)是双曲线y＝上的两点，且x1＞0＞x2，则y1________y2(填“＞”“＝”或“＜”)．14、如图，已知点P（4，2），过点P作PM⊥x轴于点M，PN⊥y轴于点N，双曲线=交PM于点A，交PN于点B．若四边形OAPB的面积为5，则=_____．15、如果函数是反比例函数，且当时随的增大而增大，此函数的解析式是___________________.16、设函数y＝与y＝－2x－6的图象的交点坐标为(a，b)，则＋的值是________．17、已知矩形ABCD的四个顶点均在反比例函数y＝的图象上，且点A的横坐标是2，则矩形ABCD的面积为________．18、如图，直线y=x﹣2与x轴、y轴分别交于点A和点B，点C在直线AB上，且点C的纵坐标为﹣1，点D在反比例函数y=的图象上，CD平行于y轴，S△OCD=，则k的值为________．三、解答题19、若y＝(m＋3)xm2－10是反比例函数，试求其函数表达式．20、某三角形的面积为15，它的一边长为cm，且此边上高为cm，请写出与之间的关系式，并求出时，的值．21、如图，在平面直角坐标系中，直线与轴交于点，与双曲线在第二象限内交于点（-3，）．⑴求和的值；⑵过点作直线平行轴交轴于点，连结AC,求△的面积.22、已知反比例函数，（k为常数，k≠1）．（1）若点A（1，2）在这个函数的图象上，求k的值；（2）若在这个函数图象的每一分支上，y随x的增大而增大，求k的取值范围；（3）若k=13，试判断点B（3，4），C（2，5）是否在这个函数的图象上，并说明理由．23、为预防甲型H1N1流感，某校对教室喷洒药物进行消毒．已知喷洒药物时每立方米空气中的含药量y（毫克）与时间x（分钟）成正比，药物喷洒完后，y与x成反比例（如图所示）．现测得10分钟喷洒完后，空气中每立方米的含药量为8毫克．（1）求喷洒药物时和喷洒完后，y关于x的函数关系式；（2）若空气中每立方米的含药量低于2毫克学生方可进教室，问消毒开始后至少要经过多少分钟，学生才能回到教室？（3）如果空气中每立方米的含药量不低于4毫克，且持续时间不低于10分钟时，才能杀灭流感病毒，那么此次消毒是否有效？为什么？参考答案1、D2、D3、A.4、C5、B6、B7、C8、A9、10、y=-．11、12、13、> 14、315、16、-217、18、3 19、y＝20、；时相应地值为6（cm）21、（1）a=2，b=1（2）3 22、（1）k=3；（2）k＜1；（3）点C不在函数的图象上．23、（1）①（0≤x＜10），②（x≥10）；（2）40分钟；（3）本次消毒有效．答案详细解析【解析】1、反比例函数的一般式是（k≠0），所以A.是反比例函数，错误；B.是反比例函数，错误；C.是反比例函数，错误；D.不是反比例函数，正确．故选：D.2、试题解析：∵点A（-2，5）在反比例函数y=（k≠0）的图象上，∴k的值是：k=xy=-2×5=-10．故选D．3、试题分析：把x=时，y=8代入入y=（k≠0），解得k=×8=﹣4．所以函数的解析式为y=．故选：A．考点：待定系数法求反比例函数解析式．4、把点（1，-1）分别代入四个反比例函数解析式可得：；；；；∴图象过点（1，-1）的反比例函数是：.故选C.5、根据双曲线的图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系S=|k|即可求得k的值．解：由于点M是反比例函数（k＞0）图象上一点，则S△MOP=|k|=1；又由于k＞0，则k=2．故选B．6、分析：根据反比例函数的性质判断出的正负情况，然后比较大小即可．详解：∵反比例函数的k=−3<0，∴反比例函数图象位于第二、四象限，∵∴∴故选B.点睛：考查反比例函数的图象与性质，反比例函数当时，图象在第一、三象限.在每个象限，y随着x的增大而减小，当时，图象在第二、四象限.在每个象限，y随着x的增大而增大.7、试题解析：由题意得则故选C.8、∵反比例函数的图象在二四象限，∴k＜0．∵PA⊥x轴于点A，且S△PAO=2，∴k=-4，∴反比例函数的解析式为y=-.故选A.9、设y与的反比例关系式为y=（k≠0），将x=4，y=1代入，得k=2，所以y与的反比例关系式为.将x=2代入上式，得y==.10、试题分析：根据轴对称的定义，利用点Q（2，4），求出P点坐标，将P点坐标代入解析式，即可求出反比例函数解析式．试题解析：∵点Q（2，4）和点P关于y轴对称，∴P点坐标为（-2，4），将（-2，4）代入解析式得，k=xy=-2×4=-8，∴函数解析式为y=-．考点：1．待定系数法求反比例函数解析式；2．关于x轴、y轴对称的点的坐标．11、这些煤能烧的天数=煤的总吨数÷平均每天烧煤的吨数，煤的总吨数为1500，平均每天烧煤的吨数为x，∴这些煤能烧的天数为，故答案为：12、试题分析：设反比例函数的解析式为y=（k≠0），再把点A（-3，2）代入，求出k 的值即可．解：设反比例函数的解析式为y=(k≠0)，∵反比例函数的图象经过A(−3,2)，∴k=xy=(−3)×2=−6，∴反比例函数的解析式为y=.故答案为：.13、试题解析：∵反比例函数中，∴函数图象的两个分支分别位于一、三象限，且在每一象限内，随的增大而减小.∴点A位于第一象限，点B位于第三象限，故答案为：14、∵点P（4，2），∴OM=4，ON=2.∴S矩形OMPN=OM×ON=4×2=8.∵S矩形OMPN-S△OMA-S△ONB= S矩形OAP B,，∴k=315、试题解析：有题意可得：当时，随的增大而增大，函数的解析式是：点睛：反比例函数的解析式有三种形式：16、∵函数的图象与的图象的交点坐标为，∴，∴，∴.17、设点A(2,n),代入反比例函数y＝可得A点纵坐标n=,反比例函数y＝的图象既是关于直线y=x的轴对称图形,也是关于原点对称的中心对称图形,矩形也是轴对称和中心对称图形,又因为矩形ABCD的四个顶点在反比例函数图象上,所以可以求得A,B,C,D四点的坐标分别为故依据两点间的距离公式,可以求得矩形的两边长度,即可以求得矩形ABCD的面积为.18、试题解析：设CD与轴交于点E，当时，，即，那么，所以，而.点睛：在反比例函数中，是过双曲线上任意一点作轴的垂线段与两坐标轴围成的面积.19、试题分析：（1）此题只需根据反比例函数的定义式令m2-10=-1即可，且满足m+3≠0. 试题解析：由反比例函数的定义可知m2－10＝－1，①m＋3≠0，②由①得m2＝9，解得m＝±3，由②得m≠－3，∴m＝3.∴此反比例函数的表达式为y＝.20、试题分析：三角形的面积=边长×这边上高÷2，那么这边上高=2×三角形的面积÷边长，进而把相关数值代入求值即可．试题解析：∵三角形的面积=边长×这边上高÷2，三角形的面积为15cm2，一边长为xcm，此边上高为ycm，∴；当x=5时，y=6（cm）．点睛：此题考查列反比例函数关系式以及求值问题，根据三角形的面积得到求一边上的高的等量关系是解决问题的关键.21、试题分析：（1）因为直线与双曲线交于点B，将B点坐标分别代入直线与双曲线的解析式，即可解得与的值.（2）先利用直线BC平行于轴确定C点坐标为，然后根据三角形面积公式计算三角形面积即可.试题解析：（1）由两图象相交于点B，得解得：a=2,b=1(2)∵点B(-3,2), 直线∥轴，∴C点坐标为，BC=3，∴ S△ABC =.22、试题分析：（1）把点A的坐标代入函数解析式，利用待定系数法求解即可；（2）根据反比例函数图象的性质得到：k-1＜0，由此求得k的取值范围；（3）把点B、C的坐标代入函数解析式进行一一验证．试题解析：（1）∵点A（1，2）在这个函数的图象上，∴k﹣1=1×2，解得k=3；（2）∵在函数图象的每一支上，y随x的增大而增大，∴k﹣1＜0，解得k＜1；（3）∵k=13，有k﹣1=12，∴反比例函数的解析式为．将点B的坐标代入，可知点B的坐标满足函数关系式，∴点B在函数的图象上，将点C的坐标代入，由5≠，可知点C的坐标不满足函数关系式，∴点C不在函数的图象上．23、（1）分别设出喷洒药物时和喷洒完后的函数解析式，代入点（10，8）即可求解．（2）由（1）求得的反比例函数解析式，令y＜2，求得x的取值范围即可．（3）将y=4分别代入求得的正比例函数和反比例函数求得的x值作差与10比较即可得出此次消毒是否有效．解：（1）①∵当0≤x＜10时y与x成正比例，∴可设y=kx．∵当x=10时，y=8，∴8=10k．∴k=．∴（0≤x＜10）．②∵当x≥10时y与x成反比例，∴可设．∵当x=10时，y=8，∴．∴k=80．∴（x≥10）．（2）当y＜2时，即．解得x＞40．∴消毒开始后至少要经过40分钟，学生才能回到教室．（3）将y=4代入中，得x=5；将y=4代入中，得x=20；∵20﹣5=15＞10，∴本次消毒有效．。

浙教版数学八年级下册6.1《反比例函数》精选练习一、选择题1.如果直角三角形的面积一定，那么下列关于这个直角三角形边的关系中，正确的是( )A.一条直角边与斜边成反比例B.一条直角边与斜边成正比例C.两条直角边成反比例D.两条直角边成正比例2.下列函数中，y 是x 的反比例函数的是（ ）A.y=3xB.错误!未找到引用源。

C.3xy=1D.错误!未找到引用源。

3.近视眼镜的度数y(度)与镜片焦距x(m)成反比例，已知400度近视眼镜镜片的焦距为0.25 m ，则y 与x 的函数关系式为( ) A.y=400x B.y=14x C.y=100x D.y=1400x4.下列关系中的两个量，成反比例的是（ ）A.面积一定时，矩形周长与一边长B.压力一定时，压强与受力面积C.读一本书，已读的页数与余下的页数D.某人年龄与体重5.若反比例函数错误!未找到引用源。

，当x=2时，y= -6，则k 的值为（ ）A.-12B.12C.-3D.36.已知反比例函数y=k x的图象过点(2，3)，那么下列四个点中，也在这个函数上的是( ) A.(－6，1) B.(1，6) C.(2，－3) D.(3，－2)7.在函数y=错误!未找到引用源。

中，自变量x 的取值范围是( )A.x ≠0B.x>0C.x<0D.一切实数8.下列函数表达式中，y 不是x 的反比例函数的是( )A.y=3xB.y=x 3C.y=12xD.xy=129.小华以每分钟x 个字的速度书写，y 分钟写了300个字，则y 与x 的函数关系式为( )A.y=x 300B.y=300xC.y=300－xD.y=300－x x10.下列函数中，是反比例函数的为( )A.7y=xB.C.D.y=5x+411.已知y 与x －1成反比例，那么它的解析式为( )A.y=k x－1(k ≠0) B.y=k(x －1)(k ≠0) C.y=k x －1(k ≠0) D.y=x －1k(k ≠0) 12.如果直角三角形的面积一定，那么下列关于这个直角三角形边的关系中，正确的是( )A.两条直角边成正比例B.两条直角边成反比例C.一条直角边与斜边成正比例D.一条直角边与斜边成反比例二、填空题13.已知函数y=y 1＋y 2，y 1与x 成正比例，y 2与x 成反比例，且当x=1时，y=4；当x=2时，y=5；则当x=－2时，函数y 的值是 。

初中数学反比例函数基础测试题含答案一、选择题1．如图，正方形OABC 的边长为6，D 为AB 中点，OB 交CD 于点Q ，Q 是y ＝k x上一点，k 的值是（ ）A ．4B ．8C ．16D ．24【答案】C【解析】【分析】 延长根据相似三角形得到:1:2BQ OQ =，再过点Q 作垂线，利用相似三角形的性质求出QF 、OF ，进而确定点Q 的坐标，确定k 的值．【详解】解：过点Q 作QF OA ⊥，垂足为F ，OABC Q 是正方形，6OA AB BC OC ∴====，90ABC OAB DAE ∠=∠=︒=∠，D Q 是AB 的中点，12BD AB ∴=， //BD OC Q ， OCQ BDQ ∴∆∆∽，∴12BQ BD OQ OC ==， 又//QF AB Q ，OFQ OAB ∴∆∆∽，∴22213QF OF OQ AB OA OB ====+， 6AB =Q ，2643QF ∴=⨯=，2643OF =⨯=， (4,4)Q ∴，Q 点Q 在反比例函数的图象上，4416k ∴=⨯=，故选：C ．【点睛】本题考查了待定系数法求反比例函数、相似三角形的性质和判定，利用相似三角形性质求出点Q 的坐标是解决问题的关键．2．如图，点A 在双曲线4y x =上，点B 在双曲线(0)k y k x=≠上，AB x P 轴，交y 轴于点C ．若2AB AC =，则k 的值为（ ）A ．6B ．8C ．10D ．12【答案】D【解析】【分析】 过点A 作AD ⊥x 轴于D ，过点B 作BE ⊥x 轴于E ，得出四边形ACOD 是矩形，四边形BCOE 是矩形，得出ACOD S 矩形=4，BCOE S k =矩形，根据AB=2AC ，即BC=3AC ，即可求得矩形BCOE 的面积，根据反比例函数系数k 的几何意义即可求得k 的值．【详解】过点A 作AD ⊥x 轴于D ，过点B 作BE ⊥x 轴于E ，∵AB ∥x 轴，∴四边形ACOD 是矩形，四边形BCOE 是矩形，∵AB=2AC ，∴BC=3AC ，∵点A 在双曲线4y x=上， ∴ACOD S 矩形=4，同理BCOE S k =矩形，∴矩形3BCOE ACOD S S =矩形矩形=12，∴k=12，故选：D ．【点睛】本题考查了反比例函数图象上点的坐标特征，反比例系数k 的几何意义，作出辅助线，构建矩形是解题的关键．3．下列函数中，当x ＞0时，函数值y 随自变量x 的增大而减小的是（ ）A ．y ＝x 2B ．y ＝xC ．y ＝x+1D ．1y x = 【答案】D【解析】【分析】需根据函数的性质得出函数的增减性，即可求出当x ＞0时，y 随x 的增大而减小的函数．【详解】解：A 、y ＝x 2是二次函数，开口向上，对称轴是y 轴，当x ＞0时，y 随x 的增大而增大，错误； B 、y ＝x 是一次函数k ＝1＞0，y 随x 的增大而增大，错误；C 、y ＝x+1是一次函数k ＝1＞0，y 随x 的增大而减小，错误；D 、1y x=是反比例函数，图象无语一三象限，在每个象限y 随x 的增大而减小，正确； 故选D ．【点睛】本题综合考查了二次函数、一次函数、反比例函数的性质，熟练掌握函数的性质是解题的关键．4．如图直线y ＝mx 与双曲线y=k x交于点A 、B ，过A 作AM ⊥x 轴于M 点，连接BM ，若S △AMB ＝2，则k 的值是( )A．1 B．2 C．3 D．4【答案】B【解析】【分析】此题可根据反比例函数图象的对称性得到A、B两点关于原点对称，再由S△ABM=2S△AOM并结合反比例函数系数k的几何意义得到k的值．【详解】根据双曲线的对称性可得：OA=OB,则S△ABM＝2S△AOM＝2，S△AOM＝12|k|＝1，则k＝±2．又由于反比例函数图象位于一三象限，k＞0，所以k＝2．故选B．【点睛】本题主要考查了反比例函数y＝kx中k的几何意义，即过双曲线上任意一点引x轴、y轴垂线，所得矩形面积为|k|，是经常考查的一个知识点．5．给出下列函数：①y＝﹣3x+2：②y＝3x；③y＝﹣5x：④y＝3x，上述函数中符合条件“当x＞1时，函数值y随自变量x增大而增大”的是（）A．①③B．③④C．②④D．②③【答案】B【解析】【分析】分别利用一次函数、正比例函数、反比例函数的增减性分析得出答案．【详解】解：①y＝﹣3x+2，当x＞1时，函数值y随自变量x增大而减小，故此选项不符合题意；②y＝3x，当x＞1时，函数值y随自变量x增大而减小，故此选项不符合题意；③y＝﹣5x，当x＞1时，函数值y随自变量x增大而增大，故此选项符合题意；④y＝3x，当x＞1时，函数值y随自变量x增大而增大，故此选项符合题意；故选：B．【点睛】此题考查一次函数、正比例函数、反比例函数，正确把握相关性质是解题关键．6．在平面直角坐标系xoy 中，函数()20y x x =<的图象与直线1l ：()103y x b b =+<交于点A ，与直线2l ：x b =交于点B ，直线1l 与2l 交于点C ，记函数()20y x x =<的图象在点A 、B 之间的部分与线段AC ，线段BC 围城的区域（不含边界）为W ，当4233b -≤≤-时，区域W 的整点个数为（ ）A ．3个B ．2个C ．1个D ．没有【答案】D【解析】【分析】根据解析式画出函数图象，根据图形W 得到整点个数进行选择.【详解】∵()20y x x =<，过整点（-1，-2），（-2，-1），当b=43-时，如图：区域W 内没有整点，当b=23-时，区域W 内没有整点，∴4233b-≤≤-时图形W增大过程中，图形内没有整点，故选：D.【点睛】此题考查函数图象，根据函数解析式正确画出图象是解题的关键.7．若一个圆锥侧面展开图的圆心角是270°，圆锥母线l与底面半径r之间的函数关系图象大致是（）A．B．C．D．【答案】A【解析】【分析】根据圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长得到2πr=270180lπ⋅⋅，整理得l=43r（r＞0），然后根据正比例函数图象求解．【详解】解：根据题意得2πr=270180lπ⋅⋅，所以l=43r（r＞0），即l与r为正比例函数关系，其图象在第一象限．故选A．【点睛】本题考查圆锥的计算；函数的图象．8．如图，一次函数1y ax b =+和反比例函数2k y x=的图象相交于A ，B 两点，则使12y y >成立的x 取值范围是( )A ．20x -<<或04x <<B ．2x <-或04x <<C ．2x <-或4x >D ．20x -<<或4x >【答案】B【解析】【分析】 根据图象找出一次函数图象在反比例函数图象上方时对应的自变量的取值范围即可.【详解】观察函数图象可发现：2x <-或04x <<时，一次函数图象在反比例函数图象上方， ∴使12y y >成立的x 取值范围是2x <-或04x <<，故选B ．【点睛】本题考查了反比例函数与一次函数综合，函数与不等式，利用数形结合思想是解题的关键.9．如图，ABDC Y 的顶点,A B 的坐标分别是()(), 0,3 1, 0A B -，顶点,C D 在双曲线k y x=上，边BD 交y 轴于点E ,且四边形ACDE 的面积是ABE ∆面积的3倍，则k 的值为:（ ）A ．6-B ．4-C ．3-D ．12-【答案】A【解析】【分析】 过D 作DF//y 轴，过C 作//CF x 轴，交点为F ，利用平行四边形的性质证明,DCF ABO ∆≅∆利用平移写好,C D 的坐标，由四边形ACDE 的面积是ABE ∆面积的3倍，得到2,DB BE =利用中点坐标公式求横坐标，再利用反比例函数写D 的坐标，列方程求解k ．【详解】解：过D 作DF//y 轴，过C 作//CF x 轴，交点为F ，则,CF DF ⊥ABDC QY ，,CDF BAO ∴∠∠的两边互相平行，,AB DC =CDF BAO ∴∠=∠，90,DFC BOA ∠=∠=︒Q,DCF ABO ∴∆≅∆,,CF BO DF AO ∴== 设(,),k C m m由()(), 0,3 1, 0A B -结合平移可得：(1,3)k D m m ++， Q 四边形ACDE 的面积是ABE ∆面积的3倍，11()322BD BE DE CA h h BE ∴+=⨯⨯， ,,BD BE h h AC BD ==Q3DE AC BE ∴+=，4,DE BD BE BE ∴++=2,DB BE ∴=(1,3),(1,0),0,E k D m B x m++=Q ∴ 由中点坐标公式知：110,2m ++= 2m ∴=- ，(1,)1k D m m ++Q ， 3212k k ∴=+-+-， 6.k ∴=-故选A ．【点睛】本题考查的是反比例函数的图像与性质，平行四边形的性质，平移性质，中点坐标公式，掌握以上知识点是解题关键．10．下列函数：①y=-x ；②y=2x ；③1y x=-；④y=x 2 ． 当x<0时，y 随x 的增大而减小的函数有（ ）A ．1 个B ．2 个C ．3 个D ．4 个 【答案】B【解析】【分析】分别根据一次函数、反比例函数及二次函数的性质进行逐一判断即可．【详解】一次函数y ＝－x 中k ＜0，∴y 随x 的增大而减小，故本选项正确；∵正比例函数y ＝2x 中，k ＝2，∴当x ＜0时，y 随x 的增大而增大，故本选项错误；∵反比例函数1y x＝中，k ＝－1＜0，∴当x ＜0时函数的图像在第二象限，此时y 随x 的增大而增大，故本选项错误； ∵二次函数y ＝x 2，中a ＝1＞0，∴此抛物线开口向上，当x ＜0时，y 随x 的增大而减小，故本选项正确．故选B ．【点睛】本题考查的是一次函数、反比例函数及二次函数的性质，解题关键是根据题意判断出各函数的增减性．11．如图，平行于x 轴的直线与函数y ＝1k x（k 1＞0，x ＞0），y ＝2k x （k 2＞0，x ＞0）的图象分别相交于A ，B 两点，点A 在点B 的右侧，C 为x 轴上的一个动点，若△ABC 的面积为6，则k 1﹣k 2的值为（ ）A ．12B ．﹣12C ．6D ．﹣6【答案】A【解析】【分析】 △ABC 的面积＝12•AB•y A ，先设A 、B 两点坐标（其y 坐标相同），然后计算相应线段长度，用面积公式即可求解．【详解】 解：设：A 、B 点的坐标分别是A （1k m ，m ）、B （2k m ，m ）， 则：△ABC 的面积＝12•AB•y A ＝12•（1k m ﹣2k m ）•m ＝6， 则k 1﹣k 2＝12．故选：A ．【点睛】此题主要考查了反比例函数系数的几何意义，以及图象上点的特点，求解函数问题的关键是要确定相应点坐标，通过设A 、B 两点坐标，表示出相应线段长度即可求解问题．12．如图，过反比例函数()0k y x x=>的图象上一点A 作AB x ⊥轴于点B ，连接AO ，若2AOB S ∆=，则k 的值为（ ）A ．2B ．3C ．4D ．5【答案】C【解析】【分析】 根据2AOB S ∆=，利用反比例函数系数k 的几何意义即可求出k 值，再根据函数在第一象限可确定k 的符号.【详解】解：由AB x ⊥轴于点B ，2AOB S ∆=，得到122AOB S k ∆== 又因图象过第一象限, 122AOB S k ∆==，解得4k = 故选C【点睛】本题考查了反比例函数系数k 的几何意义.13．反比例函数k y x=在第一象限的图象如图所示，则k 的值可能是（ ）A ．3B ．5C ．6D ．8【答案】B【解析】【分析】 根据点（1，3）在反比例函数图象下方，点（3，2）在反比例函数图象上方可得出k 的取值范围，即可得答案.【详解】∵点（1，3）在反比例函数图象下方，∴k>3，∵点（3，2）在反比例函数图象上方， ∴3k <2，即k<6， ∴3<k<6，故选：B.【点睛】 本题考查了反比例函数的图象的性质，熟记k=xy 是解题关键.14．已知反比例函数k y x=的图象分别位于第二、第四象限，()11,A x y 、()22,B x y 两点在该图象上，下列命题：①过点A 作AC x ⊥轴，C 为垂足，连接OA .若ACO ∆的面积为3，则6k=-；②若120x x <<，则12y y >；③若120x x +=，则120y y +=其中真命题个数是（ ） A ．0B ．1C ．2D ．3 【答案】D【解析】【分析】根据反比例函数的性质，由题意可得k ＜0，y 1=,,sin cos 22x x x ππ⎡⎤∃∈-≤⎢⎥⎣⎦，y 2=2k x ，然后根据反比例函数k 的几何意义判断①，根据点位于的象限判断②，结合已知条件列式计算判断③，由此即可求得答案.【详解】 ∵反比例函数k y x=的图象分别位于第二、第四象限， ∴k<0，∵()11,A x y 、()22,B x y 两点在该图象上， ∴y 1=,,sin cos 22x x x ππ⎡⎤∃∈-≤⎢⎥⎣⎦，y 2=2k x ， ∴x 1y 1=k ，x 2y 2=k ，①过点A 作AC x ⊥轴，C 为垂足，∴S △AOC =1OC?AC 2=11x ?y k =322=， ∴6k =-，故①正确；②若120x x <<，则点A 在第二象限，点B 在第四象限，所以12y y >，故②正确； ③∵120x x +=，∴()121212120k x x k k y y x x x x ++=+==，故③正确， 故选D.【点睛】 本题考查了反比例函数的性质，反比例函数图象上点的坐标特征等，熟练掌握和灵活运用相关知识是解题的关键.15．若A （-3，y 1）、B （-1，y 2）、C （1，y 3）三点都在反比例函数y=k x （k ＞0）的图象上，则y 1、y 2、y 3的大小关系是（ ）A ． y 1＞y 2＞y 3B ． y 3＞y 1＞y 2C ． y 3＞y 2＞y 1D ． y 2＞y 1＞y 3 【答案】B【解析】【分析】反比例函数y=k x（k ＞0）的图象在一、三象限，根据反比例函数的性质，在每个象限内y 随x 的增大而减小，而A （-3，y 1）、B （-1，y 2）在第三象限双曲线上的点，可得y 2＜y 1＜0，C （1，y 3）在第一象限双曲线上的点y 3＞0，于是对y 1、y 2、y 3的大小关系做出判断．【详解】∵反比例函数y=k x（k ＞0）的图象在一、三象限， ∴在每个象限内y 随x 的增大而减小，∵A （-3，y 1）、B （-1，y 2）在第三象限双曲线上，∴y 2＜y 1＜0，∵C （1，y 3）在第一象限双曲线上，∴y 3＞0，∴y 3＞y 1＞y 2，故选：B ．【点睛】此题考查反比例函数的图象和性质，解题关键在于当k ＞0，时，在每个象限内y 随x 的增大而减小；当k ＜0时，y 随x 的增大而增大，注意“在每个象限内”的意义，这种类型题目用图象法比较直观得出答案．16．反比例函数21k y x+=的图象上有两点()11,A a y -，()21,B a y +，若12y y <，则a 的取值范围（ ）A ．1a <-B ．1a >C ．11a -<<D ．这样的a 值不存在【答案】C【解析】【分析】由210k +>得出在同一分支上，反比例函数y 随x 的增大而减小，然后结合反比例函数的图象进行求解．【详解】210k +>Q ，∴在同一分支上，反比例函数y 随x 的增大而减小，11a a -<+Q ，12y y <，∴点A ，B 不可能在同一分支上，只能为位于不同的两支上，10a ∴-<且10a +>，11a ∴-<<，故选C ．【点睛】本题考查反比例函数的图象与性质，熟练掌握反比例函数的性质是解题的关键，注意反比例函数的图象有两个分支．17．如图，矩形ABCD 的边AB 在x 轴上，反比例函数(0)k y k x=≠的图象过D 点和边BC 的中点E ，连接DE ，若△CDE 的面积是1，则k 的值是（ ）A ．3B ．4C ．25D ．6【答案】B【解析】【分析】 设E 的坐标是m n k mn =（，），， 则C 的坐标是2m n （，），求得D 的坐标，然后根据三角形的面积公式求得mn 的值，即k 的值．【详解】设E 的坐标是m n k mn =（，），，， 则C 的坐标是（m ，2n ），在mn y x = 中，令2y n =，解得：2m x =， ∵1CDE S =V ，∴111,12222m m n m n -=⨯=g 即 ∴4mn =∴4k =故选：B【点睛】本题考查了待定系数法求函数的解析式，利用mn 表示出三角形的面积是关键．18．已知反比例函数b y x=与一次函数y ax c =+有一个交点在第四象限，该交点横坐标为1，抛物线2y ax bx c =++与x 轴只有一个交点，则一次函数b c y x a a=+的图象可能是（ ） A ． B ． C ． D ．【答案】B【解析】【分析】根据题意得b ＜0，a+c ＜0，240b ac =>，可得a ＜0，c ＜0，进而即可判断一次函数b c y x a a=+的图象所经过的象限． 【详解】 ∵反比例函数b y x=与一次函数y ax c =+有一个交点在第四象限， ∴反比例函数的图象在二、四象限，即b ＜0，∵该交点横坐标为1，∴y=a+c ＜0，∵抛物线2y ax bx c =++与x 轴只有一个交点， ∴240b ac -=，即：240b ac =>，∴a ＜0，c ＜0，∴0b a>，0c a >， ∴b c y x a a=+的图象过一、二、三象限． 故选B ．【点睛】本题主要考查反比例函数与一次函数的图象和性质，掌握函数图象上点的坐标特征以及函数解析式的系数的几何意义，是解题的关键．19．如图，矩形ABCD的顶点A，B在x轴的正半轴上，反比例函数k yx =在第一象限内的图象经过点D，交BC于点E．若4AB=，2CEBE=，34ADOA=，则线段BC的长度为（）A．1 B．32C．2 D．23【答案】B【解析】【分析】设OA为4a，则根据题干中的比例关系，可得AD=3a，CE=2a，BE=a，从而得出点D和点E 的坐标(用a表示)，代入反比例函数可求得a的值，进而得出BC长.【详解】设OA=4a根据2CEBE=，34ADOA=得：AD=3a，CE=2a，BE=a∴D(4a，3a)，E(4a+4，a)将这两点代入解析得；3444kaakaa⎧=⎪⎪⎨⎪=⎪+⎩解得：a=12∴BC=AD=32故选：B【点睛】本题考查反比例函数和矩形的性质，解题关键是用含有字母的式子表示出点D、E的坐标，然后代入解析式求解.20．若函数2myx+=的图象在其象限内y的值随x值的增大而增大，则m的取值范围是（）A．m＞﹣2 B．m＜﹣2C．m＞2 D．m＜2【答案】B【解析】【分析】根据反比例函数的性质，可得m+2＜0，从而得出m的取值范围．【详解】∵函数2myx+=的图象在其象限内y的值随x值的增大而增大，∴m+2＜0，解得m＜-2．故选B．。

浙教版八年级下册数学第六章反比例函数含答案一、单选题(共15题，共计45分)1、反比例函数，当x＜0时，y随x的增大而增大，则m的值是（）A.－1B.3C.－1或3D.22、如图，已知点 A 、B分别在反比例函数的图象上，且OA ⊥OB ，则的值为（）A. B.2 C. D.43、如图，直线y=x−2与双曲线y=(k>0)在第一象限内的交点为R，与x轴的交点为P，与y轴的交点为Q；作RM⊥x轴于点M，若△OPQ与△PRM的面积是4：1，则k等于( )A. B. C.2 D.34、下列各点中，在函数y=－的图象上的是( )A.（3，1）B.（－3，1）C.（，3）D.（3，－）5、如图，在Rt△ABC中，∠ABC=90°，点B在x轴上，且B（﹣1，0），A点的横坐标是2，AB=3BC，双曲线y= （m＞0）经过A点，双曲线y=﹣经过C点，则m的值为（）A.12B.9C.6D.36、已知抛物线y=ax2+bx+c与反比例函数y= 的图象在第一象限有一个公共点，其横坐标为1，则一次函数y=bx+ac的图象可能是（）A. B. C. D.7、如图，过点C（1，2）分别作x轴、y轴的平行线，交直线y=﹣x+6于A、B 两点，若反比例函数y=（x＞0）的图象与△ABC有公共点，则k的取值范围是（）A.2≤k≤9B.2≤k≤8C.2≤k≤5D.5≤k≤88、下列各点中，在函数的图象上的点是（）A.（3，4）B.（﹣2，﹣6）C.（﹣2，6）D.（﹣3，﹣4）9、已知点A(m，4)在双曲线上，则m的值是（）A.-4B.4C.1D.-110、如图，以原点为圆心的圆与反比例函数y=的图象交于A、B、C、D四点，已知点A的横坐标为1，则点C的横坐标（）A.﹣4B.﹣3C.﹣2D.﹣111、已知反比例函数y=的图象经过点（3，2），那么下列四个点中，也在这个函数图象上的是（）A.（3，﹣2）B.（﹣2，﹣3）C.（1，﹣6）D.（﹣6，1）12、若点，，都在反比例函数的图象上，则，，的大小关系是（）A. B. C. D.13、如图，点A是反比例函数y= (x>0)图象上任意一点，AB⊥y轴于点B，点C是x轴上的一个动点，则△ABC的面积为( )A.1B.2C.4D.无法确定14、下列四个点，在反比例函数图象上的是（）。

八年级数学下册《反比例函数》练习题与答案(苏科版)一、选择题1.下列函数中，表示y 是x 的反比例函数的是( )A.x(y ＋1)＝1B.y ＝1x －1C.y ＝－1x 2D.y ＝12x 2.已知y=8x n ﹣2，若y 是x 的反比例函数，则n=( )A.1B.﹣1C.1或﹣1D.03.反比例函数y ＝n ＋5x的图象经过点(2，3)，则n 的值是( ) A.－2 B.－1 C.0 D.14.如图，菱形OABC 的顶点B 在y 轴上，顶点C 的坐标为(﹣3，2).若反比例函数y=k x(x ＞0)的图象经过点A ，则k 的值为( )A.﹣6B.﹣3C.3D.65.关于反比例函数y ＝4x的图象，下列说法正确的是( ) A.必经过点(1，1)B.两个分支分布在第二、四象限C.两个分支关于x 轴成轴对称D.两个分支关于原点成中心对称6.在反比例函数y ＝图象上有两点A(x 1，y 1)，B(x 2，y 2)，x 1＜0＜x 2，y 1＜y 2，则m 的取值范围是( )A.m ＞13B.m ＜13C.m ≥13D.m ≤137.在反比例函数y ＝k x (k<0)的图象上有两点(－1，y 1)，(-14，y 2)，则y 1－y 2的值是( ) A.负数 B.非正数 C.正数 D.不能确定8.如图，函数y 1＝x 3与y 2＝1x 在同一坐标系中的图象如图所示，则当y 1＜y 2时( )A.﹣1＜x ＜lB.0＜x ＜1或x ＜﹣1C.﹣1＜x ＜I 且x ≠0D.﹣1＜x ＜0或x ＞19.如图，反比例函数y ＝k x 的图象经过正方形ABCD 的顶点A 和中心E ，若点D 的坐标为(﹣1，0)，则k 的值为( )A.2B.﹣2C.12D.﹣1210.若在同一直角坐标系中，正比例函数y ＝k 1x 与反比例函数y ＝k 2x的图象无交点，则有( ) A.k 1＋k 2＞0 B.k 1＋k 2＜0 C.k 1k 2＞0 D.k 1k 2＜011.一司机驾驶汽车从甲地开往乙地，他以平均80千米/小时的速度用了4个小时到达乙地，当他按原路匀速返回时，汽车的速度v 千米/小时与时间t 小时的函数关系是( )A.v=320tB.v=320tC.v=20tD.v=20t12.教室里的饮水机接通电源就进入自动程序：开机加热时每分钟上升10 ℃，加热到100 ℃后停止加热，水温开始下降，此时水温(℃)与开机后用时(min)成反比例关系，直至水温降至30℃，饮水机关机.饮水机关机后即刻自动开机，重复上述自动程序.若在水温为30 ℃时，接通电源后，水温y(℃)和时间x(min)的关系如图，为了在上午第一节下课时(8：45)能喝到不超过50 ℃的水，则接通电源的时间可以是当天上午的( )A.7：20B.7：30C.7：45D.7：50二、填空题13.如图，点A 是反比例函数y ＝k x 图象上的一个动点，过点A 作AB ⊥x 轴，AC ⊥y 轴，垂足分别为B 、C ，矩形ABOC 的面积为4，则k ＝ .14.如图，在平面直角坐标系中，点A 是函数y=k x(k ＜0，x ＜0)图象上的点，过点A 与y 轴垂直的直线交y 轴于点B ，点C 、D 在x 轴上，且BC ∥AD.若四边形ABCD 的面积为3，则k 值为 .15.已知点A(－2，y 1)，B(－1，y 2)和C(3，y 3)都在反比例函数y ＝3x的图象上，则y 1，y 2，y 3的大小关系为____________(用“＜”连接).16.已知函数y=是反比例函数,且图象在第二、四象限内,则m 的值是 .17.如图，在平面直角坐标系中，反比例函数y ＝2x (x ＞0)的图象与正比例函数y ＝kx ，y ＝1kx(k ＞1)的图象分别交于点A ，B ，若∠AOB ＝45°，则△AOB 的面积是______．18.如图，矩形OABC 的边AB 与x 轴交于点D ，与反比例函数y ＝k x(k ＞0)在第一象限的图象交于点E ，∠AOD ＝30°，点E 的纵坐标为1，△ODE 的面积是433，则k 的值是 .三、解答题19.已知直线y ＝－2x 经过点P(－2，a)，反比例函数y ＝k x(k ≠0)经过点P 关于y 轴的对称点P ′. (1)求a 的值；(2)直接写出点P ′的坐标；(3)求反比例函数的解析式.20.已知y 与x 的部分取值如下表： x … －6 －5 －4 －3 －2 －1 12 3 4 5 6 … y … 1 1.2 1.5 2 3 6 －6 －3 －2 -1.5 -1.2 －1 …(1)(2)画出这个函数的图象.21.已知反比例函数y ＝k x(k 为常数，k ≠0)的图象经过点A(2，3). (1)求这个函数的解析式；(2)判断点B(－1，6)，C(3，2)是否在这个函数的图象上，并说明理由；(3)当－3＜x ＜－1时，求y 的取值范围.22.如图，一次函数y ＝x ＋4的图象与反比例函数y ＝k x(k 为常数且k ≠0)的图象交于A(﹣1，a)，B 两点，与x 轴交于点C.(1)求此反比例函数的表达式；(2)若点P 在x 轴上，且S △ACP ＝32S △BOC ，求点P 的坐标.23.某厂仓库储存了部分原料，按原计划每小时消耗2吨，可用60小时.由于技术革新，实际生产能力有所提高，即每小时消耗的原料量大于计划消耗的原料量.设现在每小时消耗原料x(单位：吨)，库存的原料可使用的时间为y(单位：小时).(1)写出y 关于x 的函数解析式，并求出自变量的取值范围.(2)若恰好经过24小时才有新的原料进厂，为了使机器不停止运转，则x 应控制在什么范围内？24.甲、乙两家商场进行促销活动，甲商场采用“满200减100”的促销方式，即购买商品的总金额满200元但不足400元，少付100元；满400元但不足600元，少付200元.乙商场按顾客购买商品的总金额打6折促销.(1)若顾客在甲商场购买了510元的商品，付款时应付多少钱？(2)若顾客在甲商场购买商品的总金额为x(400≤x＜600)元，优惠后得到商家的优惠率为p，写出p与x之间的函数关系式，并说明p随x的变化情况；(3)品牌、质量、规格等都相同的某种商品，在甲乙两商场的标价都是x(200≤x＜400)元，你认为选择哪家商场购买商品花钱较少？请说明理由.25.如图，在平面直角坐标系中有Rt△ABC，∠A＝90°，AB＝AC，A(﹣2，0)，B(0，1).(1)求点C的坐标；(2)将△ABC沿x轴的正方向平移，在第一象限内B、C两点的对应点B'、C'正好落在某反比例函数图象上.请求出这个反比例函数和此时的直线B'C'的解析式.(3)若把上一问中的反比例函数记为y1，点B′，C′所在的直线记为y2，请直接写出在第一象限内当y1＜y2时x 的取值范围.参考答案1.D2.A3.D.4.D5.D6.B.7.A8.B.9.B10.A11.B12.A13.答案为：－4.14.答案为：﹣3.15.答案为：y 2<y 1<y 3.16.答案为：﹣2.17.答案为：2.18.答案为：3 3.19.解：(1)将P(－2，a)代入y ＝2x ，得a ＝－2×(－2)＝4.(2)∵a ＝4，∴点P 的坐标为(－2,4).∴点P ′的坐标为(2,4).(3)将P ′(2,4)代入y ＝k x 得4＝k 2，解得k ＝8∴反比例函数的解析式为y ＝8x. 20.解：(1)反比例函数：y ＝－6x. (2)如图所示.21.解：(1)∵反比例函数y ＝k x的图象经过点A(2，3) 把点A 的坐标代入解析式，得3＝k 2，解得k ＝6. ∴这个函数的解析式为y ＝6x. (2)点B 不在这个函数的图象上，点C 在这个函数的图象上.理由：分别把点B ，C 的坐标代入y ＝6x可知点B 的坐标不满足函数解析式，点C 的坐标满足函数解析式∴点B 不在这个函数的图象上，点C 在这个函数的图象上.(3)∵当x ＝－3时，y ＝－2；当x ＝－1时，y ＝－6.又由k ＞0，知当x ＜0时，y 随x 的增大而减小∴当－3＜x ＜－1时，－6＜y ＜－2.22.解： (1)把点A(﹣1，a)代入y ＝x ＋4，得a ＝3∴A(﹣1，3).把A(﹣1，3)代入反比例函数y ＝k x，得k ＝﹣3. ∴反比例函数的表达式为y ＝﹣3x. (2)联立两个函数表达式：⎩⎪⎨⎪⎧y ＝x ＋4，y ＝－3x ，解得⎩⎪⎨⎪⎧x ＝－1，y ＝3，或⎩⎪⎨⎪⎧x ＝－3，y ＝1. ∴点B 的坐标为(﹣3，1).当y ＝x ＋4＝0时，得x ＝﹣4∴点C(﹣4，0).设点P 的坐标为(x ，0).∵S △ACP ＝32S △BOC ∴12×3×|x ﹣(﹣4)|＝32×12×4×1，解得x 1＝﹣6，x 2＝﹣2. ∴点P(﹣6，0)或(﹣2，0).23.解：(1)∵正方形OABC 的边OA ，OC 分别在x 轴，y 轴上，点B 的坐标为(2，2)∴C(0，2).∵D 是BC 的中点∴D(1，2).∵反比例函数y ＝k x(x ＞0，k ≠0)的图象经过点D ∴k ＝2.(2)当P 在直线BC 的上方，即0＜x ＜1时∵点P(x ，y)在该反比例函数的图象上运动，∴y ＝2x. ∴S 四边形CQPR ＝CQ ·PQ ＝x ·(2x－2)＝2－2x ；当P 在直线BC 的下方，即x ＞1时，同理求出S 四边形CQPR ＝CQ ·PQ ＝x ·(2－2x)＝2x －2 综上，S ＝⎩⎪⎨⎪⎧2x －2（x ＞1），2－2x （0＜x ＜1）. 24.解：(1)400≤x ＜600，少付200元∴应付510－200＝310(元).(2)由(1)可知少付200元∴函数关系式为：p ＝200x. ∵k ＝200，由反比例函数图象的性质可知p 随x 的增大而减小.(3)购x 元(200≤x ＜400)在甲商场的优惠金额是100元，乙商场的优惠金额是x －0.6x ＝0.4x. 当0.4x ＜100，即200≤x ＜250时，选甲商场优惠；当0.4x ＝100，即x ＝250时，选甲乙商场一样优惠；当0.4x ＞100，即250＜x ＜400时，选乙商场优惠.25.解：(1)作CN ⊥x 轴于点N∵A(﹣2，0)B(0，1)∴OB ＝1，AO ＝2在Rt △CAN 和Rt △AOB ∵∴Rt △CAN ≌Rt △AOB(AAS)∴AN ＝BO ＝1，CN ＝AO ＝2，NO ＝NA ＋AO ＝3又∵点C 在第二象限∴C(﹣3，2)；(2)设△ABC 沿x 轴的正方向平移c 个单位，则C ′(﹣3＋c ，2)，则B ′(c ，1设这个反比例函数的解析式为：y 1＝k x 又点C ′和B ′在该比例函数图象上，把点C ′和B ′的坐标分别代入y 1＝k x得﹣6＋2c ＝c解得c ＝6，即反比例函数解析式为y 1＝6x此时C ′(3，2)，B ′(6，1)，设直线B ′C ′的解析式y 2＝mx ＋n∵，∴∴直线C ′B ′的解析式为y 2＝﹣13x ＋3；(3)由图象可知反比例函数y 1和此时的直线B ′C ′的交点为C ′(3，2)，B ′(6，1) ∴若y 1＜y 2时，则3＜x ＜6.。

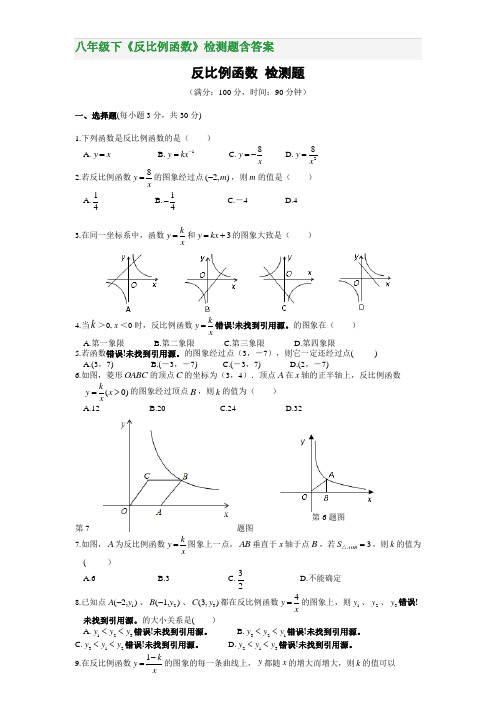
八年级下《反比例函数》检测题含答案反比例函数 检测题（满分：100分，时间：90分钟）一、选择题(每小题3分，共30分) 1.下列函数是反比例函数的是（ ）A.y x =B.1y kx -=C.8y x =-D.28y x= 2.若反比例函数8y x=的图象经过点(2,)m -，则m 的值是（ ） A.14 B.14- C.－4 D.4 3.在同一坐标系中，函数ky x=和3y kx =+的图象大致是（ ）4.当k ＞0,x ＜0时，反比例函数ky x=错误！未找到引用源。

的图象在（ ） A.第一象限 B.第二象限 C.第三象限 D.第四象限5.若函数错误！未找到引用源。

的图象经过点（3，－7），则它一定还经过点( ) A.(3，7) B.(－3，－7) C.(－3，7) D.(2，－7)6.如图，菱形OABC 的顶点C 的坐标为（3，4）．顶点A 在x 轴的正半轴上，反比例函数(0)ky x x=>的图象经过顶点B ，则k 的值为（ ）A.12B.20C.24D.32第6题图第7题图7.如图，A 为反比例函数ky x=图象上一点，AB 垂直于x 轴于点B ，若3AOB S =△，则k 的值为( ）A.6B.3C.23D.不能确定 8.已知点1(2,)A y -、2(1,)B y -、3(3,)C y 都在反比例函数4y x=的图象上，则1y 、2y 、3y 错误！未找到引用源。

的大小关系是( ）A.123y y y <<错误！未找到引用源。

B.321y y y <<错误！未找到引用源。

C.312y y y <<错误！未找到引用源。

D.213y y y <<错误！未找到引用源。

9.在反比例函数1ky x-=的图象的每一条曲线上，y 都随x 的增大而增大，则k 的值可以第19题图是（ ）A.－1B.0C.1D.2 10.已知1(1,)A y -，2(2,)B y 两点在双曲线32my x+=上，且12y y >，则m 的取值范围是（ ） A.0m < B.0m > C.32m >- D.32m <-二、填空题（每小题3分，共24分）11.已知y 错误！未找到引用源。

（新课标）苏科版八年级下册第11章反比例函数测试题（时间：90分钟满分：120分）（班级：姓名：得分：）一、选择题（第小题3分，共30分）1.已知直线y=ax（a≠0）与双曲线的一个交点坐标为（2，6），则它们的另一个交点坐标是（）A．（﹣2，﹣6）B．（﹣6，﹣2）C．（﹣2，6）D．（6，2）2. 近视眼镜的度数y（度）与镜片焦距x（m）成反比例，已知400度近视眼镜镜片的焦距为0.25 m，则y与x的函数表达式为（）A.400yx=B.14yx=C.100yx=D.1400yx=3.如图所示为反比例函数1yx=在第一象限的图像，点A为此图像上的一动点.过点A分别作AB x⊥轴和AC┴y轴，垂足分别为B,C.则四边形OBAC的面积为（）A.1B.3C.2D.44. 在反比例函数(0)ky kx=<的图像上有两点（-1，y1），（41-，y2），则y1-y2的值是（）第3题图A. 正数B.非正数C.负数D.不能确定第8题图 ADC B yxO 2y x= 3y x =-5. 已知直线y=kx （k ＞0）与双曲线y=3x 交于A （x 1,y 1）,B(x 2,y 2)两点，则x 1y 2-x 2y 1的值为（ ）A.-6 B ．-9 C ．0 D ．96. 在平面直角坐标系xOy 中，如果有点P （-2，1）与点Q （2，-1），那么下列描述：①点P 与点Q 关于x 轴对称；②点P 与点Q 关于y 轴对称；③点P 与点Q 关于原点对称；④点P 与点Q 都在y=x 2-的图像上.其中正确的是（ ）A ．①②B ．②③C ．①④D ．③④ 7.如图，A ，B 是函数2y x =的图像上关于原点对称的任意两点，BC ∥x轴，AC ∥y 轴，若△ABC 的面积记为S ，则（ ）A ．S=2B ．2＜S ＜4C ．S=4D ．S ＞4第7题图8. 如图，点A 是反比例函数y=2x (x ＞0)的图像上任意一点，AB ∥x轴交反比例函数y=－3x 的图像于点B ，以AB 为边作□ABCD ，其中C ，D 在x 轴上，则S □ABCD 为( )A．2B ．3C ．4D ．54y x ＝的图像，下列说法正确的是（ ）9. 关于反比例函数A ．必经过点（1，1）B ．两个分支分布在第二、四象限C ．两个分支关于x 轴成轴对称D ．两个分支关于原点成中心对称10.平面直角坐标系中，已知点O(0，0)，A(0，2)，B(1，0)，点P 是反比xyPQO例函数1y x =-图像上的一个动点，过点P 作PQ ⊥x 轴，垂足为点Q.若以点O ，P ，Q 为顶点的三角形与∆OAB 相似，则相应的点P 共有（ ）A ．4个B ．3个C ．2个D ．1个 第10题图二、填空题（第小题4分，共32分） 11 已知函数216(5042016)a y a x -=-，当a =_____时，它的图像是双曲线.12下列函数：①y=2x ﹣1；②20182015y x =-；③y=x 2+8x ﹣2066；④22015y x =；⑤12016y x=；⑥y=.其中是反比例函数的有 （填“序号”）.13. 若点Ｐ（a,2)在一次函数y=2x+4的图像上，它关于y 轴的对称点在反比例函数x ky =的图像上，则反比例函数的表达式为 .14.反比例函数)0(≠=k x ky 的图像在二、四象限，图像上有一点A ，过点A作AB ⊥x 轴于点B ，△AOB 的面积为2，则该双曲线的表达式为 . y 1=ax+b （a ≠0）与反15 .如图，一次函数比例函数y 2=()0≠k xk的图像交于A （1,4）,B （4,1）两点，若y 1＞y 2，则x 的取值范围是第15题图 第16题图 第17题图第18题图16. 如图，点A 是反比例函数6y x =-（x < 0）的图像上的一点，过点A 作平行四边形ABCD ，使点B,C 在x 轴上，点D 在y 轴上，则平行四边形ABCD 的面积为 17. 如图，点A 在双曲线y=x 6上，过A 作AC ⊥x 轴，垂足为C ，OA 的垂直平分线交OC 于点B ，当OA ＝4时，则△ABC 的周长为 . 18.如图，双曲线()ky k x =>0与⊙O在第一象限内交于P,Q 两点，分别过P,Q两点向x 轴和y 轴作垂线.已知点P 的坐标为（1，3）则图中阴影部分的面积为 . 三 解答题（共58分）19.（10分）已知y=2y 1-3y 2，y 1与x 成正比例，y 2与x 成反比例，当x=1时，y=1，当x=2时，y=5.（1）请你写出y 与x 之间的函数表达式； （2）当x=-1时，求y 的值.20.（10分）如图，一次函数y=kx+b 的图像与坐标轴分别交于A ，B 两点，与反比例函数my x =的图像在第二象限的交点为C ，CD ⊥x 轴，垂足为D ，若OB=2，OD=4，△AOB 的面积为1，（1）求一次函数与反比例函数的表达式； （2）直接写出当x<0时0m kx b x +->的x 的取值范围.21.（12分）已知反比例函数x k y 1-=图像的两个分支分别位于第一、三象限．y xABO第22题图（1）求k 的取值范围；（2）若一次函数y=2x+k 的图像与该反比例函数的图像有一个交点的纵坐标是4． ①求当x=-6时反比例函数y 的值；当210<<x 时，求一次函数y 的取值范围．②分）如图，一次函数b kx y +=1的图像与反比例函数)0(2>=x x my22.（12的图像交于A （1，6），B （a ，2）两点． （1）求一次函数与反比例函数的表达式； （2）直接写出1y ≥2y 时x 的取值范围．23.（14分）据媒体报道，近期“手足口病”可能进入发病高峰期，某校根据《学校卫生工作条例》，为预防“手足口病”，对教室进行“薰药消毒”.已知药物在燃烧及释放过程中，室内空气中每立方米含药量y （毫克）与燃烧时间x （分钟）之间的关系如图所示（即图中线段OA 和双曲线在A 点及其右侧的部分）.根据图像所示信息，解答下列问题：（1）写出药物燃烧及释放过程中，y 与x 之间的函数解析式及自变量的取值范围.（2）据测定，当空气中每立方米的含药量低于2毫克时，对人体无毒害作用，那么从消毒开始后，哪一时间段内师生不能进入教室？参考答案一、1.A 2..C 3.A 4.C 5.C 6.D 7.C 8. D 9.D 10.A 二、11. -4 12.. ② 13.x y 2=14. y=x 4-. 15. x ＜0或1＜x＜4． 16. 6 17. 27 18. 4三、19.解：（1）由题意可设11y k x =，22k y x=，则2132k y k x x=-.∵当x=1时，y=1，当x=2时，y=5，∴12212313452k k k k -=⎧⎪⎨-=⎪⎩解得123223k k ⎧=⎪⎪⎨⎪=⎪⎩∴23y x x =-. （2）当x=-1时，2233(1)1(1)y x x =-=⨯--=--.20.解：（1）∵OB=2，△AOB 的面积为1，∴B （-2，0），OA=1，∴A （0，-1）.可得11,2201b k k b b ⎧=-=-⎧⎪∴⎨⎨-+=⎩⎪=-⎩∴一次函数的表达式为112y x =--.∵OD=4,OD ⊥x 轴，∴C （-4，y ）.将x= - 4代入112y x =--，得y=1, ∴C(-4,1),∴14m =-,∴m= - 4, ∴反比例函数的表达式为4y x =-.(2) x<-4.21. 解：（1）∵反比例函数x k y 1-=图像的两个分支分别位于第一、三象限，∴01>-k ，∴1>k .（2）①设交点坐标为（a ，4），代入两个函数表达式，得⎪⎩⎪⎨⎧-=+=a kk a 1424 解得⎪⎩⎪⎨⎧==321k a ∴反比例函数的表达式为x y 2=.当x=-6时反比例函数y 的值为3162-=-=y .②由①可知，两图像交点坐标为（21，4），所以一次函数的表达式是y=2x+3，它的图像与y 轴交点坐标是（0，3）. 由图像可知，当210<<x 时，y 的取值范围是43<<y .22.解：（1）∵点A （1，6），B （a ，2）在x my =2的图像上，∴61=m，6=m ． 2=a m ，326==a ．∵点A （1，6），B （3，2）在函数y 1=kx+b 的图像上，∴⎩⎨⎧=+=+.23,6b k b k 解得⎩⎨⎧=-=.8,2b k∴一次函数的表达式为y 1=-2x+8，反比例函数的表达式为x y 62=．（2）1≤x ≤3．23. 解：（1）设反比例函数的解析式为y=x k，将（25，6）代入解析式，得k=25×6=150，则反比例函数的解析式为y=x 150.将y=10代入y=x 150，得x=15，故A （15，10）.所以反比例函数自变量的取值范围为x ≥15. 设正比例函数的解析式为y=nx ，将A （15，10）代入，得n=1510=32，则正比例函数的解析式为y=32x （0≤x ≤15）．（2）由32x=2，解得x=3；由x 150=2，解得x=75.所以从消毒开始后，从第3分钟开始直至第75分钟内，师生不能进入教室．。

八年级数学下册新版苏科版：第11章达标检测卷一、选择题(每题3分，共24分)1．下列关系式中，y 是x 的反比例函数的是( )A ．y ＝5xB ．y x＝3C ．y ＝1xD ．y ＝x 2－32．计划修建铁路l km ，铺轨天数为t ，每天铺轨量为s km ，则下列三个结论：①当l 一定时，t 是s 的反比例函数；②当t 一定时，l 是s 的反比例函数；③当s 一定时，l 是t 的反比例函数．其中正确的是( ) A ．①B ．②C ．③D ．①②③3．下列关于反比例函数y ＝3x的说法中，错误的是( )A ．当x ＜0时，y 随x 的增大而减小B ．双曲线在第一、三象限C ．当x ＞0时，y 随x 的增大而增大D ．当x ＞0时，函数值y ＞04．若点A (－1，y 1)，点B (1，y 2)，点C (2，y 3)是y ＝2x图像上的三个点，则y 1，y 2，y 3之间的大小关系正确的是( ) A ．y 1＞y 2＞y 3 B ．y 1＜y 2＜y 3 C ．y 3＞y 1＞y 2D ．y 1＜y 3＜y 25．某密闭容器内装有一定质量的某种气体，当改变容积V 时，气体的密度ρ是容积V 的反比例函数，当容积为5 m 3时，密度是1.4 kg/m 3，则ρ与V 之间的函数表达式为( ) A ．ρ＝V7B ．ρ＝7VC ．ρ＝7VD ．ρ＝17V6．当k ＞0时，函数y ＝k x与y ＝－kx 在同一平面直角坐标系内的大致图像是( )7．如图，直线y 1＝kx ＋1与双曲线y 2＝2x在第一象限内交于点P (1，t )，与x 轴、y 轴分别交于A ，B 两点，则下列结论错误的是( ) A ．t ＝2B ．△AOB 是等腰直角三角形C ．k ＝1D ．当x ＞1时，y 2＞y 18．如图，平行四边形OABC 的顶点A 在x 轴的正半轴上，点D (3，2)在对角线OB 上，反比例函数y ＝k x (k ＞0，x ＞0)的图像经过C 、D 两点．已知平行四边形OABC 的面积是152，则点B 的坐标为( ) A ．(4，83)B ．(92，3)C ．(5，103)D ．(245，165)二、填空题(每题2分，共20分)9．若反比例函数y ＝1－3kx的图像在第一、三象限，则 k 的取值范围是________．10．已知点(2，－2)在反比例函数y ＝kx的图像上，则这个反比例函数的表达式是____________．11．若正比例函数y ＝2x 的图像与某反比例函数的图像有一个交点的纵坐标是2，则该反比例函数的表达式为____________．12．在对物体做功一定的情况下，力F (N)与此物体在力的方向上移动的距离s (m)成反比例函数关系，其图像如图所示，点P (4，3)在图像上，则当力达到10N 时，物体在力的方向上移动的距离是________m.13．若点A (－3，y 1)，B (－2，y 2)，C (1，y 3)都在反比例函数y ＝－12x的图像上，则y 1，y 2，y 3的大小关系是______________．14．如图，函数y ＝kx ＋b (k ≠0)与y ＝m x(m ≠0)的图像相交于A (－2，3)，B (1，－6)两点，则不等式kx ＋b ＞m x的解集为____________．15．一次函数y ＝ax ＋b (a ≠0)的图像与反比例函数y ＝k x(k ≠0)的图像的两个交点分别是A (－1，－4)，B (2，m )，则a ＋2b ＝________．16．对于函数y ＝2x，当y ＜1时，x 的取值范围是________．17．在平面直角坐标系中，点A (－2，1)，B (3，2)，C (－6，m )分别在三个不同的象限．若反比例函数y ＝k x(k ≠0)的图像经过其中两点，则m 的值为________．18．点P ，Q ，R 在反比例函数y ＝k x(常数k ＞0，x ＞0)图像上的位置如图所示，分别过这三个点作x 轴、y 轴的平行线．图中所构成的阴影部分面积从左到右依次为S 1，S 2，S 3.若OE ＝ED ＝DC ，S 1＋S 3＝27，则S 2的值为________．三、解答题(19～21题每题6分，22、23题每题7分，24～26题每题8分，共56分) 19．已知反比例函数y ＝－32x. (1)写出这个函数的比例系数； (2)求当x ＝－10时函数y 的值； (3)求当y ＝6时自变量x 的值20．如图，在平面直角坐标系中，一次函数y ＝43x －2的图像与y 轴相交于点A ，与反比例函数y ＝k x在第一象限内的图像相交于点B (m ，2)，过点B 作BC ⊥y 轴于点C . (1)求反比例函数的表达式； (2)求△ABC 的面积．21．在面积为定值的一组矩形中，当矩形的一边长为7.5 cm 时，相邻的另一边长为8 cm.(1)设矩形相邻的两边长分别为x cm ，y cm ，求y 关于x 的函数表达式．这个函数是反比例函数吗？如果是，指出比例系数．(2)若其中一个矩形的一边长为5 cm ，求相邻的另一边长．22．如图，平行于y 轴的直尺(部分)与反比例函数y ＝m x(x ＞0)的图像交于A 、C 两点，与x轴交于B 、D 两点，连接AC ，若点A 、B 对应直尺上的刻度分别为5、2，直尺的宽度BD ＝2，OB ＝2.设直线AC 的表达式为y ＝kx ＋b . (1)请结合图像填空：①点A 的坐标是__________；②不等式kx ＋b ＞m x的解集是__________． (2)求直线AC 的表达式．23．如图，▱OABC 的边OA 在x 轴的正半轴上，OA ＝5，反比例函数y ＝m x(x ＞0)的图像经过点C (1，4)．(1)求反比例函数的表达式和点B 的坐标；(2)过AB 的中点D 作DP ∥x 轴交反比例函数图像于点P ，连接CP ，OP .求△COP 的面积．24．某气象研究中心观测到一场沙尘暴从发生到减弱的全过程．开始一段时间风速平均每小时增加2千米，4小时后，沙尘暴经过开阔荒漠地，风速变为平均每小时增加4千米，然后风速不变，当沙尘暴遇到绿色植被区时，风速y (千米/时)与时间x (小时)成反比例函数关系缓慢减弱，其图像如图所示．(1)这场沙尘暴的最高风速是多少千米/时，最高风速维持了几小时？ (2)当x ≥20时，求出风速y (千米/时)与时间x (小时)的函数表达式；(3)在这场沙尘暴形成的过程中，风速不超过10千米/时的时刻称为“安全时刻”，其余时刻为“危险时刻”，那么在这场沙尘暴中，“危险时刻”共有几小时？25．在函数的学习中，我们经历了“确定函数表达式——画函数图像——利用函数图像研究函数性质——利用图像解决问题”的学习过程．我们可以借鉴这种方法探究函数y ＝4x －1的性质． (1)补充下表，并在如图所示的坐标系中画出函数的图像．x … －3 －1 0 2 3 5 … y…－1－2－441…(2)观察图像，写出该函数图像的增减性特征：______________________． (3)函数y ＝4x －1的图像是由函数y ＝4x的图像如何平移得到的？并求其对称中心的坐标．(4)根据上述经验，想一想函数y ＝4x －1＋2的图像的大致位置，结合图像直接写出y ≥3时，x 的取值范围．26．如图，四边形AOBC 是矩形，反比例函数y ＝k x(k ＞0)在第一象限内的图像与矩形AOBC的边AC 、BC 分别交于点M 、N (点M 、点N 不与点C 重合)． (1)S △AOMS △BON＝__________； (2)若BN ＝14BC ，且四边形MONC 的面积为9，求反比例函数的表达式；(3)判断AM AC 与BNBC的关系，并说明理由．答案一、1．C 2．A 3．C 4．D 5．C 6．B 7．D8．B 点拨：∵反比例函数y ＝k x (k ＞0，x ＞0)的图像经过点D (3，2)，∴2＝k3，∴k ＝6，∴y ＝6x.设直线OB 的表达式为y ＝mx ， 则2＝3m ，∴m ＝23，∴直线OB 的表达式为y ＝23x ，∵反比例函数y ＝6x的图像经过点C ，∴设C (a ，6a)，其中a ＞0.∵四边形OABC 是平行四边形， ∴BC ∥OA ，S 平行四边形OABC ＝2S △OBC ， ∴点B 的纵坐标为6a，∵直线OB 的表达式为y ＝23x ，∴B (9a ，6a )，∴BC ＝9a－a ，∴S △OBC ＝12×6a ×(9a －a )，∴2×12×6a ×(9a －a )＝152，解得a ＝2或a ＝－2(舍去)， ∴B (92，3)，故选B.二、9．k ＜13 10．y ＝－4x 11．y ＝2x12．1.2 13．y 3＜y 1＜y 2 14．x ＜－2或0＜x ＜1 15．－2 16．x ＞2或x ＜017．－1 点拨：∵点A (－2，1)，B (3，2)，C (－6，m )分别在三个不同的象限，∴点C (－6，m )一定在第三象限，∴反比例函数y ＝kx(k ≠0)的图像经过B ，C 两点， ∴3×2＝－6m ， ∴m ＝－1.18．275点拨：设CD ＝DE ＝OE ＝a ，则P (k 3a ，3a )，Q (k 2a ，2a )，R (ka ，a )，∴CP ＝k 3a ，DQ ＝k 2a ，ER ＝ka，∴OG ＝AG ，OF ＝2FG ，OF ＝23GA ，∴S 1＝23S 3＝2S 2，又∵S 1＋S 3＝27，∴S 3＝815，S 1＝545，∴S 2＝275.三、19．解：(1)比例系数为－32.(2)当x ＝－10时，y ＝－32×（－10）＝320.(3)当y ＝6时，－32x ＝6，解得x ＝－14.20．解：(1)∵B 点在一次函数图像上，∴43m －2＝2， ∴m ＝3， ∴B (3，2)， ∴k ＝3×2＝6，∴反比例函数的表达式为y ＝6x.(2)∵BC ⊥y 轴，B (3，2)， ∴C (0，2)，BC ＝3.令x ＝0，则y ＝43x －2＝－2，∴A (0，－2)，∴AC ＝4， ∴S △ABC ＝12AC ·BC ＝6.21．解：(1)设y 关于x 的函数表达式为y ＝k x.不妨令x ＝7.5，则y ＝8. 将x ＝7.5，y ＝8代入y ＝k x， 得k ＝7.5×8＝60，∴y 关于x 的函数表达式是y ＝60x(x ﹥0)，这个函数是反比例函数，比例系数为60.(2)当x ＝5时，y ＝60x＝12，∴相邻的另一边长为12cm.22．解：(1)①(2，3) ② 2＜x ＜4(2)∵A 在反比例函数y ＝m x图像上， ∴m ＝2×3＝6，∴反比例函数的表达式为y ＝6x.∵BD ＝2，OB ＝2，∴OD ＝4.∴C 点的横坐标为4.将x ＝4代入y ＝6x ，得y ＝32，∴C (4，32)．将A 、C 的坐标分别代入y ＝kx ＋b ，得⎩⎪⎨⎪⎧3＝2k ＋b ，32＝4k ＋b ，解得⎩⎪⎨⎪⎧k ＝－34，b ＝92，∴直线AC 的表达式为y ＝－34x ＋92.23．解：(1)∵反比例函数y ＝m x(x ＞0)的图像经过点C (1，4)．∴m ＝1×4＝4，∴反比例函数的表达式为y ＝4x.∵四边形OABC 为平行四边形，∴BC ＝OA ＝5，BC ∥OA .∵C (1，4)， ∴点B (6，4)． (2)延长DP 交OC 于点E .∵点D 为线段BA 的中点，A (5，0)，B (6，4)， ∴点D (112，2)．令y ＝4x 中的y ＝2，则x ＝2，∴点P (2，2)， ∴PD ＝112－2＝72，∴EP ＝ED －PD ＝5－72＝32，∴S △COP ＝12EP ·y C ＝12×32×4＝3.24．解：(1)这场沙尘暴的最高风速是2×4＋4×(10－4)＝32(千米/时)，最高风速维持时间为20－10＝10(小时)．(2)设x ≥20时，y ＝k x ，将(20，32)代入，得32＝k20，解得k ＝640.所以当x ≥20时，风速y (千米/时)与时间x (小时)之间的函数表达式为y ＝640x.(3)因为4小时时的风速为2×4＝8(千米/时)，4小时后，风速变为平均每小时增加4千米，所以4.5小时时的风速为10千米/时．将y ＝10代入y ＝640x ，得10＝640x，解得x ＝64.因为64－4.5＝59.5(小时)，所以“危险时刻”共有59.5小时．25．解：(1)2 图像如图所示．(2)当x ＞1时，y 随x 的增大而减小；当x ＜1时，y 随x 的增大而减小 (3)函数y ＝4x －1的图像是由函数y ＝4x的图像向右平移1个单位得到的．对称中心的坐标为(1，0)． (4)1＜x ≤5. 26．解：(1)1(2)连接OC ，∵四边形AOBC 是矩形， ∴S △AOC ＝S △BOC ，又∵S △AOM ＝S △BON ＝12|k |＝12k ，∴S △ONC ＝S △OMC ＝12S 四边形MONC ＝92，∵BN ＝14BC ，∴S △BON ＝13S △ONC ，∴12k ＝13×92， 解得k ＝3，∴反比例函数的表达式为y ＝3x.11 (3)AM AC ＝BN BC.理由：设AC ＝a ，BC ＝b ， 则M (k b ，b )，N (a ，k a )，∴AM AC ＝k ab ，BN BC ＝k ab ， ∴AM AC ＝BN BC.。

（新课标）苏科版八年级下册反比例函数练习卷一、选择题1．下列函数中，y 是x 的一次函数的是（ ） ①6y x =-；②2y x=；③8x y =；④7y x =-．A ．①②③B ．①③④C ．①②③④D ．②③④2．一次函数y 1=kx+b 与y 2=x+a 的图象如图，则下列结论：①k ＜0；②a ＞0：③b ＞0；④x ＜2时，kx+b ＜x+a 中，正确的个数是（ ）A ．1 B.2 C.3 D.43．如图，一次函数y=ax+b 与x 轴，y 轴交于A ，B 两点，与反比例函数y=相交于C ，D 两点，分别过C ，D 两点作y 轴，x 轴的垂线，垂足为E ，F ，连接CF ，DE ，EF ．有下列四个结论：①△CEF 与△DEF 的面积相等；②△AOB ∽△FOE ；③△DCE ≌△CDF ；④AC=BD ．其中正确的结论个数是（ ） A ．1 B ．2 C ．3 D ．44．如图，直线l 1：x=1，l 2：x=2，l 3：x=3，l 4：x=4，…，与函数y=（x ＞0）的图象分别交于点A 1、A 2、A 3、A 4、…；与函数y=的图象分别交于点B 1、B 2、B 3、B 4、…．如果四边形A 1A 2B 2B 1的面积记为S 1，四边形A 2A 3B 3B 2的面积记为S 2，四边形A 3A 4B 4B 3的面积记为S 3，…，以此类推．则S 10的值是（ ） A ． B ．C ．D ．5．下图中表示一次函数n mx y +=与正比例函数mnx y =（m ，n 是常数，且mn ≠0）图像的是（ ）．6．如图6，有一种动画程序，屏幕上正方形ABCD 是黑色区域（含正方形边界），其中(11)(21)(22)(12)A B C D ，，，，，，，，用信号枪沿直线2y x b =-+发射信号，当信号遇到黑色区域时，区域便由黑变白，则能够使黑色区域变白的b的取值范围为．A ． 3<b<6B ．2<b<6C ．36b ≤≤D ．2<b<5 二、填空题7．如图，已知函数y ＝21-x+b 和y ＝21x 的图象交于点P ()2,4--，, 则根据图象可得，关于x y b x y 2121=+-=的二元一次方程组的解是____________．8．如图，菱形OABC 的顶点O 是坐标原点，顶点AxyO01 221 图6在x 轴的正半轴上，顶点B 、C 均在第一象限，OA=2，∠AOC=60°．点D 在边AB 上，将四边形OABC 沿直线0D 翻折，使点B 和点C 分别落在这个坐标平面的点B ′和C ′处，且∠C ′DB ′=60°．若某反比例函数的图象经过点B ′，则这个反比例函数的解析式为 ．9．如图,在平面直角坐标系中,直线L 经过原点,且与y 轴正半轴所夹的锐角为600,过点A （0,1）作y 轴的垂线交直线L 于点B,过点B 作直线L 的垂线交y 轴于点A 1,以A 1B 、BA 为邻边作□ABA 1C 1；过点A 1作y 轴的垂线交直线L 于点B 1,过点B 1作直线L 的垂线交y 轴于点A 2,以A 2B 1、B 1A 1为邻边做□A 1B 1A 2C 2,…；按此作法继续下去,则点Cn 的坐标是_______．10．如图放置的△OAB 1，△B 1A 1B 2，△B 2A 2B 3，…都是边长为2的等边三角形，边AO 在y 轴上，点B 1，B 2，B 3，…都在直线y=33x 上，则A 2015的坐标是 ．11．两个反比例函数xy 3=，xy 6=在第一象限内的图像如图所示，点1P ，2P ，3P ，…，2013P 在函数xy 6=的图像上，它们的横坐标分别是1x ，2x ，3x ，…，2013x ，纵坐标分别是1，3，5，…，共2013个连续奇数，过点1P ，2P ，3P ，…，2013P 分别作y 轴的平行线，与函数xy 3=的图像交点依次是1Q （1x ，1y ），2Q （2x ，2y ），3Q （3x ，3y ），…，2013Q （2013x ，2013y ），则 2013y . 12．如图，在反比例函数位于第一象限内的图象上取一点P 1，连结OP 1，作P 1A 1^x 轴，垂足为A 1，在OA 1的延长线上截取A 1 B 1= OA 1，过B 1作OP 1的平行线，交反比例函数的图象于P 2，过P 2作P 2A 2^x 轴，垂足为A 2，在OA 2的延长线上截取A 2 B 2= B 1A 2，连结P 1 B 1，P 2 B 2，则的值是 ． 三、解答题13．如图，在平面直角坐标系中，O 是坐标原点，点A 坐标为（2，0），点B 坐标为（0，b ）（b ＞0），点P 是直线AB 上位于第二象限内的一个动点，过点P 作PC 垂直于x 轴于点C ，记点P 关于y 轴的对称点为Q ，设点P 的横坐标为a ．（1）当b=3时：①求直线AB 相应的函数表达式；②当S △QOA =4时，求点P 的坐标；（2）是否同时存在a 、b ，使得△QAC 是等腰直角三角形？若存在，求出所有满足条件的a 、b 的值；若不存在，请说明理由．14．如图，在矩形OABC中，OA=3，OC=5，分别以OA、OC 所在直线为x轴、y轴，建立平面直角坐标系，D是边CB上的一个动点（不与C、B重合），反比例函数k=yx（0k>）的图象经过点D且与边BA交于点E，连接DE．（1）连接OE，若△EOA的面积为2，则k= ；（2）连接CA，DE与CA是否平行？请说明理由；（3）是否存在点D，使得点B关于DE的对称点在OC上？若存在，求出点D的坐标；若不存在，请说明理由．15．如图，直线y=x+2与x轴交于点A，与y轴交于点B，动点P从点A开始沿折线AB﹣BO以1cm/s的速度运动到点O．设点P运动的时间为t（s），△PAO面积为S（cm2）．（坐标轴的单位长度为cm）（1）当点P在线段AB上运动到与点O距离最小时，求S的值；（2）在整个运动过程中，求S与t之间的函数表达式；（3）当点P运动几秒后，△PAO面积为2cm2？16．图1，梯形ABCD中，AD∥BC，AB=AD=DC=5，BC=11．一个动点P从点B出发，以每秒1个单位长度的速度沿线段BC方向运动，过点P作PQ⊥BC，交折线段BA-AD于点Q，以PQ为边向右作正方形PQMN，点N在射线BC上，当Q点到达D 点时，运动结束．设点P的运动时间为t秒（t＞0）．（1）当正方形PQMN的边MN恰好经过点D时，求运动时间t的值；（2）在整个运动过程中，设正方形PQMN与△BCD的重合部分面积为S，请直接写出S与t之间的函数关系式和相应的自变量t的取值范围；（3）如图2，当点Q在线段AD上运动时，线段PQ与对角线BD交于点E，将△DEQ沿BD翻折，得到△DEF，连接PF．是否存在这样的t，使△PEF是等腰三角形？若存在，求出对应的t的值；若不存在，请说明理由．参考答案1．B ． 2．B ． 3．C4．D 5．C 6．C 7．24-=-=y x 8．y=﹣．9．（-4n-13,4n ）． 10．（20153，2017）．11．5.2012 12．13．（1）①y=－1．5x+3 ②P （32－ ，4）（2）⎩⎨⎧=-=22b a 或⎪⎩⎪⎨⎧=-=132b a14．（1）4；（2）DE ∥AC ，理由见试题解析；（3）D （0.96，5）． 15．(1)32;(2) S=043()423(44223)t t t t ≤≤+≤+⎧⎪⎨⎪⎩﹣＜；(3) 433秒或2+23秒16．（1）t=4；（2）S=22210()9()1128203243447)?1222(12734)8(t t t t t t t t t ≤+≤≤-+≤⎧⎪⎪⎪⎪⎨-+-⎪⎪⎪⎪⎩＜＜＜＜；（3）存在，当t=4、4811或4011时，△PEF 是等腰三角形．。

浙教版八年级下册数学第六章反比例函数含答案一、单选题(共15题，共计45分)1、以正方形ABCD两条对角线的交点O为坐标原点，建立如图所示的平面直角坐标系，双曲线y=经过点D，则正方形ABCD的面积是（）A.10B.11C.12D.132、如图，在平面直角坐标系中，△OAB的顶点A在x轴正半轴上，OC是△OAB 的中线，点B，C在反比例函数的图象上，则△OAB的面积等于（）A.2B.3C.4D.63、反比例函数y=（k≠0）的图象经过点（-2，3），则该反比例函数图象在（）A.第一、三象限B.第二、四象限C.第二、三象限D.第一、二象限4、在闭合电路中，电流I，电压U，电阻R之间的关系为：I＝．电压U（伏特）一定时，电流I（安培）关于电阻R（欧姆）的函数关系的大致图象是（）A. B. C. D.5、若是反比例函数，则a的取值为（）A.1B.-1C.±1D.任意实数6、下列说法正确的是A.两条对角线互相垂直且相等的四边形是正方形B.任意两个等腰三角形相似 C.一元二次方程，无论a取何值，一定有两个不相等的实数根 D.关于反比例函数，y的值随x值的增大而减小7、如图，双曲线与直线交于点M，N，并且点M坐标为(1，3)点N坐标为(-3，-1)，根据图象信息可得关于x的不等式的解为( )A. B. C. D.8、某气球内充满了一定质量的气体，在温度不变的条件下，气球内气体的压强p(Pa)是气球体积V(m3)的反比例函数，且当V=1.5m3时，p=16000Pa，当气球内的气压大于40000Pa时，气球将爆炸，为确保气球不爆炸，气球的体积应( )A.不小于0.5m 3B.不大于0.5m 3C.不小于0.6m 3D.不大于0.6m 39、若点M（x，y）满足，则点M所在象限是（）A.第一、三象限B.第二、四象限C.第一、二象限D.不能确定10、反比例函数y=的图象上有两个点为（1，y1），（2，y2），则y1与y2的关系是( )A.y1＞y2B.y1＜y2C.y1=y2D.无法判断11、一次函数与反比例函数( )的图象的形状大致是（）A. B. C.D.12、如果点（-a，-b）在反比例函数y＝的图象上，那么下列各点中，在此图象上的是（）A.(a，b)B.(b，－a)C.(－a，b)D.(－b，a)13、如图，在平面直角坐标系中，将一块含有45°的直角三角板按照如图方式摆放，顶点A、B的坐标为（1，4）、（4，1），直角顶点C的坐标为（4，4），若反比例函数的图象与直角三角板的边有交点，则k的取值范围为（）A. B. C. D.14、如图，反比例函数y=的图象经过直角三角形OAB的顶点A，D为斜边OA 的中点，则过点D的反比例函数的解析式是（）A.y=B.y=-C.y=D.y=15、若反比例函数的图象位于第二、四象限内，则m的取值范围是（）A.m＞0B.m＜0C.m＞1D.m＜1二、填空题(共10题，共计30分)16、如图，已知点A，C在反比例函数y= （a＞0）的图象上，点B，D在反比例函数y= （b＜0）的图象上，AB∥CD∥x轴，AB，CD在x轴的两侧，AB=3，CD=2，AB与CD的距离为5，则a﹣b的值是________．17、已知函数的图象经过点(1，3)，且与x轴没有交点，写出一个满足题意的函数的解析式________.18、已知，是反比例函数图象上两个点的坐标，且，请写出一个符合条件的反比例函数的解析式________．19、在平面直角坐标系中，点A的坐标为（5，0），点C的坐标为（0，4），四边形ABCO为矩形，点P为线段BC上的一动点，若△POA为等腰三角形，且点P在双曲线y= 上，则k值可以是________．20、在平面直角坐标系中，A为反比例函数y＝﹣（x＞0）图象上一点，点B的坐标为(4，0)，O为坐标原点，若的面积为6，则点A的坐标为________.21、如图，直线y=x向下平移b个单位后得直线l，l与函数y=（x＞0）相交于点A，与x轴相交于点B，则OA2﹣OB2=________ ．22、如图，过反比例函数y=图象上三点A、B、C分别作直角三角形和矩形，图中S1+S2=5，则S3=________ ．23、如图，A（4，0），B（3，3），以AO，AB为边作平行四边形OABC，则经过C点的反比例函数的解析式为________．24、若反比例函数的图象经过第一、三象限，则 k的取值范围是________.25、如果反比例函数y＝(k是常数，k≠0)的图象经过点(2，3)，那么在这个函数图象所在的每个象限内，y的值随x值的增大而________．(填“增大”或“减小”)三、解答题(共5题，共计25分)26、已知, 与成正比例, 与成反比例，且当时,; 时, .试求当时, 的值.27、水池内有水40m3，经过排水管的时间y（h）与每小时流出的水量xm3之间的关系是反比例函数吗？28、已知一个长方体的体积是100cm3，它的长是ycm，宽是10cm，高是xcm．（1）写出y与x之间的函数关系式；（2）当x=2cm时，求y的值．29、如图，一次函数y=kx+b与反比例函数的图象交于A（m，6），B（3，n）两点．（Ⅰ）求一次函数的解析式；（Ⅱ）根据图象直接写出的x的取值范围；（Ⅲ）求△AOB的面积．30、如果y是z的反比例函数，z是x的反比例函数，那么y与x具有怎样的函数关系？参考答案一、单选题(共15题，共计45分)1、C2、B3、B4、A5、A6、C7、D9、B10、A11、C12、A13、C14、C15、D二、填空题(共10题，共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题，共计25分)27、28、30、。