河北省邢台市临西实验中学2019_2020学年高一数学下学期期末考试试题含解析.doc

河北省邢台市高一下学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共27分)1. （2分）在△ABC中，∠C=90°，=（k,1）,=(2,3),则k的值是（）A . 5B . -5C .D . -2. （2分）下列命题正确的是（）A . ac＞bc⇒a＞bB . a2＞b2⇒a＞bC . ＞⇒a＜bD . ＜⇒a＜b3. （2分）已知等差数列满足，，则前n项和取最大值时，n的值为（）A . 20B . 21C . 22D . 234. （2分）在中，内角所对的边分别为。

已知，，则（）A .C .D .5. （5分）设等比数列的前项和是，若,则（）A . 2B .C .D . 36. （2分） (2016高三上·滨州期中) 设变量x，y满足约束条件，则目标函数z=2x+y的最大值为（）A . 1B . 2C . 3D . 67. （2分）将一个等腰梯形绕着它的较长的底边所在的直线旋转一周，所得的几何体包括（）A . 一个圆台、两个圆锥B . 一个圆柱、两个圆锥C . 两个圆台、一个圆柱D . 两个圆柱、一个圆台8. （2分）已知向量+=（2，﹣8），﹣=（﹣8，16），则与夹角的余弦值为（）B . -C .D .9. （2分） (2017高三上·山东开学考) 如图中的三个直角三角形是一个体积为20cm3的几何体的三视图，则该几何体外接球的面积（单位：cm2）等于（）A . 55πB . 75πC . 77πD . 65π10. （2分）已知△ABC满足=++，则△ABC是（）A . 等边三角形B . 锐角三角形C . 直角三角形D . 钝角三角形11. （2分） (2018高二上·抚顺期末) 函数（且）的图像恒过定点，若点在直线上，其中，则的最小值为（）A . 16B . 24C . 25D . 5012. （2分） (2017高三上·太原期末) 在平行四边形ABCD中，AC与BD交于点O，E是线段OD的中点，AE的延长线与CD相交于点F，则 =（）A .B .C .D .二、填空题 (共4题；共12分)13. （1分）(2018·河南模拟) 在中，，，则 ________．14. （5分） (2018高二下·温州期中) 已知正实数满足 ,则的最小值为________．15. （1分）(2017·黄陵模拟) 如图，某数学兴趣小组为了测量西安大雁塔高AB，选取与塔底B在同一水平面内的两个测点C与D．测得∠BCD=105°，∠BDC=45°，CD=26.4m，并在C点测得塔顶A的仰角为60°，则塔高AB=________m．（≈2.45，结果精确到0.01）．16. （5分）(2020·海南模拟) 若下实数，满足，则的最小值为________.三、解答题 (共6题；共60分)17. （10分）(2017高三下·静海开学考) 已知，设函数．（Ⅰ）当，求函数f（x）的值域；（Ⅱ）当时，若f（x）=8，求函数的值．18. （10分） (2018高一上·北京期中) 已知f（x）是定义在[-1，1]上的奇函数，且f（1）=1，若任意的a、b∈[-1，1]，当a+b≠0时，总有．（1）判断函数f（x）在[-1，1]上的单调性，并证明你的结论；（2）解不等式：；（3）若f（x）≤m2-2pm+1对所有的x∈[-1，1]恒成立，其中p∈[-1，1]（p是常数），试用常数p表示实数m的取值范围．19. （10分） (2016高二上·郑州期中) 已知等差数列{an}中，a1=﹣2，公差d=3；数列{bn}中，Sn为其前n 项和，满足：2nSn+1=2n（n∈N+）（Ⅰ）记An= ，求数列An的前n项和S；（Ⅱ）求证：数列{bn}是等比数列；（Ⅲ）设数列{cn}满足cn=anbn ， Tn为数列{cn}的前n项积，若数列{xn}满足x1=c2﹣c1 ，且xn=，求数列{xn}的最大值．20. （10分） (2016高二上·绍兴期中) 已知四棱锥P﹣ABCD中，底面ABCD是直角梯形，AD∥BC，AB⊥BC，AB=AD=1，BC=2，又PB⊥平面ABCD，且PB=1，点E在棱PD上，且BE⊥PD．（1）求异面直线PA与CD所成的角的大小；（2）求证：BE⊥平面PCD；（3）求二面角A﹣PD﹣B的大小．21. （10分）(2018·凯里模拟) 已知，，设函数，.（Ⅰ）求函数的单调递增区间；（Ⅱ）若的内角，，所对的边分别为，，，且，，，求的面积.22. （10分） (2019高二上·沈阳月考) 正项数列的前项和满足 .（1）求的值；（2）证明：当，且时，；（3）若对于任意的正整数，都有成立，求实数的最大值.参考答案一、单选题 (共12题；共27分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共12分)13-1、14-1、15-1、16-1、三、解答题 (共6题；共60分)17-1、18-1、18-2、18-3、19-1、20-1、20-2、20-3、21-1、22-1、22-2、22-3、。

2019-2020学年高一下学期期末数学模拟试卷一、选择题：本题共12小题，在每小题给出的四个选项中，只有一项是符合题目要求的。

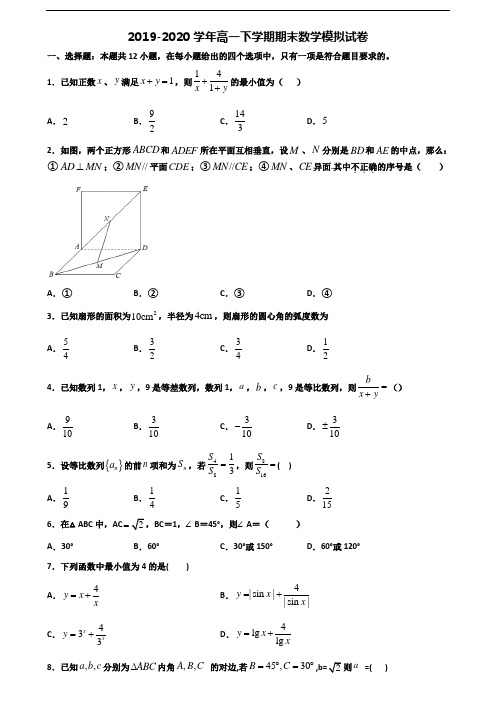
1．已知正数x、y满足1x y+=，则141x y++的最小值为（）A．2B．92C．143D．52．如图，两个正方形ABCD和ADEF所在平面互相垂直，设M、N分别是BD和AE的中点，那么：①AD MN⊥；②//MN平面CDE；③//MN CE；④MN、CE异面.其中不正确．．．的序号是（）A．①B．②C．③D．④3．已知扇形的面积为210cm，半径为4cm，则扇形的圆心角的弧度数为A．54B．32C．34D．124．已知数列1，x，y，9是等差数列，数列1，a，b，c，9是等比数列，则bx y=+（）A．910B．310C．310-D．310±5．设等比数列{}n a的前n项和为n S，若4813SS=，则816SS=( )A．19B．14C．15D．2156．在△ABC中，AC2=BC＝1，∠B＝45°，则∠A＝（）A．30°B．60°C．30°或150°D．60°或120°7．下列函数中最小值为4的是( )A．4y xx=+B．4|sin||sin|y xx=+C．433xxy=+D．4lglgy xx=+8．已知,,a b c分别为ABC∆内角,,A B C的对边,若45,30B C=︒=︒2则a=( )A ．624+ B ．622+ C ．624- D ．622- 9．下列大小关系正确的是 ( ) A. B. C.D.10．关于x 的不等式0-<bx a 的解集是(2,)+∞，则关于x 的不等式()(5)0bx a x +->的解集是（ ） A ．(,2)(5,)-∞-⋃+∞ B ．(,2)(5,)-∞⋃+∞ C ．(2,5)D ．(2,5)-11．已知函数sin()0,02y x πωϕωϕ⎛⎫=+>< ⎪⎝⎭，且此函数的图象如图所示，由点(,)P ωϕ的坐标是（ ）A ．2,2π⎛⎫⎪⎝⎭B ．2,4π⎛⎫⎪⎝⎭C ．4,2π⎛⎫⎪⎝⎭D ．4,4π⎛⎫⎪⎝⎭12．已知△ABC 的项点坐标为A （1，4），B （﹣2，0），C （3，0），则角B 的内角平分线所在直线方程为（ ） A ．x ﹣y+2＝0B ．x 2-y+2＝0C ．x 3-y+2＝0D ．x ﹣2y+2＝0二、填空题：本题共4小题 13．已知函数()sin 03y x πωω⎛⎫=+> ⎪⎝⎭的最小正周期为π，若将该函数的图像向左平移()0m m >个单位后，所得图像关于原点对称，则m 的最小值为________. 14．若关于x 的不等式220ax bx ++>的解集是11{}23x x -<<，则a b +=_________. 15．某班级有50名学生，现用系统抽样的方法从这50名学生中抽出10名学生，将这50名学生随机编号为号，并按编号顺序平均分成10组（号，号，…，号），若在第三组抽到的编号是13，则在第七组抽到的编号是______．16．已知一组数据6，7，8，8，9，10，则该组数据的方差是____. 三、解答题：解答应写出文字说明、证明过程或演算步骤。

邢台市重点名校2019-2020学年高一下学期期末考试数学试题一、选择题：本题共12小题，在每小题给出的四个选项中，只有一项是符合题目要求的。

1．若角α的终边经过点()1,2P --，则sin α=（ ）A．5-B． CD【答案】B 【解析】 【分析】根据任意角的三角函数的定义，可以直接求到本题答案. 【详解】因为点()1,2P --在角α的终边上，所以sin y rα===. 故选：B 【点睛】本题主要考查利用任意角的三角函数的定义求值.2．若直线1:2l y x a =-+与直线22:(2)2l y a x =--平行,则a =A ．1B ．1- C ．D ．±1【答案】A 【解析】由题意，直线12l l //，则22122a a ⎧-=-⎨≠-⎩，解得1a =，故选A.3．中国古代数学著作《算法统宗》中有这样一个问题：“三百七十八里关，初行健步并不难，次日脚痛减一半，六朝才得至其关，欲问每朝行里数，请公仔细算相还”.其意思为：“有一个人走378里路，第1天健步行走，从第2天起，因脚痛每天走的路程为前一天的一半，走了6天后到达目的地，可求出此人每天走多少里路.”那么此人第5天走的路程为（ ） A ．48里 B ．24里C ．12里D ．6里【答案】C 【解析】记每天走的路程里数为{a n }，由题意知{a n }是公比12的等比数列，由S 6=378，得166112112a S ⎛⎫- ⎪⎝⎭=-=378，解得：a 1=192，∴5411922a =⨯=12（里）．故选C ． 4．在ABC ∆中，角A ，B ，C 的对边分别为a ，b ，c ，且()()22222cos a c a c babc c -+-=.则B =（ ） A ．60B =︒ B ．60B =︒或120B =︒C ．30B =︒D ．90︒【答案】A 【解析】 【分析】利用余弦定理和正弦定理化简已知条件，求得cos B 的值，即而求得B 的大小. 【详解】由于()()22222cos a c a c b abc c -+-=，所以222cos 22a c b b Cac a c+-=-，由余弦定理和正弦定理得sin cos cos 2sin sin B CB A C=-，即2sin cos sin cos cos sin A B B C B C =+()sin sin B C A =+=，由于A 是三角形的内角，所以sin A 为正数，所以12cos 1,cos 2B B ==，B 为三角形的内角，所以60B =.故选：A 【点睛】本小题主要考查正弦定理和余弦定理边角互化，考查三角形的内角和定理，考查两角和的正弦公式，属于基础题.5．设函数()2,01,0x x f x x ⎧≥=⎨<⎩，则满足()()2f x f x <的x 的取值范围是（ ）A ．(),0-∞B ．()0,∞+C ．()0,1D ．()1,+∞【答案】B 【解析】 【分析】分别解0x <和0x ≥时条件对应的不等式即可. 【详解】①当0x <时，20x <，此时()()21f x f x ==，不合题意；②当0x ≥时，20≥x ，()()2f x f x <可化为222x x <即2x x <，解得0x >. 综上，()()2f x f x <的x 的取值范围是()0,∞+. 故选：B.【点睛】本题考查了分段函数不等式的解法，考查了分类讨论思想，属于基础题. 6．己知中，角所对的边分別是.若，则=( )A ．B ．1C ．2D ．【答案】B 【解析】 【分析】 由正弦定理可得． 【详解】 ∵，∴．故选B ． 【点睛】本题考查正弦定理，解题时直接应用正弦定理可解题，本题属于基础题．7．已知椭圆C ：22221(0)x y a b a b +=>>的左右焦点为F 1,F 2离心率为33，过F 2的直线l 交C 与A,B 两点，若△AF 1B 的周长为3C 的方程为( )A ．22132x y +=B ．2213x y +=C ．221128x y +=D ．221124x y +=【答案】A 【解析】 【详解】若△AF 1B 的周长为3由椭圆的定义可知443a =,3a ∴=33c e a ==,1c ∴=, 22b ∴=，所以方程为22132x y +=，故选A.考点：椭圆方程及性质8．为得到函数3sin 2y x =的图象，只需将函数3sin(23)y x =+图象上的所有点（ ）A ．向右平移3个单位长度B ．向右平移32个单位长度 C ．向左平移3个单位长度 D ．向左平移32个单位长度【答案】B 【解析】 【分析】先化简得33sin(23)3sin 22y x x ⎡⎤⎛⎫=+=+ ⎪⎢⎥⎝⎭⎣⎦，根据函数图像的变换即得解. 【详解】因为33sin(23)3sin 22y x x ⎡⎤⎛⎫=+=+⎪⎢⎥⎝⎭⎣⎦， 所以函数3sin(23)y x =+图象上的所有点向右平移32个单位长度可得到函数3sin 2y x =的图象. 故选：B 【点睛】本题主要考查三角函数图像的变换，意在考查学生对该知识的理解掌握水平和分析推理能力.9．已知函数210()210x x x f x x x ⎧++≥=⎨+<⎩，若(sin sin sin361)1f αβ++︒-=-，(cos cos cos361)3f αβ++︒+=，则cos()αβ-=（ ）A ．12B ．2C ．12-D ．2-【答案】C 【解析】 【分析】由函数()f x 的解析式，求得()11f -=-，()13f =，进而得到sin sin sin36αβ+=-︒，cos cos cos36αβ+=-︒，结合两角差的余弦公式和三角函数的基本关系式，即可求解.【详解】由题意，函数2213()010()2421021x x x x x f x x x x x ⎧⎧++≥++≥⎪==⎨⎨+<⎩⎪+<⎩，令()1f x =-，即211x +=-，即1x =-，所以()11f -=-， 令()3f x =，即213x x ++=，即1x =，所以()13f =，又因为(sin sin sin361)1f αβ++︒-=-，(cos cos cos361)3f αβ++︒+=，即(sin sin sin361)(1)f f αβ++︒-=-，(cos cos cos361)(1)f f αβ++︒+=， 所以sin sin sin3611αβ++︒-=-，cos cos cos3611αβ++︒+=， 即sin sin sin36αβ+=-︒，cos cos cos36αβ+=-︒，平方可得222sin sin 2sin sin sin 36αβαβ++=︒，222cos cos 2cos cos cos 36αβαβ++=︒， 两式相加可得22(cos cos sin sin )22cos()1αβαβαβ++=+-=， 所以cos()αβ-=12-. 故选：C. 【点睛】本题主要考查了两角和与差的余弦公式，三角函数的基本关系式的应用，以及函数的解析式的应用，其中解答中合理应用三角函数的恒等变换的公式进行运算是解答的关键，着重考查了推理与运算能力，属于中档试题.10．已知,,l m n 表示三条不同的直线，,αβ表示两个不同的平面，下列说法中正确的是（ ） A ．若//,m n n α⊂，则//m α B ．若//,m n αα⊂，则//m nC ．若,,l m l αβαβ⊥=⊥，则m β⊥D ．若,m n αα⊥⊥，则//m n【答案】D 【解析】 【分析】利用线面平行、线面垂直的判定定理与性质依次对选项进行判断，即可得到答案． 【详解】对于A ，当m α⊂时，则m 与α不平行，故A 不正确；对于B ，直线与平面平行，则直线与平面内的直线有两种关系：平行或异面，故B 不正确； 对于C ，若m β⊂，则m 与β不垂直，故C 不正确；对于D ，若两条直线垂直于同一个平面，则这两条直线平行，故D 正确； 故答案选D 【点睛】本题考查空间中直线与直线、直线与平面位置关系相关定理的应用，属于中档题． 11．平面α平面β，直线a α⊂，b β⊂ ，那么直线a 与直线b 的位置关系一定是（ ）A ．平行B ．异面C ．垂直D ．不相交【答案】D 【解析】利用空间中线线、线面、面面的位置关系得出直线a 与直线b 没有公共点. 【详解】 由题平面α平面β，直线a α⊂，b β⊂则直线a 与直线b 的位置关系平行或异面，即两直线没有公共点，不相交. 故选D. 【点睛】本题考查空间中两条直线的位置关系，属于简单题．12．已知P,A,B,C 是球O 的球面上四点，PA ⊥面ABC,0PA 2BC 6,BAC 90∠===，则该球的半径为（ ） A ．35 B ．65C ．33D ．35【答案】D 【解析】 【分析】根据PA ⊥面ABC ，0BAC 90∠=，得到三棱锥的三条侧棱两两垂直，以三条侧棱为棱长得到一个长方体，且长方体的各顶点都在该球上，长方体的对角线的长就是该球的直径，从而得到答案。

邢台市2019-2020学年高一下期末考试数学试题一、选择题：本题共12小题，在每小题给出的四个选项中，只有一项是符合题目要求的。

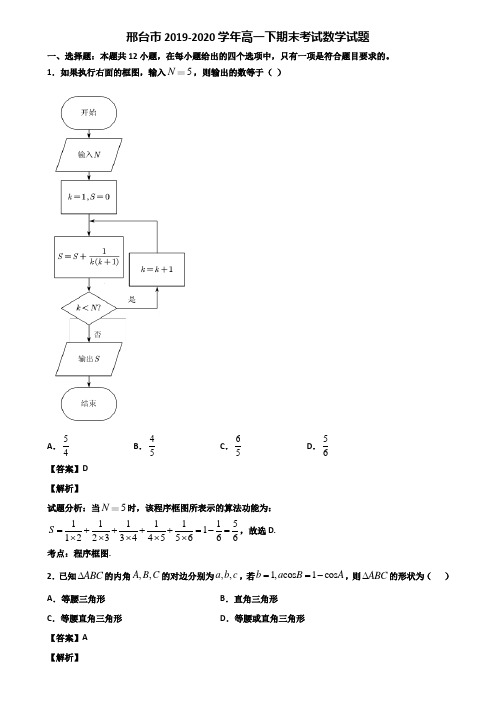
1．如果执行右面的框图，输入5N，则输出的数等于（ ）A ．54B ．45C ．65D ．56【答案】D 【解析】 试题分析：当5N时，该程序框图所表示的算法功能为：11111151122334455666S =++++=-=⨯⨯⨯⨯⨯，故选D. 考点：程序框图.2．已知ABC ∆的内角,,A B C 的对边分别为,,a b c ，若1,cos 1cos b a B A ==-，则ABC ∆的形状为（ ） A ．等腰三角形 B ．直角三角形 C ．等腰直角三角形 D ．等腰或直角三角形【答案】AABC ∆中，1,cos 1cos b a B A ==-，所以cos cos a B b b A =-.由正弦定理得：cos cos sinA B sinB sinB A =-. 所以cos ?cos ?sinA B sinB A sinB +=. 所以()sin C sinB π-=，即sinC sinB = 因为,B C 为ABC ∆的内角，所以B C = 所以ABC ∆为等腰三角形. 故选A.3．已知圆1Γ与2Γ交于两点，其中一交点的坐标为()3,4，两圆的半径之积为9，x 轴与直线()0y mx m =>都与两圆相切，则实数m =（ ） A ．158B ．74CD ．35【答案】A 【解析】 【分析】根据圆的切线性质可知连心线过原点,故设连心线y tx =,再代入()3,4,根据方程的表达式分析出12,x x 是方程()()()22234x tx tx -+-=的两根,再根据韦达定理结合两圆的半径之积为9求解即可. 【详解】因为两切线均过原点,有对称性可知连心线所在的直线经过原点,设该直线为y tx =,设两圆与x 轴的切点分别为12,x x ,则两圆方程为：()()()()()()222111222222x x y tx tx x x y tx tx ⎧-+-=⎪⎨-+-=⎪⎩,因为圆1Γ与2Γ交于两点,其中一交点的坐标为()3,4. 所以()()()22211134x tx tx -+-=①,()()()22222234x tx tx -+-=②. 又两圆半径之积为9,所以212129tx tx x x t ⋅==③联立①②可知12,x x 是方程()()()22234x tx tx -+-=的两根,化简得()268250x t x -++=,即1225x x =.代入③可得2925t =,由题意可知0t >,故35t =.因为y tx =的倾斜角是连心线所在的直线的倾斜角的两倍.故221tm t =-,故158=m .【点睛】本题主要考查了圆的方程的综合运用,需要根据题意列出对应的方程,结合韦达定理以及直线的斜率关系求解.属于难题.4．已知函数2()2cos 2f x x x =，在ABC 中，内角,,A B C 的对边分别是,,a b c ，内角A 满足()1f A =-，若a =ABC 的面积的最大值为（ ）A ．B ．2C ．4D ．【答案】B 【解析】 【分析】通过将2()2cos 2f x x x =利用合一公式变为2cos 213x π⎛⎫++ ⎪⎝⎭，代入A 求得A 角，从而利用余弦定理得到b,c,的关系，从而利用均值不等式即可得到面积最大值. 【详解】2()2cos 2f x x x ==cos 2212cos 213x x x π⎛⎫+=++ ⎪⎝⎭()2cos 211cos 2133f A A A ππ⎛⎫⎛⎫=++=-⇒+=- ⎪ ⎪⎝⎭⎝⎭，A 为三角形内角，则3A π=a =222222cos 2abc bc A b c bc bc bc bc =+-=+-≥-=，当且仅当b c =时取等号11sin 62222ABCSbc A =≤⨯⨯=【点睛】本题主要考查三角函数恒等变换，余弦定理，面积公式及均值不等式，综合性较强，意在考查学生的转化能力，对学生的基础知识掌握要求较高.5．若直线2y x =-的倾斜角为α，则sin 2α的值为（ ） A ．45B ．45-C ．45±D ．35【答案】B 【解析】 【分析】根据题意可得：tan 2α，所求式子利用二倍角的正弦函数公式化简，再利用同角三角函数间的基本由于直线2y x =-的倾斜角为α，所以tan 2α，则22222sin cos 2tan 224sin 22sin cos sin cos tan 1(2)15ααααααααα-⨯=====-++-+故答案选B 【点睛】本题考查二倍角的正弦函数公式，同角三角函数间的基本关系，以及直线倾斜角与斜率之间的关系，熟练掌握公式是解本题的关键．6．若不等式210ax ax -+≤的解集为空集，则实数a 的取值范围是（ ） A ．04a ≤≤ B ．04a <≤C ．04a <<D ．04a ≤<【答案】D 【解析】 【分析】对a 分0,0a a =≠两种情况讨论分析得解. 【详解】当0a =时，不等式为10≤，所以满足题意；当0a ≠时，2,0440a a a a >⎧∴<<⎨∆=-<⎩， 综合得04a ≤<. 故选：D 【点睛】本题主要考查不等式的恒成立问题，意在考查学生对这些知识的理解掌握水平，属于基础题. 7．下列函数中周期为π，且图象关于直线3x π=对称的函数是( )A ．2sin 23x y π⎛⎫=+⎪⎝⎭B ．2sin 26y x π⎛⎫=-⎪⎝⎭C ．2sin 23y x π⎛⎫=+ ⎪⎝⎭D ．2sin 23x y π⎛⎫=- ⎪⎝⎭【答案】B 【解析】 因为，所以选项A,B,C,D 的周期依次为又当3x π=时，选项A,B,C,D 的值依次为所以只有选项A,B 关于直线3x π=对称，因此选B.8．若直线与直线平行，则的值为（ ）A ．7B ．0或7C ．0D ．4【答案】B 【解析】 【分析】根据直线和直线平行则斜率相等，故，求解即可。

数学考生注意：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分．考试时间120分钟．2．请将各题答案填写在答题卡上．3．本试卷主要考试内容：人教A 版必修5，必修2前三章．第Ⅰ卷一、选择题1. 下列几何体中是四棱锥的是（ ）A. B.C. D.【答案】C 【解析】 【分析】由四棱锥的定义判断.【详解】因为一个多面体的一个面是四边形，其余各面是有一个公共顶点的三角形，那么这个多面体叫做四棱锥.只有C 符合， 故选：C【点睛】本题主要考查四棱锥的定义和几何特征，属于基础题.2. 已知等差数列{}n a 的前n 项和为n S ，且13a =，公差2d =，则5S =（ ） A. 30 B. 35C. 40D. 45【答案】B 【解析】 【分析】利用等差数列前n 项和公式计算即可得到答案.【详解】因为13a =，2d =，所以51545352S a d ⨯=+=． 故选：B【点睛】本题主要考查等差数列前n 项和计算，属于简单题. 3. 在ABC 中，4B π=，52sin A =，4AC =，则BC =（ ） A. 5 B. 6C. 7D. 8【答案】A 【解析】 【分析】 先建立方程sin sin BC ACA B=，再求解即可. 【详解】由正弦定理知5248,5sin sin 2BC ACBC A B⨯===． 故选：A【点睛】本题考查正弦定理，是基础题 4. 若关于x 的不等式220ax ax ++≥的解集为R ，则a 的取值范围为（ ）A. (]0,4B. []0,4C. (]0,8D. []0,8【答案】D 【解析】 【分析】分0a =和0a ≠两类情况讨论即可得答案. 【详解】解：由题知当0a =时符合条件； 当0a ≠时，20,80,a a a >⎧⎨-≤⎩解得08a <≤． 综上，a 的取值范为[]0,8． 故选：D.【点睛】本题考查一元二次不等式恒成立问题，考查分类讨论思想，是基础题.5. 已知点(2,5),(1,6)A B ，则直线AB 的倾斜角为（ ） A.34π B.23π C.3π D.4π 【答案】A 【解析】 【分析】求出直线的斜率，从而可得直线的倾斜角. 【详解】由题知直线AB 的斜率65112k -==--，故直线AB 的倾斜角为34π． 故答案为：A.【点睛】本题考查直线的倾斜角的求法，可先求出斜率，再根据两者之间的关系求出倾斜角，本题属于基础题.6. 在正项等比数列{}n a 中，2256892100a a a a ++=，则59a a +=（ ）A. 5B. 10C. 20D. 50【答案】B 【解析】 【分析】根据等比数列的性质可得8559a a a a =，从而可得所求的59a a +的值. 【详解】因为数列{}n a 为等比数列，所以()22222568955995922100a a a a a a a a a a ++=++=+=，又0n a >，所以5910a a +=．故选：B.【点睛】一般地，如果{}n a 为等比数列，n S 为其前n 项和，则有性质：（1）若,,,*,m n p q N m n p q ∈+=+，则m n p q a a a a =；（2）公比1q ≠时，则有nn S A Bq =+，其中,A B 为常数且0A B +=；（3）232,,,n n n n n S S S S S -- 为等比数列（0n S ≠ ）且公比为n q .7. 已知直线240x y +-=与直线230x my m +++=平行，则它们之间的距离为（ ）51035310【答案】C 【解析】 【分析】根据直线240x y +-=与直线230x my m +++=平行，由4034m m -=⎧⎨+≠⎩,解得m ，然后利用两平行线间的距离.【详解】因为直线240x y +-=与直线230x my m +++=平行，所以4034m m -=⎧⎨+≠⎩,解得4m =，因为直线240x y +-=与直线7202++=x y 227|4|352212--=+．故选：C【点睛】本题主要考查两直线的位置关系，还考查了运算求解的能力，属于基础题. 8. 已知a c >，b d >，则下列结论正确的是（ ） A. 22()()a b c d +>+ B. 0ab cd ad bc +--> C. ab cd > D. a b c d ->-【答案】B 【解析】 【分析】根据不等式的性质作差比较可证B 正确，举反例可说明ACD 错误． 【详解】若1,5,2,7a c b d =-=-=-=-，则22()()a b c d +<+，ab cd <，a b c d -<-，ACD 均错误．因为a c >，b d >，所以()()0ab cd ad bc a c b d +--=-->．B 正确．故选：B ．【点睛】本题考查不等式的性质，掌握不等式的性质是解题关键．应用时涉及到不等式的乘除时，不等式两边的正负对不等式的成立有决定性作用，一般比较大小可用作差法． 9. 已知直线:30l x y ++=，直线:260m x y -+=，则m 关于l 对称的直线方程为（ ） A. 630x y ++= B. 630x y -+= C. 260x y ++= D. 230x y -+=【答案】D 【解析】 【分析】先求两直线交点，再在m 上找一点（不同于交点）做关于l 的对称点，然后利用对称点与交点求出直线方程即为答案.【详解】由题知直线l 与直线m 交于点()3,0P-，且点()0,6M 在m 上，设点M 关于l 对称的点的坐标为(),N a b ，则61,630,22b aa b -⎧=⎪⎪⎨+⎪++=⎪⎩解得9,3,a b =-⎧⎨=-⎩ 则直线MN 的方程为230x y -+=，即m 关于l 对称的直线方程为230x y -+=． 故选：D【点睛】考查对称知识，求直线关于直线对称，转化成点与点关于直线对称，也可以利用求轨迹方程的方法，到角公式等.10. 已知m ，n 为两条不同的直线，α，β为两个不同的平面，给出下列命题： ①若//,m n αα⊥，则m n ⊥； ②若,//m m αβ⊥，则αβ⊥； ③若,,//m n αβαβ⊂⊂，则//m n ； ④若,m n m α⊥⊥，则//n α． 其中所有真命题的序号是（ ） A. ①② B. ①②③C. ①②④D. ②【答案】A 【解析】【分析】根据空间中线面、面面平行垂直的性质进行判断.【详解】对于①，若//,m n αα⊥，则m 可以平移到平面α上，因为n 垂直于平面α内所有直线，所以m n ⊥，故①正确；对于②，若,//m m αβ⊥，因此直线m 可以平移到平面β上，所以存在平面β内一条直线垂直于α，所以αβ⊥，故②正确； 对于③，m ，n 可能平行，也可能异面，所以③错； 对于④，n 可能平行于α，也可能n 在平面α内，所以④错.故选：A ． 【点睛】本题考查立体几何中线面位置关系，考查空间想象力.11.ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知1cos ,22c a b A b a c =+=+，则ABC 的形状为（ ） A. 等腰非等边三角形 B. 直角非等腰三角形 C. 等边三角形 D. 钝角三角形【答案】C 【解析】 【分析】先利用正弦定理将1cos 2c a b A =+中得边化成角，可以求出3B π=，再利用正弦定理将2b a c =+化简可以求出3C π=，从而判断ABC 的形状为等边三角形.【详解】1cos 2c a b A =+，由正弦定理得1sin sin sin cos 2C A B A =+，1si si n sin cos 2n A A BB A , 即1sin cos cos sin sin sin cos 2A B A B A B A +=+ sin 0A ≠，∴1cos ,23B B π==，2b a c =+，所以2sin sin sin 3B A C =+=，即sin sin 33C C π⎛⎫++=⎪⎝⎭，解得3C π=，故ABC 的形状为等边三角形． 故选：C.【点睛】本题主要考查利用正弦定理化简关系式，从而判断三角形得形状，属于基础题. 12. 在三棱锥S ABC -中，5,17,10SA BC SB AC SC AB ======，则该三棱锥外接球的表面积为（ ） A. 20π B. 25πC. 26πD. 34π【答案】C 【解析】 【分析】由于三棱锥对棱相等，可将它补成一个长方体，利用长方体求得其外接球的半径，得球表面积．【详解】因为5,17,10SA BC SB AC SC AB ======，所以可以将三棱锥S ABC-如图放置于一个长方体中，设长方体的长宽、高分别为a ，b ，c ，则有22222217,25,10,a b a c b c ⎧+=⎪+=⎨⎪+=⎩整理得22226a b c ++=，则该棱锥外接球的半径262R =，S 球2426R ππ==． 故选：C ．【点睛】本题考查求三棱锥外接球的表面积，解题关键是求出球的半径，方法是把球放在一个长方体中，三棱锥的各棱是长方体六个面上面对角线．第Ⅱ卷二、填空题13. 已知直线l 的斜率为2，且经过点()2,5--，则直线l 的一般式方程为_____________． 【答案】210x y --= 【解析】 【分析】根据直线的点斜式方程求出之后再化为一般是方程即可得答案. 【详解】解：因为直线l 的斜率为2，且经过点()2,5--， 所以直线l 的方程为52(2)y x +=+， 即210x y --=． 故答案为：210x y --=.【点睛】本题考查直线的点斜式方程，一般式方程，是基础题.14. 已知某圆柱的侧面展开图是边长为6的正方形，则该圆柱的体积为____________． 【答案】54π【解析】 【分析】根据圆柱体积公式，结合侧面展开图的性质进行求解即可 【详解】因为圆柱的侧面展开图是边长为6的正方形， 所以该圆柱的底面圆的周长为6，因此半径为3π，而圆柱的高为6， 故该圆柱的体积为23546πππ⎛⎫⨯⨯= ⎪⎝⎭．故答案为：54π【点睛】本题考查了圆柱体积公式的计算，考查了数学运算能力.15. 有A ，B ，C 三座城市，其中A 在B 的正东方向，且与B 相距100km ，C 在A 的北偏东30°方向，且与A 相距300km ．一架飞机从A 城市出发，以400km/h 的速度向C 城市飞行，飞行30min 后，接到命令改变航向，飞往B 城市，此时飞机距离B 城市__________km ．【答案】1007 【解析】 【分析】根据题意，画出三角形，根据余弦定理即可求解.【详解】如图，由题意可知100km,300km,200km,120AB AC AD BAD ===∠=︒，则22212cos 10000400002100200700002BD AB AD AB AD BAD ⎛⎫=+-⋅∠=+-⨯⨯⨯-= ⎪⎝⎭，故1007km BD =． 故答案为：7【点睛】本题考查利用余弦定理解决实际问题，属于基础题. 16. 已知正数a ，b 满足2a b +=，则2238a b ⎛⎫⎛⎫++ ⎪⎪⎝⎭⎝⎭的最小值为__________． 【答案】49 【解析】 【分析】根据正数a ，b 满足2a b +=，由223849⎛⎫⎛⎫⎛⎫⎛⎫++=++ ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭b a a b a b ，利用基本不等式求解.【详解】因为正数a ，b 满足2a b +=， 所以229438493749b a b aa b a b a b⎛⎫⎛⎫⎛⎫⎛⎫++=++=++ ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭， 当且仅当64,55a b ==时，等号成立．故答案为：49【点睛】本题主要考查基本不等式的应用，属于基础题.三、解答题17. 在等差数列{}n a 中，已知244,10a a ==． （1）求{}n a 的通项公式；（2）设{}n a 的前n 项和为n S ，若70n S =，求n 的值． 【答案】（1）32n a n =-；（2）7n =. 【解析】 【分析】（1）利用等比数列与等差数列的通项公式及其性质即可得出； （2）根据等差数列的求和公式直接计算即可.【详解】（1）设等差数列{}n a 的公差为d ，由题意得114,310,a d a d +=⎧⎨+=⎩ 解得11,3,a d =⎧⎨=⎩ 故1(1)32n a a n d n =+-=-． （2）因为{}n a 的前n 项和为n S ，所以()2137022n n n a a n nS +-===，整理得(320)(7)0n n +-=， 故203n =-（舍去）或7n =． 【点睛】本题主要考查了等差数列的通项公式，求和公式，考查了运算能力，属于中档题. 18. 求出满足下列条件的直线方程．（1）经过点(3,2)A -且与直线340x y +-=垂直； （2）经过点()2,7B 且在两条坐标轴上的截距相等．【答案】（1）3110x y -+=；（2）720,90x y x y -=+-=.【解析】【分析】（1）求出所求直线的斜率，利用点斜式方程可得所求的直线方程；（2）根据截距是否为零分类讨论，当截距不为零时可设直线的方程为0x y b ++=，代入所过的点后求出b ，从而得到所求直线的方程.【详解】解：（1）因为所求的直线与直线340x y +-=垂直，所以所求的直线的斜率为3． 又直线经过点()3,2A -，所以该直线方程为23(3)y x -=+，即3110x y -+=．（2）当所求的直线与两条坐标轴上的截距均为0时，因为直线经过点()2,7B ，所以该直线方程为720x y -=；当所求的直线与两条坐标轴上的截距相等且不为0时，则设该直线方程为0x y b ++=， 将点()2,7B 代入方程得9b =-，即所求的直线方程为90x y +-=.【点睛】本题考查直线方程的求法，一般地，确定直线方程需要两个几何要素，如知道其所过的点和斜率，或者知道截距和斜率，或知道所过的两个点，本题属于基础题.19. ABC 的内角A ，B ，C 的对边分别是a ，b ，c ，且sin 3cos b C c B =-．（1）求B ；（2）若23,4b ac ==，求ABC 的周长．【答案】（1）23B π=；（2）423+. 【解析】【分析】（1）已知等式利用正弦定理化边为角后可求得B 角；（2）利用余弦定理列出关于,a c 的关系式求得a c +后可得周长．【详解】解：（1）因为sin 3cos b C c B =-，所以sin sin 3sin cos B C C B =． 又sin 0C ≠，所以sin 3=B B ，即tan 3B =又0B π<<，所以23B π=． （2）由余弦定理得22222cos ()b a c ac B a c ac =+-=+-．因为23,4b ac ==，所以4a c +=．故ABC 的周长为423+．【点睛】本题考查正弦定理、余弦定理，解题关键是用正弦定理进行边角转换． 20. 在三棱锥D ABC -中，22AB BC ==，4DA DC AC ===，平面ADC ⊥平面ABC ，点M 在棱BC 上.（1）若M 为BC 的中点，证明：BC DM ⊥.（2）若三棱锥A CDM -的体积为3M 到平面ABD 的距离.【答案】（1）见解析；（2）217【解析】【分析】 （1）取AC 的中点O ，连接OB ，OD ，根据DA DC =，得到OD AC ⊥，由平面ADC ⊥平面ABC ，得到OD ⊥平面ABC ，OD OB ⊥，再利用OBD OCD ≅△△，得到DB DC =，根据M 为BC 的中点证明.（2）由（1）得到16-=⋅⋅D ABC V DO BC AB ，根据三棱锥A CDM -的体积为3-D ABM V ，再由等体积法求解.【详解】（1）如图所示：取AC 的中点O ，连接OB ，OD ，因为DA DC =，所以OD AC ⊥. 又因为平面ADC ⊥平面ABC ，且相交于AC ，所以OD ⊥平面ABC ，所以OD OB ⊥.因为222AB BC AC +=，所以AB BC ⊥， 所以OB OC =，所以OBD OCD ≅△△，所以DB DC =，且M 为BC 的中点， 所以BC DM ⊥.（2）18363D ABC V DO BC AB -=⋅⋅=， 所以833333D ABM V -=-=. 在ABD △中，221224(2)272ABD S =⨯-=△ 设M 到平面ABD 的距离为h ，则13ABD D ABM S h V -⋅=△， 解得21h =所以M 到平面ABD 21. 【点睛】本题考查等差线线垂直，线面垂直以及等体积法求点到面的距离，还考查了转化化归的思想和逻辑推理，运算求解的能力，属于中档题.21. 如图，在四棱柱1111ABCD A B C D -中，底面ABCD 为正方形，1AA ⊥平面ABCD ，O 为11A C 的中点，且2AB =．（1）证明：//OD 平面1AB C ．（2）若异面直线OD 与1AB 所成角的正切值为13，求三棱柱111ABC A B C -的体积． 【答案】（1）证明见解析；（2）8.【解析】【分析】 （1）连接1OB ，连接BD 交AC 于G ，连接1B G ，通过证明四边形1OB GD 为平行四边形得1//OD B G ，进而证明//OD 平面1AB C .（2）先根据异面直线OD 与1AB 所成角的正切值为13得11tan 3AB G ∠=，再证明AC ⊥平面11BB D D ，最后根据体积计算公式计算即可得答案.【详解】（1）证明：连接1OB ，连接BD 交AC 于G ，连接1B G ．易证1//OB DG ，且1OB DG =，所以四边形1OB GD 为平行四边形，所以1//OD B G ．因为1B G ⊂平面1,AB C OD ⊄平面1AB C ，所以//OD 平面1AB C ．（2）解：由（1）知，1//OD B G ，所以异面直线OD 与1AB 所成角即直线1B G 与1AB 所成角所以11tan 3AB G ∠=． 因为底面ABCD 为正方形，所以AC BD ⊥，又侧棱垂直底面，所以1BB AC ⊥．因为1BB BD B ⋂=，所以AC ⊥平面11BB D D ，所以1AC B G ⊥．因为112,tan 3AG AB G =∠=， 所以132B G =，所以11824BB =-=．故三棱柱111ABC A B C -的体积212482V =⨯⨯=．【点睛】本题考查线面平行的证明，几何体的体积的求解，是中档题.22. 在数列{}n a 中，1114,340n n a a a +=-+=．（1）证明：数列{}2n a -是等比数列．（2）设()()1(1)3131n n n n n a b +-=++，记数列{}n b 的前n 项和为n T ，若对任意的*,n n N m T ∈≥恒成立，求m 的取值范围．【答案】（1）证明见解析；（2）3,14⎡⎫-+∞⎪⎢⎣⎭. 【解析】【分析】 （1）由1340n n a a +-+=得()1232n n a a +-=-，再结合等比数列的定义即可证明； （2）先根据（1）求出432nn a =⨯+，进而得()()11(1)11(1)31313131n n n n n n n n a b ++-⎛⎫==-+ ⎪++++⎝⎭，再分n 为偶数和奇数两类情况并结合裂项求和法讨论即可.【详解】解：（1）证明：因为1340n n a a +-+=，所以134n n a a +=-，所以()1232n n a a +-=-，即()*1232n n a n N a +-=∈-． 因为114a =，所以1212a -=，故数列{}2n a -是以12为首项，3为公比的等比数列．（2）解：由（1）可得1212343n n n a --=⨯=⨯，即432n n a =⨯+，则()()()()()111(1)432(1)11(1)313131313131n n n n n n n n n n n n a b +++-⨯+-⎛⎫===-+ ⎪++++++⎝⎭． 当n 为偶数时，22311111111113131313131313131n n n n n T -+⎛⎫⎛⎫⎛⎫⎛⎫=--++++--++ ⎪ ⎪ ⎪ ⎪++++++++⎝⎭⎝⎭⎝⎭⎝⎭1111113131431n n ++=-+=-++++， 因为111431n n T +=-++是递减的，所以13414n T -<≤-． 当n 为奇数时，22311111111113131313131313131n n n n n T -+⎛⎫⎛⎫⎛⎫⎛⎫=--++++++-- ⎪ ⎪ ⎪ ⎪++++++++⎝⎭⎝⎭⎝⎭⎝⎭1111113131431n n ++=--=--+++， 因为11031n +>+，所以14n T <-． 要使对任意的*,n n N m T ∈≥恒成立，只需()max n m T ≥，即314m ≥-， 故m 的取值范围是3,14⎡⎫-+∞⎪⎢⎣⎭． 【点睛】本题考查利用递推关系证明等比数列，裂项求和法求和，分类讨论思想，数列不等式恒成立问题，考查分析解决问题的能力与运算能力，是中档题.。

2019-2020学年高一下学期期末数学模拟试卷一、选择题：本题共12小题，在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知奇函数．．．()2sin()(0,02)f x x ωϕωϕπ=+><<满足44f x f x ππ⎛⎫⎛⎫+=- ⎪ ⎪⎝⎭⎝⎭，则ω的取值不可．．能．是（ ） A ．2 B ．4C ．6D ．102．若2tan1tan 1212m ππ=-，则m =（ ）A B C ．2D ．3．矩形ABCD 中，6, 4AB =AD =，若在该矩形内随机投一点P ，那么使得ABP ∆的面积不大于3的概率是（ ） A ．18B ．16C ．14D ．124．已知向量(),2a x =，()1,b y =且,x y 为正实数，若满足2a b xy ⋅=，则34x y +的最小值为（ ）A ．5+B ．5+C ．D ．5．直三棱柱ABC —A 1B 1C 1中，BB 1中点为M ，BC 中点为N ，∠ABC ＝120°，AB ＝2，BC ＝CC 1＝1，则异面直线AB 1与MN 所成角的余弦值为 A ．1B ．45-C ．34-D ．06．△ABC 的内角A 、B 、C 的对边分别为a 、b 、c.已知a =，2c =，2cos 3A =，则b=AB C ．2D ．37．点()2,5P 关于直线0x y +=对称的点的坐标是（ ） A ．()5,2-- B ．()2,5-C ．()5,2D ．()2,5--8．已知向量()3,1a =，(3,3b =-，则向量a 在向量b 方向上的投影为（ ）A ．B ．1-C D ．19．若a 、b 、R c ∈，且a b >，则下列不等式中一定成立的是（ ） A ．a b b c +≥-B ．ac bc ≥C ．20c a b>-D ．()20a b c -≥10．已知数列{}n a 的前n 项和为n S ，直线y x =-O :2222n x y a +=+交于()*,n n P Q n N∈两点，且214n n n S PQ =.记n n b na =，其前n 项和为n T ，若存在*n N ∈，使得22n n T a λ<+有解，则实数λ取值范围是（ ）A ．3,5⎛⎫+∞ ⎪⎝⎭B ．4,5⎛⎫+∞⎪⎝⎭C ．1,2⎛⎫+∞⎪⎝⎭D ．()0,∞+11．下图所示的几何体是由一个圆柱中挖去一个以圆柱的上底面为底面，下底面圆心为质点的圆锥面得到，现用一个垂直于底面的平面去截该几何体、则截面图形可能是（ ）A ．（1）（2）B ．（2）（3）C ．（3）（4）D ．（1）（4）12．若直线1:2l y x a =-+与直线22:(2)2l y a x =--平行,则a =A ．1B ．1-C ．3±D ．±1二、填空题：本题共4小题13．ABC 的内角A B C ，，的对边分别为a ，b ，c ，若ABC 的面积为2224a b c +-，则角C =_______. 14．22cos821sin8++-的化简结果是_________.15．如果3个正整数可作为一个直角三角形三条边的边长，则称这3个数为一组勾股数．现从1,2,3,4,5中任取3个不同的数，则这3个数构成一组勾股数的概率为 ． 16．已知函数y=sin （ωx+ϕ）（ω>0, -π≤ϕ<π）的图象如图所示，则ϕ=________________ .三、解答题：解答应写出文字说明、证明过程或演算步骤。