第四章角度计量和测量技术
- 格式:ppt
- 大小:6.74 MB
- 文档页数:70

角度测量技术的基本原理和应用角度测量技术是应用于工程、导航、地理测量等领域的一种重要的测量方法。
它通过测量物体或地点之间的角度来确定其位置关系,从而帮助我们更好地理解和掌握所研究领域的特性和性质。
本文将介绍角度测量技术的基本原理和一些常见的应用。
一、基本原理角度测量技术的基本原理依赖于测量物体或地点之间的角度差异。
在测量过程中,通常使用角度计量仪器(如经纬仪、陀螺仪)来测量目标物体或地点相对于参考方向的角度。
角度计量仪器的精度和测量范围是影响角度测量精度和可行性的关键因素。
例如,经纬仪常用于测量地理位置,利用水平仪和径向刻度来测量目标位置相对于地球表面和参考方向之间的角度。
而陀螺仪则是一种精密的角度计量仪器,主要用于导航和航空领域,利用陀螺仪的旋转和惯性原理来测量目标物体或地点的角度。
在角度测量中,还常常使用三角法来计算和测量角度。
三角法是一种基于三角关系的几何学方法,用于测量和计算未知角度。
通过测量已知角度和物体间的边长关系,三角法可以推导出目标角度的大小。
二、应用领域1. 工程测量角度测量技术在工程测量中有着广泛的应用。
例如,在建筑工程中,我们需要测量建筑物之间的夹角以确保建筑物的位置和方向准确无误。
另外,在制造业中,角度测量常用于测量零件和工件之间的相对位置和角度,以确保生产过程的正确性和质量。
2. 导航定位角度测量技术对于导航和定位具有重要意义。
航海、航空和航天等领域都依赖于角度测量来确定目标物体的位置和方向。
例如,罗盘是一种常用的导航仪器,利用地球的磁场来测量船只和飞行器的方向。
另外,一些现代导航系统如全球定位系统(GPS),则利用卫星信号和三角测量原理来测量目标物体的位置和方向。
3. 地理测量角度测量技术在地理测量中也有着重要的应用。
地理测量主要研究地球表面的形状、地理位置和地形特征。
通过测量目标物体或地点之间的角度,地理学家可以绘制地图、测量地形和研究地球的变化。
例如,地球测量学使用角度测量技术来测量地球的大小、形状和旋转轴的倾斜度。




第一章角度单位与国家检定系统角度是一种重要的物理量。
角度计量是几何量计量的重要组成局部。
角度量的范围广,平面角按平面所在的空间位置可分为:在水平面内的水平角(或称方位角),在垂直面内的垂直角(或倾歪角),空间角是水平角和垂直角的合成;按量程可分为圆周分度角和小角度;按标称值可分为定角和任意角;按组成单元可分为线角度和面角度;按形成方式可分为固定角和动态角,固定角是指加工或装配成的零组件角度,仪器转动后恢复至静态时的角位置等,动态角是指物体或系统在运动过程中的角度,如卫星轨道对地球赤道面的夹角,周密设备主轴转动时的轴线角漂移,测角设备在一定角速度和角加速度运动时,输出的实时角度信号等。
对一些特定角,往往给予专门名称,如基面、轴线或准线相互间夹角为0°或180°时称为平行度,90°或270°时称为垂直度;角度量在应用时还往往引进特定的参考基准,所指的角度是对参考基准的夹角,如:水平度是以大地水平面或铅垂线为参考的倾歪角;天文方位角是以天文北为参考的水平角;经、纬度是以通过格林尼治天文台的子午线和赤道面为参考的水平角和垂直角。
第一节角度单位人类的生产、生活、战争等活动都离不开计量单位。
国际单位制了七个全然单位和两个辅助单位,这两个辅助单位确实是根基“平面角〞和“立体角〞。
平面角是在平面内的夹角,其单位是“弧度〞(rad),“弧度〞是一圆内两条半径之间的平面角,这两条半径在圆周上截取的弧长与半径相等,它所对应的角称为一弧度,一圆周所对应的圆心角等于2π弧度,π=3.1415926…。
立体角的单位为“球面度〞(sr),“球面度〞是顶点位于球心的一立体角,它在球面上所截取的面积等于以球半径为边长的正方形面积。
弧度和球面度都纯属几何单位,其定义根基上无量纲的量,但应用时,能够作为无量纲的数,也能够作为有独立量纲的量,作为有独立量纲的量时,能够作为全然单位,如角速度单位为弧度每秒(rad/s),角加速度单位为弧度每二次方秒(rad/s2)等,弧度是全然单位;当作为无量纲的数时,可作为导出单位,如:电动机的机械功率(牛顿米每秒(N·m/s)等于转矩牛顿米(N·m)和转速弧度每秒(rad/s)之积,转速的弧度在运算中自动消逝,否那么等号两边就不平衡,这确实是根基辅助单位的两重性。


四. 角度测量和经纬仪思考题1.什么是水平角?试绘图说明用经纬仪测量水平角的原理。
2.什么是竖直角?为什么测竖直角时可只瞄准一个目标?3.经纬仪测角时,若照准同一竖直面内不同高度的两目标点,其水平度盘读数是否相同?若经纬仪架设高度不同,照准同一目标点,则该点的竖直角是否相同?4.何谓视差?产生视差的原因是什么?观测时如何消除视差?5.简述电子经纬仪的主要特点。
它与光学经纬仪的根本区别是什么?6.简述编码度盘测角系统的测角原理。
7.简述光栅度盘测角系统的测角原理。
8.安置经纬仪时,对中和整平的目的是什么?若用光学对中器应如何进行?9.试述用方向观测法观测水平角的步骤。
如何进行记录、计算?有哪些限差规定?10.水平角方向观测法中的2c有何含义?为什么要计算2c并检核其互差?11.何谓竖盘指标差?如何计算和检验竖盘指标差?12.试述水平角观测中的照准误差与目标偏心误差有什么区别。
13.根据水平角观测的原理,试说明经纬仪轴系之间的关系应有哪些基本要求部分习题答案15.16. 8.3″;18. 3.4″;19. 3′26.3″22. x c=+15.1″;23. x i=-1.06″;24. –10.7″25. A. 12″; B. 12.2″; C. 13.9″26. A. 24″; B. 24.4″; C. 27.8″27. C=-8″; i=-9.7″28. 2.6″29. (1)υ=40″, (2)τ=20″, (3) c=0, (4) i=10″31. ±8.0″32. ±9.8″33. ±6.1″34. ±8.5″,±8.5″。

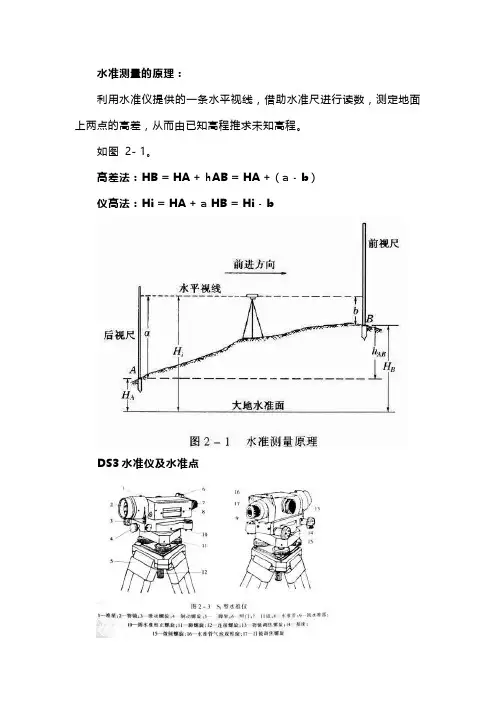
水准测量的原理:利用水准仪提供的一条水平视线,借助水准尺进行读数,测定地面上两点的高差,从而由已知高程推求未知高程。
如图2- 1。
高差法:HB = HA + hAB = HA + ( a - b )仪高法:Hi = HA + a HB = Hi - bDS3水准仪及水准点水平角测量原理(一)定义:水平角就是地面上某点到两目标的方向线铅垂投影到水平面上所成的角度,其取值范围为0 ~ 360。
(二)测角原理:如图3-1测回法测回法是测水平角的基本方法,用于两个目标方向之间的水平角的观测。
如图,设O为测站点,A、B为观测目标,用测回法观测OA与OB两方向之间的水平角β。
竖直角测量原理:(一)定义地面某点至目标的方向线与水平面之间的夹角,取值范围为–90~90。
仰角为正,俯角为负。
(二)测角原理:如图距离:两标志点之间的水平直线长度。
直线定线:把多根标杆标定在已知直线的工作。
方法有目估定线和经纬仪定线。
钢尺量距:精密钢尺量距时必须对所量距离施加尺长改正、温度改正,倾斜,即用钢尺的实际长度。
其实际长度用尺长方程式表示,它的一般形式为:l t = l + Δl + a ×l(t - t0 )视距测量:利用望远镜的视距丝装置,根据几何光学原理同时测定距离和高差的方法。
视线水平时:距离:D = k·l 高差:h = i –v斜距情况下:距离:D = kl cos2α高差:h = ( 1 / 2 ) kl sin2α+ i –v式中:l为上下丝读数之差;α为竖直角;i为仪器高;v为目标高(中丝读数);k = 100光电测距:原理:通过测定光波在两点间传播的时间计算距离的方法。
公式:D′= ( 1 / 2 )* c* t式中:c为空气中的光速;t为光波在两点间往返的时间。


测绘技术中的计量与测量方法详解在现代科技的发展和城市建设的推动下,测绘技术成为了不可或缺的重要工具。
它被广泛应用于土地规划、工程建设、地图制作等领域。
测绘技术的核心在于精确的计量和测量方法。
本文将深入探讨测绘技术中的计量与测量方法,揭示它们背后的原理和应用。
一、测绘技术中的计量方法1. 三角测量法三角测量法是测绘中最基本的一种计量方法。
它利用三角形的性质和几何原理进行测量。
通过测量三角形的边长和角度,可以计算出其他未知量,如高度、距离等。
这种方法在地球测量中被广泛应用,以确定地表上的各个地点的位置坐标。
2. 光电测量法光电测量法基于光电传感器的测距原理。
它通过测量光的反射、透射和折射现象,确定距离或角度。
这种方法常用于测量隧道和桥梁等工程结构的变形和运动情况,以及进行地形地貌的测量。
3. 雷达测量法雷达测量法利用雷达系统发射的电磁波与目标物的反射信号之间的时间差和频率差,来计算目标物的距离、速度和方向。
这种方法常用于航空测量和卫星测量等领域,以获取地球表面的高程和地物的分布情况。
二、测绘技术中的测量方法1. 电子全站仪测量法电子全站仪是一种高精度的测量仪器。
它通过测量目标点与仪器之间的水平角度和垂直角度,以及目标点与仪器之间的斜距或斜坡距离,来计算目标点的坐标。
这种方法广泛应用于建筑、道路等工程测量中,以获取各个测点的坐标和高程等信息。
2. 全球导航卫星系统测量法全球导航卫星系统,如GPS(全球定位系统)、北斗导航系统等,是一种基于卫星定位和测距原理的测量工具。
通过接收卫星发射的信号,测量接收器与卫星之间的距离和时间差,从而确定接收器的位置。
这种方法被广泛应用于航海、地图制作以及车辆定位等领域。
3. 激光扫描测量法激光扫描测量法利用激光束的扫描和反射原理,对目标物进行高精度的三维测量。
它通过扫描激光束在目标物上的反射点,获取目标物的表面形状和细节。
这种方法常用于建筑物立面的测量、文物保护等领域。