机械产品可靠性设计分析1 应力—强度干涉模型1.1 理论基础应力—强度干涉理论认为可靠性就是产品在给定的运行条件下对抗失效的能力，在机械产品中就是承受应力的能力，即应力与强度相互作用的结果。
施加在零件上的应力大于它的强度时就会发生失效。
应力施加在零件上时，强度就是阻止失效的能力。
应力或负载可以定义为机械载荷、空间变化、环境、温度等一切可能引起失效的因素。
由于强度和应力都是随机变量，所以可以用概率分布来表示。
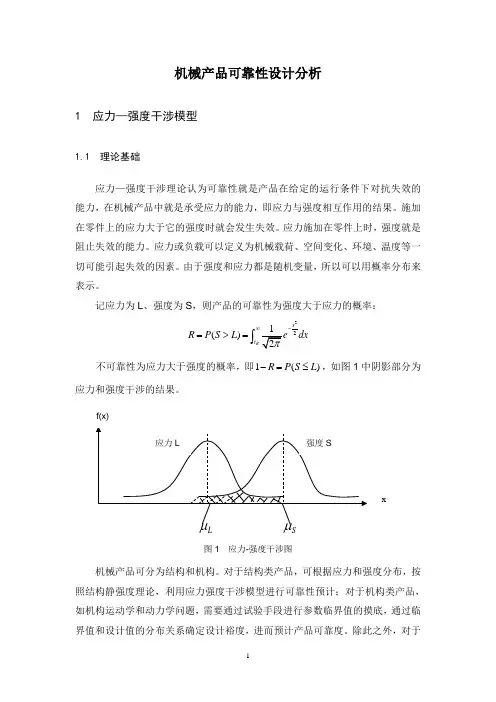
记应力为L、强度为S，则产品的可靠性为强度大于应力的概率：22()RxtR P S L dx∞-=>=⎰不可靠性为应力大于强度的概率，即1()R P S L-=≤，如图1中阴影部分为应力和强度干涉的结果。
图1 应力-强度干涉图机械产品可分为结构和机构。
对于结构类产品，可根据应力和强度分布，按照结构静强度理论，利用应力强度干涉模型进行可靠性预计；对于机构类产品，如机构运动学和动力学问题，需要通过试验手段进行参数临界值的摸底，通过临界值和设计值的分布关系确定设计裕度，进而预计产品可靠度。
除此之外，对于机械产品还存在疲劳等可靠性问题，都可以利用概率设计方法，利用机械可靠性设计的思想来进行可靠性计算。
1.2 正态分布可靠度计算方法在不很精确的概率设计法可靠性计算中，通常不考虑随机变量的实际分布而假定服从正态分布或对数正态分布，利用正态分布进行可靠度计算。
在假设应力、强度均为正态分布随机变量2(,)L LN μσ、2(,)s s N μσ且相互独立情况下，可靠性表示为：()R R t =ΦR t =或R t =式中，S μ——强度均值；L μ——应力均值； S σ——强度标准差； L σ——应力标准差；SL f μμ=； SS S C σμ=； LL LC σμ=； 当应力为一确定的量L 时，()S SLR μσ-=Φ 如果应力和强度的母体分布参数均值和方差未知时，用样本均值和样本方差来代替。
产品强度试验结果取得x n 个强度试验值1x ，2x ，…，x n x ；产品应力试验结果取得y n 个应力试验值1y ，2y ，…，y n y 。
