专题16 角平分线四大模型(解析版)
- 格式:docx
- 大小:221.79 KB
- 文档页数:24

角平分线的四大模型模型1:角平分线的点向两边作垂线如图,P是∠M O N的平分线上一点,过点P作PA⊥O M于点A,PB⊥O N于点B,则PB=PA模型分析利用角平分线的性质:角平分线上的点到角两边的距离相等,构造模型,为边相等、角相等、三角形全等创造更多的条件,进而可以快速找到解题的突破口例题1 (1)如图①,在⊥ABC中,∠C=90°,AD平分∠CAB,BC=6,BD=4,那么点D 到直线AB的距离是(2)如图②,∠1=∠2,∠3=∠4,求证:AP平分∠BAC1.如下图,在四边形ABCD中,BC>AB,AD=DC,BD平分∠ABC,求证:∠BAD+∠BCD=180°模型2:截取构造对称全等如图,P是∠M O N的平分线上的一点,点A是射线O M上任意一点,在O N上截取O B=O A,连接PB,则⊥O PB⊥⊥O PA模型实例例题2 (1)如图①所示,在⊥ABC中,AD是⊥BAC的外角平分线,P是AD上异于点A的任意一点,试比较PB+PC与AB+AC的大小,并说明理由(2)如图②所示,AD是⊥ABC的内角平分线,其它条件不变,试比较PC-PB与AC-AB 的大小,并说明理由巩固提升1.已知,在△ABC中,∠A=2∠B,CD是∠ACB的平分线,AC=16,AD=8,求线段BC的长模型3:角平分线+垂线构造等腰三角形如图,P是∠M O N的平分线上一点,AP丄O P于P点,延长AP交O N于点.B,则⊥A O B是等腰三角形.模型分析构造此模型可以利用等腰三角形的"三线合一”,也可以得到两个全等的直角三角形.进而得到对应边.对应角相等.这个模型巧妙地把角平分线和三线合一联系了起来.模型实例例题3 如图,己知等腰直角三角形ABC中,∠A=90°,AB=AC,BD平分∠ABC,C£丄BD.垂足为E.求证:BD=2C£.巩固提升1.如图,在⊥ABC中.BE是角平分线.AD丄BE.垂足为D.求证:∠2=∠1+∠C.模型4:角平分线+平行线模型分析有角平分线时.常过角平分线上一点作角的一边的平行线. 构造等腰三角形.为证明结论提供更多的条件.体现了用平分线与等腰三角形之间的密切关系.模型实例例题4 解答下列问题:(1)如图①.⊥ABC中,EF∥BC,点D在EF上,BD、CD分别平分∠ABC、∠ACB.写出线段EF 与BE、CF有什么数量关系?(2)如图②,BD平分∠ABC,CD平分外角∠ACG. DE//BC交AB于点E,交AC于点F,线段EF与BE、CF有什么数量关系?并说明理由.(3)如图③,BD 、CD 为外角∠CBM 、∠BCN 的平分线,DE //BC 交AB 延长线于点E .交AC 延长线于点F ,直接写出线段EF 与BE 、CF 有什么数关系?巩固提升1.如图, 在⊥ABC 中,∠ABC 和∠ACB 的平分线交于点E .过点E 作MN ∥BC 交AB 于M 点. 交AC 于N 点.若BM +CN =9,则线段MN 的长为 .课后练习1.已知:如图,BD 为△ABC 的角平分线,且BD=BC ,E 为BD 延长线上的一点,BE=BA ,过E 作EF △AB ,F 为垂足.下列结论:△△ABD ≌△EBC ;△∠BCE +∠BCD =180°;△AD=AE ;△BA +BC =2BF .其中正确的是( )A .△△△B .△△△C .△△△D .△△△△ 2.如图,中,,,垂足为,若,,则的长为( )A .B .C .D .4ABC ∆135ACB ∠=︒CD AB ⊥D 6AD =20BD =CD72。

专题01 角平分线的五种模型模型一、角平分线垂两边例1.如图,AD是△ABC的角平分线,且AB:AC=3:2,则△ABD与△ACD的面积之比为()A.3:2B.6:4C.2:3D.不能确定【答案】A【详解】过点D作DE⊥AB于E,DF⊥AC于F.∵AD为∠BAC的平分线,∴DE=DF,又AB:AC=3:2,∴S△ABD:S△ACD=(12AB•DE):(12AC•DF)=AB:AC=3:2.故选A.例2.如图,∠AOP=∠BOP=15°,PC//OA,PD⊥OA,若PC=4,则PD的长为___.【答案】2【详解】解:过P作PE⊥OB,交OB与点E,∵∠AOP=∠BOP,PD⊥OA,PE⊥OB,∴PD=PE,∵PC//OA,∴∠CPO=∠POD,又∠AOP=∠BOP=15°,∴∠CPO=∠BOP=15°,又∠ECP为△OCP的外角,∴∠ECP=∠COP+∠CPO =30°,在直角三角形CEP 中,∠ECP =30°,PC =4,∴PE =12PC =2,则PD =PE =2.故答案为:2. 【变式训练1】如图所示,在四边形ABCD 中,DC //AB ,∠DAB =90°,AC ⊥BC ,AC =BC ,∠ABC 的平分线交A D ,AC 于点E 、F ,则BFEF的值是___________.11221BCBC BC ==--【详解】解:如图,作FG ⊥AB 于点G ,∠DAB -90°,∴FG /AD ,∴BF EF =BGAGAC ⊥BC ,∴∠ACB =90° 又BF 平分∠ABC ,∴FG =FC 在Rt △BGF 和Rt △BCF 中BF BFCF GF=⎧⎨=⎩ ∴△BGF ≌△BCF (HL ),∴BC =BGAC =BC ,∴∠CBA =45°,∴AB =2BC1BF BG BC EF AG AB BG ∴====- 【变式训练2】如图,BD 平分ABC 的外角∠ABP ,DA =DC ,DE ⊥BP 于点E ,若AB =5,BC =3,求BE 的长.【答案】1【详解】解:过点D 作BA 的垂线交AB 于点H ,∵BD平分△ABC的外角∠ABP,DH⊥AB,∴DE=DH,在Rt△DEB和Rt△DHB中,DE DHDB DB=⎧⎨=⎩,∴Rt△DEB≌Rt△DHB(HL),∴BE=BH,在Rt△DEC和Rt△DHA中,DE DHDC DA=⎧⎨=⎩,∴Rt△DEC≌Rt△DHA(HL),∴AH=CE,由图易知:AH=AB−BH,CE=BE+BC,∴AB−BH=BE+BC,∴BE+BH=AB−BC=5−3=2,而BE=BH,∴2BE=2,故BE=1.【变式训练3,的平分线相交于点E,过点E作交AC于点F,则EF的长为.【答案】【解析】延长FE交AB于点D G H,如图所示:四边形BDEG是矩形,平分CE平分,四边形BDEG是正,,设,则,,,解得,,即,解得,.模型二、角平分线垂中间例.如图,已知,90,,BAC AB AC BD ∠=︒=是ABC ∠的平分线,且CE BD ⊥交BD 的延长线于点E .求证:2BD CE =. 【答案】见解析【详解】证明:如图,延长CE 与BA 的延长线相交于点F ,∵90,90EBF F ACF F ∠+∠=︒∠+∠=︒,∴EBF ACF ∠=∠,在ABD △和ACF 中,EBF ACF AB AC BAC CAF ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴()ABD ACF ASA △≌△,∴BD CF =,∵BD 是ABC ∠的平分线,∴EBC EBF ∠=∠.在BCE ∆和BFE ∆中,EBC EBF BE BE CEB FEB ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴()BCE BFE ASA ≌△△, ∴CE EF =,∴2CF CE =, ∴2BD CF CE ==.【变式训练1】如图,已知△ABC ,∠BAC =45°,在△ABC 的高BD 上取点E ,使AE =BC . (1)求证:CD =DE ;(2)试判断AE 与BC 的位置关系?请说明理由;【答案】(1)见解析;(2)AE BC ⊥,理由见解析;(3)【详解】(1)证明:∵BD AC ⊥,45BAC ∠=︒,∴90,45EDA BDC ABD BAD ∠=∠=︒∠=∠=︒,∴AD BD =,在Rt ADE △和Rt BDC 中,∵AD BDAE BC =⎧⎨=⎩ ∴()Rt ADE Rt BDC HL ≅,∴CD =DE ; (2)AE BC ⊥,理由如下:如图,延长AE ,交BC 于点F , 由(1)得,90EAD EBF EAD AED ∠=∠∠+∠=︒,∵AED AEF ∠=∠,∴90BEF EBF ∠+∠=︒,∴90EFB =︒,即AE BC ⊥;【变式训练2】如图,D 是△ABC 的BC 边的中点,AE 平分∠BAC ,AE ⊥CE 于点E ,且AB =10,AC =16,则DE 的长度为________【答案】3【解答】解:如图,延长CE ,AB 交于点F .AE 平分∠BAC ,AE ⊥EC ,∴∠F AE =∠CAE ,∠AEF =∠AEC =90°在△AFE 和△ACE 中,EAF EAC AE AE AEF AEC =⎧⎪=⎨⎪=⎩∠∠∠∠,∴△AFE ≌ACE (ASA ),∴AF =AC =16,EF =EC ,∴B F =6又D 是BC 的中点,∴BD =CD ,∴DE 是△CBF 的中位线,∴DE =12BF =3,故答案为:3. 【变式训练3】如图,在ABC ∆中,CD 是ACB ∠的平分线,AD CD ⊥于点D ,DE //BC 交AB 于点E ,求证:EA EB =.【答案】见解析【解答】证明:延长AD 交BC 于点F .CD 平分ACF ∠, ACD FCD ∴∠=∠.又,,AD CD CD CD ⊥=ADC ∴∆≌FDC ∆,AD FD ∴=. 又DE ∥BC ,EA EB ∴=.模型三、角平分线+平行线构造等腰三角形例.如图所示,在△ABC 中,BC =6,E 、F 分别是AB 、AC 的中点,动点P 在射线EF 上,BP 交CE 于D,∠CBP 的平分线交CE 于Q ,当CQ =13CE 时,EP +BP =________.【答案】12【解答】解:如图,延长BQ 交射线EF 于点M .E 、F 分别是AB 、AC 的中点,∴EF //BC ,∴∠CBM =∠EMBBM 平分∠ABC ,∴∠ABM =∠CBM ,∴∠EMB =∠EBM ,∴EB =EM ,∴EP +BP =EP +PM =EM CQ =13CE ,∴EQ =2CQ由EF //BC 得,△EMQ ∽△CBQ∴2 212 12EM EQEM BC EP BP BC CQ==∴==∴+=【变式训练1】如图,平分于点C ,,求OC 的长?【解析】如图所示:过点D 作交OA 于点E ,则,平分,,中,,.【变式训练2C=90°,AD平分∠CAB,BE平分∠ABC,AD、BE相交于点F,且,则AC=.【解析】过点E于G,连接CF,如图所示:分别是,CF是的平分线,,,由勾股定理可得.模型四、利用角平分线作对称例.平分.【答案】见解析【解析】证明:在AB上截取,连接DE,如图所示:.【变式训练】AD是△ABC的角平分线,过点D作DE⊥AB于点E,且DE=3,S△ABC=20.(1)如图1,若AB=AC,求AC的长;(2)如图2,若AB=5,请直接写出AC的长.【答案】(1)203;(2)253【详解】解:(1)如图1,作DF⊥AC于F,∵AD 是△ABC 的角平分线,DE ⊥AB ,DF ⊥AC ,∴DF =DE =3, 由题意得,12×AB ×3+12×AC ×3=20,解得,AC =AB =203; (2)如图2,作DF ⊥AC 于F ,∵AD 是△ABC 的角平分线,DE ⊥AB ,DF ⊥AC ,∴DF =DE =3, 由题意得,12×5×3+12×AC ×3=20,解得,AC =253. 模型五、内外模型例.如图,在△ABC 中,AB=AC ,∠A=30°,E 为BC 延长线上一点,∠ABC 与∠AC E 的平分线相交于点D ,则∠D 的度数为( )A .15°B .17.5°C .20°D .22.5°【答案】A4321DA【解析】∵∠ABC与∠AC E的平分线相交于点D,∴∠DCE=∠DCA,∠CBD=∠ABD,即.的外角的平分线CP与内角BP交于点P,若,则.【解析】平分平分又,过点P的延长线,垂足分别为点E、F、G,如图所示:由角平分线的性质可得,AP是.课后训练1.如图,BD是ABC的外角∠ABP的角平分线,DA=DC,DE⊥BP于点E,若AB=5,BC=3,则BE 的长为()A .2B .1.5C .1D .0【答案】C【详解】解:如图,过点D 作DF AB ⊥于F ,BD 是ABP ∠的角平分线,DF AB ⊥,DE ⊥BP ,DE DF ∴=,在Rt BDE 和Rt BDF 中,BD BDDE DF =⎧⎨=⎩,()Rt BDE Rt BDF HL ∴△≌△,BE BF ∴=,在Rt ADF 和Rt CDE △中,DA DCDE DF=⎧⎨=⎩,()Rt ADF Rt CDE HL ∴△≌△,AF CE ∴=,AF AB BF =-,CE BC BE =+,AB BF BC BE ∴-=+,2BE AB BC ∴=-,5AB =,3BC =,2532BE ∴=-=,解得:1BE =.故选:C .2.如图,AD 是ABC 中BAC ∠的平分线,DE AB ⊥交AB 于点E ,DF AC ⊥交AC 于点F ,若7ABC S =△,32=DE ,5AB =,则AC 的长为( )A .133B .4C .5D .6【答案】A【详解】∵AD 是ABC ∆中BAC ∠的平分线,DE AB ⊥于点E ,DF AC ⊥交AC 于点F ,∴32DF DE ==. 又∵ABCABD ACDSSS=+,5AB =,∴1313752222AC =⨯⨯+⨯⨯,∴133AC =.故选:A . 3.如图,在Rt △ABC 中,∠C =90°,∠BAC 的平分线交BC 于点D ,CD =2,BD =3,Q 为AB 上一动点,则DQ 的最小值为( )A.1B.2C.2.5D【答案】B【详解】解:作DH⊥AB于H,如图,∵AD平分∠BAC,DH⊥AB,DC⊥AC,∴DH=DC=2,∵Q为AB上一动点,∴DQ的最小值为DH的长,即DQ的最小值为2.故选:B.4.如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD 的面积是______.【答案】30【详解】过D作DE⊥AB,交BA的延长线于E,则∠E=∠C=90°,∵∠BCD=90°,BD平分∠ABC,∴DE=DC=4,∴四边形ABCD的面积S=S△BCD+S△BAD=12×BC×CD+12×AB×DE=12×9×4+12×6×4=30,故答案为:30.5.如图,在△ABC中,AD为△ABC的角平分线,DE⊥AB,垂足为E,DF⊥AC,垂足为F,若AB=5,AC=3,DF=2,则△ABC的面积为______.【答案】8【详解】解:∵AD为△ABC的角平分线,DE⊥AB,DF⊥AC,∴DE=DF=2,∴△ABC的面积=12×5×2+12×3×2=8,故答案侍:8.6.在△ABC中,∠ABC=62°,∠ACB=50°,∠ACD是△ABC的外角∠ACD和∠ABC的平分线交于点E,则∠AEB=_____︒【答案】25【详解】解:如图示:过点E ,分别作EF BD ⊥交BD 于点E ,EG AC ⊥交AC 于点G ,EH AB ⊥,交AB 延长线于点H , ∵BE 平分ABC ∠,CE 平分ACD ∠,∴EH EF =,EG EF =,∴EH EG =,∴AE 平分HAC ∠, ∵62ABC ∠=︒,50∠=°ACB ,∴6250112HAC ABC ACB ∠=∠+∠=︒+︒=︒,∴111125622EAO HAC ∠=∠=⨯︒=︒, ∵BE 平分ABC ∠,62ABC ∠=︒∴11623122EBC ABC ∠=∠=⨯︒=︒ 在AOE △和BOC 中,OBC OCB OAE AEB ∠+∠=∠+∠∴31505625AEB OBC OCB OAE ∠=∠+∠-∠=︒+︒-︒=︒,故答案是:25. 7.如图,DE ⊥AB 于E ,DF ⊥AC 于F ,若BD =CD ,BE =CF .(1)求证:AD 平分∠BAC :(2)已知AC =18,BE =4,求AB 的长. 【答案】(1)见解析;(2)10AB =.【详解】(1)证明:DE AB ∵⊥,DF AC ⊥,90E DFC ∴∠=∠=︒,在Rt BED 和Rt CFD △中,BD CD BE CF =⎧⎨=⎩,∴Rt BED Rt CFD ≅()HL ,DE DF ∴=,DE AB ∵⊥,DF AC ⊥,AD ∴平分BAC ∠;(2)解:DE DF =,AD AD =,Rt ADE Rt ADF ∴≅()HL ,AE AF ∴=,AB AE BE AF BE AC CF BE =-=-=--,184410AB ∴=--=.8.如图1,在平面直角坐标系中,△ABC 的顶点A (-4,0),B (0,4),AD ⊥BC 交BC 于D 点,交y 轴正半轴于点E (0,t )(1)当t=1时,点C 的坐标为 ; (2)如图2,求∠ADO 的度数;(3)如图3,已知点P (0,3),若PQ ⊥PC ,PQ=PC ,求Q 的坐标(用含t 的式子表示). 【答案】(1)点C 坐标(1,0);(2)∠ADO =45°;(3)Q (-3,3-t ). 【详解】(1)如图1,当t =1时,点E (0,1), ∵AD ⊥BC , ∴∠EAO +∠BCO =90°, ∵∠CBO +∠BCO =90°,∴∠EAO =∠CBO ,在△AOE 和△BOC 中,∵90EAO CBOAO BO AOE BOC ∠=∠⎧⎪=⎨⎪∠=∠︒⎩=,∴△AOE ≌△BOC (ASA ),∴OE =OC =1,∴点C 坐标(1,0). 故答案为:(1,0);(2)如图2,过点O 作OM ⊥AD 于点M ,作ON ⊥BC 于点N ,∵△AOE ≌△BOC ,∴S △AOE =S △BOC ,且AE =BC , ∵OM ⊥AE ,ON ⊥BC ,∴OM =ON ,∴OD 平分∠ADC ;AD ⊥BC ,90ADC ∴∠=︒∴∠ADO =1452ADC ∠=︒;(3)如图3,过P 作GH ∥x 轴,过C 作CG ⊥GH 于G ,过Q 作QH ⊥GH 于H ,交x 轴于F ,∵P (0,3),C (t ,0),∴CG =FH =3,PG =OC =t , ∵∠QPC =90°,∴∠CPG +∠QPH =90°, ∵∠QPH +∠HQP =90°,∴∠CPG =∠HQP ,∵∠QHP=∠G=90°,PQ=PC,∴△PCG≌△QPH,∴CG=PH=3,PG=QH=t,∴Q(-3,3-t).。
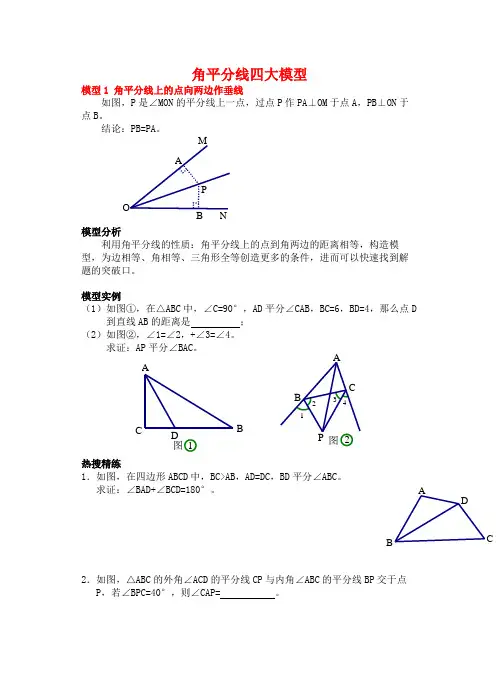
角平分线四大模型模型1 角平分线上的点向两边作垂线如图,P 是∠MON 的平分线上一点,过点P 作PA ⊥OM 于点A ,PB ⊥ON 于点B 。
结论:PB=PA 。
模型分析利用角平分线的性质:角平分线上的点到角两边的距离相等,构造模型,为边相等、角相等、三角形全等创造更多的条件,进而可以快速找到解题的突破口。
模型实例(1)如图①,在△ABC 中,∠C=90°,AD 平分∠CAB ,BC=6,BD=4,那么点D到直线AB 的距离是 ; (2)如图②,∠1=∠2,+∠3=∠4。
求证:AP 平分∠BAC 。
热搜精练1.如图,在四边形ABCD 中,BC>AB ,AD=DC ,BD 平分∠ABC 。
求证:∠BAD+∠BCD=180°。
2.如图,△ABC 的外角∠ACD 的平分线CP 与内角∠ABC 的平分线BP 交于点 P ,若∠BPC=40°,则∠CAP= 。
N M OAB P 2图4321A CP B D AB C图1A B DC模型2 截取构造对称全等如图,P 是∠MON 的平分线上一点,点A 是射线OM 上任意一点,在ON 上截取OB=OA ,连接PB 。
结论:△OPB ≌△OPA 。
模型分析利用角平分线图形的对称性,在角的两边构造对称全等三角形,可以得到对应边、对应角相等。
利用对称性把一些线段或角进行转移,这是经常使用的一种解题技巧。
模型实例(1)如图①所示,在△ABC 中,AD 是△ABC 的外角平分线,P 是AD 上异于点A 的任意一点,试比较PB+PC 与AB+AC 的大小,并说明理由;(2)如图②所示, AD 是△ABC 的内角平分线,其他条件不变,试比较 PC-PB 与AC-AB 的大小,并说明理由。
热搜精练1.已知,在△ABC 中,∠A=2∠B ,CD 是∠ACB 的平分线,AC=16,AD=8。
求线段BC 的长。
A B DCPP O N M B A 图2DP AB C D C 1图P B A ABCD2.已知,在△ABC 中,AB=AC ,∠A=108°,BD 平分∠ABC 。

角平分线四大模型模型一:角平分线上的点向两边作垂线如图,P是∠MON的平分线上一点,过点P作PA⊥OM于点A,PB⊥ON于点B,则PB=PA.模型分析:利用角平分线的性质:角平分线上的点到角两边的距离相等,构造模型,为边相等、角相等、三角形全等创造更多的条件,进而可以快速找到解题的突破口。
例1:(1)如图①,在△ABC,∠C=90°,AD平分∠CAB,BC=6cm,BD=4cm,那么点D到AB的距离是___cm(2)如图②,已知∠1=∠2,∠3=∠4,求证:AP平分∠BAC.练习1 如图,在四边形ABCD中,BC>BA,AD=DC,BD平分∠ABC.求证:∠BAD+∠C=180°练习2 如图,△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P,若∠BPC=40°,则∠CAP=()模型二:截取构造对称全等如图,P是∠MON的平分线上一点,点A是射线OM上任意一点,在ON上截取OB=OA,连接PB,则△OPB≅△OPA.模型分析:利用角平分线图形的对称性,在角的两边构造对称全等三角形,可以得到对应边、对应角相等、利用对称性把一些线段或角进行转移,这是经常使用的一种解题技巧。
例2:(1)如图①所示,在△ABC中,AD是△BAC的外角平分线,P是AD上异于点A的任意一点,试比较PB+PC与AB+AC的大小,并说明理由.(2)如图②所示.AD是△ABC的内角平分线,其他条件不变,试比较PC -PB与AC-AB的大小,并说明理由.练习 3 已知:△ABC中,∠A=2∠B,CD是∠ACB的平分线,AC=16,AD=8,求线段BC的长。
练习4 已知,如图AB=AC,∠A=108°,BD平分∠ABC交AC于D,求证:BC=AB+CD.练习5 如图,在△ABC中,∠A=100°,∠ABC=40°,BD是∠ABC的平分线,延长BD至E,使DE=AD.求证:BC=AB+CE.模型三:角平分线+垂线构造等腰三角形如图,P是∠MON的平分线上一点,AP⊥OP于P点,延长AP交ON于点B,则△AOB是等腰三角形。

角平分线四大模型互动精讲【知识梳理】模型一、角平分线+两垂线如图1,P 是∠MON 的平分线上一点,过点P 作PA ⊥OM 于点A ,PB ⊥ON 于点B 。
结论:PB=PA 。
模型二、角平分线+截长补短如图2,P 是∠MON 的平分线上一点,点A 是射线OM 上任意一点,在ON 上截取OB=OA ,连接PB 。
结论:△OPB ≌△OPA 。
图1 图2模型三、角平分线+垂线如图,P 是∠MO 的平分线上一点,AP ⊥OP 于P 点,延长AP 于点B 。
结论:△AOB 是等腰三角形。
模型四、角平分线+平行线如图,P 是∠MON 的平分线上一点,过点P 作PQ ∥ON ,交OM 于点Q 。
结论:△POQ 是等腰三角形。
图3 图4NM OABPPONM BA PONM BAQPONM【例题精讲】模型一、角平分线+两垂线例1、(1)如图①,在△ABC 中,∠C=90°,AD 平分∠CAB ,BC=6,BD=4,那么点D 到直线AB 的距离是 2 ;(2)如图②,∠1=∠2,+∠3=∠4。
求证:AP 平分∠BAC 。
例2、如图,在四边形ABCD 中,BC>AB ,AD=DC ,BD 平分∠ABC 。
求证:∠BAD+∠BCD=180°。
2图4321ACP BDABC图1ABDC模型二、角平分线+截长补短例3、已知,在△ABC 中,∠A=2∠B ,CD 是∠ACB 的平分线,AC=16,AD=8。
求线段BC 的长。
例4、(1)如图①所示,在△ABC 中,AD 是△ABC 的外角平分线,P 是AD 上异于点A 的任意一点,试比较PB+PC 与AB+AC 的大小,并说明理由;(2)如图②所示, AD 是△ABC 的内角平分线,其他条件不变,试比较PC-PB 与AC-AB 的大小,并说明理由。
ABCD图2DPA BCDC1图PBA模型三、角平分线+垂线例5、如图,已知等腰直角三角形ABC 中,∠A=90°,AB=AC ,BD 平分∠ABC ,CE ⊥BD ,垂足为E 。


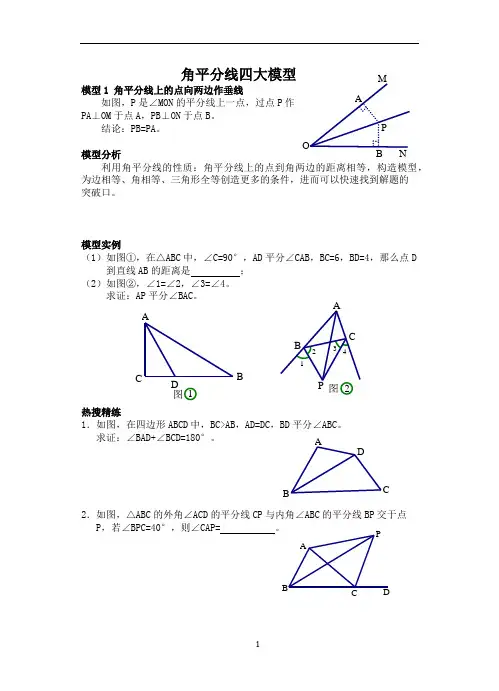
N MOA B P 2图4321A CP B D AB C图1A B D C AB D CP角平分线四大模型模型1 角平分线上的点向两边作垂线如图,P 是∠MON 的平分线上一点,过点P 作PA ⊥OM 于点A ,PB ⊥ON 于点B 。
结论:PB=PA 。
模型分析利用角平分线的性质:角平分线上的点到角两边的距离相等,构造模型,为边相等、角相等、三角形全等创造更多的条件,进而可以快速找到解题的突破口。
模型实例(1)如图①,在△ABC 中,∠C=90°,AD 平分∠CAB ,BC=6,BD=4,那么点D到直线AB 的距离是 ; (2)如图②,∠1=∠2,∠3=∠4。
求证:AP 平分∠BAC 。
热搜精练1.如图,在四边形ABCD 中,BC>AB ,AD=DC ,BD 平分∠ABC 。
求证:∠BAD+∠BCD=180°。
2.如图,△ABC 的外角∠ACD 的平分线CP 与内角∠ABC 的平分线BP 交于点 P ,若∠BPC=40°,则∠CAP= 。
16.如图,∠AOB=90°,OM平分∠AOB,将直角三角板的顶点P在射线OM上移动,两直角边分别与OA、OB相交于点C、D,问PC与PD相等吗?试说明理由.17.如图∠BAC=30°,D为角平分线上一点,DE⊥AC于E,DF∥AC且交AB于F.(1)求证:△ADF是等腰三角形.(2)若DF=10cm,求DE的长.18.如图,在△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,CD=5cm,求AB的长.19.已知:如图,∠B=∠C=90°,M是BC的中点,且DM平分∠ADC.(1)求证:AM平分∠DAB.(2)试说明线段DM与AM有怎样的位置关系?并证明你的结论.20.如图,已知∠1=∠2,P为BN上的一点,PF⊥BC于F,PA=PC.求证:∠PCB+∠BAP=180°.P O N M B A 图2DP AB C D C 1图P B A ABC DA BC DE DC BA模型2 截取构造对称全等如图,P 是∠MON 的平分线上一点,点A 是射线OM 上任意一点,在ON 上截取OB=OA ,连接PB 。

角平分线四大模型编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(角平分线四大模型)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为角平分线四大模型的全部内容。
NM OABP 2图4321A C PB D ABC图1ABDCABD CPPONM BA 第二章 角平分线四大模型模型1 角平分线上的点向两边作垂线如图,P 是∠MON 的平分线上一点,过点P 作 PA ⊥OM 于点A ,PB ⊥ON 于点B. 结论:PB=PA.模型分析利用角平分线的性质:角平分线上的点到角两边的距离相等,构造模型,为边相等、角相等、三角形全等创造更多的条件,进而可以快速找到解题的突破口。
模型实例(1)如图①,在△ABC 中,∠C=90°,AD 平分∠CAB ,BC=6,BD=4,那么点D 到直线AB 的距离是 ;(2)如图②,∠1=∠2,+∠3=∠4. 求证:AP 平分∠BAC 。
热搜精练1.如图,在四边形ABCD 中,BC 〉AB ,AD=DC ,BD 平分∠ABC 。
求证:∠BAD+∠BCD=180°.2.如图,△ABC 的外角∠ACD 的平分线CP 与内角∠ABC 的平分线BP 交于点 P ,若∠BPC=40°,则∠CAP= 。
模型2 截取构造对称全等如图,P 是∠MON 的平分线上一点,点A 是射线OM 上任意一点,在ON 上截取OB=OA ,连接PB 。
结论:△OPB ≌△OPA 。
图2DPA BC DC1图PBAABCDABCDEDCBA模型分析利用角平分线图形的对称性,在角的两边构造对称全等三角形,可以得到对应边、对应角相等。
角平分线模型的三种考法类型一、角平分线上的点向两边作垂线1已知,△ABC中,∠BAC=120°,AD平分∠BAC,∠BDC=60°,AB=2,AC=3,则AD的长是.1.如图,AC、BD是四边形ABCD的对角线,BD平分∠ABC,2∠ACD=∠ABC+∠BAC,已知∠CAD=43°,则∠BDC=.2.已知:AD是△ABC的角平分线,且AD⊥BC.(1)如图1,求证:AB=AC;(2)如图2,∠ABC=30°,点E在AD上,连接CE并延长交AB于点F,BG交CA的延长线于点G,且∠ABG=∠ACF,连接FG.①求证:∠AFG=∠AFC;②若S△ABG:S△ACF=2:3,且AG=2,求AC的长.3.在平面直角坐标系中,点A的坐标是(0,a),点B的坐标(b,0)且a,b满足a2-12a+36+a-b=0.(1)求A、B两点的坐标;(2)如图(1),点C为x轴负半轴一动点,OC<OB,BD⊥AC于D,交y轴于点E,求证:OD平分∠CDB.(3)如图(2),点F为AB的中点,点G为x正半轴点B右侧的一动点,过点F作FG的垂线FH,交y轴的负半轴于点H,那么当点G的位置不断变化时,S△AFH-S△FBG的值是否发生变化?若变化,请说明理由;若不变化,请求出相应结果.类型二、过边上的点向角平分线作垂线构造等腰三角形2已知:ΔABC中,D为BC的中点,AG平分∠BAC,CG⊥AG于G,连结DG,若AB=6,AC=4,求DG的长.1.已知:等腰直角三角形ABC中,∠ACB=90°;AC=BC;∠1=∠3;BE⊥AD.求证:BE=12 AD.2.如图,在△ABC中,∠C=90°,BC=AC,D是AC上一点,AE⊥BD交BD的延长线于E,AE=12BD,且DF⊥AB于F,求证:CD=DF类型三、利用角平分线的性质,在角两边截长补短3如图,在ΔABC中,AB>AC,AD平分∠BAC交BC于D,求证:AB-AC>BD-CD.1.如图所示,在ΔABC中,∠ACB=60°,AE,BD是ΔABC的角平分线,AE,BD交于点G,求证:GD=GE.2.阅读下面材料:小明遇到这样一个问题:如图一,△ABC中,∠A=90°,AB=AC,BD平分∠ABC,猜想线段AD与DC数量关系.小明发现可以用下面方法解决问题:作DE⊥BC交BC于点E:(1)根据阅读材料可得AD与DC的数量关系为.(2)如图二,△ABC中,∠A=120°,AB=AC,BD平分∠ABC,猜想线段AD与DC的数量关系,并证明你的猜想.(3)如图三,△ABC中,∠A=100°,AB=AC,BD平分∠ABC,猜想线段AD与BD、BC的数量关系,并证明你的猜想.3.如图,已知B(-1,0),C(1,0),A为y轴正半轴上一点,点D为第二象限一动点,E在BD的延长线上,CD交AB于F,且∠BDC=∠BAC.(1)求证:∠ABD=∠ACD;(2)求证:AD平分∠CDE;(3)若在点D运动的过程中,始终有DC=DA+DB,在此过程中,∠BAC的度数是否变化?如果变化,请说明理由;如果不变,请求出∠BAC的度数.4.如图1,点A、D在y轴正半轴上,点B、C分别在x轴上,CD平分∠ACB与y轴交于D点,∠CAO=90°-∠BDO.(1)求证:AC=BC;(2)在(1)中点C的坐标为4,0,点E为AC上一点,且∠DEA=∠DBO,如图2,求BC+EC的长;(3)在(1)中,过D作DF⊥AC于F点,点H为FC上一动点,点G为OC上一动点,(如图3),当点H在FC上移动、点G在OC上移动时,始终满足∠GDH=∠GDO+∠FDH,试判断FH、GH、OG这三者之间的数量关系,写出你的结论并加以证明.课后训练1如图,在ΔABC中,∠B=60°,AD、CE分别是∠BAC、∠ACB的平分线,AD、CE相交于点F,试判断FE和FD之间的数量关系.2如图,在ΔABC中,∠ABC=2∠C,BE平分∠ABC,交AC于E,AD⊥BE于D,求证:AC= 2BD.3如图,在△ABC中,AB=AC,∠A=100°,BD是∠ABC的平分线,延长BD至点E,DE=AD,试求∠ECA的度数.4如图1,在△ABC中,CM是AB边的中线,∠BCN=∠BCM交AB延长线于点N,2CM=CN.(1)求证AC=BN;(2)如图2,NP平分∠ANC交CM于点P,交BC于点O,若∠AMC=120°,CP=kAC,求CPCM的值.5如图,在△ABC中,AD为BC边上的高,AE是∠BAD的角平分线,点F为AE上一点,连接BF,∠BFE=45°.(1)求证:BF平分∠ABE;(2)连接CF交AD于点G,若SΔABF=SΔCBF,求证:∠AFC=90°;(3)在(2)的条件下,当BE=3,AG=4.5时,求线段AB的长.6已知△ABC中,BE平分∠ABC,BE交AC于点E,CD平分∠ACB,交AB于点D,BE与CD交于点O.(1)如图1,求证:∠BOC=90°+1∠BAC.2(2)如图2,连接OA,求证:OA平分∠BAC.(3)如图3,若∠BAC=60°,BD=4,CE=2,求ODOC的值.7已知:在ΔABC和ΔDEC中,AC=BC,DC=EC,∠ACB=∠ECD=α.(1)如图1,A,C,D在同一直线上,延长AE交BD于F,求证:AF⊥BD;(2)如图2,AE与BD交于F,G在AD上,若FG平分∠AFD,求证:点C在直线FG上.角平分线模型的三种考法类型一、角平分线上的点向两边作垂线1已知,△ABC 中,∠BAC =120°,AD 平分∠BAC ,∠BDC =60°,AB =2,AC =3,则AD 的长是.【答案】5【分析】过D 作,DE ⊥AC ,DF ⊥AB 交AB 延长线于F ,然后根据全等三角形的性质和30°角直角三角形的性质即可求解.【详解】过D 作,DE ⊥AC ,DF ⊥AB 交AB 延长线于F ,∵AD 平分∠BAC ,DE ⊥AC ,DF ⊥AB ,∴DE =DF ,∠DEC =∠DFB =90°=∠DEA ,∵∠BAC +∠BDC +∠DCE +∠DBA =360°,∠BAC =120°,∠BDC =60°,∴∠DCE +∠DBA =180°,∵∠DBF +∠DBA =180°,∴∠DCE =∠DBF ,在△DEC 和△DFB 中,∠DCE =∠DBF∠DEC =∠DFBDE =DB∴△DEC ≌△DFB AAS ,∴CE =BF ,在Rt △DEA 和Rt △DFA 中,DE =DF DA =DA ,∴Rt △DEA ≌△DFA HL ,∴AE =AF ,∵AE =AC -CE ,AF =AB +BF ,∴AC -CE =AB +BF ,∴CE +BF =AC -AB =1,∴CE =BF =12,∴AF =AB +BF =52,∵AD 平分∠BAC ,∴∠DAB =12∠BAC =60°,∴∠ADF =180°-∠DAB -∠DFB =30°,∴AD =2AF =5.【点睛】此题考查了全等三角形和角平分线的性质,解题的关键是作出辅助线构造全等三角形.1.如图,AC 、BD 是四边形ABCD 的对角线,BD 平分∠ABC ,2∠ACD =∠ABC +∠BAC ,已知∠CAD =43°,则∠BDC =.【答案】47°【分析】过D 作DE ⊥BC 于E ,DF ⊥AB 于F ,DG ⊥AC 于G ,依据DC 平分∠ACE ,BD 平分∠ABC ,利用角平分线的性质,即可得到DF =DG ,进而得出AD 平分∠CAF .再根据三角形外角的性质,即可得到∠BDC =12∠BAC ,进而得出结论.【解析】如图所示,过D 作DE ⊥BC 于E ,DF ⊥AB 于F ,DG ⊥AC 于G ,∵BD 平分∠ABC ,DE ⊥BC ,DF ⊥AB ,∴DF =DE ,∵2∠ACD =∠ABC +∠BAC ,∠ACE =∠ABC +∠BAC ,∴∠ACE =2∠ACD ,∴CD 平分∠ACE ,又∵DE ⊥BC ,DG ⊥AC ,∴DE =DG ,∴DF =DG ,又∵DF ⊥AB ,DG ⊥AC ,∴AD 平分∠CAF ,∵∠CAD =43°,∴∠CAF =86°,∠BAC =94°,∵∠DCE 是△BCD 的外角,∠ACE 是△ABC 的外角,∴∠BDC =∠DCE -∠DBC =12∠ACE -12∠ABC =12∠ACE -12∠ABC =12∠ACE -∠ABC =12∠BAC =12×94°=47°故答案为:47°.【点评】本题主要考查了角平分线的性质以及三角形外角的性质,解题的关键是掌握角平分线的性质:角的平分线上的点到角的两边的距离相等.2.已知:AD 是△ABC 的角平分线,且AD ⊥BC.(1)如图1,求证:AB =AC ;(2)如图2,∠ABC =30°,点E 在AD 上,连接CE 并延长交AB 于点F ,BG 交CA 的延长线于点G ,且∠ABG =∠ACF ,连接FG .①求证:∠AFG =∠AFC ;②若S △ABG :S △ACF =2:3,且AG =2,求AC 的长.【答案】(1)见解析;(2)①见解析;②6.【分析】(1)用ASA 证明△ABD ≌△ACD ,即得AB =AC ;(2)①证明△BAG ≌△CAE 可得AG =AE ,再用SAS 证明△FAG ≌△FAE ,即得∠AFG =∠AFC ;②过F 作FK ⊥AG 于K ,由S △ABG :S △ACF =2:3,可得S △CAE :S △ACF =2:3,S △FAE :S △ACF =1:3,而△FAG ≌△FAE ,故S △FAG :S △ACF =1:3,即得AG :AC =1:3,根据AG =2,可求AC =6.【解析】解:(1)证明:∵AD 是△ABC 的角平分线,∴∠BAD =∠CAD ,∵AD ⊥BC ,∴∠ADB =∠ADC ,在△ABD 和△ACD 中,∠BAD =∠CADAD =AD ∠ADB =∠ADC,∴△ABD ≌△ACD ASA ,∴AB =AC ;(2)①∵AB =AC ,∠ABC =30°,AD ⊥BC ,∴∠BAD =∠CAD =60°,∴∠BAG =60°=∠CAD ,在△BAG 和△CAE 中,∠BAG =∠CAEAB =AC ∠ABG =∠ACE,∴△BAG ≌△CAE ASA ,∴AG =AE ,在△FAG 和△FAE 中,AG =AE∠GAF =∠EAF AF =AF,∴△FAG ≌△FAE SAS ,∴∠AFG =∠AFC ;②过F 作FK ⊥AG 于K ,如图:由①知:△BAG ≌△CAE,∵S △ABG :S △ACF =2:3,∴S △CAE :S △ACF =2:3,∴S △FAE :S △ACF =1:3,由①知:△FAG ≌△FAE ,∴S △FAG :S △ACF =1:3,∴12AG ⋅FK :12AC ⋅FK =1:3,∴AG :AC =1:3,∵AG =2,∴AC =6.【点睛】本题主要考查了全等三角形的性质与判定,解题的关键在于能够熟练掌握全等三角形的相关知识.3.在平面直角坐标系中,点A 的坐标是(0,a ),点B 的坐标(b ,0)且a ,b 满足a 2-12a +36+a -b =0.(1)求A 、B 两点的坐标;(2)如图(1),点C 为x 轴负半轴一动点,OC <OB ,BD ⊥AC 于D ,交y 轴于点E ,求证:OD 平分∠CDB .(3)如图(2),点F 为AB 的中点,点G 为x 正半轴点B 右侧的一动点,过点F 作FG 的垂线FH ,交y 轴的负半轴于点H ,那么当点G 的位置不断变化时,S △AFH -S △FBG 的值是否发生变化?若变化,请说明理由;若不变化,请求出相应结果.【答案】(1)A (0,6),B (6,0);(2)证明见解析;(3)不变化,S △AFH -S △FBG =9.【分析】(1)由非负性可求a ,b 的值,即可求A 、B 两点的坐标;(2)过点O 作OM ⊥BD 于M ,ON ⊥AC 于N ,根据全等三角形的判定和性质解答即可;(3)由于点F 是等腰直角三角形AOB 的斜边的中点,所以连接OF ,得出OF =BF .∠BFO =∠GFH ,进而得出∠OFH =∠BFG ,利用等腰直角三角形和全等三角形的判定和性质以及三角形面积公式解答即可.【解析】解:(1)∵a 2-12a +36+a -b =0∴(a -6)2+a -b =0,∴a -6=0a -b =0 ,即a =b =6.∴A (0,6),B (6,0).(2)如图,过点O 作OM ⊥BD 于M ,ON ⊥AC 于N ,根据题意可知∠ACO +∠CAO =90°.∵BD ⊥AC ,∴∠BCD +∠CBE =90°,∴∠CAO =∠CBE .∵A (0,6),B (6,0),∴OA =OB =6.在△AOC 和△BOE 中,∠CAO =∠EBOOA =OB ∠AOC =∠BOE =90°,∴△AOC ≅△BOE (ASA ).∴OE =OC ,AC =BE ,S △AOC =S △BOE .∴12AC ∙ON =12BE ∙OM ,∴OM =ON ,∴点O 一定在∠CDB 的角平分线上,即OD 平分∠CDB .(3)如图,连接OF ,∵△AOB 是等腰直角三角形且点F 为AB 的中点,∴OF ⊥AB ,OF =FB ,OF 平分∠AOB .∴∠OFB =∠OFH +∠HFB =90°.又∵FG ⊥FH ,∴∠HFG =∠BFG +∠HFB =90°,∴∠OFH =∠BFG .∵∠FOB =12∠AOB =45°,∴∠FOH =∠FOB +∠HOB =45°+90°=135°.又∵∠FBG =180°-∠ABO =180°-45°=135°,∴∠FOH =∠FBG .在△FOH 和△FBG 中∠OFH =∠BFGOF =BF ∠FOH =∠FBG,∴△FOH ≅△FBG (ASA ).∴S △FOH =S △FBG ,∴S △AFH -S △FBG =S △AFH -S △FOH =S △FOA =12S △AOB =12×12OA ∙OB =14×6×6=9.故不发生变化,且S △AFH -S △FBG =9.【点睛】本题为三角形综合题,考查非负数的性质,角平分线的判定,等腰直角三角形的性质和判定、全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,正确添加辅助线,构造全等三角形解决问题,属于中考压轴题.类型二、过边上的点向角平分线作垂线构造等腰三角形2已知:ΔABC 中,D 为BC 的中点,AG 平分∠BAC ,CG ⊥AG 于G ,连结DG ,若AB =6,AC =4,求DG 的长.【答案】DG =1【分析】延长CG 交AB 于点E . 根据等腰三角形的判定与性质得CG =EG ,AE =AC ,再根据三角形中位线的性质得出DG =12BE =12(AB -AC ),从而得出DG 的长.【详解】解:延长CG 交AB 于点E .∵AG 平分∠BAC ,CG ⊥AG 于G ,∴CG =EG ,AE =AC =4,∴BE =AB -AC =2,∵CG =EG ,D 为BC 的中点,∴DG =12BE =1.故答案为DG =1.【点睛】本题考查等腰三角形的判定与性质,三角形中位线定理,根据题意作出辅助线,利用三角形中位线定理求解是解题的关键. 1.已知:等腰直角三角形ABC 中,∠ACB =90°;AC =BC ;∠1=∠3;BE ⊥AD .求证:BE =12AD .【答案】见解析.【分析】延长AC 、BE 交于F ,首先由ASA 证明△AEF ≌△AEB ,得到BE =12BF ,然后再次通过ASA 证明△ACD ≌△BCF ,得到AD =BF ,问题得解.【解析】证明:延长AC 、BE 交于F ,∵∠1=∠3,BE ⊥AE ,在△AEF 和△AEB 中,∠1=∠3AE =AE ∠AEF =∠AEB =90°,∴△AEF ≌△AEB (ASA),∴FE =BE ,∴BE =12BF ,∵∠ACD =∠BED =90°,∠ADC =∠BDE ,∴∠1=∠2,在△ACD 和△BCF 中,∠ACD =∠BCF =90°AC =BC ∠1=∠2,∴△ACD ≌△BCF (ASA ),∴AD =BF ,∴BE =12AD .【点睛】本题主要考查了全等三角形的判定和性质,正确作出辅助线,两次证明全等是解题关键,也考查学生的推理能力,题目比较好,有一定的难度. 2.如图,在△ABC 中,∠C =90°,BC=AC ,D 是AC 上一点,AE ⊥BD 交BD 的延长线于E ,AE =12BD ,且DF ⊥AB 于F ,求证:CD =DF 【答案】见解析【解析】证明:延长AE 、BC 交于点F . 如图所示:∵AE ⊥BE ,∴∠BEA =90°,又∠ACF =∠ACB =90°,∴∠DBC +∠AFC =∠FAC +∠AFC =90°,∴∠DBC =∠FAC ,在△ACF 和△BCD 中,∠ACF =∠BCD =90°AC =BC ∠FAC =∠DBC,∴△ACF ≌△BCD (ASA ),∴AF =BD .又AE =12BD ,∴AE =12AF ,即点E 是AF 的中点,∴AB =BF ,∴BD 是∠ABC 的角平分线,∵∠C =90°,DF ⊥AB 于F ,∴CD =DF .类型三、利用角平分线的性质,在角两边截长补短3如图,在ΔABC 中,AB >AC ,AD 平分∠BAC 交BC 于D,求证:AB -AC >BD -CD .【答案】详见解析【分析】可以在AB 上截取AE =AC ,构造三角形全等,再结合三角形三边关系可证得结论.【详解】在AB 上截取AE =AC ,则BE=AB-AC,在△AED和△ACD中,AE=AC∠EAD=∠CADAD=AD,∴△AED≌△ACD(SAS),∴DE=DC,在△BDE中,BD-DE<BE(三角形两边之差小于第三边),∴BE>BD-CD,即AB-AC>BD-CD.【点睛】本题考查了全等三角形的判定与性质,三角形三边关系,构造三角形全等是解题的关键.1.如图所示,在ΔABC中,∠ACB=60°,AE,BD是ΔABC的角平分线,AE,BD交于点G,求证:GD=GE.【答案】详见解析【分析】在AB上截AF=AD,连接FG,根据角平分线的性质、结合三角形内角和定理可得∠AGD=60°,∠AGB=120°,证明ΔADG≌ΔAFG,得GD=GF,∠AGD=∠AGF=60°,可证得ΔBGF≌ΔBGE,即可得GF=GE=GD.【解析】证明:在AB上截AF=AD,连接FG,∵AE平分∠BAC,∴∠EAC=∠EAB,又∵AG=AG,∴ΔADG≌ΔAFG ,∴GD=GF,∠AGD=∠AGF,∵∠ACB=60°,AE,BD是ΔABC的角平分线,∴∠AGB=180°-12∠CAB-12∠CBA=180°-12∠CAB+∠CBA=120°∴∠AGD=∠AGF=∠BGF=∠BGE=60°,∵∠BGF =∠BGEBG =BG∠GBF =∠GBE∴ΔBGF ≌ΔBGE ASA ,∴GF =GE ,∴GD =GE .【点睛】本题考查角平分线的性质、全等三角形的判定和性质,作辅助线是解题的关键.2.阅读下面材料:小明遇到这样一个问题:如图一,△ABC 中,∠A =90°,AB =AC ,BD 平分∠ABC ,猜想线段AD 与DC 数量关系.小明发现可以用下面方法解决问题:作DE ⊥BC 交BC 于点E :(1)根据阅读材料可得AD 与DC 的数量关系为.(2)如图二,△ABC 中,∠A =120°,AB =AC ,BD 平分∠ABC ,猜想线段AD 与DC 的数量关系,并证明你的猜想.(3)如图三,△ABC 中,∠A =100°,AB =AC ,BD 平分∠ABC ,猜想线段AD 与BD 、BC 的数量关系,并证明你的猜想.【答案】(1)CD =2AD ;(2)CD =3AD ;(3)BC =AD +BD .【分析】(1)由角平分线的性质可得AD =DE ,根据∠A =90°,AB =AC ,可得∠C =45°,由DE ⊥BC 可得△DEC 是等腰直角三角形,可得CD =2DE ,进而可得答案;(2)在BC 上截取BE =AB ,连接DE ,利用SAS 可证明△ABD ≌△EBD ,可得AD =DE ,∠BED =∠A =120°,由等腰三角形的性质可得∠C =30°,利用三角形外角性质可得∠CDE =90°,利用含30°角的直角三角形的性质即可得答案;(3)在BC 上取一点E ,使BE =BD ,作DF ⊥BA 于F ,DG ⊥BC 于G ,由角平分线的性质就可以得出DF =DG ,利用AAS 可证明△DAF ≌△DEG ,可得DA =DE ,利用外角性质可求出∠EDC =40°,进而可得DE =CE ,即可得出结论.【解析】(1)∵∠A =90°,BD 平分∠ABC ,DE ⊥BC ,∴DE =AD ,∵∠A =90°,AB =AC ,∴∠C =45°,∴△CDE 是等腰直角三角形,∴CD =2DE =2AD ,故答案为CD =2AD(2)如图,在BC 上截取BE =AB ,连接DE ,∵BD 平分∠ABC ,∴∠ABD =∠DBE ,在△ABD 和△EBD 中,AB =BE∠ABD=∠DBE BD =BD,∴△ABD ≌△EBD ,∴DE =AD ,∠BED =∠A =120°,∵AB =AC ,∴∠C =∠ABC =30°,∴∠CDE =∠BED -∠C =90°,∴CD =3DE =3AD .(3)如图,在BC 上取一点E ,是BE =BD ,作DF ⊥BA 于F ,DG ⊥BC 于G ,∴∠DFA =∠DGE =90°.∵BD 平分∠ABC ,DF ⊥BA ,DG ⊥BC ,∴DF =DG .∵∠BAC =100°,AB =AC ,∴∠FAD =80°,∠ABC =∠C =40°,∴∠DBC =20°,∵BE =BD ,∴∠BED =∠BDE =80°,∴∠FAD =∠BED .在△DAF 和△DEG 中,∠DFA =∠DGE∠FAD =∠BED DF =DG,∴△DAF ≌△DEG (AAS ),∴AD =ED .∵∠BED =∠C +∠EDC ,∴80°=40+∠EDC ,∴∠EDC =40°,∴∠EDC =∠C ,∴DE =CE ,∴AD =CE .∵BC =BE +CE ,∴BC =BD +AD .【点睛】本题考查了等腰三角形的性质的运用,角平分线的性质的运用,全等三角形的判定及性质的运用,解答时合理添加辅助线是解答本题的关键.3.如图,已知B (-1,0),C (1,0),A 为y 轴正半轴上一点,点D 为第二象限一动点,E 在BD 的延长线上,CD 交AB 于F ,且∠BDC =∠BAC .(1)求证:∠ABD =∠ACD ;(2)求证:AD 平分∠CDE ;(3)若在点D 运动的过程中,始终有DC =DA +DB ,在此过程中,∠BAC 的度数是否变化?如果变化,请说明理由;如果不变,请求出∠BAC 的度数.【答案】(1)见解析;(2)见解析;(3)不变,60°【分析】(1)根据∠BDC=∠BAC,∠DFB=∠AFC,再结合∠ABD+∠BDC+∠DFB=∠BAC+∠ACD +∠AFC=180°,即可得出结论;(2)过点A作AM⊥CD于点M,作AN⊥BE于点N.运用“AAS”证明△ACM≌△ABN得AM=AN.根据“到角的两边距离相等的点在角的平分线上”得证;(3)运用截长法在CD上截取CP=BD,连接AP.证明△ACP≌ABD得△ADP为等边三角形,从而求∠BAC的度数.【解析】(1)证明:∵∠BDC=∠BAC,∠DFB=∠AFC,又∵∠ABD+∠BDC+∠DFB=∠BAC+∠ACD+∠AFC=180°,∴∠ABD=∠ACD;(2)过点A作AM⊥CD于点M,作AN⊥BE于点N.则∠AMC=∠ANB=90°,∵OB=OC,OA⊥BC,∴AB=AC,∵∠ABD=∠ACD,∴△ACM≌△ABN(AAS),∴AM=AN,∴AD平分∠CDE(到角的两边距离相等的点在角的平分线上);(3)∠BAC的度数不变化.在CD上截取CP=BD,连接AP.∵CD=AD+BD,∴AD=PD,∵AB=AC,∠ABD=∠ACD,BD=CP,∴△ABD≌△ACP,∴AD=AP,∠BAD=∠CAP,∴AD=AP=PD,即△ADP是等边三角形,∴∠DAP=60°,∴∠BAC=∠BAP+∠CAP=∠BAP+∠BAD=60°.【点睛】此题考查全等三角形的判定与性质,运用了角平分线的判定定理和“截长补短”的数学思想方法,综合性较强.4.如图1,点A、D在y轴正半轴上,点B、C分别在x轴上,CD平分∠ACB与y轴交于D点,∠CAO=90°-∠BDO.(1)求证:AC=BC;(2)在(1)中点C的坐标为4,0,点E为AC上一点,且∠DEA=∠DBO,如图2,求BC+EC的长;(3)在(1)中,过D作DF⊥AC于F点,点H为FC上一动点,点G为OC上一动点,(如图3),当点H在FC上移动、点G在OC上移动时,始终满足∠GDH=∠GDO+∠FDH,试判断FH、GH、OG这三者之间的数量关系,写出你的结论并加以证明.【答案】(1)见解析;(2)8;(3)GH=FH+OG,证明见解析.【分析】(1)结合题意易得∠CAO=∠CBD,从而易证△CAO≌△CBD AAS得到结论;(2)如图所示,过D作DN⊥AC于N点,结合(1)易证得Rt△BDO≌Rt△EDN HL及Rt△CDO≌Rt△CDN HL,由全等三角形的性质可求解;(3)如图所示,在x轴的负半轴上取OM=FH,连接DM,易证得△DFH≌△DOM SAS,得到DH= DM及∠1=∠ODM,结合题意易得∠GDH=∠GDM,再证得△GDH≌△GDM SAS得到MG=GH从而得到结论.【解析】(1)证明:∵∠CAO=90°-∠BDO,∠CBD=90°-∠BDO,∴∠CAO=∠CBD,∵CD平分∠ACB,∴∠ACD=∠BCD,在△CAD和△CBD中,∠CAO=∠CBD ∠ACD=∠BCD CD=CD,∴△CAD≌△CBD AAS,∴AC=BC;(2)解:由(1)知∠DEA=∠DBO=∠CAD,∴BD=AD=DE,如图所示,过D作DN⊥AC于N点,∵CD平分∠ACB,∴DO=DN,在Rt△BDO和Rt△EDN中,BD=DE DO=DN,∴Rt△BDO≌Rt△EDN HL,∴BO=EN,在Rt△CDO和Rt△CDN中,CD=CD DO=DN,∴Rt△CDO≌Rt△CDN HL,∴CO=CN,∴BC+EC=BO+OC+CN-EN=2OC=8;(3)GH=FH+OG.∵CD平分∠ACB,在x轴的负半轴上取OM=FH,连接DM,如图所示:在△DFH和△DOM中,DF=DO∠DFH=∠DOM OM=FH, ∴△DFH≌△DOM SAS,∴DH=DM,∠1=∠ODM,∴∠GDH=∠1+∠2=∠ODM+∠2=∠GDM,在△GDH和△GDM中,DH=DM∠GDH=∠GDM DG=DG,∴△GDH≌△GDM SAS,∴MG=GH,∴GH=MG=OM+OG=FH+OG.【点睛】本题考查了角平分线的性质,全等三角形的判定和性质的综合运用;解题的关键是熟练掌握全等三角形的判定和性质的综合运用.课后训练1如图,在ΔABC中,∠B=60°,AD、CE分别是∠BAC、∠ACB的平分线,AD、CE相交于点F,试判断FE和FD之间的数量关系.【答案】详见解析【分析】如图,过点F作FH⊥BC,FG⊥AB,垂足分别为H、G,根据角平分线,可得点F是ΔABC的内心,则有FG=FH,继而根据三角形内心的性质可得∠FDH=∠FEG,从而可得ΔFDH≌ΔFEG,继而可得FE=FD.【详解】FE=FD,理由如下:如图,过点F作FH⊥BC,FG⊥AB,垂足分别为H、G.∵F是∠BAC,∠ACB的平分线AD、CE的交点,∴F为ΔABC的内心,∴FG=FH.∵∠B=60°,∴∠FAC+∠FCA=12∠BAC+∠BCA=60°,又∵∠FDH=∠B+∠BAD=60°+∠BAD;∠FEG=∠BAD+∠FAC+∠FCA=60°+∠BAD,∴∠FDH=∠FEG,又GH=FH,∴ΔFDH≌ΔFEG,∴FD=FE.【点睛】本题考查了三角形的内心的性质,全等三角形的判定与性质解题的关键是注意数形结合思想的应用,注意辅助线的作法.2如图,在ΔABC中,∠ABC=2∠C,BE平分∠ABC,交AC于E,AD⊥BE于D,求证:AC=2BD.【答案】详见解析【分析】延长BD至N,使DN=BD,易得AD垂直平分BN,继而证得AE=EN,则可证得结论.【详解】延长BD至N,使DN=BD,连接AN.∵AD⊥BE,∴AD垂直平分BN,∴AB=AN,∴∠N=∠ABN,又∵BE平分∠ABC,∠ABC=2∠C,∴∠ABN=∠NBC=∠C,∴∠NBC=∠C,∴AN∥BC,∴∠C=∠NAC,∴∠NAC=∠N,∴AE=EN,∵BE=EC,∴AC=BN=2BD.【点睛】本题考查了等腰三角形的性质与判定、线段垂直平分线的性质以及平行线的判定与性质.注意掌握辅助线的作法,注意数形结合思想的应用.3如图,在△ABC中,AB=AC,∠A=100°,BD是∠ABC的平分线,延长BD至点E,DE=AD,试求∠ECA的度数.【答案】40°【分析】在BC上截取BF=AB,连接DF,通过证明△ABD≌△FBD SAS,可得∠DFC=180°-∠A= 80°,再通过证明△DCE≌△DCF SAS,即可求得∠ECA=∠DCB=40°【详解】解:如图,在BC 上截取BF =AB ,连接DF ,∵BD 是∠ABC 的平分线,∴∠ABD =∠FBD ,在△ABD 和△FBD 中,AB =FB ,∠ABD =∠FBD ,BD =BD ,∴△ABD ≌△FBD SAS ,∴∠BFD =∠A ,AD =DF ,∴DE =DF ,∴∠DFC =180°-∠A =80°,又∵∠ABC =∠ACB =40°,∴∠FDC =60°,∵∠EDC =∠ADB =180°-∠ABD -∠A =60°,∴∠EDC =∠FDC ,在△DCE 和△DCF 中,DE =DF ,∠EDC =∠FDC ,DC =DC ,∴△DCE ≌△DCF SAS ,故∠ECA =∠DCB =40°.【点睛】本题考查了全等三角形的问题,掌握全等三角形的性质以及判定定理是解题的关键.4如图1,在△ABC 中,CM 是AB 边的中线,∠BCN =∠BCM 交AB 延长线于点N ,2CM =CN.(1)求证AC =BN ;(2)如图2,NP 平分∠ANC 交CM 于点P ,交BC 于点O ,若∠AMC =120°,CP =kAC ,求CP CM的值.【答案】(1)见解析;(2)2k k +1【分析】(1)延长CM 至点D ,使CM =DM ,可证ΔACM ≅ΔBDM ,由全等三角形的性质从而得出AC =BD ,根据题目已知,可证ΔDCB ≅ΔNCB ,由全等三角形的性质从而得出BN =BD ,等量代换即可得出答案;(2)如图所示,作CQ =CP ,可证ΔCPO ≅ΔCQO ,由全等三角形的性质相等角从而得出∠1=∠2=∠3,进而得出∠4=∠5,故可证ΔNOB ≅ΔNOQ 等量转化即可求出CP CM的值.【详解】(1)如图1所示,延长CM 至点D ,使CM =DM ,在△ACM 与△BDM 中,CM =DM∠AMC =∠BMD AM =BM,∴ΔACM ≅ΔBDM ,∴AC =BD ,∵2CM =CN ,∴CD =CN ,在△DCB 与△NCB 中,CD =CN∠DCB =∠NCB CB =CB,∴ΔDCB ≅ΔNCB ,∴BN =BD ,∴AC =BN ;(2)如图所示,∵∠AMC =120°,∴∠CMN =60°,∵NP 平分∠MNC ,∠BCN =∠BCM ,∠PNC +∠BCN =12∠AMC =60°,∴∠CON =120°,∠COP =60°,∴∠CMN +∠BOP =180°,作CQ =CP ,在△CPO 与△CQO 中,CQ =CP∠QCO =∠PCO CO =CO,∴ΔCPO ≅ΔCQO ,∴∠1=∠2=∠3,∴∠4=∠5,在△NOB 与△NOQ 中,∠4=∠5∠BNO =∠QNO NO =NO,∴ΔNOB ≅ΔNOQ ,∴BN =NQ ,∴CN =CP +NB ,∴2CM =CP +AC ,设AC =a ,∴CP =ka ,CM =a (k +1)2,∴CP CM=2k k +1.【点睛】本题考查全等三角形的综合应用,掌握全等三角形的判定与性质是解题的关键.5如图,在△ABC 中,AD为BC 边上的高,AE 是∠BAD 的角平分线,点F 为AE 上一点,连接BF ,∠BFE =45°.(1)求证:BF平分∠ABE;(2)连接CF交AD于点G,若SΔABF=SΔCBF,求证:∠AFC=90°;(3)在(2)的条件下,当BE=3,AG=4.5时,求线段AB的长.【答案】(1)见解析(2)见解析(3)7.5【分析】(1)根据AE是∠BAD的角平分线和∠BFE=45°得2∠FBA+2∠BAF=90°,再结合AD为BC边上的高得出∠EBF=∠FBA即可证明;(2)过点F作FM⊥BC于点M,FN⊥AB于点N,证明△ABF≅△CBF,得出∠AFB=∠CFB,再根据∠BFE=45°,解出∠AFB=∠CFB=135°即可证明;(3)根据△ABF≅△CBF及AD为BC边上的高证明△AFG≅△CFE,得出AG=EC=4.5,再根据BE= 3,解得BC=BE+EC=7.5,结合△ABF≅△CBF即可求出AB=BC=7.5;【详解】(1)证明:∵AE是∠BAD的角平分线,∴∠BAD=2∠BAF.∵∠BFE=45°,∴∠FBA+∠BAF=45°.∴2∠FBA+2∠BAF=90°.∵AD为BC边上的高,∴∠EBF+∠FBA+2∠BAF=90°.∴∠EBF=∠FBA.∴BF平分∠ABE.(2)过点F作FM⊥BC于点M,FN⊥AB于点N,∵BF平分∠ABE,且FM⊥BC,FN⊥AB,∴FM=FN.∵SΔABF=SΔCBF,∴AB=BC,∵BF平分∠ABE,∴∠ABF=∠CBF,在△ABF和△CBF中,AB=BC∠ABF=∠CBF BF=BF∴△ABF≅△CBF(SAS),∴∠AFB=∠CFB,∵∠BFE=45°,∴∠AFB =∠CFB =135°,∴∠AFC =90°,(3)∵△ABF ≅△CBF ,∴AF =FC ,∠AFC =90°,∴∠AFC =∠EFC ,∵AD 为BC 边上的高,∴∠ADE =90°,∴∠EAD +∠AEC =∠FCE +∠AEC ,∴∠EAD =∠FCE .在△AFG 和△CFE 中,∠EAD =∠FCEAF =CF∠AFC =∠EFC∴△AFG ≅△CFE (ASA ).∴AG =EC =4.5,∵BE =3,∴BC =BE +EC =7.5,∵△ABF ≅△CBF ,∴AB =BC =7.5.【点睛】本题主要考查了全等三角形的证明以及性质运用,角平分线的判定以及基本性质,熟练掌握全等三角形的几种判定方法以及角平分线的判定是解答该题的关键.6已知△ABC 中,BE 平分∠ABC ,BE 交AC 于点E ,CD 平分∠ACB ,交AB 于点D ,BE与CD 交于点O .(1)如图1,求证:∠BOC =90°+12∠BAC .(2)如图2,连接OA ,求证:OA 平分∠BAC .(3)如图3,若∠BAC =60°,BD =4,CE =2,求OD OC的值.【答案】(1)见解析(2)详见解析(3)23【分析】(1)由角平分线的性质得出∠OBC=12∠ABC,∠OCB=12∠ACB,由三角形的内角和定理得出∠ABC+∠ACB=180°-∠BAC,∠BOC+∠OBC+∠OCB=180°,代入即可得出结论;(2)过点O作ON⊥BC于N,OM⊥AB于M,OK⊥AC于K,证明OM=OK,则点O在∠BAC的平分线上,即可得出结论;(3)过点B作BH⊥CD交CD的延长线于点H,过点O作OF平分∠BOC交BC于点F,过点O作ON⊥BC于N,OM⊥AB于M,证明∠BOF=∠BOD,∠COF=∠COE,由角平分线的性质得出∠OBF=∠OBD,∠OCF=∠OCE,由ASA证得△BOF≌△BOD,BF=BD=4,由ASA证得△COF≌△COE,CF=CE=2,求出BC=6,由S△BOD:S△BOC=12OD⋅BH:12OC⋅BH=OD:OC,S△BOD:S△BOC=12BD⋅OM:12BC⋅ON=BD:BC,进行计算即可得出结论.【详解】(1)证明:∵BE平分∠ABC,CD平分∠ACB,∴∠OBC=12∠ABC,∠OCB=12∠ACB,∵∠ABC+∠ACB+∠BAC=180°,∴∠ABC+∠ACB=180°-∠BAC,∵∠BOC+∠OBC+∠OCB=180°,∴∠BOC=180°-∠OBC+∠OCB=180°-12∠ABC+12∠ACB=180°-12∠ABC+∠ACB=180°-12180°-∠BAC=180°-90°+12∠BAC=90°+12∠BAC;(2)证明:如图,过点O作ON⊥BC于N,OM⊥AB于M,OK⊥AC于K,∵BE平分∠ABC,CD平分∠ACB,∴OM=ON,ON=OK,∴OM=OK,∴点O在∠BAC的平分线上,∴OA平分∠BAC;(3)解:如图,过点B作BH⊥CD交CD的延长线于点H,过点O作OF平分∠BOC交BC于点F,过点O作ON⊥BC于N,OM⊥AB于M,∵∠BAC =60°,∴∠BOC =90°+12∠BAC =120°,∴∠BOD =∠COE =180°-∠BOC =180°-120°=60°,∵OF 平分∠BOC ,∴∠BOF =∠COF =12∠BOC =60°,∴∠BOF =∠BOD ,∠COF =∠COE ,∵BE 平分∠ABC ,CD 平分∠ACB ,∴∠OBF =∠OBD ,∠OCF =∠OCE ,在△BOF 和△BOD 中,∠OBF =∠OBDBO =BO ∠BOF =∠BOD,∴△BOF ≌△BOD ASA ,∴BF =BD =4,在△COF 和△COE 中,∠OCF =∠OCECO =CO ∠COF =∠COE,∴△COF ≌△COE ASA ,∴CF =CE =2,∴BC =BF +CF =4+2=6,∵S △BOD :S △BOC =12OD ⋅BH :12OC ⋅BH =OD :OC ,S △BOD :S △BOC =12BD ⋅OM :12BC ⋅ON =BD :BC ,∴OD OC =BD BC=46=23.【点睛】本题是三角形综合题,主要考查了全等三角形的判定与性质、角平分线的判定与性质、三角形内角和定理、三角形面积的计算等知识,熟练掌握角平分线的性质与判定以及全等三角形的判定与性质是解题的关键.7已知:在ΔABC 和ΔDEC 中,AC =BC ,DC =EC ,∠ACB =∠ECD =α.(1)如图1,A ,C ,D 在同一直线上,延长AE 交BD 于F ,求证:AF ⊥BD ;(2)如图2,AE 与BD 交于F ,G 在AD 上,若FG 平分∠AFD ,求证:点C 在直线FG 上.【答案】(1)见解析(2)见解析【分析】(1)先说明∠ACB =∠ECD =12×180°=90°,根据SAS 证明ΔACE ≌ΔBCD ,得出∠CAE =∠CBD ,说明∠CAE +∠CDB =90°,即可得出答案;(2)连接CF ,过点C 作CM ⊥BD 于点M ,CN ⊥AE 于点N ,根据SAS 证明ΔBCD ≌ΔACE 得出∠CBM =∠CAN ,根据AAS 证明ΔCBM ≌ΔCAN ,得出CM =CN ,说明CF 平分∠MFN ,得出∠AFG =∠DFG ,证明∠CFM +∠MFA +∠AFG =∠CFN +∠NFD +∠DFG =180°即可得出结论.【详解】(1)证明:∵A ,C ,D 在同一直线上,∠ACB =∠ECD =α,∴∠ACB =∠ECD =12×180°=90°,∵在ΔACE 和ΔBCD 中AC =BC∠ACE =∠BCD CE =CD,∴ΔACE ≌ΔBCD SAS ,∴∠CAE =∠CBD ,∵∠CBD +∠BDC =90°,∴∠CAE +∠CDB =90°,∴∠AFD =180°-∠CAE +∠CDB =90°,∴AF ⊥BD .(2)证明:连接CF ,过点C 作CM ⊥BD 于点M ,CN ⊥AE 于点N ,如图所示:∵∠ACB =∠DCE ,∴∠ACB +∠ACD =∠ACD +∠DCE ,即∠BCD =∠ACE ,∵在ΔBCD 和ΔACE 中BC =AC∠BCD =∠ACE CD =CE,∴ΔBCD ≌ΔACE SAS ,∴∠CBM =∠CAN ,∵在ΔCBM 和ΔCAN 中∠CBM =∠CAN∠CMB =∠CNA =90°CB =CA,∴ΔCBM ≌ΔCAN ,∴CM =CN ,∵CM⊥BD,CN⊥AE,∴CF平分∠MFN,∴∠MFC=∠NFC,∵FG平分∠AFD,∴∠AFG=∠DFG,∵∠MFA=∠NFD,∴∠CFM+∠MFA+∠AFG=∠CFN+∠NFD+∠DFG,∵∠CFM+∠MFA+∠AFG+∠CFN+∠NFD+∠DFG=360°,∴∠CFM+∠MFA+∠AFG=∠CFN+∠NFD+∠DFG=180°,∴C、F、G在同一直线上,即点C在直线FG上.【点睛】本题主要考查了全等三角形的判定和性质,角平分线的性质,垂直的定义,解题的关键是作出辅助线,构造全等三角形.。
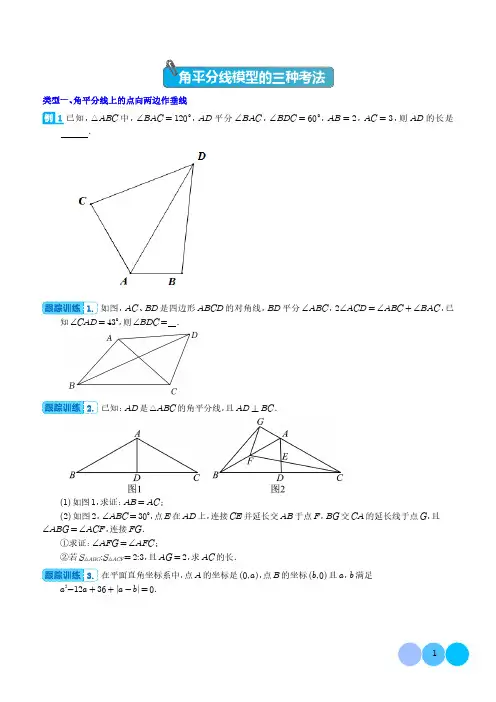
中考常考几何模型 专题16 角平分线四大模型 1、角平分线上的点向两边作垂线 如图,P 是∠MON 的平分线上一点,过点 P 作 PA⊥OM 于点 A,PB⊥ON 于点 B。 结论:PB=PA。
2、截取构造对称全等 如图,P 是∠MON 的平分线上一点,点 A 是射线 OM 上任意一点,在 ON上截取 OB=OA,连接 PB。
结论:△OPB≌△OPA。
3、 角平分线+垂线构造等腰三角形 如图,P 是∠MO 的平分线上一点,AP⊥OP 于 P 点,延长 AP 于点 B。 结论:△AOB 是等腰三角形。
4、角平分线+平行线 如图,P 是∠MO 的平分线上一点,过点 P 作 PQ∥ON,交 OM 于点 Q。结论:△POQ 是等腰三角形。 模型精练: 1.(2019•东平县二模)如图,△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P,若∠BPC=40°,则∠CAP=( )
A.40° B.45° C.50° D.60° 【点睛】根据外角与内角性质得出∠BAC的度数,再利用角平分线的性质以及直角三角形全等的判定,得出∠CAP=∠FAP,即可得出答案
【解析】解:延长BA,作PN⊥BD,PF⊥BA,PM⊥AC,
设∠PCD=x°, ∵CP平分∠ACD, ∴∠ACP=∠PCD=x°,PM=PN, ∵BP平分∠ABC, ∴∠ABP=∠PBC,PF=PN, ∴PF=PM, ∵∠BPC=40°, ∴∠ABP=∠PBC=∠PCD﹣∠BPC=(x﹣40)°, ∴∠BAC=∠ACD﹣∠ABC=2x°﹣(x°﹣40°)﹣(x°﹣40°)=80°, ∴∠CAF=100°, 在Rt△PFA和Rt△PMA中, {𝑃𝐴=𝑃𝐴𝑃𝑀=𝑃𝐹,
∴Rt△PFA≌Rt△PMA(HL), ∴∠FAP=∠PAC=50°. 故选:C. 2.(2019•桂平市期末)如图,在△ABC中,∠C=90°,AD平分∠CAB,BC=12cm,BD=8cm,那么点D到直线AB的距离是( )
A.2cm B.4cm C.6cm D.10cm 【点睛】先求出CD的长,过点D作DE⊥AB于点E,根据角平分线上的点到角的两边的距离相等的性质可得DE=CD,从而得解.
【解析】解:如图,过点D作DE⊥AB于点E, ∵BC=12cm,BD=8cm, ∴CD=BC﹣BD=12﹣8=4cm, ∵∠C=90°,AD平分∠CAB, ∴DE=CD=4cm, 即点D到直线AB的距离是4cm. 故选:B. 3.(2020•浙江自主招生)如图,在△ABC中,AD是∠A的外角平分线,P是AD上异于A的任意一点,设PB=m,PC=n,AB=c,AC=b,则(m+n)与(b+c)的大小关系是( )
A.m+n>b+c B.m+n<b+c C.m+n=b+c D.无法确定 【点睛】在BA的延长线上取点E,使AE=AC,连接EP,证明△ACP和△AEP全等,推出PE=PC,根据三角形任意两边之和大于第三边即可得到m+n>b+c.
【解析】解:在BA的延长线上取点E,使AE=AC,连接EP,
∵AD是∠A的外角平分线, ∴∠CAD=∠EAD, 在△ACP和△AEP中,{𝐴𝐸=𝐴𝐶∠𝐶𝐴𝐷=∠𝐸𝐴𝐷𝐴𝑃=𝐴𝑃, ∴△ACP≌△AEP(SAS), ∴PE=PC, 在△PBE中,PB+PE>AB+AE, ∵PB=m,PC=n,AB=c,AC=b, ∴m+n>b+c. 故选:A. 4.(2019•兰山区一模)如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=11,则线段MN的长为 11 .
【点睛】根据平行线的性质得出∠MEB=∠EBC,∠NEC=∠ECB,根据角平分线定义得出∠MBE=∠EBC,∠NCE=∠ECB,求出∠MEB=∠MBE,∠NEC=∠NCE,推出ME=BM,EN=CN即可.
【解析】解:∵MN∥BC, ∴∠MEB=∠EBC,∠NEC=∠ECB, ∵∠ABC和∠ACB的平分线交于点E, ∴∠MBE=∠EBC,∠NCE=∠ECB, ∴∠MEB=∠MBE,∠NEC=∠NCE, ∴ME=BM,EN=CN, ∵BM+CN=11, ∴EM+EN=11, 即MN=11, 故答案为:11. 5.如图,已知等腰直角三角形ABC中,AB=AC,∠BAC=90°,BF平分∠ABC,CD⊥BD交BF的延长线于点D,试说明:BF=2CD.
【点睛】作BE的中点E,连接AE、AD,根据直角三角形得到性质就可以得出AE=BE=EF,由BD平分∠ABC就可以得出∠ABE=∠DBC=22.5°,从而可以得出∠BAE=∠BAE=∠ACD=22.5°,∠AEF=45°,由∠BAC=90°,∠BDC=90°就可以得出A、B、C、D四点共圆,求出AD=DC,证△ADC≌△AEB推出BE=CD,从而得到结论.
【解析】解:取BF的中点E,连接AE,AD,
∵∠BAC=90°, ∴AE=BE=EF, ∴∠ABD=∠BAE, ∵CD⊥BD, ∴A,B,C,D四点共圆, ∴∠DAC=∠DBC, ∵BF平分∠ABC, ∴∠ABD=∠DBC, ∴∠DAC=∠BAE, ∴∠EAD=90°, ∵AB=AC, ∴∠ABC=45°, ∴∠ABD=∠DBC=22.5°, ∴∠AED=45°, ∴AE=AD, 在△ABE与△ADC中,
{∠𝐴𝐵𝐸=∠𝐷𝐴𝐶∠𝐵𝐴𝐸=∠𝐴𝐶𝐷𝐴𝐸=𝐴𝐷,
∴△ABE≌△ADC, ∴BE=CD, ∴BF=2CD. 6.如图,在△ABC中,∠ABE=2∠C,AD是∠BAC的平分线,BE⊥AD,垂足为E (1)若∠C=30°,求证:AB=2BE. (2)若∠C≠30°,求证:BE=12(AC﹣AB). 【点睛】(1)由BE⊥AD,得到∠AEB=90°,根据已知条件得到∠ABE=60°,根据三角形的内角和得到∠BAE=30°,根据直角三角形的性质即刻得到结论;
(2)根据等腰三角形的性质得到AB=AF,根据等腰三角形的性质得到∠AFE=∠ABE=2∠C,根据三角形外角的性质得到∠C=∠CBF,得到BF=CF,于是得到结论.
【解析】解:(1)∵BE⊥AD, ∴∠AEB=90°, ∵∠ABE=2∠C,∠C=30°, ∴∠ABE=60°, ∴∠BAE=30°, ∴AB=2BE; (2)∵AD是∠BAC的平分线,BE⊥AD, ∴AB=AF, ∴∠AFE=∠ABE=2∠C, ∵∠AFE=∠C+∠CBF, ∴∠C=∠CBF, ∴BF=CF, ∵BF=2BE, ∴CF=AC﹣AB=BE=2BE, ∴BE=12(AC﹣AB). 7.(2019•沂源县期末)如图,在△ABC中,AB=AC,∠ABC=40°,BD是∠ABC的平分线,延长BD至E,使DE=AD,求证:∠ECA=40°.
【点睛】在BC上截取BF=AB,连DF,根据SAS可证明△ABD≌△FBD,得出DF=DA=DE,证明△DCE≌△DCF,故∠ECA=∠DCB=40°.
【解析】证明:在BC上截取BF=AB,连DF,
∵BD是∠ABC的平分线, ∴∠ABD=∠FBD, ∴△ABD≌△FBD(SAS), ∴DF=DA=DE, 又∵∠ACB=∠ABC=40°,∠DFC=180°﹣∠A=80°, ∴∠FDC=60°, ∴∠EDC=∠ADB=180°﹣∠ABD﹣∠A=180°﹣20°﹣100°=60°, ∴△DCE≌△DCF(SAS), 故∠ECA=∠DCB=40°. 8.(2019•临洮县期末)已知△ABC中,AB=AC,∠A=108°,BD平分∠ABC,求证:BC=AC+CD.
【点睛】在线段BC上截取BE=BA,连接DE.则只需证明CD=CE即可.结合角度证明∠CDE=∠CED. 【解析】证明:在线段BC上截取BE=BA,连接DE.
∵BD平分∠ABC, ∴∠ABD=∠EBD=12∠ABC. 在△ABD和△EBD中,
{𝐵𝐸=𝐵𝐴∠𝐴𝐵𝐷=∠𝐸𝐵𝐷𝐵𝐷=𝐵𝐷,
∴△ABD≌△EBD.(SAS) ∴∠BED=∠A=108°,∠ADB=∠EDB. 又∵AB=AC,∠A=108°,∠ACB=∠ABC=12×(180°﹣108°)=36°,
∴∠ABD=∠EBD=18°. ∴∠ADB=∠EDB=180°﹣18°﹣108°=54°. ∴∠CDE=180°﹣∠ADB﹣∠EDB=180°﹣54°﹣54°=72°. ∴∠DEC=180°﹣∠DEB=180°﹣108°=72°. ∴∠CDE=∠DEC. ∴CD=CE. ∴BC=BE+EC=AB+CD. 9.(2019•自贡期中)如图,在四边形ABCD中,BC>BA,AD=DC, (1)若BD⊥CD,∠C=60°,BC=10,求AD的长; (2)若BD平分∠ABC,求证:∠A+∠C=180°.
【点睛】(1)由含30°角的直角三角形的性质求出DC,即可得出答案; (2)在BC上截取BE=BA,连接DE,推出△ABD≌△EBD,推出∠A=∠BED,AD=DE=DC,推出∠BED+∠C=180°,即可得出答案.
【解析】(1)解:∵BD⊥CD,∠C=60°, ∴∠CBD=30°, ∴DC=12BC=5,
∵AD=DC=5; (2)证明:在BC上截取BE=BA,连接DE,如图所示: ∵BD平分∠ABC, ∴∠ABD=∠EBD,