统计学原理课后习题答案 第五章 抽样及参数估计

第一章总论一、判断题1.√2.√3.×4.√5.×6.×7.×8.×二、单选题1.C2.B3.D4.B5.C6.C7.C8.A9.B 10.C 11.A三、多选题1.ABCD（题目中的“五个”应去掉）2.ABE3.BDE4.BE5.AC6.AC第二章统计调查一、判断题1.×2. ×3. ×4. ×5. √6.×7. ×8. ×9. ×10. √ 11. ×12. × 13. ×14. √ 15.√二、单选题1.B2.C3.C4.C5.C6.D7.D8.C9.D 10.D 11.D 12.C 13.A 14.C15.A 16.B 17.A 18.B 19.A 20.D三、多选题1.ABCDE2.ABE3.BDE4.ABCD5.ABCDE第三章统计整理一、判断题1.×2.×3.×4. √5.√6.√7.×8.×9.×10.× 11.√12.√二、单选题1.B2.B3.B4.A5.A6.C7.D8.C9.B 10.C 11.D 12.B 13.B三、多选题1.ADE2.CDE3.ABCD4.CD5.ACD6.ABCD7.CDE8.BC9.BCE四、计算题1.某班学生英语考试成绩频数分配表考试成绩学生人数（人）频率（ %）60 分以下（不及格）37.5060— 70（及格）615.0070— 80（中）1537.5080— 90（良）1230.0090— 100（优）410.00合计40100.002.某生产车间工人日加工零件数频数分配表零件数（件）工人人数（人）频率（%）组距组中值25—30717.50527.530—35615.00532.535—401127.50537.540—45717.50542.545—50922.50547.5合计40100.00——第 4 章综合指标一、判断题1.√2.×3.×4.√5.√6.×7.×8.×9.×10.×11.×12.√13.×14.×15.×三、单选题1. B2. D3. C4. D5. C6. D7. C8. D9. B10. A11. D12. B1. ACE 5. BCD2. ABC6. ABD3.BD7. BCDE4. BCD8. ACE五、计算题1. ⑴企业2008 年2007 年实2008 年销售计划实际完成计划际销售额额为 2007 年销售额比重销售额比重（ %）的百分比（ %）（ %）(%)甲120030122430.911021100111.27乙100025102625.91102.6900114丙180045171043.189********.27合计40001003960100993640108.79⑵ 略2.⑴ 计划完成程度26272728108 % =100100 %⑵ 设在第五年第二季度提前天X完成，则：23752791X100X9191X 45 . 5（天）即提前两个季度（ 6 个月）又 45天半完成 5 年计划。

思考与练习（第五章） BY 缪嘉伦 思考题1. 解释原假设与备择假设的含义，并归纳常见的几种建立原假设与备择假设的原则。

答：原假设（null hypothesis ）通常是研究者想悼念证据予以反对的假设，也称零假设，用H 0表示。

备择假设(alternative hypothesis)通常是研究者想悼念证据予以支持的假设，也称研究假设，用H l 或 H a 表示。

几种常见的原则：第一， 原假设和备择假设是一个完备事件组，而且相互对立。

第二， 在建立原假设时，通常是先确定备择假设，然后再确定原假设。

第三， 在假设检验中，等号“=”总是放在原假设上。

第四， 在面对某一实际问题时，由于不同的研究者有不同的研究目的，即使对同一问题也可能提出截然相反的原假设和备择假设。

第五， 假设检验的目的主要是收集证据拒绝原假设。

3.什么是显著性水平？它对于假设检验决策的意义是什么？与置信水平的区别？答：显著性水平（level of significance ）是指当原假设实际上是正确时，检验统计量落在拒绝域的概率，记为α。

它是人们事先指定的犯第I 类错误概率α的最大允许值。

显著性水平α越小，犯第I 类错误的可能性自然就越小，但犯第∏类错误的可能性随之增大。

置信水平是指变量落在置信区间的可能性，记为1-α。

4.什么是P 值？P 值检验和统计量检验有什么不同？答：P 值（P value ）就是当原假设为真时所得到的样本观察结果或更极端结果出现的概率。

如果P 值很小，说明原假设情况的发生的概率很小，而如果出现了，根据小概率原理，我们就有理由拒绝原假设，P 值越小，我们拒绝原假设的理由越充分。

总之，P 值越小，表明结果越显著。

但是检验的结果究竟是“显著的”、“中度显著的”还是“高度显著的”需要我们自己根据P 值的大小和实际问题来解决。

区别：从显著性水平来比较，如果选择的α值相同，所有检验结论的可靠性都一样；通过计算P 值，可测量出样本观测数据与原假设的值0μ的偏离程度。

第五章练习题一、单项选择题1．抽样推断的目的在于（）A．对样本进行全面调查B．了解样本的基本情况C．了解总体的基本情况D．推断总体指标2．在重复抽样条件下纯随机抽样的平均误差取决于（）A．样本单位数B．总体方差C．抽样比例D．样本单位数和总体方差3．根据重复抽样的资料，一年级优秀生比重为10%，二年级为20%，若抽样人数相等时，优秀生比重的抽样误差（）A．一年级较大B．二年级较大C．误差相同D．无法判断4．用重复抽样的抽样平均误差公式计算不重复抽样的抽样平均误差结果将（）A．高估误差B．低估误差C．恰好相等D．高估或低估5．在其他条件不变的情况下，如果允许误差缩小为原来的1/2 ，则样本容量（）A．扩大到原来的2倍B．扩大到原来的4倍C．缩小到原来的1/4D ．缩小到原来的1/26．当总体单位不很多且差异较小时宜采用（）A．整群抽样B．纯随机抽样C．分层抽样D．等距抽样7．在分层抽样中影响抽样平均误差的方差是（）A．层间方差B．层内方差C．总方差D．允许误差二、多项选择题1．抽样推断的特点有（）A ．建立在随机抽样原则基础上B．深入研究复杂的专门问题C ．用样本指标来推断总体指标D．抽样误差可以事先计算E ．抽样误差可以事先控制2．影响抽样误差的因素有（）A ．样本容量的大小B．是有限总体还是无限总体C ．总体单位的标志变动度D．抽样方法E ．抽样组织方式3．抽样方法根据取样的方式不同分为（）A ．重复抽样B ．等距抽样C ．整群抽样D ．分层抽样E ．不重复抽样4．抽样推断的优良标准是（）A ．无偏性B ．同质性C ．一致性D ．随机性E ．有效性5．影响必要样本容量的主要因素有（）A．总体方差的大小B．抽样方法元） 户）1．抽样推断和全面调查结合运用，既实现了调查资料的 _________ 性，又保证于调查资料的______ 性。

2．在其他条件不变的情况下， 样本容量与抽样误差成 _____ 比；总体各单位的标志变动度 与样本容量成 ______ 比。

第5章 参数估计●1. 从一个标准差为5的总体中抽出一个容量为40的样本，样本均值为25。

（1） 样本均值的抽样标准差x σ等于多少？（2） 在95%的置信水平下，允许误差是多少？解：已知总体标准差σ=5，样本容量n =40，为大样本，样本均值x =25， （1）样本均值的抽样标准差x σn σ405=0.7906 （2）已知置信水平1－α=95%，得 α/2Z =1.96，于是，允许误差是E =nα/2σZ 6×0.7906=1.5496。

●2.某快餐店想要估计每位顾客午餐的平均花费金额，在为期3周的时间里选取49名顾客组成了一个简单随机样本。

（3） 假定总体标准差为15元，求样本均值的抽样标准误差； （4） 在95%的置信水平下，求允许误差；（5） 如果样本均值为120元，求总体均值95%的置信区间。

解：（1）已假定总体标准差为σ=15元， 则样本均值的抽样标准误差为 x σn σ4915=2.1429 （2）已知置信水平1－α=95%，得 α/2Z =1.96，于是，允许误差是E =nα/2σZ 6×2.1429=4.2000。

（3）已知样本均值为x =120元，置信水平1－α=95%，得 α/2Z =1.96， 这时总体均值的置信区间为 nα/2x Z 0±4.2=124.2115.8可知，如果样本均值为120元，总体均值95%的置信区间为（115.8，124.2）元。

●3.某大学为了解学生每天上网的时间，在全校7500名学生中采取不重复抽样方法随机抽取36人，调查他们每天上网的时间，得到下面的数据（单位：小时）：3.3 3.1 6.2 5.8 2.34.15.4 4.5 3.2 4.4 2.0 5.4 2.66.4 1.8 3.5 5.7 2.3 2.1 1.9 1.2 5.1 4.3 4.2 3.6 0.8 1.5 4.71.41.22.93.52.40.53.62.5求该校大学生平均上网时间的置信区间，置信水平分别为90%、95%和99%。

统计学原理课后答案在学习统计学原理课程时，课后习题是非常重要的一部分，通过做习题可以更好地巩固知识点，检验自己的学习成果。

下面是统计学原理课后习题的答案，希望对大家的学习有所帮助。

1. 什么是统计学？统计学是一门研究数据收集、整理、分析和解释的学科。

它可以帮助我们更好地理解数据背后的规律和趋势，从而做出合理的决策。

2. 描述统计学和推断统计学的区别。

描述统计学是通过对已有数据进行总结、整理和分析，以便更好地理解数据的特征和规律；推断统计学则是通过对样本数据进行分析，从而推断总体的特征和规律。

3. 什么是总体和样本？总体是指我们研究的对象的全部集合，而样本是从总体中抽取出来的一部分数据。

通过对样本的分析，我们可以推断总体的特征。

4. 什么是变量？它可以分为哪些类型？变量是指在研究中可能发生变化的因素或特征。

根据变量的性质，可以分为定性变量和定量变量。

定性变量是指描述对象特征的变量，如性别、颜色等；定量变量是指可以用数字来表示的变量，如身高、体重等。

5. 什么是频数和频率？频数是指某一数值在样本或总体中出现的次数；频率是指某一数值在样本或总体中出现的比例，通常用百分比来表示。

6. 什么是概率？概率是指某一事件发生的可能性，通常用0到1之间的数值来表示，0表示不可能发生，1表示肯定发生。

7. 什么是正态分布？正态分布是一种连续的概率分布，其特点是呈钟形曲线，均值、中位数和众数重合，两侧尾部渐进于水平轴。

在实际应用中，很多自然现象和人类行为都呈现出正态分布的特征。

8. 什么是假设检验？假设检验是一种统计推断方法，用于检验关于总体参数的假设是否成立。

通过对样本数据的分析，我们可以得出对总体参数的推断结论。

9. 什么是置信区间？置信区间是指对总体参数的估计范围，通常用于估计总体参数的真实值。

置信区间的计算方法可以根据不同的总体参数和样本数据而定。

10. 什么是相关分析？相关分析是用来研究两个变量之间关系的统计方法，通过相关系数来衡量两个变量之间的相关程度。

《统计学原理》第五章习题河南电大贾天骐一．判断题部分题目1：从全部总体单位中按照随机原则抽取部分单位组成样本，只可能组成一个样本。

（）答案：×题目2：在抽样推断中，全及指标值是确定的、唯一的，而样本指标值是一个随机变量。

（）答案：√题目3：抽样成数的特点是：样本成数越大，则抽样平均误差越大。

（）答案：×题目4：抽样平均误差总是小于抽样极限误差。

（）答案：×题目5：在其它条件不变的情况下，提高抽样估计的可靠程度，则降低了抽样估计的精确程度。

（）答案：√题目6：从全部总体单位中抽取部分单位构成样本，在样本变量相同的情况下，重复抽样构成的样本个数大于不重复抽样构成的样本个数。

（）答案：√题目7：抽样平均误差反映抽样误差的一般水平，每次抽样的误差可能大于抽样平均误差，也可能小于抽样平均误差。

（）答案：√题目8：在抽样推断中，抽样误差的概率度越大，则抽样极限误差就越大于抽样平均误差。

（）答案：√题目9：抽样估计的优良标准有三个：无偏性、可靠性和一致性。

（）答案：×题目10：样本单位数的多少与总体各单位标志值的变异程度成反比，与抽样极限误差范围的大小成正比。

（）答案：×题目11：抽样推断的目的是，通过对部分单位的调查，来取得样本的各项指标。

（）答案：×题目12：用来测量估计可靠程度的指标是抽样误差的概率度。

（）答案：√题目13：总体参数区间估计必须具备三个要素即：估计值、抽样误差范围和抽样误差的概率度。

（）答案：×二．单项选择题部分题目1：抽样平均误差是（）。

A、抽增指标的标准差B、总体参数的标准差C、样本变量的函数D、总体变量的函数答案：A题目2：抽样调查所必须遵循的基本原则是（）。

A、准确性原则B、随机性原则C、可靠性原则 C、灵活性原则答案：B题目3：在简单随机重复抽样条件下，当抽样平均误差缩小为原来的1/2时，则样本单位数为原来的（）。

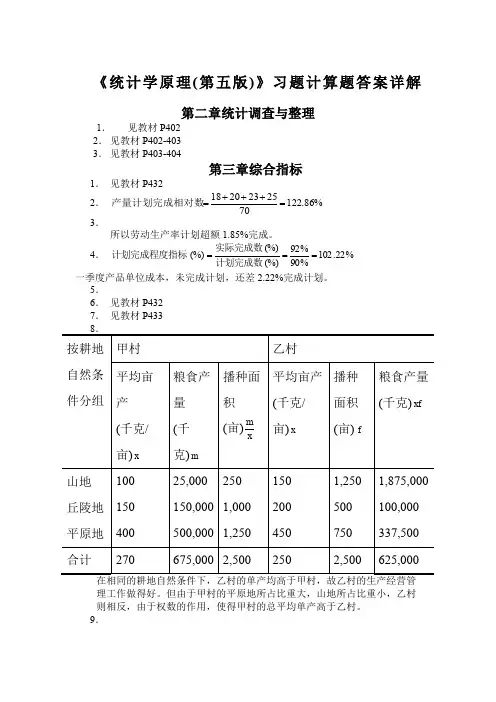
《统计学原理(第五版)》习题计算题答案详解第二章统计调查与整理1． 见教材P402 2． 见教材P402-403 3． 见教材P403-404第三章综合指标1． 见教材P4322． %86.1227025232018=+++=产量计划完成相对数3．所以劳动生产率计划超额1.85%完成。

4． %22.102%90%92(%)(%)(%)===计划完成数实际完成数计划完成程度指标 一季度产品单位成本，未完成计划，还差2.22%完成计划。

5．6． 见教材P432 7． 见教材P433理工作做得好。

但由于甲村的平原地所占比重大，山地所占比重小，乙村则相反，由于权数的作用，使得甲村的总平均单产高于乙村。

9．11．%74.94963.09222.09574.03=⨯⨯=G X 或参照课本P9912．%49.51X %49.105 08.107.105.104.102.1 X 1624632121=-=⨯⨯⨯⨯=∑⋅⋅⋅⋅⋅⋅=G ff n f f G nX X X 平均年利率：平均本利率为：(2)R=500-150=350(千克/亩) (3)“(4)根据以上计算，294.5千克/亩>283.3千克/亩>277.96千克/亩，即M 0>Me>X ，故资料分布为左偏(即下偏)。

(2) 15． 见教材P435 16． 见教材P40417．%86.1227025232018=+++=产量计划完成相对数18．%85.101%108%110%%(%)===计划为上年的实际为上年的计划完成程度指标 劳动生产率计划超额1.85%完成19． %22.102%90%92(%)(%)(%)===计划完成数实际完成数计划完成程度指标一季度产品单位成本未完成计划，实际单位成本比计划规定数高2.22%20． %105%103% %%(%) 计划为上年的计划为上年的实际为上年的计划完成程度指标=∴=1.94% %94.101103%105%% 即计划规定比上年增长计划为上年的解得：==21． 见教材P405 22． 见教材P405理工作做得好。

统计学（第四版）贾俊平 第五章 参数估计 练习题答案5.1（答案精确到小数点后两位）（1）已知：n=49，15σ=，样本均值的标准误差X σ==（2）已知：置信水平：2195%, 1.96Z αα-==，估计误差E=2151.96 4.207Z α== （3）已知120,X =置信水平：2195%, 1.96Z αα-==，E=4.20置信区间为()2120 4.20115.80,124.20X Z α±=±=5.2（答案精确到小数点后两位）（1）置信区间为28900 1.96(8646.97,9153.03)X Z α±=±=（2）置信区间为28900 1.96(8815.48,8984.52)X Z α±=±=（3）置信区间为28900 1.65(8760.55,9039.45)X Z α±=±=（4）置信区间为28900 2.58(8681.95,9118.05)X Z α±=±= 5.3 （1） 表5.3—1置信水平90%上网时间置信区间报告上网时间5.4（答案精确到小数点后两位）（1）已知N=500,n=50，132n =A. 传统方法：320.6450p ==比例置信区间为0.64(0.51,0.77)p ±=±= B. 现代方法：3220.63504p +==+比例置信区间为0.63(0.50,0.76)p ±=±=（2）已知0.8p =0.1≤得到：16n ≥5.5（1）（2）5.6已知2212121214,7,53.2,43.4,96.8,102.0n n X X s s ======，（1）置信水平195%α-=，12μμ- 置信区间为()(()122 1.86,17.74X X t v α-±= （2）置信水平199%α-=，12μμ- 置信区间为()(()1220.19,19.41X X t v α-±=5.8已知1212250,p 40%,p 30%n n ==== （答案精确到小数点后四位）（1）置信水平190%α-= ，12ππ- 的置信区间为 ()()120.10.0300,0.1700p p -±=±=（2）置信水平195%α-= ，12ππ- 置信区间()()120.10.0168,0.1832p p -±±=5.9 有Excel 得，()2212121220.241609,0.076457,0.058375,0.005846, 2.464484,0.405764s s s s F F αα-======所以，方差比的置信区间为()()22112222122, 4.051926,24.61011s s s s F F αα-⎛⎫ ⎪= ⎪ ⎪ ⎪⎝⎭5.10已知置信水平2195%,Z 1.96,120,20E αασ-====≤ 所以，222138.3Z n E σ=≥ ，取n=139。

《统计学》习题五 参考答案、单项选择题：1、抽样误差是指（ ）。

CA 在调查过程中由于观察、测量等差错所引起的误差B 人为原因所造成的误差C 随机抽样而产生的代表性误差D 在调查中违反随机原则出现的系统误差2、抽样平均误差就是（ ）。

DA 样本的标准差B 总体的标准差C 随机误差D 样本指标的标准差3、抽样估计的可靠性和精确度（ ）。

BA 是一致的B 是矛盾的C 成正比D 无关系4、在简单随机重复抽样下，欲使抽样平均误差缩小为原来的三分之一，则样本容量应（ ）。

A A 增加 8 倍B 增加 9 倍C 增加 1.25 倍D 增加 2.25 倍5、当有多个参数需要估计时，可以计算出多个样品容量 n 为满足共同的要求，必要的样本容量 一般应是（ ）。

BA 总体的标志变异程度B 允许误差的大小C 重复抽样和不重复抽样D 样本的差异程度E 估计的可靠度三、填空题：3、 实施概率抽样的前提条件是要具备（ ）。

抽样框4、 对总体参数进行区间估计时，既要考虑极限误差的大小，即估计的（ 虑估计的（ ）问题。

准确性 可靠性四、简答题：1、抽样调查与重点调查的主要不同点。

A 最小的n 值 B 最大的n 值 6、抽样时需要遵循随机原则的原因是（ C 中间的n 值 D 第一个计算出来的n 值）。

CA 可以防止一些工作中的失误B 能使样本与总体有相同的分布C 能使样本与总体有相似或相同的分布D 可使单位调查费用降低二、多项选择题：1、抽样推断中哪些误差是可以避免的（ A 工作条件造成的误差 B D 人为因素形成偏差 E2、区间估计的要素是（ A 点估计值 B D 抽样极限误差 E3、影响必要样本容量的因素主要有（ ）。

A B D系统性偏差 C 抽样随机误差 抽样实际误差）。

A C D样本的分布 C 估计的可靠度总体的分布形式）。

A B C E1、抽样推断就是根据（ ）的信息去研究总体的特征。

样本2、样本单位选取方法可分为（ ）和（ ）。

思考题与练习题参考答案【友情提示】请各位同学完成思考题和练习题后再对照参考答案。

回答正确，值得肯定；回答错误，请找出原因更正，这样使用参考答案，能力会越来越高，智慧会越来越多。

学而不思则罔，如果直接抄答案，对学习无益，危害甚大。

想抄答案者，请三思而后行！第一章绪论思考题参考答案1．不能，英军所有战机=英军被击毁的战机+英军返航的战机+英军没有弹孔的战机，因为英军被击毁的战机有的掉入海里、敌军占领区，或因堕毁而无形等，不能找回；没有弹孔的战机也不可能自己拿来射击后进行弹孔位置的调查。

即便被击毁的战机找回或没有弹孔的战机自己拿来射击进行实验，也不能从多个弹孔中确认那个弹孔是危险的。

2．问题：飞机上什么区域应该加强钢板？瓦尔德解决问题的思想：在他的飞机模型上逐个不重不漏地标示返航军机受敌军创伤的弹孔位置，找出几乎布满弹孔的区域；发现：没有弹孔区域是军机的危险区域。

3．能，拯救和发展自己的参考路径为：①找出自己的优点，②明确自己大学阶段的最佳目标，③拟出一个发扬自己优点，实现自己大学阶段最佳目标的可行计划。

练习题参考答案一、填空题1．调查。

2．探索、调查、发现。

3. 目的。

二、简答题1．瓦尔德；把剩下少数几个没有弹孔的区域加强钢板。

2．统计学解决实际问题的基本思路，即基本步骤是：①提出与统计有关的实际问题；②建立有效的指标体系；③收集数据；④选用或创造有效的统计方法整理、显示所收集数据的特征；⑤根据所收集数据的特征、结合定性、定量的知识作出合理推断；⑥根据合理推断给出更好决策的建议。

不解决问题时，重复第②-⑥步。

3．在结合实质性学科的过程中，统计学是能发现客观世界规律，更好决策，改变世界和培养相应领域领袖的一门学科。

三、案例分析题1．总体：我班所有学生；单位：我班每个学生；样本：我班部分学生；品质标志：姓名；数量标志：每个学生课程的成绩；指标：全班学生课程的平均成绩；指标体系：上学期全班同学学习的科目；统计量：我班部分同学课程的平均成绩；定性数据：姓名；定量数据：课程成绩；离散型变量：学习课程数；连续性变量：学生的学习时间；确定性变量：全班学生课程的平均成绩；随机变量：我班部分同学课程的平均成绩，每个同学进入教室的时间；横截面数据：我班学生月门课程的出勤率；时间序列数据：我班学生课程分别在第一个月、第二个月、第三个月、第四个月的出勤率；面板数据：我班学生课程分别在第一个月、第二个月、第三个月、第四个月的出勤率；选用描述统计。

抽样技术第五章课后答案抽样是统计过程中的一个重要环节，它能提供更有效的统计息。

为了获得更加精确的结果，必须使用适当的抽样方法。

抽样方法包括()。

正确地使用()是指()式中所有抽样变量均可视为相同量。

每一组()个变量与某一组()个变量之间有()种相关性。

A:无关系变量; B:线性关联变量; C:关系-线性关联变量; D:线性相似性; E:线性相关性; F:相关性：对数关系。

一、问题定义给定样本，求所需数量。

分析数据求与所需数量对应的样本。

用多组样本重复抽取一组样本。

问题定义二、问题特征问题1:随机选择一个个体，要求其按照一定的方式计算一下，该个体与被抽到的抽样组的数量相等。

问题2:问题1中要得到的抽样组的数量为：从任意数量个样本的统计意义上（单位为 k)或从任意数量个样本的统计意义上(n、 n)去推断出有多少个样本属于随机选取一种方法计算出来的数量与原问题1中随机抽取一个总样本相等的数量与原问题1中随机抽取一个总样本相等的数量之间有着相关关系。

从该角度出发考虑这种相关性，即可以得出如下结果：本题的基本思路与前面两题类似。

从已知条件出发考虑这个问题中不同群体中所占比例之间的相关性：对于某群体内所有个体来说，个体数量都是相同的比例是这样形成的: a.对于随机变量 N; b.每个个体所占比例=群体人数 b+个体人数 c= B; c.群体人数 a=(1- M) b+个体人数c=(1- N) b+个人人数 c=(1- M) c= C; d、 e、 f三种形式均不是随机变量: a.对于该群体中所有个体来说，个体总数与群体总人数之间呈现线性相关关系: b.对于该群体中所有个体来说唯一没有显著线性关系的就是 a。

三、抽样的基本原理抽样的基本原理是将所有变量用等比例形式分组，然后对每个分组进行统计，以发现该分组与总体之间的相互关系，以及分析样本中的差异。

1所示。

抽样方法分为正向抽样法和反向抽样法。

正向抽样是指将所有变量都作为等值统计量进行正比例随机抽样。

统计学原理课后习题答案第五章抽样及参数估计统计学原理课后习题答案第五章抽样及参数估计1.①由题意可知本题属于：纯随机重复抽样下的总体比例区间估计。

已知：n=1000,82882.8%1000p ==，(Z)195.45%F α=-= ,查表得/2=2Z α 由于不知总体标准差，用样本的标准差代替：p 82.8%282.8% 2.4%Z α±=±?=±即：80.4%P 85.2%≤≤所以该城市拥有彩电家庭比例的置信区间为80.4%—85.2%。

②由题意可知本题属于：重复抽样时比例的必要抽样数目。

已知： 82.8%p =，5%p ?= ，(Z)199.73%F α=-= ,查表得/2=3Z α 由于不知总体标准差，用样本的标准差代替：2222(1P)382.8%（1-82.8%）5130.05p z P n -??==≈?2.由题意可知本题属于：纯随机重复抽样下的总体平均数的抽样极限误差已知：n=100,=3x ，=0.8σ ，(Z)195%F α=-= ,查表得/2=1.96Z α/2= 1.960.16Z α?=?= 分钟 3.（1）已知：n=150,12382%150p ==，(Z)199.73%F α=-= ,查表得/2=3Z α 由于不知总体标准差，用样本的标准差代替：p 82%382%9.41%Z α±=±?=±即：72.59%P 91.41%≤≤（2）已知：n=150,=2x ，=0.75σ ，(Z)199.73%F α=-= ,查表得/2=3Z α/20.752320.2x Z αμ=±=±?=± 分钟即：1.8 2.2μ≤≤4. 已知：200σ=，30z ?= ，(Z)195%F α=-= ,查表得/2=1.96Z α 则：2222221.9620017130z z n σ?==≈? 户（1）如上图（2）40名职工的平均考核成绩为30704076.75xfx f===∑ 样本的方差为22()4777.5s122.54x x ff-===∑∑ (Z)195%F α=-= ，查表得到/2 1.96Z α=/276.75 1.911.07676.75 3.43s x Z α±=±?=± 即在95%的概率保证度下，该企业工人的平均考核成绩在73.32到80.18直接。

统计学第五章课后习题答案一、选择题1：B 、C 【解析】所谓概率抽样，就是要求对总体的每次观察（每一次抽取）都是随机试验，并且有总体相同的分布。

2：D3：A 【解析】221226'42z n n α==∆⎛⎫ ⎪⎝⎭4：B 【解析】一致性是指随着样本容量不断增大，样本统计量接近总体参数的可能性就越来越大。

或者，对于任意给定的偏差控制水平，两者间偏差高于此控制水平的可能性越来越小，接近于0。

5：AC二、计算题 1: x =425 s n 21-=72.049 s 14=8.488s =n s =15488.8=2.1448 ∆=ns n t )1(2-α=2，1448⨯2.1916=4.70 所求μ的置信区间为425-4.701<μ<425+4.70即（420.30，429.70） 2: x =1209 s n 21-=0.005 s 15 =0.0707x s =n s =160707.0=0.017671 )116(05.0-t =2.131)1(2-=∆∂n t n s =2.131×0.017671=0.04所求μ的置信区间为12.09-0.04<μ<12.09+0.04即（12.05,12.13）3:n=600,p=0.1.np=60≥5,可以认为频数n 充分大，∂=0.05.z 2α=z 25.00=1.96 ∆=1.96600.90.10⨯=0.024，因此所求一次投掷中一只概率的置信区间是0.1-0.024<ρ<0.1+0.024，即（0.076，0.124）4: N 16,p ,np 75,,n 0.05====可认为频数充分大，，2z α=0.025 1.96z =0.2431∆== 因此，所求零件长度不合格的置信区间为0.4375—0.2431<ρ<0.4375+0.2431,即（0.19,0.68）5:114820ni i y ==∑， 1114820494(30n i i y y n μ=====∑分钟） 6. n=80 ,p=0.1,np=8≥5,可以认为n 充分大，ɑ≥0.05，96.1025.02==z z α 0657.096.1809.01.0==∆⨯因此，无上网经历的学生所占比率的置信区间为0.1—0.0657<ρ<0.1+0.0657，即（0.0343,0.1657)。

第五章一、单项选择题1．抽样推断的目的在于（）A．对样本进行全面调查 B．了解样本的基本情况C．了解总体的基本情况 D．推断总体指标2．在重复抽样条件下纯随机抽样的平均误差取决于（）A．样本单位数 B．总体方差C．抽样比例 D．样本单位数和总体方差3．根据重复抽样的资料，一年级优秀生比重为10%，二年级为20%，若抽样人数相等时，优秀生比重的抽样误差（）A．一年级较大 B．二年级较大C．误差相同 D．无法判断4．用重复抽样的抽样平均误差公式计算不重复抽样的抽样平均误差结果将（）A．高估误差 B．低估误差C．恰好相等 D．高估或低估5．在其他条件不变的情况下，如果允许误差缩小为原来的1/2，则样本容量（）A．扩大到原来的2倍 B．扩大到原来的4倍C．缩小到原来的1/4 D．缩小到原来的1/26．当总体单位不很多且差异较小时宜采用（）A．整群抽样 B．纯随机抽样C．分层抽样 D．等距抽样7．在分层抽样中影响抽样平均误差的方差是（）A．层间方差 B．层内方差C．总方差 D．允许误差二、多项选择题1．抽样推断的特点有（）A．建立在随机抽样原则基础上 B．深入研究复杂的专门问题C．用样本指标来推断总体指标 D．抽样误差可以事先计算E．抽样误差可以事先控制2．影响抽样误差的因素有（）A．样本容量的大小 B．是有限总体还是无限总体C．总体单位的标志变动度 D．抽样方法E．抽样组织方式3．抽样方法根据取样的方式不同分为（）A．重复抽样 B．等距抽样 C．整群抽样D．分层抽样 E．不重复抽样4．抽样推断的优良标准是（）A．无偏性 B．同质性 C．一致性D．随机性 E．有效性5．影响必要样本容量的主要因素有（）A．总体方差的大小 B．抽样方法C．抽样组织方式 D．允许误差范围大小E．要求的概率保证程度6．参数估计的三项基本要素有（）A．估计值 B．极限误差C．估计的优良标准 D．概率保证程度E．显著性水平7．分层抽样中分层的原则是（）A．尽量缩小层内方差 B．尽量扩大层内方差C．层量扩大层间方差 D．尽量缩小层间方差E．便于样本单位的抽取三、填空题1．抽样推断和全面调查结合运用，既实现了调查资料的_______性，又保证于调查资料的_______性。

第五章 抽样推断一、单项选择题 1 2 3 4 5 6 7 8 9 10 C B A D B D C B A C 11 12 13 14 15 16 17 18 19 20 ADCADCACBD二、多项选择题1 2 3 4 5 ABCE ABDE BCE ABCE ABDE 6 7 8 9 10 ACE ADE ACD ABE CDE 11 12 13 14 15 BDE CD BC ABCD ABCDE 16 17 18 19 20 AD ACBCEABDEACE三、判断题 1 2 3 4 5 6 7 8 9 10 ×××√√×√√××四、填空题 1、变量 属性 2、正 反3、重复抽样 不重复抽样4、抽样总体 样本5、大于 N n -1 Nn 6、标准差7、样本 总体 抽样平均误差 抽样平均误差 △x = Z x σ 8、合适的样本估计量 一定的概率保证程度 允许的极限误差范围 9、随机抽样 统计分组 10、增大 增大 降低 11、大数定律 中心极限定理 12、样本容量不小（不小于30个单位） 13、大 0.514、缩小33（即0.5774） 扩大 1.1180 15、估计量（或统计量） 参数 五、简答题（略） 六、计算题1、已知条件：P = 0.5 ，n = 100 且重复抽样 求：p ≤0.45的概率 解：Z =1100)5.01(5.05.045.0)1(=-⨯-=--nP P P p则F (Z = 1) = 0.6827 所以p ≤0.45的概率为：26827.01-= 0.15865 2、解E (x 1) = E （0.5X 1 + 0.3X 2 + 0.2X 3） = 0.5 E (X ) + 0.3 E (X ) + 0.2E (X ) = E (X ) = XE (x 2) = E （0.5X 1 + 0.25X 2 + 0.25X 3）= 0.5 E (X ) + 0.25 E (X ) + 0.25E (X )= E (X ) = XE (x 3) = E （0.4X 1 + 0.3X 2 + 0.3X 3） = 0.4 E (X ) + 0.3 E (X ) + 0.3E (X ) = E (X ) = X 所以x 1、x 2、x 3都是X 的无偏估计量。