当前位置：文档之家 › 《传热学》第二章 稳态导热

《传热学》第二章 稳态导热

  • 格式：pptx
  • 大小：6.09 MB
  • 文档页数：38

下载文档原格式

  / 38

合集下载

传热学(第二章)

传热学(第二章)


(2-32)
热阻
R=
1 1 1 ( 4πλ r r2 1
(2-33)
由球坐标系一般形式的导热微分方程
1 T 1 T 1 T T (λr2 + 2 2 (λ ) + 2 (λ sin θ ) + Φ = ρcp r2 r r) r sin θ r sin θ θ θ τ
2 1
λ1
第二章
导热基本定律及稳态导热
2-3 通过平壁,圆筒壁,球壳和其他变截面物体的导热 通过平壁,圆筒壁,
1 T 1 T T T (λr + 2 (λ ) + (λ ) + Φ = ρcp τ r r r) r z z d dt 简化变为 dr (r dr ) = 0 (2-25)
⒉ 通过圆筒壁的导热 由导热微分方程式(2—12)
⒉ 通过圆筒壁的导热 根据热阻的定义,通过整个圆筒壁的导热热阻为 (2-29) 29) 与分析多层平壁—样,运用串联热阻叠加的原则,可得通过图2-9所示的多层圆筒壁的 导热热流量 2πl(t1 t4 ) Φ= (2-30) ln( d2 / d1) / λ1 + ln( d3 / d2 ) / λ2 + ln( d4 / d3) / λ3 ⒊ 通过球壳的导热 导热系数为常数,无内热源的空心球壁.内,外半径为r1,r2,其内外表面均匀 恒定温度为t1,t2,球壁内的温度仅沿半径变化,等温面是同心球面. 由傅立叶定律得: dt 各同心球面上的热流率q不相等,而热流量Φ相等. Φ = 4πr2λ dr dr Φ 2 = 4πλdt r
的热传导微分方程:
T(r,τ ) τ ρc 当 λ = const 时, 2T(r,τ ) + Φ = p T(r,τ ) λ λ τ [λT(r,τ )] + g(r,τ ) = ρcp
工程热力学与传热学 第二章 稳态热传导 基本概念

工程热力学与传热学 第二章 稳态热传导 基本概念


t—温度(0C)；
x , y , z—直角坐标
由傅里叶定律可知，求解导热问题的关键是获 得温度场。导热微分方程式即物体导热应遵循的一 般规律，结合具体导热问题的定解条件，就可获得 所需的物体温度场。
具体推导: 傅里叶定律
能量守衡定律
导热微分方程式
假定导热物体是各向同性的，物性参数为常数。 我们从导热物体中取出一个任意的微元平行六面 体来推导导热微分方程，如下图所示。
2. 说明： 导热系数表明了物质导热能力的程度。 它是物性参数 物质的种类 热力状态（温度、压力等）。
在温度t=200C时：
纯铜λ=399 w/m0C；水λ=0.599 w/m0C；干空气0C λ（固体）大--------→（液体）---------→（气体）小
隔热材料（或保温材料）----石棉、硅藻土、矿渣棉等，它 们的导热系数通常:λ < 0.2 w/m0C。
c t ( x 2t2 y 2t2 z 2t2)q'
这是笛卡儿坐标系中三维非稳态导热微分方程的一般形式。
导热微分方程式——温度随时间和空间变化的一般关系。 它对导热问题具有普遍适用的意义。
Cp t ( x2t2 y2t2 z2t2)qv
最为简单的是一维温度场的稳定导热微分方程为：
稳态温度场：物体各点的温度不随时间变动； 非稳态（瞬态）温度场：物体的温度分布随时间改变。
2. 等温面(Isothermal surface)（线）：同一时刻物体中温度 相同的点连成的面（或线）。 特点：（1）同一时刻，不同等温线（或面）不可能相交； （2）传热仅发生在不同的等温线（或面）间； （3）由等温线（或面）的疏密可直观反映出不同区域 热流密度的相对大小。
在半径r处取一厚度为dr长度为l米的薄圆筒壁。则
传热学2章稳态导热总结问答题及答案

传热学2章稳态导热总结问答题及答案

一、名词解释稳态温度场：物体内各点温度不随时间变化的温度场。

等温面 ：温度场中同一瞬间温度相同点组成的面。

热扩散率（或导温系数）：表征物体内部温度趋于一致的能力，为cρλα= 肋效率：肋片的实际散热量与假设整个肋片表面处于肋基温度下的散热量之比。

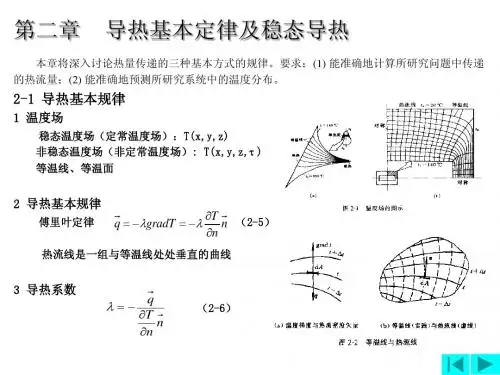
二、解答题和分析题1．写出傅里叶定律的一般形式的数学表达式，并说明其中各个符号的意义。

答：傅里叶的一般表达式为：n nt gradt q ∂∂-=-=λλ。

其中：q 是热流密度矢量；λ为导热系数，它表示物质导热本领的大小；gradt 是空间某点的温度梯度；n 是通过该点的等温线上的法向单位矢量，指向温度升高的方向，“-”号表示热量沿温度降低的方向传递。

2、写出傅里叶定律的文字表达式。

答：在导热中，单位时间内通过给定截面面积的导热量，正比于垂直该截面方向上的温度变化率和截面面积，而热量传递的方向则与温度升高的方向相反。

3、等温面与等温线的特点，不同温度的等温面(线)能相交不？答：1) 温度不同的等温面或等温线彼此不能相交；2) 在连续的温度场中，等温面或等温线不会中断，它们或者是物体中完全封闭的曲面（曲线），或者就终止与物体的边界上；3）物体的温度场通常用等温面或等温线表示，若每条等温线间的温度间隔相等时，等温线越密反映出该区域导热热流密度的越大。

不同温度的等温面(线)不能相交4．得出导热微分方程所依据的是什么基本定律?答：傅里叶定律和能量守恒定律。

5．解释材料的导热系数λ和导温系数α之间的区别和联系? （或热扩散率α的定义及物理意义。

）答：从表达式看，导温系数c ρλ/a =与导热系数成正比关系，但导温系数不但与材料的导热系数有关，还与材料的热容量(或储热能力)也有关；从物理意义看，导热系数表征材料导热能力的强弱，导温系数表征材料传播温度变化的能力的大小，两者都是物性参数。

6．将一根铁棒一端置于火炉中，另一端很快烫手，而在冬天将手置于温度相同的铁板或木板上时，铁板感觉更冰凉一些，用传热学的知识解释这些原因。

传热学课件第 二 章 稳 态 热传导

传热学课件第 二 章 稳 态 热传导


d2t d x2
m 2 t t f
1
通过肋壁的导热
一、等截面直肋的导热
4.求解：
4>.引入过余温度：<1>式变为 <4> 5>.解微分方程得温度场 <4>式为一个二阶线性齐次常微分方程，它的通解为： =C1emx+C2e-mx <5> 将边界条件<2>、<3>代入<5>即得肋片沿H方向的温度分布：
通过圆筒壁的导热
一、已知第一类边界条件
据傳里叶定律并整理后可得热流量的表达式： 1 ln d2 2l d1 式中的分母即为长度为l的圆筒壁的导热热阻。 单位为：℃/W 实际工程多采用单位管长的热流量ql来计算热流量：

t w1 t w 2
ql
Q l

t w1 t w 2
d ln d2 2 1 1
通过平壁的导热
二、已知第三类边界条件：
q
q
t f 1 t f 2
1 1 h1 h2
也可写作：q=k（tf1-tf2） （请牢记K的物理意义！） 对于冷热流体通过多层平壁的导热，可写作：
t f 1 t f 2
1 h1

i 1
n
i 1 i h2
若已知传热面积A，则热流量为：
e m x H e m x H 0 e mH e mH
d 2 m 2 d x2
or :
0
或写作：
0
ch mx H ch mH
expmx H exp mx H expmH exp mH
1
h21d x 0
传热学 第2章 稳态导热

传热学 第2章 稳态导热


t t t t c Φ x x y y z z
3、常物性且稳态:
2t 2t 2t Φ a 2 2 2 0 x y z c
如果边界面上的热流密度保持为常数，则 q | w 常数 当边界上的热流密度为零时，称为绝热边界条件
t t qw 0 0 n w n w
18
（3）第三类边界条件 给出了物体在边界上与和它直接接触的流体之 间的换热状况。 根据能量守恒，有：
返回
2.1.1 各类物体的导热机理
气体：气体分子不规则热运动时相互碰撞的结果，高温的气体分子运 动的动能更大 固体：自由电子和晶格振动 对于导电固体，自由电子的运动在导热中起着重要的作用，电的良导 体也是热的良导体 对于非导电固体，导热是通过晶格结构的振动，即原子、分子在其平 衡位置附近的振动来实现的
返回
2.2.2 定解条件
导热微分方程式是能量守恒定律在导热过程中的应用，是一切导热 过程的共性，是通用表达式。 完整数学描述：导热微分方程 + 定解条件 定解条件包括初始条件和边界条件两大类，稳态问题无初始条件 初始条件：初始时刻的状态表示为： =0，t =f (x,y,z)
边界条件： 给出了物体在边界上与外界环境之间在换热上的联系或相互作用
2、推导基本方法：傅里叶定律 + 能量守恒定律 在导热体中取一微元体
进入微元体的总能量+微元体内热源产生的能量-离开微元体的总能量= 微元体内储存能的增加
11
Ein Eg Eout Es
d 时间段内：
Ein Φx Φy Φz d Eiout Φxdx Φy dy Φz dz d
传热学第二章稳态热传导

传热学第二章稳态热传导

n w
h h
t f t f ( )
五、 热扩散系数 （thermal diffusivity）
a
物体导热能力 c 物体蓄热能力
从导热方程看：
a
t
温度变化快 扯平能力强
故，a 是评价温度变化速度的一个指标
2.3 通过平壁及圆筒壁的一维稳态导热
一、通过单层平壁的导热
0 , 则 2. Φ
t a 2 t
2
3. 稳态:
Φ a t 0 c
,则
0 4. 稳态且 Φ
t 0
2
三、其它正交坐标
1、柱坐标: (cylinder coordinate)
x r cos ; y r sin ; z z
2 t 1 t 1 2 t 2 t t a 2 2 2 2 r r r z c r
p
各类物质导热系数的范围
导热机理
气体：分子热运动 t

金属 非金属
固体：自由电子和晶格振动
t 晶格振动 阻碍自由电子运动
液体的导热机理不清
固体> 液体 > 气 ； 取决于物质的种类和温度
热绝缘（保温）材料 insulation material：<0.2W/(mK) (50
（2）固体的热导率
（a） 金属的热导率
金属 12~418W (m K)
纯金属的导热：依靠自由电子的迁移和晶格振动； 金属导热与导电机理一致，良导体也是良导热体。
银 铜 金 铝
T
10K:Cu 12000 W (m K) 15K : Cu 7000 W (m K)
《传热学讲义—第二章》

《传热学讲义—第二章》

第二章稳态导热本章重点：具备利用导热微分方程式建立不同边界条件下稳态导热问题的数学模型的能力第一节 通过平壁的导热1-1第一类边界条件研究的问题：（D 几何条件：设有一单层平■壁，厚度为a,其宽度、高度远大丁其厚度（宽度、高度 是厚度的10倍以上）。

这时可认为沿高度与宽度两个方向的温度变化率很小，温度只沿厚度 方向发生变化。

（届一维导热问题）（2） 物理条件：无内热源，材料的导热系数入为常数。

（3） 边界条件：假设平壁两侧表面分别保持均匀稳定的温度t wi 和t w2 , t wi t w2。

（为第一类边界条件，同时说明过程是稳态的）求：平■壁的温度分布及通过平■壁的热流密度值。

方法1导热微分方程：采用直角坐标系，这是一个常物性、无内热源、一维稳态导热 问题（温度只在x 方向变化）。

导热微分方程式为： 史 0 （2-1） dx 2边界条件为：t x0 t w 1 , t x t w 2（2-2）对式（2-1）连续积分两次，得其通解：t c 1x c 2t w 2 t w 1这里C 1、C 2为常数，由边界条件确定，解得：C1C 2 t w 1最后得单层平壁内的温度分布为：t t w 1 %」曳x由丁 a 、t w 1、t w 2均为定值。

所以温度分布成线性关系，即温度分布曲线的斜率是常数（温度梯度），虫―宜const（2-6）dx0—1I~Dfl ——单屋平惬(2-3)(2-4)(2-5)热流密度为：q 史—(t W l t w2) W /m2(2-7)dx若表面积为A,在此条件下，通过平壁的导热热流量则为：qA A— t W考虑导热系数随温度变化的情况:通过平壁的导热热流密度为:dt dtq 0(1 bt) —dx dx竺一1 ]bt t 0 1 2 b t W1 t W21式中，0 1 2bt W1 t W21 22 m则q —(t W1 t W2)从上式可以看出，如果以平壁的平均温度t m虹上来计算导热系数，则平壁的热流密2度仍可用导热系数为常数时的热流密度计算式:(2-8)对丁导热系数随温度线形变化，即0(1 bt),此时导热微分方程为: d dt °0 dx dx解这个方程，最后得:t2bt2bt 2 Wi W2t W2)t W1(t W it、W 一t W2说明：壁内温度不再是直线规律, 而是按曲线变化。

高等传热学_第二章_稳态导热

高等传热学_第二章_稳态导热


2-1 一维稳态导热
通过长圆筒壁（图2-2）的导热由傅里叶定律直接积分的方法。 若已知圆筒壁的内外壁面温度分别为t1和t2。注意到，圆筒壁的导
热面积在径向上是变化的，但单位长度上的总热流量ql（单位为 W/m）仍应是常量（不随r变化）。由傅里叶定律可得
分离变量并积分
ql
dt 2 r dr

x 0, x ,
并整理得到
t 0 t 0
（2-1-20）
代入以上得到的通解式(2-1-19)，可以确定其中的两个任意常数，

qV t x( x) 2
（2-1-21）
2-1 一维稳态导热
如果给定两个表面的温度分别为t1和t2，即
t t1 x , t t 2 代入以上得到的通解式(2-1-19)，可以确定其中的两个任意常数， 并整理得到
2-1 一维稳态导热
图2-1通过大平壁的导热
2-1 一维稳态导热
2-1-1 无内热源的一维导热 求解导热问题的一般思路是首先从导热微分方程和相应的定解条
件出发，解得温度场。 对于如图2-1所示的大平壁的稳态导热，已知两表面的温度分别为 t1和t2。导热微分方程简化为
其通解为
d 2t 0 2 dx

t
qv 2 r C1 ln r C2 4
（2-1-25）
2-1 一维稳态导热
r＝0处温度应该有界，即 t
r 0
，可以作为一个边界条件，
由此可得C1＝0。如果给定另一个边界条件是第一类边界条件， 即r＝R，t＝t1。代入通解可得

t t1
qv 2 2 (R r ) 4
种换热设备中，常在换热表面上增添一些肋， 以增大换热表面，达到减小换热热阻的目的。
传热学2-稳态导热new

传热学2-稳态导热new


假设单管长度为l，圆筒壁的外半 径小于长度的1/10。 一维、稳态、无内热源、常物性：
d dt (r )=0 dr dr
第一类边界条件
2013-6-14
(a)
r r1时 t t w1 r r2时 t t w22稳态导热11对上述方程(a)积分两次:
dt r c1 t c1 ln r c2 dr
[W
m]
Rl
2013-6-14
通过单位长度圆筒壁传热过程的总热阻 [mK/W]
2稳态导热 单位长度圆筒壁传热系数 [W/mK] 18
kl = 1 / Rl
例2-4（P37) 作业：2-19
思考题
为什么计算平壁导热时取单位面积，而圆筒壁
面却取单位长度？ 一维、稳态、无内热源的平壁、圆筒壁导热， 其热流、温度梯度的方向、热流量的方向、温度 曲线如何？
线性分布
t 2 t1 t q t ( A )
温度差
热阻
单位面积平壁的导 热热阻： 面积为A的热阻：
R = [m2 • ° / w] C
RA
= A
[° / w] C
热阻分析法适用于一维、稳态、无内热源的情况
2013-6-14 2稳态导热 4
金属壁一般很薄、热导率很大，
故导热热阻一般可忽略。
增大h1、h2
增大换热面积A，尤其在对流环热系数小的一侧
2013-6-14 2稳态导热 22
在一些换热设备中，在换热面上加装肋片是增大换热量的重要手段
肋壁：直肋、环肋（图2-13（P41）；等截面、变截面
2013-6-14
2稳态导热
23
等截面直肋 肋宽L 肋基 肋厚
东南大学传热学 第二章 导热基本定律及稳态导热

东南大学传热学 第二章 导热基本定律及稳态导热

第二章 导热基本定律 及稳态导热
本章重点讨论稳态导热问题。为此首先介绍 一些相关的基本知识，如温度场、温度剃度、 导热基本定律等；然后应用这些基本知识推 导出求解导热问题的微分方程；最后应用这 些微分方程求解常见的导热问题。
第一节 导热基本定律
温度场
• 定义：某一瞬间物体内的温度分布，称为温度场。 • 分类 1.按温度是否随时间而变化可分为 稳态温度场：物体内温度不随时间的变化而变化的温度场 非稳态温度场：物体内的温度随时间变化而变化的温度场 2.按温度随空间的变化可分为 一维温度场：温度只在一个方向有变化的温度场 二维温度场：温度在两个方向有变化的温度场 三维温度场：温度在三个方向有变化的温度场 • 表示：三种表示方法
n x y z
导热基本定律
• 傅立叶定律：单位时间内通过单位截面积所传 递的热量，正比例于当地垂直于截面方向上的 温度变化率，即温度剃度，其比例系数为导热 系数。
• 表示型式： A t n
n
导热系数
•
定义：
q
t n
n
• 物理意义：单位时间单位面积当温度变化率为1时，由导
热所传递的热量
• 影响因素：主要是物质的种类和物质所处的状态
第三节 通过平壁、圆筒壁、球壳和 其他变截面物体的导热
通过 平壁导热
通过 圆筒壁导热
通过 球壳导热
通过变导热 系数物体 的导热
单层平壁 多层平壁 单层圆筒壁 多层圆筒壁 单层球壳 多层球壳
通过单层平壁的导热
通过单层 平壁的导热
物理模型
数学描写
温度分布
热流量计算
数学描写
d 2t dx2 x
数学描写
温度分布
热流量计算
物理模型
《传热学》第2章-导热基本定律及稳态导热

《传热学》第2章-导热基本定律及稳态导热

影响热导率的因素：物质的种类、材料成分、温度、 湿度、压力、密度等
λ金属 > λ非金属; λ固相 > λ液相 > λ气相
不同物质的导热机理
1、气体的热导率 λ气体 ≈ 0.006 ~ 0.6 W (mo C)
0o C : λ空气 = 0.0244 W (moC) ; 20o C : λ空气 = 0.026 W (moC)
dΦv = Φ& dxdydz
v 单位时间内，微元体热力学能的增加 dU = ρc ∂t dxdydz ∂τ
导热微分方程式
dΦλ + dΦV = dU
dΦ λ
=
∂ ∂x

λ
∂t ∂x

+
∂ ∂y

λ
∂t ∂y

+
∂ ∂z

λ
∂t ∂z
dxdydz
dΦv = Φ& dxdydz
q = − dΦ n dA
直角坐标系中： q = qxi + qy j + qz k
导热基本定律
v 1822法国数学家傅里叶（Fourier）在大量实验研究的基础 上, 提出了导热基本定律—傅里叶定律。
v 对于物性参数不随方向变化的各向同性物体, 傅里叶定律度
热流密 度矢量
导热微分方程式的求解方法
积分法、分离变量法、积分变换法、数值计算法等
导热微分方程＋单值性条件＋求解方法 è温度场
圆柱坐标系（r, Φ, z）
dz
v 感兴趣的同学
课下自己推导
练习.
v 球坐标系方程 见教材P26.
=
−λ ∂t ∂n w
=0
⇒

《传热学》第2章-稳态导热

第一类边界条件： x 0 , t t w1 积分得:
控制方程
边界条件
x , t tw 2
t
dt 1 2 0 ( 1 bt ) c1 0 ( t bt ) c1 x c2 tw1 dx 2
代入边界条件，得:
1 1 2 2 ( t bt ) c 0 c , ( t bt 1 2 0 w2 w 2 ) c1 c 2 0 w1 2 w1 2 1 2 c ( t bt 2 0 w1 w1 ) 2 t w1 t w 2 1 c [ 1 b( t w1 t w 2 )] 0 1 2
tw 2 tw3
2
tw3 tw4
3
tw1 tw4 tw1 tw4 3 相加可得： q R ,1 R ,2 R ,3 R ,i
i 1
例2-1：有一锅炉炉墙，三层，内层为230mm的耐火 砖层，中间为50mm厚的保温层，外层为240mm的 红砖层，导热系数分别为1.10 W/(m.K) ，0.072 W/(m.K) ，0.58W/(m.K)，已知炉墙内外表面温度 为500℃与50℃，求炉墙的导热热流密度和红砖墙的 最高温度。
第二章 稳态导热
Steady-State Conduction —— One Dimension
主要内容
掌握稳态导热。
§2-1 §2-2 §2-3 §2-4 §2-5 §2-6
通过平壁的导热 通过复合平壁的导热 通过圆筒壁的导热 具有内热源的平壁导热 通过肋片的导热 通过接触面的导热
对各层直接应用单层大平壁的热量计算式 tw1 tw 2 tw1 tw 2 第一层平壁 : q1 , 变换 : q1 R ,1 t w1 t w 2 1 R ,1

传热学ch2稳态导热

反。
dΦ/dA为通过该点的热流密度，傅里叶定律 的热流密度表达式写为：
t q λ n
负号表示热流方向和温度梯度方向相反，即 指向温度降低的方向。 q是沿n方向传递的热流密度（严格地说热 流密度是矢量，所以q应是热流密度矢量在 n方向的分量）单位为W/m²。 t n 是物体沿n方向的温度变化率

2.1.2导热基本定律 1）傅里叶导热定律 定义式： dΦ λ dA t
n
λ——导热系数 A——传热面积，单位为m² t ——温度，单位为K
物理意义：
通过物体内某点微元面积dA，在单位时间里传 递的热量与该点处的温度梯度以及截面面积成正 比。导热基本定律说明的是通过物体中任一点导 热量的大小，热量传递的方向和温度传递的方向相
假定前提：热扰动的传递速度无限大。 不适用范围（非傅里叶导热）： 1）温度效应，导热物体的温度接近0K时； 2）时间效应，当过程的作用时间极短，与材料 本身固有的时间尺寸（松弛时间）相接近时； 3）尺度效应，当过程发生的空间尺寸极小，与 微观粒子的平均自由行程相接近时。
已知条件：无内热源、λ为定值、稳态 导热微分方程： t 0
c. 温度与热导率的关系 物体热导率随温度的变化关系比较复杂,如 图所示，但一般在某个不大的温度范围内， 可以认为二者之间成线性关系，一般写成 0 (1 bt) 其中b称为温度系数。

温度对物质的热导率具有较大的影响，同 一物体温度变化，热导率一般也发生变化。 因此，在谈论某种物体的热导率时，一般 应指明物体此时所处的温度，如果没有指 明，一般物体温度为常温。
一维稳态温度场假设肋片受到流体冷却肋基温度为t高温肋片温度沿肋高h下降由于肋片一般在长度方向肋宽方向较长所以温度在该方向不变在肋片厚度方向由于肋片很薄且大所以该方向温度也不变所以温度只在肋高方向变化是一维稳态温度场如图221则1宏观整个肋片上从肋基到肋端取为控制体则能量平衡为

传热学-第二章导热基本定律及稳态传热

1、导入微元体的净热量
d 时间X方向流入与流出微元体的热流量
dQx
- dQxdx
- qx x
dxdydz d
( t ) dxdydz d
x x
d 时间Y方向流入与流出微元体的热流量
dQy
- dQydy
- q y y
dy dxdz d
y
( t ) dxdydz d
y
2.4 导热微分方程及定解条件
影响热导率的因素：物质的种类、材料成分、温度、压力及 密度等。
2.3 导热系数
2.3.1 气体导热系数
气体导热——由于分子的无规则热运动以及分子间 的相互碰撞
1 3
vlcv
v 3RT M
V 气体分子运动的均方根 m/s L 气体分子两次碰撞之间的平均自由程 m
Cv气体的定容比热 J/kg·℃
2.3 导热系数
2.4 导热微分方程及定解条件
建立数学模型的目的：
求解温度场 t f x, y, z,
步骤： 1）根据物体的形状选择坐标系, 选取物体中的 微元体作为研究对象； 2）根据能量守恒, 建立微元体的热平衡方程式； 3）根据傅里叶定律及已知条件, 对热平衡方程式 进行归纳、整理，最后得出导热微分方程式。
通过某一微元面积dA的热流：
dA q
d
q dA
t
n
dA
t
dydz
t
dxdz
t
பைடு நூலகம்
dxdy
n
x
y
z
2.2导热的基本定律
例：判断各边界面的热流方向
2.3 导热系数
由傅里叶定律可得，导热系数数学定义的具体形式为：
q t n

第二章-稳态热传导


传热学 Heat Transfer
Shanghai Jiao Tong University
2-2 导热问题的数学描述 温度场
导热微分方程
t f ( x, y, z, )
傅立叶定律
热流量
热流密度
导热微分方程的推导：傅立叶定律 + 能量守恒定律 导入导出微元体的净热流量＋ 微元体内热源生成热＝ 微元体内能的增量 导入热流量 导出热流量 内热源生成热
第一类 第二类 第三类 导热问题的数学描述＝ 导热微分方程+定解条件
稳态导热：给定边界条件即可。 非稳态导热：给定初始条件和边界条件。
SJTU-OYH
传热学 Heat Transfer
Shanghai Jiao Tong University
2-2 导热问题的数学描述 第一类边界条件（Dirichlet条件）：给定边界上的温度值。 稳态导热： 非稳态导热： 第二类边界条件（Neumann条件）：给定边界上的热流密度值。 稳态导热： 非稳态导热： 特例：绝热边界
SJTU-OYH
传热学 Heat Transfer
Shanghai Jiao Tong University
2-3 典型一维稳态导热分析解 通过多层平壁的导热
热阻分析法
热流密度
q
t1 t n 1
t1
ri
i 1
n

t1 t n 1
i i 1 i
n
n为层数
t2
t3 t4
温度分布 第一层：
x
y
z
xdx
dxdydz
y dy
z dz
内能增量
t c dxdydz
SJTU-OYH

《传热学》第2章_稳态热传导

qt1t235 W3 /m 2
2021/5/23
第2章 稳态热传导
例2-2 一锅炉炉壁有三层材料组成，最里面的是耐火粘土砖，厚115mm，
中间层是硅藻土砖，厚125mm；最外面是石棉板，厚70mm，已知墙
壁内外表面的温度为495 ℃和60 ℃，试求每平方米炉强的热损失及分界
面上的温度。
假设：1. 一维问题；2. 稳态导热；3. 无接触热阻(界面紧密接触)
1,2，,导3 热系数
面温度t1，t4。
，1,两2,外3表
假设各层之间接触良好，可以近似地认
t2
t3 t4
为接合面上各处的温度相等
x 0
❖
第一类边界条件：
x
n i1
i
t t1 t tn1
t1
t2
t3
t4
❖
热阻：
2021/5/23
r1
1 1
....r.n.nn
三层平壁的稳态导热
关键点：界面热流密度、传热量处处相同
0时( n t)wf2()
3. 规定了边界上物体与周围流体间的表面传热系数及周围流体的 温度，称为第三类边界条件。第三类边界条件可表示为
( n t)wh(twtf )
2021/5/23
第2章 稳态热传导
4. 如果导热物体表面与温度为Te的外界环境只发生辐射传热，称为
辐射边界条件。可表示为
T nTw 4Te4
更多的热量；2. 分母是单位体积的物体温度升高1℃所需要的
热量。a越大，表示物体内部温度扯平的能力越大。
2. 等号左边一项为非稳态项，也就是热力学能增量
3. 等号右边三项为通过界面的导热而使微元体增加的能量
4. 公式最后一项为源项

传热学第二章

刘彦丰华北电力大学工程应用的两个基本目的：•能准确地预测所研究系统中的温度分布；•能准确地计算所研究问题中传递的热流。

要解决的问题：温度分布如何描述和表示？温度分布和导热的热流存在什么关系？如何得到导热体内部的温度分布？第二章导热基本定律及稳态导热刘彦丰华北电力大学本章内容简介2-1 导热基本定律2-2 导热微分方程式及定解条件2-3 通过平壁、圆筒壁、球壳和其它变截面物体的导热（一维稳态导热）2-4 通过肋片的导热分析2-5 具有内热源的导热及多维导热回答问题1和2回答问题3具体的稳态导热问题刘彦丰传热学Heat Transfer 华北电力大学一、温度分布的描述和表示像重力场、速度场等一样，物体中的温度分布称为温度场。

1、温度分布的文字描述和数学表示，如：在直角坐标系中非稳态温度场),,,(τz y x f t =稳态温度场),,(z y x f t =一维温度场二维温度场三维温度场)(x f t =),(τx f t =),(y x f t =),,(τy x f t =),,(z y x f t =),,,(τz y x f t =2-1 导热基本定律刘彦丰传热学Heat Transfer华北电力大学2、温度分布的图示法传热学Heat Transfer 2、温度分布的图示法等温线传热学Heat Transfer二、导热基本定律(傅立叶定律)1822年，法国数学家傅里叶（Fourier ）在实验研究基础上，发现导热基本规律——傅里叶定律.法国数学家Fourier: 法国拿破仑时代的高级官员。

曾于1798-1801追随拿破仑去埃及。

后期致力于传热理论，1807年提交了234页的论文，但直到1822年才出版。

刘彦丰华北电力大学在导热现象中，单位时间内通过给定截面的热量，正比于垂直于该截面方向上的温度梯度和截面面积，方向与温度梯度相反。

1、导热基本定律的文字表达：nntgradt q ∂∂−=−=λλ2、导热基本定律的数学表达：t+Δt tt-Δt刘彦丰华北电力大学3、意义已知物体内部的温度分布后，则由该定律求得各点的热流密度或热流量。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

断面周长： 断面面积：
进行负内热源处理后等截面直肋导热微分方程组如下：
（假定肋端绝热）
定义： 令：
—— 过余温度
使导热微分方程齐次化：
并解出其通解为：
代入边界条件求出c1和c2，并代入通解，得出特解：
等截面直肋的温度分布：
肋端过余温度：
肋片散热量：
当考虑肋端散热时，计算肋片散热量时可采用假想肋高
n层圆筒壁的单位管长热流量：
二、第三类边界条件
常物性时导热微分方程组如下：
根据第一类边界条件时的结果: （此时壁温tw1和tw2为未知） 与以上两个边界条件共三式变形后 相加,可消去tw1和tw2，得：
单层圆筒壁的单位管长热流量：
三、临界热绝缘直径
有绝缘层时的管道总热阻：
当dx增大时： 增 大 减 小
代入肋片效率定义，得到：
肋片效率计算式：
m和l对肋片效率的影响分析：
a. m一定时，l越大，Φ越大，但ηf越低
采用长肋可以提高散热量，但却使肋片散热有效性降低
b. l一定时，m越大，ηf越低
可采用变截面肋片设法降低m
根据肋片效率计算散热量的方法（查线图法）：
矩形及三角形直肋的肋片效率
环肋的肋片效率
h较小时
应用实例：细管，电线 电线的绝缘层外直径小于临界热绝缘直径时， 可起到散热作用
第四节 具有内热源的平壁导热
应用领域：混凝土墙壁凝固
研究对象：厚度为2δ的墙壁，内热源强度为qv， 两边为第三类边界，中间为绝热边界， 取墙壁的一半为研究对象建立导热微分方程 常物性时导热微分方程组如下：
积分两次，得：
《传热学》
第二章 稳态导热
导热微分方程：
稳态时满足：
常物性、稳态导热微分方程：
无内热源时常物性、稳态导热微分方程：
第一节 通过平壁的导热
应用领域：墙壁、锅炉壁面
一、第一类边界条件
1.单层平壁：
一维简化的假设条件：高度、宽度远大于厚度 常物性时导热微分方程组如下：
积分两次，得：
代入边界条件解出C1和C2：
单层平壁的热流密度：
多层平壁的热流密度：
第二节 通过复合平壁的导热
应用领域：空心砖，空斗墙
请同学们动脑筋思考:
空斗墙和空心砖内均存在导热系数很小的 空气孔隙，因而保温性能一定会很好吗？ 为什么？
一维简化的假设条件： 组成复合平壁的各种不同材料的导热系数相差不是很大
近似计算式：
总导热热阻的计算方法——划分单元，模拟电路
硬度匹配情形
两表面一软一硬
空隙中介质的性质
可能增大 亦可能减小， 应具体分析 必须通过对函数求极值来判断 总热阻的变化规律
对dx求导并令其为0:
从而得出：
——临界热绝缘直径
a.当dx<dc时,Rl随dx 增大而减小 b.当dx>dc时,Rl随dx 增大而增大
只有在d2<dc时， 才可能绝缘直径的场合：
λ较大时
从线图查出肋片效率ηf
第六节 通过接触面的导热
接触热阻的例子—— 镶配式肋片，缠绕式肋片 接触热阻的形成原因—— 固体表面并非理想平整 接触热阻的概念—— 接触面孔隙间气体导致 两接触面之间存在温差
接触热阻的定义：
接触热阻的影响因素： 粗糙度
减小接触热阻的措施： 表面尽量平整
挤压压力
增加挤压压力
积分一次，得： 再积分一次，得： 代入边界条件解出C1和C2：
将c1和c2代入导热微分方程，得到：
单层圆筒壁的温度分布：
通常更多情况下用直径代替半径：
将第一次积分的结果：
代入傅立叶定律：
得到：
单层圆筒壁的热流量：
长度为l的圆筒壁的热阻：
单位管长单层圆筒壁的热流量：
2.多层圆筒壁——可看作数个单层圆筒壁相互串连
肋片的类型：
肋片散热器
肋片置于管道外侧的原因：
换热器或管道内侧流体一般多为流速较高的液体， 而换热器或管道外侧流体多为流速较低的气体， 大多情况下外侧对流换热热阻最大， 对整个传热过程起支配作用
一、等截面直肋的导热
一维简化的假设条件： 肋片的高度l远大于肋片的厚度δ， 因而厚度方向温差很小，
负内热源的处理方法—— 将y方向的对流散热量 等效转化为负内热源
对于右图所示的复合平壁， 有以下两种处理方法：
a.先串联再并联的计算方法：
b.先并联再串联的计算方法：
两种处理方法结果并不完全相同，但均为合理结果 原因：将二维导热问题简化为一维导热问题，无论采取简化方法， 都必然会产生一定误差
复合平壁导热问题的注意点： 1.区域划分一定要合理，保证每个区域形状完全相同 2.每个单元的热阻必须使用总热阻，不能使用单位面积热阻 3.对于各部分导热系数相差较大的情况，总热阻必须用二维 热流影响的修正系数（教材表2－1）加以修正
将C1和C2代入导热微分方程，得到：
单层平壁的温度分布：
上式对x求导，得到：
单层平壁的热流密度：
2.多层平壁——可看作数个单层平壁相互串连 n层平壁的热流密度：
第i层与第i+1层之间接触面的温度：
二、第三类边界条件
常物性时导热微分方程组如下：
根据第一类边界条件时的结果: （此时壁温tw1和tw2为未知） 与以上两个边界条件共三式变形后 相加,可消去tw1和tw2，得：
第三节 通过圆筒壁的导热
蒸汽管
应用领域：管道
热水管（95 ℃ ～70 ℃ ，60 ℃ ～45 ℃ ） 冷冻水管（7 ℃ ～12 ℃ ）
蒸汽管道保温层
请同学们动脑筋思考:
管道保温层越厚，保温效果一定越好吗？
一、第一类边界条件
1.单层圆筒壁：
一维简化的假设条件—— 长度远大于壁厚，温度场轴对称
常物性时导热微分方程组如下：
代替实际肋高 l 一维温度场假定的检验：
请同学们思考一个问题: 肋高越大，肋的散热面积越大，因而采用 增加肋高的方法可以增加肋的散热量。这 种方法在实际换热器设计中是否可行？若 可行，是否会有某些局限性？
二、肋片效率
提出此概念的目的——衡量肋片散热的有效程度 肋片效率的定义：
肋片表面平均温度tm下的实际散热量 假定肋片表面全部处在t0时的理想散热量 其中肋片表面平均温度：
代入边界条件解出C1和C2,并代入导热微分方程，得到：
三类边界时具有内热源平壁的温度分布：
上式对x求导，得到：
三类边界时具有内热源平壁的热流密度：
当h趋于无限大时，得到：
一类边界时具有内热源平壁的温度分布：
第五节 通过肋壁的导热
肋壁的作用：加大散热面积，增强传热
应用领域：冷凝器、散热器、空气冷却器等