含参数二次函数分类讨论的方法

二次函数专题——含参二次函数完整版题型汇总含参的二次函数在高中阶段考试中经常出现，因为参数的存在使得函数形成一种动态，随着参数的变化，函数也会不同。

这就使得本来简单的二次函数变得复杂起来。

例如，考虑求解$f(x)=x-2ax$在$[2,4]$上的最大值和最小值。

由于参数的存在，这个函数是动态的。

为了解决这个问题，我们需要考虑动轴定区间问题，即对称轴随着参数的变化而变化，但是在给定区间上问最大值和最小值。

对于这个问题，需要分类讨论。

在$[2,4]$这个区间上，可能出现对称轴不在这个区间里面的情况，对称轴就在区间里面的情况，或者对称轴在区间右侧的情况。

因此，我们需要分别考虑这些情况。

具体来说，我们需要找到在整个函数的区间上，哪个数离对称轴最远。

这个分界线就应该在$2$和$4$中间的位置上，即$3$。

当对称轴在$x=3$这条线左边的时候，对称轴离$2$就比较近，离$4$就比较远；对称轴在右边的时候，离$2$就比较近，离$4$就比较远。

因此，这个函数的最大值可以表示为：f_{\max}(x)=\begin{cases}f(4)=16-8a& (a\leq 3)\\f(2)=4-4a&(a>3)\end{cases}$$当$a=3$时，放在哪边都可以。

代入上面的式子，得到$f_{\max}(x)=-8$。

因此，最大值为$-8$。

接下来，我们来讨论含参的二次函数的最大值和最小值问题。

这类问题的重点在于能否清晰地做分类讨论，得到一个分段函数的解析式。

我们可以按照对称轴的位置进行分类讨论。

首先，对于对称轴在区间左侧，且$a\leq 2$的情况，函数在$x=2$处取得最小值，即$f_{min}(x)=f(2)=4-4a$。

其次，对于对称轴在区间中间，即$24$的情况，函数在$x=4$处取得最小值，即$f_{min}(x)=f(4)=16-8a$。

另外，还有一类问题叫做定轴动区间的问题。

对于这类问题，我们同样需要进行分类讨论，只不过区间在变化。

3. 指数函数和对数函数：对于形如 f(x) = a^x 和 f(x) = log_a(x) 的指数函数和对数函数 ，其中 a 是常数，零点的情况取决于参数 a 的取值。对于指数函数，如果 a > 0，则函数没 有零点；如果 a = 0，则函数在 x = -∞ 时有一个零点；如果 a < 0，则函数在 x = -∞ 和 x = +∞ 时交替有零点。对于对数函数，如果 a > 1，则函数在 x = 1 时有一个零点；如果 0 < a < 1，则函数在 x = +∞ 时有一个零点；如果 a = 1，则函数在 x = 1 时有一个零点，且 对于所有 x ≠ 1，函数都没有零点。
函数零点参数分类讨论
在数学中，函数的零点是指函数取值为零的点，也就是方程 f(x) = 0 的解。对于一般的函 数，可以根据参数的取值进行分类讨论，以确定函数的零点。
以下是常见的函数零点参数分类讨论的几种情况：
1. 线性函数：对于形如 f(x) = ax + b 的线性函数，其中 a 和 b 是常数，零点的情况取决 于参数 a 和 b 的取值。如果 a ≠ 0，则函数有唯一的零点 x = -b/a。如果 a = 0，且 b ≠ 0 ，则函数没有零点。如果 a = 0，且 b = 0，则函数在整个实数范围内都是零。
函数零点参数分类讨论
需要注意的是，以上只是一些常见函数的零点参数分类讨论的情况，实际上每个函数的零 点情况都可能有所不同，具体要根据函分类讨论
2. 二次函数：对于形如 f(x) = ax^2 + bx + c 的二次函数，其中 a、b 和 c 是常数，零 点的情况取决于参数 a、b 和 c 的取值。根据二次方程的求根公式，可以得到零点的情况。 如果 Δ = b^2 - 4ac > 0，则函数有两个不同的实数零点。如果 Δ = 0，则函数有一个重复 的实数零点。如果 Δ < 0，则函数没有实数零点。

二次函数中的分类讨论思想一、例题分析归类：（一）、正向型是指已知二次函数和定义域区间，求其最值。

对称轴与定义域区间的相互位置关系的讨论往往成为解决这类问题的关键。

此类问题包括以下四种情形：（1）轴定，区间定；（2）轴定，区间变；（3）轴变，区间定；（4）轴变，区间变。

1. 轴定区间定例1. （2008年陕西卷）22．本小题满分14分）设函数3222()1,()21,f x x ax a x g x ax x =+-+=-+其中实数0a ≠．（Ⅰ）若0a >，求函数()f x 的单调区间；（Ⅱ）当函数()y f x =与()y g x =的图象只有一个公共点且()g x 存在最小值时，记()g x 的最小值为()h a ，求()h a 的值域；（Ⅲ）若()f x 与()g x 在区间(,2)a a +内均为增函数，求a 的取值范围．2. 轴定区间动 例2. （全国卷）设a 为实数，函数2()||1,,f x x x a a R =+-+∈，求f(x)的最小值。

3. 轴动区间定评注：已知2()(0)f x ax bx c a =++≠，按对称轴与定义域区间的位置关系，由数形结合可得()f x 在[,]m n 上的最大值或最小值。

例3．求函数)(a x x y --=在]1,1[-∈x 上的最大值。

4. 轴变区间变例4. 已知24()(0),y a x a a =->，求22(3)u x y =-+的最小值。

（二）、逆向型是指已知二次函数在某区间上的最值，求函数或区间中的参数值。

例5. 已知函数2()21f x ax ax =++在区间[3,2]-上的最大值为4，求实数a 的值。

例6. 已知函数2()2x f x x =-+在区间[,]m n 上的值域是[3,3]m n ，求m ，n 的值。

练习：1、（2008江西卷21）． 已知函数4322411()(0)43f x x ax a x a a =+-+> （1）求函数()y f x =的单调区间；（2）若函数()y f x =的图像与直线1y =恰有两个交点，求a 的取值范围．2、已知二次函数2()(21)1f x ax a x =+-+在区间3[,2]2-上的最大值为3，求实数a 的值。

通法研究Җ㊀广东㊀张㊀科㊀㊀含参函数因引入了参数使得确定的函数变得不确定,其单调性讨论问题常常涉及分类讨论思想的综合运用,能体现数学思维的深度,体现逻辑推理㊁数学运算㊁直观想象等数学核心素养,是近年来高考的高频考点之一．在实际应用中,能否深入理解问题的本质,能否明确分类的逻辑和依据是求解这类问题的难点．下面就以导函数是二次函数(或类二次函数)为例,探讨求解含参函数单调性问题的通性通法．１㊀以导函数零点的大小为分类依据例１㊀已知函数f (x )＝１３x ３－(１＋a )x ２＋４a x ＋２４a (a ɪR ),讨论函数f (x )的单调性．依题意得f ᶄ(x )＝x ２－２(１＋a )x ＋４a ＝(x －２)(x －２a ),令f ᶄ(x )＝０,得x ＝２或x ＝２a ．当２a ＜２,即a ＜１时,令f ᶄ(x )＞０,得x ＜２a 或x ＞２;令f ᶄ(x )＜０,得２a ＜x ＜２．此时,f (x )的单调递增区间是(－ɕ,２a )和(２,＋ɕ),单调递减区间是(２a ,２)．当２a ＝２,即a ＝１时,fᶄ(x )ȡ０恒成立,此时,f (x )的单调递增区间是(－ɕ,＋ɕ)．当２a ＞２,即a ＞１时,令f ᶄ(x )＞０,得x ＜２或x ＞２a ;令f ᶄ(x )＜０,得２＜x ＜２a ．因此,f (x )的单调递增区间是(－ɕ,２)和(２a ,＋ɕ),单调递减区间是(２,２a )．综上所述,当a ＞１时,f (x )的单调递增区间是(－ɕ,２),(２a ,＋ɕ),单调递减区间是(２,２a );当a ＝１时,f (x )单调递增区间是(－ɕ,＋ɕ);当a ＜１时,f (x )的单调递增区间是(－ɕ,２a )和(２,＋ɕ),单调递减区间是(２a ,２)．由此题可以知道,当导函数的零点大小不确定时,讨论函数单调性的基本步骤如图１所示．求函数f (x )的定义域ң求导函数fᶄ(x )ң求导函数的零点ң以比较零点的大小为依据进行分类ң确定函数的单调区间图１２㊀以导函数零点是否在定义域内为分类依据例２㊀已知函数f (x )＝１２x ２－２(１＋a )x ＋４a l n x ,讨论函数f (x )的单调性．依题意可得,f (x )的定义域为(０,＋ɕ),fᶄ(x )＝x －２(１＋a )＋㊀㊀㊀㊀４a x ＝(x －２)(x －２a )x(x ＞０)．当２a ɤ０,即a ɤ０时,由fᶄ(x )＞０,x ＞０,{得x ＞２;由fᶄ(x )＜０,x ＞０,{得０＜x ＜２．因此f (x )在(２,＋ɕ)上单调递增,在(０,２)上单调递减．当０＜２a ＜２,即０＜a ＜１时,由fᶄ(x )＞０,x ＞０,{得０＜x ＜２a 或x ＞２;由f (x )＜０,x ＞０,{得２a ＜x ＜２．因此,f (x )在(０,２a )和(２,＋ɕ)上单调递增,在(２a ,２)上单调递减．当２a ＝２,即a ＝１时,f ᶄ(x )ȡ０,所以f (x )在(０,＋ɕ)上单调递增．当２a ＞２,即a ＞１时,由fᶄ(x )＞０,x ＞０,{得０＜x ＜２或x ＞２a ;由fᶄ(x )＜０,x ＞０,{可得２＜x ＜２a ．因此,f (x )在(０,２)和(２a ,＋ɕ)上单调递增,在(２,２a )上单调递减．综上所述,当a ɤ０时,f (x )的单调递增区间是(２,＋ɕ),单调递减区间是(０,２);当０＜a ＜１时,f (x )的单调递增区间是(０,２a )和(２,＋ɕ),单调递０１通法研究减区间是(２a ,２);当a ＝１时,f (x )的单调递增区间是(０,＋ɕ);当a ＞１时,f (x )的单调递增区间是(０,２)和(２a ,＋ɕ),单调递减区间是(２,２a )．由此题可知当导函数的零点是否在定义域内不能确定时,讨论函数单调性的基本步骤如图２所示．求函数f (x )的定义域ң求导函数f ᶄ(x )ң求导函数的零点ң优先以导函数的零点是否在定义域内为依据进行分类ң以零点的大小为依据进行分类ң确定函数的单调区间图２３㊀以导函数是否存在零点为分类依据例３㊀(２０１８年全国卷Ⅰ理２１(１))已知函数f (x )＝１x－x ＋a l n x ,讨论f (x )的单调性．f (x )的定义域为(０,＋ɕ),且知fᶄ(x )＝－x ２－a x ＋１x ２．令f ᶄ(x )＝－x ２－a x ＋１x ２＝０,即x ２－a x ＋１＝０．当－２ɤa ɤ２时,Δɤ０,f ᶄ(x )ɤ０,此时,f (x )在(０,＋ɕ)上单调递减．当a ＜－２或a ＞２时,Δ＞０,此时方程x ２－a x ＋１＝０两根为x １＝a －a ２－４２,x ２＝a ＋a ２－４２．当a ＜－２时,两根均为负数,所以x ＞０时,f ᶄ(x )＜０,此时,f (x )在(０,＋ɕ)上单调递减．当a ＞２时,两根均为正数,此时,f (x )的单调递减区间是(０,a －a ２－４２)和(a ＋a ２－４２,＋ɕ),f (x )的单调递增区间是(a －a ２－４２,a ＋a ２－４２)．综上所述,当a ɤ２时,f (x )的单调递减区间是(０,＋ɕ);当a ＞２时,f (x )的单调递增区间是(a －a ２－４２,a ＋a ２－４２),单调递减区间是(０,a －a ２－４２)和(a ＋a ２－４２,＋ɕ)．由此题可知当不确定导函数是否存在零点(或零点的个数)时,讨论函数单调性的基本步骤如图３所示．求函数f (x )的定义域ң求导函数f ᶄ(x )ң优先以导函数是否存在零点以及零点的个数为依据进行分类ң以零点是否在定义域内为依据进行分类ң确定函数的单调区间图３４㊀以导函数的类型为分类依据例４㊀已知函数f (x )＝l n x ＋a x ２－(２a ＋１)x(a ȡ０),讨论函数f (x )的单调性．f (x )的定义域为(０,＋ɕ),且知㊀㊀f ᶄ(x )＝１x＋２a x －２a －１＝２a x ２－(２a ＋１)x ＋１x．当a ＝０时,f ᶄ(x )＝－(x －１)x(x ＞０),令f ᶄ(x )＜０,得x ＞１,f (x )的单调递减区间是(１,＋ɕ);令f ᶄ(x )＞０,得０＜x ＜１,f (x )的单调递增区间是(０,１)．当０＜a ＜１２,即１２a＞１时,fᶄ(x )＝２a (x －１２a)(x －１)x(x ＞０),令f ᶄ(x )＜０,得１＜x ＜１２a,f (x )的单调递减区间是(１,１２a );令f ᶄ(x )＞０,得０＜x ＜１或x ＞１２a ,f (x )的单调递增区间是(０,１)和(１２a,＋ɕ)．当a ＝１２,即１２a＝１时,fᶄ(x )＝(x －１)２xȡ０(x ＞０),f (x )的单调递增区间是(０,＋ɕ)．当a ＞１２,即１２a＜１时,fᶄ(x )＝２a (x －１２a)(x －１)x(x ＞０),令f ᶄ(x )＜０,得１２a＜x ＜１,f (x )的单调递减区间是(１２a ,１);令f ᶄ(x )＞０,得０＜x ＜１２a 或x ＞１,f (x )的单调递增区间是(０,１２a)和(１,＋ɕ)．１１非常道综上所述,当a ＝０时,f (x )的单调递增区间是(０,１),单调递减区间是(１,＋ɕ);当０＜a ＜１２时,f (x )的单调递增区间是(０,１)和(１２a ,＋ɕ),单调递减区间是(１,１２a );当a ＝１２时,f (x )的单调递增区间是(０,＋ɕ);当a ＞１２时,f (x )的单调递增区间是(０,１２a )和(１,＋ɕ),单调递减区间是(１２a,１)．由此题可知当导函数为类二次函数时,若其类型不确定,讨论函数单调性的基本步骤如图４所示．求函数f (x )的定义域ң求导函数f ᶄ(x )ң优先以导函数的类型为依据进行分类ң以零点的大小为依据进行分类ң确定函数的单调区间图４对含参函数单调性问题,求解的关键在于思考,相对于具体函数而言含参函数的不确定性在哪里?分类的逻辑是什么?分类的不同层次及各层次分类的依据又是什么?通过对上述例题的分析㊁求解,可以得出求解含参函数单调性问题的通性通法,即首先要明确题意,确定参数的范围和函数的定义域,其次按照导函数的类型㊁导函数是否存在零点㊁零点是否在定义域内㊁零点的大小进行分类讨论,最后进行整理和总结就能得到正确的结论．含参函数单调性问题的解决是层层递进的,在递进的过程中,因参数在不同位置,使得问题的解决出现了不确定性,为了将不确定的问题转化为确定性的问题,需进行分类讨论．对于导函数为二次型含参函数单调性的讨论,通法如下．第一步,先看二次项系数是否含有参数,若含有参数,则将系数分大于０㊁小于０和等于０三种情况进行讨论;若二次项系数为０,则将问题转化为一次函数问题去解决;若二次项系数不为０,则进入第二步．第二步,对一元二次方程的判别式分Δɤ０或Δ＞０两种情况进行讨论,若Δɤ０,则函数在定义域上单调递增或单调递减;若Δ＞０,则进入第三步．第三步,求出对应一元二次方程的两个不等实根,判断两根是否在定义域内,若两根都不在定义域内或只有一个实根在定义域内,可以借助二次函数图象来解决;若两根都在定义域内,则进入第四步．第四步,判断两个根的大小,从而使问题得解．(作者单位:广东省广州市第八十六中学)Җ㊀江西㊀吕文彬㊀㊀e xȡx ＋１和l n (x ＋１)ɤx 是两个常见的不等式,当且仅当x ＝０时,等号成立．要证明这两个不等式可以通过移项构造新函数f (x )＝e x －x －１或g (x )＝l n (x ＋１)－x ,再利用导数分别求其最小值或最大值的方法．由于证明过程比较简单,这里不再赘述,下面的解题中也将证明省略,将其直接当作结论来用．这两个不等式可直接使用,也可通过代数变形或者换元变形构造新的不等式,不管哪一种方法,在解题中都有着事半功倍的效果,可以轻松解决很多难题,简化解题步骤．下面通过举例说明,以期抛砖引玉．１㊀直接应用例１㊀(２０１７年全国卷Ⅲ理２１)已知函数f (x )＝x －１－a l n x ．(１)若f (x )ȡ０,求a 的值;(２)设m 为整数,且对于任意正整数n ,(１＋１２) (１＋１２２) (１＋１２n )＜m ,求m 的最小值．(１)a ＝１(求解过程略)．(２)因为l n (１＋x )ɤx ,故取x ＝１２k ＞０(k ＝１,２, ,n ),则l n (１＋１２k )＜１２k (k ＝１,２, ,n )．l n (１＋１２)＋l n (１＋１２２)＋ ＋l n (１＋１２n )＜１２＋１２２＋ ＋１２n ＝１－１２n ＜１,即(１＋１２)(１＋１２２) (１＋１２n )＜e ．取n ＝３,可得m ＞１３５６４＞２,而(１＋１２)(１＋１２２)(１＋１２３)＞２,又因为m 为整数,所以m 的最小值为３．此题的第(１)问其实是第(２)问的铺垫,此题将导数与数列结合起来考查．m 为整数就提示我们,只需将结果控制在两个整数之间,观察其形式,很容易联想到这两个常见的不等式．这两个不等式在此题中起放缩作用,可以将含有复杂的指数式或对２１。

微专题13 含参数二次函数的最值问题【方法技巧与总结】1、定轴定区间型：即定二次函数在定区间上的最值，其区间和对称轴都是确定的，要将函数配方，再根据对称轴和区间的关系，结合函数在区间上的单调性，求其最值（可结合图象）；2、动轴定区间型：即动二次函数在定区间上的最值，其区间是确定的，而对称轴是变化的，应根据对称轴在区间的左、右两侧和穿过区间这三种情况分类讨论，再利用二次函数的示意图，结合其单调性求解；3、定轴动区间型：即定二次函数在动区间上的最值，其对称轴确定而区间在变化，只需对动区间能否包含抛物线的定点横坐标进行分类讨论；4、动轴动区间型：即动二次函数在动区间上的最值，其区间和对称轴均在变化，根据对称轴在区间的左、右两侧和穿过区间这三种情况讨论，并结合图形和单调性处理。

【题型归纳目录】 题型一：定轴定区间型 题型二：动轴定区间型 题型三：定轴动区间型 题型四：动轴动区间型题型五：根据二次函数的最值求参数 【典型例题】 题型一：定轴定区间型例1．（2022·全国·高一专题练习）函数()232f x x x =++在区间[] 55-，上的最大值、最小值分别是（ ） A ．1124-，B ．212，C ．1424-， D ．最小值是14-，无最大值例2．（2022·全国·高一课前预习）函数y ＝x 2－2x ＋2在区间[－2，3]上的最大值、最小值分别是（ ） A ．10，5 B ．10，1 C ．5，1 D ．以上都不对例3．（2022·陕西·榆林市第十中学高一期中）若二次函数()()()24f x a x x =+-的图像经过点()0,4-，则函数()f x 在[]4,2-上的最小值为___________.例4．（2022·全国·高一专题练习）已知函数242y x x =-+-，当14x ≤≤上时y 的最小值是________例5．（2022·广西南宁·高一期末）已知函数2()25,[1,5]f x x x x =-+∈-．则函数的最大值和最小值之积为______题型二：动轴定区间型例6．（2022·全国·高一课时练习）已知函数()()20f x x mx m =->在区间[]0,2上的最小值为()g m ．（1）求函数()g m 的解析式． （2）定义在()(),00,∞-+∞上的函数()h x 为偶函数，且当0x >时，()()h x g x =．若()()4h t h <，求实数t 的取值范围．例7．（2022·全国·高一单元测试）已知函数2()2(f x x mx m m =-++∈R)．当[1,1]x ∈-时，设()f x 的最大值为M ，则M 的最小值为（ ）A ．14B ．0C ．14-D ．1-例8．（2022·全国·高一单元测试）已知函数()()2213f x x k x =-++．(1)若函数()f x 为偶函数，求实数k 的值；(2)若函数()f x 在区间[]1,3-上具有单调性，求实数k 的取值范围；(3)求函数()f x 在区间[]22-,上的最小值．例9．（2022·全国·高一专题练习）已知函数()221f x x mx =++．(1)若1m =，求()f x 在13x -≤≤上的最大值和最小值； (2)求()f x 在22x -≤≤上的最小值；(3)在区间12x -≤≤上的最大值为4，求实数m 的值．例10．（2022·广东湛江·高一期末）已知函数()()f x x x a =-.其中a R ∈，且0a >. (1)求函数()f x 的单调区间； (2)求函数()f x 在1,12⎡⎤-⎢⎥⎣⎦上的最小值.例11．（2022·上海师大附中高一期末）已知函数2(1)h x ax x=+（常数a R ∈）.(1)当2a =时，用定义证明()y h x =在区间[]1,2上是严格增函数； (2)根据a 的不同取值，判断函数()y h x =的奇偶性，并说明理由；(3)令1()()2f x h x x a x=--+，设()f x 在区间[]1,2上的最小值为()g a ，求()g a 的表达式.例12．（2022·全国·高一专题练习）已知函数()21f x x x a x R a R =+-+∈∈，，． (1)当1a =时，求函数()f x 的最小值 (2)求函数()f x 的最小值为()g a ．例13．（2022·全国·高一课时练习）已知函数()f x 是定义在R 上的偶函数，且当0x ≤时，()22f x x x =+，现已画出函数()f x 在y 轴左侧的图象，如图所示，请根据图象．(1)补充完整图象并写出函数()()f x x R ∈的增区间； (2)写出函数()()f x x R ∈的解析式；(3)若函数()()[]()211,2g x f x ax x =-+∈，求函数()g x 的最小值．例14．（2022·安徽·合肥市第十中学高一期中）设函数2()43f x x ax =-+ (1)函数f (x )在区间[1，3]有单调性，求实数a 的取值范围； (2)求函数f (x )在区间[1，3]上的最小值h (a )．题型三：定轴动区间型例15．（2022·全国·高一单元测试）已知函数()22f x x mx n =++的图象过点(0,1)-，且满足()()12f f -=．(1)求函数()f x 的解析式；(2)求函数()f x 在[],2a a +上的最小值；例16．（2022·江苏·高一单元测试）二次函数()f x 满足()()12f x f x x +-=且()01f =． (1)求()f x 的解析式；(2)当[]11x ∈-，时，不等式()2f x x m >+恒成立，求实数m 的取值范围．(3)设函数()f x 在区间[]1a a +，上的最小值为()g a ，求()g a 的表达式．例17．（2022·全国·高一期中）已知二次函数2()(0)f x ax bx c a =++≠，且满足(0)2f =，(1)()21f x f x x +-=+.(1)求函数()f x 的解析式；(2)当[,2]x t t ∈+（R t ∈）时，求函数()f x 的最小值()g t （用t 表示）．例18．（2022·全国·高一专题练习）已知函数()222f x x ax =++．(1)当1a =时，求函数()f x 在区间[)23-，上的值域； (2)当1a =-时，求函数()f x 在区间[]1t t +，上的最大值；(3)求()f x 在[]55-，上的最大值与最小值．例19．（2022·江苏南通·高一开学考试）已知关于x 的函数22 4.y x mx =-+ (1)当23x -≤≤时，求函数224y x mx =-+的最大值； (2)当23x -≤≤时，若函数最小值为2，求m 的值．例20．（2022·全国·高一专题练习）已知()f x 是二次函数，不等式()0f x <的解集是()05，，且()f x 在区间[]2-，4上的最大值是28． (1)求()f x 的解析式；(2)设函数()f x 在[]1x t t ∈+，上的最小值为()g t ，求()g t 的表达式．题型四：动轴动区间型例21．（2022·江苏·楚州中学高一期中）已知函数2()2(0)f x x ax a =-> (1)当2a =时，解关于x 的不等式3()5f x -<<(2)函数()y f x =在[],2t t +的最大值为0，最小值是-4，求实数a 和t 的值．例22．（2022·贵州毕节·高一期末）已知函数2()2(0)f x x ax a =->． (1)当3a =时，解关于x 的不等式5()7f x -<<；(2)函数()y f x =在[],2t t +上的最大值为0，最小值是4-，求实数a 和t 的值．例23．（2022·四川巴中·高一期中）已知a R ∈，函数()f x x x a =-． (1)设1a =，判断函数()f x 的奇偶性，请说明理由；(2)设0a ≠，函数()f x 在区间(),m n 上既有最大值又有最小值，请分别求出m ，n 的取值范围．（只要写出结果，不需要写出解题过程）例24．（2022·江苏苏州·高一期末）已知函数f （x ）＝x |x ﹣m |＋n . (1)当f （x ）为奇函数，求实数m 的值；(2)当m ＝1，n ＞1时，求函数y ＝f （x ）在[0，n ]上的最大值.例25．（2022·浙江·磐安县第二中学高一开学考试）已知R a ∈，函数()f x x x a =-， (1)当2a =时，写出函数()y f x =的单调递增区间； (2)当2a >时，求函数()f x 在区间[]1,2上的最小值；(3)设0a ≠，函数()f x 在(),m n 上既有最大值又有最小值，请分别求出,m n 的取值范围（用a 表示）例26．（2022·全国·高一课时练习）已知函数()()2222f x x a x a =-++，()()22228g x x a x a =-+--+．设()()(){}1max ,H x f x g x =，()()(){}2min ,H x f x g x =．记()1H x 的最小值为A ，()2H x 的最大值为B ，则A B -=______．例27．（2022·浙江·温州市第二十二中学高一开学考试）函数()f x x x a =-， (1)若()f x 在R 上是奇函数，求a 的值；(2)当2a =时，求()f x 在区间(0,4]上的最大值和最小值；(3)设0a >，当m x n <<时，函数()f x 既有最大值又有最小值，求m n 、的取值范围（用a 表示）题型五：根据二次函数的最值求参数例28．（2022·全国·高一专题练习）已知抛物线2y x bx c =-++与x 轴的一个交点为(1,0)-，且经过点(2,)c ．(1)求抛物线与x 轴的另一个交点坐标．(2)当2t x t ≤≤-时，函数的最大值为M ，最小值为N ，若3M N -=，求t 的值．例29．（2022·全国·高一专题练习）若函数f (x )＝ax 2＋2ax ＋1在[－1，2]上有最大值4，则a 的值为( ) A ．38B ．－3C ．38或－3D ．4例30．（2022·全国·高一课时练习）函数()f x x x a =-在区间()0,1上既有最大值又有最小值，则实数a 的取值范围是（ ） A ．)222,0⎡-⎣ B ．()0,222 C ．2⎡⎫⎪⎢⎪⎣⎭D ．)222,1⎡⎣例31．（2022·上海交大附中高一阶段练习）已知二次函数[]224,0,y x x x m =-+∈的最小值是3，最大值是4，则实数m 的取值范围是___________.例32．（2022·湖北黄石·高一期末）已知函数21()2f x x x =-+．若()f x 的定义域为[,]m n ，值域为[2,2]m n ，则m n +=__________．【过关测试】 一、单选题1．（2022·甘肃·民勤县第一中学高一阶段练习）有如下命题：①若幂函数()y f x =的图象过点12,2⎛⎫⎪⎝⎭，则()132f >； ②函数()()110,1x f x a a a -=+>≠的图象恒过定点()1,2； ③函数()1221log f x x x =--有两个零点； ④若函数()224f x x x =-+在区间[]0,m 上的最大值为4，最小值为3，则实数m 的取值范围是[]1,2．其中真命题的序号为（ ）． A ．①②B ．②④C ．①④D ．②③2．（2022·全国·高一专题练习）若函数2()23f x x bx a =-+在区间[0,1]上的最大值是M ，最小值m ，则M m -（ ）A ．与a 无关，且与b 有关B ．与a 有关，且与b 无关C ．与a 有关，且与b 有关D ．与a 无关，且与b 无关3．（2022·河南·郏县第一高级中学高一开学考试）已知()f x 为奇函数，且当0x >时，2()42f x x x =-+，则()f x 在区间[]4,2--上（ ） A ．单调递增且最大值为2 B ．单调递增且最小值为2 C ．单调递减且最大值为-2D ．单调递减且最小值为-24．（2022·黑龙江·哈尔滨德强学校高一期中）已知函数()22f x x x a a =-++在区间[0，2]上的最大值是1，则a 的取值范围是（ ） A ．10,2⎡⎤⎢⎥⎣⎦B ．1,2⎛⎤-∞ ⎥⎝⎦C ．1,2⎡⎫+∞⎪⎢⎣⎭D ．110,,22⎛⎫⎛⎫⋃+∞ ⎪ ⎪⎝⎭⎝⎭5．（2022·湖北·恩施土家族苗族高中高一阶段练习）已知函数2y x ax b =++（,R a b ∈）的最小值为0，若关于x 的不等式2x ax b c 的解集为{}|4x m x m <<+，则实数c 的值为（ ） A ．9B ．8C ．6D ．46．（2022·河南·濮阳一高高一期中（理））已知定义域为R 的函数()f x 满足()()13f x f x +=，且当(]01x ∈，时，()()41f x x x =-，则当(]20x ∈-，时，()f x 的最小值为（ ） A ．181-B ．127-C ．19-D ．13-7．（2022·河北省博野中学高一开学考试）已知m ，n 是关于x 的一元二次方程x 2﹣2tx +t 2﹣2t +4=0的两个实数根，则（m +2)(n +2）的最小值是（ ）. A ．7B ．11C ．12D ．168．（2022·陕西商洛·高一期末）若函数()2f x x bx c =++满足()10f =，()18f -=，则下列判断错误的是（ ）A ．1b c +=-B ．()30f =C ．()f x 图象的对称轴为直线4x =D ．f （x ）的最小值为－1二、多选题9．（2022·全国·高一课时练习）设函数()21,21,ax x a f x x ax x a -<⎧=⎨-+≥⎩，()f x 存在最小值时，实数a 的值可能是（ ） A ．2B ．-1C ．0D ．110．（2022·全国·高一课时练习）定义在R 上的奇函数()f x 在(),0∞-上的解析式()()1f x x x =+，则()f x 在[)0,∞+上正确的结论是（ ） A ．()00f =B ．()10f =C ．最大值14D ．最小值14-11．（2022·浙江省龙游中学高一期中）已知函数()221f x x mx =-+，则下列结论有可能正确的是（ ）A ．()f x 在区间[]1,2上无最大值B ．()f x 在区间[]1,2上最小值为()f mC ．()f x 在区间[]1,2上既有最大值又有最小值D ．()f x 在区间[]1,2上最大值()1f ，有最小值()2f12．（2022·全国·高一单元测试）若[]()()11,9f x x x =+∈，()22()()g x f x f x =+，那么（ ）A ．()g x 有最小值6B ．()g x 有最小值12C ．()g x 有最大值26D ．()g x 有最大值182三、填空题13．（2022·上海·复旦附中高一开学考试）已知M 、N 两点关于y 轴对称，且点M 在双曲线12y x=上，点N 在直线3yx上，设点M 的对称点坐标为(),a b ，则二次函数()2y abx a b x =-++的最小值为______．14．（2022·全国·高一专题练习）已知二次函数22y x x c =-++，当12x -≤≤时，函数的最大值与最小值的差为______15．（2022·全国·高一专题练习）若函数()221f x x ax a =-+-在[0,2]上的最小值为1-．则=a ____．16．（2022·全国·高一专题练习）设函数()2,2,x x a f x x x a ⎧≤=⎨+>⎩，若()f x 有最小值，则a 的取值范围是______． 四、解答题17．（2022·全国·高一专题练习）如图，抛物线23y ax bx =+-与x 轴交于点()1,0A -，()3,0B ，交y 轴于点C ．(1)求该抛物线的函数解析式；(2)当1m x m -≤≤时，函数23y ax bx =+-有最小值2m ，求m 的值．18．（2022·全国·高一课时练习）已知函数()()2y x x a =-+，其中R a ∈． (1)若函数的图象关于直线1x =对称，求a 的值； (2)试述函数值的变化趋势及函数的最大值或最小值．19．（2022·全国·高一专题练习）已知函数()221f x x mx =++．(1)若1m =，求()f x 在[]13，-上的最大值和最小值； (2)若()f x 在[]22-，为单调函数，求m 的值； (3)在区间[]12-，上的最大值为4，求实数m 的值．20．（2022·江西省铜鼓中学高一阶段练习）二次函数()()2210g x mx mx n m =-++>在区间[]0,3上有最大值4，最小值0.(1)求函数()g x 的解析式；(2)设()()(2)f x g x a x =+-，且()f x 在[1,2]-的最小值为3-，求a 的值.1121．（2022·全国·高一课前预习）（1）已知函数2()21f x ax ax =++在区间[-1，2]上最大值为4，求实数a 的值；（2）已知函数2()22f x x ax =-+，x ∈[-1，1]，求函数()f x 的最小值．22．（2022·天津市武清区杨村第一中学高一期末）已知函数()22f x x mx n =++的图象过点()1,1-，且满足()()23f f -=．(1)求函数()f x 的解析式：(2)求函数()f x 在[],2a a +上的最小值；(3)若0x 满足()00f x x =，则称0x 为函数()y f x =的不动点，函数()()g x f x tx t =-+有两个不相等且正的不动点，求t 的取值范围．。

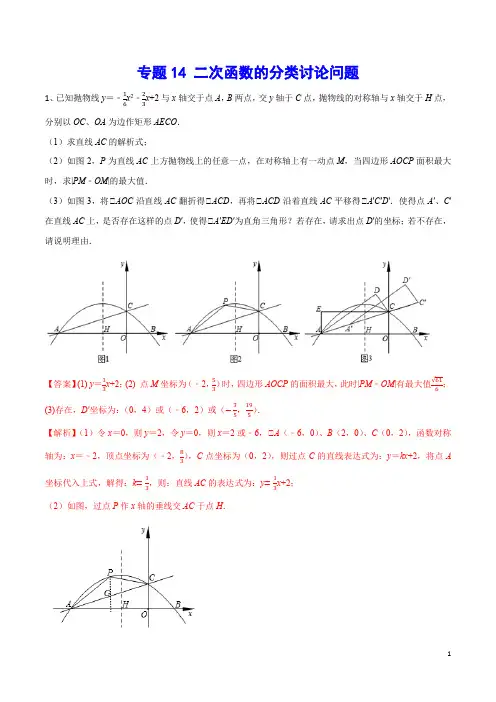
专题14 二次函数的分类讨论问题1、已知抛物线y ＝﹣16x 2﹣23x +2与x 轴交于点A ，B 两点，交y 轴于C 点，抛物线的对称轴与x 轴交于H 点，分别以OC 、OA 为边作矩形AECO ． （1）求直线AC 的解析式；（2）如图2，P 为直线AC 上方抛物线上的任意一点，在对称轴上有一动点M ，当四边形AOCP 面积最大时，求|PM ﹣OM |的最大值．（3）如图3，将△AOC 沿直线AC 翻折得△ACD ，再将△ACD 沿着直线AC 平移得△A 'C ′D '．使得点A ′、C '在直线AC 上，是否存在这样的点D ′，使得△A ′ED ′为直角三角形？若存在，请求出点D ′的坐标；若不存在，请说明理由．【答案】(1) y ＝13x +2；(2) 点M 坐标为（﹣2，53）时，四边形AOCP 的面积最大，此时|PM ﹣OM |有最大值√616； (3)存在，D ′坐标为：（0，4）或（﹣6，2）或（−35，195）．【解析】（1）令x ＝0，则y ＝2，令y ＝0，则x ＝2或﹣6，△A （﹣6，0）、B （2，0）、C （0，2），函数对称轴为：x ＝﹣2，顶点坐标为（﹣2，83），C 点坐标为（0，2），则过点C 的直线表达式为：y ＝kx +2，将点A 坐标代入上式，解得：k =13，则：直线AC 的表达式为：y =13x +2； （2）如图，过点P 作x 轴的垂线交AC 于点H ．四边形AOCP 面积＝△AOC 的面积+△ACP 的面积，四边形AOCP 面积最大时，只需要△ACP 的面积最大即可，设点P 坐标为（m ，−16m 2−23m +2），则点G 坐标为（m ，13m +2），S △ACP =12PG •OA =12•（−16m 2−23m +2−13m ﹣2）•6=−12m 2﹣3m ，当m ＝﹣3时，上式取得最大值，则点P 坐标为（﹣3，52）．连接OP 交对称轴于点M ，此时，|PM ﹣OM |有最大值，直线OP 的表达式为：y =−56x ，当x ＝﹣2时，y =53，即：点M 坐标为（﹣2，53），|PM ﹣OM |的最大值为：|√(−3+2)2+(52−53)2−√22+(53)2|=√616． （3）存在．△AE ＝CD ，△AEC ＝△ADC ＝90°，△EMA ＝△DMC ，△△EAM △△DCM （AAS ），△EM ＝DM ，AM ＝MC ，设：EM ＝a ，则：MC ＝6﹣a ．在Rt△DCM 中，由勾股定理得：MC 2＝DC 2+MD 2，即：（6﹣a ）2＝22+a 2，解得：a =83，则：MC =103，过点D 作x 轴的垂线交x 轴于点N ，交EC 于点H ．在Rt△DMC 中，12DH •MC =12MD •DC ，即：DH ×103=83×2，则：DH =85，HC =√DC 2−DH 2=65，即：点D 的坐标为（−65，185）；设：△ACD 沿着直线AC 平移了m 个单位，则：点A ′坐标（﹣6√10√10），点D ′坐标为（−65+√10185+√10），而点E 坐标为（﹣6，2），则A′D′2=(−6+65)2+(185)2=36，A′E 2=(√10)2+(√102)2=m 2√104，ED′2=(245+√10)2+(85+√10)2=m 2√101285．若△A ′ED ′为直角三角形，分三种情况讨论：△当A′D′2+A′E 2=ED′2时，36+m 2−√104=m 2+√101285，解得：m =2√105，此时D ′（−65+√10185+√10）为（0，4）；△当A′D′2+ED′2=A′E 2时，36+m 2+10+1285=m 210+4，解得：m =−8√105，此时D ′（−6510185+10）为（－6，2）；△当A′E 2+ED′2=A′D′2时，m 2√10+4+m 2√101285=36，解得：m =−8√105或m =√105，此时D ′（−65√10185√10）为（－6，2）或（−35，195）．综上所述：D 坐标为：（0，4）或（﹣6，2）或（−35，195）．2、已知抛物线1l :212y ax =-的项点为P ，交x 轴于A 、B 两点(A 点在B 点左侧)，且sin ABP ∠=．(1)求抛物线1l 的函数解析式；(2)过点A 的直线交抛物线于点C ,交y 轴于点D ,若ABC ∆的面积被y 轴分为1: 4两个部分，求直线AC 的解析式；(3)在(2)的情况下，将抛物线1l 绕点P 逆时针旋转180°得到抛物线2l ,点M 为抛物线2l 上一点，当点M 的横坐标为何值时，BDM ∆为直角三角形？【答案】（1）21128y x =-；（2）直线AC 的解析式为114y x =+；（3）点M 横坐标为16-+16--16-+16--BDM ∆为Rt ∆．【解析】（1）当0x =时，2122y ax =-=- △顶点()0,2P -，2OP = △90BOP ∠=︒，△sin OP ABP BP ∠==△BP ==△4OB ===△()4,0B ，代入抛物线1l 得：1620a -=，解得18a =，△抛物线1l 的函数解析式为21128y x =- （2）△知抛物线1l 交x 轴于A 、B 两点 △A 、B 关于y 轴对称，即()4,0-A △8AB =设直线AC 解析式：y kx b =+点A 代入得：40k b -+= △4b k =△直线AC ：4y kx k =+，()0,4D k △14|4|8||2AOD BOD S S k k ∆∆==⨯⨯= △21248x kx k -=+，整理得：2832160x kx k ---= △128x x k += △14x =-△284C x x k ==+，()284488C y k k k k k =++=+△2(84,88)C k k k ++ △21||32||2ABC C S AB y k k ∆=⋅=+ △若0k >，则:=1:4AOD OBCD S S ∆四边形 △15AOD ABC S S ∆∆= △()218325k k k =⨯+ 解得：10k =（舍去），214k = △直线AC 的解析式为114y x =+ △若k 0<，则8AOD BOD S S k ∆∆==-，()232ABC S k k ∆=-+△()218|32|5k k k -=⨯-+解得：10k =（舍去），214k =（舍去）综上所述，直线AC 的解析式为114y x =+. （3）由（2）得：()0,1D ，()4,0B△抛物线1l 绕点P 逆时针旋转180︒得到抛物线2l △抛物线2l 解析式为：22128y x =-- 设点M 坐标为21(,2)8m m --△若90BDM ∠=︒，如图1，则0m < 过M 作MN y ⊥轴于点N△90MND BOD BDM ∠=∠=∠=︒，MN m =-，22111(2)388DN m m =---=+ △90MDN BDO MDN DMN ∠+∠=∠+∠=︒ △BDO DMN ∠=∠ △BDO DMN ∆∆△BO ODDN MN=，即BO MN DN OD ⋅=⋅ △21438m m -=+解得：116m =-+，216m =--△若90DBM ∠=︒，如图2，过点M 作MQ x ⊥轴于点Q△90BQM DBM BDM ∠=∠=∠=︒，4BQ m =-，2211(2)288MQ m m =---=+ △90BMQ MBQ MBQ DBO ∠+∠=∠+∠=︒△BMQ DBO ∠=∠ △BMQ DBO ∆∆△BQ MQDO BO=，即BQ BO MQ OD ⋅=⋅△()214428m m -=+解得：116m =-+216m =--△若90BMD ∠=︒，则点M 在以BD 为直径的圆除点B 、D 外的圆周上 显然以AB 为真径的圆与抛物线2l 无交点，故此情况不存在满足的m综上所述，点M 横坐标为16-+16--16-+16--BDM ∆为Rt ∆. 3、已知：如图，一次函数y=12x+1的图象与x 轴交于点A ，与y 轴交于点B ；二次函数y=12x 2+bx+c 的图象与一次函数y=12x+1的图象交于B 、C 两点，与x 轴交于D 、E 两点且D 点坐标为（1，0） （1）求二次函数的解析式； （2）求四边形BDEC 的面积S ；（3）在x 轴上有一动点P ，从O 点出发以每秒1个单位的速度沿x 轴向右运动，是否存在点P 使得△PBC 是以P 为直角顶点的直角三角形？若存在，求出点P 运动的时间t 的值，若不存在，请说明理由． （4）若动点P 在x 轴上，动点Q 在射线AC 上，同时从A 点出发，点P 沿x 轴正方向以每秒2个单位的速度运动，点Q 以每秒a 个单位的速度沿射线AC 运动，是否存在以A 、P 、Q 为顶点的三角形与△ABD 相似，若存在，求a 的值，若不存在，说明理由．【答案】△y =12x 2−32x +1;(2)92;(3)t =1或3;(4)a =23√5或65√5【解析】（1）将B （0，1），D （1，0）的坐标代入y=12x 2+bx+c ， 得：{c ＝1b +c +12＝0，解得：{b ＝−32c ＝1故解析式y=12x 2−32x +1；（2）设C （x 0，y 0）， 则有 {y 0＝12x 0+1y 0＝12x 02−32x 0+1 ， 解得{x 0＝4y 0＝3， △C （4，3），由图可知：S=S △ACE -S △ABD ，又由对称轴为x=32可知E （2，0），△S=12AE•y 0-12AD×OB=12×4×3-12×3×1=92； （3）设符合条件的点P 存在，令P （t ，0）： 当P 为直角顶点时，如图：过C 作CF△x 轴于F ；△Rt△BOP△Rt△PCF ， △BOPF＝OP CF ，即 14−t ＝t3， 整理得t 2-4t+3=0， 解得a=1或a=3； 故可得t=1或3．（4）存在符合条件的a 值，使△APQ 与△ABD 相似， △当△APQ△△ABD 时，AP AB＝AQAD ， 解得：a=6√55；△当△APQ△△ADB 时，AP AD＝AQ AB ， 解得：a=2√53，△存在符合条件的a 值，使△APQ 与△ABD 相似，a=6√55或2√53．4、已知，抛物线y ＝﹣x 2+bx +c 经过点A （﹣1，0）和C （0，3）． （1）求抛物线的解析式；（2）在抛物线的对称轴上，是否存在点P ，使P A +PC 的值最小？如果存在，请求出点P 的坐标，如果不存在，请说明理由；（3）设点M 在抛物线的对称轴上，当△MAC 是直角三角形时，求点M 的坐标．【答案】（1）223y x x =-++；（2）当PA PC +的值最小时，点P 的坐标为()1,2；（3）点M 的坐标为()1,1、()1,2、81,3⎛⎫ ⎪⎝⎭或21,3⎛⎫- ⎪⎝⎭.【思路引导】()1由点A 、C 的坐标，利用待定系数法即可求出抛物线的解析式；()2连接BC 交抛物线对称轴于点P ，此时PA PC +取最小值，利用二次函数图象上点的坐标特征可求出点B 的坐标，由点B 、C 的坐标利用待定系数法即可求出直线BC 的解析式，利用配方法可求出抛物线的对称轴，再利用一次函数图象上点的坐标特征即可求出点P 的坐标；()3设点M 的坐标为()1,m ，则CM =，AC ==AM =AMC 90∠=、ACM 90∠=和CAM 90∠=三种情况，利用勾股定理可得出关于m 的一元二次方程或一元一次方程，解之可得出m 的值，进而即可得出点M 的坐标． 【解析】解：()1将()1,0A -、()0,3C 代入2y x bx c =-++中，得：{103b c c --+==，解得：{23b c ==，∴抛物线的解析式为223y x x =-++．()2连接BC 交抛物线对称轴于点P ，此时PA PC +取最小值，如图1所示．当0y =时，有2230x x -++=， 解得：11x =-，23x =，∴点B 的坐标为()3,0．抛物线的解析式为2223(1)4y x x x =-++=--+，∴抛物线的对称轴为直线1x =．设直线BC 的解析式为()0y kx d k =+≠， 将()3,0B 、()0,3C 代入y kx d =+中， 得：{303k d d +==，解得：{13k d =-=，∴直线BC 的解析式为3y x =-+．当1x =时，32y x =-+=，∴当PA PC +的值最小时，点P 的坐标为()1,2．()3设点M 的坐标为()1,m ，则CM =，AC ==AM =分三种情况考虑：①当90AMC ∠=时，有222AC AM CM =+，即22101(3)4m m =+-++，解得：11m =，22m =，∴点M 的坐标为()1,1或()1,2；②当90ACM ∠=时，有222AM AC CM =+，即224101(3)m m +=++-，解得：83m =， ∴点M 的坐标为81,3⎛⎫⎪⎝⎭；③当90CAM ∠=时，有222CM AM AC =+，即221(3)410m m +-=++，解得：23m =-， ∴点M 的坐标为21,.3⎛⎫- ⎪⎝⎭综上所述：当MAC 是直角三角形时，点M 的坐标为()1,1、()1,2、81,3⎛⎫⎪⎝⎭或21,.3⎛⎫- ⎪⎝⎭【方法总结】本题考查待定系数法求二次(一次)函数解析式、二次(一次)函数图象的点的坐标特征、轴对称中的最短路径问题以及勾股定理，解题的关键是：()1由点的坐标，利用待定系数法求出抛物线解析式；()2由两点之间线段最短结合抛物线的对称性找出点P 的位置；()3分AMC 90∠=、ACM 90∠=和CAM 90∠=三种情况，列出关于m 的方程．5、如图，动直线 y ＝kx+2（k ＞0）与 y 轴交于点 F ，与抛物线 y ＝14x 2+1 相交于A ，B 两点，过点 A ，B 分别作 x 轴的垂线，垂足分别为点 C ，D ，连接 CF ，DF ，请你判断△CDF 的形状，并说明理由．【答案】△CFD 是直角三角形．见解析。

含参的二次函数二次函数在初中的时候就比较重要，那么在高中阶段二次函数的考点更加重要，难度也会加大。

高中阶段比较喜欢考含有参数的二次函数，参数就会让函数形成一种动态，随着参数不同，函数是不一样的，这就使得本来简单的二次函数变得复杂起来。

例1. 求2()2f x x ax =-在[2,4]上的最大值和最小值。

解析：这道题因为参数的存在使得函数的本身是动的，在动的情况下考虑这个函数最大值和最小值的问题，这就涉及到高中比较爱考的一类问题，动轴定区间问题。

这道题中对称轴正好是x a =，随着a 不同，这个对称轴在变化，但是在给定区间上问最大值和最小值，那么就会有下面几种情况，在[2,4]这个区间上，有可能（1）这个对称轴不在这个区间里面这个时候的最大值最小值；也有可能（2）这个对称轴就在区间里面，这个时候的最值，还可能（3）对称轴在区间右侧这几个图针对这个函数并不严谨，上面的是一般函数的示意图，这道题中的函数一定是过原点的。

可以感受，随着a 的不同，最大值和最小值是不一样的，所以这种含参的动态的问题往往需要我们做的一个工作就是分类讨论。

那么函数在什么时候取到最大值呢，比如说（1），就会在4的地方取得最大值，（2）在4的地方取得最大值，（3）就会在2的地方取得最大值。

那么在整个函数的区间上，什么时候能取得最大值呢，我们就要看在这个区间上，哪个数离对称轴最远。

那么就有两种情况了，有的时候是2离得比较远，有的时候是4离得比较远，是怎么分界的呢？这个分界线就应该在2和4中间的位置上是3，当对称轴在3x =这条线左边的时候，对称轴离2就比较近，离4就比较远，对称轴在右边的时候，离2就比较近，离4就比较远。

因此这个函数的最大值，经过分类讨论之后，就会得到一个分段函数：max (4)=168(3)()(2)44(3)f a a f x f a a -≤⎧=⎨=->⎩也就是如果这个对称轴在3的左侧，也就是3a ≤的时候，离4远，在4处取得最大值，如果在右侧的话，也就是3a >的时候，离2远，在2处取得最大值。

专题1含参二次函数含参数的二次函数,由于渗透参数导致二次函数的许多性质具有不确定性,再加上绝对值进行复合或分段,求解难度加大、卡壳点增多,需要解题思维的智慧点来支撑.二次函数问题在高考数学命题中永不过时,必须积累大量智慧点,积累破解难点的学习经验.一、二次函数不同表达式间的链接问题1:已知,b c ∈R ,函数()2f x x bx c =++在()0,1上与x 轴有两个不同的交点,求()21c c b ++的取值范围.【解析】卡壳点:不会将二次函数系数与零点沟通.应对策略:参数与零点间的联系通过二次函数不同表达式间的联系来建立.问题解答:设()f x 的两个零点分别为12,x x ,且1201x x <<<,则()()()12f x x x x x =--. 于是()()()()121200,11110c f x x c b f x x ==>++==-->,从而()()()()()()2221122121211101101112216x x x x c c b c c b f f x x x x +-+-⎛⎫⎛⎫<++=++==--≤= ⎪ ⎪⎝⎭⎝⎭.由1201x x <<<知,等号不成立,所以()21c c b ++的取值范围是10,16⎛⎫⎪⎝⎭.【反思】二次函数至少有三种表达形式,即一般式、零点式和对称式,对这三种形式之间的联系不熟悉是产生解题痛点的原因,如何将目标参数与函数零点结合起来?“桥梁”就是二次函数的零点式.在确定最值时,零点式的结构给我们启示,借助基本不等式实现“元”的消失,从而获得参数的范围.二、含绝对值的二次函数结构等价转化问题2:已知函数()211f x x x a x =+-++在R 上有两个不同的零点,则实数a 的取值范围是 【解析】卡壳点:不会将复杂函数的零点转化为两个函数图象交点思考.应对策略:既含参数又有绝对值的二次函数,可将其复杂结构在其本质结构(即函数零点、方程实根、图象交点)间相互转化.1问题解答:()211f x x x a x =+-++在R 上有两个不同的零点,可转化为方程(211)a x x x +=-+-在R 上有两个不同的实根,再转化为两函数1y a x =+与()()21y g x x x ==-+-的图象有两个不同交点.而()()2221,1,11, 1.x x x g x x x x x x ⎧-+-≤=-+-=⎨--+>⎩画出1y a x =+与()y g x =的图象,如图1.显然当0a <时,开口向下的“V”形线才能与拋物线相交,“V”形线开口的大小决定它们交点的个数.根据图象可知,只需考虑方程组()21,1y a x y x x ⎧=+⎨=-+-⎩和()21,1y a x y x x ⎧=-+⎨=-+-⎩的解的情况,考虑图象相切的情形,则联立方程组所得方程()2110x a x a +-++=和2(1x -+a)10x a -+=都有唯一解. 由()()21410a a --+=得323a =-由()()21410a a +--=得323a =--所以当323323a --<<-,1y a x =+与()y g x =的图象才会有两个交点.【反思】面对复杂的代数式结构,冷静地分解代数式,尝试寻找代数式的主体结构(如二次函数与一次函数图象)间的关系,通过数形结合的方法解决.三、二次复台函数不动点转化之桥一一零点表达问题3:已知,b c ∈R ,函数()2f x x bx c =++,它的不动点为12,x x ,且212x x ->,若四次方程()()f f x x =的另两个根为34,x x ,且34x x <,试判断这四个根的大小. 【解析】卡壳点:不会将二次复合函数与函数零点建立关系.应对策略:理解函数不动点概念,将复合结构用零点式表达,并进行化简与转化. 问题解答:由题意得()()()12f x x x x x x -=--,即()()()12f x x x x x x =--+. 于是()()()()()12f f x x f x x f x x f x x ⎡⎤⎡⎤-=--+-⎣⎦⎣⎦()()()()()()12112212x x x x x x x x x x x x x x x x ⎡⎤⎡⎤=--+---+-+--⎣⎦⎣⎦()()()()()()12121211x x x x x x x x x x x x =---+-++-- ()()()()1212111x x x x x x x x ⎡⎤=---+-++⎣⎦.所以34,x x 为方程()()()121110g x x x x x =-+-++=的两个根. 由212x x ->,得()()11222120,20g x x x g x x x =-+=-+.如图2,因为二次函数()g x 的图象开口向上,所以方程()0g x =在区间(∞-,)1x 和()12,x x 上各有一个根.又34x x <,得()()31412,,,x x x x x ∞∈-∈.所以3142x x x x <<<.【反思】函数()f x 的不动点12,x x 即为方程()0f x x -=的两个实根.如何比较这四个根的大小?思路隐藏得比较深,但二次函数的零点表达式又帮助我们建立起一种联系,特别是复合函数的简单化,使我们再一次认识此函数的本来面目.二次复合函数的根的分布情况,最终用零点定理确定.四、合参二次函数抓“形式”促“结构”问题4:设()(){}()()()()()(),,min ,,,f x f xg x f x g x g x f x g x ⎧≤⎪=⎨>⎪⎩若()2f x x px q =++的图象经过两点()(),0,,0αβ,且存在整数n ,使得1n n αβ<<<+,则A.()(){}1min ,14f n f n +>B.()(){}1min ,14f n f n +<C.()(){}1min ,14f n f n +=D.()(){}1min ,14f n f n +≥【解析】卡壳点:不会将较小者函数与零点建立关系.应对策略:深刻理解较小者函数的数学符号,借助零点式进行转化.问题解答:设()()()f x x x αβ=--,图象如图3,由题意可知()()()0f n n n αβ=-->.()()()()()()111f n f n n n n n αβαβ+=--+-+-()()()()11n n n n αβαβ=--+-+- ()()()()11n n n n ααββ=-+--+- 22111,2216n n n n ααββ-++--++-⎛⎫⎛⎫≤= ⎪ ⎪⎝⎭⎝⎭ 当且仅当1,1n n n n ααββ-=+--=+-时,等号成立. 但由1n n αβ<<<+知等号不成立,所以()(){}()()21min ,1116f n f n f n f n +≤+<, 即()(){}1min ,14f n f n +<.【反思】因为()(){}()()(){}()min ,1,min ,11f n f n f n f n f n f n +≤+≤+,所以()(){}()()2min ,11f n f n f n f n +≤+.问题转化为探求()()1f n f n +的最大值,此时二次函数的零点式为探求()()1f n f n +的最大值起到了桥梁作用,对()()1f n f n +零点式的代数结构的识别为基本不等式的运用奠定了基础.任何数学问题的外在形式中必隐藏着其本质结构,对于二次函数,其表达形式至少有一般式、零点式和顶点式,它们之间联系紧密,可以相互转化.本题中抓住()()()()()()111f n f n n n n n αβαβ+=--+-+-这一智慧点,就能解决问题.五、含参二次函数抓“形态”促“化数”因为二次函数的图象是最基本的图形,若题目给出了特定区间上的抛物线,则应将抛物线补充“完整”,以帮助分析、寻找解题途径与思路.问题5:设函数()()2,f x x ax b a b =++∈R ,当214a b =+时,求函数()f x 在[]1,1-上的最小值()g a 的表达式.【解析】卡壳点:不会分类处理定区间上抛物线弧的最值. 应对策略:抓住二次函数的几何形态,分类将二次函数代数式转化.3问题解答:()22221142a a f x x ax b x ax x ⎛⎫=++=+++=++ ⎪⎝⎭,其图象的对称轴方程为2a x =-.(1)当12a -<-,即2a >时,()()2124a g a f a =-=-+,如图4.(2)当112a -≤-≤,即22a -≤≤时,()12a g a f ⎛⎫=-= ⎪⎝⎭,如图5.(3)当12a ->,即2a <-时,()()2124a g a f a ==++,如图6.所以()222,2,41,22,2, 2.4a a a g a a a a a ⎧-+>⎪⎪⎪=-≤≤⎨⎪⎪++<-⎪⎩【反思】从抛物线的形态上看,抓住对称轴2ax =-进行分类讨论,求出a 的取值范围即可得证.此问题涉及二次函数图象的形态,㧓住对称轴思考,帮助分析此二次函数的最值.六、含参二次函数抓“分类”促“分解”因为高中二次函数问题中一般含有参数或绝对值,也可能是复合或分段函数,求解时都离不开分类讨论,通过分类达到分解综合问题之目的.对于二次函数的分类,关键还是对称轴,因为它制约着二次函数的最值与值域.问题6:设()()()22222,0,43,0,k x a k x f x x a a x a x ⎧+-≥⎪=⎨+++-<⎪⎩其中a ∈R .若对任意的非零实数1x ,存在唯一的非零实数()212x x x ≠,使得()()12f x f x =成立,则k 的取值范围为【解析】卡壳点:不会从几何角度思考分段、任意、存在、含参的二层分类. 应对策略:抓住二次函数图象的对称轴分类,将综合问题按层分解. 问题解答:设()()()()22222,43g x k x a k h x x a a x a =+-=+++-.(1)若二次函数()h x 图象的对称轴在y 轴的左侧,对任意的非零实数1x 就会破坏()212x x x ≠的唯一性.(2)若二次函数()h x 图象的对称轴不在y 轴的左侧,即240a a +≤.①两个函数的图象在y 轴上不交于同一点,对任意的非零实数1x ,会破坏()212x x x ≠的唯一性; ②因为两个函数的图象在y 轴上交于同一点,即()()00g h =,所以69k a =-在[]4,0-上有解,从而[]33,9k ∈--.【反思】一个分段函数中含有二次函数(的一部分),从形上思考分类,抓住抛物线的对称轴进人第一层分类,然后抓住分段点位置进人第二层分类,思维的有序性是解决问题的关键. 强化练习1.设函数()f x 的定义域为R ,满足()()12f x f x +=,且当(]0,1x ∈时,()()1f x x x =-.若对任意(],x m ∞∈-,都有()89f x ≥-,则m 的取值范围是A.9,4∞⎛⎤- ⎥⎝⎦B.7,3∞⎛⎤- ⎥⎝⎦C.5,2∞⎛⎤- ⎥⎝⎦D.8,3∞⎛⎤- ⎥⎝⎦【解析】如答图, 作出函数图象, 可以直接排除选项 C,D.因为当 x ∈(0,1] 时, f(x) 的值域为 [−14,0], 所以 把函数值转移到 [−14,0] 上, 才能求出对应的 x 值.f(x)=2f(x −1)=4f(x −2)=−89,即 f(x −2)=−29=(x −2)(x −3), 代值检验可知 选 B.【反思】人们常常利用周期性把自变量转移到某个区间, 求得函数值, 现在反过来, 需要根据值域, 用类似周期的关系 把自变量进行转移.2.已知a ∈R ,设函数()222,1,ln ,1,x ax a x f x x a x x ⎧-+≤=⎨->⎩若关于x 的不等式()0f x ≥在R 上恒成立,则a 的取值范围为A.[]0,1B.[]0,2C.[]0,eD.[]1,e【解析】由 f(0)⩾0, 得 a ⩾0.当 0⩽a ⩽1 时, f(x)=x 2−2ax +2a =(x −a)2+2a –a 2⩾2a −a 2 =a(2−a)>0.当 a >1 时, f(1)=1>0.故当 a ⩾0 时, x 2−2ax +2a ⩾0 在 (−∞,1] 上恒成立.若 x −aln⁡x ⩾0 在 (1,+∞) 上恒成立, 即 a ⩽xln⁡x 在 (1,+∞) 上恒成立. 令 g(x)=xln⁡x , 则 g ′(x)=ln⁡x−1(ln⁡x)2.易知 x =e 为函数 g(x)=xln⁡x 在 (1,+∞) 上唯一的极小 值点, 也是最小值点.故 g(x)min =g(e)=e , 所以 a ⩽e . 综上所述, a 的取值范围为 [0,e], 故选 C.【反思】 分段函数中对二次函数进行分析判断, 对超越函数进行参变分离.3.已知λ∈R ,函数()24,,43,,x x f x x x x λλ-≥⎧=⎨-+<⎩当2λ=时,不等式()0f x <的解集是__.若函数()f x 恰有2个零点,则λ的取值范围是_.若函数()f x 恰有1个零点,则λ的取值范围是若函数()f x 恰有3个零点,则λ的取值范围是____【解析】由 f(x)<0, 解得 1<x <4.画出函数 f(x) 的图象, 如答图所示, 可以判断函数 f(x) 恰有 2 个零点, 此时 1<λ⩽3,λ>4.令 y =x −4,y =x 2−4x +3, 分析当 λ 变化时, 函数零 点的变化情况: (1) 当 λ⩽1 时, 有 1 个零点; (2) 当 1<λ⩽3 时, 有 2 个零点; (3) 当 3<λ⩽4 时, 有 3 个零点; (4) 当 λ>4 时, 有 2 个零点;【反思】 数形结合, 以形促数, 直观判断.4.已知函数()221f x ax x =++,若对任意x ∈R ,都有()()0f f x ≥恒成立,则实数a 的取值范围是_____【解析】显然 a >0, 否则, 当 x →∞ 时, 有 f(f(x)) →−∞, 不符合题意. 当 a >0 时, 函数 f(x) 的值域是 [a−1a,+∞).根据题意, 对函数 f(x) 值域中的任意一个数 t , 都有 f(x)⩾0, 因此 f(x) 没有零点, 或者 f(x) 的较大零点不超 过a−1a.即 4−4a <0, 或者 {4−4a >0,−2+√4−4a 2a ⩽a−1a, 解得实数 a 的取值范围是 [√5−12,+∞). 换一个思路: 根据对称轴 x =−1a<a−1a , 知 f(x) 在 (a−1a ,+∞) 上单调递增, 于是 f (a−1a )⩾0, 解得 a ⩾√5−12 【反思】 此问题考查学生对二次函数性质的理解运用能力, 复合结构阻碍了学生的思维, 只有抓住二次函数的重要 特征, 关于对称轴、单调性与值域的问题才能迎扨而解.5.已知函数()2221f x x x a x a =+--,当[)1,x ∞∈+时,()0f x ≥恒成立,则实数a 的取值范围是______【解析】解法 1 (分离变量法) 当 x ∈[1,+∞) 时, f(x)⩾0 恒成立等价于 ∀x ∈[1,+∞),a 2+√2x −1a − x 2−x ⩽0 恒成立, 解此不等式得⁡−√2x −1+√4x 2+6x −12⩽a ⁡⩽−√2x −1+√4x 2+6x −12. 函数 u(x)=−√2x−1+√4x 2+6x−12 在 [1,+∞) 上 单调递减, 因此 a ⩾u max =u(1)=−2.当 x ∈[1,+∞) 时, 函数 v(x)=−√2x−1+√4x 2+6x−12 ⩾x+2−√2x−12⩾1,且知 v(1)=1, 因此 a ⩽v min =v(1)=1.综上, a 的取值范围是 [−2,1].必要性: 由 f(1)⩾0, 解得 −2⩽a ⩽1. 以下解法只证明 充分性.解法 2 (直接研究 f(x) 的单调性)当 −2⩽a ⩽0 时, f(x) 在 [1,+∞) 上单调递增, 故 f(x)⩾f(1)⩾0.当 0<a ⩽1 时, x 2−√2x −1a ⩾x 2−√2x −1⩾x 2 −x ⩾0.又有 x −a 2⩾1−1=0, 相加可得 f(x)⩾0.综上,充分性得证.解法 3(直接求导法)f ′(x)=2x +1√2x−1=√2x−1−a √2x−1. 函数 y =(2x +1)√2x −1−a 在 [1,+∞) 上单调递 增, 因此 (2x +1)√2x −1−a ⩾3−a >0, 即 f ′(x)>0.∀x ∈[1,+∞), 当 a ∈[−2,1] 时, f(x) 在 [1,+∞) 上 单调递增, 故 f(x)⩾f(1)⩾0.【反思】 在不同思维基础下, 多角度思考, 学会必要性探路 和充分性证明的基本思路.6.已知()2f x ax bx c =++,其中*,,a b c ∈∈N Z ,若方程()0f x x -=的根在()0,1上,求a 的最小值.【解析】令 g(x)=f(x)−x =0 的两根为 x 1,x 2, 则 g(x)=a (x −x 1)(x −x 2).由题设知, g(0)>0,g(1)>0.g(0)g(1)=a 2x 1x 2(1−x 1)(1−x 2)⩽a 2(x 1+1−x 12)2. (x 2+1−x 22)2=a 216, 当且仅当 x 1=x 2=12 时等号成立. 又 a ∈N ∗,b,c ∈Z,g(0)>0,g(1)>0,g(0)=c ⩾1, g(1)=f(1)−1=a +b +c −1⩾1, 所以 g(0)g(1)⩾1.综上可知, a 216⩾1, 即 a 2⩾16,a ⩾4.又 a ∈N ∗, 所以 a 的最小值为 4 .【反思】 二次函数不同表达式的链接. 7.探求()2y f x x x c ==++在定区间[],(,m n m n 为常数)上的最值.【解析】 y =f(x)=x 2+x +c =(x +12)2+c −14. 设 M(c) 和 m(c) 分别表示所求的最大值和最小值.(1) 当 −12⩽m 时, f(x) 在 [m,n] 上单调递增,所以 M(c)=f(n),m(c)=f(m).(2) 当 m <−12⩽m+n 2 时, M(c)=f(n),m(c)= f (−12)=c −14. (3) 当 m+n 2<−12⩽n 时, M(c)=f(m),m(c)= f (−12)=c −14. (4) 当 −12>n 时, f(x) 在 [m,n] 上单调递减,所以 M(c)=f(m),m(c)=f(n).因此 M(c)={f(n),1⩾−(m +n),f(m),1<−(m +n), m(c)={f(m),1⩾−2m,c −14,−2n ⩽1<−2m,f(n),1<−2n.【反思】 一段抛物线弧上最值的分类思考需要整体设计. 不论是动抛物线在定区间上的最值, 还是定抛物线在动区间上的最值, 都需要根据抛物线的对称轴与定义区间的位置关 系进行分类讨论. 此问题含有字母, 抽象表达显得更为重要. 8.如果一个函数的值域与其定义域相同,则称该函数为“同域函数”.已知函数()21f x ax bx a =+++{}210,0x ax bx a x +++≥≥∣. (I)若1,2a b =-=,求()f x 的定义域;(II)当1a =时,若()f x 为“同域函数”,求实数b 的值;(III)若存在实数0a <且1a ≠-,使得()f x 为“同域函数”,求实数b 的取值范围.【解析】(I) 当 a =−1,b =2 时, f(x) 的定义域为 [0,2].(II) 当 a =1 时, f(x)=√x 2+bx +2,x ⩾0.(i) 当 −b 2⩽0, 即 b ⩾0 时, f(x) 的定义域为 [0,+∞), 值域为 [√2,+∞),所以当 b ⩾0 时, f(x) 不是“同域函数”. (ii) 当 −b 2>0, 即 b <0 时, 当且仅当 Δ=b 2−8=0 时, f(x) 是“同域函数”, 此时 b =−2√2. 综上所述, 实数 b 的值为 −2√2.(III) 设 f(x) 的定义域为 A , 值域为 B .(i) 当 a <−1 时, a +1<0, 此时 0∉A,0∈B , 从而 A ≠B,f(x) 不是“同域函数”. (ii) 当 −1<a <0 时, a +1>0. 设 x 0=−b−√b 2−4a(a+1)2a , 则 f(x) 的定义域 A =[0,x 0](1) 当 −b 2a ⩽0, 即 b ⩽0 时, f(x) 的值 域 B = [0,√a +1]. 若 f(x) 是“同域函数”, 则 x 0=√a +1, 从而 b =−(√a +1)2. 又 −1<a <0, 所以实数 b 的取值范围是(−1,0)(2) 当 −b 2a >0, 即 b >0 时, f(x) 的 值 域 B = [0,√4a(a+1)−b 24a ], 若 f(x) 是 “同域函数”, 则 x 0= √4a(a+1)−b 24a , 从而 b =√b 2−4a(a +1)(√−a −1)(∗).此时, 由 √−a −1<0,b >0 可知, (∗) 式不成立.综上所述, 实数 b 的取值范围是 (−1,0).【反思】 分析双参数时, 固定其中的一个参数, 对另一个参 数分类讨论.。

高中数学：导数中含参数的题型
高中数学：导数中含参数的题型
一、导函数是二次函数或者类二次函数形式的
注意题目中为什么没有对最高次的参数是否为零进行单独讨论？因为分子部分符号相同，很容易判断a 非负状态下的单调性，切记，切记。

二、导函数不是二次函数和类二次函数形式
能因式分解的先分解，之后求根，注意所求的根在所给出的定义域有没有意义，如果两个根中有一个或两个含有参数，则需要对比两根的大小关系，最后如果原函数有定义域，还需判断极值点和定义域端点处的位置关系。

三、最高次项系数含有参数，对该系数分类讨论
四、根
的个数不确定时，对判别式Δ分类
五、两根大小
不确定时，对两根大小分类讨论
六、不确定根是否在定义域内时，对根与定义域端点值的大小分类讨论
七、复杂问题，按顺序分类讨论。

导数中含参数问题该如何进行分类讨论
一、导函数是二次函数或者类二次函数形式的
注意题目中为什么没有对最高次的参数是否为零进行单独讨论？因为分子部分符号相同，很容易判断a 非负状态下的单调性，切记，切记。

二、导函数不是二次函数和类二次函数形式
能因式分解的先分解，之后求根，注意所求的根在所给出的定义域有没有意义，如果两个根中有一个或两个含有参数，则需要对比两根的大小关系，最后如果原函数有定义域，还需判断极值点和定义域端点处的位置关系。

三、最高次项系数含有参数，对该系数分类讨论
四、根的个数不确定时，对判别式Δ分类
五、两根大小不确定时，对两根大小分类讨论
六、不确定根是否在定义域内时，对根与定义域端点值的大小分类讨论
七、复杂问题，按顺序分类讨论。

含参数二次函数分类讨论的方法总结二次函数求最值参数分类讨论的方法分类讨论是数学中重要的思想方法和解题策略。

它是根据研究对象的本质属性的相同点和不同点，将对象分为不同种类然后逐类解决问题。

对于二次函数y=a(x-m)+n，x∈[t，s]求最值的问题，解决此类问题的基本思路为：根据对称轴相对定义域区间的位置，利用分类讨论思想方法。

为做到分类时不重不漏，可画对称轴相对于定义域区间的简图分类。

分类图如下：t+s/2为对称轴，①表示对称轴在区间［t，s］的左侧，②表示对称轴在区间［t，s］内且靠近区间的左端点，③表示对称轴在区间内且靠近区间的右端点，④表示对称轴在区间［t，s］的右侧。

然后，再根据口诀“开口向上，近则小、远则大”；“开口向下，近则大、远则小”即可快速求出最值。

含参数的二次函数求最值的问题大致分为三种题型，无论哪种题型都围绕着对称轴与定义域区间的位置关系进行分类讨论。

题型一：“动轴定区间”型的二次函数最值。

例如，求函数f(x)=x-2ax+3在x∈[0,4]上的最值。

先配方，再根据对称轴相对于区间的位置讨论，然后根据口诀写出最值。

解：f(x)=x-2ax+3=(x-a)+3-a，此函数图像开口向上，对称轴x=a。

①、当a＜0时，距对称轴x=a最近，4距对称轴x=a最远，∴x=0时，ymin=3，x=4时，ymax=19-8a。

②、当0≤a＜2时，a距对称轴x=a最近，4距对称轴x=a 最远，∴x=a时，ymin=3-a2，x=4时，ymax=19-8a。

③、当2≤a＜4时，a距对称轴x=a最近，距对称轴x=a最远，∴x=a时，ymin=3-a2，x=0时，ymax=3.④、当4≤a时，4距对称轴x=a最近，距对称轴x=a最远，∴x=4时，ymin=19-8a，x=0时，ymax=3.题型二：“区间定动轴”型的二次函数最值。

例如，已知函数f(x)=ax^2+(1-2a)x-3在[0,1]上最小值为-2，求实数a的值。

复习引入：一元一次的分类讨论：2(2)(31)2(2)0k x k x x +--+->、含参数的一元二次不等式——分类讨论1. 优先考虑十字相乘，若两根大小不确定，即分121212,,x x x x x x >=<三种情况．2. 若不能十字相乘，则考虑按判别式∆的正负分类，即分0,0,0∆>∆=∆<三种情况，结合图像法求解。

3. 按二次项系数正负是否确定：当二次项系数含参数时，按2x 项的系数a 的符号分类，即分0,0,0a a a >=<三种情况．1.2(1)0x a x a -++< 2.22560x ax a -+> 3.223()0x a a x a -++> 4.2(1)0x a x a -++< 5.2(2)20x a x a +--< 6.21()10 x a x a -++< 7.22210 x x a -+-≥1.2210x mx m -++> 2.220x kx k +-≤ 3.240x ax ++> 4.2(2)0x a x a +-+>2560()x ax ax a a R -+>∈解关于的不等式1.2210ax x ++< 2.210.ax ax +-< 3.220ax x a -+<1.21)10ax a x -++<（ 2.21)10ax a x +-->（ 3.22(1)40 mx m x -++< 4.2(32)60 ax a x -++< 5.22(1)40 ax a x -++<综合提高题1. 集合{}{}2222(1)0,540A x x a x a a B x x x =-+++<=-+≥，且A B ⊆，求a 的范围2. 集合{}(){}22320,10A x x x B x x a x a =-+≤=-++≤，且A B ⊆，求a 的范围 3. 设全集U=R ，集合{}{}22(41)40,21A x x a a B x a x a =-++≤=≤≤+，且B A ⊆，求a 的范围4. 集合{}{}22540,220A x x x B x x ax a =-+≤=-++≤，且B A ⊆，求a 的范围含参数的一元二次不等式—恒成立和无解问题（数形结合） 1.220x x a ++>的解集为R ，求a 范围 2.220x x a ++≥的解集为R ，求a 范围 3.210x ax -+≥的解集为R ，求a 范围 4.()2140x k x +-+>的解集为R ，求a 范围5.2(1)10ax a x a +-+->恒成立，求a 范围 6.210ax ax -+>恒成立，求a 范围 7.23208kx kx ++<恒成立，求k 范围 8.22(2)0ax ax a +-+<恒成立，求k 范围 9. 2(3)10mx m x -+-<恒成立，求m 范围10. 2(2)(2)10a x a x -+-+≥恒成立，求a 范围11. 2(2)2(2)-40a x a x -+-<恒成立，求a 范围12. 22(1)(1)10a x a x ----<恒成立，求a 范围13. 22(1)(1)10t x t x -+-->恒成立，求t 范围14. 22(23)(3)10m m x m x -----<恒成立，求m 范围15. 2(1)1mx m x m x m --+-函数的图像在轴下方，求实数的取值范围。

2019全国各地中考数学压轴大题函数综合八、二次函数含参数分类讨论综合问题1.（2019•宁波）如图，已知二次函数y＝x2+ax+3的图象经过点P（﹣2，3）．（1）求a的值和图象的顶点坐标．（2）点Q（m，n）在该二次函数图象上．①当m＝2时，求n的值；②若点Q到y轴的距离小于2，请根据图象直接写出n的取值范围．解：（1）把点P（﹣2，3）代入y＝x2+ax+3中，∴a＝2，∴y＝x2+2x+3，∴顶点坐标为（﹣1，2）；（2）①当m＝2时，n＝11，②点Q到y轴的距离小于2，∴|m|＜2，∴﹣2＜m＜2，∴2≤n＜11；2.（2019•杭州）设二次函数y＝（x﹣x1）（x﹣x2）（x1，x2是实数）．（1）甲求得当x＝0时，y＝0；当x＝1时，y＝0；乙求得当x＝时，y＝﹣．若甲求得的结果都正确，你认为乙求得的结果正确吗？说明理由．（2）写出二次函数图象的对称轴，并求该函数的最小值（用含x1，x2的代数式表示）．（3）已知二次函数的图象经过（0，m）和（1，n）两点（m，n是实数），当0＜x1＜x2＜1时，求证：0＜mn＜．解：（1）当x＝0时，y＝0；当x＝1时，y＝0；∴二次函数经过点（0，0），（1，0），∴x1＝0，x2＝1，∴y═x（x﹣1）＝x2﹣x，当x＝时，y＝﹣，∴乙说点的不对；（2）对称轴为x＝，当x＝时，y＝﹣是函数的最小值；（3）二次函数的图象经过（0，m）和（1，n）两点，∴m＝x1x2，n＝1﹣x1﹣x2+x1x2，∴mn＝[﹣][﹣]∵0＜x1＜x2＜1，∴0≤﹣≤，0≤﹣≤，∴0＜mn＜．3.（2019•温州）如图，在平面直角坐标系中，二次函数y＝﹣x2+2x+6的图象交x轴于点A，B（点A在点B的左侧）（1）求点A，B的坐标，并根据该函数图象写出y≥0时x的取值范围．（2）把点B向上平移m个单位得点B1．若点B1向左平移n个单位，将与该二次函数图象上的点B2重合；若点B1向左平移（n+6）个单位，将与该二次函数图象上的点B3重合．已知m＞0，n＞0，求m，n 的值．解：（1）令y＝0，则﹣，解得，x1＝﹣2，x2＝6，∴A（﹣2，0），B（6，0），由函数图象得，当y≥0时，﹣2≤x≤6；（2）由题意得，B1（6，m），B2（6﹣n，m），B3（﹣n，m），函数图象的对称轴为直线，∵点B2，B3在二次函数图象上且纵坐标相同，∴，∴n＝1，∴，∴m，n的值分别为，1．4.（2019•台州）已知函数y＝x2+bx+c（b，c为常数）的图象经过点（﹣2，4）．（1）求b，c满足的关系式；（2）设该函数图象的顶点坐标是（m，n），当b的值变化时，求n关于m的函数解析式；（3）若该函数的图象不经过第三象限，当﹣5≤x≤1时，函数的最大值与最小值之差为16，求b的值．解：（1）将点（﹣2，4）代入y＝x2+bx+c，得﹣2b+c＝0，∴c＝2b；（2）m＝﹣，n＝，∴n＝，∴n＝2b﹣m2，（3）y＝x2+bx+2b＝（x+）2﹣+2b，对称轴x＝﹣，当b≤0时，c≤0，函数不经过第三象限，则c＝0；此时y＝x2，当﹣5≤x≤1时，函数最小值是0，最大值是25，∴最大值与最小值之差为25；（舍去）当b＞0时，c＞0，函数不经过第三象限，则△≤0，∴0≤b≤8，∴﹣4≤x＝﹣≤0，当﹣5≤x≤1时，函数有最小值﹣+2b，当﹣5≤﹣＜﹣2时，函数有最大值1+3b，当﹣2＜﹣≤1时，函数有最大值25﹣3b；函数的最大值与最小值之差为16，当最大值1+3b时，1+3b+﹣2b＝16，∴b＝6或b＝﹣10，∵4≤b≤8，∴b＝6；当最大值25﹣3b时，25﹣3b+﹣2b＝16，∴b＝2或b＝18，∵2≤b≤4，∴b＝2；综上所述b＝2或b＝6；5.（2019•天门）在平面直角坐标系中，已知抛物线C：y＝ax2+2x﹣1（a≠0）和直线l：y＝kx+b，点A（﹣3，﹣3），B（1，﹣1）均在直线l上．（1）若抛物线C与直线l有交点，求a的取值范围；（2）当a＝﹣1，二次函数y＝ax2+2x﹣1的自变量x满足m≤x≤m+2时，函数y的最大值为﹣4，求m的值；（3）若抛物线C与线段AB有两个不同的交点，请直接写出a的取值范围．解：（1）点A（﹣3，﹣3），B（1，﹣1）代入y＝kx+b，∴，∴，∴y＝x﹣；联立y＝ax2+2x﹣1与y＝x﹣，则有2ax2+3x+1＝0，∵抛物线C与直线l有交点，∴△＝9﹣8a≥0，∴a≤且a≠0；（2）根据题意可得，y＝﹣x2+2x﹣1，∵a＜0，∴抛物线开口向下，对称轴x＝1，∵m≤x≤m+2时，y有最大值﹣4，∴当y＝﹣4时，有﹣x2+2x﹣1＝﹣4，∴x＝﹣1或x＝3，①在x＝1左侧，y随x的增大而增大，∴x＝m+2＝﹣1时，y有最大值﹣4，∴m＝﹣3；②在对称轴x＝1右侧，y随x最大而减小，∴x＝m＝3时，y有最大值﹣4；综上所述：m＝﹣3或m＝3；（3）①a＜0时，x＝1时，y≤﹣1，即a≤﹣2；②a＞0时，x＝﹣3时，y≥﹣3，即a≥，直线AB的解析式为y＝x﹣，抛物线与直线联立：ax2+2x﹣1＝x﹣，∴ax2+x+＝0，△＝﹣2a＞0，∴a＜，∴a的取值范围为≤a＜或a≤﹣2；6.（2019•大连）把函数C1：y＝ax2﹣2ax﹣3a（a≠0）的图象绕点P（m，0）旋转180°，得到新函数C2的图象，我们称C2是C1关于点P的相关函数．C2的图象的对称轴与x轴交点坐标为（t，0）．（1）填空：t的值为2m﹣1（用含m的代数式表示）（2）若a＝﹣1，当≤x≤t时，函数C1的最大值为y1，最小值为y2，且y1﹣y2＝1，求C2的解析式；（3）当m＝0时，C2的图象与x轴相交于A，B两点（点A在点B的右侧）．与y轴相交于点D．把线段AD原点O逆时针旋转90°，得到它的对应线段A′D′，若线A′D′与C2的图象有公共点，结合函数图象，求a的取值范围．解：（1）C1：y＝ax2﹣2ax﹣3a＝a（x﹣1）2﹣4a，顶点（1，﹣4a）围绕点P（m，0）旋转180°的对称点为（2m﹣1，4a），C2：y＝﹣a（x﹣2m+1）2+4a，函数的对称轴为：x＝2m﹣1，t＝2m﹣1，故答案为：2m﹣1；（2）a＝﹣1时，C1：y＝﹣（x﹣1）2+4，①当t＜1时，x＝时，有最小值y2＝，x＝t时，有最大值y1＝﹣（t﹣1）2+4，则y1﹣y2＝﹣（t﹣1）2+4﹣＝1，无解；②1≤t时，x＝1时，有最大值y1＝4，x＝时，有最小值y2＝﹣（t﹣1）2+4，y1﹣y2＝≠1（舍去）；③当t时，x＝1时，有最大值y1＝4，x＝t时，有最小值y2＝﹣（t﹣1）2+4，y1﹣y2＝（t﹣1）2＝1，解得：t＝0或2（舍去0），故C2：y＝（x﹣2）2﹣4＝x2﹣4x；（3）m＝0，C2：y＝﹣a（x+1）2+4a，点A、B、D、A′、D′的坐标分别为（1，0）、（﹣3，0）、（0，3a）、（0，1）、（﹣3a，0），当a＞0时，a越大，则OD越大，则点D′越靠左，当C2过点A′时，y＝﹣a（0+1）2+4a＝1，解得：a＝，当C2过点D′时，同理可得：a＝1，故：0＜a或a≥1；当a＜0时，当C2过点D′时，﹣3a＝1，解得：a＝﹣，故：a≤﹣；综上，故：0＜a或a≥1或a≤﹣．7.（2019•贵阳）如图，二次函数y＝x2+bx+c的图象与x轴交于A，B两点，与y轴交于点C，且关于直线x＝1对称，点A的坐标为（﹣1，0）．（1）求二次函数的表达式；（2）连接BC，若点P在y轴上时，BP和BC的夹角为15°，求线段CP的长度；（3）当a≤x≤a+1时，二次函数y＝x2+bx+c的最小值为2a，求a的值．解：（1）∵点A（﹣1，0）与点B关于直线x＝1对称，∴点B的坐标为（3，0），代入y＝x2+bx+c，得：，解得，所以二次函数的表达式为y＝x2﹣2x﹣3；（2）如图所示：由抛物线解析式知C（0，﹣3），则OB＝OC＝3，∴∠OBC＝45°，若点P在点C上方，则∠OBP＝∠OBC﹣∠PBC＝30°，∴OP＝OB tan∠OBP＝3，∴CP＝3；若点P在点C下方，则∠OBP′＝∠OBC+∠P′BC＝60°，∴OP′＝OB tan∠OBP′＝33，∴CP＝33；综上，CP的长为3或33；（3）若a+1＜1，即a＜0，则函数的最小值为（a+1）2﹣2（a+1）﹣3＝2a，解得a＝1（正值舍去）；若a＜1＜a+1，即0＜a＜1，则函数的最小值为1﹣2﹣3＝2a，解得：a＝﹣2（舍去）；若a＞1，则函数的最小值为a2﹣2a﹣3＝2a，解得a＝2（负值舍去）；综上，a的值为1或2．8.（2019•天津）已知抛物线y＝x2﹣bx+c（b，c为常数，b＞0）经过点A（﹣1，0），点M（m，0）是x轴正半轴上的动点．（Ⅰ）当b＝2时，求抛物线的顶点坐标；（Ⅱ）点D（b，y D）在抛物线上，当AM＝AD，m＝5时，求b的值；（Ⅲ）点Q（b+，y Q）在抛物线上，当AM+2QM的最小值为时，求b的值．解：（Ⅰ）∵抛物线y＝x2﹣bx+c经过点A（﹣1，0），∴1+b+c＝0，即c＝﹣b﹣1，当b＝2时，y＝x2﹣2x﹣3＝（x﹣1）2﹣4，∴抛物线的顶点坐标为（1，﹣4）；（Ⅱ）由（Ⅰ）知，抛物线的解析式为y＝x2﹣bx﹣b﹣1，∵点D（b，y D）在抛物线y＝x2﹣bx﹣b﹣1上，∴y D＝b2﹣b•b﹣b﹣1＝﹣b﹣1，由b＞0，得b＞＞0，﹣b﹣1＜0，∴点D（b，﹣b﹣1）在第四象限，且在抛物线对称轴x＝的右侧，如图1，过点D作DE⊥x轴，垂足为E，则点E（b，0），∴AE＝b+1，DE＝b+1，得AE＝DE，∴在Rt△ADE中，∠ADE＝∠DAE＝45°，∴AD＝AE，由已知AM＝AD，m＝5，∴5﹣（﹣1）＝（b+1），∴b＝3﹣1；（Ⅲ）∵点Q（b+，y Q）在抛物线y＝x2﹣bx﹣b﹣1上，∴y Q＝（b+）2﹣b（b+）﹣b﹣1＝﹣﹣，可知点Q（b+，﹣﹣）在第四象限，且在直线x＝b的右侧，∵AM+2QM＝2（AM+QM），∴可取点N（0，1），如图2，过点Q作直线AN的垂线，垂足为G，QG与x轴相交于点M，由∠GAM＝45°，得AM＝GM，则此时点M满足题意，过点Q作QH⊥x轴于点H，则点H（b+，0），在Rt△MQH中，可知∠QMH＝∠MQH＝45°，∴QH＝MH，QM＝MH，∵点M（m，0），∴0﹣（﹣﹣）＝（b+）﹣m，解得，m＝﹣，∵AM+2QM ＝，∴[（﹣）﹣（﹣1）]+2[（b +）﹣（﹣）]＝，∴b＝4．。

二次函数求最值参数分类讨论的方法分类讨论是数学中重要的思想方法和解题策略,它是根据研究对象的本质属性的相同点和不同点,将对象分为不同种类然后逐类解决问题．一般地,对于二次函数y=a (x -m )2+n ，x ∈[t ，s ]求最值的问题;解决此类问题的基本思路为：根据对称轴相对定义域区间的位置，利用分类讨论思想方法。

为做到分类时不重不漏，可画对称轴相对于定义域区间的简图分类。

①表示对称轴在区间［t ，s ］的左侧，②表示对称轴在区间［t ，s ］内且靠近区间的左端点，③表示对称轴在区间内且靠近区间的右端点，④表示对称轴在区间［t ，s ］的右侧。

然后，再根据口诀“开口向上，近则小、远则大”；“开口向下，近则大、远则小”即可快速求出最值。

含参数的二次函数求最值的问题大致分为三种题型，无论哪种题型都围绕着对称轴与定义域区间的位置关系进行分类讨论题型一：“动轴定区间”型的二次函数最值例１、求函数2()23f x x ax =-+在[0,4]x ∈上的最值。

分析：先配方，再根据对称轴相对于区间的位置讨论，然后根据口诀写出最值。

解：222()23()3f x x ax x a a =-+=-+-∴此函数图像开口向上，对称轴x=a①、当a ＜0时，0距对称轴x=a 最近，4距对称轴x=a 最远， ∴x=0时，min y =3，x=4时，max y =19-8a②、当0≤a＜2时，a 距对称轴x=a 最近，4距对称轴x=a 最远， ∴x=a 时，min y =3-a2，x=4时，max y =19-8a③、当2≤a ＜4时，a 距对称轴x=a 最近，0距对称轴x=a 最远， ∴x=a 时，min y =3-a2，x=0时，max y =3④、当4≤a 时，4距对称轴x=a 最近，0距对称轴x=a 最远， ∴x=4时，min y =19-8a ，x=0时，max y =3例2、已知函数2()(21)3f x ax a x =+--在区间3[,2]2-上最大值为1,求实数a 的值分析:取a=0,a ≠0，分别化为一次函数与二次函数,根据一次函数、二次函数的性质分类讨论.解:1)若a=0,则f(x)=-x-3,而f(x)在3[,2]2-上取不到最大值为1,∴a ≠0 2)若a ≠0,则2()(21)3f x ax a x =+--的对称轴为0122a x a-=(Ⅰ)若3()12f -=，解得103a =-，此时0233[,2]202x =-∈-a<0, 0()f x 为最大值，但23()120f -≠(Ⅱ) 若(2)1f =解得34a =此时013[,2]32x =-∈-0310,43a x =>=-距右端点2较远，(2)f 最大值符合条件(Ⅲ) 若0()1f x =解得32a -±=当0a =<时034[,2]2x =-∉-当302a --=<时034[,2]2x =∈-综收所述34a =或32a --=评注：此类题属于“动轴定区间”型的二次函数最值，解决此类问题的关键是讨论对称轴相对于定义域区间的位置，讨论时做到不重不漏。

含参函数单调性的分类讨论问题一、含参函数单调性讨论步骤1.求定义域；2.求导数；3.数轴标根；4.判断导数正负；5.确定函数的单调性（单调区间）.二、常见含参函数的形式分类1.一次函数形式⎪⎩⎪⎨⎧→-=→>→-=→<→+=单调区间数轴标根单调区间数轴标根(0(0)(k b x k k b x k b kx x f 2.二次函数形式))(()()(212x x x x a x f c bx ax x f --='→→++=因式分解⎪⎪⎩⎪⎪⎨⎧⎪⎩⎪⎨⎧→<>→>→→<→→=∆→→<>→=→单调区间或比较两根大小单调区间数轴标根单调区间数轴标根不能判断或一次函数讨论形式讨论参数)(0000002121x x x x a a a 3.指数函数形式（含xe ）⎩⎨⎧→++='→++='→→=根据参数分类讨论根据参数分类讨论因式分解的式子含))(()())(()()()(c bx a e xf c e b e a x f e x f x x x x题型一一次函数型例1.1讨论函数ax x x f -=ln )(的单调性.【解析】练1.1已知函数x a ax x x f )12(ln )(2+++=，讨论)(x f 的单调性.【解析】题型二二次函数型例2.1设函数2()ln f x ax a x =--，其中a R ∈，讨论()f x 的单调性.【解析】由题意，()2121'2,0ax f x ax x x x-=-=>①当0a 时，2210ax -≤，()'0f x ≤，()f x 在()0,+∞上单调递减.②当0a >时，令()0f x '=，有x =，当x ∈时，()'0f x <；当)x ∈+∞时，()'0f x >，故()f x 在上单调递减，在)+∞上单调递增.练2.11已知函数1()ln f x x a x x=-+，讨论()f x 的单调性.【解析】()f x 的定义域为(0,)+∞，22211()1a x ax f x x x x -+'=--+=-．①若2≤a ，则()0'≤f x ，当且仅当2a =，1x =时()0f x '=，所以()f x 在(0,)+∞单调递减．②若2a >，令()0f x '=得，2a x =或2a x =．当(0,)(,)22a a x -+∈+∞ 时，()0f x '<；当(,22a a x ∈时，()0f x '>．所以()f x在(0,2a，(,)2++∞a单调递减，在(,22a a +单调递增．练2.12设函数1()ln 1x f x a x x -=++，其中a 为常数．讨论函数()f x 的单调性．【解析】函数()f x 的定义域为(0,)+∞，2222(22)()(1)(1)a ax a x a f x x x x x +++'=+=++，（1）当0a ≥时，()0f x '>，函数()f x 在(0,)+∞上单调递增，（2）当0a <时，令2()(22)g x ax a x a =+++，由于22(22)44(21)a a a ∆=+-=+，①当12a =-时，0∆=，221(1)2()0(1)x f x x x --'=≤+，函数()f x 在(0,)+∞上单调递减，②当12a <-时，0,()0g x ∆<<，()0f x '<，函数()f x 在(0,)+∞上单调递减，③当102a -<<时，0∆>，设1212,()x x x x <是函数()g x 的两个零点，则1(1)a x a -++=，2(1)a x a -+=，由11a x a+-=-0a =>-，所以1(0,)x x ∈时，()0,()0g x f x '<<，函数()f x 单调递减，12(,)x x x ∈时，()0,()0g x f x '>>，函数()f x 单调递增，2(,)x x ∈+∞时，()0,()0g x f x '<<，函数()f x 单调递减，综上可知，当0a ≥时，函数()f x 在(0,)+∞上单调递增；当12a ≤-时，函数()f x 在(0,)+∞上单调递减；当102a -<<时，()f x 在(1)(0,a a -++，(1)(,)a a-++∞上单调递减，在(1)(1)(,a a a a -+-+上单调递增．例2.2已知函数32()22f x x ax =-+，讨论()f x 的单调性.【解析】2()622(3)f x x ax x x a '=-=-．令()0f x '=，得0=x 或3a x =.①若0>a ，则当(,0),3a x ⎛⎫∈-∞+∞ ⎪⎝⎭ 时，()0f x '>；当0,3a x ⎛⎫∈ ⎪⎝⎭时，()0f x '<．故()f x 在(,0),,3a ⎛⎫-∞+∞ ⎪⎝⎭单调递增，在0,3a ⎛⎫ ⎪⎝⎭单调递减；②若0=a ，()f x 在(,)-∞+∞单调递增；③若0<a ，则当,(0,)3a x ⎛⎫∈-∞+∞ ⎪⎝⎭ 时，()0f x '>；当,03a x ⎛⎫∈ ⎪⎝⎭时，()0f x '<．故()f x 在,,(0,)3a ⎛⎫-∞+∞ ⎪⎝⎭单调递增，在,03a ⎛⎫ ⎪⎝⎭单调递减.练2.21已知函数1,ln )1(21)(2>-+-=a x a ax x x f ，求)(x f 的单调区间.【解析】练2.22已知()221()ln ,R x f x a x x a x-=-+∈，讨论()f x 的单调性.【解析】因为322)11(=)(′x x x a x f －－－322)(1(=x ax x )－－，（1）当0a ≤时，(0,1)x ∈，0>)(′x f ，)(x f 单调递增，(1,)x ∈+∞，0<)(′x f ，)(x f 单调递减；（2）当0>a 时，3322+(2)(1(=2)(1(=)(′x a x a x x a x ax x x f ))－－)－－①当02a <<时，1>2a ，(0,1)x ∈或)x ∈+∞，0>)(′x f ，)(x f 单调递增，x ∈，0<)(′x f ，)(x f 单调递减；②当2a =时，1=2a，(0,)x ∈+∞，()0f x '≥，)(x f 单调递增，③当2a >时，1<2<0a ，x ∈或(1,)x ∈+∞，0>)(′x f ，)(x f 单调递增，x ∈，0<)(′x f ，)(x f 单调递减；题型三指数型例3.1已知函数2()()x x f x e e a a x =--，讨论()f x 的单调性.【解析】函数()f x 的定义域为(,)-∞+∞，22()2(2)()x x x x f x e ae a e a e a '=--=+-，①若0a =，则2()x f x e =，在(,)-∞+∞单调递增．②若0a >，则由()0f x '=得ln x a =．当(,ln )x a ∈-∞时，()0f x '<；当(ln ,)x a ∈+∞时，()0f x '>，所以()f x 在(,ln )a -∞单调递减，在(ln ,)a +∞单调递增．③若0a <，则由()0f x '=得ln(2a x =-．当(,ln())2a x ∈-∞-时，()0f x '<；当(ln()2a x ∈-+∞时，()0f x '>，故()f x 在(,ln())2a-∞-单调递减，在(ln(),)2a -+∞单调递增．练3.1已知函数2()(2)(1)x f x x e a x =-+-，讨论()f x 的单调性.。

分类讨论思想是根据题目的特点和要求，把所有研究的问题分成若干类，转化成若干个小问题，按不同情况分类，然后再逐一进行讨论、求解的思想.分类讨论思想是解答复杂问题的重要工具，尤其对于一些结论不唯一，表示形式不唯一，含有参数的复杂问题，运用分类讨论思想求解最为有效.运用分类讨论思想解题的步骤可以概括为以下几步：1.明确研究的对象.仔细分析题意，明确哪些变量、参数可直接影响所求的结果，据此确定研究的对象.常见的研究对象有参数、自变量、绝对值内部式子、方程的根，函数的定义域、直线的位置、角度等.2.明确分类标准.在确定了需要讨论的对象后，就可以选择合适的分类标准，按照其特征将所有可能会出现的情况全部罗列出来.常见的分类标准有概念、公式、定理的应用条件，代数式的意义，曲线的范围等.3.逐级讨论.在分类后，原先的复杂、困难的问题已经被分为若干个简单、容易的子问题，把所有子问题逐个逐级进行解答，计算出结果即可.当子问题也无法解答时，需要对子问题进一步分类，并且依然要遵循分类标准统一的原则，分类时要做到不重复、不遗漏任何一种情况.4.得出结论.最后需要将所有子问题的结果进行汇总，得到完整的结论.下面举例说明.例1.已知集合M ={a 2,a +1,-3}，N ={a -3,2a -1,a 2+1}，若M ∩N ={-3}，求a 的值.解：因为M ∩N ={-3}，所以-3∈N ={a -3,2a -1,a 2+1}，（1）若a -3=-3，则a =0,此时M ={1,0,-3},N ={-3,-1,1},M ∩N ={-3,1}，故不满足题意；（2）若2a -1=-3，则a =-1，此时M ={}1,0,-3，N ={}-4,-3,2，M ∩N ={}-3，满足题意；（3）若a 2+1=-3,此方程无实数解；所以a =-1.对于集合中求参数的值和参数的取值范围问题，通常要运用分类讨论思想求解.往往需讨论集合中元素的取值，集合是否为空集，含参方程是否有解.只有明确参数的不同取值会导致哪些不同的结果，找到进行分类讨论的原因，才能确定问题研究的对象和分类原则，合理进行分类.例2.设函数f ()x =a ln x +x -1x +1，其中a 为常数，试讨论函数f ()x 的单调性.解：由题意可知函数f ()x 的定义域为(0,+∞),对其求导可得f ′()x =ax 2+()2a +2x +ax (x +1)2，（1）当a ≥0时，f ′()x ≥0，则函数f ()x 在(0,+∞)上单调递增，（2）当a <0时，令g ()x =ax 2+()2a +2x +a ，可得∆=4()2a +1，①当a =-12时，∆=0，f ′()x ≤0，则函数f ()x 在(0,+∞)上单调递减，②当a <-12时，∆<0，f ′()x <0，则函数f ()x 在(0,+∞)上单调递减，③当-12<a <0时，∆>0，所以f ′()x ≤0，设x 1,x 2()x 1<x 2是函数g ()x 的两个零点，则x 1=-()a +1+2a +1a ，x 2=-()a +1-2a +1a，因为x 1=0，所以x ∈(0,x 1)时，g (x )<0，f ′()x <0，则函数f ()x 在(0,+∞)上单调递减;当x ∈(x 1,x 2)时，g (x )>0，f ′()x >0，则函数f ()x 在(0,+∞)上单调递增;当x ∈(x 2,+∞)时，g (x )<0，f ′()x <0，则函数f ()x 在(0,+∞)上单调递减.综上可知：当a ≥0时，函数f ()x 在(0,+∞)上单调递增，当a ≤-12时，函数f ()x 在(0,+∞)上单调递减，当-12<a <0时，函数f ()x 在æèççöø÷÷0，-()a +1+2a +1a ，思路探寻46(-()a+1-2a+1a,+∞)上单调递减，在(-()a+1+2a+1a,-()a+1-2a+1a)上单调递增.含参函数问题主要有两种类型，一是由于函数的概念或性质的限制，需要分类讨论参数的取值或取值范围；二是当参数为函数的系数时，需对参数进行分类讨论，此时要根据函数图象及函数对应方程的判别式来确定分类讨论的分界点.对于二次函数y=ax2+bx+c，当二次项的系数a>0时，二次函数图象的开口向上；当a=0时，该函数为一次函数；当a<0时，二次函数图象的开口向下.二次方程ax2+bx+c=0的判别式∆又决定了二次函数的零点的个数，如下表所示.因此，在讨论二次函数的零点时，可以分∆>0、=0、例3.已知函数f()x=ln xx+1+1x，当x>0且x≠1时，f()x>ln xx−1+k x，求k的取值范围.解：f()x-(ln x x-1+k x)=11-x2[2ln x+()k-1()x2-1x]，令h()x=2ln x+()k-1()x2-1x()x>0，则h′()x=()k-1()x2+1+2xx2=k()x2+1-(x-1)2x2，（1）当k≤0时，由h′()x=k()x2+1-(x-1)2x2可知，当x≠1时,h′()x<0,h()1=0，当x∈()0,1时，h()x>0，可得11-x2h()x>0，当x∈()1,+∞时，h′()x<0，可得11-x2h()x>0，所以当x>0且x≠1时，f()x-æèöøln xx-1+k x>0,即f()x>ln xx-1+k x，（2）当0<k<1时，x∈æèöø1,11-k，()k-1(x2+1)+2x>0，所以当x∈æèöø1,11-k时，h()x>0，可得11-x2h()x<0，与题意不相符；（3）当k≥1时，此时h′()x>0，可得11-x2h()x<0，与题意不相符；综上所述，k的取值范围为(-∞,0].解答含参不等式问题，通常需要运用分类讨论思想对不等式的二次项系数以及一元二次不等式对应的方程的根来进行分类讨论.若含参一元二次不等式对应的方程存在两个根，则需要讨论两根的大小关系，进而确定解集.例4.设F1，F2为椭圆x29+y24=1的两个焦点，点P为椭圆上一点，已知点P，F1，F2是一个直角三角形的三个顶点，且|PF1|>|PF2|，则PF1|PF2|=________.解：（1）若∠PF2F1=90°，则|PF1|2=|PF2|2+|F1F2|2，又|PF1|+|PF2|=6，|F1F2|=25，解得|PF1|=143，|PF2|=43，可得|PF1||PF2|=72.（2）若∠F1PF2=90°，则|F1F2|2=|PF1|2+|PF2|2，所以|PF1|2+(6-|PF1|)2=20，又|PF1|>|PF2|，可得|PF1|=4，|PF2|=2，所以|PF1||PF2|=2.综上可知，|PF1||PF2|=72或2.要求|PF1||PF2|，需寻找满足|PF1|>|PF2|的条件，分两种情况讨论Rt△PF1F2的直角所在的位置.解答几何问题，经常要讨论图形中点、直线、曲线的位置，图形的形状、角的取值范围等.总之，对于某些不确定的数量、不确定图形的形状或位置、不确定的结论等，都需运用分类讨论思想，通过分类讨论，保证其完整性，使之具有确定性.分类讨论思想是解答含参集合问题、含参函数问题、含参不等式问题、含参解析几何问题、含参数列问题的重要工具.同学们要熟练掌握分类讨论思想的应用技巧和步骤，使复杂问题简单化.（作者单位：哈尔滨师范大学教师教育学院）思路探寻47。

二次函数求最值参数分类讨论的方法分类讨论是数学中重要的思想方法和解题策略,它是根据研究对象的本质属性的相同点和不同点,将对象分为不同种类然后逐类解决问题．一般地,对于二次函数y=a (x ?m )2+n ，x ∈[t ，s ]求最值的问题;解决此类问题的基本思路为：根据对称轴相对定义域区间的位置，利用分类讨论思想方法。

为做到分类时不重不漏，可画对称轴相对于定义域区间的简图分类。

含参数的二次函数求最值的问题大致分为三种题型，无论哪种题型都围绕着对称轴与定义域区间的位置关系进行分类讨论题型一：“动轴定区间”型的二次函数最值例１、求函数2()23f x x ax =-+在[0,4]x ∈上的最值。

分析：先配方，再根据对称轴相对于区间的位置讨论，然后根据口诀写出最值。

解：222()23()3f x x ax x a a =-+=-+- ∴此函数图像开口向上，对称轴x=a①、当a ＜0时，0距对称轴x=a 最近，4距对称轴x=a 最远， ∴x=0时，min y =3，x=4时，max y =19-8a②、当0≤a＜2时，a 距对称轴x=a 最近，4距对称轴x=a 最远， ∴x=a 时，min y =3-a2，x=4时，max y =19-8a③、当2≤a＜4时，a 距对称轴x=a 最近，0距对称轴x=a 最远， ∴x=a 时，min y =3-a2，x=0时，max y =3④、当4≤a 时，4距对称轴x=a 最近，0距对称轴x=a 最远， ∴x=4时，min y =19-8a ，x=0时，max y =3 例2、已知函数2()(21)3f x ax a x =+--在区间3[,2]2-上最大值为1,求实数a 的值 分析:取a=0,a ≠0，分别化为一次函数与二次函数,根据一次函数、二次函数的性质分类讨论. 解:1)若a=0,则f(x)=-x-3,而f(x)在3[,2]2-上取不到最大值为1,∴a ≠0 2)若a ≠0,则2()(21)3f x ax a x =+--的对称轴为0122a x a-=(Ⅰ)若3()12f -=，解得103a =-，此时0233[,2]202x =-∈-a<0, 0()f x 为最大值，但23()120f -≠ (Ⅱ) 若(2)1f =解得34a =此时013[,2]32x =-∈-0310,43a x =>=-距右端点2较远，(2)f 最大值符合条件(Ⅲ) 若0()1f x =解得32a -±=当302a -+=<时034[,2]2x =-∉-当302a --=<时034[,2]2x =∈-综收所述34a =或a =评注：此类题属于“动轴定区间”型的二次函数最值，解决此类问题的关键是讨论对称轴相对于定义域区间的位置，讨论时做到不重不漏。