【校级联考】江苏省常州市教育学会2020至2021学年八年级上学期学业水平检测语文试题
- 格式:docx
- 大小:29.76 KB
- 文档页数:16

江苏省常州市八年级上学期期末学业水平调研数学卷(含答案)一、选择题1.下列成语描述的事件为随机事件的是( )A .守株待兔B .水中捞月C .瓮中捉鳖D .水涨船高2.如图,在ABC ∆中,31C ∠=︒,ABC ∠的平分线BD 交AC 于点D ,如果DE 垂直平分BC ,那么A ∠的度数为( )A .31︒B .62︒C .87︒D .93︒3.已知二元一次方程组522x y x y -=-⎧⎨+=-⎩的解为41x y =-⎧⎨=⎩,则在同一平面直角坐标系中,两函数y =x +5与y =﹣12x ﹣1的图像的交点坐标为( ) A .(﹣4,1) B .(1,﹣4) C .(4,﹣1) D .(﹣1,4)4.如图,在放假期间,某学校对其校内的教学楼(图中的点A ),图书馆(图中的点B )和宿含楼(图中的点C )进行装修,装修工人需要放置一批装修物资,使得装修物资到点A ,点B 和点C 的距离相等,则装修物资应该放置在( )A .AC 、BC 两边高线的交点处B .在AC 、BC 两边中线的交点处C .在A ∠、B 两内角平分线的交点处D .在AC 、BC 两边垂直平分线的交点处5.如图,∠AOB=60°,点P 是∠AOB 内的定点且OP=3,若点M 、N 分别是射线OA 、OB 上异于点O 的动点,则△PMN 周长的最小值是( )A .362B .332C .6D .36.人的眼睛可以看见的红光的波长约为5810cm -⨯,近似数5810-⨯精确到( ) A .0.001cmB .0.0001cmC .0.00001cmD .0.000001cm 7.下列一次函数中,y 随x 增大而增大的是( )A .y=﹣3xB .y=x ﹣2C .y=﹣2x+3D .y=3﹣x 8.如图,动点P 在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点()1,1,第2次接着运动到点()2,0,第3次接着运动到点()3,2,···,按这样的运动规律,经过第2020次运动后,动点P 的坐标是( )A .()2020,1B .()2020,0C .()2020,2D .()2019,0 9.满足下列条件的△ABC 是直角三角形的是( ) A .∠A :∠B :∠C =3:4:5B .a :b :c =1:2:3C .∠A =∠B =2∠CD .a =1,b =2,c =3 10.点P (1,﹣2)关于y 轴对称的点的坐标是( )A .(1,2)B .(﹣1,2)C .(﹣1,﹣2)D .(﹣2,1) 二、填空题11.已知点P (m ﹣2,2m ﹣1)在第二象限,则实数m 的取值范围是_____.12.如图,AD 是ABC ∆的角平分线,DE AB ⊥于E ,若18AB =,12AC =,ABC ∆的面积等于30,则DE =_______.13.根据如图所示的计算程序,小明输入的x 的值为36,则输出的y 的值为__________.14.如图,已知直线y =ax ﹣b ,则关于x 的方程ax ﹣1=b 的解x =_____.15.已知一次函数1y kx =+的图像经过点(1,0)P -,则k =________.16.如图,点E ,F 在AC 上,AD=BC ,DF=BE ,要使△ADF ≌△CBE ,还需要添加的一个条件是________(添加一个即可)17.如图,在平面直角坐标系中,函数y=﹣2x 与y=kx+b 的图象交于点P (m ,2),则不等式kx+b >﹣2x 的解集为_____.18.如图,等边△ABC 的周长是18,D 是AC 边上的中点,点E 在BC 边的延长线上.如果DE =DB ,那么CE 的长是_____.19.若代数式321x x -+有意义,则x 的取值范围是______________. 20.如图,在坐标系中,一次函数21y x =-+与一次函数y x k =+的图像交于点(2,5)A -,则关于x 的不等式21x k x +>-+的解集是__________.三、解答题21.如图,ABC ∆的三个顶点都在格点上.(1)直接写出点B 的坐标;(2)画出ABC ∆关于x 轴对称的111A B C ∆,(3)直接写出点1A 的坐标22.如图,∠AOB =90°,OA =12cm ,OB =8cm ,一机器人在点B 处看见一个小球从点A 出发沿着AO 方向匀速滚向点O ,机器人立即从点B 出发,沿BC 方向匀速前进拦截小球,恰好在点C 处截住了小球.如果小球滚动的速度与机器人行走的速度相等,并且它们的运动时间也相等.(1)请用直尺和圆规作出C 处的位置,不必叙述作图过程,保留作图痕迹;(2)求线段OC 的长.23.为落实“美丽抚顺”的工作部署,市政府计划对城区道路进行了改造,现安排甲、乙两个工程队完成.已知甲队的工作效率是乙队工作效率的32倍,甲队改造360米的道路比乙队改造同样长的道路少用3天.(1)甲、乙两工程队每天能改造道路的长度分别是多少米?(2)若甲队工作一天需付费用7万元,乙队工作一天需付费用5万元,如需改造的道路全长1200米,改造总费用不超过145万元,至少安排甲队工作多少天?24.人教版教材指出:等边三角形是三边都相等的特殊的等腰三角形.请证明:有一个角是60︒的等腰三角形是等边三角形.25.先化简,再求值:22214244x x x x x x x x +--⎛⎫-÷ ⎪--+⎝⎭,其中x =2﹣23. 四、压轴题26.如图,在ABC ∆中,90,,8ACB AC BC AB cm ∠=︒==,过点C 做射线CD ,且//CD AB ,点P 从点C 出发,沿射线CD 方向均匀运动,速度为3/cm s ;同时,点Q 从点A 出发,沿AB 向点B 匀速运动,速度为1/cm s ,当点Q 停止运动时,点P 也停止运动.连接,PQ CQ ,设运动时间为()()08t s t <<.解答下列问题:(1)用含有t 的代数式表示CP 和BQ 的长度;(2)当2t =时,请说明//PQ BC ;(3)设BCQ ∆的面积为()2S cm ,求S 与t 之间的关系式.27.已知三角形ABC 中,∠ACB =90°,点D (0,-4),M (4,-4).(1)如图1,若点C 与点O 重合,A (-2,2)、B (4,4),求△ABC 的面积;(2)如图2,AC 经过坐标原点O ,点C 在第三象限且点C 在直线DM 与x 轴之间,AB 分别与x 轴,直线DM 交于点G ,F ,BC 交DM 于点E ,若∠AOG =55°,求∠CEF 的度数;(3)如图3,AC 经过坐标原点O ,点C 在第三象限且点C 在直线DM 与x 轴之间,N 为AC 上一点,AB 分别与x 轴,直线DM 交于点G ,F ,BC 交DM 于点E ,∠NEC+∠CEF =180°,求证∠NEF =2∠AOG .28.在平面直角坐标系中,点A 、B 在坐标轴上,其中()0,A a 、(),0B b 满足|21|280a b a b --++-=.(1)求A 、B 两点的坐标;(2)将线段AB 平移到CD ,点A 的对应点为()2,C t -,如图1所示,若三角形ABC 的面积为9,求点D 的坐标;(3)平移线段AB 到CD ,若点C 、D 也在坐标轴上,如图2所示.P 为线段AB 上的一动点(不与A 、B 重合),连接OP 、PE 平分OPB ∠,2BCE ECD ∠=∠.求证:3()BCD CEP OPE ∠=∠-∠.29.观察下列两个等式:5532321,44133+=⨯-+=⨯-,给出定义如下:我们称使等式1a b ab +=-成立的一对有理数,a b 为“白马有理数对”,记为(,)a b ,如:数对5(3,2),4,3⎛⎫ ⎪⎝⎭都是“白马有理数对”. (1)数对3(2,1),5,2⎛⎫- ⎪⎝⎭中是“白马有理数对”的是_________; (2)若(,3)a 是“白马有理数对”,求a 的值;(3)若(,)m n 是“白马有理数对”,则(,)n m --是“白马有理数对”吗?请说明理由. (4)请再写出一对符合条件的“白马有理数对”_________(注意:不能与题目中已有的“白马有理数对”重复)30.在《经典几何图形的研究与变式》一课中,庞老师出示了一个问题:“如图1,等腰直角三角形的三个顶点分别落在三条等距的平行线1l ,2l ,3l 上,90BAC ∠=︒,且每两条平行线之间的距离为1,求AB 的长度”.在研究这道题的解法和变式的过程中,同学们提出了很多想法:(1)小明说:我只需要过B 、C 向1l 作垂线,就能利用全等三角形的知识求出AB 的长. (2)小林说:“我们可以改变ABC 的形状.如图2,AB AC =,120BAC ∠=︒,且每两条平行线之间的距离为1,求AB 的长.”(3)小谢说:“我们除了改变ABC 的形状,还能改变平行线之间的距离.如图3,等边三角形ABC 三个顶点分别落在三条平行线1l ,2l ,3l 上,且1l 与2l 之间的距离为1,2l 与3l 之间的距离为2,求AB 的长、”请你根据3位同学的提示,分别求出三种情况下AB 的长度.【参考答案】***试卷处理标记,请不要删除一、选择题1.A解析:A【解析】【分析】根据事件发生的可能性大小判断相应事件的类型即可.【详解】解:A.守株待兔是随机事件,故A 符合题意;B.水中捞月是不可能事件,故B 不符合题意;C.瓮中捉鳖是必然事件,故C 不符合题意;D.水涨船高是必然事件,故D 不符合题意;故选:A .本题考查了随机事件,解决本题需要正确理解必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.2.C解析:C【解析】【分析】根据垂直平分线的性质,可以得到∠C=∠ABC ,再根据角平分线的性质,得到∠ABC 的度数,最后利用三角形内角和即可解决.【详解】∵DE 垂直平分BC ,DB DC ∴=,31C DBC ︒∴∠=∠=,∵BD 平分ABC ∠,262ABC DBC ︒∴∠=∠=,180A ABC C ︒∴∠+∠+∠=,180180623187A ABC C ︒︒︒︒︒∴∠=-∠-∠=--=故选C【点睛】本题考查了垂直平分线的性质,角平分线的性质和三角形内角和,解决本题的关键是熟练掌握三者性质,正确理清各角之间的关系.3.A解析:A【解析】【分析】根据一次函数与二元一次方程组的关系进行解答即可.【详解】解:∵二元一次方程组522x y x y -=-⎧⎨+=-⎩的解为41x y =-⎧⎨=⎩∴在同一平面直角坐标系中,两函数y =x +5与y =﹣12x ﹣1的图像的交点坐标为:(-4,1)故选:A.【点睛】本题考查的是一次函数与二元一次方程组的关系,一般地,如果一个二元一次方程组有唯一解,那么这个解就是方程组对应的两条直线的交点坐标. 4.D【解析】【分析】根据线段垂直平分线的性质判断即可.【详解】作AC ,BC 两边的垂直平分线,它们的交点为P ,由线段垂直平分线的性质,P A =PB =PC ,故选:D.【点睛】本题主要考查了垂直平分线的性质,熟练掌握相关性质要点是解决本题的关键.5.D解析:D【解析】分析:作P 点分别关于OA 、OB 的对称点C 、D ,连接CD 分别交OA 、OB 于M 、N ,如图,利用轴对称的性质得MP=MC ,NP=ND ,∠BOP=∠BOD ,∠AOP=∠AOC ,所以∠COD=2∠AOB=120°,利用两点之间线段最短判断此时△PMN 周长最小,作OH ⊥CD 于H ,则CH=DH ,然后利用含30度的直角三角形三边的关系计算出CD 即可.详解:作P 点分别关于OA 、OB 的对称点C 、D ,连接CD 分别交OA 、OB 于M 、N ,如图,则MP=MC ,NP=ND ,∠BOP=∠BOD ,∠AOP=∠AOC ,∴PN+PM+MN=ND+MN+MC=DC ,∠COD=∠BOP+∠BOD+∠AOP+∠AOC=2∠AOB=120°, ∴此时△PMN 周长最小,作OH ⊥CD 于H ,则CH=DH ,∵∠OCH=30°,∴OH=12OH=32, ∴CD=2CH=3.故选D .点睛:本题考查了轴对称﹣最短路线问题:熟练掌握轴对称的性质,会利用两点之间线段最短解决路径最短问题.6.C解析:C【解析】【分析】把数还原后,再看首数8的最后一位数字8所在的位数是十万分位,即精确到十万分位.【详解】∵5⨯=0.00008,810-∴近似数5⨯是精确到十万分位,即0.00001.810-故选:C.【点睛】此题主要考查了科学记数法与有效数字,正确还原数据是解题关键.7.B解析:B【解析】【分析】根据一次函数的性质对各选项进行逐一分析即可.【详解】解:A、∵一次函数y=﹣3x中,k=﹣3<0,∴此函数中y随x增大而减小,故本选项错误;B、∵正比例函数y=x﹣2中,k=1>0,∴此函数中y随x增大而增大,故本选项正确;C、∵正比例函数y=﹣2x+3中,k=﹣2<0,∴此函数中y随x增大而减小,故本选项错误;D、正比例函数y=3﹣x中,k=﹣1<0,∴此函数中y随x增大而减小,故本选项错误.故选B.【点睛】本题考查的是一次函数的性质,即一次函数y=kx+b(k≠0)中,当k>0时,y随x的增大而增大,函数从左到右上升;k<0,y随x的增大而减小,函数从左到右下降.8.B解析:B【解析】【分析】观察可得点P 的变化规律,“()()()()44 1 4243 4, 041, 1 42, 0 43, 2n n n n P n P n P n P n ++++++,,, (n 为自然数)”,由此即可得出结论.【详解】观察, ()()()()()()0123450,01,12,0,3,2,4,0,5,1....P P P P P P ,,,, 发现规律:()()()()44 1 4243 4, 041, 1 42, 0 43, 2n n n n P n P n P n P n ++++++,,, (n 为自然数) .∵20204505=⨯∴2020P 点的坐标为()2020,0.故选: B.【点睛】本题考查了规律型中的点的坐标,解题的关键是找出规律“()()()()44 1 4243 4, 041, 1 42, 0 43, 2n n n n P n P n P n P n ++++++,,, (n 为自然数)”,本题属于中档题,难度不大,解决该题型题目时,根据点P 的变化罗列出部分点的坐标,再根据坐标的变化找出规律是关键.9.D解析:D【解析】【分析】根据三角形内角和定理判断A 、C 即可;根据勾股定理的逆定理判断B 、D 即可.【详解】A 、∵∠A :∠B :∠C =3:4:5,∠A +∠B +∠C =180°,∴∠A =45°,∠B =60°,∠C =75°,∴△ABC 不是直角三角形;B 、∵12+22≠32,∴△ABC 不是直角三角形;C 、∵∠A =∠B =2∠C ,∠A +∠B +∠C =180°,∴∠A =∠B =75°,∠C =37.5°,∴△ABC 不是直角三角形;D 、∵12+)2=22,∴△ABC 是直角三角形.故选:D .【点睛】此题主要考查利用三角形内角和定理和勾股定理判定直角三角形,熟练掌握,即可解题. 10.C解析:C【解析】关于y轴对称的点,纵坐标相同,横坐标互为相反数,由此可得P(1,﹣2)关于y轴对称的点的坐标是(﹣1,﹣2),故选C.【点睛】本题考查了关于坐标轴对称的点的坐标,正确地记住关于坐标轴对称的点的坐标特征是关键.关于x轴对称的点的坐标特点:横坐标不变,纵坐标互为相反数;关于y轴对称的点的坐标特点:纵坐标不变,横坐标互为相反数.二、填空题11.<m<2.【解析】【分析】根据第二象限内点的横坐标是负数,纵坐标是正数列出不等式组,然后求解即可.【详解】解:∵点P(m﹣2,2m﹣1)在第二象限,∴,解不等式①得,m<2,解不等式解析:12<m<2.【解析】【分析】根据第二象限内点的横坐标是负数,纵坐标是正数列出不等式组,然后求解即可.【详解】解:∵点P(m﹣2,2m﹣1)在第二象限,∴20210mm-<⎧⎨->⎩①②,解不等式①得,m<2,解不等式②得,m>12,所以,不等式组的解集是12<m<2,故答案为12<m <2. 【点睛】 本题考查了各象限内点的坐标的符号特征以及解不等式,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(−,+);第三象限(−,−);第四象限(+,−).12.2【解析】【分析】延长AC,过D 点作DF⊥AF 于F ,根据角平分线的性质得到DE=DF,由即可求出.【详解】解:如图延长AC,过D 点作DF⊥AC 于F∵是的角平分线,DE⊥AB,∴DE解析:2【解析】【分析】延长AC ,过D 点作DF ⊥AF 于F ,根据角平分线的性质得到DE=DF,由ABC ABD ACDSS S =+即可求出.【详解】解:如图延长AC ,过D 点作DF ⊥AC 于F∵AD 是ABC ∆的角平分线,DE⊥AB,∴DE =DF∵ABC ABD ACD SS S =+=30 ∴113022AB DE DF AC ⋅+⋅= ∵18AB =,12AC = ,DE =DF∴1118123022DE DE ⨯⋅+⨯= 得到 DE=2故答案为:2.【点睛】 此题主要考查了角平分线的性质,熟记概念是解题的关键.13.0【解析】【分析】根据题意,由时,代入,求出答案即可.【详解】解:∵小明输入的的值为36,∴;故答案为:0.【点睛】本题考查了代数式求值:把满足条件的字母的值代入代数式进行计算得到 解析:0【解析】【分析】根据题意,由36x =时,代入3y =-,求出答案即可. 【详解】解:∵小明输入的x 的值为36,∴3330y =-=-=; 故答案为:0.【点睛】本题考查了代数式求值:把满足条件的字母的值代入代数式进行计算得到对应的代数式的值.14.4【解析】【分析】观察图形可直接得出答案.【详解】解:根据图形知,当y =1时,x =4,即ax ﹣b =1时,x =4.故方程ax ﹣1=b 的解是x =4.故答案为4.【点睛】此题考查一次函解析:4【解析】【分析】观察图形可直接得出答案.【详解】解:根据图形知,当y=1时,x=4,即ax﹣b=1时,x=4.故方程ax﹣1=b的解是x=4.故答案为4.【点睛】此题考查一次函数与一元一次方程的联系,渗透数形结合的解题思想.15.1【解析】【分析】直接把点P(-1,0)代入一次函数y=kx+1,求出k的值即可.【详解】∵一次函数y=kx+1的图象经过点P(-1,0),∴0=-k+1,解得k=1.故答案为1.【解析:1【解析】【分析】直接把点P(-1,0)代入一次函数y=kx+1,求出k的值即可.【详解】∵一次函数y=kx+1的图象经过点P(-1,0),∴0=-k+1,解得k=1.故答案为1.【点睛】本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.16.∠D=∠B【解析】【分析】要判定△ADF≌△CBE,已经有AD=BC,DF=BE,还缺少第三组对应边相等或这两边组成的夹角相等,根据全等三角形的判定方法求解即可.【详解】∵AD=BC, D解析:∠D=∠B【解析】【分析】要判定△ADF≌△CBE,已经有AD=BC,DF=BE,还缺少第三组对应边相等或这两边组成的夹角相等,根据全等三角形的判定方法求解即可.【详解】∵AD=BC, DF=BE,∴只要添加∠D=∠B,根据“SAS”即可证明△ADF≌△CBE.故答案为∠D=∠B.【点睛】本题重点考查的是全等三角形的判定方法,熟练掌握全等三角形的知识是解答的关键,应该多加练习.三角形全等的判定定理有:边边边(SSS)、边角边(SAS)、角边角(ASA)、角角边(AAS).17.x>﹣1【解析】【分析】先利用正比例函数解析式确定P点坐标,然后观察函数图象得到,当x>﹣1时,直线y=﹣2x都在直线y=kx+b的下方,于是可得到不等式kx+b>﹣2x的解集.【详解】当解析:x>﹣1【解析】【分析】先利用正比例函数解析式确定P点坐标,然后观察函数图象得到,当x>﹣1时,直线y=﹣2x都在直线y=kx+b的下方,于是可得到不等式kx+b>﹣2x的解集.【详解】当y=2时,﹣2x=2,x=﹣1,由图象得:不等式kx+b>﹣2x的解集为:x>﹣1,故答案为x>﹣1.【点睛】本题考查了一次函数与一元一次不等式的关系:从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)﹣2x的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在﹣2x上(或下)方部分所有的点的横坐标所构成的集合.18.3【解析】【分析】由△ABC为等边三角形,D为AC边上的中点可得∠DBE=30°,由DE=DB得∠E =30°,再证出∠CDE=∠E,得出CD=CE=AC=3即可.【详解】∵△ABC为等边解析:3【解析】【分析】由△ABC为等边三角形,D为AC边上的中点可得∠DBE=30°,由DE=DB得∠E =30°,再证出∠CDE=∠E,得出CD=CE=12AC=3即可.【详解】∵△ABC为等边三角形,D为AC边上的中点,∴BD为∠ABC的平分线,且∠ABC=60°,∴∠DBE=30°,又DE=DB,∴∠E=∠DBE=30°,∵等边△ABC的周长为18,∴AC=6,且∠ACB=60°,∴∠CDE=∠ACB-∠E=30°,∴∠CDE=∠E,∴CD=CE=12AC=3.故答案为:3.【点睛】此题考查了等边三角形的性质、等腰三角形的判定以及三角形的外角性质等知识;熟练掌握等边三角形的性质,证明CD=CE是解题的关键.19.【解析】【分析】代数式有意义,则它的分母2x+1≠0,由此求得x的取值范围.【详解】∵代数式有意义,∴2x+1≠0,解得x≠.故答案为:x≠.【点睛】本题考查了分式有意义的条件. 解析:12x ≠-【解析】【分析】 代数式321x x -+有意义,则它的分母2x+1≠0,由此求得x 的取值范围. 【详解】 ∵代数式321x x -+有意义, ∴2x+1≠0, 解得x≠12-. 故答案为:x≠12-. 【点睛】本题考查了分式有意义的条件.分式有意义的条件是分母不等于零.20.【解析】【分析】根据图像解答即可.【详解】由图像可知,关于的不等式的解集是.故答案为:.【点睛】本题主要考查一次函数和一元一次不等式的关系及数形结合思想的应用.解决此类问题关键是仔细解析:2x >-【解析】【分析】根据图像解答即可.【详解】由图像可知,关于x 的不等式21x k x +>-+的解集是2x >-.故答案为:2x >-.【点睛】本题主要考查一次函数和一元一次不等式的关系及数形结合思想的应用.解决此类问题关键是仔细观察图形,注意几个关键点(交点、原点等),做到数形结合.函数y 1>y 2时x 的范围是函数y 1的图象在y 2的图象上边时对应的未知数的范围,反之亦然.三、解答题21.(1)(2,3)-;(2)画图见解析;(3)(1,1)-【解析】【分析】(1)根据平面直角坐标系中点与有序数对的对应关系解答即可;(2)ABC ∆各顶点关于x 轴对称的点A 1,B 1,C 1,然后用线段顺次连接即可;(3)根据平面直角坐标系中点与有序数对的对应关系解答即可.【详解】解:(1)点B 的坐标是(2,3)-;(2)如图,(3)点1A 的坐标是(1,1)-.【点睛】本题考查了作图-轴对称变换,熟练掌握网格结构准确找出对应点的位置是解题的关键.22.(1)详见解析;(2)103cm . 【解析】【分析】(1)作AB 的垂直平分线,交OA 于点C ,则点C 即为所求;(2)设BC =xcm ,根据题意用x 表示出AC 和OC ,根据勾股定理列出方程,解方程即可.【详解】解:(1)如图所示,作AB 的垂直平分线,交OA 于点C ,则点C 即为所求;(2)由作图可得:BC=AC,设BC=xcm,则AC=xcm,OC=(12﹣x)cm,由勾股定理得,BC2=OB2+OC2,即x2=82+(12﹣x)2,解得x=263.∴OC=12﹣263=103答:线段OC的长是103cm.【点睛】本题考查的是勾股定理的应用和基本作图:线段的垂直平分线,掌握直角三角形中,两条直角边的平方和等于斜边的平方是解题的关键.23.(1)乙工程队每天能改造道路的长度为40米,甲工程队每天能改造道路的长度为60米.(2)10天.【解析】【分析】(1)设乙工程队每天能改造道路的长度为x米,则甲工程队每天能改造道路的长度为3 2 x米,根据工作时间=工作总量÷工作效率结合甲队改造360米的道路比乙队改造同样长的道路少用3天,即可得出关于x的分式方程,解之经检验后即可得出结论;(2)设安排甲队工作m天,则安排乙队工作12006040m-天,根据总费用=甲队每天所需费用×工作时间+乙队每天所需费用×工作时间结合总费用不超过145万元,即可得出关于m的一元一次不等式,解之取其中的最大值即可得出结论.【详解】(1)设乙工程队每天能改造道路的长度为x米,则甲工程队每天能改造道路的长度为3 2 x米,根据题意得:360360332x x-=,解得:x=40,经检验,x=40是原分式方程的解,且符合题意,∴32x=32×40=60, 答:乙工程队每天能改造道路的长度为40米,甲工程队每天能改造道路的长度为60米; (2)设安排甲队工作m 天,则安排乙队工作12006040m -天, 根据题意得:7m+5×12006040m -≤145, 解得:m≥10,答:至少安排甲队工作10天.【点睛】本题考查了分式方程的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出分式方程;(2)根据各数量间的关系,正确列出一元一次不等式.24.详见解析【解析】【分析】根据题意,给出已知和求证,加以证明即可得解.【详解】已知:如下图,ABC ∆是等腰三角形,∠A =60°,证明:ABC ∆是等边三角形.证明:∵ABC ∆是等腰三角形∴AB=AC∴∠B=∠C∵∠A =60°∴∠B=∠C=18060602︒-︒=︒ ∴ABC ∆是等边三角形. 【点睛】本题主要考查了等边三角形的判定,熟练掌握等边三角形的判定证明是解决本题的关键.25.﹣21(2)x -,﹣112【解析】【分析】直接括号里面通分运算,进而利用分式的混合运算法则计算得出答案.【详解】原式= [221(2)(2)x x x x x +----]•4x x - =2(2)(2)(1)(2)4x x x x x x x x +---⋅--=24(2)4x x x x x-⋅--=﹣21(2)x -, 当x =2﹣23时, 原式=﹣112. 【点睛】 此题主要考查分式的化简求值,熟练掌握,即可解题.四、压轴题26.(1)CP=3t ,BQ=8-t ;(2)见解析;(3)S=16-2t .【解析】【分析】(1)直接根据距离=速度⨯时间即可;(2)通过证明PCQ BQC ≅,得到∠PQC=∠BCQ,即可求证; (3)过点C 作CM⊥AB,垂足为M ,根据等腰直角三角形的性质得到CM=AM=4,即可求解.【详解】解:(1)CP=3t ,BQ=8-t ;(2)当t=2时,CP=3t=6,BQ=8-t=6∴CP=BQ∵CD ∥AB∴∠PCQ=∠BQC又∵CQ=QC∴PCQ BQC ≅∴∠PQC=∠BCQ∴PQ∥BC(3)过点C 作CM⊥AB,垂足为M∵AC=BC,CM⊥AB∴AM=118422AB=⨯=(cm)∵AC=BC,∠ACB=90︒∴∠A=∠B=45︒∵CM⊥AB∴∠AMC=90︒∴∠ACM=45︒∴∠A=∠ACM∴CM=AM=4(cm)∴118t4162 22BCQS BQ CM t ==⨯-⨯=-因此,S与t之间的关系式为S=16-2t.【点睛】此题主要考查列代数式、全等三角形的判定与性质、平行线的判定、等腰三角形的性质,熟练掌握逻辑推理是解题关键.27.(1)8;(2)145°;(3)详见解析.【解析】【分析】(1)作AD⊥ x轴于D,BE⊥x轴于E,由点A,B的坐标可得出AD=OD=2,BE=EO=4,DE=6,由面积公式可求出答案;(2)作CH∥x轴,如图2,由平行线的性质可得出∠AOG=∠ACH,∠DEC=∠HCE,求出∠DEC+∠AOG=∠ACB=90°,可求出∠DEC=35°,则可得出答案;(3)证得∠NEC=∠HEC,则∠NEF=180°-∠NEH=180°-2∠HEC,可得出结论.【详解】解:(1)作AD⊥x轴于D,BE⊥x轴于E,如图1,∵A(﹣2,2)、B(4,4),∴AD =OD =2,BE =OE =4,DE =6,∴S △ABC =S 梯形ABED ﹣S △AOD ﹣S △AOE =12×(2+4)×6﹣12×2×2﹣12×4×4=8; (2)作CH // x 轴,如图2,∵D (0,﹣4),M (4,﹣4),∴DM // x 轴,∴CH // OG // DM,∴∠AOG =∠ACH,∠DEC =∠HCE,∴∠DEC+∠AOG =∠ACB =90°,∴∠DEC =90°﹣55°=35°,∴∠CEF =180°﹣∠DEC =145°;(3)证明:由(2)得∠AOG+∠HEC =∠ACB =90°,而∠HEC+∠CEF =180°,∠NEC+∠CEF =180°,∴∠NEC =∠HEC,∴∠NEF =180°﹣∠NEH =180°﹣2∠HEC,∵∠HEC =90°﹣∠AOG,∴∠NEF =180°﹣2(90°﹣∠AOG )=2∠AOG .【点睛】本题是三角形综合题,考查了坐标与图形的性质,三角形的面积,平行线的性质,三角形内角和定理,熟练掌握平行的性质及三角形内角和定理是解题的关键.28.(1)A ,B 两点的坐标分别为()0,2,()3,0;(2)点D 的坐标是141,3⎛⎫-⎪⎝⎭;(3)证明见解析【解析】【分析】(1)根据非负数的性质得出二元一次方程组,求解即可;(2)过点B 作y 轴的平行线分别与过点A ,C 作x 轴的平行线交于点N ,点M ,过点C 作y 轴的平行线与过点A 作x 轴的平行线交于点T ,根据三角形ABC 的面积=长方形CMNT 的面积-(三角形ANB 的面积+三角形ATC 的面积+三角形CMB 的面积)列出方程,求解得出点C 的坐标,由平移的规律可得点D 的坐标;(3)过点E 作//EF CD ,交y 轴于点F ,过点O 作//OG AB ,交PE 于点G ,根据两直线平行,内错角相等与已知条件得出3BCD CEF ∠=∠,同样可证OGP OPE ∠=∠,由平移的性质与平行公理的推论可得FEP OGP ∠=∠,最后根据CEP CEF FEP ∠=∠+∠,通过等量代换进行证明.【详解】解:(1)210a b --=,又∵|21|0a b --≥0, |21|0a b ∴--=0=,即210280a b a b --=⎧⎨+-=⎩, 解方程组2128a b a b -=⎧⎨+=⎩得23a b =⎧⎨=⎩, A ∴,B 两点的坐标分别为()0,2,()3,0;(2)如图,过点B 作y 轴的平行线分别与过点A ,C 作x 轴的平行线交于点N ,点M ,过点C 作y 轴的平行线与过点A 作x 轴的平行线交于点T ,∴三角形ABC 的面积=长方形CMNT 的面积-(三角形ANB 的面积+三角形ATC 的面积+三角形CMB 的面积),根据题意得,11195(2||)232(2||)5||222t t t ⎡⎤=⨯+-⨯⨯+⨯⨯++⨯⨯⎢⎥⎣⎦, 化简,得3||42t =, 解得,83t =±, 依题意得,0t <, 83t ∴=-,即点C 的坐标为82,3⎛⎫-- ⎪⎝⎭, ∴依题意可知,点C 的坐标是由点A 的坐标先向左平移2个单位长度,再向下平移143个单位长度得到的,从而可知,点D 的坐标是由点B 的坐标先向左平移2个单位长度,再向下平移143个单位长度得到的, ∴点D 的坐标是141,3⎛⎫- ⎪⎝⎭;(3)证明:过点E作//EF CD,交y轴于点F,如图所示,则ECD CEF∠=∠,2BCE ECD∠=∠,33BCD ECD CEF∴∠=∠=∠,过点O作//OG AB,交PE于点G,如图所示,则OGP BPE∠=∠,PE平分OPB∠,OPE BPE∴∠=∠,OGP OPE∴∠=∠,由平移得//CD AB,//OG FE∴,FEP OGP∴∠=∠,FEP OPE∴∠=∠,CEP CEF FEP∠=∠+∠,CEP CEF OPE∴∠=∠+∠,CEF CEP OPE∴∠=∠-∠,3()BCD CEP OPE∴∠=∠-∠.【点睛】本题综合性较强,考查非负数的性质,解二元一次方程组,平行线的性质,平移的性质,坐标与图形的性质,第(3)题巧作辅助线构造平行线是解题的关键.29.(1)35,2⎛⎫⎪⎝⎭;(2)2;(3)不是;(4)(6,75)【解析】【分析】(1)根据“白马有理数对”的定义,把数对3(2,1),5,2⎛⎫- ⎪⎝⎭分别代入1a b ab+=-计算即可判断;(2)根据“白马有理数对”的定义,构建方程即可解决问题;(3)根据“白马有理数对”的定义即可判断;(4)根据“白马有理数对”的定义即可解决问题.【详解】(1)∵-2+1=-1,而-2×1-1=-3,∴-2+1≠-3,∴(-2,1)不是“白马有理数对”,∵5+32=132,5×32-1=132,∴5+32=5×32-1,∴35,2⎛⎫⎪⎝⎭是“白马有理数对”,故答案为:3 5,2⎛⎫ ⎪⎝⎭;(2)若(,3)a是“白马有理数对”,则a+3=3a-1,解得:a=2,故答案为:2;(3)若(,)m n是“白马有理数对”,则m+n=mn-1,那么-n+(-m)=-(m+n)=-(mn-1)=-mn+1,∵-mn+1≠ mn-1∴(-n,-m)不是“白马有理数对”,故答案为:不是;(4)取m=6,则6+x=6x-1,∴x=75,∴(6,75)是“白马有理数对”,故答案为:(6,75).【点睛】本题考查了“白马有理数对”的定义,有理数的加减运算,一次方程的列式求解,理解“白马有理数对”的定义是解题的关键.30.(123【解析】【分析】(1)分别过点B,C向l1作垂线,交l1于M,N两点,证明△ABM≌△CAN,得到AM=CN,AN=BM,即可得出AB;(2)分别过点B,C向l1作垂线,交l1于点P,Q两点,在l1上取M,N使∠AMB=∠CNA=120°,证明△AMB≌△CAN,得到CN=AM,再通过△PBM和△QCN算出PM和NQ的值,得到AP,最后在△APB中,利用勾股定理算出AB的长;(3)在l3上找M和N,使得∠BNC=∠AMC=60°,过B作l3的垂线,交l3于点P,过A作l3的垂线,交l3于点Q,证明△BCN≌△CAM,得到CN=AM,在△BPN和△AQM中利用勾股定理算出NP和AM,从而得到PC,结合BP算出BC的长,即为AB.【详解】解:(1)如图,分别过点B,C向l1作垂线,交l1于M,N两点,由题意可得:∠BAC=90°,∵∠NAC+∠MAB=90°,∠NAC+∠NCA=90°,∴∠MAB=∠NCA,在△ABM和△CAN中,===AMB CNAMAB NCAAB AC∠∠⎧⎪∠∠⎨⎪⎩,∴△ABM≌△CAN(AAS),∴AM=CN=2,AN=BM=1,∴AB=22251=+;(2)分别过点B,C向l1作垂线,交l1于P,Q两点,在l1上取M,N使∠AMB=∠CNA=120°,∵∠BAC=120°,∴∠MAB+∠NAC=60°,∵∠ABM+∠MAB=60°,∴∠ABM=∠NAC,在△AMB和△CNA中,。

常州市教育学会学业水平监测八年级英语试卷2024年1月(考试范围:初中英语八年级上册)注意:本试卷共10页,全卷满分为100分,考试时间为90分钟。
考生须将答案书写在答题卡上,写在试卷上的一律无效。
期末成绩=笔试成绩×90%+口试成绩(10%)一、听力(共20小题;每小题1分,满分20分)第一部分听对话回答问题本部分共有10道小题,每小题你将听到一段对话,每段对话听两遍。
在听每段对话前,你将有5秒钟的时间阅读题目;听完后,你还有5秒钟的时间选择你认为最合适的答案。
1. What will they buy in the market?A. B. C.2. What will the weather be like tomorrow afternoon?A. B. C.3. What was the man doing when the woman called last night?A. B. C.4. What does Jenny want to be?A. B. C.5. What does Bob’s English teacher look like?A. She has long straight hair.B. She has short brown hair.C. She doesn’t wear glasses.6. What’s Alice like?A. Shy.B. Quiet.C. Humorous.7. Where did Mary go during her summer vacation?A. To Canada.B. To Australia.C. To Japan.8. Who lives the farthest from school?A. The girl.B. Allan.C. Tony.9. Why didn’t Linda come to school yesterday?A. She had a fever.B. She had a headache.C. She had a toothache.10. When may they go to the movies?A. On Saturday afternoon.B. On Sunday morning.C. On Sunday afternoon.第二部分听对话和短文回答问题你将听到一段对话和两篇短文,各听两遍。

常州市XX 学校2020〜2021学年度第一学期期中质量调研班级 姓名一、选择题(本大题共8小题,下列各题都给出代号为A 、B 、C 、D 的四个答案,其中有 且只有一个是正确的,每小题2分,共16分)1.日常生活中,我们会看到很多标志,在以下绿色食品、回收、力能、行水四个标志中,是 轴对称图形的是(▲)4.在AABC 中,ZA, NB, NC 的对边分别是。
,b, c,下列条件不能判断△ABC 是直角三角形的是(▲)A. « = 6,Z? = 8,c = 10B. a = 5,〃 = 12,c = 137 .如图,在aABC 中,AB 边的垂直平分线DE,分别与AB 边和AC 边交于点D 和点E, BC 边 的垂直平分线FG,分别与BC 边和AC 边交于点F 和点G,又4BEG 的周长为16,且GE=1, 则AC的长为(▲)A. 16B. 15C. 14D. 13八年级数学试题2020.11© ©A. B.2.下列各实数中是无理数的是(▲)22A. —B. 1.201200173.下列说法正确的是(▲)A. 2的平方根是企C. -0.3D. V3B. (-4尸的算术平方根是4C.近似数35万精确到个位D.无理数M ■的整数部分是5C. a = L 〃 = 2,c = 3D. ZA : ZB : ZC=1: 2: 35.如图,在ZkABC 中,ZC=90° , AB=10, AD 是aABC 的一条角平分线.若CD=3,D则AABD 的面积为(▲)6.如图,己知AB=AD,那么添加下列条件后,仍无法判定△ABC 丝AADC 的是(▲)A. CB=CDB. NB=ND 二90°C. ZBAC=ZDACD. ZBCA=ZDCA8.在RtZkACB中,NC=90° , NA=30° ,在直线BC或直线AC上找到一点P,使APAB是等腰三角形,则满足条件的点P的个数是(▲)A. 5个B. 6个C. 7个D. 8个二、填空题(每小题2分,共18分)9. 16的平方根是▲.10.己知aABC乌ADEF,若NB=40° , ND=30° ,则NF二▲11.若等腰三角形中有一个角是80° ,那么它的底角是一▲ 度.12.若工^至+卜+ 4| = 0,则"的立方根是一▲.14.游泳员小明横渡一条河,由于水流的影响,实际上岸地点C偏离欲达到点B 60米,结果他在水中实际游了100米,这条河宽为一▲ 米.15.如图,aABC是等边三角形,点B、C、D、E在同一直线上,且CG=CD, DF=DE,则NE二▲° .16.如图,在长方形ABCD中,AB=8, AD=10,点E为BC上一点,将AABE沿AE折叠,点B恰第16题17.如图,在AABC中,NACB=90° , AC=7cm, BC=3cm, CD为AB边上的高,点E从点B出发,在直线BC上以每秒2cm的速度移动,过点E作BC的垂线交直线CD于点F,当点E运动••▲秒时,CF=AB.三、解答题(本大题共9小题,其中18、20、21、24每题6分,19、22、23、25每题8分,26题10分,共66分)18.计算:百一(7力+,一3”*3)。


常州市八年级上学期期末学业水平调研数学卷(含答案)一、选择题1.若一次函数(2)1y k x =-+的函数值y 随x 的增大而增大,则( )A .2k <B .2k >C .0k >D .k 0<2.如图,在ABC ∆中,ABC ∠和ACB ∠的平分线相交于点F ,过F 作//DE BC ,交AB 于点D ,交AC 于点E ,若4BD =,7DE =,则线段EC 的长为( )A .3B .4C .3.5D .2 3.下列运算正确的是( )A .236a a a ⋅=B .235()a a -=-C .109(0)a a a a ÷=≠D .4222()()bc bc b c -÷-=- 4.下列各组数不是勾股数的是( )A .3,4,5B .6,8,10C .4,6,8D .5,12,13 5.在平面直角坐标系中,点P(-2,2x +1)所在的象限是( ) A .第一象限B .第二象限C .第三象限D .第四象限 6.2x -x 的取值范围( ) A .x≥2B .x≤2C .x >2D .x <2 7.变量x 与y 之间的关系是y =2x+1,当y =5时,自变量x 的值是( )A .13B .5C .2D .3.5 8.已知:如图,在△AOB 中,∠AOB =90°,AO =3cm ,BO =4cm ,将△AOB 绕顶点O ,按顺时针方向旋转到△A 1OB 1处,此时线段OB 1与AB 的交点D 恰好为AB 的中点,则线段B 1D 的长度为( )A .12cmB .1cmC .2cmD .32cm 9.下列图形中:①线段,②角,③等腰三角形,④有一个角是30°的直角三角形,其中一定是轴对称图形的个数( )A .1个B .2个C .3个D .4个10.下列交通标志图案是轴对称图形的是( )A .B .C .D .二、填空题11.某种型号汽车每行驶100km 耗油10L ,其油箱容量为40L .为了有效延长汽车使用寿命,厂家建议每次加油时邮箱内剩余油量不低于油箱容量的18,按此建议,一辆加满油的该型号汽车最多行驶的路程是_____km .12.2(5)-=_____.13.将函数y=3x+1的图象沿y 轴向下平移2个单位长度,所得直线的函数表达式为_____.14.如图,在Rt △ABO 中,∠OBA=90°,AB=OB ,点C 在边AB 上,且C (6,4),点D 为OB 的中点,点P 为边OA 上的动点,当∠APC=∠DPO 时,点P 的坐标为 ____.15.在ABC ∆中,13AC BC ==, 10AB =,则ABC ∆面积为_______. 16.已知关于x 的方程211x m x -=-的解是正数,则m 的取值范围为__________. 17.在平面直角坐标系中,(2,3)A -、(4,4)B ,点P 是x 轴上一点,且PA PB =,则点P 的坐标是__________.18.某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需时间比原计划生产450台机器所需时间相同,现在平均每天生产___台机器.19.36的算术平方根是 .20.如图①,四边形ABCD 中,//,90BC AD A ∠=︒,点P 从A 点出发,沿折线AB BC CD →→运动,到点D 时停止,已知PAD △的面积s 与点P 运动的路程x 的函数图象如图②所示,则点P 从开始到停止运动的总路程为________.三、解答题21.如图,△ABC 中,∠ACB =90°,AB =10cm ,BC =6cm ,若点P 从点A 出发以每秒1cm 的速度沿折线A ﹣C ﹣B ﹣A 运动,设运动时间为t 秒(t >0).(1)若点P 在AC 上,且满足PA =PB 时,求出此时t 的值;(2)若点P 恰好在∠BAC 的角平分线上(但不与A 点重合),求t 的值.22.如图,AO BO ⊥,DO EO ⊥,AO BO =,DO EO =.求证:AE BD =.23.先化简,再求值22333x x x x x ⎛⎫-+÷ ⎪++⎝⎭,其中2x =-24.在如图所示的正方形网格中,每个小正方形的边长都为1,△ABC 的顶点都在格点上(网格线的交点).(1)请在如图所示的网格平面内建立适当的平面直角坐标系,使点A 坐标为(﹣1,2),点B 的坐标为(﹣5,2);(画出直角坐标系)(2)点C 的坐标为( , )(直接写出结果)(3)把△ABC 先向下平移6个单位后得到对应的△A 1B 1C 1,再将△A 1B 1C 1沿y 轴翻折至△A 2B 2C 2;①请在坐标系中画出△A 2B 2C 2;②若点P (m ,n )是△ABC 边上任意一点,P 2是△A 2B 2C 2边上与P 对应的点,写出点P 2的坐标为( , );(直接写出结果)③试在y 轴上找一点Q ,使得点Q 到A 2,C 2两点的距离之和最小,此时,QA 2+QC 2的长度之和最小值为 .(在图中画出点Q 的位置,并直接写出最小值答案)25.已知:如图,ABC △和ADE △均为等腰直角三角形,90BAC DAE ∠=∠=︒,连结AC ,BD ,且D 、E 、C 三点在一直线上,2AD =,2DE EC =.(1)求证:ADB AEC △≌△;(2)求线段BC 的长.四、压轴题26.对于实数x ,若231a x ≤+,则符合条件的a 中最大的正数为X 的內数,例如:8的内数是5;7的内数是4.(1)1的内数是______,20的內数是______,6的內数是______;(2)若3是x 的內数,求x 的取值范围;(3)一动点从原点出发,以3个单位/秒的速度按如图1所示的方向前进,经过t秒后,动点经过的格点(横,纵坐标均为整数的点)中能围成的最大实心正方形的格点数(包括正方形边界与内部的格点)为n,例如当1t=时,4n=,如图2①……;当4t =时,9n=,如图2②,③;……①用n表示t的內数;②当t的內数为9时,符合条件的最大实心正方形有多少个,在这些实心正方形的格点中,直接写出离原点最远的格点的坐标.(若有多点并列最远,全部写出)27.阅读并填空:如图,ABC是等腰三角形,AB AC=,D 是边AC延长线上的一点,E在边AB上且联接DE交BC于O,如果OE OD,那么CD BE=,为什么?解:过点E作EF AC交BC于F所以ACB EFB∠=∠(两直线平行,同位角相等)D OEF∠=∠(________)在OCD与OFE△中()________COD FOEOD OED OEF⎧∠=∠⎪=⎨⎪∠=∠⎩所以OCD OFE△≌△,(________)所以CD FE=(________)因为AB AC=(已知)所以ACB B=∠∠(________)所以EFB B∠=∠(等量代换)所以BE FE=(________)所以CD BE=28.如图,A点的坐标为(0,3),B点的坐标为(﹣3,0),D为x轴上的一个动点且不与B,O重合,将线段AD绕点A逆时针旋转90°得线段AE,使得AE⊥AD,且AE=AD,连接BE 交y 轴于点M .(1)如图,当点D 在线段OB 的延长线上时,①若D 点的坐标为(﹣5,0),求点E 的坐标.②求证:M 为BE 的中点.③探究:若在点D 运动的过程中,OM BD的值是否是定值?如果是,请求出这个定值;如果不是,请说明理由.(2)请直接写出三条线段AO ,DO ,AM 之间的数量关系(不需要说明理由).29.在等腰△ABC 与等腰△ADE 中,AB =AC ,AD =AE ,∠BAC =∠DAE ,且点D 、E 、C 三点在同一条直线上,连接BD .(1)如图1,求证:△ADB ≌△AEC(2)如图2,当∠BAC =∠DAE =90°时,试猜想线段AD ,BD ,CD 之间的数量关系,并写出证明过程;(3)如图3,当∠BAC =∠DAE =120°时,请直接写出线段AD ,BD ,CD 之间的数量关系式为: (不写证明过程)30.在ABC 中,AB AC =,D 是直线AB 上一点,E 在直线BC 上,且DE DC =. (1)如图1,当D 在AB 上,E 在CB 延长线上时,求证:EDB ACD ∠=∠;(2)如图2,当ABC 为等边三角形时,D 是BA 的延长线上一点,E 在BC 上时,作//EF AC ,求证:BE AD =;(3)在(2)的条件下,ABC ∠的平分线BF 交CD 于点F ,连AF ,过A 点作AH CD ⊥于点H ,当30EDC ∠=︒,6CF =时,求DH 的长度.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【解析】【分析】根据一次函数图象的增减性来确定(k-2)的符号,从而求得k的取值范围.【详解】∵在一次函数y=(k-2)x+1中,y随x的增大而增大,∴k-2>0,∴k>2,故选B.【点睛】本题考查了一次函数图象与系数的关系.在直线y=kx+b(k≠0)中,当k>0时,y 随x的增大而增大;当k<0时,y随x的增大而减小.2.A解析:A【解析】【分析】根据△ABC中,∠ABC和∠ACB的平分线相交于点F.求证∠DBF=∠FBC,∠ECF=∠BCF,再利用两直线平行内错角相等,求证出∠DFB=∠DBF,∠CFE=∠BCF,即BD=DF,FE=CE,然后利用等量代换即可求出线段CE的长.【详解】解:∵∠ABC和∠ACB的平分线相交于点F,∴∠DBF=∠FBC,∠ECF=∠BCF,∵DF//BC,交AB于点D,交AC于点E.∴∠DFB=∠DBF,∠CFE=∠BCF,∴BD=DF=4,FE=CE,∴CE=DE-DF=7-4=3.故选:A.【点睛】本题考查了平行线的性质和角平分线的性质,解决本题的关键是正确理解题意,熟练掌握平行线和角平分线的性质,能够找到相等的量.3.C解析:C【解析】【分析】根据同底数幂的乘法、除法、积的乘方和幂的乘方进行计算即可.【详解】A. a2 a3=a5,故A错误;B. (−a2)3=−a6,故B错误;C. a10÷a9=a(a≠0),故C正确;D. (−bc)4÷(−bc)2=b2c2,故D错误;故答案选C.【点睛】本题考查了同底数幂的相关知识点,解题的关键是熟练的掌握同底数幂的乘法与除法的运算.4.C解析:C【解析】【分析】根据勾股数的定义:有a、b、c三个正整数,满足a2+b2=c2,称为勾股数.由此判定即可.【详解】解:A、32+42=52,能构成勾股数,故选项错误;B、62+82=102,能构成勾股数,故选项错误C、42+62≠82,不能构成勾股数,故选项正确;D、52+122=132,能构成勾股数,故选项错误.故选:C.【点睛】本题考查勾股数,解答此题要深刻理解勾股数的定义,并能够熟练运用.5.B解析:B【解析】【分析】【详解】∵-20,2x+10,∴点P (-2,2x+1)在第二象限,故选B.6.A解析:A【解析】【分析】二次根式有意义,被开方数为非负数,即x-2≥0,解不等式求x的取值范围.【详解】∴x−2≥0,解得x≥2.故答案选A.【点睛】本题考查了二次根式有意义的条件,解题的关键是熟练的掌握二次根式有意义的条件. 7.C解析:C【解析】【分析】直接把y=5代入y=2x+1,解方程即可.【详解】解:当y=5时,5=2x+1,解得:x=2,故选:C.【点睛】此题主要考查了函数值,关键是掌握已知函数解析式,给出函数值时,求相应的自变量的值就是解方程.8.D解析:D【解析】【分析】先在直角△AOB中利用勾股定理求出AB=5cm,再利用直角三角形斜边上的中线等于斜边的一半得出OD=12AB=2.5cm.然后根据旋转的性质得到OB1=OB=4cm,那么B1D=OB1﹣OD=1.5cm.【详解】∵在△AOB中,∠AOB=90°,AO=3cm,BO=4cm,∴AB=5cm,∵点D为AB的中点,∴OD=12AB=2.5cm.∵将△AOB绕顶点O,按顺时针方向旋转到△A1OB1处,∴OB1=OB=4cm,∴B1D=OB1﹣OD=1.5cm.故选:D.【点睛】本题主要考查勾股定理和直角三角形的性质以及图形旋转的性质,掌握“直角三角形斜边上的中线等于斜边的一半”是解题的关键.9.C解析:C【解析】【分析】直接利用轴对称图形的性质分别分析得出答案.【详解】解:①线段,是轴对称图形;②角,是轴对称图形;③等腰三角形,是轴对称图形;④有一个角是30°的直角三角形,不是轴对称图形.故选:C.【点睛】本题考查的知识点是轴对称图形的定义,理解定义内容是解此题的关键.10.B解析:B【解析】【分析】【详解】A图形中三角形和三角形内部图案的对称轴不一致,所以不是轴对称图形;B为轴对称图形,对称轴为过长方形两宽中点的直线;C外圈的正方形是轴对称图形,但是内部图案不是轴对称图形,所以也不是;D图形中圆内的两个箭头不是轴对称图象,而是中心对称图形,所以也不是轴对称图形.故选B.二、填空题11.【解析】【分析】设行驶xkm,由油箱内剩余油量不低于油箱容量的,列出不等式,即可求解.【详解】设该型号汽车行驶的路程是xkm,∵油箱内剩余油量不低于油箱容量的,∴﹣x+40≥40×,解解析:【解析】【分析】设行驶xkm,由油箱内剩余油量不低于油箱容量的18,列出不等式,即可求解.【详解】设该型号汽车行驶的路程是xkm,∵油箱内剩余油量不低于油箱容量的18,∴﹣10100x+40≥40×18,解得:x≤350,答:该辆汽车最多行驶的路程是350km,故答案为:350.【点睛】本题主要考查一元一次不等式的实际应用,找出不等量关系,列出一元一次不等式,是解题的关键.12.5【解析】根据二次根式的性质知:5.解析:5【解析】=5.13.y=3x-1【解析】∵y=3x+1的图象沿y轴向下平移2个单位长度,∴平移后所得图象对应的函数关系式为:y=3x+1﹣2,即y=3x﹣1.故答案为y=3x﹣1.解析:y=3x-1【解析】∵y=3x+1的图象沿y轴向下平移2个单位长度,∴平移后所得图象对应的函数关系式为:y=3x+1﹣2,即y=3x﹣1.故答案为y=3x﹣1.14.(,)【解析】【分析】根据题意,△ABO为等腰直角三角形,由点C坐标为(6,4),可知点B为(6,0),点A为(6,6),则直线OA为,作点D关于OA的对称点E,点E恰好落在y轴上,连接CE,解析:(185,185)【解析】【分析】根据题意,△ABO为等腰直角三角形,由点C坐标为(6,4),可知点B为(6,0),点A为(6,6),则直线OA为y x=,作点D关于OA的对称点E,点E恰好落在y轴上,连接CE,交OA于点P,则点E坐标为(0,3),然后求出直线CE的解析式,联合y x=,即可求出点P的坐标.【详解】解:在Rt△ABO中,∠OBA=90°,AB=OB,∴△ABO是等腰直角三角形,∵点C在边AB上,且C(6,4),∴点B为(6,0),∴OB=6=AB,∴点A坐标为:(6,6),∴直线OA的解析式为:y x=;作点D关于OA的对称点E,点E恰好落在y轴上,连接CE,交OA于点P,∴∠APC=∠OPE=∠DPO,OD=OE,∵点D是OB的中点,∴点D的坐标为(3,0),∴点E的坐标为:(0,3);设直线CE的解析式为:y kx b=+,把点C、E代入,得:643k bb+=⎧⎨=⎩,解得:163kb⎧=⎪⎨⎪=⎩,∴直线CE的解析式为:136y x=+;∴136y xy x⎧=+⎪⎨⎪=⎩,解得:185185xy⎧=⎪⎪⎨⎪=⎪⎩,∴点P 的坐标为:(185,185); 故答案为:(185,185). 【点睛】 本题考查了一次函数的图像和性质,等腰直角三角形的性质,以及线段动点问题,正确的找到P 点的位置是解题的关键.15.60【解析】【分析】根据题意可以判断为等腰三角形,利用勾股定理求出AB 边的高,即可得到答案.【详解】 如图作出AB 边上的高CD∵AC=BC=13, AB=10, ∴△ABC 是等腰三角形,解析:60【解析】【分析】根据题意可以判断ABC ∆为等腰三角形,利用勾股定理求出AB 边的高,即可得到答案.【详解】如图作出AB 边上的高CD∵AC=BC=13, AB=10,∴△ABC 是等腰三角形,∴AD=BD=5,根据勾股定理 CD 2=AC 2-AD 2,22135-,12ABC SCD AB =⋅=112102⨯⨯=60, 故答案为:60.【点睛】 此题主要考查了等腰三角形的判定及勾股定理,关键是判断三角形的形状,利用勾股定理求出三角形的高.16.m>1且m≠2.【解析】【分析】先解关于x的分式方程,求得x的值,然后再依据“解是正数”建立不等式求m的取值范围.【详解】原方程整理得:2x-m=x-1解得:x=m-1因为x>0,所以解析:m>1且m≠2.【解析】【分析】先解关于x的分式方程,求得x的值,然后再依据“解是正数”建立不等式求m的取值范围.【详解】原方程整理得:2x-m=x-1解得:x=m-1因为x>0,所以m-1>0,即m>1.①又因为原式是分式方程,所以,x≠1,即m-1≠1,所以m≠2.②由①②可得,则m的取值范围为m>1且m≠2.故答案为:m>1且m≠2.【点睛】考核知识点:解分式方程.去分母,分母不等于0是注意点.17.(,0)【解析】【分析】画图,设点的坐标是(x,0),因为PA=OB,根据勾股定理可得:AC2+PC2=BD2+ PD2.【详解】已知如图所示;设点的坐标是(x,0),因为PA=OB根据勾解析:(1912,0)【解析】【分析】画图,设点P的坐标是(x,0),因为PA=OB,根据勾股定理可得:AC2+PC2=BD2+PD2.【详解】已知如图所示;设点P的坐标是(x,0),因为PA=OB 根据勾股定理可得:AC2+PC2=BD2+PD2所以32+(x+2)2=42+(4-x)2解得1912 x=所以点P的坐标是(1912,0)故答案为:(1912,0)【点睛】考核知识点:勾股定理.数形结合,根据勾股定理建立方程是关键.18.200【解析】【分析】【详解】设现在平均每天生产x台机器,则原计划可生产(x﹣50)台,根据现在生产600台机器的时间与原计划生产450台机器的时间相同,等量关系为:现在生产600台机器时解析:200【解析】【分析】【详解】设现在平均每天生产x台机器,则原计划可生产(x﹣50)台,根据现在生产600台机器的时间与原计划生产450台机器的时间相同,等量关系为:现在生产600台机器时间=原计划生产450台时间,从而列出方程:600450x x50=-,解得:x=200.检验:当x=200时,x(x﹣50)≠0.∴x=200是原分式方程的解.∴现在平均每天生产200台机器.19.【解析】试题分析:根据算术平方根的定义,36的算术平方根是6.故答案为6.考点:算术平方根.解析:【解析】试题分析:根据算术平方根的定义,36的算术平方根是6.故答案为6.考点:算术平方根.20.11【解析】【分析】根据函数图象可以直接得到AB、BC和三角形ADB的面积,从而可以求得AD 的长,作辅助线CE⊥AD,从而可得CD的长,进而求得点P从开始到停止运动的总路程,本题得以解决.【解析:11【解析】【分析】根据函数图象可以直接得到AB、BC和三角形ADB的面积,从而可以求得AD的长,作辅助线CE⊥AD,从而可得CD的长,进而求得点P从开始到停止运动的总路程,本题得以解决.【详解】解:作CE⊥AD于点E,如下图所示,由图象可知,点P从A到B运动的路程是3,当点P与点B重合时,△PAD的面积是212,由B到C运动的路程为3,∴321 222 AD AB AD⨯⨯==解得,AD=7,又∵BC//AD,∠A=90°,CE⊥AD,∴∠B=90°,∠CEA=90°,∴四边形ABCE是矩形,∴AE=BC=3,∴DE=AD-AE=7-3=4,∴2222 345,CD CE DE =+=+=∴点P 从开始到停止运动的总路程为: AB+BC+CD=3+3+5=11.故答案为:11【点睛】本题考查了根据函数图象获取信息,解题的关键是明确题意,能从函数图象中找到准确的信息,利用数形结合的思想解答问题.三、解答题21.(1)254t =;(2)323t =. 【解析】【分析】(1)根据中垂线性质可知,作AB 的垂直平分线,与AC 交于点P ,则满足PA=PB ,在Rt △ABC 中,用勾股定理计算出AC=8cm ,再用t 表示出PA=t cm ,则PC=()8t -cm ,在Rt △PBC 中,利用勾股定理建立方程求t ;(2)过P 作PD ⊥AB 于D 点,由角平分线性质可得PC=PD ,由题意PC=()t 8-cm ,则PB=()()6t 8=14t ---cm ,在Rt △ABD 中,利用勾股定理建立方程求t.【详解】(1)作AB 的垂直平分线交AB 于D ,交AC 于P ,连接PB ,如图所示,由垂直平分线的性质可知PA=PB ,此时P 点满足题意,在Rt △ABC 中,2222AC=AB BC =106=8--cm ,由题意PA= t cm ,PC=()8t -cm ,在Rt △PBC 中,222PC +BC =PB ,即()2228t +6=t -,解得25t=4(2)作∠CAB 的平分线AP ,过P 作PD ⊥AB 于D 点,如图所示∵AP 平分∠CAB ,PC ⊥AC ,PD ⊥AB ,∴PC=PD在Rt △ACP 和Rt △ADP 中,AP=AP PC=PD ⎧⎨⎩∴()Rt ACP Rt ADP HL ≅∴AD=AC=8cm∴BD=AB-AD=10-8=2cm由题意PD=PC=()t 8-cm ,则PB=()()6t 8=14t ---cm ,在Rt △ABD 中,222PD +BD =PB即()()222t 8+2=14t -- 解得32t=3【点睛】 本题考查了勾股定理的动点问题,熟练运用中垂线性质和角平分线性质,找出线段长度,利用勾股定理建立方程是关键.22.见解析【解析】【分析】利用SAS 证出△AOE ≌△BOD ,然后根据全等三角形的性质即可得出结论.【详解】解:∵AO BO ⊥,DO EO ⊥,∴∠DOE =∠AOB =90°∴∠DOE +∠AOD =∠AOB +∠AOD∴∠AOE=∠BOD在△AOE 和△BOD 中AO BO AOE BOD EO DO =⎧⎪∠=∠⎨⎪=⎩∴△AOE ≌△BOD (SAS )∴AE BD =【点睛】此题考查的是全等三角形的判定及性质,掌握利用SAS 判定两个三角形全等是解决此题的关键.23.29x ,92【解析】【分析】 原式括号内两项通分并利用同分母分式的减法运算法则计算,同时利用除法法则变形,约分得到最简结果,把x 的值代入计算即可求出值.【详解】22333x x x x x ⎛⎫-+÷ ⎪++⎝⎭, 22(3)(3)333x x x x x x x⎛⎫-++=-⋅ ⎪++⎝⎭ 2933x x x +=⋅+ 29x=当x =2992x == 【点睛】此题考查了分式的化简和求值,熟练掌握运算法则是解本题的关键.24.(1)见解析;(2)(-2,5);(3)①见解析;②点P 2的坐标为(﹣m ,n ﹣6);③【解析】【分析】(1)建立适当的平面直角坐标系,根据点A 坐标为(﹣1,2),点B 的坐标为(﹣5,2)即可画出直角坐标系;(2)根据坐标系即可写出点C 的坐标;(3)把△ABC 先向下平移6个单位后得到对应的△A 1B 1C 1,再将△A 1B 1C 1沿y 轴翻折至△A 2B 2C 2;①即可在坐标系中画出△A 2B 2C 2;②若点P (m ,n )是△ABC 边上任意一点,P 2是△A 2B 2C 2边上与P 对应的点,即可写出点P 2的坐标;③根据对称性即可在y 轴上找一点Q ,使得点Q 到A 2,C 2两点的距离之和最小,进而可以求出QA 2+QC 2的长度之和最小值.【详解】(1)∵点A 坐标为(﹣1,2),点B 的坐标为(﹣5,2),如图所示:即为所画出的直角坐标系;(2)根据坐标系可知:点C的坐标为(﹣2,5),故答案为:﹣2,5;(3)把△ABC先向下平移6个单位后得到对应的△A1B1C1,再将△A1B1C1沿y轴翻折至△A2B2C2;①如图即为坐标系中画出的△A2B2C2;②点P(m,n)是△ABC边上任意一点,P2是△A2B2C2边上与P对应的点,∴点P2的坐标为(﹣m,n﹣6),故答案为:﹣m,n﹣6;③根据对称性可知:在y轴上找一点Q,使得点Q到A2,C2两点的距离之和最小,∴连接A2C1交y轴于点Q,此时QA2+QC2的长度之和最小,即为A 2C 1的长,A 2C 1=2,∴QA 2+QC 2的长度之和最小值为2.故答案为:2.【点睛】此题主要考查平面直角坐标系中三角形的平移以及对称性的运用,熟练掌握,即可解题.25.(1)详见解析;(2)10BC =【解析】【分析】(1)根据等式的基本性质可得∠DAB =∠EAC ,然后根据等腰直角三角形的性质可得DA =EA ,BA =CA ,再利用SAS 即可证出结论;(2)根据等腰直角三角形的性质和勾股定理即可求出DE ,从而求出EC 和DC ,再根据全等三角形的性质即可求出DB ,∠ADB=∠AEC ,从而求出∠BDC=90°,最后根据勾股定理即可求出结论.【详解】证明:(1)∵90BAC DAE ∠=∠=︒∴∠DAE -∠BAE =∠BAC -∠BAE∴∠DAB =∠EAC∵ABC ∆和ADE ∆均为等腰直角三角形∴DA =EA ,BA =CA在△ADB 和△AEC 中DA EA DAB EAC BA CA =⎧⎪∠=∠⎨⎪=⎩∴△ADB ≌△AEC(2)∵ADE △是等腰直角三角形,2AD AE ==∴222AD AE +=,∵2DE EC =∴EC=112DE =, ∴DC=DE +EC=3∵△ADB ≌△AEC ∴DB=EC=3,∠ADB=∠AEC∵∠ADB=∠ADE +∠BDC ,∠AEC=∠ADE +∠DAE=∠ADE +90°∴∠BDC=90°在Rt △BDC 中,BC ==【点睛】此题考查的是等腰直角三角形的性质、全等三角形的判定及性质和勾股定理,掌握等腰直角三角形的性质、全等三角形的判定及性质和利用勾股定理解直角三角形是解决此题的关键. 四、压轴题26.(1)2,7,4;(2)83x ≥;(3)①t 的内数=有2个,离原点最远的格点的坐标有两个,为()8,4-±.【解析】【分析】(1)根据内数的定义即可求解;(2)根据内数的定义可列不等式2331x ≤+,求解即可;(3)①分析可得当1t =时,即t 的内数为2时,4n =;当4t =时,即t 的内数为3时,9n =,当5t =时,即t 的内数为4时,16n =……归纳可得结论;②分析可得当t 的内数为奇数时,最大实心正方形有2个;当t 的内数为偶数时,最大实心正方形有1个;且最大实心正方形的边长为:t 的內数-1,即可求解.【详解】解:(1)22311=⨯+,所以1的内数是2;232017⨯+>,所以20的内数是7;23614⨯+>,所以6的内数是4;(2)∵3是x 的內数,∴2331x ≤+, 解得83x ≥; (3)①当1t =时,即t 的内数为2时,4n =;当4t =时,即t 的内数为3时,9n =,当5t =时,即t 的内数为4时,16n =,……∴t的内数n=;②当t的内数为2时,最大实心正方形有1个;当t的内数为3时,最大实心正方形有2个,当t的内数为4时,最大实心正方形有1个,……即当t的内数为奇数时,最大实心正方形有2个;当t的内数为偶数时,最大实心正方形有1个;∴当t的內数为9时,符合条件的最大实心正方形有2个,由前几个例子推理可得最大实心正方形的边长为:t的內数-1,∴此时最大实心正方形的边长为8,离原点最远的格点的坐标有两个,为()8,4-±.【点睛】本题考查图形类规律探究,明确题干中内数的定义是解题的关键.27.见解析【解析】【分析】先根据平行线的性质,得到角的关系,然后证明OCD OFE△≌△,写出证明过程和依据即可.【详解】解:过点E作//EF AC交BC于F,∴ACB EFB∠=∠(两直线平行,同位角相等),∴D OEF∠=∠(两直线平行,内错角相等),在OCD与OFE△中()()()COD FOEOD OED OEF⎧∠=∠⎪=⎨⎪∠=∠⎩对顶角相等已知已证,∴OCD OFE△≌△,(ASA)∴CD FE=(全等三角形对应边相等)∵AB AC=(已知)∴ACB B=∠∠(等边对等角)∴EFB B∠=∠(等量代换)∴BE FE=(等角对等边)∴CD BE=;【点睛】本题考查了全等三角形的判定和性质,平行线的性质,解题的关键是由平行线的性质正确找到证明三角形全等的条件,从而进行证明.28.(1)①E(3,﹣2)②见解析;③12OMBD,理由见解析;(2)OD+OA=2AM或OA﹣OD=2AM【解析】【分析】(1)①过点E作EH⊥y轴于H.证明△DOA≌△AHE(AAS)可得结论.②证明△BOM≌△EHM(AAS)可得结论.③是定值,证明△BOM≌△EHM可得结论.(2)根据点D在点B左侧和右侧分类讨论,分别画出对应的图形,根据全等三角形的判定及性质即可分别求出结论.【详解】解:(1)①过点E作EH⊥y轴于H.∵A(0,3),B(﹣3,0),D(﹣5,0),∴OA=OB=3,OD=5,∵∠AOD=∠AHE=∠DAE=90°,∴∠DAO+∠EAH=90°,∠EAH+∠AEH=90°,∴∠DAO=∠AEH,∴△DOA≌△AHE(AAS),∴AH=OD=5,EH=OA=3,∴OH=AH﹣OA=2,∴E(3,﹣2).②∵EH⊥y轴,∴∠EHO=∠BOH=90°,∵∠BMO=∠EMH,OB=EH=3,∴△BOM≌△EHM(AAS),∴BM=EM.③结论:OMBD=12.理由:∵△DOA≌△AHE,∴OD=AH,∵OA=OB,∴BD=OH,∵△BOM≌△EHM,∴OM=MH,∴OM=12OH=12BD.(2)结论:OA+OD=2AM或OA﹣OD=2AM.理由:当点D在点B左侧时,∵△BOM≌△EHM,△DOA≌△AHE∴OM=MH,OD=AH∴OH=2OM,OD-OB=AH-OA∴BD=OH∴BD=2OM,∴OD﹣OA=2(AM﹣AO),∴OD+OA=2AM.当点D在点B右侧时,过点E作EH⊥y轴于点H∵∠AOD=∠AHE=∠DAE=90°,∴∠DAO+∠EAH=90°,∠EAH+∠AEH=90°,∴∠DAO=∠AEH,∵AD=AE∴△DOA≌△AHE(AAS),∴EH=AO=3=OB,OD=AH∴∠EHO=∠BOH=90°,∵∠BMO=∠EMH,OB=EH=3,∴△BOM≌△EHM(AAS),∴OM=MH∴OA+OD= OA+AH=OH=OM+MH=2MH=2(AM+AH)=2(AM+OD)整理可得OA﹣OD=2AM.综上:OA+OD=2AM或OA﹣OD=2AM.【点睛】此题考查的是全等三角形的判定及性质、旋转的性质和平面直角坐标系,掌握全等三角形的判定及性质、旋转的性质和点的坐标与线段长度的关系是解决此题的关键.29.(1)见解析;(2)CD=2AD+BD,理由见解析;(3)CD=3AD+BD【解析】【分析】(1)由“SAS”可证△ADB≌△AEC;(2)由“SAS”可证△ADB≌△AEC,可得BD=CE,由直角三角形的性质可得DE=2AD,可得结论;(3)由△DAB≌△EAC,可知BD=CE,由勾股定理可求DH=32AD,由AD=AE,AH⊥DE,推出DH=HE,由CD=DE+EC=2DH+BD=3AD+BD,即可解决问题;【详解】证明:(1)∵∠BAC=∠DAE,∴∠BAD=∠CAE,又∵AB=AC,AD=AE,∴△ADB≌△AEC(SAS);(2)CD=2AD+BD,理由如下:∵∠BAC=∠DAE,∴∠BAD=∠CAE,又∵AB=AC,AD=AE,∴△ADB≌△AEC(SAS);∴BD=CE,∵∠BAC=90°,AD=AE,∴DE=2AD,∵CD=DE+CE,∴CD=2AD+BD;(3)作AH⊥CD于H.∵∠BAC=∠DAE,∴∠BAD=∠CAE,又∵AB=AC,AD=AE,∴△ADB≌△AEC(SAS);∴BD=CE,∵∠DAE=120°,AD=AE,∴∠ADH=30°,∴AH=12 AD,∴DH,∵AD=AE,AH⊥DE,∴DH=HE,∴CD=DE+EC=2DH+BD+BD,故答案为:CD+BD.【点睛】本题是结合了全等三角形的性质与判定,勾股定理等知识的综合问题,熟练掌握知识点,有简入难,层层推进是解答关键.30.(1)见解析;(2)见解析;(3)3【解析】【分析】(1)根据等腰三角形的性质和外角的性质即可得到结论;(2)过E作EF∥AC交AB于F,根据已知条件得到△ABC是等边三角形,推出△BEF是等边三角形,得到BE=EF,∠BFE=60°,根据全等三角形的性质即可得到结论;(3)连接AF,证明△ABF≌△CBF,得AF=CF,再证明DH=AH=12CF=3.【详解】解:(1)∵AB=AC,∴∠ABC=∠ACB,∵DE=DC,∴∠E=∠DCE,∴∠ABC-∠E=∠ACB-∠DCB,即∠EDB=∠ACD;(2)∵△ABC是等边三角形,∴∠B=60°,∴△BEF是等边三角形,∴BE=EF,∠BFE=60°,∴∠DFE=120°,∴∠DFE=∠CAD,在△DEF与△CAD中,EDF DCADFE CADDE CD∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△DEF≌△CAD(AAS),∴EF=AD,∴AD=BE;(3)连接AF,如图3所示:∵DE=DC,∠EDC=30°,∴∠DEC=∠DCE=75°,∴∠ACF=75°-60°=15°,∵BF平分∠ABC,∴∠ABF=∠CBF,在△ABF和△CBF中,AB BCABF CBFBF BF=⎧⎪∠=∠⎨⎪=⎩,△ABF≌△CBF(SAS),∴AF=CF,∴∠FAC=∠ACF=15°,∴∠AFH=15°+15°=30°,∵AH⊥CD,∴AH=12AF=12CF=3,∵∠DEC=∠ABC+∠BDE,∴∠BDE=75°-60°=15°,∴∠ADH=15°+30°=45°,∴∠DAH=∠ADH=45°,∴DH=AH=3.【点睛】本题考查了全等三角形的判定与性质,等腰三角形和直角三角形的性质,三角形的外角的性质,等边三角形的判定和性质,证明三角形全等是解决问题的关键.。

江苏省常州市教育学会2019-2020学年八年级上学期期末语文试题学校:___________姓名:___________班级:___________考号:___________一、字词书写1.给下列划线的字注音或根据拼音写出相应的汉字。
读朱自清笔下黑布大马guà( ),深青色棉袍,蹒跚( )走到铁道边的背影,我们读到了浓浓父爱;读茅盾笔下没有婆suō ( )姿态,没有屈曲盘旋的虬( )枝的白杨树,我们感受到质朴之美;读汪曾祺笔下昆明雨季里味极鲜yú( )的青头菌、牛肝菌,我们感受到了自然之美。
二、基础知识综合2.按语气,句子可分为陈述句、疑问句、感叹句、祈使句,指出下列句子的类型。
(1)请把我的歌,带回你的家,请把我的微笑留下。
(_______)(2)如果能够对公共事业有所贡献,我就会认为自已是最幸福的人。
(_______)三、综合性学习3.请用-句话连贯简明地转述“积极废人”的内涵。
(限50字以内)积极废人是指这样一种人:他们有这样的通病,爱给自己立flag(意指公开树立的目标),心态积极向上,但想偷懒的念头太多,永远做不到,执行力太差,行动宛如废物。
他们往往会在间歇性享乐后恐慌,时常为自己的懒惰自责。
4.请根据我国传统节日的特点,在横线上续写两个句子。
好传统我们代代传承。
春节,我们贴福舞狮共贺新禧;清明,我们踏青祭祖缅怀先人;,;,;重阳,我们登高祈福长寿延年。
四、选择题5.下列各句中,词语运用不恰当的一句是()A.我最近非常担忧,令媛成绩退步厉害,我想请您赐教。
B.推开门,那种叫作“理解”的东西,如圣灵一般翩然而至。
C.那声音是轻柔、甜美、透明的,仿佛悄悄滑过钢琴的琴键,从肖邦手下流出。
D.欢迎来到青果巷,我是这里的解说员,我将竭诚为您服务!五、句子默写6.默写。
(1)______________________,恨别鸟惊心。
(2) 角声满天秋色里_____________________。

2020一2021 学年度第一学期期末学业水平调研测试八年级物理说明:1.全卷共6页, 满分为100分, 考试用时80分钟.2.答卷前, 考生务必用黑色字迹的签字笔或钢笔在答题卡填写自己的学校、姓名、班别、座位号.用2B 铅笔填涂考生信息.3.选择题每小题选出答案后, 用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑.如需改动, 用橡皮擦干净后, 再选涂其他答案, 答案不能答在试题上.4.非选择题必须用黑色字迹钢笔或签字笔作答、答案必须写在答题卡各题目指定区域内相应位置上; 如需改动, 先划掉原来的答案, 然后再写上新的答案; 不准使用铅笔和涂改液.不按以上要求作答的答案无效.5.考生务必保持答题卡的整洁.考试结束时, 将答题卡交回.一、单项选择题(本题7 小题, 每小题3 分,共21 分)在每小题列出的四个选项中, 只有一个是正确的, 请把答案卡上对应题目所选的选项涂黑.1g 看电视转播百米赛跑时, 我们感觉运动员跑得很快, 但实际上他们始终处在屏幕内。
运动员跑得很快所选取的参照物是A g比赛场地背景B g运动员本身C g看电视的人D g电视2g 一个中学生正常步行5min, 这个中学生行走的路程约是A g1500mB g1000mC g350mD g150m3g在同一架钢琴上,弹奏C调"3(m i)"和"1(d o)"这两个音,以下说法正确的是A g音色一定不同B g音调一定不同C g响度一定不同D g音调、音色和响度都不同5g 如图中画出了光线通过透镜(图中未画出)的情形, 其中是凸透镜的是A g a、b、c、dB g b、dC g aD g c第 5 题图6g 医生在发烧病人身上擦拭酒精溶液, 可以达到降低体温的效果, 他的依据是A g酒精熔化时吸热B g酒精液化时吸热C g酒精汽化时吸热D g酒精升华时吸热7g 用天平秤称量一个空纸盒的质量, 然后将纸盒剪碎后再放到天平秤上称, 前后两次称量的质量相比A g相等B g变大C g变小D g不能确定,每次称量都不同二、填空题(本大题7 小题, 每空1 分, 共21 分)8g光在真空中传播的速度是_m k/;超声波在真空中传播速度是,它在水中的传播速度是5400_m k s,合m k/。

溧阳市2020~2021学年度第一学期期末质量调研测试八年级物理试题2021.11一、单项选择题:(下列各题的四个选项中,只有一项最符合题意。
每小1.5分,共21分)1.下列关于声音的说法中正确的是A.“低声轻语”主要说明了声音的音调低B.“尖声尖叫”主要说明了声音的音调高C.“震耳欲聋”主要说明了声音的音调高D.“闻其声而知其人”主要是根据音调来判断的2.下列几种估测最符合实际情况的是A人步行的速度约为1.4 m/min B.正常人的脉搏为70HzC.课桌的高度约为75dmD.全新的2B铅笔长约18cm3.有些物理量的大小不易直接观测,但它变化时引起其它量的变化却容易直接观测,用易观测的量显示不易观测的量是研究物理问题的一种方法,例如:发声音叉的振动可以通过激起水花来体现.以下实例中采用的研究方法与上述方法相同的是A.研究光现象时,引入光线用来描述光的传播路径和方向B.研究熔化现象时,比较冰、蜂蜡的熔化特点C.液体温度计利用液柱长度的变化来显示温度高低D.研究平面镜成像时,为了比较像与物体的大小,选用两支相同的蜡烛4.秋季的一个周末,地处江南地区的阳天气又闷又热,小明听天气预报说北方有一股弱冷空气南下,江南地区将会有一场小雨,气象台这样说的理由是A.江南地区的暖湿气流中有大量的水蒸气,水蒸气遇到冷空气迅速液化,形成降雨B.冷空气中有大量的水蒸气,遇到江南地区的暖湿气流,迅速液化,形成降雨C.冷空气把北方的水森气带到了江南地区D.江南地区的这场小与冷空气的到来无关5.北方塞冷的冬天,居民楼的玻璃上会结“冰花”,当拿起湿抹布去擦时,抹布却粘在了玻璃上,以下对上述现象的分析正确的是A.“花”是窗外的水蒸气凝固形成的B.“冰花”是屋内的水蒸气凝固形成的C.抹布粘在了玻璃上是因为发生了凝固现象D.抹布粘在了玻璃上是因为发生了凝华现象6.如图所示,志愿者骑车经过广场,最右边的志者认为自己是静止的,那么他所选取的参照物最有可能是A.前方的志愿者B.旁边的体育场馆C.地面D.迎面来的三轮车7下列现象中,由光的折射引起的是A.日食的形成B.放大镜把字放大B.C.拱桥“倒影” D.汽车“后视镜”8.关于如图所示的声现象,下列分析正确的是A.甲中敲打鼓面,附近的烛焰动,说明声音可以传递信息B.乙中车间工人佩戴耳罩,是在声源处减弱噪声C.丙中弹吉它时,增大搜动弦的力度可以增大声音的响度D.丁中抽出罩内空气,听到钟声音变小,说明发声体振动减弱9.如图所示,一细束绿光经三棱镜折射后,在光屏上a点处形成一个色光斑.现保持入射光位置及方向不变,仅将绿光改为红光,以下说法正确的是A.保持光屏位置不变,红色光近仍在a点处B.保持光屏位置不变,红色光斑在a点下方C.将光屏向左平移,红色光仍可落在a点处D.将光屏向右平移,红色光斑仍可落在a点处10.将一只玩具鹦鹉(如图甲所示)紧靠凸透镜,然后渐远离透镜的过程中,通过凸透镜观察到三个不同的像(如图乙所示),以下说法正确的是A.三个像中a、c是实像B.三个像中a、c是虚像C.三个像出现的先后顺序是c、a、bD.三个像出现的先后顺序是c、b、a11.如图所示是某物体做直线运动时的路程随时间变化的图像,由图像知下列说法错误的是A.5s时,物体通过的路程为2.5mB.整个20时间内,物体的平均速度为0.2msC.物体在20内都做匀速直线运动D.物体在05s内的速度比1020s内的連度大12.将物体放在距凸透镜20m处时,可在凸透镜另一的光屏上成一个倒立、放大的清晰像。
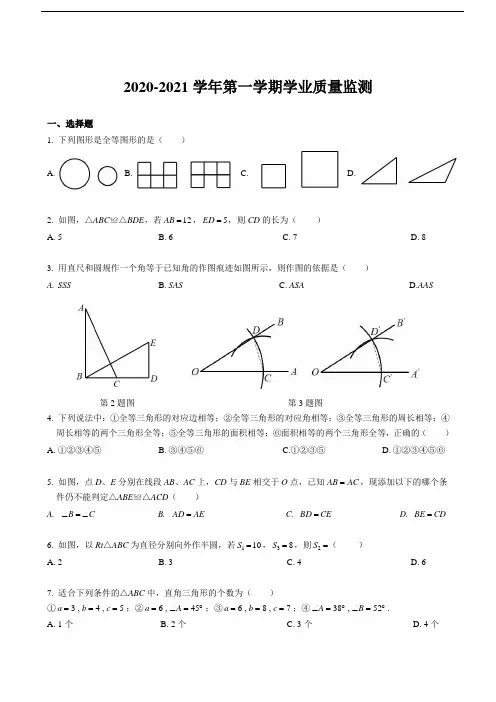
2020-2021 学年第一学期学业质量监测一、选择题1. 下列图形是全等图形的是()A. B. C. D.2. 如图,△ABC ≌△BDE ,若 AB = 12 , ED = 5,则 CD 的长为( )A. 5B. 6C. 7D. 83. 用直尺和圆规作一个角等于已知角的作图痕迹如图所示,则作图的依据是( )A. SSSB. SASC. ASAD.AAS第 2 题图第 3 题图4. 下列说法中:①全等三角形的对应边相等;②全等三角形的对应角相等;③全等三角形的周长相等;④ 周长相等的两个三角形全等;⑤全等三角形的面积相等;⑥面积相等的两个三角形全等,正确的( )A. ①②③④⑤B. ③④⑤⑥C.①②③⑤D. ①②③④⑤⑥5. 如图,点 D 、E 分别在线段 AB 、AC 上,CD 与 BE 相交于 O 点,已知 AB = AC ,现添加以下的哪个条件仍不能判定△ABE ≌△ACD ( )A. ∠B = ∠CB. AD = AEC. BD = CED. BE = CD6. 如图,以 Rt △ABC 为直径分别向外作半圆,若 S 1 = 10 , S 3 = 8 ,则 S 2 =( )A. 2B. 3C. 4D. 67. 适合下列条件的△ABC 中,直角三角形的个数为( )① a = 3 , b = 4 , c = 5 ;② a = 6 , ∠A = 45︒ ;③ a = 6 , b = 8 , c = 7 ;④ ∠A = 38︒ , ∠B = 52︒ .A. 1 个B. 2 个C. 3 个D. 4 个8.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a +b)2 = 21 ,大正方形的面积为13,则小正方形的面积为()A. 3B. 4C. 5D. 6第5 题图第6 题图第8 题图二、填空题(每题2 分,共计20 分)9.如图,一扇窗户打开后,用窗钩AB 可将其固定,这里运用的几何原理是.10.△ABC≌△ADE,如果AB = 5 ,BC = 7 ,AC = 6 ,那么DE 的长是.11. 如图,△ABC≌△ADE,∠B = 80︒,∠C = 30︒,∠DAC =15︒,则∠EAC =.12.如图,△ABC 中,AD⊥BC 于D,要使△ABD≌△ACD,若根据“HL”判定,还需要加条件.第9 题图第11 题图第12 题图第13 题图13.如图,△ABC 中,∠AEB =∠AEC ,BE =CE ,直接使用“SAS”可判定.14.如图,某同学把三角形玻璃打碎三块,他要去配一块完全一样的,结果他带了第3 片去,他所用到的原理是(用文字语言表述)第14 题图第15 题图第17 题图第18 题图15.园丁住宅小区有一块草坪如图所示,已知AB = 3 ,BC = 4 ,DA =13,DC =12 ,且AB⊥BC,这块草坪的面积是.16.一个三角形的三边长为7,24,25,则此三角形最长边上的高为.17.如图,将一根长24 的筷子,置于底面直径为5,高为12 的圆柱形水杯中,设筷子露在杯子外面的长度为h,则h 的取值范围是.18.如图,在边长为3 的正方形ABCD 的外部作Rt△AEF ,且AE =AF =1 ,连接DE ,BF ,BD ,则DE 2 +BF 2 =.三、解答题(本大题共7 题,共计56 分)19.(8 分)如图,A、B 两建筑物位于河的两岸,为了测量它们的距离,可沿河岸作一条直线MN,且使MN⊥AB 于点B,在BN 上截取BC =CD ,过点D 作BD⊥MN,使点A、C、E 在同一直线上,则DE 的长就是A、B 两建筑物之间的距离,请说明理由.20.(8 分)已知:如图,A、C、F、D 在同一直线上,AF =DC ,AB∥DE,AB =DE ,求证:(1)△ABC≌△DEF;(2)BC∥EF.21.如图,∠C =∠BDE ,AE =BE ,点D 在AC 边上,∠DEC =∠BEA.(1)求证:△AEC≌△BED;(2)若∠DEC = 40︒,求∠BDA 的度数.22.(8 分)如图,AE=AF ,AB =AC ,DE⊥BA,点E 为垂足,DF⊥AC,点F 为垂足. 求证:BD =CD .23.(8 分)如图,一架长为5 米的梯子AB 斜靠在与地面OM 垂直的墙ON 上,梯子底端距离墙的距离OB的长为3 米.(1)求梯子顶端与地面的距离OA 的长.(2)若梯子顶点A 下滑1 米到C 点,求梯子的底端向右滑到D 的距离.24.(8 分)观察下表中的每一组值:(1)根据表中前四组a,b,c 值的变化规律,第5 组中b =;c =. 第n 组中a =;b =;c =.(2)试证明以表中每组a,b,c 为边的三角形都是直角三角形.25.(8 分)如图,已知△ABC 中,AB =AC = 12 厘米,BC = 9 厘米,∠B =∠C ,点D 为AB 的中点. (1)如果点P 在线段BC 上以3 厘米/秒的速度由B 向C 运动,同时点Q 在线段CA 上由C 点向A 点运动.①若点Q 的运动速度与点P 的运动速度相等,1 秒钟时,△BPD 与△CQP 是否全等,请说明;②点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度为多少时,能够使△BPD≌△CPQ?(2)若点Q 以②的运动速度从点C 出发,点P 以原来运动速度从点B 同时出发,都逆时针沿ABC 的三边运动,求多长时间点P 与点Q 第一次在△ABC 的哪条边上相遇?⎨⎨一、选择题1~8:BCACDABC月考试卷答案二、填空题9. 三角形稳定性10. 711. 55°12. AB =AC13.∆AEB ≅ ∆AEC14.两角及其夹边对应相等的两个三角形全等 15.36 16.1682517. 11 ≤ h ≤ 1218.20三、证明题19. 应用全等三角形判定 ASA 20.(1)∵ AF = DC∴ A F - CF = DC - CF ∴ AC = DF ∵ AB / /DE ∴ ∠A = ∠D在∆ABC 和∆DEF 中 ⎧ AB = DE ⎪∠A = ∠D ⎪⎩AC = DF ∴ ∆ABC ≅ ∆DEF (SAS )(2)∵ ∆ABC ≅ ∆DEF ∴ ∠BCF = ∠EFC ∴ BC / /EF∴ ∠ACB = ∠DFE21.(1)∵ ∠DEC = ∠BEA即∠AEC = ∠BED 在∆AEC 和∆BED 中 ⎧∠C = ∠BDE ⎪∠AEC = ∠BED ⎪⎩AE = BE ∴ ∠DEC + ∠DEA = ∠BEA + ∠DEA∴ ∆AEC ≅ ∆BED (AAS ) (2)40°⎩ ⎨⎨ ∴ 2 22. 证明:∵ DE ⊥ AE , DF ⊥ AF∴ ∠E = ∠F = 90︒在 Rt ∆ADE 和 Rt ∆ADF 中 ⎧ AD = AD⎨AE = AF∴ Rt ∆ADE ≅ Rt ∆ADF (HL ) ∴ ∠EAD = ∠FAD 在∆ABD 和∆ACD 中 ⎧ AB = AC ⎪∠BAD = ∠CAD ⎪⎩AD = AD ∴ ∆ABD ≅ ∆ACD (SAS ) ∴ B D = CD23.(1)4,(2)124.(1)b =60,c =61, a = 2n + 1, b = 2n 2 + 2n , c = 2n 2 + 2n + 1(2)通过化简可得a 2 + b 2 = c 2 ,满足勾股定理,则以 a 、b 、c 为边的三角形都是直角三角形 25.(1)①全等,若V p = V q ,则 BP = CQ1s 时, BP = CQ = 3 ∵ BC = 9 ∴ CP = 9 - 3 = 6 ∵D 为 AB 中点,AB =12 ∴ BD = 1 AB = 62 ∴ B D = CP∴ ∆BPD ≅ ∆CQP (SAS )②4cm /s ,当 BP ≠ CQ 时,设时间为 t要使∆BPD ≅ ∆CPQ ,只要 BP = CP , BD = CQ 即可⎧3t = 9 - 3t ⎧t = 3 ⎪ ⎩6 = vt⎨ ⎪⎩v = 4∴Q 的速度为 4cm /s(2)24s ,第一次在 BC 边上相遇。

常州市教育学会学业水平监测八年级地理2021.01说明:测试形式为开卷书面考试。
可查阅地理课本及相关资料,但不得相互讨论和互借资料。
考试时间为60分钟。
试卷满分为100分。
一、单项选择题(每题2分,共30题,共60分)1.歌曲《我爱你中国》中"当灿烂的太阳跳出了你东海的碧波,你的帕米尔高原上依然是群星闪烁",产生这种现象的原因主要是A.所跨纬度多B.所跨经度多C.海陆差异大D.地形起伏大2.除夕,漠河镇上冰灯闪烁,海南岛依然鲜花盛开。
这是由于我国领土A.所跨纬度多B.所跨经度多C.海陆差异大D.地形起伏大3.我国固有领土黄岩岛位于A.东海B.南海C.黄海D.渤海4.我国海域辽阔,素有"天然鱼仓"之称并拥有我国最大渔场的海域是A.黄海B.东海C.南海D.渤海5.均为与我国隔海相望的岛国是A.韩国、蒙古、巴基斯坦B.日本、文莱、印度尼西亚C.蒙古、马来西亚、日本D.朝鲜、尼泊尔、菲律宾6.在我国边疆省区中,邻国最多的是A.云南省B.黑龙江省C.西藏自治区D.新疆维吾尔自治区我国东西横跨5200多千米,南北纵贯5500多千米,各地自然环境和人文风情各不相同,呈现出显著的区域地理差异。
据此回答7~9题。
7.世界上绝大多数动植物都能在我国找到适合生长的地方,主要是因为我国A.雨热同期B.夏季普遍高温D.季风气候显著C.气候复杂多样8.受地理环境的影响,我国南、北方地区形成了具有地域特色的人文风情,有关这种地域差异的描述,不符合实际情况的是A.民间体育——南赛马北滑雪B.饮食习惯——南米北面C.民居风格——南尖顶北平顶D.传统交通——南船北马9.春节,家住我国南方地区的陈超同学想去外地观赏冰灯和冰雕。
陈超的旅行路线最有可能是A.拉萨一广州B.常州一哈尔滨C.乌鲁木齐一桂林D.南京一海口下图为我国四省份轮廓示意图,读图并结合课本回答10~12题。
10.《沁园春·长沙》"独立寒秋,湘江北去,橘子洲头"描绘的是A.甲B.乙C.丙D.丁11.四省份中人口密度最小的是A.甲B.乙C.丙D.丁12.四省份中少数民族种类最少的是A.甲B.乙C.丙D.丁读下图,完成13~16题。

常州市教育学会学业水平监测八年级英语试卷2022年1月(考试范围:初中英语八年级上册)注意:本试卷分第一卷(选择题)和第二卷(非选择题)两部分。
第一卷第1至7页,答案全部做在答题纸上。
答题纸在第8页。
第二卷第9至10页,答案做在试卷上。
共100分。
考试时间为90分钟。
交卷时只将7-10页收回。
期末成绩=笔试成绩x90%+口试成绩( 10%)第一卷(共66分)一、听力(共20小题;每小题1分,满分20分) 略二、单项选择(共10小题;每小题1分,满分10分)从A、B、C、D四个选项中,选出可以填入空白处的最佳选项。
21. The sentence structure of“We call the baby panda Xi Wang." is.A. S+V+PB. S+V+OC. S+V4 IO+DOD. S+V+DO+OC22. Because of all the social workers' hard work, the city won the with COVID-19 in such a short time.A. discussionB. huntingC. fight .D. Sickness23. The doctors did what they could his sick daughter.A. to saveB. savingC. saveD. Saved24. --- Can I have some more juice, Mum?--- Sorry dear, but there is left.A. a littleB. noneC. nothingD. no25. People were waiting for the traffic lights an SUV ran into the crowd(人群). Three persons died and ten were hurt.A. whenB. while .C. becauseD. If26. In the poem, the word“shower" rhymes with“ ”A. towelB. hourC. slowerD. window27.--You play with fire.-You are right. Fire be very dangerous sometimes.A. shouldn't; mustB. may not; canC. mustn't; canD. may not; must28. The boys are busy the new pictures on the wall to make it more beautiful.A. putting onB. putting upC. putting awayD. putting in29. He turned around_and found that his mother seemedA. quiet; sadlyB. quietly; sadC. quiet; sadD. quietly; sadly30. --There s a heavy storm. As a result, M. Black cannot fly here to speak to us today.----I really look forward to meeting him.A. You're welcome!B. Take care! .C. What a shame!D. No way!三、完形填空(共10小题;每小题1分,满分10分)阅读下面短文,掌握其大意,然后从每小题所给的A、B、c、D四个选项中,选出可以填入空白处的最佳选项。
【市级联考】江苏省常州市2021・2021学年八年级第一学期期末数学试题学校:姓名:班级:考号:一、单项选择题1.在以下黑体大写英文字母中,不是轴对称图形的是〔〕A. TB. IC. ND. H2.以下各点中,位于第四象限的点是〔〕A. 〔3,-4〕B. 〔3,4〕C. 〔-3,4〕D. 〔-3, 口〕3.小亮的体重为47.95kg,用四舍五入法将47.95精确到0.1的近似值为〔〕A. 48B. 48.0C. 47D. 47.94.假设一个三角形的三边长分别为3、4、5,那么这个三角形最长边上的中线为〔〕A. 1.8B. 2C. 2.4D. 2.55.一次函数y = kx + b,函数值y随自变量x的增大而减小,且kb<0,那么函数y = kx + b的图象大致是〔〕6.如图,点B、E、C、F在同一条直线上,AB//DE, AB = DE.要用SAS证实^ABC ^^DEF,可以添加的条件是〔〕A. NA = 4B. AC//DFC. BE = CFD. AC = DF7 .如图,在△ ABC 中,AB.AC 的垂直平分线分别交BC 于点E 、F,假设NBAC = 112°,8•小苏和小林在如图①所示的跑道上进行4x50米折返跑.在整个过程中,跑步者距起 跑线的距离〕'〔单位:〃?〕与跑步时间/ 〔单位:S 〕的对应关系如图②所示.以下表达 正确的选项是〔〕.A.两人从起跑线同时出发,同时到达终点8 .小苏跑全程的平均速度大于小林跑全程的平均速度 C.小苏前15s 跑过的路程大于小林前15s 跑过的路程 D.小林在跑最后100m 的过程中,与小苏相遇2次二、填空题9 . 4的平方根是 ______ .10 .点P 〔—3,4〕,关于y 轴对称的点的坐标为.11 .在实数J 证,0.3,、污,一^中,无理数有 __________________ 个・7 2 12 .假设点〔m,m + l 〕在函数y =—gx + 2的图象上,那么门1=. 13 .以下关于建立平而直角坐标系的熟悉,合理的有.①尽量使更多的点在坐标轴上:②尽量使图形关于坐标轴对称:③建立坐标系沟通 了 “数〞与“形〞之间的联系.14 .如图,在等边^ABC 中,D 、E 分别是边AB 、AC 上的点,且AD = CE,那么 ^ADC+^BEA =\C 42: D. 44图①那么4阳为〔 〕15 .如图,在AABC 中,ZC=90° , AD 平分NCAB, AC=6, AD=7,那么点 D 到直线AB的距离是16 .己知A ABC 的三条边长分别为3, 4, 6,在A ABC 所在平面内画一条直线,将A ABC分割成两个三角形,使其中的一个是等腰三角形,那么这样的直线最多可画 条.三、解做题17 .阅读理解:•.・/< 正 <6,即 2c 有<3, :.\<y/5-\<2. .•.、后一1的整数局部为1.的小数局部为〔6一 1〕-1 =有一2解决问题:a 是加―3的整数局部,b 是J 访—2的小数局部,求〔―a[+〔b + 5〕2 的平方根.18.如图〔1〕所示,在A, B 两地间有一车站C, 一辆汽车从A 地出发经C 站匀速驶往 B 地•如图〔2〕是汽车行驶时离C 站的路程y 〔千米〕与行驶时间x 〔小时〕之间的函数关 系的图象.〔1〕填空:a=km, AB 两地的距离为 km :〔2〕求线段PM 、MN 所表示的y 与x 之间的函数表达式:〔3〕求行驶时间x 在什么范围时,小汽车离车站C 的路程不超过60千米?②描点: ③连线〔2〕观察图象,当x 时,y 随x 的增大而增大; 〔3〕结合图象,不等式|x|<x + 2的解集为.AEB24.某产品每件本钱10元,试销阶段每件产品的销售价x 〔元〕与产品的日销售量y 〔件〕之间的关系如表:日销售量y是销售价x的一次函数.〔1〕求日销售量y 〔件〕与每件产品的销售价x 〔元〕之间的函数表达式;〔2〕当每件产品的销售价定为35元时,此时每日的销售利润是多少元?25. 〔1〕问题解决:①如图1,在平面直角坐标系xOy中,一次函数y = ;x + l与x轴交于点A,与y轴交于点B,以AB为腰在第二象限作等腰直角4ABC, ZBAC = 90 , 点A、B的坐标分别为A、B.②求①中点C的坐标.小明同学为了解决这个问题,提出了以下想法:过点C向x轴作垂线交x轴于点D.i青你借助小明的思路,求出点C的坐标:〔2〕类比探究:数学老师表扬了小明同学的方法,然后提出了一个新的问题,如图2,在平面直角坐标系xOy中,点A坐标〔0,-6〕,点B坐标〔8,0〕,过点B作x轴垂线1,点P是1上一动点,点D是在一次函数y = -2x + 2图象上一动点,假设.APD是以点D 为直角顶点的等腰直角三角形,请直接写出点D与点P的坐标.参考答案1.c【解析】【分析】根据轴对称图形的概念对各个大写字母判断即可得解.【详解】解:A、“T〞是轴对称图形,故本选项不合题意;B、“I〞是轴对称图形,故本选项不合题意;C、“N〞不是轴对称图形,故本选项符合题意;D、“H〞是轴对称图形,故本选项不合题意.应选:C.【点睛】此题考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两局部折卷后可重合. 2. A【分析】根据平而直角坐标系中点的坐标特征解答即可,第四象限内点的横坐标大于0,纵坐标小于0.【详解】•第四象限内点的横坐标大于0,纵坐标小于0,位于第四象限.应选A.【点睛】此题考查了平面直角坐标系中点的坐标特征.第一象限内点的坐标特征为〔+,+〕,第二象限内点的坐标特征为〔-,+〕,第三象限内点的坐标特征为第四象限内点的坐标特征为〔+,-〕, x轴上的点纵坐标为0, y轴上的点横坐标为0.3. B【解析】试题解析:47.95精确到0.1的近似值为48.0.应选B.4. D【解析】【分析】根据勾股定理逆定理判断出三角形是直角三角形,然后根据直角三角形斜边上的中线等于斜边的一半解答即可.【详解】••• 32+42=25=52,,该三角形是直角三角形,/. —x5 = 2.5.2应选:D.【点睛】此题考查了直角三角形斜边上的中线等于斜边的一半的性质,勾股定理的逆定理,判断出直角三角形是解题的关键.5. A【解析】【分析】根据一次函数的性质得到k<0,而kb<0,那么b>0,所以一次函数y=kx+b的图象经过第二、四象限,与y轴的交点在x轴上方,据此即可求得答案.【详解】•.•一次函数y=kx+b, y随着x的增大而减小,.,.k<0,•♦.一次函数y=kx+b的图象经过第二、四象限;Vkb<0,•••图象与丫轴的交点在x釉上方,一次函数丫=1^+1〕的图象经过第一、二、四象限,应选A.【点睛】此题考查了一次函数的图象:一次函数丫=1^^^ 〔k、b为常数,四〕是一条直线,当k>0, 图象经过第一、三象限,y随x的增大而增大:当k<0,图象经过第二、四象限,y随x的增大而减小:图象与y轴的交点坐标为(0, b).6. C【分析】根据AB〃DE得出NB=NDEF,添加条件BC=EF,那么利用SAS定理证实△ABCgADEF. 【详解】解:VAB/7DE,,NB=NDEF,可添加条件BC=EF,理由:•・•在AABC和4DEF中,AB = DENB = ZDEF ,BC = EF.,.△ABC^ADEF (SAS);应选c.【点睛】此题考查三角形全等的判定方法,判定两个三角形全等时,必需有边的条件,假设有两边一角对应相等时,角必需是两边的夹角.7. D【解析】【分析】根据三角形内角和定理求出NC+NB=68°,根据线段垂直平分线的性质得到EC=E4, FB =M,根据等腰三角形的性质得到NEAC=NC, NFAB=NB,计算即可.【详解】解:•••ZBAC = 112°,"C + 4 = 68,••• EG、FH分别为AC、AB的垂直平分线,.•.EC = EA, FB = FA,.•.4AC = /C, 4AB = 4, ...4AC + /AB = 68,.-.^EAF=44 »应选:D.【点睛】此题主要考查线段的垂直平分线的性质等几何知识.线段的垂直平分线上的点到线段的两个端点的距离相等.8. D【解析】【详解】A.由图可看出小林先到终点,A错误;B.全程路程一样,小林用时短,所以小林的平均速度大于小苏的平均速度,B错误:C.第15秒时,小苏距离起点较远,两人都在返回起点的过程中,据此可判断小林跑的路程大于小苏跑的路程,C错误;D.由图知两条线的交点是两人相遇的点,所以是相遇了两次,正确.应选D.9.±2.【解析】试题分析:;(±2)2=4,・・・4的平方根是±2.故答案为±2.考点:平方根.10.(3,4)【解析】【分析】此题比拟容易,考查平而直角坐标系中两个关于坐标轴成轴对称的点的坐标特点:关于y轴对称的点,纵坐标相同,横坐标互为相反数.【详解】解:首先可知点P(-3,4),再由平面直角坐标系中关于y轴对称的点的坐标特点:横坐标互为相反数,纵坐标不变,可得:点P关于y轴的对称点的坐标是(3,4).故答案为:〔3,4〕.【点睛】解决此题的关键是掌握好对称点的坐标规律:〔1〕关于x轴对称的点,横坐标相同,纵坐标互为相反数:〔2〕关于y轴对称的点,纵坐标相同,横坐标互为相反数:〔3〕关于原点对称的点,横坐标与纵坐标都互为相反数.11.2【解析】【分析】根据无理数的概念判断即可.【详解】解:框=4, 0.3,斤,是有理数,",一色是无理数, 2故答案为:2.【点睛】此题考查的是无理数的概念,掌握无限不循环小数叫做无理数是解题的关键.12.3【解析】【分析】根据点〔皿,〃计1〕在函数〕,=-Lx+2的图象上,可以求得/〃的值,此题得以解决. 2【详解】解:•.•点〔m,m + l〕在函数y = —;x + 2的图象上,/. m +1 = — m + 2,22 解得,m = 7, 32故答案为:—.【点睛】此题考查一次函数图象上点的坐标特征,解答此题的关键是明确题意,利用一次函数的性质解答.13.【解析】【分析】根据平面直角坐标系的性质判断即可.【详解】解:以下关于建立平面直角坐标系的熟悉,合理的有①尽量使更多的点在坐标轴上:②尽量使图形关于坐标轴对称:③建立坐标系沟通了“数〞与“形〞之间的联系, 故答案为: 【点睛】此题考查了关于X轴、y轴对称的点的坐标,以及轴对称图形,熟练掌握平面直角坐标系的性质是解此题的关键.14.180【分析】根据等边三角形的性质,得出各角相等各边相等,AO=C£利用SAS判定△ADCQXCEB,从而得出NACD=NC8E,所以N3CO+NCBE=NBCO+NACO=NAC8 =60°,进而利用四边形内角和解答即可.【详解】解:•.♦△ABC是等边三角形・./A = NACB = 60,AC = BC vAD = CE/.△ADC^A CEB(SAS).•2ACD = /CBE/BCD + NCBE = 4CD + NACD = ZACB = 60 ./. 4OC = ]20 ,NDOE = 120, /. NADC + —BEA = 360 - 60 -120 =180,故答案为180.【点睛】此题考查了等边三角形的性质及全等三角形的判定方法,常用的判定方法有SSS,SAS,AAS, HL等.15.V13【分析】作小_LA8于£,根据勾股定理求出CD的长,根据角平分线的性质解答即可.【详解】作£>E_LAB 于E,••• ZC = 90°. AC = 6, AD = 7,CD=4A D1-AC1=A/13-AO平分NC48, ZC = 90° »DE±AB>DE = DC = y/i3.故答案为JT?.【点睛】此题考查的是勾股定理,角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.【分析】根据等腰三角形的性质分别利用AB, AC为底以及为腰得出符合题意的图形即可.【详解】解:如下图:B,当BJ=AC1, AC = CC2, AB = BC3, AC4 = CC4 , AB = AC〞 AB = AC6,BG=CX:7时,都能得到符合题意的等腰三角形.故答案为7.【点睛】此题主要考查了等腰三角形的判定以及应用设计与作图等知识,正确利用图形分类讨论得出是解题关键.17.±5.【分析】估算确定出“与人的值,代入原式计算即可求出平方根.【详解】解:•.•16 <19 <25,4 < <5 ».-.1< V19-3<2..二a = 1,v25<26<36./. 5 < >/26 < 6,・・・3<回-2<4,/. b = >/26-5 ,.二(-a)3 + (b + 5尸=-1 + 26 = 25 ,那么25的平方根是±5.【点睛】此题考查了估算无理数的大小,以及平方根,熟练掌握估算的方法是解此题的关键.18.〔1〕 240 390;〔2〕 PM所表示的函数关系式为:yi=150-60x, MN所表示的函数关系式为:y,=60x-150;〔3〕1.5h4x<3.5h,小汽车离车站C的路程不超过60千米.【解析】【分析】〔1〕根据图象中的数据即可得到A, B两地的距离;〔2〕根据函数图象中的数据即可得到两小时后,货车离.站的路程丁2与行驶时间x之间的函数关系式:〔3〕根据题意可以分相遇前和相遇后两种情况进行解答.【详解】解:〔1〕由题意和图象可得,a = = 240 千米,2.5A, B两地相距:150+240 = 390千米,故答案为:240, 390〔2〕由图象可得,A与C之间的距离为150km汽车的速度—=60km / h ,2.5PM所表示的函数关系式为:y,=150-60xMN所表示的函数关系式为:y2=60x-150⑶由力=60得150—60x=60,解得:x = 1.5由丫2=6.得60x-150 = 60,解得:x=3.5由图象可知当行装时间满足:1.5h<x<3.5h,小汽车离车站C的路程不超过60千米【点睛】此题考查一次函数的应用,解答此题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想和函数的思想解答.19.x=±2.【解析】【分析】直接利用平方根的性质计算得出答案.【详解】解:•.•3x2=12,x2 =4»x = ±2 •【点睛】此题主要考查了平方根,正确把握平方根的定义是解题关键.20.8-72 •【解析】【分析】直接利用零指数器,负指数箱的性质以及绝对值、立方根的性质分别化简得出答案.【详解】解:原式=3 + 1-〔应-1〕 + 3= 3 + 1-72 + 1 + 3=8-应.【点睛】此题主要考查了实数运算,正确化简各数是解题关键.21.见解析【解析】【分析】由中线性质得AE = CE = ;AC, AO = BO =〕AB,再证AE = A£>,由〔SAS〕, 得可证3E = CQ.【详解】证实:・・・8石、CQ是中线,A AE = CE = -AC, AD = BD = -AB 92 2*/ AB = AC ,:.AE = AD^在“MC和aEAB中,AD = AE< ZA = N A , AC = AB/. ^DAC^^EAB(SAS),.*. BE = CD.【点睛】此题考核知识点:全等三角形.解题关键点:灵活运用全等三角形判定和性质证线段相等.22.见解析.【分析】欲证实A8=AC,只要证实NA8C=NAC8即可:【详解】证实:AB,DF1AC./. /BED = NCFD = 90 .在RbBDE 和RtaCDF 中,BE-CF BD = CD{/.RtABDE^RtACDF(HL),/. 4BD = /CD,*r BD = CD ./. ^DBC = ^DCB ,/. ^DBC+/BD = ZDCB + 々CD,即/ABC = NACB,/. AB = AC.欲证实AB = AC,只要证实/ABC = /ACB即可:【点睛】此题考查全等三角形的判定和性质,等腰三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.23.(1)①见解析,②,③见解析;(2) x>0; (3) x>-l 【解析】【分析】(1)根据函数值填表即可:(2)根据图象得出函数性质即可:(3)根据图象得出不等式的解集即可.【详解】解:(1)①填表正确②③画函数图象如下图:(2)由图象可得:x>0时,y随x的增大而增大;(3)由图象可得:不等式|x|<x + 2的解集为x>—1:故答案为:2: 0; >0; x>-l.(1)根据函数值填表即可:(2)根据图象得出函数性质即可;(3)根据图象得出不等式的解集即可.【点睛】此题考查了一次函与不等式的关系,一次函数的图象等知识点.注意:求正比例函数,只要一对X,〕,的值就可以,由于它只有一个待定系数:而求一次函数〕,=依+〃,那么需要两组X, y的值.24.〔1〕y = -x + 40;〔2〕此时每天利润为125元.【解析】试题分析:〔1〕根据题意用待定系数法即可得解:〔2〕把工二35代入〔1〕中的解析式,得到销量,然后再乘以每件的利润即可得.试题解析:〔1〕设了 =丘+0,将x = 15, y = 25和x = 20,y = 20代入,得:〔25 = \5k+b仅=-1 ,,解得:,20 = 20k+b〃 = 40:.y = -x + 40:〔2〕将x = 35代入〔1〕中函数表达式得:>* = -35 + 40 = 5,••・利润= (35 — 10)x5 = 125 (元), 答:此时每天利润为125元.25. (1)①(一4,0)(0,1),②C(—5,4); (2) D(0,2), P(8,2)或D【分析】〔1〕利用坐标轴上点的特点建立方程求解,即可得出结论:〔2〕先构造出△AECgABQA,求出AE, CE,即可得出结论:〔3〕同〔2〕的方法构造出△AF.g/XOGP 〔A4S〕,分两种情况,建立方程求解即可得出结论.【详解】解:〔1〕针对于一次函数y = [x + l,令x = 0,・・・B(O,1),令y = 0,—x +1 = 0 ,4x ——4,A(-4,0),故答案为(Y,l), (0/):(2)如图1由(1)知,A(-4,0), B(0,l),,,.OA = 4, OB = 1,过点C作CE_Lx轴于E,NAEC = 4OA=90,NCAE + NACE = 90,/BAC = 90 ,.•./CAE + NBAO = 90 ,/. /CAE = /ABO,•.•△ABC是等腰直角三角形,AC = AB,ZAEC = ZBOA = 90 在ZiAEC 和aBOA 中,,ZCAE = ZABO ,AC = BA.-.△AEC^A BOA(AAS),.,.CE = OA = 4, AE = OB = 1 >/.OE = OA+AE = 5,・•・C(-5,4):(3)如图2, •.•过点D作DF_Ly轴于F,延长FD交BP于G,,点D在直线y = -2x + 2上,,设点D(m,_2m+2),/. F(0,-2m + 2),・.・BP_Lx轴,B(8,0),/.G(8,-2m+2),同(2)的方法得,△AFDg^DGP(AAS),.-.AF=DG, DF=PG,如图2, DF=m,•.•DF+DG = DF+AF=8,.\m+|2m-8| = 8,/. m*或m = 0.3当m = 0时,G(8,2), DF=O,/.PG = O,.•.P(8,2),当m ="时,G 8,一当|, DF = —, 3 V 3 ) 3/. PG=竺,即:D(0,2), P(8,2)或D件(1)利用坐标轴上点的特点建立方程求解,即可得出结论;(2)先构造出^AEC乌aBOA,求出AE, CE,即可得出结论:⑶同(2)的方法构造出△AFD GA DGP(AAS),分两种情况,建立方程求解即可得出结论.【点睛】此题是一次函数综合题,主要考查了全等三角形的判定和性质,方程的思想,构造全等三角形是解此题的关键.。
常州市2020~2021学年度教育学会学业水平监测八年级物理试卷2021年1月常州市教育学会中学物理专业委员会______市(区)学校______ 班级_______ 姓名________ 学号_______一、单项选择题(每小题2分,共30分)1. 在使用小提琴前,乐师常旋动琴弦轴以调节琴弦的松紧,俗称“定弦”,这主要是为了改变声音的()A. 振幅B. 响度C. 音调D. 音色2. 有一种电子牙刷,工作时能发出超声波,超声波能抵达普通牙刷刷不到的地方,使得刷牙既干净又舒服。
该牙刷工作时,使用者听不见超声波,原因是()A. 超声波不能传递能量B. 超声波的音量太低,所以人耳听不到C. 超声波的频率太低,所以人耳听不到D. 超声波的频率太高,所以人耳听不到3. 下列声音中,属于噪声是()①音乐厅里演奏“命运”交响曲②图书馆阅览室响起的手机铃声③小明上课回答问题的说话声④邻居装修房屋的电锯声A. ①②B. ①③C. ②④D. ③④4. 如图所示,舞台上经常用喷撒干冰(固态二氧化碳)的方法制造“白雾”以渲染气氛.对白雾的形成,小明的解释是:(1)干冰升华吸热使周围环境温度降低;(2)气态二氧化碳液化形成白雾.以上解释( )A. 仅第一句话存在科学性错误B. 仅第二句话存在科学性错误C. 两句话都存在科学性错误D. 两句话都没有科学性错误5. 下列自然现象中,由凝固而形成的是()A. 屋檐下挂着的冰凌B. 草叶上裹着的白霜C. 荷叶上滚动着的露珠D. 枝头上覆盖着的白雪6. 100℃的水蒸气比等量的100℃的沸水对人体造成的烫伤更严重,这是因为()A. 水蒸气是气体,更容易钻进人的皮肤B. 水蒸气的温度比沸水的温度高C. 水蒸气液化时要放出大量的热D. 水蒸气液化时要吸收大量的热7. 在严寒的雪域边疆,边防战士生活非常艰苦,为解决饮水问题,经常从野外取雪加热烧成开水。
图中能正确、完整描述“把雪加热烧成开水”过程的图象是()A.B.C.D.8. 如图所示,这是晚上汽车在干燥的沥青路面和潮湿的沥青路面上行驶时的大灯部分光路简图,在晚上开车时()A. 干燥的路面发生镜面反射B. 潮湿的路面更容易发生漫反射C. 对面无车时,驾驶员看潮湿的路面暗于看干燥的路面D. 照射到干燥路面的光不遵循光的反射定律9. 如图所示为潜水艇的潜望镜结构图。