PID算法Matlab仿真程序和C程序

这篇文章是关于基于Matlab的PID控制仿真课程设计的，主要内容包括PID控制的基本原理、Matlab的应用、课程设计的目的和意义、课程设计的具体步骤和具体操作步骤。

文章采用客观正式的语气，结构合理，旨在解释基于Matlab的PID控制仿真课程设计的重要性和实施方法。

1. 简介PID控制是一种常见的控制算法，由比例项（P）、积分项（I）和微分项（D）组成，可以根据被控对象的实际输出与期望输出的偏差来调整控制器的输出，从而实现对被控对象的精确控制。

Matlab是一种强大的数学建模与仿真软件，广泛应用于工程领域，尤其在控制系统设计和仿真方面具有独特优势。

2. PID控制的基本原理PID控制算法根据被控对象的实际输出与期望输出的偏差来调整控制器的输出。

具体来说，比例项根据偏差的大小直接调整输出，积分项根据偏差的积累情况调整输出，微分项根据偏差的变化速度调整输出。

三者综合起来，可以实现对被控对象的精确控制。

3. Matlab在PID控制中的应用Matlab提供了丰富的工具箱，其中包括控制系统工具箱，可以方便地进行PID控制算法的设计、仿真和调试。

利用Matlab，可以快速建立被控对象的数学模型，设计PID控制器，并进行系统的仿真和性能分析，为工程实践提供重要支持。

4. 课程设计的目的和意义基于Matlab的PID控制仿真课程设计，旨在帮助学生深入理解PID控制算法的原理和实现方法，掌握Matlab在控制系统设计中的应用技能，提高学生的工程实践能力和创新思维。

5. 课程设计的具体步骤（1）理论学习：学生首先需要学习PID控制算法的基本原理和Matlab在控制系统设计中的应用知识，包括控制系统的建模、PID控制器的设计原理、Matlab的控制系统工具箱的基本使用方法等。

（2）案例分析：学生根据教师提供的PID控制实例，在Matlab环境下进行仿真分析，了解PID控制算法的具体应用场景和性能指标。

（3）课程设计任务：学生根据所学知识，选择一个具体的控制对象，如温度控制系统、水位控制系统等，利用Matlab建立其数学模型，设计PID控制器，并进行系统的仿真和性能分析。

计算机控制技术实验指导书（MATLAB版）机电学院杨蜀秦编2012-11-19实验一 连续系统的模拟PID 仿真一、基本的PID 控制 在模拟控制系统中，控制器最常用的控制规律是PID 控制。

模拟PID 控制系统原理框图如图1-1所示。

图1-1 模拟PID 控制系统原理框图PID 控制规律为：⎪⎪⎭⎫⎝⎛++=⎰dt t de T dt t e T t e k t u DtI p )()(1)()(0或写成传递函数的形式⎪⎪⎭⎫ ⎝⎛++==s T s T k s E s U s G D I p 11)()()( Ex1 以二阶线性传递函数ss 251332+为被控对象，进行模拟PID 控制。

输入信号)2.0*2sin()(t t r π=，仿真时取3,1,60===d i p k k k ，采用ODE45迭代方法，仿真时间10s 。

仿真方法一：在Simulink 下进行仿真，PID 控制由Simulink Extras 节点中的PID Controller 提供。

仿真程序：ex1_1.mdl ，如图1-2所示。

图1-2 连续系统PID 的Simulink 仿真程序连续系统的模拟PID 控制正弦响应结果如图1-3所示。

图1-3 连续系统的模拟PID 控制正弦响应仿真方法二：在仿真一的基础上，将仿真结果输出到工作空间中，并利用m 文件作图。

仿真程序：ex1_2.mdl ，程序中同时采用了传递函数的另一种表达方式，即状态方程的形式，其中[]0,01,1330,25010==⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-=D C B A ，如图1-4所示。

m 文件作图程序：ex1_2plot.mclose all ;plot(t,rin,'k',t,yout,'k'); xlabel('time(s)'); ylabel('r,y');二、线性时变系统的PID 控制 Ex2 设被控对象为Jss Ks G +=2)(，其中)2sin(300400),6sin(1020t K t J ππ+=+=，输入信号为)2sin(5.0t π。

题目：以PID控制进行系统仿真学院自动化学院专业班级工业自动化111班学生姓名黄熙晴目录1 引言 (1)1.1本论文研究内容 (1)2 PID控制算法 (1)2.1模拟PID控制算法 (1)2.2数字式PID控制算法 (3)2.3PID控制算法的改进 (5)2.3.1微分项的改进 (5)2.3.2积分项的改进 (9)2.4模糊PID控制算法 (11)2.4.1模糊推理的系统结构 (12)2.4.2 PID参数在线整定原则 (12)2.5PID控制器研究面临的主要问题 .................................. 错误！未定义书签。

3 MATLAB编程和仿真 (13)3.1PID控制算法分析 (13)3.2MATLAB仿真 (15)4结语 (20)参考文献...................................................................................... 错误！未定义书签。

1 引言PID控制器以其结构简单、稳定性好、工作可靠、调整方便而成为工业控制的主要技术之一。

光学表面等离子共振生物传感技术受温度影响很大，因此设计高精度的温度控制器对于生物分析仪十分重要。

研究PID的控制算法是PID控制器整定参数优化和设定的关键技术之一。

在工业过程控制中，目前采用最多的控制方式依然是PID方式。

它具有容易实现、控制效果好、鲁棒性强等特点，同时它原理简单，参数物理意义明确，理论分析体系完整，并为工程界所熟悉，因而在工业过程控制中得到了广泛应用。

在实际的应用中，许多被控过程机理复杂，具有高度非线性、时变不确定性和纯滞后等特点，特别是在噪声、负载扰动等因素的影响下，参数复杂烦琐的整定过程一直困扰着工程技术人员。

为了减少参数整定的工作量，克服因环境变化或扰动作用造成系统性能的降低，就要提出一种PID控制参数的自动整定。

1.2本论文研究内容本文在介绍传统的PID控制算法，并对传统算法改进后，在学习的基础上提出一种模糊参数自整定方法，这种模糊控制的PID算法必须精确地确定对象模型。

Matlab控制系统工具箱的PID控制设计指南导言控制系统工具箱是Matlab提供的一个用于分析和设计控制系统的工具包。

其中，PID控制是最常用且广泛应用的一种控制算法。

本文将介绍Matlab控制系统工具箱中PID控制的设计指南，帮助读者快速掌握PID控制的原理和实践技巧。

一、PID控制简介PID控制是一种基于比例、积分和微分的控制方法，适用于各种不确定性和变化的系统。

PID控制器通过实时测量系统的误差（e），并计算比例项（P）、积分项（I）和微分项（D）的乘积和，调整输出控制信号（u），进而实现对系统的稳定控制。

二、PID控制的数学模型PID控制器可以用以下的数学模型表示：u(t) = Kp * e(t) + Ki * ∫e(t)dt + Kd * △e(t)/dt其中，u(t)表示控制器的输出，e(t)表示误差，Kp、Ki和Kd分别代表比例、积分和微分控制器的增益参数。

PID控制的目标是调整这些参数以使误差最小化。

三、PID控制器的参数调节PID控制器的性能和稳定性取决于增益参数的设置。

Matlab控制系统工具箱提供了多种方法来自动或手动地调节这些参数。

1. 自动调参方法Matlab提供了一些自动调参的函数，如pidtune和pidtool。

这些函数可以根据系统的频率响应和稳定性指标，自动选择合适的PID参数。

使用这些方法可以节省调试时间，但需要注意调参结果的合理性和系统实际需求的匹配性。

2. 手动调参方法手动调参是一种通过试验和调整来寻找最佳PID参数的方法。

Matlab中可以使用step函数或PID Controller Tuner App来进行手动调参。

这种方法需要对系统的特性和动态响应有一定的了解，并经过多次试验和优化来寻找最佳参数。

四、PID控制器的性能分析在设计PID控制器时，除了调节参数之外，还需要进行性能分析来评估控制质量和稳定性。

Matlab控制系统工具箱提供了一些常用的性能指标和分析工具。

控制系统PID参数整定方法的MATLAB仿真1. 引言PID控制器是一种常见的控制算法，广泛应用于自动控制系统中。

其通过调节三个参数：比例增益（Proportional gain）、积分时间常数（Integral time constant）和微分时间常数（Derivative time constant），实现对被控对象的稳态误差、响应速度和稳定性等性能指标的调节。

PID参数的合理选择对控制系统的性能至关重要。

本文将介绍PID控制器的经典整定方法，并通过MATLAB软件进行仿真，验证整定方法的有效性。

2. PID控制器的整定方法2.1 手动整定法手动整定法是根据经验和试错法来选择PID参数的方法。

具体步骤如下：1.将积分时间常数和微分时间常数设为零，仅保留比例增益，将比例增益逐渐增大直至系统产生较大的超调现象。

2.根据超调响应的情况，调整比例增益，以使系统的超调量接近所需的范围。

3.逐步增加微分时间常数，观察系统的响应速度和稳定性。

4.增加积分时间常数，以减小系统的稳态误差。

手动整定法的优点是简单易行，但需要经验和反复试验，对控制系统要求较高。

2.2 Ziegler-Nichols整定法Ziegler-Nichols整定法是一种基于试探和试错法的自整定方法，该方法通过调整系统的输入信号，观察系统的输出响应，从而确定PID参数。

具体步骤如下：1.将I和D参数设为零，仅保留P参数。

2.逐步增大P参数，直到系统的输出出现大幅度的振荡。

3.记录下此时的P参数值，记为Ku。

4.根据振荡的周期Tp，计算出系统的临界增益Kc = 0.6 * Ku。

5.根据系统的类型选择相应的整定法则：–P型系统：Kp = 0.5 * Kc，Ti = ∞，Td = 0–PI型系统：Kp = 0.45 * Kc，Ti = Tp / 1.2，Td = 0–PID型系统：Kp = 0.6 * Kc，Ti = Tp / 2，Td = Tp / 82.3 Cohen-Coon整定法Cohen-Coon整定法是基于频域曲线拟合的方法，主要应用于一阶和二阶系统的整定。

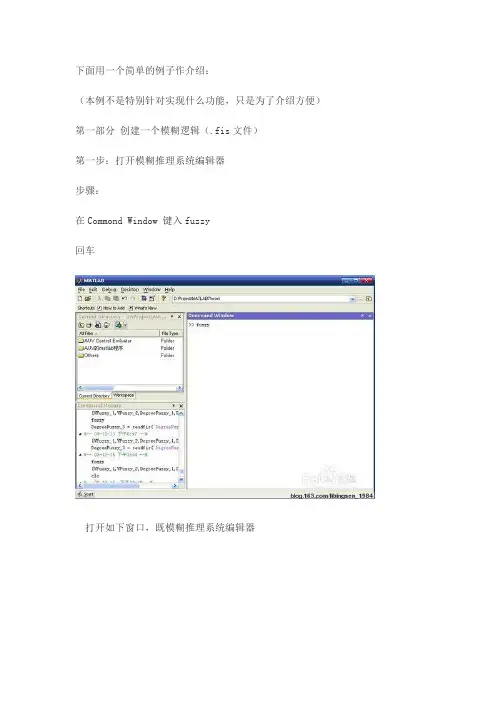
下面用一个简单的例子作介绍：（本例不是特别针对实现什么功能，只是为了介绍方便）第一部分创建一个模糊逻辑（.fis文件）第一步：打开模糊推理系统编辑器步骤：在Commond Window 键入fuzzy回车打开如下窗口，既模糊推理系统编辑器第二步：使用模糊推理系统编辑器本例用到两个输入，两个输出，但默认是一个输人，一个输出步骤：1、添加一个输入添加一个输出得如下图2、选择Input、output(选中为红框)，在Name框里修改各输入的名称并将And method 改为prod，将Or method 改为 probor提示：在命名时’_’在显示时为下标，可从上图看出。

第三步：使用隶属函数编辑器该编辑器提供一个友好的人机图形交互环境，用来设计和修改模糊推理系中各语言变量对应的隶属度函数的相关参数，如隶属度函数的形状、范围、论域大小等，系统提供的隶属度函数有三角、梯形、高斯形、钟形等，也可用户自行定义。

步骤：1、双击任何一个输入量（In_x、In_y）或输出量打开隶属度函数编辑器。

2、在左下处Range和Display Range处添加取值范围，本例中In_x和In_y的取值范围均为[0 10], Out_x和Out_y的取值范围均为[0 1]3、默认每个输入输出参数中都只有3个隶属度函数，本例中每个输入输出参数都需要用到五个，其余几个需要自己添加：选中其中一个输入输出参数点击Edit菜单，选Add MFS…打开下列对话框将MF type设置为trimf(三角形隶属度函数曲线，当然你也需要选择其他类型) 将Number of MFs 设置为2点击OK按钮同样给其他三个加入隶属度函数4、选中任何一个隶属度函数（选中为红色），在Name 中键入名称，在Type中选择形状，在Params中键入范围，然后回车如下图：5、关闭隶属函数编辑器第四步：使用规则编辑器通过隶规则编辑器来设计和修改“IF...THEN”形式的模糊控制规则。

matlab自整定pid算法
MATLAB中有多种方法可以自整定PID算法，以下是其中两
种常见的方法：
1. Ziegler-Nichols方法：
- 首先，将PID控制器的P和I增益设置为零，将D增益设置
为一个较小的非零值。

- 增加P增益，直到系统出现持续的高频振荡。

记录下此时的
P增益，记为Ku。

- 根据振荡的周期T，计算出临界增益Kc：Kc = 0.6 * Ku。

- 将PID控制器的增益重新设置为零，根据以下公式计算PID
控制器的增益：Kp = 0.6 * Kc，Ki = 1.2 / (T * Kc)，Kd = 0.075 / (T * Kc)。

- 将这些增益值设置到PID控制器中，进行实际的控制。

2. AMIGO方法：
- 首先，收集系统的开环响应数据，包括输入信号和输出信号。

- 使用AMIGO工具箱读取数据并进行预处理。

- 选择合适的模型结构，例如一阶传递函数、二阶传递函数等。

- 使用AMIGO工具箱中的模型校准方法，例如最小二乘法或
极大似然法，将模型参数校准到实际数据中。

- 根据得到的模型参数，计算PID控制器的增益值。

- 将这些增益值设置到PID控制器中，进行实际的控制。

根据具体的系统和要求，可以选择适合的自整定方法，并使用MATLAB进行实现。

PID算法matlab程序：clc;clear;close alltic%打开计算CPU时间的计时器desired=1;%期望值feed1=1;%可用阻尼系数B代替，feed2=1;%可以用弹簧系数K代替，B=feed1;K=feed2;Kp=2;%比例项KpKi=0.01;%积分项KiKd=0.01;%微分项Kddt=0.01;%采样时间Time=10;%总共仿真时间(s)n=round(Time/dt);%采样数量%预分配所有数据以优化仿真时间Prop(1:n+1)=0;Der(1:n+1)=0;Int(1:n+1)=0;I(1:n+1)=0;PID(1:n+1)=0;FeedBack(1:n+1)=0;Output(1:n+1)=0;Error(1:n+1)=0;state1(1:n+1)=0;STATE1(1:n+1)=0;state2(1:n+1)=0;STATE2(1:n+1)=0;for i=1:nError(i+1)=desired-FeedBack(i);%输入PID控制器的误差Prop(i+1)=Error(i+1);%比例项误差Der(i+1)=(Error(i+1)-Error(i))/dt;%微分项误差Int(i+1)=(Error(i+1)+Error(i))*dt/2;%积分项误差I(i+1)=sum(Int);%积分误差的总和PID(i+1)=Kp*Prop(i)+Ki*I(i+1)+Kd*Der(i);%%%可以使用你自己的系统替换以下五行STATE1(i+1)=sum(PID);%使用PID计算积分state2(i+1)=(STATE1(i+1)+STATE1(i))*dt/2;%经过第一个积分器后的输出STATE2(i+1)=sum(state2);%对第一个积分器的结果求和以求第二个积分器的结果Output(i+1)=(STATE2(i+1)+STATE2(i))*dt/2;%第二个积分器的输出结果FeedBack(i+1)=state2(i+1)*feed1+Output(i+1)*feed2;end01234567891000.20.40.60.811.21.4Time (sec)simulink 仿真：tsim =toc %仿真时间T =0:dt:Time;%原系统的阶跃响应num =[1];den =[111];c =step(num,den,T);%画图结果Reference =desired*ones(1,i+1);plot(T,Reference,'r',T,c,'g',T,Output,'b')xlabel('Time (sec)')legend('Desired','Original','PID-Control')仿真结果：有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）仿真结果：。

pid控制器matlab仿真PID控制是最早发展的自动控制策略之一，PID控制系统由比例单元（P）、积分单元（I）和微分单元（D）组成。

具有简单易懂，使用中不需精确的系统模型等先决条件，因而成为应用最为广泛的控制器。

PID控制的参数自动调整是通过智能化调整或自校正、自适应算法来实现。

当被控对象的结构和参数不能完全掌握，或得不到精确的数学模型时，控制理论的其它技术难以采用时，系统控制器的结构和参数必须依靠经验和现场调试来确定，这时应用PID控制技术最为方便。

即当我们不完全了解一个系统和被控对象，或不能通过有效的测量手段来获得系统参数时，最适合用PID控制技术。

PID控制，实际中也有PI和PD控制。

PID控制器就是根据系统的误差，利用比例、积分、微分计算出控制量进行控制的。

本文首先从PID理论出发，建立模型，讨论系统的稳定性，快速性，准确性。

利用MATLAB对PID控制的参数进行仿真，设计不同的参数，以使系统满足所要求的性能指标。

2、控制领域有一个很重要的概念是反馈，它通过各种输出值和它们各自所需值的实时比较的度量―各种误差，再以这些误差进行反馈控制来减少误差。

这样形成的因果链是输入、动态系统、输出、测量、比较、误差、输入构成的一个环路，因而也构成了包含原动态系统在内的一个新的动态闭环系统。

采用反馈的基本原因是要在不确定性存在的条件下达到性能目标。

许多情况下，对于系统的了解是不全面的，或者可用的模型是基于许多简化的假设而使它们变得不透彻。

系统也可能承受外界干扰，输出的观测常受噪声干扰。

有效的反馈能减少这些不确定性的影响，因为它们可以补偿任何原因引起的误差。

反馈概括了很广泛的概念，包括当前系统中的许多回路、非线性和自适应反馈，以及将来的智能反馈。

广义的讲，反馈可以作为描述和理解许多复杂物理系统中发生的循环交互作用的方式。

在实际的过程控制和运动控制系统中，PID占有相当的地位，据统计，工业控制中PID 类控制器占有90％以上。

模糊pid控制matlab程序
模糊PID控制是一种结合模糊控制和PID控制的方法，它可以
在控制系统中应对非线性和不确定性。

在MATLAB中，实现模糊PID
控制可以分为以下几个步骤：
1. 定义模糊系统，首先，需要使用MATLAB中的Fuzzy Logic Toolbox来定义模糊系统。

可以使用fuzzy函数来创建一个模糊系
统对象，并定义输入、输出和隶属函数等参数。

2. 设计模糊控制器，接下来，需要设计模糊控制器。

可以使用fisedit函数来打开模糊逻辑编辑器，通过编辑器来定义模糊控制
器的输入、输出和规则等。

3. 整合PID控制器，在MATLAB中，可以使用pid函数来创建
一个PID控制器对象。

然后，将模糊控制器和PID控制器整合在一起，可以通过串联、并联或级联的方式来实现模糊PID控制。

4. 闭环控制，最后，将设计好的模糊PID控制器应用于闭环控
制系统中。

可以使用sim函数来进行仿真，观察系统的响应和性能。

需要注意的是，模糊PID控制的设计涉及到模糊集合的定义、隶属函数的选择、规则的设置等，需要根据具体的控制对象和要求来进行调整和优化。

同时，对于PID控制器的参数调节也需要谨慎处理，可以使用MATLAB中的工具箱来进行参数整定和性能分析。

总的来说，实现模糊PID控制的MATLAB程序需要综合运用模糊逻辑工具箱和控制系统工具箱，通过适当的建模和调节来实现模糊PID控制器的设计和应用。

PID 控制算法的matlab 仿真PID 控制算法是实际工业控制中应用最为广泛的控制算法，它具有控制器设计简单，控制效果好等优点。

PID 控制器参数的设置是否合适对其控制效果具有很大的影响，在本课程设计中一具有较大惯性时间常数和纯滞后的一阶惯性环节作为被控对象的模型对PID 控制算法进行研究。

被控对象的传递函数如下：()1d sf Ke G s T sτ-=+ 其中各参数分别为30,630,60f d K T τ===。

MATLAB 仿真框图如图1所示。

图12 具体内容及实现功能2.1 PID 参数整定PID 控制器的控制参数对其控制效果起着决定性的作用，合理设置控制参数是取得较好的控制效果的先决条件。

常用的PID 参数整定方法有理论整定法和实验整定法两类，其中常用的实验整定法由扩充临界比例度法、试凑法等。

在此处选用扩充临界比例度法对PID 进行整定，其过程如下：1) 选择采样周期 由于被控对象中含有纯滞后，且其滞后时间常数为60d τ=，故可选择采样周期1s T =。

2) 令积分时间常数i T =∞，微分时间常数0d T =，从小到大调节比例系数K ，使得系统发生等幅震荡，记下此时的比例系数k K 和振荡周期k T 。

3) 选择控制度为 1.05Q =，按下面公式计算各参数：0.630.490.140.014p k i k d k s kK K T T T T T T ====通过仿真可得在1s T =时，0.567,233k k K T ==，故可得：0.357,114.17,32.62, 3.262p i d s K T T T ====0.0053.57p s i i p d d sK T K T K T K T ====按此组控制参数得到的系统阶跃响应曲线如图2所示。

010020030040050060070080090010000.20.40.60.811.21.41.61.8图2由响应曲线可知，此时系统虽然稳定，但是暂态性能较差，超调量过大，且响应曲线不平滑。