襄州区2017—2018学年度上学期期末学业质量调研测试八年级数学试题及答案

FDBCAE 八年级数学试题上学期期末考试一、选择题（每小题3分,共30分） 1．下列图形中轴对称图形是（ ）Ａ Ｂ Ｃ Ｄ２,.已知三角形的三边长分别是3，8，x ，若x 的值为偶数，则x 的值有( )A.6个B.5个C.4个D.3个３.一个多边形截去一个角后，形成的多边形的内角和是2520°，则原多边形的边数是( )A.15或16B.16或17C.15或17D.15.16或174.如图，△ACB ≌△A'CB'，∠BCB'＝30°，则∠ACA'的度数为( )A.20°B.30°C.35°D.40°５, 等腰三角形的两边长分别为5cm 和 10cm ，则此三角形的周长是（ ）A.15cmB. 20cmC. 25cmD.20cm 或25cm6.如图，已知∠CAB ＝∠DAB ，则添加下列一个条件不能使△ABC ≌△ABD 的是( ) A.AC ＝AD B.BC ＝BD C.∠C ＝∠D D.∠ABC ＝∠ABD7.如图，已知在△ABC 中，CD 是AB 边上的高，BE 平分∠ABC ，交CD 于点E ，BC ＝5，DE ＝2，则△BCE 的面积等于( )A.10B.7C.5D.4 8．若()22316m x x+-+是完全平方式,则m 的值等于( )A. 3B. -5C.7D. 7或-19．如图，在△ABC 中，AB =AC ，BE=CD ，BD =CF ，则∠EDF 的度数为 （ ） A ．1452A ︒-∠ B ．1902A ︒-∠ C ．90A ︒-∠ D ．180A ︒-∠第10题 10．如上图，等腰Rt △ABC 中，∠BAC ＝90°，AD ⊥BC 于点D ，∠ABC 的平分线分别交AC 、AD 于E 、F 两点，M 为EF 的中点，AM 的延长线交BC 于点N ，连接DM ，下列结论：① DF ＝DN ；② △DMN 为等腰三角形；③ DM 平分∠BMN ；④ AE ＝32EC ；⑤ AE ＝NC ，其中正确结论的个数是（ ）A ．2个B ．3个C ．4个D ．5个二、填空题（每小题3分,共24分）11．计算:()()312360.1250.2522⨯-⨯⨯- = 12,在实数范围内分解因式:3234a ab - = 13.若2,3,mn xx ==则2m nx+=14．若A （x ，3）关于y 轴的对称点是B （﹣2，y ），则x=__________，y=__________，点A 关于x 轴的对称点的坐标是__________．15,如图，△ABC 中，DE 是AC 的垂直平分线，AE ＝3 cm ，△ABD 的周长是13 cm ，则△ABC 的周长为 _________第15题图 第17题图16,已知等腰三角形一腰的垂直平分线与另一腰所在直线的夹角为40°，求此等腰三角形的顶角为17．如图，∠AOB ＝30°，点P 为∠AOB 内一点，OP ＝8．点M 、N 分别在OA 、OB 上，则△PMN 周长的最小值为__________18. 如图所示，在△ABC 中，∠A =80°，延长BC 到D ，∠ABC 与∠ACD 的平分线相交于A 1点，∠A 1BC 与∠A 1CD 的平分线相交于A 2点，依此类推，∠A 4BC 与∠A 4CD 的平分线相交于A 5点，则∠A 5的度数是 。

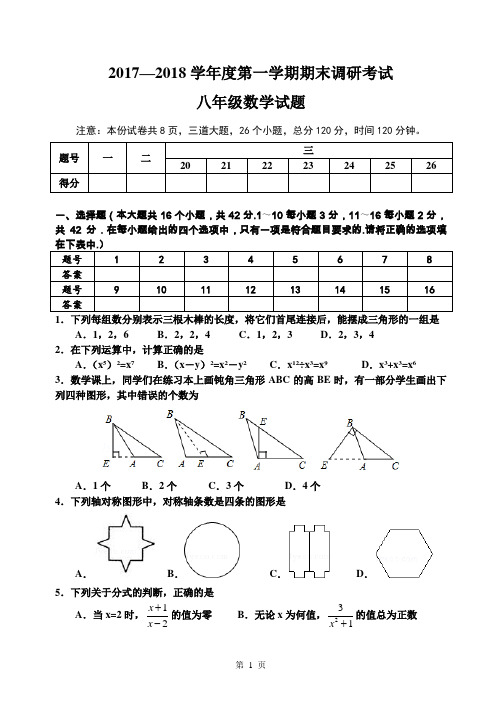
2017—2018学年度第一学期期末调研考试八年级数学试题注意：本份试卷共8页，三道大题，26个小题，总分120分，时间120分钟。

一、选择题（本大题共16个小题，共42分.1～10每小题3分，11～16每小题2分，共42分．在每小题给出的四个选项中，只有一项是符合题目要求的.请将正确的选项填在A．1，2，6 B．2，2，4 C．1，2，3 D．2，3，42．在下列运算中，计算正确的是A．（x5）2=x7B．（x－y）2=x2－y2C．x12÷x3=x9D．x3+x3=x63．数学课上，同学们在练习本上画钝角三角形ABC的高BE时，有一部分学生画出下列四种图形，其中错误的个数为A．1个B．2个C．3个D．4个4．下列轴对称图形中，对称轴条数是四条的图形是A．B．C．D．5．下列关于分式的判断，正确的是A．当x=2时，12xx+-的值为零B．无论x为何值，231x+的值总为正数C ．无论x 为何值，31x +不可能得整数值 D ．当x≠3时，3x x -有意义6．如图，已知AB=AC ，AD=AE ，若要得到“△ABD ≌△ACE”，必须添加一个条件，则下列所添条件不恰当的是A ．BD=CEB ．∠ABD=∠ACEC ．∠BAD=∠CAED ．∠BAC=∠DAE 7．若把分式2x yxy+中的x 和y 都扩大3倍，且x+y≠0，那么分式的值 A ．扩大3倍 B ．不变 C ．缩小3倍 D ．缩小6倍 8．若x=－2，y=12，则y （x+y ）+（x+y ）（x －y ）－x 2的值等于 A ．－2 B ．12C ．1D ．－19．如图，在△ABC 中，DE 是AC 的垂直平分线，AC=6cm ，且△ABD 的周长为13cm ，则△ABC 的周长为A ．13cmB ．19cmC ．10cmD ．16cm10.观察等式（2a ﹣1）a+2=1，其中a 的取值可能是A ．﹣2B ．1或﹣2C ．0或1D ．1或﹣2或0 11．下列计算中正确的是A ．22155b a a b ab -⨯=-- B ．32x y x y ya b a b a b+--=+++ C ．m m n m n n m n ÷⨯= D ．1224171649xy xy a xy a -⎛⎫⎛⎫÷=⎪ ⎪⎝⎭⎝⎭12．如图，C 在AB 的延长线上，CE ⊥AF 于E ，交FB 于D ，若∠F=40°，∠C=20°，则∠FBA 的度数为A ．50°B ．60°C ．70°D ．80°13．若y －x=－1，xy=2，则代数式－12x 3y+x 2y 2－12xy 3的值是 A ．2 B ．－2 C ．1 D ．－114．图1是一个长为 2a ，宽为2b （a ＞b ）的长方形，用剪刀沿图中虚线（对称轴）剪开，把它分成四块形状和大小都一样的小长方形，然后按图2那样拼成一个正方形，则中间空的部分的面积是A ．a 2－b 2B ．（a －b ）2C ．（a+b ）2D ．ab15．如图，△ABC的顶点坐标分别为A（4，4）、B（2，1）、C（5，2），沿某一直线作△ABC的对称图形，得到△A′B′C′，若点A的对应点A′的坐标是（3，5），那么点B的对应点B′的坐标是A．（0，3）B．（1，2）C．（0，2）D．（4，1）16．如图，点E是BC的中点，AB⊥BC，DC⊥BC，AE平分∠BAD，下列结论：①∠AED=90°②∠ADE=∠CDE ③DE=BE ④AD=AB+CD，四个结论中成立的是A．①②④B．①②③C．②③④D．①②二、填空题（本大题共3小题，共10分.17～18小题各3分；19小题有2个空，每空2分.把答案写在题中横线上）17．一个多边形的每一个外角都为36°，则这个多边形是边形．18．若x2+2（m－3）x+16是一个完全平方式，那么m应为．19．对于实数a、，b，定义运算⊗如下：a⊗b=()(),0,0bba ab aa ab a-⎧>≠⎪⎨≤≠⎪⎩，例如：2⊗4=2－4=116，计算[4⊗2] =，[2⊗2]×[3⊗2]=．三、解答题（本大题共7小题，共68分．解答应写出文字说明、证明过程或演算步骤）20．计算（本题满分8分）如图，在平面直角坐标中，△ABC各顶点都在小方格的顶点上．（1）画出△ABC关于x轴对称的图形△A1B1C1；（2）在y轴上找一点P，使PA+PB1最短，画出图形并写出P点的坐标．21．（本题满分9分）先化简，再求值：2214411a aa a a-+⎛⎫-÷⎪--⎝⎭，其中－2＜a≤2，请选择一个a的合适整数代入求值．22．（本题满分9分）两个大小不同的等腰直角三角形三角板如图①所示放置，图②是由它抽象出的几何图形，B，C，E在同一条直线上，连接DC，（1）请找出图②中的全等三角形，并给予证明（结论中不得含有未标识的字母）；（2）求证：DC⊥BE．23．（本题满分9分）先阅读以下材料，然后解答问题．将一个多项式分组后，可提公因式或运用公式继续分解的方法是因式分解中的分组分解法，一般的分组分解法有四种形式，即“2+2”分法、“3+1”分法、“3+2”分法及“3+3”分法等．如“2+2”分法：ax+ay+bx+by=（ax+ay）+（bx+by）=a（x+y）+b（x+y）=（x+y）（a+b）请你仿照以上方法，探索并解决下列问题：（1）分解因式：x2－y2－x－y；（2）分解因式：9m2－4x2+4xy－y2；24．（本题满分10分）如图，已知BD平分∠ABC，AB=AD，DE⊥AB，垂足为E．（1）求证：AD∥BC；（2）若DE=6cm，求点D到BC的距离；（3）当∠ABD=35°，∠DAC=2∠ABD时，①求∠BAC的度数；②证明：AC=AD．25．（本题满分11分)随着城际铁路的正式开通，从甲市经丙市到乙市的高铁里程比普快里程缩短了90km，运行时间减少了8h，已知甲市到乙市的普快列车里程为1220km．高铁平均时速是普快平均时速的2.5倍．（1）求高铁列车的平均时速；（2）某日王先生要从甲市去距离大约780km的丙市参加14：00召开的会议，如果他买到当日9：20从甲市到丙市的高铁票，而且从丙市火车站到会议地点最多需要1小时．试问在高铁列车准点到达的情况下，它能否在开会之前20分钟赶到会议地点？26．(本题满分12分)如图1，△ABC是边长为5cm的等边三角形，点P，Q分别从顶点A，B同时出发，沿线段AB，BC运动，且它们的是速度都为1厘米/秒．当点P到达点B时，P、Q两点停止运动．设点P的运动时间为t（秒）．（1）当运动时间为t秒时，BQ的长为厘米，BP的长为厘米；（用含t 的式子表示）（2）当t为何值时，△PBQ是直角三角形；（3）如图2，连接AQ、CP，相交于点M，则点P，Q在运动的过程中，∠CMQ会变化吗？若变化，则说明理由；若不变，请求出它的度数．参考答案及评分标准说明：1.在阅卷过程中，如果考生还有其它正确解法，可参照评分参考酌情给分；2.填空题缺少必有的单位或答案不完整不得分；3.坚持每题评阅到底的原则,当考生的解答在某一步出现错误,影响了后继部分时,如果该步以后的解答未改变这一题的内容和难度,可视影响的程度决定后面部分的给分,但不得超过后继部分应给分数的一半;如果这一步后面的解答有较严重的错误，就不给分；4.解答右端所注分数，表示正确做到这一步应得的累积分数.一、(本大题有16小题，共43分.1~10每小题各3分，11~16每小题各2分)二、(本大题有3个小题，共10分.17~18小题个3分；19小题有2个空，每空2分) 17．十；18．－1或7；19．16，．三、（本大题有7小题，共68分）20.解：（1）如图所示：△A1B1C1为所求作的三角形；……………………….……4分（2）如图，……………………………………………………………………..…..……7分点P的坐标为：（0，1）．………………………………………………………...………8分21．解：原式=……………………………………………………….2分=……………………………………………………………………………4分=，………………………………………………………………………………………6分当a=－1时，…………………………………………………………………….…………8分原式=．……………………………………………..……………………………9分22．（1）解：△BAE≌△CAD，证明如下：……………………………………………1分∵△ABC，△DAE是等腰直角三角形，∴AB=AC，AD=AE，∠BAC=∠DAE=90°．……………………………..……………2分∠BAE=∠DAC=90°+∠CAE，………………………………………………………...…4分在△BAE和△DAC中∴△BAE≌△CAD（SAS）．………………………………………………………………6分（2）证明：∵△ABC，△DAE是等腰直角三角形，∴∠B=45°，∠BCA=45°，……………………………………………………………..…7分∵△BAE≌△CAD．∴∠DCA=∠B=45°．………………………………………………………………………8分∴∠BCD=∠BCA+∠DCA=90°，∴DC⊥BE．…………………………………………………………………………………9分23．解：（1）原式=（x2－y2）－（x+y）…………………………………………………2分=（x+y）（x－y）－（x+y）…………………………….……………………………….…3分=（x+y）（x－y－1）；……………………………………………….………………………4分（2）原式=9m2－（4x2－4xy+y2）……………………………………………………….6分=（3m）2－（2x－y）2…………………………………………………………………….8分=（3m+2x－y）（3m－2x+y）. ……………………………………………………….……9分24．（1）证明：∵AB=AD，∴∠ADB=∠ABD…………………………………………………….………..……………1分又∵BD平分∠ABC，即∠ABD=∠DBC，∴∠ADB =∠DBC，…………………………………………………………..……………2分∴AD∥BC；…………………………………………………………………………………3分（2）解：作DF⊥BC交BC的延长线于F．∵BD平分∠ABC，DE⊥AB，DF⊥BC，∴DF=DE=6cm；即点D到BC的距离为6cm. ……………………………………………………..……5分（3）①解：∵BD平分∠ABC，∴∠ABC=2∠ABD=70°，…………………………………………………………..….…6分∵AD∥BC，∴∠ACB=∠DAC=70°，……………………………………………………………….…7分∴∠BAC=180°－∠ABC－∠ACB=180°－70°－70°=40°．……………………………8分②证明：∵∠ABC=70°，∠ACB=70°，∴∠ABC=∠ACB，∴AB=AC，…………………………………………………………………………………9分又∵AB=AD，∴AC=AD．………………………………………………………………………………..10分25．解：（1）设普快的平均时速为x千米/小时，高铁列车的平均时速为2.5x千米/小时，根据题意得，……………..……………………………………………………..…………1分－=8，…………………………………………..………………….……4分解得：x=96，……………..………………5分经检验，x=96是原分式方程的解，且符合题意，……………..………………………6分则2.5x=240，答：高铁列车的平均时速为240千米/小时；………………………………..…………7分（2）780÷240=3.25，则坐车共需要3.25+1=4.25（小时），……………………………………..…………..…9分从9：20到13：40，共计4小时，………………………………...…………………10分因为4小时＞4.25小时，所以王先生能在开会之前到达．………………………………………………..………11分26．解：（1）t；（5－t）；………………………..………………….…………..………2分（2）∵△ABC是等边三角形，∴∠B=60°．①当∠PQB=90°时，∵∠B=60°，∴∠BPQ=30°，∴PB=2BQ，得5－t=2t，解得，t=，………………………………………………………………………………4分②当∠BPQ=90°时，∵∠B=60°，∴∠BQP=30°，∴BQ=2BP，得t=2（5－t），解得，t=，………………………………………………………………...…………6分∴当t的值为或时，△PBQ为直角三角形；…………………………..………7分（3）∠CMQ不变，∠CMQ=60°理由如下：………………………………….……8分∵△ABC是等边三角形，∴AB=AC，∠B=∠BAC=60°，由题意可知：AP=BQ，在△ABQ与△CAP中，，∴△ABQ≌△CAP（SAS），…………………………………………………..………10分∴∠BAQ=∠ACP，∴∠CMQ=∠ACP+∠CAM=∠BAQ+∠CAM=∠BAC=60°，∴∠CMQ不会变化，总为60°．………………………..……………………………12分。

2017-2018学年度第一学期期末调研考试八年级数学试卷一、 选择题（本题共16小题，总分42分。

1~6小题，每题2分；7~16小题，每题3分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

请将正确选项的代号填1．计算32y y ⋅等于A ．5yB ．6yC ．8yD ． 9y 2. 不论x 取何值，下列分式总有意义的是A ．1+x xB ．22x x +C ．12+x xD ．x x 12+3．计算)2(42x y x -÷-的结果是A ．2B ．y x 32C ．y x 32-D ．xy 2 4．代数式c ab b a 323128+中各项的公因式是A ．238b a B ．24ab C ．abc 4 D ． c b a 3324 5．点P(-1,-3)关于x 轴对称的点Q 的坐标为A ．(1,-3)B ．(-1,3)C ．(1,3)D ．(-1,-3) 6．下列说法正确的是A ．三角形具有稳定性B ．四边形具有稳定性C ．五边形具有稳定性D ．以上都不对7．若三角形的三边长分别为1、x 、8，且x 为整数，则x 的值是A ．6B ．7C ．8D ．9 8.五边形的内角和是A ．︒180B ．︒360C ．︒540D ．︒7209. AD 是ABC ∆的中线，若用1S 表示ABD ∆的面积，用2S 表示ACD ∆的面积，则1S 与2S 的大小关系是A ．1S >2SB ．1S =2SC ．1S <2SD ．以上都有可能 10．在字母N M D C B A 、、、、、所示图形中，是轴对称图形的有A ．1个B ．2个C ．3个D ．4个11．ABC ∆中，若5:2:2C :B :A =∠∠∠,则ABC ∆的形状是A ．锐角三角形B ．直角三角形C ．等腰三角形D ．等边三角形 12．用直尺和圆规作一个角的平分线的示意图如图所示， 则能说明BOC AOC ∠=∠的依据是全等三角形的 对应角相等。

2017-2018学年八年级上学期期末检测数学试题（时间120分钟 满分120分）一、单选题（共12题：每小题3分，共36分） 1.下列图形中，是轴对称图形的是（ ）ABCD2.等腰三角形有一个角等于70°，则它的底角是（ ） A.70°B.55°C.60°D.70°或55°3.如图，点P 是∠BAC 的平分线AD 上一点，PE ⊥AC 于点E.已知PE=3，则点P 到AB的距离是（ ） A.3 B.4C.5D.64.如图，在△ABC 中，BO ，CO 分别平分∠ABC 和∠ACB ，则∠BOC 与∠A 的大小关系是（ ） A. ∠BOC=2∠AB. ∠BOC=90°+∠AC. ∠BOC=90°+12∠A D. ∠BOC=90°－12∠A 5.下列叙述中：①任意一个三角形的三条高至少有一条在此三角形内部；②以a ，b ，c 为边(a ，b ，c 都大于0，且a+b>c)可以构成一个三角形；③一个三角形内角之比为3:2:1，此三角形为直角三角形；④有两个角和一条边对应相等的两个三角形全等； 是真命题的有（ ）个 A.1B.2C.3D.46.如图，下列条件中，不能证明△ABC ≌△DCB 的是（ ） A.AB=DC ，AC=DBB.AB=DC ，∠ABC=∠DCBC.BO=CO ，∠A=∠DD.AB=DC ，∠ACB=∠DBC7.如图，在△ABC 中，AB=AC ，∠A=30°，以C 为圆心，CB 的长为半径作圆弧，交AB 于点D ，连接CD ，则∠ACD 等于（ ）A.30°B.45°C.60°D.75°8.若关于x 的分式方程223m x x x+=-无解，则m 的值为（ ） A.－1.5B.1C.－1.5或2D.－0.5或－1.59.如图，把一张矩形纸片ABCD 沿EF 折叠后，点A 落在CD 边上的点A ＇处，点B落在点B ＇处，若∠2=40°，则图中∠1的度数为 A.115° B.120° C.130°D.140°10.初三体育素质测试，某小组5名同学成绩如下所示，有两个数据遮盖，如图：那么被遮盖的两个数据依次是（ ） A.35 2B.36 4C.35 3D.36 311.如图，在Rt △ABC 中，∠C=90°，以顶点A 为圆心，适当长为半径画弧，分别交边AC 、AB 于点M 、N ，再分别以点M 、N 为圆心，大于12MN 的长为半径画弧，两弧交于点P ，作射线AP 交边BC 于点D ，若CD=4，AB=15，则△ABD 的面积是（ ） A.15B.30C.45D.6012.甲、乙二人做某种机械零件，已知甲每小时比乙多做6个，甲做90个所用的时间与乙做60个所用的时间相等.如果设甲每小时做x 个零件，那么下面所列方程中正确的是（ ） A.90606x x =- B.90606x x =+ C.90606x x =+ D.90606x x =- 二、填空题（共5小题：每小题3分，共15分）13.如图，C 、D 点在BE 上，∠1=∠2，BD=EC.请补充一个条件：__________，使△ABC≌△FED.14.若点P1（a+3，4）和P2（－2，b－1）关于x轴对称，则a=__________,b=__________.15.某大学自主招生考试只考数学和物理，计算综合得分时，按数学占60%，物理点40%计算.已知孔明数学得分为95分，综合得分为93分，那么孔明物理得分是__________分.16.为选拔一名选手参加全国中学生游泳锦标赛自由泳比赛，我市四名中学生参加了男生100米自由泳训练，他们成绩的平均数x及其方差S2如下表所示：如果选拨一名学生去参赛，应派__________去.17.如图，在平面直角坐标系中，△AA1C1是边长为1的等边三角形，点C1在y 轴的正半轴上，以AA1=2为边长画等边△AA2C2；以AA2=4为边长画等边△AA2C3，…，按此规律继续画等边三角形，则点nA的坐标为__________.三、解答题（共8题，共69分）18.（每小题4分，共8分）（1）11322xx x-=---（2）113262xx x-=--19.（7分）先化简，再求值：234441112a aa aa a a-+⎛⎫-+÷+-⎪++-⎝⎭，并从-1，0，2中选一个合适的数作为a的值代入求值.20.（6分）当a=2017，b=2018时，代数式4422222a b b aa ab b a b--⨯-++的值为.21.（8分）如图，△ABC、△CDE均为等腰直角三角形，∠ACB=∠DCE=90°，点E在AB上.求证：△CDA≌△CEB.22.（每小问4分，共8分）如图，在△ABC中，BC边的垂直平分线交AC边于点D，连接BD.（1）如图CE=4，△BDC的周长为18，求BD的长.（2）求∠ADM=60°，∠ABD=20°，求∠A的度数.23.（每小问4分，共8分）某汽车站站北广场将于2018年底投入使用，计划在广场内种植A、B两种花木共6600棵，若A花木数量是B花木数量的2倍少600棵。

2017-2018学年八年级上学期期末学业水平测试数学试卷一、选择题（本大题共8小题，共24分）1. 如图，小明书上的三角形被墨迹遮挡了一部分，但他很快想到办法在作业本上画了一样的三角形，那么这两个三角形完全一样的依据是()A. AASB. ASAC. SSSD. SAS2. 下列计算正确的是()A. a2+a3=a5B. a2⋅a3=a6C. a6÷a3=a3D. (a3)2=a93. 如图，等边三角形ABC，AB=3，点D，E，F分别是AB，BC，CA的中点，点P是线段DF上的一动点，连接BP，EP，则△BPE周长的最小值是()A. 3B. 3.5C. 4D. 4.54. 计算(1−a)(a+1)的结果正确的是()A. a2−1B. 1−a2C. a2−2a−1D. a2−2a+15. 下列各式①2mπ、②xy x+y、③2x−y3、④2a−ba中，是分式的有()A. ①②③B. ②④C. ③④D. ②③④6. 下列图案是轴对称图形的是()A. B. C. D.7. 如果把分式0.2xx+3y中的x和y都扩大为原来的10倍，那么分式的值()A. 扩大10倍B. 缩小10倍C. 是原来的100倍D. 不变8. 如图，七边形ABCDEFG中，AB，ED的延长线交于点O，若∠1，∠2，∠3，4的外角和等于210∘，则∠BOD的度数为()A. 30∘B. 35∘C. 40∘D. 45∘二、填空题（本大题共3小题，共9分）9. 要使分式x−2x+2有意义，则x的取值为______．10. 如图，由九个等边三角形组成的一个六边形ABCDEF，当图中最小的等边三角形的边长为1cm时，这个六边形ABCDEF的周长为______cm．11. 如图，三角形纸片ABC中，AB=AC，∠BAC=120∘，BC=16，折叠纸片，使点C和点A重合，折痕与AC，BC交于点D和点E，则折痕DE的长为______．三、计算题（本大题共1小题，共8.0分）12. 如图①，一个长为2a、宽为2b的长方形，沿图中的虚线用剪刀均匀的分成四个小长方形，然后按图②的形状拼成一个正方形．(1)观察图②，请用两种不同的方法求图②中阴影部分的面积．方法1：______(只列式，不化简)方法2：______(只列式，不化简)(2)请写出(a+b)2，(a−b)2，ab三个式子之间的等量关系：______．(3)根据(2)题中的等量关系，解决如下问题：若x+y=2，xy=3，求x−y的值．4四、解答题（本大题共5小题，共42分）13. 某校八年级1班参加校迎新年集市活动，购进A，B两种款式的贺年卡，购买A款卡片共用780元，购买B款卡片共用640元，A款卡片的数量是B款卡片数量的1.5倍，A款卡片每张的进价比B款卡片每张的进价少3元．(1)求A、B两种款式的贺年卡各购进了多少张？(2)如果按进价提高60%标价出售，经过一段时间后，A款卡片全部卖完，B款卡片还剩一半，同学们决定将剩下的B款卡片按标价的五折抛售，很快全部卖完.求本次活动中该班共获利多少？14. 如图，在△ABC中，AB=AC，BE⊥AC于点E，CD⊥AB于点D，BE、CD相交于点F，连接AF．求证：(1)△AEB≌△ADC；(2)AF平分∠BAC．)−115. 计算：(−1)2018−(5−1)0+(−2)2+(1316. 如图，已知点D是等边三角形ABC中BC边所在直线上的点，连接AD，过点D作∠ADF=60∘，DF与∠ACB的邻补角的平分线交于点F．(1)如图①，当点D在线段BC上时，过点D作DE//AC，且交AB于点E.求证：BD=BE；(2)如图①，在(1)的条件下，求证：BC=CD+CF；(3)如图②，当点D在线段BC的延长线上时，(2)中线段BC，CD，CF之间的数量关系式还成立吗？若成立，请加以证明；若不成立，请写出线段BC，CD，CF之间新的数量关系式，并说明理由．17. 如图，在平面直角坐标系中，△C的顶点分别为A(5,3)，B(1,−3)，C(3,−4)．(1)画出△ABC关于y轴对称的△A1B1C1；(2)写出△A1B1C1各顶点坐标；(3)求△ABC的面积．参考答案BCDBB CDA9. x≠−210. 30解：设EF=x，∴等边三角形的边长依次为x，x+x+1，x+1，x+2×1，x+2×1，x+3×1，∴六边形周长是2x+1+2(x+1)+2(x+2×1)+(x+3×1)=7x+9，∵DE=2EF，即x+3=2x，∴x=3cm，∴周长为7x+9=30cm．11.83解：∵AB=AC，∠BAC=120∘∴∠B=∠C=30∘∵折叠∴∠EAC=∠C=30∘，∠ADE=∠CDE=90∘，AE=EC∵∠BAE=∠BAC−∠EAC∴∠BAE=90∘，且∠B=30∘∴BE=2AE∵BC=EC+BE=16∴EC=16∵∠C=30∘，∠EDC=90∘∴CE=2DE∴DE=8 312. (a−b)2；(a+b)2−4ab；(a−b)2=(a+b)2−4ab解：(1)方法1：(a−b)2；方法2：(a+b)2−4ab；(2)(a−b)2=(a+b)2−4ab；故答案为：(1)(a−b)2，(a+b)2−4ab；(2)(a−b)2=(a+b)2−4ab；(3)根据题意得：(x−y)2=(x+y)2−4xy=4−3=1，则x−y=±1．13. 解：(1)设B款卡片购进x张，则A款卡片购进1.5x张，根据题意得：780 1.5x +3=640x，解得：x=40，经检验，x=40是方程的解且符合实际意义，1.5x=60，答：A款卡片购进60张，B款卡片购进40张，(2)B款卡片每张进价：64040=16元，A款卡片每张进价：16−3=13元，13×60%×60+16×60%×20−16×[1−(1+60%)×0.5]×20=468+192−64=596(元)，答：本次活动中该班共获利596元．14. 证明：(1)∵BE⊥AC，CD⊥AB，∴∠AEB=∠ADC=90∘，在△AEB与△ADC中∠AEB=∠ADC∠BAE=∠CADAB=AC，∴△AEB≌△ADC(AAS)，(2)∵△AEB≌△ADC，∴AE=AD，在Rt△AEF与Rt△ADF中，AF=AFAE=AD，∴Rt△AEF≌Rt△ADF(HL)，∴∠EAF=∠DAF，∴AF平分∠BAC．15. 解：原式=1−1+2+3=5．16. (1)证明：∵DE//AC，∴∠BDE=∠BCA=60∘，∠BED=∠BAC=60∘，∴∠BDE=∠BED=60∘，∴△BDE是等边三角形，∴BD=BE；(2)证明：∵BA=BC，BD=BE，∴EA=DC，∵∠BED=60∘，∴∠AED=120∘，∵CF是∠ACB的邻补角的平分线，∴∠ACF=60∘，∴∠DCF=120∘，∴∠AED =∠DCF ，∵∠ADF =60∘，∠BDE =60∘，∴∠ADE +∠FDC =60∘，∵∠ADE +∠DAE =∠BED =60∘，∴∠DAE =∠FDC ，在△AED 和△DCF 中，∠AED =∠DCF AE =DC ∠EAD =∠CDF，∴△AED≌△DCF ，∴DE =CF ，∴BC =CD +BD =CD +DE =CD +CF ；(3)解：(2)中线段BC ，CD ，CF 之间的数量关系式不成立， 理由如下：作DG //AC 交DF 于G ，则∠CGD =∠ACF =60∘，∠CDG =∠ACB =60∘， ∴△CDG 为等边三角形，∠ACD =∠FGD =120∘， ∴CG =CD =DG ，∵∠BDA +∠ADG =60∘，∠FDG +∠ADG =60∘， ∴∠BDA =∠FDG ，在△ACD 和△FGD 中，∠ACD =∠FGD DC =DG ∠ADC =∠FDG，∴△ACD≌△FGD ，∴AC =FG ，∴BC =FG ，∴CF =CG +GF =CD +BC ．17. 解：(1)如图所示：△A 1B 1C 1，即为所求；(2)△A 1B 1C 1各顶点坐标分别为：A 1(−5,3)，B 1(−3,−4)，C 1(−1,−3)；(3)S △ABC =7×4−12×4×6−12×7×2−12×2×1=8．。

2017—2018学年度第一学期期末教学质量检测八年级数学答案一、选择题：二、填空题：三、解答题：20.（1）解：原式=)1323(2333232++--÷-⨯ ………………………2分=324236---- ……………………………………………… 3分=323-- ……………………………………………………………4分（2）解：①如图所示；……………………………………………6分②100°. ………………………………………………………8分 21.解：（1）这个魔方的棱长为：4643=； ………………………2分 （2）每个小正方体的棱长为：4÷2=2…………………………3分阴影部分的边长为：2282222==+=CD ……4分阴影部分的面积为：8)22(22==CD ………………5分 （其它解法参照此标准给分）（3）根据图可知122-=a …………………………………6分a a a --+-2)1)(1(=（1122--）（1122+-）－1222+- =（22322)222--⨯-…………………………………………………7分=223248+--=225-…………………………………………………………………………8分 22.解：原式=[())1(11+-+x x x －()1)1(1+--x x x ]÷()()1122-+-x x x …………………………2分=()()1111-++-+x x x x ÷()()1122-+-x x x………………………………………………3分=()()()()2112112--+⨯-+x x x x x………………………………………………4分=24-x ……………………………………………………………………………5分 ()0322123221-+-=πx =22222421+⨯-⨯…………………………………………………………6分=2222+- …………………………………………………………………7分=22+ …………………………………………………………………………8分当22+=x 时，原式=22242224==-+. ………………………10分23.（1）解：∵BD 是等边△ABC 的中线，∴BD ⊥AC ，BD 平分AC . …………………………………………………1分∵AB =6∴AD =3………………………………………………………………………2分∴由勾股定理得，33363222=-=-=AD AB BD ………………………………4分（2）证明∵BD 是等边△ABC 的中线，∴BD 平分∠ABC ∴∠DBE ＝12∠ABC ＝30° …………………………………………………5分又∵CE ＝CD∴∠E ＝∠CDE ，∠E ＝12∠ACB ＝30°.∴∠DBE ＝∠E . …………………………………………………………6分∴DB ＝DE . ∵DF ⊥BE∴DF 为底边上的中线． ∴BF ＝EF . ………………………………………………………………7分 （3）解：∵AD ＝CD ，CE ＝CD ∴CE ＝CD =3 ∴BE ＝BC ＋CE=9 ……………………………………………………8分 ∵∠DBE ＝30°，DB ＝33∴DF =21DB ＝21×33=233……………………………………9分∴△BDE 的面积=432723392121=⨯⨯=⋅DF BE…………………10分 24.解：（1）60. ……………………………………………………………………………1分（2）设乙队单独施工，需要x 天才能完成该项工程，根据题意可得：31+16×（x1601+）=1，……………………………………………………3分解得：x =40，……………………………………………………………4分经检验x =40是原方程的根，…………………………………………………5分答：乙队单独施工，需要40天才能完成该项工程； （3）设乙队参与施工y 天才能完成该项工程，根据题意可得：601×30+y ×401≥1，……………………………………………………7分解得：y≥20，…………………………………………………………8分答：乙队至少施工20天才能完成该项工………………………………… 10分25.解：（1）BD=CE，BC= CE+CD；…………………………………………………2分（2）不成立，存在的数量关系为BC= CE－CD．……………………………3分理由：如图11-2，∵∠BAC=∠DAE=90°∴∠BAC+∠CAD =∠DAE+∠CAD即∠BAD=∠CAE …………………………………………………………4分在△ABD和△ACE中，，∴△ABD≌△ACE （SAS），………………………………………………5分∴BD=CE，…………………………………………………………………6分∴BD=BC+CD，即CE=BC+CD，∴BC =CE－CD；…………………………………………………………7分（3）如图11-3，∵∠BAC=∠DAE=90°∴∠BAC－∠BAE=∠DAE－∠BAE即∠BAD=∠CAE …………………………………………………………8分在△ABD和△ACE中，，∴△ABD≌△ACE （SAS），………………………………………………10分∴BD=CE，∴CD=BC+BD=BC+CE，…………………………………………………11分∵BC=6，CE=2，∴CD=6+2=8．……………………………………………………………12分。

2017—2018学年度第一学期期末检测试卷八年级数学A 卷 B 卷题号一二三2324252627总 分得分A 卷（100分）一、选择题（每小题4分，共40分）1、-8的立方根为 （ ）A ．2B ．-2C ．±2D ．±42、实数, -π, , , 0, 3 , 0.1010010001……中，无理数的71132-4个数是 （ ）A ．2B ．3C ．4D ．53、下列图形中是中心对称图形的为 （ ）4、下列运算正确的是 （ ）A. B. C. D.623a a a =⨯633x x =）（1055x x x =+3325b a ab ab -=-÷-）（）（5、分解因式结果正确的是 （ ）32b b a -A 、B 、C 、D 、)(22b a b -2)(b a b -))((b a b ab -+))((b a b a b -+6、通过估算，估计 76 的大小应在 （ ）A ．7～8之间B ．8.0～8.5之间C ．8.5～9.0之间D ．9～10之间7、下列图形中是旋转对称图形有 （ ）①正三角形 ②正方形 ③三角形 ④圆 ⑤线段A.个B.个C.个D.个54328、已知a 、b 、c 是三角形的三边长，如果满足，则0108)6(2=-+-+-c b a 三角形的形状是 （ ）A ．底与边不相等的等腰三角形B ．等边三角形C ．钝角三角形D ．直角三角形9、如图：在菱形ABCD 中，AC=6，BD=8，则菱形的边长为 （ ）A ．5B ．10C ．6D ．810、如图，□ABCD 中，对角线AC 和BD 交于O ，若AC =8，BD =6，则AB 长的取值范围是 （ ）A ．B ．71<<AB 42<<AB C ．D ．86<<AB 43<<AB 二、填空题（每小题4分，共32分）11、的算术平方根是________;3612、.计算： .()[]=+-222322221n m mn n m 13、多项式是完全平方式，则m = .6422++mx x 14、如图,在平行四边形ABCD 中,EF∥AD,GH∥AB,EF 、GH10题图9题图相交于点O,则图中共有____ 个平行四边形.15、已知，如图，网格中每个小正方形的边长为1，则四边形ABCD 的面积为 .16、已知：等腰梯形的两底分别为和，一腰长为，则它的对cm 10cm 20cm 89角线的长为 ．cm 17、□中，是对角线，且，，则ABCD BD BD BC =︒=∠70CBD =∠ADC 度．三、解答题（共28分）19、（每小题4分，共8分）因式分解（1） （2）22916y x -22242y xy x +-20、(本题8分) 先化简，再求值:，其中()()()()224171131x x x x +--++-12x =-15题图18题图A B CD 14题H G F EO21、（每小题3分，共6分）在如图的方格中，作出△ABC 经过平移和旋转后的图形：（1）将△ABC 向下平移4个单位得△；C B A '''（2）再将平移后的三角形绕点顺时针方向旋转90度。

2017-2018学年八年级数学上学期期末考试试题（考试时间120分钟，总分150分）第Ⅰ卷（选择题，共30分）一、选择题（每小题3分，共30分)每小题均有四个选项，其中只有一项符合题目要求，答案填在答题卡上．1．下已知⎩⎪⎨⎪⎧x ＝1y ＝2是二元一次方程组⎩⎪⎨⎪⎧ax ＋y ＝－12x －by ＝0的解，则a ＋b 的值是（ ）（A ）2 （B ）－2 （C ）4 （D ）－42．将直尺和直角三角板按如图方式摆放（ACB ∠为直角），已知130∠=︒，则2∠的大小是( )A. 30︒B. 45︒C. 60︒D. 65︒3．在这学期的六次体育测试中，甲、乙两同学的平均成绩一样，方差分别为1.5， 1.0，则下列说法正确的是（ ）（A ）乙同学的成绩更稳定 （B ）甲同学的成绩更稳定（C ）甲、乙两位同学的成绩一样稳定 （D ）不能确定哪位同学的成绩更稳定 4. 如图，以两条直线1l ，2l 的交点坐标为解的方程组是（（A ）⎩⎪⎨⎪⎧x －y ＝12x －y ＝1 （B ）⎩⎪⎨⎪⎧x －y ＝－12x －y ＝－1 （C ）⎩⎪⎨⎪⎧x －y ＝－12x －y ＝1 （D ）⎩⎪⎨⎪⎧x －y ＝12x －y ＝－15．如图，长方体的底面边长分别为2cm 和3cm ，高为6cm. 如果用一根细线从点A 开始经过4个侧面缠绕一圈达到点B ，那么所用细线最短需要（ ） （A ）11cm （B ）234cm （C ）(8＋210)cm （D ）(7＋35)cm 6. 16的平方根是（ ）（A ）±4 （B ）±2 （C ）4 （D ）4- 7.在平面直角坐标系中，下列的点在第二象限的是（ ）A B 3cm2cm6cm8．如图，AC ∥DF ，AB ∥EF ，若∠2＝50°，则∠1的大小是（ ） （A ）60° （B ）50° （C ）40° （D ）30°9．一次函数y ＝x ＋1的图像不经过（ ）（A ）第一象限 （B ）第二象限 （C ）第三象限 （D ）第四象限 10. 满足下列条件的△ABC ，不是直角三角形的是（ ） （A ）b 2－c 2＝a 2（B ）a:b:c ＝3:4:5 （C ）∠A: ∠B: ∠C ＝9:12:15 （D ）∠C ＝∠A －∠B 第Ⅱ卷（非选择题，共70分） 二、填空题(每小题4分，共l6分) 11. 计算：(－2)2＝ ．12．李老师最近6个月的手机话费（单位：元）分别为：27，36，54，29，38，42，这组数据的中位数是 ． 13、点A(-2，3)关于x 轴对称的点B 的坐标是14、如图，直线l 过正方形ABCD 的顶点B ，点A 、点B 到直线l 的距离分别是3和4，则该正方形的面积是 。

2017-2018学年八年级数学上学期期末考试试题（考试时间120分钟，总分150分）第Ⅰ卷（选择题，共30分）一、选择题（每小题3分，共30分)每小题均有四个选项，其中只有一项符合题目要求，答案填在答题卡上．1．下已知⎩⎪⎨⎪⎧x ＝1y ＝2是二元一次方程组⎩⎪⎨⎪⎧ax ＋y ＝－12x －by ＝0的解，则a ＋b 的值是（ ）（A ）2 （B ）－2 （C ）4 （D ）－42．将直尺和直角三角板按如图方式摆放（ACB ∠为直角），已知130∠=︒，则2∠的大小是( )A. 30︒B. 45︒C. 60︒D. 65︒3．在这学期的六次体育测试中，甲、乙两同学的平均成绩一样，方差分别为1.5，1.0，则下列说法正确的是（ ）（A ）乙同学的成绩更稳定 （B ）甲同学的成绩更稳定（C ）甲、乙两位同学的成绩一样稳定 （D ）不能确定哪位同学的成绩更稳定 4. 如图，以两条直线1l ，2l 的交点坐标为解的方程组是（（A ）⎩⎪⎨⎪⎧x －y ＝12x －y ＝1 （B ）⎩⎪⎨⎪⎧x －y＝－12x －y ＝－1 （C ）⎩⎪⎨⎪⎧x －y ＝－12x －y ＝1 （D ）⎩⎪⎨⎪⎧x －y ＝12x －y ＝－15．如图，长方体的底面边长分别为2cm 和3cm ，高为6cm. 如果用一根细线从点A 开始经过4个侧面缠绕一圈达到点B ，那么所用细线最短需要（ ） （A ）11cm （B ）234cm （C ）(8＋210)cm （D ）(7＋35)cm 6. 16的平方根是（ ）（A ）±4 （B ）±2 （C ）4 （D ）4- 7.在平面直角坐标系中，下列的点在第二象限的是（ ）A B 3cm2cm6cm（A）（2，1）（B）（2，－1）（C）（－2，1）（D）（－2，－1）8．如图，AC∥DF，AB∥EF，若∠2＝50°，则∠1的大小是（）（A）60°（B）50°（C）40°（D）30°9．一次函数y＝x＋1的图像不经过（）（A）第一象限（B）第二象限（C）第三象限（D）第四象限10. 满足下列条件的△ABC，不是直角三角形的是（）（A）b2－c2＝a2（B）a:b:c＝3:4:5（C）∠A: ∠B: ∠C＝9:12:15 （D）∠C＝∠A－∠B第Ⅱ卷（非选择题，共70分）二、填空题(每小题4分，共l6分)11. 计算：(－2)2＝．12．李老师最近6个月的手机话费（单位：元）分别为：27，36，54，29，38，42，这组数据的中位数是．13、点A(-2，3)关于x轴对称的点B的坐标是14、如图，直线l过正方形ABCD的顶点B，点A、点B到直线l的距离分别是3和4，则该正方形的面积是。

2017—2018学年度第一学期期末考试八年级数学试题温馨提示：1.本试卷分第Ⅰ卷和第Ⅱ卷两部分，共4页.满分100分，考试用时90分钟.考试结束后，将试题卷和答题卡一并交回.2.答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、准考证号、座号填写在试题卷和答题卡规定的位置上.3.第Ⅰ卷每小题选出答案后，必须用0.5毫米黑色签字笔将该答案选项的字母代号填入答题卡的相应表格中，不能答在试题卷上.4.第Ⅱ卷必须用0.5毫米黑色签字笔作答，答案必须写在答题卡各题目指定区域内相应的位置，不能写在试题卷上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带.不按以上要求作答的答案无效.第Ⅰ卷（选择题共30分）一、选择题：本大题共10个小题,在每小题的四个选项中只有一个是正确的,请把正确的选项选出来，并将该选项的字母代号填入答题卡的相应表格中.每小题选对得3分,满分30分. 1．在下列长度的三条线段中，能组成三角形的是A．1,2,3 B．3,8,4 C．10,6,5 D．2,4,22．下列图形：①角，②线段，③等腰三角形，④直角三角形，其中是轴对称图形的有A．①②③④ B．①②③C．②④D．①③3．△ABC中，若∠B =∠A+10°，∠C=∠B+10°，则下列结论错误的是A．∠C=∠A+20°B．∠A=50°C．∠B的外角是130°D．△ABC是一个锐角三角形4．下列数据能唯一确定三角形的形状和大小的是A．∠A=50°，∠B =60°，∠C=70°B．AB=6，∠B =70°，∠C=60°C．AB=4，BC =5，∠C=60°D．AB=4，BC =5，CA=105．下列运算正确的是A ．2222x x x =B ．326()x x =C ．3412(2)8x x -=D ．734()()x x x -÷-=-6．下列各因式分解正确的是A ．22(2)(2)(2)x x x -+-=-+B ．2221(1)x x x +-=-C ．22441(21)x x x -+=-D ．242(2)(2)x x x x -=+-7．若分式12x x -+的值为0,则x 应满足的条件是 A ．x =-2 B ．x =0 C.x =1或x =-2 D ．x =18.下列计算错误的是A ．0.220.77a b a b a b a b++=--B ．3223x y x x y y=C ．1a bb a-=--D ．123c c c+= 9．如图，为了促进当地旅游发展，某地要在三条公路围成的一块平地上修建一个度假村.要使这个度假村到三条公路的距离相等，应修建在△ABC 的 A ．两条中线的交点处B ．两条角平分线的交点处C ．两条高的交点处D ．两条边的垂直平分线的交点处10．如图，△ABC 的周长为30cm ，把△ABC 的边AC 对折，使顶点C 和点A 重合，折痕交BC 边于点D ，交AC 边于点E ，连接AD ，若AE =4cm ，则△ABD 的周长是 A ．22 cm B ．20 cm C ．18 cm D ．15 cm（第9题图）第Ⅱ卷（非选择题 共70分）二、填空题：本大题共8个小题，每小题3分，满分24分. 11．点（-7,9）关于y 轴对称的点的坐标是 ．12．计算：0220183--+-（）= ． 13．如果216x kx ++可运用完全平方公式进行因式分解，那么k 的值是 ． 14．张明3小时清点完一批图书的一半，李强加入清点另一半图书的工作，两人合作1.2小时清点完另一半图书.如果李强单独清点这批图书需要 小时． 15．一个多边形的内角和比它的外角和的3倍多180°，则它是 边形． 16．如图，∠1=∠2，∠3=∠4，∠BDC =130°，则∠A = ．17．在Rt△ABC 中，∠ACB =90°，BC =2.1cm ，CD ⊥AB ，在AC 上取一点E ，使EC =BC ，过点E 作EF ⊥AC 交CD 的延长线于点F ，若EF =4cm ，则AE = cm ． 18．如图，∠A =61°，∠C ′=47°,△ABC 与△A ′B ′C ′关于直线l 对称，则∠B =____ ．三、解答题：本大题共7个小题，满分46分. 解答时请写出必要的演推过程.19．先化简，再求值：222693293x x x x x x-+-÷--+，其中2018x =-.20．计算：（1）23215)()ab ab a b --÷-（； （2）222)()()6x y x y x y y +-+--（. 21．分解因式：（1）4811m -； （2）43242025ab ab ab -+.22. 两个小组同时开始攀登一座600m 高的山，第一组的攀登速度是第二组的1.2倍，他们比第二组早20min 到达顶峰，两个小组的攀登速度各是多少m/min ？如果山高是h m ，第一组的攀登速度是第二组的a 倍，并比第二组早t min 到达峰顶，则请直接写出两组的攀登速度各是多少m/min ？23. 如图，在平面直角坐标系中，点A 的坐标为（-2,0），△AOB 是等边三角形，点C 为OA 延长线上的一个动点，以BC 为边在第二象限中作等边△BCE ，连接EA 并延长EA 交y 轴于点F .（1）求∠EAB 的度数；（2）如果点C 再向左移动3个单位长度，则点F 的位置变化情况是 .24. 如图，在△ABC 中，AD ⊥BC ，BE ⊥AC ，垂足分别为D ，E ，AD 和BE 相交于点F ，DF =EF ，延长CF 交AB 于点G .（1）图中共有 个等腰三角形，共有 对全等三角形； （2）求证：CG 垂直平分AB .G FEDCBA（第23题图）（第24题图）2017—2018学年第一学期八年级数学试题参考答案及评分标准二、填空题：（每题3分，共24分）11.(7,9)； 12．89-； 13．±8； 14．4； 15．九； 16.80°； 17．1.9； 18.72°. 三、解答题：（共46分）19.解：222693293x x x x x x-+-÷--+ =2(3)(3)2(3)(3)3x x x x x x -+-+-- ……………………………………… 4分 = 2x -. ……………………………………… 5分 当2018x =-时，原式=-2018-2=-2020. …………………………… 6分20．解：（1）23215)()ab ab a b --÷-（ =362215a b a b a b --÷ ………………………………… 2分=321625a b ---- ………………………………… 3分 =1b. ………………………………… 4分（2）222)()()6x y x y x y y +-+--（ =22222446x xy y x y y ++-+- ……………………………………6分 =24xy y -. ……………………………………7分 21．解：（1）4811m -=22(91)(91)m m +- ………………………………… 2分 =2(91)(31)(31)m m m ++-. ………………………………… 4分（2）43242025ab ab ab -+=22(42025)ab b b -+ ………………………………… 5分=22(25)ab b - . ………………………………… 7分 22．解：设第二组的攀登速度为x m/min ，根据题意，列出方程600600201.2x x+=……………………………… 3分 解得 x =20 ……………………………… 4分经检验，x =20是原方程的解. ……………………………… 5分此时，1.2x =24 ……………………………… 6分 答：第一组的速度为24m/min 第二组的速度为20m/min ；如果山高是h m ，第一组的攀登速度是第二组的a 倍，并比第二组早t min 到达峰顶，则第一组的速度为ah h t -m/min 第二组的速度为ah hat-m/min. …………………… 8分 23．（1）解：∵△AOB 和△BCE 是等边三角形，∴BE =BC ,BA =BO ，∠EBC =∠ABO =∠AOB =60°，…………………… 3分 ∴∠EBC +∠ABC =∠ABO +∠ABC ，即∠EBA =∠CBO ，…………………… 4分 ∴△EBA ≌△CBO (SAS) …………………………………… 5分 ∴∠EAB =∠AOB =60°. …………………………………… 6分（2）如果点C 再向左移动3个单位长度，则点F 的位置变化情况是 保持不变 .…………………………………… 8分24． （1）图中共有 2 个等腰三角形，共有 6 对全等三角形；……2分 （2）证明：∵AD ⊥BC ，BE ⊥AC ，∴∠AEF =∠CEF =90°, ∠BDF =∠CDF =90°，∴∠CEF =∠CDF =90°, ∠AEF =∠BDF =90°，………………3分 在△CEF 和△CDF 中90,CEF CDF EF DF CF CF ∠=∠=︒⎧⎪=⎨⎪=⎩，∴△CEF ≌△CDF (HL) …………………………………… 5分 ∴∠ACG =∠BCG ，CE =CD . ………………………………… 6分 在△AEF 和△BDF 中90,AEF BDF EF DF EFA DFB ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩，∴△AEF ≌△BDF (ASA) …………………………………… 8分 ∴AE =BD ,∴CE +AE =CD +BD ，即AC =BC ，…………………………… 9分 又∠ACG =∠BCG ，∴CG 垂直平分AB . …………………………………… 10分。

2017-2018学年度第一学期期末教学质量检测八年级数学试题（时间：120分钟）友情提示：亲爱的同学，你好！今天是你展示才能的时候，只要你仔细审题，认真答题，你就会有出色的表现！1.考生务必将姓名、班级、座号、准考证号填写在答题卡规定的位置上。

2.本试题分第Ⅰ卷和第Ⅱ卷，共25道小题。

3.第Ⅰ卷是选择题，共8道小题，每小题选出的答案后，用2B铅笔把答题卡上对应的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其它答案标号，答案不能答在试卷上。

4.第Ⅱ卷是填空题和解答题，共17小题，答案必须用0.5毫米黑色签字笔写在答题卡题目指定区域内相应的位置，不能写在试题上；如需改动，先划掉原来的答案，然后再写上新的答案。

不按以上要求作答的答案无效。

5.考试结束只上交答题卡。

第Ⅰ卷一、选择题：下列每小题都给出标号为A、B、C、D的四个结论，其中只有一个是正确的，请将所选答案的字母标号涂在答题卡的相应位置。

1.3的相反数是（）A、3B、-3C、3D、-32.在平面直角坐标系中，点P（-2,3）关于x轴的对称点坐标为（）A、（-2,3）B、（2，-3）C、（-2，-3）D、（3，-2）3.下列语句：①三角形的内角和是180°；②作为一个角等于一个已知角；③两条直线被第三条直线所截，同位角相等；④延长线段AB到C，使BC=AB，其中是命题的有（）A、①②B、②③C、①④D、①③4.方程组的解是（）A、 B、 C、 D 、5.若一次函数y=kx+b，（k，b为常熟，且k≠0）的图像经过点（1,2）且y随x的增大而减小，则这个函数的表达式可能是（）A、y=2x+4B、y=3x-1C、y=-3x-1D、y=-2x+46.如图，∠AOB的边OA为平面反光镜，一束光线从OB上的C点射出，经OA上的D点反射后，反射光线DE恰好与OB平行，若∠AOB=40°，则∠BCD的度数是（）A、60°B、80°C、100°D、120°x +|y-2|=0，则（x+y）2017的值为（）7.若3A、-1B、1C、±1D、08.若一组数据10,9.a，12,9的平均数是10，则这组数的方差是（）A、0.9B、1C、1.2D、1.4第Ⅱ卷二、填空题：请把正确答案填写在答题卡的相应位置9.实数7的整数部分是_______10.命题“对顶角相等”的条件是_______________ ，结论是___________ 。

2017-2018学年湖北省襄阳市襄州区八年级（上）期末数学试卷一、选择题（本大题共10小题，每小题3分，共30分）1．（3分）下列美丽的图案中是轴对称图形的个数有（）A．1个B．2个C．3个D．4个2．（3分）下列物品不是利用三角形稳定性的是（）A．自行车的三角形车架B．三角形房架C．照相机的三脚架 D．放缩尺3．（3分）到三角形三条边的距离都相等的点是这个三角形的（）A．三条中线的交点 B．三条高的交点C．三条边的垂直平分线的交点D．三条角平分线的交点4．（3分）如图，点A、D、C、E在同一条直线上，AB∥EF，AB=EF，∠B=∠F，AE=10，AC=7，则CD的长为（）A．5.5 B．4 C．4.5 D．35．（3分）已知点A的坐标为（﹣2，3），点B与点A关于x轴对称，点C与点B关于y轴对称，则点C关于x轴对称的点的坐标为（）A．（2，﹣3）B．（﹣2，3）C．（2，3）D．（﹣2，﹣3）6．（3分）如果把分式中的x 和y 都扩大2倍，则分式的值（ ）A ．扩大4倍B ．扩大2倍C ．不变D ．缩小2倍7．（3分）下列计算正确的是（ ）A ．x 4•x 4=x 16B ．（a 3）2•a 4=a 9C ．（ab 2）4÷（﹣ab ）2=﹣ab 4D ．（a ﹣1b 3）2=8．（3分）如果分式的值为零，那么x 等于（ ）A ．1B ．﹣1C ．0D ．±19．（3分）若分式，则分式的值等于（ ）A ．﹣B ．C ．﹣D ．10．（3分）如图，C 为线段AE 上一动点（不与点A ，E 重合），在AE 同侧分别作正三角形ABC 和正三角形CDE ，AD 与BE 交于点O ，AD 与BC 交于点P ，BE 与CD 交于点Q ，连接PQ ．以下五个结论：①AD=BE ；②PQ ∥AE ；③AP=BQ ；④DE=DP ； ⑤∠AOB=60°．其中正确的结论的个数是（ ）A ．2个B ．3个C ．4个D ．5个二、填空题：（本大题共6个小题，每小题3分，共18分）请将每小题正确答案写在题中横线上11．（3分）在△ABC 中，∠A=60°，∠B=40°，则∠C 的度数是 ．12．（3分）若x2+mx+n分解因式的结果是（x+2）（x﹣1），则m+n的值为．13．（3分）a+b=2，ab=﹣2，则a2+b2= ．14．（3分）若2m=a，32n=b，m，n为正整数，则23m+10n= ．15．（3分）如图，∠AOB=30°，∠AOB内有一定点P，且OP=12，在OA上有一点Q，OB上有一点R，若△PQR周长最小，则最小周长是16．（3分）在等腰△ABC中，AB=AC，一边上的中线BD将这个三角形的周长分为15和12两个部分，则该等腰三角形的底边长为．三、简答题：（本大题共9个小题，共72分）解答应写出演算步骤或文字说明，并将答案写在对应的答题区域内17．（8分）分解因式：（1）81x4﹣16；（2）8ab3+2a3b﹣8a2b218．（6分）化简求值：（x﹣y+）（x+y﹣），其中x=97，y=3．19．（8分）解方程：（1）=；（2）﹣=20．（6分）在创建文明城市的进程中，我市为美化城市环境，计划种值树木60万棵，由于志愿者的加入，实际每天植树比原计划多20%，结果提前5天完成任务，求原计划每天植树多少万棵？21．（8分）如图，在△ABC中，BD平分∠ABC，（1）作图：作BC边的垂直平分线分别交BC，BD于点E，F（用尺规作图法，保留作图痕迹，不要求写作法）；（2）在（1）的条件下，连接CF，若∠A=60°，∠ABD=24°，求∠ACF的度数．22．（8分）如图，BD是△ABC的角平分线，DE⊥AB，DF⊥BC，垂足分别为E，F（1）求证：BE=BF；（2）若△ABC的面积为70，AB=16，DE=5，求BC的长．23．（8分）如图1，在四边形ABCD中，DC∥AB，AD=BC，BD平分∠ABC．（1）求证：AD=DC；（2）如图2，在上述条件下，若∠A=∠ABC=60°，过点D作DE⊥AB，过点C作CF⊥BD，垂足分别为E、F，连接EF．判断△DEF的形状并证明你的结论．24．（8分）在Rt△ABC中，∠ACB=90°，AC=BC，CD是∠ACB的角平分线，点E，F分别是边AC，BC上的动点，AC=4，设AE=x，BF=y．（1）若x+y=3，求四边形CEDF的面积；（2）当DE⊥DF时，如图2，试探索x、y之间的数量关系．25．（12分）如图1所示，在Rt△ABC中，∠C=90°，点D是线段CA 延长线上一点，且AD=AB，点F是线段AB上一点，连接DF，以DF为斜边作等腰Rt△DFE，连接EA，EA满足条件EA⊥AB．（1）若∠AEF=20°，∠ADE=50°，BC=2，求AB的长度；（2）求证：AE=AF+BC；（3）如图2，点F是线段BA延长线上一点，探究AE、AF、BC之间的数量关系，并证明你的结论．参考与试题解析一、选择题（本大题共10小题，每小题3分，共30分）1．【解答】解：第一个图形是轴对称图形，第二个图形不是轴对称图形，第三个图形是轴对称图形，第四个图形是轴对称图形，综上所述，是轴对称图形的有3个．故选：C．2．【解答】解：放缩尺是利用了四边形的不稳定性，而A、B、C选项都是利用了三角形的稳定性，故选：D．3．【解答】解：∵角的平分线上的点到角的两边的距离相等，∴到三角形的三边的距离相等的点是三条角平分线的交点．故选：D．4．【解答】解：∵AB∥EF，∴∠A=∠E，在△ABC和△EFD中，，∴△ABC≌△EFD（A SA），∴AC=ED=7，∴AD=AE﹣ED=10﹣7=3，∴CD=AC﹣AD=7﹣3=4．5．【解答】解：点A的坐标为（﹣2，3），点B与点A关于x轴对称，得B（﹣2，﹣3）．点C与点B关于y轴对称，得C（2，﹣3）．则点C关于x轴对称的点的坐标为（2，3），故选：C．6．【解答】解：把分式中的x和y都扩大2倍后得：==2•，即分式的值扩大2倍．故选：B．7．【解答】解：A、结果是x4，故本选项不符合题意；B、结果是a10，故本选项不符合题意；C、结果是a2b6，故本选项不符合题意；D、结果是，故本选项符合题意；故选：D．8．【解答】解：∵分式的值为零，∴，解得x=﹣1．故选：B．9．【解答】解：整理已知条件得y﹣x=2xy；∴x﹣y=﹣2xy将x﹣y=﹣2xy整体代入分式得====．故选：B．10．【解答】解：①△ABC和△DCE均是等边三角形，点A，C，E在同一条直线上，∴AC=BC，EC=DC，∠BCE=∠ACD=120°∴△ACD≌△ECB∴AD=BE，故本选项正确；②∵△ACD≌△ECB∴∠CBQ=∠CAP，又∵∠PCQ=∠ACB=60°，CB=AC，∴△BCQ≌△ACP，∴CQ=CP，又∠PCQ=60°，∴△PCQ为等边三角形，∴∠QPC=60°=∠ACB，∴PQ∥AE，故本选项正确；③∵∠ACB=∠DCE=60°，∴∠BCD=60°，∴∠ACP=∠BCQ，∵AC=BC，∠DAC=∠QBC，∴△ACP≌△BCQ（ASA），∴CP=CQ，AP=BQ，故本选项正确；④已知△ABC、△DCE为正三角形，故∠DCE=∠BCA=60°⇒∠DCB=60°，又因为∠DPC=∠DAC+∠BCA，∠BCA=60°⇒∠DPC＞60°，故DP不等于DE，故本选项错误；⑤∵△ABC、△DCE为正三角形，∴∠ACB=∠DCE=60°，AC=BC，DC=EC，∴∠ACB+∠BCD=∠DCE+∠BCD，∴∠ACD=∠BCE，∴△ACD≌△BCE（SAS），∴∠CAD=∠CBE，∴∠AOB=∠CAD+∠CEB=∠CBE+∠CEB，∵∠ACB=∠CBE+∠CEB=60°，∴∠AOB=60°，故本选项正确．综上所述，正确的结论是①②③⑤．故选：C．二、填空题：（本大题共6个小题，每小题3分，共18分）请将每小题正确答案写在题中横线上11．【解答】解：由三角形内角和定理得：∠C=180°﹣∠A﹣∠B=80°，故答案为：80°．12．【解答】解：∵x2+mx+n分解因式的结果是（x+2）（x﹣1），∴x2+mx+n=x2+x﹣2，∴m=1，n=﹣2，∴m+n=1﹣2=﹣1，故答案为﹣1．13．【解答】解：∵a2+b2=（a+b）2﹣2ab，而a+b=2，ab=﹣2，∴a2+b2=22﹣2×（﹣2）=8．故答案为8．14．【解答】解：32n=25n=b，则23m+10n=23m•210n=a3•b2=a3b2．故答案为：a3b2．15．【解答】解：设∠POA=θ，则∠POB=30°﹣θ，作PM⊥OA与OA 相交于M，并将PM延长一倍到E，即ME=PM．作PN⊥OB与OB相交于N，并将PN延长一倍到F，即NF=PN．连接EF与OA相交于Q，与OB相交于R，再连接PQ，PR，则△PQR即为周长最短的三角形．∵OA是PE的垂直平分线，∴EQ=QP；同理，OB是PF的垂直平分线，∴FR=RP，∴△PQR的周长=EF．∵OE=OF=OP=12，且∠EOF=∠EOP+∠POF=2θ+2（30°﹣θ）=60°，∴△EOF是正三角形，∴EF=12，即在保持OP=12的条件下△PQR的最小周长为12．故答案为：1216．【解答】解：根据题意，①当15是腰长与腰长一半时，AC+AC=15，解得AC=10，所以底边长=12﹣×10=7；②当12是腰长与腰长一半时，AC+AC=12，解得AC=8，所以底边长=15﹣×8=11．所以底边长等于7或11．故答案为：7或11．三、简答题：（本大题共9个小题，共72分）解答应写出演算步骤或文字说明，并将答案写在对应的答题区域内17．【解答】解：（1）原式=（9x2+4）（9x2﹣4）=（9x2+4）（3x+2）（3x﹣2）；（2）原式=2ab（4b2+a2﹣4ab）=2ab（a﹣2b）2．18．【解答】解：原式=•=•=（x+y）（x﹣y）=x2﹣y2，当x=97，y=3时，原式=972﹣32=（97+3）×（97﹣3）=100×94=940．19．【解答】解：（1）去分母，得：2x=5（x﹣3），去括号，得：2x=5x﹣15，移项，合并同类项，得：3x=15，∴x=5，经检验，x=5是原方程的解，∴x=5；（2）去分母，得：3（3x﹣1）﹣6×2=5，去括号，得：9x﹣3﹣12=5，移项，合并同类项，得：9x=20，∴x=，经检验，x=是原方程的解，∴x=．20．【解答】解：设原计划每天植树x万棵，则实际每天植树1.2x 万棵，根据题意得：﹣=5，解得：x=2， 经检验，x=2是原方程的解，且符合题意．答：原计划每天植树2万棵．21．【解答】解：（1）BC 边的垂直平分线EF 如图所示；（2）∵BD 平分∠ABC ，∠ABD=24°，∴∠FBC=24°，∵EF 垂直平分BC ，∴BF=CF ，∴∠FCB=∠FBC=24°，在△FDC 中，∠FDC=∠A+∠ABD=60°+24°=84°，∠DFC=∠FCB+∠FB C=24°+24°=48°，∴∠ACF=180°﹣84°﹣48°=48°．22．【解答】解：（1）∵DE ⊥AB ，DF ⊥BC ，∴∠BED=∠BFD=90°，∵BD 是△ABC 的角平分线，∴∠EBD=∠FBD ，在△BDE 和△BDF 中，∵，∴△DBE≌△DBF（AAS），∴BE=BF；（2）∵BD是△ABC的角平分线，DE⊥AB，DF⊥BC，∴DF=DE=5，∴S△ABD=AB•DE=40，∴S△BCD=BC•DF=70﹣40=30，∴BC=12．23．【解答】（1）证明：∵DC‖AB，∴∠CDB=∠ABD，又∵BD平分∠ABC，∴∠CBD=∠ABD，∴∠CDB=∠CBD，∴BC=DC，又∵AD=BC，∴AD=DC；（2）△DEF为等边三角形，证明：∵BC=DC（已证），CF⊥BD，∴点F是BD的中点，∵∠DEB=90°，∴EF=DF=BF．∵∠ABC=60°，BD平分∠ABC，∴∠BDE=60°，∴△DEF为等边三角形．24．【解答】解：（1）在图1中，过点D作DG⊥AC于点G，DH⊥BC于点H．∵∠ACB=90°，AC=BC，CD是∠ACB的角平分线，∴∠A=∠B=∠ACD=∠BCD=45°，∴AD=CD=BD．∵在等腰直角三角形ACD中，DG⊥AC，∠A=45°，∴DG=AG=AC=2，同理：DH=2．∵S△CDE=CE•DG=4﹣x，S△CDF=CF•DH=4﹣y，∴S四边形CEDF=S△CDE+S△CDF=（4﹣x）+（4﹣y）=8﹣（x+y）=5；（2）当DE⊥DF时，∠EDF=90°．∵CD⊥AB，∴∠ADE+∠EDC=∠EDC+∠CDF=90°，∴∠ADE=∠CDF．在△ADE与△CDF中，，∴△ADE≌△CDF（ASA），∴AE=CF，∴AE+BF=CF+BF=BC，即x+y=4．25．【解答】解：（1）在等腰直角三角形DEF中，∠DEF=90°，∵∠1=20°，∴∠2=∠DEF﹣∠1=70°，∵∠EDA+∠2+∠3=180°，∴∠3=60°，∵EA⊥AB，∴∠EAB=90°，∵∠3+∠EAB+∠A=180°，∴∠4=30°，∵∠C=90°，∴AB=2BC=4；（2）如图1，过D作DM⊥AE于D，在△DEM中，∠2+∠5=90°，∵∠2+∠1=90°，∴∠1=∠5，∵DE=FE，在△DEM与△EFA中，，∴△DEM≌△EFA，∴AF=EM，∵∠4+∠B=90°，∵∠3+∠EAB+∠4=180°，∴∠3+∠4=90°，∴∠3=∠B，在△DAM与△A BC中，，∴△DAM≌△ABC，∴BC=AM，∴AE=EM+AM=AF+BC；（3）如图2，过D作DM⊥AE交AE的延长线于M，∵∠C=90°，∴∠1+∠B=90°，∵∠2+∠MAB+∠1=180°，∠MAB=90°，∴∠2+∠1=90°，∠2=∠B，在△ADM与△BAC中，，∴△ADM≌△BAC，∴BC=AM，∵EF=DE，∠DEF=90°，∵∠3+∠DEF+∠4=180°，∴∠3+∠4=90°，∵∠3+∠5=90°，∴∠4=∠5，在△MED与△AFE中，，∴△MED≌△AFE，∴ME=AF，∴AE+AF=AE+ME=AM=BC，即AE+AF=BC．。

襄城区2017—2018学年度上学期期末测试八年级数学试题（时间：120分钟 满分：120分）★ 祝 考 试 顺 利 ★注意事项：1. 答卷前，考生务必将自己的姓名、考试号涂填在答题卡上指定的位置。

2. 选择题每小题选出答案后，用2B 铅笔将答题卡上对应题目的答案标号涂黑，如需改动， 用橡皮擦干净后，再选涂其它答案标号，答在试题卷上无效。

3. 非选择题（主观题）用0.5毫米的黑色墨水签字笔直接答在答题卡上每题对应的答题区 域内，答在试题卷上无效。

作图一律用2B 铅笔或0.5毫米黑色签字笔。

4. 考试结束后，请将本试题卷和答题卡一并上交。

一、选择题：（本大题共10个小题，每小题3分，共30分）在每小题给出的四个选项中，只有一项是符合题目要求的，请将其序号在答题卡上涂黑作答.1. 以下列各组线段为边,能组成三角形的是： A.1cm,2cm,3cm B.2cm,5cm,8cm C.3cm,4cm,5cm D. 4cm,5cm,11cm2. 下列各式中,正确的是：A.5552t t t =⋅ B.624t t t =+ C.1243t t t =⋅ D.532t t t =⋅ 3. 下面四个图形分别是节能、节水、低碳、绿色食品标志,是轴对称图形的是：4. 如图,AB=DB,∠1=∠2,请问添加下面哪个条件不能判定△ABC ≌△DBE ： A.BC=BE B.AC=DE C.∠BAC=∠D D.∠C=∠E12第7题图第8题图第4题图F D DEBCABABCE5. 下列各式由左到右的变形中,属于分解因式的是：A.an am n m a +=+)(B.C.D. 6. 要使分式735-x x有意义,则x 的取值范围是： 2222))((cb a b ac b a --+=--x x x x x 6)4)(4(6162+-+=+-)12(55102-=-x x x xA.37≠x B.37>x C.37<x D.37=x 7. 如图,在已知的△ABC 中,按以下步骤作图:①分别以B,C 为圆心,以大于21BC 的长为半径作弧,两弧相交于两点M,N;②作直线MN 交AB 于点D,连接CD.若CD=AC,∠A=50°,则∠ACB 的度数为: A.90° B.95° C.100° D.105°8. 如图,AD 是△ABC 的中线,E,F 分别是AD 和AD 延长线上的点,且DE=DF,连接BF,CE.下列说法中正确的个数是:①CE=BF;②△ABD 和△ADC 的面积相等;③BF ∥CE;④CE,BF 均与AD 垂直. A.4个 B.3个 C.2个 D.1个 9. 已知一个多边形的每一个外角都等于18°,下列说法错误的是： A.这个多边形是二十边形 B.这个多边形的内角和是3600°C.这个多边形的外角和是360°D.这个多边形的每个内角都是162°10. 某厂接到加工720件衣服的订单,预计每天做48件,正好按时完成,后因客户要求提前5天交货,设每天应多做x 件才能按时交货,则x 应满足的方程为： A.54872048720=+-x B.54872048720+=+x C.572048720=-x D.54872048720=-+x 二、填空题：（本大题共6个小题，每小题3分，共18分）把答案填在答题卡的对应位置的横线上.11.三角形的三边长分别为12,8,5+x ,则x 的取值范围是______________. 12.如图所示,AB=AC,AD=AE,∠BAC=∠DAE,若∠1=34°,∠2=22°,则∠3=_________. 13.计算:20182017)25.0()4(-⨯-=__________.231第14题图第16题图第12题图E DCBCA14.如图,在△ABC 中,∠BAC=90°,∠B=60°,AD ⊥BC 于D,若BC=16,则CD=__________. 15.若关于x 的方程0113=--+x ax 无解,则a 的值为____________. 16.如图,在△ABC 中,∠ACB=90°,△ABD 是△ABC 的轴对称图形.点E 在AD 上,点F 在AC 的延长线上.若点B 恰好在EF 的垂直平分线上,并且AE=5,AF=13,则DE=_________. 三、解答题：（本大题共9个小题，共72分）解答应写出文字说明、证明过程或演算步骤，并且写在答题卡上每题对应的答题区域内.17.（本小题满分6分）如图,点E 、A 、C 在同一条直线上,AB ∥CD,∠B=∠E,AC=CD.求证:BC=ED.E A计算: (1)632422)2(x x x x -+⋅ (2)210)2()21()21(-----++19.（每小题4分,共8分）因式分解: (1)3222a x a ax ++ (2)x x x 8)1)(9(--+20.（每小题4分,共8分） 解方程: (1)12544+=-x x (2)1)3)(2(102+-+=+x x x x21.（本小题满分6分）先化简,再求值:296)252(2-+-÷-++m m m m m ,其中1-=m .22.（本小题满分6分）如图,在所给的网格图中,完成下列各题. (1)画出格点△ABC 关于直线DE 的对称 △A 1B 1C 1;(2)若点A 的坐标为)3,4(-,点B 的坐标为)2,2(-, 则C 1的坐标为________; (3)在DE 上画出点P,使PB+PC 最小.23.（本小题满分10分）2017年3月以来,各种品牌的“共享单车”(俗称“小黄车”)陆续登陆我市中心城区.由于人口密度不同,襄城区与樊城区每1000人中“小黄车”的投放数量也不相同.据相关部门调查统计:襄城区与樊城区每1000人中“小黄车”的投放数量的乘积,恰好是襄城区每1000人中所投放“小黄车”数量的5倍多40辆.(1)如果襄城区每1000人中“小黄车”的投放数量是8辆,并且投放在襄城区的“小黄车”的总数量是3760辆,那么襄城区的人口总数是多少?(2)如果襄城区每1000人中“小黄车”的投放数量是x 辆,那么樊城区每1000人中“小黄车”的投放数量可用含x 的代数式表示为___________;(3)如果“小黄车”在襄城区与樊城区的实际投放总量分别是4480辆与5600辆,并且两个区的人口总和是112万人.请求出(2)中的x .已知:点D 是等边△ABC 的边AB 上任意一点,以CD 为底边在CD 的左侧构造顶角为120°的等腰△CDE.(1)如图1,求证:∠ECB 与∠EDB 互补;(2)如图2,延长BC 至F,使得CF=BD,连接EF 、EB,求证:EF=EB; (3)如图3,在(2)的条件下,连接AE,求证:∠EAD=∠EDA.图3图2图1FECFE CAB AABD D25.（本小题满分10分）已知:在△ABC 中,∠BAC=90°,AB=AC.将△ABC 按如图所示的位置放置在平面直角坐标系中,使得点A ),0(m 落在y 轴的负半轴上,使得点B )0,(n 落在x 轴的正半轴上,点C 在第二象限,并且n m ,满足0258622=+-++n m n m .(1) 由题意可知:OA=_________,OB=_________(直接写答案); (2) 求点C 的坐标;(3) △ABC 的斜边BC 交y 轴于D,直角边AC 交x 轴于E.在AC 上截取AF=CE,连接 DF.探究线段DF 、AD 、BE 的数量关系并证明你的结论.襄城区2017-2018学年度上学期期末测试八年级数学试题参考答案一.选择题二.填空题11.61<<x 12.56° 13.25.0- 14.12 15. 1或3- 16.4 （第15题只填一种情况并且对了的,给2分;若填了两种情况,但有一种错误的,给0分）三.解答题17.证明: ∵AB ∥CD…………............…………………………1分 ∴∠BAC=∠ECD……………………………………2分∴在△ABC 和△CED 中⎪⎩⎪⎨⎧=∠=∠∠=∠CD AC ECD BAC E B ………….......………………4分∴△ABC ≌△CED……………………....…………5分 ∴BC=ED………...........................…………………6分 18. （1）解:原式=66628x x x -+……….........................…………………2分 =67x ………...........................................…………………4分 （2）解:原式=4121--………....................................…………………6分 =45-………............................................…………………8分 19. (1)解：原式＝)2(22a ax x a ++…….....................................…………………2分 ＝2)(a x a +…….................................................…………………4分(2)解：原式＝x x x x 8992--+-……................................…………………6分 ＝92-x …….........................…...............................………………7分＝)3)(3(-+x x …….........................…..................………………8分 20.（1）解：方程两边乘)12)(4(+-x x ，得)4(5)12(4-=+x x …………………................…………………1分 解得 8-=x ………………………………...........................……2分 检验：当8-=x 时，0)12)(4(≠+-x x ………..………………3分 所以原分式方程的解是8-=x ……………………………………4分 （2）解： 方程两边乘)3)(2(-+x x ，得)3)(2(10)3(-++=+x x x x ……….................................…………..……5分解得 2-=x ........................................……………………………………6分检验：当2-=x 时，0)3)(2(=-+x x 因此2-=x 不是原分式方程的解……7分 所以原分式方程无解...............................……………………………………8分21.解:原式2)3(2]252)2)(2([--⋅----+=m m m m m m ..............................…………..……1分 233223(m )(m )m m (m )+--=⋅--................................................…………..……2分 33-+=m m ..............................……..................................................……..……4分 当1-=m 时,原式213131-=--+-=.............................................…………..……6分22.解:(1)如右图所示;(2) )5,1(;(3) 如右图点P 即为所求.(每问2分,共计6分)23.(1)47083760=÷..............…………………......................…………................……1分4700001000470=⨯........................…………………………….............………2分答:襄城区的人口总数是470000人...................................................................…3分(2)xx 405+...........................................................………………………...…………6分 （3）11200001000405560010004480=⨯++⨯xx x............................…7分 解得:8=x ...................................................................................…8分 经检验: 8=x 是原方程的解并且符合实际意义.....................…9分答:(2)中的x 等于8....................................................................…10分 (本题三问按3分+3分+4分,计分)24.(1)证明:∵△ABC 是等边三角形 ∴∠B ＝60º ................................................................................................…1分 又∵∠ECB+∠B+∠BDE+∠DEC=︒=︒⨯-360180)24(................................…2分∴∠ECB+∠BDE=︒360－∠B －∠DEC=360º－60º－120º=180º即∠ECB 与∠BDE 互补....................................................................................…3分(2)证明:∵∠ECB+∠BDE=180º,∠ECB+∠ECF=180º∴∠BDE=∠ECF........................................................…4分∴在△ECF 和△EDB 中⎪⎩⎪⎨⎧=∠=∠=DE CE EDB ECF BD CF∴△ECF ≌△EDB……………………………………5分 ∴EF ＝EB.................................................................…6分(3)证明:由(2)知△ECF ≌△EDB ∴EF ＝EB, ∠F ＝∠DBE. ∴∠F=∠EBC.∴∠DBE=∠EBC ………………….....…………………7分∵△ABC 是等边三角形∴BA=BC ………………………................……………8分∴在△BEC 和△BEA 中⎪⎩⎪⎨⎧=∠=∠=BA BC EBA EBC BE BE∴△BEC ≌△BEA ..............……………………………………9分 ∴CE ＝AE又∵CE ＝DE∴AE=DE∴∠EAD=∠EDA ......………………………………..……10分 (本题三问按3分+3分+4分,计分)25.解：(1)3,4;………………….........……..….................…2分 (2)过点C 作CM ⊥y 轴于M ∵ CM ⊥y 轴,x 轴⊥y 轴∴∠AOB ＝∠CMA ＝90º∴∠OAB+∠OBA ＝90º又∵∠BAC ＝∠OAB+∠MAC ＝90º∴∠OBA ＝∠MAC …..….............................................…3分 在△OBA 和△MAC 中⎪⎩⎪⎨⎧=∠=∠∠=∠AC AB CMA AOB MAC OBA∴△OBA ≌△MAC…..…..........................................…4分 ∴MA=OB=4,CM=OA=3 ∴OM=MA －OA=4－3=1∴点C 的坐标为)1,3(-…..…...................................…5分(3)AD+DF=BE,理由如下:…..…..............................................................…6分 在y 轴上截取AG=BE,连接CG由(2)知∠EBA ＝∠GAC 在△ABE 和△CAG 中⎪⎩⎪⎨⎧=∠=∠=AG BE GAC EBA CA AB∴△ABE ≌△CAG …..…................................................................…7分 ∴AE ＝CG, ∠ACG ＝∠BAE ＝90º ∵AF ＝CE∴AF+EF ＝CE+EF 即CF ＝CG ∵∠BAC ＝90º,AB ＝AC ∴∠ACB ＝45º∴∠GCB ＝∠ACG －∠ACB ＝90º－45º＝45º∴∠GCD ＝∠FCD …..…................................................................…8分在△GCD 和△FCD 中⎪⎩⎪⎨⎧=∠=∠=CD CD FCD GCD CF CG∴△GCD ≌△FCD …..…..............................................................…9分 ∴DF ＝DG∵AD+DG ＝AG∴AD+DF ＝BE …..…..................................................................…10分 (本题三问按2分+3分+5分,计分;第3问还有其它方法,请比照给分)。

襄州区2017—2018学年度上学期期中学业质量调研测试八年级数 学 参 考 答 案(说明：此答案是参考答案，若学生答题出现其他解法，请参照给分。

）一、 选择题（每小题3分，共30分）11. 90º； 12. -1； 13.A8； 14. 23b a ； 15. 12; 16. 7,11. 三、解答题（共72分） 17.（每小题4分，共8分）解：（1）原式=)49)(49(22-+x x ………………2分 =)23)(23)(49(2-++x x x ………………4分 （2）原式=)44(222ab a b ab -+………………2分 =2)2(2b a ab -………………4分 18.（本题6分）解：原式=yx xy y x y x xy y x +-+∙-+-4)(4)(22………………1分 =y x xyy xy x y x xy y xy x +-++∙-++-42422222………………2分 =yx y x y x y x +-∙-+22)()(………………3分 =22))((y x y x y x -=-+………………4分 当97=x ，3=y 时，原式=22397-=（97+3）（97-3）………………5分=100×94=940………………6分 19. （每小题4分，共8分）解：（1）去分母，得)3(52-=x x ………………1分 去括号，得1552-=x x移项，合并同类项，得153=x ………………2分 ∴5=x ………………3分 经检验，5=x 是原方程的解， ∴5=x ………………4分（2）去分母，得526)13(3=⨯--x ………………1分去括号，得51239=--x移项，合并同类项，得209=x ………………2分∴920=x ………………3分 经检验，920=x 是原方程的解，∴920=x ………………4分20.(本题6分）解：设原计划每天植树x 万棵，依据题意可列方程5%)201(6060=+-xx ………………2分 解这个方程得，2=x ………………4分经检验， 2=x 是原方程的解，所以 2=x ……………5分答：原计划每天植树2万棵.………………6分21.（本题8分）解：（1）如图：EF 即为所求做的BC 边上的垂直平分线；…………3分 （2）∵ BD 平分∠ABC ，∠ABD=24°，∴ ∠FBC=24°………………4分 ∵ EF 垂直平分BC ，∴ BF=CF ………………5分 ∴ ∠FCB=∠FBC=24° 在△FDC 中，∠FDC=∠A+∠ABD=60°+24°=84° ……………6分 ∠DFC=∠FCB+∠FBC=24°+24°=48° ………………7分 ∴ ∠ACF=180°-84°-48°=48° ………………8分22.（本题8分）（1）证明：∵DE ⊥AB ，DF ⊥BC ，∴∠BED=∠BFD=90°，………………1分 ∵BD 是△ABC 的角平分线，∴∠EBD=∠FBD ，………………2分 又∵BD=BD ，∴△DBE ≌△DBF ，………………3分 ∴BE=BF ；………………4分（2）解：∵BD 是△ABC 的角平分线，DE ⊥AB ，DF ⊥BC ，∴DF=DE=5，………………5分∴，………………6分 ∴=70﹣40=30，∴BC=12．………………8分23.(本题8分) 解：（1）证明：∵DC‖=AB ，∴∠CDB=∠ABD ，………………1分 又∵BD 平分∠ABC ，∴∠CBD=∠ABD，∴∠CDB=∠CBD，………………2分∴BC=DC，又∵AD=BC，………………3分∴AD=DC；………………4分（2）△DEF为等边三角形，证明：∵BC=DC（已证），CF⊥BD，∴点F是BD的中点，………………5分∵∠DEB=90°，∴EF=DF=BF．………………6分∵∠ABC=60°，BD平分∠ABC，∠BDE=60°，………………7分∴△DEF为等边三角形．………………8分24.(本题8分)解：（1）如图，过点D作DG⊥AC于点G，DH⊥BC于点H∵∠ACB=90°，AC=BC，CD是∠ACB的角平分线∴∠A=∠B=∠ACD=∠BCD=45°，∴AD=CD=BD ………………1分∵在等腰直角三角形ACD中，DG⊥AC，∠A=45°∴DG=AG=AC=2同理DH=2 ………………2分∵S△CDE=CE•DG=4﹣x，S△CDF=CF•DH=4﹣y，………………3分∴S四边形CEDF=S△CDE+S△CDF=（4﹣x）（4﹣y）=8﹣（x+y）=5；……………4分（2）当DE⊥DF时，∠EDF=90°∵CD⊥AB∴∠ADE+∠EDC=∠EDC+∠CDF=90°∴∠ADE=∠CDF，又∵∠A=∠DCF=45°， AD=CD，………………6分在△ADE与△CDF中，，∴△ADE≌△CDF ………………7分∴AE=CF∴AE+BF=CF+BF=BC 即x+y=4．………………8分25.（本题12分）解：（1）在等腰直角三角形DEF中，∠DEF=90°，∵∠1=20°，∴∠2=∠DEF﹣∠1=70°，………………1分∵∠EDA+∠2+∠3=180°，∴∠3=60°，………………2分∵EA⊥AB，∴∠EAB=90°，∵∠3+∠EAB+∠A=180°，∴∠4=30°，………………3分∴AB=2BC=4；………………4分（2）如图1，过D作DM⊥AE于D，在△DEM中，∠2+∠5=90°，∵∠2+∠1=90°，∴∠1=∠5，………………5分∵DE=FE，在△DEM与△EFA中，，∴△DEM≌△EFA，………………6分∴AF=EM，∵∠4+∠B=90°，∵∠3+∠EAB+∠4=180°，∴∠3+∠4=90°，∴∠3=∠B，在△DAM与△ABC中，，∴△DAM≌△ABC，………………7分∴BC=AM，∴AE=EM+AM=AF+BC；………………8分（3）AE+AF=BC.证明：如图2，过D作DM⊥AE交AE的延长线于M，∵∠C=90°，∴∠1+∠B=90°，∵∠2+∠MAB+∠1=180°，∠MAB=90°，∴∠2+∠1=90°，∠2=∠B，………………9分在△ADM与△BAC中，，∴△ADM≌△BAC，∴BC=AM，………………10分∵EF=DE，∠DEF=90°，∵∠3+∠DEF+∠4=180°，∴∠3+∠4=90°，∵∠3+∠5=90°，∴∠4=∠5，在△MED与△AFE中，，∴△MED≌△AFE，………………11分∴ME=AF，∴AE+AF=AE+ME=AM=BC，即AE+AF=BC．………………12分。

2017—2018学年度第一学期期末教学质量检测八年级数学答案 一、选择题： 题号 1 2 3 4 5 6 7 8 答案A DB BCD A C 题号9 10 11 12 13 14 15 16 答案 B D C B C D A B二、填空题：题号17 18 19 答案 15 ∠A ＝∠D 或AB=ED 或 ∠ACB ＝∠DFE 或AC ∥DF 22或（2）3；（2）1-n 或 12-n三、解答题：20.（1）解：原式=)1323(2333232++--÷-⨯ ………………………2分 =324236---- ……………………………………………… 3分 =323-- ……………………………………………………………4分（2）解：①如图所示；……………………………………………6分②100°. ………………………………………………………8分21.解：（1）这个魔方的棱长为：4643=； ………………………2分（2）每个小正方体的棱长为：4÷2=2…………………………3分 阴影部分的边长为：2282222==+=CD ……4分阴影部分的面积为：8)22(22==CD ………………5分（其它解法参照此标准给分）（3）根据图可知122-=a …………………………………6分a a a --+-2)1)(1(=（1122--）（1122+-）－1222+-=（22322)222--⨯-…………………………………………………7分 =223248+--=225-…………………………………………………………………………8分图122.解：原式=[())1(11+-+x x x －()1)1(1+--x x x ]÷()()1122-+-x x x …………………………2分 =()()1111-++-+x x x x ÷()()1122-+-x x x………………………………………………3分 =()()()()2112112--+⨯-+x x x x x ………………………………………………4分 =24-x ……………………………………………………………………………5分 ()0322123221-+-=πx =22222421+⨯-⨯…………………………………………………………6分 =2222+- …………………………………………………………………7分 =22+ …………………………………………………………………………8分 当22+=x 时，原式=22242224==-+. ……………………… 10分 23.（1）解：∵BD 是等边△ABC 的中线，∴BD ⊥AC ，BD 平分AC . …………………………………………………1分∵AB =6∴AD =3………………………………………………………………………2分 ∴由勾股定理得，33363222=-=-=AD AB BD ………………………………4分（2）证明∵BD 是等边△ABC 的中线，∴BD 平分∠ABC∴∠DBE ＝12∠ABC ＝30° …………………………………………………5分 又∵CE ＝CD∴∠E ＝∠CDE ，∠E ＝12∠ACB ＝30°. ∴∠DBE ＝∠E . …………………………………………………………6分∴DB ＝DE .∵DF ⊥BE∴DF 为底边上的中线．∴BF ＝EF . ………………………………………………………………7分（3）解：∵AD ＝CD ，CE ＝CD∴CE ＝CD =3∴BE ＝BC ＋CE =9 ……………………………………………………8分 ∵∠DBE ＝30°，DB ＝33∴DF =21DB ＝21×33=233……………………………………9分 ∴△BDE 的面积=432723392121=⨯⨯=⋅DF BE …………………10分 24.解：（1）60. ……………………………………………………………………………1分（2）设乙队单独施工，需要x 天才能完成该项工程，根据题意可得：31+16×（x 1601+）=1，……………………………………………………3分 解得：x =40，……………………………………………………………4分经检验x =40是原方程的根，…………………………………………………5分答：乙队单独施工，需要40天才能完成该项工程；（3）设乙队参与施工y 天才能完成该项工程，根据题意可得：601×30+y ×401≥1，……………………………………………………7分 解得：y ≥20， …………………………………………………………8分答：乙队至少施工20天才能完成该项工 ………………………………… 10分25.解：（1）BD =CE ，BC = CE +CD ； …………………………………………………2分（2）不成立，存在的数量关系为BC = CE －CD ． ……………………………3分理由：如图11-2，∵∠BAC =∠DAE =90°∴∠BAC +∠CAD =∠DAE +∠CAD即∠BAD =∠CAE …………………………………………………………4分在△ABD 和△ACE 中，，∴△ABD ≌△ACE （SAS ）， ………………………………………………5分∴BD =CE ， …………………………………………………………………6分∴BD =BC +CD ，即CE =BC +CD ，∴BC = CE －CD ； …………………………………………………………7分（3）如图11-3，∵∠BAC =∠DAE =90°∴∠BAC －∠BAE =∠DAE －∠BAE即∠BAD =∠CAE …………………………………………………………8分在△ABD 和△ACE 中，，∴△ABD ≌△ACE （SAS ），………………………………………………10分∴BD=CE，∴CD=BC+BD=BC+CE，…………………………………………………11分∵BC=6，CE=2，∴CD=6+2=8．……………………………………………………………12分小课堂：如何培养自主学习能力？自主学习是与传统的接受学习相对应的一种现代化学习方式。

2017—2018学年第一学期期末学业水平测试八年级数学试题温馨提示:1.本试卷分第Ⅰ卷和第Ⅱ卷两部分，共5页。

满分为120分。

考试用时100分钟。

考试结束后，只上交答题卡。

2.答卷前，考生务必用0.5毫米黑色签字笔将自己的学校、班级、姓名、准考证号、考场、座号填写在答题卡规定的位置上，并用2B 铅笔填涂相应位置。

3．第Ⅰ卷每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号。

答案不能答在试题卷上。

4.第Ⅱ卷必须用0.5毫米黑色签字笔作答，答案必须写在答题卡各题目指定区域内相应的位置，不能写在试题卷上；不准使用涂改液、胶带纸、修正带。

不按以上要求作答的答案无效。

第Ⅰ卷（选择题）一、选择题：本大题共12小题，共36分，在每小题给出的四个选项中，只有一项是正确的，请把正确的选项选出来．每小题选对得3分，选错、不选或选出的答案超过一个均记零分. 1.下列根式中不是最简二次根式的是（A ）13 （B ）12 （C ）42+a （D ）2 2.无论a 取何值时，下列分式一定有意义的是（A ）221aa + （B ）21aa +（C ）112+-a a（D ）112+-a a 3.如图，ABC ABD ∠=∠,要使ABC ABD ∆≅∆,还需添加一个条件，那么在①AC AD =；②BC BD =；③C D ∠=∠；④CAB DAB ∠=∠这四个关系中可以选择的是（A ）①②③ （B ）①②④ （C ）①③④ （D ）②③④4.如图是用直尺和圆规作一个角等于已知角的示意图， 则说明∠A ′O ′B ′＝∠AOB 的依据是 （A ）SSS （B ）SAS （C ）ASA （D ）AAS（第4题图）5.如图，36DBC ECB ∠=∠=︒,72BEC BDC ∠=∠=︒,则图中等腰三角形的个数是 （A ） 5 （B ） 6 （C ） 8（D ） 96.下列运算：（1）a a a 2=+；（2）1243a a a =⨯；（3）()22ab ab = ；（4）()632a a =-.其中错误的个数是（A ） 1 （B ） 2 （C ） 3 （D ） 4 7.若A b a b a +-=+22)()(，则A 等于（A ）ab 2 （B ）ab 2- （C ）ab 4- （D ）ab 48.练习中，小亮同学做了如下4道因式分解题，你认为小亮做得正确的有 ①)1)(1(3-+=+x x x x x ②222)(2y x y xy x -=+- ③1)1(12+-=+-a a a a ④)4)(4(1622y x y x y x -+=- （A ）1个（B ）2个（C ）3个（D ）4个9.关于x 的分式方程101m x x -=+的解，下列说法正确的是 （A ）不论m 取何值，该方程总有解（B ）当1m ≠时该方程的解为1mx m=- （C ）当1,0m m ≠≠且时该方程的解为1mx m=-（D ）当2m =时该方程的解为2x = 10.如果把分式yx x 34y3-中的x 和y 的值都扩大为原来的3倍，那么分式的值（A ）扩大为原来的3倍 （B ）扩大6倍 （C ）缩小为原来的12倍 （D ）不变11.如图，将矩形纸片ABCD 折叠，使点D 与点B 重合，点C 落在C ′处，折痕为EF ，若AB=4，BC=8，则△BC ′F 的周长为（A ）12 （B ）16 （C ）20 （D ）2412．如图，AD 是△ABC 的角平分线，DE ⊥AC ，垂足为E ，BF ∥AC 交ED 的延长线于点F ，若BC 恰好平分∠ABF ，AE ＝2EC ，给出下列四个结论：①DE ＝DF ；②DB ＝DC ；③AD ⊥BC ；④AB ＝3BF ，其中正确的结论共有（A ）①②③ （B ）①③④ （C ）②③ （D ）①②③④第Ⅱ卷（非选择题）二、填空题：本大题共6小题，共24分，只要求填写最后结果，每小题填对得4分． 13.在△ABC 中，∠C=90°，BC=16，∠BAC 的平分线交BC 于D ，且BD ：DC=5：3， 则D 到AB 的距离为_____________．14.已知等腰三角形的一个内角为50°，则顶角角的大小为________________. 15.分解因式：322318122xy y x y x -+- =__________________________________. 16.若362+-mx x 是一个完全平方式，则m=____________________.17.当x 的值为 ，分式242x x -+的值为0.18.如果直角三角形的三边长为10、6、x ，则最短边上的高为______．三、解答题：本大题共6个小题，满分60分．解答时请写出必要的演推过程． 19.（本小题满分8分） （1）计算：)35()35(45205152+--+-. （2）计算：2(3)(3)(2)a b a b a b ---+-20.（每小题5分，共10分）根据要求，解答下列问题： （1）计算：()()()()x x x x x-+--÷-123286234（2）化简：)111(3121322-+--+-⨯--x x x x x x . 21.（本小题满分10分）如图，已知点E 是∠AOB 的平分线上一点，EC ⊥OB ，ED ⊥OA ，C 、D 是垂足.连接CD ， 且交OE 于点F ．（1）求证：OE 是CD 的垂直平分线． （2）若∠AOB=60°，求证：OE=4EF ．22.（本小题满分10分）如图，已知B 、C 、E 三点在同一条直线上，△ABC 与△DCE 都是等边三角形.其中线段 BD 交AC 于点G ，线段AE 交CD 于点F.求证：（1）△ACE ≌△BCD ；（2）△GFC 是等边三角形.23.（本小题满分12分）如图，中，，若动点 P 从点C 开始，按的路径运动，且速度为每秒1cm ，设出发的时间为t 秒． （1）出发2秒后，求的周长． （2）问t 满足什么条件时，为直角三角形？ （3）另有一点Q ，从点C 开始，按的路径运动，且速度为每秒2cm ，若P 、Q 两点同时出（第21题图）发，当P 、Q 中有一点到达终点时，另一点也停止运动当t 为何值时，直线PQ 把的周长分成相等的两部分？24.（本小题满分10分）如图所示，港口A 位于灯塔C 的正南方向，港口B 位于灯塔C 的南偏东60°方向，且港口B 在港口A 的正东方向的135公里处.一艘货轮在上午8时从港口A 出发，匀速向港口B 航行.当航行到位于灯塔C 的南偏东30°方向的D 处时，接到公司要求提前交货的通知，于是提速到原来速度的1.2倍，于上午12时准时到达港口B ，顺利完成交货.求货轮原来的速度是多少？2017—2018学年第一学期期末学业水平测试八年级数学试题参考答案一、选择题（本大题12个小题，每小题3分，共36分）题号 1 2 3 4 5 6 7 8 9 10 11 12 答案BDDACCDBCAAD二、填空题（本大题6个小题，每小题4分，共24分）13.6； 14.50°或80°； 15.232）（y x xy --；AC B第24题图D16.21±； 17.2 ； 18. 8或10 三、解答题（本大题6个小题，共60分） 19.（本小题满分10分）解：（1）原式=)35(453525-++- …………………………2分 =125453525-++- …………………………3分 =1256- ………………………………………………5分（2）2(3)(3)(2)a b a b a b ---+-= 2222944b a a ab b -+-+ ……………4分= 2134b ab - ……………5分20.（每小题5分，共10分）化简： 解：原式()()xx x x x23234322--+-+-=……………4分x x x x x23234322++--+-=23-=x . ……………5分（2）原式＝()()()⎪⎭⎫ ⎝⎛++-+---⨯-+--1111311132x x x x x x x x ……２分 ＝111+++--x xx x ……………４分 ＝11+x . ……………5分21.（本小题满分10分）解：（1）∵OE 是∠AOB 的平分线，EC ⊥OB ，ED ⊥OA ，OE=OE ，∴Rt △ODE ≌Rt △OCE （AAS ）， …………………………2分 ∴OD=OC ，∴△DOC 是等腰三角形， …………………………3分 ∵OE 是∠AOB 的平分线，∴OE 是CD 的垂直平分线. …………………………5分 （2）∵OE 是∠AOB 的平分线，∠AOB=60°，∴∠AOE=∠BOE=30°， ………………6分∵EC⊥OB，ED⊥OA，∴OE=2DE，∠ODF=∠OED=60°，…………………………8分∴∠EDF=30°，∴DE=2EF，…………………………9分∴OE=4EF．…………………………10分22.（本小题满分10分）证明：（1）∵△ABC与△DCE都是等边三角形，∴AC=BC，CE =CD，∠ACB =∠DCE=60°， ------------------------3分∴∠ACB+∠ACD =∠DCE+∠ACD，即∠ACE =∠BCD，∴△ACE≌△BCD（SAS）. ----------------------------5分（2）∵△ABC与△DCE都是等边三角形，CD=ED，∠ABC =∠DCE=60°（此步不再赋分），由平角定义可得∠GCF=60°=∠FCE， ---------------------7分又由（1）可得∠GDC=∠FEC，∴△GDC≌△FEC（AAS）. ----------8分∴GC=FC, --------------------------9分又∠GCF=60°，∴△GFC是等边三角形. -----------------------10分23.解：，，动点P从点C开始，按的路径运动，速度为每秒1cm，出发2秒后，则，，，的周长为：；-----------------3分，动点P从点C开始，按的路径运动，且速度为每秒1cm，在AC上运动时为直角三角形，，当P在AB上时，时，为直角三角形，，，解得：，，，速度为每秒1cm，，综上所述：当或为直角三角形；-----------------8分当P点在AC上，Q在AB上，则，直线PQ把的周长分成相等的两部分，，；当P点在AB上，Q在AC上，则，直线PQ把的周长分成相等的两部分，，，当或6秒时，直线PQ把的周长分成相等的两部分．-------------12分24.（本小题满分10分）解：根据题意，A ∠=90°，ACB ∠=60°，ACD ∠=30°， ∴603030DCB ∠=︒-︒=︒, 906030B ∠=︒-︒=︒， ∴DCB B ∠=∠∴CD BD = -----------2分 ∵A ∠=90°，ACD ∠=30° ∴2CD AD =∴2BD AD = -----------4分 又135AB =∴45AD =,,90BD = -----------5分 设货轮原来的速度是x 公里/时，列方程得45901281.2x x+=- ----------8分 解得 x =30 ----------9分 检验，当x =30时，1.2x ≠0. 所以，原分式方程的解为x =30.答: 货轮原来的速度是30公里/时. -----------10分注意：评分标准仅做参考，只要学生作答正确，均可得分。

湖北省襄阳市襄州区2017-2018学年八年级数学上学期期中试题襄州区2017—2018学年度上学期期中学业质量调研测试八年级数 学 参 考 答 案一、 选择题（每小题3分，共30分）二、 填空题（每小题3分，共18分）11. 90º； 12. 100º； 13.AB=DE(答案不唯一，只要正确即可）； 14. 1； 15. ①④; 16. 5. 三、解答题（共72分） 17.（本题6分）解：在△ABC 中，∵∠B=40°，∠C=60°∴∠BAC=180°-∠B-∠C=180°-40°-60°=80°…………2分 ∵AE 是的角平分线， ∴∠EAC=12∠BAC=12×80°=40°，………………3分 ∵AD 是△ABC 的高，∴∠ADC=90°， ∴在△ADC 中，∠DAC=180°-∠ADC-∠C=180°-90°-60°=30°，………………5分 ∴∠DAE=∠EAC-∠DAC=40°-30°=10°．………………6分18.（本题6分）证明：∵ AE ＝BF ，∴AE ＋EF ＝BF ＋EF ，即AF ＝BE ，………………2分 在△ADF 和△BCE 中，AD BCA B AF BE =⎧⎪∠=∠⎨⎪=⎩………………4分 ∴ ADF BCE ∆≅∆ ………………5分 ∴ DF=CE. ………………6分19. （本题7分）证明：连接CM ；等腰Rt △ABC 中，CM 是斜边AB AB 的中线， ∴CM ⊥BM,∠B ＝∠A ＝45º, ………………2分 ∠BCM ＝MCE ＝90º×21＝45º ………………3分 ∴∠BCM ＝∠MCE ＝∠B, ………………4分 ∴CM=BM ， ………………5分 又∵BD=CE ，∴△MBC ≌△MCE ；………………6分∴MD=ME ． ………………7分20.(本题8分）（1）如图所示，BP 即为所求作的角平分线；…………3分 （2）证明：∵AD ⊥BC,∴∠ADB ＝90º,∴∠BPD ＋∠PBD ＝90º;…………4分 ∵∠BAC ＝90º,∴∠AQP ＋ABQ ＝90º,…………5分 ∵∠ABQ ＝∠CBQ,∴∠BPD ＝∠AQP, …………6分 ∵∠APQ ＝∠BPD,∴∠ABQ ＝∠AQP, …………7分 ∴AP ＝AQ …………8分 21.（本题8分） (1)证明：AE 和BD 相交于点,O AOD BOE ∴∠=∠.在AOD ∆和BOE ∆中，,2A B BEO ∠=∠∴∠=∠.…………2分 又12,1,BEO AEC BED ∠=∠∴∠=∠∴∠=∠.…………4分在AEC ∆和BED ∆中，(),A B AE BEAEC BED ASA AEC BED ∠=∠⎧⎪=∴∆≅∆⎨⎪∠=∠⎩.…………5分 （2）,,AEC BED EC ED C BDE ∆≅∆∴=∠=∠.…………6分在EDC ∆中，,142,69EC ED C EDC =∠=∴∠=∠=，…………7分∴∠=∠=.…………8分BDE C6922.（本题8分）证明：(1) ∵AD=CD，A C∠=∠…………1分∵DE AB⊥，DF BC⊥∴0∠=∠=…………2分90AED CFD∴ADE CDE∆≅∆…………3分(2) ∵ADE CDE∆≅∆，∴AE＝CF,DE=DF,…………4分∴∠DEF=∠DFE,…………5分∵∠BEF＝180º－∠DEF－∠DEA,∠BFE＝180º－∠DFE－∠DFC∴BEF BFE∠=∠…………6分∴BE=BF, …………7分∵DE=DF,∴DB垂直平分EF.…………8分23.(本题9分)解：（1）（2，3）；…………2分（2）如图所示(图略）；…………4分（3）如图所示（图略）：…………6分D（﹣2，﹣3）或（﹣5，3）或（﹣5，﹣3）．……………9分24.(本题10分)解：解：（1）证明：∵CD和BE是△ABC的两条高，∴∠A=∠ACD+∠A=90°，∴∠ABE=∠ACD，………………1分∵∠ACD=∠CBE，∴∠ABE=∠CBE，∵∠BEA=∠BEC=90°，………………2分在△BAE 与△BCE 中，，∴△BAE ≌△BCE ，∴BA=BC ； ………………4分（2） BH=2AE ………………5分证明：∵∠BDC=90°，∠BCD=45°，∴BD=DC ， ………………6分∵∠BDH=∠CDA=90°， 在△BDH 与△CDA 中，，∴△BDH ≌△CDA ，∴BH=AC ， ………………7分∵BE ⊥AC ，∴AC=2AE ，∴BH=2AE. ………………8分（3）DG ＝DH,DF ⊥FC,BE 平分∠ABC （答案较多，只要正确就好）………10分 25.（本题10分）解:(1)∵Rt △ABC 中,∠C=90°，∠A ＝60°,∴∠B ＝30°， ………………1分又∵AB ＝10cm, …………2分∴AM ＝AB －BM ＝10－2t, AN ＝t ； ………………3分(2)∵△AMN 是以MN 为底的等腰三角形,∴AM=AN,即10-2t=t, ………………5分∴当t=310时,△AMN 是以MN 为底边的等腰三角形; ………………6分 (3)当MN ⊥AC 时,MN ∥BC,∵∠C ＝90°,∠A ＝60°,∴∠B ＝30°, ………………7分∵MN ∥BC,∴∠NAP=30°,∴AN ＝21AM,∴t ＝21(10-2t ）， ………………8分 ∴t ＝2.5, ………………9分∴当t ＝2.5时,MN ∥BC. ………………10分。