实用文库汇编之圆的周长提高练习题

2020年北师大版六年级数学上册章节常考题精选汇编（提高版）第一章《圆》一．选择题1．（2019秋•怀柔区期末）数学课上，同学们把一个圆形纸片沿它的半径平均分成若干份以后剪开，用它们拼成一个面积不变的近似的长方形．这个长方形的周长是16.56厘米，这个圆形纸片的面积是( )平方厘米．A ．12.56B ．16.56C ．8.28【解答】解：圆的半径是：16.56(2 3.142)÷+⨯16.56(2 6.28)=÷+16.568.28=÷2=（厘米）圆的面积是：23.142⨯3.144=⨯12.56=（平方厘米）答：这个圆形纸片的面积是12.56平方厘米．故选：A ．2．（2019秋•丰台区期末）一个圆的半径由4厘米增加到9厘米，面积增加了( )平方厘米．A ．25πB ．16πC ．65πD ．169π【解答】解：9944ππ⨯⨯-⨯8116ππ=-65π=（平方厘米）答：面积增加了65π平方厘米．故选：C ．3．（2019秋•丰台区期末）从直径4分米的圆形钢板上挖去一个直径2分米的圆，求剩余部分的面积．下面列式正确的是( )A ．22(42)2ππ÷-B ．22[(42)(22)]π÷-÷C ．22(42)π÷D ．22[(42)(22)]π÷+÷【解答】解：422÷=（分米）221÷=（分米）2221ππ⨯-⨯22(21)π=⨯-(41)π=⨯-3π=（平方分米）答：剩下部分的面积是3π平方分米．即列式正确的是22[(42)(22)]π÷-÷．故选：B ．4．（2019春•泰兴市期末）世界上第一个把圆周率的值精确到六位小数的数学家是( )A ．刘徽B ．祖冲之C ．欧几里德【解答】解：世界上第一个把圆周率的值精确到六位小数的数学家是祖冲之．故选：B ．5．（2017秋•涟源市校级期末）在边长2a 的正方形里面画一个最大的圆，则正方形的面积与圆的面积之比是( )A ．2:1B ．4:1C ．4:πD ．:4π 【解答】解：222(2):[()]2a a π⨯ 224:a a π=4:π=， 答：正方形的面积与圆的面积的比是4:π．故选：C ．二．填空题6．（2019秋•望城区期末）要剪一个周长是12.56厘米的圆形纸片，它的半径是 厘米，这个圆形纸片的面积是 平方厘米．【解答】解：12.56 3.1422÷÷=（厘米）23.142⨯3.144=⨯12.56=（平方厘米）答：这个圆形纸片的面积是12.56平方厘米．故答案为：2、12.56．7．（2019秋•丹江口市期末）把一个圆沿半径分成若干等份，然后拼成一个近似的长方形，量得这个长方形的长是25.12厘米，这个圆的半径是厘米，面积是平方厘米．【解答】解：25.12 3.148÷=（厘米）2⨯=（平方厘米）3.148200.96答：这个圆的半径是8厘米，面积是200.96平方厘米．故答案为：8；200.96．8．（2019秋•中山区期末）一个圆环，内圆的直径是4厘米，外圆的直径是8厘米，圆环的面积是平方厘米．【解答】解：422÷=（厘米）÷=（厘米）82422⨯-3.14(42)=⨯-3.14(164)=⨯3.1412=（平方厘米）37.68答：圆环的面积是37.68平方厘米．故答案为：37.68．9．（2018秋•虹口区期末）将一个半径为5厘米的圆沿半径剪成2个半径相同的扇形，已知大扇形面积为小扇形的4倍，则两个扇形的周长差为厘米．+=【解答】解：415412 3.145()⨯⨯⨯-553=⨯31.45=（厘米）18.84答：两个扇形的周长差为18.84厘米．故答案为：18.84．10．（2018秋•浦东新区期末）如果一个半径为2cm的圆的面积恰好与一个半径为4cm的扇形面积相等，那么这个扇形的圆心角度数为 ．【解答】解：23.142⨯3.144=⨯12.56=（平方厘米）设这个扇形的圆心角度数为x 度， 23.14412.56360x ⨯⨯= 3.141612.56360x ⨯⨯= 12.5612.5690x ⨯=190x = 90x =答：这个扇形的圆心角度数为90度．故答案为：90度．11．（2018秋•上海期末）已知扇形的半径是2cm ，面积是243cm π，那么扇形的圆心角是 度；扇形的周长是 cm ．【解答】解：设扇形的圆心角的度数是n ︒2423360n ππ= 3603n =÷120n =1203.142222360⨯⨯⨯+⨯ 4.194≈+ 8.19=（厘米）答：扇形的圆心角是120度；扇形的周长是8.19cm ．故答案为：120，8.19．三．判断题12．（2019秋•碑林区校级期末）大圆的圆周率与小圆的圆周率相等． √ ． （判断对错）【解答】解：因为任意圆的圆周率=圆的周长÷圆的直径，圆周率是一个定值，用π表示，所以大圆的圆周率与小圆的圆周率相等．故判断为：√．13．（2019秋•惠州期末）圆的周长与它直径的比值是3.14． ⨯ （判断对错）【解答】解：圆的周长与直径的比值是圆周率π， 3.14π≈，所以原题说法错误；故答案为：⨯．14．（2020•法库县）直径是圆内最长的线段． √ （判断对错）【解答】解：通过直径的定义可知：在一个圆中，圆内最长的线段是圆的直径的说法是正确的； 故答案为：√．15．（2018秋•白云区期末）一个圆的周长是1256m ，半径增加了1m 后，面积增加了23.14m ． ⨯ （判断对错）【解答】解答：原来周长半径为：1256 3.142200()m ÷÷=原来面积为：23.14200200125600()m ⨯⨯=增加后的半径是2001201+=（米）增加的面积为：3.14201201 3.14200200⨯⨯-⨯⨯3.14(201201200200)=⨯⨯-⨯3.14401=⨯21259.14()m =答：面积增加了21259.14m ．所以原题说法错误．故答案为：⨯．16．（2011秋•浦东新区期末）用圆规画圆，圆的大小是由圆规的两脚之间的距离来决定． √ （判断对错）．【解答】解：由分析可知：用圆规画圆，圆规两脚间的距离是圆的半径，半径决定圆的大小．故答案为：√．17．圆转化成长方形后，面积不变，周长不变． ⨯ （判断对错）【解答】解：如图圆转化成长方形后，面积不变，周长比原周长多了两条半径的长度．原题的说法名错误．故答案为：⨯．四．计算题18．（2018秋•营山县期末）求图中形阴影部分的面积．（可以直接用π表示，也可以π取3.14)【解答】解：1025()÷=cm2⨯-⨯÷⨯3.14510522=-78.5502=cm28.5()答：阴影部分的面积是228.5cm．19．（2019•郑州模拟）计算阴影部分的面积．【解答】解：20210÷=（厘米）2⨯-⨯2020 3.1410=-⨯400 3.14100=-400314=（平方厘米）86答：阴影部分的面积是86平方厘米．20．（2019春•蓬溪县期末）公园有一个周长31.4米的圆形喷水池，现在准备在它的周围种植一圈宽1米的草皮（如图），种植草皮的面积是多少平方米？【解答】解：水池的半径：31.4 3.1425÷÷=（米）草坪的面积：223.14[(51)5]⨯+-3.14[3625]=⨯-3.1411=⨯34.54=（平方米）答：种植草皮的面积是34.54平方米．21．（2018秋•涿州市期末）一个座钟的分针长20厘米，45分钟后，分针尖端走过的长度是多少厘米？【解答】解：3.14202(4560)⨯⨯⨯÷ 33.14404=⨯⨯ 3.1430=⨯94.2=（厘米）答：分针尖端走过的长度是94.2厘米．22．（2016秋•建瓯市期中）大圆的半径是10厘米，小圆的半径是8厘米．那么环形的面积是多少？【解答】解：223.14(108)⨯-3.14(10064)=⨯-113.04=（平方厘米）答：圆环的面积是113.04平方厘米．23．一个圆的直径是12厘米，若半径延长13，则面积是原来的多少倍？ 【解答】解：因为圆的面积与半径的平方成正比，所以面积是原来的：21(1)3+ 24()3= 169= 答：面积是原来的169倍． 24．一块正方形铁板，在上面画一个最大的圆，已知圆的周长是18.84分米．这块铁板的面积是多少平方分米？【解答】解：18.84 3.146÷=（分米）6636⨯=（平方分米）答：这块铁板的面积是36平方分米．六．解答题25．（2019秋•文水县期末）画一画，算一算．（1）量出下面线段的长度 厘米．（取整厘米数）（2）在线段AB 上取一点O ，使:1:2AO OB =（3）以点O 为圆心．OA 长为半径画一个圆，并算出这个圆的面积．【解答】解：（1）量得线段的长度是6厘米．（2）6(12)÷+63=÷2=（厘米）所以AO 的长度是2厘米，如下图：（3）这个圆是以点O为圆心，2厘米为半径的圆，如下图：圆的面积：23.142⨯=⨯3.144=（平方厘米）12.56答：这个圆的面积是12.56平方厘米．故答案为：2．26．（2019秋•灵武市期末）看图计算：（1）已知图中三角形的面积是50平方厘米，圆的面积是多少平方厘米？（2）计算如图的表面积和体积．（单位：米）【解答】解：（1）设圆的半径是r厘米，则根据三角形的面积是50平方厘米，可得2250r÷=，所以2502100r=⨯=，因此圆的面积为：⨯=（平方厘米）．3.14100314答：圆的面积是314平方厘米．（2）(535232)2⨯+⨯+⨯⨯(15106)2=++⨯312=⨯62=（平方米）； 53230⨯⨯=（立方米）； 答：这个长方体的表面积是62平方米，体积是30立方米．27．（2019秋•汉南区期末）公园里有一个直径是8米的圆形花坛，在花坛周围有一条宽2米的小路．这条石子小路的面积是多少？【解答】解：内圆半径是：824÷=（米)223.14[(42)4]⨯+-3.14[3616]=⨯-3.1420=⨯62.8=（平方米）答：石子路的面积有62.8平方米．28．（2019秋•孝昌县期末）公园里有一个圆形花坛，花坛半径是10米，现在要进行扩建，要求扩建后花坛的半径是原来的32．扩建后花坛的面积比原来面积大多少平方米？ 【解答】解：2233.14[(10)10]2⨯⨯- 3.14[225100]=⨯-3.14125=⨯392.5=（平方米）； 答：扩建后花坛的面积比原来面积大392.5平方米．29．（2019秋•宜宾期中）如果大圆的半径等于小圆的直径，则大圆半径是小圆半径的 倍．小圆的面积是大圆面积的()()． 【解答】解：设小圆的半径为r ，则大圆的半径为2r ，22r r ÷=小圆面积：大圆面积22:[(2)]r r ππ=⨯22:[4]r r ππ=1:4 ；如果大圆的半径等于小圆的直径，则大圆半径是小圆半径的2倍，小圆的面积是大圆面积的14．故答案为：2、14．。

圆的周长提高练习题（4）一、填空1．一只羊栓在一块草地中央的树桩上，树桩到羊颈的绳长是 3米。

这只羊可以吃到（）平方米地面的草。

2．一根 2米长的铁丝，围成一个半径是30厘米的圆，（接头处不计），还多（）米，围成的面积是（）3．用一根 10.28米的绳子，围成一个半圆形，这个半圆的半径是（），面积是（）4．从一个长8分米，宽5分米的长方形木板上锯下一个最大的圆，这个圆的面积是（）5．大圆的半径等于小圆的直径，大圆的面积是小圆面积的（） 20．一个圆的周长扩大3倍，面积就扩大（）倍。

6.用三根同样长的铁丝分别围成一个长方形、一个正方形、和一个圆，其中（）面积最小，（）面积最大。

7.一种钟表的分针长5cm，1小时分针尖端走过的距离是（）分米，分针所扫过的面积（）平方分米。

二、解决问题1、一个圆形花圃直径8米，用四分之三种兰花，兰花的种植面积是多少？2、一个圆形花坛的半径是10米，沿着花坛的周围每隔5米种一盆花，一共可以种盆花？3、阿姨要用藤条做5个圆环，每隔圆环的直径是20分米，5个圆环的接头处共需要10分米。

30米的藤条够用吗？4、一种零件的横截面是一个圆环，外圈半径是0.5米，内圈半径是0.4米.这种零件横截面的面积是多少平方米？5、有一个圆形拱门，门高2米。

这个拱门的门框是多少米？拱门的面积是多少平方米？6、一个花坛的周长是47.1米。

小明在花坛周围滚铁环，铁环直径是30厘米，围着花坛转一周，铁环要转多少圈？《圆的面积》教学设计教学内容：六年级数学上册第67-68页圆的面积。

教学目标：1：认知目标理解圆的面积的含义；理解和掌握圆的面积公式。

2：过程与方法目标经历圆的面积公式的推导过程，体验实验操作，逻辑推理的学习方法。

3：情感目标引导学生进一步体会“转化”的数学思想，初步了解极限思想；体验发现新知识的快乐，增强学生的合作交流意识和能力，培养学生学习数学的兴趣。

教学重点：正确掌握圆面积的计算公式。

（专题精选）初中数学圆的难题汇编含解析一、选择题1．已知⊙O的直径CD=10cm，AB是⊙O的弦，AB=8cm，且AB⊥CD，垂足为M，则AC的长为（）A．25cm B．45 cm C．25cm或45cm D．23cm或43cm【答案】C【解析】连接AC，AO，∵O的直径CD=10cm，AB⊥CD，AB=8cm，∴AM=12AB=12×8=4cm,OD=OC=5cm,当C点位置如图1所示时，∵OA=5cm，AM=4cm，CD⊥AB，∴222254OA AM-=-=3cm，∴CM=OC+OM=5+3=8cm，∴22224845AM CM+=+=；当C点位置如图2所示时，同理可得OM=3cm，∵OC=5cm，∴MC=5−3=2cm，在Rt△AMC中22224225AM CM+=+=cm.故选C.2．如图，已知AB是⊙O的直径，CD是弦，且CD⊥AB，BC=3，AC=4，则sin∠ABD的值是（）A．43B．34C．35D．45【答案】D【解析】【分析】由垂径定理和圆周角定理可证∠ABD=∠ABC，再根据勾股定理求得AB=5，即可求sin∠ABD 的值．【详解】∵AB是⊙O的直径，CD⊥AB，∴弧AC=弧AD，∴∠ABD=∠ABC．根据勾股定理求得AB=5，∴sin∠ABD=sin∠ABC=45．故选D．【点睛】此题综合考查了垂径定理以及圆周角定理的推论，熟悉锐角三角函数的概念．3．如图，在平行四边形ABCD中，BD⊥AD，以BD为直径作圆，交于AB于E，交CD于F，若BD=12，AD：AB=1：2，则图中阴影部分的面积为（）A．3B．36ππC．312πD．48336ππ【答案】C【解析】【分析】易得AD长，利用相应的三角函数可求得∠ABD的度数，进而求得∠EOD的度数，那么一个阴影部分的面积=S△ABD-S扇形DOE-S△BOE，算出后乘2即可．【详解】连接OE，OF．∵BD=12，AD ：AB=1：2，∴AD=43 ，AB=83，∠ABD=30°，∴S △ABD =×43×12=243,S 扇形=603616,633933602OEB S ππ⨯==⨯⨯=V ∵两个阴影的面积相等，∴阴影面积=()224369330312ππ⨯--=- .故选：C【点睛】本题主要是理解阴影面积等于三角形面积减扇形面积和三角形面积．4．如图，AB 是⊙O 的直径，EF ，EB 是⊙O 的弦，且EF=EB ，EF 与AB 交于点C ，连接OF ，若∠AOF=40°，则∠F 的度数是（ ）A ．20°B ．35°C ．40°D ．55°【答案】B【解析】【分析】 连接FB ，由邻补角定义可得∠FOB=140°，由圆周角定理求得∠FEB=70°，根据等腰三角形的性质分别求出∠OFB 、∠EFB 的度数，继而根据∠EFO ＝∠EBF-∠OFB 即可求得答案.【详解】连接FB ，则∠FOB=180°-∠AOF=180°-40°=140°，∴∠FEB＝12∠FOB=70°，∵FO＝BO，∴∠OFB＝∠OBF=(180°-∠FOB)÷2=20°，∵EF＝EB，∴∠EFB＝∠EBF=(180°-∠FEB)÷2=55°，∴∠EFO＝∠EBF-∠OFB=55°-20°=35°，故选B.【点睛】本题考查了圆周角定理、等腰三角形的性质等知识，正确添加辅助线，熟练掌握和灵活运用相关知识是解题的关键.5．如图，△ABC的外接圆是⊙O，半径AO=5，sinB=25，则线段AC的长为（）A．1 B．2 C．4 D．5【答案】C【解析】【分析】首先连接CO并延长交⊙O于点D，连接AD，由CD是⊙O的直径，可得∠CAD=90°，又由⊙O的半径是5，sinB=25，即可求得答案．【详解】解：连接CO并延长交⊙O于点D，连接AD，由CD是⊙O的直径，可得∠CAD=90°，∵∠B和∠D所对的弧都为弧AC，∴∠B=∠D，即sinB=sinD=25，∵半径AO=5，∴CD=10，∴2 sin105AC ACDCD===，∴AC=4，故选：C.【点睛】本题考查了同弧所对的圆周角相等，以及三角函数的内容，注意到直径所对的圆周角是直角是解题的关键.6．如图，点I为△ABC的内心，AB=4，AC=3，BC=2，将∠ACB平移使其顶点与I重合，则图中阴影部分的周长为（）A．4.5 B．4 C．3 D．2【答案】B【解析】【分析】连接AI、BI，因为三角形的内心是角平分线的交点，所以AI是∠CAB的平分线，由平行的性质和等角对等边可得：AD=DI，同理BE=EI，所以图中阴影部分的周长就是边AB 的长．【详解】连接AI、BI，∵点I为△ABC的内心，∴AI平分∠CAB，∴∠CAI=∠BAI，由平移得：AC∥DI，∴∠CAI=∠AID，∴∠BAI=∠AID，∴AD=DI，同理可得：BE=EI，∴△DIE的周长=DE+DI+EI=DE+AD+BE=AB=4，即图中阴影部分的周长为4，故选B．【点睛】本题考查了三角形内心的定义、平移的性质及角平分线的定义等知识，熟练掌握三角形的内心是角平分线的交点是关键．7．如图，ABC ∆是O e 的内接三角形，45A ∠=︒，1BC =，把ABC ∆绕圆心O 按逆时针方向旋转90︒得到DEB ∆，点A 的对应点为点D ，则点A ，D 之间的距离是（）A ．1B ．2 C ．3 D ．2【答案】A【解析】【分析】 连接AD ，构造△ADB ，由同弧所对应的圆周角相等和旋转的性质，证△ADB 和△DBE 全等，从而得到AD=BE=BC=1.【详解】如图，连接AD ，AO ，DO∵ABC ∆绕圆心O 按逆时针方向旋转90︒得到DEB ∆，∴AB=DE ，90AOD ∠=︒，45CAB BDE ∠=∠=︒∴1452ABD AOD ∠=∠=︒（同弧所对应的圆周角等于圆心角的一半）， 即45ABD EDB ∠=∠=︒，又∵DB=BD ，∴DAB BED ∠=∠（同弧所对应的圆周角相等），在△ADB 和△DBE 中 ABD EDB AB EDDAB BED ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ADB ≌△EBD （ASA ）,∴AD=EB=BC=1.故答案为A.【点睛】本题主要考查圆周角、圆中的计算问题以及勾股定理的运用；顶点在圆上，两边都与圆相交的角角圆周角；掌握三角形全等的判定是解题的关键.8．如图，在扇形OAB中，120AOB∠=︒，点P是弧AB上的一个动点（不与点A、B重合），C、D分别是弦AP，BP的中点．若33CD=，则扇形AOB的面积为（）A．12πB．2πC．4πD．24π【答案】A【解析】【分析】如图，作OH⊥AB于H．利用三角形中位线定理求出AB的长，解直角三角形求出OB即可解决问题．【详解】解：如图作OH⊥AB于H．∵C、D分别是弦AP、BP的中点．∴CD是△APB的中位线，∴AB＝2CD＝63∵OH⊥AB，∴BH＝AH＝33∵OA＝OB，∠AOB＝120°，∴∠AOH＝∠BOH＝60°，在Rt△AOH中，sin∠AOH＝AHAO，∴AO＝336sin3AHAOH==∠，∴扇形AOB的面积为：2120612360ππ=g g，故选：A．【点睛】本题考查扇形面积公式，三角形的中位线定理，解直角三角形等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考常考题型．9．如图，已知AB是⊙O的直径，点C在⊙O上，过点C的切线与AB的延长线交于点P，连接AC，若∠A=30°，PC=3，则⊙O的半径为（）A．3B．23C．32D．23【答案】A【解析】连接OC，∵OA=OC，∠A=30°，∴∠OCA=∠A=30°，∴∠COB=∠A+∠ACO=60°，∵PC是⊙O切线，∴∠PCO=90°，∠P=30°，∵PC=3，∴OC=PC•tan30°3故选A10．如图，以Rt△ABC的直角边AB为直径作⊙O交BC于点D，连接AD，若∠DAC＝30°，DC＝1，则⊙O的半径为（）A ．2B ．3C ．2﹣3D ．1【答案】B【解析】【分析】 先由圆周角定理知∠BDA=∠ADC=90°，结合∠DAC=30°，DC=1得AC=2DC=2，∠C=60°，再由AB=ACtanC=23可得答案．【详解】∵AB 是⊙O 的直径，∴∠BDA ＝∠ADC ＝90°，∵∠DAC ＝30°，DC ＝1，∴AC ＝2DC ＝2，∠C ＝60°，则在Rt △ABC 中，AB ＝ACtanC ＝23，∴⊙O 的半径为3，故选：B ．【点睛】本题主要考查圆周角定理，解题的关键是掌握半圆（或直径）所对的圆周角是直角和三角函数的应用．11．如图，O e 中，若66OA BC AOB ⊥∠=o 、，则ADC ∠的度数为（ ）A ．33°B ．56°C ．57°D ．66°【答案】A【解析】【分析】 根据垂径定理可得»»ACAB =，根据圆周角定理即可得答案．【详解】∵OA ⊥BC ，∴»»ACAB =， ∵∠AOB=66°，∠AOB 和∠ADC 分别是»AB和»AC 所对的圆心角和圆周角， ∴∠ADC=12∠AOB=33°， 故选：A ．【点睛】 本题考查垂径定理及圆周角定理，垂直于弦的直径平分弦，并且平分这条弦所对的两条弧；在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半；熟练掌握相关定理是解题关键．12．在平面直角坐标系内，以原点O 为圆心，1为半径作圆，点P 在直线323y x =+上运动，过点P 作该圆的一条切线，切点为A ，则PA 的最小值为( )A ．3B ．2C ．3D ．2 【答案】D 【解析】【分析】先根据题意，画出图形，令直线y= 3x+ 23与x 轴交于点C ，与y 轴交于点D ，作OH ⊥CD 于H ，作OH ⊥CD 于H ；然后根据坐标轴上点的坐标特点，由一次函数解析式，求得C 、D 两点的坐标值； 再在Rt △POC 中，利用勾股定理可计算出CD 的长，并利用面积法可计算出OH 的值； 最后连接OA ，利用切线的性质得OA ⊥PA ，在Rt △POH 中，利用勾股定理，得到21PA OP =-，并利用垂线段最短求得PA 的最小值即可.【详解】如图， 令直线3x+23x 轴交于点C ，与y 轴交于点D ，作OH ⊥CD 于H ， 当x=0时，y=3D （0，3当y=033，解得x=-2，则C （-2，0），∴222(23)4 CD=+=，∵12OH•CD=12OC•OD，∴OH=2233⨯=.连接OA，如图，∵PA为⊙O的切线，∴OA⊥PA，∴2221PA OP OA OP=-=-，当OP的值最小时，PA的值最小，而OP的最小值为OH的长，∴PA的最小值为22(3)12-=.故选D.【点睛】本题考查了切线的性质，解题关键是熟记切线的性质：圆的切线垂直于经过切点的半径．若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．13．已知圆锥的三视图如图所示，则这个圆锥的侧面展开图的面积为（）A．60πcm2B．65πcm2C．120πcm2D．130πcm2【答案】B【解析】【分析】先利用三视图得到底面圆的半径为5cm，圆锥的高为12cm，再根据勾股定理计算出母线长为13cm，然后根据圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和扇形的面积公式计算．【详解】根据三视图得到圆锥的底面圆的直径为10cm，即底面圆的半径为5cm，圆锥的高为12cm，所以圆锥的母线长=225+12=13，所以这个圆锥的侧面积=12×2π×5×13=65π（cm 2）． 故选B ．【点睛】本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．也考查了三视图．14．中国科学技术馆有“圆与非圆”展品，涉及了“等宽曲线”的知识．因为圆的任何一对平行切线的距离总是相等的，所以圆是“等宽曲线”．除了例以外，还有一些几何图形也是“等宽曲线”，如勒洛只角形(图1)，它是分别以等边三角形的征个顶点为圆心，以边长为半径，在另两个顶点间画一段圆弧．三段圆弧围成的曲边三角形．图2是等宽的勒洛三角形和圆．下列说法中错误的是( )A ．勒洛三角形是轴对称图形B ．图1中，点A 到¶BC上任意一点的距离都相等 C ．图2中，勒洛三角形上任意一点到等边三角形DEF 的中心1O 的距离都相等D ．图2中，勒洛三角形的周长与圆的周长相等【答案】C【解析】【分析】根据轴对称形的定义，可以找到一条直线是的图像左右对着完全重合，则为轴对称图形.鲁列斯曲边三角形有三条对称轴. 鲁列斯曲边三角形可以看成是3个圆心角为60°，半径为DE 的扇形的重叠，根据其特点可以进行判断选项的正误.【详解】鲁列斯曲边三角形有三条对称轴，就是等边三角形的各边中线所在的直线，故正确；点A 到¶BC上任意一点的距离都是DE ，故正确; 勒洛三角形上任意一点到等边三角形DEF 的中心1O 的距离都不相等，1O 到顶点的距离是到边的中点的距离的2倍，故错误；鲁列斯曲边三角形的周长=3×60180DE DE ππ⨯=⨯ ,圆的周长=22DE DE ππ⨯=⨯ ,故说法正确.故选C.【点睛】主要考察轴对称图形，弧长的求法即对于新概念的理解．15．“直角”在几何学中无处不在，下列作图作出的AOB ∠不一定．．．是直角的是（ ） A ． B ．C ．D ．【答案】C【解析】【分析】根据作图痕迹，分别探究各选项所做的几何图形问题可解.【详解】解：选项A 中，做出了点A 关于直线BC 的对称点，则AOB ∠是直角.选项B 中，AO 为BC 边上的高，则AOB ∠是直角.选项D 中，AOB ∠是直径AB 作对的圆周角，故AOB ∠是直角.故应选C【点睛】本题考查了尺规作图的相关知识，根据基本作图得到的结论，应用于几何证明是解题关键．16．如图，将边长为2cm 的正方形ABCD 沿直线l 向右翻动（不滑动），当正方形连续翻动8次后，正方形的中心O 经过的路线长是（ ）cm ．A ．2B ．8C ．3πD ．4π【答案】D【解析】【分析】由题意可得翻转一次中心O 经过的路线长就是1个半径为1，圆心角是90°的弧长，然后进行计算即可解答．【详解】解：∵正方形ABCD cm ，∴对角线的一半＝1cm ，则连续翻动8次后，正方形的中心O 经过的路线长＝8×901180π⨯＝4π． 故选：D ．【点睛】本题考查了弧长的计算，审清题意、确定点O 的路线和长度是解答本题的关键．17．下列命题中哪一个是假命题（ ）A ．8的立方根是2B ．在函数y ＝3x 的图象中，y 随x 增大而增大C ．菱形的对角线相等且平分D ．在同圆中，相等的圆心角所对的弧相等【答案】C【解析】【分析】利用立方根的定义、一次函数的性质、菱形的性质及圆周角定理分别判断后即可确定正确的选项．【详解】A 、8的立方根是2，正确，是真命题；B 、在函数3y x =的图象中，y 随x 增大而增大，正确，是真命题；C 、菱形的对角线垂直且平分，故错误，是假命题；D 、在同圆中，相等的圆心角所对的弧相等，正确，是真命题，故选C ．【点睛】考查了命题与定理的知识，能够了解立方根的定义、一次函数的性质、菱形的性质及圆周角定理等知识是解题关键．18．若正六边形的半径长为4，则它的边长等于（ ）A ．4B ．2C ．D ．【答案】A【解析】试题分析：正六边形的中心角为360°÷6=60°，那么外接圆的半径和正六边形的边长将组成一个等边三角形，故正六边形的半径等于4，则正六边形的边长是4．故选A ． 考点：正多边形和圆．19．如图，四边形ABCD是⊙O的内接四边形，若∠BOD=86°，则∠BCD的度数是（）A．86°B．94°C．107°D．137°【答案】D【解析】【分析】【详解】解：∵∠BOD=86°，∴∠BAD=86°÷2=43°，∵∠BAD+∠BCD=180°，∴∠BCD=180°-43°=137°，即∠BCD的度数是137°．故选D．【点睛】本题考查圆内接四边形的对角互补．②圆内接四边形的任意一个外角等于它的内对角（就是和它相邻的内角的对角）．20．如图，四边形ABCD为⊙O的内接四边形．延长AB与DC相交于点G，AO⊥CD，垂足为E，连接BD，∠GBC=50°，则∠DBC的度数为（）A．50°B．60°C．80°D．90°【答案】C【解析】【分析】根据圆内接四边形的性质得：∠GBC=∠ADC=50°，由垂径定理得：··，则∠CM DMDBC=2∠EAD=80°．【详解】如图，∵四边形ABCD为⊙O的内接四边形，∴∠GBC=∠ADC=50°．∵AE⊥CD，∴∠AED=90°，∴∠EAD=90°﹣50°=40°，延长AE交⊙O于点M．∵AO⊥CD，∴··，∴∠DBC=2∠EAD=80°．CM DM故选C．【点睛】本题考查了圆内接四边形的性质：圆内接四边形的任意一个外角等于它的内对角，还考查了垂径定理的应用，属于基础题．。

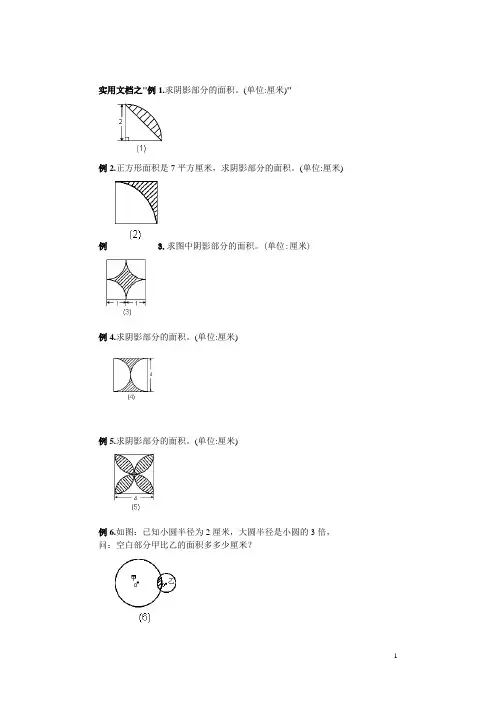
实用文档之"例1.求阴影部分的面积。

(单位:厘米)"例2.正方形面积是7平方厘米，求阴影部分的面积。

(单位:厘米) 例 3.求图中阴影部分的面积。

(单位:厘米)例4.求阴影部分的面积。

(单位:厘米)例5.求阴影部分的面积。

(单位:厘米)例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米？例7.求阴影部分的面积。

(单位:厘米)例8.求阴影部分的面积。

(单位:厘米)例9.求阴影部分的面积。

(单位:厘米)例10.求阴影部分的面积。

(单位:厘米)例11.求阴影部分的面积。

(单位:厘米)例12.求阴影部分的面积。

(单位:厘米)例13.求阴影部分的面积。

(单位:厘米)例14.求阴影部分的面积。

(单位:厘米)例15.已知直角三角形面积是12平方厘米，求阴影部分的面积。

例16.求阴影部分的面积。

(单位:厘米)例17.图中圆的半径为5厘米,求阴影部分的面积。

(单位:厘米)例18.求阴影部分的面积。

(单位:厘米)例19.正方形边长为2厘米，求阴影部分的面积。

例20.如图，正方形ABCD的面积是36平方厘米，求阴影部分的面积。

例21.如图，正方形边长为8厘米，求阴影部分的面积。

例21.如图，三角形ABC是直角三角形，阴影部分甲比阴影部分乙面积大28平方厘米，AB=40厘米。

求BC的长度。

.例22求阴影部分的面积例23求阴影部分的周长与面积例24求阴影部分的周长与面积例25求阴影部分的周长与面积例26求阴影部分的周长与面积例27求阴影部分的周长与面积例28求阴影部分的周长与面积例29求阴影部分的面积例30求阴影部分的面积例31正方形面积是7平方厘米，求阴影部分的面积和周长。

(单位:厘米)例32求图中阴影部分的面积和周长。

(单位:厘米)例33求图中阴影部分的面积和周长。

(单位:厘米)例34求图中阴影部分的面积和周长。

(单位:厘米)例35求图中阴影部分的面积和周长。

必考专题：圆应用题（真题汇编）数学六年级上册人教版1．（2022上·河南信阳·六年级统考期末）下图中，大圆面积与小圆面积的比是5∶3，已知阴影部分的面积是12平方厘米，占小圆面积的14。

大圆的面积是多少平方厘米？2．（2022上·河南信阳·六年级统考期末）在一个圆形花坛的周围每隔1.57米放一盆花，一共放了20盆花，这个花坛的直径是多少米？3．（2022上·河南信阳·六年级统考期末）一块圆形玉佩（如图）。

外圈是环形玉石，中间镶嵌圆形黄金。

这块玉佩所用玉石的面积是多少平方厘米？4．（2021上·湖南长沙·六年级统考期末）小杰在边长10cm的正方形中画了一个最大的圆（如图）。

求图中阴影部分的面积？( 取3.14)5．（2022上·河南南阳·六年级统考期末）如图三角形ABC是一个等腰直角三角形，AB＝BC＝10分米，图中涂色部分的面积是多少平方分米？6．（2022上·湖南永州·六年级期末）有一个周长是94.2米的圆形草坪，公园准备为它安装自动旋转喷灌装置进行喷灌。

（1）应将这个喷灌装置安装在草坪的什么位置合适？（2）现有射程为30米、20米、15米三种装置，你认为应选哪种比较合适？为什么呢？7．（2021上·河南郑州·六年级统考期末）如图（单位：厘米），长方形的周长是多少厘米？（请写出你的思考过程）8．（2022上·海南省直辖县级单位·六年级统考期末）宾馆大厅里有一个圆形的吊灯，周长是62.8分米，这个吊灯的面积是多少平方分米？9．（2022上·广东江门·六年级统考期末）图中正方形的边长是6厘米。

（1）在圆内画一个圆心角是90°的扇形。

（保留找圆心痕迹）（2）如果把这个圆剪去，剩下部分的面积是多少平方厘米？10．（2022上·山东济南·六年级校考期末）一个周长是50.24厘米的圆，半径增加了4厘米，面积增加了多少平方厘米？11．（2022上·辽宁鞍山·六年级统考期末）中国建筑中经常能见到“外方内圆”和“外圆内方”的设计。

圆的周长和面积演习题(二)一.填空（基本题）：1.圆的周长老是直径长度的（）倍多一些.这个倍数是个固定的数,我们把它叫做（）,用字母（）暗示.2.用字母暗示圆周长的公式是（）或（）.3.自行车的车轮滚动一周,所行的旅程是车轮的（）.4.要画一个半径为4厘米的圆,圆规的两脚应叉开（）厘米;要画一个周长是18.84厘米的圆,圆规的两脚应叉开（）厘米.5.大圆直径是小圆直径的3倍,大圆周长是小圆周长的（）倍.6.一个周长是12.56厘米的圆,半径是（）厘米.列式：7.做r=20cm的铁圈100个,须要铁丝（）米.列式：8.把一块边长是10分米的正方形铁片,剪成一个最大的圆形,这个圆的周长是（）.列式：二.剖析题意,写公式,解决问题（进步题）1.一种压路机的前轮直径是6分米,假如它每分钟转3周,它每分钟进步若干？2.一只大钟,分钟长60厘米,2个小时后,分针的尖端走了若干厘米？3.一根铁丝长18.84米,绕成10个圈,每个圆形圈的半径是若干？4.一根铁丝正好折成一个等边三角形,它的边长为31.4厘米,假如把同样长的铁丝围成一个圆,这个圆的直径长若干厘米？三、求暗影部分的周长和面积一.填空1.一个圆形桌面的直径是2米,它的面积是（）平方米.2．已知圆的周长,求d=（）,求r=（）. 3．环形面积S＝（）.4．圆的半径扩展2倍,直径就扩展（）倍,周长就扩展（）倍,面积就扩展（）倍.5．用圆规画一个周长50.24厘米的圆,圆规两脚尖之间的距离应是（）厘米,画出的这个圆的面积是（）平方厘米.20．一个圆的周长扩展3倍,面积就扩展（）倍.6．大圆半径是小圆半径的4倍,大圆周长是小圆周长的（）倍,小圆面积是大圆面积的（）.7．圆的半径增长5倍,圆的周长增长（）,圆的面积增长（）.8．一个半圆的周长是20.56分米,这个半圆的面积是（）平方分米.9．将一个圆平均分成1000个完整雷同的小扇形,割拼成近似的长方形的周长比本来圆周长长10厘米,这个长方形的面积是（）平方厘米.10．在一个面积是16平方厘米的正方形内画一个最大的圆,这个圆的面积是（）平方厘米;再在这个圆内画一个最大的正方形,正方形的面积是（）平方厘米.11．大圆半径是小圆半径的3倍,大圆面积是84.78平方厘米,则小圆面积为（）平方厘米.12．大圆半径是小圆半径的2倍,大圆面积比小圆面积多12平方厘米,小圆面积是（）平方厘米.13．鼓楼中间岛是半径10米的圆,它的占地面积是（）平方米.14．小华量得一根树干的周长是75.36厘米,这根树干的横截面大约是（）平方厘米15．一只羊栓在一块草地中心的树桩上,树桩到羊颈的绳长是3米.这只羊可以吃到（）平方米地面的草.16．一根2米长的铁丝,围成一个半径是30厘米的圆,（接头处不计）,还多（）米,围成的面积是（）17．用一根10.28米的绳索,围成一个半圆形,这个半圆的半径是（）,面积是（）18．从一个长8分米,宽5分米的长方形木板上锯下一个最大的圆,这个圆的面积是（）19．大圆的半径等于小圆的直径,大圆的面积是小圆面积的（）20．用三根同样长的铁丝分离围成一个长方形.一个正方形.和一个圆,个中（）面积最小,（）面积最大.二.断定（1）经由过程圆心的线段,叫做圆的直径.（）（2）周长是地点圆直径的3.14倍.（）（3）统一个圆内,半径是直径的一半.（）（4）任何圆的圆周率都是π.（）（5）半径是2厘米的圆,它的周长和面积相等.（）（6）两个圆的面积相等,则两个圆的半径必定相等.（）（7）假如一个圆的直径缩小2倍,那么它的周长也缩小2倍,面积则缩小4倍（）四.运用题1．一个环形的外圆半径是8分米,内圆半径5分米,求环形的面积？2.环形的外圆周长是18.84厘米,内圆直径是4厘米,求环形的面积？3．校园圆形花池的半径是6米,在花池的四周修一条1米宽的水泥路,求水泥路的面积是若干平方米？4．将一根长100米的绳索,绕一棵大树20圈少48厘米,这棵大树横截面面积是若干平方厘米？5.（1）轧路机前轮直径1.2米,每分钟滚动6周.1小时能进步若干米？（2）自行车轮胎外直径71厘米,每分钟滚动100圈.经由过程一座1000米的大桥约需几分钟？（3）在一张长７厘米,宽４厘米的长方形纸上剪一个直径为２厘米的圆,最多可以剪几个？6．一个水缸,从里面量,缸口直径是50厘米,缸壁厚5厘米.要制做一个缸盖,使它正好盖住缸口的外沿,这个缸盖的面积是若干平方厘米？假如在缸盖的边沿贴上一圈金属（不计接头）,这个金属条长若干厘米？7．一种自行车轮胎外直径35.36厘米,假如平均每分钟转100圈,经由过程长1670米的武汉长江大桥,须要若干分钟？（得数保存整数）8、一根铁丝长37.68米,在一根圆形木棒上正好绕200圈,木棒横截面的半径是若干厘米？9.一根铁丝长6.28米,正好在一棵树的1米高处的树干处绕了10圈,那么这棵树的1米高处的树干的横截面的直径是若干厘米？10.一个时钟的时针长20厘米,假如走一日夜,那么它的尖端所走过的旅程有多长？时针所扫过的面积有多大？11.一辆自行车的直径是0.4米,假如小明骑着这辆自行车以每分钟100圈的速度经由一座桥,一共用了3分钟,那么这座桥有多长？12.李大爷靠墙围了一个半径是10米的半圆形养鸡场,用了多长的篱笆？这个养鸡场有多大？假如不靠墙围,那么须要多长的篱笆？1、一辆自行车车轮外直径为0.6米,小华骑自行车从家到黉舍,假如每分钟迁移转变100周,他从家到黉舍动身10分钟到达黉舍,小华家距黉舍若干米？2、火车轮的外直径长0.9米,假如它分钟转400周,那么这列火车每小时进步若干千米？3、一辆自行车轮胎的外直径是70厘米,假如车轮平均每分钟转100圈,半小时可以行若干米？4、一个圆形花园直径8米,用四分之三种兰花,兰花的栽种面积是若干？5、在一张边长10厘米的正方形纸上剪一个最大的圆后,这个圆周长和面积各是若干？6、在一张周长为4厘米的正方形硬纸板上,剪一个最大的圆,剩下部分的面积是若干平方厘米？7、用两根长12.56厘米的铁丝分离围成一个正方形和一个圆,哪个面积大？大若干？8、在一个长8分米,宽5分米的白铁皮上剪下一个最大的圆,剪去的边角料的面积是若干平方分米？9、一种零件的横截面是一个圆环,外圈半径是0.5米,内圈半径是0.4米.这种零件横截面的面积是若干平方米？。

章节测试题1.【答题】已知半圆的半径是，则计算它的周长算式是（）.A. B.C. D.【答案】D【分析】此题考查的是半圆的周长.注意半圆的周长是圆的周长的一半+圆的直径．【解答】半圆的周长为.选D.2.【答题】圆的周长和直径越大，圆周率就越大．（）【答案】×【分析】此题考查的是圆周率的认识．【解答】圆周率是圆的周长与直径的比值，是一个固定不变的数，不随周长和直径的变化而变化.故此题是错误的.3.【答题】圆周率就是圆的周长除以直径的商．（）【答案】✓【分析】此题考查的是圆周率的认识.【解答】根据圆周率的定义可知，圆周率是圆的周长除以直径的商.故此题是正确的.4.【答题】圆的周长与它的直径的比值是.（）【答案】✓【分析】根据圆周率的含义：圆的周长和它直径的比值叫做圆周率，进而得出结论.【解答】根据圆周率的含义，圆的周长与它的直径的比值，所以原题的说法是正确的.5.【答题】如图，阴影部分的周长是（）cm．A.πB.2πC.4πD.2.5π【答案】B【分析】要求阴影部分的周长，先根据圆的周长的计算公式“C=πd”分别求出小圆的周长和大圆的周长，进而求出大圆的半圆弧的长，继而根据“阴影部分周长=大圆半圆弧的长+小圆的周长”进行解答即可．【解答】π×2÷2+π×（2÷2）=π+π=2π（厘米），所以阴影部分的周长是2πcm．6.【答题】两个圆的周长不相等，是因为它们的（）A.圆心位置不同B.半径不同C.圆周率不同【答案】B【分析】根据“圆心决定圆的位置，半径决定圆的大小”和“圆的周长=2πr”进行分析，进而得出结论．【解答】由“圆的周长=2πr”可知：圆的周长和半径、圆周率有关系.因为圆周率不变，所以只与半径有关，则两个圆的周长不相等，是因为半径不同．7.【答题】一辆赛车绕半径为100米的圆形跑道逆时针行驶一周，外轮比内轮多跑4π米，则两轮之间距离为（）A.2π米B.1米C.2米D.4米【答案】C【分析】外轮比内轮多跑4π米，指的是两个圆的周长差，所以用周长差除以圆周率即可求出两圆的直径差，再除以2即可求出半径差，即两个轮子之间的宽度.【解答】4π÷π÷2=2（米）.8.【答题】在400米道上进行200米赛跑，弯道部分是半圆，半径为36米，每条跑道宽1.2米，第4道与第1道起跑线相差（）米.A.1.21πB.2.4πC.3.6πD.36π【答案】C【分析】因为跑道长400米，所以跑200米，只跑路程的一半，所以第4道与第1道起跑线相差（4-1）个1.2米，据此解答即可.【解答】1.2×（4-1）×π=3.6×π=3.6π，故选C.9.【答题】丽丽测得一棵树树干的周长是1.57米，这棵树树干的直径大约是（）米．A.0.25B.0.5C.2D.3.14【答案】B【分析】此题就是求周长为1.57米的圆的直径，根据圆的周长公式可得，圆的直径=周长÷π，由此计算即可解决问题．【解答】1.57÷3.14=0.5（米），所以这棵树树干的直径为0.5米．10.【答题】画一个周长是18.84厘米的圆，圆规的两脚之间的距离应该是（）厘米．A.3B.6C.9D.12【答案】A【分析】圆规两脚之间的距离即为这个圆的半径，由圆的周长公式即可解决问题．【解答】18.84÷3.14÷2=3（厘米），答：圆规的两脚之间的距离应该是3厘米．11.【答题】画一个周长是15.7cm的圆时，圆规两脚间的距离应取（）A.5cmB.15.7cmC.2.5cmD.3.14cm【答案】C【分析】求圆规两脚之间的距离实际上是求这个圆的半径，圆的周长已知，则可以利用圆的周长=2πr，求出这个圆的半径．【解答】15.7÷（2×3.14）=15.7÷6.28=2.5（厘米），所以两脚之间的距离是2.5厘米．12.【答题】一个挂钟的时针长2.5厘米，一昼夜这根时针的尖端走了（）A.15.7厘米B.31.4厘米【答案】B【分析】根据题意知道，时针一昼夜走了两个圆的周长，由此根据圆的周长公式C=2πr，即可求出答案．【解答】3.14×2.5×2×2=3.14×5×2=3.14×10=31.4（厘米），所以一昼夜这根时针的尖端走了31.4厘米.13.【答题】要把圆的周长扩大到原来的4倍，半径应（）A.扩大到原来的2倍B.扩大到原来的4倍C.扩大到原来的8倍【答案】B【分析】根据圆的周长C=2πr可得：圆的周长与半径成正比例，由此即可解答．【解答】根据题干分析可得，圆的周长与半径成正比例，所以把圆的周长扩大到原来的4倍，半径应扩大到原来的4倍．14.【答题】已知半圆形所在圆的直径是6厘米，那么这个半圆形的周长是（）厘米．A.15.42B.9.42C.18.84D.14.13【分析】半圆的周长=整圆的周长的一半+一条直径的长度，据此代入数据即可解答．【解答】3.14×6÷2+6=9.42+6=15.42（厘米），所以这个半圆的周长是15.42厘米．15.【答题】一台拖拉机，后轮直径是前轮的2倍，后轮转动4圈，前轮转动（）圈．A.2B.4C.8D.16【答案】C【分析】根据题意，可设前轮直径为d，那么后轮直径为2d，根据圆的周长公式可计算出前轮滚动一圈的周长和后轮滚动一圈的周长，再用后轮行的周长的路程乘4就是后轮共行的路程，已知前轮行的总路程等于后轮行的总路程，可用后轮行走的总路程除以前轮滚动一圈长度就是前轮滚动的圈数，列式解答即可得到答案．【解答】设前轮直径为d，那么后轮直径为2d，后轮行的路程为：4×2πd=8πd，前轮行的圈数为：8πd÷dπ=2（圈）.所以前轮转动8圈．16.【答题】一个圆的直径是3厘米，它的周长是（）A.9.42厘米B.12.56厘米C.8.52厘米【答案】A【分析】本题考察的知识点是圆的周长公式.【解答】已知直径，求周长，用公式：Ｃ＝πd.17.【答题】半圆的周长就是圆周长的一半. ( )【答案】×【分析】如图所示，半圆的周长应是圆周长的一半再加一条直径.【解答】半圆的周长应是圆周长的一半再加一条直径，所以原题的说法是错误的.18.【答题】一个圆的周长是直径的3.14倍. ( )【答案】×【分析】因为圆的周长C＝，所以一个圆的周长是直径的倍.【解答】因为圆的周长C＝，所以一个圆的周长是直径的倍.所以原题的说法是错误的.19.【答题】直径越大，圆周率越大；直径越小，圆周率越小.( )【答案】×【分析】根据圆周率的含义：圆的周长和它的直径的比值叫做圆周率.圆周率是一个定制，用字母“”表示.【解答】根据圆周率的含义，圆周率是一个定值，所以原题的说法是错误的.20.【答题】一个圆的周长是25.12厘米，它的直径是______厘米.【答案】8【分析】根据圆的周长C=πd，所以直径＝圆的周长÷，由此解答.【解答】25.12÷3.14＝8（厘米）.。

一、圆的综合真题与模拟题分类汇编（难题易错题）1．如图1，直角梯形OABC中，BC∥OA，OA=6，BC=2，∠BAO=45°．（1）OC的长为；（2）D是OA上一点，以BD为直径作⊙M，⊙M交AB于点Q．当⊙M与y轴相切时，sin∠BOQ=；（3）如图2，动点P以每秒1个单位长度的速度，从点O沿线段OA向点A运动；同时动点D以相同的速度，从点B沿折线B﹣C﹣O向点O运动．当点P到达点A时，两点同时停止运动．过点P作直线PE∥OC，与折线O﹣B﹣A交于点E．设点P运动的时间为t （秒）．求当以B、D、E为顶点的三角形是直角三角形时点E的坐标．【答案】（1）4；（2）35；（3）点E的坐标为（1，2）、（53，103）、（4，2）．【解析】分析：（1）过点B作BH⊥OA于H，如图1（1），易证四边形OCBH是矩形，从而有OC=BH，只需在△AHB中运用三角函数求出BH即可．（2）过点B作BH⊥OA于H，过点G作GF⊥OA于F，过点B作BR⊥OG于R，连接MN、DG，如图1（2），则有OH=2，BH=4，MN⊥OC．设圆的半径为r，则MN=MB=MD=r．在Rt△BHD中运用勾股定理可求出r=2，从而得到点D与点H重合．易证△AFG∽△ADB，从而可求出AF、GF、OF、OG、OB、AB、BG．设OR=x，利用BR2=OB2﹣OR2=BG2﹣RG2可求出x，进而可求出BR．在Rt△ORB中运用三角函数就可解决问题．（3）由于△BDE的直角不确定，故需分情况讨论，可分三种情况（①∠BDE=90°，②∠BED=90°，③∠DBE=90°）讨论，然后运用相似三角形的性质及三角函数等知识建立关于t的方程就可解决问题．详解：（1）过点B作BH⊥OA于H，如图1（1），则有∠BHA=90°=∠COA，∴OC∥BH．∵BC∥OA，∴四边形OCBH是矩形，∴OC=BH，BC=OH．∵OA=6，BC=2，∴AH=0A﹣OH=OA﹣BC=6﹣2=4．∵∠BHA=90°，∠BAO=45°，∴tan∠BAH=BHHA=1，∴BH=HA=4，∴OC=BH=4．故答案为4．（2）过点B作BH⊥OA于H，过点G作GF⊥OA于F，过点B作BR⊥OG于R，连接MN、DG，如图1（2）．由（1）得：OH =2，BH =4． ∵OC 与⊙M 相切于N ，∴MN ⊥OC ． 设圆的半径为r ，则MN =MB =MD =r ． ∵BC ⊥OC ，OA ⊥OC ，∴BC ∥MN ∥OA ． ∵BM =DM ，∴CN =ON ，∴MN =12（BC +OD ），∴OD =2r ﹣2，∴DH =OD OH -=24r -．在Rt △BHD 中，∵∠BHD =90°，∴BD 2=BH 2+DH 2，∴（2r ）2=42+（2r ﹣4）2． 解得：r =2，∴DH =0，即点D 与点H 重合，∴BD ⊥0A ，BD =AD ． ∵BD 是⊙M 的直径，∴∠BGD =90°，即DG ⊥AB ，∴BG =AG ． ∵GF ⊥OA ，BD ⊥OA ，∴GF ∥BD ，∴△AFG ∽△ADB ， ∴AF AD =GF BD =AG AB =12，∴AF =12AD =2，GF =12BD =2，∴OF =4，∴OG同理可得：OB AB ，∴BG =12AB ．设OR =x ，则RG x ．∵BR ⊥OG ，∴∠BRO =∠BRG =90°，∴BR 2=OB 2﹣OR 2=BG 2﹣RG 2， ∴（2﹣x 2=（）2﹣（x ）2．解得：x =5，∴BR 2=OB 2﹣OR 2=（2﹣（5）2=365，∴BR =5．在Rt △ORB 中，sin ∠BOR =BR OB35．故答案为35． （3）①当∠BDE =90°时，点D 在直线PE 上，如图2．此时DP =OC =4，BD +OP =BD +CD =BC =2，BD =t ，OP =t ． 则有2t =2． 解得：t =1．则OP =CD =DB =1． ∵DE ∥OC ，∴△BDE ∽△BCO ，∴DE OC =BD BC =12，∴DE =2，∴EP =2， ∴点E 的坐标为（1，2）． ②当∠BED =90°时，如图3．∵∠DBE =OBC ，∠DEB =∠BCO =90°，∴△DBE ∽△OBC ，∴BEBC =2DB BE OB ∴，∴BE =5t ． ∵PE ∥OC ，∴∠OEP =∠BOC ．∵∠OPE =∠BCO =90°，∴△OPE ∽△BCO ，∴OEOB =25OPBC∴，=2t，∴OE=5t．∵OE+BE=OB=255，∴t+5t=25．解得：t=53，∴OP=53，OE=55，∴PE=22OE OP-=103，∴点E的坐标为（51033，）．③当∠DBE=90°时，如图4．此时PE=PA=6﹣t，OD=OC+BC﹣t=6﹣t．则有OD=PE，EA=22PE PA+=2（6﹣t）=62﹣2?t，∴BE=BA﹣EA=42﹣（62﹣2t）=2t﹣22．∵PE∥OD，OD=PE，∠DOP=90°，∴四边形ODEP是矩形，∴DE=OP=t，DE∥OP，∴∠BED=∠BAO=45°．在Rt△DBE中，cos∠BED=BEDE=2，∴DE=2BE，∴t=22（t﹣22）=2t﹣4．解得：t=4，∴OP=4，PE=6﹣4=2，∴点E的坐标为（4，2）．综上所述：当以B、D、E为顶点的三角形是直角三角形时点E的坐标为（1，2）、（51033，）、（4，2）．点睛：本题考查了圆周角定理、切线的性质、相似三角形的判定与性质、三角函数的定义、平行线分线段成比例、矩形的判定与性质、勾股定理等知识，还考查了分类讨论的数学思想，有一定的综合性．2．如图，AB 为⊙O 的直径，AC 为⊙O 的弦，AD 平分∠BAC ，交⊙O 于点D ，DE ⊥AC ，交AC 的延长线于点E ．（1）判断直线DE 与⊙O 的位置关系，并说明理由； （2）若AE ＝8，⊙O 的半径为5，求DE 的长．【答案】（1）直线DE 与⊙O 相切（2）4 【解析】试题分析：（1）连接OD ，∵AD 平分∠BAC ，∴EAD OAD ∠∠＝，∵OA OD ＝，∴ODA OAD ∠∠＝，∴ODA EAD ∠∠＝，∴EA ∥OD ，∵DE ⊥EA ，∴DE ⊥OD ，又∵点D 在⊙O 上，∴直线DE 与⊙O 相切 （2）如图1，作DF ⊥AB ，垂足为F ，∴DFA DEA 90∠∠︒＝＝，∵EAD FAD ∠∠＝，AD AD ＝，∴△EAD ≌△FAD ，∴AF AE 8＝＝，DF DE ＝，∵OA OD 5＝＝，∴OF 3＝，在Rt △DOF 中，22DF 4OD OF -＝＝，∴AF AE 8＝＝ 考点：切线的证明，弦心距和半径、弦长的关系点评：本题难度不大，第一小题通过内错角相等相等证明两直线平行，再由两直线平行推出同旁内角相等．第二小题通过求出两个三角形全等，从而推出对应边相等，接着用弦心距和弦长、半径的计算公式，求出半弦长．3．如图，在锐角△ABC 中，AC 是最短边．以AC 为直径的⊙O ，交BC 于D ，过O 作OE ∥BC ，交OD 于E ，连接AD 、AE 、CE ． （1）求证：∠ACE=∠DCE ；（2）若∠B=45°，∠BAE=15°，求∠EAO 的度数；（3）若AC=4，23CDF COE S S ∆∆=，求CF 的长．【答案】（1）证明见解析，（2）60°；（3）43【解析】 【分析】（1）易证∠OEC =∠OCE ，∠OEC =∠ECD ，从而可知∠OCE =∠ECD ，即∠ACE =∠DCE ； （2）延长AE 交BC 于点G ，易证∠AGC =∠B +∠BAG =60°，由于OE ∥BC ，所以∠AEO =∠AGC =60°，所以∠EAO =∠AEO =60°； （3）易证12COE CAES S=，由于23CDF COES S=，所以CDF CAES S =13，由圆周角定理可知∠AEC =∠FDC =90°，从而可证明△CDF ∽△CEA ，利用三角形相似的性质即可求出答案． 【详解】（1）∵OC =OE ，∴∠OEC =∠OCE ．∵OE ∥BC ，∴∠OEC =∠ECD ，∴∠OCE =∠ECD ，即∠ACE =∠DCE ； （2）延长AE 交BC 于点G ．∵∠AGC 是△ABG 的外角，∴∠AGC =∠B +∠BAG =60°． ∵OE ∥BC ，∴∠AEO =∠AGC =60°． ∵OA =OE ，∴∠EAO =∠AEO =60°．（3）∵O 是AC 中点，∴12COE CAESS =． 23CDF COES S=，∴CDF CAES S=13． ∵AC 是直径，∴∠AEC =∠FDC =90°． ∵∠ACE =∠FCD ，∴△CDF ∽△CEA ，∴CF CA =3，∴CF =3CA =43．【点睛】本题考查了圆的综合问题，涉及平行线的性质，三角形的外角的性质，三角形中线的性质，圆周角定理，相似三角形的判定与性质等知识，需要学生灵活运用所学知识．4．函数是描述客观世界运动变化的重要模型，理解函数的本质是重要的任务。

（完整版）圆的周长的练习题圆的周长的练习题圆的周长提高练习题一、计算下列各题，并熟记它们的得数。

∏=3.14 2∏= 3∏= 4∏= 5∏=6∏= 7∏= 8∏= 9∏= 10∏=二、填空（基础题）：1、圆的周长总是直径长度的（）倍多一些。

这个倍数是个固定的数，我们把它叫做（），用字母（）表示。

2、用字母表示圆周长的公式是（）或（）。

3、自行车的车轮滚动一周，所行的路程是车轮的（）。

4、要画一个半径为4厘米的圆，圆规的两脚应叉开（）厘米；要画一个周长是18.84厘米的圆，圆规的两脚应叉开（）厘米。

5、大圆直径是小圆直径的3倍，大圆周长是小圆周长的（）倍。

6、圆的直径扩大3倍，周长就（）倍，圆的周长缩小4倍，半径就（）。

7、在一个长5厘米，宽3厘米的长方形中花一个最大的圆，这个圆的半径式（）厘米。

8、把一块边长是10分米的正方形铁片，剪成一个最大的圆形，这个圆的周长是（）。

列式：9、用铁丝把2根横截面直径都是20厘米的圆木捆在一起，如果接头处铁丝长5厘米，那么捆一周至少需要（）厘米的铁丝。

三、判断1、圆的半径都相等。

2、半圆的周长等于圆周长的一半。

3、两端在圆上的线段，直径最长。

4、将一个圆的半径扩大2倍，它的直径比原来圆的直径扩大4倍。

5、车轮滚动一周所行的路程就是这个车轮的周长。

（）6、大圆的圆周率大于小圆的圆周率。

（）三、分析题意，写公式，解决问题（提高题）1、用一根3.14分米的铁丝围成一个正方形，它的边长是多少？如果围成一个圆，这个圆的半径是多少厘米？2、一个半圆的直径10分米，这个半圆的周长多少分米？3、一个圆形花坛的直径是8m ，在花坛的周围摆放盆花,每隔1.57 m 放一盆，一共可以放几盆花？4、一只挂钟的分针长20厘米，经过30分钟后，分针的尖端所走的路程是多少厘米？经过45分钟呢？5、一只挂钟分针的针尖在41小时内，正好走了25.12厘米。

它的分针长多少？ 6、小军用一根30米长的绳子测一棵树的直径，在树干上绕了10圈多了1.74米。

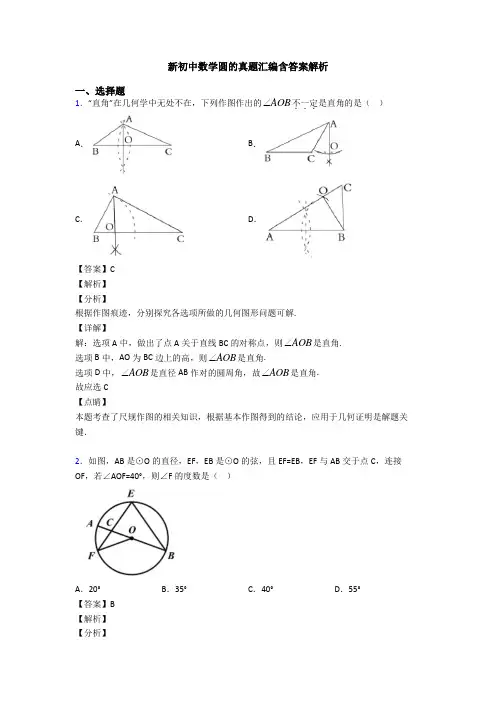
新初中数学圆的真题汇编含答案解析一、选择题1．“直角”在几何学中无处不在，下列作图作出的AOB ∠不一定．．．是直角的是（ ） A ． B ．C ．D ．【答案】C【解析】【分析】根据作图痕迹，分别探究各选项所做的几何图形问题可解.【详解】解：选项A 中，做出了点A 关于直线BC 的对称点，则AOB ∠是直角.选项B 中，AO 为BC 边上的高，则AOB ∠是直角.选项D 中，AOB ∠是直径AB 作对的圆周角，故AOB ∠是直角.故应选C【点睛】本题考查了尺规作图的相关知识，根据基本作图得到的结论，应用于几何证明是解题关键．2．如图，AB 是⊙O 的直径，EF ，EB 是⊙O 的弦，且EF=EB ，EF 与AB 交于点C ，连接OF ，若∠AOF=40°，则∠F 的度数是（ ）A ．20°B ．35°C ．40°D ．55°【答案】B【解析】【分析】连接FB，由邻补角定义可得∠FOB=140°，由圆周角定理求得∠FEB=70°，根据等腰三角形的性质分别求出∠OFB、∠EFB的度数，继而根据∠EFO＝∠EBF-∠OFB即可求得答案.【详解】连接FB，则∠FOB=180°-∠AOF=180°-40°=140°，∴∠FEB＝12∠FOB=70°，∵FO＝BO，∴∠OFB＝∠OBF=(180°-∠FOB)÷2=20°，∵EF＝EB，∴∠EFB＝∠EBF=(180°-∠FEB)÷2=55°，∴∠EFO＝∠EBF-∠OFB=55°-20°=35°，故选B.【点睛】本题考查了圆周角定理、等腰三角形的性质等知识，正确添加辅助线，熟练掌握和灵活运用相关知识是解题的关键.3．已知，如图，点C，D在⊙O上，直径AB=6cm，弦AC，BD相交于点E，若CE=BC，则阴影部分面积为（）A．934π-B．9942π-C．39324π-D．3922π-【答案】B【解析】【分析】连接OD、OC，根据CE=BC，得出∠DBC=∠CEB=45°，进而得出∠DOC=90°，根据S阴影=S 扇形-S△ODC即可求得．【详解】连接OD、OC，∵AB 是直径,∴∠ACB=90°，∵CE=BC ，∴∠CBD=∠CEB=45°，∴∠COD =2∠DBC=90°，∴S 阴影=S 扇形−S △ODC =2903360π⋅⋅ −12×3×3=94π −92. 故答案选B.【点睛】本题考查的知识点是扇形面积的计算，解题的关键是熟练的掌握扇形面积的计算.4．如图，ABC ∆是O e 的内接三角形，45A ∠=︒，1BC =，把ABC ∆绕圆心O 按逆时针方向旋转90︒得到DEB ∆，点A 的对应点为点D ，则点A ，D 之间的距离是（）A ．1B 2C 3D ．2【答案】A【解析】【分析】 连接AD ，构造△ADB ，由同弧所对应的圆周角相等和旋转的性质，证△ADB 和△DBE 全等，从而得到AD=BE=BC=1.【详解】如图，连接AD ，AO ，DO∵ABC ∆绕圆心O 按逆时针方向旋转90︒得到DEB ∆，∴AB=DE ，90AOD ∠=︒，45CAB BDE ∠=∠=︒ ∴1452ABD AOD ∠=∠=︒（同弧所对应的圆周角等于圆心角的一半）， 即45ABD EDB ∠=∠=︒，又∵DB=BD ，∴DAB BED ∠=∠（同弧所对应的圆周角相等），在△ADB 和△DBE 中 ABD EDB AB EDDAB BED ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ADB ≌△EBD （ASA ）,∴AD=EB=BC=1.故答案为A.【点睛】本题主要考查圆周角、圆中的计算问题以及勾股定理的运用；顶点在圆上，两边都与圆相交的角角圆周角；掌握三角形全等的判定是解题的关键.5．如图，在扇形OAB 中，120AOB ∠=︒，点P 是弧AB 上的一个动点（不与点A 、B 重合），C 、D 分别是弦AP ，BP 的中点．若33CD =，则扇形AOB 的面积为（ ）A ．12πB ．2πC ．4πD ．24π【答案】A【解析】【分析】 如图，作OH ⊥AB 于H ．利用三角形中位线定理求出AB 的长，解直角三角形求出OB 即可解决问题．【详解】解：如图作OH⊥AB于H．∵C、D分别是弦AP、BP的中点．∴CD是△APB的中位线，∴AB＝2CD＝63∵OH⊥AB，∴BH＝AH＝33∵OA＝OB，∠AOB＝120°，∴∠AOH＝∠BOH＝60°，在Rt△AOH中，sin∠AOH＝AH AO，∴AO＝336 sin3AHAOH==∠，∴扇形AOB的面积为：2120612360ππ=g g，故选：A．【点睛】本题考查扇形面积公式，三角形的中位线定理，解直角三角形等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考常考题型．6．已知锐角∠AOB如图，（1）在射线OA上取一点C，以点O为圆心，OC长为半径作»PQ，交射线OB于点D，连接CD；（2）分别以点C，D为圆心，CD长为半径作弧，交»PQ于点M，N；（3）连接OM，MN．根据以上作图过程及所作图形，下列结论中错误的是（）A．∠COM=∠COD B．若OM=MN，则∠AOB=20°C．MN∥CD D．MN=3CD【答案】D【解析】【分析】由作图知CM=CD=DN，再利用圆周角定理、圆心角定理逐一判断可得．【详解】解：由作图知CM=CD=DN，∴∠COM=∠COD，故A选项正确；∵OM=ON=MN，∴△OMN是等边三角形，∴∠MON=60°，∵CM=CD=DN，∴∠MOA=∠AOB=∠BON=13∠MON=20°，故B选项正确；∵∠MOA=∠AOB=∠BON=20°，∴∠OCD=∠OCM=80°，∴∠MCD=160°，又∠CMN=12∠AON=20°，∴∠MCD+∠CMN=180°，∴MN∥CD，故C选项正确；∵MC+CD+DN＞MN，且CM=CD=DN，∴3CD＞MN，故D选项错误；故选：D．【点睛】本题主要考查作图-复杂作图，解题的关键是掌握圆心角定理和圆周角定理等知识点．7．如图，以Rt△ABC的直角边AB为直径作⊙O交BC于点D，连接AD，若∠DAC＝30°，DC＝1，则⊙O的半径为（）A．2 B．3C．2﹣3D．1【答案】B【解析】【分析】先由圆周角定理知∠BDA=∠ADC=90°，结合∠DAC=30°，DC=1得AC=2DC=2，∠C=60°，再由AB=ACtanC=23可得答案．【详解】∵AB是⊙O的直径，∴∠BDA＝∠ADC＝90°，∵∠DAC＝30°，DC＝1，∴AC＝2DC＝2，∠C＝60°，则在Rt△ABC中，AB＝ACtanC＝23，∴⊙O的半径为3，故选：B．【点睛】本题主要考查圆周角定理，解题的关键是掌握半圆（或直径）所对的圆周角是直角和三角函数的应用．的扇形无重叠地围成一个圆锥，则这个圆锥的高8．如图，用半径为12cm，面积272cm为（）A ．12cmB ．6cmC ．6√2 cmD ．63 cm 【答案】D【解析】 【分析】 先根据扇形的面积公式计算出扇形的圆心角，再利用周长公式计算出底面圆的周长，得出半径．再构建直角三角形，解直角三角形即可．【详解】 72π=212360n π⨯ 解得n=180°，∴扇形的弧长=18012180π⨯=12πcm ． 围成一个圆锥后如图所示：因为扇形弧长=圆锥底面周长即12π=2πr解得r=6cm ，即OB=6cm根据勾股定理得OC=22126=63-cm ，故选D ．【点睛】本题综合考查了弧长公式，扇形弧长=用它围成的圆锥底面周长，及勾股定理等知识，所以学生学过的知识一定要结合起来．9．木杆AB 斜靠在墙壁上，当木杆的上端A 沿墙壁NO 竖直下滑时，木杆的底端B 也随之沿着射线OM 方向滑动．下列图中用虚线画出木杆中点P 随之下落的路线，其中正确的是（ ）A ．B ．C ．D ．【答案】D【解析】解：如右图，连接OP，由于OP是Rt△AOB斜边上的中线，所以OP=12AB，不管木杆如何滑动，它的长度不变，也就是OP是一个定值，点P就在以O为圆心的圆弧上，那么中点P下落的路线是一段弧线．故选D．10．如图，在Rt△ABC中，∠ABC=90°，AB=23，BC=2，以AB的中点为圆心，OA的长为半径作半圆交AC于点D，则图中阴影部分的面积为( )A 532π-B532π+C．23πD．432π【答案】A【解析】【分析】连接OD，过点O作OH⊥AC，垂足为 H，则有AD=2AH，∠AHO=90°，在Rt△ABC中，利用∠A的正切值求出∠A=30°，继而可求得OH、AH长，根据圆周角定理可求得∠BOC =60°，然后根据S阴影=S△ABC-S△AOD-S扇形BOD进行计算即可.【详解】连接OD，过点O作OH⊥AC，垂足为 H，则有AD=2AH，∠AHO=90°，在Rt△ABC中，∠ABC=90°，AB=23，BC=2，tan∠A=23323BCAB==，∴∠A=30°，∴OH=12OA=32，AH=AO•cos∠A=33322⨯=，∠BOC=2∠A=60°，∴AD=2AH=3，∴S阴影=S△ABC-S△AOD-S扇形BOD=()26031132323222360π⨯⨯⨯-⨯⨯-=5342π-，故选A.【点睛】本题考查了垂径定理，圆周角定理，扇形面积，解直角三角形等知识，正确添加辅助线，熟练掌握和灵活运用相关知识是解题的关键.11．一个圆锥的侧面展开图是半径为1的半圆，则该圆锥的底面半径是（）A．13B．12C．34D．1【答案】B【解析】【分析】根据侧面展开图的弧长等于圆锥的底面周长，即可求得底面周长，进而即可求得底面的半径长．【详解】圆锥的底面周长是：π；设圆锥的底面半径是r，则2πr=π．解得：r=12．故选B．【点睛】本题考查了圆锥的计算，正确理解理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键，理解圆锥的母线长是扇形的半径，圆锥的底面圆周长是扇形的弧长．12．如图，ABC ∆是一块绿化带，将阴影部分修建为花圃.已知15AB =，9AC =，12BC =，阴影部分是ABC ∆的内切圆，一只自由飞翔的小鸟将随机落在这块绿化带上，则小鸟落在花圃上的概率为（ ）.A ．16 B ．6π C ．8π D ．5π 【答案】B【解析】【分析】由AB=5，BC=4，AC=3，得到AB 2=BC 2+AC 2，根据勾股定理的逆定理得到△ABC 为直角三角形，于是得到△ABC 的内切圆半径=4+3-52=1，求得直角三角形的面积和圆的面积，即可得到结论．【详解】解：∵AB=5，BC=4，AC=3，∴AB 2=BC 2+AC 2，∴△ABC 为直角三角形，∴△ABC 的内切圆半径=4+3-52=1， ∴S △ABC =12AC•BC=12×4×3=6， S 圆=π，∴小鸟落在花圃上的概率=6π ， 故选B ．【点睛】本题考查几何概率，直角三角形内切圆的半径等于两直角边的和与斜边差的一半及勾股定理的逆定理，解题关键是熟练掌握公式.13．2cm 的正方形ABCD 沿直线l 向右翻动（不滑动），当正方形连续翻动8次后，正方形的中心O 经过的路线长是（ ）cm ．A．82B．8 C．3πD．4π【答案】D【解析】【分析】由题意可得翻转一次中心O经过的路线长就是1个半径为1，圆心角是90°的弧长，然后进行计算即可解答．【详解】解：∵正方形ABCD的边长为2cm，∴对角线的一半＝1cm，则连续翻动8次后，正方形的中心O经过的路线长＝8×901180π⨯＝4π．故选：D．【点睛】本题考查了弧长的计算，审清题意、确定点O的路线和长度是解答本题的关键．14．如图，AB是⊙O的直径，AC是⊙O的切线，OC交⊙O于点D，若∠ABD＝24°，则∠C 的度数是（）A．48°B．42°C．34°D．24°【答案】B【解析】【分析】根据切线的性质求出∠OAC，结合∠C＝42°求出∠AOC，根据等腰三角形性质求出∠B＝∠BDO，根据三角形外角性质求出即可．【详解】解：∵∠ABD＝24°，∴∠AOC＝48°，∵AC是⊙O的切线，∴∠OAC＝90°，∴∠AOC+∠C＝90°，∴∠C＝90°﹣48°＝42°，故选：B．【点睛】考查了切线的性质，圆周角定理，三角形内角和定理，解此题的关键是求出∠AOC的度数，题目比较好，难度适中．15．如图，3个正方形在⊙O直径的同侧，顶点B、C、G、H都在⊙O的直径上，正方形ABCD的顶点A在⊙O上，顶点D在PC上，正方形EFGH的顶点E在⊙O上、顶点F在QG 上，正方形PCGQ的顶点P也在⊙O上．若BC＝1，GH＝2，则CG的长为（）A．125B．6C．21+D．22【答案】B【解析】【分析】【详解】解：连接AO、PO、EO，设⊙O的半径为r，OC=x，OG=y，由勾股定理可知：22222222211{22r xr x x yr y=++=++=++（）①（）②（）③，②﹣③得到：x2+（x+y）2﹣（y+2）2﹣22=0，∴（x+y）2﹣22=（y+2）2﹣x2，∴（x+y+2）（x+y﹣2）=（y+2+x）（y+2﹣x）．∵x+y+2≠0，∴x+y﹣2=y+2﹣x，∴x=2，代入①得到r2=10，代入②得到：10=4+（x+y）2，∴（x+y）2=6．∵x+y＞0，∴x+y=6，∴CG=x+y=6．故选B．点睛：本题考查了正方形的性质、圆、勾股定理等知识，解题的关键是设未知数列方程组解决问题，难点是解方程组，利用因式分解法巧妙求出x的值，学会把问题转化为方程组，用方程组的思想去思考问题．16．如图，四边形ABCD 内接于圆O ，DA DC =，50CBE ∠=︒，AOD ∠的大小为（ ）A ．130°B ．100°C ．20°D ．10°【答案】A【解析】【分析】 先求出∠ABC 的大小，根据内接四边形角度关系，得到∠ADC 的大小，从而得出∠C 的大小，最后利用圆周角与圆心角的关系得∠AOD 的大小.【详解】∵∠CBE=50°∴∠ABC=130°∵四边形ABCD 是内接四边形∴∠ADC=50°∵AD=DC∴在△ADC 中，∠C=∠DAC=65°∴∠AOD=2∠C=130°故选：A【点睛】本题考查圆的性质，主要是内接四边形对角互补和同弧对应圆心角是圆周角2倍，解题中，我们要充分利用圆的性质进行角度转换，以便得到我们需要的角度.17．如图，有一圆锥形粮堆，其侧面展开图是半径为6m 的半圆，粮堆母线AC 的中点P 处有一老鼠正在偷吃粮食，此时，小猫正在B 处，它要沿圆锥侧面到达P 处捕捉老鼠，则小猫所经过的最短路程长为（ ）A ．3mB ．33C ．35D ．4m【答案】C【解析】【分析】【详解】如图，由题意得：AP =3，AB =6，90.BAP ∠=o ∴在圆锥侧面展开图中223635.BP m =+=故小猫经过的最短距离是35.m故选C.18．若正六边形的半径长为4，则它的边长等于（ ）A ．4B ．2C ．23D ．43【答案】A【解析】试题分析：正六边形的中心角为360°÷6=60°，那么外接圆的半径和正六边形的边长将组成一个等边三角形，故正六边形的半径等于4，则正六边形的边长是4．故选A ． 考点：正多边形和圆．19．如图，AB 是⊙O 的直径，弦CD ⊥AB 于点M ，若CD ＝8 cm ，MB ＝2 cm ，则直径AB 的长为（ ）A ．9 cmB ．10 cmC ．11 cmD ．12 cm【答案】B【解析】【分析】 由CD ⊥AB ，可得DM=4．设半径OD=Rcm ，则可求得OM 的长，连接OD ，在直角三角形DMO 中，由勾股定理可求得OD 的长，继而求得答案．【详解】解：连接OD ，设⊙O 半径OD 为R,∵AB是⊙O的直径，弦CD⊥AB于点M，∴DM=12CD=4cm，OM=R-2,在RT△OMD中，OD²=DM²+OM²即R²=4²+(R-2)²,解得：R=5,∴直径AB的长为:2×5=10cm．故选B．【点睛】本题考查了垂径定理以及勾股定理．注意掌握辅助线的作法及数形结合思想的应用．20．如图，AB是⊙O的直径，点C是⊙O上一点，点D在BA的延长线上，CD与⊙O交于另一点E，DE=OB=2，∠D=20°，则弧BC的长度为（）A．23πB．13πC．43πD．49π【答案】A【解析】【分析】连接OE、OC，如图，根据等腰三角形的性质得到∠D=∠EOD=20°，根据外角的性质得到∠CEO=∠D+∠EOD=40°，根据等腰三角形的性质得到∠C=∠CEO=40°，根据外角的性质得到∠BOC=∠C+∠D=60°，根据求弧长的公式得到结论.【详解】解：连接OE、OC，如图，∵DE=OB=OE，∴∠D=∠EOD=20°，∴∠CEO=∠D+∠EOD=40°，∵OE=OC，∴∠C=∠CEO=40°，∴∠BOC=∠C+∠D=60°，∴»BC的长度=260?2360π⨯=23π，故选A.【点睛】本题考查了弧长公式：l=••180n Rπ（弧长为l，圆心角度数为n，圆的半径为R），还考查了圆的认识及等腰三角形的性质及三角形外角的性质，熟练掌握等腰三角形的性质和三角形外角性质是关键．。

《圆的周长》练习题一、填空题。

1.圆中最长的线段是6厘米，这个圆的周长是（）厘米。

2.画一个周长为37.68厘米的圆，圆规两脚间的距离应是（）。

3.一个圆的半径扩大2倍，周长扩大（）倍。

4.一个圆的周长为12.56厘米，将它切成两个半圆后，每个半圆的周长为（）厘米。

5.一只大挂钟的时针长60厘米，分针长80厘米，一天内这只大挂钟分针尖端经过路程总长（）米。

6.用面积为9平方分米的正方形铁皮，剪成一个面积最大的圆形铁片，铁片的周长为（）分米。

7.把一个圆分割成两个相等的半圆后，它的周长增加了6厘米，原来这个圆的面积是（）。

8.在一张长60厘米、宽40厘米的长方形纸片中，最多能剪（）个直径为4厘米的圆。

9.两个圆的半径之和是6厘米已知大圆周长是25.12厘米，小圆的周长是（）厘米。

10.在一个长10厘米，宽5厘米的长方形里，画一个最大的圆，这个圆的半径是（）分米。

11.圆的半径从10厘米减少到8厘米，周长减少（）厘米。

12.一个圆的周长、直径、半径的和是18.56厘米，这个圆的半径是（）厘米。

二、操作题。

1.如图所示，已知正方形的边长是3厘米，求阴影部分周长。

三、应用题。

1.一个圆形花圃，直径为12米，在它的周围沿外侧铺一条2米宽的小路，在小路的外侧围上篱笆，篱笆有多长？2.一个长方形的周长与一个半径25分米的圆周长相等，已知长方形的长是4米，长方形的面积是多少平方米？《圆的周长》练习题一、填空题。

1.圆周率表示同一个圆内（）与（）的倍数关系，保留两位小数约是（）。

同一个圆内周长是直径的（）倍，是半径的（）倍。

2.把一个圆规两脚尖分开 4.5厘米画一个圆，这个圆的半径是（），直径是（），周长是（）。

3.在一个长是6厘米，宽是4厘米的长方形内，剪一个最大的圆，这个圆的直径是（），周长是（）。

4.一根电线长94.2厘米,用它围成一个正方形,边长是(),用它围成一个等边三角形,边长是(),用它围一个圆，半径是（）。

小学数学北师版六年级上册填空题1、圆规两脚间的距离是 3 厘米，画出的圆的周长是（）厘米，面积是（）平方厘米。

2、圆的周长9.42 分米，它的直径是（）分米，面积是（）平方分米。

3、将一个直径8 厘米的圆形纸片沿直径对折后，得到一个半圆，这个半圆的周长是（）厘米，面积是（）平方厘米。

14、小圆半径是大圆半径的3，小圆与大圆的周长比是（），面积比是（）。

5、甲乙两圆的周长比是2：3，其中一个圆的面积是18，另一个圆的面积可能是（），也可能是（）。

6、正三角形有（）条对称轴，正方形有（）条对称轴，正五边形有（）条对称轴，由此推算，正n 边形估计有（）条对称轴。

7、圆的半径是 6 厘米，它的周长是（），面积是（）。

8、一个半圆形，半径是 3 厘米，周长是（），面积是（）。

9、一个圆的周长是 12.56 厘米，它的直径是（），面积是（）。

10、一张圆桌面的周长是376.8 厘米，要在它上面配一块圆形玻璃，这块圆形玻璃的面积是（）。

11、用一根长 10.28 米绳子，围成一个半圆形，这个半圆的半径是（）米，面积是（）平方米。

12、在长 5 厘米、宽 4 厘米的长方形中画一个最大的圆，这个圆的周长是（），面积是（）。

13、一个圆的半径扩大 3 倍，直径扩大（）倍，周长扩大（）倍，面积扩大（）倍。

14、两个圆的直径比是3： 2，则它们的半径比是（），周长比是（），面积比是（）。

15、一个挂钟，分针长50 厘米，时针长 40 厘米，分针的尖端转一圈的长度是（），时针转一周扫过的面积是（）。

16、甲、乙两圆的周长之比是3： 5，则甲圆面积比乙圆面积小（--）。

17、把一个圆分成若干等份，剪开拼成一个近似的长方形。

这个长方形的长相当于（），长方形的宽就是圆的（）。

因为长方形的面积是（），所以圆的面积是（）．18、圆的直径是 6 厘米，它的周长是（），面积是（）。

19、圆的周长是 25.12 分米，它的面积是（）。

20、甲圆半径是乙圆半径的 3 倍，甲圆的周长是乙圆周长的（），甲圆面积是乙圆面积的（）。

小数估算练习题在数学中，小数估算是一种常见的数值计算方法，它可以帮助我们近似地确定数值结果，尤其在日常生活中的实际问题中非常实用。

通过小数估算，我们可以快速得到一个大致的数值，方便进一步计算或做出决策。

下面是一些小数估算练习题，帮助你提升估算能力。

1. 估算圆的周长对于一个直径为12.6米的圆，我们可以通过小数估算来计算它的周长。

解答：首先，我们知道圆的周长公式为C = πd，其中d为直径，π取近似值3.14。

根据这个公式，我们可以估算出C ≈ 3.14 × 12.6 ≈ 39.564米。

所以，圆的周长约为39.564米。

2. 估算百分比某次考试中，有60名学生参加了考试，其中有36名学生成绩合格。

我们可以通过小数估算来计算合格率。

解答：首先，我们可以计算出合格率为(36/60) × 100% ≈ 60%。

3. 估算金额在购物时，了解商品的实际价格非常重要。

我们可以通过小数估算来计算商品的实际价格。

解答：例如，一件原价为78.5元的商品打八折。

我们可以计算出实际价格为78.5 × 0.8 = 62.8元。

所以，该商品的实际价格约为62.8元。

4. 估算距离旅行中，我们常常需要估算两地之间的距离。

我们可以通过小数估算来计算两地之间的大致距离。

解答：例如，两地之间的实际距离为256.3千米。

我们可以估算出大致距离为250千米左右。

5. 估算面积对于某块不规则形状的土地，我们可以通过小数估算来计算其面积。

解答：例如，一块土地的长约为15.7米，宽约为8.9米。

我们可以估算出面积为15.7 × 8.9 ≈ 139.33平方米。

通过以上小数估算练习题，我们可以发现小数估算的应用非常广泛。

它可以帮助我们高效地解决实际问题，做出合理的决策。

在实际生活中，我们经常需要对数值进行快速估算，以便更好地理解问题、分析情况或做出决策。

因此，掌握小数估算的技巧是非常重要的。

总结：小数估算是一种常见的数学计算方法，可以帮助我们近似地确定数值结果。

圆的全集汇编及解析一、选择题1．如图，用半径为12cm ，面积272cm π的扇形无重叠地围成一个圆锥，则这个圆锥的高为（ ）A ．12cmB ．6cmC ．6√2 cmD ．63 cm【答案】D【解析】【分析】先根据扇形的面积公式计算出扇形的圆心角，再利用周长公式计算出底面圆的周长，得出半径．再构建直角三角形，解直角三角形即可．【详解】 72π=212360n π⨯ 解得n=180°，∴扇形的弧长=18012180π⨯=12πcm ． 围成一个圆锥后如图所示：因为扇形弧长=圆锥底面周长即12π=2πr解得r=6cm ，即OB=6cm根据勾股定理得22126=63-，故选D ．【点睛】本题综合考查了弧长公式，扇形弧长=用它围成的圆锥底面周长，及勾股定理等知识，所以学生学过的知识一定要结合起来．2．如图，已知AB 是⊙O 是直径，弦CD ⊥AB ，AC 2，BD =1，则sin ∠ABD 的值是( )A ．22B ．13C ．223D ．3【答案】C【解析】【分析】 先根据垂径定理，可得BC 的长，再利用直径对应圆周角为90°得到△ABC 是直角三角形，利用勾股定理求得AB 的长，得到sin ∠ABC 的大小，最终得到sin ∠ABD【详解】解：∵弦CD ⊥AB ，AB 过O ，∴AB 平分CD ，∴BC =BD ，∴∠ABC =∠ABD ，∵BD =1，∴BC =1，∵AB 为⊙O 的直径，∴∠ACB =90°，由勾股定理得：AB =()22222213AC BC +=+=， ∴sin ∠ABD =sin ∠ABC =223AC AB = 故选：C ．【点睛】本题考查了垂径定理、直径对应圆周角为90°、勾股定理和三角函数，解题关键是找出图形中的直角三角形，然后按照三角函数的定义求解3．将直尺、有60°角的直角三角板和光盘如图摆放，A 为60°角与直尺的交点，B 为光盘与直尺的交点，AB =4，则光盘表示的圆的直径是( )A ．4B ．3C ．6D ．43【答案】B【解析】【分析】设三角板与圆的切点为C ，连接OA 、OB ，根据切线长定理可得AB=AC=3，∠OAB=60°，然后根据三角函数，即可得出答案.【详解】设三角板与圆的切点为C ，连接OA 、OB ，由切线长定理知，AB =AC =3，AO 平分∠BAC ，∴∠OAB =60°，在Rt △ABO 中，OB =AB tan ∠OAB 3∴光盘的直径为3故选：B ．【点睛】本题主要考查了切线的性质，解题的关键是熟练应用切线长定理和锐角三角函数.4．下列命题中，是假命题的是( )A ．任意多边形的外角和为360oB ．在ABC V 和'''A B C V 中，若''AB A B =，''BC B C =，'90C C ∠=∠=o ，则ABC V ≌'''A B C VC ．在一个三角形中，任意两边之差小于第三边D ．同弧所对的圆周角和圆心角相等【答案】D【解析】【分析】根据相关的知识点逐个分析．【详解】解：A. 任意多边形的外角和为360o ,是真命题；B. 在ABC V 和'''A B C V 中，若''AB A B =，''BC B C =，'90C C ∠=∠=o ，则ABC V ≌'''A B C V ，根据HL ，是真命题；C. 在一个三角形中，任意两边之差小于第三边，是真命题；D. 同弧所对的圆周角等于圆心角的一半，本选项是假命题.故选D ．【点睛】本题考核知识点：判断命题的真假. 解题关键点：熟记相关性质或定义．5．如图，AB是⊙O的直径，EF，EB是⊙O的弦，且EF=EB，EF与AB交于点C，连接OF，若∠AOF=40°，则∠F的度数是（）A．20°B．35°C．40°D．55°【答案】B【解析】【分析】连接FB，由邻补角定义可得∠FOB=140°，由圆周角定理求得∠FEB=70°，根据等腰三角形的性质分别求出∠OFB、∠EFB的度数，继而根据∠EFO＝∠EBF-∠OFB即可求得答案.【详解】连接FB，则∠FOB=180°-∠AOF=180°-40°=140°，∴∠FEB＝12∠FOB=70°，∵FO＝BO，∴∠OFB＝∠OBF=(180°-∠FOB)÷2=20°，∵EF＝EB，∴∠EFB＝∠EBF=(180°-∠FEB)÷2=55°，∴∠EFO＝∠EBF-∠OFB=55°-20°=35°，故选B.【点睛】本题考查了圆周角定理、等腰三角形的性质等知识，正确添加辅助线，熟练掌握和灵活运用相关知识是解题的关键.6．已知某圆锥的底面半径为3 cm，母线长5 cm，则它的侧面展开图的面积为（）A ．30 cm 2B ．15 cm 2C ．30π cm 2D ．15π cm 2【答案】D【解析】 试题解析：根据圆锥的侧面展开图的面积计算公式得：S ＝RL π＝15π故选D.7．如图，边长为1的正方形ABCD 绕点A 逆时针旋转45°后得到正方形AB 1C 1D 1，边B 1C 1与CD 交于点O ，则图中阴影部分的面积是（ ）A ．224π--B ．224π-+ C ．142π+ D ．142π- 【答案】B【解析】【分析】先根据正方形的边长，求得CB 1=OB 1=AC-AB 1=2-1，进而得到211(21)2OB C S =-V ，再根据S △AB1C1=12，以及扇形的面积公式即可得出图中阴影部分的面积． 【详解】连结DC 1，∵∠CAC 1＝∠DCA ＝∠COB 1＝∠DOC 1＝45°，∴∠AC 1B 1＝45°，∵∠ADC ＝90°，∴A ，D ，C 1在一条直线上，∵四边形ABCD 是正方形，∴AC 2OCB 1＝45°，∴CB 1＝OB 1∵AB 1＝1，∴CB 1＝OB 1＝AC ﹣AB 1＝2﹣1， ∴211111(21)22OB C S OB CB ∆=⋅⋅=-， ∵1111111111222AB C S AB B C =⋅=⨯⨯=V ， ∴图中阴影部分的面积＝2245(2)11(21)22360224ππ⨯⨯---=-+． 故选B ．【点睛】本题考查了旋转的性质，正方形性质、勾股定理以及扇形面积的计算等知识点的综合应用，主要考查学生运用性质进行计算的能力．解题时注意：旋转前、后的图形全等．8．如图，ABC V 中，90ACB ∠=︒，O 为AB 中点，且4AB =，CD ，AD 分别平分ACB ∠和CAB ∠，交于D 点，则OD 的最小值为（ ）．A ．1B ．22C 21D ．222【答案】D【解析】【分析】 根据三角形角平分线的交点是三角形的内心，得到DO 最小时，DO 为三角形ABC 内切圆的半径，结合切线长定理得到三角形为等腰直角三角形，从而得到答案．【详解】解：Q CD ，AD 分别平分ACB ∠和CAB ∠，交于D 点，D ∴为ABC ∆的内心，OD ∴最小时，OD 为ABC ∆的内切圆的半径，,DO AB ∴⊥过D 作,,DE AC DF BC ⊥⊥ 垂足分别为,,E F,DE DF DO ∴==∴ 四边形DFCE 为正方形，O Q 为AB 的中点，4,AB =2,AO BO ∴==由切线长定理得：2,2,,AO AE BO BF CE CF r ======sin 4522,AC BC AB ∴==•︒=222,CE AC AE ∴=-=Q四边形DFCE为正方形，,CE DE∴=222,OD CE∴==-故选D．【点睛】本题考查的动态问题中的线段的最小值，三角形的内心的性质，等腰直角三角形的性质，锐角三角函数的计算，掌握相关知识点是解题关键．9．在Rt△ABC中，∠ACB=90°.AC=8，BC=3，点D是BC边上动点，连接AD交以CD为直径的圆于点E，则线段BE长度的最小值为( )A．1 B．32C．3D．52【答案】A【解析】【分析】根据直径所对的圆周角为直角可知∠CED=90°，则∠AEC=90°，设以AC为直径的圆的圆心为O，若BE最短，则OB最短，根据直角三角形斜边上的中线等于斜边的一半可得OE=12AC=4，在Rt△OBC中，根据勾股定理可求得OB=5，即可得解.【详解】解：连接CE，∵E点在以CD为直径的圆上，∴∠CED=90°，∴∠AEC=180°-∠CED=90°，∴E点也在以AC为直径的圆上，设以AC为直径的圆的圆心为O，若BE最短，则OB最短，∵AC=8，∴OC=12AC=4，∵BC=3，∠ACB=90°，∴OB=22OC BC=5，∵OE=OC=4，∴BE=OB-OE=5-4=1.故选A.【点睛】本题考查了直径所对的圆周角为直角，直角三角形的性质和勾股定理.10．如图，以Rt△ABC的直角边AB为直径作⊙O交BC于点D，连接AD，若∠DAC＝30°，DC＝1，则⊙O的半径为（）A．2 B3C．23D．1【答案】B【解析】【分析】先由圆周角定理知∠BDA=∠ADC=90°，结合∠DAC=30°，DC=1得AC=2DC=2，∠C=60°，再由3【详解】∵AB是⊙O的直径，∴∠BDA＝∠ADC＝90°，∵∠DAC＝30°，DC＝1，∴AC＝2DC＝2，∠C＝60°，则在Rt△ABC中，AB＝ACtanC＝23，∴⊙O的半径为3，故选：B．【点睛】本题主要考查圆周角定理，解题的关键是掌握半圆（或直径）所对的圆周角是直角和三角函数的应用．11．如图，⊙O的直径CD＝10cm，AB是⊙O的弦，AB⊥CD，垂足为M，OM：OC＝3：5，则AB的长为（）A91B．8cm C．6cm D．4cm【答案】B【解析】【分析】由于⊙O的直径CD＝10cm，则⊙O的半径为5cm，又已知OM：OC＝3：5，则可以求出OM＝3，OC＝5，连接OA，根据勾股定理和垂径定理可求得AB．【详解】解：如图所示，连接OA．⊙O的直径CD＝10cm，则⊙O的半径为5cm，即OA＝OC＝5，又∵OM：OC＝3：5，所以OM＝3，∵AB⊥CD，垂足为M，OC过圆心∴AM＝BM，在Rt△AOM中，22AM=5-3，∴AB＝2AM＝2×4＝8．故选：B．【点睛】本题考查了垂径定理和勾股定理的应用，构造以半径、弦心距和弦长的一半为三边的直角三角形，是解题的关键.12．如图，在Rt ABC △中，90ACB ∠=︒，30A ∠=︒，2BC =．将ABC V 绕点C 按顺时针方向旋转n 度后得到EDC △，此时点D 在AB 边上，斜边DE 交AC 边于点F ，则n 的大小和图中阴影部分的面积分别为（ ）A ．302，B ．602，C ．360，D ．603， 【答案】C【解析】试题分析：∵△ABC 是直角三角形，∠ACB=90°，∠A=30°，BC=2，∴∠B=60°，AC=BC×cot ∠33AB=2BC=4，∵△EDC 是△ABC 旋转而成，∴BC=CD=BD=12AB=2， ∵∠B=60°，∴△BCD 是等边三角形，∴∠BCD=60°，∴∠DCF=30°，∠DFC=90°，即DE ⊥AC ，∴DE ∥BC ，∵BD=12AB=2， ∴DF 是△ABC 的中位线，∴DF=12BC=12×2=1，CF=12AC=12×23=3， ∴S 阴影=12DF×CF=12×3=32． 故选C ．考点：1.旋转的性质2.含30度角的直角三角形．13．已知线段AB 如图，(1)以线段AB 为直径作半圆弧»AB ，点O 为圆心；(2)过半径OA OB 、的中点C D 、分别作CE AB DF AB ⊥⊥、，交»AB 于点E F 、；(3)连接,OE OF ．根据以上作图过程及所作图形，下列结论中错误的是( )A ．CE DF =B ．»»AE BF =C ．60EOF ∠=︒D ． =2CE CO【答案】D【解析】【分析】 根据作图可知AC CO OD DB ===,据此对每个选项逐一判断即可.【详解】根据HL 可判定ECO FDO ≅V V ,得CE DF =，A 正确；∵过半径OA OB 、的中点C D 、分别作CE AB DF AB ⊥⊥、，连接AE ，CE 为OA 的中垂线，AE OE =在半圆中，OA OE =∴OA OE AE ==,AEO △为等边三角形，60EOF =o ∠AOE=∠FOD=∠, C 正确；∴圆心角相等，所对应的弧长度也相等，»»AE BF=，B 正确 ∵60,90EOC =o o ∠AOE=∠,∴=3CE CO ，D 错误【点睛】本题考查了全等三角形的判定和性质，勾股定理等知识点，解题的关键在于证明60o ∠AOE=.14．如图，抛物线y ＝ax 2﹣6ax+5a （a ＞0）与x 轴交于A 、B 两点，顶点为C 点．以C 点为圆心，半径为2画圆，点P 在⊙C 上，连接OP ，若OP 的最小值为3，则C 点坐标是（ ）A ．5252B ．（4，﹣5）C ．（3，﹣5）D ．（3，﹣4）【答案】D【解析】【分析】首先根据二次函数的解析式求出点A 、B 、C 三点的坐标，再由当点O 、P 、C 三点共线时，OP 取最小值为3，列出关于a 的方程，即可求解．【详解】∵2650y ax ax a a +-=（＞） 与x 轴交于A 、B 两点， ∴A （1，0）、B （5，0），∵226534y ax ax a a x a =+=---（） ， ∴顶点34C a （，-）， 当点O 、P 、C 三点共线时，OP 取最小值为3，∴OC ＝OP+2＝5， 29165(0)a a +=> ，∴1a = ，∴C （3，﹣4），故选：D ．【点睛】本题考查了二次函数的图象和性质，解题的关键是明确圆外一点到圆上的最短距离即该点与圆心的距离减去半径长．15．如图，点I 是Rt △ABC 的内心，∠C ＝90°，AC ＝3，BC ＝4，将∠ACB 平移使其顶点C 与I 重合，两边分别交AB 于D 、E ，则△IDE 的周长为（ ）A．3 B．4 C．5 D．7【答案】C【解析】【分析】连接AI、BI，根据三角形的内心的性质可得∠CAI＝∠BAI，再根据平移的性质得到∠CAI＝∠AID，AD＝DI，同理得到BE＝EI，即可解答.【详解】连接AI、BI，∵∠C＝90°，AC＝3，BC＝4，∴AB225AC BC∵点I为△ABC的内心，∴AI平分∠CAB，∴∠CAI＝∠BAI，由平移得：AC∥DI，∴∠CAI＝∠AID，∴∠BAI＝∠AID，∴AD＝DI，同理可得：BE＝EI，∴△DIE的周长＝DE+DI+EI＝DE+AD+BE＝AB＝5故选C．【点睛】此题考查了平移的性质和三角形内心的性质，解题关键在于作出辅助线16．如图，点A、B、C、D、E、F等分⊙O，分别以点B、D、F为圆心，AF的长为半径画弧，形成美丽的“三叶轮”图案．已知⊙O的半径为1，那么“三叶轮”图案的面积为（）A ．π+332B ．π-332C ．33π+ D ．33π-【答案】B【解析】【分析】连接OA 、OB 、AB ，作OH ⊥AB 于H ，根据正多边形的中心角的求法求出∠AOB ，根据扇形面积公式计算．【详解】 连接OA 、OB 、AB ，作OH ⊥AB 于H ，∵点A 、B 、C 、D 、E 、F 是⊙O 的等分点，∴∠AOB=60°，又OA=OB ，∴△AOB 是等边三角形，∴AB=OB=1，∠ABO=60°，∴2211()2-3 ∴“三叶轮”图案的面积=（2601360π⨯⨯-123×6=π-332， 故选B ．【点睛】本题考查的是正多边形和圆、扇形面积的计算，掌握正多边形的中心角的求法、扇形面积公式是解题的关键．17．如图，四边形ABCD 内接于⊙O ，F 是¶CD上一点，且¶¶DF BC =，连接CF 并延长交AD 的延长线于点E ，连接AC ．若∠ABC=105°，∠BAC=25°，则∠E 的度数为（ ）A．45°B．50°C．55°D．60°【答案】B【解析】【分析】先根据圆内接四边形的性质求出∠ADC的度数，再由圆周角定理得出∠DCE的度数，根据三角形外角的性质即可得出结论．【详解】∵四边形ABCD内接于⊙O，∠ABC=105°，∴∠ADC=180°﹣∠ABC=180°﹣105°=75°．∵»»，∠BAC=25°，DF BC∴∠DCE=∠BAC=25°，∴∠E=∠ADC﹣∠DCE=75°﹣25°=50°．【点睛】本题考查圆内接四边形的性质，圆周角定理.圆内接四边形对角互补.在同圆或等圆中，同弧或等弧所对的圆心角相等，而同弧所对的圆周角等于圆心角的一半，所以在同圆或等圆中，同弧或等弧所对的圆周角相等.18．如图，在⊙O中，OC⊥AB，∠ADC＝26°，则∠COB的度数是（）A．52°B．64°C．48°D．42°【答案】A【解析】【分析】由OC⊥AB，利用垂径定理可得出，再结合圆周角定理及同弧对应的圆心角等于圆周角的2倍，即可求出∠COB的度数．【详解】解：∵OC⊥AB，∴，∴∠COB＝2∠ADC＝52°．故选：A．【点睛】考查了圆周角定理、垂径定理以及圆心角、弧、弦的关系，利用垂径定理找出是解题的关键．19．如图，⊙O过点B、C，圆心O在等腰直角△ABC的内部，∠BAC＝90°，OA＝1，BC＝6，则⊙O的半径为（）A．23B．13C．4 D．32【答案】B【解析】【分析】如下图，作AD⊥BC，设半径为r，则在Rt△OBD中，OD=3－1，OB=r，BD=3，利用勾股定理可求得r.【详解】如图，过A作AD⊥BC，由题意可知AD必过点O，连接OB；∵△BAC是等腰直角三角形，AD⊥BC，∴BD=CD=AD=3；∴OD=AD-OA=2；Rt△OBD中，根据勾股定理，得：22+BD OD13故答案为：B.【点睛】本题考查了等腰直角三角形的性质和勾股定理的应用，解题关键是利用等腰直角三角形ABC判定点O在AD上.20．如图所示，AB为⊙O的直径，点C在⊙O上，且OC⊥AB，过点C的弦CD与线段OB 相交于点E，满足∠AEC＝65°，连接AD，则∠BAD等于()A．20°B．25°C．30°D．32.5°【答案】A【解析】【分析】连接OD，根据三角形内角和定理和等边对等角求出∠DOB＝40°，再根据圆周角定理即可求出∠BAD的度数．【详解】解：连接OD，∵OC⊥AB，∴∠COB＝90°，∵∠AEC＝65°，∴∠OCE＝180°﹣90°﹣65°＝25°，∵OD＝OC，∴∠ODC＝∠OCD＝25°，∴∠DOC＝180°﹣25°﹣25°＝130°，∴∠DOB＝∠DOC﹣∠BOC＝130°﹣90°＝40°，∴由圆周角定理得：∠BAD＝12∠DOB＝20°，故选：A．【点睛】本题考查了圆和三角形的问题，掌握三角形内角和定理、等边对等角、圆周角定理是解题的关键．。

2021年人教版小学数学六年级上册第五单元圆第二节圆的周长同步训练（I）卷姓名:________ 班级:________ 成绩:________亲爱的小朋友，经过一段时间的学习，你们掌握了多少知识呢？今天就让我们来检测一下吧！一定要仔细哦！一、单选题 (共5题；共14分)1. （6分）用圆规画一个周长是18.84厘米的圆，圆规两脚之间的距离是（）厘米。

A . 2B . 3C . 62. （2分）(2011·佛山) 有两个大小不同的圆，直径都增加1厘米，则它们的周长（）A . 大圆增加得多B . 小大圆增加得多C . 增加得一样多3. （2分） (2020三上·巴南期末) 下面三个图形中，（）的周长最长.A .B .C .4. （2分）圆的半径为6厘米，若半径增加2厘米，则周长增加（）A . 4π厘米B . 6π厘米C . 8π厘米D . 2π厘米5. （2分）下面半圆的周长是（）A . 25.12厘米B . 12.56厘米C . 20.56厘米D . 30.56厘米二、判断题 (共5题；共10分)6. （2分）两个圆的周长相等，那么这两个圆的面积也相等。

7. （2分）判断对错.圆的周长总是圆直径的3.14倍8. （2分）在圆形鸡场的四周围上篱笆，求篱笆的长就是求圆的周长。

9. （2分）半径是5厘米的圆，它的周长和面积相等。

10. （2分）半圆的周长是它所在圆的周长的一半，半圆的面积是它所在圆的面积的一半。

三、填空题 (共3题；共11分)11. （5分）刘大爷用篱笆围一个半圆形菜园．（1）篱笆长________米？（2）菜园的面积是________平方米？12. （1分）(2011·广州模拟) 一个周长为20厘米的大圆内有许多小圆，这些小圆的圆心都在大圆的一个直径上．则小圆的周长之和为________厘米．13. （5分）如图．已知这个“太极图”的直径是8厘米，则阴影部分的圆长是________厘米，面积是________平方厘米．四、解答题 (共1题；共10分)14. （10分）一辆自行车的车轮直径是70厘米，自行车车轮每分钟转100周。