分数的意义练习题(1)

分数意义练习题分数是数学中的一个重要概念，它可以帮助我们表示部分和整体之间的关系。

掌握分数的意义对于学习数学和解决实际问题非常重要。

下面我将通过一些练习题来帮助大家更好地理解分数的意义。

1. 小明将一块长方形巧克力平均分成4份，他吃掉了其中的3/4，那么他吃掉了巧克力的几分之几？解析：将巧克力平均分成4份，表示整体被分成了4份，也就是1份的大小是整体的1/4。

小明吃掉了其中的3/4，也就是他吃掉了整体的3/4份。

所以他吃掉了巧克力的3/4÷1/4=3份的大小，也就是整体的3/4。

2. 有一块长方形蛋糕，小红吃掉了其中的1/3，小明吃掉了剩下的1/4，那么他们两个一共吃掉了蛋糕的几分之几？解析：小红吃掉了蛋糕的1/3，也就是整体的1/3份。

小明吃掉了剩下的1/4，也就是整体的1/4份。

他们两个一共吃掉了蛋糕的1/3+1/4=7/12份的大小，也就是整体的7/12。

3. 一辆汽车在一小时内以60公里的速度行驶，那么15分钟内它行驶了多少公里？解析：一小时有60分钟，所以15分钟是整体的15/60=1/4。

汽车在一小时内行驶了60公里，所以在15分钟内行驶了整体的1/4×60=15公里。

通过以上的练习题，我们可以看到分数的意义在实际问题中的应用。

分数可以帮助我们表示部分和整体之间的关系，帮助我们解决各种实际问题。

掌握分数的意义可以帮助我们更好地理解数学知识，提高解决问题的能力。

除了以上的练习题，我们还可以通过一些生活中的例子来深入理解分数的意义。

比如，我们可以想象一下自助餐厅中的食物摆放在一个长方形的餐盘中，我们可以根据自己的需求，将整体分成几份，并选择其中的几份食物。

这个过程就是利用分数的意义来表示我们选择的部分和整体之间的关系。

在学习分数的过程中，我们还需要注意分数的大小比较。

当分母相同时，分子越大，分数越大；当分子相同时，分母越大，分数越小。

比如，1/2比1/3大，因为2>3；而1/4比1/2小，因为4>2。

分数的意义【例题1】填空：有一块布长5米，正好可以做6条童裤。

每条童裤用这块布的（），每条童裤用布（）米。

【练习1】填空：把18个桃子平均分给2只小猴，每只猴子分得桃子总数的（）每只猴子分得（）个桃子。

【例题2】填空：7米的1/9和1米的（）相等，1千克的（）和3千克的1/4相等。

【练习2】（1）填空：5/8kg表示把（）kg平均分成（）份，取这样的（）份：也表示把（）kg平均分成（）份，取其中的（）份。

（2）判断：8kg的1/9和1kg的8/9一样重。

（）【例题3】填空：五年级人数的1/6与六年级人数的1/7相等。

（）年级人数多一些。

【练习3】选择：下面两根彩带露出的部分同样长，两根相比（）A.甲长B.乙长C.同样长D.无法比较长短【例题4】选择：一班和二班各有1/2的人参加合唱比赛。

那么，比较参加合唱比赛的人数（）A.班人多B.二班人多C.两班一样多D.无法确定【练习4】选择（1）小红与小兰放学回家后，小红喝了一杯水的1/2，小兰也喝了一杯水的1/2。

那么，比较她们的喝水量，（）。

A.小红多B.小兰多C.两人一样多D.无法确定（2）妈妈买了一个西瓜，爸爸吃了它的1/2，明明吃了剩下的1/2。

（）吃得多。

A.爸爸B.明明C.两人一样多D.无法确定（3）在为希望工程捐款的活动中，小明捐了零花的1/4，小芳捐了零花钱的3/4，（）捐的多。

A.小明B.小芳C.两人一样多D.无法确定【例题5】有两根同样长的电线，第一根剪去米1/2，第二根剪去它的1/2，哪根电线剩下的长？【练习5】两堆同样重的沙子，第一堆运走1/3吨，第二堆运走1/3。

哪堆沙子运走的质量多？【例题6】选择：将一根绳子剪成两段，第段长二米，第二段占全长的二，两段绳子相比较，（）A.一样长B.第一段长C.第二段长D.无法确定【练习6】选择：将一根铁丝剪成两段，第一段长2/5米，第二段占全长的2/5，两段铁丝相比较，（）A.一样长B.第一段长C.第二段长D.无法确定【例题7】选择：把一根绳子对折3次，每段是全长的（）。

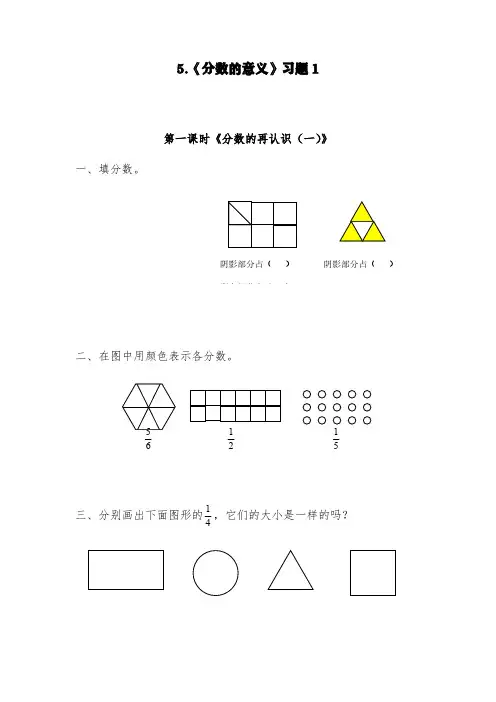
分数的意义（一）一、填空。

（1）的表示把单位“1”平均分成（）份，取其中的（）（2 把全班同学平均分成5个小组，2个小组占全班人数的（）。

这里的单位“1”是（）。

（3）把3m长的绳子平均分成5段，每段占全长的（）。

（4）女职工人数占全厂人数的，男职工占全厂人数的（）（5）的分数单位是（），再加上（）个这样的分数单位就是1。

（6）6个是（），（）个是。

（7）（）个是1，1里面有（）个。

（8）读作（），它由（）个组成。

二、判断。

（1）分数单位是的分数有7个。

（2）分数单位相同的分数，分母也相同。

（）（3）一堆苹果的一定比另一堆苹果的多。

（）三、选择。

（1）在分数中，决定分数单位大小的是（）A、单位“1”B、分子C、分母D、分数值（2）把一根木料锯成5段，锯下一段所用的时间是完成这项工作所用时间的（）A、B、C、D、（3）分子相同的分数，（）A、它们分数单位相同B、所含分数单位的个数相同C、分数的大小相同（4）1kg糖溶化在水中，糖是糖水的（）A 、B 、C、四、思考。

1、将分数这样循环排列下去，第50个分数是哪能个数。

2、把红花、黄花、紫花按红、红、黄、黄、黄、紫、紫的顺序排列。

（1）第101朵是什么颜色？（2）101朵花中有多少朵黄花？（3）黄花占101朵花的几分之几？分数的意义（二）一、填空1、=（）÷（）（）÷27=5÷（）= 23÷49=2、kg表示把（）kg平均分成（）份，取其中的（）份，是（）kg，也表示把（）kg平均分成（）份，取其中的（）份，每份是（）kg。

二、判断。

1、把一个正方形的纸对折一次后，再对折一次，每一小块占正方形的。

（）2、分数中的分子、分母都不可以为0。

（）3、1÷6可以写成。

（）三、选择1、把3m长的绳子平均分成8段，第段是全长的（），每段长（）m。

2、吨可以表示（），也可以表示（）。

3、7分是1时的（），7kg是1吨的（），7个月是一年的（）。

分数的意义专项练习题1、把单位“1”平均分成若干份，表示这样的…份或儿份的数叫做分数。

表示其中一份的数就是分数单位。

2、分数与除法的关系：分数是一种数，除法是一种运算。

除法中被除数相当于分数的分子，除数相当于分数的分母，商相当丁•分数值。

3真分数——分子比分母小假分数——分子比分母大或等于分母由分数和整数组成的分数叫带分数。

4、分数的基本性质：分数的分子和分母同时乘或除以相同的数，分数的大小不变。

5、最简分数：分数的分子和分母的公因数只有1,这样的分数叫做最简分数。

6、约分：把一个分数化成同它相等，但分子分母都比较小的分数，这个过程叫做约分。

通过约分可将一个分数化成最简分数。

7、通分：把异分母分数分别化成和原来分数相等的同分母分数的过程叫通分。

8、分数大小的比较：分母相同，分子大的这个分数就大；分子相同，分母小的这个分数就大；分母或分子不同的分数，一般先通分再比较。

9、分数与小数互化1）分数化成小数的方法：运用分数与除法的关系，用分子除以分母2）小数化成分数的方法：把小数改写成分母是10、100、1000, ??的分数，再约分成最简分数。

典型试题一、填空1.用分数表示下列各图中的阴影部分。

2.在括号里填上适当的分数。

400千克=吨75厘米=米15分=吋50平方分米=平方米30时=日3.把一根5米铁丝平均截成8段，每段占全长的，3 段占全长的，每段长米。

4.的分数单位是，它有个这样的分数单位，再加个这样的分数单位后为2.5.把3米长的铁丝平均截成7段，每段长米，每段长是3米的。

796.和9相比较，分数值大的是，分数单位大的是。

17.和1米的相等，11小吋的和2小吋的相等。

318•分数单位是的最简真分数有，分子是5的假分数有，其屮最大的是，最小的5是。

9.甲数=2X2X3X5,乙数=2X3X3,甲乙两数的最大公约数是，最小公倍数是。

10•甲=2X5XA,乙=2X7XA,甲、乙两个数的最小公倍数是210, A是。

《分数的意义（一）》练习题一、填空。

1. 将一个物体或许多物体看成一个整体，它可以用自然数（ ）来表示，通常把它叫做（ ）。

2.把（ ）平均分成若干份，表示其中1份或者几份的数，叫做分数。

表示其中的（ ）份的数，我们叫做分数单位。

3.52的分数单位是（ ），21的分数单位是（ ）。

4. 把8个苹果平均分成4份，每份是8个苹果的（ ）。

5.76的分数单位数（ ），它是由（ ）个这样的分数单位组成的。

3个51是（ ）。

二、用分数表示每个图里的涂色部分。

三、圈一圈，填一填。

（1）卷心菜的21是（ ）个。

（2）白菜的21是（ ）个。

（3）草莓的21是（ ）个。

四、选一选。

1.一个图形的31是，这个图形的是（ ）。

A. B. C.2. 明明看来一本书的43，小小看了一本书的43，两人看的页数（ ）。

A. 一样多 B.无法比较 C.明明多五、一个图形41的是△△，请试着画出这个图形的43。

六、根据分数涂色。

（1）用下面的长方形面积表示某班学生总数，其中男生占全班学生人数的43。

（2）用下面几个图形表示清泉小学运动队的学生，其中男生占运动队总人数的32。

答案与解析一、1.【解析】根据单位“1”的意义直接求解，即将一个物体或许多物体看成一个整体，它可以用自然数1来表示，通常把它叫做单位“1”。

【答案】1；单位“1”。

4.【解析】此题把8个苹果看做单位“1”，根据分数的意义求解。

【答案】41。

5.【解析】根据分数单位的意义求解。

【答案】71；6；53。

二、【解析】根据分数的意义直接求解，即分的总份数做分母，阴影部分的份数做分子。

【答案】61；43；41；32；42。

三、【解析】21表示把单位“1”平均分成2份，表示这样一份的数，据此意义圈一圈，进而得出相关数据。

【答案】6；5；10。

四、1.【解析】31是1个，33里面有3个31，则有3个。

【答案】B 。

2.【解析】两人书不一定相同，则单位“1”不同，所以无法比较。

分数的意义题10道
分数的意义题10道
分数是数学中重要的概念之一，它可以帮助我们进行精确的计算和描述，广泛应用于日常生活和各个学科领域。

下面将给出10道关于分数意义的题目，帮助我们深入理解分数的概念和应用。

1. 请用一句话描述分数的含义是什么？答案：分数是用来表示整数之间的部分关系的数。

2. 请解释分数的分子和分母分别表示什么？答案：分数的分子表示部分的数目，而分母表示整体的数目。

3. 将下列混合数转化为带分数：23/5。

答案：4 3/5
4. 将下列带分数转化为假分数：5 2/3。

答案：17/3
5. 将下列分数化简到最简形式：8/12。

答案：2/3
6. 将下列分数转化为小数：3/4。

答案：0.75
7. 将下列小数转化为分数：0.6。

答案：3/5
8. 用分数形式表示以下图形中黑色部分的面积占比。

[图片]
答案：3/8
9. 小明吃掉了一块披萨的3/5，小红吃掉了另一块披萨的1/4，那么他们吃掉了所有披萨的多少比例？答案：11/20
10. 若一条绳子已经剪断了3/4的长度，剩下的长度是原
来的多少比例？答案：1/4
通过以上10道题目，我们可以深入了解分数的含义和应用。

分数的概念在日常生活中有许多实际应用，例如表示比例，计算面积和体积，比较大小等。

了解分数的意义不仅仅是为了在数学中应用，还能帮助我们更好地理解和解决实际问题。

分数的意义练习题分数的意义练习题分数表示一个数是另一个数的几分之几，或一个事件与所有事件的比例。

下面是店铺想跟大家分享的分数的意义练习题，欢迎大家浏览。

一、填一填1、分数单位是37的最大真分数是（），最小假分数是（）2、的分子加上9，要使分数的大小不变，分母应（）。

3、 =（）÷24 = 0.375＝＝15÷（）4、米既可以看作 3米的，又可以看作（）米的。

5、把5米长的铁丝平均截成8段，每段长（）米，每段是5米的（）。

6、把8公顷地平均分成15份，每份是这块地的（），每份是（）公顷。

7、的分数单位是( )，它有（）个这样的'分数单位。

再添( )个这样的分数单位就是1。

8、的分数单位是（），它有（）个这样的分数单位。

再添( )个这样的分数单位就是最小的质数。

9、的分数单位是（），它有（）个这样的分数单位。

再添( )个这样的分数单位就是最小的质数。

10、在这个分数中，当a是（）时，分数值是1 ；当a是（）时，分数值是2,当a 是( )时,这个分数的分数单位是。

11、把、0.9、、这四个数，从小到大排列起来。

12、在（）里填上适当的最简分数。

80厘米＝（）米 32时= ( )日 700千克＝（）吨350平方分米＝（）平方米 4时45分＝（）时3升400毫升= ( )升 35立方分米=（）立方米13、甲数是乙数的因数，它们的最大公因数是（），最小公倍数是（）。

14、a÷ b=5，它们的最大公因数是（），最小公倍数是（）。

二、判断题1、分数的分子和分母同时乘以任何数，分数大小都不变。

………………（）2、分数的分母越大，它的分数单位就越小。

……………………………… ( )3、把单位“1”分成若干份，表示这样一份或几份的数,叫做分数………( )4、所有的假分数的值都大于1。

…………………………………………( )5、两个分数相等，它们的分数单位一定相等。

………… ……………( )6、在分数中，分母越小，它的分数单位就越小。

《分数的意义》练习题一、填空。

（）若干份，表示这样的（）或者（）的数叫做分数，表示其中一份的数叫做（）。

1. 把单位“1”2. 表示的意义是（）．表示的意义是（）。

3. 把单位“1”平均分成10份，其中的7份就是（），它的分数单位是（）。

4. 的分数单位是（），它有（）个这样的分数单位．的分数单位是（），它有（）个这样的分数单位。

5. 把4米的绳子平均分成5段，每段占全长的（），每段的长是（）米。

），错的打“×”二、判断。

（对的打“√”1. 把单位“1”分成3份，其中的2份就是．（）2. 3米的和1米的一样长．（）3. 分母越大的分数，分数单位越大．（）4. 五（2）班有男生25人，女生23人，男生人数占全班人数的．（）三、选择题。

1. 分子相同的分数（）。

①分数单位相同②分数的大小相同③所含的分数单位的个数相同2. 在、、三个分数中，最大的分数是（）。

①②③3.把3吨化肥平均分成5份，每份重（）吨。

①②③4. 男生人数占全班的，则女生人数占全班的（）。

①②③分数的意义和性质练习一、填空。

（35%）（1）在下面的括号里填上适当的分数。

40平方分米＝（）平方米75厘米＝（）米350千克＝（）吨（2）表示（），还可以表示（）。

（3）的分数单位是（），它有（）个这样的分数单位。

（4）在下面的○里填上“＞”、“＜”或“＝”符号。

○0.125 ○1 4○3 6.5千米○6千米（5）在下面的括号里填上适当的数。

是（）个0.875＝＝（6）3米长的铁丝平均分成8段，每段长（）米，用小数表示是（）米。

（7）8和9的最大公因数是（），最小公倍数是（）。

12和72的最大公因数是（），最小公倍数是（）。

（8）一个数3、5、7分别除都余1，这个数最小是（）。

（9）一项工程必须在30天完成，平均每天完成全部工程的（）。

7天完成这项工程的（）。

19天完成这项工程的（）。

（10）两个数的最小公倍数是180，最大公因数是30，其中一个数是90，另一个数是（）。

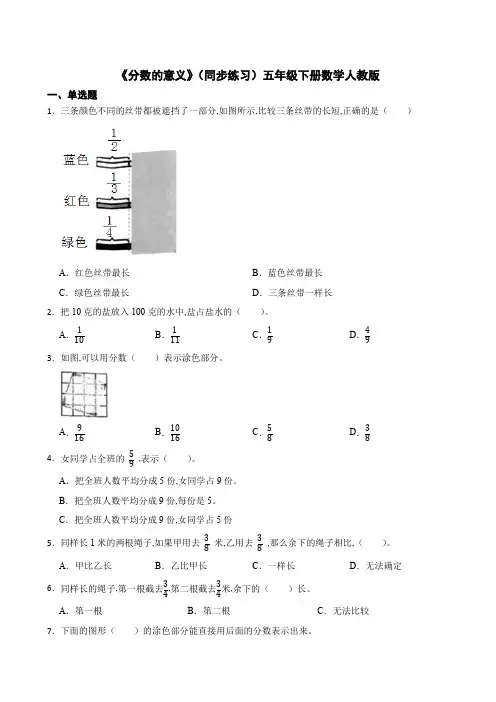
《分数的意义》（同步练习）五年级下册数学人教版一、单选题1．三条颜色不同的丝带都被遮挡了一部分,如图所示,比较三条丝带的长短,正确的是（）A．红色丝带最长B．蓝色丝带最长C．绿色丝带最长D．三条丝带一样长2．把10克的盐放入100克的水中,盐占盐水的（）。

A．110B．111C．19D．493．如图,可以用分数（）表示涂色部分。

A．916B．1016C．58D．3 84．女同学占全班的59,表示（）。

A．把全班人数平均分成5份,女同学占9份。

B．把全班人数平均分成9份,每份是5。

C．把全班人数平均分成9份,女同学占5份5．同样长1米的两根绳子,如果甲用去38米,乙用去38,那么余下的绳子相比,（）。

A．甲比乙长B．乙比甲长C．一样长D．无法确定6．同样长的绳子,第一根截去34,第二根截去34米,余下的（）长。

A．第一根B．第二根C．无法比较7．下面的图形（）的涂色部分能直接用后面的分数表示出来。

A．B．C．8．把10克的精盐放入100克的水中,精盐占盐水的（）A．19B．110C．1119．一杯牛奶,第一次喝了这杯牛奶的15,第二次喝了余下的45,第二次喝了这杯牛奶的()A．15B．45C．425D．162510．与12÷ 45结果相等的式子是()。

A．12÷5×4B．12÷4×5C．12÷4÷5D．12×5×4 11．（）堆梨子最多。

A．第一堆B．第二堆C．第三堆12．把2米长的绳子平均分成5份,每份长（）。

A．15米B．25C．25米二、判断题13．在38中,8表示其中的8份,3表示平均分成了3份。

（）14．把一个苹果分成2份,每份是这个苹果的 12。

（ ） 15．如果a÷b= b a （a=0）,那么 b a里面有b 个 1a 。

（ ） 16．把一个西瓜切成5份,每份一定是这个西瓜的 15。

分数的意义和性质练习题分数的意义和性质练习题分数是数学中一个重要的概念，它在我们的日常生活中也有着广泛的应用。

分数可以表示一个整体被分成若干等份，每份的大小就是分数的分子和分母所表示的数值。

在这篇文章中，我们将通过一些练习题来探讨分数的意义和性质。

练习题一：小明有一块巧克力，他想把它平均分给他的两个朋友。

这块巧克力的重量是1/2千克。

每个朋友将得到多少千克的巧克力？解答：将巧克力平均分给两个朋友，意味着将1/2千克的巧克力分成两份。

所以，每个朋友将得到1/2 ÷ 2 = 1/4千克的巧克力。

练习题二：小红在超市买了一盒饼干，盒子里有3/4盒饼干。

如果她吃掉了1/2盒，还剩下多少盒饼干？解答：盒子里有3/4盒饼干，而小红吃掉了1/2盒。

我们可以先计算出1/2盒饼干的数量，即3/4 × 1/2 = 3/8盒饼干。

所以，还剩下3/4 - 3/8 = 3/8盒饼干。

练习题三：小明和小红一起做作业，他们共用了1/3小时。

如果小明用了1/4小时，那么小红用了多长时间？解答：小明用了1/4小时，而他们共用了1/3小时。

我们可以先计算出1/3小时的时间，即1/3 - 1/4 = 1/12小时。

所以，小红用了1/12小时。

通过这些练习题，我们可以看到分数在实际问题中的应用。

分数可以帮助我们表示整体被分成若干等份的情况，并且可以计算每份的大小。

在练习题一中，我们将巧克力平均分给朋友，通过分数的运算，得到每个朋友得到的巧克力的重量。

在练习题二中，我们计算了剩下的饼干的数量，同样通过分数的运算，得到了最终的结果。

在练习题三中，我们利用分数的运算，计算出了小红用的时间。

除了上述的应用之外，分数还有一些重要的性质。

首先，分数可以表示小于1的数，也可以表示大于1的数。

例如，1/2表示小于1的数，而3/2表示大于1的数。

其次，分数可以进行加减乘除的运算。

我们可以通过分数的运算，求得最终的结果。

最后，分数还可以进行比较大小的运算。

小学数学分数的意义练习题1. 将以下分数化简为最简形式：a) 6/9b) 12/16c) 15/25d) 24/362. 将以下分数转换为百分数：a) 3/5b) 4/10c) 7/8d) 2/33. 比较以下分数的大小，使用 >、< 或 = 进行填空：a) 2/3 ____ 4/5b) 5/8 ____ 3/4c) 1/2 ____ 2/4d) 3/7 ____ 5/74. 用最小公倍数填空：a) 3/4 + 2/5 = ____/20b) 5/6 + 3/8 = ____/24c) 2/3 - 1/6 = ____/6d) 7/10 - 4/5 = ____/105. 简化以下混合数：a) 3 1/2b) 4 2/3c) 5 3/4d) 6 5/66. 用分数填空：a) 在12个相等的部分中，7个是什么分数？b) 如果一个蛋糕被切成8个相等的部分，我们吃了5/8，还剩下几个部分？c) 一辆车在4小时内行驶了3/5 的距离，还剩下几小时的路程？d) 一个游泳池的3/4 被填满了，还剩下的1/2 应该填满多少？7. 解答以下问题并用分数表示：a) 如果一条绳子剪成了3段，其中一段的长度是3/8，另一段的长度是5/8，第三段的长度是多少？b) 如果一个水果篮子里有18个苹果，1/3 的苹果是红色的，1/6 的苹果是绿色的，剩下的苹果是什么颜色的，有多少个？c) 在一块土地上，有2/7 种植了果树，1/4 种植了蔬菜，剩下的土地用来种植了多少？8. 在下列情景中，将给定问题转化为数学表达式，并解决之：a) 如果一个书架上有30本书，其中2/5 是小说，其他的是非小说书籍，非小说书籍有多少本？b) 在一个班级里有25名学生，其中的4/5 是女生，男生占学生总数的百分之几？9. 以下是某个城市的气温变化情况，将其表示为分数：a) 上午：8°C, 下午：12°C, 晚上：4°Cb) 上午：-2°C, 下午：6°C, 晚上：-4°Cc) 上午：15°C, 下午：18°C, 晚上：12°C10. 小明今天早上跑了5/8 公里，下午又跑了2/5 公里。

分数的意义练习题和答案1、0<0/15<0.5, 口中的数字可能是几？2、3/5比0. □中的数大，口中的数字可能是几？3、把2. 375化成分数4、在括号里填上适当的数。

化成有限小数//不能化成有限小数/62/5、写出几个比1/5大，又比1/4小的分数。

6、三个人做同样的零件，王师傅5分钟做了4个，李师傅4分钟做了3个，马师傅7分钟做了6个。

他们谁做得最快？7、教学楼和校门之间有一条90米长的人行道为了迎接校庆，五年级同学在人行道的两侧每隔5米插一面彩旗。

后来发现彩旗间距太远，打算把彩旗拔下来，每隔3米插一面。

有多少而彩旗可以不用动？8、一个分数的分子比分母小36,约分后是3/7。

这个分数是多少？9、将一个分数用2约分一次，用3约分两次，得1/4。

这个分数是多少？10、幼儿园买回60把铅笔和40块橡皮。

要把这两种文具分别平均分给中班的小朋友，结果铅笔多了4把，橡皮少了2块。

中班最多有多少人？11、一根彩带，每5米截一段余4米，每9米截一段也余4米，这根彩带最短是多少米？12、分别用边长为3cm和4cm的正方形纸片铺长12cm、宽9cm的长方形，哪种纸片能将这个长方形正好铺满？还有哪些边长是整理米数的正方形纸片也能正好铺满这个长方形？13、9/12的分子减去6,要使分数的大小不变，分母应该减去多少？变化后的分数是多少？14、下面各种情况，分数大小变化有什么变化？分子扩大到原来的8倍，分母不变。

分数分子缩小到原来的1/4,分母不变。

分数分母扩大到原来的5倍，分子不变。

分数15、把一个最简假分数化成带分数后分子减少了8, 这个假分数可能是多少？16、一个带分数，它的分数部分的分子是3,将它化成假分数后分子是31。

这个带分数可能是多少？17、有一个分数，①如果分子和分母都加上1,则分数变为1/2；②如果分子和分母都减去1,则分数变为2/5。

求这个分数。

18、有一个分数，分子加3后可约为5/6,分子减3后可约为1/3O求这个分数。

分数的意义和性质练习试题一、分数的意义和性质1．一个分数用2约分了2次，用3约分了1次，得到的最简分数是．求原来的分数是________．【答案】【解析】【解答】解：故答案为：【分析】根据分数的基本性质，把这个分数的分子和分母同时乘3、2、2即可求出原来的分数。

2．一个最简分数，如果把它的分子除以2，分母乘3后，就得到．这个最简分数是________【答案】【解析】【解答】解：故答案为：【分析】可以采用倒推的方法，把现在的分数的分子乘2，分母除以3，这样就能计算出原来的分数。

3．一排电线杆，原来每两根之间的距离是30米，现在改为45米，如果开始的一根不移动，至少再隔________又会有一根电线杆可以不移动？【答案】 90米【解析】【解答】 30=2×3×5，45=3×3×5，所以30和45的最小公倍数是2×3×3×5=90.故答案为：90米.【分析】根据题意可知，要求至少再隔多少米又会有一根电线杆可以不移动，就是求30和45的最小公倍数，据此解答.4．和这两个分数（）。

A. 意义相同B. 分数单位相同C. 大小相同【答案】 C【解析】【解答】和这两个分数的意义和分数单位都不同，但是它们的大小相同。

故答案为：C。

【分析】根据题意可知，这两个分数的分母不同，所以分数的意义和分数单位都不同，将约分可得，据此解答。

5．的分子减少3，要使分数的大小不变，分母应该（）。

A. 减少3B. 减少6C. 减少4D. 增加4【答案】 C【解析】【解答】解：6-3=3，6÷3=2；8÷2-4=4，分母应该减少4。

故答案为：C。

【分析】用原来的分子减去3求出现在的分子，然后计算分子缩小的倍数，把分母也缩小相同的倍数，然后确定分母应该减少的数即可。

6．下面四个数中最大的是（）。

A. B. C. 0.43 D.【答案】 D【解析】【解答】解：，，=0.45，所以最大的数是。

分数的意义练习题及答案一、填空题1. 一个整体可以用自然数1来表示，把它平均分成若干份，表示其中这样一份的数叫做分数单位。

表示其中若干份的数叫做分数。

2. 把单位“1”平均分成若干份，表示其中1份的数叫做分数单位，表示其中几份的数叫做分数。

3. 一个分数的分子在（）叫做真分数。

4. 一个分数的分子大于或等于分母的分数叫做假分数，假分数大于或等于1。

5. 把一个分数化成小数的方法是：用分子除以分母。

二、选择题1. 下列分数中，最小的是（）A. 1/3B. 2/3C. 3/4D. 4/52. 把一个分数的分子和分母同时乘上2，这个分数的大小（）A. 不变B. 变大C. 变小D. 无法确定3. 一个分数的分子比分母小，这个分数是（）A. 假分数B. 真分数C. 整数D. 无法确定三、判断题1. 把单位“1”平均分成若干份，表示这样一份或几份的数叫做分数。

（对/错）2. 一个分数的分子比分母大，这个分数是真分数。

（对/错）3. 真分数都小于1。

（对/错）四、计算题1. 计算下列分数的和：1/4 + 2/32. 将下列分数化成小数：3/83. 计算下列分数的差：5/6 - 1/2五、解答题1. 一个长方形的长是10厘米，宽是5厘米，它的面积是多少平方厘米？如果把这个面积看作单位“1”，那么它的1/5是多少平方厘米？2. 一个班级有40名学生，其中1/4的学生参加了数学竞赛，那么参加数学竞赛的学生有多少人？3. 一个分数的分子是分母的2倍，如果分母是6，那么这个分数是多少？六、应用题1. 一块布料的总面积是12平方米，如果用去它的3/4，那么用去了多少平方米？2. 一个水果店有苹果和梨两种水果，苹果的重量是梨的3/2倍，如果梨的重量是40千克，那么苹果的重量是多少？3. 一个班级有60名学生，其中男生占3/5，女生占2/5，这个班级有多少名男生和女生？答案：一、填空题1. 分数2. 分数3. 分母4. 假分数5. 用分子除以分母二、选择题1. A2. A3. B三、判断题1. 对2. 错3. 对四、计算题1. 11/122. 0.3753. 1/3五、解答题1. 面积是50平方厘米，1/5的面积是10平方厘米。

分数的意义练习题及答案分数的意义练习题及答案在学习数学的过程中，分数一直是我们不可避免地要面对的一个重要概念。

分数的意义和应用十分广泛，无论是在日常生活中还是在学术领域中，我们都会频繁地遇到分数的概念和运算。

为了更好地掌握和理解分数的意义，下面将给出一些练习题及答案，希望能够帮助读者更好地理解和应用分数。

1. 小明有一块巧克力，他打算将这块巧克力平均分给他的三个朋友。

如果巧克力的重量是120克，每个朋友能得到多少克的巧克力？答案：将巧克力平均分给三个朋友，意味着要将120克的巧克力分为三等份。

所以每个朋友能得到的巧克力重量为120克÷ 3 = 40克。

2. 一辆汽车以每小时60公里的速度行驶，行驶了2小时后停下来休息。

这段时间内汽车行驶的总距离是多少公里？答案：汽车以每小时60公里的速度行驶了2小时，所以汽车行驶的总距离为60公里/小时× 2小时 = 120公里。

3. 小明的爸爸每天早上跑步，他每次跑5公里。

如果他连续跑了3天，总共跑了多少公里？答案：小明的爸爸每天早上跑5公里，连续跑了3天。

所以他总共跑了5公里/天× 3天 = 15公里。

4. 一箱苹果有36个，小红买了其中的1/4个苹果，小明买了其中的1/3个苹果，还剩下多少个苹果？答案：一箱苹果有36个，小红买了1/4个苹果，小明买了1/3个苹果。

所以剩下的苹果个数为36个 - （1/4个苹果 + 1/3个苹果）= 36个 - 9个 - 12个 =15个。

5. 小明的爸爸每天工作8小时，其中1/4的时间用于开会，1/8的时间用于午饭，剩下的时间用于工作。

他每天工作多少小时？答案：小明的爸爸每天工作8小时，其中1/4的时间用于开会，1/8的时间用于午饭。

所以他剩下的时间用于工作为8小时 - （1/4 × 8小时+ 1/8 × 8小时）= 8小时 - 2小时 - 1小时 = 5小时。

通过以上的练习题，我们可以看到分数在实际生活中的应用。

《分数的意义和性质》习题第1节分数的意义1．填一填。

（1）一个物体、一些物体等都可以看作一个（），把这个（）平均分成（），这样的（）或（）都可以用（）来表示。

（2）—个整体可以用自然数（）来表示，通常把它叫做（）。

（3）56是把单位“1”平均分成（）份，表示这样的（）份，它的分数单位是（）。

（4）4个17是（）；58里面有（）个（）（）（5）把12个苹果平均分成3份，这里的单位“1”是（），每份是这些苹果的（），毎份有（）个苹果。

（6）把3m平均分成2份，这里的单位“1”是（），每份是3m的（）。

2．判断。

（对的打“√”，错的打“×”）（1）一堆苹果分成4份，每份占这堆苹果的14。

（）（2）1和单位“1”相等。

（）（3）把5米长的绳子平均分成7段，每段占全长的57。

（）（4）任何一个物体组成的整体都可以看成单位“1”。

（）3．（1）一盒巧克力共有16块，平均分给4位同学，每块巧克力是这盒巧克力的（），每人分得（）块，每人分到的是这盒巧克力的（）。

（2）35表示把（）平均分成（）份，表示这样的（）份。

它的分母是（），表示（）；分子是（），表示（）。

4．下面各图的涂色部分分别占全图的几分之几？5．下列表示图中涂色部分的分数对吗？如果不对，请根据分数重新画图。

6．把单位“1”平均分成6份，表示这样的a 份的数是几？7．五（1）班共有51名同学，其中女生有28人，男生占全班同学的几分之几？女生占全班同学的几分之几？第2节 分数与除法1．在括号里填上适当的分数或整数。

5dm ＝（ ）m 205 mL ＝（ ）L 6分＝（ ）时 41cm 2 ＝（ ）dm 2 9dm 2 ＝（ ）m 2 43 千克＝（ ）吨 2．在下面的（ ）里填上适当的数。

815=÷（ ）（ ） 3=7÷（ ）（ ） 79=9÷（ ） 66=21÷（ ）3．填下面表中的空格。

分数与除法的关系 除号 被除数 除数 商 分数线4．北京奥运会要进行16夫，已进行了3天，完成了全部赛程的几分之几？剩下的还有几分之几？5．工程队13天完成一项工程，平均每天完成这项工程的几分之几？5天可以完成这项工程的几分之几？6．解放小学有男教师35人，女教师165人，男、女教师各占总人数的几分之几？ 7．一个分数的分母比分子的5倍多4，分子与分母的和是76，这个分数是多少？ 8．一个长方形的周长是32 cm ，长是10 cm ，求宽是周长的几分之几。

分数的意义练习一一、填空1、“一块菜地的1/6种了黄瓜”中，把（）看作单位“1”，平均分成（）份，种黄瓜的是这样的（）份。

2、的整数部分是（），分数部分是（），分数单位是（），它有（）个这样的单位。

3、把5米长的绳子平均分成8段，每段长（）/（）米。

4、１块烧饼的( ) ，与３块烧饼的( ) 相等。

5、把8公顷地平均分成15份，每份是这块地的（），每份是（）公顷。

6、王师傅5分钟加工17个零件，李师傅加工20个零件需要6分钟；张师傅7分钟加工23个零件。

（）的工效最高。

7、把3米平均分成4份，每份占1米的（）/（），是（）/（）米。

8、把4吨煤平均分给5户居民，平均每户居民分得总吨数的（）/（），每户居民分得（）/（）吨。

9、男生２８人，女生２３人，女生人数是男生人数的 ( )男生人数是全班的( )10、７÷１２= ( ) =（）÷（）11、“红气球是气球总数的5/6”中，把（）看作单位“1”，平均分成（）份，红气球是这样的（）份。

12、把一根4米长的绳子平均分成5段，每段长（）米，每段长占全长的13、李、王、陈三位师傅做同一种零件。

李师傅4小时做了3个，王师傅10小时做了7个，陈师傅做17个用了20小时，谁做得快？14、修一条4千米长的水渠，5天修完，平均每天修（）千米，相当于1千米的（）。

15、一盒巧克力共有16块，平均分给4位同学，每块巧克力是这盒巧克力的（），每人分得（）块，每人分到的是这盒巧克力的（）。

二、拓展应用。

1、有一块花布长7米，正好可以做9条同样大小的童裤。

（1）每条童裤用这块布的几分之几？（2）每条童裤用布几分之几米？2、有一串彩珠共56颗，按“2红3绿4黄”的顺序依次排列，第56颗是什么颜色？三种颜色的珠子分别占总数的几分之几？3、把2米长的绳子对折两次，这时每段绳子占全长的几分之几，每段绳子长多少米？4、把3块同样的饼干平均分给4个人，每人分得块。

它是1块饼干的，是3块的。

冀教版四年级数学下册第四单元分数的意义练习题（1）⼀、⽤分数表⽰每个图⾥的涂⾊部分。

( ) ( )( ) ( )( ) ( ) ⼆、填空1、有12个苹果，把它平均分成四份，每份是这些苹果的) () (，是（）个，三份是)()(，是（）个；把这些苹果平均放在三个果盘中，每盘是这些苹果的)()(，是（）个，⼆盘是)()(，是（）个；把这些苹果平均放在六个果盘中，每盘是这些苹果的)()(，是（）个，五盘是)()(，是（）个。

2、1⾓是1元的) () (，是)()(元。

1分⽶的101是)()(分⽶，是( )厘⽶。

3、⼀盘草莓30个，⼩红已经吃了13，⼩红吃了（）个？还剩下)()(没吃，是（）个。

4、59 ⾥⾯有（）个19 ，（）个110 是910；1⾥⾯有（）个101 ，有（）个 151。

34⾥⾯有3个（），2⾥⾯有（）个15 ，10个113 是（），（）个115 是1315。

5、⼥⽣⼈数占全班⼈数的49 。

表⽰把（）看做单位“1”，平均分成（）份，（）占其中的4份。

6、在下⾯括号⾥天上适当的分数。

3分⽶=（）⽶ 17分=（）⼩时 250千克=（）吨 70厘⽶=（）⽶97千克=（）吨 53⼩时=（）⽇49⽶=（）千⽶ 35平⽅分⽶=（）平⽅⽶7、4÷9=( )9 10÷12=（） ( )÷( )= 35638、当X=（）时， 4X =2；当X=（）时，4X =1。

9、37 表⽰把( )平均分成( )份,取其中的( )份。

10、把⼀根3⽶长的绳⼦平均截成8段，每段是这根绳⼦的( )( ) ，每段长（）⽶。

11、37 的分数单位是( ),它有（）个这样的分数单位,再添上( )个这样的分数单位就是1。

12、 1的58 与5的（）相等，4个17等于1的（）。

13、把8⽶长的铁丝，平均分成9段，每段占全长的（），每段长（）⽶。

三、涂⼀涂，填⼀填。

1、这些△的61是( )个，在1图中画出来。