c语言递归实现最大公约数源码

c语言求两个数最大公约数,穷举法的时间复杂度C语言求两个数最大公约数，穷举法的时间复杂度在计算机科学领域中，我们经常需要解决各种数学问题，例如求两个数的最大公约数。

而在C语言中，我们可以使用穷举法（也称为暴力法）来求解最大公约数。

在本篇文章中，我们将深入探讨C语言中求两个数最大公约数的问题，并分析穷举法的时间复杂度。

1. 最大公约数的概念最大公约数指的是两个或多个整数共有约数中最大的一个。

在数学上，常用的求最大公约数的方法有辗转相除法、更相减损术和质因数分解法等。

而在计算机科学中，我们可以使用穷举法来求解最大公约数。

下面，我们将以C语言为例，介绍如何使用穷举法来求解两个数的最大公约数。

2. C语言求最大公约数在C语言中，我们可以使用穷举法来求解两个数的最大公约数。

穷举法的基本思路是从较小的数开始，逐渐减小，直到找到两个数的一个公约数为止。

以下是一个简单的C语言程序示例：```c#include <stdio.h>int gcd(int a, int b) {int min = a < b ? a : b;int max = a > b ? a : b;int result = 0;for (int i = 1; i <= min; i++) {if (min % i == 0 && max % i == 0) {result = i;}}return result;}int main() {int a, b;printf("请输入两个整数：");scanf("%d %d", &a, &b);printf("它们的最大公约数是：%d\n", gcd(a, b)); return 0;}```3. 穷举法的时间复杂度穷举法的时间复杂度可以通过一个简单的分析得出。

在上面的C语言程序中，我们使用了一个for循环来进行穷举。

c语言最大公约数和最小公倍数最大公约数和最小公倍数是数学中常用的概念，也是在编程中经常需要用到的知识点。

在C语言中，我们可以通过简单的算法来计算两个数的最大公约数和最小公倍数。

首先，让我们来了解一下最大公约数和最小公倍数的定义。

最大公约数，又称为最大公因数，是指两个或多个整数共有的约数中最大的一个。

最小公倍数，又称为最小公倍数，是指能够被两个或多个整数同时整除的最小的一个数。

接下来，我们分别介绍如何计算最大公约数和最小公倍数的算法。

1.最大公约数的计算：最大公约数有多种计算方法，这里我们介绍常用的欧几里得算法。

欧几里得算法，也叫辗转相除法，基于以下原理：-如果a能被b整除，那么a和b的最大公约数是b；-如果a不能被b整除，那么a和b的最大公约数等于b和a除以b的余数的最大公约数。

根据这个原理，我们可以用递归的方式来实现最大公约数的计算。

代码如下：```cint gcd(int a, int b) {if(b == 0) {return a;} else {return gcd(b, a % b);}}```这段代码中的gcd函数用于计算a和b的最大公约数。

如果b等于0，那么a就是最大公约数；否则，递归调用gcd函数，传入b和a 除以b的余数，直到b等于0。

2.最小公倍数的计算：最小公倍数可以通过最大公约数来计算。

根据以下公式可以得到最小公倍数：最小公倍数= (a * b) /最大公约数(a, b)可以编写一个函数来计算最小公倍数，代码如下：```cint lcm(int a, int b) {int gcdVal = gcd(a, b);return (a * b) / gcdVal;}```这段代码中的lcm函数用于计算a和b的最小公倍数。

它首先调用gcd函数来计算a和b的最大公约数，然后用a和b的乘积除以最大公约数得到最小公倍数。

以上就是计算最大公约数和最小公倍数的算法。

在C语言中，我们可以使用这些算法来方便地计算任意两个整数的最大公约数和最小公倍数。

C语⾔实现求最⼤公约数的三种⽅法⽬录题⽬描述问题分析代码实现⽅法⼀：穷举法⽅法⼆：辗转相除法⽅法三：更相减损法题⽬描述求任意两个正整数的最⼤公约数问题分析最⼤公因数，也称最⼤公约数、最⼤公因⼦，指两个或多个整数共有约数中最⼤的⼀个。

a，b的最⼤公约数记为（a，b），同样的，a，b，c的最⼤公约数记为（a，b，c），多个整数的最⼤公约数也有同样的记号。

求最⼤公约数有多种⽅法，常见的有质因数分解法、短除法、辗转相除法、更相减损法。

与最⼤公约数相对应的概念是最⼩公倍数，a，b的最⼩公倍数记为[a，b]。

——百度百科最⼤公因数的求法有不少，本⽂我将采⽤穷举法、辗转相除法、更相减损法三种⽅法，求两个正整数的最⼤公约数（最⼤公因数）。

代码实现⽅法⼀：穷举法穷举法（列举法），是最简单最直观的⼀种⽅法。

具体步骤为：先求出两个数的最⼩值min（最⼤公约数⼀定⼩于等于两个数的最⼩值），接着从最⼩值min递减遍历（循环结束条件为i > 0），如果遇到⼀个数同时为这两个整数的因数，则使⽤break退出遍历（退出循环），这时的遍历值i即为两个正整数的最⼤公约数。

#include <stdio.h>/*** @brief 获取两个正整数的最⼤公因数（穷举法）* @param num1 第⼀个正整数* @param num2 第⼆个正整数* @return 最⼤公因数*/int Get_Max_Comm_Divisor(int num1, int num2){int i = 0;//获取两个整数的最⼩值int min = num1 < num2 ? num1 : num2;//从两个数的最⼩值开始递减遍历for(i = min; i > 0; i--){//i为num1和num2的公倍数if(num1 % i == 0 && num2 % i == 0)break;}return i;}int main(){int num1 = 0, num2 = 0;puts("请输⼊两个正整数.");scanf("%d%d", &num1, &num2);printf("最⼤公约数为%d.\n", Get_Max_Comm_Divisor(num1, num2));运⾏结果⽅法⼆：辗转相除法辗转相除法⼜称欧⼏⾥得算法，是指⽤于计算两个⾮负整数a，b的最⼤公约数。

详解C语⾔求两个数的最⼤公约数及最⼩公倍数的⽅法求两个正整数的最⼤公约数思路：这是⼀个很基本的问题，最常见的就是两种⽅法，辗转相除法和辗转相减法。

通式分别为 f(x, y) = f(y, x%y), f(x, y) = f(y, x - y) (x >=y > 0)。

根据通式写出算法不难，这⾥就不给出了。

这⾥给出《编程之美》上的算法，主要是为了减少迭代的次数。

对于x和y，如果y = k * y1, x= k * x1，那么f(x, y) = k * f(x1, y1)。

另外，如果x = p * x1，假设p为素数，并且y % p != 0，那么f(x, y) = f(p * x1, y) = f(x1, y)。

取p = 2。

参考代码：//函数功能: 求最⼤公约数//函数参数: x,y为两个数//返回值: 最⼤公约数int gcd_solution1(int x, int y){if(y == 0)return x;else if(x < y)return gcd_solution1(y, x);else{if(x&1) //x是奇数{if(y&1) //y是奇数return gcd_solution1(y, x-y);else //y是偶数return gcd_solution1(x, y>>1);}else //x是偶数{if(y&1) //y是奇数return gcd_solution1(x>>1, y);else //y是偶数return gcd_solution1(x>>1, y>>1) << 1;}}}求最⼩公倍数：最常⽤的是辗转相除法，有两整数a和b：① a%b得余数c②若c=0，则b即为两数的最⼤公约数③若c≠0，则a=b，b=c，再回去执⾏①下⾯⾮递归版本：int gcd_solution2(int x, int y){int result = 1;while(y){int t = x;if(x&1){if(y&1){x = y;y = t % y;}elsey >>= 1;}else{if(y&1)x >>= 1;else{x >>= 1;y >>= 1;result <<= 1; }}}return result * x; }。

【C语⾔程序设计】C语⾔求最⼤公约数（详解版）！问题描述求任意两个正整数的最⼤公约数（GCD）。

问题分析如果有⼀个⾃然数a能被⾃然数b整除，则称a为b的倍数，b为a的约数。

⼏个⾃然数公有的约数，叫做这⼏个⾃然数的公约数。

公约数中最⼤的⼀个公约数，称为这⼏个⾃然数的最⼤公约数。

根据约数的定义可知，某个数的所有约数必不⼤于这个数本⾝，⼏个⾃然数的最⼤公约数必不⼤于其中任何⼀个数。

要求任意两个正整数的最⼤公约数即求出⼀个不⼤于其中两者中的任何⼀个，但⼜能同时整除两个整数的最⼤⾃然数。

算法设计思路有两种：第⼀种：采⽤穷举法按从⼩到⼤（初值为1，最⼤值为两个整数当中较⼩的数）的顺序将所有满⾜条件的公约数列出，输出其中最⼤的⼀个；第⼆种，按照从⼤（两个整数中较⼩的数）到⼩（到最⼩的整数1）的顺序求出第⼀个能同时整除两个整数的⾃然数，即为所求。

我们将对第⼆种思路进⾏详细说明。

两个数的最⼤公约数有可能是其中的⼩数，所以在按从⼤到⼩顺序找寻最⼤公约数时，循环变量i的初值从⼩数n开始依次递减，去寻找第⼀个能同时整除两整数的⾃然数，并将其输出。

需要注意的是，虽然判定条件是i>0，但在找到第⼀个满⾜条件的i值后，循环没必要继续下去；如，25和15，最⼤公约数是5，对于后⾯的4、3、2、1没必要再去执⾏，但此时判定条件仍然成⽴，要结束循环只能借助break语句。

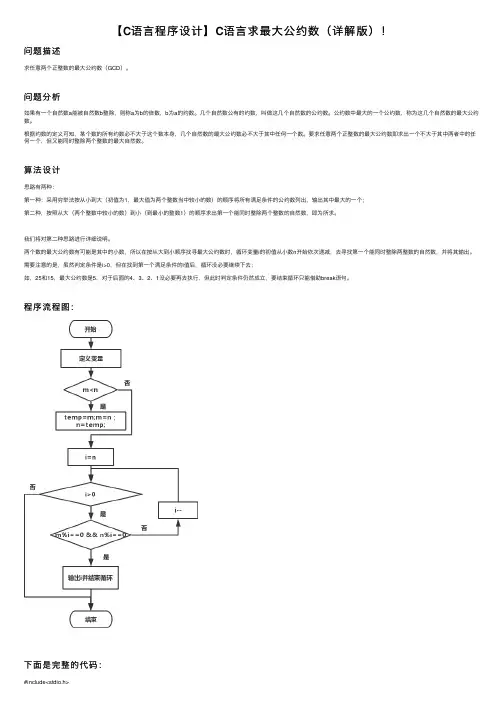
程序流程图：下⾯是完整的代码：#include<stdio.h>int main(){int m, n, temp, i;printf("Input m & n:");scanf("%d%d", &m, &n);if(m<n) /*⽐较⼤⼩，使得m中存储⼤数，n中存储⼩数*/{ /*交换m和n的值*/temp=m;m=n;n=temp;}for(i=n; i>0; i--) /*按照从⼤到⼩的顺序寻找满⾜条件的⾃然数*/if(m%i==0 && n%i==0){/*输出满⾜条件的⾃然数并结束循环*/printf("The GCD of %d and %d is: %d\n", m, n, i);break;}return0;}运⾏结果：Input m & n:100 125The GCD of 125 and 100 is: 25不管你是转⾏也好，初学也罢，进阶也可，如果你想学编程，进阶程序员~【值得关注】我的！【点击进⼊】全栈程序员正在等你加⼊~。

《C 语言输出最大公约数和最小公倍数》在 C 语言编程中，计算最大公约数和最小公倍数是非常常见的需求之一。

它们是数学中的基本概念，对于计算机科学以及实际问题中都具有重要的意义。

本文将深入探讨如何在 C 语言中输出最大公约数和最小公倍数，并结合实际问题进行分析和应用。

## 1. 最大公约数让我们明确最大公约数的定义。

最大公约数，英文为 Greatest Common Divisor，通常缩写为 GCD，是两个整数的共同约数中最大的一个。

在 C 语言中，我们可以使用欧几里得算法来高效地计算两个数的最大公约数。

欧几里得算法的基本思想是通过不断取余的方式，直到余数为 0，那么除数就是最大公约数。

以下是 C 语言中计算最大公约数的代码示例：```cint gcd(int a, int b) {if (b == 0) {return a;} else {return gcd(b, a % b);}}```在上述代码中，我们定义了一个名为 `gcd` 的函数，它接收两个整数参数 `a` 和 `b`，然后通过递归调用自身来计算最大公约数。

这种递归的实现思路非常巧妙，而且在实际的程序中也能够高效地运行。

## 2. 最小公倍数接下来，让我们来讨论最小公倍数。

最小公倍数，英文为 Least Common Multiple，通常缩写为 LCM，是两个整数的共同倍数中最小的一个。

在C 语言中，我们可以通过最大公约数来计算最小公倍数，因为有一个基本的性质：两个整数的最大公约数与它们的最小公倍数的乘积等于这两个整数的乘积。

以下是 C 语言中计算最小公倍数的代码示例：```cint lcm(int a, int b) {return a / gcd(a, b) * b;}```在上述代码中，我们定义了一个名为 `lcm` 的函数，用来计算两个整数的最小公倍数。

通过调用之前我们定义的 `gcd` 函数，可以非常方便地实现对最小公倍数的计算。

1写两个函数，分别求两个整数的最大公约数和最小公倍数，用主函数调用这两个函数, 并输出结果。

这两个数由键盘输入。

程序设计：#include<stdio.h>int hcf(int x,int y){int t;if(xvy){t=x;x=y;y=t;} while((t=x%y)!=0){x=y;y=t;}return y;} int lcf(int x,int y,int m){return x*y/m;}int main(){int hcf(int,int);int lcf(int,int,int);int x,y,h,l;printf("请输入两个数："); scanf("%d%d"，&x,& y);h=hcf(x,y);l=lcf(x,y,h);printf("最大公约数为：h=%d\n最小公倍数为：l=%d\n",h,l); return 0; }运行结果：2求方程ax A2+bx+c=0的根，用3个函数分别求当：b A2-4ac大于0、等于0和小于0时的根并输出结果。

从主函数输入a，b, c的值。

程序设计：#include<stdio.h>#include<math.h>void g_two(double a,double b,double c) {double x1,x2;x1=(-b+sqrt(b*b-4*a*c))/(2*a); x2=(-b-sqrt(b*b-4*a*c))/(2*a);printf("方程的两个根为：x仁％f\nx2=%f\n",x1,x2); }void g_one(double a,double b,double c){double x;x=(-b)/(2*a);printf("方程的两个根为：x1=x2=%f\n",x);}void g_zone(double a,double b,double c){printf("无解\n");}void main(){void g_two(double,double,double);void g_one(double,double,double);void g_zone(double,double,double); double a,b,c,t;printf("请输入a、b、c 的值："); scanf("%lf%lf%lf", &a,&b,& c); t=b*b-4*a*c;if(t>0)g_two(a,b,c);else if(t==0)g_one(a,b,c);elseg_zone(a,b,c);}运行结果：3.写一个判断素数的函数，在主函数输入一个整数，输出是否是素数的信息。

利用递归求两个数的最大公约数(利用辗转相除法)最大公约数，也叫做最大公因数，是指两个或多个整数共有的约数中最大的一个。

求两个数的最大公约数可以使用递归方法，特别是采用辗转相除法。

所谓辗转相除法，是指通过不断地用较小的数去除较大的数，然后再用除数去除余数，直到最后余数为0为止。

最后一个不为0的除数即为最大公约数。

下面我们就来看一个具体的例子，以便更好地理解递归求解最大公约数的方法。

假设我们要求解的两个数是36和48。

首先，我们使用48去除36，得到余数为12。

然后，将36作为新的被除数，余数12作为新的除数，再进行一次相除操作。

我们用36去除12，得到余数0。

此时，我们得到的不为0的除数12就是最大公约数。

我们可以使用递归方法来实现这个过程。

首先，设定递归函数gcd(a, b)表示求解a和b的最大公约数。

如果b等于0，那么gcd(a, b)就等于a；如果b不等于0，那么gcd(a, b)等于gcd(b, a%b)。

这样，我们就可以利用递归不断地缩小问题规模，直到规模最小为止。

接下来，我们将上述方法转化为函数的形式，方便我们进行编程实现。

```pythondef gcd(a, b):if b == 0:return aelse:return gcd(b, a % b)```在调用这个函数时，我们只需要传入要求解的两个数即可。

```pythonresult = gcd(36, 48)print("36和48的最大公约数为：" + str(result))```通过以上步骤，我们成功地求解出了36和48的最大公约数，即12。

这个方法不仅仅适用于36和48，对于任意两个正整数，我们都可以采用相同的方法求解它们的最大公约数。

在实际应用中，求解最大公约数经常用于简化分数、约分、化简等操作。

比如，在算术题中，我们需要将一个分数化简为最简形式，就需要求解其分子和分母的最大公约数，然后将分子和分母都除以这个最大公约数，得到最简形式的分数。

c语言中用递归法求两个数的最大公约数
在C语言中，可以使用递归方法来求两个数的最大公约数（Greatest Common Divisor, GCD）。

这里给出一个基于欧几里得算法（Euclidean Algorithm）的递归实现：
```c
#include <stdio.h>
int gcd(int a, int b) {
// 基本情况：如果b为0，则a是最大公约数
if (b == 0)
return a;
// 递归情况：应用性质1或性质2
else
return gcd(b, a % b);
}
int main() {
int x, y;
printf("请输入两个整数: ");
scanf("%d %d", &x, &y);
printf("所输入两数的最大公约数为: %d\n", gcd(x, y));
return 0;
}
```
在这个程序中，`gcd()`函数接收两个参数 `a` 和 `b`。

它首先检查基本情况，即当 `b` 为0时返回 `a` 作为最大公约数。

否则，它会递归地调用自身，将 `b` 和 `a` 对 `b` 取模的结果作为新的参数。

这个过程会一直持续下去，直到达到基本情况为止。

这种递归实现利用了欧几里得算法的基本原理：对于任何两个正整数 `a` 和 `b`，它们的最大公约数与 `b` 和`a` 除以 `b` 的余数的最大公约数相同。

C语言课程设计专业：电气工程及其自动化班级：电气11姓名：学号：指导教师：兰州交通大学自动化与电气工程学院2012 年7月6日1 基本题目1.1题目编写函数，求取两个整数m,n的最大公约数和最小公倍数。

1.2 题目分析图1 程序流程图1.3 程序# include<stdio.h>int max(int a,int b);int main(){printf("请输入两个整数");int m,n,p;scanf("%d%d",&m,&n);p=m*n;printf("最大公约数为：%d最小公倍数为：%d\n",max(m,n),p/max(m,n));return 0;}int max(int a,int b){int c;while (a!=b){if(a<b){c=a;a=b;b=c;}a=a-b;}return b;}1.4 程序的运行结果图2 基本题目运行结果2 改错题目2.1 改正后程序#include <stdio.h>#include <conio.h>main(){int i=0,j;char ch;while((ch=getch())!='\r'){i++;printf("%c",ch);}printf("you type %d characters\n",i);}2.2 程序运行结果图3 正确程序运行结果3 综合题目3.1 题目综合题目为：《班级通讯录》。

3.2 数据结构对上述题目进行分析，定义结构体数据结构如下：struct Person{char name[10]; //姓名char num[15]; //号码char age[8]; //年龄char adds[20]; //住址struct Person *next;};3.3 程序的主要功能通过该系统实现对通讯录信息进行录入、显示、修改、删除、排序、保存等操作的管理。

使用欧几里得算法计算两个正整数的最大公约数c语言使用欧几里得算法计算两个正整数的最大公约数是计算机领域中的经典问题之一，尤其在c语言中，这一算法广泛应用。

本文将探讨欧几里得算法的原理和实现方法，并深入介绍在c语言中如何编写代码来实现这一计算过程。

一、欧几里得算法原理欧几里得算法，又称辗转相除法，是一种用于计算两个正整数的最大公约数的算法。

其原理非常简单，即通过反复用较大数除以较小数，然后用除数去除余数，直至余数为0时，除数即为这两个正整数的最大公约数。

二、欧几里得算法实现在c语言中，可以通过递归或迭代的方式来实现欧几里得算法。

下面分别介绍这两种实现方法。

1. 递归实现递归是一种简洁而优雅的解决问题的方式，对于欧几里得算法也同样适用。

以下是c语言中使用递归实现欧几里得算法的代码示例：```cint gcd(int a, int b) {if (b == 0) {return a;} else {return gcd(b, a % b);}}```在这段代码中，函数gcd接受两个正整数参数a和b，返回它们的最大公约数。

当b等于0时，即找到了最大公约数，返回a的值；否则，递归调用gcd函数，传入参数为b和a除以b的余数。

2. 迭代实现除了递归，欧几里得算法还可以通过迭代的方式进行实现。

以下是c语言中使用迭代实现欧几里得算法的代码示例：```cint gcd(int a, int b) {while (b != 0) {int temp = a % b;a = b;b = temp;}return a;}```在这段代码中，使用while循环来不断更新a和b的值，直至b等于0，最终a的值就是这两个正整数的最大公约数。

三、个人观点欧几里得算法作为计算最大公约数的经典算法，不仅在c语言中得到了广泛的应用，也为其他编程语言提供了宝贵的思路。

其简洁、高效的特点使之成为解决相关问题的首选算法之一。

在实际开发中，对欧几里得算法的理解和掌握能够帮助我们更好地应对相关计算问题，提高代码的执行效率和性能。

定义函数gcd( m, n),用递归法求m和n的最大公约数。

使用辗转相除法求最大公约数的在数学中，最大公约数是指两个或多个整数共有约数中最大的一个。

找出两个整数的最大公约数是一个基本的数学问题。

求解最大公约数的过程中可以使用一种叫做辗转相除法的算法，通过不断地取模和交换两个数的位置来实现。

同时，我们也可以通过定义函数来实现求两个数的最大公约数。

本文将探究如何定义函数gcd(m, n)并使用递归法求m和n的最大公约数，同时还将详细介绍辗转相除法的实现过程和优化方式。

一、gcd函数的定义及递归法求解我们可以将定义函数gcd(m, n)作为解决两个整数最大公约数的一个基本步骤。

定义该函数时，我们需要考虑以下几个因素：1、函数名：gcd，表示求最大公约数。

2、参数：m，n分别表示两个整数。

3、返回值：一个整数，表示m和n 的最大公约数。

在实现gcd函数时，使用递归法是一种常见的方式。

递归是指在程序执行过程中，出现调用自身的情况。

递归函数必须具有一个出口，否则递归会一直进行下去，直到程序发生错误。

对于求两个整数最大公约数的问题，我们可以通过递归来不断将原问题简化成更小的问题，最终求出答案。

具体代码实现如下：``` python def gcd(m, n): if n == 0: return m else: return gcd(n, m % n) ```上述代码中，如果n为0，则返回m；否则，将n和m%n（即m除以n的余数）作为gcd函数的参数，并再次调用自身。

通过不断递归，当n为0时，返回的即为m和n的最大公约数。

二、辗转相除法的实现过程辗转相除法是一种求两个整数最大公约数的常用算法。

该算法基于一个简单的事实：两个整数的最大公约数等于其中较小的数和两数相除余数的最大公约数。

假设要求a和b的最大公约数，设a>b，则有以下辗转相除法的实现步骤：1、用a除以b，得到商q和余数r。

2、如果r为0，则b为最大公约数。

信息安全数学基础之欧几里德算法一、引言信息安全是当今社会互联网时代不可或缺的重要组成部分，信息安全的基础是数学理论，而欧几里德算法作为一种基本的数学算法，被广泛应用在信息安全领域中。

本文将通过对欧几里德算法的介绍和C语言代码实现，为读者提供深入了解和学习欧几里德算法的基础知识。

二、欧几里德算法原理欧几里德算法，又称辗转相除法，是求两个整数的最大公约数的一种方法。

其原理是通过重复利用两个整数的除法求余运算，将两个整数逐步缩小直至其最大公约数被求出。

具体步骤如下：1. 设两个整数为a和b，其中a>b；2. 用b去除a，得到余数r；3. 将b赋值给a，将r赋值给b；4. 重复2、3步骤，直到r等于0，此时b即为a和b的最大公约数。

三、C语言实现欧几里德算法下面给出了C语言实现欧几里德算法的代码：```#include <stdio.h>// 欧几里德算法int euclid_algorithm(int a, int b) {int r; // 余数while (b > 0) {r = a b;a = b;b = r;}return a;}int main() {int num1, num2, gcd; // 输入的两个整数和它们的最大公约数printf("请输入两个整数：");scanf("d d", num1, num2);gcd = euclid_algorithm(num1, num2);printf("d和d的最大公约数为：d\n", num1, num2, gcd); return 0;}```四、欧几里德算法应用举例以输入两个整数为24和36的情况为例，当运行上述C语言代码时，得到的输出结果为：```请输入两个整数：24 3624和36的最大公约数为：12```这表明欧几里德算法成功地求出了24和36的最大公约数，验证了欧几里德算法的有效性和正确性。

输入两个正整数a、b，求a、b的最大公约数。

要求采
用递归函数实现。

求最大公约数的递归函数
1. 程序思路
欧几里得算法（辗转相除法）：如果两个数的最大公约数是d，那么a 可以表示成d的倍数，即a=md，同理可以表示b=nd，其中m和n都是整数。

可以采用如下方法求d：
1. 如果a能够被b整除，那么d=b；
2. 如果a不能被b整除，那么d等于b和a除以b的余数c的最大公约数。

即d=gcd(b,c)。

2. 代码实现
用函数gcd(a,b)表示a和b的最大公约数。

```python
def gcd(a,b):
if b==0:
return a
else:
return gcd(b,a%b)
```
3. 测试样例
输入a=12，b=18，输出6。

4. 复杂度分析
时间复杂度：O(log(max(a,b)))，即递归深度为log(max(a,b))。

空间复杂度：O(log(max(a,b)))，即递归深度为log(max(a,b))。

最大公约数c语言最大公约数是数学中的一个概念，它是指两个或多个整数共同的约数中最大的一个。

最大公约数也可以用来计算两个或多个数之间的最小公倍数。

最大公约数在很多领域都有重要的应用，比如在几何中，最大公约数可以用来表示两个要素之间的最大相关性；在代数中，最大公约数可以用来分解多项式；在统计学中，最大公约数可以用来计算样本数据之间的最大共性等等。

计算最大公约数一般有两种方法，一种方法是使用辗转相除法，另一种方法是使用穷举法。

而在c语言中，两者都可以实现。

首先，我们以辗转相除法为例，介绍如何在c语言中实现最大公约数。

辗转相除法是求最大公约数的一种常用方法，它的原理是：用较大的数除以较小的数，再用除数除以余数，直到余数为0时，所得的最后一个除数即为这两个数的最大公约数。

在c语言中，想要实现辗转相除法，可以使用while 循环，依次将较小的数作为除数，较大的数作为被除数，然后求出余数，把余数作为新的被除数，重复上述步骤，当余数为0时，所得的最后一个除数即为最大公约数。

下面是c语言求最大公约数的辗转相除法程序：int gcd(int x, int y) //gcd (x，y) 代表求x，y 的最大公约数 { int temp; if (x < y) { temp = x; x = y; y = temp; } while (y != 0) { temp = x % y; x = y; y = temp; }return x; }其次，我们来介绍穷举法在c语言中如何实现最大公约数的计算。

穷举法是求最大公约数的一种常用方法，它的原理是：从1开始，逐个判断两个数能否同时被整除，直到找到最大的一个可以被两个数同时整除的数，即为最大公约数。

在c语言中，想要实现穷举法，可以使用for循环，从1开始，逐个判断两个数能否被整除，如果可以，则把当前的数作为最大公约数，如果不可以，则把当前的数加1，重复上述步骤，直到可以被两个数同时整除的数，即为最大公约数。

c++最大公约数辗转相除法
以下是使用辗转相除法求最大公约数的C++代码：cpp
#include <iostream>
using namespace std;
int gcd(int a, int b) {
if (b == 0) {
return a;
} else {
return gcd(b, a % b);
}
}
int main() {
int num1, num2;
cout << "请输入两个整数：" << endl;
cin >> num1 >> num2;
int result = gcd(num1, num2);
cout << "它们的最大公约数是：" << result << endl;
return 0;
}
在上面的代码中，gcd函数使用递归实现了辗转相除法。

当其中一个数为0时，返回另一个数作为最大公约数。

否则，将其中一个数除以另一个数取余数，并将余数和另一个数作为参数递归调用gcd函数。

最后，主函数从用户输入中获取两个整数，调用gcd函数并输出最大公约数。