(完整版)小学奥数找规律

第1讲寻找规律一、知识要点按照一定次序排列起来的一列数，叫做数列。

如自然数列：1，2，3，4，……双数列：2，4，6，8，……我们研究数列，目的就是为了发现数列中数排列的规律，并依据这个规律来填写空缺的数。

按照一定的顺序排列的一列数，只要从连续的几个数中找到规律，那么就可以知道其余所有的数。

寻找数列的排列规律，除了从相邻两数的和、差考虑，有时还要从积、商考虑。

善于发现数列的规律是填数的关键。

二、精讲精练【例题1】在括号内填上合适的数。

（1）3，6，9，12，（），（）（2）1，2，4，7，11，（），（）（3）2，6，18，54，（），（）举一反三1：1.在下面的括号里填上合适的数。

（1）2，4，6，8，10，（），（）（2）1，2，5，10，17，（），（）2.按规律填数。

（1）2，8，32，128，（），（）（2）1，5，25，125，（），（）3.先找规律再填数。

12，1，10，1，8，1，（），（）【例题2】先找出规律，再在括号里填上合适的数。

（1）15，2，12，2，9，2，（），（）（2）21，4，18，5，15，6，（），（）（3）3,4,7,3,4,10,3,4,13，（），（），（）举一反三2：1.按规律填数。

（1）2，1，4，1，6，1，（），（）（2）3，2，9，2，27，2，（），（）2.在括号里填上适当的数。

（1）18，3，15，4，12，5，（），（）（2）1，15，3，13，5，11，（），（）3.找规律填数。

（1）4，7，8，4，6,13,4,5,18，（），（），（）（2）1,2,3,2,4,6,3,8,9，（），（），（）【例题3】先找出规律，再在括号里填上合适的数。

（1）2，5，14，41，（）（2）252，124，60，28，（）（3）1，2，5，13，34，（）（4）1，4，9，16，25，36，（）练习3：1.按规律填数。

（1）2，3，5，9，17，（），（）（2）2，4，10，28，82，（），（）2.按规律填数。

第1周寻找规律（一）——寻找数列的变化规律数列：按照一定顺序排列的一串数叫做数列。

如：1,2,3,4,5,6〃〃〃或者 2,4,6,8,10,12〃〃〃等等寻找数列变化规律的一般方法：一．根据每组相邻两个数之间的关系，找出规律，推断出所要填的数；二．根据相隔的每两个数的关系，找出规律，推断出所要填的数；三．从整体上把握数据之间的联系，找出规律；一、观察相邻两个数之间的关系，找出规律①作差法——通过作差观察两数之间的差是否有一定的规律②观察相邻两数之间倍数关系是否存在一定的规律每相邻两个数的差相等——等差数列【王牌例题1】先找出下列数排列的规律，并根据规律在括号里填上适当的数。

（1） 1，4，7，10，（），16，19【补充-例题】先找出下列数排列的规律，并根据规律在括号里填上适当的数。

55，49，43，37，( ), 31 ,25这类每相邻两个数的差都相等的数列叫做等差数列课堂练习：举一反三1（1）2，6，10，14，（），22，26（3）33，28，23，（），13，（），3每相邻两个数之间的倍数关系都相等——等比数列【王牌例题1】先找出下列数排列的规律，并根据规律在括号里填上适当的数。

（2） 1， 2 ，4, 8，16，（），64，（）【补充-例题】先找出下列数排列的规律，并根据规律在括号里填上适当的数。

192，（），48, 24, 12, 6 ，（）这类每相邻两个数之间的倍数关系都相等都的数列叫做等比数列课堂练习：举一反三1（6）2，6，18，（），162，（）（7）128，64，32，（），8，（），2每相邻两个数的差成等差或等比【王牌例题2】先找出下列数排列的规律，然后在括号里填上适当的数。

1，2，4，7，（），16，22课堂练习-举一反三2（2）1，4，9，16，25，（），49，64（4）53，44，36，29，（），18，（），11，9，8（8）3， 4， 6，10，18，（），二、观察相隔的每两个数之间的关系，找出规律【王牌例题3】先找出规律，然后在括号里填上适当的数。

找规律奥数题200道题目1已知数列{1, 4, 7, 10, 13, ...}，请问数列的第100项为多少？解题思路：观察数列可以发现，每一项相比前一项都增加了3。

因此，可以通过如下公式求第n项：a_n = 3n - 2。

代入n=100，得到第100项为a_100 = 3*100 - 2 = 298。

题目2计算1 + 2 + 3 + ... + 100的和。

解题思路：这是一个等差数列求和的问题，可以使用求和公式来解答。

求和公式为S = (n/2)(a_1 + a_n)，其中S表示和，n表示项数，a_1表示首项，a_n表示末项。

代入题目中的情况，我们有S = (100/2)(1 + 100) = 5050。

因此，1 + 2 + 3 + ... + 100 = 5050。

题目3已知数列{1, 2, 4, 7, 11, ...}，请问数列的第10项为多少？解题思路：观察数列可以发现，每一项相比前一项都增加了递增的数字。

首先确定递增数字的规律，我们可以发现，递增的数字是从2开始不断加1的。

因此，我们可以通过如下公式求第n项：a_n = a_{n-1} + (n - 1)。

代入n=10，得到第10项为a_10 = a_9 + 9 = 11 + 9 = 20。

题目4求斐波那契数列的第20项。

解题思路：斐波那契数列是一个经典的数列，每一项都是前两项的和。

因此，可以通过递归或迭代的方法求解。

这里我们使用迭代的方法。

首先，我们初始化前两项为0和1。

然后，从第3项开始，每一项都等于前两项的和。

重复这个过程，直到求得第20项。

递归公式为a_n = a_{n-1} + a_{n-2}。

a =0b =1for i in range(2, 21):c = a + ba = bb = c# 第20项为a计算得到的第20项为6765。

题目5已知数列{2, 4, 8, 16, 32, ...}，请问数列的第10项为多少？解题思路：观察数列可以发现，每一项相比前一项都乘以2。

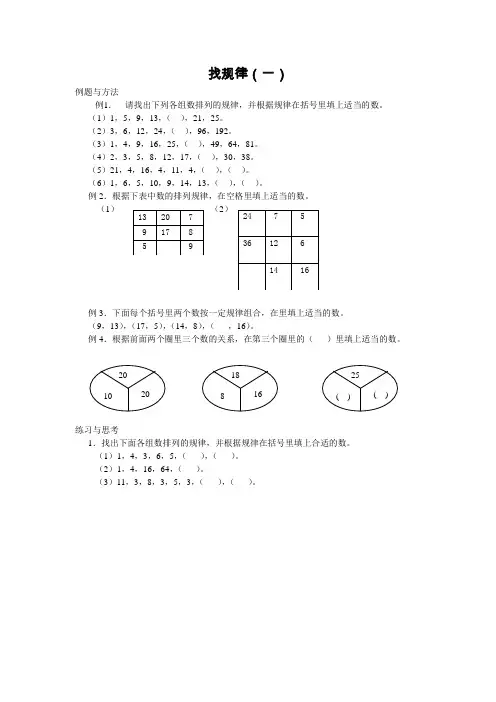
找规律（一）
例题与方法
例1． 请找出下列各组数排列的规律，并根据规律在括号里填上适当的数。

（1）1，5，9，13，（ ），21，25。

（2）3，6，12，24，（ ），96，192。

（3）1，4，9，16，25，（ ），49，64，81。

（4）2，3，5，8，12，17，（ ），30，38。

（5）21，4，16，4，11，4，（ ），（ ）。

（6）1，6，5，10，9，14，13，（ ），（ ）。

例2．根据下表中数的排列规律，在空格里填上适当的数。

（1）
（2）
例3．下面每个括号里两个数按一定规律组合，在里填上适当的数。

（9，13），（17，5），（14，8），（ ，16）。

例4．根据前面两个圈里三个数的关系，在第三个圈里的（ ）里填上适当的数。

练习与思考
1．找出下面各组数排列的规律，并根据规律在括号里填上合适的数。

（1）1，4，3，6，5，（ ），（ ）。

（2）1，4，16，64，（ ）。

（3）11，3，8，3，5，3，（ ），（ ）。

（4）0，1，3，8，21，（）。

2．找规律，在空格里填上适当的数。

（1）
（2）
3．下面括号里和两个数是按一定规律组合，根据规律在里填上适当的数。

（1）（8，7），（6，9），（10，5），（，13）。

（2）（1，3），（5，9），（7，13），（9，）。

4．根据前面两个圈里三个数的关系，在第三个圈里的（）里填上适当的数。

(1) (2)
(2)。

小学奥数竞赛找规律一、引言小学奥数竞赛是一个培养学生数学思维、启发学生创造力的重要途径。

其中，找规律是竞赛中的一个重要题型，它需要学生发现序列或图形中的规律，并按照规律进行推理、预测和计算。

本文将介绍小学奥数竞赛中找规律题的特点和解题方法。

二、特点1. 多样性：小学奥数竞赛中的找规律题目形式多样，包括数字序列、图形序列、比例关系和变量代换等。

2. 灵活性：解决找规律题的方法多种多样，没有固定的解题公式，需要学生善于发现特点和思考创造性解决问题的方法。

3. 基础要求：找规律题的解答过程需要基本的数学概念和推理能力，需要学生有扎实的数学基础和良好的逻辑思维能力。

三、解题方法1. 观察法：首先观察给出的数字序列或图形序列，尝试找出其中的规律。

观察时可注意数值、位置、形状、颜色等方面的变化。

2. 推理法：根据观察的规律进行推理，找出序列或图形中的隐藏规律。

可以通过数学运算、替换等方法进行推理。

3. 验证法：找到可能的规律后，进行验证是否适用于其他数字或图形。

通过验证可以确认规律的正确性。

4. 创新法：当常规方法无法找到规律时，可以尝试用创新的思维方式，如逆向思维、扩张思维、模式转换等，寻找不同角度的规律。

四、案例分析以下是一个数字序列的找规律题案例：1, 4, 9, 16, ?观察这个序列，可以发现每个元素是前一个元素的平方。

根据这个规律，下一个元素应该是 25。

五、总结在小学奥数竞赛中，找规律是一个重要的题型，需要学生发现序列或图形中的规律，并进行推理、预测和计算。

解决找规律题可以使用观察法、推理法、验证法和创新法等方法，善于运用多种方法能提高解题的准确性和创造性。

希望本文对大家在小学奥数竞赛中的找规律题有所帮助。

参考资料：[1] 张文君. (2015).《小学奥数竞赛教材：找规律与推理》. 北京: ___.[2] 王春秀. (2019).《小学奥数考点讲义：找规律（数学奥赛解题思维培养丛书）》. 北京: ___.。

三年级奥数教案之找规律（合集五篇）第一篇：三年级奥数教案之找规律三年级奥数教案（一）专题一找规律教学目标培养学生的观察与逻辑推理能力教学重难点找规律的方法和技巧找规律是小学奥数中的经典，是经常出现的一种类型题，它考的是学生的观察力和逻辑推理能力，充分的寻找两者之间的联系，为以后的学习打下基础。

一．数按一定规律排列的一列数叫做数列，例如1,2,3,4,5,6,7,8,9,10，......就是自然数排成的数列，每个数比前一个大1，第n个数就是n。

数列中的每一个数叫做这个数列的项，其中第1个数称为这个数列的第1项，第2个数称为第2项......通过观察数列，可以发现它的内在规律，填出所缺的数，这里的规律应力求简单明了。

寻找数列的排列规律，除了从相邻两数的和、差考虑，有时还要从积、商考虑。

善于发现数列的规律是填数的关键。

例1 在括号内填上合适的数。

（1）3，6，9，12，（），（）（2）1，2，4，7，11，（），（）（3）2，6，18，54，（），（）解析：（1）在数列3，6，9，12，（），（）中，前一个数加上3就等于后一个数，相邻两个数的差都是3，根据这一规律，可以确定答案；（2）在数列1，2，4，7，11，（），（）中，第一个数增加1等于第二个数，第二个数增加2等于第三个数，也就是相邻两个数的差依次是1，2，3，4……这样下一个数应为11增加5，再下一个数应比刚刚那个数大6，所以答案就出来了。

（3）在数列2，6，18，54，（），（）中，后一个数是前一个数的3倍，根据这一规律可知道答案。

例2 先找出规律，再在括号里填上合适的数。

（1）15，2，12，2，9，2，（），（）；（2）21，4，18，5，15，6，（），（）；解析：（1）在15，2，12，2，9，2，（），（）中隔着看，第一个数减3是第三个数，第三个数减3是第五个数，第二、四、六的数不变。

根据这一规律，可以确定答案。

（2）在21，4，18，5，15，6，（），（）中，隔着看第一个数减3为第三个数，第三个数减3为第五个数。

小学四年级奥数经典例题之举一反三（第1讲和第2讲）文档目录：第1讲找规律（一）第2讲找规律（二）第1讲找规律（一）一、知识要点观察是解决问题的根据。

通过观察，得以揭示出事物的发展和变化规律，在一般情况下，我们可以从以下几个方面来找规律：1．根据每组相邻两个数之间的关系，找出规律，推断出所要填的数；2．根据相隔的每两个数的关系，找出规律，推断出所要填的数；3．要善于从整体上把握数据之间的联系，从而很快找出规律；4．数之间的联系往往可以从不同的角度来理解，只要言之有理，所得出的规律都可以认为是正确的。

二、精讲精练【例题1】先找出下列数排列的规律，并根据规律在括号里填上适当的数。

1，4，7，10，（），16，19【思路导航】在这列数中，相邻的两个数的差都是3，即每一个数加上3都等于后面的数。

根据这一规律，括号里应填的数为：10+3=13或16－3=13。

像上面按照一定的顺序排列的一串数叫做数列。

练习1：先找出下列各列数的排列规律，然后在括号里填上适当的数。

（1）2，6，10，14，（），22，26（2）3，6，9，12，（），18，21（3）33，28，23，（），13，（），3（4）55，49，43，（），31，（），19（5）3，6，12，（），48，（），192（6）2，6，18，（），162，（）（7）128，64，32，（），8，（），2（8）19，3，17，3，15，3，（），（），11，3..【例题2】先找出下列数排列的规律，然后在括号里填上适当的数。

1，2，4，7，（），16，22【思路导航】在这列数中，前4个数每相邻的两个数的差依次是1，2，3。

由此可以推算7比括号里的数少4，括号里应填：7+4=11。

经验证，所填的数是正确的。

应填的数为：7+4=11或16-5=11。

练习2：先找出下列数排列的规律，然后在括号里填上适当的数。

（1）10，11，13，16，20，（），31（2）1，4，9，16，25，（），49，64（3）3，2，5，2，7，2，（），（），11，2（4）53，44，36，29，（），18，（），11，9，8（5）81，64，49，36，（），16，（），4，1，0（6）28，1，26，1，24，1，（），（），20，1（7）30，2，26，2，22，2，（），（），14，2（8）1，6，4，8，7，10，（），（），13，14【例题3】先找出规律，然后在括号里填上适当的数。

小学四年级数学奥数题库100道及答案(完整版)1. 简便计算：25×125×32答案：25×125×32 = 25×125×4×8 = (25×4)×(125×8) = 100×1000 = 1000002. 找规律填数：1，4，9，16，（），36答案：25 （规律是平方数，1²= 1，2²= 4，3²= 9，4²= 16，5²= 25，6²= 36）3. 两数相除，商是8，余数是16，被除数、除数、商和余数的和是463，求被除数是多少？答案：设除数为x，则被除数为8x + 16。

8x + 16 + x + 8 + 16 = 463，9x + 40 = 463，9x = 423，x = 47，被除数= 8×47 + 16 = 3924. 小明在计算加法时，把一个加数个位上的9 看成了6，把十位上的3 看成了8，结果得到的和是100，正确的和是多少？答案：个位少加了：9 - 6 = 3，十位多加了：80 - 30 = 50，正确的和是：100 + 3 - 50 = 535. 一桶水，连桶重250 千克，用去一半水后，连桶还有145 千克，问桶里原来有多少千克水？桶重多少千克？答案：水的一半重：250 - 145 = 105（千克），水重：105×2 = 210（千克），桶重：250 - 210 = 40（千克）6. 鸡兔同笼，共有头30 个，脚86 只，求鸡兔各有多少只？答案：假设全是鸡，兔：(86 - 30×2)÷(4 - 2) = 13（只），鸡：30 - 13 = 17（只）7. 等差数列3、7、11、15、…，第20 项是多少？答案：公差为4，第20 项= 3 + (20 - 1)×4 = 798. 有一堆棋子，按照“二黑三白”的顺序排列，第28 颗棋子是什么颜色？答案：28÷(2 + 3) = 5（组）......3（颗），所以是白色。

小学奥数找规律题1.问题描述小学奥数中，找规律题是一种常见的题型。

这类题目要求学生观察给定的数列、图形或规律，并找出其中的规律，从而推断下一个数、下一个图形或者给出符合规律的答案。

本文将介绍小学奥数中常见的找规律题类型，并给出解题方法和示例。

2.规律题类型2.1 数列找规律题数列找规律题是小学奥数中最常见的题型之一。

通常，这类题目给出一组数字，要求学生找出其中的规律，并推断下一个数字。

常见的数列找规律题类型包括等差数列、等比数列和特殊数列。

2.1.1 等差数列等差数列是指数列中相邻两项之间的差都相等的数列。

在等差数列中，每一项都是前一项加上一个常数得到的。

例如，1、3、5、7、9即是一个等差数列，其中公差为2。

解决等差数列找规律题的方法是观察相邻两项的差值，确定公差，进而推断下一个数字。

示例给定数列1、4、7、10、13，求下一个数字。

解：观察相邻两项的差值，可得差值都为3，因此这是一个等差数列，下一个数字为13+3=16。

2.1.2 等比数列等比数列是指数列中相邻两项之间的比值都相等的数列。

在等比数列中，每一项都是前一项乘以一个常数得到的。

例如，2、4、8、16、32即是一个等比数列，其中公比为2。

解决等比数列找规律题的方法是观察相邻两项的比值，确定公比，进而推断下一个数字。

示例给定数列2、6、18、54、162，求下一个数字。

解：观察相邻两项的比值，可得比值都为3，因此这是一个等比数列，下一个数字为162×3=486。

2.1.3 特殊数列特殊数列是指不符合等差或等比规律的数列。

在特殊数列中，每一项的求法不满足常见的规律。

解决特殊数列找规律题的方法是观察数列的特点，可能需要思考数学的性质或者进行一定的计算。

示例给定数列1、1、2、3、5，求下一个数字。

解：观察数列，可以发现这是一个斐波那契数列，下一个数字为3+5=8。

2.2 图形找规律题图形找规律题是小学奥数中另一种常见的题型。

这类题目给出一组图形，要求学生找出其中的规律，并推断下一个图形。

小学二年级下册数学奥数知识点讲解第 11课《找规律法》试题附答案笫十一讲找规律祛观察、搜集己知事矢 从甲发现具有规律性的线索，用以探焉未知事件的 奥秘，是人类智力活动的主要內容.数学上有很多材料可用以来模拟这种活銳培养学注这方面的能力. 例1观察数列的前面几项，找岀规律，写岀该数列的第100项来？12345, 23451, 3951N 45123, ■-例2把写上1?1|100£100个号码的牌子，偉卩面那祥依次分发给四个人.你 知這第『珂牌子会落到谁的手里字小明小英小方小军例3四个小功物换开始小乩 小魏 小兔和小猫分别坐在1、2、3, 4 号位子上（如下圏所示）•第一次它们上下两制啓仏 第二次左右换位.第三次 又上下交换.第四次左右交换•这样一6交换下去，问十次换包扁 小兔坐在第 几号座位上7例4从1开始，每隔两个数写岀一个数，得到一列数，求这列数前第100个数是多少令L 4 7, 10. 13,…例5茴图游戏先画第一代，一个再画第二代.左△下面画出两条銭 段*左一条钱段的末罐又画一个△,左另一条的末端蔺一人6 商第三代，在 笫二代的△下面文画岀两条线段，一条末端茴△・另一条末端画6 而在笫二 代的。

的下面画一条线.线的末端再画一个…一直煦此画下去（见下 图）-问第十次的△和O 共有多少个？S E E3EQO 00002 3ft---- 3-答案第十一讲找规律法观察.搜集己知事实.从中岌现具有规律性的銭報 用以探需未知事件的 奥秘，是人类智力活动的主要内容.数学上有很多材料可用以来模拟这种活动、培界学生这方面的能力. 例1观察数列的前面几项，找岀规律，与出该数列的第100项来？12345, 234B1, 34512> 45123,…解’为了寻找规律.再多写岀几项出来。

并给以编号’1 2 3 4 5 612345, 23451, 34512, 45123, 51234, 12345, 7 8 9 10 U 12 2345L 34512, 45123, 51234, 12345, 2345L廿細巩察，可发现该数列的第电项同第1项，•第7项同兼项"第倾同第3 项•…也就是说该数列各项的出现具有周期性，他们是循环出现的，一个循环 节包含100-5=20.可见第100项与勲项.第10项一拝（项数都能被遵除）,即第100项是 51234. 例2把写上1到10哒血个号码的牌子，像下面那样依次分发给四个人，你 知置第73号牌子会落到谁的手里？解；仔细观察，你会发现；分给」卜明的牌子号码是匚齡乞13,…，号码除以4余1,00 0 y m国回分给小英的牌子号码是2, 6, 10, 14,…，号码除以4余2； 分给小方的牌子号码是3, 7, 11,…，号码除以4余3,分给小军的牌子号码是4, 8, 12,…，号码除以4余0 （整除）・ 因此，试用4除73看看余几？73*4=18 •余 1可见73号牌会落到小明的手里. 这就是运用了如下的规律：小明小英小芳小军用这种规律预测第几号牌子发给谁，是很容易的，请同学们自己再试一试. 例3四个小动物换位，开始水鼠、小猴、小兔和小猫分别坐在1、2、3、4 号位子上（如下图所示）.第一次它们上下两排换位，第二次左右换位，第三次 又上下交换，第四次左右交换.这样一直交换下去，问十次换位后，小兔坐在第 几号座位上？解；为了能找出变化规律，再接着写岀几次换位情况，见下图.肝住小兔的位置进行观察:叫2猴兔L 2貓鼠彳*很1 2鼠4兔开始第一汝交换它到了第1号位；它到了第2号位； 它到了第4号位' 它到了第3号位， 它又到了第1号位 可以岌现，每经过四次换位后，小兔又回到了原未的位置，利用这个规律 以及10-4二2・・・余2,可知：第十次换位后，小兔的座位同第二次换位后的位置一样，即左第二号位. 如果再仔细地把换位图连续起来研究研究，可以发现，随着一次次地交 换， 小兔的座位按顺时针旋转， 小鼠的座位按逆时针旋转，<1、寮的座位按顺时针旋转，小猫的座位按逆时针旋转，按这个规律也可以预测任何小动物在交换几次后的座位•例4从1开始，每隔两个数写岀一个数，得到一列数，求这列数的第100个 数是多少？1, 4, 7, 10, 13,…解：不难看岀，这是一个等差数列，它的后一项都比相邻的前一项大3,即 公差二3,还可臥发现：笫2项等于第1项加1个公差即4=1+1X3.第一次换位后, 笫二次换位后, 第三次换位后, 第四次换位后, 第五次换位后第3项等于第1项加2个公差即7=1+2 X 3.第4项等于第1项加3个公差即10二1+3X3.第5项等于第1项加4个公差即13二1+4X3.可见笫"项等于笫1项加(n-1)个公差，即|第口项=笫1项十Gl) X公差按这个规律，可求出:第10035=1+ c 100-1) x 3=1+99X3=238.例5画图游戏先画第一代，一个△,再画笫二代，在△下面画岀两条线段，在一条线段的末端又画一个厶，在另一条的末端画一个O；画第三代，在第二代的△下面又画出两条线段，1条末端画4,另1条耒端画O；而在第二代的0的下面画一条线，线的末端再画一个△；…一直照此画下去(见下图)，问第十次的△和O共有多少个？—第一代—第二代—第三代解：按着画图规则继续画出几代，以便于观察，以期从中找岀图形的生成规律，见下图.第一代△第三代7 △第五代貝P △ Vb △ 6 第^AOAZXOZXOA AO A Z O数一数，各代的图形（包括△利0）的个数列成下表;第几代 — 二 三 四 五 六 • • • 图形个数 1 2 3 5 8 12• • •可以发现各代图形个数组成一个数列，这个数列的生成规律是，从第三项 起每一项都是前面两项之和.援此规律接着把数列写下去，可得出第十代的△和 O 共有別个（见下表）：第几项 —— 二 三 四 五 六 七 A 九 十 十一 十二 • •• 图形个数 1 2 3 5 8 13 21 34 55 89 144 233• • •这就是著名的裴波那契数列•裴波那契是意大利的数学家，他生活在距今大 约七百多年以前的时代.例6如下图所示，5个大小不等的中心有孔的圜盘，按大的在下、小的在上 的次序套在木桩上构成了一座圆盘塔.现在要把这座圆盘塔移到另一个木桩上. 规定移动时妾遵守一个条件，每搬一次只许拿一个圆盘而且任何吋侯大圆盘都 不能压住小圆盘•假如还有第三个木桩可作临时存放圆盘之用•问把这5个圆盘全 部移到另一个木桩上至少需要搬动多少次？（下图所示）第二代 第四代 △△O解：先从最简单情形试起.①当仅有一个圆盘时，显然只需搬动一次（见下贝图）•②当有两个圆盘时，只需搬动3次（见下图）.(0)③当有三个圆盘时,总结.找规律，①当仅有一个圆盘时，只需搬1次.③ 当有三个圆盘时，必须先妄把上面的两个小的圆盘搬到临时桩上，见上 图中的（1） ~（3）•由前面可知，这需要搬动3次,然后把最下层的最大圆盘搬 一次到中间桩上，见图（4）,之后再扌巴上面的两个搬到中间桩上，这又需搬3 次，见图中（5）~⑺.所以共搬动2X3+1 h 次.⑥推论，当有4个圆盘时，就需要先扌巴上面的3个圆盘搬到临吋桩上，需要7 次，然后把下面的大圆盘搬到中间桩上（1次），之后再把临时桩上的3个圆盘 搬到中间桩上，这又需妄了次，所以共需搬动2XM 二15次.⑤可见当有5个圆盘时，要把它按规定搬到中间桩上去共需要:2X15+1=31 次.这样也可以与岀一个一股的魯式（叫递推公式）20Xtij 一种情况的搬动次数+1=后一种情况的赧动次数对于有更多圆盘的情况可由这个公式算岀来.国盘个数 1 2 34567 8 9 10搬动次数 137 15 31 63 127 255 511 1023• • •逬一步进行考察，并联想到另一个数列2n 1 23 4 5 6 78 9 102n148163264128 256 512 1024当圆到©-小m-羊后<5>若把n个圆盘搬动的次数写成g 把两个表对照后可得出进行蠡r如接把圆酬代入计算就行了’祕再松松式那样习题十11.先计算下面的前几个算式，找出规律，再继续往下写出一些算式,① IX 9+2二② 9X9+7=12X9+3二98X9+6二123X9+4= 987X9+5 二1234* 9+5= 9876X 9+4=• I •• • •Z先计算下面的奇妙算式，找岀规律，再继续写岀一些算式’19+9X9二118+98X9二1117+987X3=11116+9876X9=111115+98765X9=• • •3•先计算下面的前几个算式，找岀规律，再继续写岀一些算式：1X1=lixu=111X111=1111X1111=11111X11111=• • •4•有一列数是2、9、8、2、…，从第三个数起：每一个数都是它前面的两个数相乘积的个位数字（比如第三个数蹴是2X9=8的个位数字）.问这一列数的第1Q0个数是几？5.如杲全体自然数按下表逬行排列，那么数1000应在哪个字母下面？6.如果自然数如下图所示排成四列，问101在哪个字母下面?7.3X3的末位数字是9, 3X3X3的末位数是7, 3X 3X3X3的末位数字是L. 求35个羿目乘的结杲的耒位数字是几？二年级奥数下册：第十一讲找规律法习题解答习题十一解答1.① 1X9^2=11L2X 9+3=111123X9^4=1111L234X 9+5^1111112345X94-6=111111123456X9+7=11111111234567X^+8=1111111.112345678 X9+9=L1U11.11L②9 X 9+7=8898X9+6=888ggyx g+5=gg889876X2+0=8888898765X9+3=888888987654X9+2=88888889876543X9+1=88888888・2.19+9X9=100118+98X^10001117+987X9=1000011116+9876X9=100000111115+98765 xg 二100000011111141-987654X9=1000000011111113+9876543X^=100000000111111112+98765432x9=10000000001111111111+987654321X9= 10000000000.3.1X1=111X11=121111X111=123211111X1111=123432111111X11111=123454321111111X111111=123456543211111111x1111111=123456765432111111111X11111111=123456787654321111111111X111111111=123456789876543214.解：按数列的生成规律再多写岀一些数来，再仔细观察，找出规律：2、9、& 2、6、2、2^ 4、8^ 2、6、2^ 2、4. 8、2、6、2、2、4、…可见，除最前面的两个数2和9以外，*、2、6、2、2、4这六个数依次重复岀现.因此可利用这个规律，按下面的方法找岀第100个数岀来：100-2=98,98* 6=16—2.即笫100个数与这六个数的第2个数相同，即笫100个数是2.5.解：不难发现，每个字母下面的数除以7的亲数都是相同的•如第1列的三个数1、8和15,除以7时的余数都是h第2列的三个数2、9和16,除以T时的余数都是2；第3列的三个数3. 10和17,除以7的余数都是3；…•利用这个规律，可求出第1000个自然数在哪个字母下面：1000-7=142'-6所以1000在字母F 的下面.6. 解：可以这样找出排列的规律性：全体自然数依次循环排列在A 、B 、C 、 D 、D 、C 、B 、21个字母的下面，且卩依上题解题方法：101-8=12*-5.可知101与5均排在同一字母下面，即在D 的下面.7•解；从简单情况做起，列表找规律；仔细观察可发现，乘积的末位数字的岀现有周期性的规律：看相乘的3的个 数除以4的余数，余1.时，积的末位数字是3,畲2吋，积的末位数字是9,余3时，积的末位数字是7,整除时，积的末位数字是1,35-4=8-3所以这个积的末位数字是7・。

小学数学奥数训练：探索规律专项练习试卷及答案(50道解答题有详细答案解析)小学数学奥数训练：探索规律专项练试卷及答案（50道解答题有详细答案解析）1、在大于1000的整数中，找出所有被34除后商与余数相等的数，那么这些数的和是多少?2、动脑筋，探索规律。

1.2×2.1=11.2×2.11=111.2×2.111=1111.2×2.1111=.2×2.=你发现了什么规律？3、按照规律接着画出第4幅图。

第10幅图中一共有()个点。

4、用火柴棒摆出图形。

摆第1个图形要4根火柴棒。

那么摆第5个图形要多少根火柴棒?5、一张桌子坐4人，两张桌子并起来坐6人，三张桌子并起来坐8人，…照这样计算，10张桌子并成一排可坐多少人？如果一共有26人，需要并多少张桌子？6、图形三角形个数所需火柴数1234……………10n3579 (1001)(1)10个三角形需要几根洋火？摆n个呢？(2)如果有1001根火柴可以摆几个三角形？共20页，第1页7、观察：÷3=﹣3，差．÷4=﹣4，请再写出两个数，使它们的商等于它们的8、已知1+3=4=2，1+3+5=9=3，1+3+5+7=16=4，1+3+5+7+9=25=5，...(1)仿照上例，计算：1+3+5+7+ (99)(2)按照上述纪律，请你用自然数n（n≥1）表示一般纪律．22229、下列图案由边长相等的黑、白两色小正方形按一定规律拼接而成。

照如许画下去，第10个图形中分别有几何个玄色小正方形和白色小正方形？你能说明个中的道理吗？10、有一个挂钟，每小时敲一次钟，几点敲几下，钟敲6下，5秒钟敲完，钟敲12下，几秒钟敲完？11、观察点子图，找一找有什么纪律，想一想，第8个方框里有______个点，第20个方框内呢？12、图(1)是一个三角形，分别连接这个三角形三边的中点得到图(2)，再分别连接图(2)中间的小三角形三边的中点，得到图(3)．按这样的方法继续下去，第100个图形有多少个小三角形？共20页，第2页13、用三条边都是l厘米的三角形拼图形，按如下规律拼下去．想一想：用29个如许的三角形拼成的图形是什么图形？14、（2012•成都）一串分数：，，，，，，，，，…（1）是此串分数中的第多少个分数？（2）第115个分数是多少？15、（2013•长沙）有这样一串数、、、、、、、、、…（1）第407个分数是多少？（2）从开始，前407个分数的和是几何？16、（2011•海港区）判断推理．三角形个数1个2个3个4个…小棒的根数3根5根7根9根…观察图形和表格，如果要摆100个三角形，需要多少根小棒？要摆n个三角形，需要多少根小棒？17、观察下图，按规律填表。